- 1Mathematical and Statistical Methods Group, Wageningen University and Research, Wageningen, Netherlands
- 2Freiburg Center for Data Analysis and Modeling, University of Freiburg, Freiburg, Germany
Uncertainty is ubiquitous in biological systems. For example, since gene expression is intrinsically governed by noise, nature shows a fascinating degree of variability. If we want to use a model to predict the behaviour of such an intrinsically stochastic system, we have to cope with the fact that the model parameters are never exactly known, but vary according to some distribution. A key question is then to determine how the uncertainties in the parameters affect the model outcome. Knowing the latter uncertainties is crucial when a model is used for, e.g., experimental design, optimisation, or decision-making. To establish how parameter and model prediction uncertainties are related, Monte Carlo approaches could be used. Then, the model is evaluated for a huge number of parameters sets, drawn from the multivariate parameter distribution. However, when model solutions are computationally expensive this approach is intractable. To overcome this problem, so-called spectral expansion (SE) methods have been developed to quantify prediction uncertainty within a probabilistic framework. Such SE methods have a basis in, e.g., computational mathematics, engineering, physics, and fluid dynamics, and, to a lesser extent, systems biology. The computational costs of SE schemes mainly stem from the calculation of the expansion coefficients. Furthermore, SE effectively leads to a surrogate model which captures the dependence of the model on the uncertainty parameters, but is much simpler to execute compared to the original model. In this paper, we present an innovative scheme for the calculation of the expansion coefficients. It guarantees that the model has to be evaluated only a restricted number of times. Especially for models of high complexity this may be a huge computational advantage. By applying the scheme to a variety of examples we show its power, especially in challenging situations where solutions slowly converge due to high computational costs, bifurcations, and discontinuities.
1 Introduction
Every mathematical model in systems biology is subject to uncertainty and incomplete knowledge (Geris and Gomez-Cabrero, 2016; Gutenkunst et al., 2007; Mitra and Hlavacek, 2019; van Mourik et al., 2014). This can be in the form of unknown model structure, unknown model parameters and imperfect experimental data. Characterizing and quantifying these sources is crucial, as the uncertainty can translate into inaccuracies in the model predictions. Information about the quality of model predictions is vital when applied as support for decision-making or optimization routines such as experimental design and parameter estimation (Raue et al., 2013). The aim of uncertainty quantification (UQ) is to determine the likeliness of certain outcomes, given that some aspects of the system under study are not (exactly) known.
Generally, uncertainty is distinguished into two classes (Bruno, 2007; Ghanem et al., 2017; Le Maître and Knio, 2010). The first class is so-called aleatoric uncertainty. Aleatoric uncertainty stems from the intrinsic variability found in the system under consideration, for this reason it is also referred to as statistical uncertainty. For example, in the case of parameter estimation, this uncertainty is related to the fact that parameters may essentially vary over the system components (e.g., cells) (Elowitz et al., 2002), so that for the system as a whole only a distribution of parameter values can be estimated, and not one precise value per parameter. Gene expression noise is often a source of varying conditions (e.g., initial conditions or protein production rates) in cells resulting in variability of process parameters such as the protein production rate (Thattai and van Oudenaarden, 2001; Elowitz et al., 2002; Blake et al., 2003; Lev, 2014; Schultheiß Araújo et al., 2017).
In contrast, the second class of uncertainty, termed epistemic (or systemic) uncertainty, is caused by a lack of information (Bruno, 2007; Ghanem et al., 2017; Le Maître and Knio, 2010). For example, in parameter estimation, uncertainty in the estimates may be caused by imperfect data sets that contain noisy, incoherent, or even missing data points (Sullivan, 2015). In such cases, the uncertainty can in principle be reduced by performing extra experiments (Banga and Balsa-Canto, 2008; Kreutz and Timmer, 2009; Barz et al., 2010), but practical restrictions often prohibit this.
In biological systems both types of uncertainty are typically present (Geris and Gomez-Cabrero, 2016). In terms of modelling, both are usually dealt with by employing a probabilistic framework (Kirk et al., 2016), in which model parameters are represented according to a probability density function (PDF) (van Mourik et al., 2014; Bruno, 2007). The choice of the type of PDF and the corresponding distribution of parameters is usually based on previous knowledge. For example, the case of a completely unknown parameter is described by a uniform distribution on a broad (positive) interval. In other cases a parameter could be known to follow a normal or lognormal distribution with known mean and variance, established in previously performed experiments (Tsigkinopoulou et al., 2018).
Among the field of UQ, Monte Carlo (MC) methods are most commonly used (Barbu and Zhu, 2020; James, 1980). In an MC approach the parameter PDFs are sampled and model responses for each sample recorded, thus providing a distribution of model outcomes and an indication of the uncertainty therein (e.g., by analyzing the distribution moments). These methods are simple in their implementation and are widely applicable. However, for models that have a large number of parameters or are computationally expensive, these MC procedures are often not feasible (Bruno, 2007; Le Maître and Knio, 2010).
As an alternative to MC, meta-modelling techniques, also referred to as surrogate modelling, are frequently adopted to deal with models that would otherwise be intractable. Support vector machines (Noble, 2004), artificial neural networks (Tadeusiewicz, 2015) and Bayesian networks (Wilkinson, 2007) are examples meta-modelling techniques used in systems biology. In this work, we focus on spectral expansion (SE) methods, an approach that is widely used in engineering systems (Ghanem et al., 2017; Le Maître and Knio, 2010) and to a lesser extent in biological systems (Martin-Casas and Mesbah, 2016; Paulson et al., 2019; Streif et al., 2014; Renardy et al., 2018) for UQ purposes. In such an approach the model response is represented in the form of a series expansion. The advantage of such a representation is that an approximation of the model response is obtained for all values of the parameters at once. This allows immediate evaluation of statistics of the model outcome, either analytically or through sampling of the stochastic parameters, which can be done significantly faster than through MC methods for models that are problematic and computationally expensive (Xiu and George, 2002).
These advantages come at the cost of the need to calculate expansion coefficients. For this, two classes of spectral methods are in use. In the first class the governing equations of the model are reformulated such that each variable is represented by a spectral expansion. This results in a system of differential equations for the expansion coefficients and is known as intrusive spectral projection (Bruno, 2007). In the second class, based on so-called non-intrusive spectral projection, the expansion coefficients are determined without changing the original model equations (Eldred et al., 2008). This is the line followed in this paper. The advantage of a non-intrusive approach is that it requires only straightforward deterministic model evaluations and does not involve any reformulation of the model. It is particularly attractive in case of models where intrusive methods would become too laborious.
In the past, SE methods have been shown to converge very slowly or not at all for models involving non-smooth functions (Joel Chorin, 1974; Le Maıtre et al., 2004). This is indeed a critical challenge for biological models, which often show complex, non-linear behaviour such as bifurcations and spatial discontinuities. In this work, we provide a scheme for non-intrusive spectral projection that may overcome these problems. It is easy to implement and we show its power through applying it to a number of various biological models. The scheme straightforwardly allows the use of different basis functions for the expansion, such as Haar wavelets in case of models with bifurcations. We also present a simple segmentation method resulting in a piecewise continuous approximation of the model at hand which helps to deal with complex models avoiding the necessity of high order expansions. The examples treated in this paper have been chosen such that each one shows how a specific problem can be overcome. The MATLAB code used for each example is publicly available on GitHub (see Section 8)
2 Methods
2.1 Spectral expansion
Let us consider a model
where
The underlying model could be of any type, e.g., an ODE, a PDE, an algebraic, or a statistical model. This implies that
This meta-model can be used to determine the distribution of the model response
where
where
The most commonly used method for determining the coefficients in the SE approach is through Gaussian quadrature schemes (Bruno, 2007). Here, we propose an alternative scheme. It is applicable to any set of orthonormal functions, allowing the flexibility to tackle different modelling challenges. A key feature in the scheme is the introduction of the symmetric matrix:
Since this matrix is symmetric, its eigenvalues
where
The striking point here is that this expansion requires evaluation of the model only
2.2 Practical aspects
Here, we treat some specific aspects of the method presented above.
2.2.1 PDFs and basis functions
We already mentioned Legendre and Hermite polynomials as possible basis functions for SE. Legendre polynomials are defined over the interval
As mentioned above, Legendre are related to the standard uniform distribution
To obtain a uniformly distributed random variable
A lognormally distributed random variable
Equations 7–9 show the most common transformations. Other transformations are, of course, possible as well. where
2.2.2 Multiple uncertainty parameters
Typically, biological models involve more than one random parameter, which means that the SE basis
As other similar approaches, SE suffers from the curse of dimensionality (Ghanem et al., 2017; Xiu, 2007). Note from Equation 10 that the number of times the model has to be evaluated scales as
2.2.3 Correlated uncertainty parameters
To handle correlated parameters we propose transforming the basis functions. Here, we discuss the case of two correlated parameters; in Supplementary Material S2 we show the general case. Let
where the functions
with
2.2.4 Segmentation
In cases where either an expansion to high order is needed to obtain the requested approximation accuracy or the model is computationally expensive, one needs to switch to optimised or more effective methods (Le Maître and Knio, 2010; Sullivan, 2015). Models that show complex response surfaces (e.g., bifurcations) will require high order expansions to capture the inherent complexity. To overcome these problems, we present here a simple and easy to implement scheme that segments the parameter intervals into subintervals, yielding a piecewise continuous approximation of the original function. Within each of these segments we then perform a separate expansion. In this approach we have to deal with a trade-off: the number of expansions is increased, but per expansion we have a (much) lower order of expansion. Below, we argue why the second positive aspect greatly counterbalances the first negative aspect.
To determine the segments we define a scaling function
This scaling function
Upon a variable transformation
After segmentation, the expansion on the interval
where
We can also define an index function to select
Using both index functions we can finally write the segmented reconstruction as:
The number of model solutions required now scales as
To illustrate this with an example, we take a system with 2 species of interest and 5 uncertainty parameters
2.2.5 Haar wavelet expansion
Traditional SE methods are known to have difficulties with capturing discontinuous behaviour (Joel Chorin, 1974; Le Maıtre et al., 2004). Spectral convergence is only observed when solutions are sufficiently regular and continuous. Just like Fourier expansions, SE suffers from Gibbs phenomena at discontinuities, resulting in slow convergence (Le Maître and Knio, 2010). Haar wavelets have been suggested to overcome these difficulties (Le Maıtre et al., 2004; Sullivan, 2015). In contrast to global basis functions like the aforementioned polynomial systems, wavelet representations lead to localized decompositions, resulting in increased robustness at the cost of a slower convergence rate (Sullivan, 2015; Le Maître and Knio, 2010). Here, we discuss that Haar wavelets can be easily incorporated in the framework presented above and in Example IV in Section 3.4 we show how they can be applied in practice.
As mother wavelet we take
By introducing a scaling factor
Given the uncertainty parameter
By concatenating the indices
2.2.6 Sensitivity analysis
In sensitivity analysis one quantifies the effects of changes in the parameters on the variability of the model response. Here, we show how our SE approach allows for sensitivity analysis in an elegant way. In the case of local sensitivity analysis, small parameter variations around a certain point in parameter space are used to determine the effect on the model output (Brian, 2013). This sensitivity is estimated via calculation of the partial derivatives of model output with respect to parameters, evaluated in that point (Ingalls, 2008). Alternatively, global sensitivity approaches do not specify a specific point in parameter space (Saltelli, 2008). For example, Sobol indices are a popular sensitivity measure as they provide a measure of global sensitivity and accurate information for most models (Ilya, 2001). Sobol indices are based on the decomposition of the variance of the output
where I is the multi-index set of all variables and
where
In this way the relative contribution of parameter
2.3 Monte Carlo sampling
In the examples in Section 3.5 we compare SE with Monte Carlo sampling. For efficiency reasons we apply Quasi Monte Carlo methods using Sobol sequences, since these show a faster rate of convergence than standard sequences of pseudorandom numbers (Soboĺ, 1990). In order to test for convergence, we use the so-called blocking method. In this method the error is estimated in a straightforward manner. The quantity of interest (i.e., the model response
2.4 Summary of implementation
In this section we provide an overview of the steps needed to arrive at a meta-model using SE:
1. Determine which of the model parameters is stochastic in nature and decide upon an appropriate PDF for such parameters.
2. Choose a truncation degree
3. Based on the PDF in the previous steps, calculate the appropriate basis functions
4. Determine the
where
For Hermitian polynomials
5. Calculate the eigenvalues
6. Calculate
7. Calculate
8. Arrive at the metamodel
9. Eventually, apply post-processing through, e.g., sensitivity analysis.
3 Results
To test the performance of the present SE approach in biological simulations, we have chosen six typical examples. Through these examples, we show how to deal with several challenges usually encountered in systems biology.
The first example has only one uncertainty parameter. Its simplicity allows comparison between the results of our approach with an exact solution.
The second example concerns a biochemical reaction network and is higher dimensional, i.e., it contains more than one uncertainty parameters. We use it to highlight the advantages of segmentation.
The third example is the glycolytic oscillator, which shows bifurcations, i.e., different dynamic behaviour for different parameter sets (Strogatz, 1994). We use it to demonstrate the power of global sensitivity analysis, which in the SE framework can be achieved without significant additional computational costs once the SE coefficients have been calculated. In addition, this example allows us to show the use of mixed expansions, since the parameter PDFs follow different distributions. This leads to a combination of different families of basis functions, thus highlighting the flexibility of the SE approach when applied to varying input uncertainties.
The fourth and fifth examples have a spatial dimension. First, we consider the Schnakenberg model which is a well-known model of pattern formation and comes with challenges such as shifts from non-patterning to patterning regions (D Murray, 2007). In this example we demonstrate the advantage of using Haar wavelets over polynomial basis functions for systems with bifurcations. Second, we study a model describing pattern formation in plants, more specifically patterning of the hairs found on top of leaves, so-called trichomes (Bouyer et al., 2008). In this model we show how to adapt the approach such that the computational costs are reduced as much as possible by carefully choosing the quantity of interest, without changing the standard set of steps.
The final example is a model of plasmid transfection, where we consider correlated parameter distributions. This model predicts the distribution of two different plasmid constructs among a population of dividing cells. Upon division the plasmids are distributed among the daughter cells according to a bivariate Poisson distribution.
3.1 Example I. Exponential decay: comparing performance of SE to MC and an analytical solution
For this example case, we consider the simple reaction consisting of one decaying species:
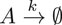
Its dynamics is described by
We assume that
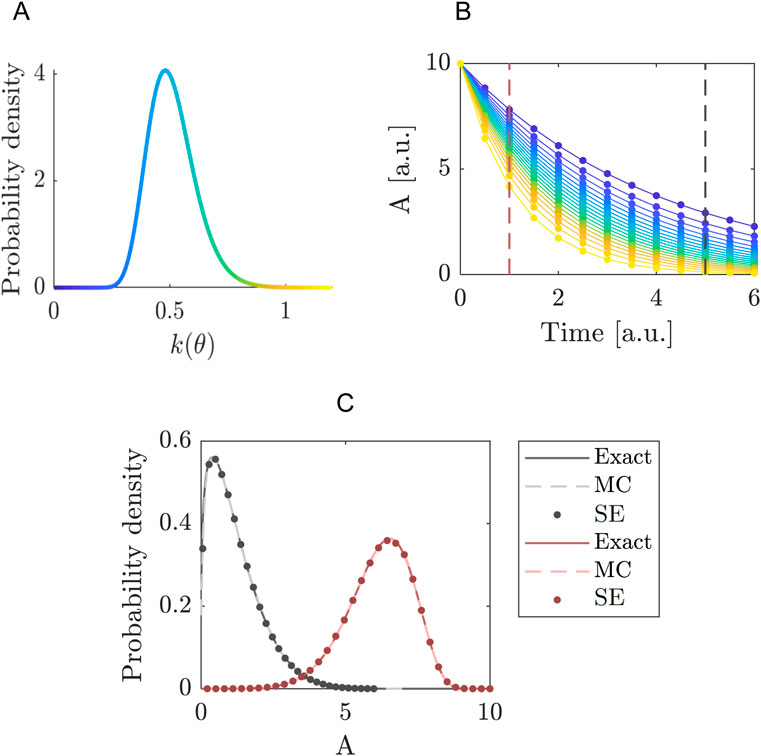
Figure 1. Quantifying the uncertainty propagated by the decay rate in the exponential decay model. (A) Probability density function of the decay rate
Next, we determine how the uncertainty in
In Figure 1, we focus on the distributions of
with kernel function
3.2 Example II. Biochemical reaction network: segmentation to deal with higher dimensions
In this example we present a simple model with multiple uncertainty parameters. It allows us to illustrate the computational advantage of segmentation as explained in Section 2.2.4. The model describes the dynamics of two proteins




In this network, the proteins
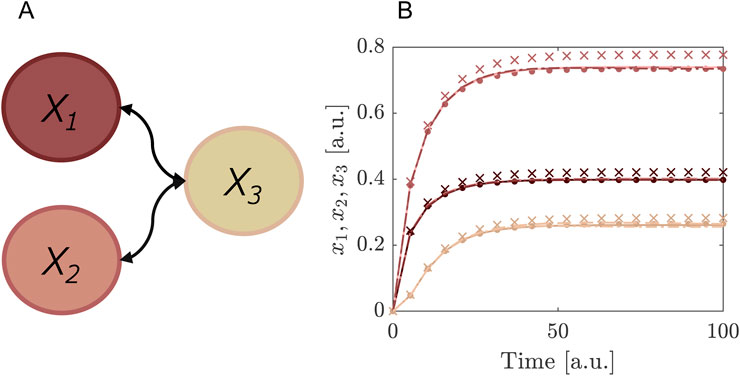
Figure 2. Comparing the segmented expansion with the standard non-segmented expansion. (A) Interaction scheme of the model in Equations 35–37. Note that
We use for the parameters

Table 1. Benchmarking of segmented and non-segmented expansion. An overview of the number of model evaluations
Dividing the parameter intervals into smaller sub-intervals is a relatively straightforward and simple way to circumvent huge computation times. Other, more intricate methods have been developed to tackle models with an even larger amount of parameters (Blatman and Sudret, 2010b; Xiu, 2007; Nobile et al., 2008). For example, using an adaptive algorithm that is based on classical statistical learning tools can result in a “sparse” SE, that consists of only the significant coefficients in the expansion, thereby reducing the computational cost. This method has been tested on models of stochastic finite element analysis with up to 21 parameters (Blatman and Sudret, 2010b).
3.3 Example III. Glycolytic oscillator: different uncertainty PDFs and global sensitivity
Living cells obtain energy by breaking down sugar in the biochemical process called glycolysis. In yeast cells, this glycolysis was observed to behave in an oscillatory fashion, where the concentration of various intermediates were increasing and decreasing within a period of several minutes (Hess and Boiteux, 1968). This glycolytic oscillator can be modelled as a two-component system with a negative feedback (Strogatz, 1994):
where
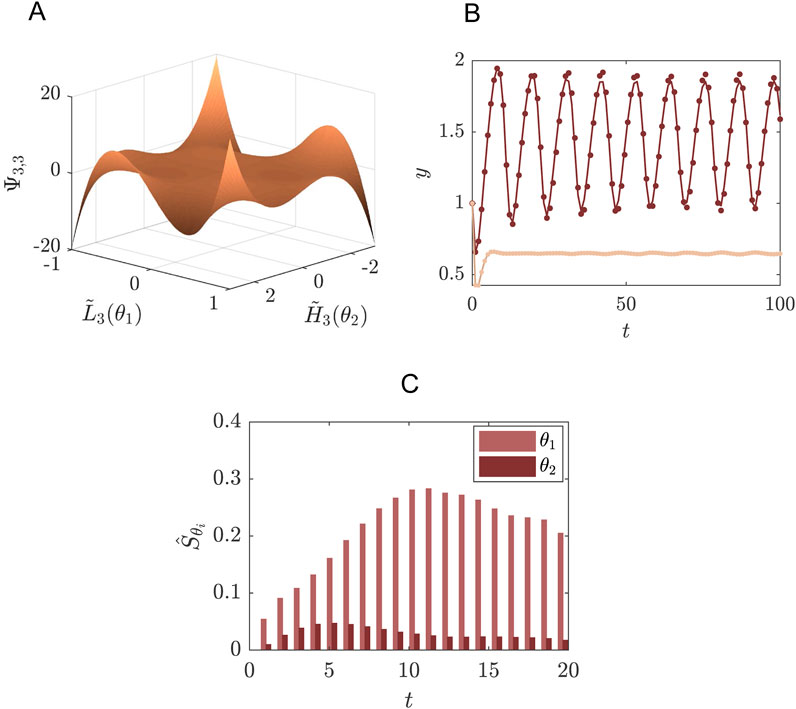
Figure 3. Example of a system of glycolysis as defined in Equations 38, 39 where SE is performed for the concentration of species
The distributions of the uncertainty parameters were chosen such that they include the bifurcation point from stable limit cycle to the stable fixed point (Figure 3). For the purpose of this example we are interested in the concentration of
In post-processing we may use the SE coefficients to determine the first order Sobol indices for the parameters
3.4 Example IV. Schnakenberg model: dealing with spatial discontinuities
In this example we introduce a spatial component. We consider the Schnackenberg model, which is one of the simplest, but yet realistic two-species system that can produce spatially oscillating solutions and therefore has become a prototype for reaction diffusion systems. The Schnakenberg model consists of the following (dimensionless) equations for the concentrations
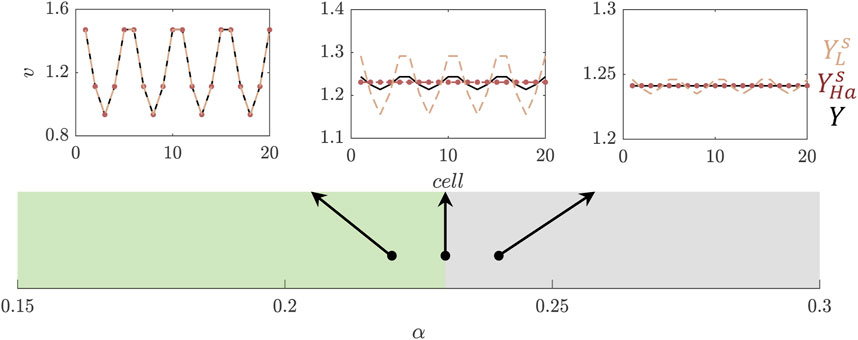
Figure 4. Reconstruction of the concentration of species
SE using polynomial basis functions is known for being inaccurate in regions that contain discontinuities (Le Maître and Knio, 2010; Le Maıtre et al., 2004; Joel Chorin, 1974). In this example, the lack of convergence in SE can be seen along the boundary of the patterning space (TS) in Figure 4, where the expansion by Legendre polynomials is indicated with the dashed lines. For the reconstruction of concentration
3.5 Example V. Trichome patterning: dealing with spatial discontinuities
As an extra example of pattern formation we consider a model that describes trichomes. Trichomes are hairs found on the epidermal layer of leaves. In Arabidopsis Thaliana these trichomes form a regular pattern, where each trichome is separated by around three to four epidermal cells (Hülskamp, 2004). The model studied here consists of three proteins and their interactions which can explain features of trichome patterning (Bouyer et al., 2008; Pesch and Hülskamp, 2004). Protein transpararant testa glabra1 (TTG1) binds to the transcription factor glabra3 (GL3) which together form a trichome-promoting complex, called the activating complex (AC) (Bouyer et al., 2008). Experimental data suggests that TTG1 is depleted from cells neighbouring a trichome (Bouyer et al., 2008). For this reason the interaction between TTG1 and GL3 is modelled in a substrate-depletion form (Figure 5), where TTG1 acts as a substrate for the formation of AC (Bouyer et al., 2008). After non-dimensionalisation this model consists of four parameters, none of which have been experimentally determined, highlighting the substantial amount of uncertainty within this model (Pesch and Hülskamp, 2009; Scheres, 2000). Here, we examine the propagation of uncertainty in the parameters to the predicted pattern.
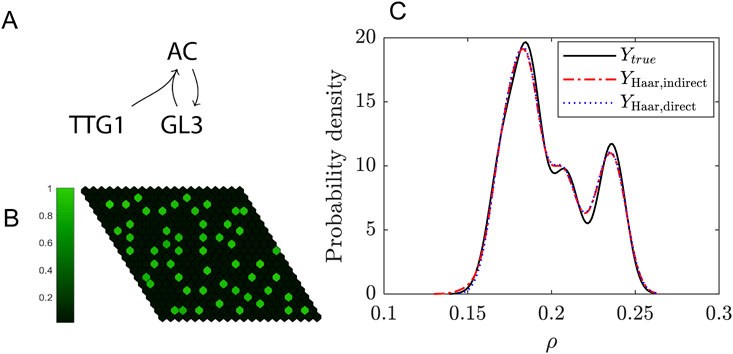
Figure 5. Uncertainty quantification for the trichome system. (A) Schematic of the model. (B) Example of a simulation of the model on a 20-by-20 grid. The colorbar indicates the levels of the activating complex (AC) in the cells relative to the maximum. (C) Probability density function of the trichome density in the Turing Space using either the indirect (dashed red line) or direct expansion (dotted blue line) method and for comparison the solution of the real model (solid black line). A resolution level of 3 (i.e., a total of 16 wavelets) has been used for the expansion.
The trichome patterning is described by the following set of coupled ODEs (Bouyer et al., 2008):
where
In this example we focus on the parameter
where
Our present goal is to study the uncertainty in
where
Our second, direct approach is to directly reconstruct
Similarly, as we did for
In other words, we only solve the system and determine the trichome density if the parameter set falls within the Turing space. This lends robustness to the SE for the non-smooth parts of the function
One of the nice features of this Example is that it illustrates there are multiple ways in which the uncertainty in the output can be captured: first, an indirect method (Equation 46) where the model output consists of concentration profiles from which the pattern features have to be extracted in post-processing, and second, by taking the density as model output (Equations 47, 48). In Figure 5 results for the indirect and direct approaches are compared. We conclude that both have similar levels of accuracy and in both cases the expansions converge to the real solution at resolution level N = 6, which means a summation of 128 wavelets. The PDF in Figure 5 is constructed using
3.6 Example VI. Plasmid transfection: dealing with correlated parameters
It can happen that in parameter space a structure occurs, i.e., that the multivariate joined probability cannot be written as a product of univariate distributions. In this section we exemplify how to handle such a case. As an example we choose the transfection of mammalian cells (e.g., Human embryonic kidney cells, HEK293) with two plasmids: plasmid
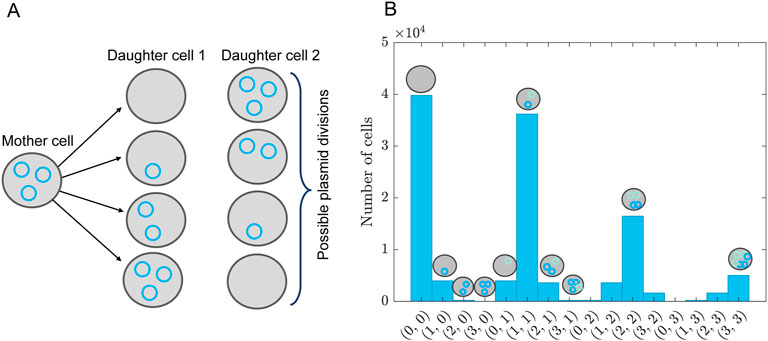
Figure 6. Plasmid distribution model. (A) Schematic overview of plasmid distribution upon cell division, showing all possible combinations of how to divide three plasmids among two daughter cells. This is for a single type of plasmid. The probability of finding these combinations is given by Equation 56. (B) Distribution of plasmid combinations for two types of plasmids, assuming a bivariate Poisson distribution given by Equation 59 with
Denoting by
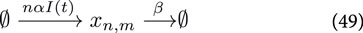
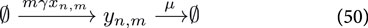
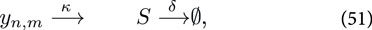
where
For sake of clarity we keep the system simple and ignore all complicating effects, such as gene expression noise, maturation of the reporter construct (e.g., GFP). However, for transient transfections of the mammalian cells, we need to take into account the distribution of plasmids among the cells, which is not constant due to cell division. The set of Ordinary Differential Equations describing the reactions given by Equations 49–51 read:
The parameter
We assume that the rate of dilution of the plasmids corresponds to the growth rate of the cells, i.e., plasmids are lost upon division. In reality, the plasmids are also degraded, but we assume the time scale of this degradation is much longer than the experimental duration and can therefore be ignored. To model the partition of plasmids upon cell division we assume that any partition of the number of plasmids is possible, see, for example, Figure 6A. The probability of finding a certain partition is given by the binomial distribution
where
We treat the plasmid uptake as a Poisson process, i.e., the number of plasmids inside a cell is Poisson distributed. Assuming that the mean number of plasmid taken up is the same for
where
The correlation between
In Figure 7A we show
Note the dependence on the parameter
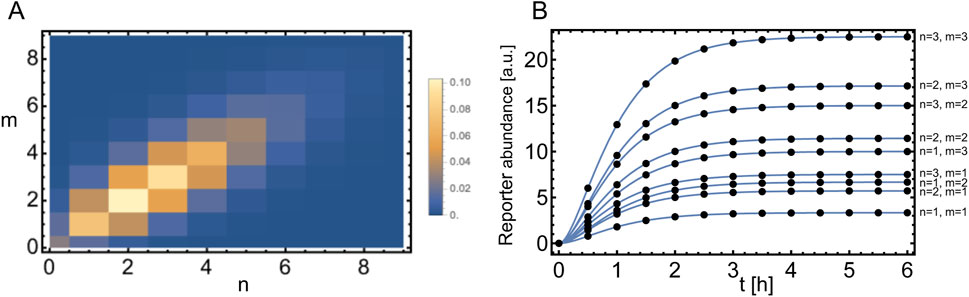
Figure 7. Expansion with respect to a bivariate Poisson distribution. (A) Bivariate Poisson distribution given by Equation 59 with
We first consider a system in which the mammalian cells do not secrete the reporter molecule, e.g., YFP. In this case we set
where
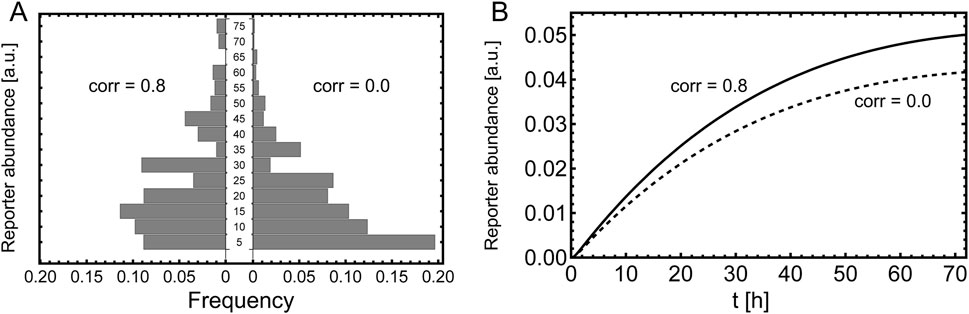
Figure 8. Measurement of the reporter. Comparison of correlated and un-correlated plasmid uptake. (A) Histogram of the single cell readout, measured 6 h after induction. The parameters are the same as stated in Figure 7 and the histogram is calculated according Equation 64 with
Next, we consider a segregated reporter, e.g., SEAP. In this case the reporter abundance in the bulk is measured instead of single cell measurements. The temporal evolution of the bulk reporter is governed by Equations 52–55. In Figure 8B one can see that the dynamics of the reporter is clearly different due to correlation of the plasmid uptake.
4 Discussion and conclusion
In this paper we have presented an efficient and widely-applicable version of spectral expansion to quantify the effect of parameter uncertainty on model outcomes. The present scheme is based on non-intrusive spectral projection and makes use of expansions in terms of some orthonormal set of basis functions., e.g.,,polynomial functions or wavelets. The orthonormal properties of those basis functions are utilized to develop a novel scheme to determine the expansion coefficients. It has the attractive property that it is computationally very fast. The scheme is similar to the Golub-Welsh algorithm known from Gaussian quadrature (Golub and Welsch, 1969). In the latter procedure the roots of the polynomials used play an essential role (Bruno, 2007). In our new scheme this role is played by the eigenvalues of a matrix, which can be calculated very fast. Our method does not require modification of the model equations. This is in general the main advantage of non-intrusive methods: there is no need to recast the model into a probabilistic framework. Instead, the random behaviour of parameters is accounted for through a set of deterministic simulations of the process for a restricted number of parameter values. These values are chosen such that they reflect the uncertainties in the parameters. To test the performance of our method we applied it to a number of different models (Example I) a model of exponential decay (Example II) a biochemical reaction network (Example III) the glycolytic oscillator (Example IV) the Schnakenberg model, and (Example V) a trichome model. Examples IV and V deal with spatial pattern formation, and, finally, Example VI illustrates SE for correlated parameters. For each test case, the results of the SE are compared to, if available, analytical solutions and/or and Monte Carlo simulations. In these comparisons we mostly focus on the accuracy of SE. Although the computational advantage is an important reason for using SE techniques, we do not focus on that aspect since it has already been extensively explored elsewhere; see, for example, (Zein et al., 2013; Bruno, 2007; Fajraoui et al., 2017).
The accuracy of the reconstruction by SE depends on the choice of expansion order and the appropriate choice of basis functions. While the latter choice is determined by the PDFs of the input parameters, the choice of expansion order has to be chosen by the user. For example, in Examples I and III we chose
In some cases the expansion order has to be chosen prohibitively large. For such a situation we propose an extended approach that segments the parameter interval into subintervals, essentially zooming in on these sub-intervals such that a lower expansion order can be used in each sub-interval. In Example II we have shown that this segmentation approach can greatly reduce the computational costs, thus providing a way to circumvent the curse of dimensionality. Such adaptations are nearly always required in high-dimensional cases and segmentation is a relatively simple and straight-forward method to tackle dimensionality problems yielding a piecewise continuous approximation to the original function. It is an alternative for so-called sparse SE methods, that utilise only a small subset of the basis functions in order to limit the amount of model evaluations (Blatman and Sudret, 2010b; Xiu, 2007; Nobile et al., 2008).
Convergence of the SE may be poor in regions of the parameter space around a bifurcation (Ghanem et al., 2017), due to the use of smooth basis functions to represent non-smooth model behaviour. This effect is often illustrated by the Gibbs phenomenon in Fourier expansions, where the spectral basis consisting of smooth sine and cosine functions is not suitable, giving rise to slow and even lack of correct convergence. Since smooth functions like the Hermite and Legendre polynomials will fail to describe steep or discontinuous solutions, we explored the use of Haar wavelets. Wavelets naturally allow localised decompositions and this leads to more robust behaviour (Le Maıtre et al., 2004). We show in Example IV (Schnakenberg model) the advantages of using Haar wavelets over polynomials by focusing on the region in parameter space where the system jumps from spatially heterogeneous to spatially homogeneous dynamics. Although around this bifurcation point an expansion in terms of Haar wavelets also turned out to show slow convergence, the accuracy of the expansion is much better than when Legendre polynomials are used. In the vicinity of bifurcations Haar wavelets thus provide a useful tool for biological systems which feature discontinuities. In Example V (trichome pattern formation) we have highlighted the flexibility of the method: some quantities, e.g., the scalar quantity of trichome density, can either be directly expanded or indirectly. By making use of that adaptability the number of model evaluations can be reduced while the level of accuracy is maintained. Finally, in Example VI we illustrate how to handle correlated parameters by means of correlated plasmid uptake by mammalian cells. We show how single-cell or bulk readout can be calculated using SE.
Overall, the approach presented here consists of a number of easy-to-implement steps and is applicable to a great variety of systems that would be computationally costly when analysed in the context of uncertainty quantification in the usual way. We therefore believe that this approach could provide a valuable asset for the toolkit of computational systems biology.
Data availability statement
The code is publicly available at: https://github.com/AnnaDeneer/SpectralExpansion.
Author contributions
AD: Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. JM: Conceptualization, Methodology, Writing–original draft, Writing–review and editing. CF: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Writing–original draft, Writing–review and editing, Methodology.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. CF received funding from FET-Open research and innovation actions grant under the European Union’s Horizon 2020 (CyGenTiG; grant agreement 801041).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsysb.2024.1419809/full#supplementary-material
References
Banga, J. R., and Balsa-Canto, E. (2008). Parameter estimation and optimal experimental design. Essays Biochem. 45, 195–209. doi:10.1042/BSE0450195
Barbu, A., and Zhu, S.-C. (2020). Monte Carlo methods. Singapore: Springer Singapore. doi:10.1007/978-981-13-2971-5
Barz, T., Arellano-Garcia, H., and Wozny, G. (2010). Handling uncertainty in model-based optimal experimental design. Industrial and Eng. Chem. Res. 49 (12), 5702–5713. doi:10.1021/ie901611b
Berger, J., Hauber, J., Hauber, R., Geiger, R., and Cullen, B. R. (1988). Secreted placental alkaline phosphatase: a powerful new quantitative indicator of gene expression in eukaryotic cells. Gene 66 (1), 1–10. doi:10.1016/0378-1119(88)90219-3
Berkhout, P., and Plug, E. (2004). A bivariate Poisson count data model using conditional probabilities. Stat. Neerl. 58 (3), 349–364. ISSN 1467-9574. doi:10.1111/j.1467-9574.2004.00126.x
Blake, W. J., Kaern, M., Cantor, C. R., and Collins, J. J. (2003). Noise in eukaryotic gene expression. Nature 422 (6932), 633–637. doi:10.1038/nature01546
Blatman, G., and Sudret, B. (2010a). Efficient computation of global sensitivity indices using sparse polynomial chaos expansions. Reliab. Eng. and Syst. Saf. 95 (11), 1216–1229. doi:10.1016/j.ress.2010.06.015
Blatman, G., and Sudret, B. (2010b). An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probabilistic Eng. Mech. 25 (2), 183–197. doi:10.1016/j.probengmech.2009.10.003
Bouyer, D., Geier, F., Kragler, F., Schnittger, A., Pesch, M., Wester, K., et al. (2008). Two-dimensional patterning by a trapping/depletion mechanism: the role of TTG1 and GL3 in Arabidopsis trichome formation. PLoS Biol. 6 (6), e141. ZSCC: NoCitationData[s0]. doi:10.1371/journal.pbio.0060141
Bowman, A. W., and Azzalini, A. (1997). Applied smoothing techniques for data analysis: the kernel approach with S-Plus illustrations, Vol. 18. Oxford: OUP.
Brian, P. I. (2013). Mathematical Modeling in systems biology. An introduction. MIT Press. 0-262-01888-8.
Bruno, S. (2007). Uncertainty propagation and sensitivity analysis in mechanical models–contributions to structural reliability and stochastic spectral methods. Habilit. Dir. Des. Rech. Univ. Blaise Pascal, Clermont-Ferrand, Fr. 147.
Christian, P. (2004). “Robert and George casella,” in Monte Carlo statistical methods (New York, New York, NY: Springer Texts in Statistics. Springer). 978-1-4419-1939-7 978-1-4757-4145-2. doi:10.1007/978-1-4757-4145-2
D Murray, J. (2007). Mathematical biology: I. An introduction, Vol. 17. Springer Science and Business Media.
Eldred, M., Webster, C., and Constantine, P. (2008). “Evaluation of non-intrusive approaches for wiener-askey generalized polynomial chaos,” in 49th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics, and materials conference, 16th AIAA/ASME/AHS adaptive structures conference, 10th AIAA non-deterministic approaches conference, 9th AIAA gossamer spacecraft forum, 4th AIAA multidisciplinary design optimization specialists conference, 1892.
Elowitz, M. B., Levine, A. J., Siggia, E. D., and Swain, P. S. (2002). Stochastic gene expression in a single cell. Sci. (New York, NY) 297 (5584), 1183–1186. doi:10.1126/science.1070919
Fajraoui, N., Marelli, S., and Sudret, B. (2017). On optimal experimental designs for sparse polynomial chaos expansions. arXiv Prepr. arXiv:1703.05312.
Ghanem, R., Higdon, D., and Owhadi, H. (2017). Handbook of uncertainty quantification, Vol. 6. Springer.
Golub, G. H., and Welsch, J. H. (1969). Calculation of gauss quadrature rules. Math. Comput. 23 (106), 221–230. doi:10.2307/2004418
Gutenkunst, R. N., Waterfall, J. J., Casey, F. P., Brown, K. S., Myers, C. R., and Sethna, J. P. (2007). Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 3 (10), 1871–1878. doi:10.1371/journal.pcbi.0030189
Hess, B., and Boiteux, A. (1968). Mechanism of glycolytic oscillation in yeast, i. aerobic and anaerobic growth conditions for obtaining glycolytic oscillation. Biol. Chem. 349 (2), 1567–1574. doi:10.1515/bchm2.1968.349.2.1567
Hülskamp, M. (2004). Plant trichomes: a model for cell differentiation. Nat. Rev. Mol. Cell Biol. 5 (6), 471–480. doi:10.1038/nrm1404
Ilya, M. S. (2001). Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 55 (1-3), 271–280. doi:10.1016/s0378-4754(00)00270-6
Ingalls, B. (2008). Sensitivity analysis: from model parameters to system behaviour. Essays Biochem. 45, 177–193. ISSN 0071-1365. doi:10.1042/bse0450177
James, F. (1980). Monte Carlo theory and practice. Rep. Prog. Phys. 43 (9), 1145–1189. doi:10.1088/0034-4885/43/9/002
Joel Chorin, A. (1974). Gaussian fields and random flow. J. Fluid Mech. 63 (1), 21–32. doi:10.1017/s0022112074000991
Kirk, P., Silk, D., and Stumpf, M. P. H. (2016). “Reverse engineering under uncertainty,” in Uncertainty in biology (Springer), 15–32.
Kreutz, C., and Timmer, J. (2009). Systems biology: experimental design. FEBS J. 276 (4), 923–942. doi:10.1111/j.1742-4658.2008.06843.x
Le Maître, O., and Knio, O. M. (2010). Spectral methods for uncertainty quantification: with applications to computational fluid dynamics. Springer Science and Business Media.
Le Maıtre, O. P., Knio, O. M., Najm, H. N., and Ghanem, R. G. (2004). Uncertainty propagation using wiener–haar expansions. J. Comput. Phys. 197 (1), 28–57. doi:10.1016/j.jcp.2003.11.033
Lev, S. (2014). Noise in biology. Rep. Prog. Phys. 77 (2), 026601–026629. doi:10.1088/0034-4885/77/2/026601
Liu, P., Shi, J., Wang, Y., and Feng, X. (2013). Bifurcation analysis of reaction-diffusion schnakenberg model. J. Math. Chem. 51 (8), 2001–2019. doi:10.1007/s10910-013-0196-x
Martin-Casas, M., and Mesbah, A. (2016). Discrimination between competing model structures of biological systems in the presence of population heterogeneity. IEEE life Sci. Lett. 2 (3), 23–26. doi:10.1109/lls.2016.2644645
Mitra, E. D., and Hlavacek, W. S. (2019). Parameter estimation and uncertainty quantification for systems biology models. Curr. Opin. Syst. Biol. 18, 9–18. doi:10.1016/j.coisb.2019.10.006
Nobile, F., Tempone, R., and Webster, C. G. (2008). A sparse grid stochastic collocation method for partial differential equations with random input data. SIAM J. Numer. Analysis 46 (5), 2309–2345. doi:10.1137/060663660
Noble, W. S. (2004). Support vector machine applications in computational biology. Kernel methods Comput. Biol. 71 (92), 71–92. doi:10.7551/mitpress/4057.003.0005
Ogura, H. (1972). Orthogonal functionals of the Poisson process. IEEE Trans. Inf. Theory 18 (4), 473–481. ISSN 0018-9448. doi:10.1109/TIT.1972.1054856
Olver, F. W. J. (2010). in NIST handbook of mathematical functions hardback and CD-ROM (Cambridge University Press). Available at: https://books.google.de/books?id=3I15Ph1Qf38C.National institute of standards, and technology (U.S.)
Paulson, J. A., Martin-Casas, M., and Ali, M. (2019). Fast uncertainty quantification for dynamic flux balance analysis using non-smooth polynomial chaos expansions. PLoS Comput. Biol. 15 (8), e1007308. doi:10.1371/journal.pcbi.1007308
Pesch, M., and Hülskamp, M. (2004). Creating a two-dimensional pattern de novo during arabidopsis trichome and root hair initiation. Curr. Opin. Genet. and Dev. 14 (4), 422–427. doi:10.1016/j.gde.2004.06.007
Pesch, M., and Hülskamp, M. (2009). One, two, three models for trichome patterning in arabidopsis? Curr. Opin. plant Biol. 12 (5), 587–592. doi:10.1016/j.pbi.2009.07.015
Raue, A., Schilling, M., Bachmann, J., Matteson, A., Schelke, M., Kaschek, D., et al. (2013). Lessons learned from quantitative dynamical modeling in systems biology. PloS one 8 (9), e74335. doi:10.1371/journal.pone.0074335
Renardy, M., Yi, T.-Mu, Xiu, D., and Chou, C.-S. (2018). Parameter uncertainty quantification using surrogate models applied to a spatial model of yeast mating polarization. PLoS Comput. Biol. 14 (5), e1006181. doi:10.1371/journal.pcbi.1006181
Saltelli, A. (2008). Global sensitivity analysis: the primer. Chichester, England ; Hoboken, NJ: John Wiley. 978-0-470-05997-5. OCLC: ocn180852094.
Scheres, B. (2000). Non-linear signaling for pattern formation? Curr. Opin. plant Biol. 3 (5), 412–417. doi:10.1016/s1369-5266(00)00105-9
Schultheiß Araújo, I., Pietsch, J. M., Keizer, E. M., Greese, B., Balkunde, R., Fleck, C., et al. (2017). Stochastic gene expression in Arabidopsis thaliana. Nat. Commun. 8 (1), 2132–2139. doi:10.1038/s41467-017-02285-7
Silverman, B. W. (1986). Density estimation for statistics and data analysis, Vol. 26. New York, United States: CRC Press.
Soboĺ, I. M. (1990). Quasi-Monte Carlo methods. Prog. Nucl. Energy 24 (1-3), 55–61. doi:10.1016/0149-1970(90)90022-w
Streif, S., Petzke, F., Ali, M., Findeisen, R., and Braatz, R. D. (2014). Optimal experimental design for probabilistic model discrimination using polynomial chaos. IFAC Proc. Vol. 47 (3), 4103–4109. doi:10.3182/20140824-6-za-1003.01562
Strogatz, S. H. (1994). “Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering,” in Studies in nonlinearity (Addison-Wesley Pub). 978-0-201-54344-5.
Sudret, B. (2008). Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. and Syst. Saf. 93 (7), 964–979. doi:10.1016/j.ress.2007.04.002
Sullivan, T. J. (2015). Introduction to uncertainty quantification. Springer International Publishing. ISBN ISBN 978-3-319-23395-6.
Tadeusiewicz, R. (2015). Neural networks as a tool for modeling of biological systems. Bio-Algorithms Med-Systems 11 (3), 135–144. doi:10.1515/bams-2015-0021
Tan, E., Chin, C. S. H., Lim, Z. F. S., and Ng, S. K. (2021). HEK293 cell line as a platform to produce recombinant proteins and viral vectors. Front. Bioeng. Biotechnol. 9, 796991. ISSN 2296-4185. doi:10.3389/fbioe.2021.796991
Thattai, M., and van Oudenaarden, A. (2001). Intrinsic noise in gene regulatory networks. PNAS 98 (15), 8614–8619. doi:10.1073/pnas.151588598
Tsigkinopoulou, A., Hawari, A., Uttley, M., and Breitling, R. (2018). Defining informative priors for ensemble modeling in systems biology. Nat. Protoc. 13 (11), 2643–2663. doi:10.1038/s41596-018-0056-z
van Mourik, S., Ter Braak, C., Stigter, H., and Molenaar, J. (2014). Prediction uncertainty assessment of a systems biology model requires a sample of the full probability distribution of its parameters. PeerJ 2, e433. doi:10.7717/peerj.433
Vincent, D., Sudret, B., and Deheeger, F. (2013). Metamodel-based importance sampling for structural reliability analysis. Probabilistic Eng. Mech. 33, 47–57. doi:10.1016/j.probengmech.2013.02.002
Wilkinson, D. J. (2007). Bayesian methods in bioinformatics and computational systems biology. Briefings Bioinforma. 8 (2), 109–116. doi:10.1093/bib/bbm007
Xiu, D. (2007). Efficient collocational approach for parametric uncertainty analysis. Commun. Comput. Phys. 2 (2), 293–309.
Xiu, D., and George, Em K. (2002). The wiener–askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 24 (2), 619–644. doi:10.1137/s1064827501387826
Yoshida, N., and Sato, M. (2009). Plasmid uptake by bacteria: a comparison of methods and efficiencies. Appl. Microbiol. Biotechnol. 83 (5), 791–798. ISSN 0175-7598. doi:10.1007/s00253-009-2042-4
Zein, S., Colson, B., and Glineur, F. (2013). An efficient sampling method for regression-based polynomial chaos expansion. Commun. Comput. Phys. 13 (4), 1173–1188. doi:10.4208/cicp.020911.200412a
Keywords: systems biology, computational systems biology, mathematical modelling, spectral expansion, surrogate models
Citation: Deneer A, Molenaar J and Fleck C (2024) Spectral expansion methods for prediction uncertainty quantification in systems biology. Front. Syst. Biol. 4:1419809. doi: 10.3389/fsysb.2024.1419809
Received: 18 April 2024; Accepted: 27 August 2024;
Published: 03 October 2024.
Edited by:
Claudio Angione, Teesside University, United KingdomReviewed by:
Marissa Renardy, Applied BioMath, United StatesDaniela Besozzi, University of Milano-Bicocca, Italy
Copyright © 2024 Deneer, Molenaar and Fleck. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christian Fleck, Y2hyaXN0aWFuLmZsZWNrQGZkbS51bmktZnJlaWJ1cmcuZGU=
 Anna Deneer1
Anna Deneer1 Jaap Molenaar
Jaap Molenaar Christian Fleck
Christian Fleck