Distinct mechanisms underlie electrical coupling resonance and its interaction with membrane potential resonance

Neurons in oscillatory networks often exhibit membrane potential resonance, a peak impedance at a non-zero input frequency. In electrically coupled oscillatory networks, the coupling coefficient (the ratio of post- and prejunctional voltage responses) could also show resonance. Such coupling resonance may emerge from the interaction between the coupling current and resonance properties of the coupled neurons, but this relationship has not been clearly described. Additionally, it is unknown if the gap-junction mediated electrical coupling conductance may have frequency dependence. We examined these questions by recording a pair of electrically coupled neurons in the oscillatory pyloric network of the crab Cancer borealis. We performed dual current- and voltage-clamp recordings and quantified the frequency preference of the coupled neurons, the coupling coefficient, the electrical conductance, and the postjunctional neuronal response. We found that all components exhibit frequency selectivity, but with distinct preferred frequencies. Mathematical and computational analysis showed that membrane potential resonance of the postjunctional neuron was sufficient to give rise to resonance properties of the coupling coefficient, but not the coupling conductance. A distinct coupling conductance resonance frequency therefore emerges either from other circuit components or from the gating properties of the gap junctions. Finally, to explore the functional effect of the resonance of the coupling conductance, we examined its role in synchronizing neuronal the activities of electrically coupled bursting model neurons. Together, our findings elucidate factors that produce electrical coupling resonance and the function of this resonance in oscillatory networks.

1 Introduction

In oscillatory circuits, neurons and synapses are subject to inputs that often span a range of frequencies. Whether they respond more favorably in one frequency range, and whether such frequency selectivity can be altered in different states, may impact the dynamics of the circuit output. Many neurons exhibit a frequency-dependent property known as membrane potential resonance, characterized as a maximal subthreshold impedance at a non-zero (resonance) frequency (Hutcheon and Yarom, 2000). When measured with oscillatory current injection, this corresponds to the voltage amplitude response being maximal to oscillatory current input at that frequency. Membrane potential resonance typically arises through interactions of passive properties of the neuron and the kinetics of voltage gated ionic currents (Hutcheon and Yarom, 2000). The resonance frequency of neurons has been shown to correlate with the network frequency in several systems (Wu et al., 2001; Bykhovskaia et al., 2004; Tohidi and Nadim, 2009; Moca et al., 2014). Membrane potential resonance is one form of preferred frequency response observed in neural circuits, but other circuit properties such as synaptic strengths and firing rate can also have a preferred frequency at which the output is maximized and such preferred frequencies are also often termed resonance (Izhikevich et al., 2003; Richardson et al., 2003; Drover et al., 2007; Ledoux and Brunel, 2011; Tseng et al., 2014; Rau et al., 2015; Stark et al., 2022).

In neural circuits coupled through gap junction-mediated electrical coupling, any input that causes membrane potential oscillations in one neuron could produce oscillations in its coupled partners (Landisman et al., 2002; Long et al., 2004). In electrically coupled networks where individual neurons exhibit membrane potential resonance, both the postjunctional neuron’s membrane potential and the coupling coefficient (the ratio of post- and prejunctional voltages) can also exhibit preferred frequency responses (Curti et al., 2012; Stagkourakis et al., 2018). However, it is not known if coupling resonance reflects the properties of the electrical coupling, those of the coupled neurons, or if it emerges from the interaction between the two. Electrical coupling is an important factor in generating neural oscillations (Posłuszny, 2014; Coulon and Landisman, 2017; Traub et al., 2018; Alcamí and Pereda, 2019) and, as we showed in a previous study, membrane potential resonance can directly influence the network oscillation frequency through electrical coupling (Chen et al., 2016). It is therefore important to understand how resonance properties of neurons can interact through electrical coupling.

We examined this question by recording pairs of electrically coupled neurons that show resonance in the oscillatory pyloric network of the crab, Cancer borealis. This circuit includes two bursting pyloric dilator (PD) neurons that are known to exhibit membrane potential resonance at a frequency close to the pyloric circuit oscillation frequency (Tohidi and Nadim, 2009; Fox et al., 2017). These two neurons are strongly electrically coupled to each other and, during normal activity, exhibit synchronous slow-wave oscillations that support their bursting activity (Marder and Eisen, 1984). We took advantage of the fact that we could examine the PD neurons’ membrane potential resonance and their coupling properties simultaneously to quantify the frequency dependent properties of the neurons, the coupling coefficient, and the coupling current (measured in voltage clamp). We found that all three components exhibit frequency selectivity, but with distinct preferred frequencies. Although resonance in the coupling coefficient has been previously reported, this is, to our knowledge, the first report of resonance in the coupling current.

We used mathematical analysis and computational modeling to explain the mechanism underlying resonance in the coupling coefficient, and what factors determine its resonance frequency. We then examined potential circuit mechanisms that may give rise to resonance in the coupling current and explored how such a resonance may influence network synchronization.

2 Materials and methods

2.1 Preparation and electrophysiology recordings

All experiments were performed on wild-caught adult male crabs (Cancer borealis) purchased from local seafood suppliers in Newark, NJ. Prior to experiments, animals were kept in artificial sea water tanks at 13 C. Before dissection, crabs were anesthetized by placing them on ice for 30 min. The STNS was dissected out following standard protocols (Blitz et al., 2004; Tohidi and Nadim, 2009), placed in a Petri dish coated with clear silicone elastomer (Sylgard 184; Dow Corning) and superfused with C. borealis saline, containing (in mM) 11 KCl, 440 NaCl, 13 CaCl₂, 26 MgCl₂, 11.2 Trizma base, and 5.1 maleic acid (pH = 7.4–7.5). A petroleum jelly well was built around the STG for constant superfusion of chilled (10–12°C) saline during the experiment.

PD neurons were identified by their characteristic intracellular waveforms and by matching their activities to the spikes on the corresponding motor nerves. Extracellular activities of motor nerves were recorded with a differential AC amplifier (Model 1700; A-M Systems), using stainless-steel pin wire electrodes placed inside and outside of small petroleum jelly wells built around the nerves. Intracellular recordings, current clamp and voltage clamp experiments were done with Axoclamp 900 A amplifiers (Molecular Devices). The STG was desheathed and the neuron cell bodies were impaled with sharp glass electrodes, prepared with a Flaming-Brown P-97 Puller (Sutter Instruments) and filled with 0.6 M K₂SO₄ + 20 mM KCl solution (15–30 MΩ electrode resistance). All electrophysiological data were digitized at 5–10 KHz with a Digidata 1440 A data acquisition board (Molecular Devices).

2.2 Measuring electrical coupling resonance and membrane potential resonance

We measured the membrane potential and electrical coupling resonance in pairs of PD neurons, in both current clamp experiments and voltage clamp experiments, with dual two-electrode recordings. In all experiments, we recorded the voltage in both the pre- and the postjunctional neurons (V_pre and V_post) and the current injected into them (I_pre and I_post). In current clamp experiments, a ZAP (Impedance Amplitude Profile) current was injected into the prejunctional neuron and produced oscillation in both V_pre and V_post. The ZAP function was given by

$\begin{array}{l}{I}_{ZAP}=I_{\max }\cos \left(2\pi f\left(t\right)\right)\\ f\left(t\right)=\frac{f_{\mathrm{lo}}}{L}\left(e^{Lt}-1\right)\\ L=\frac{1}{t_{\max }}\log \left(\frac{f_{\mathrm{hi}}}{f_{\mathrm{lo}}}\right)\end{array}$

where f(t) swept a range of frequencies as a function of time, t, from f_lo = 0.1 Hz to f_hi = 4 Hz. I_max = 3 nA and produced a V_pre roughly ranging from −60 mV to −30 mV. t_max is the total duration of the ZAP waveform which, in most trials was at least 100 s. Additionally, to avoid transients, we always started the ZAP function with 2 pre-cycles of a sinusoidal current applied at the lowest frequency (f_lo = 0.1 Hz) that smoothly transitioned into the ZAP waveform. When measuring in voltage clamp, the same ZAP function was applied to the prejunctional voltage V_pre to force it to alternate between −60 and −30 mV, while the postjunctional neuron was held at a constant voltage of V_post = −60 mV. The prejunctional impedance (Z_pre), the postjunctional impedance (Z_post), the coupling coefficient (CC) and the coupling conductance (G_c) were calculated as shown in Table 1.

TABLE 1

TABLE 1. List of notations. All symbols in the table are functions of the input frequency f. The symbol $\widehat{X}$ refers to the Fourier transform of X. In this manuscript we use the symbols below to denote the norm (|·|) of the complex values obtained by the Fourier transforms.

All factors measured as a function of frequency, in current or voltage clamp, were fit with a sixth-degree polynomial in MATLAB (The MathWorks Inc.) and the resonance frequency and amplitude were estimated as the peak amplitude of the fit curve and the frequency at which the maximum amplitude was achieved.

All experimental measurements involving electrical coupling were done in the presence of 100 nM tetrodotoxin citrate (TTX; Biotium) saline to block action potentials as well as the descending neuromodulatory inputs, and 5 µM picrotoxin (PTX; Sigma) to block chemical synapses within the STG, all of which are inhibitory.

2.3 Data and statistical analysis

All experimental data analysis was done using scripts written in MATLAB, and statistical comparisons were done in SigmaPlot 12 (SyStat Software Inc.). Critical significance level was set to α = 0.05. Unless otherwise indicated, all error bars in the figures represent standard error of the mean.

2.4 Model of coupled resonant neurons

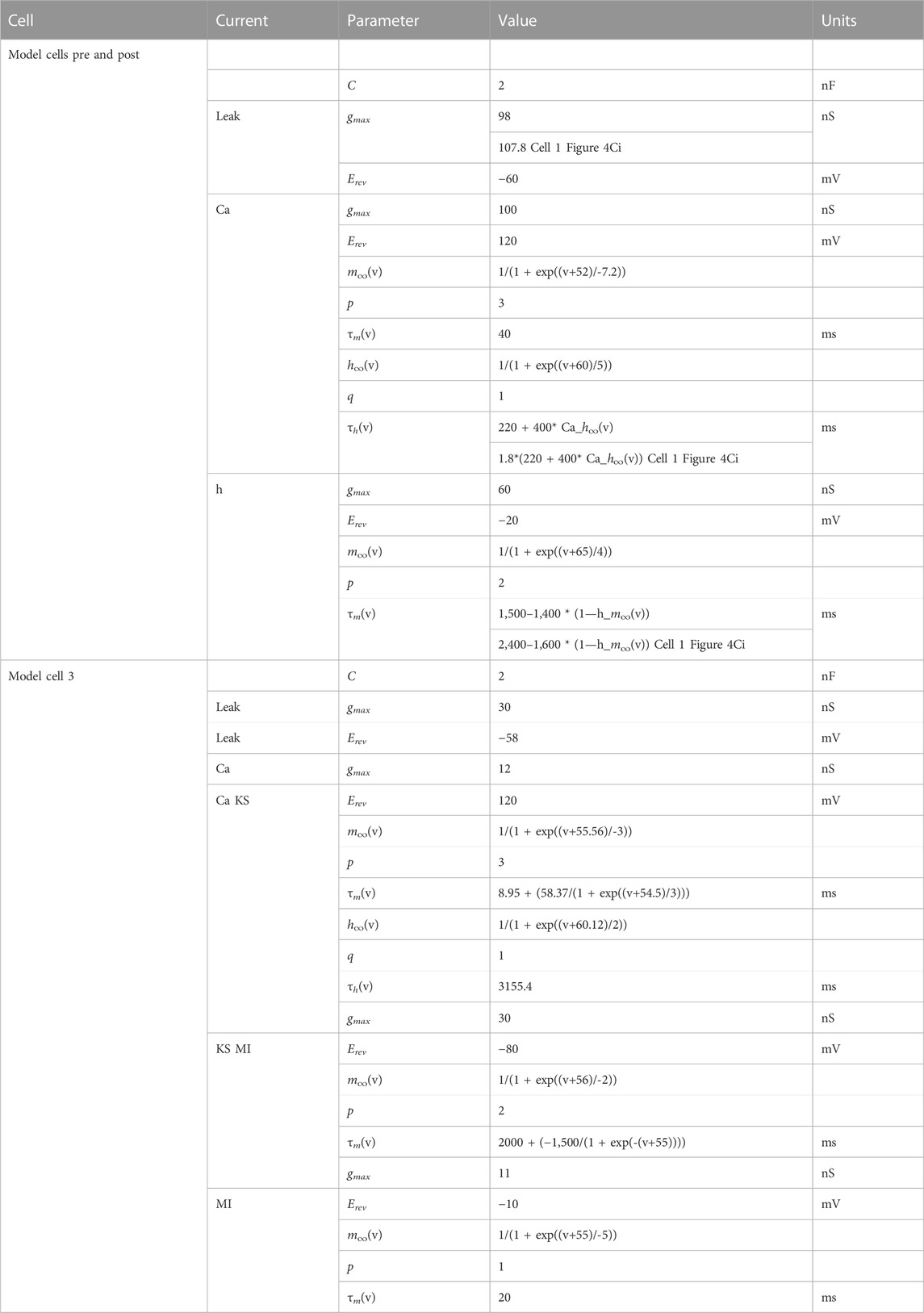
We made biophysical models of coupled resonant neurons of Figures 4A, 5, using single compartment neurons having the Hodgkin-Huxley type currents given in Table 2. The model structure and parameters for the model neurons were implemented from the PD neuron resonance properties as previously described (Fox et al., 2017). Simulations were performed in NEURON 8.0 through the Python 3.8 interface. Analyses were conducted through custom Python scripts using scipy 1.5 and numpy 1.19 packages. All simulations for this study are available on https://github.com/fnadim/ECouplingResonance.

TABLE 2

TABLE 2. Parameters of the coupled resonant neurons.

2.5 Ball-and-stick model

The ball-and-stick model neurons were built using a point neuron, modeled as a sphere of diameter 100 μm, coupled to a single neurite of length 1,000 μm, divided into 101 compartments. Two forms of the neurite were used, as described in the Results. One was a standard cylinder of diameter 10 µm. The other was a tapered cylinder with diameter tapering (proximally-to-distally) linearly from 20 to 0.5 µm. The parameters used to build the model were R_m = 10000 Ωcm², R_a = 100 Ωcm, Cm = 1 μF/cm². For adding resonance, all compartments were modeled according to the parameters given in Table 2. Simulations were preformed in NEURON as described above.

2.6 Model of coupled bursting neurons

The model consisted of two neurons coupled with symmetric electrical coupling. Each neuron was built as a two-compartment biophysical model, consisting of a soma/neurite (SN) and an axon (A) compartment. The soma/neurite compartment included a leak and a low-threshold (T-type) inactivating calcium current, which effectively made it a calcium spike oscillator (Torben-Nielsen et al., 2012). The axon compartment included Hodgkin-Huxley type leak, fast sodium and delayed rectifier potassium currents, which allowed it to spike but only when the input from the soma/neurite compartment produced a calcium spike. The combination produced a bursting neuron. The neuron obeyed the following standard Hodgkin-Huxley type current balance equations:

$\begin{array}{l}{C}_{SN}\frac{d{V}_{SN}}{dt}=I_{L-SN}+I_{Ca}+I_{axial}+I_c\\ C_A\frac{d{V}_{SN}}{dt}=I_{L-A}+I_{Na}+I_K-I_{axial}\end{array}$

where C_x and $I_{L-x}=g_{L-x}\left(V-E_{L-x}\right)$ denote the membrane capacitance and leak current of the compartments (x = SN or A), $I_{axial}=g_{axial}\left(V_{SN}-V_A\right)$ is the axial current between the two compartments. The electrical coupling current is $I_c=G_c\left(V_{SN}-V_{SN2}\right)$, where V_SN2 is the voltage of the other neuron’s SN compartment and G_c is the coupling conductance, which may be frequency-dependent (see below). The ionic currents are given as

$I_{ion}={\overline{g}}_{ion}{m}_{ion}^p{h}_{ion}^q\left(V-E_{ion}\right)$

where ion = Ca, Na or K, ${\overline{g}}_{ion}$ is the maximal conductance, and m_ion and h_ion denote the activation and inactivation gating variables governed by

$\frac{dx}{dt}=\frac{1}{{\tau }_x}\left[x_{\infty }\left(V\right)-x\right]$

(x = m_ion or h_ion). The activation and inactivation powers, p and q, are non-zero integers. The model equations and parameters are provided in Table 3. The parameters of the two neurons were chosen so that, in isolation, their bursting frequencies differed by about 10%.

TABLE 3

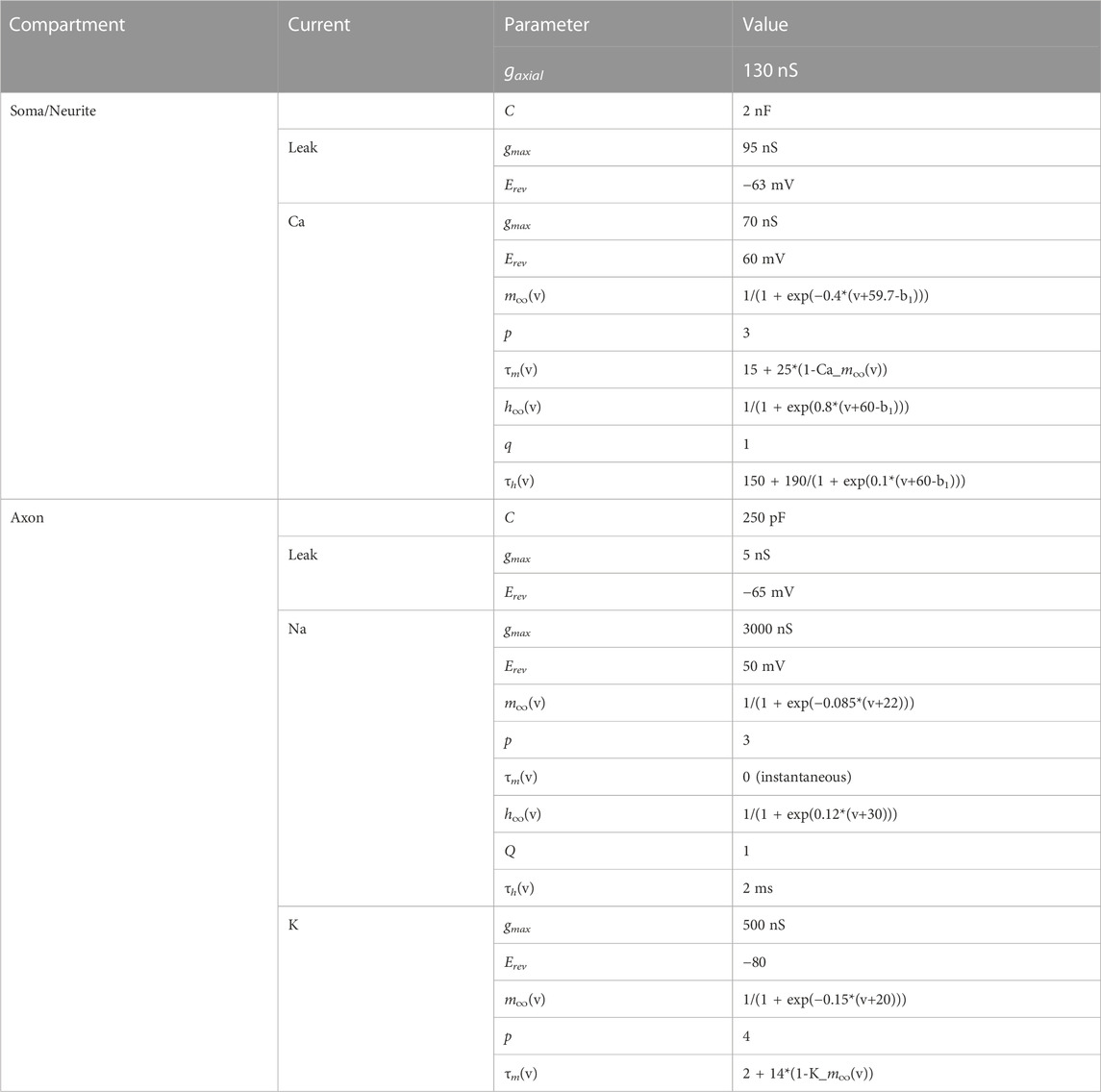
TABLE 3. Parameters of the coupled bursting neurons. a₁, b₁ and c₁ are scaling parameters. For cell 1, a₁ = 0, b₁ = 0, c₁ = 1; for cell 2, a₁ = 0.412241, b₁ = −0.0282679, c₁ = 1.125. All capacitances in pF, conductances in nS, time constants in ms.

The G_c frequency dependence was modeled to show resonance at f = 0.75 Hz according to the following equation:

$G_c=2.625{\overline{G}}_c\left[e^{-0.1f}-e^{-5f}\right]$

where 2.625 is a scaling factor so that $G_c={\overline{G}}_c$ at the resonance frequency.

Simulations were done in C, using a 4th order Runge-Kutta numerical integrator. The two cells always started with identical initial conditions and each run was 25 s. A 15 s window, ending 1 s before the simulation end (to remove filtering artifacts), was used for measurements of synchrony. The two voltage waveforms were sampled at 1 KHz The Slow waveform was obtained by low-pass filtering the waveforms with a moving average window of length 81 ms. The Fast waveform was obtained as the difference between the Full waveform and the Slow waveform. The level of synchrony was measured as, R², the square of the correlation coefficient between the (Full, Slow or Fast) waveforms of the two cells in this time window. All analysis was done in MATLAB.

3 Results

3.1 The coupling coefficient between the PD neurons exhibits resonance at a distinct frequency from their membrane potential resonance

The two PD neurons are very similar in their ionic current expression and anatomical structure and therefore considered to be functionally equivalent, if not identical (Marder and Eisen, 1984; Bucher et al., 2005; Schulz et al., 2006). During normal pyloric activity, these two neurons exhibit synchronous slow-wave oscillations that support their bursting activity (Figure 1A). This synchronous activity arises primarily from their electrical coupling to one another and to the pyloric pacemaker, the anterior burster (AB) neuron (Marder and Eisen, 1984). The electrical coupling strength between the two PD neurons can be determined in the classical way as the coupling coefficient (CC), measured as the ratio of the voltage change of the postjunctional neuron to that of the prejunctional neuron (Figure 1B):

$CC=\frac{\Delta V_{post}}{\Delta V_{pre}}.$

FIGURE 1

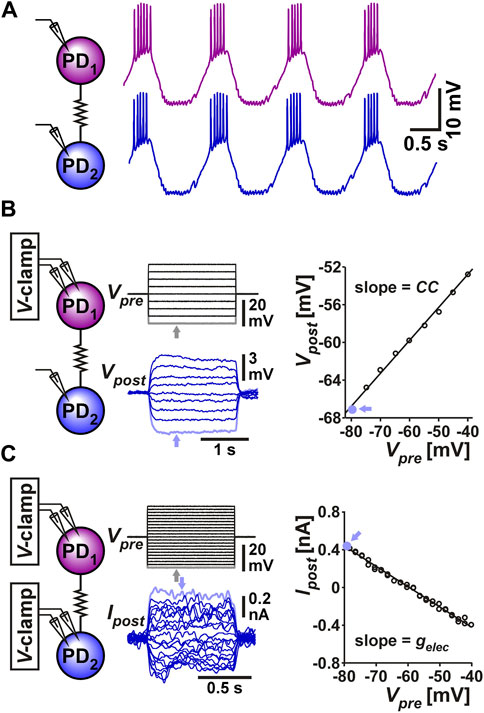
FIGURE 1. The two PD neurons produce synchronized slow wave bursting due to their strong electrical coupling. (A) Somatic recording of the two PD neurons shows that they produce bursting oscillations that are synchronized in their slow-wave activity. (B) Measurement of coupling coefficient between the two PD neurons. The prejunctional PD₁ neuron is voltage clamped with steps ranging from −80 to −40 mV from a holding potential of −60 mV. The postjunctional PD₂ neuron membrane potential is recorded in current clamp. The coupling coefficient CC is measured as the slope of the linear fit to the values of V_post plotted vs. V_pre. Each data point is the mean value of voltage during the step, as seen in the grey point, corresponding to the lowest steps (arrows). (C) Measurement of coupling conductance between the two PD neurons. The prejunctional PD₁ neuron is voltage clamped as in panel B, while the postjunctional PD₂ neuron is voltage clamped at a steady holding potential of −60 mV (not shown). The coupling conductance G_c is measured as the slope of the linear fit to the values of I_post plotted vs. V_pre. Each data point is the mean value the step, as seen in the grey point, corresponding to the lowest V_pre and highest I_post steps (arrows).

A more direct measure of the strength of coupling, which does not depend on the input resistance of the postjunctional neuron can be obtained by voltage clamping both neurons, stepping the voltages of the (arbitrarily-designated) prejunctional neuron and measuring the current flow to the postjunctional cell. The coupling conductance (G_c) can be measured as (Figure 1C):

$G_c=\frac{\Delta I_{post}}{\Delta V_{pre}}.$

The PD neurons are bursting oscillators and, additionally, these neurons show membrane potential resonance at a frequency correlated with their burst frequency (Tohidi and Nadim, 2009; Tseng and Nadim, 2010; Fox et al., 2017). We were interested in knowing whether the coupling strength between the two PD neurons (the PD-PD coupling) depends on, or is influenced by, their oscillation frequency and, if so, if the coupling also shows resonance. In the context of this manuscript, resonance is defined as a neuronal property that produces a maximum response to oscillatory input at a non-zero frequency. To compare any frequency dependence of the electrical coupling and that of the individual neurons, it was necessary to measure these two factors simultaneously. To do so, we arbitrarily designated the two PD neuron as pre- and postjunctional, injected a sweeping-frequency sinusoidal (ZAP) current into the prejunctional PD neuron and measured the voltage responses in both pre-and postjunctional PDs (Figure 2A). We then switched the pre and post designations and repeated the protocol. In the trials shown here, the ZAP function frequency is swept from 0.1 to 4 Hz, a range that covers the natural burst frequency of PD neurons which is typically between 0.5 and 2.5 Hz. In several trials we also changed the direction of the frequency sweep to go from high to low frequency. There was no difference in our measurements when the direction of the sweeping frequency of the ZAP current was reversed.

FIGURE 2

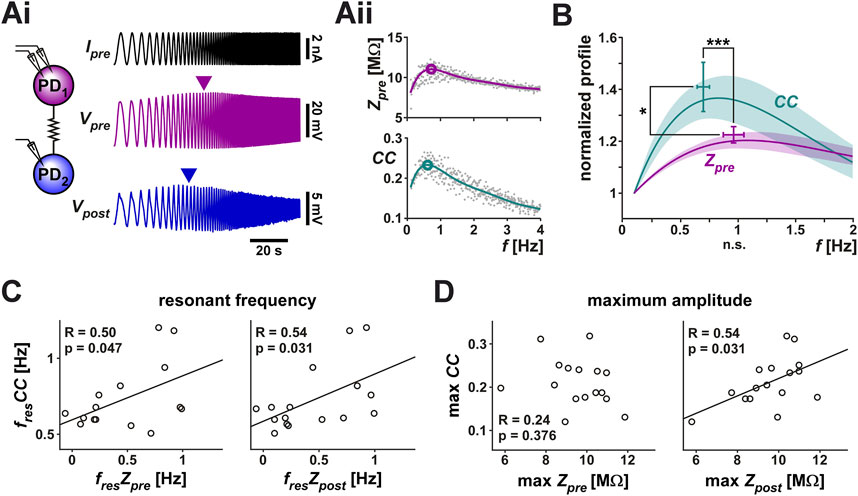
FIGURE 2. The coupling coefficient (CC) between the two PD neurons shows resonance. A ZAP current, sweeping a frequency range of 0.1–4 Hz, was applied to one PD neuron to simultaneously measure the voltage changes in both PD neurons. (Ai) Both neurons showed a peak amplitude response at an intermediate frequency (marked by arrowheads). Schematic shows the two coupled neurons monitored in current clamp. (Aii) The prejunctional impedance (Z_pre) and CC of the data shown in Ai. A 6th order polynomial fit (smooth curves) to the raw data was used to measure the peak amplitude and resonance frequency (circled). (B) Z_pre and CC have distinct resonances. Averaged frequency profiles of CC and Z_pre are shown, both normalized to their amplitude at 0.1 Hz. CC had a smaller resonance frequency than Z_pre (p < 0.001) and higher resonance power (p = 0.037). N = 19, paired Student’s t-test. (C, D) The resonance frequency of CC was correlated with the resonance frequency of both Z_pre and Z_post (C), while its maximum amplitude was only correlated with that of Z_post (D).

In 19 out of 28 measurements, both the prejunctional membrane impedance (Z_pre; Table 1) and the coupling coefficient (CC) showed clear resonance (Figure 2B). Note that the peak values shown in the figure do not exactly match the peak of the mean profile (solid line) since the peak of the average of multiple non-linear curves is determined by the overall shapes of the individual curves, not just by their peaks. In response to the ZAP current, however, Z_pre and CC showed distinct frequency profiles (Figure 2B): CC had a lower resonance frequency (0.70 ± 0.20 Hz) than Z_pre (0.97 ± 0.36 Hz) and the normalized peak amplitude of CC was larger than that of Z_pre. Additionally, the resonance frequency of CC was correlated with the resonance frequency of both the prejunctional and postjunctional impedance (Z_pre and Z_post, Figure 2C), while its maximum amplitude was only correlated with that of Z_post (Figure 2D).

3.2 Electrical coupling conductance shows a preferred frequency (resonance)

Membrane potential resonance can be measured using both current clamp and voltage clamp methods, each providing its own advantage. Current clamp measurements allow the membrane potential to change freely and therefore, voltage-dependent ionic currents can also influence the membrane potential. This method allows one to observe neuronal responses in a manner closer to their natural biological activity and, in general, current clamp measurements provide a more realistic value of the impedance amplitude (Rotstein and Nadim, 2019). However, because the electrical coupling coefficient is influenced by the input resistance of the postjunctional neuron, it is not a direct measure of the strength of electrical coupling (Bennett, 1966; Mann-Metzer and Yarom, 1999). A direct estimate of the electrical coupling conductance, G_c, requires measuring the current flowing between the two coupled neurons (Table 1) and, to obtain an accurate measurement of the ionic current, the membrane potentials must be constrained using the voltage clamp method, as we showed in Figure 1C.

To directly measure whether the coupling conductance G_c is influenced by frequency, we voltage clamped both PD neurons at a holding potential of −60 mV. We then applied a ZAP function voltage waveform (ranging from −60 to −30 mV) to the prejunctional neuron, while holding the postjunctional neuron at a steady voltage of −60 mV (Figure 3Ai). This allowed us to simultaneously measure the currents flowing in the pre- and postjunctional neurons (I_pre and I_post) in response to the change in the frequency of V_pre. As seen in the example in the figure, I_pre showed a clear minimum in response to the voltage ZAP, indicating a minimum in the neuronal admittance (the reciprocal of impedance) value. This simply reflects the membrane potential resonance in the prejunctional PD neuron as measured in voltage clamp (Tseng and Nadim, 2010) (Figure 3Aii, top panel). Interestingly, in response to the prejunctional ZAP function, the postjunctional current, I_post, did not remain constant in amplitude but had a clear maximum amplitude at a non-zero frequency. Therefore, the PD-PD coupling conductance, G_c, also showed a peak at this frequency (Figure 3Aii, bottom panel).

FIGURE 3

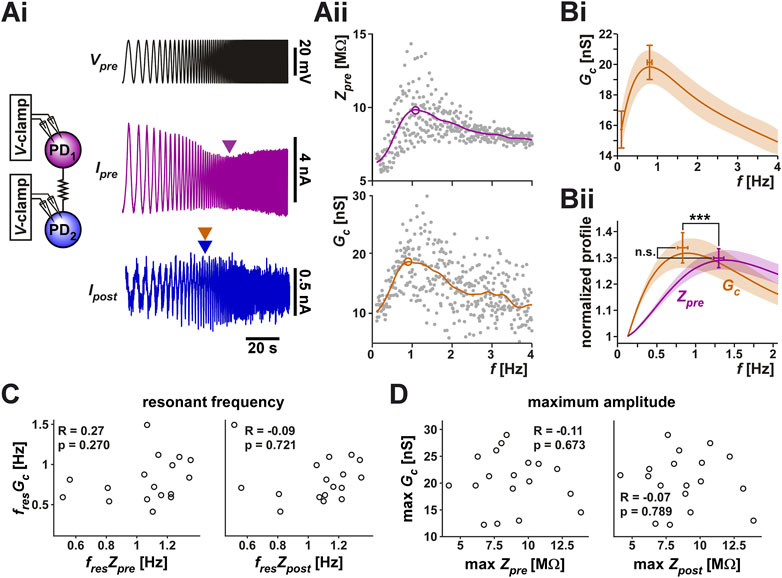
FIGURE 3. The coupling conductance shows a frequency-dependent resonance which is distinct from the resonance of the coupled PD neurons. (Ai) The two PD neurons were voltage clamped, the prejunctional neuron with a ZAP waveform, sweeping a frequency range of 0.1–4 Hz and a voltage range of −60 to −30 mV, while the postjunctional neuron was held at constant holding potential of −60 mV (not shown), and the current flow in both neurons was measured. I_pre showed a minimum value at an intermediate frequency, reflecting the intrinsic resonance of the prejunctional neuron (magenta arrowhead), while I_post showed a peak at a distinct frequency (blue/bronze arrowheads). Schematic represents the two coupled neurons in voltage clamp. (Aii) The prejunctional impedance (Z_pre) and G_c measured from the data shown in Ai. A 6th order polynomial fit (smooth curves) to the raw data was used to measure the peak amplitude and resonance frequency (circled). The peak of G_c corresponds to the bronze color arrowhead in (Ai). (Bi) The frequency profile of G_c across experiments shows a peak below 1 Hz. (Bii) Z_pre and G_c have distinct resonances. Averaged frequency profiles of G_c and Z_pre are shown, both normalized to their amplitude at 0.1 Hz. G_c had a smaller resonance frequency than Z_pre (p < 0.001) but comparable resonance power Z_PD (p = 0.525). N = 20, paired Student’s t-test. (C, D) Neither the resonance frequency (C), nor the resonance amplitude (D) of G_c was correlated with that of Z_pre or Z_post.

Unlike the measurements with the step protocol, in which the directionality of the electrical coupling had little influence, we found that the two directions of the coupling often produced slightly different results. Therefore, in this part of the study, we treated the PD1 to PD2 and the PD2 to PD1 in each preparation independently. In 20 of the 28 measured cases, G_c showed resonance. Figure 3Bi shows the averaged resonance profile of these 20 electrical connections.

Because Z_pre and G_c have different units, their amplitudes cannot be directly compared. Yet it is useful to examine how much larger each of these factors is at its peak compared to its baseline. In fact, membrane potential resonance power is often measured as a ratio of the peak impedance Z_max to the impedance at zero frequency (i.e., the input resistance). We used the values of Z_pre and G_c at the lowest frequency (0.1 Hz) as a proxy for the zero-frequency values and normalized these curves to this value for each experiment (Figure 3Bii). A paired comparison between G_c and the impedance profile (Z_pre; see Table 1) of the prejunctional neuron showed no difference in their relative amplitudes. However, G_c had a significantly lower resonance frequency (0.80 ± 0.26 Hz) than Z_pre (1.27 ± 0.23 Hz). Also, note that the resonance frequencies for Z_pre were different between current clamp and voltage clamp experiments, because, as described above, Z_pre measured in current clamp is influenced by non-linear actions of voltage-gated ionic currents. Finally, unlike with the coupling coefficient CC, we did not observe any correlation between Z_pre or Z_post and G_c either in frequency (Figure 3C) or in amplitude (Figure 3D). This is consistent with the hypothesis that G_c reflects the properties of the electrical coupling and not those of the coupled neurons.

3.3 Modeling elucidates how resonance of the coupling coefficient CC arises

Frequency dependence of electrical coupling may emerge from the properties of the coupled neurons, may be a property of the junctional coupling itself, or arise from the interaction of the two. To demonstrate how resonance of the coupling coefficient CC could arise from the membrane potential resonance properties of the coupled neurons, we coupled two biophysical models that capture the resonance properties of the isolated PD neuron (Fox et al., 2017) with a constant electrical coupling coefficient (parameters for the model given in Table 2). We injected a ZAP current into one neuron and measured the voltage responses of both neurons (Figure 4Ai). Current injection to PD model neuron 1 resulted in membrane potential resonance, mainly due to the intrinsic properties of this neuron, and current flow through the electrical coupling to PD model neuron 2 produces membrane potential resonance in the second neuron. In this simulation, the two PD model neurons were identical and therefore, when isolated, had identical impedance profiles (Z₁ = Z₂ in Figure 4Aii). Coupling only slightly changed the impedance profile of either neuron compared to its profile when isolated (Z_pre compared to Z₁; Z_post compared to Z_2; see Table 1 for notations). In this simulation, the CC vs. frequency curve also showed resonance, with a resonance peak frequency at a value close to, but different from, that of the coupled neurons. This gave rise to the question what factors determine the resonance frequency of CC.

FIGURE 4

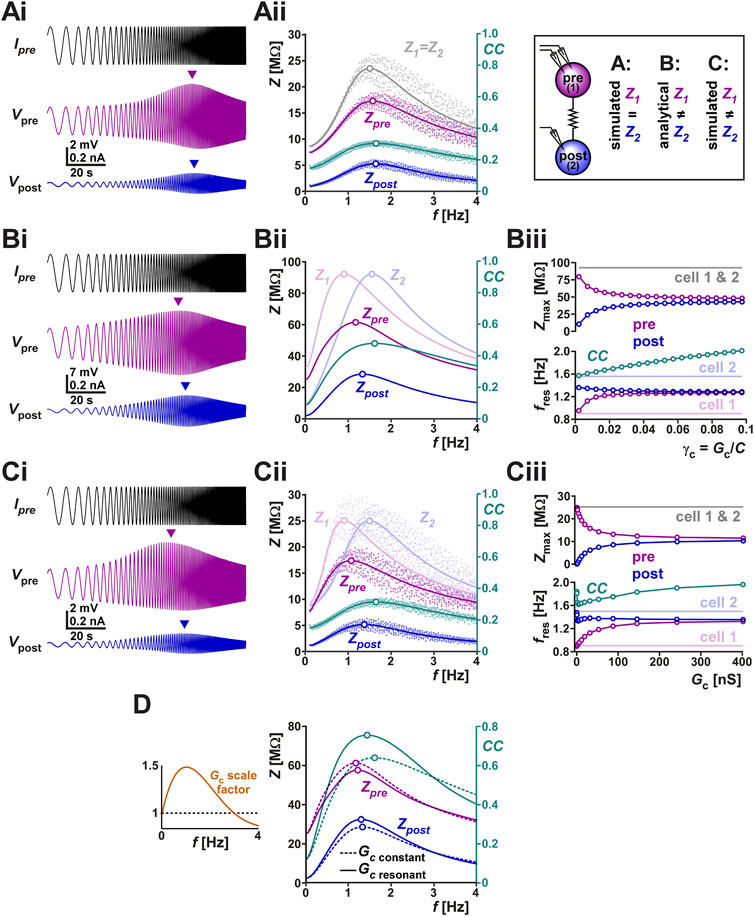
FIGURE 4. (A) The right panel schematically shows the protocols of this figure, in which we examine the current-clamp responses of two coupled identical biophysical model neurons (A), two coupled linear resonators with distinct resonance frequencies measured analytically (B) and two coupled biophysical model neurons with distinct resonance frequencies (C). (Ai) Two identical biophysical model neurons (parameters in Table 2) were coupled (G_c = 20 nS) and a ZAP current sweeping frequencies of 0.1–4 Hz was injected in both neurons to measure the changes in their membrane potentials. Arrows in Ai show the peak (resonance) values in membrane potential amplitudes. (Aii) Membrane impedance amplitudes of the pre- and postjunctional model neurons (Z_pre and Z_post, respectively) of panel (Ai) shown in raw form (dots) and with a non-linear curve fit (solid curves). The impedance profile of the isolated identical pre- and post-junctional cells (1 and 2) are also shown in gray. The coupling coefficient (CC) shows a resonance frequency at a value close to those of Z_pre and Z_post. The peak (resonance) frequencies are shown as open circles. (Bi) Simulation of a ZAP current injected in one of two coupled linear resonators, shown for comparison with the biophysical simulations. (Bii) Analytical calculations (see Supplementary Appendix SA1) show that coupling two linear resonators with distinct resonance frequencies (shown in Bi) brings the resonance peaks (open circles) closer to each other. Z_pre and Z_post show the impedance amplitude profiles of the coupled neurons whose isolated impedance profiles are shown in Z₁ and Z₂. In contrast, resonance frequency of CC does not fall between those of Z₁ and Z₂. (Biii) Bottom panel shows the resonance frequencies (f values of open circles in Bi) as a function of increasing coupling conductance γ_c (=G_c/C; C is the membrane capacitance). Top panel shows the resonance amplitudes (Z values of open circles in Bii). (C) Panels (Ci–Ciii) show simulations of two coupled biophysical neurons [as in (A)], confirming the findings of the analytical model (panel B). Panel descriptions are the same as in (B). Cell 1 was made to have a different resonance frequency by adjusting the parameters as indicated in Table 2. Cell 2 is identical to that of panel (A). (D) The linear model is used to compare the effect of G_c resonance on the coupling coefficient CC. The left panel shows the two cases compared. In one (scale factor of 1), G_c is kept constant whereas in the other G_c is scaled by an inverted U function, mimicking the resonance measured experimentally in Figure 3 B. The right panel compares Z_pre, Z_post and CC for the two cases, using the linear models of panel (B). Note the amplification of CC and the shift in its resonance frequency when G_c shows resonance.

To address this question, we switched to linear resonator neurons in which the impedance profile can be mathematically calculated (Richardson et al., 2003; Rotstein and Nadim, 2014). The full analysis is provided in Supplementary Appendix SA1. In the linear system of two coupled resonator neurons, the value of the coupled impedance profiles, as a function of the respective uncoupled profiles is given by

$\begin{array}{l}{\mathbf{Z}}_{pre}=\frac{{{\mathbf{Z}}_{\mathbf{2}}}^{-1}+G_c}{\left({{\mathbf{Z}}_{\mathbf{1}}}^{-1}+G_c\right)\left({{\mathbf{Z}}_{\mathbf{2}}}^{-1}+G_c\right)-G_c^2}\\ {\mathbf{Z}}_{post}=\frac{G_c}{\left({{\mathbf{Z}}_{\mathbf{1}}}^{-1}+G_c\right)\left({{\mathbf{Z}}_{\mathbf{2}}}^{-1}+G_c\right)-G_c^2}.\end{array}$

(Supplementary Equation SA1.8 of the Appendix with notations of Table 1) and the value of CC reduces to the ratio of the amplitudes of the two impedance profiles.

$CC=\frac{Z_{post}}{Z_{pre}}=\frac{G_c}{‖{{\mathbf{Z}}_{\mathbf{2}}}^{-1}+G_c‖}.$(1.1)

Here, Z₂ is the complex impedance profile of the postjunctional neuron when isolated (Z₂ is the amplitude of the complex Z₂, i.e., Z₂ = ||Z₂||). Note that for linear resonator neurons, CC only depends on the impedance of the (isolated) postjunctional neuron and not on that of the prejunctional neuron. Although this result does not generally hold for non-linear (e.g., biological) resonators, it still provides a very good approximation in most cases, in addition to a clearer conceptual understanding of the phenomenon.

The coupled linear resonators provide insight into how electrical coupling influences the resonance properties of the neurons as well as that of CC. For instance, the simulation of two electrically coupled linear resonators (as described in Supplementary Appendix SA1) and injected with a ZAP current shows distinct peak amplitudes in the pre- and post-junctional neuron’s membrane potentials (Figure 4Bi). In fact, coupling two linear resonators with the same maximal amplitude, but distinct resonance frequencies, shifted the resonance frequencies of both neurons toward values in between those of the isolated neurons (Figure 4Bii; compare peak frequencies of Z_pre and Z_post with Z₁ and Z₂). The resonance frequency Z_post fell between Z_pre and Z₂. The postjunctional impedance profile (Z_post: which is V_post/I_pre in Figure 4Ai; see Table 1 for definition) always had a lower amplitude than the prejunctional profile (compare Z_pre and Z_post in Figure 4Bii). In Figure 4Bii, we also show the frequency-dependent profile of CC for comparison (note the different scales). Here, the resonance frequency of CC was close to that of Z₂.

Interestingly, however, the resonance frequency of CC was not constrained to fall between the resonance frequencies of Z₁ and Z₂. This can be readily observed using the linear resonator models when current was injected in the cell with lower resonance frequency (cell 1 in Figure 4Bii) and the electrical coupling conductance was increased. When the electrical coupling conductance was small, the resonance frequency of CC was close to that of Z₂, but when G_c was increased, this frequency also increased monotonically (Figure 4Biii bottom panel). Not surprisingly, increasing the strength of coupling also caused the resonance frequencies (Figure 4Biii bottom panel) and maximum pre- and postjunctional impedance values (Figure 4Biii top panel) to converge to the same value. These predictions of the analytical linear models can be confirmed by simulating a biophysical model of two coupled resonator neurons. Figure 4Ci shows such a simulation, which is based on the same neurons as in panel Ai, except that the prejunctional neuron’s parameters have been changed to allow for a lower resonance frequency while keeping the same resonance amplitude. The findings for Z_pre, Z_post and CC (Figure 4Cii) are qualitatively similar to those of the linear model, as is the dependence of the resonance frequencies and peak resonance values of these attributes as a function of G_c (Figure 4Ciii). The only small difference between the biophysical and linear models arises at very small G_c values, where, in the biophysical model (Figure 4Ciii), Z_post and CC show a non-monotonic dependence on G_c.

One can also use the coupled linear resonators to predict how a frequency-dependent G_c influences the measured coupling coefficient. To make this comparison, we scaled G_c as a function of frequency in a manner similar to what we had measured in the biological system (Figure 3Bii and left panel of Figure 4D). A comparison of the resulting CC and the CC obtained with a constant G_c value across frequencies showed that the resonance frequency of G_c can clearly amplify the amplitude of CC, by bringing the Z_pre and Z_post curves closer to each other in this range (Figure 4D right panel).

3.4 Can coupling conductance resonance result from network connectivity?

When both neurons are voltage-clamped, the prejunctional neuron with a fixed-amplitude sinusoidal waveform and the postjunctional neuron at a constant holding voltage (Figure 5Ai), the amplitude of the ionic current change recorded in the postjunctional neuron (I_post, which is also the coupling current I_c) is proportional to the coupling conductance G_c and independent of any resonant properties of either neuron. This follows from the fact that

$I_{post}=I_c=G_c\left(V_{pre}-V_{post}\right)$

where V_pre and V_post are controlled by voltage clamp and G_c is constant. Although this is an obvious result, it is informative. We demonstrated this in the simulation shown in Figure 5Aii, where the prejunctional model neuron was voltage-clamped with a ZAP function (range −60 to −45 mV) and the prejunctional neuron was held at a steady voltage of −60 mV (parameters for the model given in Table 2). The current (I_pre) in the prejunctional neuron showed a minimum, while the current flowing to the postjunctional neuron (I_post) did not change with the frequency of the ZAP function (Figure 5Aiii). This is also clear from our calculations for the coupled linear resonators in voltage clamp as shown in Supplementary Appendix SA1 (Supplementary Equation SA1.11).

FIGURE 5

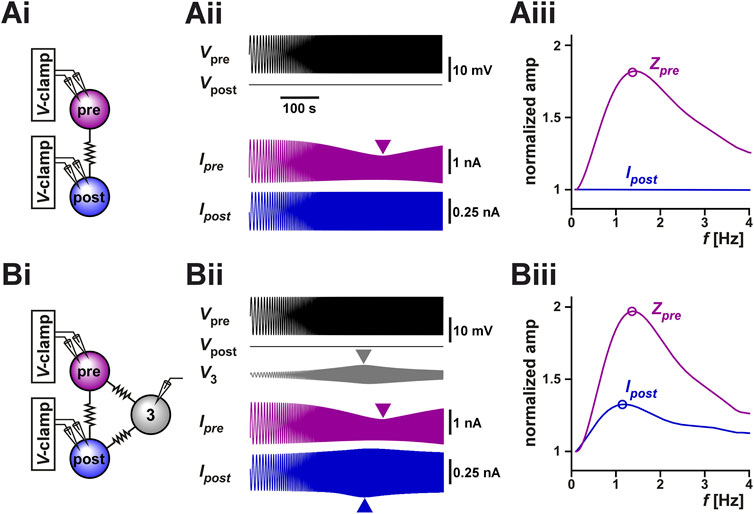
FIGURE 5. Coupling to a third resonant neuron can produce resonance in the coupling current between two voltage-clamped neurons. (A) The coupling current between two identical model neurons with resonant properties was measured in voltage clamp [schematic in (Ai)]. The prejunctional neuron was voltage clamped with a ZAP waveform spanning from 0.1 Hz to 4 Hz and voltage range of −60 to −45 mV. The postjunctional neuron was voltage clamped at a holding potential of −60 mV. The postjunctional current amplitude showed no frequency dependence (Aii). As a function of input frequency, the prejunctional impedance shows resonance, but the post junctional current remains constant. For comparison, Z_pre and I_post are normalized to their value at 0.1 Hz. (B) The same protocol as A, but the two neurons are both coupled to a third (identical) neuron which is not voltage clamped [schematic in (Bi)]. The addition of the third cell leads to a frequency-dependent response in the voltage of the third neuron (Bii) and in resonance in the postjunctional current (Biii). For comparison, Z_pre and I_post are normalized to their value at 0.1 Hz.

However, when these two neurons are part of a circuit of electrically coupled neurons, even when both neurons are voltage-clamped, the measurement of I_post may not have a constant amplitude at all input frequencies due to circuit connectivity. For example, if both neurons are electrically coupled to a third neuron whose voltage can vary freely, indirect current flow through the third neuron may affect the amplitude of I_post. Indeed, in the pyloric circuit, the two biological PD neurons are electrically coupled to the anterior burster (AB) neuron (Marder and Eisen, 1984) and, in our experiments described above, we did not control or monitor the activity of the AB neuron. It is therefore possible that the apparent resonance we observed in our experimental measurement of I_post (Figure 3Ai) was due to the uncontrolled changes in the voltage of the AB neuron. To test this possibility, we coupled the model neurons of Figure 5Ai to a third neuron with the same resonance properties and ran the same voltage clamp protocol (parameters given in Table 2). Indeed, we observed that even though the pre- and postjunctional neurons were voltage-clamped, the voltage of the third coupled neuron (marked 3 in Figures 5Bi,5Bii) showed a peak at an intermediate frequency. Thus, the resonance of neuron 3 resulted in an apparent resonance in our measured I_post, because in this case

$I_{post}=G_c\left(V_{post}-V_{pre}\right)+G_c\left(V_{post}-V_3\right).$

A normalized comparison between the impedance profile V_pre and I_post (Figure 5Biii) shows that even when the three neurons are identical in their properties (and therefore have the same isolated resonance frequency), I_post may show resonance at a different frequency, as we had observed in our experimental measurements of Figure 3. Therefore, a potential mechanism for electrical coupling current resonance is through frequency preference inherited from other electrically coupled cells.

3.5 Space clamp issues

Voltage clamp measurements of distal currents are inevitably subject to space clamp errors (To et al., 2022). Considering that gap junctions are most probably located at a distal location to the soma (Otopalik et al., 2019a), it is likely that our voltage-clamp estimate of G_c, or even our measurement of Gc resonance is affected by space clamp errors. To examine the extent of such an error, we used a multi-compartmental ball-and-stick model of the PD neurons to estimate the effect of coupling distance from the somatic recording site on G_c. Two ball-and-stick models were examined (Figure 6 schematics), one with a standard cylindrical neurite of constant diameter (10 µm), the other with a tapering diameter (20–0.5 µm). As described in a recent detailed study (Otopalik et al., 2019b), the tapered model is a better estimate of the structure of STG neurons.

FIGURE 6

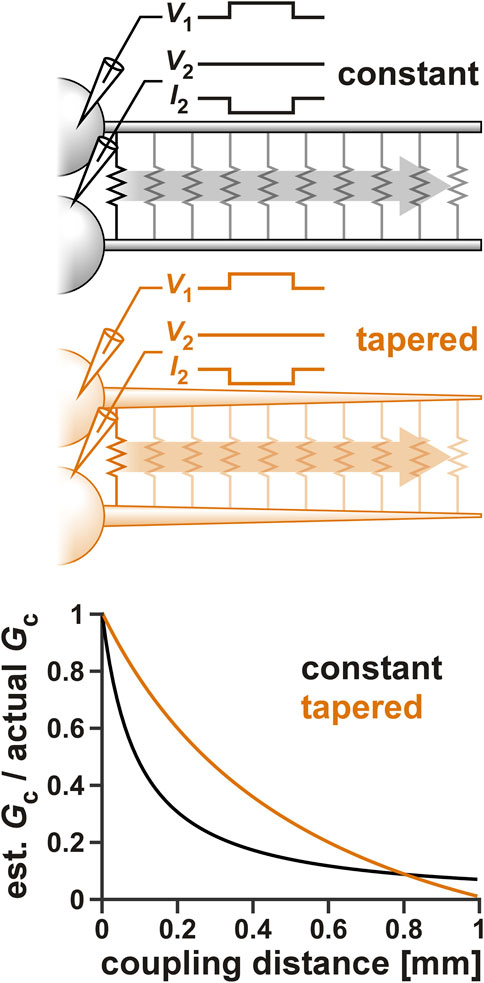
FIGURE 6. The effect of space clamp error on the measurement of G_c. Two ball-and-stick models were examined, one with a standard cylindrical neurite of constant diameter (10 µm), the other with a tapering diameter (20–0.5 µm). Neurite lengths were set to 1,000 µm and the position of the electrical coupling was shifted from the beginning to the end of the neurite, as shown schematically in the top panels. Both somas were voltage clamped and step voltage was applied to one cell. G_c was calculated from the current measured in the second soma. The bottom panel shows the effect of the electrical coupling position on the measurement G_c.

To estimate the effect of coupling position on G_c, the somas of both ball-and-stick model neurons were voltage clamped and a voltage step (from V_hold to V₁) was applied to one (cell 1), while the other (cell 2) was held at a constant voltage (V_hold). G_c was then measured as

$G_c=I_2/\left(V_1-V_{hold}\right).$

When the position of the coupling was changed along the neurite, the estimated G_c attenuated (Figure 6). The extent of attenuation was much less for the tapered neurite compared to the standard one, except at the very tip, where the tapered neurite became very small in diameter. This was consistent with the findings of Otopalik et al. (2019b) in which they estimated attenuation of a chemical synaptic input. However, considering that the two PD neurons have a relatively strong apparent coupling coefficient, we estimate the coupling position to be no further than halfway along the tapered neurite. Additionally, when we added the ionic currents that produce resonance (Table 2) to these neurons, there was little resonance effect measured in G_c (data not shown).

3.6 Potential function of electrical coupling resonance

We used computational modeling to understand the potential function of resonance in the electrical coupling conductance in this system. We used a computational model of two electrically coupled bursting neurons and chose the parameters of the two neurons to produce bursting oscillations with different cycle frequencies when uncoupled. We then coupled the two neurons and examined the synchronization of their activity at different electrical conductance strengths (Figure 7A). The level of synchronization was measured as the coefficient of determination (R²) between the two voltage waveforms (Lane et al., 2016). We measured the synchrony of the full bursting waveforms between the two neurons (full). In addition, we lowpass-filtered the traces to measure the synchrony of only the slow waves (slow), and high pass-filtered to measure the synchrony of only the spiking activity (fast).

FIGURE 7

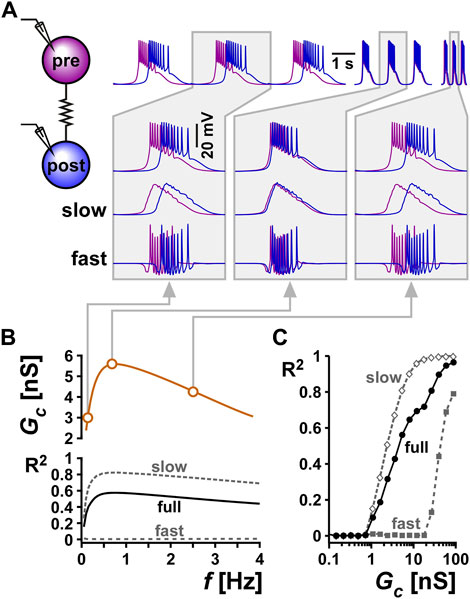
FIGURE 7. Resonance in the coupling conductance influences the level of synchrony between two model bursting neurons. (A) The level of synchrony between two model bursting neurons, coupled with a resonant G_c (schematic), depends on the network oscillation frequency. The three columns show superimposed phase-locked oscillations of two model bursting neurons at three frequencies. The second row is a zoom in to a single burst. The third row shows lowpass filtered traces (slow), highlighting the level of asynchrony of the burst slow waves. The bottom row shows the high pass filtered traces (fast = full - slow), highlighting the lack of synchrony of spiking activity. Gray boxes correspond to frequencies and G_c values as shown in panel (B) (B) Coupling conductance is modeled to show resonance at f = 0.75 Hz. The level of synchrony between the two coupled neurons, measured as a coefficient of determination R² of their voltage waveforms depends on the network frequency. Changing the network frequency increases synchrony of the slow and full waveforms, but not the fast spiking activity. (C) R² increases with the coupling conductance.

To examine the effect of resonance in G_c on the synchrony between the two neurons, we produced a G_c frequency profile similar to that observed experimentally (compare G_c vs. f in Figure 7B with Figure 3Bi). Although the two model neurons had different intrinsic burst frequencies, they always oscillated with the same frequency (i.e., they were phase locked) when coupled. To understand the role of G_c resonance, we changed this burst frequency by modifying the intrinsic properties of the bursting neurons (see Methods). We found that when the two cells oscillated at either low or high frequencies, where the G_c was smaller, the slow wave synchrony between the two neurons was smaller (Figure 7C, Bi, Biii). In contrast, when the network frequency matched the G_c resonance frequency, the level of synchronization was maximal (Figure 7C). In contrast to the slow wave, the fast spiking activity of the two neurons was not noticeably altered by frequency. When G_c was kept constant as a function of frequency, then network frequency did not affect the level of synchrony between the two neurons, either in the slow wave or in the spiking activity. The level of synchrony in this case was determined simply by the value of the electrical coupling conductance G_c.

4 Discussion

Gap junction-mediated electrical coupling between neurons is well known to lead to synchronization of their electrical activity (Gutierrez et al., 2013; Marder et al., 2017; Alcamí and Pereda, 2019; Vaughn and Haas, 2022). However, as a number of modeling studies have shown, in certain conditions it can also promote anti-synchrony (Sherman and Rinzel, 1992; Chow and Kopell, 2000; Bem and Rinzel, 2004). It is commonly assumed that electrical coupling acts primarily as a lowpass filter so that slow voltage changes, such as burst envelopes and subthreshold oscillations, are transmitted more effectively than fast ones such as action potentials (Galaretta and Hestrin, 1998; Connors and Long, 2004; Placantonakis et al., 2006). However, more recent studies that have explored electrical coupling in oscillatory networks have found that the interaction the intrinsic properties of neurons and the electrical coupling could result in a band-pass filtering of the coupling coefficient, such that the coupling coefficient is highest around a “resonance” frequency (Armstrong-Gold and Rieke, 2003; Curti et al., 2012; Stagkourakis et al., 2018). Such bandpass-filtering has been attributed to the properties of voltage-gated ion channels or subthreshold resonance in the coupled neurons (Curti et al., 2012; Alcamí and Pereda, 2019), thus suggesting that the subthreshold resonance frequency can play a significant role in setting the frequency of a network of electrically coupled neurons.

Here, we found similar results in the PD neurons of the crab pyloric circuit. The two PD neurons produce ongoing synchronous bursting activity, are strongly electrically coupled (Figure 1) and show membrane potential resonance (Figure 2; Tohidi and Nadim, 2009). We found that the coupling coefficient of these neurons also shows resonance, but at a much lower frequency than that of their membrane potential resonance (Figure 2). The CC resonance frequency, however, was strongly correlated with both that of the pre- and postjunctional neuron. A combined modeling and mathematical analysis showed that although with increased coupling strength the resonance frequencies measured in the coupled neurons converges to the same value, the CC resonance frequency does not necessarily fall between these two values (Figure 4C). In fact, our mathematical calculations, based on coupled linear resonators, showed that in response to oscillatory input, CC behaves very much like it does in response to a direct current input: It depends on a non-linear combination of the coupling conductance and the impedance of the postjunctional, but not prejunctional, neuron [Eq. 1.1; also see (Alcamí and Pereda, 2019)]. Thus, at least to the first order (linear) approximation, the resonance properties of the prejunctional neuron have no influence on the CC resonance frequency, which can fall well outside the range of resonance frequencies of the neurons. This finding is important in the light of the above-mentioned fact that CC resonance frequency is often considered to be a determinant of the network oscillation frequency (Curti et al., 2012; Stagkourakis et al., 2018).

The second, perhaps more surprising, finding of our study is that when we measured the current flow between the coupled PD neurons in voltage clamp, we found that the measured coupling was both frequency-dependent in its amplitude and had a resonance frequency distinct from the intrinsic resonance of the PD neurons. For direct current flow between voltage-clamped coupled neurons, this finding inevitably leads to the conclusion that the coupling conductance G_c is frequency-dependent. There are some caveats, however, that should be considered when drawing such a conclusion. First, voltage clamp is often subject to lack of space clamp. If gap junctions that lead to electrical coupling are present in a distal location from the voltage-clamped somata, it is possible that space clamp issues may somehow result in the appearance of frequency-dependence in the coupling current. A structured multi-compartmental ball-and-stick model of the coupled neurons showed that changing the position of the electrical coupling away from the soma reduced the apparent amplitude of the measured G_c, but this reduction was only drastic when the coupling position was far from the soma (Figure 6). Additionally, consistent with previous findings showing that the stomatogastric neurons are electrotonically compact (Otopalik et al., 2019b), a tapered neurite showed a much smaller attenuation of the measured G_c. Attenuation was only greater when the coupling position was very distal to the soma, an unlikely possibility considering that the biological PD neurons have a large coupling coefficient. However, with the same model we did not find significant resonance in the measured coupling current, indicating that our measured resonance of G_c is unlikely to be due to a space clamp error. The second caveat in drawing a conclusion that G_c is frequency-dependent is that both PD neurons are strongly coupled to the pyloric pacemaker AB neuron, which was neither voltage-clamped nor photo ablated (Miller and Selverston, 1979) here. In fact, a computational model of the three-neuron coupled circuit showed that a free-running AB neuron may indeed result in an apparent resonance of the coupling current measured between the two PD neurons (Figure 5Biii). Although we did not resolve the caveat of coupling to additional neurons in the current study, our unpublished results indicate that there is a possibility that frequency-dependence may in fact in part be inherent to the electrical coupling conductance. These findings showed that peptide neuromodulators that activate the same ionic current in the pyloric pacemaker neurons have an opposite effect on shifting both the frequency and amplitude of resonance in the coupling current (Li et al., 2017). This result cannot be explained by coupling to a free-running AB neuron which is modulated the same way by the two peptides. Consequently, the gap junction channels may in fact have kinetics that allows for bandpass filtering. Although it is know that current flow through gap junctions may have complex and functional voltage-dependent properties (examples in Coleman et al., 1995; Vaughn and Haas, 2022), to our knowledge, such a frequency-dependent filtering property of gap junctions has not been previously reported.

Previous studies have suggested that different resonant properties of different circuit components collectively influence network frequency (Lovett-Barron et al., 2017). However, it remains to be determined to what extent CC or G_c resonance interacts with other frequency-dependent properties of a network. We showed, however, that resonance in G_c or the coupling current would amplify the resonance properties of CC (Figure 4D). In addition, one functional consequence of the frequency-dependence of the coupling is intuitively clear if the network frequency may be subject to context-dependent changes. We demonstrated this using a coupled network of two intrinsically distinct model neurons. Although at all frequencies tested, the two neurons remained phase locked, their degree of synchronization was effectively determined by the frequency-dependent properties of the coupling conductance (Figure 7). In an oscillatory network such as the crab pyloric network, where network frequency depends on multiple factors including neuromodulation and temperature, it is reasonable to assume that the degree of synchronization between the PD neurons may be influenced indirectly by the factors that modify network frequency. Although the experimental verification of these functional consequences remains to be performed, our combined experimental and modeling findings indicate that the resonance properties of electrical coupling may play a central role in shaping the output of oscillatory networks.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

XL and FN conceived and designed the experiments and analysis. XL, performed all experimental analysis. OI, HR, and FN designed and performed the computational modeling. HR performed all mathematical analysis. XL and FN wrote the manuscript draft. All authors contributed to the conceptual understanding of the findings and edited the manuscript.

Funding

Supported by NIH grant R01-MH060605 (FN and DB), and NSF grants DMS-1608077 (HR) and IOS-2002863 (HR).

Acknowledgments

The authors thank Dr. Jorge Golowasch for his input and comments, and Dr. Alberto Pereda for helpful comments on the original recordings of G_c resonance.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsysb.2023.1122433/full#supplementary-material

References

Alcamí, P., and Pereda, A. E. (2019). Beyond plasticity: The dynamic impact of electrical synapses on neural circuits. Nat. Rev. Neurosci. 20 (5), 253–271. doi:10.1038/s41583-019-0133-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Armstrong-Gold, C. E., and Rieke, F. (2003). Bandpass filtering at the rod to second-order cell synapse in salamander (Ambystoma tigrinum) retina. J. Neurosci. 23 (9), 3796–3806. doi:10.1523/JNEUROSCI.23-09-03796.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Bem, T., and Rinzel, J. (2004). Short duty cycle destabilizes a half-center oscillator, but gap junctions can restabilize the anti-phase pattern. J. Neurophysiol. 91, 693–703. doi:10.1152/jn.00783.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, M. V. (1966). Physiology of electrotonic junctions. Ann. N. Y. Acad. Sci. 137 (2), 509–539. doi:10.1111/j.1749-6632.1966.tb50178.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Blitz, D. M., Beenhakker, M. P., and Nusbaum, M. P. (2004). Different sensory systems share projection neurons but elicit distinct motor patterns. J. Neurosci. 24 (50), 11381–11390. doi:10.1523/JNEUROSCI.3219-04.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Bucher, D., Prinz, A. A., and Marder, E. (2005). Animal-to-animal variability in motor pattern production in adults and during growth. J. Neurosci. 25 (7), 1611–1619. doi:10.1523/JNEUROSCI.3679-04.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Bykhovskaia, M., Polagaeva, E., and Hackett, J. T. (2004). Mechnisms underlying different facilitation forms at the lobster neuromuscular synapse. Brain Res. 1019 (1-2), 10–21. doi:10.1016/j.brainres.2004.05.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Li, X., Rotstein, H. G., and Nadim, F. (2016). Membrane potential resonance frequency directly influences network frequency through electrical coupling. J. Neurophysiol. 116 (4), 1554–1563. doi:10.1152/jn.00361.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

Chow, C., and Kopell, N. (2000). Dynamics of spiking neurons with electrical coupling. Neur. Comp. 12, 1643–1678. doi:10.1162/089976600300015295

PubMed Abstract | CrossRef Full Text | Google Scholar

Coleman, M. J., Meyrand, P., and Nusbaum, M. P. (1995). A switch between two modes of synaptic transmission mediated by presynaptic inhibition. Nature 378 (6556), 502–505. doi:10.1038/378502a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Connors, B. W., and Long, M. A. (2004). Electrical synapses in the mammalian brain. Annu. Rev. Neurosci. 27 (1), 393–418. doi:10.1146/annurev.neuro.26.041002.131128

PubMed Abstract | CrossRef Full Text | Google Scholar

Coulon, P., and Landisman, C. E. (2017). The potential role of gap junctional plasticity in the regulation of state. Neuron 93 (6), 1275–1295. doi:10.1016/j.neuron.2017.02.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Curti, S., Hoge, G., Nagy, J. I., and Pereda, A. E. (2012). Synergy between electrical coupling and membrane properties promotes strong synchronization of neurons of the mesencephalic trigeminal nucleus. J. Neurosci. 32 (13), 4341–4359. doi:10.1523/JNEUROSCI.6216-11.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

Drover, J. D., Tohidi, V., Bose, A., and Nadim, F. (2007). Combining synaptic and cellular resonance in a feed-forward neuronal network. Neurocomputing 70 (10-12), 2041–2045. doi:10.1016/j.neucom.2006.10.135

PubMed Abstract | CrossRef Full Text | Google Scholar

Fox, D. M., Tseng, H. A., Smolinski, T. G., Rotstein, H. G., and Nadim, F. (2017). Mechanisms of generation of membrane potential resonance in a neuron with multiple resonant ionic currents. PLoS Comput. Biol. 13 (6), e1005565. doi:10.1371/journal.pcbi.1005565

PubMed Abstract | CrossRef Full Text | Google Scholar

Galaretta, M., and Hestrin, S. (1998). Frequency-dependent synaptic depression and the balance of excitation and inhibition in the neocortex. Nat. Neurosci. 1 (7), 587–594. doi:10.1038/2822

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutierrez, G. J., O'Leary, T., and Marder, E. (2013). Multiple mechanisms switch an electrically coupled, synaptically inhibited neuron between competing rhythmic oscillators. Neuron 77 (5), 845–858. doi:10.1016/j.neuron.2013.01.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutcheon, B., and Yarom, Y. (2000). Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci. 23, 216–222. doi:10.1016/s0166-2236(00)01547-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Izhikevich, E. M., Desai, N. S., Walcott, E. C., and Hoppensteadt, F. C. (2003). Bursts as a unit of neural information: Selective communication via resonance. Trends Neurosci. 26 (3), 161–167. doi:10.1016/S0166-2236(03)00034-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Landisman, C. E., Long, M. A., Beierlein, M., Deans, M. R., Paul, D. L., and Connors, B. W. (2002). Electrical synapses in the thalamic reticular nucleus. J. Neurosci. 22 (3), 1002–1009. doi:10.1523/jneurosci.22-03-01002.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

Lane, B. J., Samarth, P., Ransdell, J. L., Nair, S. S., and Schulz, D. J. (2016). Synergistic plasticity of intrinsic conductance and electrical coupling restores synchrony in an intact motor network. Elife 5, e16879. doi:10.7554/eLife.16879

PubMed Abstract | CrossRef Full Text | Google Scholar

Ledoux, E., and Brunel, N. (2011). Dynamics of networks of excitatory and inhibitory neurons in response to time-dependent inputs. Front. Comput. Neurosci. 5, 25. doi:10.3389/fncom.2011.00025

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Bucher, D. M., and Nadim, F. (2017). Different neuromodulators directly influence gap junction-mediated electrical coupling strength in oscillatory networks. Soc. Neurosci. Abstr. 42, 155–105.

Google Scholar

Long, M. A., Landisman, C. E., and Connors, B. W. (2004). Small clusters of electrically coupled neurons generate synchronous rhythms in the thalamic reticular nucleus. J. Neurosci. 24 (2), 341–349. doi:10.1523/jneurosci.3358-03.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Lovett-Barron, M., Andalman, A. S., Allen, W. E., Vesuna, S., Kauvar, I., Burns, V. M., et al. (2017). Ancestral circuits for the coordinated modulation of brain state. Cell 171, 1411–1423.e1417.

PubMed Abstract | CrossRef Full Text | Google Scholar

Mann-Metzer, P., and Yarom, Y. (1999). Electrotonic coupling interacts with intrinsic properties to generate synchronized activity in cerebellar networks of inhibitory interneurons. J. Neurosci. 19 (9), 3298–3306. doi:10.1523/jneurosci.19-09-03298.1999

PubMed Abstract | CrossRef Full Text | Google Scholar

Marder, E., and Eisen, J. S. (1984). Electrically coupled pacemaker neurons respond differently to same physiological inputs and neurotransmitters. J. Neurophysiol. 51 (6), 1362–1374. doi:10.1152/jn.1984.51.6.1362

PubMed Abstract | CrossRef Full Text | Google Scholar

Marder, E., Gutierrez, G. J., and Nusbaum, M. P. (2017). Complicating connectomes: Electrical coupling creates parallel pathways and degenerate circuit mechanisms. Dev. Neurobiol. 77 (5), 597–609. doi:10.1002/dneu.22410

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, J. P., and Selverston, A. (1979). Rapid killing of single neurons by irradiation of intracellularly injected dye. Science 206 (4419), 702–704. doi:10.1126/science.386514

PubMed Abstract | CrossRef Full Text | Google Scholar

Moca, V. V., Nicolic, D., Singer, W., and Muresan, R. C. (2014). Membrane resonance enables stable robust gamma oscillations. Cereb. Cortex 24, 119–142.

PubMed Abstract | CrossRef Full Text | Google Scholar

Otopalik, A. G., Lane, B., Schulz, D. J., and Marder, E. (2019a). Innexin expression in electrically coupled motor circuits. Neurosci. Lett. 695, 19–24. doi:10.1016/j.neulet.2017.07.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Otopalik, A. G., Pipkin, J., and Marder, E. (2019b). Neuronal morphologies built for reliable physiology in a rhythmic motor circuit. Elife 8, e41728. doi:10.7554/eLife.41728

PubMed Abstract | CrossRef Full Text | Google Scholar

Placantonakis, D. G., Bukovsky, A. A., Aicher, S. A., Kiem, H. P., and Welsh, J. P. (2006). Continuous electrical oscillations emerge from a coupled network: A study of the inferior olive using lentiviral knockdown of connexin36. J. Neurosci. 26 (19), 5008–5016. doi:10.1523/JNEUROSCI.0146-06.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Posłuszny, A. (2014). The contribution of electrical synapses to field potential oscillations in the hippocampal formation. Front. Neural Circuits 8, 32. doi:10.3389/fncir.2014.00032

PubMed Abstract | CrossRef Full Text | Google Scholar

Rau, F., Clemens, J., Naumov, V., Hennig, R. M., and Schreiber, S. (2015). Firing-rate resonances in the peripheral auditory system of the cricket, Gryllus bimaculatus. J. Comp. Physiol. A Neuroethol. Sens. Neural Behav. Physiol. 201 (11), 1075–1090. doi:10.1007/s00359-015-1036-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Richardson, M. J., Brunel, N., and Hakim, V. (2003). From subthreshold to firing-rate resonance. J. Neurophysiol. 89 (5), 2538–2554. doi:10.1152/jn.00955.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

Rotstein, H. G., and Nadim, F. (2014). Frequency preference in two-dimensional neural models: A linear analysis of the interaction between resonant and amplifying currents. J. Comput. Neurosci. 37 (1), 9–28. doi:10.1007/s10827-013-0483-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Rotstein, H. G., and Nadim, F. (2019). Frequency-dependent responses of neuronal models to oscillatory inputs in current versus voltage clamp. Biol. Cybern. 113 (4), 373–395. doi:10.1007/s00422-019-00802-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Schulz, D. J., Goaillard, J. M., and Marder, E. (2006). Variable channel expression in identified single and electrically coupled neurons in different animals. Nat. Neurosci. 9 (3), 356–362. doi:10.1038/nn1639

PubMed Abstract | CrossRef Full Text | Google Scholar

Sherman, A., and Rinzel, J. (1992). Rhythmogenic effects of weak electrotonic coupling in neuronal models. Proc. Natl. Acad. Sci. U. S. A. 89 (6), 2471–2474. doi:10.1073/pnas.89.6.2471

PubMed Abstract | CrossRef Full Text | Google Scholar

Stagkourakis, S., Pérez, C. T., Hellysaz, A., Ammari, R., and Broberger, C. (2018). Network oscillation rules imposed by species-specific electrical coupling. Elife 7, e33144. doi:10.7554/eLife.33144

PubMed Abstract | CrossRef Full Text | Google Scholar

Stark, E., Levi, A., and Rotstein, H. G. (2022). Network resonance can be generated independently at distinct levels of neuronal organization. PLoS Comput. Biol. 18 (7), e1010364. doi:10.1371/journal.pcbi.1010364

PubMed Abstract | CrossRef Full Text | Google Scholar

To, M. S., Honnuraiah, S., and Stuart, G. J. (2022). Voltage clamp errors during estimation of concurrent excitatory and inhibitory synaptic input to neurons with dendrites. Neuroscience 489, 98–110. doi:10.1016/j.neuroscience.2021.08.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Tohidi, V., and Nadim, F. (2009). Membrane resonance in bursting pacemaker neurons of an oscillatory network is correlated with network frequency. J. Neurosci. 29 (20), 6427–6435. doi:10.1523/JNEUROSCI.0545-09.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Torben-Nielsen, B., Segev, I., and Yarom, Y. (2012). The generation of phase differences and frequency changes in a network model of inferior olive subthreshold oscillations. PLoS Comput. Biol. 8 (7), e1002580. doi:10.1371/journal.pcbi.1002580

PubMed Abstract | CrossRef Full Text | Google Scholar

Traub, R. D., Whittington, M. A., Gutiérrez, R., and Draguhn, A. (2018). Electrical coupling between hippocampal neurons: Contrasting roles of principal cell gap junctions and interneuron gap junctions. Cell Tissue Res. 373 (3), 671–691. doi:10.1007/s00441-018-2881-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Tseng, H. A., Martinez, D., and Nadim, F. (2014). The frequency preference of neurons and synapses in a recurrent oscillatory network. J. Neurosci. 34 (38), 12933–12945. doi:10.1523/JNEUROSCI.2462-14.2014

PubMed Abstract | CrossRef Full Text | Google Scholar

Tseng, H. A., and Nadim, F. (2010). The membrane potential waveform of bursting pacemaker neurons is a predictor of their preferred frequency and the network cycle frequency. J. Neurosci. 30 (32), 10809–10819. doi:10.1523/jneurosci.1818-10.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaughn, M. J., and Haas, J. S. (2022). On the diverse functions of electrical synapses. Front. Cell Neurosci. 16, 910015. doi:10.3389/fncel.2022.910015

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, N., Hsiao, C. F., and Chandler, S. H. (2001). Membrane resonance and subthreshold membrane oscillations in mesencephalic V neurons: Participants in burst generation. J. Neurosci. 21 (11), 3729–3739. doi:10.1523/JNEUROSCI.21-11-03729.2001

PubMed Abstract | CrossRef Full Text | Google Scholar