- 1Department of Biostatistics, St. Jude Children’s Research Hospital, Memphis, TN, United States
- 2Department of Preventive Medicine, Northwestern University, Feinberg School of Medicine, Chicago, IL, United States
- 3Eisai Inc., Woodcliff Lake, NJ, United States
- 4Department of Bioinformatics and Biostatistics School of Public Health and Information Sciences, University of Louisville, Louisville, KY, United States
In the context of high-throughput data, the differences in continuous markers between two groups are usually assessed by ordering the p-values obtained from the two-sample pooled t-test or Wilcoxon–Mann–Whitney test and choosing a stringent cutoff such as 10–8 to control the family-wise error rate
1 Introduction
In the context of genetic analysis, it is quite common to compare hundreds of thousands of genetic features such as gene expressions or DNA methylations between cases and controls. The well-known two-sample t-test or its robust analog Wilcoxon rank sum test has been commonly utilized to obtain p-values for comparing genetic features between the two groups at each locus. These p-values are then ordered and chosen to control the family-wise error rate
When a study involves testing the differences between several thousands of genes between cases and controls, then it may be reasonable to assume that the sample size would be fixed for all comparisons. However, the p-values for comparing a gene expression profile between the two groups would still be affected by the effect size (standardized difference in the mean expression levels), underlying distributional assumptions (usually normality), and inequality of the variances for the two groups. In the context of a multiple-hypotheses setting, it is clear that
In the parametric setting, it is well known that the pooled two-sample t-test is optimal for comparing the two means when the underlying distributions are normal and have equal variances. When the variances are not equal, then one uses the Behrens–Fisher statistic with the Satterthwaite approximation; see Welch (1937) and Satterthwaite (1946).
However, it is also well known that these assumptions are rarely met in practice, and an alternative is to use non-parametric approaches that impose fewer conditions on the underlying distributions. For the two-sample location problem, one is often interested in comparing the medians of the two populations, and the widely used Wilcoxon–Mann–Whitney (WMW) test is distribution-free, if the two distributions are continuous and have the same shape. Pratt (1964) has shown that the test does not maintain type I error if the variances are different. Fligner and Policello (1981) proposed a modified WMW statistic for unequal variances but assumed the two populations to be symmetric. Brunner and Munzel (2000) and Neubert and Brunner (2007) further extended the non-parametric statistics to more general situations by further relaxing the underlying assumptions.
In general, it is well recognized, for example, Hampel et al. (1986) showed that the parametric tests would be optimal, that is, they would be valid and have the optimal power, when the underlying assumptions are satisfied. On the other extreme are the non-parametric tests that have minimal assumptions on the underlying distribution, but a price is paid in terms of loss of power. However, when there are modest departures from the target family (usually normal), robust methods serve as a viable alternative as they provide significant gain in power while maintaining the type I error control. In the context of the two-sample problem, assuming the underlying distributions to be in the neighborhood of the normal family with equal variances, Srivastava et al. (1992) and Mudholkar et al. (1991) have proposed robust test procedures based on L-statistics. In particular, the approach based on trimmed means, which is based on the concept of trimming the extreme observations, seems appealing and has shown better operating characteristics particularly for the distributions that are heavier tailed than normal.
It would be a daunting task to test the underlying distributional assumption and the homogeneity of variances at each locus and then use the appropriate test statistic based on the results of those tests. Even if one performed that, one will have to account for the increased number of tests being performed and the conditional nature of the p-values in the second stage. Pounds and Rai (2009) adopted the concept of an assumption adequacy averaging approach, which incorporates an assessment of the assumption of normality and weighs the results of the two alternative approaches based on whether the assumption of normality is satisfied or not. However, their approach does not extend to the situations where the assumptions of normality and homoscedasticity may be violated simultaneously.
The hallmarks of a “good” robust procedure should be that which is able to control the type I error rate and provide significant gain in power when the underlying assumptions are violated. Also, it should be able to maintain the type I error control with minimal loss in power when the underlying assumptions hold. The literature is filled with robust test procedures proposed for comparing two populations, and it is worthwhile to note that majority of them assess the type I error control at the traditional level of
In this study, we propose a robust analog of the Behrens–Fisher statistic based on trimmed means that is robust to the violations of underlying assumptions of normality and homogeneity. We use the asymptotic normality of trimmed means, derived by Huber (1970), to obtain the asymptotic distribution of the proposed test statistic. Then, using the first two moments of the proposed test statistics and regression methods, we obtain finite sample approximations to make the statistics useful in small sample sizes. The proposed statistic provides for a robust alternative for comparing two distributions that may not be normal and may be heteroscedastic. It is interesting to note that the proposed test statistic has the best performance for skewed distributions as well. However, in the context of high-throughput studies, the results based on the p-value approach will also be affected by the correlations among the test statistics by virtue of the correlation among genes. In this development, we focus our attention on developing a test statistic that will provide valid p-values when the assumptions of normality and homoscedasticity are violated with the understanding that one could use the approaches described in Benjamini and Yekutieli (2007) or Sun and Cai (2009) to conduct inference with correlated p-values. In Section 2, we provide the details of the motivating example. In Section 3, the background information regarding trimmed means and their asymptotic properties are discussed. In Section 4, a brief account of the Behrens–Fisher statistic for two samples is provided. In Section 5, we propose the new test statistic and obtain null distribution approximations for the proposed test statistic for finite samples. In Section 6, the details of the simulation study to evaluate the performance of the proposed test statistic in terms of type I error control and power properties and its comparison with the existing approaches are provided. In Section 7, the usefulness of the proposed test procedure is demonstrated by applying it to the DNA methylation data. Section 8 is dedicated to discussions and miscellaneous comments.
2 Motivating Example
Teschendorff et al., (2010) conducted a study to investigate the mechanism of diabetic nephropathy by comparing 27580 markers from a genome-wide methylation array between cases and controls. These data were submitted by the authors to the NCBI Gene Expression Omnibus (http://www.ncbi.nlm.nih.gov/geo) under accession nos. GSE20067 and can be easily downloaded. There were 97 cases who had type 1 diabetes (T1D) and nephropathy and 98 controls who had T1D but with no evidence of renal disease. The purpose of this study was to identify the markers that would be differentially expressed between the two groups. Cao et al. (2013) used the two-sample t-test and converted them to p-values to identify the proportions of DNA methylations that were different between the two groups. They further showed that the monotonicity assumption required for the validity of the
Cao et al. (2013) used the raw proportions of methylation which range between 0 and 100%. However, in practice, the logit transformation is often used before applying any test procedure. The benefit of using this transformation is that it transforms the proportions on a scale that ranges from −∞ to ∞ and possibly achieves variance stabilization; see Box (1953). We checked the assumption of normality in cases and controls and equality of variances between the two groups for all markers using Shapiro and Wilk (1965) and the F-test (Box, 1953) at different significance levels on the raw and logit-transformed methylation data. The results for the logit transformation (raw) are reported, and the results for the raw data were slightly worse.
At the conventional level of
Thus, it is obvious that the assumption of normality and/or equality of variance, in general, is questionable, and robust methods that are robust to such violations should be used. In the following section, we provide the background of the trimmed means and their asymptotic distribution.
3 Trimmed Means and Asymptotic Results
3.1 Trimmed Means
In the univariate case for one sample problem, let
where
where
is the Winsorized variance, and
3.2 Asymptotic Results
Huber (1970) justified the studentization in light of the asymptotic normal distribution of the trimmed means. Specifically, he showed that when the underlying distribution
where
It may be noted that
where
Now, if we fix the distribution
where
Using the aforementioned asymptotic theory, Mudholkar et al. (1991) refined the approximation for one-sample trimmed
4 Two-Sample Behrens–Fisher Trimmed
In the univariate setting for the two-sample problem, let
where
where
5 Trimmed
5.1 Trimmed t Statistic
For the two-sample problem discussed in Section 4, Yuen (1974) substituted trimmed means and Winsorized variances in place of means and variances in (11) and proposed a robust analog of the Behrens–Fisher statistic as:
where
Now, assuming the underlying distribution to be normal, that is,
Then, using
which reduces to
where
Remark: It may be noted that in the aforementioned derivation, the underlying distribution is fixed to normal, that is,
5.2 Null Distribution Approximation
In this section, we have combined the large sample theory of Section 3 and the results of a Monte Carlo study to develop a scaled Student’s
Furthermore, by dividing the numerator and denominator of (16) by
where
where
where
In order to render
That is, the test statistic (16) can be approximated by:
However, based on the simulations, it was seen that with the finite sample correction in (20) the strict type I error control could not be achieved; see Table 2 (Column 8).
Then, using simulation studies and the logic that a slightly conservative test can be obtained by making the degrees of freedom smaller (the tails would become a little bit heavier), we obtained the modified degrees of freedom
Then, obtain the scalar
That is, the test statistic in (16) can be approximated by :
The performance of the test statistic (16) using the null distribution approximations given in (20) and (23) were evaluated using extensive simulation studies described in the next section.
6 Simulations
6.1 Simulation Setup
Extensive simulation studies were performed to evaluate the performance of the proposed test statistics
It may be noted that the mWMW or its generalizations proposed by Neubert and Brunner (2007) test the general hypothesis of
Simulations were conducted where a single hypothesis was simulated and examined at increasingly stringent significance levels of α to mimic the situation of testing multiple hypotheses but assuming the underlying distribution to be same for the two groups. Five families of distributions were considered: normal, contaminated normal, combined normal and uniform (contaminated with normal/uniform distribution), cauchy (all symmetric continuous distributions), and transformed beta (skewed continuous distribution). Although, the theory and derivation of the test statistic in (16) assumes the underlying distributions to be symmetric, it may be argued that, after appropriate trimming, the “middle” of the skewed distribution may also resemble the “middle” of the normal distribution, and it may be reasonable to apply and evaluate the performance of the trimmed test statistic for skewed distributions as well. In addition, in situations where hundreds and thousands of gene expressions are compared, it is likely that some underlying distributions may be skewed in real-life setting. So we included beta distribution in our simulation studies to mimic such a situation.
An independent simulation study was undertaken to compare the type I error control of
From Supplementary Table S1, it is clear that Yuen’s approach, based on the Welch-type approximation, cannot control type I error for normal distribution at stringent levels of
For beta distribution (skewed), neither
The results for the contaminated normal and combined normal and uniform suggest that both methods are conservative with
In another independent simulation study, from each of the distributions mentioned before, random samples of sizes
To further evaluate the performance of the tests three possible scenarios arise for various combinations of σ1 and σ2 for normal, contaminated normal and contaminated with normal/uniform distributions as described later.
6.1.1 Normal
Scenario I: σ1 = σ2 represents the case of two normal distributions with equal variances.
Scenario II: σ1 < σ2 represents the case where variance of the second population is larger, and in evaluating power, it corresponds to the situation that the variance is larger for the second population with larger mean, that is,
Scenario III: σ1 > σ2 represents the case where variance of the first population is larger, and in evaluating power, it corresponds to the situation that the variance is smaller for the second population with larger mean (μ2 > μ1 = 0).
6.1.2 Contaminated Normal
Scenario I: σ1 = σ2 represents the case of two normal distributions with unequal variances (no contamination).
Scenario II: σ1 < σ2 represents the situation that the variance of the contaminated part of the distribution is larger, that is, contamination with the normal distribution with “outliers”.
Scenario III: σ1 > σ2 represents the situation that the variance of the contamination part of the distribution is smaller, that is, contamination with the normal distribution with “inliers”.
6.1.3 Combined Normal and Uniform
Scenario I: σ1 = σ2 represents the case of two contaminated normal distributions, contaminated with normal/uniform (N/U) distribution, with equal variances.
Scenario II: σ1 < σ2 represents that the variance of contamination part of the distribution with N/U is larger, that is, contamination is done with “outliers” coming from N/U distribution.
Scenario III: σ1 > σ2 represents that the variance of contamination part of the distribution with N/U is smaller, that is, contamination is done with “inliers” coming from N/U distribution.
For cauchy and transformed beta, the distributions were simulated for the parameters given in Table 1.
6.2 Simulation Results
For ease of readability, we have reported the ratio of empirical estimate of type I error/expected level of significance, that is,
Based on our extensive simulation studies, it is clear that for all the distributions under study, the empirical type I error rates were better controlled for both trimmed tests,
Remark: In practice, the choice of trimming proportions would be critical. Our recommendation, supported by our simulation studies, is to use 15% trimming proportions because trimming less than that provides results that would be similar to the normal setting (type I error control often not maintained) and trimming more than that results in more conservative tests and loss of power. In general, higher proportion of trimming would be recommended for settings where the underlying distribution may be very heavy tailed. However, this would not be known a priori and would be a daunting task to check at each loci, particularly, in the context of high-throughput data, but a 15% trimming provides a balance between not trimming enough to trimming too much and generally provides reasonably good results for all underlying distributions (including asymmetric distribution) studied in our simulation studies.It may also be noted that we compared the null distributions at two levels of
6.2.1 Normal Distribution
Null Distribution: As seen from Figure 1A, it is clear that, in general, the type I error control at
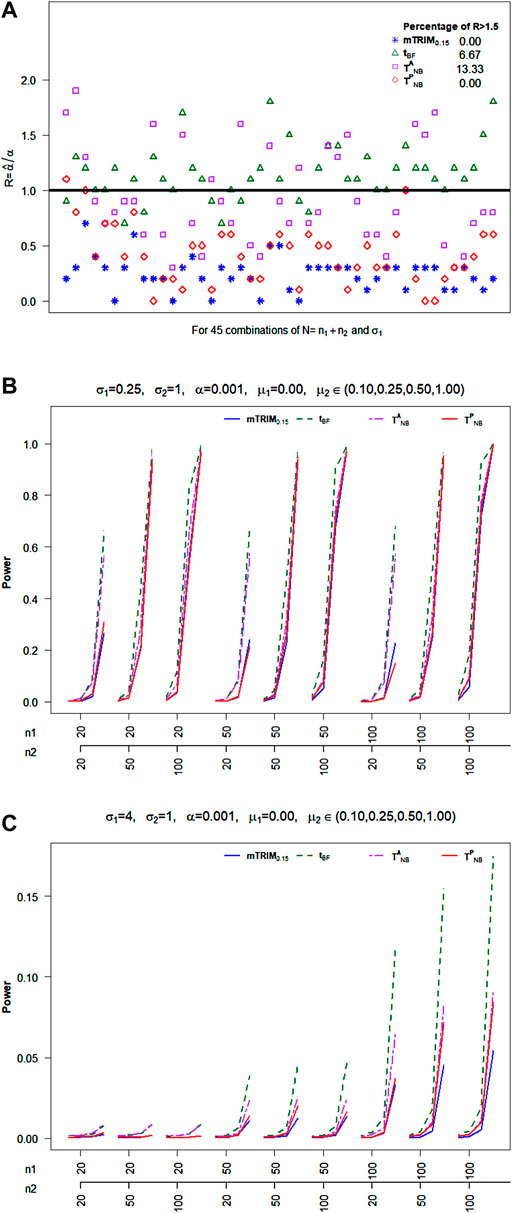
FIGURE 1. (A) Plot of ratio
Power Properties: For Scenario I, with
6.2.2 Combined Normal and Uniform
Null Distribution: From Figure 2A, it is clear that
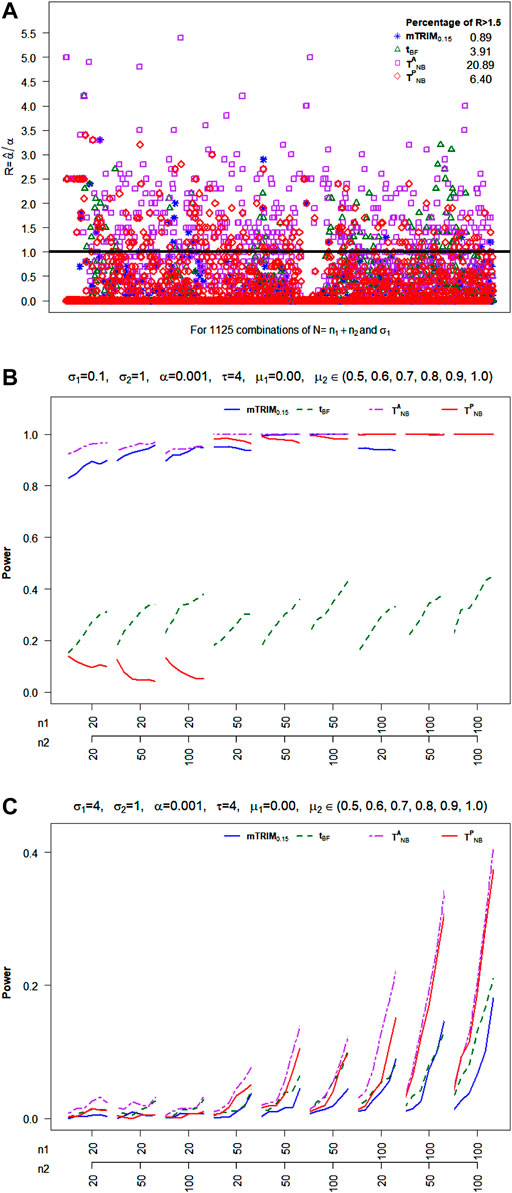
FIGURE 2. (A) Plot of ratio
6.2.3 Cauchy Distribution
For cauchy distribution, from Figure 3A, it is very clear that
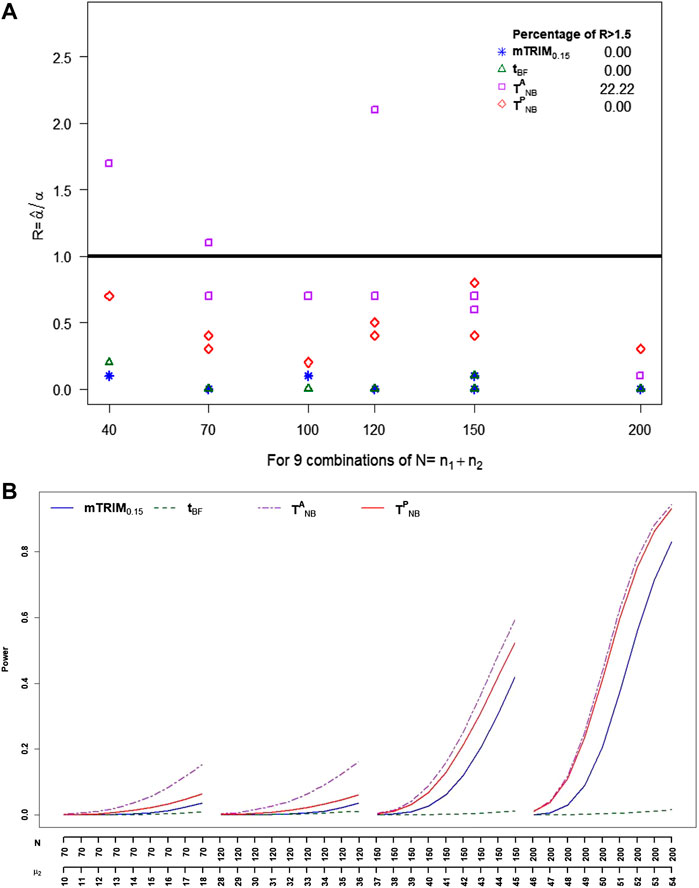
FIGURE 3. (A) Plot of ratio
6.2.4 Skewed Transformed Beta
For skewed transformed beta distribution, from Figure 4A, it is very clear that none of the four tests can control type I error well. The percentage of times the type I errors exceeds 1.5 threshold for
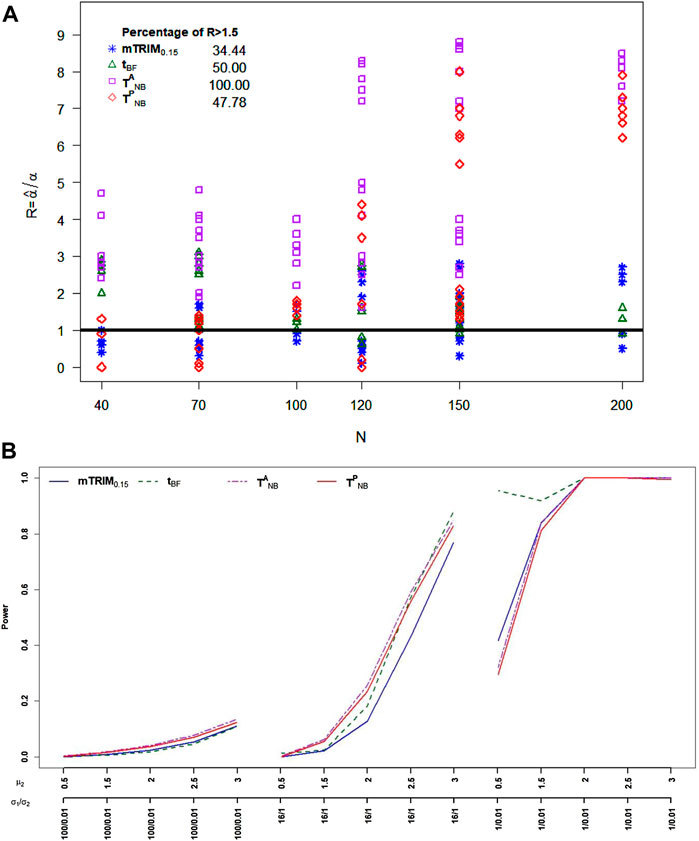
FIGURE 4. (A) Plot of ratio
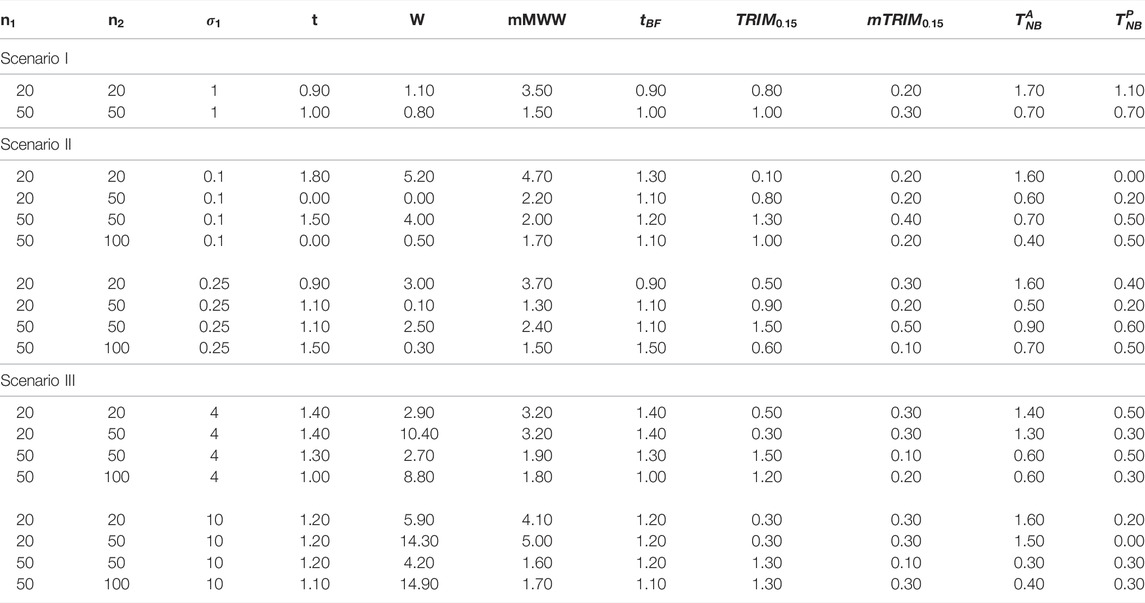
7 Application to DNA Methylation Data
We downloaded the data from the NCBI Gene Expression Omnibus website and applied all the approaches discussed before to the example to evaluate their relative performances.
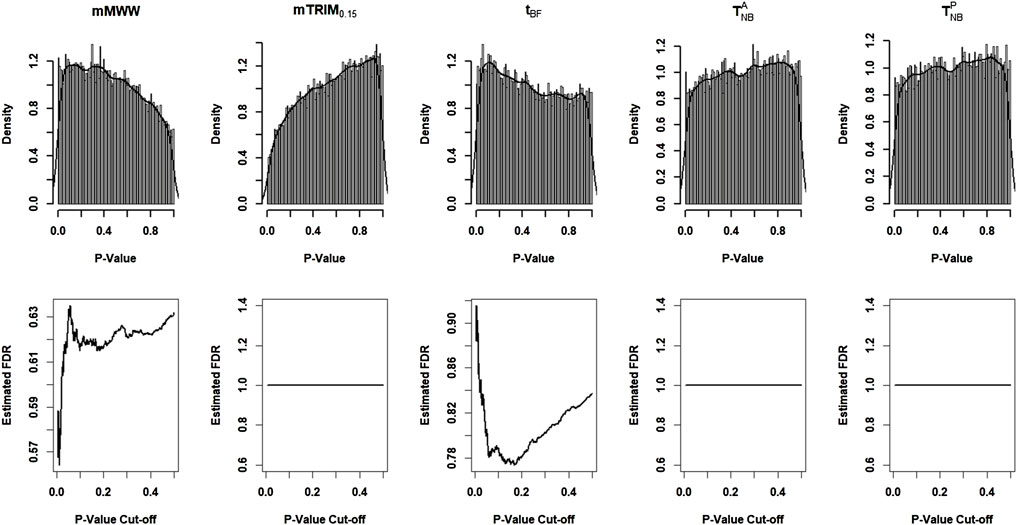
Figure 5 shows the histogram of p-values with the density estimates and the estimated FDR as a function of p-value cutoffs. The estimated non-null proportion are 0, 0.09, 0.28, 0.00005, and 0 corresponding to
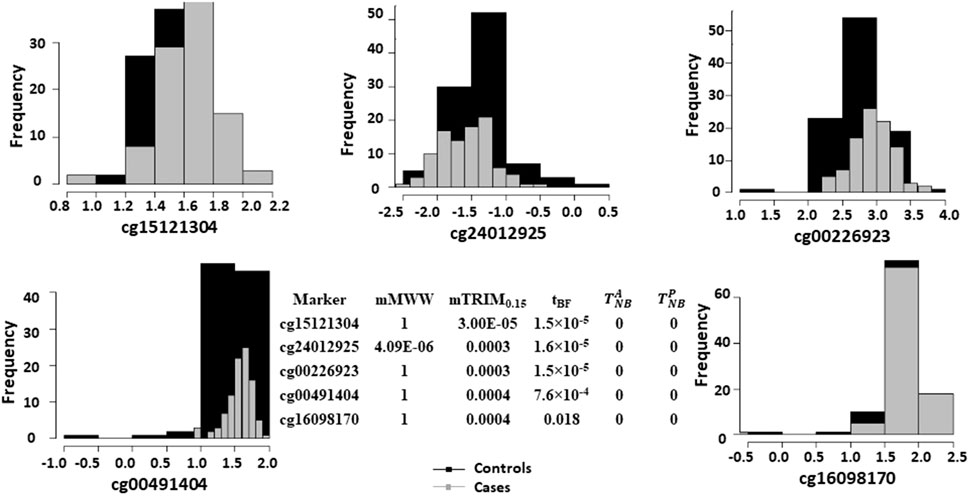
FIGURE 6. Histograms of logistic transformed methylation data for the five most significant markers based on the mTRIM0.15 method and corresponding p-values for all the five methods.
8 Discussion
The proposed trimmed analog of the Behrens–Fisher statistic is robust in the sense that it can strictly maintain the type I error rate compared to the alternatives currently available in the literature and at the same time can provide significant gain in power when the underlying distributions may be in the neighborhood of normal with possibly unequal variances. However, it is possible that for some other underlying distributions and for some parameter combinations, other test procedures may outperform
In a genome wide association study of a continuous outcome, often, we are interested in testing if the continuous outcomes corresponding to three genotypes are same or not. Furthermore, in a gene expression analysis of k samples, based on multiple dose levels, we could be interested in knowing if the gene expressions among k-sample are different or not. To address these issues, the commonly used parametric method will be ANOVA analysis if the data follow normal distribution; otherwise, the alternative of ANOVA will be the Kruskal and Wallis, 1952. However, similar to the two-sample comparison discussed in the study, it may be perceived that the two most popular methods may not be able to maintain type I error rate at a given significance level and may lose significant statistical power when the underlying distributions may not be normal and possibly heteroscedastic. We are currently in the process of investigating it and extending our approach to k-sample heteroscedastic case.
Often, the comparison in the two-sample case or k-sample case needs to be adjusted for covariates of interest that may be associated with the phenotype of interest. We are currently in the process of developing approaches that would provide robust comparisons after adjusting for the covariates.
Although the motivation and presentation of the method lies in identifying genetic features different between two groups, it is also readily applicable to any epidemiology studies of comparing continuous variables between two groups and any clinical trial of comparing continuous responses for two treatments. We have implemented the proposed method in R program (Supplementary Note S1). The method can be easily applied to compare the continuous variables between two groups from one to hundreds of thousands of tests.
Data Availability Statement
The methylation array data can be downloaded from publicly available data base at NCBI Gene Expression Omnibus (http://www.ncbi.nlm.nih.gov/geo) under accession no. GSE20067.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research work of GK, SM, HZ, and DS was supported by the Grant CA21765 from the National Institutes of Health (NIH) and by the American Lebanese and Syrian Associated Charities (ALSAC). SR’s work was partially supported by the Wendell Cherry in Clinical Trial Research.
Conflict of Interest
Author LZ was employed by Eisai Inc.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsysb.2022.877601/full#supplementary-material.
References
Aspin, A. A. (1948). An Examination and Further Development of a Formula Arising in the Problem of Comparing Two Mean Values. Biometrika 35, 88–96. doi:10.1093/biomet/35.1-2.88
Benjamini, Y., and Yekutieli, D. (2007). The Control of False Discovery Rate in Multiple Testing under Dependence. Ann. Stat. 29, 1165–1188.
Box, G. E. P. (1953). Non-Normality and Tests on Variances. Biometrika 40 (3/4), 318–335. doi:10.2307/2333350
Brunner, E., and Munzel, U. (2000). The Nonparametric Behrens-Fisher Problem: Asymptotic Theory and a Small-Sample Approximation. Biom. J. 42, 17–25. doi:10.1002/(sici)1521-4036(200001)42:1<17::aid-bimj17>3.0.co;2-u
Cao, H., Sun, W., and Kosorok, M. R. (2013). The Optimal Power Puzzle: Scrutiny of the Monotone Likelihood Ratio assumption in Multiple Testing. Biometrika 100 (2), 495–502. doi:10.1093/biomet/ast001
Chow, S. C., Shao, J., and Wang, H. (2008). Sample Size Calculations in Clinical Research. Chapman & Hall/CRC, Taylor and Francis Group.
Fagerland, M. W., and Sandvik, L. (2009). Performance of Five Two-Sample Location Tests for Skewed Distributions with Unequal Variances. Contemp. Clin. Trials 30, 490–496. doi:10.1016/j.cct.2009.06.007
Fligner, M. A., and Policello, G. E. (1981). Robust Rank Procedures for the Behrens-Fisher Problem. J. Am. Stat. Assoc. 76, 162–168. doi:10.1080/01621459.1981.10477623
Hampel, F. R., Ronchetti, E. M., Rousseeuw, P. J., and Stahel, W. A. (1986). Robust Statistics: The Approach Based on Influence Functions. New York: John Wiley and Sons.
Huber, P. J. (1970). “Studentizing Robust Estimates,” in Nonparametric Techniques in Statistical Inference. Editor M. L. Puri (Cambridge, England: Cambridge University Press), 453–463.
Janssen, A. (1997). Studentized Permutation Tests for non-i.i.D. Hypotheses and the Generalized Behrens-Fisher Problem. Stat. Probab. Lett. 36, 9–21. doi:10.1016/s0167-7152(97)00043-6
Kang, G., Ye, K., Liu, N., Allison, D. B., and Gao, G. (2009). Weighted Multiple Hypothesis Testing Procedures. Stat. Appl. Genet. Mol. Biol. 8, 1–22. doi:10.2202/1544-6115.1437
Kruskal, W. H., and Wallis, W. A. (1952). Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 47 (260), 583–621. doi:10.1080/01621459.1952.10483441
Lee, A. F. S. (1995). Coefficients of lee-gurland Two-Sample Test on normal Means. Commun. Stat. - Theor. Methods 24 (7), 1743–1768. doi:10.1080/03610929508831583
Lee, A. F. S., and Gurland, J. (1975). Size and Power of Tests for equality of Means of Two normal Populations with Unequal Variances. J. Am. Stat. Assoc. 70, 933–941. doi:10.1080/01621459.1975.10480326
Mudholkar, A., Mudholkar, G. S., and Srivastava, D. K. (1991). A Construction and Appraisal of Pooled Trimmed-Tstatistics. Commun. Stat. - Theor. Methods 20, 1345–1359. doi:10.1080/03610929108830569
Neubert, K., and Brunner, E. (2007). A Studentized Permutation Test for the Non-parametric Behrens-Fisher Problem. Comput. Stat. Data Anal. 51, 5192–5204. doi:10.1016/j.csda.2006.05.024
Pagurova, V. I. (1968). On a Comparison of Means of Two normal Samples. Theor. Probab. Appl. 13, 527–534. doi:10.1137/1113069
Pounds, S., and Rai, S. N. (2009). Assumption Adequacy Averaging as a Concept for Developing More Robust Methods for Differential Gene Expression Analysis. Comput. Stat. Data Anal. 53 (5), 1604–1612. doi:10.1016/j.csda.2008.05.010
Robins, J. M., van DER Vaart, A., and Ventura, V. (2000). Asymptotic Distribution ofPValues in Composite Null Models. J. Am. Stat. Assoc. 95, 1143–1156. doi:10.1080/01621459.2000.10474310
Satterthwaite, F. E. (1946). An Approximate Distribution of Estimates of Variance Components. Biometrics Bull. 2, 110–114. doi:10.2307/3002019
Shapiro, S. S., and Wilk, M. B. (1965). An Analysis of Variance Test for Normality (Complete Samples). Biometrika 52 (3–4), 591–611. doi:10.1093/biomet/52.3-4.591
Srivastava, D. K., Mudholkar, G. S., and Mudholkar, A. (1992). Assessing the Significance of Difference between Two Quick Estimates of Location. J. Appl. Stat. 19 (3), 405–416. doi:10.1080/02664769200000036
Storey, J. D. (2002). A Direct Approach to False Discovery Rates. J. R. Stat. Soc. Ser. B Stat. Methodol. 64, 479–498. doi:10.1111/1467-9868.00346
Sun, W., and Tony Cai, T. (2009). Large-scale Multiple Testing under Dependence. J. R. Stat. Soc. Ser. B Stat. Methodol. 71, 393–424. doi:10.1111/j.1467-9868.2008.00694.x
Teschendorff, A. E., Menon, U., Gentry-Maharaj, A., Ramus, S. J., Weisenberger, D. J., Shen, H., et al. (2010). Age-dependent DNA Methylation of Genes that Are Suppressed in Stem Cells Is a Hallmark of Cancer. Genome Res. 20 (4), 440–446. doi:10.1101/gr.103606.109
Tukey, J. W., and McLaughlin, D. H. (1963). Less Vulnerable Confidence and Significance Procedures for Location Based on a Single Sample: Trimming/Winsorization I. Sankhya, A 25, 331–352.
Welch, B. L. (1949). Further Note on Mrs. Aspin’s Tables and on Certain Approximations to the Tabled Function. Biometrika 36, 293–296.
Welch, B. L. (1947). The Generalization of “Student’s” Problem when Several Difference Population Variances Are Involved. Biometrika 34 (1-2), 28–35. doi:10.2307/2332510
Welch, B. L. (1937). The Significance of the Difference between Two Means when the Population Variances Are Unequal. Biometrika 29, 350–362.
Keywords: Behrens–Fisher problem, false discoveries, robustness, trimmed means, robust trimmed test
Citation: Kang G, Mirzaei SS, Zhang H, Zhu L, Rai SN and Srivastava DK (2022) Robust Behrens–Fisher Statistic Based on Trimmed Means and Its Usefulness in Analyzing High-Throughput Data. Front. Syst. Biol. 2:877601. doi: 10.3389/fsysb.2022.877601
Received: 16 February 2022; Accepted: 11 April 2022;
Published: 02 June 2022.
Edited by:
Rongling Wu, The Pennsylvania State University (PSU), United StatesReviewed by:
Tao He, San Francisco State University, United StatesXiaoxi Shen, Texas State University, United States
Copyright © 2022 Kang, Mirzaei, Zhang, Zhu, Rai and Srivastava. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Deo Kumar Srivastava, a3VtYXIuc3JpdmFzdGF2YUBzdGp1ZGUub3Jn
 Guolian Kang
Guolian Kang Sedigheh S. Mirzaei
Sedigheh S. Mirzaei Hui Zhang
Hui Zhang Liang Zhu3
Liang Zhu3 Shesh N. Rai
Shesh N. Rai Deo Kumar Srivastava
Deo Kumar Srivastava