Stefano Panzeri
1* Mathew E. Diamond
2,3*
- 1 Robotics, Brain and Cognitive Sciences Department, Italian Institute of Technology, Genova, Italy
- 2 Cognitive Neuroscience Sector, International School for Advanced Studies, Trieste, Italy
- 3 Italian Institute of Technology- SISSA Unit, Trieste, Italy
Computational analyses have revealed that precisely timed spikes emitted by somatosensory cortical neuronal populations encode basic stimulus features in the rat’s whisker sensory system. Efficient spike time based decoding schemes both for the spatial location of a stimulus and for the kinetic features of complex whisker movements have been defined. To date, these decoding schemes have been based upon spike times referenced to an external temporal frame – the time of the stimulus itself. Such schemes are limited by the requirement of precise knowledge of the stimulus time signal, and it is not clear whether stimulus times are known to rats making sensory judgments. Here, we first review studies of the information obtained from spike timing referenced to the stimulus time. Then we explore new methods for extracting spike train information independently of any external temporal reference frame. These proposed methods are based on the detection of stimulus-dependent differences in the firing time within a neuronal population. We apply them to a data set using single-whisker stimulation in anesthetized rats and find that stimulus site can be decoded based on the millisecond-range relative differences in spike times even without knowledge of stimulus time. If spike counts alone are measured over tens or hundreds of milliseconds rather than milliseconds, such decoders are much less effective. These results suggest that decoding schemes based on millisecond-precise spike times are likely to subserve robust and information-rich transmission of information in the somatosensory system.
Introduction
Explorations of sensory processing are founded on the model that, if two sensory stimuli can be discriminated, their associated neural representations must be in some way distinct (for reviews see e.g., Petersen et al., 2002a ; Quian Quiroga and Panzeri, 2009 ; Panzeri et al., 2010 ). A fundamental challenge, then, is to discover the essential differences in the neural representations of two perceptually discriminable stimuli.
Behaving rats can perform whisker-mediated texture discriminations between tactile stimuli in as little as 100 ms between first touch and choice action, as shown by Figure 4 in von Heimendahl et al. (2007) . Thus, the signal supporting their decision must reside in spike trains of some tens or at most a few hundred milliseconds (Diamond et al., 2008 ). Well before any recordings are collected during the course of active sensory discriminations, it is crucial to delineate candidate coding mechanisms under more controlled conditions so that the data obtained from the behaving animal can be interpreted profitably. Although there are many cases where neural activity collected in the absence of any quantitative hypothesis has proven uninterpretable (Prigg et al., 2002 ), the notion somehow survives that the search for potential coding mechanisms should not be undertaken except from the perspective of documented sensory capacities (Stuttgen, 2010 ). In contrast, our view is that the starting point is to ask what signals neuronal populations are capable of carrying, and by what principles. In this way, models and assumptions can be ruled out or reinforced in parallel with the collection of new data sets.
Information theory has proved to be a profitable way to evaluate the salient differences between the neural representations of sensory events and the potential mechanisms by which neurons convey signals about stimuli. In rat whisker cortex, information theoretic studies have highlighted the potentially important role of spike times in encoding sensory information: the knowledge of the timing of spikes with millisecond precision adds large amounts of information that cannot be gained by counting the spikes over tens or hundreds of millisecond (Panzeri et al., 2001 ; Petersen et al., 2001 ; Arabzadeh et al., 2006 ). When stimuli are presented to anesthetized animals, the experimenter, of course, knows the stimulus timing. As a result, most spike timing based codes that have been proposed rely on stimulus time knowledge. For example, in rat whisker cortex the short latency of neural responses carries almost all the information that neurons transmit about stimulus location, yet the latency is calculated with respect to a known stimulus onset time (Panzeri et al., 2001 , 2003b ; Petersen et al., 2001 , 2002a ,b ).
Latency codes are the simplest and most prominent case of information encoding by spike times measured with an external temporal reference, and they offer a number of significant computational advantages. First-spike coding is metabolically efficient, and is the fastest possible way to encode information (no neural message can be faster than a first-spike-time). Van Rullen and Thorpe (2001) have argued that first-spike coding is the only way information can be encoded compatible with the speed of processing in the visual system. Latency coding is also a convenient way to represent analog variables in a format ready for further computation (Hopfield, 1995 ). However, a potential problem arises if latencies are measured with respect to the stimulus onset. Since the brain, unlike the experimenter, does not have direct access to the time of stimulus onset, it is uncertain whether this timing could be used. Indeed, we have investigated the issue of the robustness of spike timing codes during naturalistic whisker deflections (Arabzadeh et al., 2006 ). We found that in cortex the information in spike times of single neurons or of small populations was largely lost if the decoder had imprecise knowledge of the stimulus time (Arabzadeh et al., 2006 ).
Encoding of information by latency has been reported not only in the rat whisker system but also in other different sensory modalities (e.g., Gawne et al., 1996 ; Furukawa et al., 2000 ; Muller et al., 2001 ; Reich et al., 2001 ; Foffani et al., 2004 , 2008 , 2009 ; Chechik et al., 2006 ). The consistent finding that latency coding is informative at the cortical level raises the question of whether, and how, information in precise spike times of cortical neurons can be read out by other brain areas even without independent knowledge of the stimulus time.
The problem of decoding the information in precise spike times could be solved if the sensory input were generated in response to an active motor command, in which case the time of the command could constitute an estimate of stimulus time. For example, rats sweep their vibrissae toward objects of interest (Kleinfeld et al., 2006 ) and they may be able to register incoming spike trains with respect to their own whisker protraction with a resolution of some tens of milliseconds (Kleinfeld et al., 2006 ; Diamond et al., 2008 ). However, it seems unlikely that motor “efference copy” possesses the necessary temporal resolution to align first-spike times with ms precision (von Heimendahl et al., 2007 ). Still, even if motor commands do not constitute a ms-precise clock, they may serve as a “window of expectation”, and within such windows the brain may use spike timing relative to an internal reference frame to extract a representation of the stimulus (Hopfield, 1995 ; Van Rullen and Thorpe, 2001 ; Brody and Hopfield, 2003 ; Johansson and Birznieks, 2004 ; Kayser et al., 2009 ; Panzeri et al., 2010 ). Timing relative to an internal reference frame could be defined either from spike times within a single neuron’s train, or as relative timing between multiple neurons. The feasibility of this “relative timing” population code has been demonstrated on simulated networks (Van Rullen and Thorpe, 2001 ) and at the peripheral level (Johansson and Birznieks, 2004 ; Gollisch and Meister, 2008 ; Saal et al., 2009 ).
In this article, we investigate the feasibility of decoding fine-scale relative spike timing information in cortex by considering somatosensory cortical recordings in response to instantaneous whisker deflections. We are particularly interested in testing whether decoders based upon relative spike times can operate robustly even in the presence of spontaneous activity (which complicates the estimates of response latencies of individual neurons), and in understanding whether they can provide information beyond what can be extracted by counting spikes over coarser time scales. The information that we attempt to extract from the spike trains is the identity of the deflected whisker. Knowing which whisker has contacted an object is thought to be part of the process of object localization, in which rats have excellent capacities (Diamond et al., 1999 , 2008 ; Harris et al., 1999 ; Mehta et al., 2007 ; Knutsen and Ahissar, 2009 ).
The article is organized as follows. After reviewing concepts and results from information theory showing the role of spike timing in encoding whisker information, we present methods for stimulus decoding in the absence of externally added knowledge of the stimulus time course. We apply these methods, as a feasibility test, to data from anesthetized rats. We show that stimulus site can be decoded from millisecond-precise population spike times without absolute stimulus time knowledge.
Information Theoretic Analysis
The information that a single neuron or a neuronal population response conveys about the stimulus can be quantified by Shannon’s Mutual Information formula (Cover and Thomas, 1991 ), abbreviated hereafter as Information:
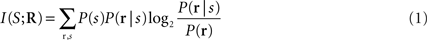
where P(s) is the probability of presentation of stimulus s, P(r | s) is the probability of observing response r given presentation of stimulus s, and P(r) is the probability of observing response r across all trials to any stimulus. This equation quantifies the maximal reduction of uncertainty (i.e., the gain in information) about the stimuli obtained from a single-trial observation of a neuronal response (averaged over all stimuli and responses). Information is measured in bits (1 bits corresponds to a reduction of uncertainty by a factor of two), and is an upper bound on the amount of knowledge about stimuli that can be extracted by any decoding algorithm operating on neural responses. By evaluating the information carried by different ways of defining and quantifying the response r, we can evaluate the capacity of different candidate neural codes.
The computation of information requires the estimation of the stimulus-conditional response probabilities. These probabilities are not known a priori and must be measured experimentally from a finite number of trials. The estimated probabilities suffer from finite sampling errors, which induce a systematic error (bias) in estimates of the information (Panzeri et al., 2007 ). In this article, unless otherwise stated we used the following procedure to correct for the bias when computing information from real data. First, to facilitate the sampling of its probability, we considered responses r which are discrete in nature or which are binned into some discrete set of possible responses. Although the discretization facilitates the sampling of neural response probabilities, the information measures still suffer from limited sampling bias. We thus used a quadratic extrapolation procedure (Strong et al., 1998 ) to estimate and subtract the bias of each information quantity.
Information theory has been shown to be a useful tool to validate or exclude potential information-carrying mechanisms, such as firing rate, temporal firing patterns of single-neurons, and firing synergies among multiple neurons (Theunissen and Miller, 1995 ; Nirenberg and Latham, 1998 ; Borst and Theunissen, 1999 ; Victor, 2000 , 2006 ; Nirenberg et al., 2001 ; Panzeri and Schultz, 2001 ; Golledge et al., 2003 ; Panzeri et al., 2003a ; Schneidman et al., 2003 ; Foffani et al., 2004 ; Schnupp et al., 2006 ; Nelken and Chechik, 2007 ; Scaglione et al., 2008 ; Montani et al., 2009 ; Petersen et al., 2009 ; Quian Quiroga and Panzeri, 2009 ).
The Data Set
Before presenting the information analysis, we briefly illustrate and describe the dataset of single neuron recordings from the somatosensory cortex of rats that we will use for all the analyses in this article. These data were originally published in Lebedev et al. (2000 ). In the following, we provide an overview of the experimental conditions.
Adult male Wistar rats weighing approximately 350 g were used. Anesthesia was induced by urethane (1.5 g/kg of body weight). The subject was placed in a stereotaxic apparatus and left somatosensory cortex was exposed by a craniotomy. Anesthesia was held at a depth characterized by a bursting rate and local field potential frequency of 0.5–8 Hz (Erchova et al., 2002 ). An array of six tungsten microelectrodes with 300 ± 50 μm separation between adjacent electrode tips was advanced into the cortical barrel field. Neurons in barrel-column D2 and surrounding D-row barrel-columns were sampled. Neuronal activity was amplified and band-pass filtered in the range 300–7,500 Hz. Action potentials were digitized at 25 kHz and stored on a PC.
All whiskers were trimmed to a 3-mm length. Individual whiskers were deflected by piezoelectric wafer positioned just below the whisker shaft, 2 mm from the skin. The stimulus was an up-down step function of 80-μm amplitude and 100 ms duration delivered once per second 50 times for each vibrissa. The stimulated vibrissae were C1-3, D1-3, E1-3, gamma, and delta. Single-unit action potentials were discriminated using a template-matching algorithm written in MATLAB (Mathworks, Inc, Natwick, MA, USA). Classified action potentials were time-stamped with 0.1 ms resolution.
Information Carried by Spike Timing Measured Aligned to an External Reference Frame
To introduce the concept of extracting information from neural responses using knowledge of the stimulus time, we review the previously reported results (Panzeri et al., 2001 ) concerning the stimulus location information carried by spike counts and spike times of single neurons recorded in barrel D2.
This analysis was based on a post-stimulus time window 0–T, where T was varied parametrically in the range 5–40 ms in steps of 5 ms. To evaluate spike count information, the “response” r on each trial was simply the number of spikes occurring in the time window 0–T. To evaluate spike timing information, the window 0–T was broken into bins of size Δt, where Δt is the temporal precision at which spike times are considered. Different values of Δt (from 20 to 2.5 ms) were used. The overall contribution of temporal encoding was then quantified as the difference between the spike timing and the spike count information. The resulting information calculation corresponds to the amount of knowledge available to an observer that can read spike times with a resolution of Δt. Since in both the spike count and the spike timing analysis the post-stimulus window and the presence and timing of spikes were measured with respect to the stimulus time, the implicit assumption of this analysis is that the downstream system reading information has precise knowledge of the stimulus onset time.
Given that typical spike counts for barrel cortical neurons are low, in this particular dataset we could compute the mutual information reliably using the so-called series expansion method (Panzeri and Schultz, 2001 ), which provides a data-robust information evaluation. Using this formalism and the associated sampling bias corrections (Panzeri and Schultz, 2001 ), we addressed whether spike timing was important for the coding of the location of the stimulated whisker. Further, we asked what were the most important components of the code.
The time course of information (averaged over a population of 106 cells recorded in barrel D2) is shown in Figure 1 A. Early in the response (0–10 ms post-stimulus onset), the spike count provided almost as much information (90% on average) as spike times measured with precision Δt = 5 ms. Later, however, there was a significant advantage for the timing code: at 40 ms, spike times sampled at precision Δt = 5 ms provided 55% more information than did total spike counts.
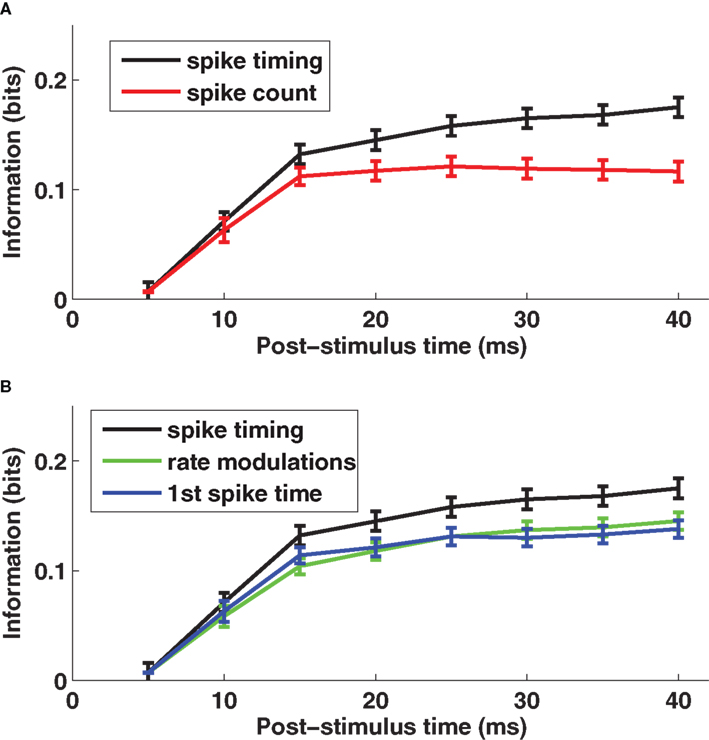
Figure 1. The encoding of stimulus location by single neuron spike times with knowledge of external clock. (A) The post-stimulus time course of the information about stimulus site available from two different neural codes provided the decoder knows stimulus time. Results are plotted as average (±SEM) across cells of the mutual information functions. The black line denotes the spike timing information obtained when sampling spikes with temporal resolution Δt = 5 ms, and the red line denotes the spike count information. (B) The post-stimulus time course of the total information carried by spike times (black line) obtained when sampling spikes with temporal resolution Δt = 5 ms, compared to the information carried by the time-varying firing rate (green line) and to the information computed using only the timing of the first spike on each trial (blue line), both obtained with the same resolution Δt = 5 ms. Results are plotted as average (±SEM) across all recorded cells. Figure modified from results presented in Panzeri et al. (2001 ).
What is the temporal resolution of the readout necessary to extract the entire quantity of information? To answer this question, we varied the width Δt of the time bins in the range 2.5–20 ms. We found that the transmitted information increased steadily with decreasing Δt, with more than 50% additional information transmitted using precision Δt = 2.5 ms compared to Δt = 20 ms (Panzeri et al., 2001 ). This suggests spike times carry their information using a temporal precision of a few milliseconds.
Further, we asked what were the most important components of the code. We used the series expansion formalism (Panzeri and Schultz, 2001 ) to separate the contribution of stimulus modulation of the time-dependent firing rates from the contribution of correlations between spike times. At 40 ms post-stimulus onset, firing rate modulations conveyed 83% of the total information (Figure 1 B). The contribution to information of correlations between the spike times was smaller (17%) (Panzeri et al., 2001 ).
To understand whether response latency played a special part in the spike timing code, we compared the information transmitted using all spikes after whisker deflection on each trial to that using only the first spike after whisker deflection. The result (Figure 1 B) was that 83% of the total information in the spike train for 0–40 ms was available in the time of the first spike alone. Moreover, for each time step in the 0–40 ms interval, the first spike accounted for essentially all of the information in firing rate modulation (Figure 1 B). Hence, the only information bearing part of the time-varying firing rate modulations was the response onset.
The conclusion is that individual rat somatosensory cortical neurons encode stimulus location largely by differences in time-varying firing rate, and that the response latency measured with millisecond resolution is the key symbol in this code. This encouraged us to look for a decoding mechanism based upon the relative spike latency of different neurons, the goal of the current work.
Information Carried by Spike Timing Measured without an External Reference Frame
We address the problem of decoding without stimulus time knowledge by considering the single-whisker deflection data reviewed in previous sections. This dataset is particularly interesting for our purpose because the population carried, at both the single neuron and the neuronal-pairs level, essentially all information about stimulus location in the timing of the first spike emitted post-stimulus deflection (Panzeri et al., 2001 ; Petersen et al., 2001 ). Therefore it is particularly important to understand if the information content of these spike times can be decoded without a precise knowledge of the stimulus time.
Columnar Population Latencies and Columnar Population Spike Counts in Response to Single-Whisker Deflection
Let us start by examining population activity in a single trial. Figure 2 A shows the responses of 100 non-simultaneously recorded neurons in column D2 to one deflection of whisker D2 at time t = 0. The neurons are treated as if recorded simultaneously – the effect of non-simultaneity of recordings will be addressed later by simulations. Approximately 10 ms after stimulus onset, there was a sharp increase in firing rate which led many neurons to fire nearly simultaneously (gray area in Figure 2 A). By 50 ms after stimulus onset, activity had almost returned to baseline level (Figure 2 A). Responses of these neurons to deflection of a different whisker (D1) are shown in panel 2B, where spikes were now more distributed in time. Figures 2 C,D shows the summed activity of column D2 units in response to deflection of whiskers D1 and D2. The response to the topographically matching whisker was stronger, had shorter latency and was more uniformly timed across the population.
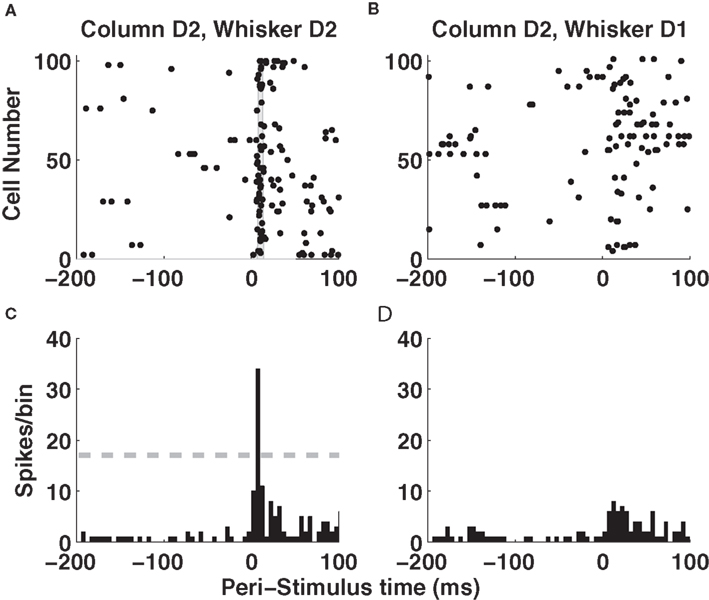
Figure 2. Single-trial responses of a barrel column to whisker deflection. (A) Raster plots of the spike times emitted in a single example trial by 100 neurons recorded non-simultaneously in barrel-column D2 around the time of deflection of the principal whisker D2. The gray area denotes the time window around 10 ms when many neurons synchronously fire their first post-stimulus spike. (B) Raster plots of the spike times emitted in a single example trial by 100 neurons recorded non-simultaneously recorded in barrel-column D2 around the time of deflection of the whisker D1. (C) The time course (sampled in 5-ms bins) of the summed activity of the whole population of D2 neurons around the time of deflection of D2 whisker in the same trial plotted in (A). The dashed horizontal line plots the threshold used to detect a “columnar synchronous response” (CSR) event. (D) The time course of the summed activity of the whole population of D2 neurons around the time of deflection of D1 whisker in the same trial plotted in (B).
Let us now consider how a downstream observer may decode such population activity. As shown in Figure 1 , the information carried by single neurons was only a fraction of a bit and thus was not high enough to support reliable stimulus discrimination; therefore, if the whole rat can localize tactile stimuli, decoding must be done at the population level. We have previously shown that pooling of neurons located within the same column (i.e., summing their population activity) does not lead to any loss of information about whisker identity (Panzeri et al., 2003b ); we will therefore consider in the following the summed population activity within a column.
It is tempting to reason that, without accurate knowledge of stimulus time it would be more efficient to count spikes over relatively large time windows, because coarse measures may be more robust to stimulus time uncertainty. To evaluate this hypothesis, we investigated how decoding accuracy using the summed spike count of the columnar population over long response windows depends on the knowledge of the stimulus time. A decoder based on columnar population spike counts exploits the fact that more spikes are emitted in response to the stimulation of the principal whisker than to any other whisker, both in the anesthetized (Petersen et al., 2002a ) and awake, behaving brain (von Heimendahl et al., 2007 ). Figure 3 A (left part) shows a scatterplot of the summed spike counts of 100 cells in barrel D2 on each trial in a 0–50 ms post-stimulus window. In this window, high spike counts correspond to stimulation of principal whisker D2 and low spike counts correspond to stimulation of the non-principal whisker D1. The distribution of counts is well separated and only two trials out of 96 would be confusable. However, since spike counts are stimulus-modulated only briefly following the stimulation, this excellent discriminability can be achieved only if the decoder knows when to count the spikes. Suppose the decoder is uncertain about stimulus time, and therefore erroneously counts spikes comprising non-stimulus-driven activity, for example in the −500 to +50 peri-stimulus time. In this case, the population spike counts cannot be correctly decoded in most trials (Figure 3 A, right part). The conclusion, perhaps counterintuitive, is that integrating columnar spike counts over long windows is not an effective way to make the neural code robust to errors in the estimation of the stimulus time. In this data set, population spike counts can only be decoded with some knowledge of the stimulus time.
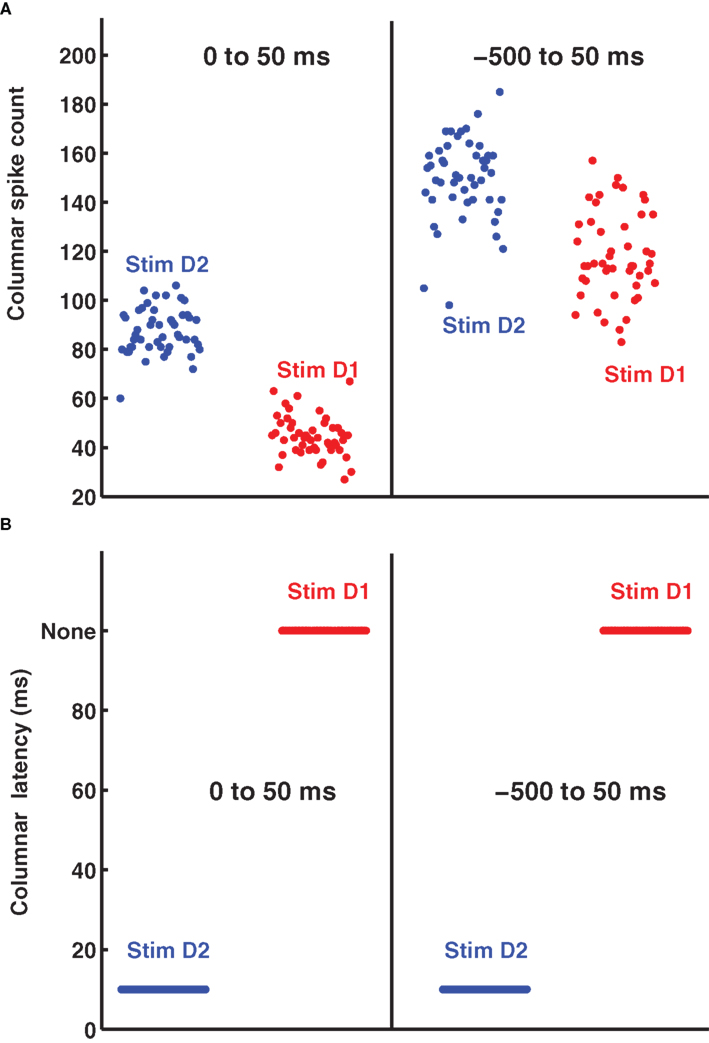
Figure 3. The distribution of single trial D2-columnar spike counts and of columnar latencies. (A) Reports the scatter plot of the single-trial summed spike count of a population of 100 neurons in barrel D2 over all the trials available to deflection of whisker D2 (blue dots) and whisker D1 (red dots). The left and right part of (A) report respectively the spike counts obtained in the 0 to 50 ms and −500 to 50 ms peri-stimulus window respectively. (B) Shows the scatter plot of the timing of columnar latency (defined as the timing of single-trial synchronous columnar response events) of a population of 100 neurons in barrel D2 over all trials to deflection of whisker D2 (blue dots) and whisker D1 (red dots). The left and right part of (B) show, respectively, the results obtained in the 0 to 50 ms and −500 to 50 ms peri-stimulus window.
An alternative hypothesis is that registering the time course of population response with high temporal precision can actually make the code more robust to the stimulus time errors. Figures 2 A,B shows that the first spikes emitted by the 100 neurons in barrel D2 after stimulation of their principal whisker are much more precisely timed than second spikes or than spikes emitted in response to a non-principal whisker. This suggests that we can indeed use the precisely aligned response latencies of individual neurons to define a “columnar synchronous response” (CSR) event characterized by the firing of at least a certain fraction f of neurons within a short interval of Δt ms (see illustration in Figure 2 C). The fraction f of neurons firing and the width of the time window Δt are free parameters. In this article, we use f = 0.17 and Δt = 5 ms (as in Figure 2 C), because we found empirically that these values were optimal. We systematically searched for CSR events by moving a sliding window of size Δt = 5 throughout the peri-stimulus time. The event occurred only in the window [10–15] ms after deflection of the principal whisker, and never during spontaneous activity or after stimulation of a non-principal whisker. This result is exemplified in one selected trial in Figures 2 C,D but (as shown in Figure 3 B), it holds for all trials. Thus, detecting spike synchrony at fine temporal precision leads to 100%-correct detection of the stimulation of the principal whisker D2. In stark contrast to the spike count code, CSR detection was not degraded by the inclusion of spontaneous activity periods due to incorrect stimulus onset knowledge, because no CSR ever occurred during spontaneous activity (Figures 2 D and 3 B). In addition, since the response onset always happened 10–15 ms after deflection of the principal whisker (Figure 3 B), CSR can specify the stimulus timing with a few milliseconds of precision, as well as the identity of the stimulus. A similar mechanism has been proposed for detection of the high-speed whisker jumps that occur during texture palpation (Jadhav et al., 2009 ). Of course, the mechanism works if a decoder can perform a CSR detection operation such as that done by a post-synaptic neuron with an integration time constant of a few milliseconds and a fixed threshold for firing (Ayling, 2008 ; Stuttgen and Schwarz, 2010 ).
Information Content of Population Latencies and Counts in a Single Column
The above analysis suggests that detecting the population response leads to a more reliable and robust decoding of stimulus identity as opposed to simply counting all the spikes in the population over long time windows. We studied in more detail how the performance of the two candidate decoding schemes depends on both the size of the columnar population and on the amount of uncertainty about the stimulus time.
We considered a population of n sequentially recorded neurons in column D2, and varied n parametrically from 1 to 100. We computed how much information the population encoded about whether whisker D1 or D2 was stimulated. Perfect discrimination corresponds to 1 bit of information. We assumed that the decoder has only imprecise knowledge about when whisker deflection will occur and, as a consequence, processes both periods of spontaneous activity preceding the stimulus as well as the stimulus-evoked response. We mimicked this by quantifying the columnar population responses from a time X before the stimulus time to a post-stimulus time T = 50 ms. Larger values of X correspond to higher uncertainty about the stimulus application time. The parameter X was varied between −500 ms and 0 ms (i.e., exact knowledge of stimulus time). There are other ways to model uncertainty about stimulus time when the events are presented continuously and the purpose is to select between potential stimulus features rather than select between evoked and spontaneous activity (e.g., Arabzadeh et al., 2006 ). For detection of the onset of a stimulus, the method used here has two advantages. First, spontaneous activity is one of the greatest problems for measuring latency, and so its inclusion is a stringent and relevant test for the robustness of latency codes. Second, it is a simple but reasonable way to model a coarse “window of stimulus expectation” that may for example accompany the motor commands initiating active whisking.
For any choice of X, we considered the information carried by two types of neural codes, the columnar spike count and the columnar latency code, as described next. For the columnar spike count we quantified the response r (Eq. 1) as the total number of spikes emitted within the window by all neurons in the population (as in the example of Figures 2 and 3 ). To compute the information encoded by the columnar latency, we detected CSR events (as explained above and illustrated in Figure 2 C); we called the time at which the first CSR event was detected in a certain barrel in a given trial the “columnar latency” and we used it as the variable r in Eq. 1.
We first considered the case in which the stimulus time is known precisely (X = 0 ms). The corresponding dependence of information on the population size is plotted in Figure 4 A. With a single cell (n = 1), the columnar latency reduces to the first-spike latency, and the columnar population spike count matches the single cell spike count. Consequently, the information values for columnar latency and columnar count equal those previously reported (Panzeri et al., 2001 ) for single neuron first-spike latency and single neuron spike count (0.15 bits and 0.10 bits respectively). The information available in both columnar counts and columnar latencies increased steeply with the population size n (Figure 4 A). When considering n = 100 cells, 1 bit of information (corresponding in this case to 100% correct discrimination) was available from columnar latencies and 0.89 bits were available from columnar counts. Thus, when stimulus time is known precisely the information available in columnar latency is higher than that available from counts over a large range of population size, but the information gain by columnar latency is moderate.
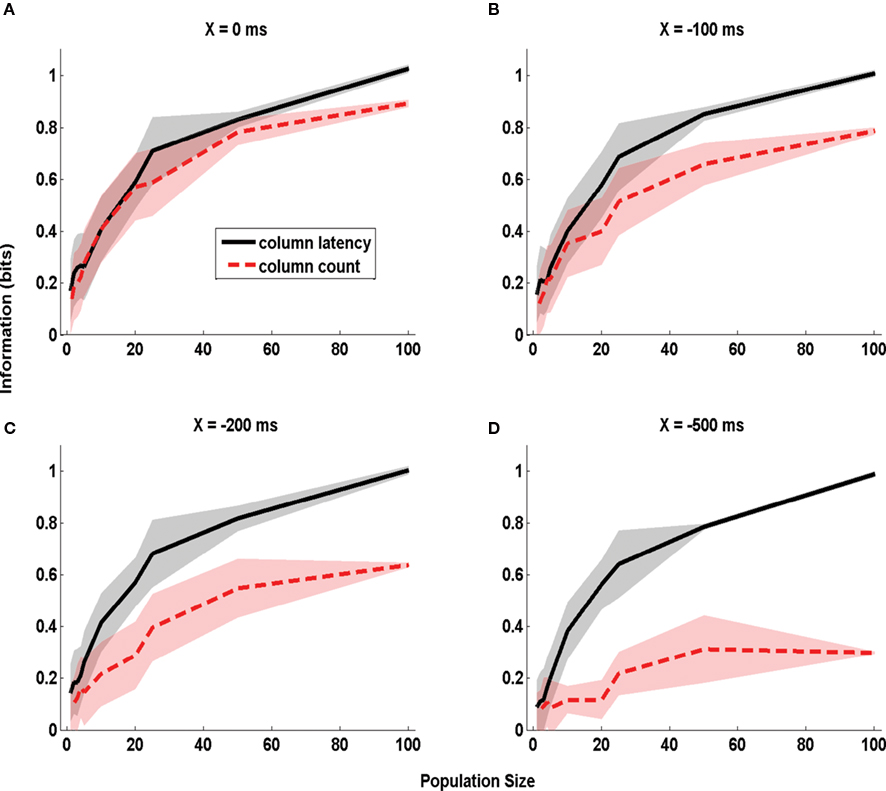
Figure 4. The dependence of information obtained by decoding the activity of one column on stimulus time uncertainty X. The information about whether whisker D1 or D2 was deflected, obtained by the summed counts (red line) or the latency of synchronous population activity (black line) of a population of neurons located in a single column (barrel D2). The information is computed in a time window starting X ms before stimulus onset and extending to 50 ms post-stimulus, and is plotted as a function of the size of the population of D2 neurons considered. (A–D) Report information values which were obtained when using respectively the values 0, −100, −200, and −500 ms for the parameter X quantifying the uncertainty about the stimulus time. Results are plotted as average (±SD; colored area) across all analyzed subgroups of cells with the specified population size.
The situation was different when there was stimulus time uncertainty of 500 ms (i.e. X = −500ms; Figure 4 D). For small population sizes there was essentially no advantage in columnar latencies over counts. For single cells (n = 1), the information available in latencies (0.1 bits) was similar to that available in counts (0.09 bits). This is because for small population sizes the columnar latency reduces to a single neuron first-spike latency code, and the latter is difficult to extract without knowledge of the stimulus time. However, as the population size increased, the information available in population latencies increased much more steeply than the information available in population counts. This is because the population latency, but not the spike count code, became robustly separable from the pre-stimulus activity. For n = 100 cells, perfect stimulus discriminability (1 bit) was achieved by the population latency code, but a much poorer discriminability (0.30 bits) was achieved by the spike count.
Intermediate values of stimulus time uncertainty (X = −100 and −200 ms, Figures 4 B,C) led to an intermediate increase of the information advantage of using population latencies rather than counts. For populations larger than 10 neurons, the larger the error in stimulus time knowledge, the larger was the information advantage of a columnar latency code. An information of 0.6 bits could be extracted from the columnar latency code with as few as 25 cells even in total absence of stimulus time knowledge. Once the uncertainty in the stimulus time exceeded 200 ms, extracting the same 0.6 bits from the spike count code could not be achieved for any population size.
In the above analysis, varying the parameter X affected both the amount of uncertainty about the stimulus time and (in the case of spike counts) the duration of the integration time window. To check that window variation did not confound our estimate of the effect of stimulus time ignorance, we repeated the same analysis as in Figure 4 but using a different parameterization of stimulus time uncertainty. Now we used sliding windows of equal duration (50 ms), but parametrized stimulus time uncertainty by varying the time step Y by which this sliding window was shifted with respect to the correct stimulus onset. The information was, as above, relative to stimulus site D1 or D2. The dependence of extracted information on Y is reported in Figure 5 . It is clear that the information in the columnar latency was more robust to errors in the stimulus time than the information in the columnar spike counts, even when using such parametrization of the uncertainty of stimulus time.
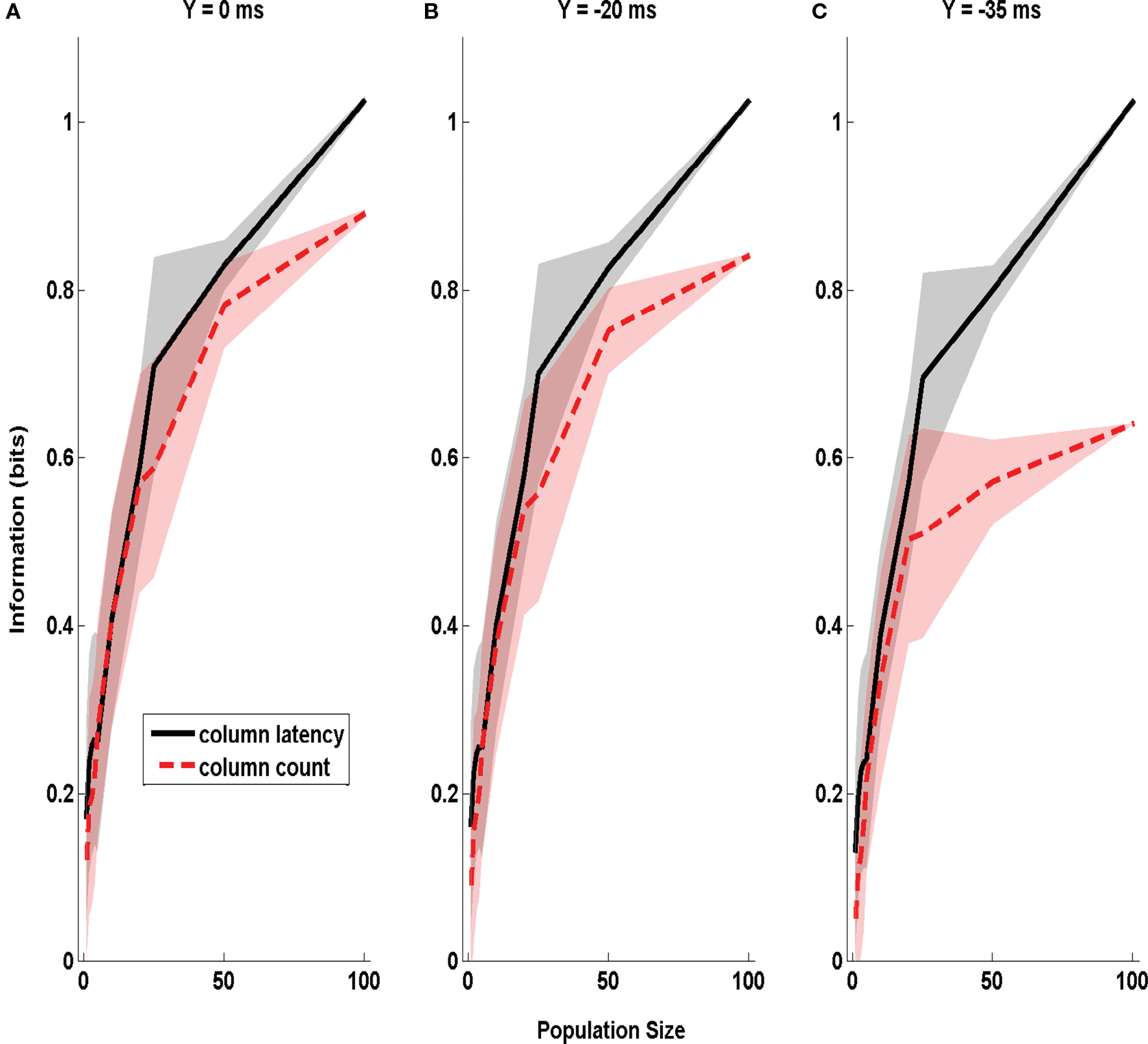
Figure 5. The dependence of Information obtained by decoding the activity of one column on stimulus time uncertainty Y. The information about whether whisker D1 or D2 was deflected, obtained by the summed counts (red line) or the latency of synchronous population activity (black line) of a population of neurons located in a single column (barrel D2). The information is computed in a time window of duration 50 ms starting Y ms before stimulus onset, and is plotted as a function of the size of the population of D2 neurons considered. (A–C) Report information values which were obtained when using respectively the values 0, −20, and −35 ms for the parameter Y quantifying the uncertainty about the stimulus time. Results are plotted as average (±SD; colored area) across all analyzed subgroups of cells with the specified population size.
In sum, decoding strategies based on the synchronized columnar population latency have multiple advantages with respect to decoding by integrating spike counts over longer windows: columnar latency decoding (1) conveys more information per cell and requires fewer cells for reliable discrimination, and (2) is more robust to uncertainty about stimulus time.
Decoding the Responses of Populations of Neurons in Multiple Barrels
Next we consider the more complex problem of decoding the activity of multiple columns to identify stimulus site from among several candidate whiskers.
We took the activity of 100 non-simultaneously recorded neurons per column from three different barrel-columns (D1, D2, and D3) in response to stimulation of whisker D1, D2, D3 or another whisker, E1, non-principal to any of the considered columns. We again considered an uncertainty X in the knowledge of the stimulus time, and again evaluated different decoding schemes based on relative latency and spike counts respectively.
Quantification of information from the populations in three columns is much more difficult than a single column: the response r of the three-column population is a three dimensional array, and the number of trials per stimulus available is not sufficient to sample in enough detail the full multivariate stimulus-response probabilities. For this reason, we computed the information available in the activity of the three columns by using an intermediate stimulus reconstruction step. Stimulus reconstruction can be operationally defined as a rule leading to the prediction of which stimulus or behavior elicited a neuronal response in a single trial. It can be mathematically defined as a function g(r) operating on the population response in any given trial and giving a prediction sP(r) of the stimulus that elicited the observed neural population response in that trial:
The information extracted through the stimulus reconstruction scheme can be quantified as follows (Quian Quiroga and Panzeri, 2009 ):
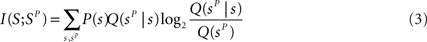
where in the above Q(sp) = ΣsP(s)Q(sp|s), and Q(sP | s) is the “confusion matrix.” Its values in a given row s and column sP of a confusion matrix represent the (normalized) number of times that a presentation of stimulus s is predicted by the decoder to be stimulus sP:
where δ is a Kronecker Delta. The decoded information I(S;SP) quantifies the total information gained when predicting the stimulus using a specific algorithm, and takes into account both the fraction of correct decoding and the spread of the decoding errors. Information theoretic inequalities ensure that I(S;SP) ≤ I(S;R). The reason I(S;SP) can sometimes be strictly less than I(S;R) is that I(S;SP) refers to a specific algorithm, whereas I(S;R) bounds the performance of all possible algorithms operating on the response r.
We computed the information I(S;SP) gained with three different decoding schemes, each corresponding to a different choice of coding scheme (i.e., a different quantification of the population response r) and of stimulus reconstruction function g in Eq. 2, as described next.
The first decoding scheme was the one based on the relative population latency of each column (in the following termed “columnar latency difference decoder”). This decoding was implemented as follows. In each trial we detected, independently in each column, the presence and timing of synchronous columnar response (CSR, as described earlier) events, exactly as described in the previous section. Then, in each trial, we decoded the stimulus by the following rule: if at least one barrel-column exhibited a CSR event, we decoded the stimulus site as being principal to the column firing the first event (note that this implies that the relative, rather than the absolute timing of each column is used for decoding). If no synchronous columnar population event was detected in the trial from any of the columns, we decoded the stimulus in that trial as whisker E1 (the only one not principal to any of the considered columns). It is important to note that the relative population latency coding scheme is a genuine form of population temporal encoding, and cannot be reduced to a simple spike count code in a short time window: events are defined separately for a population in each column, and information is computed from the relative timing of such events. In fact, when we considered fewer than n = 100 neurons in each barrel, there were several trials in which CSR events occur in more than one barrel (6% and 21% of trials on average for n = 50 and n = 25 respectively), and in this case the decoded whisker is the one principal to the barrel in which the first CSR event was evoked.
The second decoder was recruitment order. This algorithm considers the relative order in which each neuron within the population (rather than the pooled columnar activity) fires its first spike (Van Rullen and Thorpe, 2001 ; Johansson and Birznieks, 2004 ; Saal et al., 2009 ). We tested the performance of the recruitment order decoding with a procedure very close to that of (Johansson and Birznieks, 2004 ). In each trial, the first-spike latency of each neuron was measured as the time between the beginning of the sampling window and the appearance of the first spike. For each stimulated whisker, we constructed a template of the recruitment order of the neurons in response to the stimulus by sorting the neurons according to their mean rank over a set of training trials. We then used the remaining set of “test” trials to compute how well the recruitment order could predict the stimulus. For each test trial, the population response was defined as the rank order of first-spike latencies of each neuron. We then denoted the most likely whisker SP as that with the highest Spearman rank correlation to the population response of the current test trial. Two different procedures of cross-validation were employed: random division into 10 training and 38 test trials, and the leave-one-out procedure. The procedures gave equivalent results. It is important to note that the rank order coding scheme is also a genuine form of population temporal encoding.
The third decoder was the “columnar spike count decoder”, which operated on the summed spike count within each column. The population response r was a three dimensional array whose components correspond to the total spike count in columns D1, D2, and D3, respectively, and it was discretized into five equispaced classes independently in each column (the number of classes was set to five because we found empirically that this parameter choice maximized the performance of this decoder). From the training data, we computed the empirical posterior probability of joint columnar P(s | r) and then decoded the most likely stimulus, i.e.,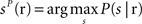 
. Cross-validation was performed as described above.
Results of the three coding schemes are reported in Figure 6 for different values of the stimulus time error X (from −500 to 0 ms) and for three different population sizes (n = 25, 50, and 100 cells per column). It is apparent that the first scheme, the columnar latency difference decoder, was the most informative and was also most robust to the stimulus time ignorance, for all population sizes considered. For example, when considering 100 cells per column (Figure 6 A), the columnar latency difference decoder yielded 100% accurate stimulus reconstructions (2 bits of information) whatever the stimulus time uncertainty X. Rank order decoding also performed well when the stimulus time was known precisely (X = 0), but was much less robust to the inclusion of periods of spontaneous activity. This is because the longer the spontaneous activity period, the higher the chance that the rank of individual neurons will be random. The columnar pooling operation removes this noise in the activation order at the single neuron level (because stimulus-evoked peaks are narrower and stronger than spontaneous peaks). Consistent with the results of Figures 2 and 3 , the spike count decoder performed well when the stimulus time was known, but it performed poorly when periods of spontaneous activity were incorporated.
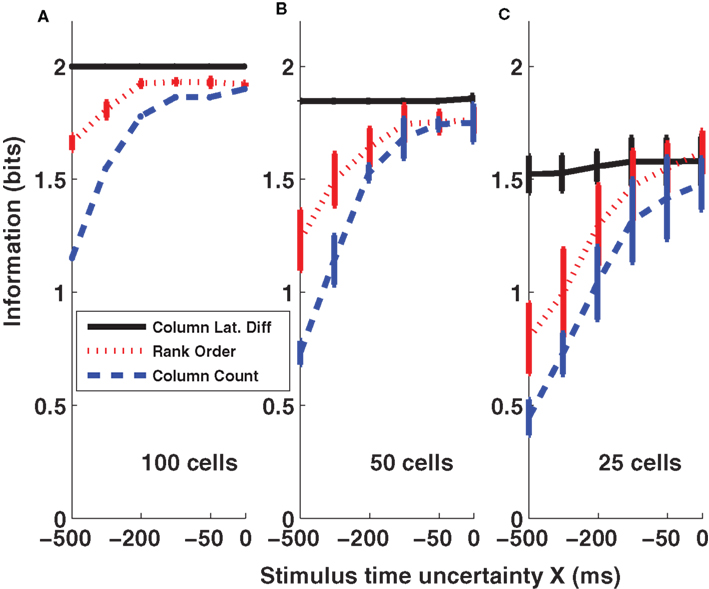
Figure 6. Information obtained by decoding the activity of three columns (barrels D1, D2, and D3). The amounts of information (Eq. 3) decoded by the columnar latency (black line), the rank order (red line) and the columnar count (blue line) decoders respectively are plotted as a function of the parameter X which quantifies the uncertainty about the stimulus time. (A–C) Plot the results obtained when using populations of 100, 50, and 25 cells in each column respectively. Results are plotted as average (±SD) across all analyzed subgroups of cells with the specified population size.
The criticism can be raised that our calculations do not take into account the effects of correlated noise, because they are based on a pseudo-simultaneous response arrays constructed by collecting together responses of non-simultaneously recorded neurons. Correlated noise may amplify the variability of the time course of the population activity (Mazurek and Shadlen, 2002 ), and by canceling such correlations our method may eliminate any strong and narrow spontaneous activity peaks in the pooled population – in effect, simulated populations may reduce “false positives” compared to real populations that contain correlated noise. To test for this, we used the procedure of Mikula and Niebur (2003) to generate correlated spike trains that matched exactly the true population-averaged PSTH of the neurons (sampled with 1-ms bins) and the true pair-wise Pearson cross-correlation value of neurons within the same column (the latter collected from a dataset of 52 D2–D2 neuronal pairs simultaneously recorded in the same conditions with a small array of electrodes, see Petersen et al., 2001 ) in each 1-ms-wide peri-stimulus time bin. When the simulated population of 100 cells per column with realistic correlation values was tested, performance of the columnar latency difference decoder as a function of X was unchanged (P > 0.3, one way ANOVA). To further check the robustness of the decoder to increased values of correlation, we increased correlations by a factor of four with respect to those present in real data. The columnar decoder then showed only a very small decrease in the decoding performance (less than 0.1 bits for each value of X compared to those reported in Figure 6 A when using 100 cells per barrel; results not shown, but see Ayling, 2008 for more details). For other studies of the effect of correlated activity on the robustness of relative-timing decoders, we refer the reader to (Chase and Young, 2007 ; Gollisch and Meister, 2008 ).
Discussion and Conclusions
The temporal precision at which neural responses carry information has been systematically investigated over the last 20 years in several sensory structures. Substantial evidence (recently reviewed in Panzeri et al., 2010 ) shows that the timing of spikes with millisecond precision carries much more information than that carried by spike counts over windows of tens or hundreds of milliseconds. However, the observation that information is carried by neural codes at a high temporal precision does not guarantee that the nervous system makes use of such codes. One of the most compelling criticisms is that temporally precise signals may not be decodable unless the downstream population has access to an equally precise external reference frame. The results presented here suggest that a precise external reference frame is not always necessary: spike timing-based decoders can work well without knowledge of the stimulus time in some conditions. Moreover, our results corroborate previous reports (Soteropoulos and Baker, 2009 ; Stuttgen and Schwarz, 2010 ) that the time course of neural population activity can be used to estimate the timing of stimulus application. We also found that, contrarily to simple intuition, relative timing codes are less degraded than spike count codes by inaccuracies in stimulus time knowledge.
Another caveat regarding spike timing coding is that in large populations there may be enough information available in spike counts to make the extra spike timing information unneeded; a ceiling effect. Our results show that, while this may be the case when the stimulus time is known with precision, in the harder task of decoding the stimulus without stimulus time knowledge, spike time mechanisms outperform those based on spike counts, and especially so as population size grows. With stimulus time uncertainty, even large populations of neurons could not be perfectly decoded by spike counts (see Figures 4 and 6 ), implying that population signals never reach a ceiling if decoded inefficiently. This suggests that previous small-population reports of encoding information by spike timing may actually underestimate (rather than overestimate) the importance of spike timing at the population level.
The results in this article were obtained considering only the encoding of simple stimuli (single-whiskers deflected in a binary manner – on/off) and need to be extended to stimulus time-free decoding of dynamic stimulus features of naturalistic complexity. There is reason to expect that the information-carrying advantage of relative timing codes over spike count codes may be even more advantageous for such stimuli. Naturalistic stimuli often consist of complex sequences of features – in the whisker system, such features include position, velocity, absolute speed, acceleration (Arabzadeh et al., 2005 ; Hipp et al., 2006 ; Lottem and Azouz, 2008 ). By reverse correlation methods, it has been shown that neurons in the sensory pathway act as “filters” for different features: they fire with varying probability and latency according to the strength of some set of features in some preceding moment (Petersen et al., 2008 ). Because neurons respond to multiple features and because the features often occur in close temporal proximity or even in temporal superposition, single-neuron decoding will always be ambiguous. To decode the sequence of features and their magnitude, a highly efficient readout of the population would be based upon the relative latencies of neurons with heightened sensitivity to specific features. For example, the firing of “high-acceleration neurons” a few milliseconds before “high-speed neurons” would signal a change in whisker direction followed by a high-speed jump. Target neurons receiving combined inputs could achieve this sort of decoding. Timing comparisons would be done not between whole columns (the condition for stimulus localization) but between sets of neurons within or across columns with varying feature selectivity.
The stimulus time-free decoding algorithms of response latencies which was presented in this study relies on the concept that there are classes of neurons activated with similar latencies by the stimulus feature to be decoded. This assumption is conceivable when considering primary cortical sensory areas, in which first-spike latency codes have been consistently reported. It however remains to be understood whether such conditions extend to higher order cortical systems where neurons can show both increases and decreases in response to a sensory stimulus or a behavioral event, or even whether constant sensory feedback in the awake behaving animal may disrupt the conditions for detection of synchronous activation of a neural population.
An important question for theoretical research is how a downstream system could learn to be selective to the “first wave” of spikes in each column that forms the basis of the stimulus-time free coding scheme. Recently, Thorpe and colleagues (Masquelier et al., 2008 , 2009 ) proposed that spike time-dependent plasticity (STDP) (Markram et al., 1997 ; Bi and Poo, 2001 ; Jacob et al., 2007 ) may provide the appropriate synaptic mechanism for learning such first spike codes: a certain “downstream” post-synaptic neuron will fire at random during the wave of first spikes at the beginning of the learning phase. When this happens, STDP reinforces the connections with all the afferents that take part in the first wave of spikes, thereby increasing the probability of the downstream neurons firing again in response to the first wave of spikes.
In general, to determine the extent to which spike time codes are used in the nervous system, it is important to establish links between the temporal precision of neural codes and behavior. The current evidence is vigorously debated (Luna et al., 2005 ; Engineer et al., 2008 ; Yang et al., 2008 ; Jacobs et al., 2009 ; Gerdjikov et al., 2010 ). While the data presented here do not speak directly to this issue, it is interesting to note that a mechanism similar to our was used by Stuttgen and Schwarz (2010 ), who demonstrated that the distribution of occurrence of such events across trials in different stimulus discrimination conditions is significantly correlated with the animal’s behavioral performance. Whisker kinetic features also seem to be encoded by CSR-like firing (Jadhav et al., 2009 ). Future developments of the clock-free method will therefore focus on decoding complex stimuli (Maravall et al., 2007 ; Petersen et al., 2008 ) and stimuli experienced by awake, behaving rats, such as those reported in von Heimendahl et al. (2007 ).
In conclusion, our results demonstrate that the precise timing of spikes emitted shortly after stimulus presentation forms the basis for an information-rich code, which is robust to the stimulus time problem at the population level. Moreover, the time course of population responses can be used by the nervous system to provide information not only about the stimulus identity but also about the stimulus time itself.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the referees for thoughtful and detailed critiques which significantly improved the revised version of the manuscript. We thank C. Kayser, R.S. Petersen, and G. Notaro for useful discussions, and M.A. Ayling for contributing to the implementation of the rank order decoding algorithm. This research was supported by the BMI project of the Italian Institute of Technology and by the San Paolo Foundation, the Human Frontier Science Program (contract RG0041/2009-C), the European Community (contract BIOTACT-21590), and the Ministry of Economic Development.
References
Arabzadeh, E., Panzeri, S., and Diamond, M. E. (2006). Deciphering the spike train of a sensory neuron: counts and temporal patterns in the rat whisker pathway. J. Neurosci. 26, 9216–9226.
Arabzadeh, E., Zorzin, E., and Diamond, M. E. (2005). Neuronal encoding of texture in the whisker sensory pathway. PLoS Biol. 3:e17.
Ayling, M. (2008). A computational analysis of the functional role of GABAergic synaptic transmission in striatal medium spiny neurons. Ph.D. thesis, Faculty of Life Sciences, University of Manchester, Manchester.
Bi, G., and Poo, M. (2001). Synaptic modification by correlated activity: Hebb’s postulate revisited. Annu. Rev. Neurosci. 24, 139–166.
Borst, A., and Theunissen, F. E. (1999). Information theory and neural coding. Nat. Neurosci. 2, 947–957.
Brody, C. D., and Hopfield, J. J. (2003). Simple networks for spike-timing-based computation, with application to olfactory processing. Neuron 37, 843–852.
Chase, S. M., and Young, E. D. (2007). First-spike latency information in single neurons increases when referenced to population onset. Proc. Natl. Acad. Sci. U.S.A. 104, 5175–5180.
Chechik, G., Anderson, M. J., Bar-Yosef, O., Young, E. D., Tishby, N., and Nelken, I. (2006). Reduction of information redundancy in the ascending auditory pathway. Neuron 51, 359–368.
Cover, T. M., and Thomas, J. A. (1991). Elements of Information Theory. New York: John Wiley & Sons, Inc.
Diamond, M. E., Petersen, R. S., and Harris, J. A. (1999). Learning through maps: functional significance of topographic organization in primary sensory cortex. J. Neurobiol. 41, 64–68.
Diamond, M. E., von Heimendahl, M., Knutsen, P. M., Kleinfeld, D., and Ahissar, E. (2008). ‘Where’ and ‘what’ in the whisker sensorimotor system. Nat. Rev. Neurosci. 9, 601–612.
Engineer, C. T., Perez, C. A., Chen, Y. H., Carraway, R. S., Reed, A. C., Shetake, J. A., Jakkamsetti, V., Chang, K. Q., and Kilgard, M. P. (2008). Cortical activity patterns predict speech discrimination ability. Nat. Neurosci. 11, 603–608.
Erchova, I. A., Lebedev, M. A., and Diamond, M. E. (2002). Somatosensory cortical neuronal population activity across states of anaesthesia. Eur. J. Neurosci. 15, 744–752.
Foffani, G., Chapin, J. K., and Moxon, K. A. (2008). Computational role of large receptive fields in the primary somatosensory cortex. J. Neurophysiol. 100, 268–280.
Foffani, G., Morales-Botello, M. L., and Aguilar, J. (2009). Spike timing, spike count, and temporal information for the discrimination of tactile stimuli in the rat ventrobasal complex. J. Neurosci. 29, 5964–5973.
Foffani, G., Tutunculer, B., and Moxon, K. A. (2004). Role of spike timing in the forelimb somatosensory cortex of the rat. J. Neurosci. 24, 7266–7271.
Furukawa, S., Xu, L., and Middlebrooks, J. C. (2000). Coding of sound-source location by ensembles of cortical neurons. J. Neurosci. 20, 1216–1228.
Gawne, T. J., Kjaer, T. W., and Richmond, B. J. (1996). Latency: another potential code for feature binding in striate cortex. J. Neurophysiol. 76, 1356–1360.
Gerdjikov, T. V., Bergner, C. G., Stuttgen, M. C., Wiblingen, C., and Schwarz, C. (2010). Discrimination of vibrotactile stimuli in the rat whisker system: behavior and neurometrics. Neuron 65, 530–540.
Golledge, H. D., Panzeri, S., Zheng, F., Pola, G., Scannell, J. W., Giannikopoulos, D. V., Mason, R. J., Tovee, M. J., and Young, M. P. (2003). Correlations, feature-binding and population coding in primary visual cortex. Neuroreport 14, 1045–1050.
Gollisch, T., and Meister, M. (2008). Rapid neural coding in the retina with relative spike latencies. Science 319, 1108–1111.
Harris, J. A., Petersen, R. S., and Diamond, M. E. (1999). Distribution of tactile learning and its neural basis. Proc. Natl. Acad. Sci. U.S.A. 96, 7587–7591.
Hipp, J., Arabzadeh, E., Zorzin, E., Conradt, J., Kayser, C., Diamond, M. E., and Konig, P. (2006). Texture signals in whisker vibrations. J. Neurophysiol. 95, 1792–1799.
Hopfield, J. J. (1995). Pattern recognition computation using action potential timing for stimulus representation. Nature 376, 33–36.
Jacob, V., Brasier, D. J., Erchova, I., Feldman, D., and Shulz, D. E. (2007). Spike timing-dependent synaptic depression in the in vivo barrel cortex of the rat. J. Neurosci. 27, 1271–1284.
Jacobs, A. L., Fridman, G., Douglas, R. M., Alam, N. M., Latham, P. E., Prusky, G. T., and Nirenberg, S. (2009). Ruling out and ruling in neural codes. Proc. Natl. Acad. Sci. U.S.A. 106, 5936–5941.
Jadhav, S. P., Wolfe, J., and Feldman, D. E. (2009). Sparse temporal coding of elementary tactile features during active whisker sensation. Nat. Neurosci. 12, 792–800.
Johansson, R. S., and Birznieks, I. (2004). First spikes in ensembles of human tactile afferents code complex spatial fingertip events. Nat. Neurosci. 7, 170–177.
Kayser, C., Montemurro, M. A., Logothetis, N., and Panzeri, S. (2009). Spike-phase coding boosts and stabilizes the information carried by spatial and temporal spike patterns. Neuron 61, 597–608.
Kleinfeld, D., Ahissar, E., and Diamond, M. E. (2006). Active sensation: insights from the rodent vibrissa sensorimotor system. Curr. Opin. Neurobiol. 16, 435–444.
Knutsen, P. M., and Ahissar, E. (2009). Orthogonal coding of object location. Trends Neurosci. 32, 101–109.
Lebedev, M. A., Mirabella, G., Erchova, I., and Diamond, M. E. (2000). Experience-dependent plasticity of rat barrel cortex: redistribution of activity across barrel-columns. Cereb. Cortex 10, 23–31.
Lottem, E., and Azouz, R. (2008). Dynamic translation of surface coarseness into whisker vibrations. J. Neurophysiol. 100, 2852–2865.
Luna, R., Hernandez, A., Brody, C. D., and Romo, R. (2005). Neural codes for perceptual discrimination in primary somatosensory cortex. Nat. Neurosci. 8, 1210–1219.
Maravall, M., Petersen, R. S., Fairhall, A. L., Arabzadeh, E., and Diamond, M. E. (2007). Shifts in coding properties and maintenance of information transmission during adaptation in barrel cortex. PLoS Biol. 5:e19.
Markram, H., Lubke, J., Frotscher, M., and Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215.
Masquelier, T., Guyonneau, R., and Thorpe, S. J. (2008). Spike timing dependent plasticity finds the start of repeating patterns in continuous spike trains. PLoS ONE 3:e1377.
Masquelier, T., Hugues, E., Deco, G., and Thorpe, S. J. (2009). Oscillations, phase-of-firing coding, and spike timing-dependent plasticity: an efficient learning scheme. J. Neurosci. 29, 13484–13493.
Mazurek, M. E., and Shadlen, M. N. (2002). Limits to the temporal fidelity of cortical spike rate signals. Nat. Neurosci. 5, 463–471.
Mehta, S. B., Whitmer, D., Figueroa, R., Williams, B. A., and Kleinfeld, D. (2007). Active spatial perception in the vibrissa scanning sensorimotor system. PLoS Biol. 5:e15.
Mikula, S., and Niebur, E. (2003). The effects of input rate and synchrony on a coincidence detector: analytical solution. Neural. Comput. 15, 539–547.
Montani, F., Ince, R. A., Senatore, R., Arabzadeh, E., Diamond, M. E., and Panzeri, S. (2009). The impact of high-order interactions on the rate of synchronous discharge and information transmission in somatosensory cortex. Philos. Trans. A Math. Phys. Eng. Sci. 367, 3297–3310.
Muller, J. R., Metha, A. B., Krauskopf, J., and Lennie, P. (2001). Information conveyed by onset transients in responses of striate cortical neurons. J. Neurosci. 21, 6978–6990.
Nelken, I., and Chechik, G. (2007). Information theory in auditory research. Hear. Res. 229, 94–105.
Nirenberg, S., Carcieri, S. M., Jacobs, A. L., and Latham, P. E. (2001). Retinal ganglion cells act largely as independent encoders. Nature 411, 698–701.
Nirenberg, S., and Latham, P. E. (1998). Population coding in the retina. Curr. Opin. Neurobiol. 8, 488–493.
Panzeri, S., Brunel, N., Logothetis, N. K., and Kayser, C. (2010). Sensory neural codes using multiplexed temporal scales. Trends Neurosci. 33, 111–120.
Panzeri, S., Petersen, R. S., Schultz, S. R., Lebedev, M., and Diamond, M. E. (2001). The role of spike timing in the coding of stimulus location in rat somatosensory cortex. Neuron 29, 769–777.
Panzeri, S., Petroni, F., Petersen, R. S., and Diamond, M. E. (2003b). Decoding neuronal population activity in rat somatosensory cortex: role of columnar organization. Cereb. Cortex 13, 45–52.
Panzeri, S., Pola, G., and Petersen, R. S. (2003a). Coding of sensory signals by neuronal populations: the role of correlated activity. Neuroscientist. 9, 175–180.
Panzeri, S., and Schultz, S. R. (2001). A unified approach to the study of temporal, correlational, and rate coding. Neural. Comput. 13, 1311–1349.
Panzeri, S., Senatore, R., Montemurro, M. A., and Petersen, R. S. (2007). Correcting for the sampling bias problem in spike train information measures. J. Neurophysiol. 98, 1064–1072.
Petersen, R. S., Brambilla, M., Bale, M. R., Alenda, A., Panzeri, S., Montemurro, M. A., and Maravall, M. (2008). Diverse and temporally precise kinetic feature selectivity in the VPm thalamic nucleus. Neuron 60, 890–903.
Petersen, R. S., Panzeri, S., and Diamond, M. E. (2001). Population coding of stimulus location in rat somatosensory cortex. Neuron 32, 503–514.
Petersen, R. S., Panzeri, S., and Diamond, M. E. (2002a). Population coding in somatosensory cortex. Curr. Opin. Neurobiol. 12, 441–447.
Petersen, R. S., Panzeri, S., and Diamond, M. E. (2002b). The role of individual spikes and spike patterns in population coding of stimulus location in rat somatosensory cortex. BioSystems 67, 187–193.
Petersen, R. S., Panzeri, S., and Maravall, M. (2009). Neural coding and contextual influences in the whisker system. Biol. Cybern. 100, 427–446.
Prigg, T., Goldreich, D., Carvell, G. E., and Simons, D. J. (2002). Texture discrimination and unit recordings in the rat whisker/barrel system. Physiol. Behav. 77, 671–675.
Quian Quiroga, R., and Panzeri, S. (2009). Extracting information from neuronal populations: information theory and decoding approaches. Nat. Rev. Neurosci. 10, 173–185.
Reich, D. S., Mechler, F., and Victor, J. D. (2001). Temporal coding of contrast in primary visual cortex: when, what, and why. J. Neurophysiol. 85, 1039–1050.
Saal, H. P., Vijayakumar, S., and Johansson, R. S. (2009). Information about complex fingertip parameters in individual human tactile afferent neurons. J. Neurosci. 29, 8022–8031.
Scaglione, A., Foffani, G., Scannella, G., Cerutti, S., and Moxon, K. A. (2008). Mutual information expansion for studying the role of correlations in population codes: how important are autocorrelations? Neural Comput. 20, 2662–2695.
Schneidman, E., Bialek, W., and Berry, M. J. II. (2003). Synergy, redundancy, and independence in population codes. J. Neurosci. 23, 11539–11553.
Schnupp, J. W., Hall, T. M., Kokelaar, R. F., and Ahmed, B. (2006). Plasticity of temporal pattern codes for vocalization stimuli in primary auditory cortex. J. Neurosci. 26, 4785–4795.
Soteropoulos, D. S., and Baker, S. N. (2009). Quantifying neural coding of event timing. J. Neurophysiol. 101, 402–417.
Strong, S. P., Koberle, R., de Ruyter van Steveninck, R. R., and Bialek, W. (1998). Entropy and information in neuroal spike trains. Phys. Rev. Lett. 80, 197–200.
Stuttgen, M. C. (2010). Toward behavioral benchmarks for whisker-related sensory processing. J. Neurosci. 30, 4827–4829.
Stuttgen, M. C., and Schwarz, C. (2010). Integration of vibrotactile signals for whisker-related perception in rats is governed by short time constants: comparison of neurometric and psychometric detection performance. J. Neurosci. 30, 2060–2069.
Theunissen, F., and Miller, J. P. (1995). Temporal encoding in nervous systems: a rigorous definition. J. Comput. Neurosci. 2, 149–162.
Van Rullen, R., and Thorpe, S. J. (2001). Rate coding versus temporal order coding: what the retinal ganglion cells tell the visual cortex. Neural. Comput. 13, 1255–1283.
Victor, J. D. (2000). How the brain uses time to represent and process visual information(1). Brain Res. 886, 33–46.
Victor, J. D. (2006). Approaches to information-theoretic analysis of neural activity. Biol. Theory 1, 302–316.
von Heimendahl, M., Itskov, P. M., Arabzadeh, E., and Diamond, M. E. (2007). Neuronal activity in rat barrel cortex underlying texture discrimination. PLoS Biol. 5:e305.
Keywords: information theory, somatosensation, neural coding, decoding, spike patterns, population coding
Citation: Panzeri1 S and Diamond ME (2010) Information carried by population spike times in the whisker sensory cortex can be decoded without knowledge of stimulus time. Front. Syn. Neurosci. 2:17 doi: 10.3389/fnsyn.2010.00017
Received: 27 February 2010;
Paper pending published: 14 March 2010;
Accepted: 21 May 2010;
Published online: 14 June 2010
Edited by:
Per Jesper Sjöström, University College London, UKReviewed by:
Guglielmo Foffani, Hospital Nacional de Parapéjicos, Spain; Drexel University, USAMiguel Maravall, Universidad Miguel Hernández, Spain
Demetris Soteropoulos, Newcastle University, UK
Copyright: © 2010 Panzeri1 and Diamond. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence:
Stefano Panzeri, Department of Robotics, Brain and Cognitive Sciences, Italian Institute of Technology, Via Morego 30, 16163 Genova, Italy. e-mail: stefano.panzeri@iit.it
Mathew E. Diamond, Cognitive Neuroscience Sector, International School for Advanced Studies (SISSA), Via Beirut, 9 34014 Trieste, Italy. e-mail: diamond@sissa.it