Investigating factors of pedestrian safety using ordinal logistic regression in Addis Ababa City roads

Pedestrians are the most victimized group in traffic accidents, and this has raised concerns about pedestrian safety in urban Ethiopia. The aim of this study is to determine the factors that affect pedestrian safety in Addis Ababa city Roads. This study employed a concurrent mixed-methods research method and an explanatory research design. Perception-based pedestrian safety data was collected from respondents’ key informants and personal observation. Exploratory factor analysis was employed to identify significant variables. Besides, the fitness of each variable was evaluated under the assumption of ordinal logistic regression, and the effect size of significant variables was determined using the odds ratio. The result indicates pedestrians are 0.065, 0.181, 0.296, 0.324, 0.289, 0.306, 0.038, and 0.193 times less likely to be safe due to narrow sidewalk width, poor sidewalk and footpath pavement comfort, inclusivity problems of sidewalks and footpaths, illegal vehicle parking, street vending, fast vehicle speed, and absence of traffic signs and lights, respectively. Consequently, the use of ordinal logistic regression offers a practical and effective means of determining pedestrian safety factors. Better pedestrian facilities should be constructed by considering pedestrian flow and diversity. Besides, the concerned body should provide spaces for street vendors and car parking and enforce traffic rules in the appropriate system to control vehicle speed.

1 Introduction

Many countries across the world are experiencing transportation-related traffic accidents with the growth of their vehicle population and urbanization (Cabrera-Arnau et al., 2020; Soathong et al., 2019; Wang et al., 2019). The number of automobiles has increased substantially, which has a detrimental effect on the urban environment, raises the risk of accidents, and endangers public health (Alkassabany et al., 2018). As of 2020, 56 percent of people on the planet live in cities, and by 2050, that number is predicted to rise to 70 percent (UNICEF, 2022). According to this statistic, there are already more than 1 billion cars owned worldwide, and by 2050, that number is predicted to reach 2.5 billion (Sousains, 2011). This increase in the number of vehicles will increase traffic accidents problems (Welle, 2015).

Road traffic accidents are among the major public concern on a global level (UNECA, 2020; WHO, 2018) and are responsible for 20 to 50 million non-fatal injuries and for 1.35 million deaths next to TB and malaria (Eshetu, 2020; Grzelak et al., 2020; UNECA, 2020; World Bank, 2022). They are the primary cause of death for people between the ages of 15 and 29 and the second most common cause of death for kids between the ages of 5 and 14 (Alkassabany et al., 2018; World Bank, 2020). As per the worldwide status report on road safety fatalities, the following road user categories share a percentage: 36% for passengers, 6% for drivers, 1% for riders, 2% for bicycles, and 55% for pedestrians (Haile, 2018; Tulu et al., 2015a). Unfortunately, among such death of accident statistics reports, vulnerable road users such as pedestrians are becoming more involved in traffic events (Al-sahili and Jaber, 2019; Debnath et al., 2021; Levulytė et al., 2017; Lulie, 2019; Soathong et al., 2019). Consequently, one of the biggest concerns in traffic management is pedestrian safety, particularly in places where walking is the primary form of transportation.

The situation of traffic deaths strongly suffers in underdeveloped and developing nations (Hussain et al., 2022; Mukherjee and Mitra, 2022; Reich and Nantulya, 2002). Over 90% of road fatalities worldwide are thought to occur in low- and middle-income nations (Heydar et al., 2019; Lagarde, 2019; Mabunda et al., 2020; Peralta-Santos et al., 2022; Reich and Nantulya, 2002). Pedestrians, cyclists, and motorcyclists bear a disproportionate share of the burden of road traffic accidents when compared to other road users (Hussain et al., 2022; Mabunda et al., 2020). In developing nations, most pedestrian-related traffic incidents take place in urban areas (Al-Majali and Imam, 2019; Fink, 2019) due to fast traffic growth (Erga, 2019; Taddesse, 2011), and inadequately maintained transportation infrastructure, ineffective traffic management, and an unsuitable settlement layout (Aga et al., 2021; Erga, 2019; Hussain et al., 2022). The majority of their metropolitan road networks were constructed without taking pedestrian road safety into consideration (Heydar et al., 2019; Job, 2020; Stoker et al., 2015; Tulu et al., 2013a; Tulu et al., 2013b). This strongly affected the travel freedom of their pedestrian population and has attracted many researchers from diverse perspectives in bringing pedestrian friendly environments.

In Ethiopia, walking that takes the most common modality in the country experienced with high prevalence of road traffic accidents particularly in urban areas (Alemgena et al., 2018). The country’s urban centers have seen an increase in traffic injuries over time due to expansion in the number of vehicles, population, road network, and vehicle kilometers driven (Tulu et al., 2013a; UNECA, 2020). An average of 4,732 citizens per year die on Ethiopian roads; daily, almost 13 Ethiopians are killed in traffic accidents and never return home (UNECA, 2020; Vision Zero for Youth, 2021).

Pedestrians are more victimized by traffic accidents in urban areas than in rural surroundings (Alemgena et al., 2018; Tulu et al., 2015a; UNECA, 2020; World Bank, 2020) and take 33% of the traffic-injured victims (Vision Zero for Youth, 2021). The Ethiopian Federal Police Commission’s published pedestrian fatality statistics may not accurately reflect the true number of deaths among pedestrians in the nation because of issues like incomplete reporting and incorrect categorization of traffic fatalities (UNECA, 2020). On the polar opposite, policymaking and physical urban planning neglected Pedestrian safety contexts (Tulu et al., 2013b; World Bank, 2020). According to the World Bank report, 88% of urban roads in the country are built without considering the safety of the walking population (World Bank, 2020, 2022). Urban planners and policymakers lack a critical consideration of the walking population (Galanis et al., 2017) in enhancing pedestrian safety. Therefore, pedestrian safety is a contemporary challenge for large urban areas in the country and needs critical investigation by concerned groups.

Addis Ababa is the largest urban center and one of the fastest-growing cities in Ethiopia, accounting for a quarter of the country’s urban population (World Bank, 2022). In the recent decade, rapid vehicular growth observed in the city (AAUATF, 2022; World Bank, 2014) at the expense of a higher volume of pedestrian population and lower road network expansion (AACTMA, 2021; Gebresenbet and Aliyu, 2019; Transport Research Laboratory, 2012). In the city, walking shares 60–70% of the total mode of transport of the daily pedestrian population (AACTMA, 2021; Transport Research Laboratory, 2012). Besides, the city holds more than 60% of the country’s fleet volume (AACTMA, 2021). However, the city’s current road network fails to serve the fast growth of mobility demand of people and vehicles (Asres, 2018; Erga, 2019; Fenta, 2014) and intern resulted in deep-rooted problems in pedestrian safety (Erga, 2019; Zewude, 2015).

According to the report of the federal police commission (2020) cited by Vision Zero for Youth, the city of Addis Ababa was identified as one of the hotspots of traffic accident areas in the country and takes 10 and 26% of the national total traffic death tolls and injuries, respectively (Vision Zero for Youth, 2021). Pedestrians took the majority of the city’s road traffic accident burden (AACTMA, 2021; UNECA, 2020) and the fatal rate comparison in modality indicates that pedestrians were 23 times more likely to be killed than vehicle users (AACTMA, 2021). When measured per 100,000 persons, road deaths in the city have been rising over the last five years; from 2016 to 2020, pedestrian fatalities accounted for 83% of all traffic statistics (AACTMA, 2021; Alemayehu et al., 2023).

The streets of Addis Ababa were designed with cars in mind, prioritizing vehicle flow over pedestrian safety (BIGRS, 2019; Dahir, 2019; Fenta, 2014; MOT, 2020; Ruhama, 2022; World Bank, 2022). Many of the city’s streets are broad without crosswalks, sidewalks, or other traffic-calming amenities (UNECA, 2020). In Addis Ababa, pedestrians must choose between walking on the road or in the sand/mud on the roadside, creating an extremely unpleasant experience (Tulu et al., 2015a). However, the presence of a higher risk of pedestrian injury and fatality in Addis Ababa City has received increased attention in recent years, and extensive investment efforts have been devoted to improving pedestrian safety with various approaches (AACTMA, 2022).

The City Administration is now working to overcome traffic problems with major investments in building new infrastructural facilities (for walking and cycling) and awareness creation for city dwellers. For example, the city administration has been conducting “Car-Free Day” since 2019 and 16 major road sections are being closed once a month on Sunday to promote walking to reduce road accidents (AACTMA, 2022). However, the problem of pedestrian safety still prevails in the City and even increased in time and space (UNECA, 2020). As a result, researches that focus on pedestrian safety in Addis Ababa City are important to explore the aforementioned challenges.

Determining and evaluating the variables that influence the likelihood of becoming engaged in a traffic incident and pedestrian road insecurity helps to facilitate the analysis of pedestrian road safety, which is necessary to reduce and offset any negative consequences (Grzelak et al., 2020). Decisions on raising the standard of pedestrian road safety can be supported by the use of mathematical models, which enable the estimation of the strength and direction of this effect (Grzelak et al., 2020). A popular mathematical model utilized in operation studies and pedestrian traffic safety is logistic regression (Davis and Cheong, 2019; Davis et al., 2018; Ghasemzadeh et al., 2018; Hamilton et al., 2021; Jang et al., 2013; Kong and Yang, 2010; Kwigizile et al., 2011; Park et al., 2012; Siddiqui et al., 2006).

Ordinal logistic regression is an extension of logistic regression employed in identifying factors of traffic safety in the last decades. When the dependent variable of interest is categorical and contains more than two categories or levels in a sensible order, it is utilized (Bellizzi et al., 2018). Many researchers in different parts of the world such as Riccardi et al. (2022) in Great Britain; Alicioglu et al. (2020), Liu et al. (2019), and Pour-Rouholamin et al. (2017) in the United States; Asare and Mensah (2020) in Ghana; Zewude and Ashine (2016) and Bekelcho et al. (2023) in Ethiopia; Sethulakshmi and Mohan (2023) in India applied ordinal logistic regression for identifying factors associated with pedestrian safety and traffic injury. However, none of the studies considered the perception of pedestrians and were solely based on the secondary data collected from police and/or traffic administration offices.

Generally, pedestrian road safety issues are addressed in many studies throughout the world, but scholarly organized research regarding pedestrian safety in Addis Ababa is limited and lacks methodological reliability. Researchers are primarily concerned with pedestrian risk, and facility availability with health and environmental variables rather than inclining them to pedestrian safety cases. For example, Tulu et al. (2015b) examine the frequency of pedestrian crashes in Addis Ababa and determine the causes by modeling exposure and road environment variables. However, the risk factors and difficulties related to pedestrian safety were not sufficiently addressed in this study. Similarly, Amare (2019) also assesses the concern of road traffic accident factors in Addis Ababa city by taking the Kirkos sub-city as a focus of study. His analysis was based on the crash data collected from the traffic office of the city and analyzed using multiple linear regressions. However, his Method is unable to examine the contribution of each factor for pedestrian safety when responses are in categorical form which is okay for ordinal logistic regression.

Bekelcho et al. (2023) Used an ordinal logistic regression modeling technique to determine the determinant factors for crash severity levels that occurred in Addis Ababa City based on data collected from 2017 to 2020. However, their research was based on secondary data which is less trustworthy than primary data that was gathered from several offices. It neglected to take into account pedestrians’ perceptions of safety, which are the major target of the issue. In addition to crucial elements like car speed, his study did not take into account street shoe shining, street selling, facility surroundings, or other factors.

Another researcher Alemgena et al. (2018) in his study, analyzed the importance of pedestrian facilities in terms of environmental and connectivity advantage aspects in Nekemte City, but the researcher could not correlate them with pedestrian road safety aspects. Besides Aregawi (2018) assesses non-motorized transport (NMT) road segments in Addis Ababa’s Bole Sub-City in terms of quality, accessibility, and environmental importance to understand the availability of NMT facilities. However, his content coverage did not consider the evaluation of pedestrian road safety aspects. Another study conducted by Eguale (2015) explores pedestrian safety problems and their remedial solutions in the Kirkos sub-city border. His finding employed an analytical hierarchical process (AHP) based method for pedestrian safety factor identification that makes different from the current study that applied ordinal logistic regression for factor identification.

The researcher also reviewed the work of Tufa (2019) and Woldeamanuel et al. (2023) who explore the impact of street vending on pedestrian safety in the Addis Ababa sub-city borders. However, their exploration was only from the perspective of street vending and their studies do not consider other factors which are included in this study that can help to understand better the concern of pedestrian safety. Besides, their focus was mainly on the socio-economic impact of street vendors rather than the concern of safety. Regardless of the above trial, well-organized research literature related to pedestrian safety and its determining factors is not available in Addis Ababa city.

Therefore, this study employed ordinal logistic regression for analyzing factors that determine pedestrian safety in the city of Addis Ababa by taking the Piassa-Bole Bridge and Megenagna-Torihayloch corridors as a major focus to get possible answers to the questions: (i) what looks the performance of ordinal logistic regression for analyzing pedestrian safety? (ii) What are the main factors behind the pedestrian safety in the study corridors? (iii) What degree of influence do factors contribute to pedestrian safety in the study area? This study helps to generate an in-depth view of pedestrian problems for academics, officers, and other concerned groups to pin out significant directions and recommendations for a sustainable and safe pedestrian environment.

2 Research methodology

2.1 Description of the study area

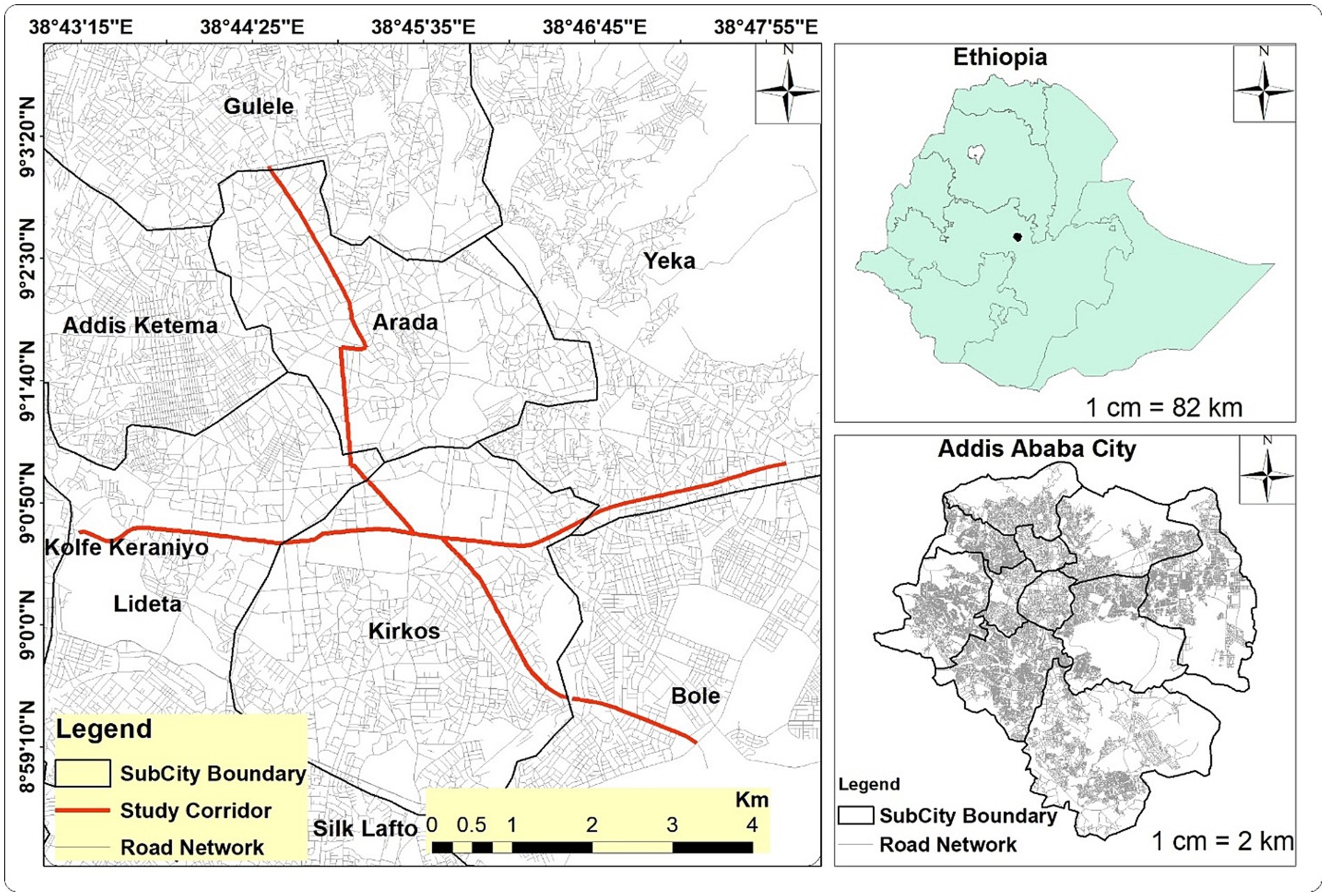
Geographically, the city is located between 8,049′55.929″ - 90 5′53.853″ North latitude and 38019.547″ -380 38′16.555″ East longitudes (see Figure 1). The terrain varies from gently sloping to steeply sloping regions with multiple stream valleys and high grades. It covers an area of 540 km² and has an average elevation of 2,500 meters above mean sea level. Its climate and weather are suitable and moderate. The fastest urban expansion is occurring in this City (World Bank, 2020, 2022). It serves as the capital of Ethiopia as well as the home base for the African Union and other international institutions. According to the World Bank (2022) Group, Addis Ababa is the home of 25% of Ethiopia’s urban population. The estimated population is 4.8 million, with an annual growth rate of 4.39% (World Bank, 2022). The city’s economy is expanding at a rate of 14% per year and currently accounts for around 50% of the GDP of the country (World Bank, 2022).

Figure 1

Figure 1. Location map of the study area.

The city boasts more than 60% of the nation’s fleet and more than 621 km of pedestrian pathways in addition to 2,561 km of asphalt, 2,030 km of gravel, and 1,850 km of cobblestone roads (AACTMA, 2021). According to the Addis Ababa City Road Transport Bureau report, the city has a total area of 3,018,319.7 m/sq. and 636,833.8 meters of sidewalk in various widths and materials (Tulu et al., 2013c; AACRTB, 2019). In Addis Ababa, walking and public transportation account for the majority of travels roughly 85% of all journeys. The percentage of walks varies greatly throughout the City (Tulu et al., 2013c; AACRTB, 2019). The extent and right of way of Addis Ababa’s road network, however, are restricted, and despite a high pedestrian flow, a sizable portion (63%) of the network lacks walkways (World Bank, 2022). The chosen road corridors for this study are those that run from Torihayloch to Megenagna and from Bole Bridge to Piassa Square. These road corridors are selected by the Addis Ababa Traffic Management Agency in a four-year non-motorized transport enhancement strategy based on high pedestrian traffic flow and black spot concentrations.

2.2 Research methods, data source and data collection tools

This study was based on a pragmatism philosophical paradigm and deductive research approach. Based on the modality of the study, a concurrent mixed research method is used to attain the objective of the study. The versatility of mixed techniques makes them ideal for careful analysis of promising concepts, which is the reasoning behind our use. Besides, an Explanatory research design is used to analyze the contributing factors of pedestrian safety.

Primary sources of data are used to collect relevant data for this study. Accordingly (i) questionnaire was employed to collect data that can be used for identifying factors influencing pedestrian safety level from respondents. (ii) Observation is also used to see the existing pedestrian walking side safety, the reality of factors with the existing environment, and other important concerns. Photographs were taken to document the existing pedestrian safety, mobility, and the current traffic situation in the study border and finally (iii) a semi-structured interview was employed to validate the response of respondents with these experts closer to pedestrian safety from Addis Ababa City Traffic Management Agency and Addis Ababa City Police Commission departments. The study also considered secondary data inputs collected from books, reports, research, and other website-based data sources.

As recommended by Onwuegbuzie and Collins (2007) and Taherdoost (2017), the sample size used in the study is determined based on the expense of the data collection, time and effort required, nature and characteristics of the target population. Accordingly, two corridors that extend from Piassa/Menilik Square to Bole Bridge and Megenagna to Torihayloch were selected using purposive sampling. The researcher then selected 384 samples of respondents (pedestrians) across two selected corridors using the convenience sampling method. This sampling method is used due to its better integration with probability that help to avoid bias when generalizing our finding.

To determine the sample size (n), the researcher used the formula set by Kothari (2004).

$\begin{array}{ll}N=\left({\mathrm{Z}}^2\mathrm{p}\mathrm{q}\right)/{\mathrm{d}}^2& (1)\end{array}$

Where: N = sample size, Z = standard normal variable at 95 percent confidence level, which is 1.81, p = estimated characteristics of the target population (0.5); q = 1- p, d = level of statistical significance set (5% margin of errors).

In addition, 10 key informants were selected from Addis Ababa City Traffic Management Agency and Addis Ababa City Police Commission departments using purposive sampling. These key informants were used to triangulate the responses forwarded by the sampled respondents.

2.3 Method of data analysis

2.3.1 Exploratory factor analysis

A major tool in multivariate statistics, factor analysis explains how underlying factors affect a set of observed variables (Alavi et al., 2020; Taherdoost et al., 2020; Williams et al., 2010; Liao and Valliant, 2012; Senaviratna and Cooray, 2019; Meles et al., 2020). It is useful for figuring out whether theoretical constructs apply to a particular set of data and how well these constructs capture the original variables (Sürücü et al., 2023). Thus, instead of considering too many variables that may be insignificant, we use basic factors that allow easy interpretation based on the advice of Barron (2018), Yong and Pearce (2013), and Thompson (2007). The suitability of the data should be confirmed before performing an EFA analysis. Therefore, this study examines the absence of outliers, missing values, multicollinearity, singularity, and the presence of enough correlation and sufficient sample size recommended by Sürücü et al. (2023) to evaluate the suitability of the data for factor analysis.

i. Outliers: Ensuring the absence of outliers and guaranteeing univariate and multivariate data normality is crucial before applying factor analysis to a dataset (Bartholomew et al., 2021; Beavers et al., 2013; Goretzko et al., 2019; Yong and Pearce, 2013). The size of the Pearson product–moment correlation coefficients, which are used to calculate the EFA results, is decreased when the data are not normal. Furthermore, the occurrence of outliers results in the creation of fake factors (Sürücü et al., 2023; Zygmont and Smith, 2014). Consequently, to improve the EFA analysis, the data distribution was examined.

ii. Correlation among Variables: The correlation coefficient, which establishes the relationship between two variables, is the fundamental statistical method used in factor analysis. A low correlation value suggests a weak association between the variables and inhibits the production of factors, whereas a high correlation value enables the creation of factors with two or fewer variables. Therefore, this study considered that the correlation coefficient of most variables should be at least 0.30 (Tabachnick and Fidell, 2007) and variables with lower correlations were excluded from the exploratory factor analysis.

iii. Missing Values: Data messiness affects EFA outcomes. Because of this, it is essential to determine whether the data set’s missing data happens in a non-random order (Yong and Pearce, 2013). To prevent inaccurate estimations, it is advised that missing value data be removed from the factor analysis (Baraldi and Enders, 2010; Beavers et al., 2013).

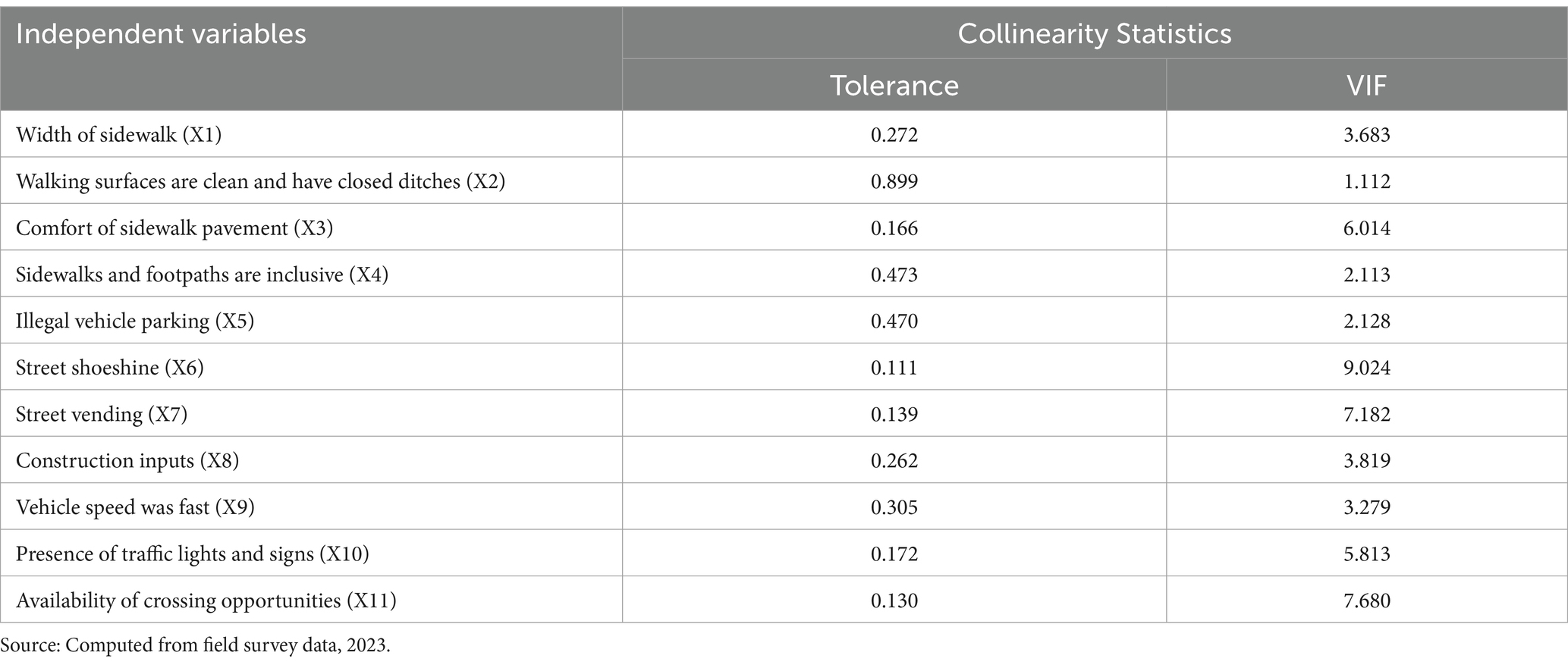
iv. Multicollinearity: It is advised by the literature to verify if the dataset exhibits multicollinearity. Multicollinearity and singularity gives unnecessarily inflated standard errors, spuriously low or high t-statistics, illogical signs and these problems may lead to invalid statistical inferences (Liao and Valliant, 2012; Senaviratna and Cooray, 2019). Therefore, problematic variables (VIF ≥ 7.5) were excluded from the factor analysis.

v. Sample Size: It is indicated that insufficient sample size can damage the factor analysis process and produce unreliable and invalid results (Goretzko et al., 2019; Goretzko and Bühner, 2022; Howard, 2015; Sürücü et al., 2023; Watkins, 2018). Therefore, caution is required for sample size, because EFA generally functions better with larger sample sizes, and larger samples lead to more stable solutions by reducing the margin of error (Beavers et al., 2013). If the sample size is too small, it is not possible to obtain generalizable or reproducible results (Sürücü et al., 2024). For this reason, this study accepted the recommendation of Sürücü et al. (2023) that confirms factor analysis not to be performed with sample sizes less than 200.

2.3.1.1 Bartlett’s test and Kaiser-Meyer-Olkin test

Bartlett’s Test of Sphericity establishes the existence of linear combinations and shows that the observed correlation matrix differs statistically from a single matrix (Beavers et al., 2013). If this condition is not satisfied, it indicates that it is impossible to construct precise and trustworthy factors (Beavers et al., 2013). The Bartlett’s Sphericity Test result in the EFA needs to be less than 0.05. If not, it is advised to repeat factor analysis with a larger sample size or without the items causing scattered correlation models from the analysis.

The Kaiser-Meyer-Olkin (KMO) Test is a metric for shared variance in items that indicates whether the sample size is adequate for exploratory factor analysis. A KMO value of 0.6 or above indicates that the value is sufficient for factor analysis (Sürücü et al., 2023). This study used 0.6 as a threshold for deciding on the reliability of KMO results for factor analysis.

2.3.1.2 Rotation methods: varimax methods

The rotation’s primary goal is to create an optimally simple structure that maximizes the amount of high loads on each variable while attempting to load each variable on the fewest possible components (Sürücü et al., 2023; Yong and Pearce, 2013). There are two types of rotation methods: orthogonal (varimax) and oblique (promax). According to Tabachnick and Fidell (2007), oblique rotations are more suited if the factors have a high degree of correlation with one another, while orthogonal rotations are more appropriate when the elements are conceptually independent (low correlation) (Tabachnick and Fidell, 2007). This study applied the orthogonal rotation method to decide how many of the variables to be retained.

2.3.1.3 Components of factor analysis: extraction

2.3.1.3.1 Principal components

Theoretically, principal component analysis presupposes that the component is a composite of observable variables or that the component is caused by the individual item scores (Beavers et al., 2013). The principal component analysis breaks down a large number of variables into fewer components to extract the maximum variation from the dataset (Alavi et al., 2020; Meyers et al., 2013; Ruengvirayudh and Brooks, 2022; Tabachnick and Fidell, 2007; Yong and Pearce, 2013), Consequently, we classify principal component analysis as a data reduction method. The numbers of factors to be retained are determined by:

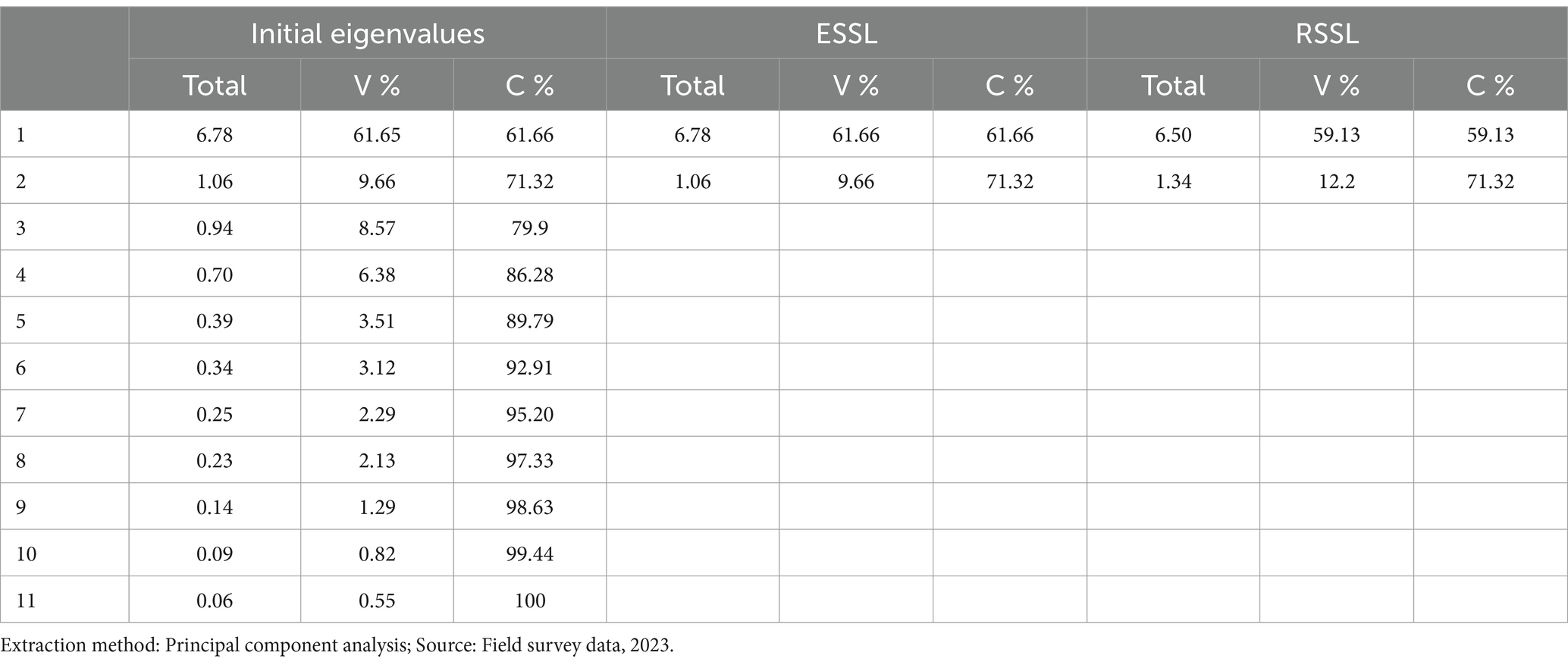
1. Eigenvalue > 1 Rule: Every component and factor has an eigenvalue, a value that indicates how much of the variance in the items linked to each factor can be accounted for by that factor (Beavers et al., 2013). Kaiser (1964) recommended that all factors with eigenvalues above 1 should be kept. However, Other researchers claim that it led to an overestimation of the number of factors to be removed (Howard, 2015; Sürücü et al., 2024), and is recommended that the Scree test be used with eigenvalues to determine how many factors to retain (Yong and Pearce, 2013).

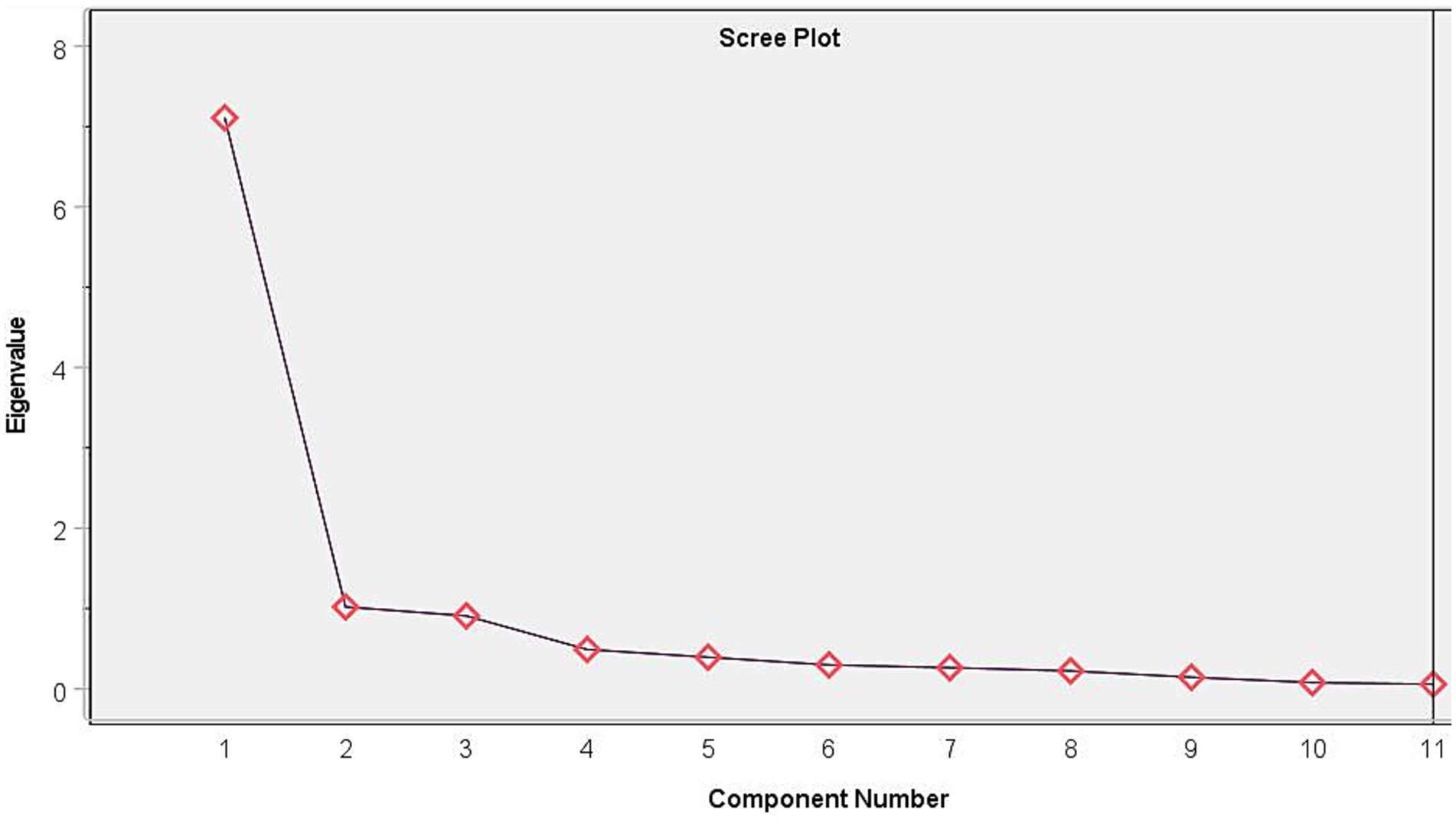
2. Scree Test: An eigenvalue graph of the factors is used in Cattell’s Scree Plot test (Goretzko et al., 2019). The factors in the graph are represented by the “x” axis, and the eigenvalues that correspond to these factors are shown by the “y” axis. The first component, which is on the far left, has the highest eigenvalue and makes up the greatest amount of variation. The breaking point is then formed by the eigenvalues bending at a specific position and constantly decreasing after that. The graph’s break point, also known as the inflection point, indicates how many components need to be kept (Goretzko et al., 2019; Sürücü et al., 2023, 2024).

3. Variance Extracted: Retaining the components that account for a specific percentage of the variation collected is a third technique to ascertain the number of factors (Beavers et al., 2013; Sürücü et al., 2023). Most researchers suggest that the variance explained should be 70–90% (Beavers et al., 2013; Sürücü et al., 2023). while, others suggest that 50% and above of the variance explained is sufficient (Brien, 2016).

2.3.2 Analysis of factors of pedestrian safety using ordinal logistic regression

Logistic regression is used to determine the impact of covariate control factors, evaluate interaction effects, estimate the likelihood of the dependent variable based on the independent variables, and quantify the effect size of the independent variables on the dependent (Hosmer and Lemeshow, 2013; Meron, 2011). Meanwhile, Ordinal logistic regression (OLR) is used to analyze ordinal response variables with more than two categories (Dlamini et al., 2020; Pratiwi and Kismiantini., 2019; Sesay et al., 2021). Therefore, ordinal logistic regression is used in this study due to the polychotomous and ordinal nature of the dependent variable.

The popular ordinal logistic regression models created for examining ordinal response variables are the proportional odds model (PO), two iterations of the partial proportional odds model with and without limitations, the continuous ratio model, and the stereotype model (O’Connell, 2006; Tesfaledet et al., 2019). However, the cumulative logit model called the proportional odds model recommended by Li and Fan (2019), Pour-Rouholamin et al. (2017), Norusis (2010), and Tesfaledet et al. (2019) is used in this study. Since the PO model yields the most readily interpretable regression result (Tesfaledet et al., 2019), it is used in this study. The selection of an appropriate link function determines the accuracy of the model output (Jeong et al., 2018). Hence, the Logit link function is used in this study.

2.3.2.1 Modeling assumption

The satisfaction of the statistical model’s assumptions determines the validity of conclusions made using contemporary statistical modeling approaches (Rosner, 2010). As a result, the following model assumptions were considered in this study.

i. The proportional odds or parallel line regression assumption: the relationship between each pair of outcome groups is the same since the coefficient that describes the relationship between the lowest versus all higher categories of the response variable are the same as those that describe the relationship between the next lowest and all higher categories (Akin and Şentürk, 2012; Ari and Yildiz, 2014; Carophine, 2016; Ombui et al., 2011). In other words, the model assumes that no input variable disproportionately affects a specific level of the outcome variable. If the assumption is violated, the modeling approach fails, which is the major consideration in the validation process (Ari and Yildiz, 2014). Parallel line test is considered to check this assumption.

ii. No Multicollinearity: Multicollinearity occurs when statistical models have two or more explanatory variables that are highly correlated with each other (Agresti, 2007). Multicollinearity leads to problems with understanding which variable contributes to the explanation of the dependent variable and assuming the absence of collinearity is an important step in ordinal regression (Agresti, 2007, 2010; Hair et al., 2010; Ringle et al., 2020). To test for this assumption, we use the VIF value of a variable less than 7.5 and a tolerance of above 0.1 (Agresti, 2007, 2019; O’Connell, 2006; Ringle et al., 2020; Shrestha, 2020).

iii. Linear relationship: The logistic regression model does not assume a linear relationship between the dependent and the independent variables but a linear relationship between the logit of the response and the explanatory variables and further does not require the independent variable to be in an interval or unbounded (Carophine, 2016).

iv. Data normality: The model makes the assumptions that all of the variables are included in the regression model and that the error terms are independent. Over the error term, no normal distribution assumption is made (Carophine, 2016).

Given an ordinal scale with K categories as the dependent variable and a vector of explanatory variables denoted by 𝒙 = (𝒙1, 𝒙2, 𝒙3,…, 𝒙p), the OLR’s cumulative logit model is described as follows with Hosmer and Lemeshow (2013) using Equation 2.

$\begin{array}{l}\mathrm{Logit}\mathbf{k}\left(\mathrm{x}\right)=\mathrm{logit}\left(\left[\mathrm{Y}\le \mathrm{s}|\mathrm{x}\right]\right)=\mathit{ln}\left(\frac{\mathrm{P}\left[\mathrm{Y}\le \mathrm{s}|\mathrm{x}\right]}{1-p\left[\mathrm{Y}\le \mathrm{s}|\mathrm{x}\right]}\right)\\ =\mathit{ln}\left(\frac{\pi 1\left(\mathrm{x}\right)+\dots +\pi s\left(\mathrm{x}\right)}{\left(\pi s+1\left(\mathrm{X}\right)+\dots +\pi s(\mathrm{x}\right)}\right)={\beta }_{0\mathrm{S}}+x_i^T\beta \end{array}\text{ (2)}$

Where s is the dependent variable (1, …, S – 1) and α₁, …, α_S − 1 is the threshold model and 𝛃 is a vector of the regression coefficient. Ordinal logistic regression with five categories of dependent variables is defined as:

$\begin{array}{ll}\mathrm{logit}\left(\mathrm{P}\left(\mathrm{Y}\le 1|\mathrm{x}\mathrm{i}\right)\right)=ln\left(\frac{\mathrm{P}\left[\mathrm{Y}\le 1|\mathrm{x}\mathrm{i}\right]}{1-p\left[\mathrm{Y}\le 1|\mathrm{x}\mathrm{i}\right]}\right)={\beta }_{01}+x_i^T\beta & (3)\end{array}$

$\begin{array}{ll}\mathrm{logit}\left(\mathrm{P}\left(\mathrm{Y}\le 2|\mathrm{x}\mathrm{i}\right)\right)=ln\left(\frac{\mathrm{P}\left[\mathrm{Y}\le 2|\mathrm{x}\mathrm{i}\right]}{1-p\left[\mathrm{Y}\le 2|\mathrm{x}\mathrm{i}\right]}\right)={\beta }_{02}+x_i^T\beta & (4)\end{array}$

$\begin{array}{ll}\mathrm{logit}\left(\mathrm{P}\left(\mathrm{Y}\le 3|\mathrm{x}\mathrm{i}\right)\right)=ln\left(\frac{\mathrm{P}\left[\mathrm{Y}\le 3|\mathrm{x}\mathrm{i}\right]}{1-p\left[\mathrm{Y}\le 3|\mathrm{x}\mathrm{i}\right]}\right)={\beta }_{03}+x_i^T\beta & (5)\end{array}$

$\begin{array}{ll}\mathrm{logit}\left(\mathrm{P}\left(\mathrm{Y}\le 4|\mathrm{x}\mathrm{i}\right)\right)=ln\left(\frac{\mathrm{P}\left[\mathrm{Y}\le 4|\mathrm{x}\mathrm{i}\right]}{1-p\left[\mathrm{Y}\le 4|\mathrm{x}\mathrm{i}\right]}\right)={\beta }_{04}+x_i^T\beta & (6)\end{array}$

$\begin{array}{ll}\mathrm{logit}\left(\mathrm{P}\left(\mathrm{Y}\le 5|\mathrm{x}\mathrm{i}\right)\right)=ln\left(\frac{\mathrm{P}\left[\mathrm{Y}\le 5|\mathrm{x}\mathrm{i}\right]}{1-p\left[\mathrm{Y}\le 5|\mathrm{x}\mathrm{i}\right]}\right)={\beta }_{05}+x_i^T\beta & (7)\end{array}$

Odds are the ratio of the probability that an event will occur divided by the probability that it will not occur (Basbas et al., 2013). They tell us how much the logit changes based on the values of the predictor variables. The odds value was calculated as follows.

$\begin{array}{ll}{\pi }_1\left(\mathrm{xi}\right)=exp\left({\beta }_{01}+\mathrm{x}{i}^T\beta \right))/\left(1+exp\left({\beta }_{01}+\mathrm{x}{i}^T\beta \right)\right)& (8)\end{array}$

$\begin{array}{ll}{\pi }_2\left(\mathrm{xi}\right)=\frac{(exp\left({\beta }_{02}+\mathrm{x}{i}^T\beta \right)}{(1+exp\left({\beta }_{02}+\mathrm{x}{i}^T\beta \right)}-\frac{(exp\left({\beta }_{01}+\mathrm{x}{i}^T\beta \right)}{(1+exp\left({\beta }_{01}+\mathrm{x}{i}^T\beta \right)}& (9)\end{array}$

$\begin{array}{ll}{\pi }_3(\mathrm{xi}=\frac{(exp\left({\beta }_{03}+\mathrm{x}{i}^T\beta \right)}{(1+exp\left({\beta }_{03}+\mathrm{x}{i}^T\beta \right)}-\frac{(exp\left({\beta }_{02}+\mathrm{x}{i}^T\beta \right)}{(1+exp\left({\beta }_{02}+\mathrm{x}{i}^T\beta \right)}& (10)\end{array}$

$\begin{array}{ll}\pi 4(\mathrm{xi}=\frac{exp\left(\beta 04+x{i}^T\beta \right)}{1+exp\left(\beta 04+x{i}^T\beta \right)}-\frac{exp\left(\beta 03+x{i}^T\beta \right)}{1+exp\left(\beta 03+x{i}^T\beta \right)}& (11)\end{array}$

$\begin{array}{ll}{\pi }_5\left(\mathrm{xi}\right)=1-{\pi }_1\left({\mathrm{x}}_i\right)-{\pi }_2\left({\mathrm{x}}_i\right)-{\pi }_3\left({\mathrm{x}}_i\right)-{\pi }_4\left({\mathrm{x}}_i\right)& (12)\end{array}$

The odds ratio is used to show the level of the tendency of a part of the population in a certain category to part of the population in other categories in a predictor variable (Agresti, 2010; Kateri and Agresti, 2013; Kleinbaum and Klein, 2010; Purnomo, 2021). The value of the odds ratio is used to interpret the ordinal logistic coefficients and is calculated using Equation 13.

$\begin{array}{ll}\Psi k=\frac{P\left(Y\le s|xk+△\right)/\mathrm{P}(\mathrm{y}>\mathrm{s}|\mathrm{x}\mathrm{k}+△}{P\left(y\le s|xk\right)/P\left(y>s|xk\right)}=exp.\left(\beta k△\right)& (13)\end{array}$

If the predicator X_K changes by ∆ units, it will give a change of exp. (B_K∆); a value of one indicates no relationship, between zero and one indicates a negative relationship, and above one indicates a positive relationship (Ali et al., 2016; Kleinbaum and Klein, 2010).

2.3.2.2 Ordinal logistic regression model evaluation

2.3.2.2.1 Model significance testing

The (log) likelihood ratio statistic is used for judging the model significance testing (Williams, 2020). This is because the Log statistic is computationally easy and is given automatically in the output of most statistical computer packages (Hilbe, 2015; Starkweather and Moske, 2011). The Likelihood Ratio statistics of this study were computed using Equation 14.

$\begin{array}{ll}\mathrm{G}=-2log\left[\frac{{{\displaystyle \prod }}_{i=1}^n{\left(\frac{ni}{n}\right)}^{ni}}{{{\displaystyle \prod }}_{i=1}^n\pi i^{yi}{\left(1-\pi i^{yi}\right)}^{1-yi})}\right]& (14)\end{array}$

Wald test (Wβi) is used to test the significance of each coefficient in the model (Muhammad and Tuti, 2013; Pasaribu et al., 2019). It was computed by dividing the maximum likelihood estimate (MLE) of the slope parameter ( $\beta i)$ by the estimate of its standard error, $\beta i$ using Equation 15.

$\begin{array}{ll}W\beta i=\frac{\beta i}{SE\left(\beta i\right)}& (15)\end{array}$

2.3.2.2.2 The goodness-of-fit tests

Compute the Pearson chi-squared and deviance statistics on the cross-classification of covariate patterns with observed and estimated response frequencies as a straightforward way to evaluate goodness of fit (Fagerland and Hosmer, 2017). Covariate patterns and response categories are tabulated to get the PR test statistics. If there are fewer covariate patterns than observations, then this method performs well (Fagerland and Hosmer, 2017). PR test of Pearson Chi-square and deviance statistics are used in this study to examine the Goodness-of-Fit test as recommended by Fagerland and Hosmer (2017), Hilbe (2015) and Hosmer and Lemeshow (2013).

$\begin{array}{ll}\mathrm{P}\mathrm{R}\left(\mathrm{X}2\right)={\displaystyle \sum }_{i=1}^2{\displaystyle \sum }_{k=1}^k{\displaystyle \sum }_{j=1}^c\frac{{\left(\widehat{\mathrm{O}}ikj-\widehat{E}ikj\right)}^2}{\widehat{E}ikj}& (16)\end{array}$

$\begin{array}{ll}\mathrm{P}\mathrm{R}\left(\mathrm{D}2\right)=2{\displaystyle \sum }_{i=1}^2{\displaystyle \sum }_{k=1}^k{\displaystyle \sum }_{j=1}^c\widehat{\mathrm{O}}ikj\ast log\frac{\widehat{\mathrm{O}}ikj}{\widehat{E}ikj}& (17)\end{array}$

Where: i represents the index of the two subgroups based on the Ôs, K is the number of observed covariate patterns because of the categorical covariates, and c is the number of response categories.

The reference distribution for both PR (χ²) and PR (D²) is the chi-squared distribution with (2 K - 1) (C - 1) - P_cat - 1 degrees of freedom, where P_cat denotes the number of dichotomous variables needed to model all the categorical covariates (substitute dummy variables for categorical covariates with more than two categories). This reference distribution adheres well to the distribution of PR (χ²) and PR (D²) under the proportional odds model (Fagerland and Hosmer, 2013, 2016; Pulkstenis and Robinson, 2004). The model’s good fit to the data is the null hypothesis for the goodness-of-fit tests. Therefore, a low p-value suggests that there is a problem with the model (Fagerland and Hosmer, 2017).

2.3.2.2.3 Parameters of estimation of coefficients

The table of Parameter estimates tells us specifically the relationship between our explanatory variables and the outcome (Adejumo and Adetunji, 2013; Hilbe, 2015). The Maximum Likelihood estimation (MLE) that maximizes the likelihood function (Liang et al., 2020) is used in this study. Its likelihood function for a sample with ‘n’ independent observations, (y_i, x_i), i = 1, 2,...,k as decided in Das and Rahman (2011) and Hosmer and Lemeshow (2013).

$\begin{array}{ll}\mathcal{𝓁}\left(\theta \right)={\displaystyle \prod }_{i=1}^n\left[{\pi }_1{\left(\mathit{xi}\right)}^{\mathrm{y}1\mathrm{i}}{\pi }_2{\left(\mathit{xi}\right)}^{\mathrm{y}2\mathrm{i}}{\pi }_3{\left(\mathit{xi}\right)}^{\mathrm{y}3\mathrm{i}}{\pi }_4{\left(\mathit{xi}\right)}^{\mathrm{y}4\mathrm{i}}\right]& (18)\end{array}$

The principle of maximum likelihood estimation (MLE) is to estimate parameter vectors by maximizing the likelihood function (Ali et al., 2016; Kleinbaum and Klein, 2010). Since the closed-form solution for θ is not possible to obtain, a numerical approach is required to estimate the parameters (Kleinbaum and Klein, 2010). Hence, the procedure used is Newton–Raphson.

$\begin{array}{ll}{\left(\theta \right)}^{\left(\mathrm{m}+1\right)}={\left(\theta \right)}^{\left(\mathrm{m}\right)}-{\left(\mathrm{H}\right)}^{-1}\left({\theta }^{\left(\mathrm{m}\right)}\right)\mathrm{g}\left({\theta }^{\left(\mathrm{m}\right)}\right)& (19)\end{array}$

Where H (θ) is a nonsingular Hussian matrix and the elements of the matrix are the second partial derivative elements of the ln-likelihood function for the parameters to be estimated. Whereas g(θ) is the gradient vector with the first partial derivative element of the ln-likelihood function for the parameter to be estimated and m is the number of iterations.

$\begin{array}{ll}\mathrm{g}\left(\theta \right)=\left(\frac{\partial lnL\left(\theta \right)}{\partial \beta 01}\frac{\partial lnL\left(\theta \right)}{\partial \beta 02}\frac{\partial lnL\left(\theta \right)}{\partial \beta 0\mathbf{k}}\frac{{\left(\partial lnL\left(\theta \right)\right)}^T}{{\left(\partial \beta \right)}^T}\right)& (20)\end{array}$

$\mathrm{H}\left(\theta \right)=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}.\\ \frac{{\partial }^{2}lnL\left(\theta \right)}{\partial \beta {01}^2}\frac{{\partial }^{2}lnL\left(\theta \right)}{\partial \beta 01\partial \beta 02}\frac{{\partial }^{2}lnL\left(\theta \right)}{\partial \beta 01\partial \beta 0k}\frac{{\partial }^{2}lnL\left(\theta \right)}{\partial \beta 01\partial \beta }\\ \frac{{\partial }^{2}lnL\left(\theta \right)}{\partial \beta {02}^2}\frac{{\partial }^{2}lnL\left(\theta \right)}{\partial \beta 02\partial \beta 0k}\frac{{\partial }^{2}lnL\left(\theta \right)}{\partial \beta 02\partial \beta }\\ \\ \frac{{\partial }^{2}lnL\left(\theta \right)}{\partial \beta 0k^2}\frac{{\partial }^{2}lnL\left(\theta \right)}{\partial \beta 0k\partial \beta }\end{array}\\ \mathit{Symmetry}\frac{{\partial }^{2}lnL\left(\theta \right)}{\partial {\beta }^T\partial \beta }\end{array}\\ \end{array}\right)\text{ (21)}$

N.B: Iteration stop if, || ${\theta }^{\left(m+1\right)}-{\theta }^{\left(m\right)}\left|\right|\le \epsilon \text{,}$where e is a very small number approaching zero.

2.3.2.2.4 Measuring strength of association

The pseudo R square value represents the proportion of variation in the outcome variable accounted for by the independent variables. The model with the largest R² statistic is “best” according to this measure (Adejumo and Adetunji, 2013). In this case, McFadden, Cox & Snell, and Nagelkerke R² value indicates the amount of variation in the dependent variable. Nagelkerke R² was more reliable than the McFadden and Cox and Snell R² in evaluating the strength of the relationship between dependent and independent variables (Smith and Mckenna, 2012). Hence, the Nagelkerke R² was opted for this study and computed by Equation 22.

$\begin{array}{ll}\mathrm{Nagelkerke}\mathrm{R}2=\left(\mathrm{R}2\mathrm{c}\mathrm{s}\right)/(1-\left(\mathrm{L}\ast {ß}^{\left(0\right)2/\pi }\right)& (22)\end{array}$

Where: L ( $ß$ ) is the log-likelihood function and L ( $ß$ ⁽⁰⁾) is the log-likelihood with the threshold.

2.3.2.2.5 Test of parallelism

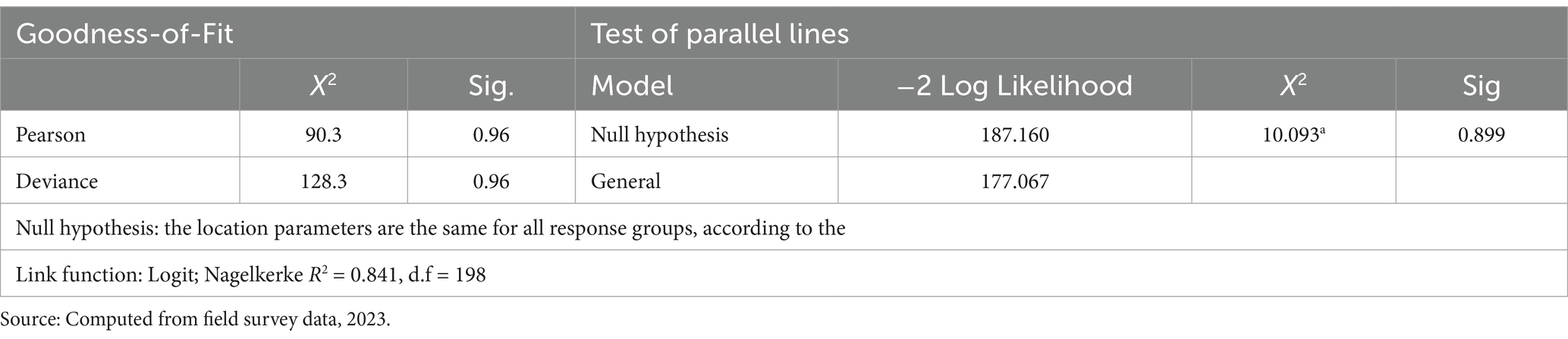
Finding out whether it is reasonable to presume that the location parameters’ values are constant across answer categories is made easier with the use of the test of parallel lines (Adejumo and Adetunji, 2013). To test the parallelism assumption −2 log-likelihood and Chi-square (X²) statistics recommended by Kleinbaum and Klein (2010) and Meron (2011) are used in this study. The link function used is appropriate if there is evidence to reject the null hypothesis (Ari and Yildiz, 2014; Fullerton and Xu, 2012; O’Connell, 2006).

2.3.2.2.6 Classification accuracy

Correctly classified response rate (CCR) is the percentage of correct observations (Alicioglu et al., 2020; Ghasemzadeh et al., 2018; Pratiwi and Kismiantini., 2019). The higher value of CCR shows a better accuracy of the output (Chen and Hughes, 2004; Ghasemzadeh et al., 2018; Hosmer and Lemeshow, 2013; Kline, 2013; Pratiwi and Kismiantini., 2019).

$\begin{array}{ll}\mathrm{C}\mathrm{C}\mathrm{R}=\frac{\mathrm{Number\; of\; correct\; prediction}}{\mathrm{Number\; of\; observation}}\ast 100& (23)\end{array}$

2.4 Variables used in the ordinal logistic regression model

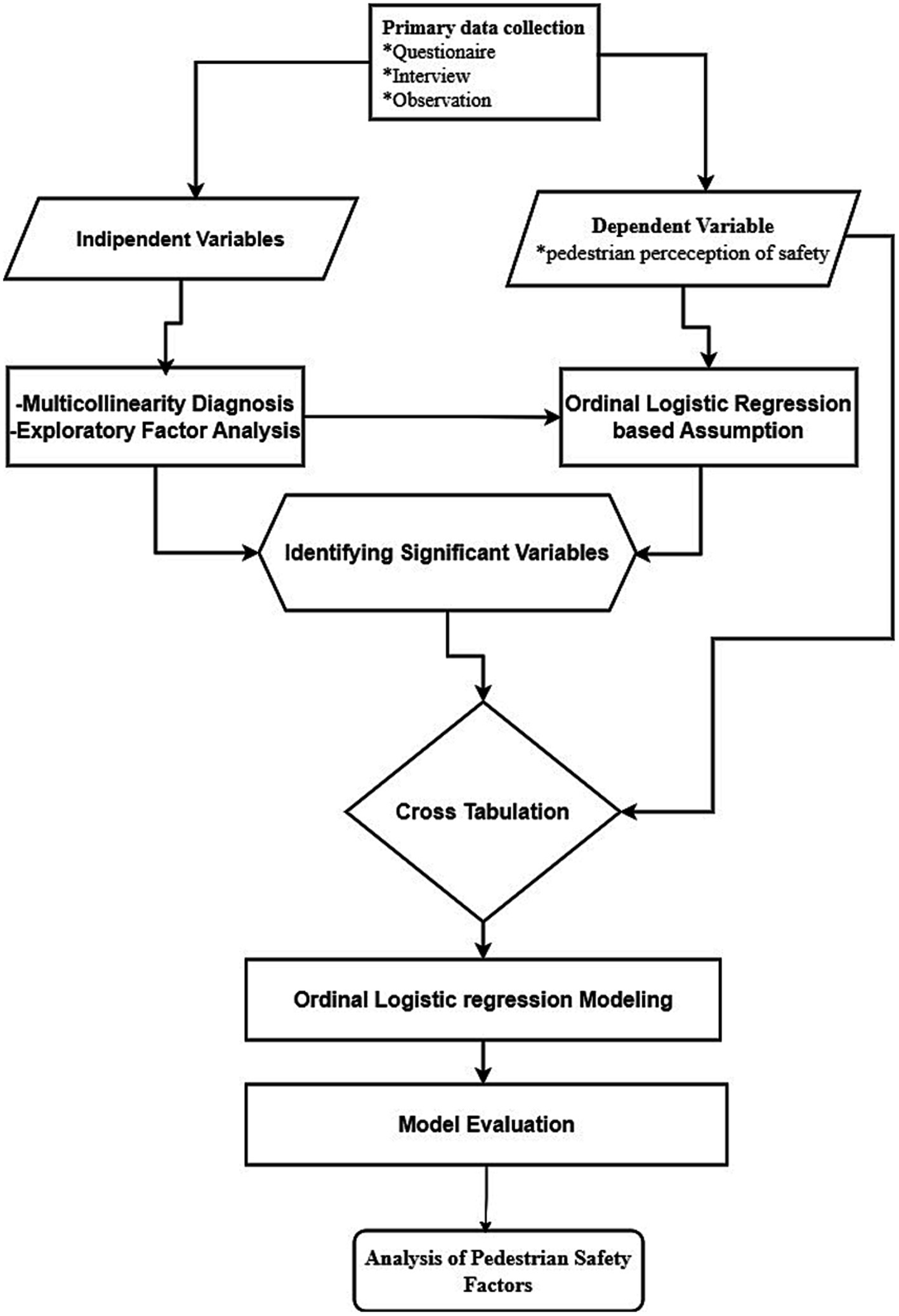
The level of perception of pedestrian safety that was considered as a dependent variable was categorized into five ordered classes of very poor, poor, fair, good, and very good and coded as 1, 2, 3, 4, and 5, respectively. Variables considered in the study were identified from research literatures and by asking experts who have closer understanding on pedestrian affairs. A total of 11 independent variables were collected from literature and experts for this study to investigate pedestrian safety. The overall methodological step followed in this study is shown in Figure 2.

Figure 2

Figure 2. Methodological framework of factors of pedestrian safety.

3 Results and discussion

3.1 Perception based pedestrian’s level of safety

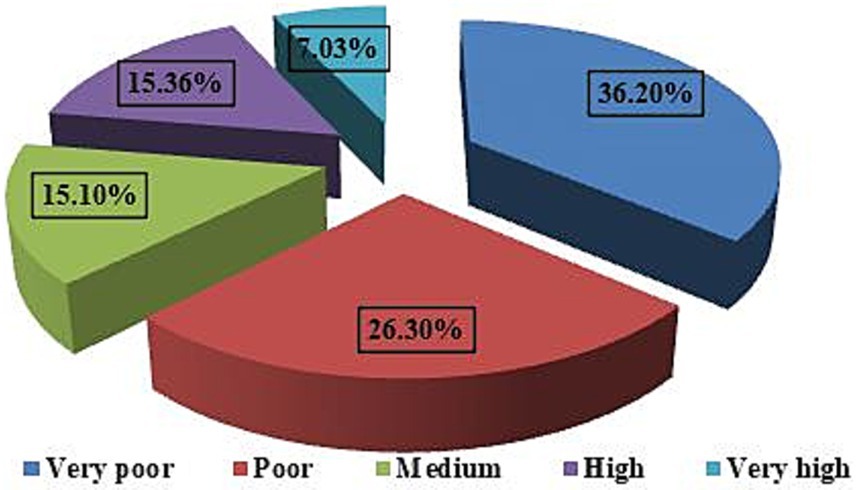
Based on Figure 1, the majority of the respondent’s safety was poor and very poor which accounts for 62.5%. Besides, 15.1% of the respondents’ feeling of safety was fair across the study corridors. On the other hand, 15.4 and 7% of the respondents reported high and very high levels of feeling of safety (See Figure 3) Based on the descriptive statistics result of Table 1, the most repeatedly reported safety score was very poor. The median and mean scores were on the poor level of safety (see Table 1). So, the result is so important to figure out major factors that affect pedestrians’ level of safety.

Figure 3

Figure 3. Safety scale of pedestrians.

Table 1

Table 1. Summary statistics output.

3.2 Demographic, socio-economic condition and pedestrian safety

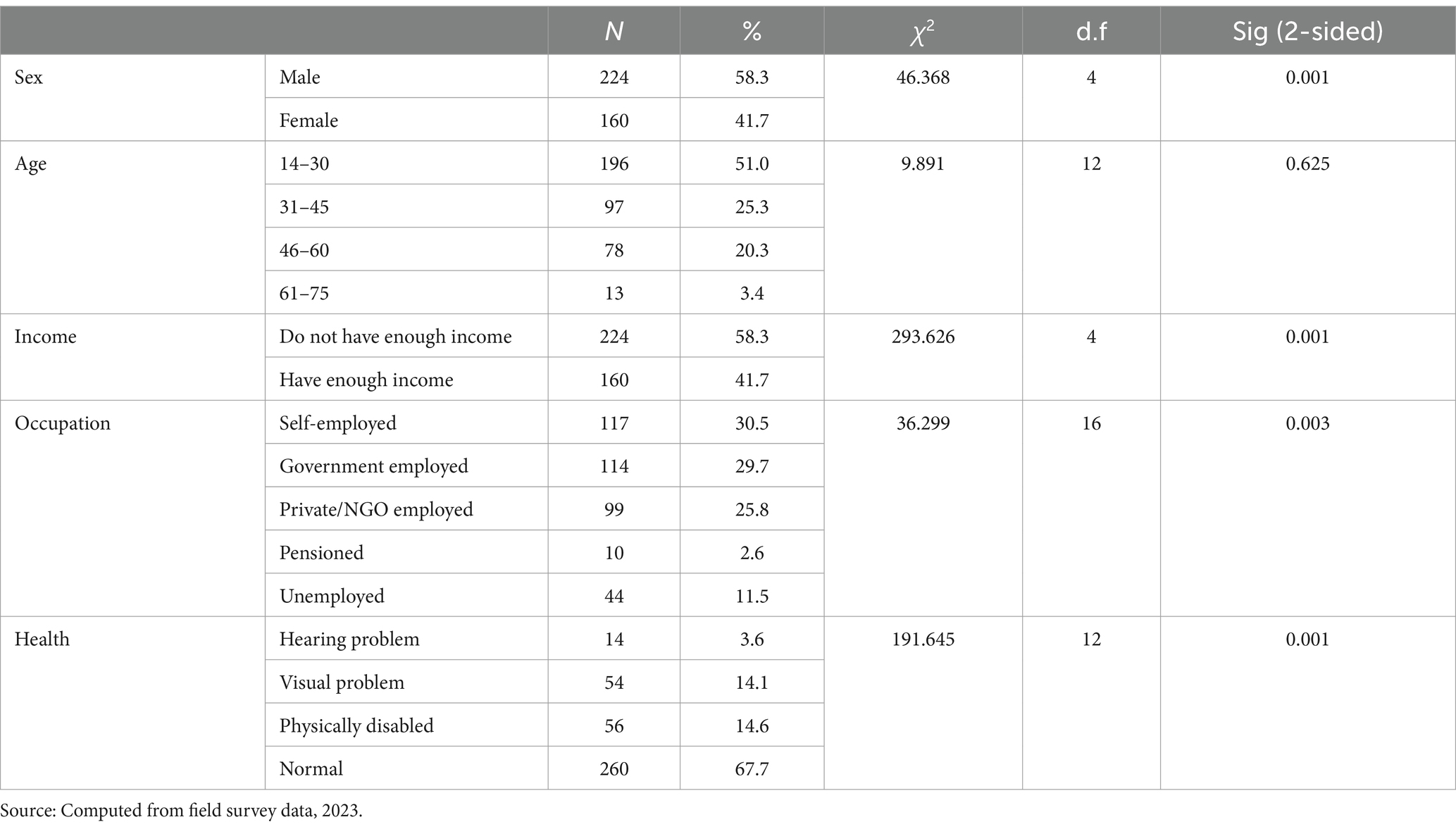
The demographic and socio-economic characteristics of the respondents such as sex, age, income, occupation, and health status were considered in this study and the result is presented in Table 2. Accordingly, from the total of 384 respondents, 224 (58.3%) were male and the remaining 160 (41.7%) were female. This implies that the sex compositions of the respondents were dominated by male pedestrians. The age category of the respondents was divided into four categories and the majority of the respondents 196 (51%) were pedestrians aged between the age of 14–30 years and followed by 31–45 years old (25.3%). Respondents aged 38–60 and 61–75 years take 78 (20.3%) and 13 (3.4%) respectively. This implies that most pedestrians (76.3%) are within the working age group. Based on income level, most of the respondents (58.3%) were those who did not have enough income for their day-to-day life.

Table 2

Table 2. Linkage of demographic and socio-economic conditions and pedestrian safety.

The employment types of pedestrians presented in Table 2 indicate that 30.5 and 29.7% were from self-employed and government-employed classes, respectively. Besides, 25.8%, 2.6 and 11.5% of the respondents belonged to NGO-employed, pensioned, and unemployed groups, respectively. This data will be helpful to see its association with pedestrian safety. Finally, the health status indicated that the majority of the respondents (67.7%) were normal respondents who did not have any health problems. On the other hand, 32.3% of the respondents have hearing, visual, and physical disability problems. According to Zarei et al. (2024), the general health condition of pedestrians has a strong relationship with pedestrian’s sense of safety. Therefore, the presence of diverse health conditions of pedestrians will help to identify pedestrian safety factors.

The chi-square test was employed to examine the presence of significant difference pedestrian safety level across the the different socio-economic status of respondents. According to Table 2, there was significant difference in perception of safety because of sex, income, occupation, and health status classes of pedestrians. However, the age of the respondent and pedestrian safety had no association (ꭓ² = 9.891, sig = 0.625). This could be due to the possibility of having lower level of safety perception among all age classes of pedestrians. Therefore, except age, demographic, and socio-economic conditions of respondents have resulted in a significant variation in safety scale among pedestrians. The finding of the study supports the work of Lin et al. (2017) and Mamun et al. (2018) who examine a linkage between pedestrian safety and demographic and socio-economic condition of pedestrians.

3.3 Data evaluation for factor analysis

The Kaiser-Meyer-Olkin (KMO) test and Bartlett’s test of Sphericity were used to evaluate the output of exploratory factor analysis (EFA). First, the Kaiser-Meyer-Olkin test of sampling adequacy assesses whether or not our sample size is sufficient for factor analysis. A value of less than 0.5 indicates the sample is too small. In this case, the value is KMO = 0.884, which means our sample size is sufficient.

The second statistic is Bartlett’s test of Sphericity which tells us whether we have an adequate number of correlations between our variables for factor analysis. In this case, we are looking for a significance value of less than our alpha level (p < 0.05). As a result, we can decide that the correlations among variables are enough for factor analysis (p < 0.001).

As factor analysis looks for relationships between variables, we establish and investigate whether there are relationships that exist between variables or not in addition to Bartlett’s test. As an assumption, there need to be at least some moderate-to-high correlations in our data (i.e., r > =0.3). Thus, cross-tabulation was used to observe the strength of the relationship. Except for one variable, i.e., the cleanness of walking surfaces and has closeness of ditches, plenty of moderate to very good correlations exist among variables (see Supplementary Table 1) and the result suggested that the analysis is appropriate. On the other hand, in factor analysis, we also want to avoid multicollinearity. According to Tabachnick and Fidell (2007) high correlation value (r ≥ 0.9) enables the creation of factors with two or fewer variables. Thus, they must be removed to avoid their disturbance in variable significance evaluation. In this study, the presence of shoeshine across pedestrian paths as a variable is removed to keep the context described above (Table 3).

Table 3

Table 3. KMO and Bartlett test (Computed from field survey data, 2023).

3.4 Selection of variables using exploratory factor analysis

3.4.1 Eigenvalues, total variance explained and scree plot

As many factors as there are variables in a factor analysis will always be extracted. In this instance, the questionnaire contains 11 variables. But the majority of these elements will be irrelevant. To decide the number of factors being kept, eigenvalues over 1, total variance, and Scree Plot are considered (see Table 4). All of the factors that are present in the data set are listed in the first three columns. The percentage of variance (%) column indicates the portion of the dataset’s volatility that each element can account for. When compared to the later elements, the initial few factors explain comparatively larger shares of the variance. The elements that we seek to extract are just those that contribute significantly to the variance.

Table 4

Table 4. Total Variance Explained (Where c, cumulative; V, variance).

3.4.1.1 Extraction sums of squared loadings (ESSL)

The middle set of columns is nearly the same as the first, but it only shows the variables that significantly contribute to the variance in our data. Only the items that meet our extraction criteria of eigenvalues greater than one are displayed in this section. The “Total” column displays each factor’s eigenvalue prior to rotation. The factor analysis produced two factors that were retrieved in our findings.

3.4.1.2 Rotation sums of squared loadings (RSSL)

After the rotation, the extracted factors’ eigenvalues are displayed in the last set of columns. Rotation maximizes the loading of each of your variables onto one while minimizing its loading on the other components. In this way, the eigenvalues are closer to each other and the factor loadings are optimized. Two factors that together accounted for 71.32% of the variance in the data were identified by the analysis.

3.4.1.3 Scree plot

This graph plots all 11 eigenvalues for two factors (see Figure 4). This can aid in visualizing the elements to maintain. An ‘elbow’ or point on the curve where the eigenvalues level out and drop off is frequently depicted in these representations. Eigenvalues that are more than this might be significant enough to keep, while the rest might not. In the scree plot curve, the graph appears to fall off after 2 factors and drop after 3. So, using this method of extraction, we can justify 2 factors here.

Figure 4

Figure 4. Scree plot diagram.

3.4.2 Rotated component matrix

To determine exactly how many factors to retain, the output of the rotated component matrix is the most important table as indicated in Supplementary Table 5. It tells how each variable loads onto each of two factors after rotation, and to what extent. This allows us to interpret what each of your extracted factors might represent. According to the result except for the 11th variable, variables have above 0.5 coefficients and are identified as important variables for the study (see Supplementary Table 2). Therefore, the 11th variable cannot be taken as a factor due to its smaller coefficient and the result approved that only those factors under component 1 fulfill the assumption.

3.5 Evaluating variables for ordinal logistic regression modeling

3.5.1 Assessing multicollinearity among independent variables

Multicollinearity increases the standard error of the regression coefficient so that the possible results of the Wald test of each independent variable will not be significant (Agresti, 2007, 2019; Muhammad and Tuti, 2013; O’Connell, 2006). In logistic regression, there must be no multicollinearity. From the selected variables shown in Table 5, two of them have VIF values above 7.5. Hence, they were removed from the list of independent/explanatory variables (see Table 5). This is good information to proceed to the ordinal logistic regression modeling. However, the fitness of each variable has to be evaluated individually before the final modeling to enhance the reliability of the model.

Table 5

Table 5. Multicollinearity diagnosis.

3.5.2 Likelihood ratio test, goodness of fit test and pseudo R²

The variable selection process helps to decrease the risk of over fitting the model by reducing the number of independent variables in the model (Larasati et al., 2011). The researchers examine every variable at a time by investigating the fit of the model statistics like likelihood ratio chi-square statistics, the goodness of fitness, and pseudo-R² as recommended by Chen and Hughes (2004) and Kline (2013). Accordingly, those variables that satisfied the parsimony of the rule of statistical outputs were identified as important variables. All variables that are considered important are used for the final modeling of the ordinal logistic regression. According to Table 4, all eleven variables have a significant statistical value of model-fitting information. All of these independent variables are statistically significant at a 95% confidence interval (p = 0.05). Hence, they are considered from the important variable lists because of their fitness to satisfy the assumption of the likelihood ratio test in the model (see Supplementary Table 3).

However, the cleanness of the surface and closing of ditches (X2), and the presence of construction inputs (X8) fail to attain the precondition of the goodness of fit test and pseudo-R² procedures (see Supplementary Table 3). Even though they have a good fit for the model based on the likelihood ratio test, the corresponding goodness of fit test indicates their poor fit in the modeling of pedestrian safety. These two factors were removed from the final modeling of pedestrian safety. Clarity of walking surface and closeness of ditches has a very low Nagelkerke R². On the contrary, the presence of construction inputs as a variable has very good performance interims of strength in explaining pedestrian safety. However, the value was not significant and that led the variable to being avoided in the modeling of pedestrian safety using the feelings of sample pedestrians.

3.5.3 Variable significance evaluation

From the 11 (eleven) independent variables, four variables, i.e., closeness of ditches along with clarity of walking surfaces, and presence of construction inputs are removed from the ordinal logistic regression modeling due to their poor fit. Furthermore, the first variable was removed from the variable list due to its lower coefficient (below 0.5) in the exploratory factor analysis. Its pseudo R² is low as compared with other independent variables (Nagelkerke =0.047). On the other hand, the presence of shoeshine and the availability of crossing opportunities were removed due to the multicollinearity problem. The rest seven variables are chosen as important variable, and are included in the final regression modeling (see Table 5 and Supplementary Table 3).

3.6 Parameter estimates and interpretation of odds ratio for pedestrian safety

The magnitude of the association between a few chosen explanatory variables and the result is explained by the table of parameter estimates. Usually, one does not interpret the threshold coefficients separately; they merely indicate the intercepts. As a result, we typically do not need to explicitly interpret the threshold settings (Adejumo and Adetunji, 2013). The odds are used to explain the direction of the relationship and whether the variable contributes to a lower or higher level of safety (see Table 6).

Table 6

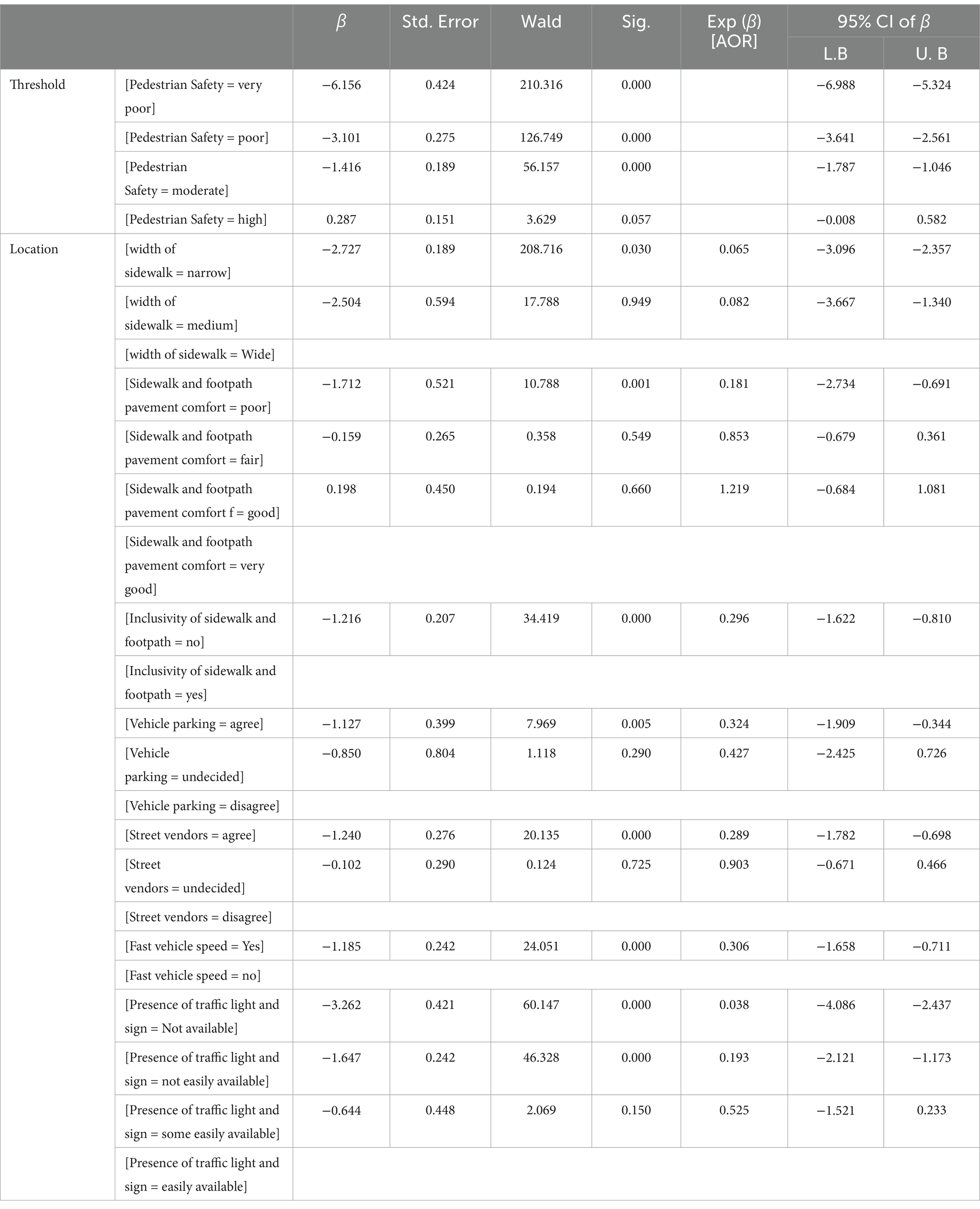
Table 6. Parameter estimates for feeling of pedestrian safety (Source: Computed from field survey data, 2023).

Sidewalks are a critical pedestrian infrastructure built for pedestrian traffic and related activities (Rodrigues et al., 2023). The degree to which walking is a convenient and secure form of transportation depends on the general features and state of sidewalks (Fonseca et al., 2022). It has been noted that wide, spotless, and well-maintained sidewalks promote safe and comfortable walking. The sidewalk’s paving materials have a big impact on how safe and comfortable it is for pedestrians. Elderly and disabled people’s mobility is restricted by slippery materials, uneven surfaces, fractures, depressions, and flooded sidewalks, all of which pose a serious risk to pedestrian safety (Hosseini et al., 2022).

According to the result of Table 6, the odds of pedestrian safety decrease by 93.5% when sidewalks become narrow in comparison to the wider one (AOR = 0.065, 95% CI = 0.030). Thus, pedestrians are more likely exposed to poor safety when the sidewalk width becomes narrow. At the same time, the result indicates that pedestrians who travel over uncomfortable sidewalk pave are 0.18 times less likely to be safe as compared to those who travel on comfortable sidewalk pavement (AOR = 0.18, 95% CI). Therefore, this study confirms the findings of Di Mascio et al. (2020), Hosseini et al. (2022), and Hosseini et al. (2022). The key informants mentioned the problem of uncomfortable pavement of footpaths and sidewalks exist in different sections of the study corridors and the researchers also observed the problem when pedestrians feel unsafe during their flow.

The inclusive nature of sidewalks and footpaths was examined as one factor of pedestrian safety. According to Humanity and Inclusion (2018) reports many of the road physical arrangements lack the tact of considering diverse travel choices in many cities of the world. As a result, many children, disabled, and old-age groups of the population suffer from traffic accidents and insecurity (Humanity and Inclusion, 2018). Based on this assertion, inclusivity was assessed as one factor in Addis Ababa mainly in the study borders. The result of Table 6 indicates the odds of failing a pedestrian to very low safety increases by 0.296 times due to failure of inclusivity of pedestrian footpaths and sidewalks. The response of the key informants also approves the problem of inclusivity of these facilities. Besides, the researcher observed non-inclusive footpaths and sidewalks that ignore the walking freedom of old aged and disabled pedestrians and almost all sites were free of facilities for them.

Pedestrians are 0.32 times less likely to be safe as a result of illegal vehicle parking (see Table 6). As observed from the site many sites of pedestrian paths are closed by vehicles and many of them stay for a longer time of days. Based on the response of Addis Ababa city administration traffic management agency staff responses, pedestrian facilities are installed for pedestrian service. But the reality on the ground is not practical. Because of this many of the pedestrians feel unsafe when they move in the study corridors. This result is consistent with the study of Idzior (2021), Gemeda (2015), and Deme (2016) who point out on-road parking as one cause of pedestrian insecurity.

Street merchants operate their unofficial businesses on sidewalks that are designed for pedestrian use. This results in a conflict over the usage of public spaces and raises the topic of whether street vendors enhance a city’s liveliness or irritate witnesses. Based on the result of Table 6, the probability of pedestrians having very poor safety increases by 0.29 times because of street vendors across pedestrian paths. This result agreed with the research findings of Tufa (2019) and Woldeamanuel et al. (2023). Street vending is an everyday event and based on repetitive observation, many of the pedestrian’s safety was disturbed due to the absence of free commuting space due to vendors.

The speed of vehicles was a very crucial risk factor for pedestrian safety in this study. According to the report in Table 6, pedestrians were 0.31 times less likely to be safe as vehicle speed is fast. The finding of this study supports the finding of Arias et al. (2021). According to the observation of the researcher, pedestrians were unsafe during fast driving speed. According to the key informant and direct observation, the legal speed is not respected and a pedestrian crash was observed practically during the survey. Finally, the study explores that pedestrians are 0.038 and 0.19 less likely to be unsafe, respectively, due to shortage and absence of traffic lights and signs. The study of Pollack et al. (2014), Olkeba et al. (2023) and Bhowmick et al. (2021) supports this argument.

3.7 Model evaluation

As explained previously, the researcher assesses the performance of an ordinal logistic model based on its model-fitting statistics and the accuracy of the predicted classification (Adejumo and Adetunji, 2013; Chen and Hughes, 2004; Larasati et al., 2011). Model-fitting statistics, including Pearson and Deviance goodness-of-fit statistics, assess how well the model fits each occurrence based on its expected and observed frequencies. In addition, the model statistics depend on the pseudo-R² statistics. Accordingly, the p-value is less than 0.05 and the chi-square statistics for model fitting information are considered statistically significant, which indicates that the model fits very well (see Table 7).

Table 7

Table 7. Model fitting information of modeling output.

Comparing the observed data for consistency with the fitted model is a standard statistical technique for determining if a model fits. Table 8 shows the standard goodness-of-fit metrics, Pearson and deviance result, based on the observed and expected frequencies. We begin with the alternative theory that there is a good fit. We conclude that we have a good model if we do not reject this hypothesis (that is, if the p-value is big) and the observed data match the model predictions. When the significant level is higher than 0.05, the Pearson and deviance statistic is deemed significant. The result from the data suggests that the model fits very well because the significant level is p is greater than 0.05 (0.96 > 0.05). The Nagelkerke R² value indicates that 84.1% of pedestrian safety is explained by all the independent variables together. The pseudo R² result of this study has better modeling performance (three fold) than Meles et al. (2020) and Bekelcho et al. (2023) that employed ordinal logistic regression for examining traffic accident severity level. So, the model has the best performance to explain the factors of pedestrian safety. The test of parallel line derived based on the recommendation of Ari and Yildiz (2014), Carophine (2016) & Ombui et al. (2011) is used for evaluating the output of the model. The parallel line assumption states that parameter estimations remain unchanged for cut-off points and that the correlation between the independent and dependent variables remains constant regardless of the categories of the dependent variable (Ali et al., 2016; Kleinbaum and Klein, 2010). Otherwise, this assumption asserts that the categories of the dependent variable are orthogonal to one another. If the assumption is incorrect, there is no parallelism (Fullerton and Xu, 2012). Likelihood Ratio statistics and ꭓ² values are used to test parallel lines assumption and examine the equality of the different categories, and decide whether the assumption holds or not. The significance value of the parallel line test is greater than alpha at 0.05 (p = 0.899). Hence, we have to accept the null hypothesis that states the location parameters are the same across the response categories and hence the link function used is appropriate (see Table 8).

Table 8

Table 8. Goodness of fit and test of parallel lines.

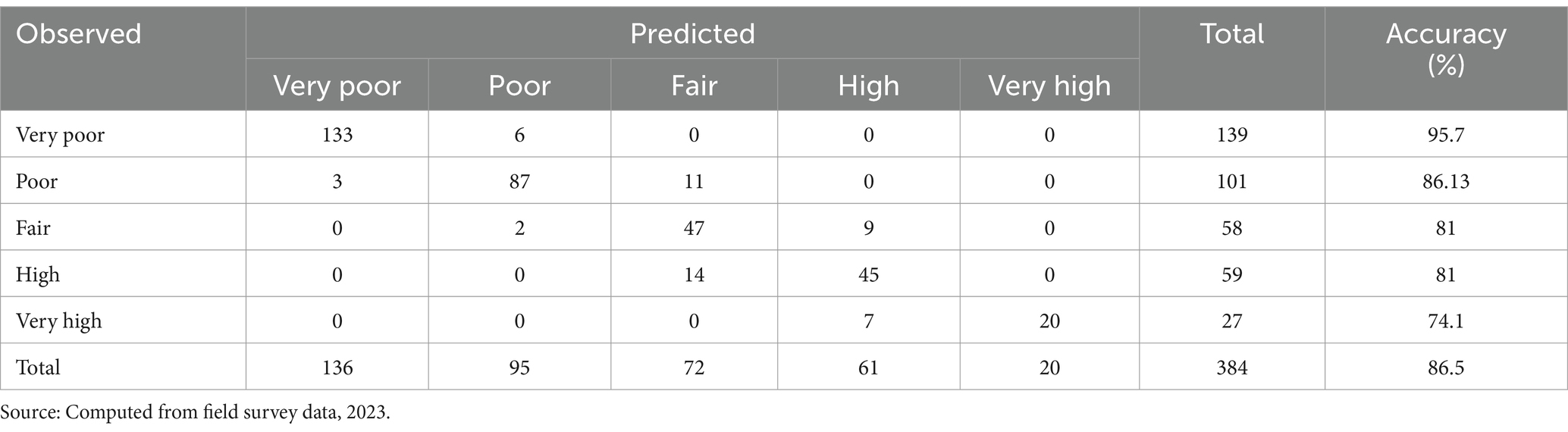
When evaluating models, the best models are those with high prediction accuracy and little likelihood of classification errors (Chen and Hughes, 2004; Kateri and Agresti, 2013; Pratiwi and Kismiantini., 2019). In this study, the correctly classified response (CCR) was derived by a linear discriminant analysis via cross-validation technique to check whether the classification accuracy was achieved or not. Table 9 demonstrates that 332 out of 384 respondents have the proper classification, yielding an accuracy rate of 86.5%. It indicates that the responses were effectively classified using the chosen model’s output.

Table 9

Table 9. Accuracy of classification.

4 Conclusion and recommendation

The challenge of rapid growth of fleet volume and fast growth of pedestrian population on travel freedom attracted the interest of many researchers from diverse perspectives. This study was conducted to explore major factors of pedestrian safety in the city of Addis Ababa. Primary and secondary data were integrated by taking Piassa to Bole Bridge and Megenagna to Torihayloch corridors as a focus of the study. The perception of pedestrians was taken as a means to identify factors under ordinal logistic regression. Finally, using the results forwarded the following conclusions are forwarded. The result of ordinal logistic regression provides higher Nagelkerke R², good-fit, reliable classification accuracy and the model can be used to list significant factors of pedestrian safety. Therefore, ordinal logistic regression analysis indicated narrow sidewalk width, lack of comfort on the pavement of the sidewalk, failure of walking facility to consider diverse road-users, Illegal vehicle parking, street-vending, fast vehicle speed and absence of traffic signs and light were strongly responsible for the lower perception of the safety of pedestrian across the study corridors. To improve the perception of safety for pedestrians, enough vehicle parking and pedestrian resting shades should be available, and local concerned bodies should provide better and alternative working sites for street merchants. Moreover, the local body should provide clear markings and signs along with appropriate speed breaking in areas having high traffic flow and sidewalk width, quality, and inclusiveness should be evaluated for the safe flow of pedestrians. Additionally, alternative crossing facilities and distributing roads should be planned in the study borders. Academicians should give focus to the concern by conducting ongoing pedestrian safety researches, consultations, and educational campaigns to the community about the impact of fast vehicle speed, illegal parking, and street vending to the community for raising awareness. Finally, further researches are highly recommended to explore new ideas for better integration of road, vehicle, and pedestrian environments.

5 Limitation of the study

The researcher tried the best and final effort to avoid limitations. However, some limitations were identified in this study. Primarily, the perception of drivers on how the pedestrian safety problem occurred was not included in examining pedestrian safety. Besides, the effect of land use pattern (the state of pedestrian safety around densely working community at schools, markets, and other commercial centers) and the role of road design, vehicular agglomeration, and road network pressure for pedestrian safety were not considered in this study. More importantly, this study did not examine and/or compare the role of each factor for pedestrian safety in different spatio temporal contexts. In this aspect, future works should employ better and advanced spatial data collection tools like mobile trucking and GPS. Therefore, the above-listed gaps have to be considered in future research works for better analysis of factors of pedestrian safety.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author/s.

Ethics statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent from the [patients/ participants OR patients/participants legal guardian/next of kin] was not required to participate in this study in accordance with the national legislation and the institutional requirements.

Author contributions

TW: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. GN: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – review & editing. RS: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

We are grateful to Ethiopia’s Ministry of Transport and Logistics (MOTL) for their continual support and eagerness to provide us with the necessary preconditions for this research study. Specifically, many thanks go to the Addis Ababa City Traffic Management Authority and Police Commission for their eagerness to provide Supportive data for this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsc.2024.1488387/full#supplementary-material

Abbreviations

AACRTB, Addis Ababa City Road Transport Bureau; AACTMA, Addis Ababa City Traffic Management Agency; AOR, Adjusted Odds Ratio; BIGRS, Bloomberg Initiative for Global Road Safety; MoT, Ministry of Transport; AAUATF, Addis Ababa Urban Age Task Force; UNECA, United Nations Economic Commission for Africa; UNICEF, United Nations Children’s Fund

References

AACRTB. (2019). Non-motorised transport: an introduction on pedestrian affair (pp. 1–36).

Google Scholar

AACTMA (2021). Addis Ababa non-motorised transport strategy implementation plan 2019–2021. Ethiopia: Addis Ababa.

Google Scholar

AACTMA (2022). Road traffic affair report. Ethiopia: Addis Ababa.

Google Scholar

AAUATF. (2022). Transport and mobility services: digital van service as alternative to private car use in Addis Ababa. In 2022 (pp. 3–12).

Google Scholar

Adejumo, A. O., and Adetunji, A. A. (2013). Application of ordinal logistic regression in the study of students’ performance: mathematical theory and modeling. Int. Inst. Sci. Technol. Educ. 3, 10–20.

Google Scholar

Aga, M. A., Woldeamanuel, B. T., and Tadesse, M. (2021). Statistical modeling of numbers of human deaths per road traffic accident in the Oromia region, Ethiopia. PLoS One 16, 1–17. doi: 10.1371/journal.pone.0251492

PubMed Abstract | Crossref Full Text | Google Scholar

Agresti, A. (2007). “An introduction to categorical data analysis” in John Wiley and Sons, vol. 2 (Hoboken, New Jersey: University of Florida).

Google Scholar

Agresti, A. (2010). Analysis of ordinal categorical data: ordinal probabilities, scores, and odds ratios. John Wiley Sons 3, 9–43. doi: 10.1002/9780470594001.ch2

Crossref Full Text | Google Scholar

Agresti, A. (2019). An introduction to categorical data analysis : In John Wiley & Sons. John Wiley & Sons.

Google Scholar

Akin, H. B., and Şentürk, E. (2012). Bireylerin Mutluluk Düzeylerinin Ordinal Lojistik Regresyon Analizi İle İncelenmesi-Analysing Levels of Happiness of Individuals With Ordinal Logistic Analysis, Öneri Dergisi, 183–193. doi: 10.14783/od.v10i37.1012000182

Crossref Full Text | Google Scholar

Al-Majali, S. R., and Imam, R. M. (2019). Analysis of pedestrian accidents in Amman. Int. J. Civil Eng. Technol. 10, 240–251.

Google Scholar

Al-sahili, K., and Jaber, A. (2019). Profile of pedestrian crashes in Nablus City, Palestine. ResearchGate, 1–13.

Google Scholar

Alavi, M., Visentin, D. C., Thapa, D. K., Hunt, G. E., Watson, R., and Cleary, M. (2020). Exploratory factor analysis and principal component analysis in clinical studies: which one should you use? J. Adv. Nurs. 76, 1886–1889. doi: 10.1111/jan.14377

PubMed Abstract | Crossref Full Text | Google Scholar

Alemayehu, M., Woldemeskel, A., Olani, A. B., and Bekelcho, T. (2023). Epidemiological characteristics of deaths from road traffic accidents in Addis Ababa, Ethiopia: a study based on traffic police records. BMC Emerg. Med. 23, 1–6. doi: 10.1186/s12873-023-00791-0

Crossref Full Text | Google Scholar

Alemgena, H., Quezon, E. T., and Umela, T. (2018). Investigation of pedestrian safety problems and its countermeasures: a case study in Nekemte City, Ethiopia. Int. J. Eng. Tech. Res. 8, 58–64.

Google Scholar

Ali, S., Ali, A., Khan, S. A., and Hussain, S. (2016). Sufficient sample size and power in multilevel ordinal logistic regression models. Comput. Math. Methods Med. 2016, 1–8. doi: 10.1155/2016/7329158

PubMed Abstract | Crossref Full Text | Google Scholar

Alicioglu, G., Sun, B., and Ho, S. S. (2020). Assessing accident risk using ordinal regression and multinomial logistic regression data generation. IEEE Xplore 1–8. doi: 10.1109/IJCNN48605.2020.9207105

Crossref Full Text | Google Scholar

Alkassabany, N., Abouelfadl, H., and Alkassabany, Y. (2018). Enhancing pedestrian safety to improve urban health. BAU J. 1, 1–17. doi: 10.54729/2789-8288.1074

Crossref Full Text | Google Scholar

Amare, M. M. (2019). Multiple regression analysis of road traffic accidents: Case study in Addis Ababa city administration : Addis Ababa University.

Google Scholar

Aregawi, A. B. (2018). Assessment of non-motorized transport infrastructure in Addis Ababa, Ethiopia (case of pedestrian and cyclists infrastructure). Can. Trans. Res. 2, 1–9.

Google Scholar

Ari, E., and Yildiz, Z. (2014). Parallel lines assumption in ordinal logistic regression and analysis approaches. Int. Interdiscip. J. Scient. Res. 1, 8–23.

Google Scholar

Arias, D., Ederer, D., Rodgers, M. O., Hunter, M. P., and Watkins, K. E. (2021). Estimating the effect of vehicle speeds on bicycle and pedestrian safety on the Georgia arterial roadway network. Accid. Anal. Prev. 161:106351. doi: 10.1016/j.aap.2021.106351

PubMed Abstract | Crossref Full Text | Google Scholar

Asare, I. O., and Mensah, A. C. (2020). Crash severity modelling using ordinal logistic regression approach. Int. J. Inj. Control Saf. Promot. 27, 412–419. doi: 10.1080/17457300.2020.1790615

PubMed Abstract | Crossref Full Text | Google Scholar

Asres, B. (2018). Analysis of land use and transportation demand interactions in Addis Ababa: A case study in Akaki Kality Sub City. MSc Thesis, Addis Ababa.

Google Scholar

Baraldi, A. N., and Enders, C. K. (2010). An introduction to modern missing data analyses. J. Sch. Psychol. 48, 5–37. doi: 10.1016/j.jsp.2009.10.001

Crossref Full Text | Google Scholar

Barron, D. (2018). Exploratory factor analysis: trinity term 2018 (pp. 1–28). Available at: https://users.ox.ac.uk/~jesu0073/Lecture%207/FactorAnalysis.pdf

Google Scholar

Bartholomew, D. C., Biu, O. E., and Arimie, C. O. (2021). Hierarchical regression modeling of some factors affecting weight of child at birth. Asian Res. J. Math. 17, 11–27. doi: 10.9734/ARJOM/2021/v17i1230345

Crossref Full Text | Google Scholar

Basbas, S., Tetou, V., and Politis, I. (2013). Ordinal and binary logistic logit models for examination of behavioral, infrastructure and perception factors influencing biking. Urban Trans. 130, 573–584. doi: 10.2495/UT130461

Crossref Full Text | Google Scholar

Beavers, A. S., Lounsbury, J. W., Richards, J. K., Huck, S. W., Skolits, G. J., and Esquivel, S. L. (2013). Practical considerations for using exploratory factor analysis in educational research. Pract. Assess. Res. Eval. 18, 1–13.

Google Scholar

Bekelcho, T., Olani, A. B., Woldemeskel, A., Alemayehu, M., and Guta, G. (2023). Identification of determinant factors for crash severity levels occurred in Addis Ababa City, Ethiopia, from 2017 to 2020: using ordinal logistic regression model approach. BMC Public Health 23, 1–15. doi: 10.1186/s12889-023-16785-3

Crossref Full Text | Google Scholar

Bellizzi, M. G., Eboli, L., Forciniti, C., and Mazzulla, G. (2018). Air transport passengers’ satisfaction: an ordered logit model. Trans. Res. Procedia 33, 147–154. doi: 10.1016/j.trpro.2018.10.087

Crossref Full Text | Google Scholar

Bhowmick, D., Winter, S., Stevenson, M., and Vortisch, P. (2021). Investigating the practical viability of walk-sharing in improving pedestrian safety. Comput. Urban Sci. 1, 21–22. doi: 10.1007/s43762-021-00020-z

PubMed Abstract | Crossref Full Text | Google Scholar

BIGRS. (2019). Design to save lives: Transforming LeGare intersection in Addis Ababa.

Google Scholar

Brien, K. O. (2016). Factor analysis: an overview in the field of measurement. Physiother. Can. 59, 142–155. doi: 10.2310/6640.2007.00004

Crossref Full Text | Google Scholar

Cabrera-Arnau, C., Curiel, R. P., and Bishop, S. R. (2020). Uncovering the behaviour of road accidents in urban areas. R. Soc. Open Sci. 7, 1–12. doi: 10.1098/rsos.191739

PubMed Abstract | Crossref Full Text | Google Scholar

Carophine, N. (2016). Ordinal logistic regression model on the factors affecting students perfomance in statistics: A case study of Maasai Mara University. Tanzania: Maasai Mara.

Google Scholar

Chen, C.-K., and Hughes, J. (2004). Using ordinal regression model to analyze student satisfaction questionnaires. IR Applications. 1, 1–13.

Google Scholar

Dahir, A. (2019). Walkability can alleviate Addis Abeba’ s traffic worries. Addis Fortune, 1–4. Available at: https://www.researchgate.net/publication/330555755%0AWalkability

Google Scholar

Das, S., and Rahman, R. M. (2011). Application of ordinal logistic regression analysis in determining risk factors of child malnutrition in Bangladesh. Nutr. J. 10, 1–11. doi: 10.1186/1475-2891-10-124

Crossref Full Text | Google Scholar

Davis, G. A., and Cheong, C. (2019). Pedestrian injury severity versus vehicle impact speed: uncertainty quantification and calibration to local conditions. Transp. Res. Rec. 2673, 583–592. doi: 10.1177/0361198119851747

Crossref Full Text | Google Scholar

Davis, J., Casteel, C., Hamann, C., and Peek-asa, C. (2018). Risk of motor vehicle crash for older adults after receiving a traffic charge: a case-crossover study. Traffic Inj. Prev. 19, 506–512. doi: 10.1080/15389588.2018.1453608

Crossref Full Text | Google Scholar

Debnath, M., Hasanat-E-Rabbi, S., Hamim, O. F., Hoque, M. S., McIlroy, R. C., Plant, K. L., et al. (2021). An investigation of urban pedestrian behaviour in Bangladesh using the perceptual cycle model. Saf. Sci. 138, 105214–105211. doi: 10.1016/j.ssci.2021.105214

PubMed Abstract | Crossref Full Text | Google Scholar

Deme, D. (2016). Traffic accident causes and countermeasures of Addis Ababa- Adama expressway : Addis Ababa Institute of Technology.

Google Scholar

Dlamini, S., Tesfamichael, S. G., Shiferaw, Y., and Mokhele, T. (2020). Determinants of environmental perceptions and attitudes in a socio-demographically diverse urban setup: the case of Gauteng Province, South Africa. Sustain. For. 12, 1–15. doi: 10.3390/su12093613

Crossref Full Text | Google Scholar

Eguale, A. (2015). Investigation of pedestrian safety problems and their remedial solutions in Addis Ababa: The case of kirkos sub city [Addis Ababa university repository]. Master Thesis

Google Scholar

Erga, D. G. (2019). Assessment of traffic congestion and its impact over selected road corridor in Addis Ababa city : Addis Ababa University Repository MSc. Thesis.

Google Scholar

Eshetu, B. (2020). Analysis of the regulation of key risk factors to road traffic accident in Ethiopia and challenges for enforcement. Bahir Dar Univ. J. Law 10, 201–232. https://heinonline.org/hol-cgi-bin/get_pdf.cgi?handle=hein.journals/bahirdjl10&section=16

Google Scholar

Fagerland, M. W., and Hosmer, D. W. (2013). Web-based supporting materials for a goodness-of-fit test for the proportional odds regression model. 32, 2235–2249.

Google Scholar

Fagerland, M. W., and Hosmer, D. W. (2016). Tests for goodness of fit in ordinal logistic regression models. J. Stat. Comput. Simul. 86, 3398–3418. doi: 10.1080/00949655.2016.1156682

Crossref Full Text | Google Scholar

Fagerland, M. W., and Hosmer, D. W. (2017). How to test for goodness of fit in ordinal logistic regression models. Stata J. 17, 668–686. doi: 10.1177/1536867X1701700308

Crossref Full Text | Google Scholar

Fenta, T. M. (2014). Demands for urban public transportation in Addis Ababa. J. Intellig. Transport. Urban Plan. 2, 121–128.

Google Scholar

Fink, A. (2019). A Mobile application for crowdsourced acquisition of urban street-view pedestrian facility data. Honors Theses 654, 1–29.

Google Scholar

Fonseca, F., Fernandes, E., and Ramos, R. (2022). Walkable cities: using the smart pedestrian net method for evaluating a pedestrian network in Guimarães, Portugal. Sustain. For. 14, 1–23. doi: 10.3390/su141610306

Crossref Full Text | Google Scholar

Fullerton, A. S., and Xu, J. (2012). The proportional odds with partial proportionality constraints model for ordinal response variables. Soc. Sci. Res. 41, 182–198. doi: 10.1016/j.ssresearch.2011.09.003

PubMed Abstract | Crossref Full Text | Google Scholar

Galanis, A., Botzoris, G., and Eliou, N. (2017). Pedestrian road safety in relation to urban road type and traffic flow. Transport. Res. Procedia 24, 220–227. doi: 10.1016/j.trpro.2017.05.111

Crossref Full Text | Google Scholar

Gebresenbet, R. F., and Aliyu, A. D. (2019). Injury severity level and associated factors among road traffic accident victims attending emergency Department of Tirunesh Beijing Hospital, Addis Ababa, Ethiopia: a cross sectional hospital-based study. PLoS One 14, 1–16. doi: 10.1371/journal.pone.0222793

Crossref Full Text | Google Scholar

Gemeda, G. (2015). Assessment of road traffic accidents along Addis Ababa-Jimma highway : Jimma University.

Google Scholar

Ghasemzadeh, A., Hammit, B. E., Ahmed, M. M., and Young, R. K. (2018). Parametric ordinal logistic regression and non-parametric decision tree approaches for assessing the impact of weather conditions on driver speed selection using naturalistic driving data. Transp. Res. Rec. 2672, 137–147. doi: 10.1177/0361198118758035

Crossref Full Text | Google Scholar

Goretzko, D., and Bühner, M. (2022). Factor retention using machine learning with ordinal data. Appl. Psychol. Meas. 46, 406–421. doi: 10.1177/01466216221089345

PubMed Abstract | Crossref Full Text | Google Scholar

Goretzko, D., Pham, T. T. H., and Bühner, M. (2019). Exploratory factor analysis: current use, methodological developments and recommendations for good practice. Curr. Psychol. 40, 3510–3521. doi: 10.1007/s12144-019-00300-2

Crossref Full Text | Google Scholar

Grzelak, M., Borucka, A., and Świderski, A. (2020). Application of the logistic regression model to assess the risk of death in road traffic accidents in the Mazowieckie Voivodeship. Transport Problems 15, 125–136. doi: 10.21307/tp-2020-054

Crossref Full Text | Google Scholar

Haile, T. (2018). Assessment of pedestrian overpass facilities along the the Addis Ababa ring road : Addis Ababa University Repository.

Google Scholar

Hair, J. F., Black, W. C., Babin, B. J., and Anderson, A. E. (2010). Overview of multivariate methods. 7th Edn. 7, 77–95.Available at: https://scholar.google.com/citations?user=CuquQ3sAAAAJ&hl=en&oi=sra

Google Scholar

Hamilton, I., Kersavage, K., Porter, R. J., Smith, K., Sanchez, J., Gayah, V., et al. (2021). An exploration of pedestrian safety through the integration of HSIS and emerging data sources: case study in Charlotte. NC. 7, 1–49. doi: 10.21949/1521675

Crossref Full Text | Google Scholar

Heydar, S., Hickford, A., McIlroy, R., Turner, J., and Bachani, A. M. (2019). Road safety in low-income countries: state of knowledge and future directions. Sustain. For. 7, 1–4. doi: 10.26552/tac.C.2019.2.1

Crossref Full Text | Google Scholar

Hilbe, J. M. (2015). “Testing and fitting a logistic model” in Practical guide to logistic regression. 1st ed (Berlin, Germany: CRC Press, Taylor & Francis Group), 71–96.

Google Scholar

Hosmer, D. W., and Lemeshow, S. (2013). Applied logistic regression. John Wiley Sons 3, 154–169. doi: 10.1002/9781118548387

Crossref Full Text | Google Scholar

Hosseini, M., Miranda, F., Lin, J., and Silva, C. T. (2022). CitySurfaces: City-scale semantic segmentation of sidewalk materials. Sustain. Cities Soc. 79, 103630–103618. doi: 10.1016/j.scs.2021.103630

Crossref Full Text | Google Scholar

Howard, M. (2015). A review of exploratory factor analysis (EFA) decisions and overview of current practices: what we are doing and how can we improve? Int. J. Human Comp. Int. 32, 51–62. doi: 10.1080/10447318.2015.1087664

Crossref Full Text | Google Scholar

Humanity and Inclusion. (2018). Inclusive urban mobility and road safety in developing countries:2018 Annual Report.

Google Scholar

Hussain, S., Goswami, A., and Gupta, A. (2022). Predicting pedestrian crash locations in urban India: an integrated GIS-based spatiotemporal HSID technique. J. Transport. Safety Secur. 15, 1–34. doi: 10.1080/19439962.2022.2048759

Crossref Full Text | Google Scholar

Idzior, M. (2021). Analysis of factors influencing pedestrians’ safety in the road traffic. Mot. Transp. 64, 24–29. doi: 10.5604/01.3001.0015.5038

Crossref Full Text | Google Scholar

Jang, K., Park, S. H., Kang, S., Song, K. H., Kang, S., and Chung, S. (2013). Evaluation of pedestrian safety pedestrian crash hot spots and risk factors for injury severity. J. Transp. Res. Board 2393, 104–116. doi: 10.3141/2393-12

Crossref Full Text | Google Scholar

Jeong, H., Sun, A. Y., Lee, J., and Min, B. (2018). A learning-based data-driven forecast approach for predicting future reservoir performance. Adv. Water Resour. 118, 95–109. doi: 10.1016/j.advwatres.2018.05.015

Crossref Full Text | Google Scholar

Job, R. F. S. (2020). Policies and interventions to provide safety for pedestrians and overcome the systematic biases underlying the failures. Front. Sustain. Cities 2, 1–8. doi: 10.3389/frsc.2020.00030

Crossref Full Text | Google Scholar

Kaiser, H. F. (1964). A Method for Determining Eigenvalues. J. Soc. Indust. Appi. Math. 12, 238–248. doi: 10.1137/0112023

Crossref Full Text | Google Scholar

Kateri, M., and Agresti, A. (2013). Bayesian inference about odds ratio structure in ordinal contingency tables. Environmetrics 24, 281–288. doi: 10.1002/env.2202

Crossref Full Text | Google Scholar

Kleinbaum, D. G., and Klein, M. (2010). Logistic regression a self-learning text: statistics for biology and health. Springer New York 3, 464–487. doi: 10.1007/978-1-4419-1742-3

Crossref Full Text | Google Scholar

Kline, R. B. (2013). Beyond significance testing: Statistics reform in the behavioral sciences. (2nd ed.). American Psychological Association. doi: 10.1037/14136-000

Crossref Full Text | Google Scholar

Kong, C., and Yang, J. (2010). Logistic regression analysis of pedestrian casualty risk in passenger vehicle collisions in China. Accid. Anal. Prev. 42, 987–993. doi: 10.1016/j.aap.2009.11.006

PubMed Abstract | Crossref Full Text | Google Scholar

Kothari, C. R. (2004). Research methodology: Methods & Techniques. 3rd Edn). New Age International (P). New Delhi, India: Limited, Publishers.

Google Scholar

Kwigizile, V., Sando, T., and Chimba, D. (2011). Inconsistencies of ordered and unordered probability models for pedestrian. J. Transp. Res. Board 2264, 110–118. doi: 10.3141/2264-13

Crossref Full Text | Google Scholar

Lagarde, E. (2019). Road traffic injuries. Encyclop. Environ. Health, 572–580. doi: 10.1016/B978-0-444-63951-6.00623-9

Crossref Full Text | Google Scholar

Larasati, A., Deyong, C., and Slevitch, L. (2011). Comparing neural network and ordinal logistic regression to analyze attitude responses. Serv. Sci. 3, 304–312. doi: 10.1287/serv.3.4.304

Crossref Full Text | Google Scholar

Levulytė, L., Baranyai, D., Sokolovskij, E., and Török, Á. (2017). Pedestrians’ role in road accidents. Int. J. Traffic Transport Eng. 7, 328–341. doi: 10.7708/ijtte.2017.7(3).04

Crossref Full Text | Google Scholar

Li, Y., and Fan, W. D. (2019). Pedestrian injury severities in pedestrian-vehicle crashes and the partial proportional odds logit model: accounting for age difference. Transp. Res. Rec. 2673, 731–746. doi: 10.1177/0361198119842828

Crossref Full Text | Google Scholar

Liang, J., Bi, G., and Zhan, C. (2020). Multinomial and ordinal logistic regression analyses with multi- categorical variables using R. Annals Transl. Med. 8, 982–988. doi: 10.21037/atm-2020-57

Crossref Full Text | Google Scholar

Liao, D., and Valliant, R. (2012). Variance inflation factors in the analysis of complex survey data. Survey Methodology. 38, 53–62.

Google Scholar

Lin, P.-S., Kourtellis, A., Zhang, Y., Guo, R., and Bialkowska-Jelinska, E. (2017). Application of demographic analysis to pedestrian safety (No. BDV25-977-30). University of South Florida. Center for Urban Transportation Research. Available at: https://rosap.ntl.bts.gov/view/dot/32333

Google Scholar

Liu, J., Hainen, A., Li, X., Nie, Q., and Nambisan, S. (2019). Pedestrian injury severity in motor vehicle crashes: an integrated spatio-temporal modeling approach. Accid. Anal. Prev. 132:105272. doi: 10.1016/j.aap.2019.105272

PubMed Abstract | Crossref Full Text | Google Scholar

Lulie, B. (2019). Estimation of level of Service of Walkways Rehabilitation Projects of Addis Ababa City roads Authority in Central Addis Ababa [Addis Ababa university repository]. Master Thesis

Google Scholar

Mabunda, M. M., Swart, L. A., and Seedat, M. (2020). Magnitude and categories of pedestrian fatalities in South Africa. Accid. Anal. Prev. 40, 586–593. doi: 10.1016/j.aap.2007.08.019

Crossref Full Text | Google Scholar

Mamun, S., Caraballo, F. J., Ivan, J. N., Ravishanker, N., Townsend, M., and Zhang, Y. (2018). Identifying association between pedestrian safety interventions and street-crossing behavior considering demographics and traffic context. J. Transp. Saf. Secur. 12, 441–462. doi: 10.1080/19439962.2018.1490369

Crossref Full Text | Google Scholar

Mascio, P. Di, D’Alessandro, D., Moretti, L., and Corazza, M. V. (2020). Walking on the safe side: a methodology to assess pavements quality conditions for pedestrian. Transportation Research Procedia, 45, 360–367. doi: 10.1016/j.trpro.2020.03.027

Crossref Full Text | Google Scholar

Meles, T. H., Mukherjee, S. C., Ryan, L., Healy, S., Mooney, R., Sharpe, L., et al. (2020). Attitudes to renewable energy technologies: Driving change in early adopter markets (No.WP20/26). UCD Centre for Economic Research Working Paper Series. Available at: https://hdl.handle.net/10419/228206

Google Scholar

Meron, D. (2011). Ordinal logistic regression analysis of correlates of crime severity. Addis Ababa, Ethiopia: Addiss Ababa University Open Acees Repository.

Google Scholar

Meyers, L. S., Gamst, G., and Guarino, A. J. (2013). “Principal components and factor analysis how” in Applied multivariate research design and interpretation (Hoboken, New Jersey: SAGE), 465–513.

Google Scholar

MOT. (2020). Ethiopia non-motorised transport strategy 2020–2029. UN-Habitat, Addis Ababa, Ethiopia.

Google Scholar

Muhammad, N., and Tuti, P. (2013). Modeling spatial ordinal logistic regression and the principal component to predict poverty status of districts in Java Island. Int. J. Stat. Appl. 3, 1–8. doi: 10.5923/j.statistics.20130301.01

Crossref Full Text | Google Scholar

Mukherjee, D., and Mitra, S. (2022). What affects pedestrian crossing difficulty at urban intersections in a developing country? Int. Assoc. Traffic Safety Sci 46, 586–601. doi: 10.1016/j.iatssr.2022.10.002

Crossref Full Text | Google Scholar

Norusis, M. J. (2010). “Ordinal Regression” in Statistical analysis for categorical data, 69–90. Available at: http://www.norusis.com/pdf/ASPC_v1, 3

Google Scholar

O’Connell, A. A. (2006). Logistic regression models for ordinal response variables: Quantitiative applications in the social science. Int. Educ. Profess. Publ. Thousand Oaks London New Delhi 146, 27–46.

Google Scholar

Olkeba, S. T., Beyecha, D. A., Merga, L. J., and Merga, B. B. (2023). Identification and prioritization of accident prone areas using accident information. A case of study of Metehara-Dengego road segment in Oromia regional state, west Hararghe zone, 1–11. doi: 10.21203/rs.3.rs-2927880/v1

Crossref Full Text | Google Scholar

Ombui, G. M., Geofrey, M., and Gichuhi, A. W. (2011). Using ordinal regression modeling to evaluate the satisfaction of Jomo Kenyatta University of Agriculture and Technology Faculty of science students. J. Agricult. Sci. Technol. 13, 164–175.

Google Scholar

Onwuegbuzie, A. J., and Collins, K. M. T. (2007). A typology of mixed methods sampling designs in social science research. Qual. Rep. 12, 281–316.

Google Scholar

Park, S., Jang, K., Park, S. H., Kim, D., and Chon, K. S. (2012). Analysis of injury severity in traffic crashes: a case study of Korean expressways. KSCE J. Civ. Eng. 16, 1280–1288. doi: 10.1007/s12205-012-1527-3

Crossref Full Text | Google Scholar

Pasaribu, F. T., Mardia, A., and Sormin, C. (2019). Ordinal logistic regression with an application to health service quality in Raden Mattaher Jambi hospital. EKSAKTA 20, 35–40. doi: 10.24036/eksakta/vol20-iss1/168

Crossref Full Text | Google Scholar

Peralta-Santos, A., Gimbel, S., Sorensen, R., Covele, A., Kawakatsu, Y., Wagenaar, B. H., et al. (2022). The neglected epidemic—risk factors associated with road traffic injuries in Mozambique: results of the 2016 INCOMAS study. PLOS Glob. Public Health 2, e0000163–e0000111. doi: 10.1371/journal.pgph.0000163

PubMed Abstract | Crossref Full Text | Google Scholar

Pollack, K. M., Gielen, A. C., Nasir, M., Ismail, M., Mitzner, M., Wu, M., et al. (2014). Investigating and improving pedestrian safety in an urban environment. Inj. Epidemiol. 1, 1–9. doi: 10.1186/2197-1714-1-11

Crossref Full Text | Google Scholar

Pour-rouholamin, M., Jalayer, M., and Zhou, H. (2017). Modelling single-vehicle, single-rider motorcycle crash injury severity: an ordinal logistic regression approach. Int. J. Urban Sci. 21, 344–363. doi: 10.1080/12265934.2017.1311801

Crossref Full Text | Google Scholar

Pratiwi, N. M.Kismiantini (2019). Implementing ordinal regression model for analyzing happiness level in Indonesia. J. Phys. Conf. Ser. 1320, 012015–012012. doi: 10.1088/1742-6596/1320/1/012015

Crossref Full Text | Google Scholar

Pulkstenis, E., and Robinson, T. J. (2004). Goodness-of-fit tests for ordinal response regression models. Stat. Med. 23, 999–1014. doi: 10.1002/sim.1659

PubMed Abstract | Crossref Full Text | Google Scholar

Purnomo, J. (2021). Factors affecting stage of cancer with accommodate indirect effect of confounding variable. AIP Conf. Proceed. 2353, 1–6. doi: 10.1063/5.0052563

Crossref Full Text | Google Scholar

Reich, M. R., and Nantulya, V. M. (2002). The neglected epidemic: road traffic injuries in developing countries. Br. Med. J. 324, 1139–1141. doi: 10.1136/bmj.324.7346.1139

Crossref Full Text | Google Scholar

Riccardi, M. R., Mauriello, F., Sarkar, S., Galante, F., Scarano, A., and Montella, A. (2022). Parametric and non-parametric analyses for pedestrian crash severity prediction in Great Britain. Sustain. For. 14, 1–44. doi: 10.3390/su14063188

Crossref Full Text | Google Scholar

Ringle, C. M., Sarstedt, M., Mitchell, R., and Gudergan, S. P. (2020). Partial least squares structural equation modeling in HRM research. Int. J. Hum. Resour. Manag. 31, 1617–1643. doi: 10.1080/09585192.2017.1416655

Crossref Full Text | Google Scholar

Rodrigues, A., Silva, H. M. R. D., Fonseca, F. P. Da, Palha, C., and Ramos, R.. (2023). The effect of sidewalk paving materials in the comfort and safety of walking: A case study in Braga, Portugal. 23rd European Colloquuium on Theoretical and Quantiative Geography, 236–237. Available at: https://hdl.handle.net/1822/85173

Google Scholar

Rosner, B. (2010). “Fundamentals of biostatistics” in Clinical trials in neurology: Design, conduct, analysis. 7th ed (Salt Lake City, Utah: Cengage Learning).

Google Scholar

Ruengvirayudh, P., and Brooks, G. P. (2022). Sample size for parallel analysis and not-so-common criteria for dimensions in factor analysis: modifying the eigenvalue > 1 Kaiser rule. Gen. Linear Model J. 46, 20–34. doi: 10.31523/glmj.046001.002

Crossref Full Text | Google Scholar

Ruhama, L. (2022). College of Development Studies Centre for regional and local development studies department: Urban land administration and management (ULAM). Addis Ababa, Ethiopia: Addis Ababa University.

Google Scholar

Senaviratna, N. A. M. R., and Cooray, T. M. J. (2019). Diagnosing multicollinearity of logistic regression model. Asian J. Probab. Stat. 5, 1–9.

Google Scholar

Sesay, R. B., Kpangay, M., and Seppeh, S. (2021). An ordinal logistic regression model to identify factors influencing students academic performance at Njala university. Int. J. Res. Scient. Innov. 8, 91–100. doi: 10.51244/IJRSI.2021.8104

Crossref Full Text | Google Scholar

Sethulakshmi, G., and Mohan, M. (2023). Identification of key determinants of personal safety perception at bus stops using proportional odds logistic regression. European Transport 9, 1–19. doi: 10.48295/ET.2023.92.9

Crossref Full Text | Google Scholar

Shrestha, N. (2020). Detecting multicollinearity in regression analysis. Am. J. Appl. Math. Stat. 8, 39–42. doi: 10.12691/ajams-8-2-1

Crossref Full Text | Google Scholar

Siddiqui, N. A., Chu, X., and Guttenplan, M. (2006). Crossing locations, light conditions, and pedestrian injury severity. J. Transport. Res. Board 1982, 141–149. doi: 10.1177/0361198106198200118

Crossref Full Text | Google Scholar

Smith, T. J., and Mckenna, C. M. (2012). An examination of ordinal regression goodness-of-fit indices under varied sample conditions and link functions. Multiple Linear Regr. Viewpoints 38, 1–7.

Google Scholar

Soathong, A., Wilson, D., Ranjitkar, P., and Chowdhury, S. (2019). A critical review of policies on pedestrian safety and a case study of New Zealand. Sustain. For. 11, 1–27. doi: 10.3390/su11195274

Crossref Full Text | Google Scholar

Sousains, J. (2011). World vehicle population tops 1Billion units. 15, 99–102. Available at: http://www.wardsauto.com/world_vehicle_population_110815/index.html (Accessed 23 January, 2023)

Google Scholar

Starkweather, J., and Moske, A. K. (2011). Multinomial Logistic Regres. 2, 1–6.

Google Scholar

Stoker, P., Garfinkel-Castro, A., Khayesi, M., Odero, W., Mwangi, M. N., Peden, M., et al. (2015). Pedestrian safety and the built environment: a review of the risk factors. J. Plan. Lit. 30, 377–392. doi: 10.1177/0885412215595438

Crossref Full Text | Google Scholar

Sürücü, L., Maslakçi, A., and Yikilmaz, İ. (2024). Exploratory factor analysis (EFA) in quantitative researches and practical considerations. Gümüşhane Univ. J. of Health Sci. 13, 947–965. doi: 10.37989/gumussagbil.1183271

Crossref Full Text | Google Scholar

Sürücü, L., Yikilmaz, İ., and Maslakçi, A. (2023). Exploratory factor analysis (EFA) in quantitative researches and practical considerations. 1–31. doi: 10.31219/osf.io/fgd4e

Crossref Full Text | Google Scholar

Tabachnick, B. G., and Fidell, L. S. (2007). “Organizing, describing, and screening data” in Experimental designs Using ANOVA, 29–67.

Google Scholar

Taddesse, W. (2011). Assessing and quantifying the level of traffic congestion at major intersections in Addis Ababa: A case for east-west corridor. Addis Ababa University Repository, MSc. Thesis.

Google Scholar

Taherdoost, H. (2017). Determining sample size; how to calculate survey sample size. Int. J. Econom. Manag. Syst. 2, 237–239.

Google Scholar

Taherdoost, H., Sahibuddin, S., and Jalaliyoon, N. (2020). Exploratory factor analysis; concepts and theory. Adv. Applied Pure Math. 27, 375–382.

Google Scholar

Tesfaledet, T., Mengistu, Y., and Nigussie, T. (2019). Application of ordinal logistic regression analysis in determining risk factors of active trachoma among rural children of aged 1-9 years old in Kaffa zone, south West Ethiopia. ARC J. Public Health Community Med. 4, 20–28. doi: 10.20431/2456-0596.0401003

Crossref Full Text | Google Scholar

Thompson, B. (2007). Exploratory and confirmatory factor analysis: understanding concepts and applications. Appl. Psychol. Meas. 31, 245–248. doi: 10.1177/0146621606290168

Crossref Full Text | Google Scholar

Transport Research Laboratory. (2012). Provision for non - motorised transport in Addis Ababa and recommendations for improvements (issue 11111024). United Nations Human Settlements Programme (UN-HABITAT).

Google Scholar

Tufa, M. A. (2019). Impact of roadside vendors and inadequate walkability infrastructures on pedestrian safety in Addis Ababa: A case study of Gulele sub-city [Addis Ababa University repository]. Master Thesis. Available at: https://www.academia.edu/download/82829365/pdf

Google Scholar

Tulu, G., Mazharul, H., Washington, S., and King, M. J. (2015a). Investigating pedestrian injury crashes on modern roundabouts in Addis Ababa, Ethiopia. Transp. Res. Rec. 2512, 1–10. doi: 10.3141/2512-01

Crossref Full Text | Google Scholar

Tulu, G., Washington, S., Haque, M., and King, M. (2015b). Investigation of pedestrian crashes on two-way two-lane rural roads in Ethiopia. Accid. Anal. Prev. 78, 118–126. doi: 10.1016/j.aap.2015.02.011

PubMed Abstract | Crossref Full Text | Google Scholar

Tulu, G., Washington, S., and King, M. (2013a). Characteristics of police-reported road traffic crashes in Ethiopia over a six year period. Proceedings of the 2013 Australasian Road Safety Research, Policing & Education Conference 28th – 30th August, 1–13.

Google Scholar

Tulu, G.., Washington, S., and King, M. (2013b). Characteristics of police-reported road traffic crashes in Ethiopia over a six year period. Peer Review Stream:Proceedings of the 2013 Australasian Road Safety Research, Policing & Education Conference, 1–14.

Google Scholar

Tulu, G., Washington, S., King, M., and Haque, M. (2013c). Why are pedestrian crashes so different in developing countries? A review of relevant factors in relation to their impact in Ethiopia. Australasian Transport Research Forum, ATRF 2013 - Proceedings. Avaialble at: https://eprints.qut.edu.au/63884/

Google Scholar

UNECA (2020). Road safety performance review in Ethiopia. Geneva: United Nation.

Google Scholar

UNICEF (2022). Strategic note on UNICEF’s work for children in urban settings. 2nd Edn.

Google Scholar

Vision Zero for Youth. (2021). Making a strong Commitment to Pedestrians with a Focus on Children. Available at: https://www.visionzeroforyouth.org›2022/11›VZY_AddisAbaba

Google Scholar

Wang, W., Yuan, Z., Yang, Y., Yang, X., and Liu, Y. (2019). Factors influencing traffic accident frequencies on urban roads: a spatial panel time-fixed effects error model. PLoS One 14, e0214539–e0214518. doi: 10.1371/journal.pone.0214539

PubMed Abstract | Crossref Full Text | Google Scholar

Watkins, M. W. (2018). Exploratory factor analysis: a guide to best practice. J. Black Psychol. 44, 219–246. doi: 10.1177/0095798418771807

Crossref Full Text | Google Scholar

Welle, B. (2015). Cities safer by design: Guidance and examples to promote traffic safety through urban and street design. 11–40.

Google Scholar

WHO. (2018). Global Status Report on Road Safety. Geneva, Switzerland: WHO. Available online: https://www.who.int/violence_injury_prevention/road_safety_status/en/ (Accessed on 23 January 2023)

Google Scholar

Williams, B., Onsman, A., and Brown, T. (2010). Exploratory factor analysis: a five-step guide for novices. J. Emerg. Primary Health Care 8, 1–13. doi: 10.33151/ajp.8.3.93

Crossref Full Text | Google Scholar

Williams, R. (2020) in Ordinal Independent Variables. eds. P. Atkinson, S. Delamont, A. Cernat, J. W. Sakshaug, and R. A. Williams (SAGE Publications Ltd), 1–7.

Google Scholar

Woldeamanuel, M., Abebe, N., and Supangkat, F. (2023). Street vending on Addis Ababa’s sidewalks: a sign of vibrancy and identity or a nuisance for pedestrians? J. Urban Aff. 45, 317–334. doi: 10.1080/07352166.2021.2014764

Crossref Full Text | Google Scholar

World Bank. (2014). Federal Democratic Republic of Ethiopia Addis Ababa urban and metropolitan transport and land use linkages strategy review: Note of proposed World Bank engagement on urban and metropolitan transport and land-use for inclusive green growth in Addis Ababa. World Bank.

Google Scholar

World Bank. (2020). Global Economic Prospects, World Bank Group. June 2020.

Google Scholar

World Bank. (2022). Addis Ababa sidewalk safety and improvement study, Project Report. Wahingiton, DC: The World Bank.

Google Scholar

Yong, A. G., and Pearce, S. (2013). A beginner’s guide to factor analysis: Focusing on exploratory factor analysis. Tutor. Quant. Methods Psychol. 9, 79–94. doi: 10.20982/tqmp.09.2p079

Crossref Full Text | Google Scholar

Zarei, M., Bazargani, H. S., Shafiee-kandjani, A. R., Dastgiri, S., Nodeh, H. R. Y., Esmaeili, E. D., et al. (2024). Relationship between general health domains and pedestrian safety behavior: a cross-sectional study. Health Scope 13, 1–8. doi: 10.5812/healthscope-141837

Crossref Full Text | Google Scholar

Zewude, A. (2015). Statistical analysis of traffic injury severity: the case study of Addis Ababa, Ethiopia. Int. J. Novel Res. Interdiscip. 2, 23–31.

Google Scholar

Zewude, B. T., and Ashine, K. M. (2016). Determinants of traffic fatalities and injuries in Wolaita zone, Ethiopia. Civil Environ. Res. 8, 38–42.

Google Scholar

Zygmont, C., and Smith, M. R. (2014). Robust factor analysis in the presence of normality violations, missing data, and outliers: empirical questions and possible solutions. Quantitative Methods Psychol. 10, 40–55. doi: 10.20982/tqmp.10.1.p040

Crossref Full Text | Google Scholar