Scalable Object Detection for Edge Cloud Environments

Object detection is an important problem in a wide variety of computer vision applications for sustainable smart cities. Deep neural networks (DNNs) have attracted increasing interest in object detection due to their potential to provide high accuracy detection performance in challenging scenarios. However, DNNs involve high computational complexity and are therefore challenging to deploy under the tighter resource constraints of edge cloud environments compared to more resource-abundant platforms, such as conventional cloud computing platforms. Moreover, the monolithic structure of conventional DNN implementations limits their utility under the dynamically changing operational conditions that are typical in edge cloud computing. In this paper, we address these challenges and limitations of conventional DNN implementation techniques by introducing a new resource-adaptive scheme for DNN-based object detection. This scheme applies the recently-introduced concept of elastic neural networks, which involves the incorporation of multiple outputs within intermediate stages of the neural network backbone. We demonstrate a novel elastic DNN design for object detection, and we show how other methods for streamlining resource requirements, in particular network pruning, can be applied in conjunction with the proposed elastic network approach. Through extensive experiments, we demonstrate the ability of our methods to efficiently trade-off computational complexity and object detection accuracy for scalable deployment.

1. Introduction

Automated object detection from visual images is important for many kinds of smart city applications, such as those involving camera-based monitoring or surveillance of areas within a city. Deep neural networks (DNNs) provide an attractive class of algorithms to apply to object detection problems. However, their computational complexity makes them unsuitable for the tighter resource constraints typical of edge cloud environments. In this paper, we develop methods for efficient DNN-based object detection in a manner that is scalable to adapt to the tighter and potentially time-varying resource constraints of edge cloud computing environments.

Consider the example of a group of surveillance drones that share edge computing resources. The devices may be able to remain in the field for longer if smaller object detection subsystems are chosen such that less computation and correspondingly less energy consumption is required. However, the drone may occasionally detect something of special note, leading to a temporary need to increase the object detection accuracy with some acceptable loss in energy efficiency or processing speed. In this case, the need for both adaptable and resource-efficient operation is evident. This paper develops novel methods for jointly providing adaptivity and resource-efficiency in edge cloud environments.

Considerable research has been conducted in recent years toward improving the execution time performance (inference speed) of DNNs (e.g., see Kim et al., 2018; Ding et al., 2019; Gong et al., 2019; Zhang et al., 2019). Research focused on execution time efficiency is of increasing interest as state-of-the-art networks continue to have more layers, and as novel applications emerge for deploying DNN-based inference at the network edge.

The use of DNNs in resource-constrained environments such as edge cloud environments requires consideration of additional metrics beyond inference accuracy. For example, energy efficiency is often very important in edge cloud environments. In such scenarios, a system designer may prefer not to utilize the highest accuracy network in favor of one that may operate for a longer duration with some acceptably small reduction in accuracy. Furthermore, there may be a desire to negotiate among speed, accuracy, and energy consumption multiple times during a deployment—e.g., as operating requirements or environmental conditions change. In such situations, it is often impractical to replace the employed neural network entirely. Moreover, it is also impractical or highly inefficient, in terms of storage utilization, to maintain multiple alternative networks on board so that they can be selected among and switched across dynamically.

A new methodology for DNN network design, called elastic neural networks (ENNs), has been introduced in recent years as an efficient, practical alternative for realizing adaptable DNN inference in compact (low-memory-footprint form) (Bai et al., 2018). ENNs enable the use of a single DNN network structure in multiple, alternative ways to achieve adaptable trade-offs among relevant operational metrics. The ENN methodology can be viewed as a modularization strategy that takes a conventional (“non-elastic”) DNN N as an input and introduces early-exits (intermediate outputs) to the backbone of N, where the early exit points are determined at design time and then selected adaptively at run-time. Each early exit point corresponds to a distinct trade-off among inference accuracy and computational complexity since the portion of the network after the early exit is switched off during inference. Each early exit point is associated with a separate network head, and each network head is optimized separately as part of the ENN training process. This approach allows the designer to construct a network with as many exit points (operational alternatives) as deemed appropriate for the application (subject to constraints imposed by the structure of N), with each additional exit point only increasing the overall network size modestly.

An important feature of the ENN methodology is, as described above, that it can be applied to arbitrary DNN backbones. This allows designers to flexibly reuse and build upon existing efforts in DNN design and optimization.

In this work, we present the first application of the ENN methodology to object detection from visual images. For the network backbone, we apply the popular Single-Shot Multibox Detector (SSD) network (Liu et al., 2016) as our starting point N. We refer to the resulting elastic network design as the elasticized SSD network, and we refer to the starting-point SSD network as the base network for the elasticized SSD. Through extensive experiments on object detection datasets, we demonstrate the effectiveness of the elasticized SSD network in providing diverse operational trade-offs with only a relatively small increase in memory requirements compared to the SSD network.

Moreover, we present the first study integrating the ENN methodology with network pruning, which is a popular method for streamlining the design of DNNs that is also of great relevance to edge cloud applications. Network pruning is defined as “a systematic process of removing the parameters of an existing network” (Blalock et al., 2020). We demonstrate that network pruning is highly complementary to the ENN methodology and that the approaches can be integrated to achieve significantly more compact ENN designs with minimal degradation in accuracy. We show, for example, that pruned ENN designs allow us to counteract the additional network size required for each exit-point network head.

The remainder of this paper is organized as follows. In section 2, we discuss related work in the literature on object detection and DNN design. In section 3, we present the proposed elasticized SSD network for object detection in edge cloud environments. In section 4, we present experimental results that evaluate the accuracy, computational complexity, and memory requirements of the elasticized SSD network, and that also provide a quantitative evaluation on the integration of pruning methods into the elasticized SSD design. In section 5, we summarize and give concluding remarks.

2. Related Work

Bai et al. originally proposed the framework of elastic neural networks (Bai et al., 2018) (ENNs). This work discussed the effects of adding early exits to an arbitrary DNN. These early exits exploit the property that feature maps constructed prior to the final network layer may contain sufficient information for proper inference. In addition to providing novel trade-offs between accuracy and inference speed, Bai showed that the proposed class of networks can also significantly improve classification accuracy for the full-network configuration (when no early exit is taken). It was anticipated that this improvement results because the early exits act as a useful regularizer at training time.

In this paper, we use Bai's ENN methodology as a starting point and present the first application of the methodology to object detection from visual images, which is an important and challenging problem for edge cloud environments. We also present the first integration of the ENN methodology with network pruning and demonstrate that both approaches—elastic networks and pruning—can be used in a complementary fashion that allows designers to streamline network implementations significantly more effectively than using either method in isolation. The pruned, elastic network approach introduced in this paper is also of special interest in edge cloud environments, where highly streamlined solutions are often required to meet tight resource constraints.

For many years, network pruning has been used to reduce the size of CNNs and avoid overfitting (LeCun et al., 1989; Ström, 1997). In the last decade, pruning has been used to reduce network storage and computation by an order of magnitude with no loss of accuracy (Han et al., 2015). The decreased storage requirements may allow an entire network to be stored on-chip rather than in DRAM, which allows for improved energy efficiency (Horowitz, 2014).

The utilization of network pruning continues to expand as well, and new strategies continue to improve the method's efficacy. For example, Molchanov et al. proposed a method that estimates the contribution of each network filter to the final loss and then prunes filters that have little estimated importance. The authors used this method on ResNet-101 to reduce the number of floating-point operations (FLOPs) by 40% with only a 0.02% loss in top-1 accuracy (Molchanov et al., 2019).

In recent years, many architectures have been developed for object detection using DNNs that consider resource-constrained environments. Tiny SSD is a recent DNN for real-time embedded object detection utilizing a non-uniform “Fire” sub-network and an optimized SSD-based convolutional layer sub-network. Tiny SSD was able to achieve a model size of 2.3 MB while still maintaining relatively high accuracy (Womg et al., 2018). Fast YOLO is another framework recently proposed to reduce parameters and power consumption while attempting to maintain accuracy (Shafiee et al., 2017). Additionally, recent networks have been developed to improve the accuracy of standard SSD networks while maintaining the network's efficiency, such as RefineDet (Zhang et al., 2018).

The approach developed in this paper goes beyond the aforementioned contributions to resource-constrained object detection by allowing system designers to balance object detection accuracy and efficiency in an adaptive manner, based on scenario-dependent operating conditions. The flexibility is achieved in a compact form through a single, configurable network, which can be deployed for efficient, adaptive operation in resource-constrained edge cloud environments.

3. Methods

Our proposed ENN for object detection is an elasticized version of the single-shot detector (SSD) network (Liu et al., 2016), as mentioned in section 1. We use a specific variant of SSD called the SSD300 network. The network, in turn, uses the VGG-16 network (Simonyan and Zisserman, 2014) as its backbone network. From a base SSD network, we add early-exits from multiple layers in the backbone network that skip the remaining backbone layers and connect directly to the layers that follow.

We selected SSD300 as the foundation for our ENN proposed in this work because it is a widely-utilized object detection network offering an often-favorable compromise between inference speed and accuracy. However, the general elasticization methodology that we apply can be readily applied to alternative object detection neural networks based on the specific needs of the application. For example, a larger network may be used if a higher mean average precision (mAP) for object detection is desired, or a smaller network with fewer early-exits may be chosen when resources are heavily constrained.

The number of early exits included in the elasticized SSD network is an important design parameter that controls the degree of configurability provided by the network. As described in section 1, each early exit corresponds to an intermediate output from the network. The set Ω of network exits is taken as the set λ₁, λ₂, …, λ_n of early exits together with the full-network exit μ, which is the conventional output of the base SSD network (i.e., the final network output as opposed to an intermediate output). The λ_is are ordered such that higher indices correspond to later exits, or equivalently, more layers from the base network that are included before the intermediate output is taken. The set of exit points in the elasticized SSD can then be expressed as Ω = {α₁, α₂, …, α_n+1}, where α_i = λ_i for i = 1, 2, …, n, and α_n+1 = μ. We refer to the value n, which is a design parameter of the elasticized network, as the elasticization degree of the network. Thus, the conventional (base) SSD network can be viewed as an elasticized network with elasticization degree 0.

In general, a larger elasticization degree provides a correspondingly larger set of trade-off options that can be selected at run-time. The costs associated with increasing the elasticization degree are increased training complexity of the network, as well as increased storage requirements for the network due to the need for an increasing number of post-exit subnetworks. More details about post-exit subnetworks will be discussed later in this section. However, we note here that the increases in training and storage costs are relatively low for the elasticized network because all of the exits in Ω are derived from a common base network. Thus, there is significant reuse of trained network parameters from across the different sub-networks that correspond to the alternative exit points in Ω. This advantage of low-overhead configurability is of particular utility in edge cloud environments.

At inference time, the inputs of the elasticized SSD network are RGB images with dimension 300 × 300 × 3 and exit position r_po, where r_po ∈ Ω. This exit position input allows the elastic network subsystem to dynamically change the exit position, where the input is controlled by the enclosing system. During operation, r_po = α_i with i ≤ n means that all portions of the network that follow α_i, including the portions that contain α_i+1, α_i+2, …, α_n+1 are effectively switched off, and therefore do not consume computational resources, that is, time or energy.

This elasticized SSD architecture is illustrated in Figure 1, where a multiplexer and switch are used to graphically depict that only a single exit point α_i is used at a given time. As shown in Figure 1, each early exit is followed by a subnetwork, which we refer to as a post-exit subnetwork. Each post-exit subnetwork consists of the layers that come after the backbone network of the base network; in our elasticized SSD design, the backbone network is VGG-16, and the base network is SSD300.

FIGURE 1

Figure 1. An illustration of the elasticized SSD network architecture.

The post-exit subnetworks are trained specifically for the elasticized network; their parameters are not inherited from the base SSD network. Additionally, each post-exit subnetwork may require alterations to the first convolutional layer to form the proper tensor shape for the remaining layers depending on the placement of the associated exit point. These alterations have been made as part of the design of the elasticized SSD network, and are opaque to users of the network. In each post-exit subnetwork, the layers after the first convolutional layer are the same regardless of the exit point.

At inference time, the post-exit subnetworks that are not in use and all layers beyond the exit point in the backbone are disabled, which improves real-time performance and energy efficiency.

When forming an ENN from an object detection network, we attach early exits to the feature-extraction subnetwork. The post-exit subnetworks are used primarily for bounding box locations and classes, i.e., localization and classification. We use this scheme because certain images may not require passing through the full feature-extraction subnetwork before having enough predictive power to perform object detection adequately, and having multiple copies of the post-exit subnetworks allows each copy to be trained independently for feature maps that have been through the same feature extraction layers. Intuitively, a different number of feature extraction layers may result in differences between classes becoming more or less subtle. If different exit points were connected to the same post-exit subnetworks, it may be difficult for localization and classification to be trained well for all exit points.

Let ESSD_x denote the active portion of our elasticized SSD network when r_po = α_x; we refer to the active portion of the network for a choice of r_po as the current path of the network. As described above, a higher value of x reduces resource consumption, typically at a cost to accuracy. The current path includes the portion of the backbone network up to α_x along with the post-exit subnetwork that follows α_x. The greater the number of path options (i.e., valid values for x), the finer the available granularity when balancing resources and network performance, but there will also be larger overhead due to the larger number of post-exit subnetworks. At the same time, significant storage savings are gained by reusing the same backbone network across all (n + 1) possible choices for the current path.

The first step in deriving an elasticized SSD network is to select the set Ω. In practice, the designer should select a set of exit points that match the desired balance between the diversity of available reconfiguration options, the least resource-intensive state deemed to have acceptable accuracy (earliest acceptable exit point), and the highest accuracy state deemed to have acceptable resource-consumption (latest acceptable exit point). In our formulation, we assume that the full-network exit is in the set of selected exit points—i.e., that μ ∈ Ω. However, this assumption can be dropped in severely resource-constrained edge cloud systems. An interesting direction for future work is the development of automated tools for deriving Ω based, for example, on a relevant multi-objective optimization formulation.

In the elasticized SSD framework, the set Γ of all candidate exit points consists of the points in the backbone network that immediately precede the Conv2d layers, as well as the full-network exit μ. It is anticipated that there would be little benefit, for example, to adding an additional exit point immediately before or after a RELU layer. Since there are 15 Conv2d layers in the backbone network, Γ consists of 16 elements—that is, if we include bypassing the backbone network entirely along with the other extreme, which is the full-network exit. We enumerate the elements of Γ, maintaining the convention that smaller indices correspond to earlier exits, as Γ = γ₁, γ₂, …, γ₁₆, where by definition, γ₁₆ = μ.

We have prototyped the elasticized SSD network using PyTorch. We refer to this prototype as the ESNO (Elasticized SSD Network for Object detection) system or simply “ESNO” for brevity. More details about ESNO and our experiments using it are presented in section 4. For the purposes of testing, the functionality for switching between ESSD_x and ESSD_y for x ≠ y in ESNO only requires the user to select r_po = y at compile time when executing the PyTorch implementation on either a CPU or GPU, once they have constructed the desired elasticized SSD configuration. In an embedded device, a physical or virtual switch could be used at run-time to dynamically change paths without the need to recompile once a final network is constructed. Embedded implementation of the elasticized network is beyond the scope of this paper; it is a useful direction for future work.

We train each path ESSD_x separately for x ∈ {1, 2, …, (n + 1)} while holding the parameters of the backbone network fixed. In our experiments, we select Ω = {γ₁₂, γ₁₃, γ₁₄, γ₁₅, μ}. This set is selected to provide the highest-accuracy collection of five configuration alternatives with which to demonstrate the proposed elasticized SSD architecture. When applying ESNO, one may choose a larger or smaller set of exit points, and convolutional layers used as exit points need not be consecutive. Our selected Ω simply provides insight into how the mAP, parameters, and FLOPs change as we exit the network prematurely. Further, our chosen set of exit points offers quantitative insight into the overhead incurred when adding four exit points to the original network, which may provide a useful degree of granularity for balancing accuracy, resources, and run-time performance in various edge cloud application scenarios.

We evaluate the various paths through the ESNO network using mean average precision (mAP), total number of floating-point operations (FLOPs), and total number of parameters in order to assess the relative trade-offs among the different paths. The FLOPs and number of parameters were determined using the pytorch-model-summary PyTorch library (Marczewski, 2020). We examined the total number of parameters and mAP achieved across each path in the elasticized SSD network to demonstrate the utility of ESSD in comparison to conventional, single-exit (non-elastic) networks. Details on these experiments are presented in section 4.

Our primary basis for comparison is the original, non-elasticized version of the ENN utilized. Specifically, we compare ESSD to the base SSD network to gain insight into the trade-off between accuracy and FLOP count, as well as the overhead incurred by the addition of early exits. Since the alternative paths reduce the number of layers used relative to the base network, our primary aim is to reduce the FLOPs used as much as possible while maintaining the highest possible accuracy.

To further streamline the efficiency of elasticized SSD implementation, we integrate network pruning into the ESNO system. We prune the network using pytorch.nn.utils.prune and use global pruning across all convolutional layers of the network, as opposed to pruning each layer independently. Our pruning technique is L1Unstructured (L1u, 2019; Paganini, 2020), which prunes the smallest weights in the network based on the L1-Norm. Unstructured pruning removes only individual weights, while structured pruning removes entire units or channels (Paganini and Forde, 2020). Our choice of L1Unstructured pruning is not compulsory when integrating pruning with the elasticized SSD architecture; any method of reducing the number of parameters while approximately maintaining accuracy can be used in place of the specific pruning strategy that is applied in ESNO. That is to say that our methodology is agnostic to the specifics of the pruning algorithm employed.

To control the degree to which pruning is performed is ESNO, we define a parameter called the pruning parameter, which we denote by ρ. This parameter is a real number within [0, 1] that determines the proportion of network parameters that are removed in the pruning process. In our experiments, we apply ρ = 0.3, which means that 30% of the network parameters across the entire network are removed during the pruning process. In section 4, we show that this setting of ρ approximately compensates for the parameter storage overhead associated with the post-exit subnetworks introduced by the elasticized SSD architecture. In other words, the total parameter storage cost associated with the post-exit layers in ESNO is approximately equal to the total parameter storage saved by applying pruning with ρ = 0.3.

We did not choose to use iterative pruning, in which multiple iterations of pruning and retraining are performed before reaching the desired, reduced network. That is, we pruned all of the network parameters at once followed by a single iteration of retraining. We chose this method because the percentage of parameters that we have pruned is relatively low; therefore, iterative pruning may not be needed to maintain accuracy as network parameters are reduced. However, ESNO can readily be adapted to incorporate iterative pruning to reduce the number of parameters as much as possible while maintaining accuracy to within a tolerable range. Detailed results related to our use of pruning in ESNO are presented in section 4.

Algorithm 1 provides a pseudocode sketch of the integrated process of pruning and training that is used to optimize the ESNO system for a given set of designer-selected exit points Ω. The application of pruning is enabled or disabled based on a Boolean-valued parameter pruning_enabled, which is set by the network designer. The initial training stage, which occurs immediately after pruning, trains the full SSD300 network using the available training data. After that, the backbone network is “frozen,” which means that its trained parameters are fixed for the remainder of the overall optimization process represented by Algorithm 1. The subsequent training operations then examine the post-exit subnetworks one at a time, and optimize these separately with the backbone parameters held fixed. The result of the overall optimization process is a pruned and trained configuration of the elasticized SSD architecture based on Ω.

ALGORITHM 1

Algorithm 1. ESSD TRAINING

4. Experimental Results

To evaluate the ESNO system, we began with an existing PyTorch implementation of SSD (DeGroot and Brown, 2019). We then added four exit points throughout the VGG-16 backbone of the network, thus creating five possible path options. As described in section 3, the set of exit points was selected as Ω = {γ₁₂, γ₁₃, γ₁₄, γ₁₅, μ}. The network, together with this set of exit points, was pruned and trained using the process summarized in Algorithm 1.

For each training step in Algorithm 1, we employed stochastic gradient descent (SGD) on the Pascal Visual Object Classes (VOC) 2007 and 2012 datasets (Everingham et al., 2007, 2012). To train the five alternative paths defined by Ω, ESNO first trained ESSD_n+1—that is, the path corresponding to the standard SSD network without exiting the backbone early. The backbone was then frozen, along with the post-exit subnetwork for the path ESSD_n+1. Then the remaining four post-exit subnetworks were trained separately while ensuring that the backbone network was not affected by alternate paths through early-exits.

For all of the training and inference experiments reported in this section, we used a desktop computer system equipped with an AMD Ryzen 5 3600 6-Core 12-Thread CPU, an MSI GeForce RTX 2070 Super 8 GB Gaming X Trio GPU, G.skill Trident Z Neo 32 GB (4 × 8) 3,600 MHz Memory, and Sabrent Rocket 2 TB PCIe 4.0 NVMe SSD storage.

First, we report on experiments performed using ESNO with pruning disabled. We trained each of the five candidate paths with an initial learning rate of 1 × 10⁻³, a batch size of 16, a momentum of 0.9, and a weight decay of 5 × 10⁻⁴. With the exception of the batch size, we chose these parameters because they were the same values used in the original SSD experiments (Liu et al., 2016). The batch size was set to 16 instead of 32 due to hardware constraints on the platform used for training. Each path was trained for 100,000 iterations, and the learning rate was reduced by a factor of 10 at 50,000, 70,000, and 90,000 iterations. These settings served as a standard basis for comparison across the five alternative network paths in the ESNO system. A summary of parameters used is provided in Table 1 for convenience.

TABLE 1

Table 1. Summary of parameters used during training.

After the ESNO optimization process of Algorithm 1 was complete, we determined the number of parameters and FLOPs encountered along each path. The results of this analysis are summarized in Table 2. The results show a considerable reduction in parameters as we move earlier in the sequence (α₁, α₂, …, α₅) of early exits. For example, ESSD₁ contains about 31% fewer parameters than ESSD₅.

TABLE 2

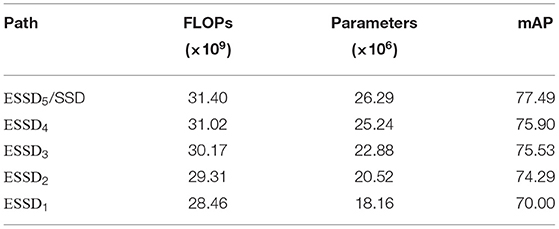
Table 2. Comparison of FLOP counts, parameter counts, and mAP levels for different paths in the trained ESNO system with pruning disabled.

With pruning disabled, the elasticized SSD network derived from the ESNO system contains a total of 3.97 × 10⁷ parameters in total while the original SSD network contains 2.63 × 10⁷ parameters. This amounts to approximately 51% overhead for the creation of our 5-path elastic network. To investigate the capability of ESNO to offset the overhead incurred, we enabled pruning in Algorithm 1 with ρ =0.3. After pruning, the training process in ESNO proceeded using the same training parameters as those that were applied in the pruning-disabled experiments. We then tested the trained, pruned, elastic network using the same methods as the non-pruned network. A summary of the results is provided in Table 3.

TABLE 3

Table 3. Results from the ESNO system with pruning enabled (ρ = 0.3).

With 30% of the entire network pruned, the number of parameters in the elasticized network is reduced to 2.77 × 10⁷. At the same time, accuracy is maintained to within 2% absolute mAP for each of the five alternative paths through the network (compared to the corresponding paths in the unpruned version). The application of pruning is also seen to reduce the size of the network to approximately the same size as the original, non-elastic SSD. In one case, namely ESSD₄, the accuracy improved slightly after pruning and retraining.

Figure 2 illustrates examples of object detection results produced by the five different exits α₁, α₂, …, α₅ for our elasticized SSD network on a given input image frame. The results were obtained from the network derived with pruning enabled and ρ = 0.3. The illustration gives a visual sense of the kind of results that can be obtained for multiple objects in a single image for the various paths through the elasticized network. From Figure 2, we can see that all five exits detected all of the same objects, with the exception that the earliest exit failed to detect the two closest people.

FIGURE 2

Figure 2. Example of the elasticized single-shot multibox detector network output after 30% pruning. Top-left−ESSD₅, Top-right−ESSD₄, Mid-left−ESSD₃, Mid-right−ESSD₂, Bottom−ESSD₁.

In general, one could empirically derive a matrix detailing the trade-offs between accuracy and FLOP count for any ENN design. Recall that, in this work, n + 1 is the number of possible paths through the network. One could use a two-dimensional matrix Z with dimensions (n + 1) × 2 such that Z[k][0] and Z[k][1], respectively, denote the measured FLOP count and accuracy when k is the exit point. There are many methods for deriving such a matrix. A simple method is for the designer to use pytorch-model-summary, as we have in our experiments, for each path option. This method identifies Z[i][0] and Z[i][1] for i = 1 to n + 1. We can determine Z for our model using the data shown in Table 2. A run-time controller for an edge cloud system may then select a path option based on Z to satisfy efficiency criteria while meeting an accuracy threshold set by the designer. The trade-off criteria should be selected based on the structure of the elasticized network and the designer's needs. Each elasticized network may act as a single node in an edge cloud system, and the cooperating networks need not be homogeneous. For example, differing accuracy thresholds may be selected for certain nodes in locations of higher importance to keep these nodes in a state of higher accuracy. Our results in section 4 for a single node provide insight into the advantages of elasticized networks when scaling an edge cloud system to many ENN nodes.

5. Conclusions

In this paper, we have developed a novel elastic neural network architecture for the detection of objects from visual images, and we have presented a prototype implementation of the architecture called the Elasticized SSD Network for Object detection (ESNO). ESNO provides capabilities to adaptively reconfigure object detection operation across diverse trade-offs between inference accuracy and computational cost.

Additionally, the alternative operating points of the reconfigurable network are achieved by reusing a major portion of the network across all of the operating points. This reuse enables the reconfigurable network architecture to be deployed in a storage-efficient manner (in terms of the required number of network parameters), which is important in relation to the resource constraints that are typical of edge cloud environments.

We also presented the first integration of the elastic neural network methodology with network pruning and demonstrate that both approaches— elastic networks and pruning—can be used in a complementary fashion that allows designers to streamline network implementations significantly more effectively than using either method in isolation. Our experimental results demonstrate the effectiveness of the ESNO architecture in providing diverse operational trade-offs with only a relatively small increase in storage requirements compared to the original (non-elastic) SSD network. Moreover, with pruning, the overhead incurred from elastic neural networks—due to the post-exit subnetworks—can be readily compensated for at minimal or no cost to accuracy while providing a resource-adaptive design that is favorable for edge cloud environments.

Useful directions for future work include the development of automated tools for deriving the set of exit points in the ESNO architecture and developing optimized implementations of the ESNO architecture that are suitable for deployment on resource-constrained, embedded computing platforms.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

RH is the primary author of this document and lead contributor to the research and experiments presented. MU is the secondary contributor to the research and experiments. SB is a contributor to the manuscript and the primary advisor on the topic. AM and ZL served as additional advisors on the work. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, Y., Bhattacharyya, S. S., Happonen, A. P., and Huttunen, H. (2018). “Elastic neural networks: a scalable framework for embedded computer vision,” in 2018 26th European Signal Processing Conference (EUSIPCO), (Rome: IEEE), 1472–1476.

Google Scholar

Blalock, D., Ortiz, J. J. G., Frankle, J., and Guttag, J. (2020). What is the state of neural network pruning? arXiv preprint arXiv:2003.03033.

Google Scholar

DeGroot, M., and Brown, E. (2019). ssd.pytorch. Available online at: https://github.com/amdegroot/ssd.pytorch

Ding, R., Liu, Z., Chin, T.-W., Marculescu, D., and Blanton, R. D. (2019). “Flightnns: lightweight quantized deep neural networks for fast and accurate inference,” in Proceedings of the 56th Annual Design Automation Conference 2019 (Las Vegas, NV), 1–6.

Google Scholar

Everingham, M., Van Gool, L., Williams, C. K. I., Winn, J., and Zisserman, A. (2007). The PASCAL Visual Object Classes Challenge 2007 (VOC2007) Results. Avaialble online at: http://www.pascal-network.org/challenges/VOC/voc2007/workshop/index.html

Google Scholar

Everingham, M., Van Gool, L., Williams, C. K. I., Winn, J., and Zisserman, A. (2012). The PASCAL Visual Object Classes Challenge 2012 (VOC2012) Results. Available online at: http://www.pascal-network.org/challenges/VOC/voc2012/workshop/index.html

Google Scholar

Gong, R., Liu, X., Jiang, S., Li, T., Hu, P., Lin, J., et al. (2019). “Differentiable soft quantization: Bridging full-precision and low-bit neural networks,” in Proceedings of the IEEE International Conference on Computer Vision (Seoul), 4852–4861.

Google Scholar

Han, S., Pool, J., Tran, J., and Dally, W. (2015). Learning both weights and connections for efficient neural network. arXiv preprint arXiv:1506.02626.

Google Scholar

Horowitz, M. (2014). “Energy table for 45nm process,” in Stanford VLSI Wiki.

Kim, E., Ahn, C., and Oh, S. (2018). “Nestednet: Learning nested sparse structures in deep neural networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Salt Lake City, UT), 8669–8678.

Google Scholar

L1u (2019). torch.nn.utils.prune.l1_unstructured - pytorch 1.7.0 documentation. Available online at: https://pytorch.org/docs/stable/generated/torch.nn.utils.prune.l1_unstructured.html

LeCun, Y., Denker, J., and Solla, S. (1989). Optimal brain damage. Adv. Neural Inform. Proc. Syst. 2, 598–605.

Google Scholar

Liu, W., Anguelov, D., Erhan, D., Szegedy, C., Reed, S., Fu, C.-Y., et al. (2016). “Ssd: Single shot multibox detector,” in European Conference on Computer Vision (Amsterdam: Springer), 21–37.

Google Scholar

Marczewski, A. (2020). Pytorch-Model-Summary 0.1.2. Available online at: https://pypi.org/project/pytorch-model-summary/

Google Scholar

Molchanov, P., Mallya, A., Tyree, S., Frosio, I., and Kautz, J. (2019). “Importance estimation for neural network pruning,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Long Beach), 11264–11272.

Paganini, M. (2020). Pruning Tutorial. Available online at: https://pytorch.org/tutorials/intermediate/pruning_tutorial.html

Paganini, M., and Forde, J. (2020). On iterative neural network pruning, reinitialization, and the similarity of masks.

Shafiee, M. J., Chywl, B., Li, F., and Wong, A. (2017). Fast yolo: a fast you only look once system for real-time embedded object detection in video. arXiv preprint arXiv:1709.05943.

Google Scholar

Simonyan, K., and Zisserman, A. (2014). Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556.

Google Scholar

Ström, N. (1997). Phoneme probability estimation with dynamic sparsely connected artificial neural networks. Free Speech J. 5:2.

Google Scholar

Womg, A., Shafiee, M. J., Li, F., and Chwyl, B. (2018). “Tiny ssd: A tiny single-shot detection deep convolutional neural network for real-time embedded object detection,” in 2018 15th Conference on Computer and Robot Vision (CRV) (Toronto, ON: IEEE), 95–101.

Google Scholar

Zhang, J., Pan, Y., Yao, T., Zhao, H., and Mei, T. (2019). “dabnn: a super fast inference framework for binary neural networks on arm devices,” in Proceedings of the 27th ACM International Conference on Multimedia (Nice), 2272–2275.

Google Scholar

Zhang, S., Wen, L., Bian, X., Lei, Z., and Li, S. Z. (2018). “Single-shot refinement neural network for object detection,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Salt Lake City, UT), 4203–4212.

Google Scholar