Resilient Intersection Management With Multi-Vehicle Collision Avoidance

In this paper, we propose a novel decentralised agent-based mechanism for road intersection management for connected autonomous vehicles. In our work we focus on road obstructions causing major traffic delays. In doing so, we propose the first decentralised mechanism able to maximise the overall vehicle throughput at intersections in the presence of obstructions. The distributed algorithm transfers most of the computational cost from the intersection manager to the driving agents, thereby improving scalability. Our realistic empirical experiments using SUMO show that, when an obstacle is located at the entrance or in the middle of the intersection, existing state of the art algorithms and traffic lights show a reduced throughput of 65–90% from the optimal point without obstructions while our mechanism can maintain the throughput up to 94–99%.

1. Introduction

Traffic congestion is one of the key factors of air pollution, causing losses in economic efficiency, as well as having wider impacts on health and climate change (May, 2013). For example, in the US alone, congestion is estimated to cost around US$305B (Schneider, 2018). A key contributing factor to congestion in urban road networks is the poor management of intersections using standard traffic lights. Despite a number of recent advances in traffic lights management, they rarely consider traffic in dynamic situations, e.g., accidents or road constructions, which are common occurrences. These situations interrupt the flow, causing a congestion surge at the intersection level or even at the network level. Ignoring these real-world issues can put people's lives at risk and increase the cost of transportation.

At the same time, the increasing adoption of Connected Autonomous Vehicles (CAVs)¹ presents an opportunity to make a step change from the status quo. Indeed, according to KPMG, 25% of the vehicles on the road will be fully autonomous by 2030 (KPMG, 2015). It is thus not difficult to imagine a future where nearly all vehicles will be fully autonomous. Moreover, work in the Artificial Intelligence (AI) community has sought to address the problem of intersection management with CAVs since the early 2000s, including the seminal work by Dresner and Stone (2008). They proposed a grid model of intersection and simple heuristic called First Come First Served (FCFS), considering the intersection as a central agent that allocates paths and time-slots to the incoming vehicles. Since their work, a number of approaches have emerged in the field (Vasirani and Ossowski, 2009; Carlino et al., 2013; Liu et al., 2013; Zohdy and Rakha, 2016; Lin et al., 2017; Isele et al., 2018; Vu et al., 2018). However, to date, most works ignore two important elements: (i) the dynamism of intersection topology, e.g., unequal numbers of lanes or heterogeneous traffic directions (ii) the resiliency of mechanism against the obstructions across the intersection.

To address the latter, a simple solution for the obstructions is to close the obstructed lane(s), e.g., with a red traffic light, and wait until the problem is resolved. However, doing so results in long delays which can be avoided if there is enough space to route around obstructions. Instead, obstructions can be treated as a part of the collision avoidance problem. This problem is widely studied in the robotics community, even though they are not explicitly designed for road intersection (Rebai et al., 2009; Savkin and Wang, 2014; Kim and Kwon, 2015; Pudics et al., 2015; Savkin and Li, 2018). Adapting the robotics algorithms to the road environment presents a certain challenge. In particular, there are different physical constraints. For example, robots can turn more easily and occupy a smaller footprint.

Against this background, we propose a new resource reservation intersection management mechanism that ensures obstructions can be avoided. In addition, it reduces the reliance on the intersection manager to compute paths through decentralised computation of dynamic trajectories for individual vehicles. By so doing, our mechanism is resilient to obstructions and reduces computational cost at the intersection manager compared to the centralised FCFS. More specifically, our approach allows vehicles to use as much space as is available within the intersection and endow them with more intelligent path planning and conflict resolution. In particular, we build on the work by Savkin and Li (2018) who provide a computationally and space-efficient approach to collision avoidance². We, therefore, adapt it to consider the constraints from the traffic intersection management problem. Thus, this paper advances the state of the art in the following ways:

1. First, we introduce a computationally decentralised method for the FCFS mechanism by having vehicles responsible for path prediction and conflicts resolution against other reservations using minimal information provided by the intersection manager.

2. Second, we propose a new path prediction algorithm with a collision avoidance extension customised for intersection management, that guarantees safe paths and adaptability to different intersection topology.

3. We then empirically show that our mechanism algorithm can significantly outperform improved extensions of traffic lights and FCFS that account for potential collisions with obstructions. Specifically, we evaluate our mechanism on Simulation of Urban MObility (SUMO), a realistic simulator. Overall, the experiments show that we can maintain up to 94–99% of the optimal performance while traffic lights and FCFS can achieve up to only 65–90%.

The rest of this paper is structured as follows. Second section describes related work. A description of the model and relevant definitions and assumptions are presented in the third section. Fourthly, the details of our algorithm including behaviour of the driver agents and the intersection agent are provided. The fifth section evaluates our algorithm against realistic traffic settings. The last section concludes.

2. Related Work

In addition to Dresner and Stone (2008) other related work includes Vasirani and Ossowski (2009), Carlino et al. (2013), Liu et al. (2013), Au et al. (2015), and Vu et al. (2018). The main objectives of these works are to optimise the efficiency of the intersection (either based on incentives or waiting time) or to scale up the solution (e.g., consider multi-intersection systems or large numbers of vehicles). Most of these assume a centralised system where the an intersection manager performs all of the computation.

Specifically, Vasirani and Ossowski (2009) proposed a market-inspired approach for intersection management that explicitly schedules the access through bidding. Their method is designed in a scalable manner, which can be extended to cover a road network or multiple intersections. However, due to the heterogeneous vehicles' bidding power, the reduction in overall delays cannot be guaranteed, especially in rush hours. In the same vein, an auction-based method proposed by Carlino et al. (2013) also experiences similar issues.

Moreover, recently, Vu et al. (2018) proposed an approach based on a distributed constraint optimisation solution that aims to account for surges in traffic flow. This solution addresses the risk of a single point of failure of such centralised systems by distributing the computation across multiple CAVs. However, their distributed approach requires significantly high communication costs, approximately 10⁵ times more messages than FCFS. Furthermore, unlike Dresner and Stone (2008), Vasirani and Ossowski (2009), Carlino et al. (2013), and Liu et al. (2013), Zohdy and Rakha (2016) proposed an intersection Cooperative Adaptive Cruise Control (iCACC), allowing multiple vehicles to cross the intersection as a group or platoon simultaneously. The results show that the delays can be reduced by 90% compared to the stop sign control.

In general, while these approaches consider variations in traffic flow of different kinds, they ignore the dynamism inherent in the real world. For example, many approaches study only regular intersection topology where a number of lanes are symmetrically equal. More importantly, vehicle trajectories are often assumed to be static without considering any intervention cases, e.g., road obstructions. Therefore, these approaches are more likely to be vulnerable to real-world scenarios.

Furthermore, as we consider the problem of collision avoidance, there are many recent relevant works from the robotics domain (e.g., Rebai et al., 2009; Savkin and Wang, 2014; Kim and Kwon, 2015; Pudics et al., 2015; Savkin and Li, 2018). In particular, Kim and Kwon (2015) proposed an algorithm that uses an ordinary camera sensor accomplishing lane following navigation while also avoiding obstacles. Similarly, Pudics et al. (2015) uses a 360-degree camera as a sensor that can provide rich information. With several calibrations and image processing methods, the obstacles can be detected and avoided.

However, unlike Kim and Kwon (2015) and Pudics et al. (2015), Savkin and Li (2018) proposed a simplified and more computationally efficient collision avoidance method that only uses 2D range finding sensors. Despite having a 2D sensor, the information is sufficient to determine obstacle existence and provide several tangent lines between the robot and the edge of the obstacles. More precisely, the robot will choose a tangent line to move along avoiding a head-on blockage before continue moving on the obstacle's boundary. Nevertheless, adapting such algorithms to the road environment presents some difficulties, mainly due to the physical differences between robots and vehicles, such as turning or steering movements, occupancy, speed, and, more importantly, centrifugal force.

3. The Traffic Model

This section describes how we model the vehicles, obstacles and the intersection in our study system. Specifically, we base our model on the original FCFS model (Dresner and Stone, 2008) that considers a road intersection managed by an Intersection Manager Agent or IMA³. The intersection agent is able to grant its resource (time-slotted space in the intersection) to each vehicle—driver agent or DA—to coordinate each vehicle's movement. Later, our traffic intersection management mechanism will be explained in detail.

3.1. Vehicles

We define A_t = {a₁...a_n} as a set of DAs in our system at time t. Each a_i ∈ A_t is modelled with its own properties: position pos_i, velocity v_i, width w_i, length l_i, minimum gap between the agent and the leading agent, and the orientation θ_i. All agents in A_t have the same value of maximum velocity v_max and accelerating rate α.

3.2. Obstacles

In this paper, we only focus on static obstructions (e.g., road construction) that occur either within the intersection or at the entrance of intersection. We assume the following about the obstacles:

1. Each obstacle is unmovable and free shape.

A virtual safe ring around is defined to ensure safety.

2. The obstacles can only position in either (1) in the intersection area or (2) at the exit of the lanes.

3. The IMA has full knowledge of the obstacles' position and safe ring and also is able to pass these details to the DAs.

Let O be an obstacle our system, and it is modelled with its own properties such as the position, the radius of the obstacle r(O), the radius of the safe ring r_safe(O), the circle around the obstacle C(O), and the circle of the safe ring C_safe(O).

3.3. The Intersection

Unlike the perfectly configured intersection in Dresner's work where the number of lanes and traffic directions are identical in all directions, we look at more general or non-symmetrical intersections, i.e., with unequal numbers of lanes or nonidentical traffic directions. Additionally, when obstacles are located nearby, this type of intersections has a realistic impact on the traffic, which allows us to study the disruption cause by obstacles in more detail. Moreover, this type of intersection can be seen extensively in many urban areas such as New Delhi, Bangkok, and Manhattan. We, therefore, model the intersection after a real and non-symmetrical intersection in Manhattan that intersects between Park Av South and East 23rd Street. Note that our algorithm works with different intersection settings as well.

In this work, the access of vehicles are scheduled based on the cell-based space reservation similar to Dresner and Stone (2008) where the centre of the intersection is discretised as a grid composed of a number of cells (k) (see Figure 1). These cells help DAs keep track of their used space and time-slots according to the predicted paths and also use to detect conflicts with other DAs preventing overlapping reservations (explains more in section 3). Specifically, this method supports dynamic vehicles trajectories that may happen due to the collision avoidance while several contemporary methods do not (e.g., Zohdy and Rakha, 2016; Lin et al., 2017; Vu et al., 2018).

FIGURE 1

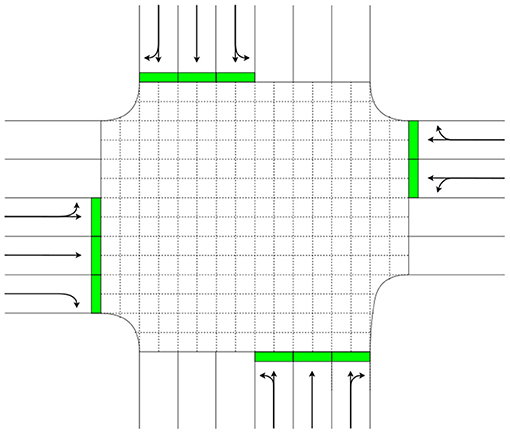
Figure 1. This figure illustrates the topology of intersection in Manhattan where the space in the middle of the intersection is virtually divided into squared cells. The arrows represent directions of the traffic.

However, whenever an obstacle is positioned at the exit of the lane, the vehicles in that lane must perform lane changing to avoid the blockage before they begin crossing. These movements interrupt the flow, resulting in increasing delays. Therefore, we introduce an extension to this cell-based approach. In particular, the grid is extended from the intersection area to cover the area around the obstacle according to the position (see Figure 2). The benefit of this extended section is to have the lane-changing movements combine with the crossing movements, allowing those movements to be reserved as one. As a result, DAs can make a reservation promptly after arriving at the queuing area, bypassing the delays that lane-changing movements may cause.

FIGURE 2

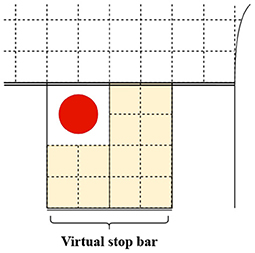
Figure 2. The extended area whenever obstacle is positioned at the exit of the lane. The circle represents the obstacle, and the highlighted area is where the grid is extended.

Additionally, to aid the queuing, a virtual stop bar is defined in front of the extended grid. The virtual stop bar's distance is calculated using the Gipps lane-changing model (Gipps, 1986). By limiting the lane changing speed to 25 km/h, a safe distance can be derived, ~7.5 m. DAs explicitly slow down until meeting that speed before changing the lane.

Moreover, to decentralise the system, we introduce a new piece of information for the IMA to hold called a reservation map, which is requestable by the DAs. This map contains a 2D-array of cells, and each cell also contains a vector of numbers representing its specific reserved timestamps. Simply put, this map allows the DAs to determine when and how long each cell is reserved and able to perform the conflict resolution on their own.

4. Resilient Intersection Management With Multi-Vehicle Collision Avoidance

Having defined the elements of the model, we next define our resilient intersection management mechanism that ensure the computation is distributed while incorporating collision avoidance. The purpose of distributing the computation is to address the high computational load for the IMA which is considered to be the main drawback of Dresner and Stone (2008). We thus propose a new mechanism called Resilient Intersection Management with Multi-vehicle Collision Avoidance (RIMMCA). Next, we detail the behaviour of the DAs and the IMA in the system.

4.1. Driver Agents Behaviour

DAs have to execute the following operations to reserve the time-slotted space.

1. Ask for information about the target lane (important for path prediction), the reservation map (i.e., which cells in the intersection are already reserved) and obstructions from the intersection agent once they arrive at the waiting area.

2. Initiate path prediction with or without collision avoidance depending on the presence of obstructions.

3. Resolve the conflict that may arise due to the previous reservations.

4. Send a requesting message containing the vehicle properties and the predicted path to the intersection agent and then wait for a confirmation.

• If the request is rejected, go back to step (1)

• If the request is confirmed, begin the crossing.

5. Notify the intersection agent that they have left the intersection area.

The main feature of decentralisation in our algorithm is that the driver agents are fully responsible for computations in two operations: path prediction (2) and conflict resolution (3). The key objective of these two operations is to find a conflict-free path from the agents' position to the target lane.

4.1.1. Path Prediction

This operation simulates the agents' movements step by step from their position to the target lane. It modifies the orientation of agents, θ_i, mimicking a steering mechanism while moving toward the assigned target lane. The output of this operation is called a predicted path $p_i=\{<po{s}_i^{t+1},{\theta }_i^{t+1}>,...,<po{s}_i^{t+s},{\theta }_i^{t+s}>\}$, where t + s is the end timestamp of this path vector.

However, this prediction is only applicable in non-obstructed situations. Therefore, we introduce an alternative method that predicts a sub-optimal path avoiding collisions with obstacles, which is explained in the next section.

4.1.2. Path Prediction With Obstructions

Here we explain how the agents perform path prediction even when obstructions exist with two main procedures.

A. Obstruction detection function: This function task is to determines the need for collision avoidance. Upon DAs' arrival at the intersection, the DAs must execute the normal path prediction retrieving an initial predicted path. The obstruction is detected when the distance between one of the waypoints in the predicted path and the centre of the obstacle's circle is smaller than r_safe(O). If an obstruction is found, the initial predicted path is discarded, and the DAs execute the path prediction with collision avoidance instead. Nevertheless, the collision avoidance still requires this function in the process, which is referred to as obstruction_detection(). Particularly, the usage is highlighted at line 8 in Algorithm 1.

ALGORITHM 1

Algorithm 1: Collision avoidance.

B. Collision avoidance algorithm:

Here, we explain how the DAs can move to the target lane without causing any collisions. Our algorithm is designed based on the model proposed by Savkin and Li (2018). However, we adapt their models to suit the intersection environment. In their model, a robot agent has to explore a restricted area until it is fully discovered, which requires the robot to constantly check for the collisions against walls. While, in our case, since the position of the obstacle is static, the algorithm is modified to check for the collisions only when needed, which is more suitable to our environment and more computationally efficient than Savkin and Li (2018). Moreover, due to the differences between robots and vehicles, the physical constraints of each vehicle are taken into account, e.g., the maximum steering angle and maximum turning velocity. This is to prevent such sharp turns or potential accidents in the real environment.

Specifically, the key algorithm is described in Algorithm 1, which mainly records the obstructed-free path per time step while updating the vehicle's position and orientation. The obstructed-free path of each DA can be broken down into three main parts of movement as follow:

1. Avoid the blockage that DA follows the tangent line T between its entry point and obstacles' safe ring C_safe(O)⁴, line 5, 6, and 13.

2. Follow the C_safe(O) curve that DA moves along the safe ring until the obstruction is no longer detected (using obstruction detection function), line 7–10 and 13.

3. Continue to steer and move forward from the end position in (2) to the entry of the target lane, line 11–13.

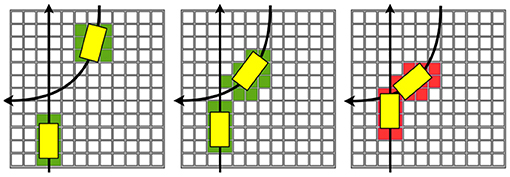
The movement (3) acts as a recovery mechanism forcing the agent to go back to the initial aiming direction while using the least possible space. The example of these movements is shown in Figure 3.

FIGURE 3

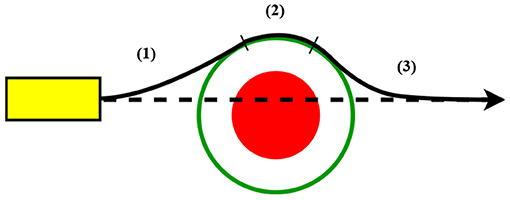
Figure 3. The predicted path considering the obstacle, where the solid line represents path from the collision avoidance algorithm while the dashed line represents the normal predicted path.

Now, our driver agents can predict a path either with or without consideration of obstructions. Next, this predicted path is processed further in the conflict resolution operation.

4.1.3. Conflict Resolution

Although the predicted path is already defined, the DAs cannot begin crossing immediately due to the conflicts that may arise against other reservations. An example of this situation is shown in Figure 4. By following the first come first served principle, a typical solution is to have the DA that comes later wait for a certain time, waiting time, letting the DAs that come before pass through first until no conflicts left, then the DAs that comes later can continue moving.

FIGURE 4

Figure 4. An example of a conflict between two paths.

Specifically, our conflict resolution algorithms composed of three main steps:

1. Calculate to-be-reserved cells and their timestamps by projecting a_i ∈ A_t vehicle's body using width w_i, length l_i, and $<po{s}_i^h,{\theta }_i^h>$ in the predicted path p_i on the intersection grid per timestamp h which starts from t + 1 and keep increasing by 1.

2. Check potential conflicted timestamp $q_{a_i}=\left\{q_{a_i}^{begin},...,q_{a_i}^{end}\right\}$ by overlapping the to-be-reserved cells with the reservation map (retrievable from IMA), where $q_{a_i}^{begin}$ is the timestamp conflict firstly occurs, and $q_{a_i}^{end}$ is the timestamp conflict ends.

3. Shift the begin timestamp of the predicted path p_i by waiting time = |q_ai| + 1.

However, the conflicts may even occur again after the shifting. To resolve this issue, the DAs must keep repeating the conflict checking (2) and timestamp shifting (3) until the predicted path is free from any conflicts.

In terms of the total computational cost for each DA, the cost required for path prediction for a vehicle a_i is in the order ${O}((w_{cell}·k_{a_i})/v_i)$ and for conflict resolution is ${O}(k)$ where w_cell is the width of cell, k_ai is the number of cells used by a_i, and k is the total number of cells.

Lastly, the DAs construct the requesting message with two pieces of information: the properties of the vehicle and the conflict-free path and send it to the IMA. We term the DA that sends out the message as the requesting DA. With our decentralised approach the IMA thus has only two tasks left, namely, verifying the request and sending an approval. We next explain the function of this agent in more detail.

4.2. Intersection Manager Agent Behaviour

Unlike the original FCFS, the IMA does perform neither path prediction nor conflict resolution since the path (or requested path) is already included in the requesting message. However, due to concurrency issues that occur in practice, to maintain the synchronisation between agents, the IMA must be responsible for the final permission granting process. In this process, the IMA verifies the validity of the requested path against the current state of the reservation map.

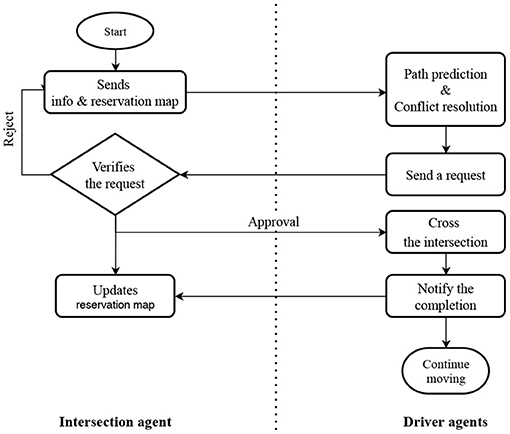
Specifically, the IMA simulates all the movements of the requesting DA and the previously granted DAs with respect to the timestamps while looking for reservation conflicts. If there is no conflict, the IMA will send an approval message with reservation details back to the requesting DA and update the reservation map as usual. However, the conflict may occur when a requesting message of a_i+1 arrives after the reservation map has already been updated by accepting a request from a_i. In this case, the request will be rejected, and a_i+1 has to start the path prediction and conflict resolution from the beginning. The overall interaction flow between the IMA and DAs can be seen as a flow chart in Figure 5.

FIGURE 5

Figure 5. The interactions flow between the IMA and DAs.

To compare the computational cost with the original FCFS, in FCFS the cost for the IMA is ${O}[(w_{cell}·k_{a_i})/v_i]+{O}(k)$ per requesting message. This is due to the path prediction and the conflict resolution operations. While, with our approach the computational cost is reduced to ${O}(k)$ per requesting message. This opens an opportunity to replicate the function of IMA across multiple nodes, i.e., the vehicles, since the computational cost is reasonably small.

Furthermore, our distributed method can reduce the overall number of messages compared to FCFS. This is because, in RIMMCA, DAs can internally resolve the reservation conflicts before sending requests to IMA. While, in FCFS, DAs notice the conflicts only when IMA notifies them via messages. Table 1 shows a comparison of an average number of messages between our method and FCFS. Indeed, it can be seen that with 1,500 vehicles our method requires more messages than FCFS. However, as the number of vehicles increases where the conflicts are likely to occur, our RIMMCA requires significantly less messages than FCFS.

TABLE 1

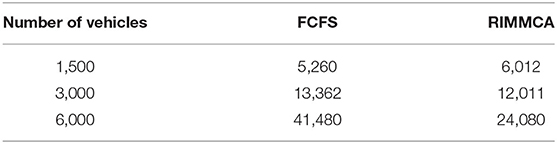
Table 1. Average number of messages in comparison between FCFS and RIMMCA, under different number of vehicles.

5. Empirical Evaluation

We aim to benchmark our RIMMCA model against two intersection controls: traffic lights (TL) and FCFS. To do so, we chose the open-source traffic simulator SUMO (Simulation of Urban MObility) (Krajzewicz et al., 2002). With the client-server based Traffic Control Interface (TraCI) (Wegener et al., 2008) available in SUMO, external applications can be built upon allowing simulated vehicles to be controlled at run time. With this feature, FCFS and RIMMCA algorithms can be implemented on the simulated intersections enabling coordination between DAs and IMA. To do so, two important modifications were made to the SUMO: (1) the vehicles can progress beyond the stop bar at any specific time even though the traffic lights are red⁵ (2) the vehicles can ignore their car following models when they are crossing the intersection⁶.

5.1. Obstacles Placement

Since SUMO does not support the placement of obstacles, in the following we explain how we deal with obstacles in the simulation. For an in-lane obstacle, we place an immobile vehicle at a specific position on the lane, which partially reduces the lane's available space. It sometimes even blocks the lane exit or entry depending on the position of the obstacle. However, by using the SUMO vehicle objects as obstacles, all simulated vehicles can respond to the blockage themselves (e.g., changing lane and choosing the best driving lane; Erdmann, 2015), without any manipulation from the algorithms. This means that, in the evaluation process, there is no collision avoidance extension required for both TL and FCFS.

Nevertheless, an obstacle in the intersection cannot be expressed with the immobile vehicle in the same way as in-lane obstacles. Otherwise, the car following model from Krauß et al. (1997) will force the crossing vehicles to stop in the middle of the intersection and eventually cause a deadlock (only for TL). Our solution is to represent this obstacle with a point of interest, a circle-shape object provided by SUMO despite having no physical meaning. Moreover, since no study has considered obstructions in the intersection to date, we have to evaluate our algorithm against the naive collision avoidance extension of TL and FCFS, which is a lane closing solution. Specifically, any lanes that are blocked by the obstruction will be closed throughout the run. We refer to the lane closing solution of TL and FCFS as TL-LC and FCFS-LC.

We separate the experiment into two main types: in-lane obstruction type and in-intersection obstruction type. In the first type, to create situations that significantly worsen the throughput, an obstacle is placed at the exit of the left most lane (see Figure 6A). This left most lane is more likely to have a long queue due to the left turn trajectory that heavily conflicts with other trajectories. Having only one obstacle at this position can seriously affect overall traffic throughput. In the second type, we place the obstacle in the middle of the intersection aiming to create three-lane blocking scenarios (see Figure 6B). This three-lane blocking is sufficient to show its effect on the throughput but still maintain a good flow. When more than three lanes are blocked, the throughput becomes poor and even fluctuate whenever the position is changed, and it is difficult to acquire accurate results. This is due to the non-symmetric intersection design.

FIGURE 6

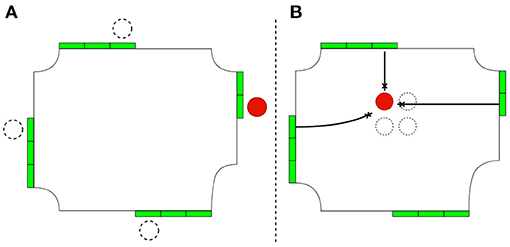
Figure 6. This figure shows example placements of obstacles where the red circle represents the obstacle, while the dashed circles represent the possible alternative positions of the obstacle. The left part (A) shows in-lane obstructions, while the right part (B) shows in-intersection obstructions.

Note that the purpose of this obstacle placement is to demonstrate how our method performs with baseline cases, not to exhaust the algorithm with such complex situations. For example, in the case of the bigger obstacle, this means more lanes will be blocked, which significantly worsens the performance of TL-LC and FCFS-LC approaches in terms of queue lengths and delays. While, RIMMCA does not rely on the lane-closure approach, the bigger obstacle only has a moderate effect on the results. Evaluation with this case would appear to have considerably better performance than TL and FCFS, which is considered an unfair comparison and overstating the results.

Moreover, with regards to the case of multiple obstruction types at the same time, it will introduce an entirely new problem to the system, namely, multiple obstructions. The solution to this problem would require a more complex algorithm. Even though our proposed method can be modified to avoid obstacles one by one, the resulting manoeuvring path would be only sub-optimal. An additional optimisation process would be required to address this aspect, which will be another challenge to our method. Still, this is beyond our current research scope.

5.2. Experimental Settings

Unlike Dresner and Stone (2008), where FCFS is tested in the ideal conditions, we test our model on the real intersection which is a replica of the intersection in Manhattan. Given that our focused intersection is located in New York, real traffic data is available via New York State Department of Transportation (2016). This dataset provides the average daily traffic count of each road in 2016 allowing us to estimate the value of traffic flow. Specifically, the flow is between 2,300 and 2,500 vehicles/hour, including 10% peak-time increase. Additionally, to create more practical traffic state, we weigh this flow across the two roads based on their actual usage, 67.46% on Park Av South and 32.54% on East 23rd Street. Given this, all simulated vehicles can be generated distributively and realistically per each run.

We leave all vehicles' attributes as default. These attributes include width 1.8 m, length 5 m, maximum speed 11.18 m/s (≈ 40 km/h), acceleration 2.6 m/s², deceleration 4.5 m/s², minimum gap 2.5 m, and etc. The size of the obstacles are r(O) = 2.5 m, r_safe(O) = 4.5 m. Only one obstacle will be placed per run (i.e., simulation instance).

Note that the obstacle safe distance, r_safe(O), is defined using three factors, obstacle radius r(O), vehicle's width w_i, and additional safe gap g_safe. Specifically, r_safe(O) is equal to:

$\begin{array}{ll}{r}_{safe}(O)=r(O)+(w_i/2)+g_{safe}& (1)\end{array}$

Where SUMO passenger vehicle's width (w_i) = 1.8 m, and g_safe is set to be 1.1 m. Hence, r_safe(O) = 4.5 m as stated. Also, the additional safe gap can be changed dynamically depending on specific vehicle types.

5.3. Experimental Results and Discussions

We set each run to be 1 h simulation time with randomly generated input flow and vehicles trips (from the estimated traffic flow and the usage weight). For the evaluation, three traffic measurement units: flow rate (vehicles/hour or veh/h), queue length (metre) and delays (seconds/veh or s/veh) were chosen. Moreover, to gain more accurate results, each experiment was also repeated more than 20 runs. The values reported below are the average over 20 runs.

5.3.1. No Obstructions

We initially set up obstruction-free experiments to see the optimal performance of traffic lights, FCFS and RIMMCA. The results show that traffic lights are significantly outperformed by FCFS and RIMMCA, while both FCFS and RIMMCA show similar results. To be exact, the optimal performance of traffic lights is the flow rate of 1569.8 veh/h, queuing length of 33.28 m, and delays of 93.43 s/veh. While, the optimal performance of FCFS and RIMMCA are similar and is much higher than the traffic lights, with the flow rate of 2, 402 veh/h, queuing length of ≈ 0.13−0.15 m and delays of 0.01 s/veh. Note that the flow rate and the delays are recorded at the end of each simulation.

Next, we perform experiments with the two obstruction types: in-lane obstruction and in-intersection obstruction.

5.3.2. In-lane Obstructions

We created four different in-lane obstruction scenarios by placing obstacles at four distinct positions (see Figure 6A). The results show that the performance of TL significantly drops to the flow rate of 1023.75 veh/h, queuing length of 44.85 m, and delays of 162.01 s/veh. Similarly, the performance of FCFS also drops to the flow rate of 2371.75 veh/h, queuing length of 11.2 m, and delays of 1.61 s/veh. While, RIMMCA can maintain its performance to be close to its optimal point with the flow rate of 2380 veh/h, queuing length of 0.25 m and delays of 0.03 s/veh.

Due to the obstacles at the entry of the lane, the queuing length values become higher in both TL and FCFS, but not in RIMMCA. This is because in TL and FCFS, when vehicles are blocked, they have to perform the lane changing, and it tends to interrupt the flow resulting in a long queue and high delays. While, in RIMMCA the lane changing movements (only to avoid collisions) are already included in the reserved path, vehicles only have to follow the scheduled time-slots. Figure 7 shows the average queuing length over time of TL, FCFS and RIMMCA.

FIGURE 7

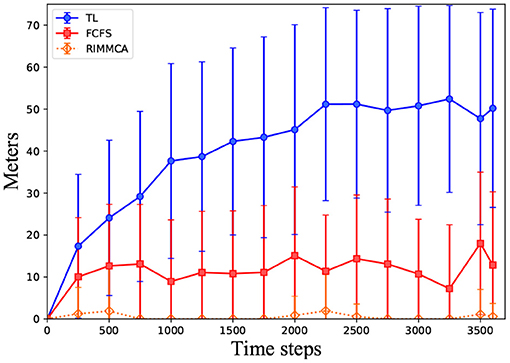
Figure 7. Average queuing length results with standard deviation of four different in-lane obstruction scenarios (20 runs per scenario).

By using the optimal performance without obstructions as a baseline, the traffic lights and FCFS offer the flow rate ≈ 65 and ≈ 98% of the optimal point, while RIMMCA offers 99% of the optimal point. From the results, it can be seen that RIMMCA can outperform both traffic lights and FCFS even with the presence of in-lane obstacles.

5.3.3. In-intersection Obstruction

Given four possible obstacle positions (see Figure 6B), we were able to create four distinct in-intersection obstruction scenarios. With this type of obstructions, even though the amount of the incoming lanes is greatly reduced due to the lane-closing solution it affects the performance of each intersection control differently. For TL-LC, the performance is better than in-lane obstruction case with the flow rate of 1416.7 veh/h, queuing length of 42 m, and delays of 118.82 s/veh. For FCFS-LC, the flow rate drops to 2, 170 veh/h, while the performance in queuing length and delays are better, 1.3 m and 0.6 s/veh. Meanwhile, RIMMCA slightly loses its performance when compare to the in-lane obstruction case with the flow rate of 2, 260 veh/h, queuing length of 2.73 m, and the delays of 4.7 s/veh. The comparison graph of queuing length between three intersection controls with this obstruction type is shown in Figure 8.

FIGURE 8

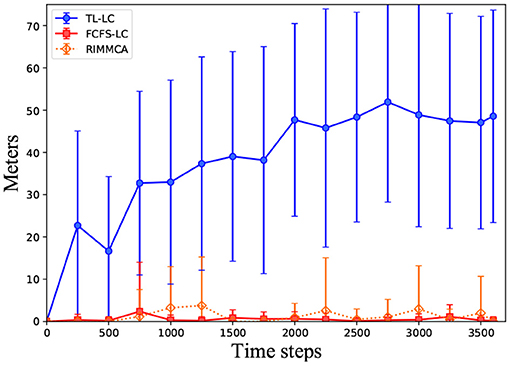
Figure 8. Average queuing length results with standard deviation of four different in-intersection obstruction scenarios (20 runs per scenario).

Comparing FCFS-LC and RIMMCA, the average queuing length of FCFS is better (smaller) than RIMMCA. This is because the required space of the obstructed-free paths are overlapping with other normal paths causing some DAs to wait longer, which results in increase of overall waiting time. However, even though RIMMCA has to sacrifice some efficiencies in the queuing length and delays, RIMMCA still outperforms both TL-LC and FCFS-LC in terms of the flow rate. Specifically, with the presence of in-intersection obstacles, RIMMCA can offer the flow rate up to ≈ 94% of the optimal point, while the TF-LC and FCFS-LC offer only ≈ 90% of the optimal point. The overall comparison between three intersection controls can be seen in Table 2.

TABLE 2

Table 2. A performance comparison table between three intersection controls in different experiment scenarios.

To conclude, the experiments of in-lane and in-intersection obstructions show that RIMMCA is more robust to obstructions in terms of flow rate compared to TL and FCFS, whether obstructions are either in-lane or in-intersection.

6. Conclusion and Future work

Many intersection management approaches only consider well behaved environments, and this means they are unable to cope with unexpected situations such as obstructions. To this end, we presented a resilient intersection management method with multi-vehicle collision avoidance. Our model offers decentralised computation of multiple vehicles to cross the intersection while avoiding collisions with obstacles. Without obstructions, our decentralised approach is shown to achieve a similar performance to FCFS. However, with obstructions, our realistic empirical study shows that our model is more robust to obstructions interfering with some crossing paths and maintain throughput or flow rate up to 94–99% of the optimal performance without obstructions, while traffic lights and FCFS can maintain only up to 65–90% of the optimal performance without obstructions.

Future work will investigate how robust RIMMCA is to communication drop-outs. Also, we plan to consider scenarios with dynamic obstacles and having multiple obstacles at the same time.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

PW wrote the first draft of the paper. All authors contributed to conception and design of the study, paper revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^A CAV is a vehicle that is capable of driving itself without human interference and wirelessly communicate and exchange information with other devices outside the vehicle and external networks (SMMT, 2017).

2. ^In this paper, collision refers to the collision between obstacle and vehicle, not between vehicles themselves.

3. ^The IMA typically sits within the infrastructure at the intersection and communicates with nearby vehicles using typical RF communications.

4. ^The size of C_safe(O) is adaptable to different vehicles' width.

5. ^The red traffic lights are required to aid the DAs waiting, indeed, according to the calculated waiting time.

6. ^This enables more close distance between vehicles allowing FCFS and RIMMCA to achieve their best performance.

References

Au, T.-C., Zhang, S., and Stone, P. (2015). “Autonomous intersection management for semi-autonomous vehicles,” in Handbook of Transportation, ed D. Teodorović (New York, NY: Routledge), 88–104.

Google Scholar

Carlino, D., Boyles, S. D., and Stone, P. (2013). “Auction-based autonomous intersection management,” in 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013) (The Hague), 529–534. doi: 10.1109/ITSC.2013.6728285

CrossRef Full Text | Google Scholar

Dresner, K., and Stone, P. (2008). A multiagent approach to autonomous intersection management. J. Artif. Intell. Res. 31, 591–656. doi: 10.1613/jair.2502

CrossRef Full Text | Google Scholar

Erdmann, J. (2015). “Sumo's lane-changing model,” in Modeling Mobility with Open Data, eds M. Behrisch, and M. Weber (Berlin: Springer), 105–123. doi: 10.1007/978-3-319-15024-6_77

CrossRef Full Text | Google Scholar

Gipps, P. G. (1986). A model for the structure of lane-changing decisions. Transport. Res. Part B Methodol. 20, 403–414. doi: 10.1016/0191-2615(86)90012-3

CrossRef Full Text | Google Scholar

Isele, D., Rahimi, R., Cosgun, A., Subramanian, K., and Fujimura, K. (2018). “Navigating occluded intersections with autonomous vehicles using deep reinforcement learning,” in 2018 IEEE International Conference on Robotics and Automation (ICRA) (Brisbane, QLD), 2034–2039. doi: 10.1109/ICRA.2018.8461233

CrossRef Full Text | Google Scholar

Kim, Y., and Kwon, S. (2015). A heuristic obstacle avoidance algorithm using vanishing point and obstacle angle. Intell. Service Robot. 8, 175–183. doi: 10.1007/s11370-015-0171-4

CrossRef Full Text | Google Scholar

KPMG (2015). Connected and Autonomous Vehicles the UK Economic Opportunity. Technical report, KPMG.

Krajzewicz, D., Hertkorn, G., Rössel, C., and Wagner, P. (2002). “Sumo (simulation Q17 of urban mobility)-an open-source traffic simulation,” in Proceedings of the 4th middle East Symposium on Simulation and Modelling (MESM20002) (Sharjah), 183–187.

Google Scholar

Krauß, S., Wagner, P., and Gawron, C. (1997). Metastable states in a microscopic model of traffic flow. Phys. Rev. E 55:5597. doi: 10.1103/PhysRevE.55.5597

CrossRef Full Text | Google Scholar

Lin, P., Liu, J., Jin, P. J., and Ran, B. (2017). Autonomous vehicle-intersection coordination method in a connected vehicle environment. IEEE Intell. Transp. Syst. Mag. 9, 37–47. doi: 10.1109/MITS.2017.2743167

CrossRef Full Text | Google Scholar

Liu, K., Chan, E., Lee, V., Kapitanova, K., and Son, S. H. (2013). Design and evaluation of token-based reservation for a roadway system. Transp. Res. Part C 26, 184–202. doi: 10.1016/j.trc.2012.09.001

CrossRef Full Text | Google Scholar

May, A. D. (2013). Urban transport and sustainability: the key challenges. Int. J. Sustain. Transp. 7, 170–185. doi: 10.1080/15568318.2013.710136

CrossRef Full Text | Google Scholar

New York State Department of Transportation (2016). Traffic Data Viewer. New York State Department of Transportation.

Google Scholar

Pudics, G., Szabó-Resch, M. Z., and Vámossy, Z. (2015). “Safe robot navigation using an omnidirectional camera,” in 2015 16th IEEE International Symposium on Computational Intelligence and Informatics (CINTI) (Budapest), 227–231. doi: 10.1109/CINTI.2015.7382928

CrossRef Full Text | Google Scholar

Rebai, K., Benabderrahmane, A., Azouaoui, O., and Ouadah, N. (2009). “Moving obstacles detection and tracking with laser range finder,” in 2009 International Conference on Advanced Robotics (Munich), 1–6.

Google Scholar

Savkin, A. V., and Li, H. (2018). A safe area search and map building algorithm for a wheeled mobile robot in complex unknown cluttered environments. Robotica 36, 96–118. doi: 10.1017/S0263574717000194

CrossRef Full Text | Google Scholar

Savkin, A. V., and Wang, C. (2014). Seeking a path through the crowd: Robot navigation in unknown dynamic environments with moving obstacles based on an integrated environment representation. Robot. Auton. Syst. 62, 1568–1580. doi: 10.1016/j.robot.2014.05.006

CrossRef Full Text | Google Scholar

Schneider, B. (2018). Traffic's Mind-Boggling Economic Toll. Bloomberg CityLab. Available online at: https://www.bloomberg.com/news/articles/2018-02-07/new-study-of-global-traffic-reveals-that-traffic-is-bad (accessed November 2019).

SMMT (2017). Connected and Autonomous Vehicles. Technical report, SMMT.

Google Scholar

Vasirani, M., and Ossowski, S. (2009). “A market-inspired approach to reservationbased urban road traffic management,” in Proceedings of the 8th International Conference on Autonomous Agents and Multiagent Systems, Vol. 1 (Budapest), 617–624.

Google Scholar

Vu, H., Aknine, S., and Ramchurn, S. D. (2018). “A decentralised approach to intersection traffic management,” in Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI-18 (Stockholm), 527–533. doi: 10.24963/ijcai.2018/73

CrossRef Full Text | Google Scholar

Wegener, A., Piórkowski, M., Raya, M., Hellbrück, H., Fischer, S., and Hubaux, J.-P. (2008). “Traci: an interface for coupling road traffic and network simulators,” in Proceedings of the 11th Communications and Networking Simulation Symposium (Ottawa, ON), 155–163. doi: 10.1145/1400713.1400740

CrossRef Full Text | Google Scholar

Zohdy, I. H., and Rakha, H. A. (2016). Intersection management via vehicle connectivity: the intersection cooperative adaptive cruise control system concept. J. Intell. Transp. Syst. 20, 17–32. doi: 10.1080/15472450.2014.889918

CrossRef Full Text | Google Scholar