Energy, Exergy, Entropy Generation Minimization, and Exergoenvironmental Analyses of Energy Systems-A Mini-Review

Ordonez, Juan C.; Cavalcanti, Eduardo J. C.; Carvalho, Monica

doi:10.3389/frsus.2022.902071

MINI REVIEW article

Front. Sustain., 04 May 2022

Sec. Quantitative Sustainability Assessment

Volume 3 - 2022 | https://doi.org/10.3389/frsus.2022.902071

This article is part of the Research Topic Thermoeconomic and Environmental Analyses of Energy Systems View all 5 articles

Energy, Exergy, Entropy Generation Minimization, and Exergoenvironmental Analyses of Energy Systems-A Mini-Review

$\nJuan C. Ordonez$ Juan C. Ordonez¹^*

Eduardo J. C. Cavalcanti²

Monica Carvalho³

¹Department of Mechanical Engineering, FAMU-FSU College of Engineering, Energy and Sustainability Center, Center for Advanced Power Systems, Florida A&M University, Florida State University, Tallahassee, FL, United States
²Department of Mechanical Engineering, Federal University of Rio Grande Do Norte (UFRN), Natal, Brazil
³Department of Renewable Energy Engineering, Center of Alternative and Renewable Energy, Federal University of Paraiba, Joao Pessoa, Brazil

Meeting the growing energy demands has become a crucial challenge, which should employ energy integration and benefit from the extraction of the maximum thermodynamic potential of the resources consumed. This brief review presents an overview of the essential elements of the methods of energy, exergy, entropy generation minimization, and exergoenvironmental analyses. In combination, these methodologies constitute a powerful toolbox for the design, analysis, and optimization of energy systems. The quantification of energy and environmental impacts provided by them is essential in guiding toward system designs that are consistent with current energy and environmental needs.

1. Introduction

Population growth, increased energy demands, and the need for imminent environmental actions to reduce greenhouse gas emissions challenge humanity's approaches and implementation of energy conversion processes and demand careful consideration of the tools and methods used for the design and evaluation of such processes.

Within the umbrella of thermodynamics, the methods of entropy generation minimization, energy, exergy, second law, and exergoenvironmental analysis are methodological frameworks that provide quantitative information about the use of resources, the conversion efficiencies, and environmental impact. Together, these methods can play an important role in the design and optimization of our future energy infrastructure (e.g., increased renewable generation, hydrogen infrastructure).

This mini-review is structured as follows: Section 2 covers energy and exergy analysis; Section 3 addresses entropy generation minimization; and Section 4 with exergoenvironmental analysis. The intention is to provide a brief description of the central aspects of the approaches and direct the reader to works in the literature that further develop and illustrate the central ideas.

2. Energy and Exergy Analysis

Energy analysis is based on the first law of thermodynamics, which states the principle of conservation of energy (Figure 1A). There should be a balance of useful, dissipated, and remaining energy (maximum extractable work, frictional losses, and unutilized energy, respectively) (Yip and Elimelech, 2012). Energy assessments evaluate the energy content of final and intermediate products, losses and several shares of energy associated with mass flows at the inputs and outputs (Carvalho and da Silva, 2018), which can help establish energy efficiency and conservation strategies. Efficiencies are calculated as the ratios of energy quantities and are employed to evaluate and compare different systems (Terzi, 2018).

FIGURE 1

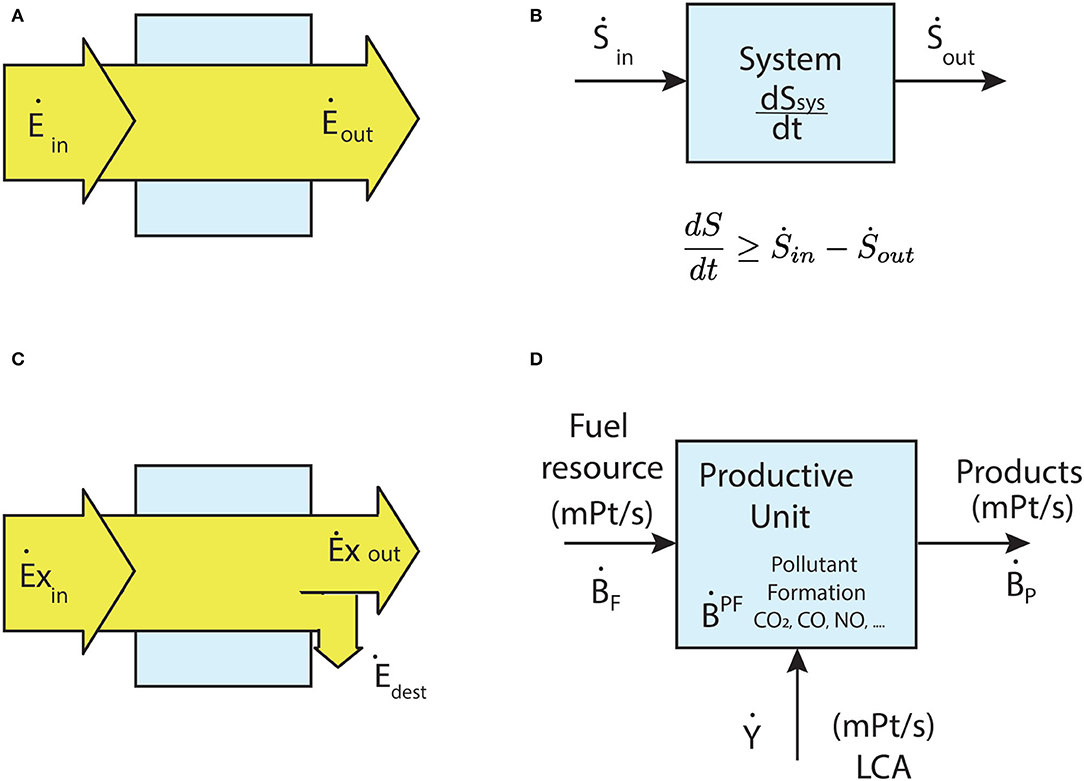
Figure 1. (A) Energy balance under steady-state process; (B) System entropy change and entropy transfers; (C) Illustration of exergy destruction in a process; (D) Exergoenvironmental balance of productive unit based on SPECO approach.

However, energy analysis does not consider the thermodynamic quality of the energy flows involved. Losses can be estimated, but there is only limited information about the optimal conversion of energy (Hammond, 2007). As energy cannot be created or destroyed, but is rather degraded along processes, the quality of energy can be evaluated by another thermodynamic property: exergy (Rant, 1956; Szargut, 1996; da Silva et al., 2017).

Introducing the second law of thermodynamics and the concept of exergy, it is possible to define differences in energy quality. As mentioned by Tsatsaronis (1993), the second law goes a step further than the first law by establishing the “true thermodynamic value of an energy carrier, and the real thermodynamic inefficiencies and losses from processes or systems.” The concept of exergy is extremely useful for this purpose, and enables the assessment and comparison of processes and systems in a rational and meaningful manner (Dincer and Rosen, 2020). It enables the quantification of performance limits for industrial processes, for example, Baumgärtner and Arons (2003) used it to quantify the amount of waste output in industrial production due to inefficiencies.

Exergy is a combined property of a system and the environment as it depends on the states of the system and environment. In most engineering applications, exergy is usually constituted of physical and chemical exergy shares.

Exergy is a measure of usefulness and a measure of potential to cause change, which means that exergy can be an effective indicator of potential environmental impacts (Assad and Rosen, 2021). An exergy analysis allows pinpointing the thermodynamic losses and inefficiencies associated with each unit of the energy system (Figure 1C). Because it provides a direct measure of the losses occurring, exergy analysis is a very efficient tool to improve the overall efficiency and to guide toward the sustainability of the process. Besides exergy, other quantities such as ascendency (Ulanowicz, 1997), have been described as goal functions that provide information about energy flows in relation to a reference state. Exergy and ascendency (measure of the information and flows embodied in an ecological network) have been combined (Carvalho and Serra, 2019) to provide richer and useful information for the synthesis and design of complex energy systems. Other environmental performance concepts have been employed to assess the impacts associated with the use of resources, such as the eco-exergy concept that extends and adapts exergy analysis to ecosystem modeling (Jørgensen and Nielsen, 2007) and eMergy (Odum, 1995), which has been used as a complementary goal function to exergy in the study of ecosystems.

Because of exergys property of value (energy quality), its concept can be extended and combined with economics, leading to the concept of thermoeconomics (or exergoeconomics). The environmental aspect can also be accounted for in exergoenvironmental (Meyer et al., 2009) and thermoenvironmental (de Abreu et al., 2021) assessments.

3. Entropy Generation Minimization

The mathematical formulation of the entropy change experienced by a thermodynamic system by Clausius (Clausius, 1879), expresses the second law as an inequality. The strength of this inequality is quantified by the entropy generation (Bejan, 1996a). In this way, the entropy generation can be seen as a metric of the irreversibility of a process executed by a thermodynamic system. Consider a thermodynamic system (Figure 1B). The entropy generation is given by,

\begin{array}{l} Ṡ_{g e n} = \frac{d S}{d t} - Ṡ_{i n} + Ṡ_{o u t} \geq 0, & (1) \end{array}

where, Ṡ_gen represents the rate of entropy generation, dS/dt represents the rate of change of the system entropy, Ṡ_in the rate of entropy transfer into the system (via mass and/or heat transfer interactions), and, similarly, Ṡ_out represents the rate of entropy transfer out of the system (via heat transfer interactions and/or mass interactions).

The Gouy-Stodola theorem (Gouy, 1889; Stodola, 1905) relates the rate of entropy generation with the rate of lost available work (Ẇ_lost) and puts in equal footing the efforts to maximize available work and those of minimizing entropy generation. For a system, with an environment at temperature T₀, the Gouy-Stodola theorem states that,

\begin{array}{l} Ẇ_{l o s t} = T_{0} Ṡ_{g e n} . & (2) \end{array}

The concept of entropy generation served as a catalyst for the integration of heat transfer and thermodynamics due to the inherent irreversibility associated with heat transfer interactions and the impact of those irreversibilities in the thermodynamic performance of energy systems (Bejan, 1980). Having the ability to quantify the degree of irreversibility by means of a function (the entropy generation), that depends on the path followed by the thermodynamic process and on geometrical parameters of the system design, gave birth to the method of Entropy Generation Minimization (EGM) (Bejan, 1982).

The EGM method enables the formulation of constrained optimization problems in which the objective function is the entropy generation, the degrees of freedom typically involve operational and geometrical parameters, and the constraints are associated with the finite resources (heat transfer areas, system volume, etc.).

The method encompasses both modeling and optimization, and can be seen as a sequence of three steps:

• Step 1: a model for the system is constructed using the laws of thermodynamics as framework. Fluxes and interactions are incorporated into the model from related disciplines, typically heat transfer and fluid mechanics.

• Step 2: the entropy generation (or its rate) is computed.

• Step 3: the entropy generation is minimized by solving a constrained optimization problem.

In Step 1, fluxes tend to bring into the model geometrical features of the system, which can become degrees of freedom. The entropy generation computation in step 2 is usually in one of two forms. A local one, expressed in terms of partial differential equations which tends to be used in connection with CFD approaches or a lumped one in which spatial dimensionality is reduced. Step 3 can in occasions be accomplished analytically, but often requires numerical approaches. In principle any suitable function minimization approach can be used in Step 3, however, care must be taken to enforce the limitations imposed by the physics on the degrees of freedom to avoid solutions that are mathematically valid but inconsistent with the physics.

In order to illustrate a sample of the wide variety of problems covered within the EGM literature, Table 1 presents groups of systems that have received special attention and basics aspects of the underlying optimizations.

TABLE 1

Table 1. Examples of entropy generation minimization and thermodynamic optimizations.

4. Exergoenvironmental Analysis

Exergoenvironmental analyses help evaluate and understand how environmental impacts are formed, and identify the most predominant burdens in a specific process. Meyer et al. (2009) have developed this methodology for energy conversion systems, combining an environmental indicator with the respective exergy flows to produce an environmental impact rate, as shown by Equation (3).

\begin{array}{l} Ḃ = b Ė & (3) \end{array}

where Ḃ is the environmental impact rate (Pts/s or mPts/s); b is the environmental impact per exergy unit (Pts/kJ or mPts/kJ) and Ė is the exergy rate (kW). Other exergy flows, such as heat transfer and power are associated using the same equation .

Traditionally, the Eco-indicator 99 method has been employed to calculate the environmental impacts, expressed in points (Pts) or milipoints (mPts). The absolute value of the points is not very relevant as its main purpose is to compare relative differences between products or components (Goedkoop et al., 2000). The value of 1 mPt is representative for one thousandth of the yearly environmental load of one average European inhabitant. Some values of pollutant emissions based on environmental indicator 99, in mPt/kg, are CO₂: 5.45; CO: 8.36; SO₂: 1499.37; NO: 4217.74; NO₂: 2749.36 (Goedkoop and Spriensma, 2001).

The SPecific Exergy COsting method (SPECO) is applied in the exergoenvironmental analysis , separating exergy in thermal, mechanical, and chemical terms (Lazzaretto and Tsatsaronis, 2006) have described the systematic and general methodology of SPECO based on the definition of fuel and product for each component. This definition considers the desired result produced and the resources expended to generate it. The product is equal to the sum of: All exergy to be considered at the outlet plus all the exergy increases between inlet and outlet, which are the purpose of the component. Moreover, the fuel is equal to the sum of: All exergy to be considered at the inlet plus all the exergy decreases between inlet and outlet, which are used for the purpose of the component.

Based on the fuel (F) and product (P) principles, the fuel (Ḃ_F and product Ḃ_P environmental impact rates are calculated, as follows:

\begin{array}{l} Ḃ_{F} = b_{F} \cdot Ė_{F} & (4) \end{array}

\begin{array}{l} Ḃ_{P} = b_{P} \cdot Ė_{P} & (5) \end{array}

Where: b_F and b_F are the specific environmental impacts per exergy unit of fuel and product (mPt/kJ), respectively. Ė_F and Ė_P are the exergy rates of the fuel and product (kW), respectively.

Exergoenvironmental balances must be developed for each component, according to Equations (6) and (7). The environmental impact rate of the product is equal to the environmental impact rate of the fuel plus the environmental impact rates of the component and the formation of pollutants.

\begin{array}{l} Ḃ_{P} = Ḃ_{F} + Ḃ^{P F} + Ẏ & (6) \end{array}

\begin{array}{l} b_{p} \cdot Ė_{P} = b_{F} \cdot Ė_{F} + (Ḃ^{P F} + Ẏ) & (7) \end{array}

Where: Ḃ^PF is the environmental impact rate associated with the formation of pollutants, and Ẏ the environmental impact rate of the component.

Ḃ^PF occurs, for example, when there is combustion and it is evaluated according to Equation 8:

\begin{array}{l} Ḃ^{P F} = \sum b^{P F} \cdot (ṁ_{o} - ṁ_{i}) & (8) \end{array}

Where: b^PF is the specific environmental impact per mass unit of each pollutant formed in combustion. ṁ_o and ṁ_i are the mass flow rates of pollutant formation that exit and enter the component, respectively. For more details on exergoenvironmental balances, auxiliary equations, and pollutant formation the readers are directed to Cavalcanti et al. (2021) and Cavalcanti and Carvalho (2021). Although, Cavalcanti and Carvalho (2021) is an exergoeconomic application of a solar hybrid trigeneration system, the balances are similar (financial costs, c, are substituted by environmental impacts, b).

The scheme of the exergoenvironmental balance based on the SPECO approach is shown in Figure 1D.

Some components, such as gas cleaning units, throttling valves, and coolers operating at temperatures above the ambient temperature, do not have a thermodynamic product. Components for which the definition of an useful product is not possible, are called dissipative components. They contribute to exergy destruction without gaining something thermodynamically useful (Lazzaretto and Tsatsaronis, 2006). Following the SPECO approach, the environmental impact rate of a dissipative component can be charged to the component(s) that serve it; apportioned to the system component(s) served by it; or completely charged to the final product(s). Cavalcanti and Carvalho (2021) applied this approach in the context of a cryogenic heat exchanger for natural gas liquefaction.

Regarding the component-related environmental impact rate (Ẏ), it is evaluated by means of a Life Cycle Assessment (LCA) in terms of Pts or mPts, as shown in Equation (9).

\begin{array}{l} Ẏ = \frac{Y}{n_{y} n_{h} 3600} & (9) \end{array}

Where: n_y is the number of years of operation and n_h is the operation hours per year.

Component-related environmental burden, as well as the formation of pollutants, can be obtained via LCA (using a specific LCA software, such as SimaPro or GaBi) or using the environmental impact tables from the Eco-indicator 99 method (Cavalcanti, 2017). The life cycle inventory of a component can include the extraction of raw materials, manufacture, transportation, operation and maintenance, and final disposal.

The exergoenvironmental assessment also includes some important parameters (environmental impact rate, relative difference, and exergoenvironmental factor). The environmental impact rate related to exergy destruction is evaluated by average environmental impact per exergy unit of fuel:

\begin{array}{l} Ḃ_{D} = b_{f} \cdot Ė_{D} & (10) \end{array}

The relative difference (r_b) indicates the potential for reducing the environmental impact and the effort associated with that reduction. The average environmental impacts rate per exergy unit of the product (b_P) can be reduced with less effort in the component with higher r_b value. It is calculated as follows:

\begin{array}{l} r_{b} = \frac{b_{P} - b_{F}}{b_{F}} & (11) \end{array}

Finally, the exergoenvironmental factor (f_b), assesses the significance of environmental impacts associated with a component against the overall environmental impacts. The environmental impact related with a component encompasses its LCA (Ẏ) plus the environmental impact due to pollutant formation. The environmental impacts relative to exergy destruction (Ḃ_D) consider the exergy destruction and exergy efficiency. f_b is evaluated as follows:

\begin{array}{l} f_{b} = \frac{Ẏ + Ḃ^{P F}}{Ẏ + Ḃ^{P F} + Ḃ_{D}} & (12) \end{array}

A low value of (f_b) indicates which component has dominant rate of exergy destruction exergy in relation to the environmental impact rate associated with the component. This component should have its efficiency improved to reduce exergy destruction rate, thus improving its environmental performance.

There have been other thermodynamic indicators combined with LCA, such as the Cumulative Exergy Demand (CExD, Bösch et al., 2007), Cumulative Exergy Extraction from the Natural Environment (CEENE, Dewulf et al., 2007), and Solar Energy Demand (SED, Rugani et al., 2011). Exergoenvironmental assessments have traditionally employed the Eco-indicator 99 method, but other, properly supported, environmental impact assessment methods can be used. Recognizing that communication of results is crucial, indicators at a midpoint level may be preferred for specific communication purposes as it is easier to express results in terms of greenhouse gas (GHG) emissions than “Points.” Exergoenvironmental assessments could benefit from the use of environmental impact methods and indicators that are easily understandable. Carvalho and Delgado (2017) mentioned that GHG emissions are suitable to communicate the results of environmental studies and have received pronounced visibility due to their popularity (an example of exergoenvironmental assessment with GHG emissions can be found in Carvalho et al., in press).

5. Conclusions

The thermodynamic methods of analysis presented here rely on the concepts of exergy, and entropy generation to assess system performance by means of metrics that quantify the levels of irreversibility.

Attaching weights associated with environmental impact and cost, to exergy terms, the methodologies are extensible to environmental and economic analyses. The design framework formed this way can help guide efforts toward systems and new energy infrastructures that make efficient use of the resources available to them while minimizing their environmental footprint.

We have focused mostly on the advantages and applicability of the methods presented. A review of the literature shows that the use and conclusions reached with the methodologies are sometimes in conflict. These discrepancies tend to arise from subtle assumptions that modify the boundaries of the system and the time frames of the impacts under consideration. Some of these differences have been documented in the literature. For example, Gyftopoulos (1997) presented arguments against claims on restrictions on the range of validity of thermodynamics; the agreement/ disagreement between maximum power extraction and minimum entropy generation is documented in Bejan (1996b), Salamon et al. (2001), and Bejan (2016); and the applicability (or not) of the Carnot efficiency limit to electrochemical engines (fuel cells) (Gaggioli and Dunbar, 1993; Haynes, 2001; Lutz et al., 2002; Haseli, 2018). There has also been a critique of exergy as a measurement of the quality of products, in the sense that the concept of quality is broader and much more complex than that of thermodynamic exergy, which leaves theoretical space remaining for future exploration, as mentioned by Sieniutycz (2016). Tsatsaronis (1999) mentioned the lack of a formal procedure for using the results of exergy assessments prevents its widespread adoption, which is prevented by component interactions not being taken properly into account. Sciubba (2010) presented counterarguments to the claim that emergy is an exergy-based procedure.

The reader is invited to explore the arguments and counterarguments as an exercise that should highlight the importance of a clear definition of the system, its boundaries, and all underlying assumptions. Selecting metrics and indicators requires caution. Some have demonstrated tremendous applicability; however, some, presented as new, are simple reformulations of previously established ones and lack the necessary scrutiny.

Author Contributions

JO, EC, and MC: conceptualization, methodology, writing—original draft preparation, writing—review and editing, visualization, and project administration. JO: supervision. All authors contributed to the article and approved the submitted version.

Funding

JO acknowledges support from the Department of Energy: This material is based upon work supported by the Department of Energy under Award Number(s) DE-FE0032084. MC wishes to acknowledge the support of the National Council for Scientific and Technological Development (CNPq, Brazil) through Research Productivity grant nÂž 307394/2018-2.

Author Disclaimer

This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Assad, M., and Rosen, M. A. (2021). Design and Performance Optimization of Renewable Energy Systems. Academic Press.

Google Scholar

Badescu, V., Baracu, T., Avram, R., Grigore, R., and Patrascu, M. (2018). “On the design and optimization of constructal networks of heat exchangers by considering entropy generation minimization and thermoeconomics,” in Proceedings of the Romanian Academy, Vol. 19 (Bucharest), 273–278.

Google Scholar

Baumgärtner, S., and Arons, J. d. S. (2003). Necessity and inefficiency in the generation of waste: a thermodynamic analysis. J. Ind. Ecol. 7, 113–123. doi: 10.1162/108819803322564389