
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Sustain., 25 April 2022
Sec. Sustainable Chemical Process Design
Volume 3 - 2022 | https://doi.org/10.3389/frsus.2022.856836
Natural gas (NG) production has significantly increased in the past decade as new unconventional oil and gas wells are being discovered. NG as obtained from the wellhead requires processing before being considered as pipeline grade. The process consists of the removal of acidic gases followed by dehydration. NG processing is associated with toxic emission having substantial environmental and health impact. Difficulty in NG processing arises from varied flow rate and uncertain feed composition that provides a challenge in efficient design as well as finding the optimal operating condition. The present work used a stochastic approach to characterize natural gas composition and its importance on the product and waste emission is studied. Under the uncertain feed composition, optimal operating condition of the controllable variables was attained by a reliability-based robust multi-objective optimization (RBRMOO) technique that mitigates BTEX emission while fulfilling NG pipeline specification. Chemical process simulator is used to find the impact of the control process settings and variation of uncertain feed condition on NG dehydration and BTEX emission. The best prediction models were developed using machine learning algorithm, chosen from a family of metamodels. RBRMOO is performed using metaheuristic algorithm to determine the optimal process condition of the control variables. The impact of uncertain feed composition in process modeling and subsequent optimization demonstrates optimal process condition where the rate of emission is lower by ~83 ton/yr when compared to that from the deterministic model where median value of uncertain feed composition is used for analysis, portraying the limitations of traditional sustainability assessment methods that do not account for uncertainty.
Natural gas (NG) processing consists of the sweetening followed by dehydration. In the dehydration unit, triethylene glycol (TEG) is primarily used to remove water from NG. In the process of dehydration volatile organic compounds (VOCs) like benzene, toluene, ethylbenzene, isomers of xylene (BTEX) is also absorbed in TEG. During the regeneration process of TEG substantial amount of the absorbed BTEX along with other VOCs are discharged into the atmosphere causing harmful environmental as well as a health hazard needing strict regulation of the process. It is found that dehydration process control variables have significant effect on BTEX emission mitigation (Braek et al., 2001; Mukherjee and Diwekar, 2021b). Regulation of some of these control variables to reduce emission may have adverse effect on dehydration of the gas. To investigate the effect of different control variables, extensive simulation has been performed under uncertain feed condition and a metamodel based robust multi-objective optimization is performed that incorporates reliability constraint.
Theoretical and experimental studies of the dehydration and related emission from NG processing is conducted to identify perfect operating conditions. Gupta et al. (1996) studied optimum process condition for TEG loss minimization using sensitivity analysis. Rahimpour et al. (2013) optimizes operating conditions of dehydration plant obtained from process simulation to improve dew point of dry gas, glycol usage, emission of greenhouse gas. Jacob (2014) have studied the effects of the control variables like glycol circulation rate, flow rate of stripping gas, and reboiler temperature on dry gas water content. They have also studied effect of design parameter like number of treys in the absorber. Ranjbar et al. (2015) have used the HYSYS® process simulator for parametric optimization of TEG dehydration plant. Kamin et al. (2017) have used HYSYS® data to create a response surface model for optimizing dehydration plant. Neagu and Cursaru (2017) have studied impact of stripping gas flow rate and the reboiler temperature on the dry gas water content and regeneration of TEG. Chebbi et al. (2019) has optimized process parameter including TEG circulation rate and concentration, and design parameter like number of trays in the absorber to minimize the capital cost and operating cost like utility, TEG pumping, and stripping gas rate. Mukherjee and Diwekar (2021b) has conducted a multi-objective optimization (MOO) taking into consideration both economic and environmental impact for a sustainable solution. Sustainable design has three pillars; economic, environmental, and societal (Mukherjee et al., 2015). Traditionally, greenhouse gas (GHG) emission is used as a yardstick for environmental impact assessment of chemical process (Sikdar et al., 2017; Mukherjee et al., 2020). Mukherjee and Diwekar (2021b) have performed BTEX emission mitigation through control variable optimization. Optimization process applied so far has used constant feed condition. In reality, uncertain feed condition either in the form of flow rate and/or composition is prevalent in natural gas sources (Bullin and Krouskop, 2009; Sureshjani et al., 2020). Thus, in the present work optimal performance of natural gas dehydration plant under feed composition uncertainty has been studied using advanced data analysis with machine learning and metaheuristic algorithm.
Chemical process operation involves uncertainty in various forms; inlet feed composition, flow rate, or data-related, including metamodeling (Mukherjee and El-Halwagi, 2018; Mukherjee et al., 2020). The uncertainty due to metamodeling is addressed by Mukherjee and Diwekar (2021a). Uncertainty in the flow rate is primarily due to declining production with time and can be addressed by optimal fracturing of the wells (Oke et al., 2018, 2019). In some case, optimal design capacity of NG processing plant can be used to handle declining production (Asani et al., 2021). Uncertainty in composition is caused by various factors including geological formation. For a given geological formation, the fracture shale in hydraulically fractured reservoirs is heterogeneous in nature leading to uncertainty (Sureshjani et al., 2020). Variation of composition of shale gas is observed between different shale play (Bullin and Krouskop, 2009). In some cases, substantial variation in composition can be found within the same shale play. In the present work impact of feed composition uncertainty in the operational optimization of NG processing has been addressed. In optimization under uncertainty, the ensemble average of the probable scenarios is optimized, resulting in a robust optimal condition. However, a robust operation does not necessarily promise with certainty a reliable process operation in the face of wide range of unknown distributions. A reliability-based optimization in the light of uncertain process variables can ascertain trust ability of the result (Boroson and Missoum, 2015; Abebe et al., 2017).
This paper proposes a reliability-based robust multi-objective optimization (RBRMOO) technique to find the optimal control variables under feed composition uncertainty for NG processing system. Data-driven metamodeling is performed with machine-learning algorithms, followed by stochastic optimization using a metaheuristic technique. RBRMOO is an active area of research in engineering (Lobato et al., 2020). Multi-objective optimization (MOO) for design and operation of chemical process system are sensitive to external noises. A robust multi objective optimization (RMOO) results in stable performance that is least sensitive to uncertain process condition. However, robust design and operation are not necessarily capable of providing optimal solutions that satisfy prescribed reliability levels of the process performance. Abubakar et al. (2015) has analyzed reliability of chemical process system. In reliability analysis, the process is stimulated for various conditions that the system may come across and analyze response. Libotte et al. (2020) has developed a model for reliability based robust multi objective optimization for design of chemical process where the probability of system failure is considered for optimization. In this work, we have developed a RBRMOO model for real time optimal operation of chemical process system. For reliability assessment of the NG dehydration plant, the deterministic process simulator is assumed to act as a digital twin of a real process system that can simulate hypothetical scenarios is coupled with a stochastic model. For a robust and reliable NG process operation, the RBRMOO applies a hybrid algorithm combining robust multi-objective optimization (RMOO) and reliability-based multi-objective optimization (RBMOO) to obtain robust optimal process condition that applies reliability as constraints. Through the RBRMOO algorithm we can enhance the robustness of the emission minimization effect with reliability as constraints for dry gas water contents.
Chemical processes differ both in type, scale, and properties. Thus, a standard list of variables to be controlled for optimal operation does not exist. Important variable selection can be done with multivariate statistics, machine learning or other parameter estimation methods (Li et al., 2004; Mukherjee et al., 2013; Mukherjee, 2017). Mukherjee and Diwekar (2021b) have been used Lasso, a machine learning algorithm for important variables selection in NG dehydration process. Surrogate models are generated using support vector regression (SVR) (Vapnik et al., 1996). The model is used to quantify the effects of the uncertain and control variables on dependent variables. The SVR-based process model is used for optimization of the process with metaheuristic algorithm, efficient ant colony optimization (EACO), to obtain optimal values of control variables that minimizes BTEX emission at different limits of the water content of the processed gas. In this work, we quantify the effect of uncertainties with probability density. The objective function is changed from deterministic to expected value and the constraint is changed to a probability function that obey the reliability condition. EACO is an efficient algorithm that has been extensively used in chemical engineering, including computer aided molecular design (CAMD) (Mukherjee et al., 2017). The present work developed an algorithmic framework for surrogate model based robust chemical process optimization that uses reliability as constraint and demonstrated the significance of incorporating source stream composition uncertainty in process optimization by the value of stochastic solution (VSS). The goal of the present work is to find an optimal operating condition that is reliable and environmentally friendly.
The next section describes natural gas dehydration process and emission from the process under feed composition uncertainty. Process simulation method implemented for data generation, modeling with SVR, and RBRMOO is explained in the solution methodology section. This is followed by results from modeling and RBRMOO with SVR-EACO strategy for the dehydration process. Finally a brief discussion of the results are given followed by conclusions.
Triethylene glycol (TEG) is the most preferred solvent in industries for NG dehydration. Dehydration process comprises an absorption and a stripping unit. The absorption unit is a tray or packed column where lean TEG entering the tower from the top is used to absorb water from wet gas in a countercurrent manner. Rich TEG coming out from the bottom of the absorber is subsequently regenerated in a regenerator column. Stripping gas obtained from part of the dry gas is injected into the reboiler. The TEG after regeneration is recycled back for absorption. Along with water vapor, aromatics are also absorbed in the absorber that is eventually released into the atmosphere primarily from the regenerator. Traditional methods adopted for BTEX/VOC mitigation like incineration, flaring, or condensation are not environmentally friendly. Process control variables that impacts BTEX/VOC emission may also affect the dry gas dew point. Thus, the problem has to be solved using multi-objective optimization (MOO) technique where the dehydration process must achieve the emission goal along with meeting dry gas due point requirement.
Traditionally, chemical process optimization assumes a constant flow rate and composition, ignoring uncertainty associated with the process. The uncertain inputs can be defined by an associated probability distribution. Impact of the uncertain feed composition is observed in a wide range of distribution of the uncertain output variables namely dry gas water content and BTEX emission. Figure 1 shows NG processing with uncertain feed composition and propagation through the process resulting uncertain output variables. In case uncertainty is considered for robust multi-objective optimization (RMOO), reliability of the process to meet the threshold of the output variables are unknown. In our previous work, a deterministic solution is performed where the median value of the feed composition is used for optimization. Under uncertain feed composition, the output variables (dry gas water and BTEX emission) at the optimal process condition will also vary, following a distribution and may exceed the limit as predicted by the median feed condition. Thus, a reliability based stochastic optimization is performed for robust solution that meets the reliability criteria as required.
Stochastic simulation of the NG processing is conducted for response analysis. In this process, the uncertain and control input variables are generated using MATLAB. For the uncertain variables (feed composition), a normal distribution is assumed and for the control variables (process parameters), a uniform distribution is selected for our analysis. From different sampling techniques including Monte Carlo (MC), Latin Hypercube, importance sampling, Hamersley Sequence Sampling (HSS), etc. (Mukherjee and Diwekar, 2016), Halton sequence has been used that has high dimensional uniformity similar to the HSS for the control variables and MC sampling is used for uncertain variables (Wang and Hickernell, 2000). Uncertainty and reliability analysis is performed using the response of the system at stochastic condition. A surrogate model is generated, and the reliability (in terms of dry gas water content) and environmental safety margin (in terms of BTEX emission) of NG processing system is obtained. The framework is shown in Figure 2.
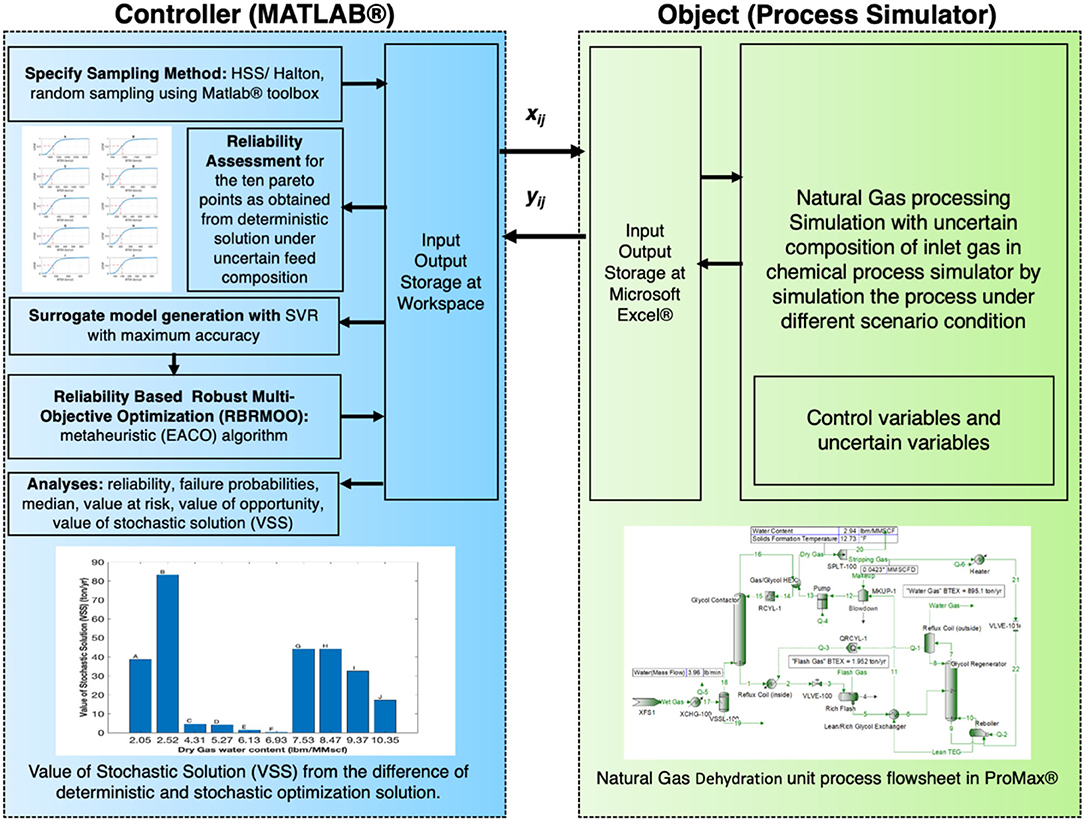
Figure 2. Framework for random variable generation, process simulation, data-based metamodeling, reliability estimation, reliability based robust multi-objective optimization, and value of stochastic solution estimation of natural gas dehydration process.
The steps involved in generating the natural gas process response under uncertain condition, surrogate model creation and RBRMOO for BTEX emission mitigation are:
(1) The entire process system is defined.
(2) The range and type of distribution of uncertain input variables and control variables of the NG process system are defined.
(3) Sample of the uncertain variables and control variables are generated using MC and Halton sequence respectively in MATLAB.
(4) Response of the NG processing system were generated using ProMax process simulator.
(5) Process performance criteria, constraints, and bounds are specified.
(6) SVR-based metamodels of the process are generated for the two different responses, BTEX emission and dry gas water content, using MATLAB for optimization.
(7) Reliability analysis is performed with LSF to obtain the probability of failure to meet the performance targets in MATLAB.
(8) Stochastic optimization is performed under specified limit of probability of failure to meet the dry gas water constraints threshold in MATLAB.
(9) The constraints are adjusted in every iteration following the threshold to obtain the Pareto optimal solution.
The ProMax model of the NG processing system is simulated for various uncertain feed compositions and the overall response with regard to the BTEX emission and dry gas water was noted. The performance of a chemical process system under stochastic conditions is determined by state space variables (q), control variables (c), uncertain inputs and modeling parameters (x), and equipment sizes (d). A standard optimization formulation (Edgar et al., 2001):
Where f is the function to be minimized and e and g are the equality and inequality constraints respectively. The state variables q are dependent on other control variables c. The inequality constrain can be represented as:
Through reliability analysis we can identify the region in the operating space that can achieve the process target while fulfilling the constraints. Through reliability analysis we can obtain the values of the control variables that meets the performance target. A threshold or failure criteria that can be determined based on process requirements like meeting the water content limit of dry gas or meeting a regulation target like BTEX emission are generally used to set the performance target. The multidimensional state space of the input variables can be divided into safe operating region and failure region using the limit state function (LSF), G(X) ≥ 0. Here X is the vector space of the input variables. Suppose there are n uncertain input variables. With n variables, we can create an n-1 dimensional hyperplane known as the failure surface that divides the input variable space into a safe and a failure region. Figure 3 shows a two-dimensional vector space with the failure surface. In the present problem, when the system response y(x) (in the present problem either dry gas water content or BTEX emission) is greater than a threshold θ i.e. y(x) ≥ θ, we called it a failure. The LSF is defined as:
Here LSF (G(X) ≥ 0) is a constraint to the optimization problem that satisfies one of the performance targets for the system. For example, in the present problem when the performance is defined by the dry gas water content, we have a failure when G(X) ≥ 0 i.e. the dry gas water content exceeds the threshold limit. When G(X) < 0, dry gas water is less than the performance target and the system is considered to be safe i.e. without failure. The probability of failure is defined as:
In case of n variables, a joint probability distribution function (FX(x)) can constitute the failure probability Pf (Thoft-Cristensen and Baker, 1982). Each process uncertain variables (x) i.e. inlet feed composition of NG is defined by a probability distribution. The Pf is obtained by integrating the joint probability distribution function (FX(x)) subject to G(X) ≥ 0 as:
The response of the entire wet gas dehydration process is obtained from PorMax® simulated for five hundred data points. Random realizations of the input variables are used to find the random response of the entire NG processing system. The Pf is estimated with stochastic simulation using an indicator function I(x) that shifts integration of Equation 5 to real space domain (Melchers, 1999) given as:
The indicator I(x) in this problem has a value of 1 when the response (e.g. dry gas water content) indicates failure satisfying the LSF, (i.e. G(X) ≥ 0, DryG exceeds threshold linit) and 0 otherwise. For a sample size of S, the indicator count can be used to estimate Pf as:
For a NG dehydration unit due to the varied feed composition, the process should have robust operating conditions. Here, two different goals need to be achieved: maximum drying efficiency and minimum toxic release. Thus, a robust multi-objective optimization RMOO problem needs to be solved. To obtain a reliable and robust process that fulfills multi-objectives criteria, a composite algorithm named Reliability-based Robust Multi-objective Optimization (RBRMOO) that applies both Reliability-based Multi-objective Optimization (RBMOO), and Robust Multi-objective Optimization (RMOO) method for a robust optimal solution that fulfills the reliability constraints.
In RBMOO, we find an optimal solution where the failure probability (P_fDryW, probability of dry gas water content exceeds the threshold θDryW) is less than or equal to the target probability (P0). The RBMOO formulation is defined as:
where the objective functions fBTEX denotes the output variables BTEX emission, is the m − dimensional vector of uncertain input variables and is the n − dimensional vector of the important control variables, yBTEX and yDryW are the functions for the output variables BTEX emission and dry gas water content respectively estimated with machine learning SVR, and wfBTEX and wfDryW are the vector of parameters for the functions yBTEX and yDryW respectively, g and h are other inequality and equality constraints respectively and li and ui are the lower and upper bound of the control variables ci, respectively. It is to be noted that the probability of dry gas water content to meet the threshold θDryW is 1 − Pf_DryW.
The uncertain input variables (x) fluctuations will result in variations in the product (yBTEX and yDryW) performance. The problem is generally handled by a robust optimization method. The RMOO is formulated as:
where E is the expected value. EfBTEX and EfDryW are the objective functions that denotes the expected values of BTEX emission and dry gas water content respectively.
Using the equations for RBMOO and RMOO, the reliability-based robust multi-objective optimization (RBRMOO) formulation is:
In the present problem, the objective of mathematical programming is to find the optimal values of the process variables so that impact on the environment in terms of BTEX emission (EfBTEX) is minimized while fulfilling the constraint on the probability of failure P_fDryW. The solution of multi-objective optimization is to find the trade-offs between the two conflicting objectives. Our two objectives, improved drying efficiency and BTEX mitigation which comprises economic and environmental aspects respectively are conflicting in nature. Thus, different process variables' impact can show completely dissimilar trends. The RBRMOO is solved similar to constraint method to generate a set of preferred Pareto optimal solutions which provides the trade-off surface. The optimization is solved repeatedly by changing the value of the threshold θDryW to generate the Pareto set. The task is performed in three steps. Firstly, SVR based process models for yBTEX(x,c, wfBTEX) and yDryW(x, c, wfDryW) has been developed, followed by finding the expected value and probability estimation, and finally optimizing the input space of the process model control variables (c) using EACO. The data used to develop the SVR model is given as Supplemental Document.
Figure 4 is the algorithmic flow diagram for reliability-based robust multi-objective optimization of natural gas dehydration process under feed composition uncertainty. The overall process has six steps: identify the control and uncertain variables and their mode of distribution and range of operation, dataset generation using efficient sampling techniques, ProMax process simulation with uncertain variables and random operating conditions, metamodel generation using SVR, probability of failure estimation, reliability based stochastic optimization using EACO through probabilistic estimation of the objective and probability of failure to meet constraint threshold. The optimal points as obtained from stochastic solution (RBRMOO) are compared with the deterministic solution (MOO) and Value of Stochastic Solution (VSS) is evaluated. Assuming ProMax® simulated process data as that from actual plant, the optimal points as obtained from the deterministic and stochastic optimization methods are evaluated in the process simulator for process performance assessment.
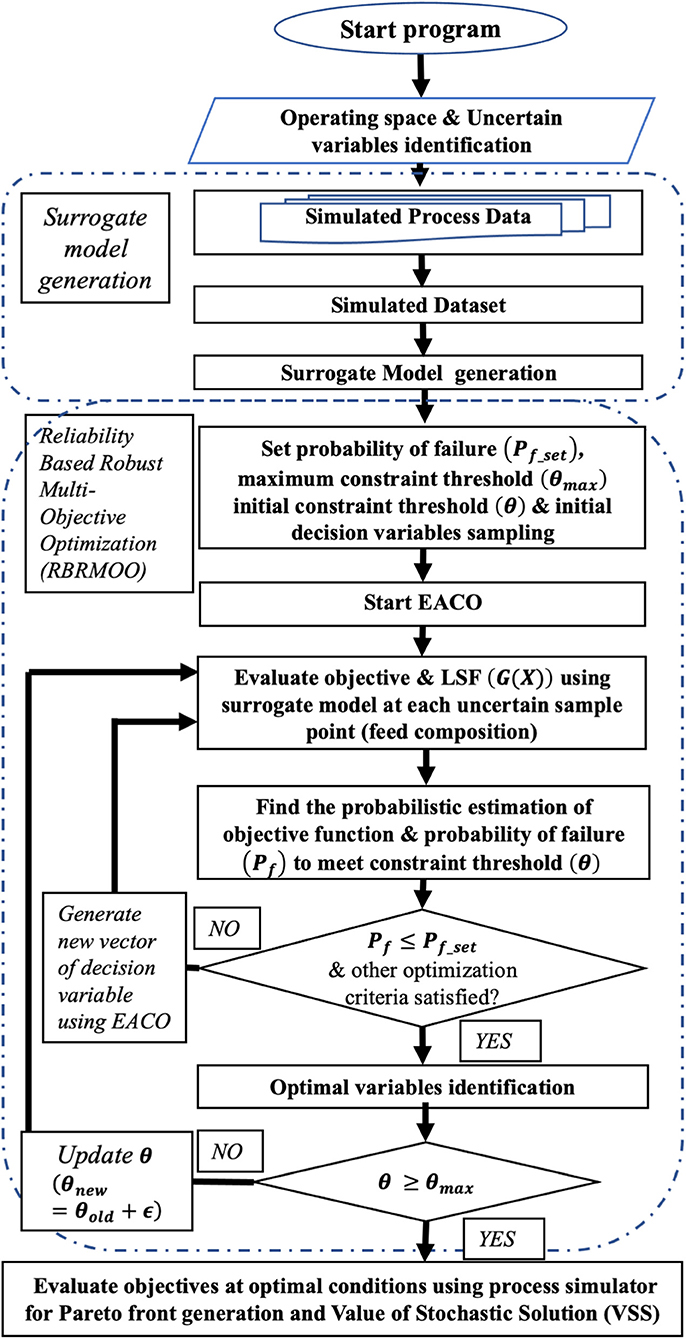
Figure 4. Algorithmic flow diagram for optimization of natural gas dehydration process with RBRMOO method.
Chemical process variables may vary over time leading to failure of the system to meet the specifications. To assess the reliability of the NG dehydration process in fulfilling the dry gas water limit or meet the BTEX emission threshold as predicted by deterministic optimization method, different uncertain variables in the process needs to be identified and varied over their possible range and distribution. In the present work, the feed composition is varied as in Figure 1. The reliability is evaluated by the probability of failure to comply the emission threshold and/or meeting the dry gas water limit.
The benchmark performance of NG dehydration system is generated by constant feed composition. In reality, uncertain feed stream composition can lead to divergence from the benchmark solution. Considering process control variables like Glycol circulation rate, Absorber pressure, Reboiler Temperature and Stripping gas rate as constant, the reliability of the dehydration process to fulfill any set point like benchmark set by deterministic solution will depend on the amount of uncertainty in the feed streams from NG sources. At the constant feed composition, the multi-objective condition is revealed by 10 Pareto optimal points as obtained by Mukherjee and Diwekar (2021b). The process conditions at the Pareto points are shown in Table 1.
The benchmark as obtained from constant feed condition at the 10 optimal conditions of NG dehydration system emits BTEX and dry gas water as shown by the performances of the process. When the feed compositions are normally distributed around the mean, the output emission and dry gas water content from the system can vary significantly resulting in the failure to meet the benchmark performance as obtained from steady feed composition.
Chemical process response is function of the control variables as well as uncertain process conditions. In the present work, we have considered uncertain feed conditions of the process. The selection of the rage of the control variables are based on literature (Braek et al., 2001). For a feed rate of 17.5 MMSCFD, the range of variables used by Braek et al. (2001) as well as the optimal condition as found by their analysis is given in Mukherjee and Diwekar (2021b). Based on the parametric study, Braek et al. (2001) has selected the glycol circulation rate and the stripping gas flow rate as significant parameters for optimization. They have also modified the flash tank pressure and the reboiler temperature. The molar percentage of the inlet components (uncertain variables) are assumed to vary normally around the mean value. The control variables can be varied by the operators uniformly within the range of operation. The distribution of the decision (control) variables and uncertain variables (feed compositions) as used for reliability estimation and stochastic optimization is shown in Table 2.
The process model is simulated for five hundred realizations of random input samples obtained from normally distributed data as shown in Figure 1. Using the input-output data, nonlinear response yBTEX(x,c, wfBTEX) and yDryW(x, c, wfDryW) is generated for BTEX emission and dry gas water content respectively. The analysis is conducted with sample size of 500. The corresponding output distribution of BTEX emission and dry gas water at the process decision variables as in optimal condition E in Table 1 is also shown in Figure 1. The cumulative distribution function of BTEX emission and dry gas water at the 10 Pareto optimal points as in Table 1 is shown in Figures 5A,B respectively. In face of uncertain feed composition, the dehydration unit can fail either in creating sufficient dryness and/or emitting excess BTEX than what is obtained from deterministic solution. To find the probability of failure of the dehydration unit, we have taken the optimal amount of BTEX emission and dry gas water as obtained from deterministic solution in Table 1 as the set point. The probability of failure is estimated by the frequency of time the amount of emission and dry gas water is equal to or exceeds the limit specified by the set point.
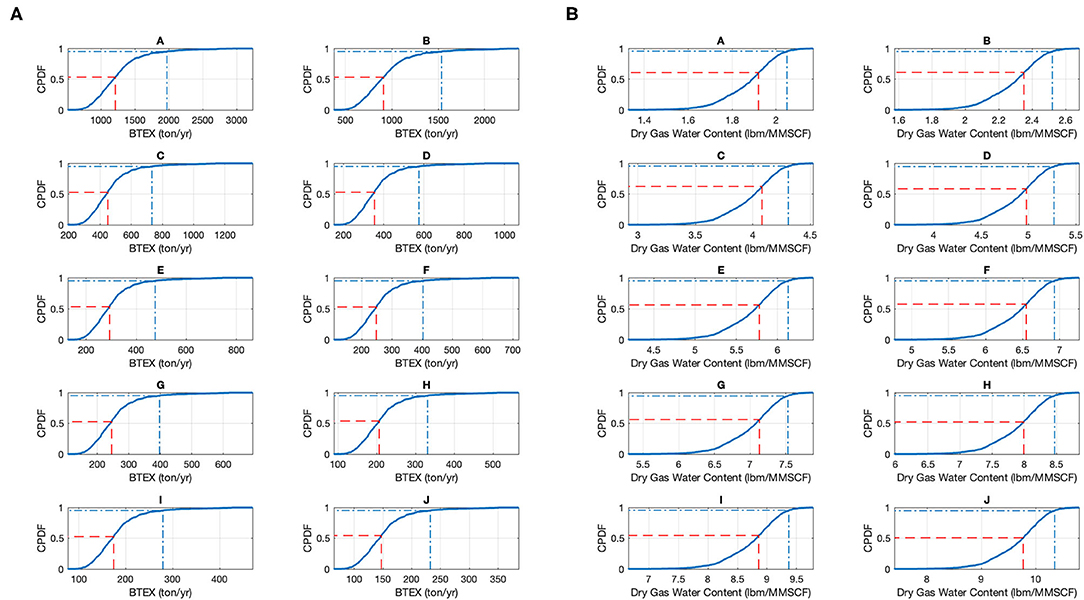
Figure 5. (A) Probability distribution of BTEX emission from uncertain NG process feed compositions generated with 500 sample points at the 10 Pareto optimal points from deterministic solution. The reliability of the system when BTEX emission is less than the amount as given in Table 1 lies between 0.54 and 0.53%; (B) Probability distribution of dry gas water content from uncertain NG process feed compositions generated with 500 sample points at the 10 Pareto optimal points from deterministic solution. The reliability of the system when dry has water is less than the amount as given in Table 1 lies between 0.62 and 0.51%.
From BTEX emission, the cumulation distribution at the 10 Pareto optimal points is shown in Figure 5A. From the distribution, the probability of failure (Pf) obtained is between 0.46 and 0.47 as shown in Figure 6A. Thus, the reliability (1 − Pf) of the dehydration process to emit BTEX as predicted by the benchmark obtained from deterministic solution is as high as 54% and as low as 53% reliable. Similar analysis for dry gas water content is shown in Figure 5B. Here the probability of failure (Pf) is found to be between 0.38 and 0.49 as shown in Figure 6B. Thus, the reliability (1 − Pf) of the dehydration process to produce dry gas as per the benchmark is found to be as high as 62% and as low as 51% reliable. Figures 5A,B also shows process performance where the dehydration unit is 95% reliable in terms of BTEX emission and dry gas water content respectively.
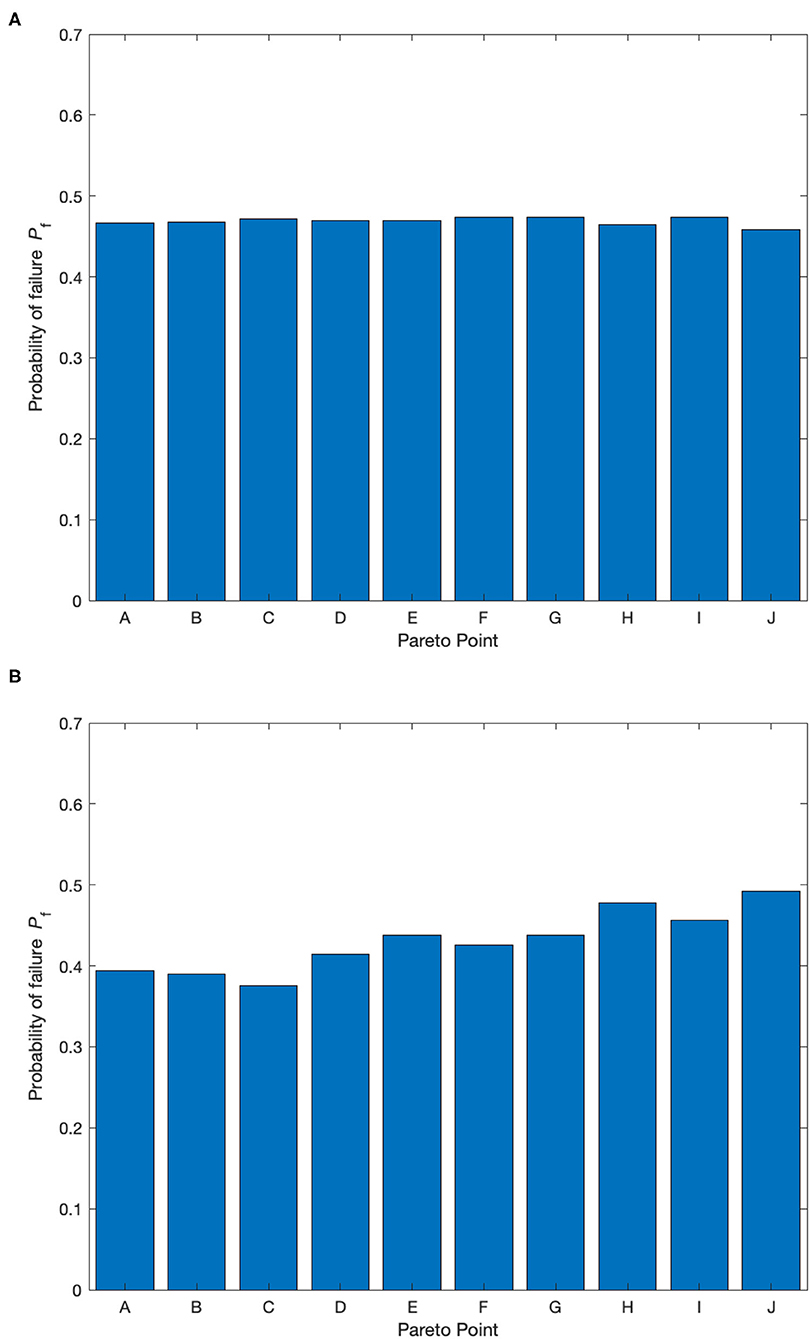
Figure 6. (A) At the 10 Pareto optimal points as obtained from MOO, the probability of failure when BTEX emission exceeds as given in Table 1 lies between 0.46 ≤ Pf ≤ 0.47; (B) At the 10 Pareto optimal points as obtained from MOO, the probability of failure when BTEX emission exceeds as given in Table 1 lies between 0.38 ≤ Pf ≤ 0.49.
Using ε − constrained method, Pareto optimal points are generated solving RBRMOO as shown in Equation 15 to Equation 19 that compares dry gas water content with BTEX emissions. Table 3 shows the optimization results. For the Pareto point A, optimization is performed by minimizing BTEX emission for minimum moisture content or maximum dryness possible. Thereafter, for the Pareto points B to I, BTEX emission minimization is obtained by increasing in steps the dry gas water limit from that obtained at Pareto point A up to 10 lbm/MMscf . The constraint on the probability of failure to meet the dry gas water limit Pf_DryW = 0.05. The process conditions at the optimal points from A to I as listed in Table 3 is simulated in process simulator in the face of uncertain feed condition and the set point for probability of failure Pf of 0.05 or 95% reliable is identified as shown in Figures 7A,B respectively for both BTEX emission and dry gas water respectively.
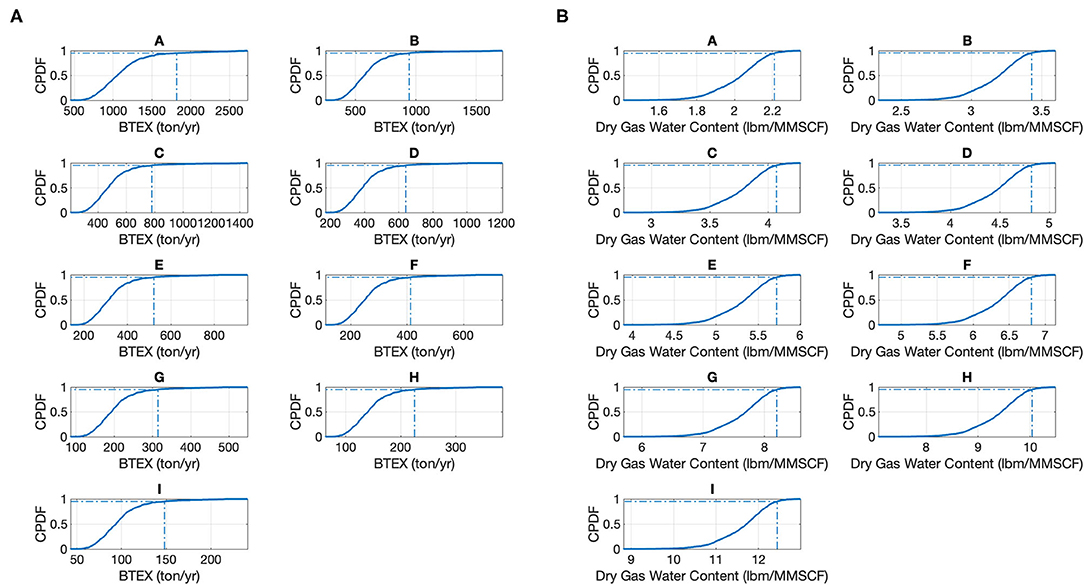
Figure 7. (A) Probability distribution of BTEX emission from uncertain NG process feed compositions generated with 500 sample points at the nine Pareto optimal points as obtained from stochastic solution (RBRMOO). The reliability of the system when BTEX emission is less than the amount as given in Table 3 is 0.95%; (B) Probability distribution of dry gas water from uncertain NG process feed compositions generated with 500 sample points at the nine Pareto optimal points as obtained from stochastic solution (RBRMOO). The reliability of the system when DryG is less than the amount as given in Table 3 is 0.95%.
The Pareto optimal points as obtained from RBRMOO stochastic solution and MOO deterministic solution are shown in Figure 8. From the two types of simulation, the optimal performance is obtained where the system is 95% reliable in face of uncertainty. The Pareto front reveals that the dry gas water decreases at the cost of increased BTEX emission. Natural gas needs to be dried to have a maximum moisture content 7 lbm/MMscf. Balanced operating conditions obtained from the RBRMOO as tabulated in Table 3 lies between Pareto points C and F. The overall optimal solution is at Pareto point E where BTEX emission (521.10 ton/yr), as well as dry gas water (5.72 lbm/MMscf). From the 500 realizations used for our analysis, the maximum BTEX emission was found to be 2,302.54 ton/yr, and that of dry gas water was 14.30 lbm/MMscf. The optimal operating conditions at the Pareto point “E” when compared with the maximum values reveals that RBRMOO have decreased dry gas water and BTEX emission by 60% and 77.37% respectively and the result is reliable for more that 95% of the time.
Tables 4, 5 shows the probabilistic characteristics of BTEX emission and dry gas water respectively at the nine Pareto optimal points as obtained from RBRMOO. At the mean (μ) feed composition as given in Table 1, the BTEX emission and dry gas water at the Pareto point E is 313.84 ton/yr and 5.31 lbm/MMscf respectively. From Table 4 it can be seen that at Pareto point E, the P95 value of BTEX emission is 521.1 ton/yr. The difference imply that traditional analysis may misrepresent BTEX emission from the process by ≅ 39.77%. Similarly, from Table 5 at Pareto point E, the P95 value of the dry gas water content is 5.72 lbm/MMscf suggest that traditional analysis approach may misrepresent dry gas water content of the process by ≅ 7.17%. Thus, traditional analysis has overpredicted the emission and dryness.
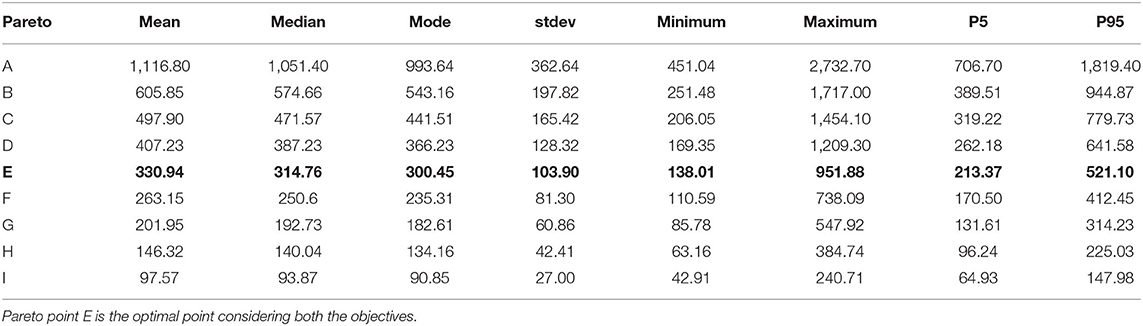
Table 4. Characteristics of BTEX emission at the Pareto optimal points as obtained from stochastic solution (ton/yr).
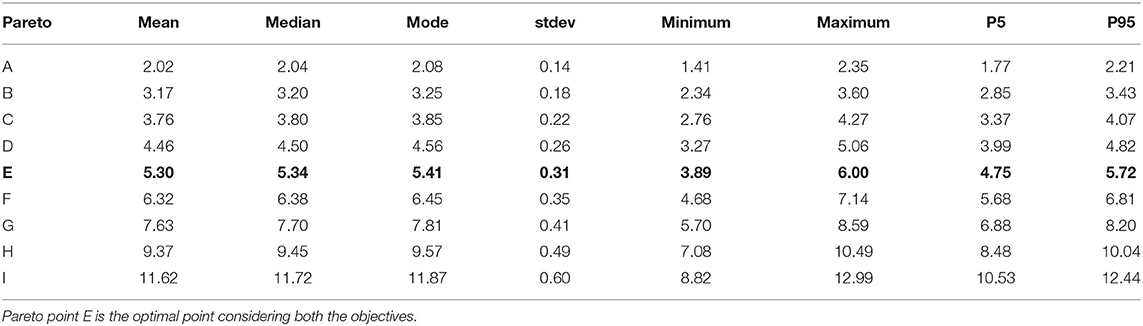
Table 5. Characteristics of dry gas water content at the Pareto optimal points as obtained from stochastic solution (lbm/MMscf).
Looking at the statistical characteristics of the distribution of BTEX emission in Table 4 suggests that at Pareto point E, the award zone (P5) when the emission is low and the risk zone (P95) when the emission is high is found to be 213.37 and 521.1 ton/yr respectively with the standard deviation is as high as 31.40% of the mean value. On the other hand, the statistical characteristics of the distribution of dry gas water content in Table 5 suggests that at Pareto point E the standard deviation of the dry gas water content is only 5.85% of the mean value.
VSS is estimated by comparing BTEX emission at different dry gas water content at optimal conditions suggested by RBRMOO stochastic and MOO deterministic solution. The difference between optimization as used in Mukherjee and Diwekar (2021b) obtained at the average value of the uncertain variable (in the present case feed composition) when compared with optimization as used in the present work by propagating the uncertainties through the model and using the probability of failure as constraint, is defined as the Value of the Stochastic Solution, VSS. Figure 8 shows the Pareto optimal points as predicted by stochastic and deterministic optimization. Figure 8 shows the P95 of the two objectives, BTEX emission and dry gas water content obtained from chemical process simulation at the optimal conditions. To compare BTEX emission at a specific dry gas water level as obtained from the stochastic and deterministic method, interpolation was used using the following equations:
Where the superscripts S and D are used to represent stochastic and deterministic solutions respectively. Dry gas water and BTEX emission as obtained from stochastic and deterministic solution and the interpolated value of BTEX as obtained using Equations 23-26 is shown in Table 6.
The VSS is obtained from the difference of deterministic and stochastic solution (interpolated) is shown in Figure 9. From the results we can see that emission savings as much as 83.17 tons per year.
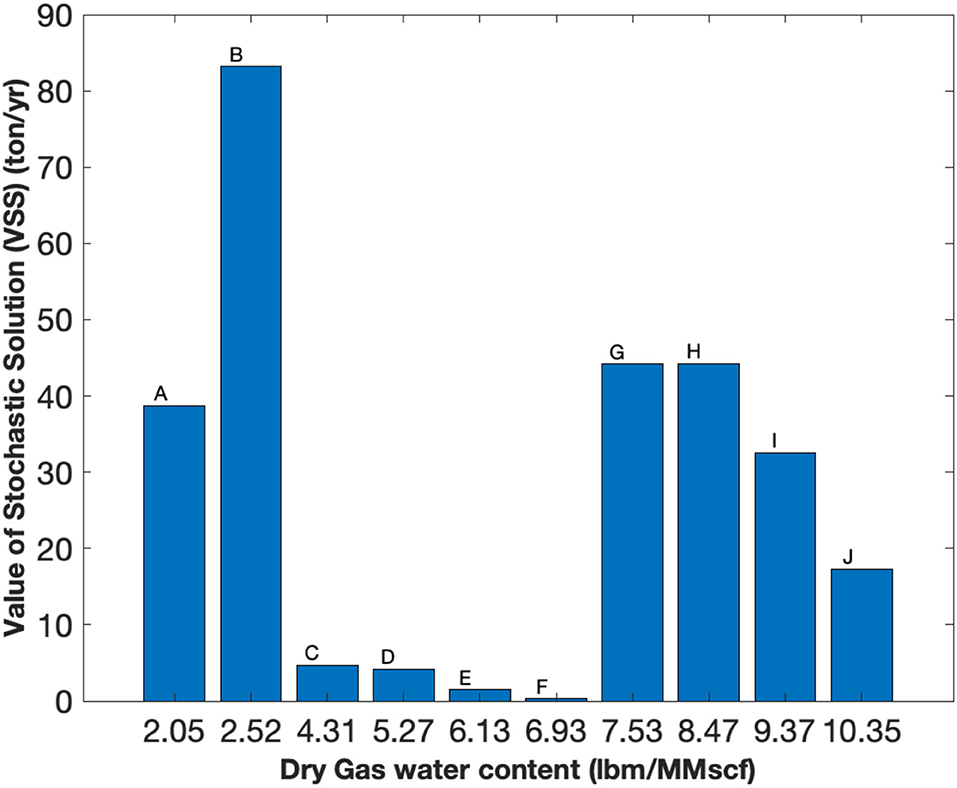
Figure 9. The difference between deterministic and stochastic optimization solution shown by the Value of the Stochastic Solution (VSS).
From the Pareto optimal solutions in Table 3, points C to F are appropriate for plant operation. At these points, dry gas water content is between 4 to 7 lbm/MMscf as recommended by Mokhatab et al. (2015) with modest BTEX emission. RBRMOO is performed by propagating the uncertainty through the model and setting the probability of failure as constraint. For reduced moisture level in dry gas, RBRMOO has resulted in identifying optimal process conditions that mitigates BTEX emission as high as 83.17 ton/yr when compared to that from deterministic optimization. At the optimal points C to F, we can also find that the difference between the stochastic and deterministic simulations are minimal. On the other hand, when the constraint on the dry gas water limit is too low or high, the difference between the stochastic and deterministic simulations are maximal.
A hybrid method is applied that uses SVR and EACO for metamodeling, probability of failure analysis and reliability based robust optimization of TEG dehydration process under feed composition uncertainty. SVR is a machine learning technique that is used for two different process model development, one for dry gas water content and the other for BTEX emission. Reliability based robust multi-objective optimization (RBRMOO) of the control variables in the input space of the SVR models is performed using EACO. Here, the ensemble average of BTEX emission is minimized with constraint on the probability of failure to meet the threshold of dry gas water content using ε − constraint method. The hybrid approach involving SVR and EACO for RBRMOO to obtain a Pareto optimal solution is novel. The method is applicable for an exclusive historical process data-based modeling and optimization under uncertainty where the predicted process performance is reliable.
While structural reliability assessment in civil construction and quality reliability analysis and reliability-based optimization in manufacturing process is relatively common, reliability assessment as well as reliability based chemical process performance analysis as well as optimizing the process using reliability constraint is not a prevalent practice. Developing a robust and reliability-based optimization framework presented in this work is key to ensure safer, more reliable and efficient chemical process operation that can support chemical engineers as they seek to improve plant safety, reliability in environmental and economic performance. Reliability based robust process performance optimization can increase the prospect for early fault detection by assessing the operational specifications in real time. The methodology presented in this work is one of those key steps necessary to implement traditional process simulators as digital twins. Availability of the optimal performance measures during process operation would greatly assist operators and other stake holders to ensure reliable operation. The results from this work support the usage of this framework in ensuring reliable performance of chemical processes under uncertainty. Although this paper focuses on natural gas dehydration plant, the proposed approach is also applicable for reliability based optimal operation of typical engineering process system.
This work has addressed optimal operation of NG dehydration process under feed composition uncertainty. The optimal control variables and the assessment of reliability in predicting process performance under uncertain feed composition has been addressed. Traditionally, optimal operating condition of chemical process system are obtained using first principle-based model of the mass and energy balance. A constant flow rates and concentration is assumed. In contrary, process generally encounter fluctuations especially in the feed streams with uncertain flow rates and/or concentration. Target of emission and dehydration set has a limited probability to be fulfilled. A novel data driven approach is proposed that applies the principle of reliability under uncertainty to enhance NG dehydration reliability. Under uncertain feed composition, a limited reliability is observed to meet the benchmark set by deterministic optimization.
In the present work, reliability based robust multi-objective optimization framework has been developed. The optimal condition promises reliable operation of NG dehydration process under uncertainty of the system. The present work shows how to theoretically decide on the set point under uncertain inlet composition for enhanced reliability of the dehydration operation. Traditionally, NG processing operates under uncertain feed composition distributed around a median value. In case some changes are incorporated either in the mean feed composition or other process condition, analysis as proposed can be performed to readjust the optimal process condition to ascertain reliable operation of the system.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
The author confirms being the sole contributor of this work and has approved it for publication.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsus.2022.856836/full#supplementary-material
Abebe, M., Park, J. W., and Kang, B. S. (2017). Reliability-based robust process optimization of multi-point dieless forming for product defect reduction. Int. J. Adv. Manufact. Technol. 89, 1223–1234. doi: 10.1007/s00170-016-9172-5
Abubakar, U., Sriramula, S., and Renton, N. C. (2015). Reliability of complex chemical engineering processes. Comput. Chem. Eng., 74, 1–14. doi: 10.1016/j.compchemeng.2014.12.013
Asani, R. R., Mukherjee, R., and El-Halwagi, M. M. (2021). Optimal selection of shale gas processing and NGL recovery plant from multiperiod simulation. Process Integrat. Optimizat. Sustain. 5, 123–138. doi: 10.1007/s41660-020-00140-9
Boroson, E., and Missoum, S. (2015). “Reliability-Based Design Optimization of Nonlinear Energy Sinks,” in presented at the Eleventh World Congress of Structural and Multidisciplinary Optimisation (WCSMO-11), Sydney, Australia, p. 7–12.
Braek, A. M., Almehaideb, R. A., Darwish, N., and Hughes, R. (2001). Optimization of process parameters for glycol unit to mitigate the emission of BTEX/VOCs. Process Safety Environ. Protect. 79, 218–232. doi: 10.1205/095758201750362262
Bullin, K. A., and Krouskop, P. E. (2009). Compositional variety complicates processing plans for US shale gas. Oil Gas J. 107, 50–55.
Chebbi, R., Qasim, M., and Jabbar, N. A. (2019). Optimization of triethylene glycol dehydration of natural gas. Energy Rep. 5, 723–732. doi: 10.1016/j.egyr.2019.06.014
Edgar, T. F., Himmelblau, D. M., and Lasdon, L. S. (2001). Optimization of Chemical Processes. New York, NY: McGraw-Hill, p. 672.
Gupta, A., Ansari, N. A. K. R., Rai, R., and Sah, A. K. (1996). “Reduction of glycol loss from gas dehydration unit at offshore platform in bombay offshore-a case study,” in Abu Dhabi International Petroleum Exhibition and Conference. Society of Petroleum Engineers.
Jacob, N. C. G. (2014). Optimization of Triethylene Glycol (Teg) Dehydration in a natural gas processing plant. Int J Res Eng Res Eng Technol 3, 346–350. doi: 10.15623/ijret.2014.0306064
Kamin, Z., Bono, A., and Leong, L. Y. (2017). Simulation, and optimization of the utilization of triethylene glycol in a natural gas dehydration process. Chem. Product Process Model. 12, 4. doi: 10.1515/cppm-2017-0017
Li, R., Henson, M. A., and Kurtz, M. J. (2004). Selection of model parameters for off-line parameter estimation. IEEE Transact. Control Syst. Technol. 12, 402–412. doi: 10.1109/TCST.2004.824799
Libotte, G. B., Lobato, F. S., Neto, F. D. M., and Platt, G. M. (2020). A Novel Reliability-based Robust Design Multi-objective Optimization Formulation Applied in Chemical Engineering. arXiv preprint arXiv:2006.00101.
Lobato, F. S., da Silva, M. A., Cavalini, A. A. Jr, and Steffen, V. Jr (2020). Reliability-based robust multi-objective optimization applied to engineering system design. Eng. Optimizat. 52, 1–21. doi: 10.1080/0305215X.2019.1577413
Melchers, R. E. (1999). Structural Reliability Analysis and Prediction. West Sussex: John Wiley and Sons Ltd, p. 456.
Mokhatab, S., Poe, W. A., and Mak, J. Y. (2015). Chapter 7 - Natural Gas Dehydration in HANDBOOK OF Natural Gas Transmission and Processing: Principles and Practices. New York, NY: Gulf professional publishing.
Mukherjee, R. (2017). Selection of Sustainable Process and Essential Indicators for Decision Making using Machine Learning Algorithms. Process Integrat. Optimizat. Sustain. 1, 153–163. doi: 10.1007/s41660-017-0011-4
Mukherjee, R., Asani, R. R., Bopanna, N., and El-Halwagi, M. M. (2020). Performance evaluation of shale gas processing and NGL recovery plant under uncertainty of the feed composition. J. Nat. Gas Sc. Eng. 83, 103517. doi: 10.1016/j.jngse.2020.103517
Mukherjee, R., and Diwekar, U. M. (2016). Comparison of monte carlo and quasi-monte carlo technique in structure and relaxing dynamics of polymer in dilute solution. Comput. Chem. Eng. 84, 28–35. doi: 10.1016/j.compchemeng.2015.08.014
Mukherjee, R., and Diwekar, U. M. (2021a). Optimizing TEG dehydration process under metamodel uncertainty. Energies 14, 6177. doi: 10.3390/en14196177
Mukherjee, R., and Diwekar, U. M. (2021b). Multi-objective optimization of the TEG dehydration process for BTEX emission mitigation using machine-learning and metaheuristic algorithms. ACS Sustain. Chemistr. Eng. 9, 1213–1228. doi: 10.1021/acssuschemeng.0c06951
Mukherjee, R., and El-Halwagi, M. M. (2018). Reliability of CHO symbiosis networks under source streams uncertainty. Smart Sustainable Manuf. Syst. 2, 132–153. doi: 10.1520/SSMS20180022
Mukherjee, R., Gebreslassie, B., and Diwekar, U. M. (2017). Design of novel polymeric adsorbents for metal ion removal from water using computer-aided molecular design. Clean Technol. Environ. Policy 19, 483–499. doi: 10.1007/s10098-016-1236-6
Mukherjee, R., Sengupta, D., and Sikdar, S. K. (2013). Parsimonious use of indicators for evaluating sustainability systems with multivariate statistical analysis. Clean Technol. Environ. Policy 15, 699–706. doi: 10.1007/s10098-013-0614-6
Mukherjee, R., Sengupta, D., and Sikdar, S. K. (2015). Sustainability in the context of process engineering. Clean Technol. Environ. Policy 17, 833–840. doi: 10.1007/s10098-015-0952-7
Neagu, M., and Cursaru, D. L. (2017). Technical and economic evaluations of the triethylene glycol regeneration processes in natural gas dehydration plants. J. Nat. Gas Sci. Eng. 37, 327–340. doi: 10.1016/j.jngse.2016.11.052
Oke, D., Majozi, T., Mukherjee, R., Sengupta, D., and El-Halwagi, M. M. (2018). Simultaneous energy and water optimisation in shale exploration. Processes 6, 86. doi: 10.3390/pr6070086
Oke, D., Mukherjee, R., Sengupta, D., Majozi, T., and El-Halwagi, M. M. (2019). Optimization of water-energy nexus in shale gas exploration: from production to transmission. Energy 183, 651–669. doi: 10.1016/j.energy.2019.06.104
Rahimpour, M. R., Saidi, M., and Seifi, M. (2013). Improvement of natural gas dehydration performance by optimization of operating conditions: a case study in Sarkhun gas processing plant. J. Nat. Gas Sci. Eng. 15, 118–126. doi: 10.1016/j.jngse.2013.10.001
Ranjbar, H., Ahmadi, H., Sheshdeh, R. K., and Ranjbar, H. (2015). Application of relative sensitivity function in parametric optimization of a tri-ethylene glycol dehydration plant. J. Nat. Gas Sci. Eng. 25, 39–45. doi: 10.1016/j.jngse.2015.04.028
Sikdar, S. K., Sengupta, D., and Mukherjee, R. (2017). Measuring Progress Towards Sustainability. Cham: Springer International Publishing.
Sureshjani, M. H., Ahmadi, M., and Fahimpour, J. (2020). Uncertainty quantification in heterogeneous tight/shale reservoirs from analysis of transient/boundary-dominated production data. J. Nat. Gas Sci. Eng. 20, 103342. doi: 10.1016/j.jngse.2020.103342
Thoft-Cristensen, P., and Baker, M. J. (1982). Structural Reliability Theory and Its Applications. Berlin: Springer Berlin Heidelberg, p. 268.
Vapnik, V., Golowich, S., and Smola, A. (1996). Support vector method for function approximation, regression estimation and signal processing. Adv. Neural Inform. Process. Syst., 9, 281–287.
Keywords: TEG dehydration process, BTEX mitigation, limit state function (LSF), reliability based robust multi-objective optimization (RBRMOO), value of stochastic solution (VSS)
Citation: Mukherjee R (2022) Reliability-Based Robust Multi-Objective Optimization (RBRMOO) of Chemical Process Systems: A Case Study of TEG Dehydration Plant. Front. Sustain. 3:856836. doi: 10.3389/frsus.2022.856836
Received: 17 January 2022; Accepted: 22 March 2022;
Published: 25 April 2022.
Edited by:
Thokozani Majozi, University of the Witwatersrand, South AfricaReviewed by:
José María Ponce-Ortega, Michoacana University of San Nicolás de Hidalgo, MexicoCopyright © 2022 Mukherjee. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rajib Mukherjee, cm11a2hlMEBnbWFpbC5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.