A Thermodynamic Measure of Sustainability

A novel thermodynamic approach to the quantification of the “degree of sustainability” is proposed and discussed. The method includes a rigorous -and innovative- conversion procedure of the so-called externalities that leads to their expression in terms of the exergy of their equivalent primary resources consumption. Such a thermodynamic approach suggests a detailed re-evaluation of the concept of sustainability because it is well-known that the Second Law strictly negates the possibility for any open and evolving system to maintain itself in a “sustainable” state without availing itself of a continuous supply of low-entropy (i.e., high specific exergy) input. If a human society is modeled as an open system, its capacity to “grow sustainably” depends not only on how it uses non-renewable resources, but also on the rate at which it exploits the renewable ones. The necessary inclusion of different forms of energy- and material flows in such an analysis constitutes per se an argument in favor of a resource-based exergy metrics. While it is true that the thermodynamically oriented approach proposed here neglects all of the non-thermodynamic attributes of a “sustainable system” (in the Bruntland sense), it is also clear that it constitutes a rigorous basis on which different physically possible scenarios can be rigorously evaluated. Non-thermodynamic indicators can be still used at a “second level analysis” and maintain their usefulness to indicate which one of the “thermodynamically least unsustainable” scenarios is most convenient from an ethical or socio-economic perspective for the considered community or for the society as a whole. The proposed indicator is known as “Exergy Footprint,” and the advantages of its systematic application to the identification of “sustainable growth paths” is discussed in the Conclusions.

Introduction

After a debate that lasted for several decades, environmental considerations have been accepted as an essential -and necessary- part of the assessment of energy conversion systems. As of the time of this writing, several paradigms are in place to identify and quantify the “anthropogenic environmental impact,” and major Environmental and Governmental Agencies shelved the crude “emission level control” of the ‘80s to prescribe comprehensive and detailed analysis of the local and global implications of the interactions of anthropic processes with the biosphere (both locally and at large). In fact, the large majority of current regulations go well-beyond the simple “assessment of ecological damage” (intended simply as “pollution”). Quantifiers of such interactions, known as Environmental Indicators (EI in the following), have been and are still being proposed and applied to different systems under diverse scenarios and with different system boundaries, to provide a sufficiently accurate and reliable decision support basis for decision makers. The definition of a reliable and robust EI invariably poses some problems: for example, some of the most popular EIs are based on a restricted number of control parameters (quality of air, public health, social equity, etc.) and offer only an incomplete measure of the actual environmental impact. Moreover, most of the “sustainability” indicators currently adopted in Biosciences are not rooted on rigorous thermodynamic principles and often require rather arbitrarily “weighed” decisions on the part of the analyst, which may generate confusion among final users. This paper proposes a method to construct thermodynamically correct Environmental Indicators to rigorously address the problem of “sustainability.” Approaching the problem under this point of view, it becomes immediately clear that if the problem is tackled starting from fundamental principles a thermodynamic redefinition of the very concept of sustainability is necessary. In fact, Second Law negates the possibility for any open and evolving system to maintain itself in a “sustainable” state without availing itself of a continuous supply of low-entropy input^1,2. Therefore, the idea that “future generations” may successfully “satisfy their needs” (UN, 1987) while their resource base is irreversibly dwindling leads either to the enforcement of an untenable Malthusian level of numerosity control of the population (Sciubba and Zullo, 2009) or to an extreme degree of “prosperous de-growth” (Galor and Moav, 2001; Martínez-Alier et al., 2010) in all likeliness unacceptable by our progeny.

A Brief Critical Analysis of the Sustainability Concept

The modern concept of environmental sustainability dates back to the early ‘60s, when the then dominating view of technology-driven economic growth came under the fire of a generic criticism based on the perception that the quality of the environment is closely linked to economic development. Admittedly, in those years academic support for the “steady state” economy (i.e., no-growth in mass throughput) was less than lukewarm, but as public opinion became strongly involved through the environmental movements, public Agencies and Governments became actively involved, promoting new procedures and issuing new regulations (Paul, 1998). Perhaps the most important step was the 1968 foundation of the Club of Rome), followed by their publication in 1972 of Limits to Growth (Club of Rome, 1972). Other initiatives followed, like the establishment of the Worldwatch Institute in 1975, and finally the term sustainable development was officially coined by the United Nations Commission (usually referred to as the “Brundtland Commission” from the name of its president, Gro Harlem Brundtland). It must be mentioned that the Commission report was largely based on the suggestions formulated in the previous decade by Daly and Costanza (Daly, 1977, 1996; Costanza et al., 1997). This 1987 report (UN, 1987), Our Common Future, contains the (too) often cited definition of “development which meets the needs of the present without compromising the ability of future generations to meet their own needs.”

In the last four decades, the concept was further developed, leading to the United Nations Millennium Declaration (September 2000 in Rio de Janeiro) which set out eight “United Nations Millennium Development Goals” (MDG), to be achieved by 2015, committing world leaders to fight poverty, hunger, disease, illiteracy, environmental degradation, and discrimination against minorities (UNEP, 1992). Following suit, the World Summit on Sustainable Development (WSSD, Johannesburg 2002), produced the first political declaration (the “Johannesburg Plan of Implementation”) setting global goals and targets on the access to water, sanitation and modern energy services, on increasing energy primary-to-final use efficiency, on the exploitation of renewable energy sources, on establishing and maintaining sustainable fisheries and forests, on the enforcement of a more accurate monitoring and management of chemicals, etc. The rationale here was that of decoupling environmental degradation from economic growth and of achieving “sustainable patterns of consumption and production.”

The term “eco-development” had already appeared in the UN Environment Program review in 1978, and its most important feature was the recommendation that environmental and developmental ideas be considered concurrently. The paradigmatic definition of the Brundtland Commission elaborated on this approach, but it contains two rather obscure points that need clarification:

a) The concept of “needs,” explicitly defined as the essential needs of individuals, including obviously their socio-economical rights to which overriding priority should be given. Specifically, who is in charge of dictating a standard for these “needs” that is acceptable to the entire world population? And if “local needs” are regarded as necessary, what supernational Authority is responsible for their definition and updates? Most importantly perhaps, how are the “needs of the future generations” established, especially in view of the fact that “sustainable development” planning requires long-term decisions and policies?

b) The idea that a simple change in consumers' attitude and an improvement in final energy uses, coupled with the expected technological advances, may suffice to allow for a perennial “sustainable development,” be it with or without a growth in the global material throughput (Daly, 1996).

Some scholars correctly observed already in those early years that it is exactly the vagueness of the definition of the “sustainability issue” that made it palatable to decision makers worldwide: it is becoming painfully clear today that “sustainable development” is something everyone can agree to, but that merely positing it does not provide exact guidelines on how to achieve its goal.

Today, we are faced with practical questions such as: What does sustainable development really mean for different communities? How can we put the concept into practice? How do we know if we are transitioning toward a sustainable world? These questions demand for a measure of environmental effects, both at local and global scales, and this is why current “environmental policy declarations” make explicit use of both local and global EI, defined (EPA, 2008) as “… a numerical value that helps provide insight into the state of the environment or human health… Indicators are developed based on quantitative measurements or statistics of environmental condition that are tracked over time.” They “… can be developed and used at a wide variety of geographic scales, from local to regional to national levels. By monitoring the environment using indicators … (it is possible to)… share meaningful environmental information with the public, and ensure that high-quality environmental decisions are made.”

Another problem is that the concept of sustainability is not only rather fuzzy (a criticism that nowadays most schools of thought agree upon) but that it also lacks a rigorous scientific foundation. The very idea that a chemically and thermally non-homogeneous open system of constant total mass may be “sustainable” tout court (i.e., that it may remain in its -possibly dynamic- state “forever”) conflicts with the dictates of the Second Law of Thermodynamics (Valero-Delgado et al., 2011). The main problem is that the currently accepted definitions of “sustainability,” “sustainable development,” “sustainable growth” etc. make implicit or explicit recourse not only to exact physical sciences (to which thermodynamic laws apply), but also to several different branches of knowledge like Economics, Social- and Political Sciences, all of which are intrinsically ruled by “value judgements” that cannot be easily falsified in Popper's sense³ and are in general axiomatically posited⁴. The (too!) often published “three pillars paradigm” (Figure 1) that asserts that the concept of Sustainability stems out of three fields of knowledge, Social, Economics and Environmental sciences, has been strongly criticized by influential scholars (Thompson, 2017; Purvis et al., 2019), but the idea is so catchy and so heavily publicized, even on public media, that most decision makers take it for granted.

FIGURE 1

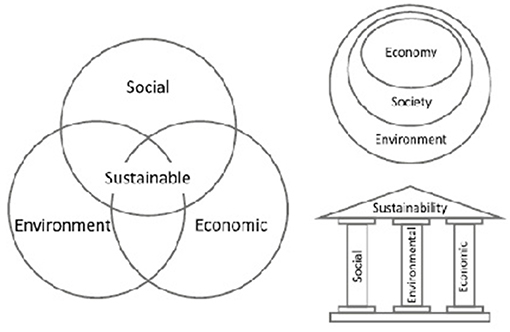
Figure 1. The concept of the three pillars of sustainability (adapted from Purvis et al., 2019).

The approach taken in this paper is in this perspective frankly “reductionist.” When addressing problems like “rational resource exploitation” and “equitable resource distribution”, the role of Physical Sciences is predominant: it is rather clear that a resource-based metrics is less biased and must be favored, and as a consequence the non-thermodynamic attributes of a “sustainable system” ought to be considered at a “second step level” and be carefully reformulated in terms of their primary resource equivalent. In such a perspective, it is clear that the inherent fuzziness of the current concept of “sustainability” is due to the neglect of the fundamental separation between its thermodynamic⁵ basis, that should be the plinth on which possible “pillars” rest, and the socio-economic one, which falls under the domain of different branches of science, is measured by different quantifiers, and ought to consider the thermodynamic part as a preliminary filter and therefore abandon the glorious idea that a “sustainable state” be attainable by a simple resource re-allocation.

Environmental Indicators as Quantifiers of the State of a System

Environmental Indicators are used at different aggregation levels in industrial, economic, social and environmental studies as a synthetic and significant way of “representing reality.” They facilitate a concise and reproducible information exchange between specialists (scientists at large) and non-specialists (herein collectively denominated “decision makers,” including in this term the public opinion). As their name implies, EIs ought to be quantifiers that measure the “environmental quality” at a local, industrial, regional, national or global scale and should be used to directly compare -and possibly integrate- different scenarios. A careful examination of most of these quantifiers reveals that the problems lie in the link between the formulation of each indicator and the phenomenological model it subsumes. Combining some widely accepted inventories of necessary properties of an Environmental Indicator (Jackson et al., 2000; Dale and Beyeler, 2001; Gong and Wall, 2001; Sciubba, 2013) we can extract a useful conceptual list of evaluation criteria:

a) The EI must be expressed by a -possibly simple- numeric or alphanumeric expression, i.e., they are scalars;

b) The application of an EI to real world situation must produce results that can be unambiguously ranked (from “bad” to “good,” from “desirable” to “damaging,” etc.);

c) The EI must be calculated on the basis of easily measurable, intrinsic properties of both the system to which it refers (= the potential “polluter source”) and of the (local or global) environment (the “polluted system”);

d) The EI must be properly normalized, so that it may be used to compare different communities under different environmental conditions, or different scenarios and time series for the same community;

e) The EI must be calculated on the basis of an unambiguous, reproducible method under a well-defined set of fundamental assumptions;

f) The EI must be anticipatory, i.e., it can be used both for diagnostic and prognostic purposes;

g) The EI must comply with the accepted laws of physics.

In conclusion, the EI that we shall consider in the present study are a) purely thermodynamic; b) resource- based; c) global; d) exergy-based. The fourth attribute is justified by the well-established record of results brought about by the adoption of exergy in the analysis of technical systems (Dewulf et al., 2008).

Thermodynamics and Resource Exploitment

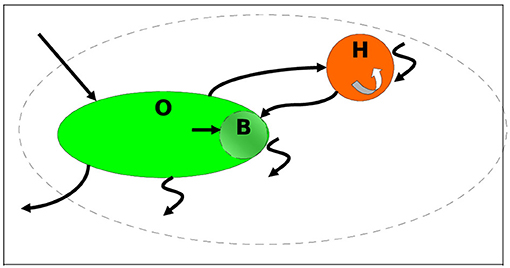
The fundamental idea of this study is that a human society can be modeled as a (non-equilibrium) thermodynamic system (Demirel, 2007; Lebon and Jou, 2008). In such an approach, the relationship between a “human society” (H) and “the environment” (O) can be quantified using thermodynamic tools. Since diverse forms of energy flows are involved that cannot be simply algebraically combined (like for instance chemical energy, thermal energy, human labor etc.), and since it is rather obvious that “thermodynamic sustainability” is inextricably linked to the Second Law, we shall use without further justification exergy⁶ as the sole quantifier for our considerations (for a definition of exergy and a detailed discussion on its properties and applications, see for example (Fratzscher, 1965; Moran, 1982; Szargut et al., 1988; Wall, 1997; Wall and Gong, 2001).

Methodological Remarks

In an Exergy Analysis every material flow is attributed an equivalent “exergetic power” by multiplying its mass flowrate by the specific exergy of the material, Ė_j = ṁ_je_j⁷. Immaterial flows carry different exergy amounts depending on both the energy intensity and “type”: mechanical and electrical power carries an exergy equal to its value in W, while thermal energy flows possess an exergy content equal to their enthalpic value multiplied by a temperature-dependent factor lower than unity that reflects their inability to be completely converted into work (Moran, 1982). Chemical energy flows (e.g., “heat of reaction”) are attributed an exergy equivalent by means of an exergy evaluation of the reactants and products and of the reference environment in which the reaction takes place (Kotas, 1985).

The Exergy Budget

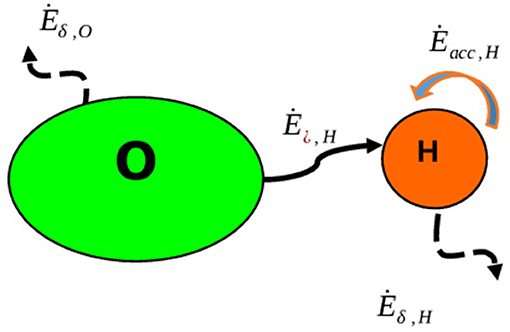
Exergy is not conserved: in every real process a portion of the incoming exergy is destroyed (annihilated) by irreversibility: in fact, this destruction is proportional to the irreversible entropy generation rate (Gouy-Stodola theorem). In the following of this paper, the exergy destruction rate is denoted by Ė_δ, and it is important to notice that it denotes in fact a fictitious “flow” that does not correspond to any physical quantity: it is but a mere arithmetical expedient to represent the difference between the input and the output so that we may formally talk of an exergy “balance.” In time-dependent processes it is often useful to include an “accumulation” term whose rate Ė_acc quantifies the amount of incoming exergy converted into internal “production processes” within the system: in a transparent reference to biological systems, this corresponds to a “growth” and its integral in time is sometimes denoted as “embodied exergy” (Yantovsky, 1994). In the following, since one of the systems (“H”) is an anthropic community (an industrial sector, a city, a Country…), this accumulation measures for example the cumulative exergy of the goods generated internally (industrial commodities, construction, consumer goods, etc.). Natural flows (wind, irradiation, water flows…) also carry an exergy that can be calculated according to the same rules. Referring specifically to the “system society,” its input Ė_in consists in material flows of ores, fossil fuels and goods from the environment and immaterial flows like solar radiation, hydraulic- and wind power, geothermal power etc., also originated in the environment. This inflow of (low-entropy) material and immaterial streams feeds the conversion processes inside of the system that convert the primary resources into final exergy use (consumer goods, buildings, transportation systems, food, etc.). Since all real processes are irreversible, at each step in the conversion chain a portion of the incoming exergy flow is destroyed (annihilated), and the cumulative destruction is denoted by Ė_δ,H. The system also discharges “waste” into the environment, both as scrapped material byproducts and process effluents or as -generally low temperature- thermal flows: their cumulative amount is referred to as Ė_W,H.

Time Evolution of H

Every anthropic system, be it a single production line, a city or an entire Country, is an open system evolving in time. But in Classical Thermodynamics the concept of “time” has no meaning and all processes are analyzed assuming they may be described by a succession of (quasi-) equilibrium states. When we deal with natural systems time becomes though an essential parameter, because the time history of the systems object of the study is really what we are after. Therefore, the “balances” described in this context must be intended as integral values over the entire duration of the time window of interest. In the model we are proposing, this time dependence is enforced in two ways:

a) The “internal dynamics” of each system are allowed to vary in a prescribed fashion: for instance, with reference to Figure 2, the growth rate of H, measured by Ė_acc is specified as a f(t) (this is equivalent to defining a scenario to which the model is applied), and the history of system evolution becomes a function of this quantity and of the boundary conditions;

b) The boundary conditions (Ė_in, Ė_out, Ė_b) may display in turn a time dependence (daily, seasonal, or otherwise) that is not considered as an internal variable of the system and depends on the considered scenario as well.

FIGURE 2

Figure 2. The constant-mass open-system model with accumulation in H (growth).

In general, the evolution of a system on a realistically extended time scale can be described by an initial and usually rather flat transient, possibly followed by a more or less steady condition of a variable duration and by a final “approach of the limit” for very long times. Since our goal here is to describe a possible model, in the following we shall assume that all systems under examination have a characteristic evolution time much longer than the window of observation, so that they may be treated as “dynamically steady” systems.

Closed Systems

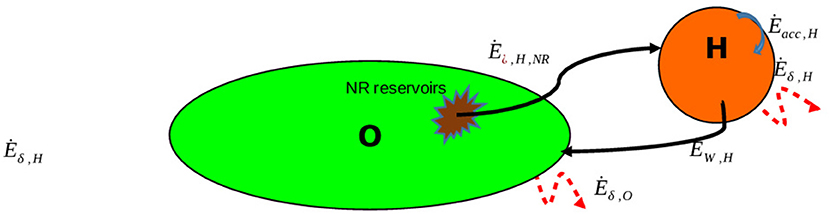
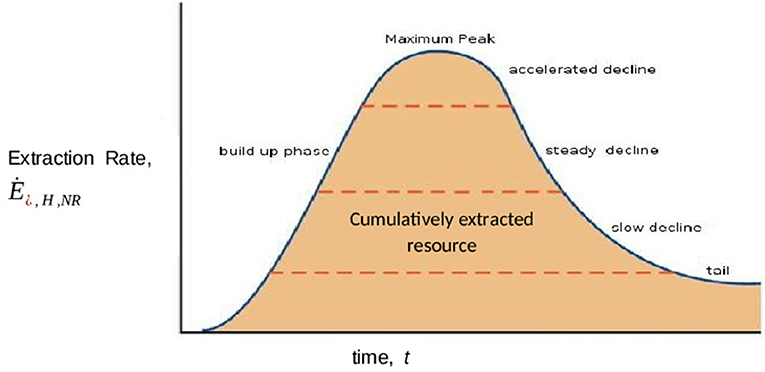
Consider first (Figure 3) a “closed system model”: let us identify the environment O with “planet Earth,” modeled as a closed system (no external material or immaterial inputs), and consider a scenario in which a society H grows in time by mining some materials and tapping some energy out of O's reservoirs: it is convenient to combine both fluxes into a single exergy flux Ė_in,H,NR. Under the additional (albeit irrelevant for our present purposes) assumption of a Hubbertian extraction rate, the interaction of the two systems will evolve as shown in Figure 4: the resources are gradually exhausted, and when the∫Ė_in,H,NR dt reaches the value E_0,NR, the cumulative exergy content of the NR reservoirs in O at the initial time, their extraction necessarily ceases⁸ and the accumulation rate becomes necessarily negative and inevitably leads to the disappearance of H. Clearly, a non-sustainable scenario.

FIGURE 3

Figure 3. The closed-system model of society/environment interaction.

FIGURE 4

Figure 4. Qualitative representation of the time evolution of Ė_in,H in a closed system.

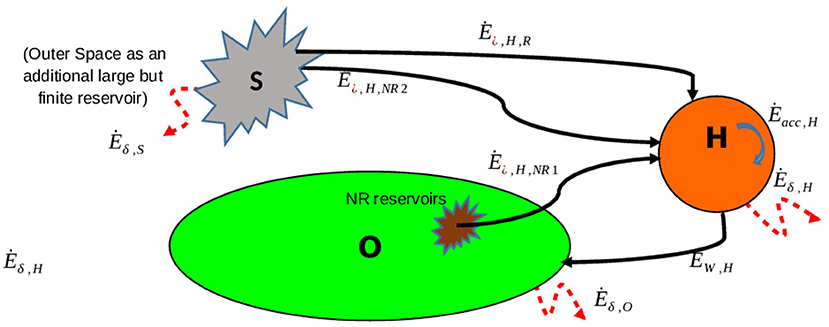
Notice that if we wish to account for space exploration and consider that humanity may be able to exploit resources from an additional series of reservoirs located in other celestial bodies, the above conclusions would still stand, provided one expands the original control volume to include the extra-terrestrial “sources” S (Figure 5). The timescale of the scenario obviously changes, but the long-term outlook remains the same: any “closed system” model negates the possibility of a “thermodynamic sustainable state” for the composite system, unless a steady state is reached for which the accumulation is driven solely by the renewable portion of the incoming resources (Sciubba and Zullo, 2009):

$\begin{array}{ll}{Ė}_{acc,H}={Ė}_{in,H,R}-{Ė}_{W,H}+{Ė}_{\delta ,H}& (1)\end{array}$

Equation 1 is valid under the assumption that the waste flow is sufficiently “small” to be completely buffered by O's internal dynamics.

FIGURE 5

Figure 5. The closed-system model extended to out-of-earth reservoirs.

Open Systems

Things change though if we adopt an open system model (Figure 6) in which O receives a steady influx of (material or immaterial) exergy from outer space and H feeds both on renewable (Ė_in,H,R) and non-renewable (Ė_in,H,NR) resources.

FIGURE 6

Figure 6. The open-system model with accumulation in H (growth).

The exergy budget for the environment O reads:

$\begin{array}{ll}{Ė}_{in}-{Ė}_{out}={Ė}_B-{Ė}_{W,H}+{Ė}_{in,H,R}+{Ė}_{in,H,NR}+{Ė}_{\delta ,O}& (\mathrm{2a})\end{array}$

It is convenient to introduce a subsystem B of O [that we shall call “immediate surroundings” following (Moran and Sciubba, 1994)] that represents the portion of the environment that directly participates to the biodegradation. Its exergy budget is:

$\begin{array}{ll}{Ė}_B+{Ė}_{w,H}={Ė}_{\delta ,B}& (\mathrm{2b})\end{array}$

The societal system H has also its own exergy budget:

$\begin{array}{ll}{Ė}_{in,H}-{Ė}_{w,H}={Ė}_{acc,H}+{Ė}_{\delta ,H}& (\mathrm{2c})\end{array}$

And considering the entire combined system O∪B∪H, the global system budget is:

$\begin{array}{ll}{Ė}_{in}-{Ė}_{out}={Ė}_{\delta ,O}+{Ė}_{\delta ,H}+{Ė}_{\delta ,B}& (\mathrm{2d})\end{array}$

Equation (2a) indicates that in the long run the fossil reservoirs will be exhausted, and therefore in the context of our search for a possible sustainable state the term Ė_in,H,NR ought to be set equal to zero. Equation (2b) reveals that the flux Ė_B denotes a primary exergy “investment” by O to biodegrade (by buffering, dilution and diffusion processes) the effluents of H that cumulatively carry an exergy Ė_w,H. Equation (2c) expresses the “steadiness” condition requiring that the algebraic sum of the exergy flow rates absorbed, discharged, accumulated and destroyed by H be equal to zero at all times, and finally equation (2d) constitutes the global balance for the combined system (O ∪H). Notice that subsystem B has been introduced here for computational convenience only: “immediate surroundings” is an intentionally vague denomination for that part of the biosphere providing the exergy flux for bio-recovery through a complex cascade of processes fed by a portion of the instantaneous difference Ė_in − Ė_out. In our model Ė_B is a “service” provided by O to H (through B) to compensate for the changes that would otherwise be induced by the wastes Ė_w,H on the steady-state of O: biodegradation is an “output” from O and takes up (uses and consumes) some of the external input Ė_in. Not surprisingly, this equation suggests that there is a “primary resource cost” to the growth of a society H.

In spite of the oversimplification embedded in such a model, the meaning of equations (2) is clear: a steady state is indeed possible for H, as long as a sufficient external exergy flow rate is available to the system. This result is in line with previous statements by several Authors (Boltzmann, 1905; Lotka, 1922; Schroedinger, 1945; Boulding, 1966) about life being “maintained by the planet exergy destruction rate”⁹. The above example demonstrates the meaning of “thermodynamic sustainability.” Clearly, such a simplified model falls short of accounting for even the most basic phenomenological evolutionary scenarios (accumulation of exergy in the form of fossil fuels and ores, different timescales for the biodegradation action of the biosphere, etc.).

Thermodynamically Sustainable Growth

Natural systems are complex and display non-linear behavior, because they possess self-regulating mechanisms consisting of a vast web of positive and negative feedback processes that operate concurrently and regulate the carrying, regeneration, and assimilation capacity of the respective systems. As stated above, they are clearly in “non-equilibrium”: how does the model of Figure 6 account for situations in which, for instance, H “grows” in time and is non-homogeneous? To get some insight, let us analyze the term Ė_acc,H that represents the “accumulation” (embodiment) of exergy into H: such an embodiment can be material (mined ores are transformed into artifacts) and/or immaterial (exergy extracted from O is consumed in the production processes). Equation (2c) can be recast in a more useful form by assuming that the biodegradation effort be proportional to the exergy of the waste flows:

$\begin{array}{ll}{Ė}_b=\kappa {Ė}_{w,H}& (3)\end{array}$

Where κ is a (not necessarily linear and not necessarily scalar) function of the respective thermodynamic states of O and H and of the intensity of the waste flux: κ = κ(O, H, Ė_w,H). The balance for H becomes:

$\begin{array}{ll}{Ė}_{acc,H}={Ė}_{in,H}-\frac{{Ė}_b}{\kappa }-{Ė}_{\delta ,H}& (4)\end{array}$

We can now use equations (2d) and (4) to assess the thermodynamic sustainability of the open system (O∪H):

a) A positive rate of accumulation in H is possible if the exergy input rate Ė_in,H from O to H is larger than the sum of the waste exergy discharged by H and of the internal rate of exergy destruction in the society;

b) For a constant Ė_in − Ė_out, the admissible rate of accumulation decreases if the biodegradation service requested of B increases (larger amount of wastes or higher κ, i.e., more polluting wastes);

c) A higher conversion efficiency on the part of H is reflected both in a lower Ė_w,H and a lower Ė_δ,H and results in an increase of the admissible accumulation rate;

d) Combining equation (4) and (2d), we obtain:

$\begin{array}{ll}{Ė}_{acc,H}={Ė}_{in}-{Ė}_{out}-(1+\kappa ){Ė}_{w,H}-{Ė}_{\delta ,O}-{Ė}_{\delta ,H}& (5)\end{array}$

Which sets a global upper limit to the accumulation rate Ė_acc,H.

Equations (2–5) constitute therefore a suitable, and global, model for assessing the thermodynamic sustainability of a human society interacting with an open environment. On this basis it is therefore possible to derive proper global indicators. In fact, the above representation of the composite system O∪H enables analysts to apply standard concepts of exergy analysis and define at least three different forms of “efficiency”: an “intrinsic efficiency” of H is obtained by calculating the ratio of the useful product of all processes enacted within its boundaries (Ė_acc,H) to the total incoming exergy flux Ė_in,H:

$\begin{array}{ll}{\eta }_H=\frac{{Ė}_{acc,H}}{{Ė}_{H,in}}=1-\frac{{Ė}_{w,H}+{Ė}_{\delta ,H}}{{Ė}_{H,in}}& (6)\end{array}$

The reciprocal of η_H, c_H, is an “exergy cost” that measures the exergy rate [in W] needed to produce a unitary rate of accumulation:

$\begin{array}{ll}{c}_H=\frac{{Ė}_{H,in}}{{Ė}_{acc,H}}& (7)\end{array}$

Both η_H and c_H are indeed global EIs, because they neither explicitly nor implicitly relate to “local” conditions around or within H, and relevant, because they provide a quantitative measure of how well H “exploits” the exergy flow it extracts from O. H could increase its accumulation capability either by reducing Ė_δ,H (i.e., improving its internal processes to reduce irreversibility and therefore increase η_H and decrease c_H) or/and Ė_w,H (i.e., reducing the unused portion of Ė_in,H released as waste into O by implementing more effective recycling procedures).

If we consider that the environment uses a portion of its exergy supply (Ė_B) to buffer the waste it receives from H, another measure of efficiency can be defined:

$\begin{array}{ll}{\eta }_{H,extended}=\frac{{Ė}_{acc,H}}{{Ė}_{H,in}+{Ė}_{B,O}}=\frac{{Ė}_{acc,H}}{{Ė}_{H,in}+\kappa {Ė}_{w,H}}& (8)\end{array}$

This appears to be a better efficiency indicator, because it accounts for the gross exergy input into H and includes the “hidden” load placed by H on the environment by forcing some biodegradation action. Its reciprocal, the cost c_H,ext, measures the exergy Watts needed to produce a unitary rate of accumulation including the environmental “service” provided by B:

$\begin{array}{ll}{c}_{H,ext}=\frac{{Ė}_{H,in}+\kappa {Ė}_{w,H}}{{Ė}_{acc,H}}& (9)\end{array}$

From the “combined system” point of view the useful exergy flux available for the accumulation in H is though Ė_in − Ė_out, so that a global system efficiency can be defined:

$\begin{array}{ll}{\eta }_{H\cup O}=\frac{{Ė}_{acc,H}}{{Ė}_{in}-{Ė}_{out}}& (10)\end{array}$

Its reciprocal, the cost c_H∪O, measures the gross exergy Watts needed to produce a unitary rate of accumulation, i.e., a global “production cost”:

$\begin{array}{ll}{c}_{H,ext}=\frac{{Ė}_{in}-{Ė}_{out}}{{Ė}_{acc,H}}& (11)\end{array}$

The above indicators provide a global measure of the ability of H to interact with O and exploit a given portion of the overall available “fuel,” defined as the difference between the incoming (low entropy) exergy flux and the (high entropy) portion re-radiated by O. The cost defined by equation (11) represents the total amount of primary exergy Ė_in − Ė_out needed to “produce” a unit of accumulated exergy Ė_acc,H: this is the “thermodynamic impact” of H's growth on the environment.

The method can be extended to more than one system interacting with O and also easily manipulated to include interactions between several systems H₁, H₂…: notice that the above defined costs are time dependent and can be used to assess the evolution of the interplay between systems and the environment and of the state of the combined system O + H₁ + H₂ etc.

Notice also that a continuously decreasing value of either one of the above efficiency indicators in time (or, which is equivalent, an increase in the costs) signals a situation in which H (or indeed the combined system O∪H) may be on a thermodynamically unsustainable path: in fact, Ė_acc,H = 0 is the limit case of “steadiness” (survival with no growth) and Ė_acc,H < 0 indicates negative growth, an obviously unsustainable condition. In conclusion, both the efficiency indicators and the costs are proper EI.

Exergy Based Indicators

While the above exergy-based description is perfectly suitable to evaluate the primary resources (solar irradiation, water, air and material taken directly from some natural reservoir in the environment surrounding the system), exergy per se is not a proper quantifier for secondary resources, i.e., resources on which some “work” or “action” has been performed by a system to bring them to the state at which they cross the control surface. The correct measure of the “exergy cost” of such pre-treated resources is the total amount of natural resources directly and indirectly expended in their transformation from the “state 0” to the state in which they cross the boundary of the system, measured in units of exergy. This is their embodied exergy content¹⁰. Quite clearly, the identification of the production chains (the direct one and all of the indirect processes that generate the individual externally manufactured inputs) and the definition of the limits for the indirect exergy supply (i.e., the proper identification of the relevant control volume) are crucial issues in such an approach.

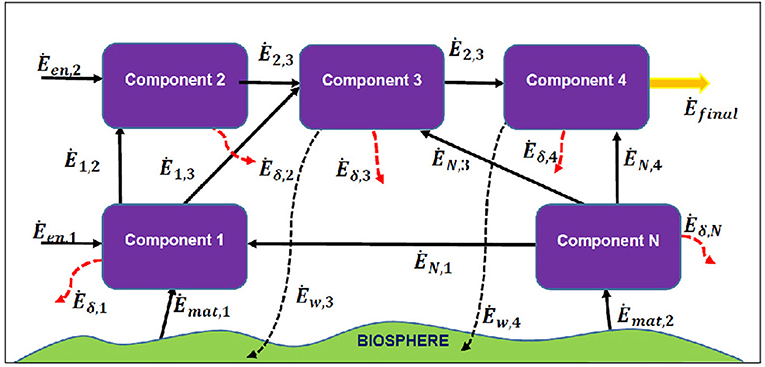
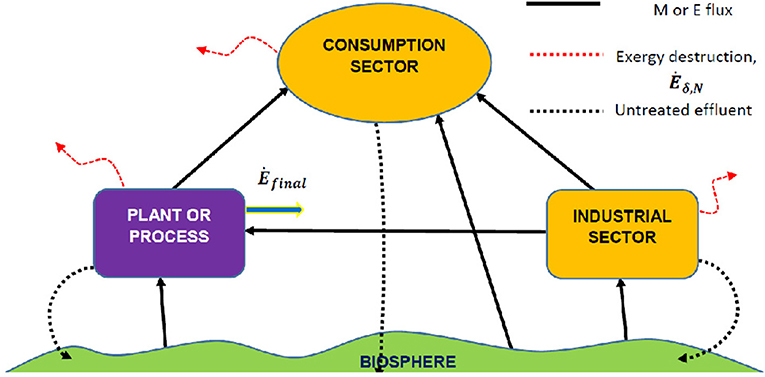
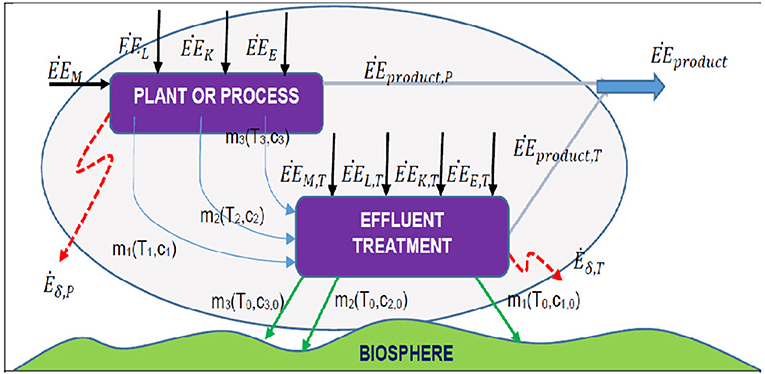
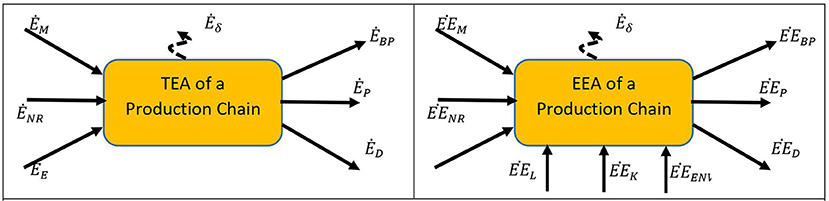
The embodied exergy content of a product or service can be calculated following, for instance, the Cumulative Exergy Content CExC (Szargut et al., 1988), the Thermo-Ecological (or Exergo-Ecological) Cost TEC (Szargut, 1995, 1999, 2005) or the Extended Exergy EEA (Sciubba, 1998, 2001; Colombo et al., 2013) methods. All three methods maintain that any external intervention that adds or subtracts exergy from a stream before it crosses the control surface can be accounted for in terms of expended primary exergy. Since the terms in the balance equations (2) through (5) are completely quantifiable and homogeneous, the expenditures related to these external interventions can be algebraically added. The most popular methods used to derive exergy-based EIs, namely, the CExC, the TEA and the EEA, are presented and compared in the following sections, with the purpose of illustrating the difference between their respective EIs and to assess their commensurability (i.e., the existence of a procedure to convert one into the other). The three procedures are examined separately, with reference to the respective “control volumes” depicted in Figure 7 (CExC), Figure 8 (TEA) and Figure 9 (EEA)¹¹.

FIGURE 7

Figure 7. The control volume for a Cumulative Exergy Consumption (CExC) analysis.

FIGURE 8

Figure 8. The control volume for a Thermo-Ecological (TEA) analysis.

FIGURE 9

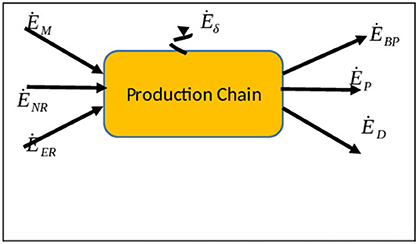
Figure 9. For the calculation of the thermo-ecological exergy cost tec. Ė_M, exergy rate of materials; Ė_NR, exergy rate of non-renewables; Ė_R, exergy rate of renewable energy carriers; Ė_D, exergy rate of effluents; Ė_P, exergy rate of main product; Ė_BP, exergy rate of by-products; Ė_δ, exergy destruction rate.

The Cumulative Exergy Consumption

This method was introduced by Szargut (1967) and perfected in later works by his group (Szargut et al., 1988; Szargut, 1999). It consists in the analysis of the complete line of production of a material good from raw materials to the final product: the corresponding control volume is shown in Figure 7. The rationale of CExC is that the exergy expenditure necessary to produce a material commodity (i.e., the exergy embodied in it) is equal to the sum of all exergy contributions along the production line. The assumptions are as follows:

a) All raw materials entering the control volume directly from the Environment possess a “raw exergy” equal to their reference exergy (Valero et al., 1986);

b) Materials that enter the control volume after having undergone a pre-treatment are attributed an exergy content equal to their raw value plus all of the exergy expenditures necessary for the pretreatment;

c) At each generic i-th production step, a portion of the incoming exergy flow is rejected to the environment in the form of “byproducts”: these flows, be they discharges, scrap material, or rejected energy that may be in principle recycled in different production lines, are collectively denominated Ė_w,i;

d) The incoming exergy flows include both renewable and non-renewable sources;

e) The exergy outflow from production step i to production step i + 1 is considered a “product” of step i and a “fuel” for step i + 1: Ė_out,i = Ė_in,i+1: since the sum of the inputs into component i (Ė_in,i) is in turn the “fuel” for its “product” Ė_out,i, and ${Ė}_{out,i}={Ė}_{in,i}-{Ė}_{w,i}-{\stackrel{.}{E}}_{\delta ,i}$, a “cumulative exergy cost” for the final (N-th) product of a technological production line can be defined as:

$\begin{array}{l}cex{c}_N=\frac{{\stackrel{.}{{\displaystyle \sum }E}}_{in,j}}{{Ė}_N}\\ =\frac{{Ė}_{in,total}}{\left[{Ė}_{in,1}-{\displaystyle {\sum }_1^N}{Ė}_{w,i}-f\left({\displaystyle {\sum }_1^N}{Ė}_{\delta ,i}\right)\right]}>1\left[J/J\right]& (12)\end{array}$

Where the function $f\left({\sum }_1^N{Ė}_{\delta ,i}\right)$, a process structure function, is used instead of the simple ${\sum }_1^N{Ė}_{\delta ,i}$to account for non-linear production chains (in the presence of a loop in the process flow diagram, the exergy destructions cannot be simply added, because of feedback effects).

The above definitions imply that if a product is generated starting from the very same raw materials by two different technological lines having different amounts of irreversible losses, its cexc assumes two different values. Thus, the cexc is a genuine measure of the environmental load posed on the primary resources available in the environment, and therefore a proper EI.

If M_X kg/yr of a (material or immaterial) commodity with a specific exergy e_X [J/kg] are generated per unit time, the total $CEx{C}_{X}isequaltocex{c}^{*}{M}_X^{*}{ex}_{X.}$ [J_{primaryexergyresources}/yr]. In the case of multiple products, proper allocation rules are suggested by Szargut (2005). The CExC does not contain any reference to the monetary circuit of the society in which the plant is located and is thus a purely technological EI. Since though neither the exergy destruction nor the exergy of the discharges are good indicators of environmental damage, the CExC must be regarded only as an indicator of the degree of resource exploitation.

The Thermo-Ecological Cost Analysis

Szargut later introduced (Szargut, 1995, 1999; Szargut et al., 2002) the Thermo-Ecological Analysis, TEA, to include in the CExC the environmental externality: the relevant control volume is shown in Figures 7, 8. The thermo-ecological cost tec (Szargut used the symbol ξ) is defined (Thermo-Ecological Portal, 2020) as “the cumulative consumption of non-renewable exergy connected with the fabrication of a particular product with inclusion of additional consumption resulting from the necessity of compensation of environmental losses caused by rejection of harmful substances to the environment.” Obviously, the analysis must be conducted in a life-time sense.

The thermoecological cost tec is calculated as a ratio of exergy flows, and constitutes a measure of the primary non-renewable exergy directly or indirectly consumed in the production line under analysis. It can be determined by solving a set of thermoecological cost balance equations. With reference to Figure 8, the rationale behind the calculation of the tec is the following:

a) The non-renewable exergy input is a net resource consumption (extracting ores and fossil fuels has a negative effect on O);

b) The processing of a material input and the generation of “secondary” energy carriers are affected by two sources of potential environmental damage: the exergy spent in the extraction and in the preparation of finished and semi-finished materials (i.e., their CExC, which includes the primary exergy consumed in the production line and has a negative effect on O), and the emissions generated in their preparation (direct negative effect on O);

c) The effluents may cause potential damage because of thermal- or chemical pollution on O (direct negative effect on O);

d) The by-products and the main product share the TEC according to exergy-based allocation rules (Serra and Torres, 2003).

Once the mass- and energy balances of the process have been calculated, its exergy flow diagram can be constructed (in a way similar to that of CExC) to identify the non-renewable portion of the TEC of the material- and energy flows Ė_M and Ė_NR. The “environmental damage” portion of the TEC for each flow is computed by means of the so-called monetary indices of harmful impact (Szargut, 2005)¹²:

$\begin{array}{ll}{\zeta }_k=\frac{E_{tot,NR}{w}_k}{GD{P}_D+{\displaystyle {\sum }_k}{P}_k{w}_k}& (14)\end{array}$

Where E_tot,NR [J] is the annual exergy consumption of non-renewable natural resources, w_k [€/J] is a monetary coefficient of ecological damage per exergy unit of the k-th effluent, GDP_D [€] is the Gross Cumulative Product of the Domestic sector in the region where the process is located and P_k [J] the annual production of the k-th effluent rejected to the environment in the geographical domain of interest [for a detailed discussion, see the Thermoecological Portal (Thermo-Ecological Portal, 2020)]. The tec measures the average cost in terms of primary exergy caused by the direct and indirect “environmental damage” caused by each technological chain in the country where it is located. For example, for a process whose only relevant emission is CO₂, the total cost (CExC+TEC) for M_X kg/yr of the X commodity becomes

$\begin{array}{l}M(cexc*e{x}_X+te{c}_{S,CO2})=\frac{{Ė}_{in,1,S}}{\left[{Ė}_{in,1,S}-{\displaystyle {\sum }_1^N}{Ė}_{w,i,S}-f_S\left({\displaystyle {\sum }_1^N}{Ė}_{\delta ,i}\right)\right]}\\ +{\displaystyle \sum _k}{\zeta }_{k,S}& (15)\end{array}$

A TEC analysis is more involved than a CExC one: additional, strongly disaggregated data are needed to calculate the total consumption of the Domestic sector, the total emission of each pollutant in the country, and the monetary index of harmfulness of each pollutant σ_j needed for the calculation of the w_j in equation (14). In his original formulation, Szargut adopted the regulated pollutant taxation values, but he also maintained that a more rational value for σ may be obtained by an iterative application of the TEC method.

The TEC has been criticized on two accounts: first, its calculation is perforce based on an extremely disaggregated and not easily accessible database; second, the definition of the index of harmful impact depends explicitly on the GDP_D, which is known to be poorly correlated to the monetary circulation in a society (Meadows and Randers, 1992; Mebratu, 1998; Mudacumura et al., 2005; Martínez-Alier et al., 2010). A third objection, raised here for the first time, is that a low tec is no guarantee of sustainability: even if the non-renewable resources used in a production process were completely substituted by non-renewable ones, the society as a whole might have a cumulative resource consumption rate Ė_in,H higher than that available in the Environment (see equation 5).

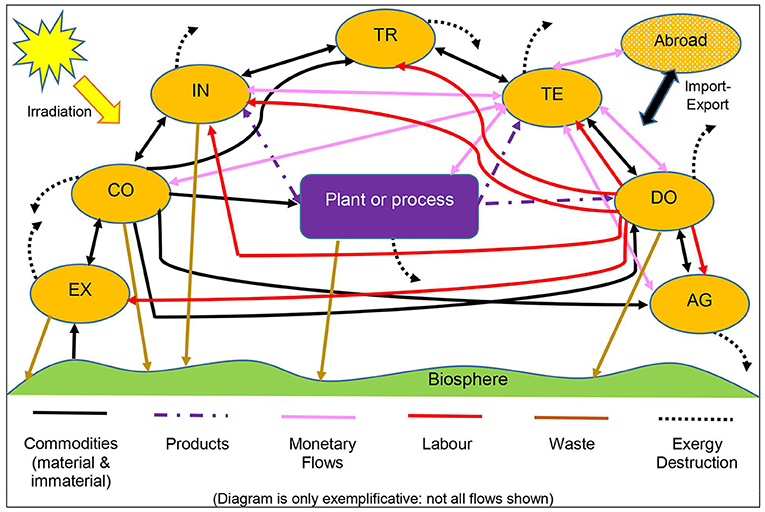
The Extended Exergy Accounting Method

The EEA method (Sciubba, 1998, 2001, 2021) is for all purposes an extension of the CExC. Its fundamental axiom is that the three Externalities (Labor, Capital and Environmental Cost) can be assigned “equivalent exergy values,” under a set of assumptions derived from an exergy budget of the region in which the process is located. With reference to Figure 10, the assumptions are:

a) The exergy “inflow” consists of both renewable and non-renewable physical streams into H and of the “imported” material and immaterial exergy flows from other regions;

b) A specific “extended exergy” [J/kg or J/unit] is defined as the equivalent exergy of each production factor: ee_energy = e_energy + ee_{externalities}; ee_material = e_material + ee_{externalities}. In practice, the cexc plus the externality “costs”;

c) A portion of the total exergy influx Ė_in,H is “used” to sustain the population (included in its totality in the Domestic sector). This portion is called extended exergy of Labor, ${\stackrel{.}{EE}}_L$, and is set equal to αĖ_in, α < 1 being an econometric coefficient external to the theory that must be derived from the global exergy budget of the Country (Sciubba, 2011);

d) The monetary circulation in the Country, M_e, is converted into another extended exergy flux, the Extended Exergy of Capital, ${\stackrel{.}{EE}}_K=\beta {\stackrel{.}{EE}}_L=\alpha \beta {Ė}_{in}$. The econometric coefficient β is also external to theory and must be calculated on the basis of financial/monetary data relevant to the Country under examination (Sciubba, 2011; Colombo et al., 2013; Biondi and Sciubba, 2021). Using statistical labor and monetary data, it is possible to calculate the specific extended exergy of Labor ee_L [J/workhour] and of Capital ee_K [J/€]. These quantities represent the amount of primary exergy resources needed to generate 1 workhour and 1 monetary unit, respectively;

e) All EE forms are homogeneous and enjoy the additive property. Being “costs,” they also admit of a conservation equation (cost balance).

FIGURE 10

Figure 10. The control volume for an Extended Exergy Accounting (EEA) analysis.

EEA can be applied equally well to individual production lines, but its natural targets are very large complex systems like Cities, Industrial districts and Countries, where both the CExC and the TEC may run into congruency problems. In the case of a Country, the region in which the process is located is subdivided (Figure 10) in 7 Sectors: Domestic (DO), Extractive (EX), Conversion (CO), Industrial (IN), Transportation (TR), Tertiary (TE) and Agricultural (AG). Each Sector exchanges fluxes of extended exergy with other sectors, with the environment and/or with another system called “Abroad” that accounts for the import/export. Every single process S exchanges extended exergy fluxes with some of the sectors; in particular, ${\stackrel{.}{EE}}_L$ is assumed to be originated only in DO, and ${\stackrel{.}{EE}}_K$ in TE. Imported commodities are handled through TE.

Once the above quantities are known, a balance for the EE_j of each individual production line is performed, resulting in a specific extended exergy cost, ee_c [J_{primaryexergy}/unit] that reflects the total amount of primary exergy resources consumed for the production of 1 unit of product X.

To calculate the Environmental externality, EEA adopts a remediation approach (Figure 11): to eliminate (or maintain within the regulated limits) the emission of m_k [kg/s] of pollutant k, a (fictitious or real) process is inserted downstream of S that uses additional primary exergy to reduce the concentration c_k to its limit value (c_k0 or c_k,regulated) before discharging the exhaust into the environment. This additional consumption (per unit of product of S) consists of materials $({\stackrel{.}{E}E}_M)$, energy (${\stackrel{.}{EE}}_E$), labor (${\stackrel{.}{EE}}_L$) and capital (${\stackrel{.}{EE}}_K$): the normalized sum of these quantities, denominated ee_ENV, is added to the ee_c.

FIGURE 11

Figure 11. Illustrative sketch of the procedure for the calculation of EE_env in EEA. ${\stackrel{.}{EE}}_{product}={\stackrel{.}{EE}}_{product,P}\pm {\stackrel{.}{EE}}_{product,T}+{\stackrel{.}{EE}}_{M,T}+{\stackrel{.}{EE}}_{E,T}+{\stackrel{.}{EE}}_{L,T}+{\stackrel{.}{EE}}_{K,T}$.

The calculation of the ee_c requires a similar data mining effort as the TEC: highly disaggregated data are needed for each Sector, for the technologically feasible effluent treatment processes and for the econometric coefficients α and β. Procedures to calculate the latter in terms of monetary and statistical employment data are reported in (Estervåg, 2003; Dewulf et al., 2008; Seçkin et al., 2012; Colombo et al., 2013; Dai et al., 2014; Biondi and Sciubba, 2021).

Comparison Between TEA and EEA

Both the tec and the eec are genuine resource consumption quantifiers, since both express a measure of the “environmental load” placed on system O by activities originating in H. They are obviously correlated (a production line with a minimal tec is likely to also have a minimal eec), and thus it is interesting to investigate whether the correlation admits of a mathematical expression.

For the sake of comparison, consider a process that produces N units/(unit time) of a commodity and emits m kg of CO₂ per unit. Let us also assume that the product exergy e_P, the exergy of the discharges e_D, the amount of non-renewables Ė_NR and the exergy destruction rates are known. The ee_c is:

$\begin{array}{l}e{e}_{c,X}=[{ee}_{M}N+e{e}_E{Ė}_X+e{e}_L{Ẇ}_X+e{e}_K{\stackrel{.}{K}}_X\\ +e{e}_{ENV}{ṁ}_{X,N,CO2}]/N\left[J/unit\right]& (16)\end{array}$

In the case of multiple products, proper allocation rules are suggested in (Sciubba, 2001; Colombo et al., 2013): they are formally the same as those adopted in TEC, but the structure of equation (16) allows for a more disaggregated account for the individual contributions (Labor, Capital and Environmental Remediation Cost), thus making the allocation easier. A perusal of equations (15, 16) suggests that the numerical values emerging from the calculation of the cexc+tec and ee_c are incommensurable, which is confirmed by a simple virtual experiment. Consider the reasonably realistic “sustainable” scenario described below:

i) Each single component of the process (or society) is optimized and is affected by the minimum attainable degree of irreversibility: $\left({\sum }_1^N{Ė}_{\delta ,i}\right)=min$; the sum of the exergy destructions extended to all components (or sectors) is the smallest one possible with the current technological level;

ii) The configuration (connectivity) of each conversion process is optimized so that the propagation of irreversibility from one component to the other is also minimized: $f_s\left({\sum }_1^N{Ė}_{\delta ,i}\right)=min$;

iii) Each effluent k-including all of the rejected flows Ė_w,1,S- is conveyed to a treatment plant that reduces its temperature to T₀ + ε and its concentration to c_0,k + Δc_kb, ε being a small quantity (say, 1-2K), c_0k the standard concentration of k in the environment and Δc_kb the buffering capacity of the environment for k.

Under the above scenario, equation (15) simplifies to:

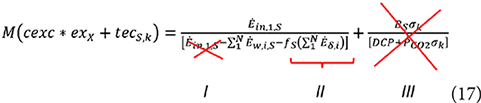
Because term I is completely offset by the environmental buffering (that requires only renewable resources), term II is minimal (assumption ii) and term III is zero because no non-renewable resources are used to reduce the potential ecological damage. Thus, the cumulative exergy consumption attains its minimum value.

Equation (16) becomes:

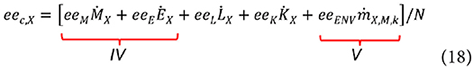
Here, both IV and V reach their minima, the former because irreversibility is minimized within the system and the latter because the posited assumptions minimize ee_ENV. Of consequence, the extended exergy cost only attains its minimum value if the Capital and Labor terms are minimized as well. Even in such a case though, because of the inclusion in ee_c of the equivalent primary exergy consumption of Labor and Capital production factors, the two minima (tec_min and eec_min) cannot be transformed one into the other by a rational formula: in fact, they not only differ numerically, but cannot be consistently rescaled, because:

A – The RHS of equation (18) contains terms (${\stackrel{.}{EE}}_{L,X}$ and ${\stackrel{.}{EE}}_{K,X}$) that are not included in equation (17);

B – The calculation of the environmental externality is performed according to two completely different criteria. Figure 12 illustrates the different types of “flows” considered by the two methods.

FIGURE 12

Figure 12. For the comparison of the tec with the eec.

The Exergy Footprint

In light of the above considerations, we can now introduce a novel indicator, the Exergy Footprint ExF, defined (Sciubba, 2012) as the amount of primary exergy (in J) globally consumed over the life of a commodity, including material, energy, labor, capital and environmental remediation costs and calculated on a life-time basis.

The ExF is the integral in time of the eec, and it is clear that the Second Law places a lower limit to its numerical value: even if we could adopt a “perfect recycling,” some external exergy source would be necessary to sustain the process and compensate for the exergy destruction. We recover here the idea that thermodynamic sustainability (eec = 1 when calculated for the whole Society) is impossible: therefore it would be more proper to speak of a “degree of unsustainability,” ξ = (eec-1)/eec.

The ExF provides useful -and unique- information at several levels:

a) If two different technological chains produce a (material or immaterial) commodity X, the one with the lower ExF is less unsustainable;

b) Since the environmental remediation cost is included in the calculation, “cleaner” technologies have -ceteris paribus- a lower Ex;

c) If a process modification is considered that changes the “energy mix” of the input or of the output (for instance replacing an electrical boiler with a fossil-fueled one or vice versa), the ExF automatically accounts for the different “quality” of the input or output. The same is true for material substitution: if one or more material inputs are substituted with others having a different cexc and a different eec, this is automatically reflected in the Ex;

d) At a more aggregated level, the Ex can be used to assess the degree of unsustainability of different infrastructures. For example, between two planned road paths, or between a bridge over a river vs. a tunnel, or between two different sites for an airport, etc.;

e) At an even more aggregated level, the Ex can provide unique information about the different degree of unsustainability of different societal policies, like what energy mix to adopt, whether or not to promote specific energy conversion systems or agricultural productions, whether to import materials or finite goods from other countries or produce them inland, etc.

Conclusions

The current concept of “sustainability,” though almost acritically accepted by media and decision makers, is far too vague to be amenable to practical and meaningful scientific use. In a thermodynamic sense, a closed system is never sustainable (unless it is at equilibrium, i.e., “dead”), and an open one may be sustainable or not depending on whether the exergy input rate is higher (or not) than the sum of the exergy destruction and accumulation rates within the system, augmented by the exergy expenditure required by the environment to buffer the effect of the effluents. It is therefore important to realize that there are two facets to a “sustainable development”: the first is of thermodynamic nature, governed by the relevant system equations described in this paper, and the second described by socio-economical indices, whose interpretation is outside of the bounds of Thermodynamics. As for the former, it is convenient to adopt exergy as a general quantifier, because it not only attributes a thermodynamically correct value to any type of flux, but also directly relates irreversibility to unsustainability: reversible processes are intrinsically sustainable (too bad there is none known in the Universe!).

It is rather clear that the socio-economical interpretation must be supported by the thermodynamic one, in the sense that if a system “uses” the incoming exergy flow in a way that leads to a total net depletion rate of (fossil or renewable) exergy sources, no societal organizational form can survive in the long run unless new exergy inputs are provided at a sufficient rate. It is true that the specific form of the societal organization may affect -ceteris paribus- the exergy depletion rate, but this does not imply that such a “minimum exergy consumption” society may be acceptable from an ethical point of view: this decision implies a value choice and is outside of the realm of Thermodynamics. Studies that do not separate these two issues are therefore bound to reach wrong and misleading conclusions.

Indicators of the “resource efficiency” of a system (be it a production line, a natural species, a human settlement, an entire nation) can be defined only in the thermodynamic system logic and at the largest system physical scale: they are termed here “global.” It is important to realize that “local” indicators are completely legitimate, but since they are by definition concerned either with a set that generally includes non-thermodynamically relevant quantities or with a limited subset of the state variables of the system, they cannot be taken as genuine indicators of the degree of sustainability as formulated above.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^One of the Reviewers correctly remarked that secondary fuels (biomass) is in fact a “high entropy” resource, but that its use brings advantages in terms of the Environmental Externality. A more correct classification would refer to such resources as “low Extended Exergy” fuels (see section The Extended Exergy Accounting Method below).

2. ^A related issue, not specifically addressed in this study, is that of re-evaluating on a Thermodynamic basis some of the local indicators adopted in biological, social and ethnological sciences. Such EIs t are usually based on a “numerosity” index of a selected population (the indicator species) and on its time evolution in the environmental niche of observation. For a more detailed discussion (Sciubba, 2013).

3. ^Popper's falsificationist methodology (Popper, 1979) holds that scientific theories are characterized by entailing predictions that future observations might reveal to be false. But to be falsified, a theory must be complete (it must contain an exact definition of its domain of application and of the relevant boundary conditions) and consequential (all of its predictions can be derived by some fundamental axioms by a procedure devoid of arbitrariness).

4. ^A paradigmatic example is the longstanding debate between advocates of a strong population control and supporters of a “prosperous way down” (see Galor and Moav, 2001; Sciubba and Zullo, 2009; Martínez-Alier et al., 2010) for a detailed analysis of the issue). Both approaches address the same problem (resource exhaustion), but the proposed solutions diverge rather radically and are in fact incommensurable, since they are based on completely different premises that involve value judgements.

5. ^We include in this “thermodynamic basis” also the biological, biophysical and environmental sciences at large.

6. ^In the context of this paper, exergy is the minimum amount of adiabatic work necessary to bring a system from an initial state S₀ of equilibrium with the environment to an arbitrary final state S₁ by means of processes that involve solely S and the environment. For a complete and rigorous treament of the topic (see Moran, 1982; Kotas, 1985).

7. ^The specific exergy of materials (see for example Szargut, 2005).

8. ^This is the well-known “Hubbert scenario”, currently known to represent an oversimplification of the actual resource exploitation curve. Among other weaknesses, it neglects changes in the extraction/refining technology and in the final demand. It is used here only to exemplify what would be the long-term situation of a “fossils only” society. A more rigorous analysis is presented in Sciubba and Zullo (2009).

9. ^Boltzmann (“…The general struggle for existence of animal beings is therefore not a struggle for raw materials – these, for organisms, are air, water and soil, all abundantly available– nor for energy, which exists in plenty in any body in the form of heat, but a struggle for entropy,” Boltzmann, 1905) and Schroedinger (“What an organism feeds upon is negative entropy,” Schroedinger, 1945) expressed the same principle in terms of entropy production, which is equivalent to exergy destruction. Lotka (1922) used the expression “consumption of available energy”.

10. ^The concept of “embodied exergy” was first proposed by Yantovsky (1994).

11. ^CexC, TEC and EEA owe a significant portion of their theoretical foundation to Thermo-Economics, a method originated in Eastern Germany in the late ‘50es (Rant, 1956; Elsner and Fratzscher, 1959; Bosnjakovic, 1965; Fratzscher, 1965), reframed in a monetary context in the US by Tribus, El-Sayed and Evans in the 70'es (El-Sayed and Gaggioli, 1989; El Sayed, 2003) and reformulated in its current form by Tsatsaronis (1984) and Valero (Valero et al., 1986; Serra and Torres, 2003) in the 80'es. The original TE paradigm adopts a monetary measure in its cost definition, the TEC -using the very same formalism- introduces a purely exergy cost similar to those described in section 4 above. The CExC avoids any reference to monetary units, and the EEA is an extension of the CExC (see below, section The Extended Exergy Accounting Method) that makes use of the TE cost allocation rules.

12. ^Notice that the calculation scheme presented in the Thermo-Ecological Portal (2020) is slightly different from, and probably not as rigorous as, the one originally proposed by Szargut (2005): here, equation (14) is taken from the original formulation, while the first part (the extended balance that includes the non-renewables) is adapted from the Thermoecological portal.

References

Biondi, A., and Sciubba, E. (2021). Extended Exergy Analysis (EEA) of Italy, 2013-2017. Energies 14:2767. doi: 10.3390/en14102767

CrossRef Full Text | Google Scholar

Boltzmann, L. (1905). The Second Law of Thermodynamics (Theoretical Physics and Philosophical Problems). New York, NY: Springer-Verlag. doi: 10.1007/978-94-010-2091-6_2

CrossRef Full Text | Google Scholar

Bosnjakovic, F. (1965). Die Bewertung Wärmetechnischer Prozesse mit Hilfe der Exergie, in Energie und Exergie. VDI-Fachgruppe: Die Anwendung des Exergiebegriffs in der Energietechnik.

Boulding, K. (1966). The Economics of the Coming Spaceship Earth, Proc. VI “Resources for the Future” Forum on Environmental Quality in a Growing Economy. Washington DC.

Google Scholar

Club of Rome (1972). Limits to Growth. Washington, DC.

Google Scholar

Colombo, E., Rocco, M., and Sciubba, E. (2013). Advances in exergy analysis. A novel assessment of the extended exergy accounting method. Appl. Enviro. 113, 1405–1420. doi: 10.1016/j.apenergy.2013.08.080

CrossRef Full Text | Google Scholar

Costanza, R., d'Arge, R., de Groot, R., Farber, S., Grasso, M., Hannon, B., et al. (1997). The value of the world's ecosystem services and natural capital. Nature 387, 253–260. doi: 10.1038/387253a0

CrossRef Full Text | Google Scholar

Dai, J., Chen, B., and Sciubba, E. (2014). Ecological accounting for China based on Extended Exergy - A sustainability perspective. Renew. Sustain. En. Rev. 37, 334–347. doi: 10.1016/j.rser.2014.05.022

CrossRef Full Text | Google Scholar

Dale, V. H., and Beyeler, S. C. (2001). Challenges in the development and use of ecological indicators. Ecol. Ind. 1:6. doi: 10.1016/S1470-160X(01)00003-6

CrossRef Full Text | Google Scholar

Daly, H. (1977). Steady-State Economics. Washington, DC: Freeman pub.

Google Scholar

Daly, H. (1996). Beyond Growth. The Economics of Sustainable Development. Boston, MA: Beacon Press.

Google Scholar

Demirel, Y. (2007). Nonequilibrium Thermodynamics, 2nd Edn. Amsterdam: Elsevier. doi: 10.1016/B978-044453079-0/50016-X

CrossRef Full Text | Google Scholar

Dewulf, J., Langenhove, H., Muys, B., Bruers, S., Bakshi, B. R., Grubb, G. F., et al. (2008). Exergy its potential and limitations. Environ. Sci. Technol. 42, 2221–2232. doi: 10.1021/es071719a

PubMed Abstract | CrossRef Full Text | Google Scholar

El Sayed, Y. M. (2003). The Thermo-Economics of Energy Conversion. Oxford: Elsevier.

Google Scholar

El-Sayed, Y. M., and Gaggioli, R. A. (1989). A critical review of second law costing methods part I and II. J. Energy Res. Technol. 111, 1–15. doi: 10.1115/1.3231402

CrossRef Full Text | Google Scholar

Elsner, N., and Fratzscher, W. (1959). Die Bedeutung der Exergieflussbilder fur die Untersuchung Waermetechnischer Anlagen. Energietechn 7, 68–74.

EPA, Environmental Protection Agency. (2008). Report on the Environment. Washington, DC.

Google Scholar

Estervåg (2003). Energy, exergy, and extended-exergy analysis of the Norwegian society. Energy 30, 649–675. doi: 10.1016/j.energy.2004.05.025

CrossRef Full Text | Google Scholar

Fratzscher, W. (1965). Die Bedeutung der Exergie für die Energiewirtschaft. Wiss. Zeitsch. der Techn. Hochs. Chemie Leuna-Merseburg 7, 81–87.

Galor, O., and Moav, O. (2001). Evolution and growth. Eur. Econ. Rev. 45, 718–729. doi: 10.1016/S0014-2921(01)00112-X

CrossRef Full Text | Google Scholar

Gong, M., and Wall, G. (2001). On exergy and sustainable development-Part 2. Indicators and methods. Exergy Int. J. 1, 217–233. doi: 10.1016/S1164-0235(01)00030-9

CrossRef Full Text | Google Scholar

Jackson, L. E., Kurtz, J. C., and Fisher, W. S. (2000). Evaluation Guidelines for Ecological Indicators, EPA/620/R-99/005.

Google Scholar

Kotas, T. (1985). The Exergy Method of Thermal Plant Analysis, Butterworths. London: Academic Press.

Lebon, G., and Jou, D. (2008). Understanding Non-Equilibrium Thermodynamics. Foundations, Applications, Frontiers. Heidelberg: Springer Verlag. doi: 10.1007/978-3-540-74252-4

CrossRef Full Text | Google Scholar

Lotka, A. J. (1922). Contribution to the energetics of evolution. Proc. Natl. Acad. Sci. U.S.A. 8, 147–151. doi: 10.1073/pnas.8.6.147

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez-Alier, J., Unai, P., Franck-Dominique, V., and Zaccai, E. (2010). Sustainable de-growth. Mapping the context, criticisms and future prospects of an emergent paradigm. Ecol. Econ. 69, 1741–1747. doi: 10.1016/j.ecolecon.2010.04.017

CrossRef Full Text | Google Scholar

Meadows, D., and Randers, J. (1992). Beyond the Limits. London: Earthscan Pub.

Google Scholar

Mebratu, D. (1998). Sustainability and sustainable development historical and conceptual review. Env. Impact Asses. Rev. 18, 493–520. doi: 10.1016/S0195-9255(98)00019-5

CrossRef Full Text | Google Scholar

Moran, M. J., and Sciubba, E. (1994). Exergy analysis-principles and practice. JERT 116:1994. doi: 10.1115/1.2906818

CrossRef Full Text | Google Scholar

Moran, M. J. (1982). Availability Analysis. A Guide to Efficient Energy Use. London: Prentice-Hall.

Google Scholar

Mudacumura, G. M., Mebratu, D., and Shamsul Haque, M. (2005). Sustainable Development Policy and Administration. Boca Raton, FL: CRC press.

Google Scholar

Paul, B. D. (1998). A history of the concept of sustainable development: literature review. Ann. Univ. Oradea Fasc. 17.

Google Scholar

Popper, K. (1979). The Two Fundamental Problems of the Theory of Knowledge [Manuscript (1933) Published in German (1979). T. Eggers Hansen (ed.)]. English translation (2009). London; New York, NY: Routledge Pub.

Google Scholar

Purvis, B., Mao, Y., and Robinson, D. (2019). Three pillars of sustainability in search of conceptual origins. Sustain. Sci. 14, 681–695. doi: 10.1007/s11625-018-0627-5

CrossRef Full Text | Google Scholar

Rant, Z. (1956). Exergie, ein neues Wort für technische Arbeitsfähigkeit. Forsch. Ing. Wesens 22, 36–37.

Google Scholar

Schroedinger, E. (1945). What Is Life? The Physical Aspect of the Living Cell. New York, NY: Macmillan Pub.

Sciubba, E. (1998). “A novel exergetic costing method for determining the optimal allocation of scarce resources,” in Proc. CPOTE 1998, Contemporary Problems in Thermal Engineering, A. Ziebik ed, Gliwice (Poland), 311–324.

Sciubba, E. (2001). Beyond thermoeconomics? The concept of extended exergy accounting and its application to the analysis and design of thermal systems. IJE 1, 68–84. doi: 10.1016/S1164-0235(01)00012-7

CrossRef Full Text | Google Scholar

Sciubba, E. (2011). A revised calculation of the econometric factors α and β for the extended exergy accounting method. Ecol. Mod. 222, 1060–1066. doi: 10.1016/j.ecolmodel.2010.11.003

CrossRef Full Text | Google Scholar

Sciubba, E. (2012). An exergy based Ecological Indicator as a measure of our resource use footprint. Int. J. Exergy 10, 239–266. doi: 10.1504/IJEX.2012.046811

CrossRef Full Text | Google Scholar

Sciubba, E. (2013). Can an environmental indicator valid both at the local and global scales be derived on a thermodynamic basis? Ecol. Indicat. 29, 125–137. doi: 10.1016/j.ecolind.2012.12.008

CrossRef Full Text | Google Scholar

Sciubba, E. (2021). Exergy as a thermodynamic measure of the degree of (un)sustainability of a human society. Energy Rep. 5, 62–69. doi: 10.1016/j.egyr.2018.12.001

CrossRef Full Text

Sciubba, E., and Zullo, F. (2009). Exergy-based population dynamics a thermodynamic view of the 'sustainability' concept. J. Ind. Ecol. 15, 172–184. doi: 10.1111/j.1530-9290.2010.00309.x

CrossRef Full Text | Google Scholar

Seçkin, C., Sciubba, E., and Bayulken, A. R. (2012). An application of the Extended Exergy Accounting method to the Turkish Society, year (2006). Energy 40, 151–163. doi: 10.1016/j.energy.2012.02.018

CrossRef Full Text | Google Scholar

Serra, L., and Torres, C. (2003). Structural Theory of Thermoeconomics, Enc. Of Life-Support Sciences. London: EOLSS Pub.

Google Scholar

Szargut, J. (1967). Towards a rational evaluation of steam prices. Gospodarka Cieplna 5, 104–106.

Google Scholar

Szargut, J. (1995). Exergy and Ecology, Proc. IV W. shop on Second Law Analysis of Energy Systems, M. Moran & E. Sciubba Eds. Roma.

Google Scholar

Szargut, J. (1999). Depletion of Unrestorable Natural Exergy Resources as aMeasure of the Ecological Cost, Proc. ECOS'99, Ishida M, Kataoka H, Moran MJ, G. Tsatsaronis Eds (Tokyo).

Szargut, J. (2005). The Exergy Method. Technical and Ecological Applications. Southhampton: WIT press.

Szargut, J., Morris, D. R., and Steward, F. R. (1988). Exergy Analysis of Thermal, Chemical, Metallurgical Processes. New York, NY: Hemispere Pub.

Szargut, J., Ziebik, A., and Stanek, W. (2002). Depletion of the unrestorable natural exergy resources as a measure of the ecological cost. Energy Conver. Manage. 42, 1149–1163. doi: 10.1016/S0196-8904(02)00005-5

CrossRef Full Text | Google Scholar

Thermo-Ecological Portal (2020). Available online at: http://www.~exergoecology.com

Thompson, P. B. (2017). The Spirit of the Soil. Agriculture and Environmental Ethics. New York, NY: Routledge Pub. doi: 10.4324/9781315559971

CrossRef Full Text | Google Scholar

Tsatsaronis, G. (1984). Combination of Exergetic and Economic Analysis in Energy-Conversion Processes, Proc. European Congr. Energy Economics & Management in Industry. Algarve: Pergamon Press.

UN (1987). Report of the World Commission on Environment and Development - Our Common Future. Oxford: Oxford U. Press.

UNEP, United Nations Environment Program (1992). Rio Declaration on Environment and Development. Available online at: http://www.unesco.org/education/nfsunesco/pdf/RIO_E.PDF

Valero, A., Lozano, M. A., and Muñoz, M. (1986). A General Theory of Exergy Savings - 1. On the Exergetic Cost, Proc. ASME Computer-Aided Engineering of Energy Systems. Anaheim.

Google Scholar

Valero-Delgado, A., Valero-Capilla, J., and Gómez, B. (2011). The crepuscular planet. A model for the exhausted continental crust. Energy 36, 694–707. doi: 10.1016/j.energy.2010.09.034

CrossRef Full Text | Google Scholar

Wall, G. (1997). Energy, society and morals. J. Hum. Values 3, 193–206. doi: 10.1177/097168589700300206

CrossRef Full Text | Google Scholar

Wall, G., and Gong, M. (2001). Exergy and sustainable development, Part 1. Conditions and concepts. Int. J. Exergy 1:6. doi: 10.1016/S1164-0235(01)00020-6

CrossRef Full Text | Google Scholar

Yantovsky, E. I. (1994). Energy and Exergy Currents (An Introduction to Exergonomics). New York, NY: Nova Science Pub.

List of Symbols