Evaluation of Sustainability Determinants of Small Farming Systems via Participatory Modeling and Fuzzy Multi-Criteria Processes: The Case Study of Heliciculture in Greece

Feasibility and sustainability of small-scale farming systems are the most critical factors that determine future investments of urban agro-farming while promoting eco-systematic livelihood development and biodiversity. The determination and the diversification of the ambivalent and heterogeneous factors that affect the investment decision making of small farming systems is studied in this work via the application of participatory modeling methodology of regional stakeholders. Defuzzification of the participants' categorical feedback is succeeded applying Fuzzy Analytical Hierarchy Process (F-AHP) to set the pairwise weight matrix of the determinants suggested by the stakeholders. At a second phase, an innovative Fuzzy Cognitive Map (FCM) model is utilized to determine the weighted inter-causalities between all agricultural, environmental, and socio-economic criteria from the F-AHP output. Apart from the concept circumscription, we use the FCM to provide an in-depth scenario analysis including steady state and dynamic evaluation of driver concepts to receiver concepts in the model. The methodology is applied for the case study of heliciculture farming systems in Greece. Results show that sustainability is affected primarily by agricultural and inventory factors and secondarily by social and environmental factors identifying such cradle-to-farm gate life cycle assessment to be of low carbon footprint.

Introduction

As the Food and Agriculture Organization (FAO, 2017) suggests, and (Dutta et al., 2020) applies in different adaptation strategies, agricultural transitioning toward sustainable development plays an important role in the 2030 Agenda for global rural economic progress. This development includes a whole repertoire of methodologies and approaches for agricultural planning. These methodologies however must be evaluated first to become the pillars based on which competent authorities will establish policies for this development. Even more explicitly, the transitioning of traditional small-scale farming systems (especially in the southern European countries) must abnegate traditional methodologies assuming: (a) low or no-cost water, (b) fertilizers and infrastructures, and (c) undergo the necessary changes in levels of urbanization and rural markets to maintain viability and profitability. For this transition to be digested and become the base in agricultural development for the southern European countries, the societal acceptance is critical since, it boosts local residents to further investing into autonomous farming systems. At the same time, such initiatives generate additional residential income, employment, food sustainability, and fight poverty in the underdeveloped European regions.

Farmers of small-scale agricultural systems are vulnerable to market stability and product price fluctuation thus, they must make greater efforts in order to take advantage of economies of agricultural micro-scale (Markou et al., 2020). Additional efforts for the small crop-oriented and livestock-oriented farms in southern Europe to overcome the disadvantage of low profitability also must include: (a) the intensification of group membership in a participatory modeling fashion, (b) the focusing on the principal components toward farm sustainability, and (c) the diversity of Mediterranean-type farming systems that blends the morphology of low vegetation regions with the idiosyncrasies of mild temperate climate conditions (Stylianou et al., 2020). For all the above reasons, there is a need to design and implement multi-stakeholder hierarchical governance structures that run various scenario analyses based of the critical determinants which affect agricultural development. This will allow the establishment of regional policies that are based on the diversity of various target farming systems according to the relative importance of the considered determinants (Hawkes and Halliday, 2017).

Determining suitable and profitable agricultural development can be evaluated based on a multitude of criteria, physical environment variables and spatial data. Many of the abovementioned attributes are defined with categorical values of linguistic terms rather than numeric values. Furthermore, the criteria involved may be emanated from diverse and heterogeneous methodological categories carrying uneven weight importance. To deal with the decision-making problem of initiating a new agriculture structure assuming sustainable productivity suitability and profitability, fuzzy soft computing methodologies are introduced in this paper. Initially, participatory modeling is applied via recording of experts' and direct stakeholders' opinions. This increases the methodological effectiveness and efficiency of our approach by empowering competent authorities, professionals, and academia groups to improve the validity of the developed solutions. The recording of opinions of the above social groups carries data of fuzzy nature thus, methodologies such as F-AHP and FCM are chosen due to their ability to cope with: (a) fuzzification and defuzzification processes of data morphology, (b) subjectivities of experts in the field, and (c) revealing the most influential criteria and parameters (Zhao et al., 2019; Kokkinos and Karayannis, 2020; Kokkinos et al., 2020; Lak Kamari et al., 2020). At a second step, F-AHP is activated to assist: (a) the discovery all the important determinants that affect small-farming system development, (b) the clustering of all determinants into uncover categories, (c) the calculation of the relative importance between the criteria, either in the same category or cross-categorical, and (d) the normalization (defuzzification) of the critical weights values within the range of [0, 1]. The final step is the use of FCM as an innovative tool to utilize the inter-causalities between all criteria pairs and investigate the trend of agricultural development (increase or decrease) according to the selective increase or decrease of critical parameters (drivers). This can be achieved by analyzing the steady state characteristics of the map as well as the best- and worst-case scenarios in relation to the specific influential parameter at hand.

The above framework of methodologies is applied into the case study of small heliciculture farming systems in Greece as a paradigm for the proof of correctness. We have selected this type of small-farming activity because heliciculture shows alternative agricultural features especially due to contradictive social relations or differences of the influential actors (Gelabert et al., 2014). Even though there are several research works that focus on the efficiency of snail breeding within open or semi-open type agricultural systems, most of these attempts concentrate their findings into the economic efficiency of the projects without taking into account the technological, environmental and social impacts generated (Libois and Codjia, 2001). The primary purpose of this research work is to develop a flexible scenario analysis and decision-making tool that investigates the effect of agricultural/technological, environmental, and socio-economic parameters to optimize the snail production while maintaining overall sustainability of the farming system operation.

Original Contribution of the Current Research

Our research contribution is innovative in many aspects with the most critical to be:

• The participatory modeling methodology and the variety of Multi-Criteria Decision Making (MCDM) methods which utilize Fuzzy Logic constitutes a holistic approach that investigates and mitigates the uncertainties raised toward investing into heliciculture farming.

• The inclusion of an enriched repertoire of influential criteria that impact the decision making of investing in sustainable small farming systems. More specifically, this research analyzes the interoperability of these factors at the level of FCMs even though the relative importance matrix in F-AHP process is formed separately for each criteria category.

• The proposed methodology transcends similar fuzzy-based methodologies since it carries the advantage of being easily understood by the regional stakeholders. This is due to the relative advantage of FCMs and their characteristic of explainability as to the “whys” and “how's” in terms of the concepts involved. More specifically, the utilization of the FCM gives to the stakeholders a tool of interaction that explains the inter-causalities between the cultural differences and regional agricultural behaviors in relation to snail farming (Bennardo and Kronenfeld, 2011). Additionally, a variety of different scenarios including the steady state, worst, and best cases of the FCM allows us to determine alternative farming decisions toward sustainable agro-economy.

Materials and Methods

Fuzzy Set Theory and Fuzzy Analytic Hierarchy Process

In relation to the main principles of feasibility and sustainability, small farming agriculture is critically important for the local and regional agro-economies. The additional prerequisites of ecology, organic production, health, and profitability affect the existence and the regular operation of small farms in a way that cannot be directly computed and evaluated using crisp numeric values. For that reason, fuzzy sets (Zadeh, 1965) can be used to provide uncertainty evaluations of information represented by linguistic and categorical variables. Fuzzy set modeling is an extension of classical sets carrying the characteristic of membership defined as a function of participation, or a level of uncertainty, or the part of imprecision in a linguistic variable. Through a well-defined transformation (called defuzzification) the membership value can be transformed to a real number within the range of [0, 1]. Current research in MCDM problems always provides an analysis of pairwise comparisons between the criteria that participate in the decision making process and are expressed by fuzzy linguistics (Wang and Peng, 2020).

On the other hand, Analytic Hierarchy Process (AHP) is a well-known method that utilizes the expert and/or stakeholder opinions and judgements. The method compares all criteria imposed by the experts with each other aiming to discover the interlinks and mutual importance relations of all considered criteria pairs (Wang and Chin, 2011). However, AHP is applied under the assumption that experts' opinion is recorded using crisp numeric scales. Unfortunately, a considerable portion of decision-making problems must deal with the fact that, when surveying stakeholders, vagueness is introduced in answers. Hence, fuzzy-based opinions are to be expressed by linguistic-type values on specific categorical asked variables. Apparently, it was soon found that the inclusion of fuzzy sets in determination of relative importance is critical in dealing with this type of data. F-AHP which was discovered by (Chang, 1996), brings into effective action the triangular fuzzy numbers as a method to defuzzify vagueness when estimating the relative importance of interlinked criteria collection (Lu et al., 2007; Chan et al., 2008; Chamodrakas et al., 2010; Kilincci and Onal, 2011). The method allows the calculation of the pairwise importance comparison matrix of the criteria used to determine a targeted decision. More specifically, let a triangular membership function fuzzy number be defined by the fuzzy triplet (l, m, u) corresponding to the low-medium-high possible crisp values. Such numbers will be called as Triangular Fuzzy Numbers (TFN). Note that (l ≤ m ≤ u) to avoid interference with the relative crisp limits. Using the previous definition of the membership functions, Figure 1 depicts the spanning of the membership function μ(x) within the range [0, 1] which is rigorously shown in the following definition formula:

$\begin{array}{ll}\mu \left(x\right)=\left\{\begin{array}{cc}\frac{x-l}{m-l}& l\le x\le m\\ \frac{u-x}{u-m}& m\le x\le u\\ 0& \text{otherwise}\end{array}\right\}\text{ using the fuzzy triplet }(l,m,u)& (1)\end{array}$

FIGURE 1

Figure 1. The presentation of a triangular fuzzy number.

Linguistic variables are handled setting up a nine-step fuzzy triangular scale. This scale has an equivalent nine-level numeric scale as discussed recently in (Liu et al., 2020) and given in Table 1:

TABLE 1

Table 1. Interlink between fuzzy linguistic values, triangular-fuzzy and numeric scale.

Furthermore, several researchers have added to the membership function algebra a set of operations like the regular algebra (Kahraman et al., 2003; Ullah et al., 2020). It is critical to present these operation as they are essential in computing the pairwise comparison matrix between the criteria used in the methodology (Chan et al., 2008; Chamodrakas et al., 2010). Assuming $\tilde{Q}$ a triangular fuzzy number we depict the inverse/reciprocal, the addition, the subtraction, the multiplication, the inner product, and the summation operations using the fuzzy theory:

$\begin{array}{ll}\tilde{Q}=(l,m,u)& (2)\end{array}$

$\begin{array}{ll}{(\tilde{Q})}^{-1}={(l,m,u)}^{-1}=\left(\frac{1}{u},\frac{1}{m},\frac{1}{l}\right)& (3)\end{array}$

$\begin{array}{ll}{\tilde{Q}}_1\oplus {\tilde{Q}}_2=\left(l_1,m_1,u_1\right)\oplus \left(l_2,m_2,u_2\right)=(l_1+l_2,m_1+m_2,u_1+u_2)& (4)\end{array}$

$\begin{array}{ll}{\tilde{Q}}_1-{\tilde{Q}}_2=\left(l_1,m_1,u_1\right)-\left(l_2,m_2,u_2\right)=(l_1-u_2,m_1-m_2,u_1-l_2)& (5)\end{array}$

$\begin{array}{ll}{\tilde{Q}}_1\otimes {\tilde{Q}}_2=\left(l_1,m_1,u_1\right)\otimes \left(l_2,m_2,u_2\right)=(l_1{l}_2,m_1{m}_2,u_1{u}_2)& (6)\end{array}$

Let us also assume an n-criteria analysis for a specific problem. The corresponding relative importance comparison matrix is given in the form:

$\begin{array}{l}\tilde{Q}=\left[\begin{array}{cccc}{\tilde{Q}}_{11}& {\tilde{Q}}_{12}& \cdots & {\tilde{Q}}_{1n}\\ {\tilde{Q}}_{21}& {\tilde{Q}}_{22}& \dots & {\tilde{Q}}_{2n}\\ ⋮& ⋮& \dots & ⋮\\ {\tilde{Q}}_{n1}& {\tilde{Q}}_{n2}& \dots & {\tilde{Q}}_{nn}\end{array}\right]\\ =\left[\begin{array}{cccc}(l_{11}{m}_{11}{u}_{11})& (l_{12}{m}_{12}{u}_{12})& \cdots & (l_{1n}{m}_{1n}{u}_{1n})\\ (l_{21}{m}_{21}{u}_{21})& (l_{22}{m}_{22}{u}_{22})& \dots & (l_{2n}{m}_{2n}{u}_{2n})\\ ⋮& ⋮& \dots & ⋮\\ (l_{n1}{m}_{n1}{u}_{n1})& (l_{n2}{m}_{n2}{u}_{n2})& \dots & (l_{nn}{m}_{nn}{u}_{nn})\end{array}\right]\\ for\begin{array}{c}i=1..n\\ j=1..n\end{array}& (7)\end{array}$

The method first finds the relative importance 2-dimensional array in the fuzzy scale computing the geometric mean. At a second step it defuzzifies the fuzzy 2-dimensional array converting back to a crisp output using the operation:

$\begin{array}{ll}{\tilde{F}}_i=\tilde{R}\otimes {\tilde{G}}_i={\left({\displaystyle \sum _{i=1}^n}\sqrt[n]{{\displaystyle \underset{j=1}{\prod ^n}}{\tilde{Q}}_{ij}}\right)}^{-1}\otimes \sqrt[n]{{\displaystyle \underset{j=1}{\prod ^n}}{\tilde{Q}}_{ij}}& (8)\end{array}$

where ${\tilde{G}}_i$ denotes the result found by the geometric mean for criterion Q_i, R corresponds to the inverse of the sum of ${\tilde{G}}_i$, and ${\tilde{F}}_i$ represents the fuzzy weight for criterion Q_i.

Since ${\tilde{F}}_i$ are still TFN, they need to be de-fuzzified. The defuzzification method is based on the “center of area”. The method is proposed by (Chou and Chang, 2008) and it produces a crisp number from a TFN using the equation below:

$\begin{array}{ll}{M}_i=\frac{l{\tilde{F}}_i+m{\tilde{F}}_i+u{\tilde{F}}_i}{3}& (9)\end{array}$

where M_i is of crisp numeric mode. However, all relevant crisp weights in the method need to be normalized so that their summation adds up to 1, giving a definite ranking of importance. The normalization formula follows:

$\begin{array}{ll}{N}_i=\frac{M_i}{{\sum }_{i=1}^n{M}_i}& (10)\end{array}$

Let us consider an n-criteria relative importance matrix $\tilde{Q}$, with TFN weights where, every element ${\tilde{Q}}_{ij}$ indicates the importance between criterion C_i and C_j respectively. Assume that ${\tilde{Q}}_{ij}=\frac{1}{{\tilde{Q}}_{ji}}$ indicating a reciprocal matrix. If for every triplet of criteria i,j,k it holds that ${\tilde{Q}}_{ik}={\tilde{Q}}_{ij}{\tilde{Q}}_{jk}$ then all matrix entries satisfy the transitivity property. Such matrices are called consistent. For such matrices we define, ω to be an eigenvector (of order n) and λ to be an eigenvalue if and only if ${\tilde{Q}}_{ij}.\omega ={\lambda }_{max}.\omega$ and λ_max ≥ n. Note that, λ_max is the largest eigenvalue of the comparison matrix, and n is the dimension of the matrix. Also, the difference between λ_max and n represents the level of inconsistency of the stakeholder responses in the study. Note that λ_max is computed on the defuzzified TFN after application of the geometric mean above and on the mean-vector of the defuzzified comparison matrix.

The consistence index (CI) for a comparison matrix can be computed with the use of the following equation.

$\begin{array}{ll}CI=\frac{{\lambda }_{max}-n}{n-1}& (11)\end{array}$

Finally, the consistency ratio (CR) represents the difference in consistency between the given evaluation matrix and a random matrix (Saaty, 1980) and it is given by

$\begin{array}{ll}CR=\frac{CI}{RI(n)}& (12)\end{array}$

where RI(n) is the corresponding Random Index that is directly depended on the value of n i.e., the size of the matrix. The values of RI(n) for 3 ≤ n ≤ 9 are given by the sequence (0.58, 0.9, 1.12, 1.24, 1.32, 1.41 and 1.45) respectively according to (Golden, 1989).

FCMs as a Tool for MCDM

Fuzzy cognitive maps are semi-quantitative graph-based models, mostly suited for modeling expert and stakeholder participation, concerning a specific scientific domain of interest. Proposed by Kosko (Kosko, 1986, 1992) FCMs are consisted of nodes which represent concepts that inter-operate and they are interlinked with edges representing causal relationships between any pair of concepts. The edges of the FCM are valued with a fuzzy weight that indicates the extend (positive or negative) of these relations. At any step of the inference process, the FCM may be considered as a state vector. This allows to treat the FCM as a dynamical neural network system converging to a steady state. In a similar way to F-AHP, the measure of the inter-causalities between any two concepts in FCMs can be a fuzzy number between −1 and 1. The range of values traverses from a negative (inversely analogous) exceptionally solid causality to a positive exceptionally solid impact (Novak and Cañas, 2008). More specifically, the causalities between concepts C_j and C_i can be:

• W_ij > 0, indicating a positive causality,

• (ii) W_ij < 0, showing a negative causality, and

• (iii) W_ij = 0, showing no causality.

An example of an FCM along with the adjacency matrix of concept inter-causalities is shown in Figure 2.

FIGURE 2

Figure 2. A typical FCM and the corresponding adjacency matrix of causalities.

Assume that at time-t the activation function is applied to the map. Then all the C_i’s get the value $X_i^t$ because of the overall influence of all causalities emanated from all concepts that are connected to C_i at iteration-k. The value X_i denotes the overall influence emanating from all concepts C_j to C_i such that i ≠ j (inference). The inference modeling is borrowed from the neural networks applying a collection of inference models. Among them, the most popular inference models are: (a) Kosko's inference, (b) Modified Kosko's inference, and (c) Rescale inference. The activation functions of these models are depicted in the following equations in this respective manner:

$\begin{array}{ll}{X}_i(k+1)=f\left({\displaystyle \sum _{j=1,j\ne i}^N}{w}_{ji}\times X_j(k)\right)& (13)\end{array}$

$\begin{array}{ll}{X}_i(k+1)=f\left(X_i(k)+{\displaystyle \sum _{j=1,j\ne i}^N}{w}_{ji}\times X_j(k)\right)& (14)\end{array}$

$\begin{array}{ll}{X}_i(k+1)=f\left((2\times X_i(k)-1)+{\displaystyle \sum _{j=1,j\ne i}^N}{w}_{ji}\times (2\times X_j(k)-1)\right)& (15)\end{array}$

The set of most popular transformation functions used (i.e., the predefined threshold for activations to stop) in the inference procedure are: (a) sigmoid, (b) bivalent, (c) trivalent, and (d) hyperbolic as given below:

$\begin{array}{ll}f(x)=\frac{1}{1+e^{-\lambda x}}& (16)\end{array}$

$\begin{array}{ll}f\left(x\right)=\{\begin{array}{c}1x>0\\ 0x\le 0\end{array}& (17)\end{array}$

$\begin{array}{ll}f\left(x\right)=\{\begin{array}{c}1x>0\\ 0x=0\\ -1x<0\end{array}& (18)\end{array}$

$\begin{array}{ll}f(x)=tanh(\lambda \times x)& (19)\end{array}$

where λ > 0 be real number that denotes the steepness of f and x is the value A_i(k) on the equilibrium point. From the transformations above, the sigmoidal function always converges steeply between 0 and 1.

Using the experts' help, the map concepts along with their intercausal relationships are determined initially. The values are crisp numeric within the range [−1, 1]. In case that linguistic values are used, these are defuziffied at a later stage. Post processing can also be applied by experts to re-evaluate the structure and the interconnections of the FCM. This process leads to an improvement of the FCM via the use of fuzzy conditional statements and fuzzy rules as (Groumpos and Anninou, 2017) suggest. The algorithm applied now follows:

Step 1: Experts define the FCM concepts C_i which correspond to the criteria analyzed.

Step 2: Every expert considers every possible pair of concepts to determine their causal relationship. If there exists one in the mode of (positive, negative, neutral), a value within [−1, 1] is given. There are three different cases between two concepts C_i and C_j:

• w_ij ≥ 0 indicating that when C_i increases, the same result is caused to concept C_j.

• w_ij ≤ 0 indicates that an increase or decrease to C_i causes the inverse effect to C_j.

• w_ij = 0 indicates no relation between concepts C_i and C_j.

Note that the influential effect between the two concepts C_i and C_j is defined by |w_ij|. In each step of the inference process of the FCM, the state of each concept is reevaluated using the inference rule:

$\begin{array}{ll}{A}_i(k)=f\left(k_1{A}_i\left(k-1\right)+{\displaystyle \sum _{j=1,j\ne i}^N}{w}_{ji}\times A_j\left(k-1\right)\right)& (20)\end{array}$

In the case that either there are no experts or the experts' knowledge is highly diverse resulting a collection of FCMs with minimum concept overlapping, a variety of learning methodologies can be used in a similar way as in the neural network processes. More specifically there are three categories of FCM learning methodologies: (a) Hebbian-based, (b) Population-based, and (c) Hybrid. The Hebbian methods apply either the Hebbian law or variations of this on available data to adjust the causal weights by Dickerson and Kosko (1994), Huerga (2002), and Papageorgiou et al. (2004). Population-based algorithms (evolution-based, particle swarm optimization and simulated annealing) use models that mimic the input data in a similar way as in function optimization for the case of genotype development adopted by biology (Mateou et al., 2005; Stach et al., 2005; Alizadeh et al., 2007). Finally, hybrid learning blends the previous two methodologies using advanced search capabilities and determining the weight matrix as (Zhu and Zhang, 2008) proposes.

Sustainability of Small Farming Systems

There is an urgent necessity lately to assess the sustainability of small farming systems. Assessing the sustainability influential factors is the most important step in improving current farming practices to guarantee the agricultural, environmental, economic, and social viability of such small-scale systems. Unfortunately, in most cases, such assessing and evaluating methodologies are foreign to farmers. However, academia and other experts may provide to the farmers such information as a collection of dynamically assessed case studies. This alternative gives the ability to the farmers to bypass the theoretical part of the methodology and concentrate on the application specifics. Such case studies may be used collectively to:

• summarize and characterize bidirectional interactions of agricultural determinants,

• link and cluster systemic sustainability indicators into categories of common scientific domain and,

• form the data repositories used from the researchers to create MCDM frameworks that can provide optimized decision support systems to farmers.

However, all known methods used to evaluate sustainability suffer from noticeable levels of uncertainties introduced into the evaluation process. This is caused by the characterization of certain factors using linguistic and fuzzy variables due to the dynamic nature of such systems. Therefore, a clear set of criteria/objectives is needed along with a descriptive methodology so the farmers can adapt to specific farm management practices in order to achieve sustainability. Toward this direction, a participatory modeling approach is used to first establish the criteria of every category, and then determine the interoperability of these criteria. This method enhances the adaptation and the explainability of the decision-making modeling by providing to farmers and other stakeholders with a holistic view of the problem and the interlinking of the diverse parameters participating. In relation to small farming systems, it is prominent that the research expert first describes the criteria to the stakeholders (farmers, competent authorities etc.) providing evidence of the importance of criteria. Stakeholders are then engaged to evaluate the criteria and provide individual scores filling up their own relative importance matrix. To calculate the weighted sum (see fuzzy set operations above) post-processing is needed to convert the linguistic/categorical type values. The F-AHP succeeds to compute the correct ordering of criteria according to relative importance. In the case of long multi-criteria lists, separate F-AHP calculations can order the criteria of each category. Several works of F-AHP related to agriculture and small farming systems specifically have shown significant results in prioritizing the most important operational factors of the farms focusing in sustainability (Papageorgiou et al., 2016; Galdeano-Gómez et al., 2017; Damani, 2019; Rao et al., 2019; Karimi et al., 2020; Tzouramani et al., 2020). At the same time the FCM utilization for predicting productivity or yield in specific farming systems has been studied in several research works (Mourhir et al., 2017; Bahri et al., 2020; Shahrin et al., 2020; Tsadiras et al., 2020).

In this work a logical architecture which embeds both methodologies is proposed as shown in Figure 3. Initially, experts propose the set of important criteria emanating from various scientific domains (agricultural, social, environmental, and economic). At a second phase stakeholders are invited to participate on the design of this strategic planning via participatory modeling. While experts set the criteria stakeholders determine the level of their absolute importance as well as their relative importance. As aforementioned, first F-AHP computes the relative importance matrix of the criteria, thus giving a normalized weight rating between 0 and 1. At the second phase, an FCM is involved for assessing the influence of all driver concepts (the initiators that drive the decision to start a farming system). The receiver concepts of the FCM are set according to the specific scenario analysis that is analyzed. For most cases of farming systems, this relates to the yield prediction or economic productivity. Apart from the steady state of the FCM according to the inputs coming from the F-AHP, best- and worst-case scenarios are also studied to predict trends (positive or negative) for the receiver concepts.

FIGURE 3

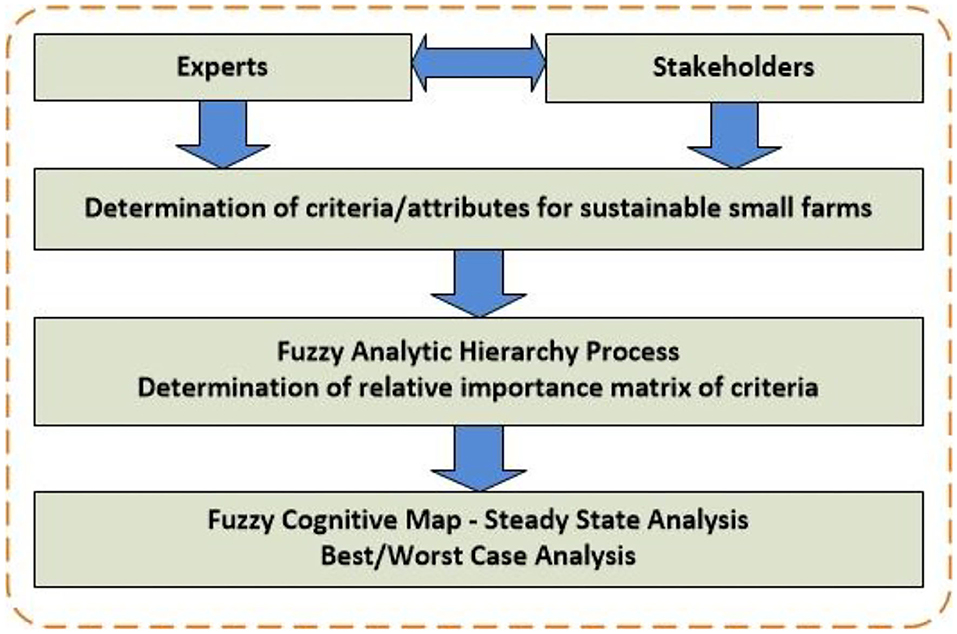
Figure 3. Logical architecture of the study: intermix of SF-AHP and FCM in scenario analysis of small farming systems.

Sustainability of Heliciculture Small Farming Systems in Europe and Greece

Edible snails are a profoundly valued food in numerous European nations. Especially in France reaches utilization levels of quantities of around 40,000 tons for every year (Daguzan, 1989; Kiebre-Toe et al., 2003). In Spain, national consumption rates reached almost 16,000 tons for the year 2008 indicating that there is a trend and a mainstream toward higher rates. Be that as it may, like France and other European nations, the greater part of the snails devoured are gathered from the wild and only about 3% of the overall utilization comes from heliciculture, which makes it an interesting agricultural and zootechnic activity (Segade et al., 2011). On the other hand, in Greece, due to the favorable climatic conditions, the traditional nature of the agricultural sector and the intense interest of mainly young people, there is significant potential for the growth of the Snail-farming sector. According to the latest available data from the Ministry of Rural Development and Food (2014) 255 snail farms were recorded. The average size of snail farms is small (0.82 ha for the open farms and 0.18 ha for the net-covered greenhouses), while very few are more than 1.5 ha. Snail farms have been set up and operated without a clear operating framework as far as it concerns parameters such as livestock management, environmental impact, and welfare indicators.

Edible snails are a nutritious food and an excellent source of protein, fatty acids, carbohydrates, vitamins, and minerals. The commercial interest is not only in gastronomy but also in the fields of pharmacy, dermatology and cosmetology (Bonnemain, 2005; Tsoutsos et al., 2009; FAO, 2011; Hatziioannou et al., 2014). Studies in snail farming have been carried out in laboratory (de Vaufleury and Gimbert, 2009) or in farms (Daguzan, 1985, 1989; Dupont-Nivet et al., 2000; Toader-Williams and Bentea, 2010; Toader-Williams and Sara, 2010). The scientific knowledge on farmed snail nutrition remains limited (Jess and Marks, 1998; García et al., 2006; Milinsk et al., 2006; Toader-Williams and Bentea, 2010). The chemical composition, organoleptic and physical properties of farmed snails have not been studied extensively or have not been correlated with the snail farming system (Linhart and Thompson, 1995; Milinsk et al., 2003).

F-AHP Methodology for the Case Study

This paper investigates the influential factors of snail production in the Greek region. It represents a categorization of these factors into: (a) snail farming geo-technological, (b) environmental, (c) economic, and (d) social. The geo-technological category includes the most critical determinants in relation to snail farming. This category spans not only to snail-specific factors (e.g., snail species) but also to the oriented infrastructure needed for this farming type (intensive or extensive), as well as the equipment and the facilities utilized. In relation to environmental indicators, snail farming is environmentally friendly in terms of pollutant emissions. The quantity of nitrates lost to groundwater and surface water is insignificant for this farming type and, there are not any snail farming practices that directly or indirectly reflect any impact to the environment. However, some primary climatological parameters are tightly coupled with snail production such as geographical location, pollution, light intensity, precipitation, and humidity. Furthermore, various managerial and economic determinants directly affect the viability of snail farming. Farm income and efficiency are depended on the stability of production and the stability of the market. At the same time, snail farming systems are autonomous units of special characteristics and thus not very popular, making the market more competitive. The economic sustainability is also interlinked with some important social pillars including the decent livelihood and fair-trading practices as the two most important.

For the above reasons, the results of this research shed light in some of the most important problems of the Greek snail-farming sector. The need for the project implementation is mandatory after the unplanned development of the snail-farming sector during the last decades. Due to improved handling procedures, quality product certification and product labeling, value-added products can be developed. The designing of novel products will lead to the growth of the snail-farming sector and the processing industry with a positive impact on the Greek economy. The following Table 2 tabulates all the critical factors clustered according to the four categories above. Special prioritization is given however to the geo-technological (operational) factors as the most critical when focusing on maximizing snail production. Table 2 entries are due to experts' knowledge and the outcomes of extensive literature in heliciculture previously mentioned in this subsection.

TABLE 2

Table 2. Candidate criteria for sustainable heliciculture farming.

The process design of interviewing the stakeholders is depicted in the following plan: First the authors created four questionnaires, one for each of the criteria categories using the exact names of the criteria shown in Table 2. The questionnaires were based on questions to reflect the pairwise comparisons between any pair of concepts. An example questionnaire for the geo-technological category of criteria is included in the Supplementary Material. At a second phase, the authors have explained the stakeholders the basics of the F-AHP methodology and asked the stakeholders to answer the questionnaires with a number between 1-9 that corresponds to a fuzzy linguistic value as shown in Table 1. This was chosen for speeding up the answering process. The set of stakeholders included 12 farmers that are owners of a small snail farming unit. Four out of the previous farmers are also involved with other types of small farming systems which focus on various sustainability and environmental protection orientation. All stakeholders are from the broader region of Thessaly and south-western Macedonia Greece. The stakeholder assessments were done on an individual basis. However, stakeholder group decision making was considered and to achieve this individual stakeholder responses were summarized into one representative via geometric mean (Cortés-Aldana et al., 2009; Oblak and Glavonjić, 2015).

This small group of farmers is utilized because it does not only provide significant knowledge to the problem at hand but also it provides co-designing of the models. These farmers are considered to have the most experience on all the specific features of snail farming. This approach yields many benefits, including strategic planning, effective model application and utilization of the regional social capital. The number of stakeholders is however small but, there is not any availability on increasing the participation of this group. For the case of Greece, heliciculture is not popular yet. More specifically, for the region of Thessaly and south-western Macedonia (current case study), the group of stakeholders represents more than fifty percent of the total group of farmers. Any other synthesis of the stakeholder group would yield variations on the results which would be driven by target groups that do not directly relate to the cultivation process.

The outcomes of the pairwise comparison questionnaires were analyzed using a C-code program based on the F-AHP algorithms to obtain the final ranking for each criterion. The program run four times (once for each criterion category). The analysis was obtained from the aggregated geometric means data discussed above. The consistency ratio (CR) was calculated according to the given equation that relates λmax to find the consistency index (CI) and the random consistency index (RI) from the predefined values for number of criteria greater or equal to 3. In this study CR threshold was set to 0.10 according to (Kordi and Brandt, 2012; Saaty and Vargas, 2012).

FCM Methodology for the Case Study

The same set of stakeholders as in F-AHP were conducted to provide participatory scenario development via FCMs (van Vliet et al., 2010; Gray et al., 2013). The utilization of the same stakeholders is due to the following reasons: (a) credibility of responses since this group is the most appropriate group of people to evaluate the recognition of the scenario designed and how plausible it is, (b) relevance (i.e., the ability of the stakeholders to estimate the relevance of the concepts to end users (note that the farmers are also end users), (c) legitimacy (the ability to recognize if the concepts used cover the widest possible range of perspectives), and (d) creativity (the ability to recognize if the FCM design cover future possible implications of unexpected events that might affect the snail production).

Along these lines, the stakeholders were invited to fill out the questionnaire created for the construction of inter-causalities in the FCM. This questionnaire is also included in the Supplementary Material. The participants were asked to rate the relevance between any one of the 23 concepts in total to the snail production using a nine-point scale (1–9) spanning from “totally irrelevant” to “totally relevant.” No new concepts were introduced to promote absolute similarity between the F-AHP approach and the literature outcomes. At the end of the process, causal links and positive/negative interactions between concepts were indicated by the stakeholders. The final value of each inter-causality represents the consensus opinion of all participants as a causality mean. Note that all criteria are included in one map as opposed to the F-AHP approach where separate analyses were made for each criteria category. The receiver concept of the map is the snail production to find and analyze what are the most critical driver-concepts that affect the snail production. Fuzzy values are incorporated in the map in the following aspect: Participants are informed about the Likert-scale used and how this is equivalent to the corresponding linguistic values. The map outcome shows a trend of increase or increase of the snail production as driver concepts range their causality values from the worst case (minimum increase/decrease) to the best case (maximum increase/decrease).

Results and Discussion

F-AHP Methodology for Criteria Ranking

The AHP analysis presented in this study utilizes the literature reviews of Kurka and Blackwood (2013), Massawe et al. (2019), and Fekadu and Negese (2020). The criteria importance was considered for suitability of heliciculture farming systems to maximize production. This importance was calculated via a combination of literature review, expert's opinion (academia) and farmers' responses to questionnaires dedicated to fill out the relative comparison matrix. More specifically, twelve farmers were identified and volunteered to provide their opinions based on the set of criteria from Table 2 focusing on the production aspect. The selection of the stakeholders was primarily due to their prior engagement to snail farming. The questionnaire was extensive but straightforward since it contained the same type of questions in the form “How important do you think that Criterion C_i is compared to Criterion C_j?” The stakeholders were invited to answer four questionnaires, one for each category of criteria. The questionnaire of the geo-technological criteria category is given in the Supplementary Material.

The sequence of steps according to the algorithm of F-AHP is shown in the following tables: Table 3 depicts the initial (before fuzzification) initial pairwise comparison matrix and the fuzzy and defuzzified weights for the geo-technological category, Table 4 for the environmental category, Table 5 for the economics category and Table 6 for the social category of criteria, respectively.

TABLE 3

Table 3. Fuzzy AHP for technological category.

TABLE 4

Table 4. Fuzzy AHP for environmental category.

TABLE 5

Table 5. Fuzzy AHP for economics category.

TABLE 6

Table 6. Fuzzy AHP for social category.

Tables 3–6 present the ordering of weight criteria in their own categories of analysis. Specifically, the Norm Crisp value shown in the right column denotes the ranking of criteria given a value between 0 and 1 with the summation of all weights to be 1. The criteria performing the best from each category are:

• Geo-Technological oriented criteria: A6 (density and biomass) found to be the most critical factor of the category with weight of 0.163423 with the second to be A7 (reproduction performance). For this case, the strategy is to gain high levels of biomass and density of animals in the field where they live (studies have shown that snail move within very small distances). This in conjunction to high reproduction rates to ensure high productivity.

• Environmental oriented criteria: B2 (water quality requirement) with weight 0.217747 followed by the B5 (humidity) with weight 0.194744 are the two important factors from the environmental sector. This finding shows that stakeholders do prefer fields that secure the water availability and believe that water quantity (adequate levels of humidity) as well as water quality (non-contaminated) do play a significant role in the snail production levels (count production and/or meat production).

• Economic oriented criteria: C1 (stability of annual production) with weight 0.290428 is highlighted as the most influential parameter in this category. It is the stakeholders' rigid opinion that the stability of the field annual production is more important than to gain high production levels for 1 year followed by low levels afterwards. This indicates that farmers prefer a secure environment where they act and produce as opposed to opportunistic type agricultural activities.

• Social oriented criteria: criterion D1 (decent livelihood (capacity development)) and D2 (fair trading practices) from the social category depict same importance levels with weight 0.285239 indicating that for the Greek farmer society it is very important the gaining of a decent livelihood through a small heliciculture farm under the precondition that the produced livestock will be moved via local and regional commerce channels that secure fair trading practices.

FCM Construction and Dynamic Scenario Analysis

To design a good scenario analysis tool using the most significant criteria and how their combination influences the production of small heliciculture farms, the same group of stakeholders (farmers) and experts (researchers) contributed their experience and perceptions. More specifically, after they were informed how to construct an FCM, they used the criteria as concepts of the map and for every pair of concepts (C_i,C_j) they specified the causalities for both directions (C_iC_j) and (C_jC_i) respectively. In the case of no causalities, the value of 0 is assigned else a normalized value in the range [0, 1]. Note that this process provides an automatic defuzzification of the edge-weight fuzzy linguistic values. Afterwards, results were entered in the online software called MentalModeler (http://www.mentalmodeler.org, 2020) as shown in Figure 4. Even though there is high complexity of the resulted FCM, it is worthy to recognize: (a) most causalities (edges) to be positive (blue colored), (b) there is only one receiver concept (only incoming edges) which is the “production” and (c) there is a minimal set of inverses (negative) causalities indicated meaning that there is mainly unidirectional influence among concepts.

FIGURE 4

Figure 4. High complexity FCM due to concept density and unidirectional causalities.

Furthermore, the general FCM statistics under the steady state analysis are shown in Table 7. At the same time, Table 8 also depicts the In-degree and Out-degree of each concept, the type of concept (driver, ordinary and receiver) and the Centrality which is a measure of the overall influence of the concept in the model showing the conceptual weight/importance of individual concepts.

TABLE 7

Table 7. General FCM statistics.

TABLE 8

Table 8. Categorization, indegree, outdegree, centrality and type of concepts in the FCM.

The hierarchy index of the FCM model was found of value 0.122 and this value (near the range of 0) according to (Özesmi and Özesmi, 2004) makes the model highly democratic. The problem under study for the collective case (i.e., inclusion of all concepts in the map as opposed to separate maps for each category of concepts) affects the in/out degree of all concepts and of course the overall. The concept of the highest centrality is the one of “production” as expected, but concepts such as “reproduction performance,” “rearing duration and growth rate,” and “feed (quantity, quality)” present high centrality also. This is reasoned because of the high influence they also perform to the rest of the concepts. At the same time, this high centrality/influence was also expected from the previous F-AHP analysis where the same concepts/criteria reached the highest relative normalized importance.

Dynamic FCM Scenario Analysis

For the resulted FCM an adequate set of scenarios/simulations was implemented to fully exploit the substance of the causalities between the concepts. The FCM inferences iteratively as a neural network until it converges after a certain number of epochs using the Kosko clamping methodology (Kosko, 1992). According to this technique, a special focus is turned to a subset of concepts in terms of how the change of their values affects the increase or decrease of the receiver concepts and how the system reaches an equilibrium state (steady state). It is more critical to use the driver concepts for clamping as opposed to the ordinary concepts since they are the primary factors that influence the receiver concept. In general, the clamping affects all the concepts that they are mutually interdepended and for that reason it is important for these concepts when they change states. Thus, dynamic scenarios of the FCM are implemented through the clamping of the concepts and the adjacency matrix of the cognitive map to assess the impact of the perturbations on the steady state of the model (Aguilar, 2005). When we examine trends, it is more critical to use the driver concepts for clamping as opposed to the ordinary concepts since they are the primary factors that influence the receiver concept. For the same reason, receiver concepts are never used in clamping simply do not influence any concept. A typical clamping simulation is depicted in Figure 5 which shows that for all the concepts participating in the inference procedure, convergence is reach after 5 iterations of the FCM and that in the steady state the variance of converged values is small since all concepts stop to trigger a new inference after getting a value between 0.71516 and 0.98695.

FIGURE 5

Figure 5. The convergence values and the activation curves for the FCM concepts.

After extensive research on the subject, this is a unique study that attempts to examine the quantified influence of:

• the most important driver concepts of the “extensive farming (open field),” the “intensive farming (net-covered greenhouses)” and the “geographic location” and

• the most critical technological concepts of “density and biomass,” “reproduction performance,” “rearing duration and growth rate,” and “feed (quantity, quality)”

to the “production” of a heliciculture small farming system thus indicating the uniqueness of the study. For this reason, steady state statistics of the FCM were considered as the starting point to perform the best case and worst-case scenarios as to the influence of the aforementioned factors to the production of the farming system. For the worst-case scenario, we fix the starting value of the driver concepts to be 0.1. On the contrary, the best scenario case mandates the fixing of the driver concept values to be 1. Figure 6 shows the worst-case scenario results where we observe a 5% decrease trend on the production receiver concept as compared to the original steady state scenario.

FIGURE 6

Figure 6. Worst case scenario: driver concepts get value of 0.1 (comparison to the steady state).

It is also significant to observe that the biggest (among all concepts) decrease occurs on the “social diversity” concept as a result of small driver concept values with the second one in decrease to be the “humidity.” The explanation is given by the fact that, intensive or extensive field farms drastically affect the levels of humidity needed for the growth of the biomass and subsequently the growth of snails. The connection of the social diversity is indirect via the “farmed snail species” and the “geographic location” as the third driver.

On the contrary, Figure 7 presents the best-case case influence of the snail production rate as this depends on the driver concepts. For this scenario, all driver concepts are set to maximum value one. The effect of the inference under these conditions results in a production rate trend increase to be of 7%. The same increase is shown in the pollution concept where the humidity concept is the third rated with an increase of 5%. The increase of production was expected due to the maximization of the extensive and intensive farming. At the same time, extensive farming has maximum effect according to experts with the humidity of the farming system.

FIGURE 7

Figure 7. Best case scenario: driver concepts get value of 1 (comparison to the steady state).

Conclusions

In this research, a two-modeling methodology for evaluating the feasibility and sustainability of small farming systems was proposed. The focus of the study was to provide a prototype DSS to assist farmers' engagement to heliciculture. Both methods are appearances of participatory modeling. The annual production of the farm was the objective for maximization preserving sustainability. Stakeholders were invited to provide opinions for the relative importance between the criteria set. The F-AHP the model succeeded to identify the most significant criteria for each criteria category i.e., the primary components in the decision-making process. The geo-technological category of concepts is the most interesting since it contains all primary agricultural factors involved. From this category, density/biomass, reproduction performance and feed have found to be the most critical aspects that determine the production rate of heliciculture farming systems. From the environmental category, water quality as well as humidity (especially for the intensive field type) seem to play very important role toward maximization of production. At the same time, the aspects of production and market stability and workplace and health security and social diversity prove to be more important from the economics and the social categories, respectively. F-AHP outcomes were fed to an FCM to determine intra-causalities of concepts/criteria. This analysis was twofold: (a) the system was let to reach a steady state identifying the final concept participation and (b) dynamic-based scenario analysis to highlight the effect of driver concepts to the production receiver concept. Additionally, a variety of simulations were applied altering the learning methodology used for the FCM and setting driver concept values between the range of best and worst case.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

Ethical review and approval was not required for the study on human participants, in accordance with the local legislation and institutional requirements. The participants provided their consent to participate in this study.

Author Contributions

MH and KK contributed to conception, wrote the manuscript, and designed the study. MH organized the database. KK performed the statistical analysis. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsus.2021.629408/full#supplementary-material

References

Aguilar, J. (2005). A survey about fuzzy cognitive maps papers. Int. J. Comput. Cogn. 3, 27–33.

Google Scholar

Alizadeh, S., Ghazanfari, M., Jafari, M., and Hooshmand, S. (2007). Learning FCM by tabu search. Int. J. Comput. Sci., 2, 142–149.

Google Scholar

Bahri, O., Mourhir, A., and Papageorgiou, E. I. (2020). Integrating fuzzy cognitive maps and multi-agent systems for sustainable agriculture. Euro-Medit. J. Environ. Integr. 5:7. doi: 10.1007/s41207-020-0143-8

CrossRef Full Text | Google Scholar

Bennardo, G., and Kronenfeld, D. B. (2011). Types of collective representations: cognition, mental architecture, and cultural knowledge. A Companion to Cognitive Anthropology, 82–101. Available online at: https://onlinelibrary.wiley.com/doi/pdf/10.1002/9781444394931#page=96

Google Scholar

Bonnemain, B. (2005). Helix and drugs: snails for western health care from antiquity to the present. Evidence-Based Complementary and Alternative Medicine, 2. Accessed November 9, (2020). Available online at: https://www.hindawi.com/journals/ecam/2005/583043/ doi: 10.1093/ecam/neh057

PubMed Abstract | CrossRef Full Text | Google Scholar

Chamodrakas, I. D., Batis, D., and Martakos, E. (2010). Supplier selection in electronic marketplaces using satisficing and fuzzy AHP. Expert Syst. Appl. 37, 490–498. doi: 10.1016/j.eswa.2009.05.043

CrossRef Full Text | Google Scholar

Chan, F. T., Kumar, N., Tiwari, M. K., Lau, H. C., and Choy, K. (2008). Global supplier selection: a fuzzy-AHP approach. Int. J. Prod. Res. 46, 3825–3857. doi: 10.1080/00207540600787200

CrossRef Full Text | Google Scholar

Chang, D. Y. (1996). Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 95, 649–655. doi: 10.1016/0377-2217(95)00300-2

CrossRef Full Text | Google Scholar

Chou, S.-W., and Chang, Y.-C. (2008). The implementation factors that influence the ERP (Enterprise Resource Planning) benefits. Dec. Support Syst. 46, 149–157. doi: 10.1016/j.dss.2008.06.003

CrossRef Full Text | Google Scholar

Cortés-Aldana, F. A., García-Melón, M., Fernández-de-Lucio, I., Aragonés-Beltrán, P., and Poveda-Bautista, R. (2009). University objectives and socioeconomic results: a multicriteria measuring of alignment. Eur. J. Oper. Res. 199, 811–822. doi: 10.1016/j.ejor.2009.01.065

CrossRef Full Text | Google Scholar

Daguzan, J. (1985). Nitrogenous excretion in a pulmonate gastropod: elona quimperiana (de ferussac) from western brittany. Comp. Biochem. Physiol. B Comp. Biochem. 80, 103–107. doi: 10.1016/0305-0491(85)90429-8

CrossRef Full Text | Google Scholar

Daguzan, J. (1989). Snail Rearing or Heliciculture of Helix Aspersa Muller. Monograph - British Crop Protection Council. Available online at: https://agris.fao.org/agris-search/search.do?recordID=US201301749665.

Google Scholar

Damani, O. (2019). Design of Farm Assessment Index (FAI) for a holistic comparison of farming practices: case of organic and conventional farming systems from two indian states. Agroecol. Sust. Food Syst. 43, 329–357. doi: 10.1080/21683565.2018.1547941

CrossRef Full Text | Google Scholar

de Vaufleury, A., and Gimbert, F. (2009). Life history traits of the snail helix aperta born from tunisia raised in a laboratory environment: influence of photoperiod. C. R. Biol. 332, 795–805. doi: 10.1016/j.crvi.2009.04.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Dickerson, J. A., and Kosko, B. (1994). Virtual worlds as fuzzy cognitive maps. Presence 3, 173–189. doi: 10.1162/pres.1994.3.2.173

CrossRef Full Text | Google Scholar

Dupont-Nivet, M., Coste, V., Coinon, P., Bonnet, J. C., and Blanc, J. M. (2000). Rearing density effect on the production performance of the edible snail helix aspersa müller in indoor rearing. Ann. Zoot. 49, 447–456. doi: 10.1051/animres:2000135

CrossRef Full Text | Google Scholar

Dutta, S., Maiti, S., Garai, S., Abrar, F., Jha, S. K., Bhakat, M., et al. (2020). Analyzing adaptation strategies to climate change followed by the farming community of the Indian Sunderbans using Analytical Hierarchy Process. J. Coastal Conserv. 24, 1–14. doi: 10.1007/s11852-020-00779-z

CrossRef Full Text | Google Scholar

FAO (2011). Farming Systems Report, Rome: Food and Agriculture Organization of the United Nations. Available online at: http://www.fao.org/3/a-an535e.pdf

FAO (2017). Leveraging Food Systems for Inclusive Rural Transformation. The State of Food and Agriculture 2017. Rome: Food and Agriculture Organization of the United Nations.

Fekadu, E., and Negese, A. (2020). GIS assisted suitability analysis for wheat and barley crops through AHP approach at yikalo sub-watershed, Ethiopia. Cogent Food Agricul. 6:1743623. doi: 10.1080/23311932.2020.1743623

CrossRef Full Text | Google Scholar

Galdeano-Gómez, E., Aznar-Sánchez, J. A., Pérez-Mesa, J. C., and Piedra-Muñoz, L. (2017). Exploring synergies among agricultural sustainability dimensions: an empirical study on farming system in almería (Southeast Spain). Ecol. Econ. 140, 99–109. doi: 10.1016/j.ecolecon.2017.05.001

CrossRef Full Text | Google Scholar

García, A., Perea, J. M., Mayoral, A., Acero, R., Martos, J., Gómez, G., et al. (2006). Laboratory rearing conditions for improved growth of juvenile helix aspersa müller snails. Lab. Anim. 40, 309–316. doi: 10.1258/002367706777611505

PubMed Abstract | CrossRef Full Text | Google Scholar

Gelabert, C., Bargas, S. D., Rositano, F., and González, O. (2014). Heliciculture activity in Argentina from the soft systems approach. Arch. Zoot. 63, 97–108. doi: 10.4321/S0004-05922014000100010

CrossRef Full Text | Google Scholar

Golden, B. L. (1989). The Analytic Hierarchy Process: Applications and Studies. New York, NY: Springer-Verlag. doi: 10.1007/978-3-642-50244-6

CrossRef Full Text | Google Scholar

Gray, S. A., Gray, S., Cox, L. J., and Henly-Shepard, S. (2013). “Mental modeler: a fuzzy-logic cognitive mapping modeling tool for adaptive environmental management,” in 2013 46^th Hawaii International Conference on System Sciences (Grand Wailea, Maui, HI: IEEE), 965–973. doi: 10.1109/HICSS.2013.399

CrossRef Full Text | Google Scholar

Groumpos, P. P., and Anninou, A. P. (2017). A critical overview of modelling methods and decision support systems for complex dynamic systems. Ann. Fac. Eng. Hunedoara-Int. J Eng. 15.

Google Scholar

Hatziioannou, M., Issari, A., Neofitou, C., Aifadi, S., and Matsiori, S. (2014). Economic analysis and production techniques of snail farms in Southern Greece. World J. Agricul. Res. 2, 276–279. doi: 10.12691/wjar-2-6-5

CrossRef Full Text | Google Scholar

Hawkes, C., and Halliday, J. (2017). What makes Urban Food Policy Happen? Insights from Five Case Studies. Report. International Panel of Experts on Sustainable Food Systems. Available online at: https://openaccess.city.ac.uk/id/eprint/19325/

Google Scholar

Huerga, A. V. (2002). A Balanced Differential Learning Algorithm In Fuzzy Cognitive Maps. 16th Int. Catalonia: Workshop Qualitat. Reason.

Google Scholar

Jess, S., and Marks, R. J. (1998). Effect of temperature and photoperiod on growth and reproduction of helix aspersa var. maxima. J. Agric. Sci. 130, 367–372. doi: 10.1017/S0021859698005346

CrossRef Full Text | Google Scholar

Kahraman, C., Cebeci, U., and Ulukan, Z. (2003). Multi-criteria supplier selection using fuzzy AHP. Logist. Inform. Manag. 16, 382–394. doi: 10.1108/09576050310503367

CrossRef Full Text | Google Scholar

Karimi, V., Karami, E., Karami, S., and Keshavarz, M. (2020). Adaptation to Climate Change Through Agricultural Paradigm Shift. Environment, Development and Sustainability. Springer. doi: 10.1007/s10668-020-00825-8

CrossRef Full Text | Google Scholar

Kiebre-Toe, M. B., Borges, E., Maurin, F., Richard, Y., and Kodjo, A. (2003). Study of Gram negative bacteria flora in breeding snails (Helix aspersa). Revue de Médecine Vétérinaire (France). Available online at: https://agris.fao.org/agris-search/search.do?recordID=FR2004000096.

Google Scholar

Kilincci, O., and Onal, S. A. (2011). Fuzzy AHP approach for supplier selection in a washing machine company. Expert Syst. Appl. 38, 9656–9664. doi: 10.1016/j.eswa.2011.01.159

CrossRef Full Text | Google Scholar

Kokkinos, K., and Karayannis, V. (2020). Supportiveness of low-carbon energy technology policy using fuzzy multicriteria decision-making methodologies. Mathematics 8:1178. doi: 10.3390/math8071178

CrossRef Full Text | Google Scholar

Kokkinos, K., Karayannis, V., and Moustakas, K. (2020). Circular Bio-economy via energy transition supported by fuzzy cognitive map modeling towards sustainable low-carbon environment. Sci. Total Environ. 721:137754. doi: 10.1016/j.scitotenv.2020.137754

PubMed Abstract | CrossRef Full Text | Google Scholar

Kordi, M., and Brandt, S. A. (2012). Effects of increasing fuzziness on analytic hierarchy process for spatial multicriteria decision analysis. Comput. Environ. Urban Syst. 36, 43–53. doi: 10.1016/j.compenvurbsys.2011.07.004

CrossRef Full Text | Google Scholar

Kosko, B. (1986). Fuzzy cognitive maps. Int. J. ManeMachine Studies. 24, 65–75. doi: 10.1016/S0020-7373(86)80040-2

CrossRef Full Text | Google Scholar

Kosko, B. (1992). Neural Networks and Fuzzy Systems: A Dynamical Systems Approach to Machine Intelligence. New York, NY: Prentice-Hall.

Google Scholar

Kurka, T., and Blackwood, D. (2013). Participatory selection of sustainability criteria and indicators for bioenergy developments. Renew. Sust. Energy Rev. 24, 92–102. doi: 10.1016/j.rser.2013.03.062

CrossRef Full Text | Google Scholar

Lak Kamari, M., Isvand, H., and Alhuyi Nazari, M. (2020). Applications of multi-criteria decision-making (MCDM) methods in renewable energy development: a review. Renew. Energy Res. Appl. 1, 47–54. doi: 10.22044/RERA.2020.8541.1006

CrossRef Full Text | Google Scholar

Libois, R., and Codjia, J. C. (2001). [Snails and mushrooms to the rescue of sustainable developpement [Benin]]. Revue Trimestrielle de Conservation de la Nature et de Gestion Durable d'Ardenne et Gaume. Available online at: https://agris.fao.org/agris-search/search.do?recordID=BE2002000844.

Linhart, Y. B., and Thompson, J. D. (1995). Terpene-based selective herbivory by helix aspersa (Mollusca) on Thymus Vulgaris (Labiatae). Oecologia 102, 126–132. doi: 10.1007/BF00333320

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Eckert, C. M., and Earl, C. (2020). A review of fuzzy AHP methods for decision-making with subjective judgements. Expert Syst. Appl. 161:113738. doi: 10.1016/j.eswa.2020.113738

CrossRef Full Text | Google Scholar

Lu, L. Y., Wu, C. H., and Kuo, T. C. (2007). Environmental principles applicable to green supplier evaluation by using multi-objective decision analysis. Int. J. Prod. Res. 45, 4317–4331. doi: 10.1080/00207540701472694

CrossRef Full Text | Google Scholar

Markou, M., Stylianou, A., Giannakopoulou, M., and Adamides, G. (2020). Identifying business-to-business unfair trading practices in the food supply chain: the case of cyprus. New Medit. 19, 19–34. doi: 10.30682/nm2001b

CrossRef Full Text | Google Scholar

Massawe, B. H., Kaaya, A. K., and Slater, B. (2019). Involving Small Holder Farmers in the Agricultural Land Use Planning Process Using Analytic Hierarchy Process in Rice Farming Systems of Kilombero Valley, Tanzania, February. Available online at: http://www.suaire.sua.ac.tz/handle/123456789/2776

Google Scholar

Mateou, N. H., Moiseos, M., and Andreou, A. S. (2005). “Multi-objective evolutionary fuzzy cognitive maps for decision support,” in Proceeding IEEE Congr Evol Comput. (Edinburgh: IEEE), 824–830. doi: 10.1109/CEC.2005.1554768

CrossRef Full Text | Google Scholar

Milinsk, M. C., das Graças Padre, R., Hayashi, C., de Oliveira, C. C., Visentainer, J. V., de Souza, N. E., et al. (2006). Effects of feed protein and lipid contents on fatty acid profile of snail (Helix Aspersa Maxima) meat. J. Food Comp. Anal. 19, 212–216. doi: 10.1016/j.jfca.2004.09.011

CrossRef Full Text | Google Scholar

Milinsk, M. C., das Graças Padre, R., Hayashi, C., de Souza, N. E., and Matsushita, M. (2003). Influence of diets enriched with different vegetable oils on the fatty acid profiles of snail helix aspersa maxima. Food Chem. 82, 553–558. doi: 10.1016/S0308-8146(03)00010-4

CrossRef Full Text | Google Scholar

Mourhir, A., Papageorgiou, E. I., Kokkinos, K., and Rachidi, T. (2017). Exploring precision farming scenarios using fuzzy cognitive maps. Sustainability 9:1241. doi: 10.3390/su9071241

CrossRef Full Text | Google Scholar

Novak, J. D., and Cañas, A. J. (2008). The Theory Underlying Concept Maps and How to Construct and Use Them. Technical Report IHMC CmapTools 2006-01 Rev 01-2008. Florida Institute for Human and Machine Cognition, Pensacola, Florida, USA. [Online] URL: Available online at: http://Cmap.Ihmc.Us/Publications/Researchpapers/Theoryunderlyingconceptmaps.Pdf

Oblak, L., and Glavonjić, B. (2015). A model for the evaluation of radio advertisements for the sale of timber products. Drvna Ind. 65, 303–308. doi: 10.5552/drind.2014.1357

CrossRef Full Text | Google Scholar

Özesmi, U., and Özesmi, S. L. (2004). Ecological models based on people's knowledge: a multi-step fuzzy cognitive mapping approach. Ecol. Modell. 176, 43–64. doi: 10.1016/j.ecolmodel.2003.10.027

CrossRef Full Text | Google Scholar

Papageorgiou, E., Stylios, C. D., and Groumpos, P. P. (2004). Active Hebbian learning algorithm to train fuzzy cognitive maps. Int. J. Approx. Reason. 37, 219–249. doi: 10.1016/j.ijar.2004.01.001

CrossRef Full Text | Google Scholar

Papageorgiou, E. I., Kokkinos, K., and Dikopoulou, Z. (2016). “Fuzzy sets in agriculture,” in Fuzzy Logic in Its 50th Year: New Developments, Directions and Challenges, edited by Cengiz Kahraman, Uzay Kaymak, and Adnan Yazici. Studies in Fuzziness and Soft Computing (Cham: Springer International Publishing), 211–233. doi: 10.1007/978-3-319-31093-0_10

CrossRef Full Text | Google Scholar

Rao, C. S., Kareemulla, K., Krishnan, P., Murthy, G. R. K., Ramesh, P., Ananthan, P. S., et al. (2019). Agro-ecosystem based sustainability indicators for climate resilient agriculture in india: a conceptual framework. Ecol. Indic. 105, 621–633. doi: 10.1016/j.ecolind.2018.06.038

CrossRef Full Text | Google Scholar

Saaty, T. L. (1980). The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation. New York, NY: McGraw-Hill International Book Coy.

Google Scholar

Saaty, T. L., and Vargas, L. G. (2012). “A new approach to the middle east conflict: the analytic hierarchy process,” in Models, Methods, Concepts & Applications of the Analytic Hierarchy Process. International Series in Operations Research & Management Science, Vol. 175 (Boston, MA: Springer). doi: 10.1007/978-1-4614-3597-6_15

CrossRef Full Text | Google Scholar

Segade, P., Crespo, C., García, N., García-Estévez, J. M., Arias, C., and Iglesias, R. (2011). Brachylaima Aspersae n. Sp. (Digenea: Brachylaimidae) infecting farmed snails in nw spain: morphology, life cycle, pathology, and implications for heliciculture. Vet. Parasitol. 175, 273–286. doi: 10.1016/j.vetpar.2010.10.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Shahrin, S., Krupnik, T. J., Aravindakshan, S., and Groot, J. C. J. (2020). Mental models and the potential for crop intensification in coastal Bangladesh: how do farmers' perceptions reflect proposed agricultural development pathways? Available online at: https://repository.cimmyt.org/bitstream/handle/10883/20941/62499.pdf?sequence=1

Stach, W., Kurgan, L. A., Pedrycz, W., and Reformat, M. (2005). Genetic learning of fuzzy cognitive maps. Fuzzy Sets Syst. 153, 371–401. doi: 10.1016/j.fss.2005.01.009

CrossRef Full Text | Google Scholar

Stylianou, A., Sdrali, D., and Apostolopoulos, C. (2020). Capturing the diversity of mediterranean farming systems prior to their sustainability assessment: the case of cyprus. Land Use Policy 96:104722. doi: 10.1016/j.landusepol.2020.104722

CrossRef Full Text | Google Scholar

Toader-Williams, A., and Bentea, M. (2010). Comparative study on the adaptation and growth dynamics of the helix pomatia and helix aspersa muller terrestrial snails under different feeding regimes. Sci. Papers Anim. Sci. Biotechnol. 43, 143–150.

Google Scholar

Toader-Williams, A., and Sara, A. (2010). Studies on the edible terrestrial snails helix aspersa muller food conversion ratio in a confined microclimate system. Sci. Papers Anim. Sci. Biotechnol. 43, 133–142.

Google Scholar

Tsadiras, A., Pempetzoglou, M., and Viktoratos, I. (2020). Making predictions of global warming impacts using a semantic web tool that simulates fuzzy cognitive maps. Comput Econ. doi: 10.1007/s10614-020-10025-1

CrossRef Full Text | Google Scholar

Tsoutsos, D., Kakagia, D., and Tamparopoulos, K. (2009). The efficacy of helix aspersa müller extract in the healing of partial thickness burns: a novel treatment for open burn management protocols. J. Dermatol. Treat. 20, 219–222. doi: 10.1080/09546630802582037

PubMed Abstract | CrossRef Full Text | Google Scholar

Tzouramani, I., Mantziaris, S., and Karanikolas, P. (2020). Assessing sustainability performance at the farm level: examples from greek agricultural systems. Sustainability 12:2929. doi: 10.3390/su12072929

CrossRef Full Text | Google Scholar

Ullah, K., Garg, H., Mahmood, T., Jan, N., and Ali, Z. (2020). Correlation coefficients for t-spherical fuzzy sets and their applications in clustering and multi-attribute decision making. Soft Computing 24, 1647–1659. doi: 10.1007/s00500-019-03993-6

CrossRef Full Text | Google Scholar

van Vliet, M., Kok, K., and Veldkamp, T. (2010). Linking stakeholders and modelers in scenari o studies: the use of Fuzzy Cognitive Maps as a communication and learning tool. Futures 42, 1–14. doi: 10.1016/j.futures.2009.08.005

CrossRef Full Text | Google Scholar

Wang, W. M., and Peng, H. H. (2020). A fuzzy multi-criteria evaluation framework for urban sustainable development. Mathematics 8:330. doi: 10.3390/math8030330

CrossRef Full Text | Google Scholar

Wang, Y. M., and Chin, K. S. (2011). Fuzzy analytic hierarchy process: a logarithmic fuzzy preference programming methodology. Int. J. Approx. Reas. 52, 541–553. doi: 10.1016/j.ijar.2010.12.004

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Inform. Control 8, 338–353. doi: 10.1016/S0019-9958(65)90241-X

CrossRef Full Text | Google Scholar

Zhao, N., Xu, Z., and Ren, Z. (2019). Hesitant fuzzy linguistic prioritized superiority and inferiority ranking method and its application in sustainable energy technology evaluation. Inform. Sci. 478, 239–257. doi: 10.1016/j.ins.2018.11.022

CrossRef Full Text | Google Scholar

Zhu, Y., and Zhang, W. (2008). “An integrated framework for learning fuzzy cognitive map using RCGA and NHL algorithm,” in International Conference Wireless Communication Network Mobile Computation (Dalian). doi: 10.1109/WiCom.2008.2527

CrossRef Full Text | Google Scholar