Reliability of a non-invasive method to calculate buffer capacity after exhaustive cycling exercise of 20 s to 12 min: a pilot study

Traditionally, buffer capacity (β) is measured on muscle biopsies by measuring changes in muscle pH in relation to exposure of standardized quantities of hydrochloric acid. This is an invasive approach requiring specific equipment and trained personnel which limits its usability in a normal training context. Assessing β using capillary blood lactate concentration (BLC) and pH values has been proposed as a more practical and cost-effective approach. The reliability of the input BLC and pH data on the calculations of β after maximal sprint and endurance exercise has not yet been investigated and was major aim of our study. Eleven subjects performed six maximal performance tests ranging from 20 s to 12 min duration over a 2-week period. All subjects were familiarized with the test conditions. For each performance test, pre and posttest BLC and pH was measured and used to calculate β using the Henderson-Hasselbach equation. As BLC_pre and pH_pre values showed poor reliability, β calculations were repeated using constants for BLC_pre (1.23 mmol·L⁻¹) and pH_pre (7.426) chosen from the average values in the experimental data. Test-retest reliability for BLC_pre (ICC: 0.12, 95% CI −0.49–0.65, n.s.) and pH_pre (ICC: 0.40, 95% CI −0.22–0.79, n.s.) was poor, whereas BLC_post (ICC: 0.95, 95% CI 0.82–0.99, p < 0.05) and pH_post (ICC: 0.89, 95% CI 0.65–0.97, p < 0.05) displayed good to excellent reliability. Good reliability was observed for β calculated from the Henderson-Hasselbalch equation utilizing BLC_post and pH_post only (ICC: 0.86, 95% CI 0.55–0.96, p < 0.05). The validity of this method in comparison with gold-standard methods needs further scientific investigation.

1 Introduction

Intense muscular activity involving a high energy contribution from non-oxidative pathways, is associated with large ionic changes in the muscle, including the accumulation of hydrogen ions (H⁺). While the role H⁺ has in causing muscle fatigue has been questioned (1–3) and is still under investigation, the accumulation of H⁺ has been shown to contribute to a reduction in exercise performance by affecting muscle fatigue (4, 5) and the perception of effort (central fatigue) (6). Proton accumulation depends on both the production and removal of H⁺. The intra- and extracellular buffer systems act to reduce the buildup of free H⁺ and reduces the fluctuations in cellular pH during high-intensity (non-steady-state) exercise (7). Muscle buffer capacity (β_m) has been reported to be higher in highly trained team-sport athletes, sprinters and rowers than in marathon runners or untrained subjects (8, 9). This suggests that athletes involved in sports with a greater anaerobic demand may have a greater β_m. However, the results of cross-sectional studies do not allow us to conclude whether this greater β_m is due to event selection, or the type of training undertaken. Buffer capacity can be improved by specific training. High-intensity training with bouts of 120%–140% of the anaerobic threshold has been shown to improve β_m with 17%–25% (10, 11) whereas moderate intensity training (11) or high-repetition resistance training (12) did not improve β_m. Pretraining β_m negatively correlated with changes in β_m following high-intensity training (13). Increasing β_m by consuming sodium bicarbonate has been shown to be effective in improving buffer capacity and maximal exercise performance of 30 s to 12 min duration, typically associated with high accumulation of H⁺ (14–18). The ergogenic effects of sodium bicarbonate supplements seems to be more pronounced in individuals with lower β_m or training status (19). Therefore, knowing the individual's β_m provide essential information to make informed decisions on training or supplement interventions.

Traditionally, β_m is measured on muscle biopsies by measuring changes in muscle pH in relation to the exposure of standardized quantities of hydrochloric acid (HCl). From the fitted titration trend line, the subject's β_m is calculated (20). Alternatively, β_m can also be assessed based on the ratio of the pre-post exercise lactate concentration (Δlactate) over the pre-post exercise pH (ΔpH) in muscle tissue (8, 21). Skeletal muscle ³¹P magnetic resonance spectroscopy (³¹P MRS) can be utilized as a non-invasive approach to investigate muscle metabolism in resting and exercising subjects (22, 23). Unfortunately, all these measuring techniques of β_m are expensive, invasive (muscle biopsies), time consuming and require laboratory equipment and trained personnel to perform the measurements and data analysis. Consequently, these methods are hardly applicable in the context of physical training and performance monitoring of athletes. Sahlin et al. demonstrated that blood lactate and blood pH mimics the behavior of lactate and pH in the exercising muscle tissue (21). This can be explained by the co-transport of lactate and H⁺ from the intracellular to the extracellular space by the lactate-proton transporters, monocarboxylate transporter 1 (MCT1) and 4 (MCT4) (24–26). The lactate/H⁺ co-transport seems to be the most important system to remove H⁺ from the intracellular to the extracellular space during high-intensity exercise (24, 25). The intracellular accumulation of H⁺ depends on the extracellular H⁺ concentration. H⁺ efflux out of the muscle cell has been reported to be inhibited by extracellular acidosis (27) and enhanced by a greater extracellular buffer concentration (28). Therefore, lactate and H⁺ accumulation in the blood might be useful markers for lactate and H⁺ accumulation in the exercising muscle and valid input data to calculate β (29). Whereas traditional measuring techniques of β are expensive, invasive, time consuming, and therefore, are difficult to implement during physiological monitoring of athletes, assessing β from pH and lactate in capillary blood samples might overcome such issues.

To obtain reliable calculations of β, the reliability of input data must be ensured. Sources of variability are found in the analyzer used and in biological variability. The reliability and validity of lactate analyzers is extensively investigated (30–32). The within-sample standard deviations for handheld lactate analyzers are in general <0.5 mmol·l⁻¹ with greater imprecision (>1 mmol·l⁻¹) for lactate concentrations >15 mmol·l⁻¹ (30, 31, 33) as can be observed after short maximal exercise. The biological variability in the pre-exercise lactate response is ∼30% (34, 35). How these sources of variability affect the calculation of β is not yet investigated.

The purpose of this study is to investigate the test-retest reliability of the variables for calculating β (i.e., pre- and posttest blood lactate concentration and pH). We hypothesize that these input variables display robust reliability allowing for further calculation of β. Secondly, we investigate the consistency of the calculation of β under varying test conditions. We hypothesize that the calculation of β is independent of the test duration in maximal, non-steady state efforts.

2 Materials and methods

2.1 Subjects

Eleven endurance trained male subjects (mean ± SD: age 32.2 ± 15.2 years, mass 70.9 ± 6.7 kg, height 180.4 ± 6.6 cm, body fat 14 ± 5.6%, $\dot{V}{\mathrm{O}}_{2\max }$ 4.18 ± 0.48 L·min⁻¹, $v\mathrm{L}{\mathrm{a}}_{\max }$ 0.46 ± 0.08 mmol·L⁻¹·s⁻¹) gave their informed written consent to take part in the study. All subjects were familiar with laboratory exercise testing on the cycle ergometer. The study protocol was approved by the ethics committee of the Hildesheim University, Germany.

2.2 Study protocol

The subjects performed three experimental sessions over a two-week period and completed six maximal performance tests of 20 s to 12 min duration (Figure 1). These test durations were selected because they are associated with large accumulation of hydrogen ions (H⁺) in the muscle and blood and are affected by alterations in buffer capacity (16–18). The day before the experiments the subjects were allowed to perform maximum of 1 h of low-intensity training. Furthermore, the subjects were encouraged to consume ∼3 h before the exercise test a standardized meal (∼2,700 kJ; 71% carbohydrate, 15% fat, 14% protein). To avoid fluctuations of initial muscle glycogen content, they were asked to adopt an identical training and food regimen for all subsequent experimental exercise sessions (36). To account for diurnal variation, subjects reported to the experimental sessions at the same time of the day. All cycling tests were performed on the subject's personal racing bike mounted on a calibrated cycle ergometer (Cyclus 2, Leibzig, Germany). The Cyclus 2 is an electromagnetically braked ergometer and measures power output with an accuracy error of 2% according to the manufacturer. The gear ratio was fixed at either 53 × 12 or 52 × 12, depending on the front chainring of the subject's bicycle. The cycling tests were performed in an air-conditioned exercise laboratory (19°C, 60% relative humidity) and supervised by trained personnel. The subjects were verbally encouraged to perform all tests with maximal effort. During all tests, air ventilation was provided to assist body cooling (37).

Figure 1

Figure 1. Overview of the experimental tests.

2.2.1 Experimental session 1

At the first visit to the laboratory, the subjects body length, body mass and body composition (Seca, BCA 525, Hamburg Germany) were measured. After these measurements, subjects performed a 10 min warm-up at a self-selected cadence at 1.5 W·kg⁻¹. This warm-up phase was followed by 3 min of passive recovery to reduce the aerobic energy contribution in the subsequent sprint. A capillary blood sample was taken from a hyperaemic earlobe (Finalgon®, Frankfurt, Germany) to determine pre-test blood lactate concentration (BLC_pre) (EKF, Biosen C-line, Barleben, Germany) and blood pH (pH_pre) (Radiometer ABL 90 Flex, Copenhagen, Denmark).

The first test consisted of a 20 s isokinetic sprint at 120 rev·min⁻¹. During the sprint subjects had to maintain a seated position. The initial load of the ergometer was set at three times the fat free mass of the subjects (in Newton) and was activated at 60 rev·min⁻¹ (SPR1). After the sprint the subjects rested 10 min seated on the saddle, without pedaling. During this period of passive rest, post-test capillary blood samples were taken at 1-min intervals to capture the highest lactate (BLC_post) and lowest pH (pH_post) values. The maximal lactate accumulation rate $(v\mathrm{L}{\mathrm{a}}_{\max })$ was calculated using the formula below (38, 39):

$v\mathrm{L}{\mathrm{a}}_{\max }={\displaystyle \frac{\mathrm{BL}{\mathrm{C}}_{\mathrm{post}}-\mathrm{BL}{\mathrm{C}}_{\mathrm{pre}}}{20\mathrm{s}-t_{\mathrm{alac}}}}$

T_alac = time (s) from time 0 to 3% drop in peak power (39, 40).

Thereafter, the subjects cycled for minimum 15 min at 1.5 W·kg⁻¹ to promote recovery between tests. The level of recovery was controlled by measuring BLC. Subjects with BLC exceeding 2 mmol·L⁻¹ extended active recovery with 3 min. To assess test-retest reliability, the isokinetic test was repeated with identical ergometer settings, post-exercise recovery procedures and BLC and pH measurements (SPR2). After these 2 sprint-tests a ramp protocol was performed to assess $\dot{V}{\mathrm{O}}_{2\max }$. The test started at 100 W. Workload increased every 30 s with 20 W until volitional exhaustion. The subjects were allowed to use their preferred cadence (97 ± 7 rev·m⁻¹). Breathing gases were analyzed (Omnical Sport, Maastricht Instruments, The Netherlands) and heart rate recorded (Polar, Kempele, Finland). A maximal effort was established when 2 or more of the following criteria were met (41):

• Plateau in $\dot{V}{\mathrm{O}}_2$ (<120 ml·min⁻¹) despite an increase in workload

• Maximal heart rate within 10 beats of age predicted maximal heart rate (220-age)

• RER > 1.1

• BLC > 8.0 mmol·L⁻¹

2.2.2 Experimental session 2

On the second laboratory visit, subjects performed a 10 min warm-up at a self-selected cadence at 1.5 W·kg⁻¹. At the end of the warm-up, a capillary blood sample was taken from a hyperaemic earlobe to determine BLC_pre and pH_pre. Thereafter, a 6 min maximal time trial (TT₆) was performed. The subjects were instructed to achieve the highest possible average power output for the given test duration. The subjects could adjust their workload intensity (5 W steps) at any time. The subject performed the test in the seated position. They used the same pedaling frequency as from the ramp test (experimental session 1). After the time trial, the subjects rested 10 min seated on the saddle, without pedaling. During this period of passive rest, post-test capillary blood samples were taken at 1-min intervals for BLC_post and pH_post determination.

2.2.3 Experimental session 3

On the third laboratory visit, subjects performed a 10 min warm-up at a self-selected cadence at 1.5 W·kg⁻¹. At the end of the warm-up, a capillary blood sample was taken from a hyperaemic earlobe to determine BLC_pre and pH_pre. The subjects completed two maximal time trials of 3 min (TT₃) and 12 min (TT₁₂) duration, interspersed with ∼25 min recovery. The subjects were instructed to achieve the highest possible average power output for the given test duration. The subjects could adjust their workload intensity (5 W steps) at any time. The subject performed the test in the seated position. They used the same pedaling frequency as from the ramp test (experimental session 1). After each time trial, the subjects rested 10 min seated on the saddle, without pedaling. During this period of passive rest, post-test capillary blood samples were taken at 1-min intervals for BLC_post and pH_post determination. Thereafter, the subjects cycled for minimum 15 min at 1.5 W·kg⁻¹ to promote recovery between tests. The level of recovery was controlled by measuring BLC. Subjects with BLC exceeding 2 mmol·L⁻¹ extended active recovery with 3 min.

2.3 Calculation of buffer capacity

The buffer capacity (β) was calculated according to Equations 1, 2, using the Henderson-Hasselbalch equation (42). The Henderson-Hasselbalch equation is a mathematical formula that describes the relationship between the pH of a solution, the dissociation constant of an acid (pKa), and the ratio of the conjugate base to the undissociated acid. It is frequently used in biochemistry to calculate the pH of buffer systems. The dissociation constant (pK_a) for lactate was set at 3.87. The transformation of the Henderson-Hasselbalch equation into the equation applied in this study is presented in the Supplementary Materials.

$\mathrm{Method}1:\beta 1={\displaystyle \frac{\left({\displaystyle \frac{\mathrm{BL}{\mathrm{C}}_{\mathrm{post}}}{{10}^{(\mathrm{p}{\mathrm{H}}_{\mathrm{post}}-3.87)}}-{\displaystyle \frac{\mathrm{BL}{\mathrm{C}}_{\mathrm{pre}}}{{10}^{(\mathrm{p}{\mathrm{H}}_{\mathrm{pre}}-3.87)}}}}\right)}{\mathrm{p}{\mathrm{H}}_{\mathrm{post}}-\mathrm{p}{\mathrm{H}}_{\mathrm{pre}}}}(1)$

Pre-examination of the BLC_pre and pH_pre data revealed low test-retest reliability (Table 1). Therefore, we calculated β with the measured pretest values as well as with a constant BLC_pre and pH_pre. For this purpose, we used the average BLC_pre (1.23 mmol·L⁻¹) and pH_pre values (7.426) from all tests, to obtain representative constants (Equation 2).

$\mathrm{Method}2:\beta 2={\displaystyle \frac{\left({\displaystyle \frac{\mathrm{BL}{\mathrm{C}}_{\mathrm{post}}}{{10}^{(\mathrm{p}{\mathrm{H}}_{\mathrm{post}}-3.87)}}-{\displaystyle \frac{1.23}{{10}^{(7.426-3.87)}}}}\right)}{\mathrm{p}{\mathrm{H}}_{\mathrm{post}}-7.426}}(2)$

Table 1

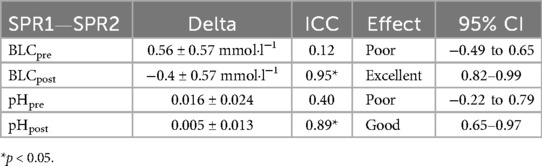
Table 1. Intraclass correlation coefficients (ICC) (95% CI): Pre-exercise blood lactate concentration (BLC_pre), pre-exercise pH (pH_pre), post-exercise BLC (BLC_post) and pH (pH_post). SPR1, first isokinetic sprint; SPR2, second isokinetic sprint; (details see methods section).

2.4 Statistical analysis

Raw data was processed using Microsoft Excel (version 16.92, Redmond, USA). Statistical analyses (Mean, standard deviations, repeated measures ANOVA) were performed using GRAPHPAD PRISM (version 10 GraphPad Prism Software, Boston, USA). The Shapiro Wilk test was used to evaluate the normality of the data. Descriptive statistics were calculated for all variables and presented as mean ± standard deviation (SD).

The reliability of the β calculations depends on the test-retest reliability of the input data. Therefore, the reliability of pre and post BLC and pH values for the sprint tests was quantified using intraclass correlation coefficients (ICC) (JASP statistical software, version 0.19 for Apple Silicon, The Netherlands). The reliability of the β calculations for the sprint tests was assessed using ICC. ICC values less than 0.5, between 0.5 and 0.75, between 0.75 and 0.9 and greater than 0.9 are indicative of poor, moderate, good and excellent reliability, respectively (43).

The consistency of the pre and post BLC and pH values and β1 and β2 under varying test conditions was evaluated with a repeated measures ANOVA and Pearson correlation coefficients. Bland–Altman plot analysis (expressed as the mean ± 1.96 SD) was used to quantify the bias and the range of agreement between SPR1 and SPR2 for BLC_pre, BLC_post, pH_pre, pH_post, β1 and β2 with 95% limits of agreement.

A probability level of p < 0.05 was set as the criterion for acceptance of statistical significance.

3 Results

3.1 Reliability of input data and buffer capacity

Mean values (±SD) for the measured BLC and pH data are shown in Figure 2. BLC_pre for the first sprint test was lower compared to the other performance tests (Δ ∼ 0.4 mmol·L⁻¹). PH_pre values were similar between the different test conditions (∼7.425). BLC_post were similar in the sprint tests and TT₁₂ (∼8.6 mmol·L⁻¹) and lower than for the other endurance tests (∼11.5 mmol·L⁻¹). An inverse pattern was observed for pH_post values, with pH values for the ramp test and TT₃ and TT₆ being significantly lower (∼7.2) compared to the pH_post after the sprint tests and TT₁₂ (∼7.28).

Figure 2

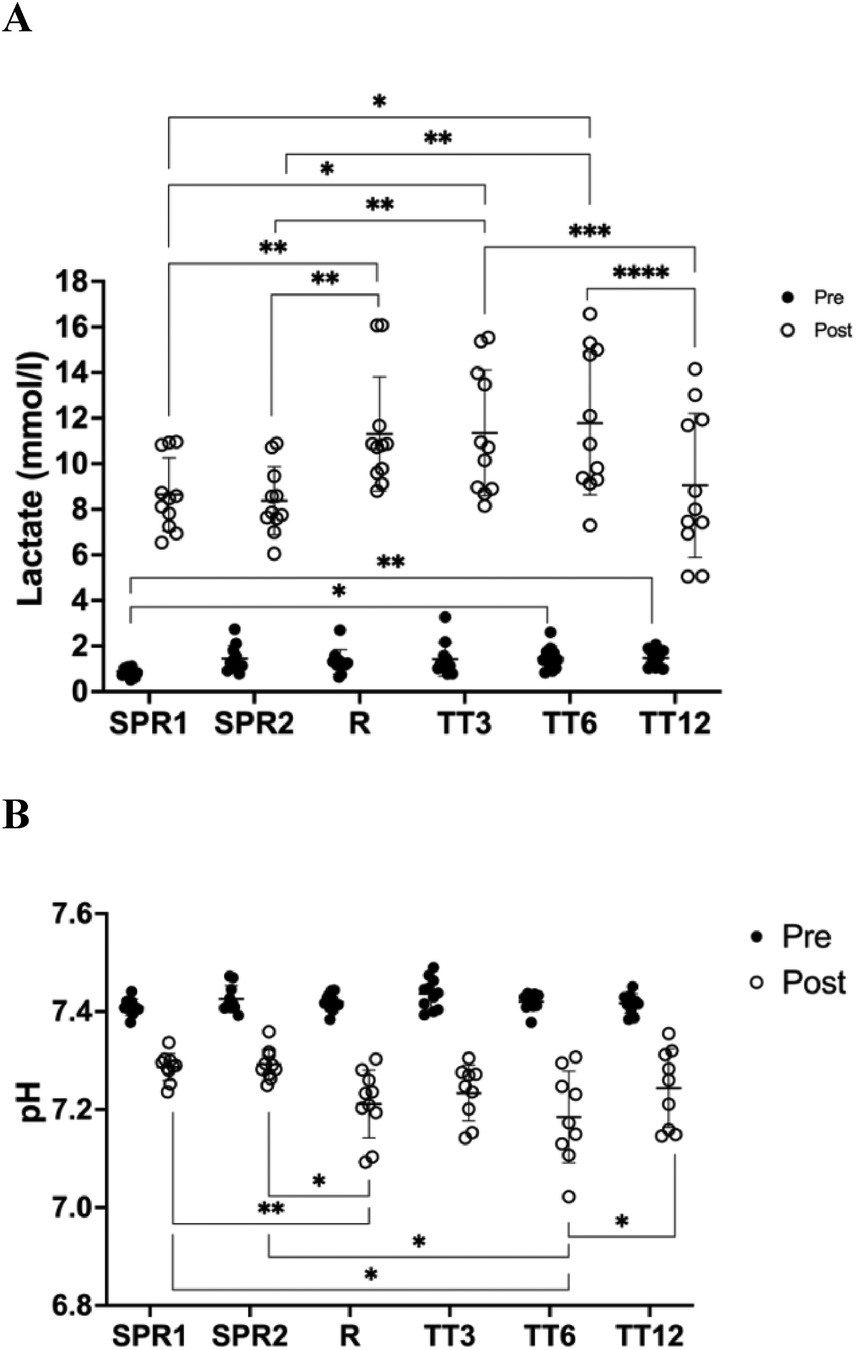
Figure 2. Blood lactate concentration (BLC) (A) and pH (B) (mean ± SD). SPR1, first isokinetic sprint; SPR2, second isokinetic sprint; Ramp, maximal ramp test protocol; TT₃, 3 min maximal time trial; TT₆, 6 min maximal time trial; TT₁₂, 12 min maximal time trial (details see methods section). Repeated measures ANOVA: *p < 0.05, **p < 0.01, ***p < 0.001.

Test-retest reliability for BLC_pre (ICC 0.12, 95% CI −0.49–0.65, n.s.) and pH_pre (ICC 0.40; 95% CI −0.22–0.79, n.s.) was poor. Test-retest reliability for BLC_post (ICC 0.95, 95% CI 0.82–0.99, p < 0.05) and pH_post were good to excellent (ICC0.89, 95% CI 0.65–0.97, p < 0.05) (Table 1).

Test-retest reliability (ICC) for β1 was poor (ICC 0.26, 95% CI −0.38–0.73) n.s.). Good reliability was observed for β2 (ICC 0.86, 95% CI 0.55–0.96, p < 0.05) (Table 2).

Table 2

Table 2. Intraclass correlation coefficients (ICC) of calculated buffer capacity (β1 and β2). SPR1, first isokinetic sprint; SPR2, second isokinetic sprint; (details see methods section).

3.2 Consistency of buffer capacity under varying test conditions

β1 ranged between 210 and 255 μmol·l⁻¹·pH⁻¹ for the sprint tests and between 207 and 245 μmol·l⁻¹·pH⁻¹ for the endurance tests, without significant differences between the tests (Figure 3A). β2 ranged from 209 to 245 μmol·l⁻¹·pH unit⁻¹. β2 was significantly higher in TT₆ compared to TT₁₂ (Δ 31 μmol·l⁻¹·pH unit⁻¹) and similar in all other conditions (Figure 3B).

Figure 3

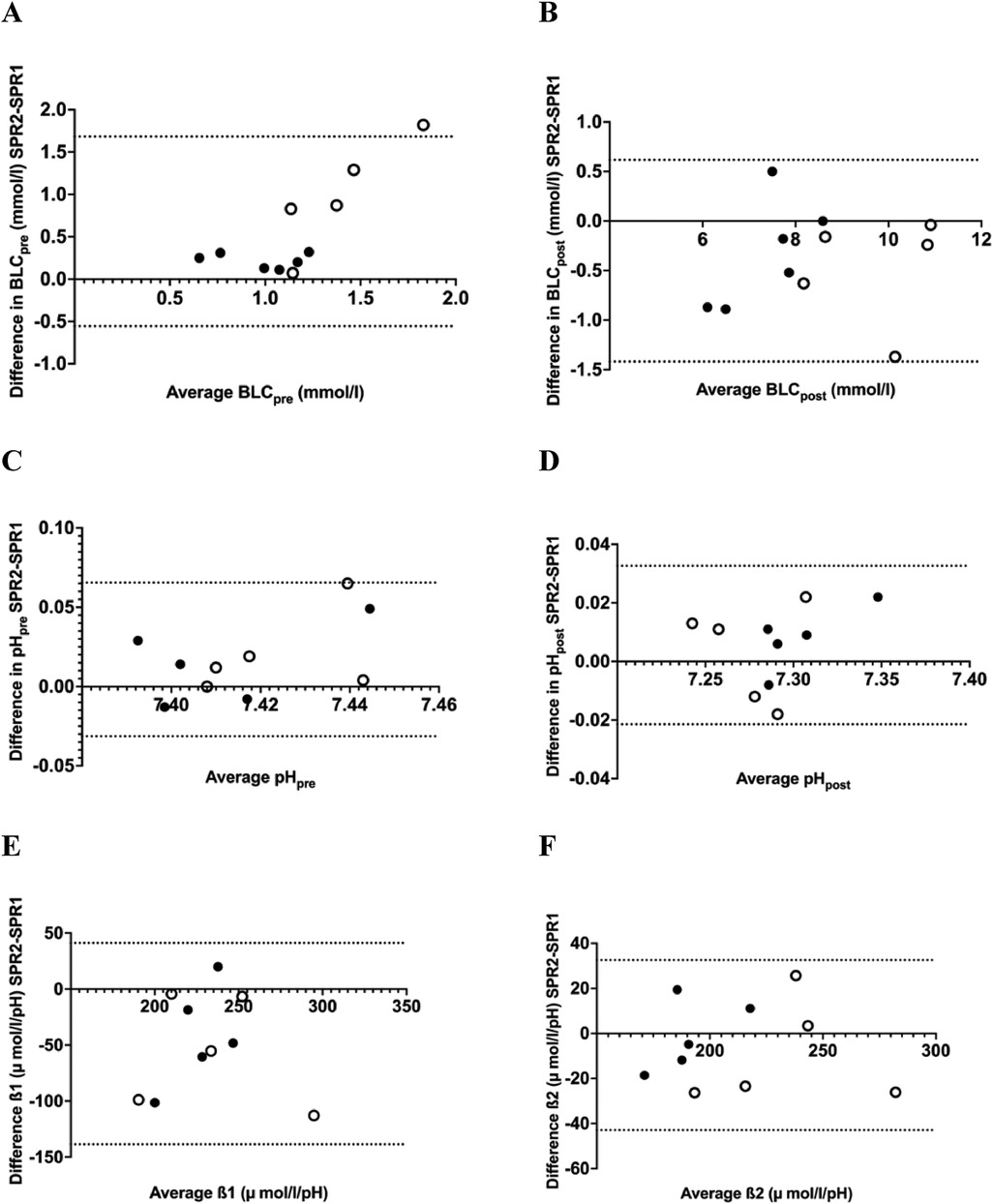
Figure 3. Bland-Altman plots comparing SPR1 and SPR2 for pre-exercise blood lactate concentration (BLC) (A), post-exercise BLC (B), pre-exercise pH (C) post-exercise pH (D) buffer capacity (β1) (E) and β2 (F) open symbols represent subjects with νLa_max ≥ 0.5 mmol·L⁻¹·s⁻¹.

Buffer capacity (β1 and β2) derived from the time trial tests is strongly correlated (r = 0.60–0.86, p < 0.05) (Supplementary Figures S1A,B). No significant correlations were observed between the buffer capacity calculated from the time trial tests in comparison with the buffer capacity calculated from the sprint test (r = 0.18–0.51, n.s.).

4 Discussion

The present study was designed to evaluate the test-retest reliability of pre- and posttest BLC and pH to calculate extracellular buffer capacity (β) during maximal cycling exercise. Secondly, we investigate the consistency of the calculation of β under varying test conditions. The main findings of the present investigation are:

(i) We observed poor reliability for the pretest BLC and pH data.

(ii) We observed good to excellent reliability for the posttest BLC and pH data.

(iii) We observed good reliability for β utilizing BLC_post and pH_post only (β2)

(iv) The calculated β was similar between the test conditions, however β derived from the sprint tests or time trial tests cannot be used interchangeably.

4.1 Reliability of input data

The BLC_pre ranged between 0.5–2.7 mmol·l⁻¹ and BLC_post ranged between 5.7–10.9 mmol·l⁻¹ which was comparable to earlier observations in maximal sprint tests of 10–30 s duration in physically active individuals (44–46). Closer examination of our data revealed that in 4 of the 5 subjects with a νLa_max ≥ 0.5 mmol·L⁻¹·s⁻¹, had elevated BLC_pre in the second sprint (0.8–1.8 mmol·L⁻¹) whereas this was not observed in the subjects with νLa_max < 0.5 mmol·L⁻¹·s⁻¹ (Figure 4A). Apparently in these subjects 10 min of passive followed by ∼20 min of active recovery was not sufficient to restore the BLC to pre-test levels. This result exceed the biological variability of ∼30% for pre-exercise BLC that have been reported in the literature (34, 47) and may have contributed to the reduced reliability in the pre-test BLC.

Figure 4

Figure 4. Buffer capacity calculated with method 1 (β1) (A) and method 2 (β2) (B) (mean ± SD). SPR1, first isokinetic sprint; SPR2, second isokinetic sprint; Ramp, maximal ramp test protocol; TT₃, 3 min maximal time trial; TT₆, 6 min maximal time trial; TT₁₂, 12 min maximal time trial (details see methods section). Repeated measures ANOVA: *p < 0.05.

The pH_pre values ranged between 7.378 and 7.472, in line with literature data (9, 15, 47). The pH_pre was not significantly different between trials, however displayed poor reliability. This is not entirely surprising given the small interindividual variation in baseline pH (9, 47, 48) which might affect the correlation (49). Average pH_post values ranged between 7.185–7.292, with the lowest value observed in TT₆. These data correspond well with earlier observations after supra-maximal exercise (9, 50, 51). Our data showed good reliability for pH_post.

4.2 Test consistency for buffer capacity determination

The buffer capacity (β) was calculated from pre- and posttest BLC and pH data using the Henderson-Hasselbalch equation (42). The Henderson-Hasselbalch equation is a mathematical formula that describes the relationship between the pH of a solution, the dissociation constant of an acid (pKa), and the ratio of the conjugate base to the undissociated acid. The average buffer capacity calculated from this method (β1) ranged between 207 and 255 μmol·l⁻¹·pH⁻¹, without significant differences between the tests. As the resting values for BLC and pH had poor reliability, we recalculated the buffer capacity replacing this data with the average BLC_pre and pH_pre values (method β2). The average buffer capacity calculated from this method (β2) yield similar values compared to β1, except for the first sprint test (Δ 40 μmol·l⁻¹·pH⁻¹). Normative data on muscle buffer capacity (in µmol H⁺·g muscle dry-weight⁻¹·pH⁻¹) is abundantly available in the scientific literature in non-exercising subjects (8, 9), sprint-, teamsport- (9) and endurance athletes (9, 10, 52). Muscle buffer capacity is typically higher in athletes compared to non-athletes, and sprint athletes compared to endurance athletes (9). To the best of our knowledge, reference data for extracellular buffer capacity is not yet documented in the scientific literature. Therefore, the data in our study cannot be compared to literature data.

4.3 Strengths and limitations

Our study provided quantitative data on the reliability of BLC and pH measurement pre and post exercise for the calculation of extracellular buffer capacity. We consider our methodological approach to ensure high data quality as a strength of this study. We tested trained cyclists familiar with maximal exercise testing in a laboratory to prevent learning or training effects. The measurements were performed by trained personal using bench-top lactate and pH analyzers to minimize sources of measurement error. It has repeatedly been shown that handheld lactate analyzers lack the accuracy of bench-top machines (30–32). Most (30, 32), but not all handheld lactate analyzers (31, 32) are undersensitive at higher lactate concentrations (above ∼8 mmol·L⁻¹) and this could jeopardize the calculation of buffer capacity. For example, using our mathematical method, a difference of 1 mmol·l⁻¹ in post exercise BLC would result in ∼12% difference in β and almost double the typical error of the titration technique on muscle biopsies (53). This means that the proposed mathematical method is sensitive to the quality of the input data and therefore lab accurate equipment is recommended to ensure good data quality. The use of bench-top analyzers can also be seen as a limitation of our experimental methodology as such expensive equipment limit the useability in the sports training context.

Some limitations of this study should be acknowledged. In 35% of our subjects 10 min of passive followed by ∼20 min of active recovery was not sufficient to restore the BLC to pre-test levels. It has repeatedly shown that active recovery is effective to accelerate BLC recovery to pre-test levels (54–56). For instance Menzies et al. demonstrated that 20 min at 80%–100% of the lactate threshold intensity (LT1) was sufficient to restore BLC to pre-test levels, but longer recovery times were needed at lower exercise intensities (56). In our study, subjects cycled 15–20 min at 1.5 W·kg⁻¹ and this might have been a too low intensity for complete BLC recovery. Adjusting the recovery intensity to 80%–100% of LT1 could have accelerated BLC recovery and improved test-retest reliability of BLC_pre data.

Secondly, our sample size was small (n = 11) compared to the recommended sample size for this type of research (n = ∼30) (57). Unfortunately, testing larger samples was not possible at the time of data collection due to COVID restrictions for laboratory exercise testing. Therefore, we consider our study rather a pilot study and generalization of our results should be done with care. Thirdly, we did not include a gold standard reference method for buffering capacity in our protocol to test validity of the calculated buffer capacity. The evaluation of the validity of our methods requires additional scientific investigation.

4.4 Conclusions

Post-exercise BLC and pH, but not pre-exercise BLC and pH, displayed good levels of reliability and can be utilized to calculate buffer capacity using maximal exercise tests of 3 to 12 min duration.

Whether the disposed methodology to assess buffer capacity will yield similar results as golden standard procedures needs further scientific investigation.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by Ethics Committee of the Hildesheim University (Germany). The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

SG: Writing – review & editing, Supervision. AK: Writing – review & editing, Formal Analysis. SW: Writing – review & editing, Conceptualization, Methodology. JW: Writing – review & editing, Investigation. RV: Investigation, Writing – review & editing, Data curation, Formal Analysis, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

AK, SW, JW, RS were employed by INSCYD GmbH.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspor.2025.1546117/full#supplementary-material

References

1. Robergs RA, Ghiasvand F, Parker D. Biochemistry of exercise-induced metabolic acidosis. Am J Physiol Regul Integr Comp Physiol. (2004) 287:R502–16. doi: 10.1152/ajpregu.00114.2004

PubMed Abstract | Crossref Full Text | Google Scholar

2. Cairns SP. Lactic acid and exercise performance: culprit or friend? Sports Med. (2006) 36:279–91. doi: 10.2165/00007256-200636040-00001

PubMed Abstract | Crossref Full Text | Google Scholar

3. Westerblad H. Acidosis is not a significant cause of skeletal muscle fatigue. Med Sci Sports Exerc. (2016) 48:2339–42. doi: 10.1249/MSS.0000000000001044

PubMed Abstract | Crossref Full Text | Google Scholar

4. Woodward M, Debold EP. Acidosis and phosphate directly reduce myosin’s force-generating capacity through distinct molecular mechanisms. Front Physiol. (2018) 9:862. doi: 10.3389/fphys.2018.00862

PubMed Abstract | Crossref Full Text | Google Scholar

5. Fitzgerald LF, Bartlett MF, Kent JA. Muscle fatigue, bioenergetic responses and metabolic economy during load- and velocity-based maximal dynamic contractions in young and older adults. Physiol Rep. (2023) 11:e15876. doi: 10.14814/phy2.15876

PubMed Abstract | Crossref Full Text | Google Scholar

6. Hureau TJ, Broxterman RM, Weavil JC, Lewis MT, Layec G, Amann M. On the role of skeletal muscle acidosis and inorganic phosphates as determinants of central and peripheral fatigue: a ³¹ P-MRS study. J Physiol. (2022) 600:3069–81. doi: 10.1113/JP283036

PubMed Abstract | Crossref Full Text | Google Scholar

7. Juel C. Regulation of pH in human skeletal muscle: adaptations to physical activity. Acta Physiol. (2008) 193:17–24. doi: 10.1111/j.1748-1716.2008.01840.x

PubMed Abstract | Crossref Full Text | Google Scholar

8. Sahlin K, Henriksson J. Buffer capacity and lactate accumulation in skeletal muscle of trained and untrained men. Acta Physiol Scand. (1984) 122:331–9. doi: 10.1111/j.1748-1716.1984.tb07517.x

PubMed Abstract | Crossref Full Text | Google Scholar

9. Edge J, Bishop D, Hill-Haas S, Dawson B, Goodman C. Comparison of muscle buffer capacity and repeated-sprint ability of untrained, endurance-trained and team-sport athletes. Eur J Appl Physiol. (2006) 96:225–34. doi: 10.1007/s00421-005-0056-x

PubMed Abstract | Crossref Full Text | Google Scholar

10. Weston AR, Myburgh KH, Lindsay FH, Dennis SC, Noakes TD, Hawley JA. Skeletal muscle buffering capacity and endurance performance after high-intensity interval training by well-trained cyclists. Eur J Appl Physiol. (1997) 75:7–13. doi: 10.1007/s004210050119

PubMed Abstract | Crossref Full Text | Google Scholar

11. Edge J, Bishop D, Goodman C. The effects of training intensity on muscle buffer capacity in females. Eur J Appl Physiol. (2006) 96:97–105. doi: 10.1007/s00421-005-0068-6

PubMed Abstract | Crossref Full Text | Google Scholar

12. Edge J, Hill-Haas S, Goodman C, Bishop D. Effects of resistance training on H+ regulation, buffer capacity, and repeated sprints. Med Sci Sports Exerc. (2006d) 38:2004–11. doi: 10.1249/01.mss.0000233793.31659.a3

PubMed Abstract | Crossref Full Text | Google Scholar

13. Edge J, Bishop D, Goodman C. Effects of chronic NaHCO₃ ingestion during interval training on changes to muscle buffer capacity, metabolism, and short-term endurance performance. J Appl Physiol. (2006) 101:918–25. doi: 10.1152/japplphysiol.01534.2005

PubMed Abstract | Crossref Full Text | Google Scholar

14. Costill DL, Verstappen F, Kuipers H, Janssen E, Fink W. Acid-base balance during repeated bouts of exercise: influence of HCO₃. Int J Sports Med. (1984) 5:228–31. doi: 10.1055/s-2008-1025910

PubMed Abstract | Crossref Full Text | Google Scholar

15. Nielsen HB, Hein L, Svendsen LB, Secher NH, Quistorff B. Bicarbonate attenuates intracellular acidosis. Acta Anaesthesiol Scand. (2002) 46:579–84. doi: 10.1034/j.1399-6576.2002.460516.x

PubMed Abstract | Crossref Full Text | Google Scholar

16. Maughan RJ, Burke LM, Dvorak J, Larson-Meyer DE, Peeling P, Phillips SM, et al. IOC Consensus statement: dietary supplements and the high-performance athlete. Br J Sports Med. (2018) 52:439–55. doi: 10.1136/bjsports-2018-099027

PubMed Abstract | Crossref Full Text | Google Scholar

17. Grgic J, Pedisic Z, Saunders B, Artioli GG, Schoenfeld BJ, McKenna MJ, et al. International society of sports nutrition position stand: sodium bicarbonate and exercise performance. J Int Soc Sports Nutr. (2021) 18:61. doi: 10.1186/s12970-021-00458-w

PubMed Abstract | Crossref Full Text | Google Scholar

18. de Oliveira LF, Dolan E, Swinton PA, Durkalec-Michalski K, Artioli GG, McNaughton LR, et al. Extracellular buffering supplements to improve exercise capacity and performance: a comprehensive systematic review and meta-analysis. Sports Med. (2022) 52:505–26. doi: 10.1007/s40279-021-01575-x

PubMed Abstract | Crossref Full Text | Google Scholar

19. Peart DJ, Siegler JC, Vince RV. Practical recommendations for coaches and athletes: a meta-analysis of sodium bicarbonate use for athletic performance. J Strength Cond Res. (2012) 26:1975–83. doi: 10.1519/JSC.0b013e3182576f3d

PubMed Abstract | Crossref Full Text | Google Scholar

20. Mannion AF, Jakeman PM, Willan PL. Determination of human skeletal muscle buffer value by homogenate technique: methods of measurement. J Appl Physiol. (1993) 75:1412–8. doi: 10.1152/jappl.1993.75.3.1412

PubMed Abstract | Crossref Full Text | Google Scholar

21. Sahlin K, Harris RC, Nylind B, Hultman E. Lactate content and pH in muscle samples obtained after dynamic exercise. Pflugers Arch Eur J Physiol. (1976) 367:143–9. doi: 10.1007/BF00585150

Crossref Full Text | Google Scholar

22. Kemp GJ, Thompson C, Taylor D, Radda G. Proton ef¯ux in human skeletal muscle during recovery from exercise. Eur J Appl Physiol. (1997) 76:462–71. doi: 10.1007/s004210050276

Crossref Full Text | Google Scholar

23. Meyerspeer M, Boesch C, Cameron D, Dezortová M, Forbes SC, Heerschap A, et al. ³¹ P magnetic resonance spectroscopy in skeletal muscle: experts’ consensus recommendations. NMR Biomed. (2021) 34:e4246. doi: 10.1002/nbm.4246

Crossref Full Text | Google Scholar

24. Bangsbo J, Johansen L, Graham T, Saltin B. Lactate and H+ effluxes from human skeletal muscles during intense, dynamic exercise. J Physiol. (1993) 462:115–33. doi: 10.1113/jphysiol.1993.sp019546

PubMed Abstract | Crossref Full Text | Google Scholar

25. Juel C. Lactate-proton cotransport in skeletal muscle. Physiol Rev. (1997) 77:321–58. doi: 10.1152/physrev.1997.77.2.321

PubMed Abstract | Crossref Full Text | Google Scholar

26. Pilegaard H, Domino K, Noland T, Juel C, Hellsten Y, Halestrap AP, et al. Effect of high-intensity exercise training on lactate/H+ transport capacity in human skeletal muscle. Am J Physiol. (1999) 276:E255–261. doi: 10.1152/ajpendo.1999.276.2.E255

PubMed Abstract | Crossref Full Text | Google Scholar

27. Hirche HJ, Hombach V, Langohr HD, Wacker U, Busse J. Lactic acid permeation rate in working gastrocnemii of dogs during metabolic alkalosis and acidosis. Pflügers Arch. (1975) 356:209–22. doi: 10.1007/BF00583833

PubMed Abstract | Crossref Full Text | Google Scholar

28. Mainwood GW, Worsley-Brown P. The effects of extracellular pH and buffer concentration on the efflux of lactate from frog sartorius muscle. J Physiol. (1975) 250:1–22. doi: 10.1113/jphysiol.1975.sp011040

PubMed Abstract | Crossref Full Text | Google Scholar

29. Hasanli M, Nikooie R, Aveseh M, Mohammad F. Prediction of aerobic and anaerobic capacities of elite cyclists from changes in lactate during isocapnic buffering phase. J Strength Cond Res. (2015) 29:321–9. doi: 10.1519/JSC.0000000000000640

PubMed Abstract | Crossref Full Text | Google Scholar

30. Bonaventura JM, Sharpe K, Knight E, Fuller KL, Tanner RK, Gore CJ. Reliability and accuracy of six hand-held blood lactate analysers. J Sports Sci Med. (2015) 14:203.25729309

PubMed Abstract | Google Scholar

31. Crotty NM, Boland M, Mahony N, Donne B, Fleming N. Reliability and validity of the lactate pro 2 analyzer. Meas Phys Educ Exerc Sci. (2021) 25:202–11. doi: 10.1080/1091367X.2020.1865966

Crossref Full Text | Google Scholar

32. Mentzoni F, Smith J, Johnson A, Lee M, Patel R, Davis K, et al. Precision and accuracy of four handheld blood lactate analyzers across low to high exercise intensities. Eur J Appl Physiol. (2024) 124(12):3781–8.39158591

PubMed Abstract | Google Scholar

33. Baldari C, Bonavolontà V, Emerenziani GP, Gallotta MC, Silva AJ, Guidetti L. Accuracy, reliability, linearity of accutrend and lactate pro versus EBIO plus analyzer. Eur J Appl Physiol. (2009) 107:105–11. doi: 10.1007/s00421-009-1107-5

PubMed Abstract | Crossref Full Text | Google Scholar

34. Panteghini M, Pagani F. Biological variation of lactate and pyruvate in blood. Clin Chem. (1993) 39:908. doi: 10.1093/clinchem/39.5.908

PubMed Abstract | Crossref Full Text | Google Scholar

35. Widjaja A, Morris RJ, Levy JC, Frayn KN, Manley SE, Turner RC. Within- and between-subject variation in commonly measured anthropometric and biochemical variables. Clin Chem. (1999) 45:561–6. doi: 10.1093/clinchem/45.4.561

PubMed Abstract | Crossref Full Text | Google Scholar

36. Pohl A, Schünemann F, Schaaf K, Yang W, Heck H, Heine O, et al. Increased resting lactate levels and reduced carbohydrate intake cause νLa.max underestimation by reducing net lactate accumulation—a pilot study in young adults. Physiol Rep. (2024) 12:e70020. doi: 10.14814/phy2.70020

PubMed Abstract | Crossref Full Text | Google Scholar

37. Van Schuylenbergh R, Vanden Eynde B, Hespel P. Effects of air ventilation during stationary exercise testing. Eur J Appl Physiol. (2004) 92:263–6. doi: 10.1007/s00421-004-1087-4

PubMed Abstract | Crossref Full Text | Google Scholar

38. Mader A. Energiestoffwechselregulation, erweiterungen des theoretischen Konzepts und seiner Begründungen – Nachweis der praktischen Nützlichkeit der Simulation des Energiestoffwechsels. In: Mader A, Allmer H, editors. Computersimulation. Möglichkeiten zur Theoriebildung und Ergebnisinterpretation. Brennpunkte der Sportwissenschaft. Sankt Augustin: Academia (1994), Vol. 8, p. 124–62.

Google Scholar

39. Heck H, Schulz H, Bartmus U. Diagnostics of anaerobic power and capacity. Eur J Sport Sci. (2003) 3:1–23. doi: 10.1080/17461390300073302

Crossref Full Text | Google Scholar

40. Weber S. Calculation of Performance-determining parameters of Metabolic Activity at the Cellular Level by Means of Cycle Ergometry [Berechnung leistungsbestimmender Parameter der metabolischen Aktivität auf zellulärer Ebene mittels fahrradergometrischer Untersuchungen]. Köln: Dtsch. Sporthochsch (2003).

Google Scholar

41. Balady GJ, Arena R, Sietsema K, Myers J, Coke L, Fletcher GF, et al. Clinician’s guide to cardiopulmonary exercise testing in adults: a scientific statement from the American Heart Association. Circulation. (2010) 122:191–225. doi: 10.1161/CIR.0b013e3181e52e69

PubMed Abstract | Crossref Full Text | Google Scholar

42. Hasselbalch KA. Die Berechnung der Wasserstoffzahl des Blutes aus der freien und gebundenen Kohlensäure desselben, und die Sauerstoffbindung des Blutes als Funktion der Wasserstoffzahl. Julius Springer (1916). Available online at: https://books.google.be/books?id=YSCvYgEACAAJ

Google Scholar

43. Koo TK, Li MY. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J Chiropr Med. (2016) 15:155–63. doi: 10.1016/j.jcm.2016.02.012

PubMed Abstract | Crossref Full Text | Google Scholar

44. Dunst AK, Hesse C, Feldmann A, Holmberg HC. A novel approach to determining the alactic time span in connection with assessment of the maximal rate of lactate accumulation in elite track cyclists. Int J Sports Physiol Perform. (2023) 18:157–63. doi: 10.1123/ijspp.2021-0464

PubMed Abstract | Crossref Full Text | Google Scholar

45. Yang W-H, Park S-Y, Kim T, Jeon H-J, Heine O, Gehlert S. A modified formula using energy system contributions to calculate pure maximal rate of lactate accumulation during a maximal sprint cycling test. Front Physiol. (2023) 14:1147321. doi: 10.3389/fphys.2023.1147321

PubMed Abstract | Crossref Full Text | Google Scholar

46. Meixner B, Nusser V, Koehler K, Sablain M, Boone J, Sperlich B. Reliability of power output, maximal rate of capillary blood lactate accumulation, and phosphagen contribution time following 15-s sprint cycling in amateur cyclists. Physiol Rep. (2024) 12:e16086. doi: 10.14814/phy2.16086

PubMed Abstract | Crossref Full Text | Google Scholar

47. Diaz-Garzon J, Fernandez-Calle P, Aarsand AK, Sandberg S, Buno A. Biological variation of venous acid-base status measurands in athletes. Clin Chim Acta. (2021) 523:497–503. doi: 10.1016/j.cca.2021.11.001

PubMed Abstract | Crossref Full Text | Google Scholar

48. Saunders B, Sale C, Harris RC, Morris JG, Sunderland C. Reliability of a high-intensity cycling capacity test. J Sci Med Sport. (2013) 16:286–9. doi: 10.1016/j.jsams.2012.07.004

PubMed Abstract | Crossref Full Text | Google Scholar

49. Bates BT, Zhang S, Dufek JS, Chen FC. The effects of sample size and variability on the correlation coefficient. Med Sci Sports Exerc. (1996) 28:386–91. doi: 10.1097/00005768-199603000-00015

PubMed Abstract | Crossref Full Text | Google Scholar

50. Messonnier L, Kristensen M, Juel C, Denis C. Importance of pH regulation and lactate/H ⁺ transport capacity for work production during supramaximal exercise in humans. J Appl Physiol. (2007) 102:1936–44. doi: 10.1152/japplphysiol.00691.2006

PubMed Abstract | Crossref Full Text | Google Scholar

51. Danaher J, Gerber T, Wellard RM, Stathis CG. The effect of β-alanine and NaHCO₃ co-ingestion on buffering capacity and exercise performance with high-intensity exercise in healthy males. Eur J Appl Physiol. (2014) 114:1715–24. doi: 10.1007/s00421-014-2895-9

PubMed Abstract | Crossref Full Text | Google Scholar

52. Parkhouse WS, McKenzie DC, Hochachka PW, Ovalle WK. Buffering capacity of deproteinized human vastus lateralis muscle. J Appl Physiol. (1985) 58:14–7. doi: 10.1152/jappl.1985.58.1.14

PubMed Abstract | Crossref Full Text | Google Scholar

53. McGinley C, Bishop DJ. Influence of training intensity on adaptations in acid/base transport proteins, muscle buffer capacity, and repeated-sprint ability in active men. J Appl Physiol. (2016) 121:1290–305. doi: 10.1152/japplphysiol.00630.2016

PubMed Abstract | Crossref Full Text | Google Scholar

54. Monedero J, Donne B. Effect of recovery interventions on lactate removal and subsequent performance. Int J Sports Med. (2000) 21:593–7. doi: 10.1055/s-2000-8488

PubMed Abstract | Crossref Full Text | Google Scholar

55. Gmada N, Bouhlel E, Mrizak I, Debabi H, Ben Jabrallah M, Tabka Z, et al. Effect of combined active recovery from supramaximal exercise on blood lactate disappearance in trained and untrained man. Int J Sports Med. (2005) 26:874–9. doi: 10.1055/s-2005-837464

PubMed Abstract | Crossref Full Text | Google Scholar

56. Menzies P, Menzies C, McIntyre L, Paterson P, Wilson J, Kemi OJ. Blood lactate clearance during active recovery after an intense running bout depends on the intensity of the active recovery. J Sports Sci. (2010) 28:975–82. doi: 10.1080/02640414.2010.481721

PubMed Abstract | Crossref Full Text | Google Scholar

57. Mondal D, Vanbelle S, Cassese A, Candel MJ. Review of sample size determination methods for the intraclass correlation coefficient in the one-way analysis of variance model. Stat Methods Med Res. (2024) 33:532–53. doi: 10.1177/09622802231224657

PubMed Abstract | Crossref Full Text | Google Scholar