Vector-based analysis of cortical activity associated with dumbbell exercise using functional near-infrared spectroscopy

The mechanisms via which the brain and muscles work together remain poorly understood. The use of vector-based fNIRS, to propose a new metric and imaging method to understand neural activation during dumbbell-lifting exercises. This method can simultaneously measure oxyhemoglobin (oxyHb) and deoxyHb levels so that the angle k: Arctan (deoxyHb/oxyHb) represents the degree of oxygen exchange in the brain and can be used to quantify the distribution of oxygen consumption. The amplitude L of the vector reflects the intensity of the response caused by the amount of change in Hb. This study used vector-based fNIRS to simultaneously measure the left primary motor cortex (left M1), multiple peripheral regions, and the right biceps brachii muscle. The subjects were seven healthy adults. The task was a dumbbell-lifting exercise involving flexion and extension of the elbow joints of both arms. Dumbbell weights of 0 (no dumbbell), 4.5, and 9.5 kg were used. During dumbbell exercise, oxygen exchange increased in the left M1, indicating increased local oxygen consumption. Around the left M1, the cerebral oxygen exchange decreased, and oxygen supply increased without cerebral oxygen consumption. The spatial agreement between the maximum value of oxygen exchange k and L during the task was <20%. Therefore, the dumbbell-lifting exercise task study reported here supported the hypothesis that cerebral oxygen consumption associated with neural activation does not coincide with the distribution of cerebral oxygen supply. The relationship between the brain oxygen supply from the site of increased oxygen exchange in the brain and its surrounding areas can be quantified using the vector method fNIRS.

Introduction

Studies of brain oxygenation during high-intensity exercise (Rupp and Perrey, 2008) and walking (Khan et al., 2021) have been performed using functional near-infrared spectroscopy (fNIRS). Physical activity induces local cerebral oxygen consumption and demand for oxygen supply. However, conventional brain functional imaging currently does not include a method for distinguishing oxygen consumption from oxygen supply simultaneously. Thus, the spatial distribution between oxygen consumption and supply in the brain that accompanies exercise remains largely unknown.

In fNIRS, variations in the ratio between changes in oxyhemoglobin (oxyHb) and deoxyHb are observed according to the site, thus reflecting the spatial distribution of oxygen consumption and supply. It is known that fNIRS is capable of measuring the fast oxygen response in capillary events (FORCE) associated with neuronal responses, defined as the FORCE effect (Kato, 2004).

The FORCE effect indicates tissue hypoxia with an increase in deoxyHb and a decrease in oxyHb, reflecting increased oxygen consumption. It has been reported that a temporary FORCE occurred in the primary motor cortex (M1) at the onset of a hand grasping task, and deoxyHb decreased and oxyHb increased around M1, reflecting oxygen supply (Akiyama et al., 2006). In a task that activated the supplementary motor area (SMA), deoxyHb and oxyHb were increased in the SMA. OxyHb increased and deoxyHb fell slightly in the sensory-motor cortex and the pre-SMA (Hatakenaka et al., 2007). Several reports have shown that oxyHb analysis alone cannot accurately detect the localization of neuroactivation (Cyranoski, 2011; Takahashi et al., 2011) and that functional images of increasing oxyHb may differ from the actual distribution of oxygen consumption (Kato, 2018, 2021).

Detecting changes in early deoxygenation has been considered a more useful spatial indicator of neuronal activity than increases in oxyHb or cerebral blood volume (CBV) because they occur in a more limited area (Ances, 2003; Kato, 2004; Khan et al., 2021). However, the oxygen consumption and supply triggered by neuroactivation cannot be evaluated simultaneously based on deoxyHb alone. In terms of technological advances, earlier NIRS was used as a cerebral oxygen monitor that could be measured over the scalp, and it was not until July 1991 that it was first successfully demonstrated that fNIRS could detect regional brain function (Kato, 2018). In addition, there was a lack of theory to quantitatively integrate neural activation from multiple sites (channels) and indices (Kato et al., 1993; Ferrari and Quaresima, 2012).

A vector-based model of cerebral oxygen regulation (CORE model; Kato, 2006, 2013) can explain variations in the ratios of concentration changes in oxyHb and deoxyHb without exception. Vector-based fNIRS allows the integration of the dynamics of oxyHb and deoxyHb changes in multiple channels on the same vector coordinates, thus enabling the detection of oxygen dynamics as differences between CORE vectors. Oxygen consumption associated with neuroactivation can be classified into one of eight phases according to the combination of the CORE vector components, i.e., oxyHb, deoxyHb, CBV, and cerebral oxygen exchange (COE). Using vector-based fNIRS, the patterns of FORCE in the language area were analyzed and classified into five levels based on variations in oxygen consumption (Yoshino and Kato, 2012).

A technique has been proposed for detecting and imaging the spatial distribution of neuroactivation by differentiating the phase distributions of oxygen consumption and oxygen supply (Kato et al., 2003; Kato, 2018). Temporal FORCE effects were reported to be detected 2–3 s after the onset of the stimulus task. Therefore, it was hypothesized that when neural activity is strongly induced, the FORCE effect occurs over a larger spatial area and for a longer period of time. Furthermore, it is assumed that the oxygen consumption and oxygen supply distributions do not coincide with the oxygen consumption distribution due to neural activation during exercise when the FORCE effect strongly appears. As a result, when oxygen consumption increases in the M1 and a strong FORCE effect is induced, a mechanism to supply fresh blood to the area around M1 could be detected. Therefore, the task of lifting heavier dumbbells has been chosen, which could be predicted to elicit strong neural activity in M1.

To identify differences in the strength of neuroactivation, measurements were taken from the M1 and surrounding sites using vector-based fNIRS during exercise tasks using three different dumbbell weights and report a new imaging method for differentiating between oxygen consumption and supply.

Materials and methods

Subjects

The subjects of this study were seven healthy adults: six males and one female; the mean age was 33.3 ± 8.0 years. The participants had some experience in sports before age 20, but had not received any intensive strength training for at least 1 year.

All participants were identified as being right-handed based on the Edinburgh Handedness Inventory. The study was explained to the subjects in writing and orally, and they provided prior written consent for participation in and reporting of this study.

The experimental procedure complied with the principles of the Declaration of Helsinki. All subjects received full explanation of the procedures and provided written informed consent for participation in the study. This study was reviewed and approved by the Ethics Committee of KatoBrain Co., Ltd. which included outside members.

fNIRS measurement

A multi-channel NIRS apparatus (ETG-100) monitored localized changes in oxyHb and deoxyHb. The scalp was irradiated at each site with two wavelengths of near-infrared light (780 and 830 nm) from a semi-conductor laser using three optical fibers. Three avalanche photodiodes detected light passing through the head. Hb concentration measurements were recorded at a sampling rate of 10 Hz.

Measurements were collected from a total of seven channels (Figure 1). Channel 1 was positioned directly over the left M1, and the remaining six channels were arranged around it: channel 2 lateral to the precentral knob, channel 3 in the premotor area, channel 5 in the SMA, and channels 4, 6, and 7 over the postcentral gyrus. The distance between emitter and detector probes was 30 mm. The M1 was identified using a technique for pre-measurement identification of target cortex sites that utilizes the distance between points of reference on the scalp from the subject's MRI (Murakoshi and Kato, 2006). The right M1 was measured by fNIRS simultaneously with the left M1. However, the analysis was limited to the left-hemisphere channel.

FIGURE 1

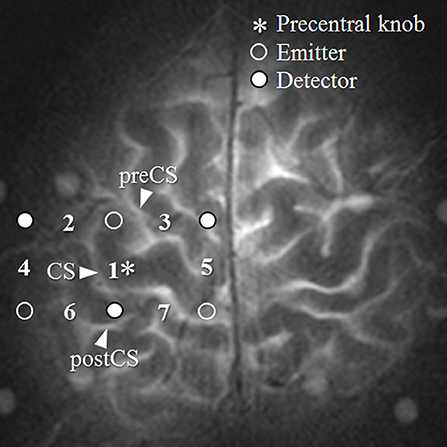
Figure 1. Region of measurement. The numbers between the detectors and emitters are channel numbers. CS, central sulcus.

Experimental procedure

The task used in this study to investigate the effects of the strength of neural activity was a dumbbell-lifting exercise that involved flexing and extending the elbow joints of both arms. It has been reported that movement-related cortical potentials increase more for isometric contractions of the elbow flexors under a heavy load than they do under a light load (Oda et al., 1996). Therefore, there were three different weights: 0 kg (no dumbbell), and dumbbells weighing 4.5 and 9.5 kg. One trial consisted of flexing and extending a given weight 12 times. Repetitions were paced at 3 s (Tamaki et al., 1994), for a total of 36 s per trial, with a 60 s resting period between trials. Each repetition lasted for 1.5 s, for a total of 3 s. Five trials with each weight made up a trial set. After completing a trial set for one weight, the subject went on to the next, heavier weight. The training order was always from lightest to heaviest, with participants always set to be most fatigued on the heaviest trial set.

For the 0 and 4.5 kg tasks, a total of 35 trials performed by the seven subjects were used for analysis. For the 9.5 kg task, one subject completed only one trial and another subject only four because the weight was too heavy, and a total of 30 trials were used for analysis.

The weight of the dumbbells that can be lifted could be different for each individual.

However, the neural activity to M1 and its surrounding sites is expected to be higher with the dumbbell weighing more. Therefore, instead of selecting the dumbbell weight that produces maximal voluntary muscle contraction, a uniform dumbbell weight was set.

Theory of vector-based analysis

A vector-based model of CORE

The CORE model (Kato, 2004, 2006, 2013) can simultaneously detect seven indices reflecting the oxygen consumption and supply caused by neuroactivation. OxyHb and deoxyHb have different chemical properties (paramagnetic or diamagnetic) arising from differences in the bonding of oxygen molecules (Pauling and Coryell, 1936). The axes oxyHb (ΔO) and deoxyHb (ΔD) define an orthogonal vector coordinate plane. Rotating this ΔO/ΔD vector plane by 45° counterclockwise results in an orthogonal vector coordinate plane comprising a (ΔO + ΔD) axis and a (ΔD –ΔO) axis. The (ΔO + ΔD) vector can be defined as the CBV vector (ΔCBV), and the (ΔD –ΔO) vector can be considered as the COE vector (ΔCOE).

The relationship among the four axes, ΔO, ΔD, ΔCBV, and ΔCOE, is described by the following square matrix:

$\begin{array}{ll}\left(\begin{array}{c}\Delta O+\Delta D\\ -\Delta O+\Delta D\\ \end{array}\right)=\left(\begin{array}{cc}1& 1\\ -1& 1\\ \end{array}\right)\left(\begin{array}{c}\Delta O\\ \Delta D\\ \end{array}\right)=\left(\begin{array}{c}\Delta CBV\\ \Delta COE\\ \end{array}\right)& (1)\end{array}$

$\begin{array}{ll}\left(\begin{array}{c}\Delta O\\ \Delta D\\ \end{array}\right)=\frac{1}{2}\left(\begin{array}{cc}1& -1\\ 1& 1\\ \end{array}\right)\left(\begin{array}{c}\Delta CBV\\ \Delta COE\\ \end{array}\right)& (2)\end{array}$

The polar coordinate plane comprising these four axes is termed as the CORE vector plane and the vector tracks on the polar coordinate as CORE vectors (Figure 2). The vectors have four components, i.e., ΔO, ΔD, ΔCBV, and ΔCOE, and the analysis of the CORE vectors allows handling these four Hb indices as the components of a wave.

FIGURE 2

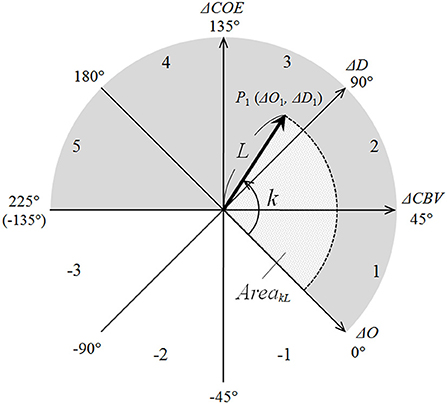
Figure 2. CORE vector coordinates. Values for k (in degrees) are shown at the tips of the axes. Phase numbers are shown in each octant arc.

On the CORE vector plane, a positive value for ΔCBV indicates increasing ΔCBV and a negative value for ΔCBV indicates decreasing ΔCBV; moreover, a positive value for ΔCOE indicates increasing ΔCOE and shows hypoxic change, and a negative value for ΔCOE indicates decreasing ΔCOE and shows hyperoxic change. In other words, ΔCOE reflects increasing or decreasing cerebral oxygen extraction from the capillaries to the cells.

Phase components of CORE vectors

The phases on the CORE vector plane are quantitatively defined indices of the degree of oxygen exchange that reflect the strength of oxygen consumption. Phase is defined by the angle k, the ratio of ΔD to ΔO. k is the angle between a CORE vector and the positive ΔO axis and is determined as follows:

$\begin{array}{l}k=Arctan\left(\frac{\Delta D}{\Delta O}\right)=Arctan\left(\frac{\Delta COE}{\Delta CBV}\right)+45^{°}\\ \left(-135^{°}\leqq k\leqq 225^{°}\right)& (3)\end{array}$

It is a quantitative index indicating the degree of oxygen consumption over a certain period. k = 0° is on the positive ΔO axis and coincides with the oxygen density of arterial blood. Thus, an increase or decrease in k indicates a change in oxygen density. The eight octants of 45° on the vector plane in Figure 1 can be classified into activation phases (Phases 1 through 5) and non-activation phases (Phases −1 through −3). Phase 1 (0 < ΔD < ΔO; ΔCOE < 0 < ΔCBV) and Phase 2 (0 < ΔO < ΔD; 0 < ΔCOE < ΔCBV) are canonical activation, showing increases in both ΔD and ΔO. Phase 3 (ΔO < 0 < ΔD; 0 < ΔCBV < ΔCOE) is hypoxic–hyperemic activation, showing a decrease in ΔO together with an increase in ΔCBV. Phase 4 (ΔO < 0 < ΔD; ΔCBV < 0 < ΔCOE) and Phase 5 (ΔO < ΔD < 0; ΔCBV < 0 < ΔCOE) are hypoxic–ischemic activation, showing an increase in ΔCOE together with a decrease in ΔCBV. Conversely, Phases −1 through −3 indicate non-activation and show decreases in both ΔD and ΔCOE. Oxygen consumption during neuroactivation can be considered higher during the activation phases vs. the non-activation phases.

The scalar L

The scalar L between point P₁ (ΔO ₁, ΔD ₁) and the origin can be described by the following equation:

$\begin{array}{ll}L=\sqrt{{\left(\Delta O_1\right)}^2+{(\Delta D_1)}^2}=\frac{1}{\sqrt{2}}\sqrt{{(\Delta CO{E}_1)}^2+{(\Delta CB{V}_1)}^2},& (4)\end{array}$

where L represents the intensity of Hb changes (oxyHb and deoxyHb); i.e., the scalar component L of the CORE vector also includes ΔCBV and ΔCOE.

The contribution percentage of ΔO and ΔD to L is calculated by squaring both sides of Equation (4).

$\begin{array}{ll}1={\left(\frac{\Delta O}{L}\right)}^2+{\left(\frac{\Delta D}{L}\right)}^2& (5)\end{array}$

$\begin{array}{ll}\text{Percentage contributed by }\Delta \text{O}:{\left(\frac{\Delta O}{L}\right)}^2\times 100\left(\%\right)& (6)\end{array}$

$\begin{array}{ll}\text{Percentage contributed by }\Delta \text{D}:{\left(\frac{\Delta D}{L}\right)}^2\times 100\left(\%\right)& (7)\end{array}$

The following relationship exists between L and the angle k:

$\begin{array}{ll}\left(\begin{array}{c}\Delta COE\\ \Delta CBV\\ \end{array}\right)=L\left(\begin{array}{c}cosk\\ sink\\ \end{array}\right)& (8)\end{array}$

In this way, CORE vectors have properties of waves: phase (k) and intensity (L). The imaging of k indicates the phase distribution of oxygen consumption, whereas the imaging of ΔO shows the distribution of oxygen supply. The distribution of the percentages of contribution by ΔO indicates the relative contribution of ΔO that is affected by changes in k with respect to L.

Oxygen regulation index

A new index was created to reflect phase and amplitude (L). The area created by the rotational motion of the CORE vector is defined on the vector plane using L_t and the radian of k ($k_{\text{t}}^{\text{rad}}$), as follows:

$\begin{array}{ll}{Area}_{kL}={\displaystyle \sum _{\text{n}=1}^{\text{n}}}\frac{1}{2}{k^{\text{rad}}}_t•{L_{\text{t}}}^2,& (9)\end{array}$

where n is the number of trials analyzed for all subjects An Area_kL is a cumulative area encompassed by the CORE vector track; that is, the area swept out by L_t over the range of k_t degrees from the positive ΔO axis (k = 0°) during t seconds from task initiation. A positive value for Area_kL indicates an area increasing in the direction of increased oxygen exchange degree (0° < k), and a negative value indicates an area increasing in the direction of increased oxygen not used for oxygen exchange (k < 0°).

Vector-based analysis

Measurements performed over 36 s during a trial and 36 s after a trial were used for analysis. Functional imaging was performed using seven indices: the four-vector components (ΔO, ΔD, ΔCBV, and ΔCOE) of the addition vectors during the tasks, phase (k), the scalar (L), and the oxygen regulation index (Area_kL).

The time-course changes were averaged, with each trial onset set as zero. The time-course changes in ΔCBV and ΔCOE were calculated from the time-course changes in ΔO and ΔD using Equations (1) and (2). Vector tracks were plotted using task onset as the origin and the grand averages calculated for all trials for each component. No baseline normalization or motion correction was performed as a preprocessing step for the analysis, as these may distort the phase of oxygen exchange (Kato, 2021).

CORE addition vectors during and after the tasks were calculated to observe total changes across the task time. The cumulative sums of ΔCBV and ΔCOE grand averages were determined, and the CORE addition vectors were plotted using those values. Imaging of each vector component (ΔO, ΔD, ΔCBV, and ΔCOE) was carried out using the cumulative sums recorded during the task. Imaging of k and L was performed using Equations (3) and (4), with values determined from the CORE addition vectors. Imaging of Area_kL was carried out based on Equation (9) based on the cumulative sums of the area determined from k and L of the single-trial CORE addition vectors.

The phase distribution of a CORE vector was determined by first classifying k for each trial into the appropriate octant and then calculating the ratio of the number of trials in each phase to the total number of trials for analysis for each task. Phase distribution for the sites surrounding the left M1 was calculated by averaging the phase distributions of all surrounding channels.

Spatial concordance between k and L was calculated as the ratio of the number of trials in which the maximum values for k and L coincided with the number of trials in the analysis of each task.

The percent contribution of ΔO and ΔD to L was calculated using Equations (6) and (7). Values for L of the CORE addition vectors and the cumulative sums of ΔD and ΔO were used for the calculation. The contribution rates for the sites surrounding the left M1 were averaged from the contribution rates of all channels. Differences in contribution rates were calculated by subtracting the percentages for ΔO from those for ΔD.

Statistics

Multiple analysis of variance and post-hoc multiple comparison tests (Scheffe's) were performed using ΔCBV and ΔCOE for all trials to determine the significance of differences between the left M1 and the averages of the surrounding sites. Statistical tests were performed for k, L, and the Area_kL, to determine the significance of differences between the left M1 and the averages of surrounding sites. Independent t-tests were used for L and the Area_kL, and Watson's U2 test was used for k. Differences in phase distribution between the left M1 and the surrounding sites were compared using Fisher's exact test for each phase.

Results

Time courses and functional images of CORE vector components

Figure 3A shows the average time courses for each vector component during and after the tasks. Figure 3B is a functional image of the four-vector components during a task. At the left M1 (channel 1), ΔO decreased for the 4.5 and 9.5 kg tasks, whereas ΔD and ΔCBV increased. However, in the surrounding sites, ΔO increased, and ΔD and ΔCOE decreased. The left M1, where the maximum decrease in ΔO occurred, was surrounded by a high oxygen supply (increased ΔO), in a donut-like shape. The sites of maximum increase in ΔD and ΔCOE were the left M1 for the 4.5 and 9.5 kg tasks and the SMA (channel 5) for the 0 kg task. ΔCBV increased in both the left M1 and the surrounding sites, not indicating localization. At 9.5 kg, the rate of the maximum increase of each vector component at the left M1 was 0% for ΔO, 0% for ΔCBV, 56.7% for ΔD, and 63.3% for ΔCOE.

FIGURE 3

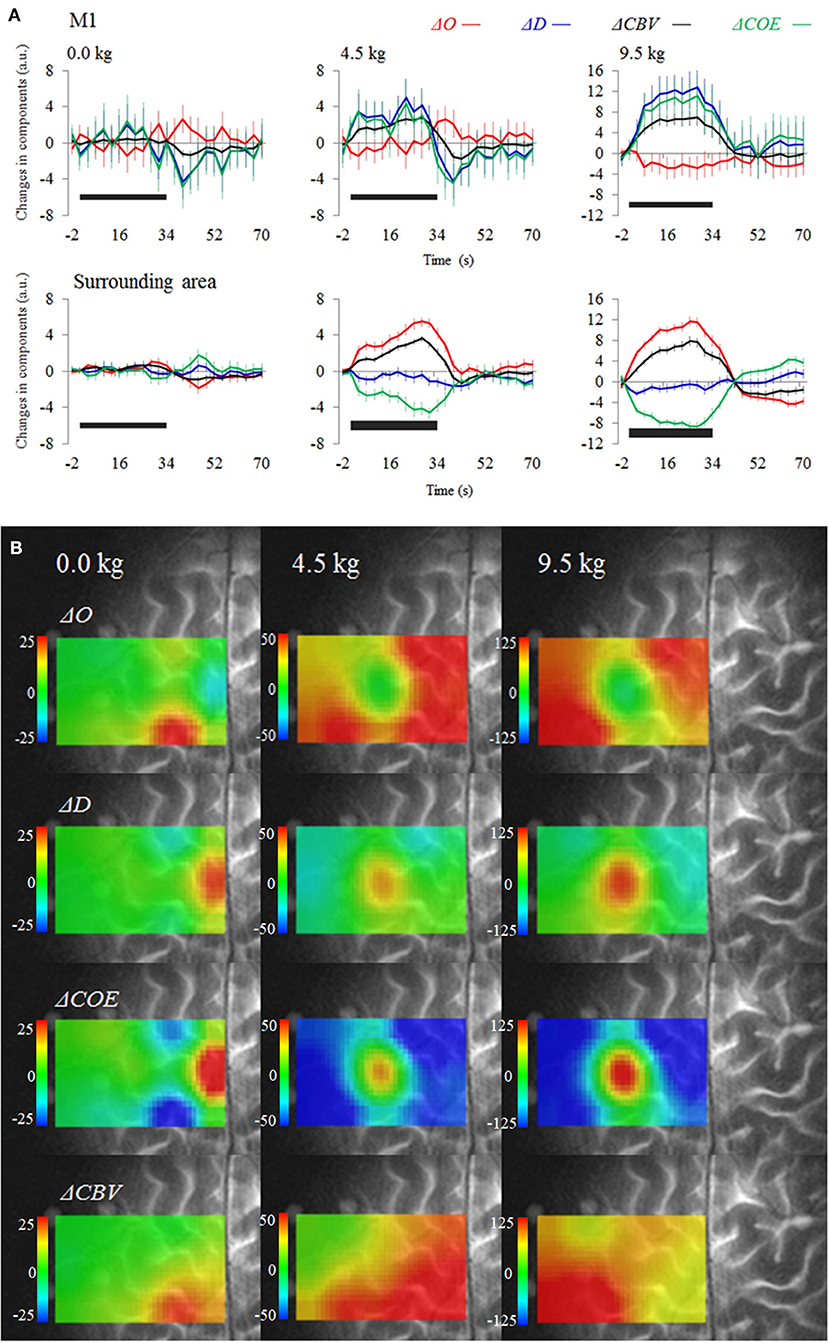
Figure 3. (A) Average time courses and standard error for the four-vector components at the left M1 and surrounding sites (averaged). (B) Functional images show changes in the vector components during a task. The black bars on the figure represent the period of the dumbbell exercise.

Functional images using k, L, and the new index Area_kL

Figure 4 provides functional images of k, L, and the Area_kL. The SMA was the site with the maximum increase in k at 0 kg. At 4.5 and 9.5 kg, the left M1 showed the maximum increase in k, whereas oxygen consumption decreased in the surrounding area. The maximum increase in L appeared not at the left M1, but in the surrounding area. The spatial concordance of the maximum increases in k and L was low; 11.4% at 0 kg, 17.1% at 4.5 kg, and 20.0% at 9.5 kg.

FIGURE 4

Figure 4. Functional images of three indices (k, L, and Area_kL) during tasks.

The spatial concordance of the maximum increases in k and Area_kL increased as the dumbbell weight increased; 37.1% at 0 kg, 54.3% at 4.5 kg, and 76.7% at 9.5 kg. Area_kL showed a significantly greater increase at the left M1 compared with the surrounding area (4.5 and 9.5 kg) (P < 0.01), indicating increased oxygen consumption. The site of maximum increase in Area_kL was the SMA at 0 kg. The imaging of Area_kL emphasized the changes at the left M1 and SMA and allowed the detection of a small increase in oxygen consumption at the left M1 that could not be detected in images of the single-vector components or L.

Differentiation of phase during and after motor exercise

Figure 5 displays the CORE addition vectors during the task (36 s) and after the task (36 s) at each channel.

FIGURE 5

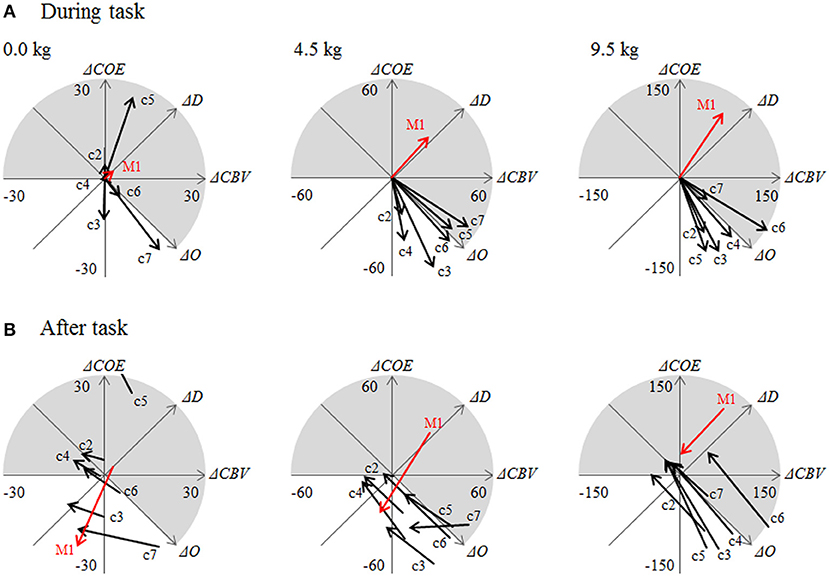
Figure 5. (A) Addition vectors during a task (0–36 s) and (B) after the task (36–72 s). c2 through c7 are the numbers of channels in the area surrounding the left M1, as shown in Figure 2.

Table 1 shows the phase distribution of the CORE addition vectors at the left M1 and surrounding sites.

TABLE 1

Table 1. Phase distribution (%) of the CORE vectors during the tasks.

Vectors for the 4.5 and 9.5 kg tasks showed significant differences between the left M1 and the surrounding sites (P < 0.01). The most common phase at the left M1 was Phase 3, indicating hypoxic–hyperemic activation. The percent occurrence of Phase 3 at the left M1 was 31.4% at 0 kg, 54.3% at 4.5 kg, and 46.7% at 9.5 kg, which were all significantly higher than those detected in the surrounding sites (Table 1). At this time, k was 83.9° at 0 kg, 93.8° at 4.5 kg, and 101.6° at 9.5 kg, which were also significantly higher than those detected in the surrounding sites (P < 0.05). Vectors in the surrounding sites were significantly concentrated in Phases −1 and −2, which are non-activation phases. In the surrounding area, k ranged from −118.3° to 135.2° at 0 kg, from −34.0° to 11.6° at 4.5 kg, and from −25.5° to 14.0° at 9.5 kg.

After the tasks, the phase differences between the left M1 and the surrounding sites disappeared. The direction of the vectors changed and moved toward the origin.

During the task, L increased significantly with increased dumbbell weight at both the left M1 and the surrounding area (P < 0.01). In the 4.5 and 9.5 kg tasks, there was no significant difference between L at the left M1 and the surrounding sites. In this way, the CORE vectors showed specific phase distributions according to site and task.

Contribution rate of ΔO and ΔD related to L change

Table 2 reports the relative contributions of ΔO and ΔD to L during the tasks. The contribution percentages from ΔO and ΔD were different for each measurement channel. At the left M1, the contribution of ΔO was small, at < 4.0%, whereas the contribution of ΔD was more than 96%, which represented a difference of ~92%.

TABLE 2

Table 2. Average contribution to L and differences in the relative contributions of ΔD and ΔO during a task.

At the sites surrounding the left M1, the contribution rate was higher for ΔO than for ΔD. Differences in the contribution rates of ΔO and ΔD increased as the dumbbell weights became heavier: 12.8% at 0 kg, 65.8% at 4.5 kg, and 83.8% at 9.5 kg. Namely, the donut-shaped image surrounding the site of maximum increase in oxygen consumption became clearer as the dumbbell weight increased from 0 to 4.5 kg and then to 9.5 kg, reflecting the increase in oxygen supply (ΔO increase) in the area surrounding the M1 unaccompanied by oxygen consumption as the dumbbell weight increased.

Although at 0 kg L was smaller at the left M1 than it was at the surrounding sites (Figure 5), the contribution of ΔO at the left M1 was lower (1.1%) than it was at the surrounding sites (56.4%).

Discussion

Spatial distribution of COE

Differences in the distribution of oxygen consumption are quantifiable using the images of k, which represents the degree of oxygen exchange. During dumbbell exercises, oxygen exchange increased at the left M1, indicating a localized increase in oxygen consumption. In the area surrounding the left M1, oxygen exchange decreased, and oxygen supply increased unaccompanied by oxygen consumption. The spatial concordance between the maximum values for the degree of oxygen exchange during a task and L, which reflects the intensity of Hb changes, was <20%. The contribution rates of ΔO and ΔD differed according to the measurement site. Therefore, the hypothesis that the distribution of oxygen consumption associated with neural activation does not coincide with the distribution of oxygen supply was supported in the motor task study.

Interestingly, an increasing difference in the relative contribution of ΔO and ΔD in the area surrounding the M1 was found as the dumbbell weights increased, which suggests that oxygen supply in the surrounding area is regulated concerning the site of increasing oxygen consumption. Even at sites of increased oxygen consumption, the contribution of ΔO was found to be low. It is believed that neural activity and local cerebral blood flow (CBF) increase or decrease relatively correlatedly. Similarly, local CBF and local CBV are also thought to increase or decrease in correlation. However, it is thought that, in brain regions where COE has increased markedly because of a rapid and sustained increase in oxygen consumption relative to oxygen supply, there is a mechanism of cerebral blood circulation that promotes replenishment from surrounding sites with sufficient oxygen supply.

Neural activity may not always correlate with local CBV or CBF when it has a strong impact on the COE homeostasis for the whole brain, as in the results of this study. The detection of an excessive increase in ΔCBV rather than an increase in ΔCOE around the near regions of rapidly increasing oxygen consumption was not previously known and therefore has not been incorporated into conventional models of cerebral circulation regulation (Roy and Sherrington, 1890; Lassen, 1959). A new model of whole brain circulation regulation is needed that can explain the mechanisms that maintain COE homeostasis for the whole brain.

Using the vector method fNIRS, it is necessary to study further how the oxygen supply in the brain is regulated from the site of increased oxygen exchange in the brain and its surrounding areas. The nature of the mechanisms that regulate the simultaneous oxygen supply at sites of increased oxygen exchange is also an important research topic at the level of whole brain regulation and at the level of more microscopic cell populations. As the weight of dumbbells lifted increases or the subject's muscle fatigue increases, the mechanisms that attempts to maintain COE homeostasis for the whole brain may be more likely to be strongly detected by vector method fNIRS. Thus, the closer to maximal voluntary muscle contraction, the more brain-muscle coordination may be required.

Compared with previous studies using verbal tasks (Kato et al., 2003; Yoshino and Kato, 2012), the present results suggest that, during muscle training, oxygen consumption and oxygen supply are controlled in areas of the cortex within a few centimeters square.

The FORCE, which is an oxygen-consuming response that occurs in a high neuroactivation site, has been observed in invasive human studies using optical imaging (Suh et al., 2006). However, it does not report that the phenomenon of oxygen supply surrounding the FORCE effect in the form of a doughnut has occurred, as obtained in this experiment. The strong and persistent FORCE effect on the homeostasis of oxygen exchange for the whole brain, as obtained in this experiment, may be a different brain mechanism from the temporary FORCE that has been previously reported (Kato, 2004, 2018).

It has been shown that γ-aminobutyric acid (GABA) concentrations during a motor learning task decrease in the left M1 and increase around it (Gudberg et al., 2012).

Studies using proton magnetic resonance spectroscopy have shown interactions between M1 and its surrounding sites in neurotransmitters (Umesawa et al., 2020; Maruyama et al., 2021). Although this method cannot measure intracellular and extracellular GABA separately, it could be used in conjunction with the vector method fNIRS to clarify the relationship between oxygen metabolism and GABA. However, because the dumbbell task is not a motor learning task, it does not necessarily elicit the same response as the strength training task. Further evidence and discussion of the physiological link between GABA and oxygen kinetics are needed.

Advantages of vector-based analysis

The CORE model of 2-dimensional analysis of ΔO and ΔD was used to simultaneously generate functional distribution images using seven indices, including oxygen exchange.

The advantage of vector-based fNIRS is that multiple indices with different physiological significance can be compared to understand better neurovascular-coupling mechanisms and neuro-oxygen coupling that accompany neuroactivation. Conversely, these indices cannot be separately detected using the fMRI BOLD signal, which includes the effects of both oxyHb and deoxyHb changes (Yamamoto and Kato, 2002).

Unlike the other component images, the oxygen exchange images were able to indicate both high oxygen exchange sites, such as Phase 3 sites (common in the M1), and reduced oxygen exchange sites, such as Phase −1 (more common in the surrounding area), even though ΔCBV increased in the same way in both types of sites. The fact that the M1 site was most frequently a Phase 3 site (ΔCOE increased more than ΔCBV) reflects the fact that the increase in ΔD attributable to oxygen consumption exceeds the increase in ΔO from oxygen supply. Together with k, the ΔD and ΔCOE indices (reflecting oxygen consumption) increased most at the SMA for 0 kg, and at the M1 for 4.5 and 9.5 kg. However, the sites showing maximum increases in the ΔO, ΔCBV, and L indices (strongly affected by blood supply) did not coincide with the M1. Phase −1 is a non-activation phase, and I also observed that it did not reflect neuroactivation in a language task (Yoshino and Kato, 2012). In Phase −1, ΔO increases and ΔD decreases, which has been considered a typical fNIRS activation pattern; however, oxygen consumption is low in this phase, and it has become clear that it does not indicate a site where activation is strong. Based on our results, an increase in ΔCBV at a site does not necessarily imply an increase in oxygen demand. Variations were found in the oxygen exchange response concerning the amount of increase in ΔO or ΔCBV. For example, it was reported that, during a motor task, CMRO₂ did not increase significantly at the M1, whereas CBF did (Vafaee et al., 2012); conversely, CBF did not increase significantly in the visual cortex, although CMRO₂ did (Mintun et al., 2001).

Possibilities and limitations of vector-based fNIRS

Area_kL, which combines the indices k and L, proved to be useful for clearly imaging slight neuroactivation at the left M1 and SMA during a 0 kg task. Increased oxygen exchange, rather than the intensity of oxygen supply, coincided with the neuroactivation site. This result shows that the location and intensity of neuroactivation cannot be accurately estimated from the intensity of Hb concentration changes. Mintun et al. (2001) strongly suggested that increased CBF is caused by factors other than oxygen demand. The response at the M1 was in danger of being overlooked, masked by the intensity of ΔO. However, even small Hb changes, such as those from cognitive tasks, can provide dynamic oxygen consumption and oxygen supply images if Area_kL is used.

Because the dumbbell load in our study was sufficient to cause a systemic cardiovascular response, it is possible that systemic circulatory changes or scalp perfusion were included in the ΔO increases in the sites surrounding M1 (Kato et al., 1999). However, the donut-shaped excessive oxygen supply response generated in the area surrounding the neuroactivation site cannot be explained simply by changes in the systemic circulation. The most recent study (Kato, 2021) showed that vector-based fNIRS was less susceptible to artifacts from whole-body cardiovascular responses and motion. In other words, detecting localized increases in k may allow us to discount the broader influence of circulation and the autonomous nervous system.

I also observed an increase in k in a prior study of passive word listening (1.5-s tasks) that was unlikely to cause systemic circulation changes (Yoshino and Kato, 2012). It is important to note that the use of baseline normalization or motion correction to preprocess the data for analysis may distort the phase of oxygen exchange. For a rigorous study, it is interesting to use data from short channels where the distance between probes detects only the scalp. Even in such a comparative study, it may not be possible to conclude that systemic changes are not involved in brain responses.

When describing the exercise during validation, the loads used were 0, 4.5, and 9.5 kg, citing previous research showing that cortical potentials increase more with heavier loads (Tamaki et al., 1994). Due to the lack of information on the maximum voluntary muscle contraction of the participants' biceps curls, it is impossible to determine whether these loads were truly heavy for the participants. Bearability for loads varies from person to person; what may be light for one person may be heavy for another. It is necessary to study the COE distribution when using dumbbells of a weight that cannot be lifted and the relationship between maximal voluntary muscle contraction and oxygen exchange. By focusing on the strong FORCE effect and the surrounding oxygen supply response using the vector-based fNIRS, it may be possible to distinguish whether the subject's inability to lift the dumbbell is due to muscle fatigue or brain fatigue, or whether the patient is capable of lifting the dumbbell but does not intentionally try to do so.

Conclusion

Vector-based fNIRS allows to image the spatial dissociation between oxygen consumption and supply in the brain during the dumbbell exercises. Based on seven indexes, vector-based fNIRS can image aspects of motor activation that other brain functional imaging modalities cannot detect. Moreover, vector-based fNIRS is a useful brain measurement method for understanding how increased oxygen exchange in M1 causes hypoxia and how the area surrounding the M1 provides fresh blood volume. The comparison of k, L, an index reflecting the local oxygen exchange distribution and its intensity obtained from vector-based fNIRS, with indices such as CBV, COE, OxyHb, DeoxyHb, CBF, and CMRO2 will be an important topic for future fNIRS studies to interpret oxygen dynamics better.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the author, without undue reservation.

Ethics statement

The studies involving human participants were reviewed and approved by the Ethics Committee of KatoBrain Co. Ltd. The patients/participants provided their written informed consent to participate in this study.

Author contributions

TK contributed to conception and design of the study, organized the data, and wrote the draft of the manuscript.

Acknowledgments

This study was partly supported by Akira Endo, M.D., Ph.D. for supervision of task design and the physical care of subjects during the experiment, and Patricia Yonemura, Hiroshi Kato and Enago (www.enago.jp) for the English language review.

Conflict of interest

Author TK was employed by KatoBrain Co., Ltd.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akiyama, T., Ohira, T., Kawase, T., and Kato, T. (2006). TMS orientation for NIRS-functional motor mapping. Brain Topogr. 19, 1–9. doi: 10.1007/s10548-006-0007-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Ances, B. M. (2003). Coupling of changes in cerebral blood flow with neural activity: what must initially dip must come back up. J. Cereb. Blood Flow Metab. 24, 1–6. doi: 10.1097/01.WCB.0000103920.96801.12

PubMed Abstract | CrossRef Full Text | Google Scholar

Cyranoski, D. (2011). Thought experiment. Nature 469, 148–149. doi: 10.1038/469148a

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferrari, M., and Quaresima, V. (2012). A brief review on the history of human functional near-infrared spectroscopy (fNIRS) development and fields of application. Neuroimage 63, 921–935. doi: 10.1016/j.neuroimage.2012.03.049

PubMed Abstract | CrossRef Full Text | Google Scholar

Gudberg, C. A., Stagg, C. J., Near, J., and Johansen-Berg, H. (2012). “Motor learning and offline processes of consolidation associated with rapid GABA modulation,” in 18th Annual Meeting of the Organization for Human Brain Mapping (Beijing).

Google Scholar

Hatakenaka, M., Miyai, I., Mihara, M., Sakoda, S., and Kubota, K. (2007). Frontal regions involved in learning of motor skill-A functional NIRS study. Neuroimage 34, 109–116. doi: 10.1016/j.neuroimage.2006.08.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Kato, T. (2004). Principle and technique of NIRS imaging for human brain FORCE: fast-oxygen response in capillary event. Proc. ISBET 1270, 85–90. doi: 10.1016/j.ics.2004.05.052

CrossRef Full Text | Google Scholar

Kato, T. (2006). Apparatus for Evaluating Biological Function. U.S. Patent No 7,065,392. Washington, DC: U.S. Patent and Trademark Office.

Kato, T. (2013). Apparatus for Evaluating Biological Function, a Method for Evaluating Biological Function, a Living Body Probe, a Living Body Probe Mounting Device, a Living Body Probe Support Device and a Living Body Probe Mounting Accessory. U.S. Patent No 8,406,838. Washington, DC: U.S. Patent and Trademark Office.

Google Scholar

Kato, T. (2018). Vector-Based Approach for the Detection of Initial Dips Using Functional Near-Infrared Spectroscopy, Neuroimaging - Structure, Function and Mind, Sanja Josef Golubic. IntechOpen. Available online at: https://www.intechopen.com/chapters/63385 (accessed August 30, 2022).

Google Scholar

Kato, T. (2021). Biological Function Measurement Device, and Biological Function Measurement Method, and Program. U.K. Patent GB2595162, Application Number 202,111,659. Newport: Intellectual Property Office.

Kato, T., Kamei, A., Takashima, S., and Ozaki, T. (1993). Human visual cortical function during photic stimulation monitoring by means of near-infrared spectroscopy. J. Cereb. Blood Flow Metab. 13, 516–520 doi: 10.1038/jcbfm.1993.66

PubMed Abstract | CrossRef Full Text | Google Scholar

Kato, T., Kumoi, M., and Koike, T. (2003). “Temporal spatial imaging of k-ratio and k-angle as oxygen exchange ratio between oxyhemoglobin and deoxyhemoglobin,” in 9th Annual Meeting of the Organization for Human Brain Mapping, Vol. 19 (Suppl) (New York, NY), 673.

Kato, T., Yamashita, Y., Sugihara, K., Furusho, J., Tazaki, I., Tanaka, D., et al. (1999). “Cerebral autonomic functional test using human functional near-infraredgraphy (fNIR),” in 5th Annual Meeting of the Organization for Human Brain Mapping, Vol. 9 (Dusseldorf).

Khan, H., Naseer, N., Yazidi, A., Eide, P. K., Hassan, H. W., and Mirtaheri, P. (2021). Analysis of human gait using hybrid EEG-fNIRS-based BCI system: a review. Front. Hum. Neurosci. 14, 613254. doi: 10.3389/fnhum.2020.613254

PubMed Abstract | CrossRef Full Text | Google Scholar

Lassen, N. A. (1959). Cerebral blood flow and oxygen consumption in man. Physiol. Rev. 39,183–238. doi: 10.1152/physrev.1959.39.2.183

PubMed Abstract | CrossRef Full Text | Google Scholar

Maruyama, S., Fukunaga, M., Sugawara, S. K., Hamano, Y. H., Yamamoto, T., and Sadato, N. (2021). Cognitive control affects motor learning through local variations in GABA within the primary motor cortex. Sci. Rep. 11, 18566. doi: 10.1038/s41598-021-97974-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Mintun, M. A., Lundstrom, B. N., Snyder, A. Z., Vlassenko, A. Z., Shulman, G. L., and Raichle, M. E. (2001). Blood flow and oxygen delivery to human brain during functional activity: theoretical modeling and experimental data. Proc. Natl. Acad. Sci. U. S. A. 98, 6859–6864. doi: 10.1073/pnas.111164398

PubMed Abstract | CrossRef Full Text | Google Scholar

Murakoshi, A., and Kato, T. (2006). “Navigating system of cranio-cerebral anatomical correlation for COE: Cerebral functional mapping of oxygen exchange,” in 12th Annual Meeting of the Organization for Human Brain Mapping, Vol. 31(suppl) (Florence). Available online at: https://www.sciencedirect.com/journal/neuroimage/vol/31/suppl/S1

Oda, S., Shibata, M., and Moritani, T. (1996). Force-dependent changes in movement-related cortical potentials. J. Electromyogr. Kinesiol. 6, 247–252. doi: 10.1016/S1050-6411(96)00010-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Pauling, L., and Coryell, C. D. (1936). The magnetic properties and structure of hemoglobin, oxyhemoglobin and carbonmonoxyhemoglobin. Proc. Natl. Acad. Sci. U. S. A. 22, 210–216. doi: 10.1073/pnas.22.4.210

PubMed Abstract | CrossRef Full Text | Google Scholar

Roy, C., and Sherrington, C. (1890). On the regulation of the blood-supply of the brain. J. Physiol. 11, 85–158. doi: 10.1113/jphysiol.1890.sp000321

PubMed Abstract | CrossRef Full Text | Google Scholar

Rupp, T., and Perrey, S. (2008). Prefrontal cortex oxygenation and neuromuscular responses to exhaustive exercise. Eur. J. Appl. Physiol. 102, 153–163. doi: 10.1007/s00421-007-0568-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Suh, M., Bahar, S., Mehta, A., and Schwartz, T. (2006). Blood volume and hemoglobin oxygenation response following electrical stimulation of human cortex. Neuroimage 31, 66–75. doi: 10.1016/j.neuroimage.2005.11.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Takahashi, T., Takikawa, Y., Kawagoe, R., Shibuya, S., Iwano, T., and Kitazawa, S. (2011). Influence of skin blood flow on near-infrared spectroscopy signals measured on the forehead during a verbal fluency task. Neuroimage 57, 991–1002 doi: 10.1016/j.neuroimage.2011.05.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamaki, T., Uchiyama, S., Tamura, T., and Nakano, S. (1994). Changes in muscle oxygenation during weight-lifting exercise. Eur. J. Appl. Physiol. 68, 465–469. doi: 10.1007/BF00599514

PubMed Abstract | CrossRef Full Text | Google Scholar

Umesawa, Y., Matsushima, K., Atsumi, T., Kato, T., Fukatsu, R., Wada, M., et al. (2020). Altered GABA concentration in brain motor area is associated with the severity of motor disabilities in individuals with autism spectrum disorder. J. Autism Dev. Disord. 50, 2710–2722. doi: 10.1007/s10803-020-04382-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Vafaee, M. S., Vang, K., Bergersen, L. H., and Gjedde, A. (2012). Oxygen consumption and blood flow coupling in human motor cortex during intense finger tapping: implication for a role of lactate. J. Cereb. Blood Flow Metab. 32, 1859–1868. doi: 10.1038/jcbfm.2012.89

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamamoto, T., and Kato, T. (2002). Paradoxical correlation between signal in functional magnetic resonance imaging and deoxygenated haemoglobin content in capillaries: a new theoretical explanation. Phys. Med. Biol. 47, 1121–1141. doi: 10.1088/0031-9155/47/7/309

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoshino, K., and Kato, T. (2012). Vector-based phase classification of initial dips during word listening using near-infrared spectroscopy. Neuroreport 23, 947–951. doi: 10.1097/WNR.0b013e328359833b

PubMed Abstract | CrossRef Full Text | Google Scholar