The wedge-pentahedra method (WPM): Topographic reduction of local terrain in the context of solar system surface gravimetry and robotic exploration

In classical gravimetry, different corrections are applied, e.g. to correct for the measurement elevation above a reference plane and the gravitational attraction of the material lying between the measurement point and reference plane. Additionally, and especially in non-flat regions, a correction for the topography is generally needed. While this contribution is relatively small on spherical celestial objects, it can be more important for irregularly shaped bodies, such as small bodies or some natural satellites. With the surface gravity being much smaller, the relative importance of the topographic correction increases, while the approximation errors of the surface will become larger. In this work, the novel Wedge-Pentahedra Method (WPM) for topographic correction for (near-) surface gravimetric measurements and simulations is presented that allows precise topographic corrections for asteroids and natural satellites. For a first study, the WPM is applied to the Martian moon Phobos. Taking an exemplary surface location, a high-resolution artificial terrain is added to the surrounding, and the gravitational influence of this topography compared to the original surface is assessed. It is found that the influence of topography on the surface gravity of a small body such as Phobos can be in the order of a few percent, making it an important correction not only for surface gravity science, but likewise for landing and surface operations, to best ensure the mission success. Therefore, the here presented WPM opens a manifold of possible future applications in the context of Solar System exploration, regarding both space science and space technology.

1 Introduction

In classical (Terrestrial) gravimetry, different corrections, sometimes also referred to as reductions, are applied to gravimetric measurements (Hammer, 1939). A generally used concept is the Bouguer anomaly, accounting for 1) the Bouguer correction, 2) the free-air gradient and 3) the terrain (topography) correction. Other types of corrections exists, but those are not discussed here. The Bouguer correction considers the gravitational effect of material between the measurement point (i.e. the gravimeter location) and a reference datum (Vaníc et al., 2001), e.g. the geoid or an arbitrary datum. The free-air gradient accounts for the increased distance to the centre of the central body (e.g. Talwani et al., 1973). Therefore, at higher-altitude surface locations, the Bouguer correction increases the resulting gravitation depending on the subsurface material density, while the free-air gradient reduces the resulting gravitation, both compared to a lower-altitude surface position. The third contribution is the topographic reduction, where the topography in the surrounding of the gravity measurement (evaluation) point is considered. Imagine a measurement at half height of a hillside: The material above the measurement point up to the peak lies above the gravimeter and “pulls up”, the resulting gravity is reduced. By the same token, from the measurement location down to the valley floor, material is “missing”, likewise decreasing the resulting gravity.

On Earth, the topographic effect is largest in mountainous regions, e.g. up 40 arcseconds in the Alps (Barzaghi et al., 2016), and elsewhere much smaller; often this correction has even be neglected (Heck and Seitz, 2007). When applied, the topographic, or mass, reduction can generally be done using tesseroids, prisms or points masses (Heck and Seitz, 2007). On the local scale, e.g. considering local surface gravimetry, tesseroids appear not suitable for a flat-Earth assumption. Point masses, or mass concentrations (mascons), result in largest computation uncertainties on the surface (Park et al., 2010; Meißenhelter et al., 2022), making it less suitable for surface measurement compared to air-/water-/spacecraft-based measurements, providing some separation between the approximated surface and the gravimeter. Regarding prisms, it is possible to obtain an analytical and therefore precise solution for right rectangular 2D (Talwani et al., 1973) or 3D prisms, e.g. Heck and Seitz (2007). However, this assumes a flat-topped rectangular top surface, which again is only an approximation of the real surface (Urbancic et al., 2017). The prism approximation therefore leads to a manifold of plateaux, giving a discontinuous surface and neglecting the surface slopes.

While the topographic correction might be oftentimes negligible on the Earth, the relative contribution will increase with decreasing gravity, e.g. on Mars and the Moon. For example, the Mars science laboratory (MSL) onboard gravity model differed from the local Martian gravity by − 4.4 mm/s² (Brugarolas, 2017), which is equal to about 0.12% of the Martian gravity, leading to vertical touchdown velocity errors roughly equal to the 3σ error and resulting in the recommendation to include corrections for local gravity (including topography) to avoid damages to a (planetary) lander in the final landing phase¹. Moreso, the effect will be even larger on small Solar System bodies (SSSB) and small natural satellites (SNS) such as the Martian moons Phobos and Deimos (hereafter generally: small bodies (SB)). To date, one gravimetric study was performed on the Moon (Talwani et al., 1973) and one on Mars (Lewis et al., 2019). Currently, the GRAvimeter for small Solar System bodies (GRASS) (Noeker et al., 2021, 2022) is being developed for surface gravimetry on the secondary of the asteroid system Dimorphos (Karatekin et al., 2021). Solar System surface gravimetry therefore demands a method well-suitable to account for local topography reduction in the proximity of the surface, avoiding the above mentioned top-surface approximation.

We will therefore address two main problems in this paper. After introducing the shape file and topography file used in this work (Section 2), we provide a geometric method to merge high-resolution 2D terrain data with a lower-resolution global shape file, exemplary demonstrating this on the Martian moon Phobos (Section 3). For example, this method can proof valuable if an existing small body (SB) shape file can be locally augmented by high resolution, local terrain observations. With this, we continue by solidifying the local high-resolution surface by creating wedge-pentahedra (Section 4) and we evaluate in-closed form the gravitation contribution (Section 5) wedge-wise using the polyhedral method (PM) (Werner and Scheeres, 1996) applied per-wedge. To show the working of the newly developed Wedge-Pentahedra Method (WPM), we further provide here a verification by comparing the resulting gravitation with a single, same-sized cube. Lastly, the gravitational influence of the surface with artificial topography is compared to the corresponding smooth surface of identical extend. This change in gravitation is also computed relative to the absolute resulting surface gravitation.

2 Shape file and DEM

2.1 Shape file

For demonstration of the newly developed WPM, we use the Martian moon Phobos and the latest shape file by Willner et al. (2014). The reported extend of this shape is represented with its radii, being 13.03 km × 11.40 km × 9.14 km, with a volume of 5,742 ± 35 km³ and a density of 1,860 kg/m³ (Willner et al., 2014). The shape model, with a nominal resolution of 100 m/pixel, was developed based on imagery data from the Mars Express Mission (MEX) and the Viking orbiter cameras.

2.2 Digital elevation model

While the above introduced shape file of Phobos is one of the most detailed in the Solar System, the resolution is still limited to 1/100 ppmeter (pixel-per-meter, comparable to pixel-per-degree (ppd)). Therefore, in order to have a high-resolution surrounding surface, an artificial digital elevation model (DEM) will be applied to the Phobian surface, kindly provided by Miyamoto (2021)². Obviously, any 2D DEM, being artificial or real, can be used for this method, meaning that gravity data analysis augmented by the observed high-resolution (local) topography can be performed following a successful mission.

The original, dimensionless data set contains 10,001 points squared, thus it is spanned in a horizontal plane, here referred to as the X-Y-plane from point (1|1) to (10,001|10,001), where the points correspond to the array position. The elevation value in these array positions is here referred to the corresponding (vertical) Z-coordinate. These “array coordinates” are completely arbitrary and can therefore be projected on any surface area. To quantify the DEM, the minimum, maximum, mean and standard deviation (std.) of the (original) DEM Z-coordinates are provided in Table 1. Given the very large amplitude of the full DEM (Table 1), and to exclude individual features, such as a very large and deep crater, we take a subset of the DEM, quadratically spanned from data points (1,000|1,000) to (2,000|2,000). Variation of the here chosen terrain subset provides an additional variable for future test cases, with entirely different local terrain. Surface plots of the (unscaled) full DEM and the chosen subset are provided in the Supplementary Material of this work. For a good visualization, only every 50th and fifth points are displayed, respectively. Note should be taken of the different scale of the Z-axes.

TABLE 1

TABLE 1. Key values of unscaled artificial DEM (Miyamoto, 2021²), at full (original) resolution. Shown is the full data set of size 10, 001² and the used subset spanned as a square between points (1,000|1,000) and (2000|2000). The first line shows the values of the full data set and the second line shows the same figures for a subset of the DEM used in this work. The data set is dimensionless, but the presented values are treated as meters.

3 Merging topographic data and shape file

For SBs, the knowledge of their shapes, and thus the available associated shape file resolution is limited. Especially for objects that have not been visited by spacecraft, the shape file is usually solely based on Earth-based observations. Even for bodies that were target of a flyby such as Phobos, the shape file resolution is limited despite the good quality of the data. Generally, the presence of a lower resolution global shape (e.g. 0.01 ppmeter) file and high resolution local shape file (e.g. better than 0.1 ppmeter) is a realistic combination. For example, the NASA DART spacecraft will kinetically impact Dimorphos to demonstrate planetary defense technology (Cheng et al., 2012). This will return high-resolution information on the shape file, but obviously only on the side/region of impact. The same is true for the Juventas CubeSat landing on Dimorphos (Goldberg et al., 2019), and the MMX mission with a planned rover deployment (Ulamec et al., 2019) and a surface-sample-acquisition-manoeuvre (Kuramoto et al., 2022). All these examples have in common that they will return detailed surface information on the surface surrounding the landing point/rover operation region. Likewise, in preparation of surface operations/landing, more detailed topographic observations of possible landing regions are obtained just-in-time, allowing additional planning using the here developed method.

Different solutions and proposals exists that consider (local) surface observations in the context of larger scale mapping. For example, Haase et al. (2019) used Apollo 17 astronaut imagery for angular measurements to precisely determine coordinates of landmarks and equipment. Details on the topography, and more specifically the surface roughness, of Itokawa were derived by Abe et al. (2006) using LIDAR observations. However, both approaches were very specific to individual features/locations, and did not return systematic improvements in the mapping of the surrounding on an areal level. On the contrary, a prime example of obtaining a high-resolution terrain model on a local scale is the surrounding of the Huygens landing site on Titan. Using (stereo-) imagery from the descent, Soderblom et al. (2007) derived an unprecedented DEM of the Titanian surface, “only” surrounding the landing Huygens landing site. Alternatively, regarding surface exploration to map the surrounding, a legged surface vehicle with a ranging sensor was presented by Kweon et al. (1989) together with a method to construct and combine elevation maps. Overall, it is therefore reasonable to assume that a high-resolution DEM will be available for the surrounding proximity of landing sites on extraterrestrial surfaces, without going further into detail on the (2D) mapping techniques.

In order to allow for good topographic reduction, here we firstly developed a method to merge a global 3D (small body) shape file with a local 2D high (-er) resolution digital elevation model (DEM). Alternatively, the merging method can be adapted for large spherical bodies (e.g. Moon, Mars, Titan), where locally a flat surface might be assumed; this will be discussed in future work. In absence of a suitable ready-made ground-truth data set of a non-spherical SB, we use the exemplary artificial DEM introduced in Section 2.2. In a first step, the local surrounding of the evaluation point is isolated (Section 3.1) and the (artificial) high-resolution digital elevation model (DEM) surface is combined with the lower-resolution shape file (Section 3.2). This merging process described in this Section is an optional preparatory step to the WPM gravitation evaluation, described in the subsequent Sections, and might be skipped if the local topography is readily available.

3.1 Localizing the region of interest

Initially, the region of interest, i.e. the local surrounding of the point of interest, is isolated. For our evaluation (landing) region, we select one exemplary location (“evaluation point”) on Phobos to illustrate the localization of the problem. To prove the stability of the method for all macroterrains, we selected a surface point inside a depression. Rather than using the vertices of the original Wavefront (.OBJ) file to identify surface points, we have decided to take the central points as evaluation (eva.) point ${(x_{\mathit{eva.}},y_{\mathit{eva.}},z_{\mathit{eva.}})}^T$ of each face by taking the average coordinates of the three boundary vertices i, j, k:

$\left[\begin{array}{c}\hfill x_{\mathit{eva.}}\hfill \\ \hfill y_{\mathit{eva.}}\hfill \\ \hfill z_{\mathit{eva.}}\hfill \end{array}\right]=\frac{1}{3}\left[\begin{array}{c}\hfill x_i+x_j+x_k\hfill \\ \hfill y_i+y_j+y_k\hfill \\ \hfill z_i+z_j+z_k\hfill \end{array}\right](1)$

The original coordinates of the studied evaluation point at the centre of its facets is ${(x_{\mathit{eva.}},y_{\mathit{eva.}},z_{\mathit{eva.}})}^T={(-945.67m,-145.67m,-8044.33m)}^T$ and the point on the Phobian surface is indicated in the global context in Figure 1 (left).

FIGURE 1

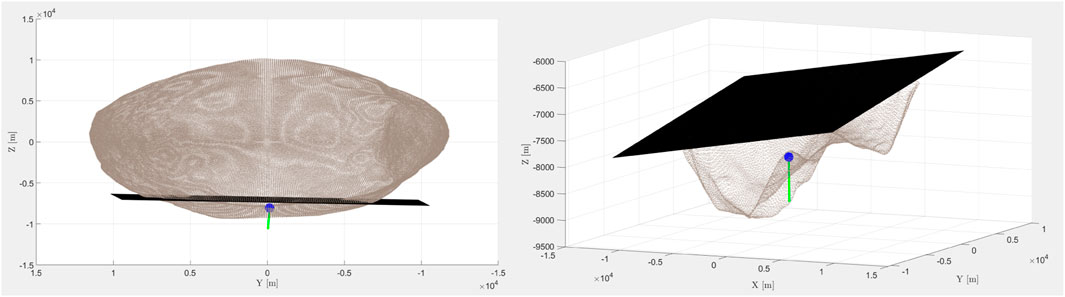
FIGURE 1. (Left) Phobos shape file with dissection plane offset by 1,000 m and evaluation point with (flipped) gravity vector (green). View in +X-direction. (Right) Local environment above dissection plane rotated with local points in proximity of the evaluation point highlighted. For better context, axes are here set equal.

In a first step, the overall shape model is used to compute the initial reference gravitation g_{ref, init} at the surface evaluation point with the well-known polyhedral method (PM) by Werner and Scheeres (1996). (This method is used here tacitly and introduced in Section 5 as it forms part in the WPM gravity evaluation.) The reference gravitation is computed with uniform density of 1,860 kg/m³ (Willner et al., 2014) and amounts to ${(g_x,g_y,g_z)}^T={(-0.1957,-0.2193,5.7880)}^T\cdot 10^{-3}m/s^2$, with a total magnitude of 5.7955⋅10⁻³ m/s² for the studied evaluation point.

With the gravitation vector in place, the first localization step is the dissection of the body. For this, a dissection plane is simply constructed by taking the evaluation point and the gravity vector as plane normal, and translating the plane by a defined distance, here 1,000 m, along the plane normal. The evaluation point, the gravity vector as plane normal, and the translational distance define the dissection plane as shown in Figure 1.

We then dissect the body along this plane and remove the points on the side away from our local point. Figure 1 (right) shows the reduced point set with the dissecting plane and the (outward-flipped) gravity vector.

Due to the arbitrary orientation of the reference gravitation g_{ref, init} in the shape file coordinate system (CS), the forthright geometric manipulation is facilitated by coordinate system rotation, such that the (outward-pointing) gravity vector aligns with the +Z′-axis in the rotated coordinate system CS′. For this, CS is rotated to becomes CS′ such that $g_{\mathit{ref,init}}={(g_x,g_y,g_z)}^T={(-0.1957,-0.2193,5.7880)}^T\cdot 10^{-3}m/s^2$ become $g_{\mathit{ref}}={(g_x^{\prime },g_y^{\prime },g_z^{\prime })}^T={(\mathrm{0,0,5.7955})}^T\cdot 10^{-3}m/s^2$, where $g_z^{\prime }$ is the magnitude of g_{ref, init}. The rotated reference gravitation vector has hence the magnitude as Z-component and the X- and Y-components are null with the exception of numerical artifacts. The rotated evaluation point coordinates are ${(x_{\mathit{eva.}}^{\prime },y_{\mathit{eva.}}^{\prime },z_{\mathit{eva.}}^{\prime })}^T={(308.39m,1259.79m,7996.54m)}^T$.

Alternatively to using the (normalized) reference gravitation vector in the above described steps, the usage of the shape surface normal was studied. However, this was found to work less reliably for irregular bodies such as Phobos. As will be shown in the next step, the method to reduce the global shape to a local shape demands sufficient surrounding material (or: surface) in all directions. The present details in the shape file of Phobos can orient the surface normal locally such that it is not helpful for the here shown implementation, i.e. not pointing in the direction of the body centre. On the contrary, the gravitation vector is generally sufficiently pointing towards the body mid-point. This is usually true for small bodies larger than Phobos, but not necessarily for even smaller bodies. On a smooth shape, such as an ellipsoid, e.g. initially assumed for Dimorphos, the gravity vector will cause a skewed dissection, making the surface normal on the smooth surface of an elongated shape preferable. Generally, the gravitational field and shape file (quality) will determine if the rotation should be done with the reference gravitation (this work) or surface normal, which will be investigated further in future work, especially for smaller bodies, or highly-elongated (e.g. dog-bone) shapes, such as 216 Kleopatra. Following a successful mission, the choice between surface normal and reference gravitation should be reconsidered for the analysis based on the latest available gravitational and observational data.

Finally, following the above introduced “vertical” translation offset, we now add a “horizontal” offset, here again exemplary Δh = 1, 000 m, but this can well vary from the vertical value and be set much larger. The terms horizontal, above/below, are artificial and only corresponds to the rotated reference frame CS′. With the “horizontal” offset Δh, we only keep the points inside a square in the X-Y-plane of side length a = 2 ×Δh = 2 × 1,000 m, centred at the evaluation point, which gives us the local surrounding for our further analysis. The rotated points above the dissection plane with the local points highlighted and isolated are shown in Figure 2. These remaining points alone form the basis for the local analysis and the superposition of the digital elevation model (DEM) that will be introduced in the next section. Clearly, the variable Δh sizes the local region of topographic investigation, and variations in this parameter influence the result. This is not only because of a different “original” surface covered, but also because of the different projection of the DEM onto that surface, recalling the inverse-squared influence of distance on gravity.

FIGURE 2

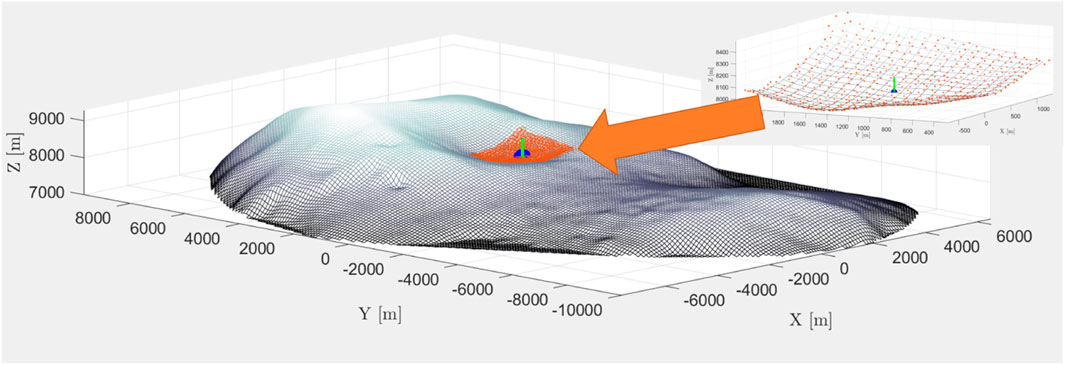
FIGURE 2. Local environment above dissection plane rotated with local points in proximity of the evaluation point highlighted. For better context, axes are set equal.

3.2 Superposition of the DEM

The localized points in the area spanning 2,000-m-squared (compare to Phobos size stated in Section 2.1) shown in Figure 2 consist of 624 points of the original shape file, therefore, we have here a one-dimensional resolution of about 25 points over 2000 m, meaning 1/80 ppmeter (slightly better than the nominal 1/100 ppmeter). While this is a good value for the global shape representation, the aim here is to artificially improve this resolution locally for the proximity terrain analysis.

The selected DEM data subset, consists of 1,000 points squared, thus of one million points. This corresponds to a resolution of 1/2 ppmeter, if projected onto the 2000-m-squared area. This resolution is too large and the number of used points has to be limited for the following reasons:

• The computation time of the algorithm, also with respect to gravity evaluation (Section 5) needs to be limited.

• The triangulation (Section 4.2) fails, if the ratio of artificial DEM to the original (smooth) resolution becomes too large.

The limitation in used points is introduced two-fold, by taking a square subset of the full DEM and by taking only every nth point of that subset data set.

For example, we take the data subset spanning from 1,000 to 2000, meaning that the points (1,000|1,000) and (2000|2000) span up the square for the subset. This subset is shown in Figure 3 (top). Hence, we have increased the surface resolution to 1,000 pixel/2000m = 1/2 ppmeter, thus we achieve a resolution 40 times better than on the original data file (1/80 ppmeter).

FIGURE 3

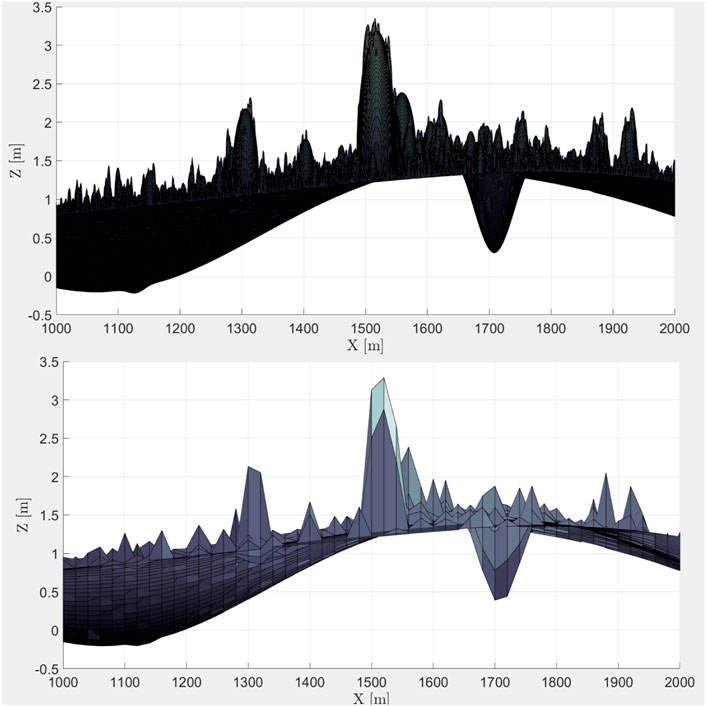
FIGURE 3. (Top) Side-view (in +Y-direction) on the subset spanned from (1,000|1,000) and (2000|2000) at the original data set resolution where all features appear smooth with a continuous surface representation. (Bottom) Same as above, but reduced resolution by taking only every 20th point.

The number of surface points can then be further reduced by only taking every nth point of the subset, reducing the number of used pixels. This is shown in Figure 3 (bottom) for every 20th point. The above calculated ground resolution therefore decreases from 1/2 ppmeter to 1/40 ppmeter. Yet, while the ground resolution now mathematically is only twice as large as the original data set, the added terrain does not disappear. Clearly visible comparing top and bottom in Figure 3, the base terrain deviation, above and below the zero-elevation plane, is only little influenced by the ground resolution at the resolution reduction. Moreover, the main features, i.e. elevations and depressions (e.g. craters) are also visible in both resolutions. Best visible when inspecting these features, however, is the difference in surface smoothness. While the surface of the original data set appears continuous and as a smooth surface (close-up inspection will still reveal discontinuous, straight facets on the “round” features), the reduced data set clearly shows the (flat) facets between the individual points. Moreover, the reduction in resolution leads to a reduction in surface features, meaning that smaller features, i.e. lying between the reduced number of points, will not appear. Likewise, the shape of surface features might be altered for this reason. The pure quantitative comparison of ground resolutions might therefore be misleading, as the DEM with lower resolution still provides much more terrain and features than the original surface. An analysis of the influence of the ground resolution is therefore included in this work. This is also important with the above mentioned computation time/algorithm for gravity and the formulation of observation requirements.

As a next step, the selected subset of the DEM with variable ground resolution (Figure 3) needs to be combined with the smooth original surface (Figure 2). This process is described step-wise in the following.

Firstly, the DEM is translated and scaled such that it lies above the reduced original surface. The vertical position “above” the original surface is only temporary and therefore arbitrary. At this stage, the DEM still has its original scaling thus within the range of −0.220 to +3.354 (Table 1), here treated as meter.

By definition, the resolution of the two data sets to be merged differs. In order to project the higher- onto the lower-resolution data grid, we perform an interpolation of the rotated original (i.e. without DEM) data set (in CS′) to match the specified (variable) resolution of the used data set. The interpolation here uses the MATLAB function griddata (option “natural”) that allows interpolation of the scattered data (here: original surface). For this, firstly a mesh is initialised with the size of the original surface (here 2000-m-squared, as highlighted in Figure 2) in the rotated reference frame CS′, with a step size equal to the (specified) DEM resolution. We then use the X′- and Y′- coordinates of this mesh for the DEM-superposition, by firstly taking the Z′-coordinate of the interpolated surface Z_{local,surface}. To this value, we add the corresponding Z-value of the DEM Z_DEM,original, multiplied by a scale factor as:

$Z_{\mathit{DEM,included}}=Z_{\mathit{local,surface}}+Z_{\mathit{DEM,original}}\cdot S_T(2)$

where S_T is the terrain scale factor. A value of S_T = 0 effectively removes the added DEM, only leaving the interpolated surface, a value of 1 is representative of the DEM plotted in Figure 3 (top) and (bottom), showing the original and resolution-reduced data, respectively. Any other value for S_T will scale the DEM accordingly, where a negative scale factor inverts the topographic profile.

In a last step, we perform a final vertical adaptation such that our evaluation point and the (newly added) artificial DEM coincide in the central evaluation point. This adaptation is arbitrary, but necessary, e.g. for the gravity evaluation. Otherwise, the evaluation point on the smooth surface could end up below the DEM surface (if the DEM locally is positive) or floating in empty space (if the DEM locally is negative).

Finally, the complete superposition of the DEM with a scale factor of S_T = 250 on the local interpolated original surface is shown in Figure 4. It is clearly visible that some of the (scaled) DEM terrain appears above and some below the original surface. This was found to be the best way of including the terrain, instead of systematically lying above or below the original surface, also with respect to the common boundary, introduced in Section 4.1.

FIGURE 4

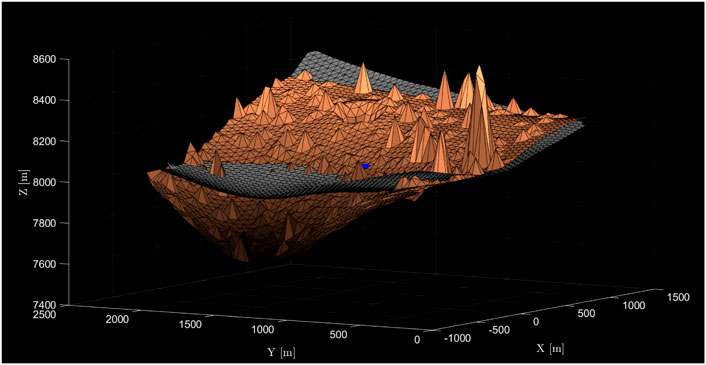
FIGURE 4. Original (smooth), interpolated surface (grey) and superpositioned DEM surface in copper. Both surfaces touch in the evaluation point (blue).

4 WPM: Solidification using wedge-pentahedra

To obtain inter-comparable results between original and DEM surface, we have to ensure a common boundary for all tested surfaces, which is done by creating a boundary frame (Section 4.1). In addition, to be able to calculate the gravitational influence of the local region, the surface has to be solidified, forming a solid volume (Section 4.2). This Section therefore describes the transition from the surface to the solid volume.

4.1 Common reference boundary

As indicated above, the geometric operations performed here need special attention towards a common boundary of the localized area. To compute the influence of the topography on the surface gravitation, we need a comparable environment, independent of the terrain scaling and realized by a common boundary frame.

For this, we start at the (central) evaluation point and span a quadrangle bound by four points (X_1,2|Y_1,2). The X-Y coordinates of these four points are simply calculated as

$X_{\mathrm{1,2}}=x_{\mathit{eva.}}^{\prime }\pm S_f\mathrm{\Delta }h(3)$

$Y_{\mathrm{1,2}}=y_{\mathit{eva.}}^{\prime }\pm S_f\mathrm{\Delta }h(4)$

where S_f (≠ S_T) is an arbitrary scale factor, chosen here as 1.001, to ensure that the frame is always outside the treated surface. Δh was above defined as the horizontal offset in the localization (here 1,000 m). The vertical (Z-) coordinate of these four points is set to be identical to the respective closest point of the DEM surface, by finding the nearest neighbour.

Starting from these four points, the frame is built in four legs, comparable to a launching gantry. Starting from one point, either the X- or Y- coordinate is kept constant. The other coordinate is varied step wise (e.g. 10 m) in one direction. The Z-value of the framing points is then again set equal to the Z-value of the closest neighbouring point of the interpolated (smooth) DEM surface, with scale factor S_T = 0 (Figure 4). By taking the smooth surface high-resolution surface, it is ensured that the frame points always find a close-by surface point for the Z-coordinate adaptation. This means, that the boundary will slightly vary for different ground resolutions, while the frame for the (interpolated) flat surface and the DEM-applied surface are always identical, which is important for a sound comparison of the DEM at that scale factor S_T.

On the local scale, it can be observed that the frame is built with small (staircase) steps of identical Z-value. This, however, does not pose a problem as no points overlap in a vertical sense. Using always the identical case for the (interpolated) flat surface and the surface with applied topography allows for the topographic reduction and the assessment of the local topography only. Finally, these frame points are added to the respective surface point sets, and they therefore play an important role in the solidification of the surface, described in the next section.

4.2 Building the local solid volume

Above, the evaluation point has been localized and rotated (Subection 3.1), the artificial DEM was superpositioned on the original surface (Section 3.2), and a reference boundary frame was built as generic boundary of the studied surface (Section 4.1).

The last step in the geometric computation is to solidify the newly created surface, i.e. creating a 3D-volume from the 2D-surface. This is required to compute the gravitational effect of the surface-forming topography, which is created by the material underlying the surface (Section 5).

In order to create a solid volume from the triangulated surface, each of the surface triangles is considered individually. The three triangle vertices are projected downwards to a common reference plane, i.e. the X-Y-coordinates are kept constant while the Z-coordinate is adapted. These total of six points form a wedge, i.e. a pentahedron, consisting of five facets, where the top triangle forms part in the DEM-surface and the bottom triangle is parallel to the X-Y-plane (Figure 5 left). Repeating this for all surface triangles, a solid volume, consisting of a multitude of pentahedra-wedges is created.

FIGURE 5

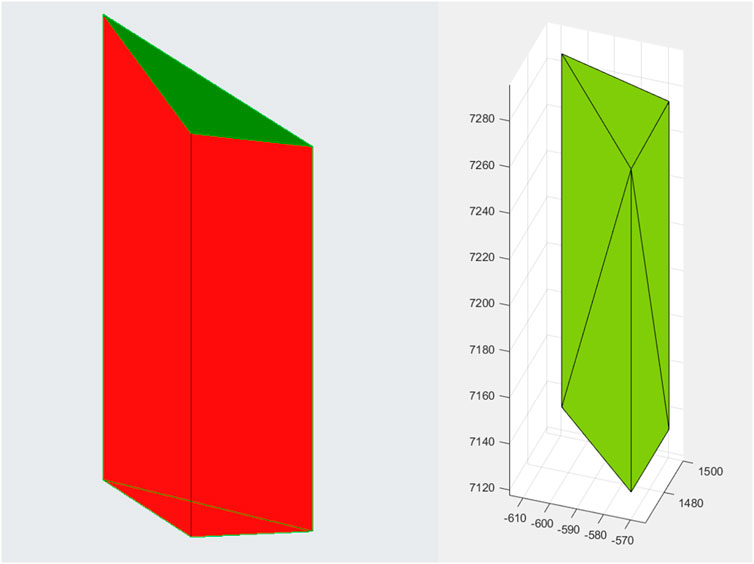
FIGURE 5. (Left) Geometry of a wedge as a pentahedron with the top surface forming part of the local surface highlighted in green. (Right) AlphaShape of wedge-pentahedron with 8 triangular facets.

For a generic algorithm, we define the projection elevation Z_bottom here as

$Z_{\mathit{bottom}}=0.9\cdot Z_{\mathit{local,min}}(5)$

where Z_local,min is the minimum Z-value of the surface. In general, the exact value (here 0.9) is not important, as long as it is kept constant between the smooth and rough surface in the topographic reduction (Section 5), similarly to the common boundary (Section 4.1). However, the down-projection distance should be large enough to always be below the anticipated surface, including the scaled DEM-surface with negative terrain such as craters. Otherwise, the superpositioned surface will appear under the projection elevation, causing the “downward” projection to fail. Likewise, projecting the surface too far down might create numerical problems as the long edges of the wedge-pentahedra become much larger than the top and bottom triangle edges.

Each of the wedges, bound with 3 + 3 = 6 vertices is now transformed to an alphaShape (α − Shape). Due to the simplicity of the (individual) wedge-pentahedra shapes, this is straight-forward. From this alphaShape, the (five) outside facets are triangulated, thus automatically splitting the (three) quadrangle facets in two triangles, giving a total of 8 facets (Figure 5 right). The advantage of this triangulation of the enclosed volume is that this format directly allows us to evaluate the gravity using the polyhedral method (PM). This evaluation is discussed further in the next Section. Showing the fully created WPM-solid is of little avail to illustrate the interior and therefore, we truncate the WPM-solidification process after 500 out of (here) 7,998 constructed wedges, showing indeed the full volume is built of individual wedges (Figure 6). As will be discussed, the advantage to evaluate the gravity pentahedron-wedge-wise is that the density can be varied per-wedge, and that the density does not have to be kept homogeneous throughout the entire volume as would be the case applying the PM to the bounding volume.

FIGURE 6

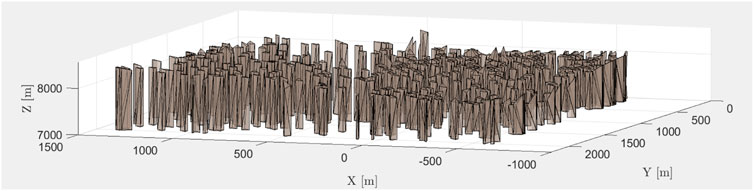
FIGURE 6. Surface solidified by WPM, truncated after 500 built wedges to show the interior of the volume.

For demonstration, we apply the solidification to the example evaluation point, once using the terrain scale factor S_T = 0 and once using a large terrain scale factor S_T = 500 to clearly visualize the added DEM. Evaluating the gravitational influence of the latter case and comparing it to the interpolated and smooth former case allows to account for the topographic reduction presented in the next Section. This is shown with the evaluation point centered (yellow) in Figure 7. Here, it is clearly visible that the common boundary frame closes the volumes off, e.g. closing of the depression on the left for S_T = 500.

FIGURE 7

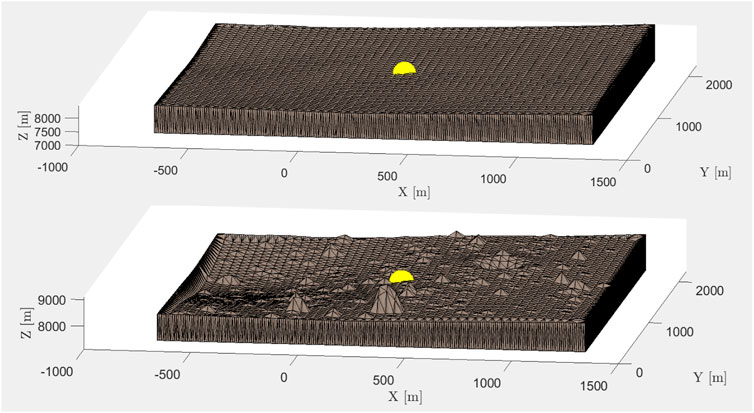
FIGURE 7. Solidified local surrounding of evaluation point (yellow) “in-crater” with local region of (2000m)² for scale factors S_T = 0 (top) and S_T = 500 (bottom).

5 WPM: Topographic reduction

With the solid in place, we can now proceed with the gravity evaluation of the local topography. In simple terms, this evaluation is done in three steps:

1) First, we compute the resulting gravity in our evaluation (eva.) point for the entire body (Phobos). For this, the homogeneous density (1,860 kg/m³, Willner et al. (2014)) is assumed. We call this gravity reference gravity: g_ref.

2) Second, we subtract the gravity of the volume bound by the local, quasi-original surface. For this, we set the DEM scale factor to S_T = 0, meaning that the surface triangulation is identical to the one to follow, yet no DEM is applied, qua definition: g_DEM=0. This is representative of the original surface with the addition of the original surface being interpolated between the (lower-resolution) original surface points.

3) Third, we then add the gravity of the same bounding volume, now with the DEM applied with the respective scale factor S_T. This gives: $g_{DEM=S_T}$.

Then the resulting gravity g_res is simply calculated with a cut-and-paste approach as

$g_{\mathit{res}}=g_{\mathit{ref}}-g_{DEM=0}+g_{DEM=S_T}(6)$

The calculated resulting gravity g_res can be compared to the reference gravity g_ref, e.g. to assess the relative change in resulting surface gravity, due to (solely) the local terrain. Generally, the relative change κ

$\kappa =\frac{g_{\mathit{res}}}{g_{\mathit{ref}}}-1(7)$

is a good measure to understand the influence on the local resulting surface gravitation due to terrain. An increase in gravity yields a positive value for κ, while a decrease returns a negative κ. This Section subsequently introduces the computation of the reference gravitation and of the gravitation per pentahedron-wedge (Section 5.1). This is then followed by a comparison of the smooth original and interpolated surface to underline the validity of the presented approach (Section 5.2). Then, the gravitational computation per-pentahedron-wedge is verified using a cube in Section 5.3.

5.1 Reference gravitation and pentahedron-wedge gravitation

The polyhedral method (PM) by Werner and Scheeres (1996) was already used tacitly in Section 3.1 to perform the initial rotation of the larger surrounding area. Here, we use an implementation by Tasev (2019). This code was verified with another implementation of the PM, by Van wal (2018) and further verified by comparing it to two different mascon implementations and to analytical solutions for a sphere and cube, as presented in Meißenhelter et al. (2022).

The gravitational attraction of any polyhedron shape with constant density ρ can be expressed as

$g\overrightarrow{(}x)=-G\rho \sum _{e\in edges}{E}_{ij}\cdot {\vec{r}}_{ij}\cdot L_{ij}+G\rho \sum _{f\in facets}{F}_{\mathit{ijk}}\cdot {\vec{r}}_{\mathit{ijk}}\cdot {\omega }_{\mathit{ijk}}(8)$

where Werner and Scheeres (1996) give the full derivation and we adapted the notation used by Van wal (2018).

As was introduced in Section 4.2, the solid volume consists of a multitude of individual pentahedra-wedges. With the surface triangulation shown in Figure 7, the gravitation of each of these wedges can be done using Eq. 8, where the number of (triangular) facets amounts to 8 and the number of edges is 12. Without question, the density of each wedge can be assigned anew, allowing a local density variation in lateral direction (and vertically in future work). Therefore, for the local gravity of the DEM, we can extend Eq. 8 by summing of the number of pentahedra-wedges z, each with variable density ρ_z as

$g\overrightarrow{(}x)=G\sum _{z\in wedges}\left(-{\rho }_z\sum _{e\in edges=12}{E}_{ij}\cdot {\vec{r}}_{ij}\cdot L_{ij}+{\rho }_z\sum _{f\in facets=8}{F}_{\mathit{ijk}}\cdot {\vec{r}}_{\mathit{ijk}}\cdot {\omega }_{\mathit{ijk}}\right).(9)$

In this work, the density ρ_z is kept constant for all pentahedra-wedges with the above introduced value of Phobos (1,860 kg/m³). It is noted that the PM is not defined on vertices or edges of the polyhedron (here: pentahedra-wedges) (Meißenhelter et al., 2022). Therefore, to avoid problems in the gravitational computation, we systematically increase the Z-component of the evaluation point generally by 0.1 m, to avoid any interference with the solidified volume. Such a distance of 10 cm is a realistic offset between surface and a gravimeter, e.g. for a landed CubeSat with a gravimeter payload, such as Juventas. For a gravimeter-carrying rover, this value could be expected to be even larger due to the ground clearance and it can be adapted accordingly. By applying this offset to all gravitation evaluations (g_ref, g_DEM=0, and $g_{DEM=S_T}$) the comparison is consistently done in the same location.

5.2 Comparing smooth original and interpolated surface

As stated above, the here presented WPM performs initially an interpolation on the lower-resolution original (regional) surface to be able to accommodate the DEM projection (Section 3.2). In this section, the influence of this interpolation will be studied to assess how close the interpolated surface corresponds to the original surface coming from the global shape file.

For this, we compare the original surface with lower resolution (here 624 surface points coming from the original surface) and we have the (generally) higher resolution interpolated surface, created in preparation of the DEM application (i.e. scale factor S_T = 0). These two surfaces are shown in Figure 8. By visual judgement, both surfaces appear identical, yet with different resolution. Therefore, additional analysis is required to assess the influence of the interpolation in detail.

FIGURE 8

FIGURE 8. Comparison of the high-resolution (interpolated) and original surface at top and bottom, respectively. Clearly, the surrounding frame boundary and centre point are identical.

To compare the two surfaces, two different assessments are performed to indirectly judge the alikeness of the two surfaces. Initially, the WPM gravitational evaluation is applied to both surfaces shown in Figure 8. As identical surfaces would yield identical surface gravitation, some expected variation serves as a measure of the similarity between the two surfaces. This analysis can be made for different resolution reduction values. Table 2 shows the resulting gravitation evaluated with the WPM on both the original and the interpolated surface. In addition, the ratio between both is provided. Likewise, the volume of the two created solid volumes from the two surfaces in computed and compared in Table 3.

TABLE 2

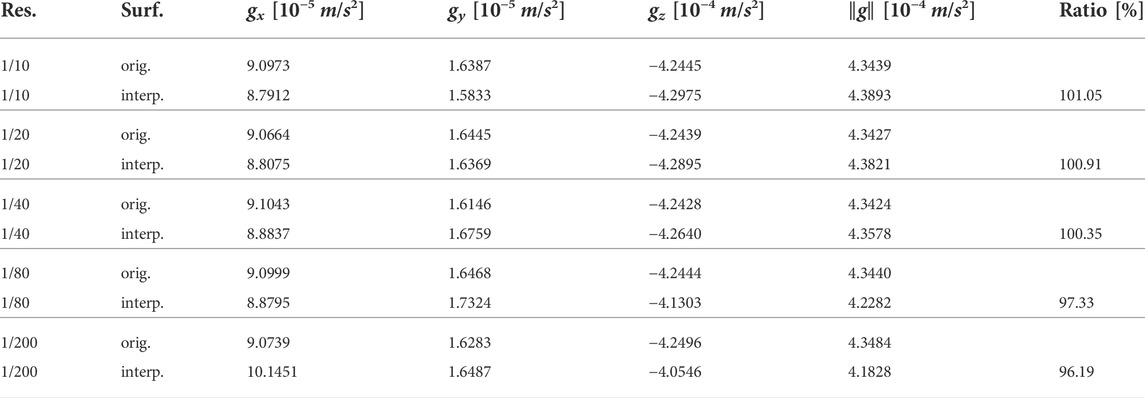
TABLE 2. Absolute WPM gravitation for local surrounding for different interpolation (interp.) resolutions (res.) compared to the WPM of the original (orig.) surface (surf.) to assess the influence of the DEM interpolation at scale factor 0. The ratio refers to the quotient of resulting WPM gravity ‖g‖ from interpolated to original surface. Resolution in ppmeter.

TABLE 3

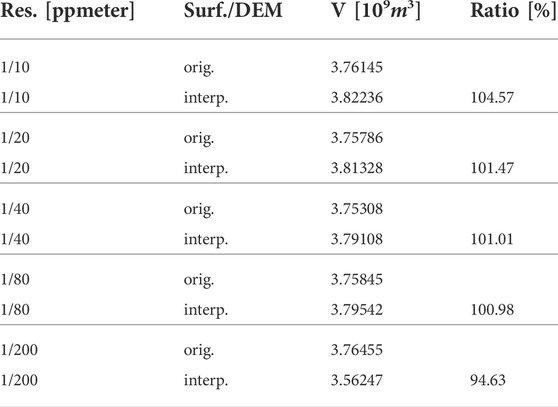
TABLE 3. Overview of bounded solid volume for different surface resolutions. This allows a comparison of the original (orig.) and interpolated (interp.) surface, using the ratio of iterp. to orig.

Regarding these two Tables, it is observable that the gravitation (Table 2) and the volume (Table 3) of the smooth (original) surface is not perfectly constant with a small yet distinct variation. Generally, one would expect this to be constant, as the WPM method is applied to the same (original) surface points. However, due to the variation in the resolution parameter, the building of the common boundary frame (Section 4.1) varies such that the Z-coordinates of the frame points, looking for the nearest neighbour, differ slightly. It is recalled that here the interpolated DEM grid is used with S_T=0, of which the resolution depends on the resolution parameter.

Nonetheless, even if the variation in gravity and volume were larger, this does not pose a problem, since the WPM topographic reduction always is concerned between a comparison between smooth surface and surface with applied DEM, both at the same resolution.

By the same token, the provided ratios must be assessed only with regards to the interpolated surface. The agreement regarding both, the gravitation of the WPM solid volume alone and the volumina are generally in good agreement, especially for 1/40 ppmeter. Here the gravitation varies only by 0.35% and the volume by about 1%. This is a very good agreement, showing that the surface interpolation in preparation of the DEM application is of very good quality. Therefore, the interpolated surface is well representative of the original surface, while some deviation due to the interpolation has been shown, as can be expected. These percentages must not be compared to the percentages presented in Section 6, where the effect of the local topography on the resulting surface gravitation is assessed.

Considering the trend of the ratios of the gravity and volume agreement, there is a clear decreasing trend. Starting with an overshoot at the highest resolution (1/10 ppmeter), the agreement decreases towards and undershoots at the coarsest resolution (1/200 ppmeter). Clearly, the “natural” interpolation switches from an over-representation (too much gravity and volume) to an under-representation (too little gravity and volume). This can be qualitatively explained with the following example. Consider an upward pointing triangle, representative of the cross-section of two facets of the original surface. To achieve a continuous (“natural”) surface representation, it is possible that the triangle is not fully inside the interpolated surface at similar or even lower resolutions due to the limited resolution, and therefore, the bound volume will be smaller. On the contrary, if distinct more points have to be fit between the three exemplary triangle points, the interpolation will yield a surface comparable to a half-circle, which would exceed the bound volume of the triangle. Of course, the overall surface interpolation is more complex and three-dimensional, yet the example provides a general explanation how the interpolation trend might change with variable resolution. Obviously, for different interpolation settings at other surface locations, the trend could likewise be inverse and yield an opposite ratio trend.

5.3 Verification of wedge-pentahedra-wise gravitation computation

Before presenting results of the gravitation computation, we have to verify that the computation of the overall gravitation of the entire considered volume can be obtained by summing the gravitation of all wedge-pentahedra that represent the identical volume (Eq. 9). For this, we apply the WPM to a flat surface with DEM scaling S_T = 0 and create a cube out of individual pentahedra-wedges. The resulting gravitation as a sum of all individual shapes is then compared to the gravitation of a single continuous cube, computed with the PM. The validity of the PM applied to a cube was shown in Meißenhelter et al. (2022), providing a very good test case for gravitational computation comparison, therefore this provides a very suitable verification case within the WPM geometric constraints. For the WPM, a simple Wavefront(.OBJ) shape file can be created with side length a = 10,000 m to represent the cube.

For the WPM cube, a surface is spanned from −5,000 m to +5,000 m in both X- and Y-direction. The surface is created and triangulated at Z = +5, 000 m and the wedges are projected downwards to Z_bottom = −5, 000 m. This is shown in Figure 9. Here, the cube with top and bottom parallel triangular facets provide a special case, where the wedges are all right prisms. The WPM cube surface is created by points every 200 m, thus creating (10,000m/200m)² ⋅ 2 = 5, 000 wedges. For the purpose of the cube, no framing using the common frame of the shape has been performed, since the flat cube surface ensures a perfect cutoff of the top surface (Section 4.1).

FIGURE 9

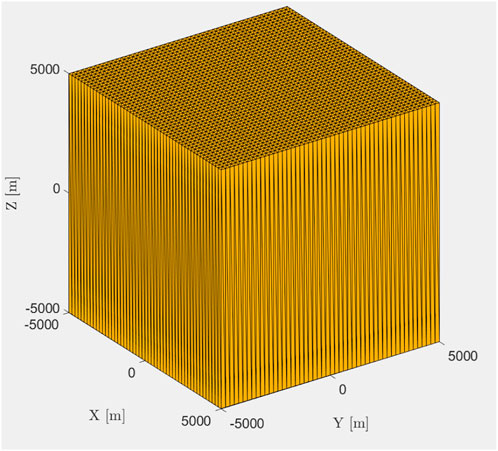
FIGURE 9. WPM applied to a created flat (10,000 m)² surface, projected from Z = +5, 000 m down to Z = −5, 000 m and thus creating a cube.

With both in place, it is possible to compare the gravitation calculated by the PM, which is a closed-form analytical solution and therefore considered as the truth, and the here developed and presented wedge-pentahedra-wise gravitation computation, calculating the gravitation as summation of the gravitation of all individual wedges. The evaluation point is done 0.1 m above the centre of the top facets, i.e. at (0, 0, 5,000.1)^Tm and the density is arbitrarily kept at 1, 860 kg/m³, like for Phobos. The resulting 3D gravitation vector components of both methods are listed in Table 4.

TABLE 4

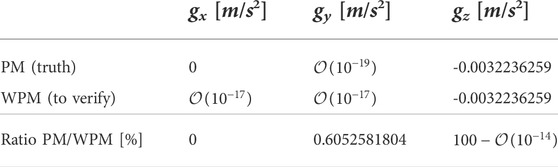
TABLE 4. Gravity verification between PM and WPM using a cube. The theoretical X- and Y-components are zero and we provide the numerically created non-zero orders of magnitude as well as the order of magnitude of the deviation of the Z-components.

Obviously, the X- and Y-components of the gravitation are expected to be zero. Indeed, both methods return near-zero values, which can be explained to be non-zero due to numerical noise. Still, the non-zero values are larger for the WPM compared to the PM, which can be expected given that within the WPM the PM is executed (here) 5,000 times, i.e. individually per pentahedron-wedge, and thus accumulating numerical noise. Clearly, the Z-component computed in both methods is in agreement, verifying the gravitation computation within the WPM.

6 Gravitational influence of the local topography

With the gravitational computation (Section 5.3) of the WPM being verified and the quality of the surface interpolation assessed (Section 5.2), the new Wedge-Pentahedra Method (WPM) can now be used to test the influence of the local topography on the surface gravity. For consistency, this will be done for the Phobian surface point used throughout this work.

Regarding the gravitational influence, we present here the assessment of two parameters, the terrain scale factor S_T and the DEM resolution (measured in pixel-per-meter (ppm)) discussed in the previous section. Firstly, the resulting gravitation at the evaluation point (Eq. 6) and the relative change due to the added topography (Eq. 7) is shown in Table 5 for different terrain scale factors S_T. Here, the ground resolution is kept constant at 10 ppmeter.

TABLE 5

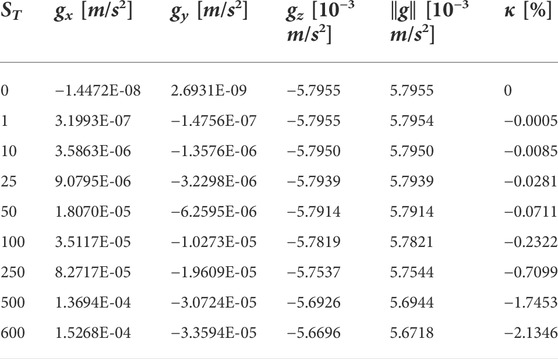
TABLE 5. Absolute gravitation for different terrain scale factors S_T for the WPM. The ratio κ provides insights on the relative change of the resulting gravitation as a function of the increased amplification of the local artificial terrain.

For the scale factor 0, the X- and Y-components are near 0 due to the applied rotation. The components are still non-zero due to the applied interpolation and numerical artifacts of the applied rotation. The scale factor 0 approximates, with some approximation error (Section 5.2), the original surface. As can be expected, the changes in gravity due to the topography increase with increasing scale factor in all three dimensions and magnitude. Therefore, also the 3D-orientation of the gravitation will vary. In this location, the ratio decreases, making the DEM gravitation smaller than the original gravitation. Here, this is due to the shape of the DEM, and, obviously, the increasing change can be inverted for a different DEM or a different evaluation location. At some tested scale factors larger than S_T=600, no result was obtained as the DEM amplitude became too large. This was discussed alongside with Eq. (5).

In the same fashion, we investigate the influence of the resolution at which the DEM is applied (Table 6). This is similar to the study presented in Table 2, however, there the DEM scale was kept constantly at S_T = 0. Here, we chose to fix the terrain scaling at S_T = 250, with a deviation of about −0.7% of the gravitation due to the added DEM (Table 5). Additionally, we track the computation time of the WPM evaluation only (thus excluding the initialization), to demonstrate the influence of the resolution on the computation time, driven by the number of pentahedron-wedges. Regarding the computation time tracked in MATLAB, the used hardware (CPU) is an Intel^® Core™ i7-8850H.

TABLE 6

TABLE 6. Absolute gravitation for different DEM resolutions compared to the WPM of the original surface to assess the influence of the DEM interpolation at scale factor 250. Computation time T for comparison of different resolutions. Compare the first κ value to Table 5 (S_T = 250).

For the resolution, other than for the scale factor, the result is less unambiguous. Generally, one could expect that with lower resolution, and thus less surface detail, we will approximate the original surface with fewer and fewer surface points spanning the DEM surface. Looking at the two highest resolutions, the absolute value of κ indeed increases from 1/10 ppmeter to 1/20 ppmeter towards 0%. However, going then to 1/40 ppmeter, the relative change again increases to κ = −0.7773%. It is hard to explain this behaviour exhaustively, but it can be expected that this shows a good example how the overall topography is steered by the chosen ground resolution, as was previously discussed with Tables 2, 3. For example, imagine a net-gravity reducing hillock with material “above” the evaluation point, again with a (simplified) 2D-triangular cross-section. This could be perfectly represented at a resolution of 1/20 ppmeter with three points, but would disappear with the peak point if the resolution is decreased to 1/40 ppmeter. Here this effect could then outweigh the general surface approximation, before this becomes again the main contribution, reducing the relative change in gravity further. Then, with further decreased ground DEM resolution, indeed the gravitation ratio increases again towards 0%, meaning that fewer details, here decreasing the resulting gravitation in sum, are represented on the lower-resolution surfaces. The second coarsest resolution of 1/80 ppmeter is indeed equal to the original shape file resolution of Phobos. Yet, while having the same resolution, the surfaces are not identical and thus κ ≠ 0%, as even with this resolution the DEM adds local topography, thus altering the original (interpolated) surface. This is even the case for 1/200 ppm, having a resolution lower than the original file, yet presenting added DEM features. Generally, while here κ < 0% it is well possible that the added DEM results in κ > 0%. This solely depends on the macroscopic (shape file) and microscopic (DEM) regional circumstances. Overall, the irregularity at 1/40 ppmeter highlights that while general trends can be expected for a variable ground resolution, the added topography will still return exceptions to such trends.

7 Discussion and future work

To date, topographic corrections on (surface) gravimetric measurements only use approximating topographic corrections, if applied at all. The here developed Wedge-Pentahedra Method (WPM) provides a novel technique for topographic reduction. Future work might compare the WPM with existing techniques to quantify the benefit of this method, which will also allow to better justify the sizing of the here introduced local surrounding, to which the DEM was applied.

While not limited to small bodies and natural satellites in the Solar System, it has been shown that, depending on the terrain amplification, the sole effect of the local surrounding topography has a non-negligible effect on the surface gravitation, important for surface gravimetry or landing/surface operations. For example, in the studied test case, the deviation in gravitation due to the terrain amounts to −0.7% for a scale factor S_T = 250. The amplification of the DEM terrain is arbitrary and larger scaling factor might, in some locations, be unrealistically large. With very good observational knowledge of the inner moon in areocentric orbit, the presented topography might be exaggerated for larger scale factors. On the contrary, considering a similar celestial body with much less known detail about the shape, large topographic variations as shown here cannot be ruled out. In any case, it is well possible to limit individual, unrealistically large features in the (artificial) DEM data set, by introducing cutoff criteria or proportional scaling.

Therefore, in absence of high-resolution ground truth data, the presented results should be understood as a priori estimates of possible topographic influences on the surface gravity. Like this, mission planning could be aided, e.g. in estimating uncertainties in the gravity for landing trajectories or rover stability. If high resolution terrain data of the selected/considered landing sites become available just before descent, final corrections might be applied and post-mission data analysis will certainly be able to include WPM corrections, which is valuable not only for surface gravimeters. Here, the analysis and variability of the DEM resolution (res.) parameter is an interesting asset, e.g. when formulating terrain/shape observation resolution requirements. Another parameter to be varied in future investigations is the size of the local surrounding (determined by Δh). This will determine the surface area surrounding the point of interest to be included in such topographic analysis regarding gravity.

The presented results are only one snapshot of a multitude of possible test cases. The presented analysis only shows the results for one exemplary surface location on one exemplary body, one artificial DEM and one local subset thereof. All these parameters can be studied further by varying them. The WPM therefore opens up a manifold of future applications across the Solar System. For example, the WPM can be used further to assess the gravity slopes on the surface of a body, i.e. the orientation of the gravity vector with respect to the local surface normal.

Likewise, while kept constant in this work, the density per-wedge can be varied to assess the influence of variation of the density. This is not limited to the “horizontal” variation, but can be extended vertically in future work. The variation of the local density is solely limited by the DEM resolution in lateral direction (determining the number of wedges) and by computation time in the subsurface direction (“vertical”). This vertical variation, stacking different right prisms or wedges above each other, will be done in future work. Moreover, the created DEM surface solid can be exported and used for illumination assessments, that will be affected by shadows of the local terrain.

Possible applications of the here developed method include, but are not limited to, small body landing (bouncing) analysis, surface operation planning, illumination assessment (shadowing, solar power etc.), or gravity science preparation. Initially targeted specifically at small, non-spherical bodies, the scope of the WPM application can be extended to larger, spherical bodies, such as the Moon and Mars. Here, a topographic reduction with very good surface representation will also be beneficial, most notably in regions with significant terrain. Good surface gravity interpretation will not only aid the science, but can be equally important in preparation of in-situ resource utilization (ISRU) or the detection of intact subsurface lava tubes.

8 Conclusion

Here, we present the implementation of the newly developed Wedge-Pentahedra Method (WPM). Using the Polyhedral Method (PM) prevalently, it provides a closed-form analytical description of the topographic influence of the local surface, while allowing the perfect triangulated description of the surface, rather than approximating it using (flat topped) prisms.

At the same time, the local density in the WPM can be varied per wedge, and further vertically, by stacking wedges or right prisms. This allows to combine the advantage of the mascon approach where the density can be assigned per mass element, while removing the disadvantage of relatively large errors at the surface, the location which is of special interest in Solar System surface gravimetry.

We have successfully verified the method by comparing the resulting gravitation of a single cube with the WPM applied to a WPM-volume equal to the cube. Further, the WPM has been applied to a surface point on Phobos and the influence of different terrain scale factors S_T and resolutions has been investigated. The influence is indeed significant for larger terrain scale factors S_T, e.g. at a scale factor of S_T=100 the effect was found to be larger than −0.1%. The DEM resolution has also an influence on the resulting gravitation, which can provide inputs to observation requirement formulation. Therefore, for Solar System gravimetry, it was shown that the topographic reduction cannot be neglected as is sometimes done on Earth, and this work provides a way to account for the local topography, especially in the context of small bodies.

Possible future applications of the here presented Wedge-Pentahedra method (WPM) are manifold and have been discussed. They are not limited to classical gravimetry and topographic reduction, but can likewise be used for mission planning, e.g. landing or rover operations. Obviously, the WPM can incorporate artificial data prior to a mission and likewise real data obtained by an exploration mission. While the effect might be largest on smaller objects in the Solar System, the method can also be applied to significant topography on the Moon, Mars and our home planet.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

MN devised and implemented the presented method, and prepared the manuscript draft. ÖK was involved in the planning and supervision of the work. MN and ÖK critically revised the manuscript and discussed the results. Both authors agree to be accountable for the content of the work.

Funding

MN acknowledges funding from the Foundation of German Business (sdw) and the Royal Observatory of Belgium (ROB) PhD grants. The authors acknowledge funding support from the PRODEX program managed by the European Space Agency (ESA) with help of the Belgian Science Policy Office (BELSPO) and from the European Union’s Horizon 2020 research and innovation program within the NEO-MAPP project.

Acknowledgments

We would like to thank Elisa Tasev and Hirdy Miyamoto for kindly providing the polyhedral method (PM) MATLAB function implementation and the artificial digital elevation model (DEM), respectively. In addition, we gratefully acknowledge Alfonso Caldiero for his help in converting the DEM file. We extend our gratitude to two anonymous reviewers for their constructive feedback.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frspt.2022.982873/full#supplementary-material

Footnotes

¹https://llis.nasa.gov/lesson/27901 accessed on 28.04.2022.

²Miyamoto, H. (2021). Personal communication, [Dataset].

References

Abe, S., Mukai, T., Hirata, N., Barnouin-Jha, O. S., Cheng, A. F., Demura, H., et al. (2006). Mass and local topography measurements of Itokawa by Hayabusa. Science 312, 1344–1347. doi:10.1126/science.1126272

PubMed Abstract | CrossRef Full Text | Google Scholar

Barzaghi, R., Carrion, D., Pepe, M., and Prezioso, G. (2016). Computing the deflection of the vertical for improving aerial surveys: A comparison between EGM2008 and ITALGEO05 estimates. Sensors 16, 1168. doi:10.3390/s16081168

PubMed Abstract | CrossRef Full Text | Google Scholar

Brugarolas, P. (2017). “Guidance, navigation and control for the entry, descent, and landing of the Mars 2020 mission,” in 40th annual guidance and control conference, Breckenridge, CO, February 2–8, 2017 (Pasadena, CA: Jet Propulsion Laboratory, National Aeronautics and Space Administration).

Google Scholar

Cheng, A., Michel, P., Reed, C., Galvez, A., Carnelli, I., and Headquarters, P. (2012). “Dart: Double asteroid redirection test,” in European Planetary Science Congress, 23–28.

Google Scholar

Goldberg, H. R., Karatekin, Ö., Ritter, B., Herique, A., Tortora, P., Prioroc, C., et al. (2019). “The Juventas cubesat in support of ESA’s Hera mission to the asteroid Didymos,” in Small satellite conference. Logan, UT: Utah State University.

Google Scholar

Haase, I., Wählisch, M., Gläser, P., Oberst, J., and Robinson, M. S. (2019). Coordinates and maps of the Apollo 17 landing site. Earth Space Sci. 6, 59–95.

Google Scholar

Hammer, S. (1939). Terrain corrections for gravimeter stations. Geophysics 4, 184–194. doi:10.1190/1.1440495

CrossRef Full Text | Google Scholar

Heck, B., and Seitz, K. (2007). A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. J. Geod. 81, 121–136. doi:10.1007/s00190-006-0094-0

CrossRef Full Text | Google Scholar

Karatekin, Ö., Ritter, B., Carrasco, J., Noeker, M., Umit, E., Van Ransbeeck, E., et al. (2021). “Surface gravimetry on Dimorphos,” in EGU General Assembly Conference Abstracts. EGU21–15901.

Google Scholar

Kuramoto, K., Kawakatsu, Y., Fujimoto, M., Araya, A., Barucci, M. A., Genda, H., et al. (2022). Martian moons exploration MMX: sample return mission to Phobos elucidating formation processes of habitable planets. Earth Planets Space 74, 12–31. doi:10.1186/s40623-021-01545-7

CrossRef Full Text | Google Scholar

Kweon, I.-S., Hebert, M., Krotkov, E., and Kanade, T. (1989). “Terrain mapping for a roving planetary explorer,” in IEEE International Conference on Robotics and Automation (IEEE), 997–1002.

Google Scholar

Lewis, K. W., Peters, S., Gonter, K., Morrison, S., Schmerr, N., Vasavada, A. R., et al. (2019). A surface gravity traverse on Mars indicates low bedrock density at Gale crater. Science 363, 535–537. doi:10.1126/science.aat0738

PubMed Abstract | CrossRef Full Text | Google Scholar

Meißenhelter, H., Noeker, M., Andert, T., Weller, R., Haser, B., Karatekin, Ö., et al. (2022). Efficient and accurate methods for computing the gravitational field of irregular-shaped bodies. In 2022 IEEE Aerospace Conference. 1–17.

Google Scholar

Noeker, M., Van Ransbeeck, E., Karatekin, Ö., and Ritter, B. (2021). “Development of a compact payload mechanism enabling continuous motorized sensor head rotation and signal transfer,” in European Space Mechanisms and Tribology Symposium (ESMATS), 20th - 24th September, 2021. Online.

Google Scholar

Noeker, M., Van Ransbeeck, E., Ritter, B., and Karatekin, Ö. (2022). “The GRASS gravimeter rotation mechanism for ESA hera mission on-board Juventas deep space CubeSat,” in Proceedings of the 46th Aerospace Mechanisms Symposium, May 11-13, 2022, 159–172. Virtual.

Google Scholar

Park, R. S., Werner, R. A., and Bhaskaran, S. (2010). Estimating small-body gravity field from shape model and navigation data. J. Guid. control, Dyn. 33, 212–221. doi:10.2514/1.41585

CrossRef Full Text | Google Scholar

Soderblom, L. A., Tomasko, M. G., Archinal, B. A., Becker, T. L., Bushroe, M. W., Cook, D. A., et al. (2007). Topography and geomorphology of the Huygens landing site on Titan. Planet. Space Sci. 55, 2015–2024. doi:10.1016/j.pss.2007.04.015

CrossRef Full Text | Google Scholar

Talwani, M., Thompson, G., Dent, B., Kahle, H., and Buck, S. (1973). Traverse gravimeter experiment.[relative gravity measurements at sites in Apollo 17 landing area]. Apollo 17 Preliminary Science Report

Google Scholar

Tasev, E. (2019). Determination of the interior structure of small bodies of the Solar System. Bruxelles: Université Libre de Belgique (BE), ISAE-SUPAERO (FR). Master’s thesis.

Google Scholar

Ulamec, S., Michel, P., Grott, M., Böttger, U., Hübers, H.-W., Murdoch, N., et al. (2019). “A rover for the jaxa mmx mission to phobos,” in 70th International Astronautical Congress (International Astronautical Federation). IAC–19.

Google Scholar

Urbancic, N., Ghent, R., Johnson, C. L., Stanley, S., Hatch, D., Carroll, K. A., et al. (2017). Subsurface density structure of Taurus-Littrow Valley using Apollo 17 gravity data. J. Geophys. Res. Planets 122, 1181–1194. doi:10.1002/2017je005296

CrossRef Full Text | Google Scholar

Van wal, S. (2018). High-fidelity simulation of small-body lander/rover spacecraft. Boulder: University of Colorado Boulder. Ph.D. thesis.

Google Scholar

Vaníc, P., Novák, P., and Martinec, Z. (2001). Geoid, topography, and the bouguer plate or shell. J. Geodesy. 75, 210–215. doi:10.1007/s001900100165

CrossRef Full Text | Google Scholar

Werner, R. A., and Scheeres, D. J. (1996). Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 castalia. Celest. Mech. Dyn. Astron. 65, 313–344. doi:10.1007/bf00053511

CrossRef Full Text | Google Scholar

Willner, K., Shi, X., and Oberst, J. (2014). Phobos’ shape and topography models. Planet. Space Sci. 102, 51–59. doi:10.1016/j.pss.2013.12.006

CrossRef Full Text | Google Scholar