Estimation of Orbital Parameters of Broken-Up Objects From In-Situ Debris Measurements

This paper briefly introduces a new approach to estimate some orbital parameters of on-orbit satellite fragmentations (specifically, the direction of angular momentum at a specific time and the time change in direction of angular momentum) from in-situ debris measurements. This approach, as in previous studies, adopts a constraint equation derived from the fact that a piece of debris detected shares the geocentric position vector with an in-situ debris measurement satellite. However, unlike previous studies, this approach does not adopt a constraint equation that can be applied to the rate of change in right ascension of the ascending node of a broken-up object. Instead, this approach determines the inclination of a broken-up object from the maximum or minimum geocentric declination at the time of detection. Then, this approach finds out a candidate for the rate of change in right ascension of the ascending node of a broken-up object by assuming a circular orbit with a radius of the geocentric distance at the time of detection. Finally, using the constraint equation adopted, this approach estimates the right ascension of the ascending node at the time of breakup and calculates a correction for the rate of change in right ascension of the ascending node. This paper also verifies that this new approach works effectively under ideal conditions where all detections are assumed to be at the line of intersection of the two orbital planes of a broken-up object and an in-situ debris measurement satellite.

1 Introduction

This study aims at an environmental estimation for tiny debris in the low Earth orbit (LEO). Whereas space debris larger than 10 cm in size are currently tracked from the ground and their orbital information is maintained and updated in some databases, those under 10 cm are not, mainly because of their low traceability. As seen in a verification experiment followed by the incident of ADEOS-II spacecraft of the Japan Aerospace Exploration Agency (JAXA), sub-millimeter-size debris can damage components of a spacecraft such as an electrical wiring harness. Therefore, building a collision flux model of sub-millimeter-size debris is urgent to mitigate the risk of their collision with spacecraft in operation.

There are two main approaches to measure an environment of sub-millimeter-size debris in LEO, that is, “ground-based” and “space-based” approaches. The former has been conducted by radar observations (Goldstein et al., 1998; Matney et al., 1999; Stokely et al., 2009). They are currently available to debris’ size limited to approximately 2 mm. On the other hand, as an example of the latter approach, in-situ debris measurement missions using debris impact sensors mounted on spacecraft body surfaces have been proposed (Ae et al., 2013; Hanada, 2013; Kitazawa et al., 2013; Bauer et al., 2014; Bauer et al., 2015; Anz-Meador et al., 2019; Oikonomidou et al., 2021) to detect micro-debris down to sub-millimeter in size.

Another advantage of those impact sensors for the in-situ debris measurement missions is that they can estimate a sub-millimeter-size debris environment more promptly than the other methods. For example, Kyushu University pursued a project for an In-situ Debris Environmental Awareness called “IDEA,” which aims at a prompt estimation of sub-millimeter-size debris environment utilizing small measurement satellites (Ae et al., 2013; Hanada, 2013). The final goal of the IDEA mission was to identify the position of on-orbit satellite fragmentations, which may generate a myriad of fragments. Whereas in conventional in-situ debris measurement approaches (McDonell et al., 1993; Aceti and Drolshagen., 1995), debris impact data on the retrieved spacecraft (or devices) have mainly time-integrated information, the proposed mission was expected to conduct a real-time measurement, that contributes to estimating a more exact orbital environment of space debris.

This study proposes a new approach to estimating some orbital parameters of on-orbit satellite fragmentations from in-situ debris measurements. Specifically, orbital elements herein indicate the direction of angular momentum at a specific time, that is, the right ascension of the ascending node (RAAN) and the inclination.

In the previous studies (Doi, 2013; Fujita et al., 2016; Furumoto et al., 2017; Kodama et al., 2019), based on a constraint equation of orbital conditions on both debris from specific on-orbit satellite fragmentations and a measurement satellite, some estimation techniques were applied for those unknown orbital parameters including in the constraint equation. Despite many refinements of the techniques applicable to actual locations of debris impact, the previously proposed methods are hard to solve the problem of converging into local minima because of the non-linear property seen in the constraint equation.

In this study, a fundamentally different approach is applied to avoid such a local minima problem. Instead of directly estimating unknown parameters of the constraint equation, the new approach firstly estimates one of the unknown orbital parameters, the inclination, by utilizing the timing that its amount coincides with the geocentric declination at the time of detection. Since the timing occurs when the geocentric declination has a maximum or minimum value, which should periodically appear during the orbital motion of measurement satellite and fragments from a specific on-orbit satellite fragmentation, we can estimate it from actual time-series observation data.

Once the inclination of the satellite fragmentation is estimated, the rate of change in RAAN can be subsequently estimated by utilizing a relationship between the two parameters implying an effect of $J_2$ perturbation. Finally, the RAAN at a specific time can be obtained from the previously estimated rate of change in RAAN.

The following sections describe the above new approach in detail, as well as the constraint equation, which strongly affects the orbital parameters for both the fragmentation debris and the measurement satellite.

2 Constraint Equation

Ae et al. (2013) have investigated the nature of orbits on which debris may contribute to the collision flux to an in-situ debris measurement satellite. For this investigation, they applied an apogee-perigee filter to known objects in the catalog to eliminate objects which never approach the measurement satellite. Then, they evaluated the collision flux into the measurement satellite due to the objects not being eliminated by the apogee-perigee filter based on a spherical finite element model. Finally, they picked up contributors to the collision flux.

Furumoto et al. (2015) and Furumoto et al. (2017) have derived a constraint equation that can be applied to the contributors picked up by Ae et al. (2013). When an in-situ debris measurement satellite detects a piece of debris, the measurement satellite and the piece of debris share the geocentric position vector at the time of detection (see Figure 1). The angular momentum vector of the piece of debris should be perpendicular to the geocentric position vector at the time of detection. Therefore, it is possible to derive a constraint equation that can be applied to the orbital plane where the piece of debris was. Letting the geocentric position vector be $\mathit{r}$ and the unit vector along the angular momentum be $e_W^{\prime }$, then the following constraint equation can be derived.

$\mathit{r}\mathbf{\cdot }{\mathit{e}}_W^{\prime }=0(1)$

Note that ${\mathit{e}}_W^{\prime }$ is given by ${\left(\sin {\mathrm{\Omega }}^{\prime }\sin i^{\prime }, -\cos {\mathrm{\Omega }}^{\prime }\sin i^{\prime }, \cos i^{\prime }\right)}^T$ in the geocentric equatorial coordinate system, where ${\mathrm{\Omega }}^{\prime }$ and $i^{\prime }$ are the RAAN and the inclination, respectively.

FIGURE 1

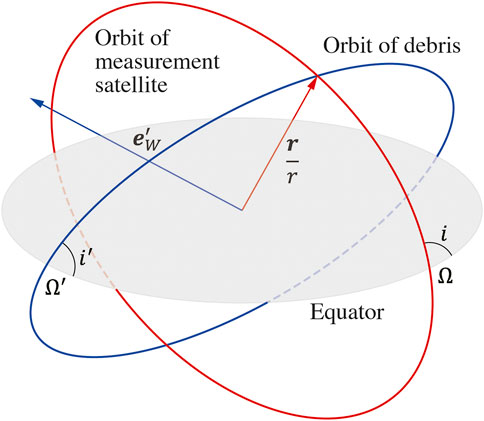
FIGURE 1. Relative orientation of orbital planes. A piece of debris detected shares the geocentric position vector with an in-situ debris measurement satellite.

Tasaki et al. (2014), Fujita et al. (2016), and Kodama et al. (2019) adopted this constraint equation to estimate some orbital parameters of a broken-up object from in-situ debris measurements. Since objects in LEO experience nodal precession or regression mainly due to $J_2$ perturbation (or Earth’s oblateness), it can be assumed that the rate of change in RAAN is constant. On this assumption, the RAAN at an arbitrary time of $t$, ${\mathrm{\Omega }}^{\prime }\left(t\right)$, can be expressed as

${\mathrm{\Omega }}^{\prime }\left(t\right)={\mathrm{\Omega }}_0^{\prime }+{\dot{\mathrm{\Omega }}}^{\prime }\left(t-t_0\right)(2)$

where ${\mathrm{\Omega }}_0^{\prime }$ is the RAAN at a specific time of $t_0$ and ${\dot{\mathrm{\Omega }}}^{\prime }$ is the rate of change in RAAN. If $t_0$ represents the time of breakup, then ${\mathrm{\Omega }}_0^{\prime }$ and $i^{\prime }$ represent the orbital plane of a broken-up object at the time of event. Since the inclination can also be assumed to be constant, the orbital parameters of a broken-up object to estimate are $i^{\prime }$, ${\mathrm{\Omega }}_0^{\prime }$ and ${\dot{\mathrm{\Omega }}}^{\prime }$. Letting $\mathit{r}={\left(x\left(t\right), y\left(t\right), z\left(t\right)\right)}^T$ and using Eq. 2, then Eq. 1 can be written in the following form:

$\left\{x\left(t\right)\sin \left[{\mathrm{\Omega }}_0^{\prime }+{\dot{\mathrm{\Omega }}}^{\prime }\left(t-t_0\right)\right]-y\left(t\right)\cos \left[{\mathrm{\Omega }}_0^{\prime }+{\dot{\mathrm{\Omega }}}^{\prime }\left(t-t_0\right)\right]\right\}\sin i^{\prime }+z\left(t\right)\cos i^{\prime }=0(3)$

Equation 3 can also be written as

$\left(\left[C_{{\dot{\mathrm{\Omega }}}^{\prime }\left(t-t_0\right)}^3\right]\mathit{r}\right).\left(\begin{array}{c}\sin {\mathrm{\Omega }}_0^{\prime }\sin i^{\prime }\\ -\cos {\mathrm{\Omega }}_0^{\prime }\sin i^{\prime }\\ \cos i^{\prime }\end{array}\right)=0$

Where $\left[C\right]$ is the rotation matrix about an axis specified by the superscript with an angle given by the subscript. Since ${\left(\sin {\mathrm{\Omega }}_0^{\prime }\sin i^{\prime }, -\cos {\mathrm{\Omega }}_0^{\prime }\sin i^{\prime }, \cos i^{\prime }\right)}^T$ is ${\mathit{e}}_W^{\prime }$ at the time of $t_0$, $\left[C_{{\dot{\mathrm{\Omega }}}^{\prime }\left(t-t_0\right)}^3\right]\mathit{r}$ is on the plane defined by ${\mathrm{\Omega }}_0^{\prime }$ and $i^{\prime }$. Kodama et al. (2019) have derived a constraint equation from this fact to find out candidates for the rate of change in RAAN. If three vectors are on the same plane, then the dot product between the cross product of the two vectors and the remaining vector must be zero. For example, if there are three detections at time $t_1$, $t_2$, and $t_3$, and the geocentric position vectors at that time are ${\mathit{r}}_{\mathrm{1}}$, ${\mathit{r}}_{\mathrm{2}}$, and ${\mathit{r}}_{\mathrm{3}}$, respectively, then the following constraint equation can be obtained.

$\left[C_{{\dot{\mathrm{\Omega }}}^{\prime }\left(t_1-t_0\right)}^3\right]{\mathit{r}}_{\mathrm{1}}.\left[\left(\left[C_{{\dot{\mathrm{\Omega }}}^{\prime }\left(t_2-t_0\right)}^3\right]{\mathit{r}}_{\mathrm{2}}\right)\times \left(\left[C_{{\dot{\mathrm{\Omega }}}^{\prime }\left(t_3-t_0\right)}^3\right]{\mathit{r}}_{\mathrm{3}}\right)\right]=0$

In this study, the above constraint equation derived by Kodama et al. (2019), which can be applied to the rate of change in RAAN, is not utilized, but only the constraint equation given by Eq. 3 is utilized.

3 New Approach

Fujita et al. (2016) and Kodama et al. (2019) have demonstrated the importance of finding out a better candidate for the rate of change in RAAN of a broken-up object when they have verified their approaches theoretically. Especially, Kodama et al. (2019) have derived a constraint equation that can be applied to the rate of change in RAAN of a broken-up object. Instead, this study determines the inclination of a broken-up object from the maximum or minimum geocentric declination at the time of detection. Then, this approach finds out a candidate for the rate of change in RAAN of a broken-up object by assuming a circular orbit with a radius of the geocentric distance at the time of detection.

Let’s imagine an oblique spherical triangle on the celestial sphere with the orbits of an in-situ debris measurement satellite and a piece of debris detected, as illustrated in Figure 2. As in the previous section, variables with prime indicate those of a piece of debris detected. Therefore, variables without prime indicate those of an in-situ debris measurement satellite. For example, $\mathrm{\Omega }$ and $i$ are the RAAN and the inclination of an in-situ debris measurement satellite, respectively.

FIGURE 2

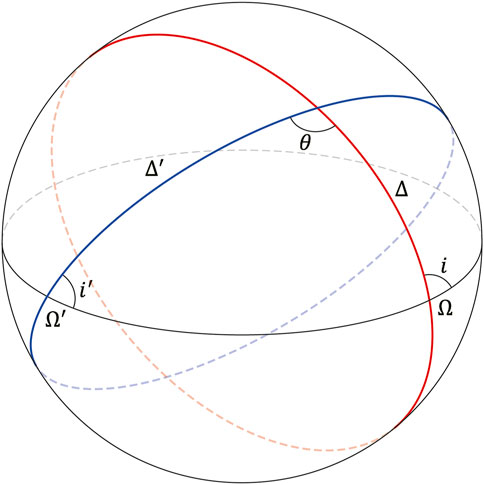
FIGURE 2. Relative orientation of orbital planes. An orbit in red represents the orbit of a measurement satellite, while the other orbit in blue represents the orbit of a piece of debris detected at the line of intersection.

From the sine formula, we obtain

$\frac{\sin \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)}{\sin \theta }=\frac{\sin \mathrm{\Delta }}{\sin i^{\prime }}=\frac{\sin {\mathrm{\Delta }}^{\prime }}{\sin \left(\pi -i\right)}$

where $\theta$ is the angle between the two orbital planes and $\mathrm{\Delta }$ is the argument of true latitude at the line of intersection of the two orbital planes. Thus,

$\sin \mathrm{}\mathrm{\Delta }\sin \theta =\sin \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)\sin i^{\prime }(4)$

$\sin \mathrm{}\mathrm{\Delta }\prime \sin \theta =\sin \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)\sin i(5)$

From analog to the cosine formula for angles, we obtain

$\cos \mathrm{}\mathrm{\Delta }\sin \theta =\cos i^{\prime }\sin i-\sin i^{\prime }\cos i\cos \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)(6)$

Therefore, $\mathrm{\Delta }$ can be calculated by using Eqs 4, 6. From the cosine formula for sides, we obtain

$\cos {\mathrm{\Delta }}^{\prime }=\cos \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)\cos \mathrm{\Delta }-\sin \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)\sin \mathrm{\Delta }\mathrm{}\cos i(7)$

Multiplying Eq. 7 by $\sin \theta$ and substituting Eqs 4, 6 into the resulting equation, then we obtain

$\cos {\mathrm{\Delta }}^{\prime }\sin \theta =-\sin i^{\prime }\cos i+\cos i^{\prime }\sin i\cos \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)(8)$

Finally, ${\mathrm{\Delta }}^{\prime }$ can be calculated by using Eqs 5, 8. Note that from the cosine law we obtain

$\cos \theta =\cos i^{\prime }\cos i+\sin i^{\prime }\sin i\cos \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)(9)$

Since the geocentric declination at the line of intersection of the two orbital planes can be expressed as $\sin \delta =\sin i\sin \mathrm{\Delta }$, it can be maximum or minimum when $d\mathrm{\Delta }/dt=0$. Therefore, it is necessary to drive the rate of change in the argument of true latitude at the line of intersection. If we differentiate Eqs 4, 6, and use Eq. 9, then we obtain

$\cos \mathrm{}\mathrm{\Delta }\sin \theta \frac{d\mathrm{\Delta }}{dt}+\sin \mathrm{\Delta }\cos \theta \frac{d\theta }{dt}=\cos \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)\sin i^{\prime }\left(\frac{d\mathrm{\Omega }}{dt}-\frac{d{\mathrm{\Omega }}^{\prime }}{dt}\right)+\sin \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)\cos i^{\prime }\frac{d{i}^{\prime }}{dt}(10)$

$-\sin \mathrm{\Delta }\sin \theta \frac{d\mathrm{\Delta }}{dt}+\cos \mathrm{\Delta }\cos \theta \frac{d\theta }{dt}=\sin i^{\prime }\cos i\sin \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)\left(\frac{d\mathrm{\Omega }}{dt}-\frac{d{\mathrm{\Omega }}^{\prime }}{dt}\right)-\left(\sin i^{\prime }\sin i+\cos i^{\prime }\cos i\cos \left(\mathrm{\Omega }-{\mathrm{\Omega }}^{\prime }\right)\right)\frac{d{i}^{\prime }}{dt}+\cos \theta \frac{di}{dt}(11)$

Subtracting Eq. 11 multiplied by $\sin \Delta$ from Eq. 10 multiplied by $\cos \Delta$, and using Eq. 4 through Eq. 7, then we obtain

$\sin \theta \frac{d\mathrm{\Delta }}{dt}=\sin i^{\prime }\cos {\mathrm{\Delta }}^{\prime }\left(\frac{d\mathrm{\Omega }}{dt}-\frac{d{\mathrm{\Omega }}^{\prime }}{dt}\right)+\sin {\mathrm{\Delta }}^{\prime }\frac{d{i}^{\prime }}{dt}-\sin \mathrm{\Delta }\cos \theta \frac{di}{dt}$

Except for special conditions such as $\sin i^{\text{′}}=0$ and $d{\mathrm{\Omega }}^{\prime }/dt=d\mathrm{\Omega }/dt$, therefore, a condition for the geocentric declination at the line of intersection to be maximum or minimum are

$\cos {\mathrm{\Delta }}^{\prime }=0 \mathrm{o}\mathrm{r} {\mathrm{\Delta }}^{\prime }=\pm \frac{\pi }{2}$

because the inclinations ($i^{\prime }$ and $i$) are not supposed to change over time.

The geocentric declination at the line of intersection can also be expressed as $\sin \delta =\sin i^{\prime }\sin {\mathrm{\Delta }}^{\prime }$. Therefore, substituting ${\mathrm{\Delta }}^{\prime }=\pm \pi /2$ into $\sin \delta =\sin i^{\prime }\sin {\mathrm{\Delta }}^{\prime }$, then we obtain $i^{\prime }=\left|\delta \right|$ or $i^{\prime }=\pi -\left|\delta \right|$. This fact means that the inclination of a broken-up object can be determined from the maximum or minimum geocentric declination at the line of intersection. Note that this approach is not available in special cases such as $\sin i^{\text{′}}=0$ and $d{\mathrm{\Omega }}^{\prime }/dt=d\mathrm{\Omega }/dt$. As will be described later, this study assumes an in-situ debris measurement satellite in a Sun-synchronous orbit. If a broken-up object is also in a Sun-synchronous orbit, then $d{\mathrm{\Omega }}^{\prime }/dt\sim d\mathrm{\Omega }/dt$. This special case is probable therefore we must come up with another approach. For example, Fujita et al. (2016) have found that multiple in-situ measurement satellites are required in such special cases. It can be identified as the special cases when the geocentric declination at the time of detection does not change over time, however.

The secular variation of RAAN due to $J_2$ perturbation is given by

${\dot{\text{Ω}}}^{\prime }=-\frac{3}{2}\frac{R_{Earth}^2{J}_2}{p^{\prime 2}}{n}^{\prime }\cos i^{\prime }(12)$

where $R_{Earth}$ is the Earth’s mean equatorial radius, $J_2\left(>0\right)$ is the second-order zonal harmonic coefficient, $p^{\prime }$ is the semi-latus rectum, and $n^{\prime }$ is the mean motion. For a broken-up object, we may be able to estimate the inclination as described previously but not the semi-latus rectum and the mean motion yet at this moment. The geocentric distance at the time of detection may be used as a semi-major axis, however. Therefore, assuming a circular orbit with a radius of the geocentric distance at the time of detection, Eq. 12 gives candidates for the rate of change in RAAN. The mean of candidates for the rate of change in RAAN may be adopted as a better candidate.

4 Verification

Doi (2013) has demonstrated the time-averaged flux per unit area per day of fragments down to 100 μm from the Chinese anti-satellite missile test using Fengyun 1C in early January 2007 to a satellite in a Sun-synchronous orbit as a function of geocentric right ascension and declination. He observed that the time-averaged flux of fragments from the test into the satellite has two peaks along the orbit of the satellite. The two peaks are exactly located at the line of intersection of the two orbital planes of the satellite and the broken-up object. Therefore, this study assumes that an in-situ debris measurement satellite may detect a piece of debris from a broken-up object at the line of intersection of the two orbital planes.

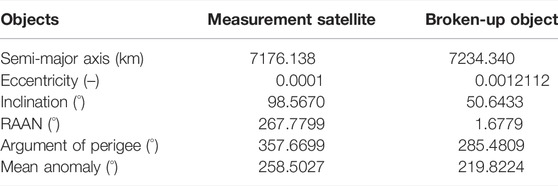
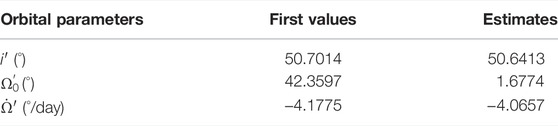
Let’s assume that an in-situ debris measurement satellite in Table 1 detects fragments from a broken-up object also in Table 1 every 5 days, with a total of 74 in 1 year. It is also assumed that all detections are at the line of intersection of the two orbital planes. Figure 3 provides the history of geocentric declination at the time of detection. It looks like two waves with different phases are plotted together. This is because there are two points along the line of intersection, where the two orbital paths are close to each other. For this study, however, it is assumed that detections are only at a point with a closer distance between the two orbital paths along the line of intersection. Note that an orbit propagator used for this study considers not only $J_2$ perturbation but also $J_3$ and $J_4$ perturbations, atmospheric drag, gravitational attraction due to Sun and Moon, and solar radiation pressure.

TABLE 1

TABLE 1. Orbital parameters at the time of breakup.

FIGURE 3

FIGURE 3. History of geocentric declination at the time of detection.

4.1 Inclination

The argument of true latitude corresponding to a given geocentric declination can be calculated by using $\sin \mathrm{\Delta }\sin i=\sin \delta$ and $\cos \mathrm{\Delta }\sin i=\cos \delta \cos \left(\alpha -\mathrm{\Omega }\right)\sin i$ where $\alpha$ represents the geocentric right ascension at the time of detection. From the history of argument of true latitude corresponding to the geocentric declination at the time of detection (see Figure 4), the argument of true latitude can be split into two ranges: $-90°<\mathrm{\Delta }<90°$ and $90°<\mathrm{\Delta }<270°$. Of course, we can split the history of geocentric declination at the time of detection into two data sets according to the two ranges of argument of true latitude. Instead, however, we may reverse the sign of geocentric declination in the latter range of argument of true latitude (i.e., $90°<\mathrm{\Delta }<270°$) to treat the history of geocentric declination at the time of detection as one data set. Figure 5 provides the history of geocentric declination at the time of detection after reversing the sign of geocentric declination, where the corresponding argument of true latitude is between 90 and 270°. Figure 5 also shows a fitted nonlinear model (periodic curve) with a solid line. With this fitted nonlinear model, we can obtain the maximum geocentric declination of 50.7014°. Therefore, the inclination of the broken-up object may be 50.7014 or 129.2986°. There are no objects with an inclination close to 129.2686°, and no further estimation could be made meaningfully in the case of 129.2986°, however. Therefore, this study decides to continue the case of 50.7014° but not the case of 129.2986°.

FIGURE 4

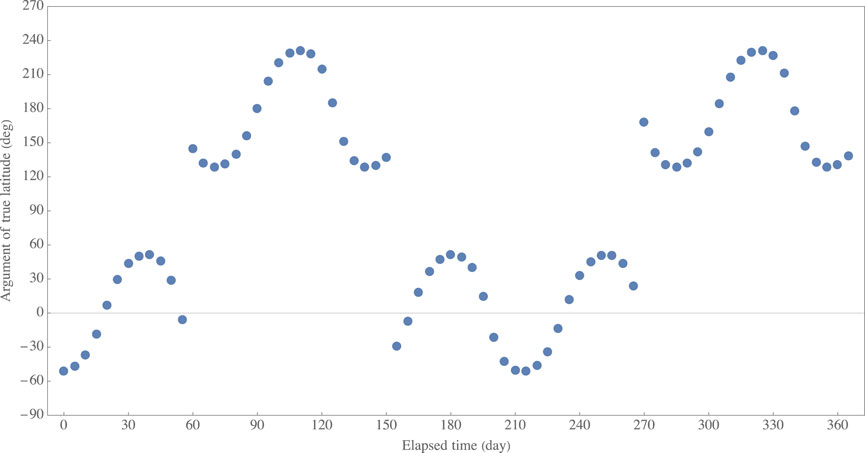
FIGURE 4. History of argument of true latitude corresponding to geocentric declination at the time of detection in Figure 3.

FIGURE 5

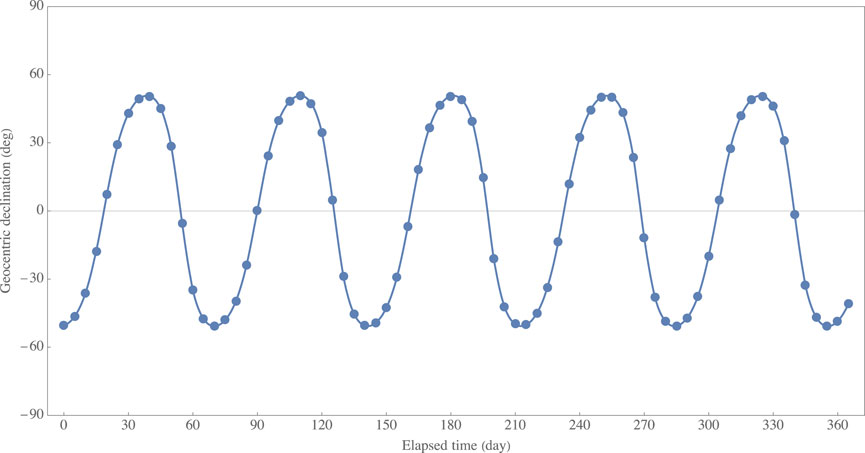
FIGURE 5. History of geocentric declination at the time of detection after reversing the sign of geocentric declination, where the corresponding argument of true latitude is between 90 and 270°. A solid line represents a fitted nonlinear model (periodic curve).

4.2 Rate of Change in Right Ascension of the Ascending Node

As described in Section 3, the rate of change in RAAN can be obtained from Eq. 12 by assuming a circular orbit with a radius of the geocentric distance at the time of detection. Applying this assumption to all data, then we can obtain candidates for the rate of change in RAAN, as shown in Figure 6. Since we do not know which candidate is better, this study adopts the mean of the candidates (i.e., −4.1755° per day as shown by a thick solid line) as a final candidate.

FIGURE 6

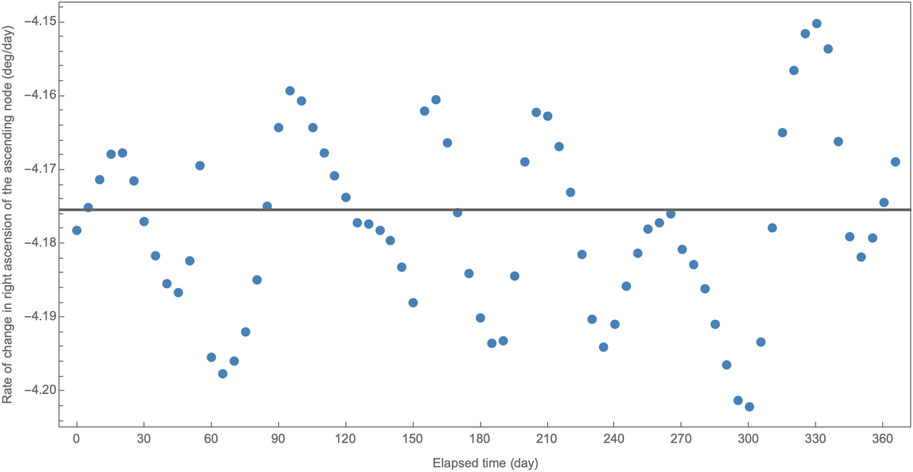
FIGURE 6. History of the rate of change in RAAN at the time of detection. A thick solid line represents the mean of the candidates.

4.3 Right Ascension of the Ascending Node

With the inclination estimated in Section 4.1 and the final candidate for the rate of change in RAAN obtained in Section 4.2, the RAAN at the time of breakup can be found as a root of the constraint equation derived in Section 2 (i.e., Eq. 3). Figure 7 shows a set of 74 constraints on ${\mathrm{\Omega }}_0^{\prime }$ and $i^{\prime }$ obtained from Eq. 3. The final candidate for the rate of change in RAAN obtained in Section 4.2 is not a true value, but all constrains intersect each other at approximately two ranges of RAAN. Since the inclination estimated in Section 4.1 is 50.7014° as shown by a thick solid line in Figure 7, the true value of the RAAN at the time of breakup may be between 0 and 40°.

FIGURE 7

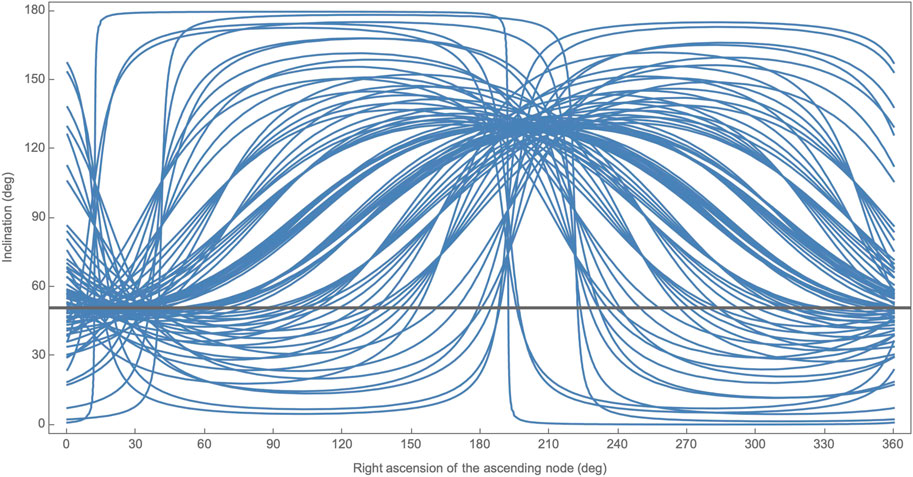
FIGURE 7. A set of 74 constrains on ${\mathrm{\Omega }}_0^{\prime }$ and $i^{\prime }$ when ${\dot{\mathrm{\Omega }}}^{\prime }=-4.1755$. A thick solid line represents the inclination estimated in Section 4.1.

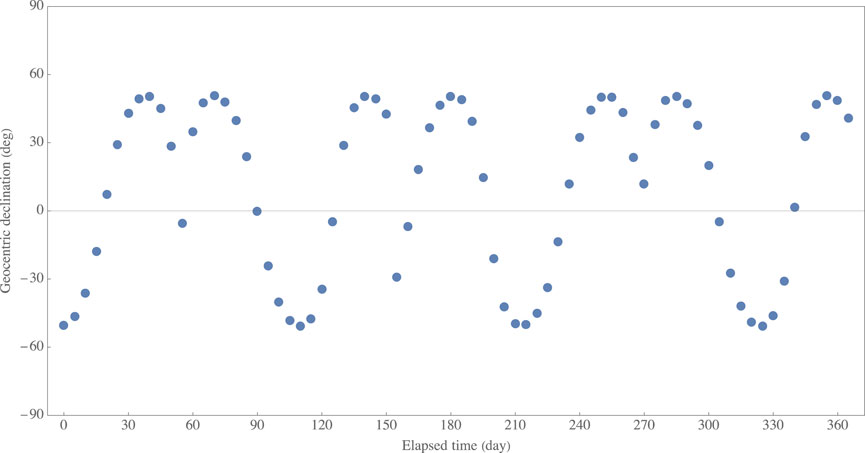
Root-finding is made by applying the constraint equation to all data. Since the candidate for the rate of change in RAAN may include an error due to assumptions made in Section 4.2, the roots found are linearly time-dependent, as demonstrated in Figure 8. Some roots are out of the trend because of some difficulties with root-finding, but most roots change linearly over time. Figure 8 also shows a fitted linear model given by $1.6467°+0.1118°\times t$ with the coefficient of determination ($R^2$) of $0.9999996$. With this fitted linear model, we can obtain the RAAN at the time of breakup and a correction for the rate of change in RAAN obtained in Section 4.2. Table 2 summarizes and compares the final estimation results with the true values.

FIGURE 8

FIGURE 8. RAAN at the time of breakup. A solid line represents a fitted linear model.

TABLE 2

TABLE 2. Final estimation results with true values.

Given the corrected rate of change in RAAN, then Figure 9 shows a set of 74 constraints on ${\mathrm{\Omega }}_0^{\prime }$ and $i^{\prime }$ obtained from Eq. 3. It can be observed clearly, as Kodama et al. (2019) demonstrated, that all constrains intersect each other at two points. This fact means that the corrected rate of change in RAAN can be expected to work in the same way as the true rate. Ultimately, the estimates obtained here can be used as first values for a nonlinear least-squares method to lead better estimates, which Tasaki et al. (2014), Fujita et al. (2016), and Kodama et al. (2019) have utilized.

FIGURE 9

FIGURE 9. A set of 74 constrains on ${\mathrm{\Omega }}_0^{\prime }$ and $i^{\prime }$ when ${\dot{\mathrm{\Omega }}}^{\prime }=-4.0657$.

4.4 Comparison

Kodama et al. (2019) found an appropriate candidate for the rate of change in RAAN and then found appropriate combinations of ${\mathrm{\Omega }}_0^{\prime }$ and $i^{\prime }$ as first values for a nonlinear least-squares method. Instead, here we adopt the inclination estimated in Section 4.1 and the final candidate for the rate of change in RAAN obtained in Section 4.2 as first values. This is because the constraints intersect each other at approximately two ranges of RAAN, as shown in Figure 7. Regarding the RAAN at the time of breakup, a worse root found in Section 4.3, that is 42.3597° at $t=365$ as in Figure 8, is adopted as a first value. Table 3 summarizes the first values for a nonlinear least-squares method and the estimation results. The estimates in Table 3 are close enough to the true values in Table 2, despite the error in the final candidate for the rate of change in RAAN obtained in Section 4.2. Compared with the present approach, the rate of change in RAAN is the same but the inclination and the RAAN at the time of breakup are slightly better. The present approach has an advantage that it needs fewer calculation steps in comparison to Kodama et al. (2019), however.

TABLE 3

TABLE 3. First values for a nonlinear least-squares method and estimation results.

5 Conclusion

This paper has proposed a new approach to estimate the direction of angular momentum of a broken-up object at a specific time from in-situ debris measurements. This new approach does not require a nonlinear least-squares method that Tasaki et al. (2014), Fujita et al. (2016), and Kodama et al. (2019) have utilized so that there is no concern to avoid local minimal solutions. In addition, this new approach does not require a constraint equation that Kodama et al. (2019) have derived to find out candidates for the rate of change in RAAN. Instead, this approach determined the inclination of a broken-up object from the history of geocentric declination at the time of detection. Then, this approach found a candidate for the rate of change in RAAN of a broken-up object by assuming a circular orbit with a radius of the geocentric distance at the time of detection. Finally, using the constraint equation derived from the fact that a piece of debris detected shares the geocentric position vector with an in-situ debris measurement satellite, this approach estimated the RAAN at the time of breakup and calculates a correction for the candidate rate of change in RAAN.

It is desirable to have more choices for the estimation approach because it leads to an increase in the flexibility of analysis. In practical use, this new approach may provide an appropriate initial value that ultimately leads to a better estimation in a nonlinear least-squares method that Tasaki et al. (2014), Fujita et al. (2016), and Kodama et al. (2019) have utilized. It is convinced that this paper has made a great contribution in this regard. When this paper has confirmed that this new approach is effective, however, all detections are assumed to be at the line of intersection of the two orbital planes of the broken-up object and the measurement satellite. Thus, it is still necessary for practical use to develop a technique to exclude or to weight detections not following the assumptions as future work. It is also necessary for practical use to clarify the conditions under which this new approach can be applied as future work. Especially, it is necessary to verify when either a broken-up object or an in-situ debris measurement satellite is in an elliptical orbit, and when both are in elliptical orbits.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

TH: Conceptualization, Methodology, Writing—Original Draft. KF: Data Curation, Writing—Review and Editing. YY: Data Curation, Writing—Review and Editing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge Dr. Yukihito Kitazawa, Haruhisa Matsumoto, Dr. Yuki Akiyama, Dr. Hideaki Hinagawa, and Dr. Shin’ichi Nakamura at JAXA for their useful advice on this study. The authors also would like to acknowledge Mr. Mahiro Tanahashi, an undergraduate student at Kyushu University, for his dedicated assistance on this study.

References

Aceti, R., and Drolshagen, G. (1995). Eureca post Flight Technology Investigations Achievements. Acta Astronautica 37, 347–360. doi:10.1016/0094-5765(95)00080-j

CrossRef Full Text | Google Scholar

Ae, K., Uetsuhara, M., and Hanada, T. (2013). “IDEA the Project for Iin-Ssitu Debris Environmental Awareness,” in Proceedings of the Sixth European Conference on Space Debris (Darmstadt, Germany. April 22–25.

Google Scholar

Anz-Meador, P., Ward, M., Manis, A., Nornoo, K., Dolan, B., Claunch, C., et al. (2019). “The Space Debris Sensor Experiment,” in The 1st International Orbital Debris Conference (Texas, USA. (NASA Technical Report JSC-E-DAA-TN74830).

Google Scholar

Bauer, W., Romberg, O., and Putzar, R. (2015). Experimental Verification of an Innovative Debris Detector. Acta Astronautica 117, 49–54. doi:10.1016/j.actaastro.2015.07.008

CrossRef Full Text | Google Scholar

Bauer, W., Romberg, O., Wiedemann, C., Drolshagen, G., and Vörsmann, P. (2014). Development of Iin-Ssitu Space Debris Detector. Adv. Space Res. 54 (9), 1858–1869. doi:10.1016/j.asr.2014.07.035

CrossRef Full Text | Google Scholar

Doi, A. (2013). A Study on Break-Up Event Identification by Measurement of Changes in Micron-Sized Debris Environment (Master Thesis). Fukuoka, Japan: Kyushu University.

Google Scholar

Fujita, K., Tasaki, M., Furumoto, M., and Hanada, T. (2016). An Orbit Determination from Debris Impacts on Measurement Satellites. Adv. Space Res. 57 (2), 620–626. doi:10.1016/j.asr.2015.11.005

CrossRef Full Text | Google Scholar

Furumoto, M., Fujita, K., and Hanada, T. (2015). Dynamic Modeling on Micron-Size Orbital Debris EnvironmentInternational Symposium on Space Technology and Science (ISTS). Japan: Kobe-Hyogo. Paper ISTS-r-12, presented at the ThirtiethJuly 4-10.

Google Scholar

Furumoto, M., Fujita, K., Hanada, T., Matsumoto, H., and Kitazawa, Y. (2017). Orbital Plane Constraint Applicable for Iin-Ssitu Measurement of Sub-millimeter-size Debris. Adv. Space Res. 59 (6), 1599–1606. doi:10.1016/j.asr.2016.12.036

CrossRef Full Text | Google Scholar

Goldstein, R. M., Goldstein, S. J., and Kessler, D. J. (1998). Radar Observations of Space Debris. Planet. Space Sci. 46 (8), 1007–1013. doi:10.1016/s0032-0633(98)00026-9

CrossRef Full Text | Google Scholar

Hanada, T. (2013). Orbital Debris Modeling and Applications at Kyushu University. Proced. Eng. 67, 404–411. doi:10.1016/j.proeng.2013.12.040

CrossRef Full Text | Google Scholar

Kitazawa, Y., Matsumoto, H., Okudaira, O., Kimoto, Y., Hanada, T., Faure, P., et al. (2013). “Research and Development on In-Ssitu Measurement Sensors for Micro-meteoroid and Small Space Debris at JAXA,” in Proceedings of the Sixth European Conference on Space Debris (Darmstadt, Germany.

Google Scholar

Kodama, Y., Furumoto, M., Yoshimura, Y., Fujita, K., and Hanada, T. (2019). Estimation of Orbital Parameters of Broken-Up Objects from In-Ssitu Debris Measurements. Adv. Space Res. 63 (1), 394–403. doi:10.1016/j.asr.2018.07.034

CrossRef Full Text | Google Scholar

Matney, M., Goldstein, R., Kessler, D., and Stansbery, E. (1999). Recent Results from Goldstone Orbital Debris Radar. Adv. Space Res. 23 (1), 5–12. doi:10.1016/s0273-1177(98)00224-5

CrossRef Full Text | Google Scholar

McDonnell, J. A. M., Deshpande, S. P., Niblett, D. H., Neish, M. J., and Newman, P. J. (1993). The Near Earth Space Impact Environment - an LDEF Overview. Adv. Space Res. 13 (8), 87–101. doi:10.1016/0273-1177(93)90572-s

CrossRef Full Text | Google Scholar

Oikonomidou, X., Braun, V., Pail, R., Gruber, T., Schummer, F., Meßmann, D., et al. (2021). “MOVE-III: An In-Situ Detector to Support Space Debris Model Validation,” in Proceedings of the Eighth European Conference on Space Debris (Virtual) (Darmstadt, Germany.

Google Scholar

Stokely, C. L., Stansbery, E. G., and Goldstein, R. M. (2009). Debris Flux Comparisons from the Goldstone Radar, Haystack Radar, and Hax Radar Prior, during, and after the Last Solar Maximum. Adv. Space Res. 44 (3), 364–370. doi:10.1016/j.asr.2009.02.005

CrossRef Full Text | Google Scholar

Tasaki, M., Fujita, K., and Hanada, T. (2014). Identifying Origin of Breakup Event by In-Ssitu Measurement in Proceedings of the Sixty-Fifth International Astronautical Congress. Toronto, Canada, 3 1958–1966.

Google Scholar