The probability analysis of ejecta particles damaging a spacecraft operating around asteroids after an artificial impact experiment: Hayabusa 2 ’s SCI operation safety study

On 5 April 2019, the Hayabusa 2 spacecraft performed the first successful artificial impact experiment on an asteroid. The Small Carry-on Impactor (SCI) device was deployed at an altitude of 500 m above Ryugu’s surface. The 2 kg copper projectile hit Ryugu’s surface in 40 min and caused the formation of an artificial crater 14.5 m in diameter. Once the SCI was deployed, the Hayabusa 2 spacecraft performed a two-week escape trajectory reaching altitudes as far as 120 km from Ryugu. The spacecraft then returned to its nominal position at 20 km altitude (Home-Position) from Ryugu for hovering control. This was done to prevent ejecta particles from seriously damaging the spacecraft and compromising its functionality. In this article, we present a method to forecast the daily probability of spacecraft damage along the selected nominal escape trajectory due to the debris cloud formed by an artificial impact. The result of the damage analysis confirmed that the selected escape trajectory experienced a small number of particle collisions under the design threshold, which would not have resulted in damage. Indeed, no damage was reported on the Hayabusa 2 spacecraft and it kept operating normally after the SCI operation. The method here presented serves as a guideline for post-impact mission operations to forecast and estimate the probability of damage to spacecraft or CubeSats operating near a small celestial body after an artificial impact experiment has occurred.

1 Introduction

The Hayabusa 2 mission is the Japanese sample and return mission launched in 2014 to the asteroid Ryugu. Ryugu’s samples were successfully returned to Earth on 6 December 2020. The Hayabusa 2 mission has been now extended to reach its new target, asteroid 1998 KY26, in 2031 (Hirabayashi et al., 2021). The Hayabusa 2 is the successor mission to JAXA’s Hayabusa mission to the asteroid Itokawa. The Hayabusa 2 spacecraft encountered Ryugu on 27 June 2018, followed by two touchdowns on February 21^st and 11 July 2019, respectively. The Hayabusa 2 spacecraft successfully performed the first artificial impact on an asteroid on 5 April 2019 (Arakawa et al., 2020). During the asteroid proximity operations, the Hayabusa 2 spacecraft was set to a base position, Home Position (HP), at 20 km above the asteroid facing the sub-Earth direction. This technique was successfully used by the Hayabusa mission and it is known as hovering¹. All operations such as trajectory conjunction maneuvers, gravity measurement, fly-around observations, cratering, and touchdowns start from HP and return to HP position after each mission operation (Tsuda et al., 2013, 2020; Saiki et al., 2022b).

The Hayabusa 2 spacecraft was equipped with a Small Carry-on Impactor (SCI), and it formed a crater of 14.5 m in size to allow the sampling of substrate asteroid materials (Saiki et al., 2017, 2020; Arakawa et al., 2020). The SCI is a compact kinetic impactor released along the HP axis at 500 m from the asteroid’s surface to create an artificial crater on it. As part of the Hayabusa 2 experiment, the spacecraft released a deployable camera (DCAM3) to observe the impact event while the mother spacecraft flew away from HP position to be placed in a safe location from the asteroid’s ejecta. An impact velocity of 2 km/s was required for the Hayabusa 2 mission to crater Ryugu (Saiki et al., 2017, 2020; 2022a). Previous work in JAXA showed that the asteroid ejecta would leave the landing site after 2 weeks, therefore allowing the Hayabusa 2 mother spacecraft to return safely at HP and continue with the scheduled mission operations (Matsumoto et al., 2011). However, the debris trail of asteroid P/2010 A2 observed by Rosetta spacecraft suggested that the debris was the result of a natural collision event occurring with the asteroid in 2009 (Snodgrass et al., 2010). Therefore, dust particles of a diameter size larger than 1 mm can last in an asteroid’s orbit for several months or years. The Ryugu asteroid is a C-type asteroid composed of regolith material with large-sized particles in the order of cm in diameter. Those large-size particles pose a great risk for the Hayabusa 2 spacecraft (Micheal et al., 2016).

In this paper, a methodology to predict the probability of damage to a spacecraft after an artificial impact on asteroids is developed. The semi-analytical method here proposed is based on formulating a two-point boundary value problem between the point of impact and the spacecraft’s position for predicting the initial state that the ejecta must have to collide with the spacecraft. This method allows one to then estimate the likelihood of a particle intercepting the spacecraft and damaging it by using cratering models. The methodology proposed allows for a fast evaluation of the probability of damage to a spacecraft after an artificial impact and it was used as a damage estimation tool during Hayabusa 2’s mission operations. The method proposed is thus of use for evaluating the risks posed to the spacecraft by the impact during the mission operations that follow the impact event. The fate of the asteroid ejecta is here investigated through numerical modeling for diameter-size dust particles from 0.1 to 1 cm. An N-Body high fidelity dynamical model called goNEAR tool (Soldini et al., 2020c; b, 2022) is used where the asteroids shape model gravity, its ephemeris, the solar radiation pressure accelerations and the effect of the Sun's, and planets’ third-body perturbations are taken into account. This is done to observe with numerical experiments if the ejecta will collide with the spacecraft. The scaling laws and the single Al plate damage model are here combined with the results from a two-point boundary value problem to assess the likelihood of damage. The methodology proposed can be adapted to artificial impact experiments, for example, for the probability of damage to LICIACube (Dotto et al., 2021) from NASA’s DART impact (Rivkin et al., 2021).

The paper is organized as follows: Section 2 provides information on the environmental perturbations that a particle experiences in the gravity regime of Ryugu. The proposed methodology to evaluate the probability of spacecraft damage after an artificial impact on an asteroid is shown in Section 3. Section 4 presents the results of our analysis specific to the SCI impact operation. Finally, an insight into the qualitative motion of ejecta particles around asteroid Ryugu is presented in Section 5.

2 Environmental perturbations

The dynamics of the ejecta around the weak gravity field of asteroids are subject to environmental perturbations as the asteroid’s irregular shape and spin ratio, the solar gravity, and solar radiation pressure. Depending on the altitude of the ejecta, some perturbations are more dominant than others. In the case of the Ryugu asteroid, the following spheres of influence can be computed following the definition given in Yu et al. (2017):

• The Hill sphere (solar tides equals the asteroid gravity):

$R_1=r_m{\left(\frac{{\mu }_a}{{\mu }_{\mathit{Sun}}}\right)}^{1/3}=110.8\left[km\right](1)$

• The sphere of influence (the asteroid gravity is dominant):

$R_2=r_m{\left(\frac{{\mu }_a}{{\mu }_{\mathit{Sun}}}\right)}^{2/5}=6.3\left[km\right](2)$

• The solar gravity equals the asteroid gravity:

$R_3=r_m{\left(\frac{{\mu }_a}{{\mu }_{\mathit{Sun}}}\right)}^{1/2}=87.4\left[m\right](3)$

where μ_a is the gravity constant of the asteroid Ryugu (30 m³/s²) and μ_Sun the gravity constant of the Sun's. $r_m=\sqrt[3]{\frac{T_o^2{\mu }_{\mathit{Sun}}}{4{\pi }^2}}$ (mean radius, Ryugu in a circular orbit around the Sun's). T_o is the orbital period and it is set to 1.3 years while r_m = 1.78 ⋅ 10⁸ [km].

The Solar Radiation Pressure (SRP) perturbation (a_srp) for dust particles is given by (Scheeres, 2012):

${\mathit{a}}_{\mathit{srp}}=-C_r{P}_0\frac{A}{m}\frac{\left(\mathit{d}-\mathit{r}\right)}{|\mathit{d}-\mathit{r}{|}^3},(4)$

where d and r are the distances of the Sun's and of the dust from the asteroid, respectively. The Sun's pressure, P₀ is 10⁸ kg km³ s⁻² m⁻², the reflectivity coefficient C_r for the dust, defined as (1 + ρ) with ρ being the reflectivity. A and m are the areas and the mass of spherical dust particles. In Table 1, four different sizes of dust particles have been used to compute the sphere of influence’s radius. Above that radius, solar radiation pressure is dominant with respect to the asteroid’s gravity.

TABLE 1

TABLE 1. Effect of the solar radiation pressure acceleration on Ryugu’s sphere of influence. Calculated by using Eqs 4, 5 and when SRP and solar tides are equal.

The values of those spheres of influence’s radii have been found as in Yu et al. (2017). Figure 1 shows the normalized solar tide (solid black line) and the SRP (dash line) scaled by Ryugu’s gravity. The picture is given in logarithmic scale and the unitary horizontal line (dash-dot line) represents the case in which the perturbation equals the gravity of the asteroid. The intersection between the dashed lines and the solid line with the unitary horizontal line gives the value of the radius of influence of the considered perturbation. The four radii of influence for four sizes of particles are summarised in Table 1, while the intersection between the solid line and the horizontal line represents the Hill sphere (R₁) that was previously computed in Eq. 1.

FIGURE 1

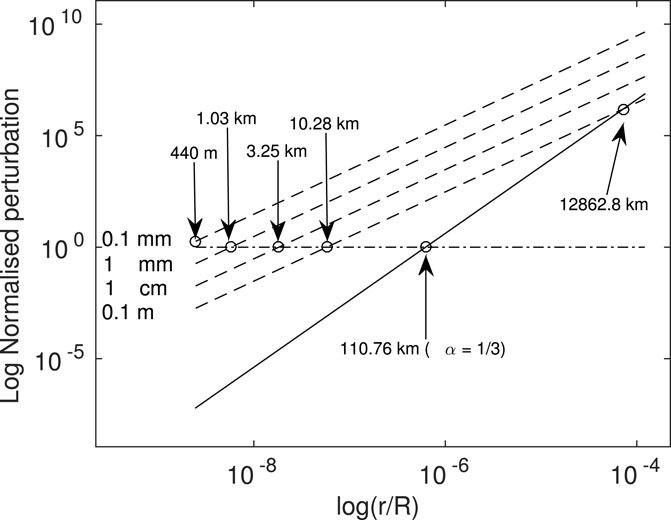
FIGURE 1. Solar radiation pressure (dashed lines) for four particle diameters (0.1 mm, 1 mm, 1 cm and 0.1 m) and solar tides (black line) scaled with Ryugu’s gravity force. This picture was done following the calculation of Yu et al. (2017) adapted for the Ryugu case.

In this case, we also add the third body perturbation of the Sun's, a_s (Scheeres, 2012):

${\mathit{a}}_s=-{\mu }_{\mathit{Sun}}\left(\frac{\mathbf{\Delta }}{|\mathbf{\Delta }{|}^3}-\frac{\mathit{r}}{|\mathit{r}{|}^3}\right),(5)$

Here, μ_Sun is the Sun’s mass parameter, Δ is the distance between the Sun's and the dust particles, and r is the distance of the dust particles with the asteroid. Figure 2 shows the planets’ third body perturbation (Figure 2A) and tides (Figure 2B) during the Hayabusa 2 mission operations. As one can see, the Sun's is the major perturbation with respect to the other planets’.

FIGURE 2

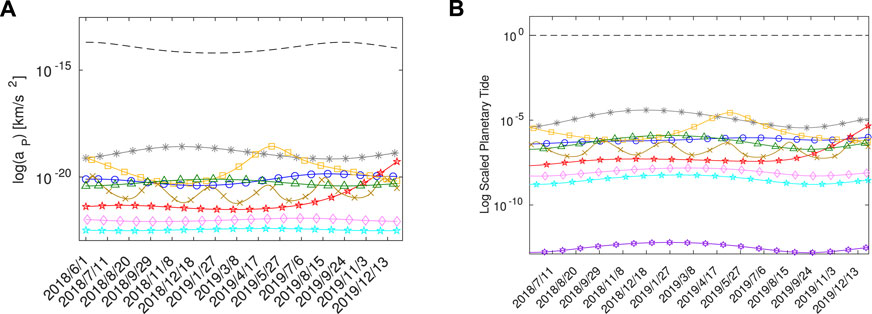
FIGURE 2. Logarithmic scaleof the third-body acceleration (A) and scaled planetary tides (B). Legend: Sun's (black dashed line), Earth (blue circles), Mars (red stars), Jupiter (gray asterisks), Mercury (Brown crosses), Venus (yellow squares), Saturn (green triangles), Uranus (pink diamonds), Neptune (light blue stars) and Pluto (violet hexagrams). These plots have been computed following Ref Yu et al. (2017).

Figure 2 shows that at the time of impact, the tides of Venus are a dominant effect to the same order as those of Jupiter. Our analysis includes the effect of all planetary tides, the Sun’s tide, and the solar radiation pressure acceleration.

3 Methodology

In this section, we present the methodology employed during the SCI operation to estimate the potential damages to the Hayabusa 2 spacecraft. We started with the knowledge of the expected SCI’s impact location of 300° in longitude and less than 20° in latitude. The predicted position dispersion is shown in Figure 3 in green.

FIGURE 3

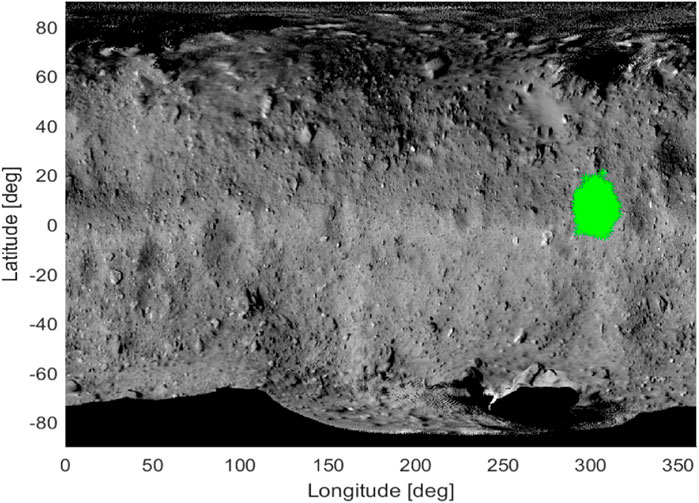
FIGURE 3. Predicted position dispersion through Monte Carlo analysis (Saiki et al., 2017, 2020).

A two-point boundary value problem was first solved between the location of the SCI impact and the position of the Hayabusa 2 spacecraft along its escape trajectory. Thus, we were able to compute the ejection velocity at the crater site that a particle would have to impact the spacecraft. Moreover, we could calculate the velocity at which the particle could hit the spacecraft and evaluate the predicted damages. Figure 4 shows a schematic representation of the problem. Given the local horizon plane (LH) in light blue, the orientation of the ejection velocity (V₀, in blue in Figure 4) is expressed in terms of azimuth (α₀, in green in Figure 4) and elevation (δ₀, in red in Figure 4). The red dashed trajectory represents the solution after optimization.

FIGURE 4

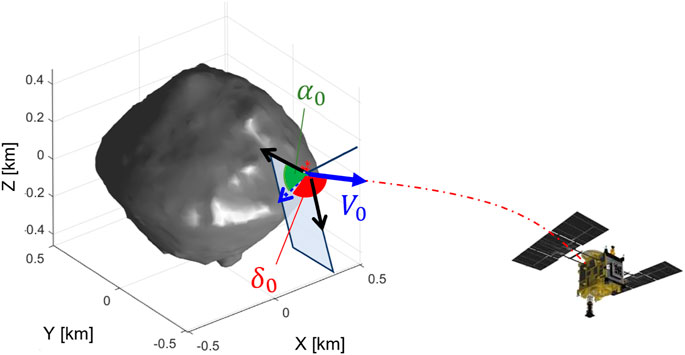
FIGURE 4. Schematic representation of the two-point boundary value problem formulation with a reference frame in body-fixed coordinates.

The Two-Point Boundary Value Problem (TPBVP) is similar to Lambert’s problem. However, in our study, the effect of environmental perturbations is taken into account. The following steps were taken:

• The Time of Flight (ToF), the initial position of the SCI impact point on Ryugu, and the final position of the location of the spacecraft along the escape trajectory were kept fixed. The area-to-mass ratio of the ejecta particle and its reflectivity coefficient, C_r were also kept fixed;

• The proposed single shooting method requires an ODE integration of the ejecta velocity guess at SCI impact (V₀ in Figure 4) which is expressed as a function of three angles and it is given by:

${\mathit{V}}_0=\left\{\begin{array}{c}\hfill V_0\cos {\delta }_0\cos {\alpha }_0\hfill \\ \hfill V_0\cos {\delta }_0\sin {\alpha }_0\hfill \\ \hfill V_0\sin {\delta }_0\hfill \end{array}\right\},(6)$

with V₀ = V_max(1 + sin x₀) where V_max is set at 2.5 km/s. The goNEAR N-Body planetary propagator was used (Soldini et al., 2020c; b, 2022) and it takes into account the planetary tides, the Sun's tide, the polyhedron gravity model of the asteroid, and the solar radiation pressure acceleration.

• The optimization problem requires minimizing the error in distance between the position of the particle at the end of the integration (t_f) and the location of the spacecraft at a fixed location along the escape trajectory. Thus, the cost function is as follows:

$\underset{{\alpha }_0,{\delta }_0,x_0}{\min }\Vert {\mathit{r}}_{HY2}-{\mathit{r}}_{ej}\left(t_f\right)\Vert .(7)$

In Eq. 7, r_HY2 is the position vector of Hayabusa 2 along the escape trajectory, which is fixed and r_ej(t_f) is the final position of the ejecta particle at the end of the integration. The boundary conditions are given as 0° < α₀ < 360°, − 90° < δ₀ < 90° and − 90° < x₀ < 0°. Note that the optimization problem is here reduced in finding three angles, α₀ (in-plane angle or azimuth), δ₀ (out-of-plane angle or elevation), and x₀ (e.g. V = V_max with x₀ = 0°).

Figure 5 shows an example of solutions for the proposed TPBVP when the size of the ejecta particles varies from 1 mm to 10 cm in diameter for different ToF. The reflectivity coefficient (C_r) of the particles is assumed to be 1.1. We selected a time interval of 1 day to forecast the probability of the ejecta hitting the Hayabusa 2 spacecraft. While the TPBVP provides a possible trajectory between the point of impact and the spacecraft, it is necessary to now calculate the probability of the dust particles being ejected at a specific azimuth (α₀) and elevation (δ₀). For further details on the Hayabusa 2’s escape trajectory, refer to Saiki et al. (2017, 2020).

FIGURE 5

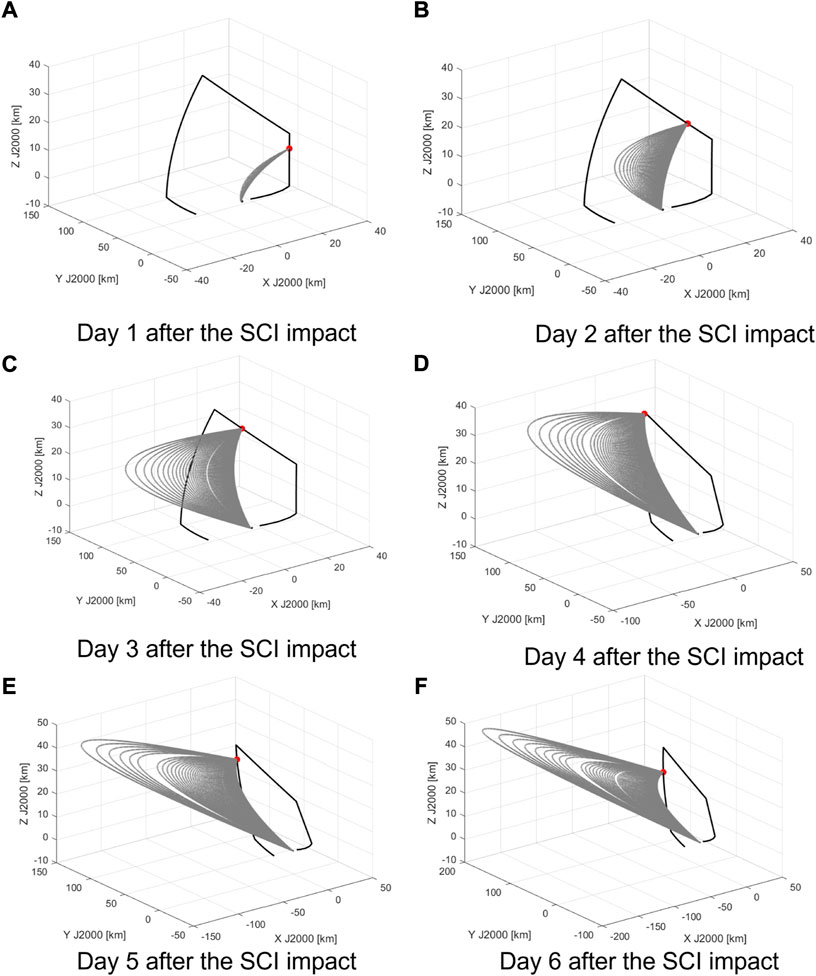
FIGURE 5. Solutions for the TPBVP for particles size in the range of 1 mm–10 cm in diameter (gray trajectories) for ToF set at 1 (A), 2 (B), 3 (C), 4 (D), 5 (E) and 6 (F) days after the SCI impact along the Hayabusa 2 escape trajectory (in black) with C_r set to 1.1.

Figure 6 shows the profile of the ejecta escape velocity at the SCI impact location, the elevation angle, and the relative ejecta-spacecraft impact speed as a function of the size of the dust particles for the solutions in Figure 5. The light blue curves represent solutions at different ToF (1, 2, 3, 4, 5, and 6 days after the SCI impact). The escape velocity of all the calculated solutions is above the theoretical value of 0.38 m/s for a point mass gravity model $(\sqrt{2{\mu }_a/r_a})$² as shown in Figure 6A (black dashed line). Figure 6B shows the elevation angle compared with the theoretical value of the scaling laws’ crater model (black dashed line) (Wada, K. et al., 2021; Arakawa et al., 2020). This highlights that, although we find potential trajectories between the SCI impact and the location of the Hayabusa 2 spacecraft by solving a TPBVP, not all the solutions found are probable when matched to the crater model theory (Wada, K. et al., 2021; Arakawa et al., 2020). Therefore, we now evaluate the probability of a number of particles being ejected at a specific azimuth and elevation. The following impact probability density function is thus assumed:

$P\left(t\right)={\int }_t^{t+\mathrm{\Delta }t}N\left(>r_{ej}\right)P_{\alpha }{P}_{\delta }dt,(8)$

where N(> r_ej) is the power-law distribution of the ejected particle size with r_ej being the ejecta radius. P_α and P_δ are the density functions of a particle being ejected from the crater at a particular azimuth, α, and elevation, δ, respectively. The power-law distribution of the ejecta particle size is given by (Holsapple and Housen, 2007; Yu et al., 2017; Wada, K. et al., 2021):

$N\left(>r_{ej}\right)={\left(\frac{r_{\mathit{max}}}{r_{ej}}\right)}^2\frac{M_{ej}}{2m_{\mathit{max}}},(9)$

where r_ej is the radius of a spherical dust particle, M_ej is the total mass of the ejected particles, r_max is the maximum particle radius set at 10 cm while m_max is the mass of a particle of 10 cm in radius, estimated as 8 kg (Wada, K. et al., 2021). The total mass of particles ejected from the crater, M_ej is approximated by computing the volume of a sphere cap:

$V_{\mathit{cap}}=\pi h\frac{\left(R_{\mathit{crater}}^2+\frac{h^2}{3}\right)}{3},(10)$

where h is the height of the cap, R_crater is the radius of the cap and it corresponds to half of the diameter of the estimated crater. Here, we investigated two extreme cases for a 20 m and 8 m crater [actual crater size (Arakawa et al., 2020)]. Finally, the total mass is computed as M_ej = V_capρ_ej where the density of the ejecta, ρ_ej, is equal to 2.5 g/cm³. Figure 7 shows the power-law distribution presented in Eq. 9 as a function of the radius of the particles.

FIGURE 6

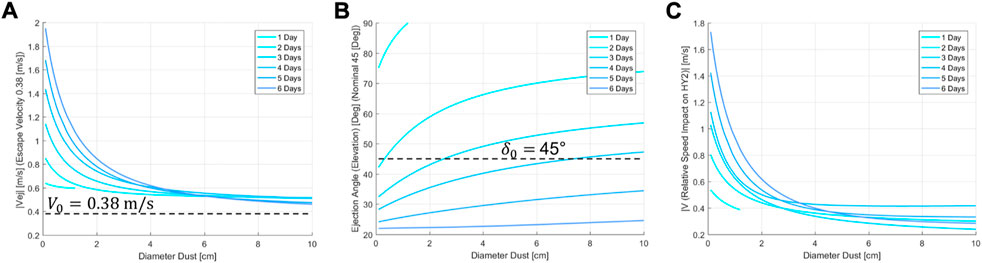
FIGURE 6. TPBVP sensitivity analysis as a function of the dust diameter (x-axis) and ToF (blue scale curves) of solutions in Figure 5: (A). ejecta escape velocity compared to the escape theoretical value of 0.38 m/s (B). Elevation angle compared to the nominal scaling law angle of 45°. (C). The relative impact speed between the ejecta particle and the Hayabusa 2 spacecraft at ToF.

FIGURE 7

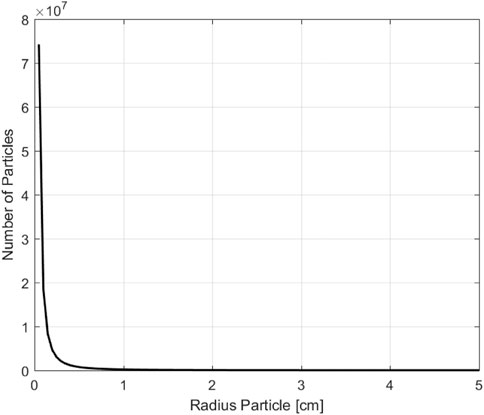
FIGURE 7. Power-law distribution of the ejected particle size (Holsapple and Housen, 2007; Yu et al., 2017; Wada, K. et al., 2021).

Given a predefined escape trajectory for the Hayabusa 2 spacecraft, the formulated TPBVP allows us to obtain the deterministic trajectory flown by a particle from the SCI impact point on Ryugu’s surface to a specific location along the Hayabusa 2’s escape trajectory. This allows us to precisely estimate the ejection speed of the particle and the impact speed with the Hayabusa 2 spacecraft regardless of the terrain conditions. The solution from the TPBVP allows us to determine the effect of the damage by estimating the speed of the impact. A sensitivity analysis is then carried out as a function of particle sizes. The probability heavily depends on the terrain condition and it provides us with an estimation of the number of particles that could impact the spacecraft. Here, the nominal case of a symmetric crater and ejecta cone is assumed as the first approximation of the number of particles that can intercept the spacecraft. Note that the artificial crater formed on Ryugu was not found to be symmetric due to the presence of boulders (Wada, K. et al., 2021). Thus, this implies that the probability along the azimuth is not uniform and certain azimuth angles are less likely to have contributed to the ejection of particles. However, the most important point of this estimation is to establish the damage effect which is quantified directly as a solution of the TPBVP while the terrain conditions affect the estimation of the overall number of particles that could intercept the spacecraft. In this case, the TPBVP has shown that the speed of the particles that would impact the spacecraft is within the design limit thus the terrain conditions do not affect the estimation of damage but rather the number of particles that intercept the spacecraft. The choice of a symmetric crater model was made as these analyses were carried out during the SCI operations and it provided an initial estimate. We can now compute the fraction of particles that would hit the spacecraft when leaving the surface of Ryugu in a specific azimuth direction, α. Thus, the density function is given by:

$P_{\alpha }=\frac{\theta }{2\pi },(11)$

where the angle θ is shown in Figure 8. Figure 8 shows the crater size in blue with diameter D and θ is computed, knowing the distance of the Hayabusa 2 spacecraft from the SCI impact point, D_hy2 and L are the distance from the SCI impact site and the Hayabusa 2 spacecraft and the spacecraft’s 8 m cross-section, respectively. The fraction of particles that can hit the spacecraft from a particular elevation direction δ is given by:

$P_{\delta }=1-\left(P\left({\delta }_{\mathit{mean}}+\mathrm{\Delta }\delta \right)-P\left({\delta }_{\mathit{mean}}-\mathrm{\Delta }\delta \right)\right),(12)$

where P is the cumulative distribution function, δ_mean = 45°, Δδ is the difference in the elevation direction between the mean value (δ_mean) and the one of the particle’s velocity (V₀) computed with the TPBVP and 1σ = 10% δ_mean which are given from the ejecta model from impact (Holsapple and Housen, 2007; Wada, K. et al., 2021; Arakawa et al., 2020). Figure 9 shows the velocity distribution in the x-y local horizon plane as a function of the elevation. The local horizon plane is defined as shown in Figure 4 (light blue plane). Equation 12 was used to obtain Figure 9, where each point in the figure represents a direction of V₀.

FIGURE 8

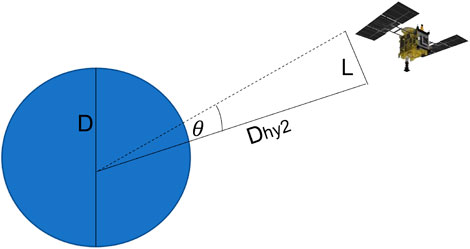
FIGURE 8. Estimation of a fraction of particles that can collide with the Hayabusa 2 spacecraft when leaving the SCI impact site at a specific azimuth.

FIGURE 9

FIGURE 9. Distribution probability of the ejecta velocity in the elevation direction.

Figure 10 shows the ejecta velocity in the x-y local horizon plane, $V_{0_{xy}}$ computed with the TPBVP method as a function of the ToF (days after impact, Figures 10A–F) and the ejecta diameter size (color bar in Figure 10). Figure 10 shows that solutions from the TPBVP for millimeter-sized particles can be found on day 1 after impact, while centimeter-sized particles could intercept the spacecraft from day 2 after impact. It is also interesting to notice how the azimuth (in-plane angle of the x-y local horizon plane in light blue in Figure 4) changes showing that on day 6 of ToF the ejecta particles share the same azimuth. Figure 11 shows the P_δ computed in Eq. 12 for the solutions shown in Figure 10. This shows that millimeter-sized particles are likely to collide with the spacecraft in the first 3 days after impact while centimeter-sized particles are more likely to collide with the spacecraft after day 4 from the SCI impact. The color associated to each histogram in Figure 11 matches the day of impact as presented in Figure 6.

FIGURE 10

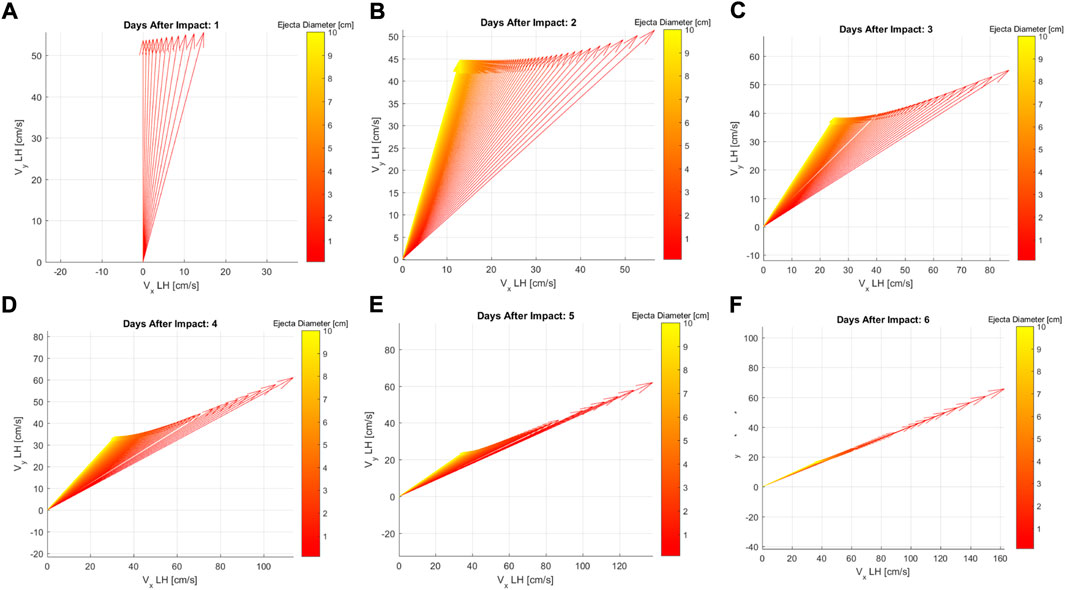
FIGURE 10. Ejection velocity as function of 1 (A), 2 (B), 3 (C), 4 (D), 5 (E) and 6 (F) days after the SCI impact and ejecta particle size.

FIGURE 11

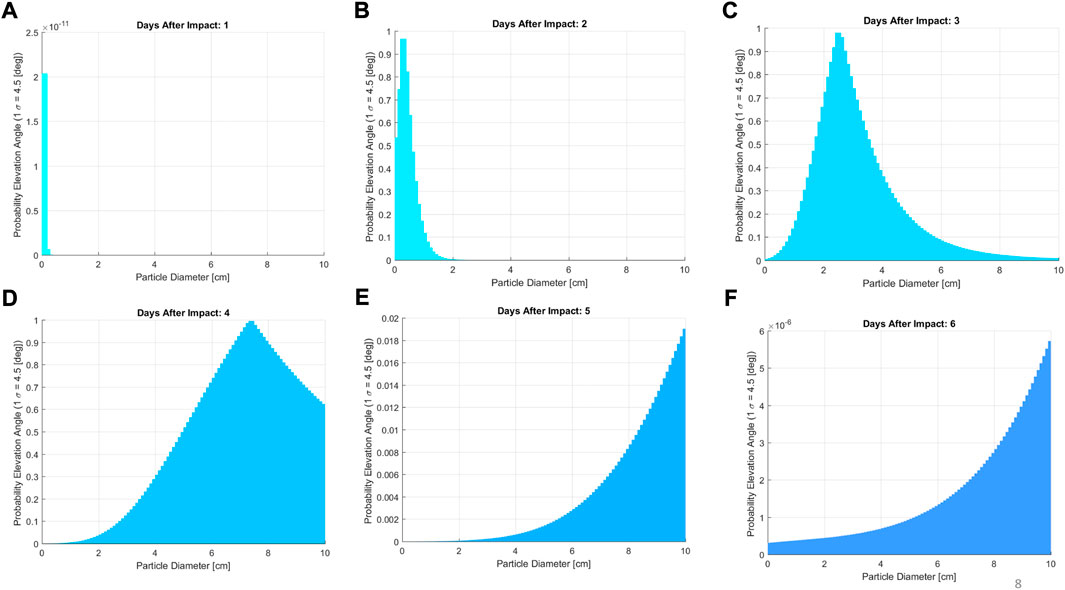
FIGURE 11. Distribution probability of the ejecta velocity in the elevation direction as a function of 1 (A), 2 (B), 3 (C), 4 (D), 5 (E) and 6 (F) days after SCI impact and ejecta particle size. The color of the histogram correspond to the day of the impact as for Figure 6.

We now want to evaluate the probability of damage (Wijker, 2008) to the spacecraft based on the relative ejecta-spacecraft impact velocity and the probability of impact. Thus, the target thickness equation is here used (Wijker, 2008):

$t=K_1{m}_p^{0.352}{v}_p^{0.875}{\rho }_p^{\frac{1}{6}},(13)$

where m_p is the projectile mass (g), in our case, a spherical ejecta particle, and v_p is the relative impact speed of the ejecta on the Hayabusa 2 spacecraft (computed with the TPBVP, Figure 6C). K₁ is the constant of the target material, assumed to be 0.55 for an Al panel of the spacecraft, ρ_p is the density (g/cm³) of the ejecta assumed as 2.5 g/cm³. The formula in Eq. 13 allows us to compute the thickness threshold, t, of a single Al plate. The acceptable penetration threshold for an Al single plate is 0.289 mm to avoid permanent damage.

4 Probability of damage results

In this section, two sizes of crater were considered of 20 m and 8 m respectively. The results of the TPBVP were used to compute how many particles per day will collide with the Hayabusa 2 spacecraft and also the thickness of penetration given in Eq. 13 was evaluated to estimate the possible damages. Tables 2, 3 show the daily forecast probability of the number of particles that could collide with the spacecraft (N/day) as for Eq. 8. This analysis is done by varying the diameter size of the ejecta particle between 0.1 and 10 cm. The TPBVP is solved to compute the collision speed on the Hayabusa 2 (HY2) spacecraft which allows computing the thickness of penetration, t (Eq. 13). Missing solutions in the N/day column imply a lack of probability that the event occurs. Indeed, only particles of 0.1 cm size can impact the spacecraft on day 1 after the SCI impact (6 April 2019). Day 2 (7 April 2019) and 3 (8 April 2019) were the most likely days for ejecta particles to collide with the spacecraft. However, the thickness of penetration is far below the damage threshold of 0.289 mm for both the 20 m and 8 m crater sizes. Figure 12 show the N/day probability for the 20 m (Figure 12A) and 8 m (Figure 12B) crater respectively. We could thus conclude that the Hayabusa 2 escape trajectory was a safe strategy to avoid the ejecta particles generated from the SCI impact. While millimeter-sized particles were likely to collide with the spacecraft two-three days after impact, centimeter-sized particles could collide with the spacecraft after day 4 (9 April 2019), causing no expected damage. The overall fraction of particles colliding with the spacecraft is negligible and although a small fraction could collide with the spacecraft, the collision speed was under the Al panel design threshold.

TABLE 2

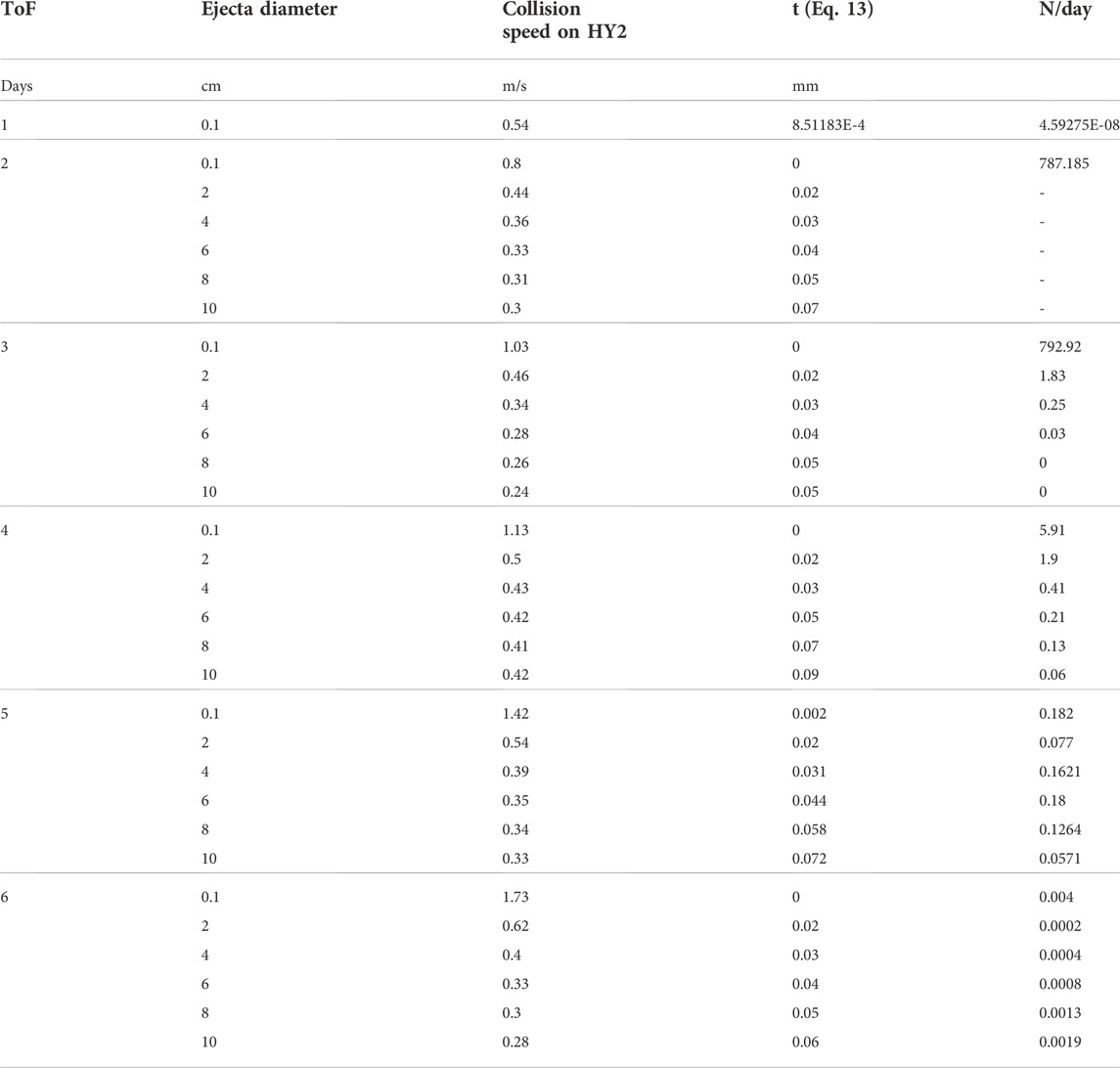
TABLE 2. Probability of the number of particles (N) per day that are predicted to collide with the Hayabusa 2 spacecraft: results for a 20 m crater.

TABLE 3

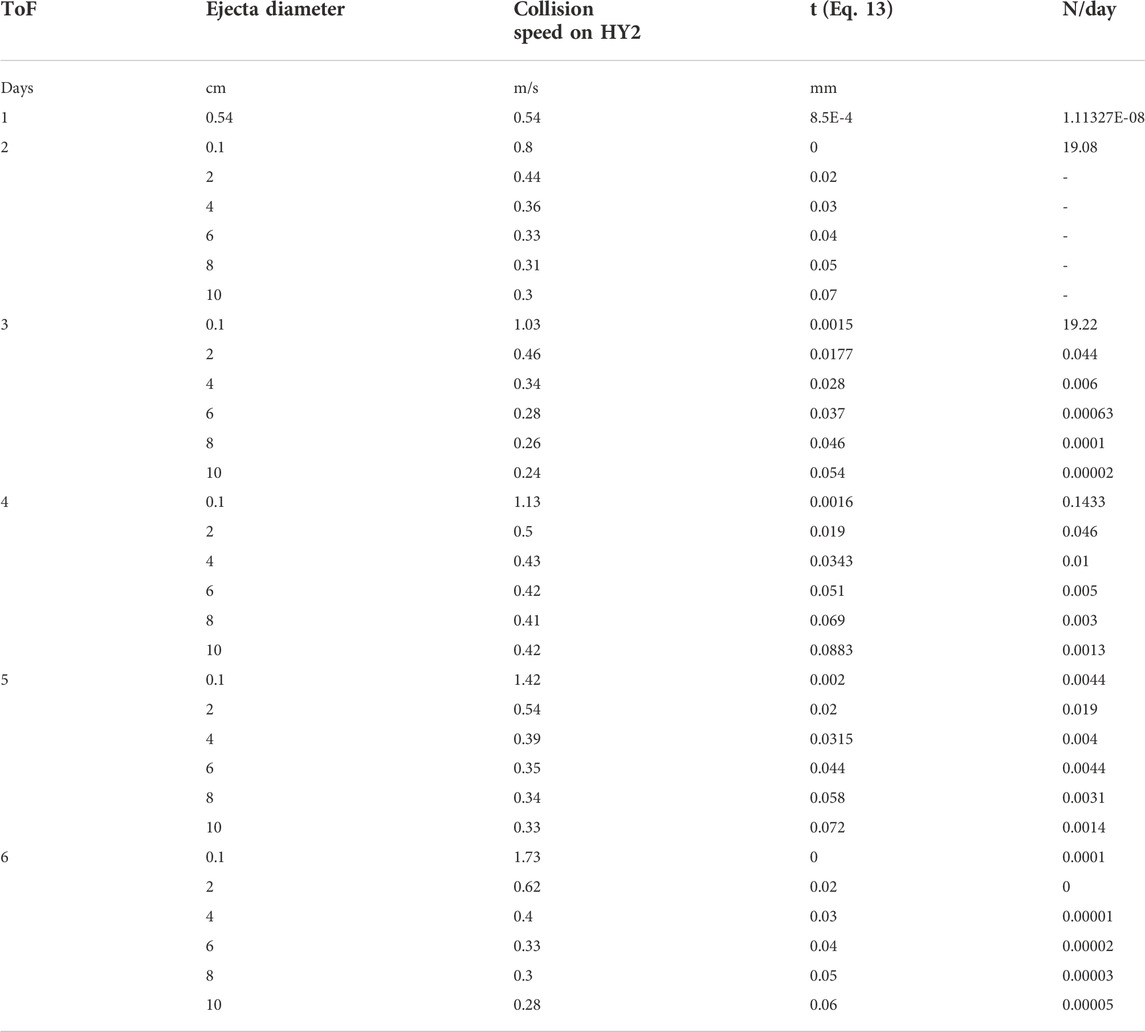
TABLE 3. Probability of the number of particles (N) per day that are predicted to collide with the Hayabusa 2 spacecraft: results for a 8 m crater.

FIGURE 12

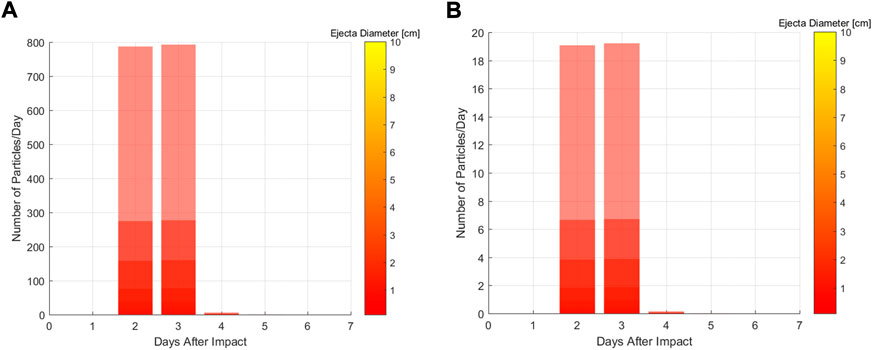
FIGURE 12. Daily forecast of the probability of the number of particles colliding with the Hayabusa 2 spacecraft for crater sizes of 20 m (A) and 8 m (B).

5 Hill problem

So far we have demonstrated that the ejecta particles from the SCI impact could not damage the spacecraft while following its escape trajectory during the SCI operation. However, it is useful to illustrate how the effect of SRP and particle size affect the qualitative motion of a particle. In Soldini et al. (2020a), the scaling laws were used as a first guess of the ejecta curtain for direct integration in an N-Body planetary model (goNEAR tool). In this study, we found that centimeter-sized particles could stay in orbit for a few weeks. Thus, we are interested in evaluating the qualitative motion of particles with ejecta speeds close to the theoretical escape value of 38 cm/s. Moreover, the two touch-down operations have also contributed to lifting off ejecta particles from the surface of Ryugu. In this section, we provide a qualitative insight into the Hill sphere of influence where the boundaries of motion, known as Zero Velocity Curves (ZVCs), can be quickly visualized. The Sun-Ryugu photogravitational Hill problem is here assumed where the Sun’s and Ryugu’s gravity is modeled as a point mass and the effect of SRP is taken into account (Soldini et al., 2020c). The Hamiltonian nature of the problem allows defining an integral of motion (Jacobi constant), thus, given an initial state of the particle, its motion could be bounded according to the value of its corresponding Jacobi constant. The Hill problem is defined in rotating coordinates with the system centered on Ryugu and the Sun's sharing a fixed distance with Ryugu with coordinates x $<$ 0 and y = z = 0. Figure 13 shows the case of the ZVC for a 10 cm size particle when the ejection velocity, V₀, is varied between 15 and 70 cm/s. The white area represents a region where the motion of the ejecta particle is possible while the green area is the so-called forbidden region of motion. The ZVC is the curve that separates the white region from the green. As shown in Figure 13, ejection speeds lower than 30 cm/s means that the particle can not escape the sphere of influence of Ryugu (i.e., either re-impact the surface or stays in orbit). Above 40 cm/s, the particle is free to escape Ryugu. The case of 35 cm/s can still provide long-term orbiting motion due to the cap shape of the Hill sphere. By increasing V₀, the ZVC tends to get closer towards the Sun's, reaching a distance from Ryugu of 1,400 km for an ejecta speed of 70 cm/s. Thus, it is possible to make use of this qualitative information for selecting a safe location for placing the spacecraft during the impact. Indeed, ejecta with a velocity below 40 cm/s would allow the spacecraft to be easily located in safe areas far from any debris if positioned inside the forbidden regions (green areas in Figure 13). Conversely, for ejecta with a velocity above 40 cm/s, the altitude of the forbidden regions reaches distances above 100 km which is the maximum distance that the Hayabusa 2 spacecraft has operated from Ryugu. In cases where the forbidden regions are at higher altitudes, the best approach is to place the spacecraft behind the asteroid to shield it from the ejecta, as was done for the Hayabusa 2 spacecraft.

FIGURE 13

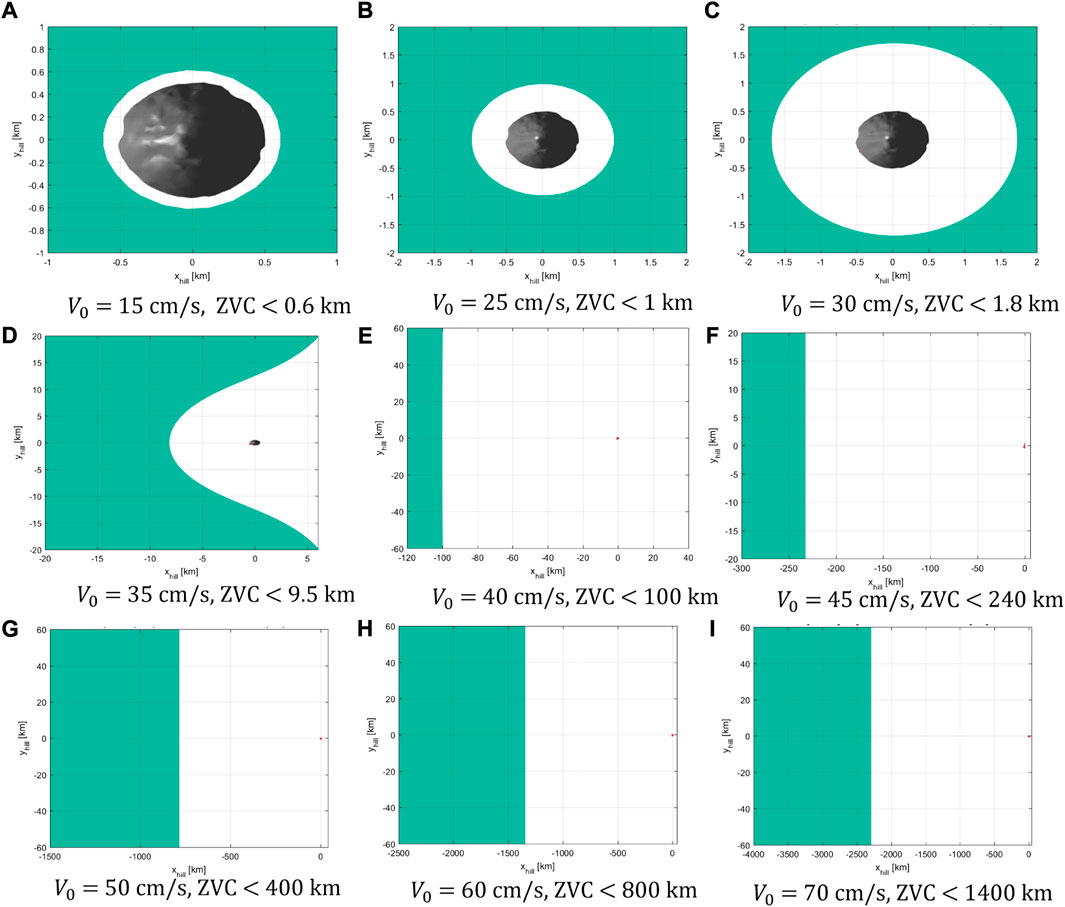
FIGURE 13. Zero velocity curves of a 10 cm particle with ejection speed increasing from 15 cm/s (A) to 70 cm/s (B). The figures from (A–I) shows a variation in the ejection speed.

Figure 14 shows the comparison of the ZVC for the size of particles of 1 mm, 1 cm, and 10 cm (columns of figures) and ejecta speeds of 30, 35, 40, and 45 cm/s (rows of figures). Millimeter-sized particles are prone to a fast escape while centimeter-sized particles require a higher ejection speed. While ejecta particles were less likely to impact the spacecraft along the escape trajectory during the SCI operation, we have here presented qualitative scenarios of bounded particle motion around Ryugu. As said, the forbidden regions represent a potentially safe space for the spacecraft to be placed during impact. However, it is expected that particles of different sizes and ejecta speeds are lifted-off by the impact, thus making it difficult to define a forbidden region that holds true for all the analyzed cases. The favorable option is to place the spacecraft in a shielding position behind the asteroid itself which was the rationale for the Hayabusa 2’s escape trajectory after the SCI impact. Nevertheless, these considerations allow us to identify the particle sizes and ejecta speeds that could pose a long-term risk for the spacecraft. In the cases where the motion of a particle is bounded or quasi-bounded to the asteroid, it can not escape the asteroid’s gravity field, thus potentially staying in long-term orbit around it as shown in Figures 13A–D and Figures 14B–F.

FIGURE 14

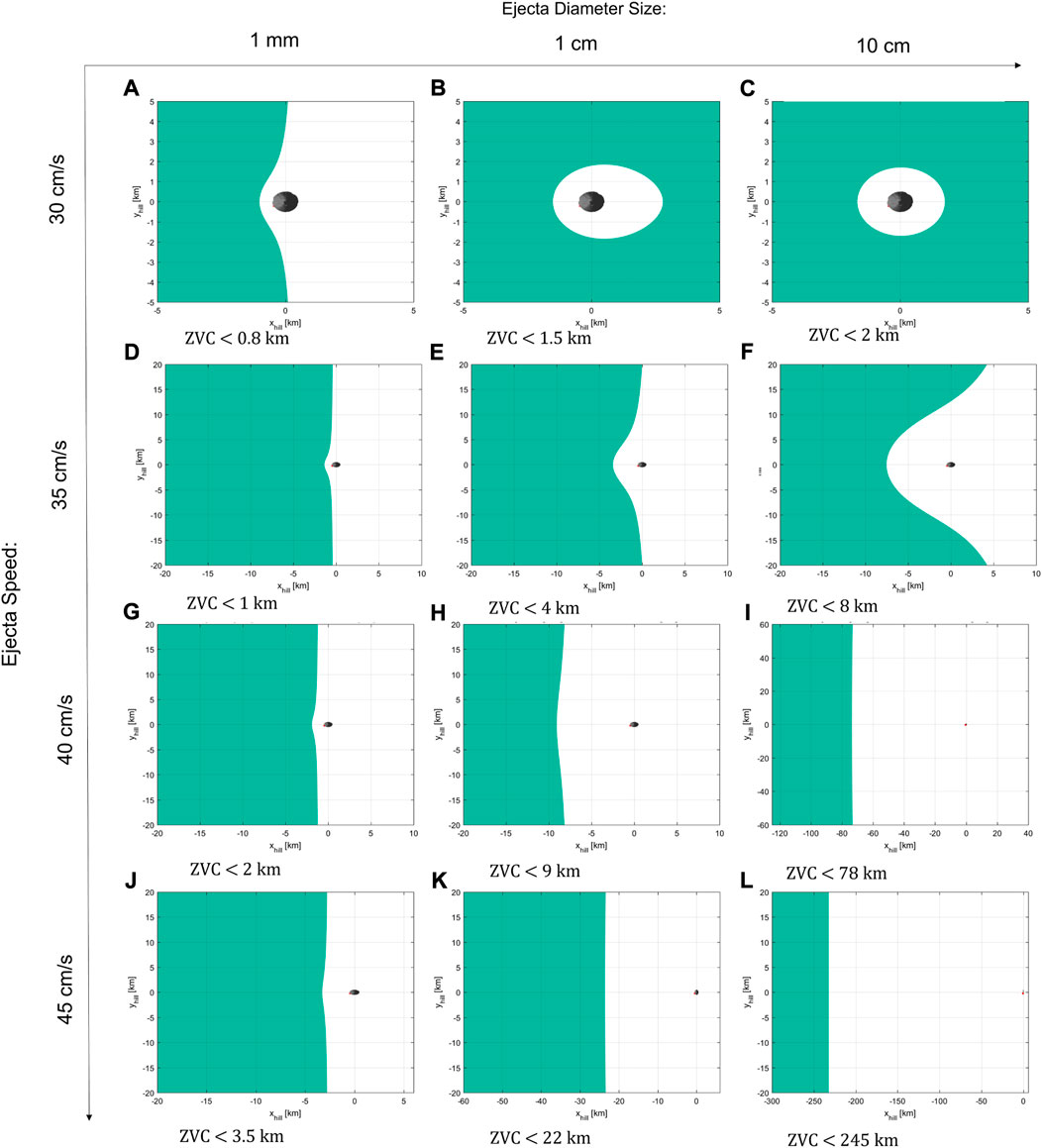
FIGURE 14. Zero velocity curves of ejecta particles of 1 mm (A,D,G,J) 1 cm (B,E,H,K) and 10 cm (C,F,I,L) size (columns of figures) as a function of the ejecta speed (rows of figures).

6 Conclusion

In this article, a two-point boundary value problem was proposed to compute the ejection speed from the SCI impact site and the relative ejecta-spacecraft impact speed. The probability for a particle to be ejected at a specific azimuth and elevation was also taken into account following the crater scaling laws. This method allowed forecasting of the number of particles per day that were likely to collide with the Hayabusa 2 spacecraft along its escape trajectory. The target thickness equation for a single Al plate was used to conclude that the SCI impact did not pose a risk to the Hayabusa 2 spacecraft. Finally, an insight into the qualitative motion of ejecta particles around Ryugu was also presented. The methodology proposed here can be easily adapted to artificial impact experiments, for example for the probability of damage to LICIACube from NASA’s DART impact.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SS has contributed on the overall methodology, analysis and results while TS and YT have contributed on the methodology section.

Acknowledgments

SS would like to thank Dr Koji Wada from PERC for providing the scaling laws’ parameters for the SCI impact.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The spacecraft does not orbit the asteroid.

²r_a is the equivalent sphere radius of the asteroid.

References

Arakawa, M., Saiki, T., Wada, K., Ogawa, K., Kadono, T., Shirai, K., et al. (2020). An artificial impact on the asteroid (162173) ryugu formed a crater in the gravity-dominated regime. Science 368, 67–71. doi:10.1126/science.aaz1701

PubMed Abstract | CrossRef Full Text | Google Scholar

Dotto, E., Della Corte, V., Amoroso, M., Bertini, I., Brucato, J., Capannolo, A., et al. (2021). Liciacube - the light Italian cubesat for imaging of asteroids in support of the nasa dart mission towards asteroid (65803) didymos. Planet. Space Sci. 199, 105185. doi:10.1016/j.pss.2021.105185

CrossRef Full Text | Google Scholar

Hirabayashi, M., Mimasu, Y., Sakatani, N., Watanabe, S., Tsuda, Y., Saiki, T., et al. (2021). Hayabusa2 extended mission: New voyage to rendezvous with a small asteroid rotating with a short period. Adv. Space Res. 68, 1533–1555. doi:10.1016/j.asr.2021.03.030

CrossRef Full Text | Google Scholar

Holsapple, K. A., and Housen, K. R. (2007). a crater and its ejecta: An interpretation of deep impact. Icarus 187, 586–597. doi:10.1016/j.icarus.2006.08.035

CrossRef Full Text | Google Scholar

Matsumoto, J., Saiki, T., Tsuda, Y., and Kawaguchi, J. (2011). Numerical analysis of particle distribution with collisions around an asteroid. Astrodyn. Symp.

Google Scholar

Micheal, P., Cheng, A., Küppers, M., Pravec, P., Blum, J., Delbo, M., et al. (2016). Science case for the asteroid impact mission (aim): A component of the asteroid impact & deflection assessment (aida) mission. Adv. Space Res. 57, 2529–2547. doi:10.1016/j.asr.2016.03.031

CrossRef Full Text | Google Scholar

Rivkin, A. S., Chabot, N. L., Stickle, A. M., Thomas, C. A., Richardson, D. C., Barnouin, O., et al. (2021). The double asteroid redirection test (DART): Planetary defense investigations and requirements. Planet. Sci. J. 2, 173. doi:10.3847/psj/ac063e

CrossRef Full Text | Google Scholar

Saiki, T., Imamura, H., Arakawa, M., Wada, K., Takagi, Y., Hayakawa, M., et al. (2017). The small carry-on impactor (sci) and the hayabusa2 impact experiment. Space Sci. Rev. 208, 165–186. doi:10.1007/s11214-016-0297-5

CrossRef Full Text | Google Scholar

Saiki, T., Mimasu, Y., Takei, Y., Yamada, M., Sawada, H., Ogawa, K., et al. (2020). Motion reconstruction of the small carry-on impactor aboard hayabusa2. Astrodyn. 4, 289–308. doi:10.1007/s42064-020-0077-6

CrossRef Full Text | Google Scholar

Saiki, T., Sawada, H., Ogawa, K., Mimasu, Y., Takei, Y., Arakawa, M., et al. (2022a). “Chapter 15 - hayabusa2’s kinetic impact experiment,” in Hayabusa2 asteroid sample return mission. Editors M. Hirabayashi, and Y. Tsuda (Netherlands: Elsevier), 291–312. doi:10.1016/B978-0-323-99731-7.00015-5

CrossRef Full Text | Google Scholar

Saiki, T., Takei, Y., Fujii, A., Kikuchi, S., Terui, F., Mimasu, Y., et al. (2022b). “Chapter 7 - overview of the hayabusa2 asteroid proximity operations,” in Hayabusa2 asteroid sample return mission. Editors M. Hirabayashi, and Y. Tsuda (Netherlands: Elsevier), 113–136. doi:10.1016/B978-0-323-99731-7.00007-6

CrossRef Full Text | Google Scholar

Scheeres, D. J. (2012). Orbital motion in strongly perturbed enviroment. New York: Springer.

Google Scholar

Snodgrass, C., Tubiana, C., Vincent, J.-B., Sierks, H., Hviid, S., Moissl, R., et al. (2010). A collision in 2009 as the origin of the debris trail of asteroid P/2010 A2. Nature 467, 814–816. doi:10.1038/nature09453

PubMed Abstract | CrossRef Full Text | Google Scholar

Soldini, S., Takanao, S., Ikeda, H., Wada, K., Yuichi, T., Hirata, N., et al. (2020a). A generalised methodology for analytic construction of 1:1 resonances around irregular bodies: Application to the asteroid ryugu’s ejecta dynamics. Planet. Space Sci. 180, 104740. doi:10.1016/j.pss.2019.104740

CrossRef Full Text | Google Scholar

Soldini, S., Takeuchi, H., Taniguchi, S., Kikuchi, S., Takei, Y., Ono, G., et al. (2022). “Chapter 13 - superior solar conjunction phase: Design and operations,” in Hayabusa2 asteroid sample return mission. Editors M. Hirabayashi, and Y. Tsuda (Netherlands: Elsevier), 241–257. doi:10.1016/B978-0-323-99731-7.00013-1

CrossRef Full Text | Google Scholar

Soldini, S., Takeuchi, H., Taniguchi, S., Kikuchi, S., Takei, Y., Ono, G., et al. (2020b). Hayabusa2’s superior solar conjunction mission operations: Planning and post-operation results. Astrodyn. 4, 265–288. doi:10.1007/s42064-020-0076-7

CrossRef Full Text | Google Scholar

Soldini, S., Yamaguchi, T., Tsuda, Y., Saiki, T., and Nakazawa, S. (2020c). Hayabusa2’s superior solar conjunction phase: Trajectory design, guidance and navigation. Space Sci. Rev. 216, 108. doi:10.1007/s11214-020-00731-5

CrossRef Full Text | Google Scholar

Tsuda, Y., Saiki, T., Terui, F., Nakazawa, S., Yoshikawa, M., and ichiro Watanabe, S. (2020). Hayabusa2 mission status: Landing, roving and cratering on asteroid ryugu. Acta Astronaut. 171, 42–54. doi:10.1016/j.actaastro.2020.02.035

CrossRef Full Text | Google Scholar

Tsuda, Y., Yoshikawa, M., Abe, M., Minamino, H., and Nakazawa, S. (2013). System design of the Hayabusa 2 - asteroid sample return mission to 1999 JU3. Acta Astronaut. 91, 356–362. doi:10.1016/j.actaastro.2013.06.028

CrossRef Full Text | Google Scholar

Wada, K., Ishibashi, K., Kimura, H., Arakawa, M., Sawada, H., Ogawa, K., et al. (2021). Size of particles ejected from an artificial impact crater on asteroid 162173 ryugu. Astron. Astrophys. 647, A43. doi:10.1051/0004-6361/202039777

CrossRef Full Text | Google Scholar

Wijker, J. J. (2008). Damage to spaceraft by meteroids and obital debris. Spacecr. Struct., Berlin, Heidelberg: Springer Berlin Heidelberg, 299–411. doi:10.1007/978-3-540-75553-1_27

CrossRef Full Text | Google Scholar

Yu, Y., Michel, P., Schwartz, S. R., Naidu, S. P., and Benner, L. A. (2017). Ejecta cloud from the aida space project kinetic impact on the secondary of a binary asteroid: I. Mechanical environment and dynamical model. Icarus 282, 313–325. doi:10.1016/j.icarus.2016.09.008

CrossRef Full Text | Google Scholar