Design and Implementation of Blind Source Separation Based on BP Neural Network in Space-Based AIS

In space-based AIS (Automatic Identification System), due to the high orbit and wide coverage of the satellite, there are many self-organizing communities within the observation range of the satellite, and the signals will inevitably conflict, which reduces the probability of ship detection. In this paper, to improve system processing power and security, according to the characteristics of neural network that can efficiently find the optimal solution of a problem, proposes a method that combines the problem of blind source separation with BP neural network, using the generated suitable data set to train the neural network, thereby automatically generating a traditional blind signal separation algorithm with a more stable separation effect. At last, through the simulation results of combining the blind source separation problem with BP neural network, the performance and stability of the space-based AIS can be effectively improved.

Introduction

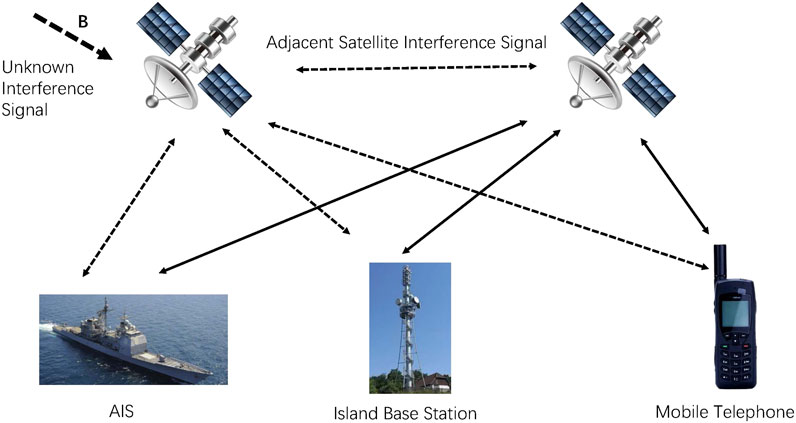
In space-based AIS (Automatic Identification System), satellite communications are one of important parts, due to the satellite orbit altitude is relatively high and the number of satellites increasing, the openness of satellite orbits makes satellite communications vulnerable to be jammed from external signals. To solve that problem, improving the efficiency of information processing, new technologies must be developed. The framework of space-based AIS is shown in Figure 1. In Figure 1, due to the openness of satellite channels, satellite communication is easily disturbed by external signals, therefore, it is great significance to study the security of satellite communication in space-based AIS (Kourogiorgas et al., 2015) (Chen et al., 2020).

FIGURE 1

FIGURE 1. Framework of space-based AIS.

Blind separation technology can improve the efficiency of signal processing without occupying excess bandwidth. With the increasing processing power of computers, neural network technology has also been introduced into blind separation technology (Lee et al., 2008; Lahat and Christian, 2016; Fu et al., 2014). In 1985, C. Jutten and J. Herault proposed a neural network recursively connecting two initial signals to two mixed signals passing through the channel, gradient descent method is used to change the network weights, the residual error of the output signal is minimized, the separation of the signal under unknown initial conditions is accomplished. In 1991, the variability of the solution of blind separation problem is completed by L. Tong. In recent years, a robust neural network blind separation algorithm is developed by A. Cichockic and R. Unbehauen (Inan and Erdogan, 2015; (Li et al., 2020; Kim et al., 2007. In (Inan and Erdogan, 2015), introduce a family of convolutive Bounded component analysis (BCA) criteria and corresponding algorithms, and prove that the global optima of the proposed criteria, under generic BCA assumptions, are equivalent to a set of perfect separators. In (Li et al., 2020), separate the mixed source signals by Particle swarm optimization (PSO) clustering. In (Kim et al., 2007), proposes a new algorithm that exploits higher order frequency dependencies of source signals in order to separate them when they are mixed.

In this paper, according to the characteristics of the neural network can find the optimal solution efficiently, a novel method is proposed, which combined blind separation and neural network, the neural network is trained with the generated appropriate data set.

The rest of this paper is organized as follows. Section Knowledge Background describes the basic knowledge of the novel algorithm, followed by the novel algorithm formulation in Section Algorithm execution process. Section Simulation Results gives the simulation details of the novel algorithm, experimental results show that the proposed algorithm has better performance and improve communication efficiency and system security significantly. Section Conclusion concludes the paper.

Knowledge Background

Blind Source Separation Model

N original signals pass through the mixed channel, the signals are statistically independent of each other, and M sensors receive the mixed signal, the mixed model of the observed signal is

$x_j\left(t\right)=\sum _{i=1}^N{a}_{ji}{s}_i\left(t\right)+n_i\left(t\right),i\in \left[\mathrm{1,2},\cdots N\right],j\in \left[\mathrm{1,2},\cdots M\right](1)$

$a_{ji}$ are the unknown mixing coefficients, $s_i\left(t\right)$are the original signals, $x_j\left(t\right)$ are the observed signals, $n_i\left(t\right)$ are the noise signals. The matrix form of formula (1) is

$\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\\ ⋮\\ x_M\left(t\right)\end{array}\right]=\left[\begin{array}{c}{a}_{11}\left(t\right)\\ a_{21}\left(t\right)\\ ⋮\\ a_{M1}\left(t\right)\end{array}\begin{array}{c}{a}_{12}\left(t\right)\\ a_{22}\left(t\right)\\ ⋮\\ a_{M2}\left(t\right)\end{array}\begin{array}{c}\cdots \\ \cdots \\ \ddots \\ \cdots \end{array}\begin{array}{c}{a}_{1N}\left(t\right)\\ a_{2N}\left(t\right)\\ ⋮\\ a_{MN}\left(t\right)\end{array}\right]\left[\begin{array}{c}{s}_1\left(t\right)\\ s_2\left(t\right)\\ ⋮\\ s_M\left(t\right)\end{array}\right]+\left[\begin{array}{c}{n}_1\left(t\right)\\ n_2\left(t\right)\\ ⋮\\ n_M\left(t\right)\end{array}\right](2)$

Among the numbers of original signal (M) and the numbers of receiving antenna(N), blind source signals can be classified into overdetermined blind separation (M < N), determined blind separation (M = N) and underdetermined blind separation (M > N) (Robert et al., 1995).

The blind source separation model in space-based AIS is slightly different from common blind separation. In this paper, consider only the signal processing methods between satellites, the probability distribution of the channel model obeys Rayleigh distribution, the probability density function is expressed as follows,

$f\left(x\right)=\frac{x}{{\sigma }^2}\exp (-\frac{x^2}{2{\sigma }^2}),x\ge 0(3)$

Back Propagation Neural Network

BP (Back Propagation) neural network was proposed by Rumelhart and McClelland in 1986, which is a multi-layer feedforward neural network trained according to error back propagation algorithm. In the BP neural network system, hidden layer connection weight learning of multi-layer neural network is solved, which has four basic features (Wu et al., 2005).

Nonlinear

Each connection unit in BP neural network has a different form, BP neural network can deal with nonlinear problems well. BP neural network contains a large number of specific connection units, and the connection mode of BP neural network is not a specific connection unit, so the BP neural network is nonlinear. The relationship between the initial data and the expected data is not linear, and a neural network is designed to train and learn the initial data and the expected data. Then the trained BP neural network system can simulate the relationship between the initial data the expected data.

Parallel Processing

BP neural network is composed of many parallel concrete join units, and the order in which these join units are used in BP neural network is parallel. That is, when the initial data is entered, these parallel concrete connection units are activated in parallel, so processing the initial data in this way is very fast.

Fault Tolerance and Associative Ability

In the system model of the human brain, data is stored separately in different places. Information processing is also similar to that in BP neural network, the initial data is stored in each concrete link unit, rather than a specific storage in a fixed. Therefore, even if some of the connection units fail and the data is lost, the main part of the data still exists, the original data can be recovered from the data body part.

Self-Learning, Self-Organization and Adaptive Ability

BP neural network can change the weight of each specific connection unit according to the initial data input. Each input of data leads to an iterative calculation and the weights are adjusted. The self-organization of BP neural network means that when the trained network inputs different types of initial data again, it can adjust the weight according to the change of the initial data type. In this case, change itself structure is called adaptive ability.

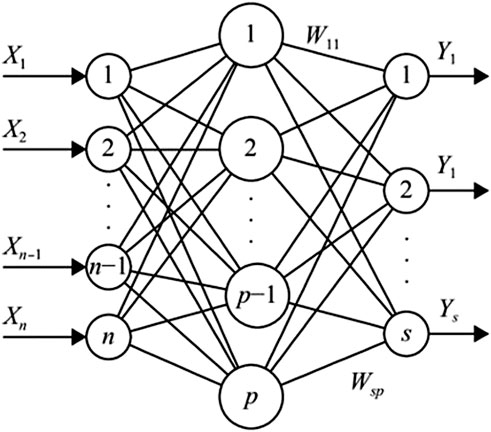
BP neural network is a kind of multi-layer feedforward network trained by using the method of transmitting data error from back to forward. It is one of the most commonly used models, which includes both the process of data propagating backwards and the process of error propagating forwards. Classic BP neural network diagram contains a data input layer, an intermediate layer, and a result output layer. The task of data input layer is to receive and detect incoming data and then send it to the neurons at the next layer, the task of intermediate layer is to process and transform the information transmitted from the upper layer accordingly and sends the information to the final layer. These three parts constitute the BP neural network, which transmit data backwards. The diagram of BP neural network is as follows in Figure 2 (Jin et al., 2000).

FIGURE 2

FIGURE 2. Diagram of BP neural network.

Frequency-Hop Signal Model

In space-based AIS, considering to the frequency-hop signal model (Loof and Pratt, 2019a) (Loof and Pratt, 2019b),

$f\left(t\right)=\sqrt{2S}{\displaystyle \sum _{k}rec{t}_{T_H}\left(t-k{T}_H-\alpha T_H\right)}•e^{j2\pi f_k\left(t-k{T}_H-\alpha T_H\right)+j\theta }+n\left(t\right),0<t\le L(4)$

In formula (4), $L$ is the length of signal, $T_H$is the hop duration, $rec{t}_{T_H}$ stands for is the rectangular window, $f_k$ is the carrier frequency of the kth hop, $\alpha T_H$ is the frequency hopping time, $\theta$ is the phase of a frequency hopping signal, $S$ is the signal power; $n\left(t\right)$ is the Gaussian white noise. The frequency hopping signal distribution in time-frequency domain is described in Figure 3. In Figure 3, the time-frequency domain image of frequency hopping signal is determined by the following three factors: the position of the kth hop in the time domain, the position of the kth hop in the frequency domain and the length of the time-frequency domain.

FIGURE 3

FIGURE 3. Frequency-hop signal distribution image in time-frequency domain.

Algorithm Execution Process

In the algorithm execution process, BP neural network is the main body of algorithm execution.

Forward Propagation

Sampling data input formula is as follows (Porter et al., 2014; Balouchestani et al., 2014; Logeswari et al., 2014),

$n_i^m={\displaystyle \sum _{j=1}^{s^{m-1}}{\omega }_i^m},y_j^{m-1}+b_i^m,m=\mathrm{1,2},\cdots M(M\ge 2)(5)$

In formula (5), $n_i^m$ stands for the connection value of neurons in m row and i column of BP neural network, M stands for the number of layers of the neural network. The output of m layer is $y^m=f^m\left(n^m\right)$, m is the number of layers of the neural network, $f^m$ is the transfer function at the mth layer. Then, the output of the first layer is $y^1=f^1(W^{1}x+b)$, the output of the last layer is $y=y^M$.

Back Propagation

Back propagation is the main characteristic of BP neural network, in this paper, BP neural network is mainly composed of four parts.

Error Function

In this paper, MSE (Mean Squared Error) function is chosen as the error function of BP network, the expression of MSE is as follows,

$F\left(z\right)=E\left(e^2\right)=E\left[{(y_i-{\stackrel{\wedge }{y}}_i)}^2\right](6)$

here, $y_i$ is the output of the BP neural network true value, ${\stackrel{\wedge }{y}}_i$ is the output of the BP neural network estimated value.

Weight Correction Method

In the above error function (6), gradient descent method as the weight correction method, the iterative formula is as follows,

$w_{i,j}^m(k+1)=w_{i,j}^m\left(k\right)-\eta \frac{\partial F}{\partial w_{i,j}^m}(7)$

$b_i^m(k+1)=b_i^m\left(k\right)-\eta \frac{\partial F}{\partial b_i^m}(8)$

here, $\eta$ stands for training rate.

Chain Rule

To minimize MSE, it’s necessary to take the partial derivative of the objective function, the chain rule is the rule that you have to follow when you take partial derivatives, suppose $F$ is the objective function, then the chain rule is as follows,

$\frac{\text{d}F\left(n\left(w\right)\right)}{dw}=\frac{dF\left(n\right)}{dn}\frac{dn\left(w\right)}{dw}(9)$

According to formula (9), formulas (7) and 8 can be expressed as,

$\frac{\text{d}F}{d{w}_{i,j}^m}=\frac{dF}{d{n}_i^m}\frac{d{n}_i^m}{d{w}_{i,j}^m}(10)$

$\frac{\text{d}F}{d{b}_i^m}=\frac{dF}{d{n}_i^m}\frac{d{n}_i^m}{d{b}_i^m}(11)$

In BP neural network, $s_i^m=\frac{\partial F}{\partial n_i^m}$ represents the sensitivity of the iteration, then formulas (10) and (11) can be expressed as

$\frac{\partial F}{\partial w_{i,j}^m}=s_i^m{y}_j^{m-1}(12)$

$\frac{\partial F}{\partial b_i^m}=s_i^m(13)$

Weights Updated

In the above process, according to gradient descent method, the connection value of the BP neural network is as follows,

$w_{i,j}^m(k+1)=w_{i,j}^m\left(k\right)-\eta {\text{s}}_i^m{y}_j^{m-1}(14)$

$b_i^m(k+1)=b_i^m\left(k\right)-\eta {\text{s}}_i^m(15)$

BP Neural Network Algorithm

According to the 3.2, the steps of BP neural network in this paper are as follows.

1) Calculate the forward propagation value of BP neural network

$n^m=W^m{y}^{m-1}+b^m,m=\mathrm{1,2},\cdots ,M(M>2)(16)$

${\text{y}}^m=f^m\left(n^m\right)(17)$

${\text{y}=\text{y}}^m(18)$

2) Calculate the back propagation value of BP neural network

$s^M=-2{\left(F^M\right)}^{\prime }\left(n^M\right)(t-y)(19)$

$s^{m-1}={\left(F^{m-1}\right)}^{\prime }\left(n^{m-1}\right){\left(W^m\right)}^T{s}^m,m=M,\cdots ,\mathrm{2,1}(M\ge 2)(20)$

3) Change connection value

$s^{m-1}={\left(F^{m-1}\right)}^{\prime }\left(n^{m-1}\right){\left(W^m\right)}^T{s}^m,m=M,\cdots ,\mathrm{2,1}(M\ge 2)(21)$

$b^m(k+1)=b^m\left(k\right)-\eta s^m(22)$

Simulation Results

Parameter Setting

In this paper, determined blind separation (M = N) is considered, the number of original signals is equal to the number of received antennas, M = N = 3, the parameters are set as follows.

Sparse Representation

Since the target signal is processed as sparse signal, the sparse processing should be carried out (Meganem et al., 2014).

Definition

Dictionary: It is a collection of waveforms, that is, an analytic function library or a signal sample library, which may not satisfy orthogonality.

Atom: Basic waveforms in dictionaries, that is the basic carrier and representation unit of information and can represent any signal by superposition.

Theorem

Atomic Decomposition Theorem:$x$is a random signal, and the dictionary $\Phi$ consists of many column vectors, each of which is an atom ${\varphi }_r$, then $x$ can be expressed as a weighted sum of some optimal atoms, $x={\displaystyle \sum _{\gamma \in \Gamma }{\alpha }_{\gamma }}{\varphi }_{\gamma }=A\alpha$, here ${\alpha }_{\gamma }$ is a decomposition coefficient, $\gamma$ is the atomic number, $\Gamma$ is the set of atomic serial numbers.

Residual Signal: In fact, it’s very difficult to match ${\alpha }_{\gamma }$ and ${\varphi }_r$, in general, random signals $x$ is obtained by means of signal approximation, $x={\displaystyle \sum _{i=1}^m{\alpha }_{{\gamma }_i}{\varphi }_{{\gamma }_i}}+r_m$, here$r_m$ is the residual signal, the smaller the value of $r_m$, the higher the matching accuracy.

Sparse Representation: Sparse representation is actually an optimization problem, that is, the signal has as few atoms as possible, but it can’t be distorted, suppose ${\Vert \alpha \Vert }_0$ is the objective function of the optimization problem, then the mathematical model of sparse representation is as follows,

$\min {\Vert \alpha \Vert }_0,s.t.x={\displaystyle \sum _{\gamma \in \Gamma }{\alpha }_{\gamma }}{\varphi }_{\gamma }(23)$

Separation Simulation Results

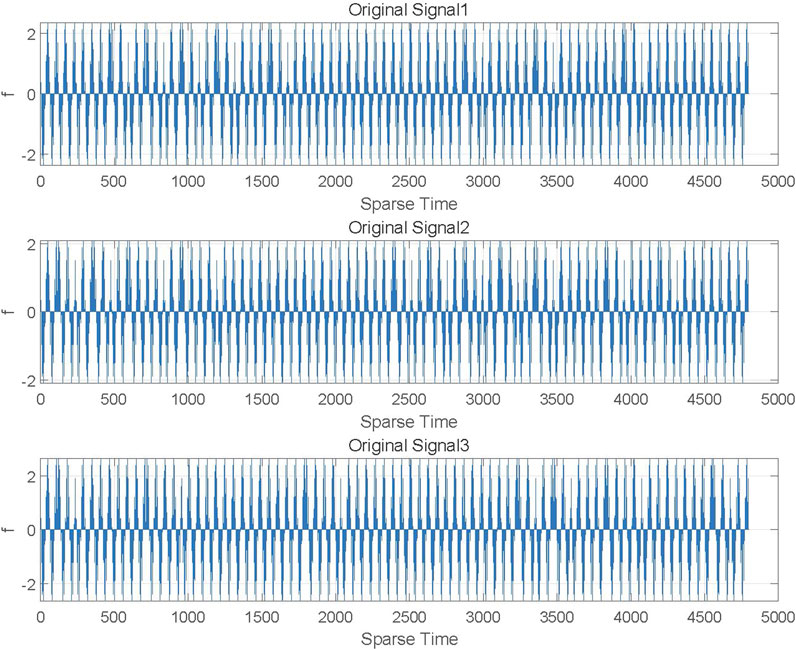
After the signal is sparse, the signal separation performance will be discussed in this subsection. In this paper, the number of transmitting antennas and receiving antennas is equal to three, the original signal are sparsely processed according to 4.2 and the waveforms are shown in Figure 4, in Figure 4, the X-axis represents sparse time and the Y-axis represents $f$, the expression for $f$ is described in formula (24),

$f=\mathbf{A}\cdot m\left(\mathbf{N}\right).\ast \cos \left(2\pi \cdot \frac{f_c}{f_s}\cdot \mathbf{N}\right)(24)$

FIGURE 4

FIGURE 4. Waveforms of original signals.

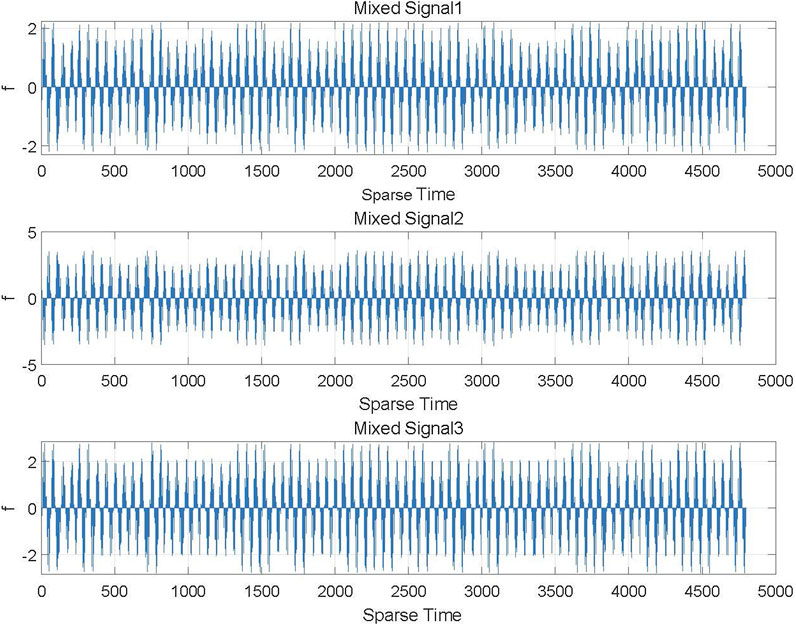
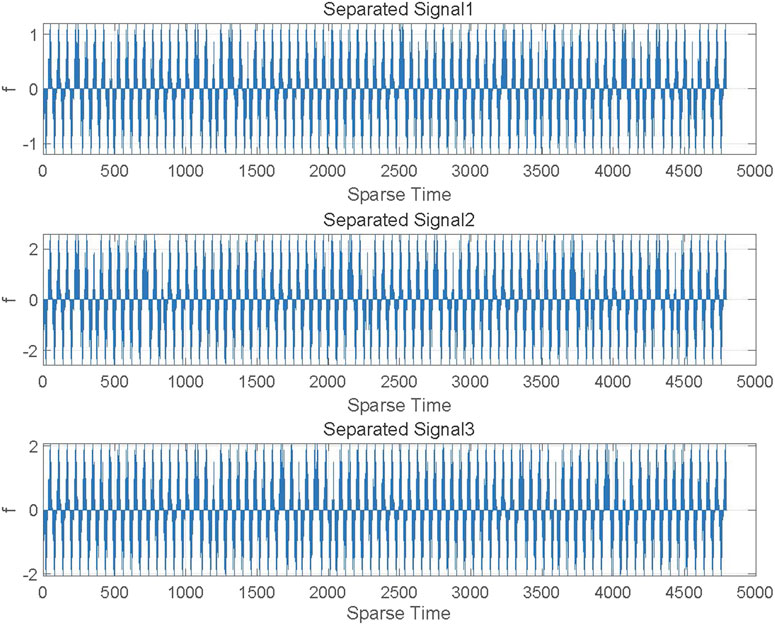
In the next experiment, we aim to separate each signal from the received mixed signals. Considering to the realistic signal transmission, we assume that the transmission channel is a Gaussian channel, the initial signal goes through the Gaussian channel and are sparsely processed according to 4.2, the mixed signal’s waveforms are shown in Figure 5.

FIGURE 5

FIGURE 5. Waveforms of mixed signals.

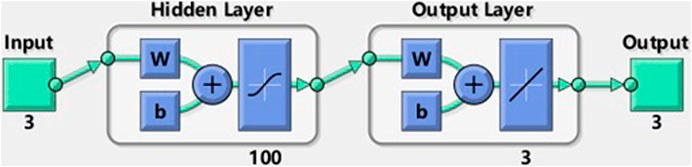
We use the proposed algorithm in this article, in BP neural network algorithm, the number of hidden layers is 100, the processing flow chart is given in Figure 6. In the data training process, 70% of the data set is used as the training set, 15% of the data set as the verification set and the remaining 15% of the data set as the test set. After the proposed algorithm in this article, the original signals are recovered efficiently, the separated signal waveforms are displayed in Figure 7. From Figure 7, it is clear that the signal waveform after separation is very similar to the original signal waveform.

FIGURE 6

FIGURE 6. Processing flow chart of BP neural network algorithm.

FIGURE 7

FIGURE 7. Waveforms of separated signals.

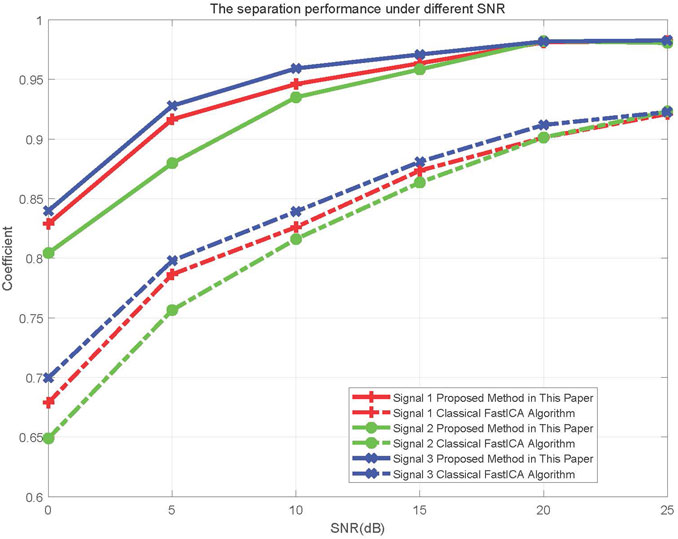
To measure the separation effect, we compare the signals in Figure 4 and Figure 7 with correlation coefficient value as the evaluation standard. The correlation coefficient expression is given in formula (25) (Li et al., 2016),

$r=\frac{{\displaystyle \sum _{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}}{\sqrt{{\displaystyle \sum _{i=1}^n{(x_i-\overline{x})}^2·{\displaystyle \sum _{i=1}^n{(y_i-\overline{y})}^2}}}}(25)$

To measure the advantages of the algorithm in this paper, we further compare the separation performance with Classical FastICA Algorithm. The algorithm performance comparison results are shown in Figure 8. In Figure 8, the algorithm has better separation performance than Classical FastICA Algorithm (Reju et al., 2010).

FIGURE 8

FIGURE 8. Separation performance comparison with classical fastICA algorithm.

Network Security Analysis

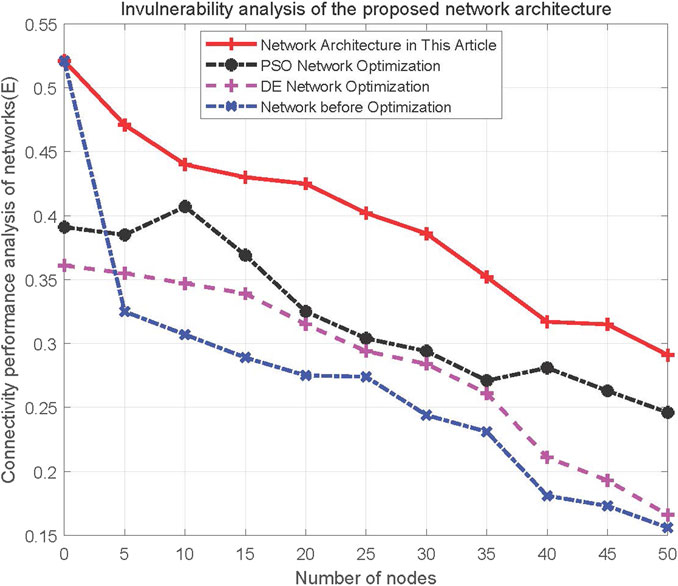
Blind separation belongs to signal processing, it can not only improve the information processing ability of the system, but also improve the security of space-based AIS network. To measure the security of the system, invulnerability analysis of space-based AIS network is used as the safety standard, the parameter settings are shown in Table 1. A cost function is constructed to measure the invulnerability analysis of the space-based AIS network in formula (26),

$E=\frac{1}{N(N-1)}{\displaystyle \sum _{i\ne j}\frac{1}{l_{ij}}}(26)$

where $l_{ij}$ is the distance of node i and node j.

TABLE 1

TABLE 1. Simulation parameters.

The results of the analysis are shown in Figure 9. The results show that: 1) The invulnerability performance of space-based AIS network under random attack has significant advantages than the DE (Differential Evolution algorithm) network optimization and PSO (Particle Swarm Optimization) network optimization; 2) As the number of nodes increases, the invulnerability of the system decreases; 3) The invulnerability performance of space-based AIS network with blind source separation was significantly better than that without blind source separation (Yang et al., 2019) (Tai et al., 2017).

FIGURE 9

FIGURE 9. Invulnerability analysis of space-based AIS network.

Conclusion

In this paper, the blind separation technique is used to deal with the conflict between signal receivers of space-based AIS network. This method not only improves the signal processing capability of the system, but also improves the security of the space-based AIS network. That fundamentally solves the security of the system and belongs to the category of Endogenous Safety and Security (ESS). Finally, the paper discusses the signal processing ability and the security of the system through the simulation experiment. The simulation results show that the algorithm in this paper has better advantages than conventional information processing methods.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

CL completed the overall idea of the paper, LZ completed the structure of the paper, ZZ, YL, and YY completed the simulation experiments.

Funding

This work is fully supported by Natural Science Foundation of China Project (61871422), Science and Technology Program of Sichuan Province (2020YFH0071), National Natural Science Foundation of China under Grant (61801319), in part by Sichuan Science and Technology Program under Grant (2020JDJQ0061), (2021YFG0099), in part by the Sichuan University of Science and Engineering Talent Introduction Project under Grant (2020RC33), Innovation Fund of Chinese Universities under Grant (2020HYA04001).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Balouchestani, M., Sugavaneswaran, L., and Krishnan, S. (2014). Advanced K-means clustering algorithm for large ECG data sets based on K-SVD approach[C]. 2014 9th International Symposium on Communication Systems, Networks and Digital Signal. Tokyo: CSNDSP), 177–182.

Chen, S., Sun, S., and Kang, S. (2020). System Integration of Terrestrial Mobile Communication and Satellite Communication——The Trends, Challenges and Key Technologies in B5G and 6G. China Commun., 156–171.

CrossRef Full Text | Google Scholar

Fu, G.-S., Phlypo, R., Li, M., Li, X.-L., and Adali, T. (2014). Blind Source Separation by Entropy Rate Minimization. IEEE Trans. Signal. Process. 62 (16), 4245–4255. doi:10.1109/tsp.2014.2333563

CrossRef Full Text | Google Scholar

Inan, H. A., and Erdogan, A. T. (2015). Convolutive Bounded Component Analysis Algorithms for Independent and Dependent Source Separation. IEEE Trans. Neural Netw. Learn. Syst. 26 (4), 697–708. doi:10.1109/tnnls.2014.2320817

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Wen., Zhao, Wei., Luo, Jia-Li., Wei, Si., and Zhen, Han. The Improvements of BP Neural Network Learning Algorithm. Proc. ICSP2000, 1647–1649.

Google Scholar

Kim, T., Attias, H. T., Lee, S.-Y., and Lee, T.-W. (2007). Blind Source Separation Exploiting Higher-Order Frequency Dependencies. IEEE Trans. Audio Speech Lang. Process. 15 (1), 70–79. doi:10.1109/tasl.2006.872618

CrossRef Full Text | Google Scholar

Kourogiorgas, C. I., Arapoglou, P., and Panagopoulos, A. D. (2015). Statistical Characterization of Adjacent Satellite Interference for Earth Stations on Mobile Platforms Operating at Ku and Ka Bands. IEEE Wireless Commun. Lett. 4 (No. 1), 82–85. doi:10.1109/lwc.2014.2374177

CrossRef Full Text | Google Scholar

Lahat, D., and Christian, J. (2016). An alternative proof for the identifiability of independent vector analysis using second order statistics[C]. ICASSP, Shanghai, 4363–4367.

Google Scholar

Lee, J.-H., Lee, T.-W., Jolesz, F. A., and Yoo, S.-S. (2008). Independent vector analysis (IVA): Multivariate approach for fMRI group study. Neuroimage 40 (1), 86–109. doi:10.1016/j.neuroimage.2007.11.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, C., Zhu, L., Luo, Z., and Zhang, Z. (20202020). “Solutions to Data Reception with Improve Blind Source Separation in Satellite Communications,” in IEEE International Symposium on Networks, Computers and Communications (ISNCC'20) (Montreal, Canada: IEEE), 1–5. doi:10.1109/isncc49221.2020.9297206

CrossRef Full Text | Google Scholar

Li, C. J., Zhu, L. D., and Zhang, Z. (2016). Non-orthogonal frequency hopping signal underdetermined blind source separation in time-frequency domain[J]. Infocommunications J. 8 (3), 1–7.

Google Scholar

Logeswari, G., Sangeetha, D., and Vaidehi, V. (2014). “A cost effective clustering based anonymization approach for storing phr in cloud[C],” in International Conference on Recent Trends (Sydney: Information Technology), 1–5.

Google Scholar

Loof, J. L., and Pratt, T. G. (2019). Blind Separation of Frequency-Hopped Signals Using a Space-Polarization Receiver. IEEE Signal. Process. Lett. 26 (No. 7), 1061–1064. doi:10.1109/lsp.2019.2918939

CrossRef Full Text | Google Scholar

Loof, J. L., and Pratt, T. G. (2019). Frequency-Hopped Signal Source Identification in Frequency-Selective Channels. IEEE Trans. Aerospace Electron. Syst. 55 (No. 6), 3316–3329.

CrossRef Full Text | Google Scholar

Meganem, I., Deville, Y., Hosseini, S., Deliot, P., and Briottet, X. (2014). Linear-Quadratic Blind Source Separation Using NMF to Unmix Urban Hyperspectral Images. IEEE Trans. Signal. Process. 62 (7), 1822–1833. doi:10.1109/tsp.2014.2306181

CrossRef Full Text | Google Scholar

Porter, R., Tadic, V., and Achim, A. (2014). Blind separation of sources with finite rate of innovation[C]. London: Signal Processing Conference (EUSIPCO), 136–140.

Reju, V. G., Soo Nqee Koh, S. N., and Ing Yann Soon, I. Y. (2010). Underdetermined Convolutive Blind Source Separation via Time-Frequency Masking. IEEE Trans. Audio Speech Lang. Process. 18 (1), 101–116. doi:10.1109/tasl.2009.2024380

CrossRef Full Text | Google Scholar

Robert, H., Zaragoza, M., and Lin, S. (1995). QPSK block-modulation codes for unequal error protection[J]. IEEE Trans. Inf. Theor. 41 (2), 576–581.

Google Scholar

Tai, W.-L., Chang, Y.-F., and Li, W.-H. (2017). An IoT notion-based authentication and key agreement scheme ensuring user anonymity for heterogeneous ad hoc wireless sensor networks. J. Inf. Security Appl. 34, 133–141. doi:10.1016/j.jisa.2017.04.002

CrossRef Full Text | Google Scholar

Wu, W., Feng, G., Li, Z., and Yuesheng, X. (2005). Deterministic Convergence of an Online Gradient Method for BP Neural, IEEE Transactions on Neural Networks. 16, 533–540. doi:10.1109/tnn.2005.844903

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., He, S., Xu, Y., Chen, L., and Ren, J. (2019). A trusted routing scheme using blockchain and reinforcement learning for wireless sensor networks. Sensors (Switzerland) 19, 4. doi:10.3390/s19040970

CrossRef Full Text | Google Scholar