
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Space Technol., 11 March 2021
Sec. Space Propulsion
Volume 2 - 2021 | https://doi.org/10.3389/frspt.2021.639819
This article provides the first results of a long-term study aimed at improving the validity of numerical modeling techniques for Electric Propulsion induced Spacecraft Charging using the Spacecraft Plasma Interaction System software. The preflight numerical model of the European Space Agency’s BepiColombo mission and its outputs are presented as a benchmark example of the present capabilities and limitations of the model. It is demonstrated that the code can obtain the spacecraft charging equilibrium by simulating the dynamic interactions between the electric propulsion system, the thruster-generated plasmas, and spacecraft systems exposed to space. The importance of including a physical description of the electron cooling in the freely expanding thruster plasmas is shown by comparing simulations with different polytropic indexes. It particularly highlights the inadequacy of treating the entire plasma as isothermal. The reported variability of the simulation outputs with numerical and physical parameters paves the way for future improvements in preflight design modeling and increased understanding of plasma thruster-induced charging processes through future comparison with available flight telemetries.
BepiColombo is an ESA/JAXA joint mission to Mercury, relying on solar electric propulsion and gravitational assists to reach its destination (Benkhoff et al., 2010). While Electric Propulsion (EP) acquired valuable heritage with deep space scientific missions (Deep Space 1, SMART-1, Hayabusa 1, Dawn, and Hayabusa 2) and through growing use on telecommunication satellites, the integration and operation of an EP system in conjunction with the host spacecraft remain a challenging task (Clark et al., 2019; Randall et al., 2019). There are numerous uncertainties associated with differences between flight and ground operations of an EP system due to an incomplete understanding of the interactions between the EP-generated plasma and the SpaceCraft (S/C). Ground test and qualifications campaigns of plasma thrusters carried out in vacuum chambers somewhat deviate from real flight conditions due to, for example, the nonnegligible chamber background pressure and the interactions of the thruster plume with the chamber walls. The thruster-spacecraft interactions are virtually impossible to fully reproduce on ground due to the physical scale of the system and the large mass-flow rate of high-power engines.
Because a thruster-generated plasma is a relatively dense and electrically active entity involved in complex surface interactions with the spacecraft, the operation of a plasma thruster is an important driver of the spacecraft electrostatic charging process. Unexpectedly high levels of charging leading to potentially damaging electrostatic parasitic discharges can compromise the nominal operation of a Solar Electric Propulsion System (SEPS) and the lifetime of its subsystems (Gollor, 2011). Therefore, design phases and test campaigns heavily rely on numerical simulations of both ground and flight operations of any EP system (Sarrailh et al., 2019). As a testimony to the unpredictability of EP-spacecraft interactions, the ESA SMART-1 technology demonstrator mission highlighted the unexpectedly strong role of the spacecraft solar arrays in the charging process. Its Hall Effect Thruster cathode formed a closed electrical loop with the solar array small biased conductors through the thruster plasma backflow, increasing the total current drawn from the cathode (Tajmar et al., 2009). These types of complex interactions are hard to predict and quantify and can compromise the success of a mission.
This article introduces and provides the first results of a long-term study of BepiColombo S/C charging aimed at improving the validity of numerical modeling techniques for Electric Propulsion induced by Spacecraft Charging using the Spacecraft Plasma Interaction System (SPIS) software. The preflight numerical model of the European Space Agency’s BepiColombo flight mission and its outputs are presented here as a benchmark example of the capabilities and limitations of the model, while a follow-up work will present new modeling improvements obtained with SPIS EP and validated through direct comparisons with flight telemetries. A detailed overview of BepiColombo and its EP system is given in Section 2 and the interactions between the thruster backflow plasma and the spacecraft are reviewed in Section 3 for future references. Section 4 details the SPIS software and the numerical model characteristics. Finally, results are presented and discussed in Section 5.
Three major stacked elements form the 6m × 3 m × 3m BepiColombo spacecraft. Shown as a schematic in Figure 1, the Mercury Transfer Module (MTM) hosts the SEPS, with the four T6 ion thrusters pointing along the +Z vector of the spacecraft reference frame. The MTM function is to transport BepiColombo’s two orbiters to Mercury: ESA’s Mercury Planetary Orbiter (MPO) and JAXA’s Mercury Magnetospheric Orbiter (MMO). The timeline of the mission major events is as follows: takeoff in October 2018, Earth flyby in April 2020, fist Venus flyby in October 2020, first Mercury flyby in October 2021, Mercury orbit insertion in December 2025, and end of nominal mission in May 2027. The cruise phase of the mission (2018–2025) is characterized by a succession of thrust arcs (SEPS on), coast arcs (SEPS off), and planetary gravitational assists until the MTM delivers the two orbiters to Mercury and retires on a solar orbit. For thermal mitigation, BepiColombo’s + Y vector will keep an angle relative to the Sun’s direction (the Solar Aspect Angle (SAA)) within
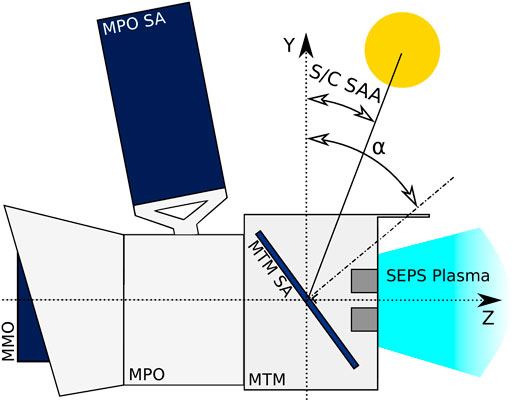
FIGURE 1. Sketch of BepiColombo in the YZ plane of the spacecraft reference frame and defined angles. The yellow disk represents the Sun, the dark gray squares two of the four T6 thrusters, while the dark blue areas are the solar cells-covered surfaces. The SEPS plasma expanding in space to generate thrust is indicated by the light blue region.
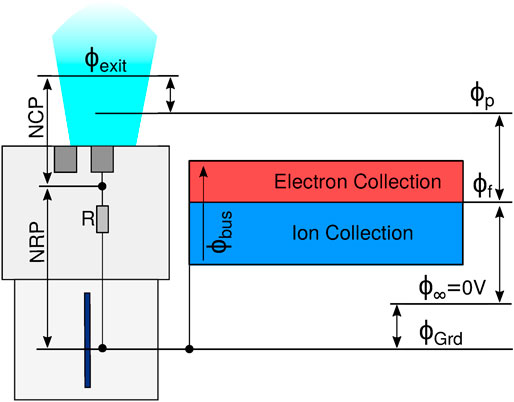
FIGURE 2. Relationships between the different potentials involved in the model. The red and blue regions depict the separation between electron and ion collecting areas of the MTM solar arrays. The NCP and NRP are the neutralizer coupling and reference potentials, respectively.
The two 14m long MTM solar arrays, supporting over 40m2 of solar cells, provide the power to operate the SEPS (≤11kW). They are located on the −X and +X sides of the spacecraft (see Figure 1) and are each made out of five panels. The solar cells are covered by radiation protecting dielectric coverglass and are connected in series through four small space-exposed conductive elements called interconnectors. They form strings of 40 cells oriented along the short edge of the SA, from a bus-bar connected to spacecraft ground to a bus-bar forming the high voltage terminal of the SA. All bus-bars run along the two long edges of the solar arrays, parallel to the X-axis of the spacecraft reference frame. Figure 3 shows a cropped section of a MTM solar panel, with the solar cells strings running vertically top to bottom from the grounded bus-bar to the high voltage bus-bar. The potential of the high voltage bus-bar is labeled
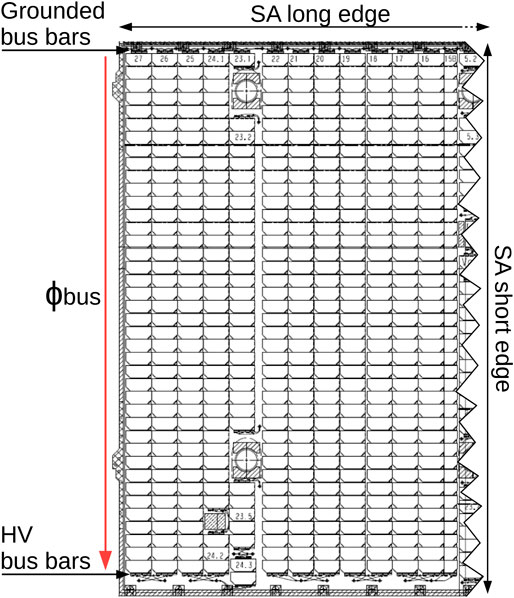
FIGURE 3. Cropped section of the photovoltaic assembly of a MTM solar panel showing main components.
While ideally the solar cells surface normal vector would keep SAA as close to
The SEPS comprises four T6 gridded ion engines, two Power Processing Units (PPU), and the flow control units. The PPU controls and distributes the power generated by the solar arrays to the thrusters subsystems. To avoid arcing damage to galvanic insulation within the PPU, the voltage between the PPU housing, which is tied to spacecraft ground, and the PPU low voltage return is constrained to be less than 50V. To guarantee this requirement, a clamping network made out of back-to-back clamping diodes mounted in parallel to a bleeder resistor R connects the low voltage return to the spacecraft ground; see Figure 4. To protect the diodes, the whole SEPS is switched off if the voltage across R exceeds
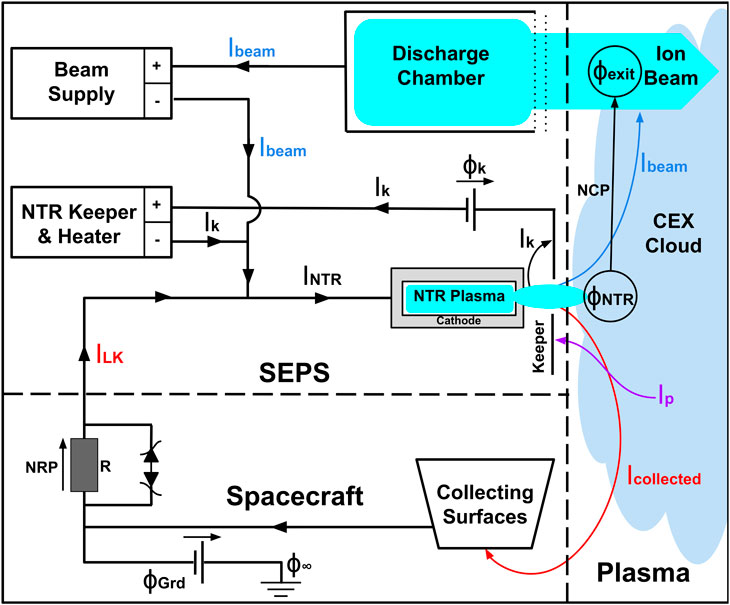
FIGURE 4. Electrical sketch of the SEPS. Current arrows represent electron flow and voltage arrows potential increase. The clamping network is composed of the bleeder resistor R and back-to-back diodes.
The T6 thruster was qualified for operation at 145mN, but its life-test was conducted at 125mN, the final nominal SEPS flight configuration (Randall et al., 2019). As the present model was made to verify the amplitude of R in the worst-case conditions, the simulations were run at 145mN. The T6 accelerates ionized xenon propellant from a discharge chamber through a potential gradient of 1850V between two grids and forms an ion beam of current
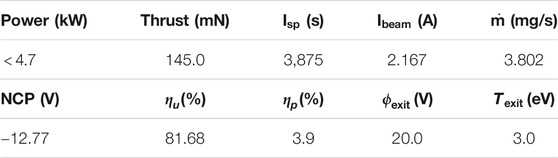
TABLE 1. T6 characteristics at full thrust in the BepiColombo flight qualification configuration.
An electron current equal to
The neutralizer plasma expands downstream of the keeper in a quasineutral spot-like plasma. A potential gradient, called the Neutralizer Coupling Potential (NCP), will form between the ion beam (of local plasma potential
An object immersed in plasma will acquire a floating potential
Focusing on the SEPS role first, the neutralizer will maintain the required negative NCP between the SEPS low voltage return and the beam plasma potential
The solar arrays are the main contributor to
The nature of the expected interactions between the thruster plasma and the spacecraft required the creation of a detailed geometric, physical, and electrical numerical model of BepiColombo, with sufficient spatial resolution over a simulation volume the scale of the spacecraft, with accurate reproduction of the plasma environment and electrical behaviors of the SEPS and the solar arrays. This is necessary for assisting mission design and improving incremental understanding of these phenomena.
The open-source simulation package SPIS is a 3D electrostatic solver based on a Particle-In-Cell approach to compute the main moments of the plasma populations’ distribution functions and solves the Vlasov Poisson system in the unstructured mesh volume surrounding a meshed spacecraft. In addition, it computes the potential distribution on the meshed spacecraft surfaces from the balance of collected and emitted plasma currents together with conducted currents through the different surface materials to spacecraft ground which are electrical coupled (circuit solver part). This code is designed to simulate spacecraft charging in various environments (low-Earth orbits, geostationary, etc.) and, more recently, during EP operations (Thiebault et al., 2015). The present work uses SPIS v5.2.4 coupled with the AISEPS package (Wartelski et al., 2013). Due to the complexity and dimensions of the system, the present model of BepiColombo employs the Particle-In-Cell (PIC) formalism with a few significant departures from the pure approach in order to accommodate computational resource limitations. Code particularities and details are hereby presented.
Due to the high plasma densities involved and the large computation volume, it is computationally too expensive to simulate every physical particle on a standard workstation. The PIC approach is employed instead to reduce the total number of particles by using macroparticles. Each macroparticle represents a great number of physical particles.
BepiColombo ion beam macroparticles,
The CEX ions macroparticles are created in the simulation volume through a Monte Carlo collision algorithm. A fast ion is changed into a slow charge-exchange ion at random neutral thermal velocity according to a collision probability function taking empirically determined cross-sections as argument (Miller et al., 2002). The two CEX collisions implemented in this model are as follows:
Since the resulting
In the classic PIC kinetic formalism, the tetrahedra composing the 3D mesh of the simulation domain need to be smaller than the local Debye length in order to resolve the sheaths and the electron dynamics. With submillimetric Debye lengths downstream of the thruster, respecting this condition in a simulation volume encapsulating BepiColombo would require an amount of memory exceeding available workstation capabilities. An alternative is to treat the neutralizer electrons as an isothermal fluid population whose density over the simulation mesh is determined by the local plasma potential according to Boltzmann’s relation:
where e is the elementary charge,
where C is a constant and γ is the polytropic index, with
To obtain the plasma potential in the simulation volume, the usual PIC approach is to solve Poisson’s equation:
where
This method gives the local plasma potential as an explicit law of the local ion density everywhere in the domain. In the isothermal case, the equivalent approach is to invert Boltzmann’s relation Eq. 1 with the quasineutral assumption to determine
The electron temperature variation is obtained by replacing the constant in Eq. 2 with the thruster reference values:
Measurements in space and laboratories report
Figure 5 displays
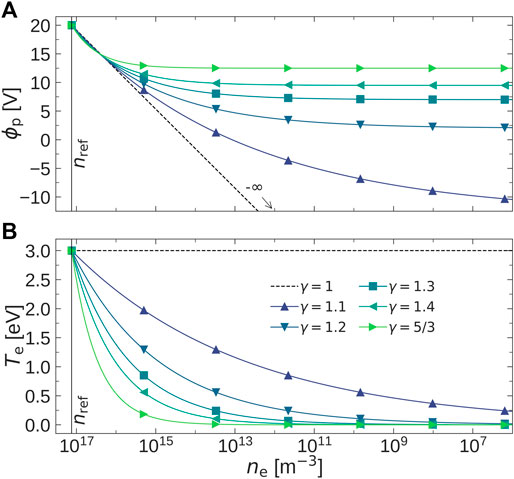
FIGURE 5. (A) Plasma potential
To reproduce the spacecraft-plasma coupling through current collection and emission, the numerical model needs to include the electrical properties of the surface materials. As a trade-off between detailed surfaces and numerical mesh density, each spacecraft surface is represented by its external surface coating material and is included in the model as a macroscopic electrical node. SPIS allows the definition of the material electric and physical properties such as surface and bulk conductivity, electron and protons induced secondary electron emission, and photoemission yields (for the main ones). Each surface node is linked to the spacecraft ground through an equivalent RC electrical circuit. Differential charging occurring between dielectric surfaces and the S/C ground is computed, accounting for dielectric thicknesses and surface and volume conductivity. Sources representing thrusters and neutralizers can also be linked to the circuit solver. A source can either be a physical source for which an actual PIC population emission in the volume draws a corresponding current from the circuit or a virtual source that only draws a current but does not generate macroparticles.
Since the quasineutrality assumption precludes reproducing the sheaths, the electron flux to the spacecraft surfaces is calculated using the following electron collection model:
where
BepiColombo surfaces are made from a variety of materials to meet the mission thermal requirements and to mitigate differential charging. The present model includes 20 different materials, corresponding to 20 different nodes in the circuit solver. In Figure 6, each color represents a different node/material.
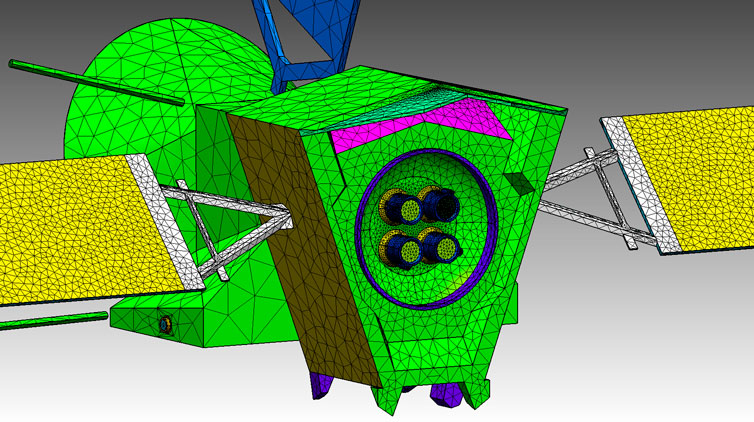
FIGURE 6. Section of BepiColombo geometrical model, showing the thruster bay with the local mesh refinements. Each color corresponds to a different material and electrical node.
Simulating the real coupling between the neutralizer plasma and the ion beam is beyond the capabilities of the present model due to the use of the quasineutral solver. To reproduce the impact of the NCP on spacecraft charging, the alternative was to define an equivalent virtual SEPS in the electrical circuit. This virtual source reproduces the total net current draw of the entire SEPS (see the corresponding dashed rectangle in Figure 4), i.e.,
Due to the interconnectors and bus-bars small dimensions and large number, their reproducing in the spacecraft geometrical model is not possible. Likewise, simulating their complex interactions with the CEX plasma, solar wind, and radiation is beyond the capabilities of SPIS. Instead, the AISEPS package implemented a simplistic approach to the interconnector plasma collection processes based on the following strong assumption: owing to the interconnectors small size, their potentials are shielded by the surrounding coverglasses and are not perceived by the bulk plasma flowing toward the solar cells. Only once inside the coverglass sheath can the plasma feel the interconnector potentials. As a result, the solar cells side of the solar array is simplified as a being entirely made out of coverglass, visible in yellow in Figure 6. Being a dielectric, the coverglass develops local differential surface potentials during plasma collection. The interconnectors potential distribution from
The outputs of the simulations are presented here to highlight the effects of the model specificity and their impact on the charging of BepiColombo. The potential for improving key aspects of the numerical modeling of electric propulsion-spacecraft charging through calibration with flight telemetries and future code improvements are discussed. This is the first step toward a more comprehensive in-flight characterization and description of the behavior of electrical thruster plumes in space. Presented results are from simulations ran at 145mN and with
The thruster ions (
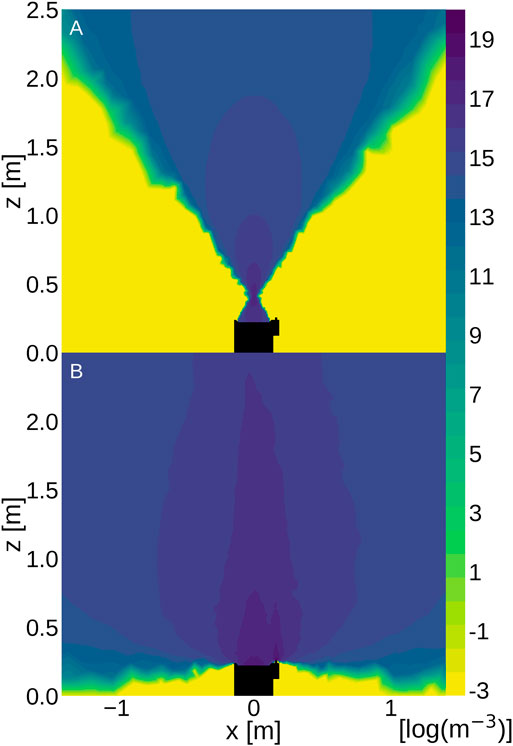
FIGURE 7. Density mappings at full thrust of (A) the total ion beam
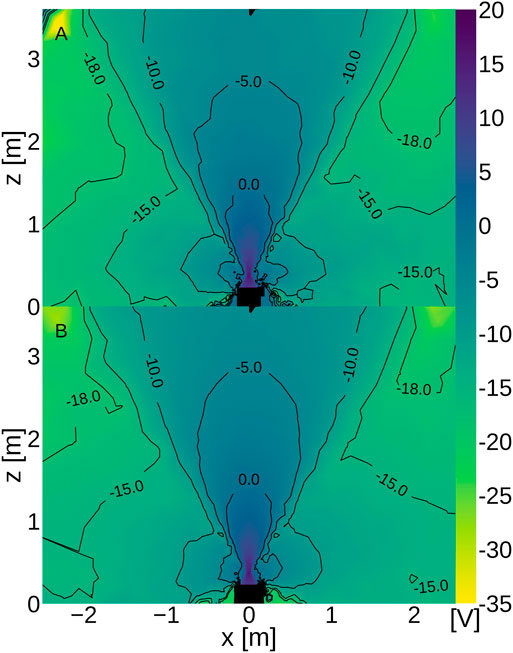
FIGURE 8. Plasma potential mapping downstream of the T6 thruster in the isothermal case calculated with (A) the quasineutral solver and (B) the Poisson solver, with
Figures 9, 10 display the entire simulation volume for the distribution of the total plasma density (ion beam + CEX) and plasma potential, respectively, for

FIGURE 9. Mapping of the plasma density around BepiColombo in the XZ plane for an arbitrary fixed spacecraft ground
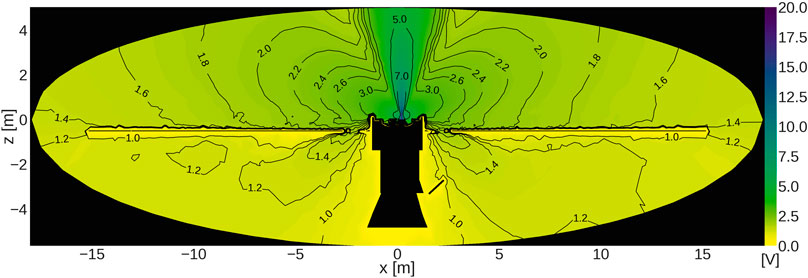
FIGURE 10. XZ mapping of the plasma potential around BepiColombo, for the same conditions as Figure 9. The plasma potential stays positive everywhere in the volume, as expected.
Taking the plasma densities right over the MTM solar arrays from Figure 9 and the corresponding electron temperatures (no reported here), the Debye sheath thicknesses at these locations range inside
In Figure 9, the CEX could reach every corner of the simulation volume as expected. The characteristic CEX side lobes are clearly visible, and it is interesting to notice how the CEX ions develop backward lobes through the yokes of the MTM solar arrays, for
The simplifications and uncertainties of the BepiColombo model have various impacts on spacecraft charging. The extend of these impacts will be covered in the following study in which the in-flight SEPS telemetries will serve as calibration data for the numerical model, allowing new refinements and consequently increasing the reliability and confidence in preflight simulation of SEPS-induced charging. To illustrate the interest of such a process, the impact of the value of γ on the equilibrium electrostatic charging of BepiColombo is reported in Figure 11. In this figure and Figure 12, each data point is an average on the ten last simulation time-steps once equilibrium was reached. The plain lines connecting data points serve as a visualization guide. The standard deviation from the mean is shown as red vertical error bars. In most cases, the error bars are smaller than the marker size. In Figure 11, BepiColombo’s frame potential

FIGURE 11. Influence of γ on four simulation outputs of interest, for the input parameters of Table 1 and
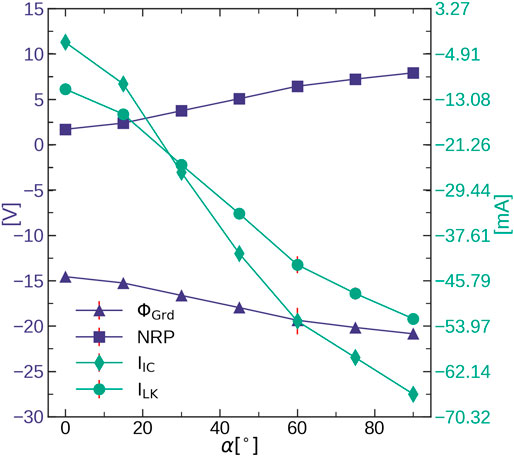
FIGURE 12. Influence of the MTM solar arrays angle α on the four simulation outputs, for
SMART-1 flight telemetries showed a cyclic variation of the spacecraft ground potential coinciding with the spacecraft orbital period. Numerical modeling allowed to attribute these variations to the rotation of the spacecraft solar arrays as in order to keep a constant SAA along the orbit, their α was varying accordingly (Tajmar et al., 2009). This change in α meant that the solar arrays interconnectors were exposed to regions of the CEX backflow plasma of varying density and temperature. Figure 12 shows that for fixed simulation inputs, a similar dependency between the interconnectors collected current (and therefore with
BepiColombo’s seven years trip to Mercury presents a unique opportunity to improve current modeling and understanding of spacecraft charging induced by the operation of a SEPS thanks to soon-to-be available flight telemetries.
Upon creating a numerical representation of the T6 thruster plasma plume reproducing ground measured plume properties, the charge-exchange collisions generate a low-energy backflow plasma, which contacts all space-exposed surfaces by following plasma potential gradients down to the negatively charged spacecraft. Due to the electrostatic nature of this diffusion, establishing physically sound plasma potentials in the simulation volume is key to obtaining a self-consistent spacecraft charging process. While the erroneous isothermal assumption leads to nonphysical and unusable results, a polytropic process with
The strong influence of some of the model numerical and physical parameters on the simulations’ outputs, such as the NRP, demonstrates how the flight telemetries of BepiColombo will allow validating and improving the new electron cooling algorithms, plasma potential solver, and interconnectors model included in the latest version of SPIS. This will in turn help improve preflight assessments of EP-induced charging and will provide invaluable insight into the variability of SEPS operation in space compared to on-ground.
The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.
This work has been conducted by FF as part of an ESA Young Graduate Traineeship initiated and supervised by OS. FC brought expertise on numerical simulation aspect (SPIS) and CC on plasma physics and electric propulsion.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frspt.2021.639819/full#supplementary-material.
SEPS Solar electric propulsion system
SPIS Spacecraft plasma interaction system
MTM Mercury transfer module
SA Solar array
SAA Solar aspect angle
NRP Neutralizer reference potential
NCP Neutralizer coupling potential
CEX Charge-exchange
Ibeam Ion beam current
IIC Current collected by the interconnectors
ILK Leakage current through the bleeder resistor;
α MTM solar array rotation angle
γ Polytropic index
Barouch, E. (1977). Properties of the solar wind at 0.3AU inferred from measurements at 1AU. J. Geophys. Res. 82, 1493–1502. doi:10.1029/JA082i010p01493
Benkhoff, J., Van Casteren, J., Hayakawa, H., Fujimoto, M., Laakso, H., Novara, M., et al. (2010). BepiColombo-Comprehensive exploration of Mercury: mission overview and science goals. Planet. Space Sci. 58, 2–20. doi:10.1016/j.pss.2009.09.020
Clark, S., Randall, P., Lewis, R., Marangone, D., Goebel, D., Chaplin, V., et al. (2019). “BepiColombo–solar electric propulsion system test and qualification approach”. in Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 September, 2019, 1–20.
Dannenmayer, K., and Mazouffre, S. (2013). Electron flow properties in the far-field plume of a Hall thruster. Plasma Sourc. Sci. Technol. 22, 035004. doi:10.1088/0963-0252/22/3/035004
Ferguson, D., and Hillard, G. (1995). Space measurement of electron current collection by space station solar arrays. AIAA Paper 1995-0486. doi:10.2514/6.1995-486
Fujii, H., and Abe, T. (2003). Current collection and discharges on high voltage solar array for space use in plasma. IEEE Trans. Plasma Sci. 31, 1001–1005. doi:10.1109/TPS.2003.818448
Goebel, D. M., and Katz, I. (2008). Fundamentals of electric propulsion: ion and Hall thrusters. New York, NY: John Wiley & Sons, 19–136. doi:10.1002/9780470436448
Gollor, M. (2011). Accommodation aspects of electric propulsion with power processing units and the spacecraft. AIAA Paper 2011-5651. doi:10.2514/6.2011-5651
Hastings, D. E., and Chang, P. (1989). The physics of positively biased conductors surrounded by dielectrics in contact with a plasma. Phys. Fluids B: Plasma Phys. 1, 1123–1132. doi:10.1063/1.858982
Hu, Y., and Wang, J. (2017). Fully kinetic simulations of collisionless, mesothermal plasma emission: macroscopic plume structure and microscopic electron characteristics. Phys. Plasmas. 24, 033510. doi:10.1063/1.4978484
Lai, S. T. (2011). Fundamentals of spacecraft charging: spacecraft interactions with space plasmas. Princeton, NJ: Princeton University Press, 53. doi:10.2307/j.ctvcm4j2n
Lieberman, M. A., and Lichtenberg, A. J. (2005). Principles of plasma discharges and materials processing. New York, NY: John Wiley & Sons, 165–206. doi:10.1002/0471724254
Markelov, G., and Gengembre, E. (2006). Modeling of plasma flow around SMART-1 spacecraft. IEEE Trans. Plasma Sci. 34, 2166–2175. doi:10.1109/TPS.2006.879098
Merino, M., Fajardo, P., Giono, G., Ivchenko, N., Gudmundsson, J.-T., Mazouffre, S., et al. (2020). Collisionless electron cooling in a plasma thruster plume: experimental validation of a kinetic model. Plasma Sourc. Sci. Technol. 29, 035029. doi:10.1088/1361-6595/ab7088
Miller, J. S., Pullins, S. H., Levandier, D. J., Chiu, Y.-h., and Dressler, R. A. (2002). Xenon charge exchange cross sections for electrostatic thruster models. J. Appl. Phys. 91, 984–991. doi:10.1063/1.1426246
Nakles, M. R., Brieda, L., Reed, G. D., Hargus, W., and Spicer, R. L. (2007). Experimental and numerical examination of the BHT-200 Hall thruster plume. AIAA Paper 2007-5305. doi:10.2514/6.2007-5305
Randall, P., Lewis, R., Clark, S., Chan, K., Gray, H., Striedter, F., et al. (2019). “BepiColombo–MEPS commissioning activities and T6 ion thruster performance during early mission operations”. in Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, September 15–20, 2019, 1–16.
Sarrailh, P., Hess, S., Villemant, M., and Mateo-Velez, J. (2019). “Simulation of plasma plume experiments with Hall Thrusters: on-ground chamber effects on measurements and extrapolation to in-flight situation”. in Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, September 15–20, 2019, 1–10.
Snyder, J., Goebel, D. M., Hofer, R. R., Polk, J. E., Wallace, N. C., and Simpson, H. (2012). Performance evaluation of the T6 ion engine. J. Propulsion Power. 28, 371–379. doi:10.2514/1.B34173
Tajmar, M., Gonzalez, J., Estublier, D., and Saccoccia, G. (2000). “Modelling and experimental verification of Hall and ion thrusters at ESTEC”. in Proceedings of the Third International Conference on Spacecraft Propulsion. Cannes, France, December 4–8, 2017. 683.
Tajmar, M., Sedmik, R., and Scharlemann, C. (2009). Numerical simulation of SMART-1 Hall-thruster plasma interactions. J. Propulsion Power. 25, 1178–1188. doi:10.2514/1.36654
Thiebault, B., Jeanty-Ruard, B., Souquet, P., Forest, J., Mateo-Velez, J.-C., Sarrailh, P., et al. (2015). SPIS 5.1: an innovative approach for spacecraft plasma modeling. IEEE Trans. Plasma Sci. 43, 2782–2788. doi:10.1109/TPS.2015.2425300
Keywords: electric propulsion, spacecraft charging, numerical modeling, plasma, electron cooling, solar array plasma interactions
Citation: Filleul F, Sutherland O, Cipriani F and Charles C (2021) BepiColombo: A Platform for Improving Modeling of Electric Propulsion-Spacecraft Interactions. Front. Space Technol. 2:639819. doi: 10.3389/frspt.2021.639819
Received: 09 December 2020; Accepted: 20 January 2021;
Published: 11 March 2021.
Edited by:
Stéphane Mazouffre, Center National de la Recherche Scientifique (CNRS), FranceReviewed by:
Laurent Garrigues, UMR5213 Laboratoire Plasma et Conversion d’Energie (LAPLACE), FranceCopyright © 2021 Filleul, Sutherland, Cipriani and Charles. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Félicien Filleul, ZmVsaWNpZW4uZmlsbGV1bEBhdWNrbGFuZC5hYy5ueg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.