Critical bifurcations in deformable membrane necks under inhomogeneous curvature: constriction frustration vs. abscissional elongation

Catenoid necks, as minimal surfaces with zero mean curvature $(K=0)$, minimize bending energy and serve as geometric scaffolds for scissional membrane remodeling. We apply the Canham–Helfrich model of flexible membranes to analyze deformable spontaneous curvature $(K_0)$, a key regulator of membrane scission events in cellular compartmentalization. To model functional membrane necking, we examine deformed catenoidal shapes with variable mean curvature $(\delta K\ne 0)$ near the minimal-energy catenoid $(K=0)$, which varies along either the constrictional or elongational pathways. Using the Euler–Lagrange equilibrium equations, we derive inhomogeneous catenoid solutions, revealing metastable singularities departing from the critical catenoid of the maximal area—a tipping point (TP) for scission. Using functional second-derivative analysis, we further examine how inhomogeneous $K_0$ affects stability. The transition between frustrated constriction and abscissional elongation is numerically analyzed through conformal solutions to the governing inhomogeneous $K_0-$ field.

1 Introduction

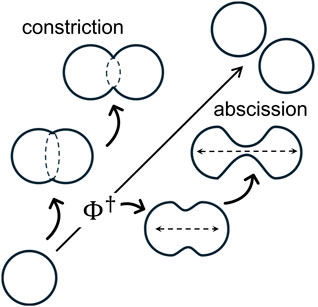
Necking processes—crucial for membrane compartmentalization—are essential to cell physiology (Morgan, 2007). Scissional pathways involve cytokinetically controlled membrane remodeling, forming cellular compartments connected by deformable necks (Morgan, 2007; Moeendarbary and Harris, 2014; McMahon and Gallop, 2005). Necking mechanisms operate within conserved membrane geometries across diverse organisms, guided by biophysical constraints (Burton and Taylor, 1997; Kozlov et al., 2014; Carlton et al., 2020; Banani et al., 2016; Westermann, 2010; Frolov et al., 2000). Mechanobiological inhomogeneities are key regulators of membrane neck remodeling across all life domains (Morgan, 2007; Moeendarbary and Harris, 2014; Burton and Taylor, 1997; Frolov et al., 2000). For instance, cell division (Carlton et al., 2020), membrane budding (Kozlov et al., 2014; Chan et al., 2022), endocytosis (Kozlov et al., 2014), organelle dynamics (Carlton et al., 2020; Westermann, 2010), and endomembrane trafficking (Banani et al., 2016) all rely on the functional regulation of membrane necks under mechanobiological control (Fletcher and Mullins, 2010; Eyckmans et al., 2011; Wang and Thampatty, 2006). Understanding inhomogeneous membrane remodeling is key to revealing how necking forces drive shape-regulatory physiological mechanisms (Chan et al., 2022). For instance, scissional motor proteins, including prokaryotic FtsZ (Margolin, 2005; Bisson-Filho et al., 2017), eukaryotic actomyosin (Rosenthal, 2017; Yano et al., 1982), and dynamin (Cooke, 1995; Ferguson et al., 2012; Hinshaw and Schmid, 1995), are known to drive radial forces through mechanical anisotropies in a constriction ring (Thanedar and Margolin, 2004; Mingorance et al., 2010; Ramirez-Diaz et al., 2021; Murrell et al., 2015; Kruse et al., 2024; Zhang et al., 2020; Antonny et al., 2016). In contrast, the mitotic spindle, a bipolar microtubule-based structure, directs abscissional axial stretching (Prosser and Pelletier, 2017; Mitchison and Salmon, 2001), ensuring proper segregation into daughter cells (Pavin and Tolić, 2016; McIntosh et al., 2012). In synthetic cell biology (Szostak et al., 2001; Blain and Szostak, 2014) and soft-active matter research (Ramaswamy, 2010; Palacci et al., 2013; Guillamat et al., 2016), lipid model membranes are widely used to reconstitute cytokinetic engines (Szostak et al., 2001), mimicking mechanobiological inhomogeneities (Osawa et al., 2008; Hutchison et al., 2016; López-Montero et al., 2012; López-Montero et al., 2013). Membrane microsystems provide insights into functionally inhomogeneous pre-scissional states, such as equatorial ring constriction (Osawa et al., 2008) and axially polarized neck elongation (Hutchison et al., 2016), both of which contribute to membrane scission in synthetic cells engineered for cytokinesis (Blain and Szostak, 2014). Figure 1 illustrates possible necking mechanisms leading to scission during membrane bending and compartment remodeling. While these membrane-bending mechanisms require energy for deformation, a tipping point (TP) determines the irreversible pathway toward final scission.

Figure 1

Figure 1. Membrane necking processes energetically regulated along curvature-bending pathways (catenoid-like) toward divisional scission. High-energy furrow constrictions contrast with abscissional elongational necks emerging during the energetically uphill process of membrane remodeling. Mechanical bifurcations may arise along these pathways, favoring one outcome over another at a critical tipping point $({\mathrm{\Phi }}^{†})$ and stabilizing topological change (divisional Goldstein terminus) through spontaneous abscission.

Theoretically, membrane inhomogeneity induces mechanical anisotropies in spontaneous curvature $(K_0)$ and surface tension $(\sigma )$ (Barrio et al., 2020; Salinas-Almaguer et al., 2022; Beltrán-Heredia et al., 2017; Horger et al., 2010), both of which are modulated by microphysical internal stresses under bending rigidity (Jülicher and Seifert, 1994; Reinhard, 2014; Seguin and Fried, 2014). Biology-inspired physical models of membrane remodeling highlight the mechanical coupling between $K_0$ and $\sigma$ (Beltrán-Heredia et al., 2017; Jülicher and Seifert, 1994; Erickson, 2009). They often recapitulate necking energy in catenoidal manifolds, which naturally minimize membrane energy—referred to as $\mathrm{\Phi }(K_0,\sigma )$. Catenoidal necks, as minimal surfaces with near-zero mean curvature $(K\approx 0)$, minimize membrane energy under boundary constraints (Spivak, 1979). These minimal-energy scaffolds enable stable neck-shaping pathways (Jia et al., 2021; Walzel et al., 2022), where inhomogeneous $K_0$ and $\sigma$ drive transitions toward regulated scission (Frolov et al., 2000; Santiago and Monroy, 2023). Rigid catenoid configurations $({\mathrm{\Phi }}_R)$ represent minimal energy necks with zero mean curvature $(K=0)$, dominated by Gaussian curvature $({\mathcal{K}}_{\mathcal{G}})$ injected from the boundaries (Santiago and Monroy, 2023; Durand, 1981; Chabanon and Rangamani, 2018). Under spontaneous curvature $K_0(\sigma )$, ${\mathrm{\Phi }}_R-$ surfaces present two extremal solutions with distinct stability (Spivak, 1979; Walzel et al., 2022): ${\mathrm{\Phi }}_0(K_0=0)$, the stable minimal-area solution, and ${\mathrm{\Phi }}^{†}(K_0\ne 0)$, a metastable critical catenoid that maximizes area (Sagan, 1992). As supercritical necks stretch, they gain stability beyond ${\mathrm{\Phi }}^{†}$, resulting in spontaneous abscission. Once ${\mathrm{\Phi }}^{†}$ is overpassed, further neck elongation induces a topological scission event, leading to the well-known Goldschmidt solution (Sagan, 1992) (see Figure 1). More specifically, the critical catenoid ${\mathrm{\Phi }}^{†}$ represents an abscission-like geometry where the supporting membrane neck reaches its maximum permissible size (Durand, 1981; Chabanon and Rangamani, 2018), which leads to a critical “tipping point” determinant for spontaneous scission (Santiago and Monroy, 2023). Hence, we analyze how mechanical gradients of membrane tension and spontaneous curvature govern neck flexibility beyond the rigid catenoid geometry. ${\mathrm{\Phi }}^{†}$ separates subcritical constricted necks of minimal area $(A_0)$ from supercritical tubular configurations of maximized area $(A_{\mathit{max}}>A_0)$, thus playing a key geometric role in balancing curvatures at a transitional bifurcation (Santiago and Monroy, 2023). Once geometrically softened, the ${\mathrm{\Phi }}^{†}-$ critical trade-off can exert abscission control, depending on coordinated curvature–composition adjustments under mechanical spontaneity (Jia et al., 2021; Walzel et al., 2022).

In this work, we investigate whether optimal abscission mechanics stem solely from rigid catenoidal neck geometry or depend on curvature-bending deformability factors, $K(\mathrm{\Phi })$, such as necking elasticity driven by spontaneous curvature $(K_0)$; in general, $K(\mathrm{\Phi })$ denotes a constitutional status shaping the neck’s curvature deformations (Durand, 1981). Using a deformable catenoidal manifold under the Canham–Helfrich Hamiltonian (Jülicher and Seifert, 1994; Santiago and Monroy, 2023), we will analyze $K_0-$ perturbed catenoid configurations, $\mathrm{\Phi }\approx {\mathrm{\Phi }}_R+\alpha {\mathrm{\Phi }}_D$, near the organizing ${\mathrm{\Phi }}^{†}-$criticality. Henceforth, the small deformation parameter, $\alpha \propto \mathrm{\Phi }-{\mathrm{\Phi }}^{†}\propto \delta K$, defines the perturbation series as adaptable curvature changes lead to optimized necking $(\delta K\ne 0)$. In a previous paper, the curvature–elasticity coupling was demonstrated to cause configurational bifurcation into two critical branches separated by an energy barrier (Santiago and Monroy, 2023); they evolved from subcritical ring-like constrictional furrows to supercritical elongated forms, passing through the critical abscissional status $({\mathrm{\Phi }}^{†})$ (Santiago and Monroy, 2023). In this study, by analyzing inhomogeneous necking pathways in deformable catenoids $({\mathrm{\Phi }}_D)$ or $D-$ catenoids, we identify the abscissional tipping point, which is closely linked to the critical ${\mathrm{\Phi }}^{†}$-catenoid, as a milestone for spontaneous scission under curvature perturbations $(\delta K\ne 0)$. This deformable state undergoes sharp changes in spontaneous curvature near criticality while minimizing the expenditure of bending free energy (first-order energy variation). In addition, mechanical stability requires inhomogeneous $K_0$ to be concave upon all of its independent variables (second-order variation) (Walzel et al., 2022; Chabanon and Rangamani, 2018). Our findings highlight the energy regulation between catenoidal neck deformation and inhomogeneous force distribution required for efficient scission.

2 Methods

2.1 Elastostatic forces: elongational stress and constrictional torque

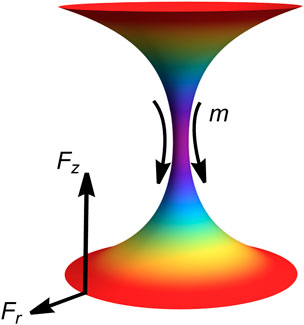
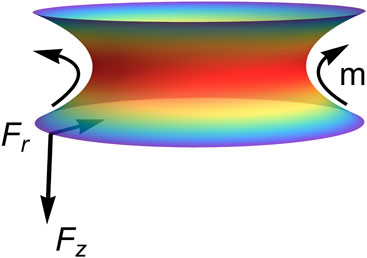
In addition to a continuum description, the system is modeled as two charged particles interacting within the inhomogeneous necking field (Santiago and Monroy, 2023; Santiago and Monroy, 2020). Figure 2 depicts the lower edge of an abscissional neck acting as a “south pole” particle exerting an elongational axial force, while the upper edge behaves as a “north pole” particle sensing this repulsive force (corresponding to the neck-connected compartment formed during abscission).

Figure 2

Figure 2. Repulsive elongational catenoid configuration. Abscissional shape in the supercritical regime with border radii $\bar{R}=3$, equatorial waist radius ${\bar{R}}_0\approx 0.2$, length $\bar{h}\approx 2.26$, and area $\bar{A}\approx 1.25$. Radial force $F_r$ and the axial force $F_z$ that act on the southern border in the case of a highly tubular-shaped membrane. Both of them are positive, while the local shaping torque $m$ (negative) is also shown. It is 0 on the borders and has the maximum negative intensity at the equatorial waist. The concave configuration of spontaneous curvature, ${\nabla }^2{K}_0<0$, with the minimal value at the neck waist (colored in blue), results in mechanical stability.

On one hand, Figure 2 presents tubular solutions (supercritical), where negative tube-shaping torque $(m<0)$ is associated with a predominantly concave spontaneous curvature (${\nabla }^2{K}_0<0$; stable). Radial and axial tensions are positive therein ($F_r>0$ and $F_z>0$), indicating effectively repulsive abscissional forces in each hemi-neck $(\nabla K_0>0)$. These elongational forces represent stable membrane flows of spontaneous curvature driven from the neck waist toward the bounding compartments. On the other hand, Figure 3 illustrates ring-like solutions (sub-critical), where positive neck-shaping torque $(m>0)$ arises from a predominantly convex spontaneous curvature (${\nabla }^2{K}_0<0$; unstable). Both radial $(F_r<0)$ and axial $(F_z<0)$ tensions are negative, reflecting attractive edge forces driven by constrictional gradients ($\nabla K_0<0$ in each hemi-neck). In biological cells, they represent constrictive flows shaping the waist ring from an internal divisional apparatus.

Figure 3

Figure 3. Attractive constrictive catenoid configuration. Constrictional membrane neck with boundary radii $\bar{R}=3$, equatorial waist radius ${\bar{R}}_0\approx 1.95$, length $\bar{h}\approx 0.66$, and area $\bar{A}\approx 0.80$. Schematic representation of the radial force $F_r$ and axial force $F_z$ that act as driving flows on the southern border in the case of a highly constricted membrane. The local constrictional shaping torque $m$ (positive) is also shown as being maximal at the equatorial waist. The convex configuration of spontaneous curvature, ${\nabla }^2{K}_0>0$, with the maximal value at the neck waist (colored in red), results in mechanical instability.

These elastostatic (virtual) charges interact with each other—either repulsively (elongation; Figure 2) or attractively (constriction; Figure 3)—through a flexible geometry influenced by a $K_0$-driven stress field that generates charges at the edge boundaries (Santiago and Monroy, 2023). Necking shape emerges from the catenoid-conformal field symmetry driven by an inhomogeneous $K_0$-elasticity Hamiltonian (Canham–Helfrich type). In mechanical terms, the south particle experiences necking stress, $\mathbf{\Sigma }$, exerted by the north particle through the inhomogeneous spontaneous curvature’s field $(K_0)$ under membrane energy density $(\sigma )$. The neck-shaping stress, $\mathbf{\Sigma }=A^{-1}(F_z,F_r)$, arises from axial tension, $F_z=\partial \sigma /\partial z$, and radial tension, $F_r=\partial \sigma /\partial r$, both generating a local necking torque, $\mathbf{m}\equiv \mathbf{\Sigma }\times \mathbf{R}$ ($A=\pi R^2$ represents the edge area where necking tensions apply). We depict these interactions on both sides of the critical catenoidal bifurcation (see Figures 2, 3). Therefore, we explore membrane abscission in critical catenoid necks that are weakly perturbed from mechanical equilibrium, focusing on elongational abscissional pathways compared to constrictional configurations. Hence, curvature-conformal necking distributions are analyzed in relation to external deformation stresses.

2.2 Necking Canham–Helfrich Hamiltonian: inhomogeneous shape equation

The starting point for calculating necking forces is the generalized Canham–Helfrich energy functional (Canham, 1970; Helfrich, 1973):

$\mathcal{H}=\frac{\kappa }{2}\int dA{\left(K-K_0\right)}^2+\int dA\sigma +{\kappa }_G\int dA{\mathcal{K}}_G,(1)$

where spontaneous curvature $(K_0)$ and surface tension $(\sigma )$ are defined to be inhomogeneous functions across the necking membrane.

The first term represents the bending energy, where $K\equiv 2H$ relates the extrinsic curvature $(K)$ with the mean curvature $(H)$ under homogeneous bending rigidity $(\kappa )$, which is considered constant across the membrane. The second term accounts for the surface energy due to the necking area $(A)$, with the surface tension $(\sigma )$ considered an inhomogeneous Lagrange multiplier. The third term fixes the Gaussian curvature $({\mathcal{K}}_G)$, where a constant saddle-splay modulus $({\kappa }_G)$ is assumed as a homogeneous parameter imposed from the neck boundaries (Capovilla et al., 2002). The CH model describes membranes as effective two-dimensional fluids, averaging microscopic interactions into globally homogeneous elasticity $\kappa$ and ${\kappa }_G$ (Helfrich, 1973; Zhong-Can and Helfrich, 1989). Due to lateral membrane fluidity, global rigidities remain homogeneous (i.e., $\kappa$ and ${\kappa }_G$ are constant) (Helfrich, 1973). In other words, the scalar free energy functional (CH) depends only on the membrane’s instantaneous geometry, with no memory of past deformations (Deserno, 2015). The energy first-variation delivers the Euler–Lagrange derivatives along the normal and longitudinal direction (Zhong-Can and Helfrich, 1989) and the boundary terms arising from the CH response of the elastic membrane projected on the edge boundaries (Capovilla et al., 2002). Under energy minimization from the generalized CH functional in Equation 1 $(\delta \mathcal{H}=0)$, the well-known shape equation is given as follows (Zhong-Can and Helfrich, 1989):

$\begin{array}{ccc}\hfill & -\hfill & \kappa {\nabla }^2\left(K-K_0\right)-\frac{\kappa }{2}\left(K-K_0\right)\left[K\left(K+K_0\right)-4{\mathcal{K}}_G\right]\hfill \\ \hfill & +\hfill & \sigma K=\mathrm{\Delta }P,\hfill \end{array}(2)$

where $\mathrm{\Delta }P$ represents the normal pressure decrease across the membrane. For an open neck that connects two separated compartments, $\mathrm{\Delta }P=0$.

The inhomogeneous shape equation in Equation 2 arises as the transverse Euler–Lagrange minimizer (Santiago and Monroy, 2023), where $K_0$ and $\sigma$ vary along the membrane coordinate. The bending rigidity $(\kappa )$ remains constant, representing isotropic fluid forces distributed in-plane along the membrane neck (Helfrich, 1973).

2.3 Membrane inhomogeneity: longitudinal membrane tension–spontaneous curvature connection

Additionally, we derive a key inhomogeneity relationship connecting changes in spontaneous curvature, $K_0$, with the necking force generator $\sigma$; this is given as follows (Santiago and Monroy, 2023):

${\partial }_a\sigma =\kappa \left(K-K_0\right){\partial }_a{K}_0,(3)$

where $({\partial }_a)$ represents the covariant derivatives, linking the spatial dependence of the two compositional fields ($K_0$ and $\sigma$), both modulated upon extrinsic curvature $(K)$ ($a$ refers to a generalized membrane coordinate). If $K_0$ is constant, $\sigma$ must also be constant, recovering the well-known homogeneous equilibrium condition (Zhong-Can and Helfrich, 1989).

The membrane in-plane inhomogeneity stated in Equation 3 arises from Euler–Lagrange longitudinal minimization (Santiago and Monroy, 2023), where $K_0(a)$ and $\sigma (a)$ co-vary together with local bending curvature stress. The curvature spontaneously imposed by the $K_0-$ field reflects fluid lateral forces distributed inhomogeneously along the membrane neck area $(A)$, while membrane tension enforces area conservation (Reinhard, 2014). Unlike thermodynamic surface tension $(\gamma )$, which represents positive surface energy per unit area ($A_0$, the reference area of a tensionless membrane), the mechanical membrane tension can be either negative in floppy membranes connected to membrane reservoirs $(\sigma <0)$ or positive when stretched ($\sigma =\gamma +K_A(A-A_0)/A_0$, with $K_A$ being the compressibility modulus). $K_0$ and excess tension, $\sigma -\gamma$, are intrinsically linked through the internal membrane pressure field $\mathrm{\Pi }(a)$ (Seguin and Fried, 2014). This inhomogeneous pressure originates from variations in membrane density (mosaicity) and compositional asymmetries between the leaflets (excess area) (Reinhard, 2014; Seguin and Fried, 2014), both driven by molecular interactions within the membrane components (Amiral and Markus, 2020). Membrane inhomogeneities from protein inclusions are effectively described by the mesoscopic parameters, $K_0(a)$ and $\sigma (a)$ (McMahon and Gallop, 2005; CampeloF et al., 2008), representing coarse-grained normal curvature and longitudinal tension, respectively. These mechanical relationships manifest in the equilibrium condition established along the longitudinal direction, as expressed in Equation 3. The transverse (Equation 2) and longitudinal (Equation 3) equilibrium equations describe quasi-static balance, where the former governs normal necking shape and the latter captures longitudinal tension, driving cortical flows. In dynamic approaches, energy dissipation from intrinsic membrane viscosity must be explicitly considered (Marino and Antonio, 2009).

2.4 Boundary conditions

Finally, boundary conditions arise from the variational principle, applied across a continuous membrane symmetry, referenced to the Darboux frame (Capovilla et al., 2002).

$\kappa \left(K-K_0\right)+{\kappa }_G{K}_T=0,(\mathrm{4a})$

$\sigma +\frac{\kappa }{2}{\left(K-K_0\right)}^2+{\kappa }_G{\mathcal{K}}_G=0,(\mathrm{4b})$

$\kappa {\nabla }_{l}K={\kappa }_G{\dot{K}}_{\tau },(\mathrm{4c})$

where $K_T$ denotes the extrinsic curvature along the surface tangent and ${\nabla }_l$ represents the curvature gradient in the longitudinal direction based on the natural moving frame of the membrane necking surface embedded in the Euclidean space (Spivak, 1979). Under minimal energy constraints established from the membrane edges, the first condition in Equation 4 requires the local torque to vanish at the boundary (Equation 4a). The second equation balances intrinsic and extrinsic curvatures with surface tension under energy conservation (Equation 4b). Crucially, an additional third condition arises from changes in constrictional torque, induced by saddle-splay elasticity within the deformed membrane, for inhomogeneous curvature along the longitudinal direction (Equation 4c) (where the dot symbol refers to the partial derivative with respect to the longitudinal coordinate, which is evaluated at the neck boundary). Such an inhomogeneous condition implies a local balance between extrinsic bending stiffness and intrinsic torques (Capovilla et al., 2002).

3 Results

3.1 Inhomogeneous necking in minimal catenoid surfaces: stability conditions

To determine conditions for mechanical stability, we first define the necking equilibrium relationships governing unperturbed configurations under the inhomogeneous force fields of membrane tension $(\sigma )$ and spontaneous curvature $(K_0)$. For minimal $R-$ catenoid surfaces with zero mean curvature $(K=0)$, as applied in the shape equation (Equation 2), the spontaneous curvature satisfies the inhomogeneous Helmholtz equation, which is given as follows:

${\nabla }^2{K}_0=2K_0{\mathcal{K}}_G,(5)$

which determines harmonic solutions for the curvature–composition force field $K_0(\mathrm{\Phi })$, driven by the covariant interaction, $\mathrm{\Phi }(l)$, between spontaneous curvature $K_0(\mathrm{\Phi })$ and Gaussian curvature ${\mathcal{K}}_{\mathcal{G}}$, remaining conserved in the absence of a topological change ($l$ represents an internal membrane length) (Spivak, 1979). This catenoid form of the shape equation represents the second-order Euler–Lagrange derivative for mechanical equilibrium $({\delta }^2\mathcal{H}=0)$, defining the stability condition for the CH energy of a necked catenoidal membrane (Walzel et al., 2022). Stability depends on the sign of the inhomogeneous term in Equation 5. Since ${\mathcal{K}}_G<0$ for any neck surface, a concave spontaneous curvature $({\nabla }^2{K}_0<0)$ ensures stability for $K_0>0$, while a convex distribution $({\nabla }^2{K}_0>0)$ leads to instability for $K_0<0$. Additionally, we derive the local relationship between spontaneous curvature, $K_0(\mathrm{\Phi })$, and surface tension, $\sigma (\mathrm{\Phi })$, which is systemically governed by the intrinsic composition-shape conformal field $(\mathrm{\Phi })$. For rigid, unperturbed $R$-catenoids $(K=0)$, integrating the inhomogeneity condition in Equation 3 over the parametric length $(ł)$ along the neck surface yields the local excess tension, which is given as follows:

$\sigma \left(l\right)-{\sigma }_0=-\frac{\kappa }{2}{K}_0^2\left(l\right),(6)$

where ${\sigma }_0(l=0)$ is an integration constant representing the lateral tension at the membrane edges. Note that Equation 6 applies to any value of $l$ along the neck and not just at the boundary, as defined in Equation 4b.

3.2 Boundary-injected Gaussian energy: necking axial stress

Interestingly, the closure relationship in Equation 6 mirrors the boundary condition in Equation 4b; by evaluating both boundary edges, the south pole edge $(B_S)$ and the north pole edge $(B_N)$ (at $l=0$), one obtains the connection $-{\sigma }_0\Rightarrow {\kappa }_G{{\mathcal{K}}_G}^{(0)}(B_S)+{\kappa }_G{{\mathcal{K}}_G}^{(0)}(B_N)$, which is rewritten as follows:

$\sigma \left[\mathrm{\Phi }\left(l\right)\right]+\frac{\kappa }{2}{K}_0^2\left[\mathrm{\Phi }\left(l\right)\right]=-{\kappa }_G{{\mathcal{K}}_G}^{\left(0\right)},(7)$

which establishes continuous energy density governed by the Gaussian edging curvature, ${{\mathcal{K}}_G}^{(0)}$, as intrinsically connected on the deformable neck from the external (reservoir) boundaries.

The constitutive shape $\mathrm{\Phi }(l)$ locally links normal necking spontaneous curvature to lateral tension forces regulated by conserved Gaussian curvature (Spivak, 1979). Positive membrane rigidness $(\kappa >0)$ implies that positive Gaussian energy injected from the boundaries corresponds to lateral negative tension $(-{\sigma }_0\iff {\kappa }_G{\mathcal{K}}_G^{(0)}>0)$, describing relaxed configurations that expand the membrane area using boundary reservoirs under elongational stress ($F_z>0$ and $m<0$; see Figure 5). Conversely, if negative Gaussian energy is extracted from the edges, the necking tension becomes positive $(-{\sigma }_0\iff {\kappa }_G{\mathcal{K}}_G^{(0)}<0)$, resulting in stressed necking configurations that contract the membrane area under constrictive stress ($F_z<0$ and $m>0$; see Figure 5). Our previous analysis examined the mechanical behavior of geometrically rigid catenoid necks ($R-$catenoids; $K=0$) with a superposed inhomogeneous spontaneous curvature field, $K_0(l)$, leading to a shape-conformal connection (fundamental $\mathrm{\Phi }\Rightarrow {\mathrm{\Phi }}_R$), under neck-shaping forces ($F_z$ and $m$) independent of curvature deformation (Santiago and Monroy, 2023). This zeroth-order analysis focused on the elastic stress tensor derived from the homogeneous Euler–Lagrange minimizer (Capovilla et al., 2002) while assuming axial force conservation along the minimal catenoid surface $(K=0)$ (Jülicher and Seifert, 1994). In this study, we extend a first-order perturbative problem under linear shape deformation $(\mathrm{\Phi }\approx {\mathrm{\Phi }}_R+\alpha {\mathrm{\Phi }}_D(K))$, starting from the rigid R-catenoid ($K=0$ and $\alpha =0$) as the fundamental state $({\mathrm{\Phi }}_R)$. We then consider deformed configurations ($\delta K\ne 0$, thus $\alpha >0$) based on catenoid-conformal solutions to the deformed state $({\mathrm{\Phi }}_D)$, modulated by the spontaneous curvature field under necking stress $(K_0)$. We begin by analyzing the $K_0-$ decorated shape equation near the critical state for minimal R-catenoid surfaces with axial revolution symmetry.

3.3 Renormalized necking configurations: critical $R^{†}$-catenoid

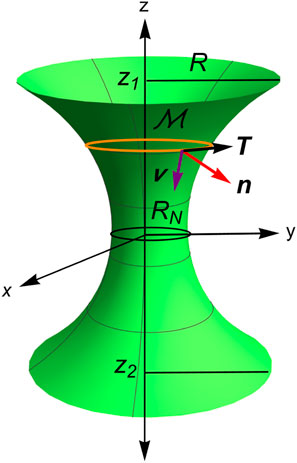
Figure 4 addresses the zeroth-order problem $({\mathrm{\Phi }}_R;\alpha =0)$, where the necking membrane is parametrized in Euclidean 3D-space using the axial $z-$ coordinate and the azimuthal angle $\varphi$; this is given by

$\mathbf{X}\left(z,\varphi \right)=\rho \left(z\right)\mathit{\rho }+z\mathbf{k},(8)$

where $\mathit{\rho }=(\cos \varphi ,\sin \varphi ,0)$ and $\mathbf{k}=(\mathrm{0,0,1})$ are the cylindrical basis and $\rho (z)$ is the radial coordinate of the surface.

Figure 4

Figure 4. Minimal R-catenoid neck. Geometric elements in the description of membranes with axial symmetry. The neck is placed at $z=0$ (the equatorial radius $R_0$), while $z_1$ and $z_2$ represent the axial coordinates of the upper and lower borders, respectively. The Darboux frame, $\mathit{\nu }=\mathbf{T}\times \mathbf{n}$, adapted to any parallel curve, is shown. The axial force and local torque exerted by the region $\mathcal{M}$ on the rest of the membrane are calculated using the stress tensor, as indicated in the text.

Henceforth, from Equation 8 the tangential vectors to the revolution surface are given by ${\mathbf{e}}_z={\rho }^{\prime }\mathit{\rho }+\mathbf{k}$ and ${\mathbf{e}}_{\varphi }=\rho \mathit{\varphi }$ so that the induced metric is found to be $g_{ab}d{\xi }^{a}d{\xi }^b=(1+{\rho }^{\prime 2})d{z}^2+{\rho }^{2}d{\varphi }^2$, where the prime symbols indicate parametric derivatives along the $z$ coordinate. Then, the infinitesimal element of area is obtained as follows: $dA=\rho \sqrt{1+{\rho }^{\prime 2}}dzd\varphi$. The unit vector normal to the surface is obtained using the following formula: $\mathbf{n}={\mathbf{e}}_{\varphi }\times {\mathbf{e}}_z/|\cdot |=(-{\rho }^{\prime }\mathbf{k}+\mathit{\rho })/\sqrt{1+{\rho }^{\prime 2}}$. The covariant derivatives, ${\partial }_z{\mathbf{e}}_z={\rho }^{″}\mathit{\rho }$ and ${\partial }_{\varphi }{\mathbf{e}}_{\varphi }=-\rho \mathit{\rho }$, imply the components of the curvature field $K_{zz}=-{\rho }^{″}/\sqrt{1+{\rho }^{\prime 2}}$, and $K_{\varphi \varphi }=\rho /\sqrt{1+{\rho }^{\prime 2}}$. Therefore, we can express the extrinsic mean curvature $(K\equiv 2H)$ and the intrinsic Gaussian curvature $({\mathcal{K}}_{\mathcal{G}})$ as functions of the radial coordinate $(\rho )$, along with its first-order $({\rho }^{\prime })$ and second-order $({\rho }^{″})$ derivatives, respectively, as follows (Durand, 1981):

$2H\left(\rho ,{\rho }^{\prime },{\rho }^{″}\right)=-\frac{{\rho }^{″}}{{\left(1+{\rho }^{\prime 2}\right)}^{3/2}}+\frac{1}{\rho \sqrt{1+{\rho }^{\prime 2}}},(9)$

${\mathcal{K}}_G\left(\rho ,{\rho }^{\prime },{\rho }^{″}\right)=-\frac{{\rho }^{″}}{\rho {\left(1+{\rho }^{\prime 2}\right)}^2}.(10)$

These Equations 9, 10 provide a frame-invariant description of curvature energy for the variational equations derived from the Canham–Helfrich Hamiltonian, minimized for the rigid R-catenoids (fundamental ${\mathrm{\Phi }}_R-$ state). However, the curvatures are size-dependent, thus necessitating scale-invariant re-parametrization.

3.4 Renormalized R-catenoid necking under spontaneous curvature

For a rigid catenoid surface $(K=0)$, the minimization relationship is provided in a scale-invariant form as $\bar{\rho }=\cosh \bar{z}$, where $\bar{\rho }\equiv \rho /R_0$ and $\bar{z}\equiv z/R_0$, with $R_0$ representing the re-normalizing radius of the equatorial waist (see Figure 4). Unlike the standard approach based on the boundary edge radius $(R_B)$ (Santiago and Monroy, 2023; Durand, 1981), this renormalized manifold parametrization expresses spatial lengths relative to the waist radius $(R_0)$ in a dimensionless form as follows:

$2\bar{H}\left(\bar{\rho },{\bar{\rho }}^{\prime },{\bar{\rho }}^{″}\right)=-\frac{{\bar{\rho }}^{″}}{{\left(1+{\bar{\rho }}^{\prime 2}\right)}^{3/2}}+\frac{1}{\bar{\rho }\sqrt{1+{\bar{\rho }}^{\prime 2}}},(11)$

${\bar{\mathcal{K}}}_G\left(\bar{\rho },{\bar{\rho }}^{\prime },{\bar{\rho }}^{″}\right)=-\frac{{\bar{\rho }}^{″}}{\bar{\rho }{\left(1+{\bar{\rho }}^{\prime 2}\right)}^2},(12)$

where $\bar{H}\equiv R_{0}H$ and ${\bar{\mathcal{K}}}_G\equiv R_0^2{\mathcal{K}}_G$. In Equations 11, 12, the derivatives are defined relative to renormalized lengths $(\bar{z}=z/R_0)$; for the rigid R-catenoids, one obtains

${\bar{K}}^{\left(R\right)}\equiv 2{\bar{H}}^{\left(R\right)}=0,(13)$

${\bar{\mathcal{K}}}_G^{\left(R\right)}=-\frac{1}{{\cosh }^4\bar{z}},(14)$

under principal curvatures given by ${\bar{K}}_{\nu }=-1/{\cosh }^2\bar{z}$ and ${\bar{K}}_T=1/{\cosh }^2\bar{z}$, where ${\bar{K}}_i\equiv R_0{K}_i$. Thus, the rigid R-catenoid is a minimal surface (Equation 13), with negative Gaussian curvature (Equation 14).

Furthermore, the inhomogeneous Helmholtz equation for the spontaneous curvature field (Equation 5) is expressed in reduced dimensionless coordinates as follows:

$\frac{1}{\bar{\rho }\sqrt{1+{\bar{\rho }}^{\prime 2}}}{\partial }_{\bar{z}}\left(\frac{\bar{\rho }}{\sqrt{1+{\bar{\rho }}^{\prime 2}}}{\partial }_{\bar{z}}\right){\bar{K}}_0=-2{\bar{K}}_0\frac{{\bar{\rho }}^{″}}{\bar{\rho }{\left(1+{\bar{\rho }}^{\prime 2}\right)}^2}.(15)$

Hence, the shape-conformal spontaneous curvature ${\bar{K}}_0\equiv K_0{R}_0$ satisfies Equation 15 on the renormalized catenoid, reducing to the scale-invariant hyperbolic form as follows (Durand, 1981):

${\bar{K}}_0^{″}+2{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\bar{z}{\bar{K}}_0=0.(16)$

Solutions to Equation 16 are given by

${\bar{K}}_0\left(\bar{z}\right)=A_1\tanh \bar{z}+A_2\mathcal{S}\left(\bar{z}\right),(17)$

where $A_1$ and $A_2$ are amplitude functions that translate the rigid necking geometry into inhomogeneous forces. The oddness imparting function $A_1$ in Equation 17 governs governs axial tensile forces inverted anti-symmetrically at the equatorial waist, while the evenness amplitude $A_2$ adjusts the spontaneous curvature to maintain mirror symmetry through the R-catenoid’s structure factor:

$\mathcal{S}\left(\bar{z}\right)\equiv 1-\bar{z}\tanh \bar{z}.(18)$

These rigid R-catenoid transformations focus on the conformal shape dependence of the matrix elements $(A_1,A_2)$ without including all the underlying physics. Specifically, they describe the spatial distributions of longitudinal axial interactions $(A_1)$ and catenoid torsional shape $(A_2)$, which are closely linked to the internal necking structure. Figure 5 illustrates necking structures conformally shaped in the rigid R-catenoid, which are given as follows from Equation 18 (Santiago and Monroy, 2023): (A) subcritical constriction furrows $({\mathcal{S}}_{\mathit{sub}}>0)$; (B) critical tipping forms at an abscissional onset $({\mathcal{S}}^{†}=0)$; and (C) supercritical elongational tubes leading to abscission $({\mathcal{S}}_{\mathit{super}}<0)$. The necking shape amplitudes $A_1$ and $A_2$ are set by the boundary conditions in Equation 4 (following appropriate renormalization in the deformed case; Equation 4). With the catenoid equatorial waist positioned at $z=0$ and boundary edges at $z_1$ and $z_2$ (see Figure 4), Equation 17 simplifies to the linear algebraic form as follows:

${\mathbf{K}}_0=\mathbb{M}\mathbf{A},(19)$

where the transference matrix holds on the catenoid form determined from the edge boundaries:

$\mathbb{M}\left({\bar{z}}_1,{\bar{z}}_2\right)=\left(\begin{array}{cc}\hfill \tanh {\bar{z}}_1\hfill & \hfill \mathcal{S}\left({\bar{z}}_1\right)\hfill \\ \hfill \tanh {\bar{z}}_2\hfill & \hfill \mathcal{S}\left({\bar{z}}_2\right)\hfill \end{array}\right),(20)$

Figure 5

Figure 5. Renormalized rigid necking configurations relative to the critical $R^{†}$-catenoid. Schematics of three stages of symmetric catenoids and their geometric elements for conformal decoration with the spontaneous curvature field ${\bar{K}}_0$. The stages (a) A and (b) B are on the subcritical regime, while the stage (c) C is on the supercritical regime. (d) Distribution of ${\bar{K}}_0$ as a function of $\bar{z}$ along the three stages depicted above. (e) Bending energy ${\bar{E}}_b\equiv E_b/(2\pi \kappa )$ (blue curve) and the total energy $\bar{E}\equiv E/(2\pi \kappa )$ (red curve). The configurational states A, B, and C identify the necking stages depicted in the panels above. We used the experimental value ${\kappa }_G/\kappa =-0.7$.

which transforms the necking vector $\mathbf{A}={(A_1,A_2)}^T$ into spontaneous curvatures imposed from the catenoid edges ${\mathbf{K}}_0={({\bar{K}}_0({\bar{z}}_1),{\bar{K}}_0({\bar{z}}_2))}^T$. Thus, the necking solutions can be determined by inverting Equation 19 as follows:

$\mathbf{A}={\mathbb{M}}^{-1}{\mathbf{K}}_0,(21)$

where an inversion matrix of Equation 21 is given as follows:

${\mathbb{M}}^{-1}=\frac{1}{\det \mathbb{M}}\left(\begin{array}{cc}\hfill \mathcal{S}\left({\bar{z}}_2\right)\hfill & \hfill -\mathcal{S}\left({\bar{z}}_1\right)\hfill \\ \hfill -\tanh {\bar{z}}_2\hfill & \hfill \tanh {\bar{z}}_1\hfill \end{array}\right).(22)$

Note that the necking amplitudes $A_1$ and $A_2$ in Equation 21 are well-defined only if $\det \mathbb{M}\ne 0$, with critical singularity occurring at the configuration where this determinant vanishes (see Equation 22):

$\det {\mathbb{M}}^{†}=\tanh {\bar{z}}_1^{†}\mathcal{S}\left({\bar{z}}_2^{†}\right)-\tanh {\bar{z}}_2^{†}\mathcal{S}\left({\bar{z}}_1^{†}\right)=0,(23)$

The root-points in Equation 23 implies a singular behavior of the necking configuration for given spontaneous curvatures ${\bar{K}}_0$. At this critical point, the catenoid satisfies maximal area conditions for given boundary constraints (Spivak, 1979; Sagan, 1992). After resolving the coupled geometry-composition system, Equation 21, the necking constants are written explicitly as follows:

$A_1\left({\bar{z}}_1,{\bar{z}}_2\right)=\frac{\mathcal{S}\left({\bar{z}}_2\right){\bar{K}}_0\left({\bar{z}}_1\right)-\mathcal{S}\left({\bar{z}}_1\right){\bar{K}}_0\left({\bar{z}}_2\right)}{\det \mathbb{M}},(24)$

$A_2\left({\bar{z}}_1,{\bar{z}}_2\right)=-\frac{\tanh \left({\bar{z}}_2\right){\bar{K}}_0\left({\bar{z}}_1\right)-\tanh \left({\bar{z}}_1\right){\bar{K}}_0\left({\bar{z}}_2\right)}{\det \mathbb{M}},(25)$

We focus on the symmetric case $({\bar{z}}_1=-{\bar{z}}_2=\pm {\bar{z}}_B)$, where the first necking constant equals 0 $(A_1=0)$, while the second one is given as follows:

$A_2\left({\bar{z}}_B\right)=\frac{{\bar{K}}_0^{\mathit{symm}}\left({\bar{z}}_B\right)}{\mathcal{S}\left({\bar{z}}_B\right)}.(26)$

Hence, the critical $R^{†}-$ catenoid emerges as a singularity in Equation 26 corresponding to the maximal area $(A_{\mathit{max}}\approx 1.19)$ (Santiago and Monroy, 2023), satisfying

$\mathcal{S}\left({\bar{z}}_B^{†}\right)\equiv 1-{\bar{z}}_B^{†}\tanh {\bar{z}}_B^{†}=0,(27)$

whose rigid geometric form enforces shape-conformal necking transformations under critical boundaries renormalized at $\pm {\bar{z}}_B^{†}\approx 1.2$ (Spivak, 1979; Sagan, 1992), corresponding to critical edge radius ${\bar{R}}^{†}\approx 1.81$ (i.e., at ${\mathcal{S}}^{†}=0$) (Santiago and Monroy, 2023). From Equation 27, the constrictive furrow-like shapes correspond to subcritical conditions (${\mathcal{S}}_{\mathit{sub}}>0$ for ${\bar{z}}_B<{\bar{z}}_B^{†}$ and $\bar{R}>{\bar{R}}^{†}$), while elongated tubular shapes correspond to supercritical conditions ($\mathcal{S}{†}_{\mathit{super}}<0$ for ${\bar{z}}_B>{\bar{z}}_B^{†}$ and $\bar{R}<{\bar{R}}^{†}$).

3.4.1 Inhomogeneous shape-conformal field: Rigid necking energy

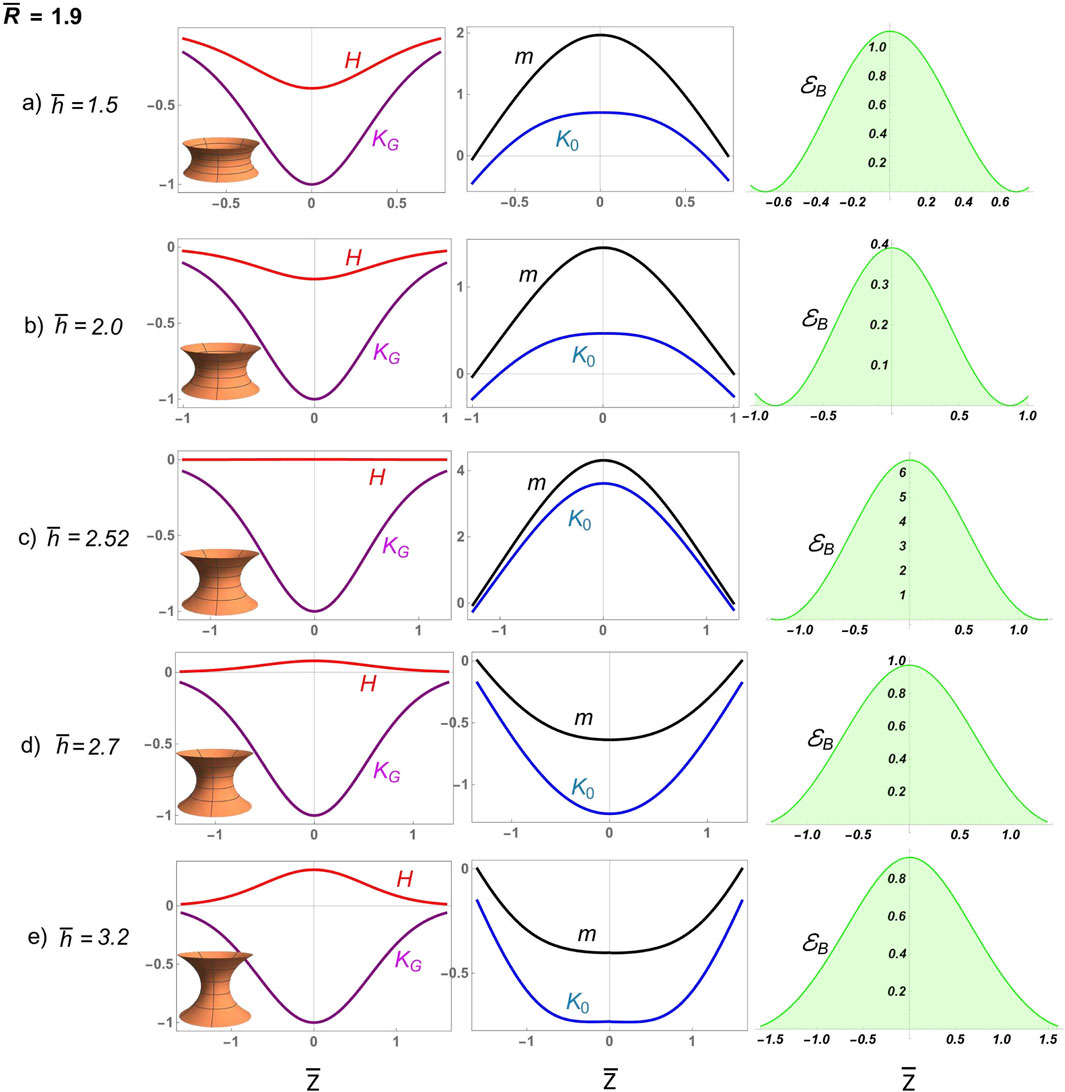
Figures 5a–c illustrate catenoid-conformal necking configurations exhibiting distinct axial and radial forces near the critical catenoid (Santiago and Monroy, 2023). At the edge boundaries, applying the renormalized boundary condition from Equation 4a yields ${\bar{K}}_0({\bar{z}}_B)=A_2({\bar{z}}_B)\mathcal{S}({\bar{z}}_B)=({\kappa }_G/\kappa ){\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2{\bar{z}}_B$. Consequently, the spontaneous curvature conformal field, ${\bar{K}}_0$, symmetrically distributes along the renormalized, scale-invariant catenoid as follows:

${\bar{K}}_0^{\mathit{symm}}\left(\bar{z}\right)=\frac{{\kappa }_G}{\kappa }\frac{{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\left({\bar{z}}_B\right)}{\mathcal{S}\left({\bar{z}}_B\right)}\mathcal{S}\left(\bar{z}\right),(28)$

with dimensionless axial coordinate $\bar{z}\in [-{\bar{z}}_B,{\bar{z}}_B]\ne {\bar{z}}^{†}$.

As shown in Figure 5d, the catenoid-conformal necking solutions for the spontaneous curvature in Equation 28 split into two different branches separated by the critical rigid catenoid $(R^{†})$, where spontaneous curvature abruptly changes the sign. In the subcritical regime $({\bar{z}}_B<{\bar{z}}_{-}^{†})$, ${\bar{K}}_0$ is negative, reaching a minimum and spreading broadly across the furrow (curve A). Near the critical point, ${\bar{K}}_0$ attains its minimum negative value as $\mathcal{S}({\bar{z}}_{-}^{†})\to 0$ (curve B). In the supercritical regime $({\bar{z}}_B>{\bar{z}}^{†})$, ${\bar{K}}_0$ remains positive but decreases significantly for highly elongated catenoids (${\bar{z}}_B\gg {\bar{z}}^{†}$; curve C). Likewise, the critical $K_0-$ singularity appears reflected in the corresponding bending energy as follows:

$\begin{array}{ccc}\hfill E_b^{\mathit{symm}}& \equiv \hfill & \frac{\kappa }{2}\int dA{\left(K_0^{\mathit{symm}}\right)}^2,\hfill \\ \hfill & =\hfill & 2\pi \frac{\kappa }{2}\frac{{\kappa }_G^2}{{\kappa }^2}\frac{{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4\left({\bar{z}}_B\right)}{{\mathcal{S}}^2\left({\bar{z}}_B\right)}{\int }_{-{\bar{z}}_B}^{{\bar{z}}_B}d\bar{z}{\cosh }^2\left(\bar{z}\right){\mathcal{S}}^2\left(\bar{z}\right),\hfill \\ \hfill & =\hfill & \pi \frac{{\kappa }_G^2}{\kappa }\frac{{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4\left({\bar{z}}_B\right)}{{\mathcal{S}}^2\left({\bar{z}}_B\right)}\mathfrak{f}\left({\bar{z}}_B\right),\hfill \end{array}(29)$

where a catenoid-conformal symmetry holds

$\mathfrak{f}\left({\bar{z}}_B\right)\equiv {\bar{z}}_B-\frac{{\bar{z}}_B^3}{3}-\frac{3}{2}{\bar{z}}_B\cosh 2z_B+\frac{1}{4}\left(5+2{\bar{z}}_B^2\right)\sinh 2{\bar{z}}_B.(30)$

Note that Equation 30 appears by the integration in Equation 29. Here, the necking work exhibits symmetry under axial revolution in the catenoid background, with the form $\mathfrak{f}(\mathcal{S},{\mathcal{S}}^{\prime },{\mathcal{S}}^{″})$ determined by the shape factor $\mathcal{S}({\bar{z}}_B)$ and its higher derivatives ${\mathcal{S}}^{\prime }$ and ${\mathcal{S}}^{″}$. As shown in Figure 5e, a critical singularity emerges in the bending energy, Equation 29, at the tipping point ${\bar{z}}_B={\bar{z}}_1^{†}\approx 1.2$. However, including the surface tension energy, $E_{\sigma }=\int dA\sigma$ (see Equation 1), which also behaves inhomogeneously under the spontaneous curvature field (Equation 7), we obtain

$\begin{array}{ccc}\hfill E& =\hfill & E_b+E_{\sigma },\hfill \\ \hfill & =\hfill & \frac{\kappa }{2}\int dA{K}_0^2+\int dA\sigma \hfill \\ \hfill & =\hfill & -{\kappa }_G\int dA{\mathcal{K}}_G\left({\bar{z}}_B\right)\hfill \\ \hfill & =\hfill & \frac{{\kappa }_G}{{\cosh }^4{\bar{z}}_B}{\int }_{-{\bar{z}}_B}^{{\bar{z}}_B}d\bar{z}{\cosh }^2\bar{z},\hfill \\ \hfill & =\hfill & 2\pi {\kappa }_G\left({\bar{z}}_B+\cosh {\bar{z}}_B\sinh {\bar{z}}_B\right){\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4{\bar{z}}_B,\hfill \end{array}(31)$

where we used the continuity condition from Equation 7, assuming conserved Gaussian curvature on the catenoid surface (Equation 14). Consequently, the total necking energy, Equation 31, becomes a smooth function, removing singularity (see Figure 5d). Note that this expression for necking energy is generally valid for any catenoid surface without topological changes.

3.5 Catenoid-conformal stress under inhomogeneous spontaneous curvature

The inhomogeneity of the spontaneous curvature, $(K_0)$, induces necking forces on the membrane, which are derived from the stress tensor, $\mathbf{\Sigma }(K,K_0,\sigma )$, associated with the total energy, $E(K,K_0,{\mathcal{K}}_{\mathcal{G}},\sigma )$. The membrane-covariant energy distribution is encoded in the stress tensor (Capovilla and Guven, 2002; Guven, 2004; Fournier, 2007) decomposed surface-covariant as follows:

${\mathbf{\Sigma }}^a={\mathrm{\Sigma }}^{ab}{\mathbf{e}}_b+{\mathrm{\Sigma }}^a\mathbf{n},(32)$

with tangential and normal components, respectively, given as follows:

$\begin{array}{ccc}\hfill {\mathrm{\Sigma }}^{ab}& =\hfill & \kappa \left(K-K_0\right)\left[K^{ab}-\frac{1}{2}\left(K-K_0\right)g^{ab}\right]-g^{ab}\sigma ,\hfill \\ \hfill {\mathrm{\Sigma }}^a& =\hfill & -\kappa {\nabla }^a\left(K-K_0\right).\hfill \end{array}(33)$

Equations 32 and Equations 33 in cylindrical coordinates, the forces per unit length, along the azimuthal and radial direction, are given by

${\mathcal{F}}_z\equiv {\mathbf{\Sigma }}^a{\nu }_a\cdot \mathbf{k}=-\frac{1}{\sqrt{1+{\rho }^{\prime 2}}}\left({\mathcal{F}}_n{\rho }^{\prime }+{\mathcal{F}}_{\nu }\right),(34)$

${\mathcal{F}}_{\rho }\equiv {\mathbf{\Sigma }}^a{\nu }_a\cdot \mathit{\rho }=\frac{1}{\sqrt{1+{\rho }^{\prime 2}}}\left({\mathcal{F}}_n-{\rho }^{\prime }{\mathcal{F}}_{\nu }\right).(35)$

Here, the unit vector field $\mathit{\nu }={\nu }^a{\mathbf{e}}_a$, as depicted in Figure 4. The normal and lateral forces unit lenght that appear in Equations 34 and Equations 35 are are, respectively, given by

${\mathcal{F}}_n=\frac{\kappa }{\sqrt{1+{\rho }^{\prime 2}}}{\left(-\frac{{\rho }^{″}}{{\left(1+{\rho }^{\prime 2}\right)}^{3/2}}+\frac{1}{\rho \sqrt{1+{\rho }^{\prime 2}}}-K_0\right)}^{\prime },(36)$

$\begin{array}{cc}\hfill {\mathcal{F}}_{\nu }=& -\sigma -\frac{\kappa K_0^2}{2}+\frac{\kappa }{2}\left(\frac{{{\rho }^{″}}^2}{{\left(1+{\rho }^{\prime 2}\right)}^3}-\frac{1}{{\rho }^2\left(1+{\rho }^{\prime 2}\right)}\right.\hfill \\ \hfill & +\left.2K_0\frac{1}{\rho \sqrt{1+{\rho }^{\prime 2}}}\right).\hfill \end{array}(37)$

In the case of minimal necking surfaces with a rigid geometry (R-catenoids; $K=0$), they simplify to

$\begin{array}{ccc}\hfill {\mathcal{F}}_n& =\hfill & -\frac{\kappa }{\sqrt{1+{\rho }^{\prime 2}}}{K}_0^{\prime },\hfill \\ \hfill {\mathcal{F}}_{\nu }& =\hfill & -\sigma -\frac{\kappa K_0^2}{2}+\frac{\kappa K_0}{\rho \sqrt{1+{\rho }^{\prime 2}}},\hfill \\ \hfill & =\hfill & {\kappa }_G{\mathcal{K}}_G\left(B_1\right)+\frac{\kappa K_0}{\rho \sqrt{1+{\rho }^{\prime 2}}}.\hfill \end{array}(38)$

Here, the $K_0-\sigma$ connection with conserved Gaussian curvature in Equation 7 is applied at the “south” generating boundary ($B_S$ at ${\bar{z}}_1$), as specified in the second oulined, Equation 38. In the dimensionless form, the corresponding catenoid-conformal results, Equations 36 and 37 are expressed in terms of the reduced axial coordinate $(\bar{z})$ as follows:

$\begin{array}{ccc}\hfill {\bar{\mathcal{F}}}_n\left(\bar{z}\right)& =\hfill & -\frac{\kappa }{\cosh \bar{z}}{\bar{K}}_0^{\prime },\hfill \\ \hfill {\bar{\mathcal{F}}}_{\nu }\left(\bar{z}\right)& =\hfill & -{\kappa }_G{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4{\bar{z}}_1+\frac{\kappa {\bar{K}}_0}{{\cosh }^2\bar{z}},\hfill \end{array}(39)$

where ${\bar{\mathcal{F}}}_i\equiv R_0^2{\mathcal{F}}_n$. By substituting Equations 39 in Equation 34, we obtain the axial force $F_z\equiv 2\pi \bar{\rho }{\bar{\mathcal{F}}}_z$,

${\bar{F}}_z\equiv \frac{{\kappa }_G}{\kappa }{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4{\bar{z}}_1-A_2\left({\bar{z}}_1,{\bar{z}}_2\right),(40)$

where $A_2$ is obtained using Equation 25, and the factor $2\pi \kappa$ has been absorbed into ${\bar{F}}_z\equiv F_z/(2\pi \kappa )$.

In the symmetric case $({\bar{z}}_1={\bar{z}}_2={\bar{z}}_B)$, the axial force is expressed in terms of the reduced boundary length $({\bar{z}}_B)$ using the catenoid-conformal expression as follows:

$\begin{array}{ccc}\hfill {\bar{F}}_z^{\mathit{symm}}& \equiv \hfill & \frac{{\kappa }_G}{\kappa }{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4{\bar{z}}_B-A_2\left({\bar{z}}_B\right),\hfill \\ \hfill & =\hfill & \frac{{\kappa }_G}{\kappa }{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4{\bar{z}}_B\left(1-\frac{1}{\mathcal{S}\left({\bar{z}}_B\right)}\right).\hfill \end{array}(41)$

The R-catenoid form factor, $\mathcal{S}({\bar{z}}_B)$, defines conformal tensional forces based on the scale-invariant catenoid size $({\bar{z}}_B)$. Hence, from Equation 41 a force singularity emerges at the critical catenoid, where ${\bar{z}}_B^{†}\approx 1.2$ (see Figure 5) (Santiago and Monroy, 2023). In the subcritical regime $({\bar{z}}_B<{\bar{z}}_B^{†})$, a positive axial force arises $({\bar{F}}_z>0)$, acting as an attractive constrictive force approaching the catenoid’s edge borders (Figure 5). Conversely, in the supercritical regime $({\bar{z}}_B>{\bar{z}}_B^{†})$, a negative elongational force $({\bar{F}}_z<0)$ indicates repulsive edge interactions leading to elongational forces in the neck (see 5). For abscissional catenoids (if ${\bar{z}}_B\gg {\bar{z}}^{†}$, then $\mathcal{S}\to \infty$), the axial force vanishes, allowing the neck borders to separate freely. Unlike the axial force, the radial force varies along the catenoid and is described by the inhomogeneous expression as follows:

${\bar{F}}_{\rho }\left(\bar{z}\right)=\left(-A_1+A_2\bar{z}\right)\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\bar{z}+\frac{{\kappa }_G}{\kappa }{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4{\bar{z}}_1\sinh \bar{z},(42)$

where $\bar{z}\in [{\bar{z}}_2,{\bar{z}}_1]$. At the equatorial waist $\bar{z}=0$, the radial force evaluates to ${\bar{F}}_{\rho }(0)=-A_1$, thus making the “south pole” shape constant $-A_1$ (as given by Equation 24, the radial force at the waist of the catenoid). For a symmetric catenoid $(\pm {\bar{z}}_1={\bar{z}}_B)$, $A_1=0$, the radial force Equation 42, result in

$\begin{array}{ccc}\hfill {\bar{F}}_{\rho }^{\mathit{symm}}\left(\bar{z}\right)=A_2\left({\bar{z}}_B\right)\bar{z}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\bar{z}+\frac{{\kappa }_G}{\kappa }{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4{\bar{z}}_B\sinh \bar{z},& \hfill & \hfill \\ \hfill =\frac{{\kappa }_G}{\kappa }\left(\frac{{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\left({\bar{z}}_B\right)}{\mathcal{S}\left({\bar{z}}_B\right)}\bar{z}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\bar{z}+{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4{\bar{z}}_B\sinh \bar{z}\right).& \hfill & \hfill \end{array}(43)$

For $\bar{z}\in [-{\bar{z}}_B,{\bar{z}}_B]$, the radial force at the waist is 0, ${\bar{F}}_{\rho }^{\mathit{symm}}(0)=0$, as expected for a generalized asymmetric R-catenoid (Santiago and Monroy, 2023). Specifically, the radial constriction force, Equation 43, at the lower boundary (south pole at $\bar{z}=-{\bar{z}}_B$) is

${\bar{F}}_{\rho }^{\mathit{symm}}\left(-{\bar{z}}_B\right)=\frac{{\kappa }_G}{\kappa }\left(\frac{{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^3\left({\bar{z}}_B\right)}{\mathcal{S}\left({\bar{z}}_B\right)}{\bar{z}}_B+{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^4{\bar{z}}_B\sinh {\bar{z}}_B\right).(44)$

For rigid R-catenoids $({\mathrm{\Phi }}_R)$, necking forces arise from geometric curvature interactions, leading to elastic-like deformations under shape-conformal stress $\bar{\mathbf{\Sigma }}\equiv ({\bar{F}}_z,{\bar{F}}_{\rho })$. The axial force ${\bar{F}}_z$ (Equation 40) represents elastic interactions between the edge boundaries, which are governed by the Gaussian curvature ${\mathcal{K}}_G$ (the southern boundary at ${\bar{z}}_1$ and the northern boundary at ${\bar{z}}_2$, with the waist at $z=0$). It arises from inhomogeneities in the catenoid’s conformal spontaneous curvature $({\bar{K}}_0)$ and generates axial necking tension $({\bar{F}}_z\equiv \partial \sigma /\partial \bar{z})$. For symmetric catenoids, ${\bar{F}}_z$ is compressive and intensifies near the critical catenoid. In the supercritical branch, after overcoming the bending energy barrier, it becomes elongational and diminishes to 0 under abscission (see Figure 5). The radial force ${\bar{F}}_{\rho }$ (Equation 40) reflects constrictive necking interactions driven by the gradient of spontaneous curvature $({\bar{K}}_0^{\prime })$. In the subcritical branch, it is outward (convex furrowing, ${\bar{K}}_0^{\prime }>0$), while in the supercritical branch, it is inward (concave tubulation, ${\bar{K}}_0^{\prime }<0$). This can also be seen in the radial force acting on the edge, Equation 44. Mechanical inhomogeneities also generate shape-conformal torque, expressed as $\bar{\mathbf{m}}$ (Santiago and Monroy, 2023); for symmetrical configurations, the neck torsional modulus is derived as follows:

$\begin{array}{ccc}\hfill \bar{m}\left(\bar{z}\right)& =\hfill & {\bar{K}}_0\left(\bar{z}\right)-\frac{{\kappa }_G}{\kappa }\mathrm{s}\mathrm{e}\mathrm{c}{\mathrm{h}}^{\mathrm{2}}\bar{\mathrm{z}},\hfill \\ \hfill & =\hfill & \frac{{\kappa }_G}{\kappa }\left(\frac{{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\left({\bar{z}}_B\right)}{\mathcal{S}\left({\bar{z}}_B\right)}\mathcal{S}\left(\bar{z}\right)-\mathrm{s}\mathrm{e}\mathrm{c}{\mathrm{h}}^{\mathrm{2}}\bar{\mathrm{z}}\right).\hfill \end{array}(45)$

For $\bar{z}\in [{\bar{z}}_1,{\bar{z}}_2]$, the shape-conformal local torque for a rigid R-catenoid peaks at the waist and drops to 0 at the boundaries. The singular point in Equation 45, shows the bifurcation in the local torque.

3.6 Deformable necking configurations: D-catenoids

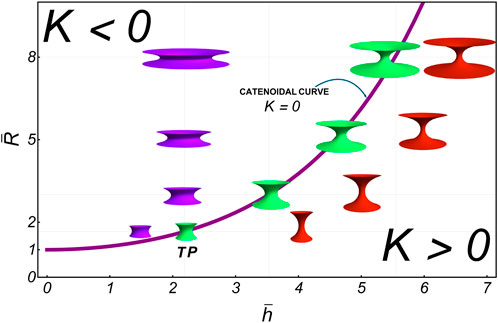
In elasticity-driven membrane necking phenomena such as cell division, endocytosis, and pore formation, necking occurs near catenoidal surfaces of minimal energy (${\mathrm{\Phi }}_R$ with $\bar{K}+\delta \bar{K}\approx 0$) but in excited deformable states under curvature-softening stresses (${\mathrm{\Phi }}_D$ for $\delta \bar{K}\ge 0$). This section examines the first-order variational problem concerning how spontaneous curvature is adaptively distributed along a deformable membrane in a linearly perturbed excited state, $\mathrm{\Phi }\approx {\mathrm{\Phi }}_R+\alpha (\delta \bar{K}){\mathrm{\Phi }}_D$, which slightly deviates from the fundamental catenoid state to improve abscissional efficiency while maintaining moderate energy consumption relative to the fundamental state, i.e., at small $\alpha (\delta \bar{K})\approx \delta \bar{K}/{\bar{K}}_0$. The deformable neck, referred to as a D-catenoid, is parametrized in cylindrical coordinates as follows (Durand, 1981):

$\bar{\rho }\left(\bar{z}\right)={\bar{R}}_N\cosh \bar{z}.(46)$

For simplicity, we consider the symmetric case, where the waist necking radius is renormalized as ${\bar{R}}_N\equiv \bar{R}/\cosh {\bar{z}}_B$, with the neck length $\bar{h}$ determined at the boundary edges ${\bar{z}}_B=\bar{h}/2$. The dimensionless overline indicates that $\bar{R}\equiv R/R_0$ and $\bar{h}=h/R_0$, which is akin to the rigid R-catenoid. In Equation 46, the necking domain $\bar{z}\in [-\bar{h}/2,\bar{h}/2]$. Notably, $\bar{\rho }(\pm {\bar{z}}_B)=\bar{R}$, which represents the renormalized border edge radius (see Figure 4). As a result, Figure 6 shows the configurational landscape of necking shapes (${\bar{R}}_N-\bar{h}$ space), where deformable D-catenoids $({\mathrm{\Phi }}_D)$ are derived by re-normalizing rigid R-catenoids of minimal energy $({\mathrm{\Phi }}_R)$. The fundamental state ${\mathrm{\Phi }}_R-$ curve represents the smallest zero-order solutions satisfying ${\bar{R}}_N=\bar{R}/\cosh {\bar{z}}_1=1$, such that the mean curvature is 0 $(\bar{K}=0)$. The TP represents the critical $R^{†}-$ catenoid of the maximum size (${\bar{A}}_{\mathit{max}}\approx 1.19$ for ${\bar{R}}^{†}\approx 1.81$ and ${\bar{z}}_B\approx 1.2$), which corresponds to the critical aspect ratio ${\bar{h}}^{†}/{\bar{R}}^{†}\approx 1.33$. D-catenoids emerge as renormalized configurations with a variable aspect. Qualitatively, when the edge radius is fixed (constant $\bar{R}$), the deformation-renormalized neck radius, $\bar{\rho }(0)={\bar{R}}_N(\bar{R},{\bar{z}}_B)$, decreases with ${\bar{z}}_B$, resulting in negative mean curvatures $(\bar{K}<0)$ along horizontally departing scissional pathways (Figure 6; below the R-catenoidal curve). Conversely, by fixing the neck height (constant $\bar{h}$), the edge radius increases with $\bar{R}$, producing positive mean curvatures $(\bar{K}>0)$ along vertically departing scissional pathways (Figure 6; above the R-catenoidal curve). According to Equation 46, the D-catenoid’s curvatures are expressed as inhomogeneous functions as follows:

${\bar{K}}^{\left(D\right)}\equiv 2{\bar{H}}^{\left(D\right)}=\pm \frac{1-{\bar{R}}_N^2}{{\bar{R}}_N}\frac{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\bar{z}}{{\mathcal{R}}^{3/2}\left(\bar{z}\right)},(47)$

${{\bar{\mathcal{K}}}_G}^{\left(D\right)}=-\frac{1}{{\mathcal{R}}^2\left(\bar{z}\right)},(48)$

note that both, Equations 47 and, 48, are governed by the structural rigidity factor

$\mathcal{R}\left(\bar{z}\right)\equiv 1+{\bar{R}}_N^2{\sinh }^2\bar{z},(49)$

Figure 6

Figure 6. Configuration space of deformable D-catenoid necking configurations renormalized from the rigid R-catenoids of minimal energy. Some shape membranes from Equation (46) in terms of the parameters $\bar{R}$ and $\bar{h}=2{\bar{z}}_B$. On the R-catenoidal curve, ${\bar{R}}_N=1$ so that $\bar{R}=\cosh \bar{h}/2$ and the basal mean curvature is 0 $({\bar{K}}_R=0)$. Deformable D-catenoids are characterized by curvature deformation $(\delta \bar{K}\ne 0)$, departing from the basal curvature $({\bar{K}}_D={\bar{K}}_R+\delta \bar{K})$. The value is negative below the R-catenoidal curve ($\bar{K}<0$ for $\delta \bar{K}<0$), while it is positive above the R-curve ($\bar{K}>0$ for $\delta K>0$). The maximal critical MC-catenoid $({\bar{R}}^{†})$ identifies the catenoid of the maximum size, such that ${\tilde{h}}_{\mathit{max}}=\bar{h}/\bar{R}\approx 1.32$ and ${\tilde{A}}_{\mathit{max}}=\bar{A}/\pi R^2\approx 1.19$, marking the metastable TP for abscission.

An even positive function defines neck rigidness based on the catenoid’s shape, remaining flexible near the neck waist ($\mathcal{R}\approx 1$ for $\bar{z}\le {\bar{R}}_N$) but being stiffened toward the edge boundaries ($\mathcal{R}\to \infty$ for $\bar{z}\gg {\bar{R}}_N$). This shape-conformal function defined in Equation 49, $\mathcal{R}=1-{\bar{R}}_N^2+{\bar{\rho }}^2$, captures deformational perturbations departing from the rigid R-catenoid shape $({\bar{K}}^{(R)}=0)$, with ${\mathcal{R}}_R=1$. Thus, we define the D-catenoid shapes as geometric shape perturbations $\mathcal{R}(\bar{z})=1\pm \delta \mathcal{R}$, where the renormalized deformation is $\delta \mathcal{R}={\bar{\rho }}^2-{\bar{R}}_N^2$. Expanding deformability up to the first order, the renormalized curvatures are approximated as follows:

${\bar{K}}^{\left(D\right)}\approx \pm \frac{1-{\bar{R}}_N^2}{\bar{\rho }}\left(1\mp \frac{3}{2}\delta \mathcal{R}\right)\approx \pm \delta \bar{K},(50)$

${\bar{\mathcal{K}}}_G^{\left(D\right)}\approx -1\pm 2\delta \mathcal{R}\approx -1\pm \delta {\bar{\mathcal{K}}}_G.(51)$

From Equations 50 and 51, we see that at the equatorial waist ($\bar{z}=0$, ${\mathcal{R}}_0=1$, and ${\bar{\rho }}_0={\bar{R}}_N$), yielding ${\bar{K}}_0=(1-{\bar{R}}_N^2)/{\bar{R}}_N$ and ${\bar{\mathcal{K}}}_{G0}=-1$. Therefore, the mean curvature for broad necking radii $({\bar{R}}_N>1)$ appears distinctly negative $(\bar{K}={\bar{K}}_R-\delta \bar{K}<0)$, which is quantitatively equivalent to $\bar{R}>\cosh {\bar{z}}_1$ (which corresponds to constrictional furrows in the upper leftmost region of the reference R-curve in Figure 6); however, for narrow necking radii $({\bar{R}}_N<1)$, it becomes positive $(\bar{K}={\bar{K}}_R+\delta \bar{K}>0)$, corresponding to $\bar{R}<\cosh {\bar{z}}_1$ (abscissional tubes in the lower rightmost side of the red R-curve). The Gaussian curvature is consistently negative in the saddle-splay region $({\bar{\mathcal{K}}}_G\approx -1\pm \delta {\bar{\mathcal{K}}}_G)$, vanishing in absolute magnitude toward the softened boundaries (${\bar{\mathcal{K}}}_G\approx 0$ at $\bar{z}\to \pm {\bar{z}}_B$).

3.6.1 Deformable neck constriction pathway

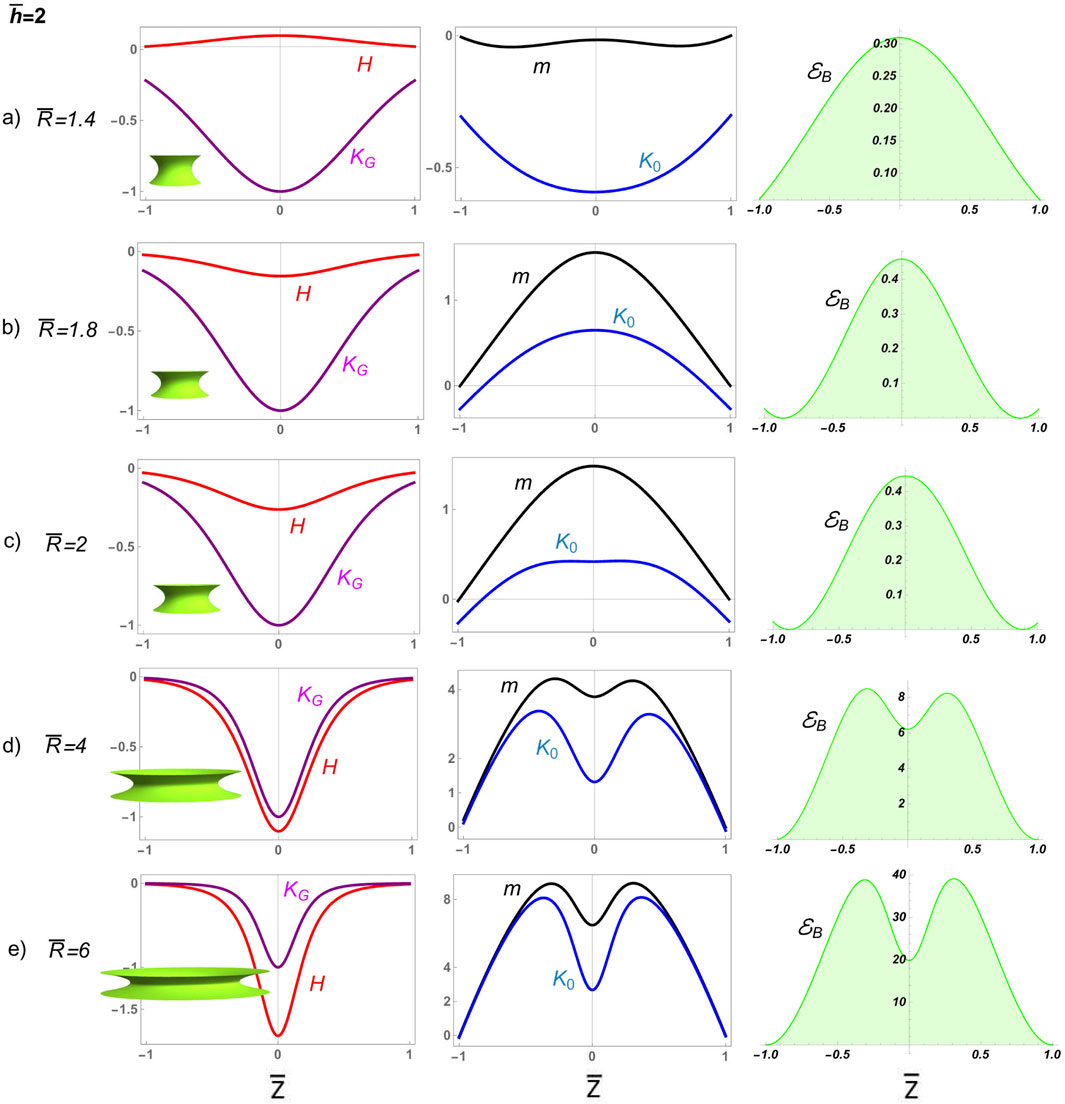
We first analyze how neck deformability affects constriction in a divisional furrow characterized by dominant convex curvature $(K<0)$. Figure 7 shows numerical solutions for deformable D-catenoids with constant length $(\bar{h}=2)$ and variable neck radii from near-critical to highly constricted supercritical $(1.4\le \bar{R}\le 6)$. Initially, $(\bar{R}\gtrsim {\bar{R}}^{†}\approx 1.2)$; in other words, the deformable curvature’s distribution results in a slightly positive mean curvature $(\bar{K}\gtrsim 0)$, which causes the neck to curve inward, forming a furrow. The deformation ${\mathrm{\Phi }}_D-$ pathway $(0.7\le \bar{R}/\bar{h}\le 3)$, intersecting the rigid ${\mathrm{\Phi }}_R$ curve above the critical catenoid at ${(\bar{R}/\bar{h})}^{†}\approx 0.75$, reveals a constriction scenario dominated by edge-attractive forces preventing abscission. This is marked by a spread distribution of Gaussian curvature $({\mathcal{K}}_G)$, evolving into strongly negative mean curvature under extreme constriction ($\bar{K}\gg 0$ at $\bar{R}\gg {\bar{R}}^{†}$; Figure 6). The inhomogeneous spontaneous curvature $({\bar{K}}_0)$ starts as negative, transitions to positive with increasing constriction, and exhibits a dip at the waist flanked by peaks, indicating lateral resistance. The constrictional shaping torque becomes strongly positive $(\bar{m}>0)$, following the same distribution as ${\bar{K}}_0$. The bending energy density increases significantly, eventually forming a bimodal distribution with a local minimum at the equatorial waist; this reflects forced constriction under varying mean curvatures. These analytical results show that narrow constrictional furrows prevent spontaneous abscission due to high curvature-induced stress, sustained by elevated bending energy $(E_b\gg \kappa )$.

Figure 7

Figure 7. Constriction pathway leading to furrow relaxation. Several stages of constriction along a D-catenoid of constant length $\bar{h}=2$. Panel (a) corresponds to a D-catenoid on the left of the catenoidal curve in Figure 6, while (b-e) are on the right. At the waist, the Gaussian curvature is normalized to ${\bar{\mathcal{K}}}_G=-1$. (a) D-catenoid with border radius $\bar{R}=6$. Gaussian curvature ${\mathcal{K}}_G$ and mean curvature $\bar{H}$ as a function of $\bar{z}$ (first column); local torque $\bar{m}$ and spontaneous curvature ${\bar{K}}_0$ as a function of $\bar{z}$ (second column); density of the bending energy ${\mathcal{E}}_B=1/2{(K-K_0)}^2$ as a function of $\bar{z}$ (third column). The experimental value for Gaussian rigidity, ${\kappa }_G/\kappa =-0.7$, was used.

3.6.2 Shape-conformal deformation under inhomogeneous spontaneous curvature

We exploit the fact that the axial force, $F_z\equiv 2\pi \bar{\rho }{\bar{\mathcal{F}}}_z$, remains constant along the surface (Jülicher and Seifert, 1994). The term ${\bar{\mathcal{F}}}_z$ is identified from Equation 34, where the renormalized necking forces are expressed in terms of the rigidity structure factor $(\mathcal{R})$ as follows:

$\begin{array}{cc}\hfill {\bar{\mathcal{F}}}_{\nu }=& \frac{{\bar{R}}_N^2{\cosh }^2\bar{z}}{{2\mathcal{R}}^3}-\frac{\mathrm{s}\mathrm{e}\mathrm{c}{\mathrm{h}}^{\mathrm{2}}\bar{\mathrm{z}}}{2{\bar{R}}_N^2\mathcal{R}}\hfill \\ \hfill & +\frac{2{\bar{R}}_N\cosh \bar{z}{K}_0\left(\bar{z}\right)}{2{\mathcal{R}}^{3/2}}-\frac{{\bar{K}}_0^2\left(\bar{z}\right)}{2}+\bar{\sigma },\hfill \end{array}(52)$

${\bar{\mathcal{F}}}_n=-\frac{1}{{\mathcal{R}}^{1/2}}{\left(\frac{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\bar{z}}{{\bar{R}}_N}-\frac{{\bar{R}}_N\cosh \bar{z}}{\mathcal{R}}-{\bar{K}}_0\right)}^{\prime },(53)$

where the ${\text{symbol\hspace{0.17em}}}^{\prime }$ denotes the derivative with respect to $\bar{z}$. Thus, shape-conformal forces renormalized into D-catenoids are given by

${\bar{F}}_z=-\frac{{\bar{R}}_N\sinh \bar{z}}{{\mathcal{R}}^{1/2}}\left({\bar{R}}_N\sinh \bar{z}{\bar{\mathcal{F}}}_n+{\bar{\mathcal{F}}}_{\nu }\right),(54)$

${\bar{\sigma }}^{\prime }=\left(\delta \bar{K}-{\bar{K}}_0\right){\bar{K}}_0^{\prime },(55)$

where Equations 52 and 53 must be substituted in Equation 54. The membrane inhomogeneties are now related by the Equation 55. The boundary conditions generalized from Equation 4 to renormalize deformable shape under variable mean curvature evaluated in D-catenoids, i.e., $\bar{K}\approx \delta \bar{K}(\delta \mathcal{R})$:

$\delta \bar{K}\left({\bar{z}}_B\right)-{\bar{K}}_0\left({\bar{z}}_B\right)=-\frac{{\kappa }_G}{\kappa }{K}_T\left({\bar{z}}_B\right),(\mathrm{56a})$

$\bar{\sigma }\left({\bar{z}}_B\right)+\frac{1}{2}{\left(\delta \bar{K}\left({\bar{z}}_B\right)-{\bar{K}}_0\left({\bar{z}}_B\right)\right)}^2=-\frac{{\kappa }_G}{\kappa }{\mathcal{K}}_G\left({\bar{z}}_B\right).(\mathrm{56b})$

Equations 56a and 56b account for the inhomogeneous spontaneous curvature field, ${\bar{K}}_0$, the corresponding surface tension, $\bar{\sigma }$, the shaping parameters ${\bar{R}}_N$ and ${\bar{z}}_B=\bar{h}/2$, and the constant axial force ${\bar{F}}_z\equiv F_z/(2\pi \kappa )$. The no-torque boundary condition (Equation 56a) determines the constant ${\bar{F}}_z$. To solve the geometry-deformability system, we specify the parameters $\bar{R}$ and ${\bar{z}}_B$ and integrate the equations from the initial conditions at ${\bar{z}}_B$. Next, we numerically evaluate the deformation-conformal equations along the two bifurcation pathways predicted at criticality (Santiago and Monroy, 2023).

4 Discussion: necking pathways on deformable D-catenoids

We examine two necking scenarios related to abscissional processes in deformable D-catenoids characterized by dominant concave curvature $(K>0)$. They are driven by inhomogeneous spontaneous curvature from the critical point imposed by the rigid geometric configuration (${\bar{R}}^{†}\approx 1.81$ and ${\bar{h}}^{†}/{\bar{R}}^{†}\approx 1.33$): A) frustrated constrictional furrows under the terminal energy barrier (supercritical); B) elongated tubes under quasi-spontaneous abscissional relaxation (cf. near-critical neck abscission). Both necking pathways, either supercritical or critical, are considered under variable aspect radius $({\bar{R}}_N)$, causing bending torque under axial neck stretching (variable $\bar{h}$ at increasing ${\bar{F}}_z$). Deformable ${\mathrm{\Phi }}_D-$ configurations are determined by varying the aspect ratio while keeping the boundary radius $(\bar{R})$ constant (Figure 5).

4.1 Constrictional furrows: supercritical abscissional frustration $(\bar{R}=5\gg {\bar{R}}^{†})$

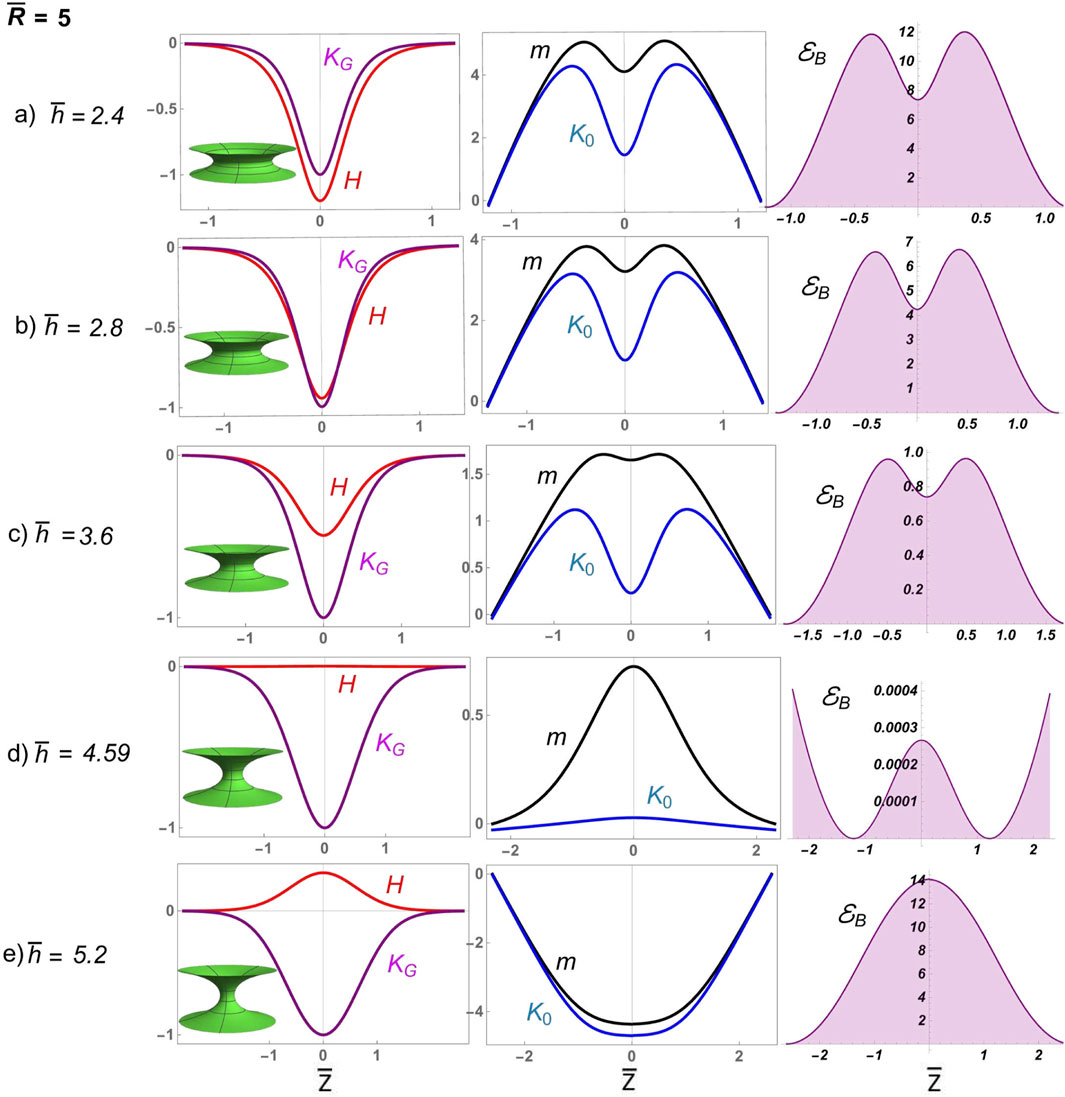
Figure 8 presents numerical solutions for deformable D-catenoids with a large neck radius, showcasing broad constrictional furrows experiencing frustrated abscission. The elongational pathway, $2.1\le \bar{R}/\bar{h}\le 0.96$, which intersects the catenoidal curve above the critical catenoid, ${(\bar{R}/\bar{h})}^{†}\approx 0.75$ (Figure 6), reveals a supercritical scenario of frustrated abscission driven by the high bending energy in the regime of extreme constriction. Initially, the furrow displays a negative mean curvature $(\bar{K}<0)$, curving inward like a saddle. The Gaussian curvature $({\bar{\mathcal{K}}}_G)$ remains negative, normalized to unity at the waist, indicating the saddle’s deepest point. The inhomogeneous spontaneous curvature $({\bar{K}}_0)$ is positive, with a dip at the waist flanked by local peaks, suggesting lateral resistance to deformation. The bending energy density exhibits a bimodal distribution with a local minimum at the equatorial waist, promoting constriction under varying mean curvatures in D-catenoids. As the surface approaches the R-catenoidal shape of minimal energy $({\mathrm{\Phi }}_R)$, where $\bar{K}$ reaches 0, ${\bar{K}}_0$ transitions from oscillating to nearly vanishing, marking the critical symmetry where tension and torsional balance at ${(\bar{R}/\bar{h})}^{†}\approx 0.75$ (Santiago and Monroy, 2023). Beyond this critical crossover, the neck transitions across the R-catenoidal curve; then, $\bar{H}$ flips positive, the surface bulges outward, and ${\bar{K}}_0$ flops negative, peaking at the waist as the membrane neck elongates. The local torque $(\bar{m})$ aligns this curvature flip–flop process, reaching its maximum at the neck waist, where constriction is greatest. Meanwhile, the bending energy, which is negligible near the calm catenoidal region, surges to a high barrier as the neck constricts further, reflecting the high energy cost of elongational deformation beyond the critical condition $(\bar{h}>{\bar{h}}^{†})$. The sharp increase in bending energy halts further elongation, trapping the system in a frustrated state unable to overcome the high energy barrier $(E_b\gg \kappa )$. This dysfunctional interplay of balanced curvatures, torque, and bending energy illustrates a membrane neck that is unable to undergo abscissional constriction $({\mathrm{\Phi }}_{\mathit{frust}}\approx {\mathrm{\Phi }}_R+\alpha {\mathrm{\Phi }}_D)$, highlighting the deformability limits in D-catenoidal configurations $(\alpha \ge 0)$.

Figure 8

Figure 8. Supercritical frustrated constrictional pathway. Several stages along a D-catenoid with border radius $\bar{R}=5$. The Panels (a-c) correspond to D-catenoids on the left of the catenoidal curve in Figure 6, while (e) is on the right. At the Gaussian curvature ${\bar{K}}_G$ has been normalized such that ${\mathcal{K}}_G=-1$ at the waist. Gaussian curvature and mean curvature $H$ as a function of $\bar{z}$ (first column); local torque $\bar{m}$ and spontaneous curvature ${\bar{K}}_0$ as a function of $\bar{z}$ (second column); density of the bending energy, ${\mathcal{E}}_B=1/2{(K-K_0)}^2$, as a function of $\bar{z}$ (third column). (a) D-catenoid of height $\bar{h}=2.4$ as an initial constrictive configuration. (d) Catenoidal shape that represents the reversibly bifurcating state with a constrictive torque concentrated in the catenoid waist, such that the mean curvature nearly vanishes $(\bar{\delta }H=0)$ under weakly positive spontaneous curvature $({\bar{K}}_0\approx 0)$, where the density of the bending energy approaches 0 $({\mathcal{E}}_B\approx 0)$. (e) Further constriction into more elongated configurations is blocked by a high bending energy barrier.

4.2 Elongational tubes: critical abscission from the metastable tipping point $(\bar{R}=1.9\approx {\bar{R}}^{†})$

The pathway to abscission under near-critical conditions reveals a regulated interplay between curvatures and forces, driven by proximity to the critical catenoid. The long elongational pathway, $1.3\le \bar{R}/\bar{h}\le 0.6$, intersects the catenoidal curve near the critical catenoid ${(\bar{R}/\bar{h})}^{†}\approx 0.75$, corresponding to ${\bar{h}}^{†}\approx 2.4$ (Figure 6) and positioning the system close to critical conditions (Figure 6). This critical elongational scenario creates a mechanical necking environment of enhanced geometry sensitivity, where subtle changes in the shape’s aspect ratio trigger pronounced mechanical responses under moderate bending energy. At small neck lengths $(\bar{h}\approx 1.5)$, the surface remains subdued, with spontaneous curvature $({\bar{K}}_0)$ requiring minimal intensity under low bending energy $(E_b\approx \kappa )$. Unlike the oscillatory behavior observed in the high-constriction supercritical regime, here, ${\bar{K}}_0$ forms a modest local peak at the waist, reflecting a tentative balance between bending and stretching forces. As the height increases and the shape morphs closer to the critical catenoid, ${\bar{K}}_0$ escalates sharply, reaching its maximum intensity at the moment of criticality. The abscissional bending energy density reaches its critical value, $E_b^{†}\approx 6\kappa$, which is lower than the high energy barrier, preventing abscission under supercritical conditions, $E_b^{(super)}\approx 15\kappa \gg E_b^{†}$ (Figure 8). This critical configuration (Figure 9C) embodies a transient yet decisive shape-energy equilibrium, where the surface achieves its most energetically efficient form. Beyond this critical point, a sudden transformation occurs. The spontaneous curvature undergoes a sudden reversal, the tipping point for starting abscissional, becoming negative with a pronounced global minimum at the waist of the D-catenoid under facilitated bending energy $(E_{\mathit{abs}}\approx \kappa )$. This inhomogeneous flipping of spontaneous curvature marks the onset of the supercritical abscissional regime $({\mathrm{\Phi }}_{\mathit{abs}}={\mathrm{\Phi }}_R-\alpha {\mathrm{\Phi }}_D)$, where the surface elongates spontaneously, and the forces driving abscission come to dominate $(\alpha <0)$. The bending energy density mirrors these transitions, remaining subdued for configurations far from the catenoid but surging intensely as the shape approaches criticality. The energetic demands at this juncture underscore the system’s struggle to transition from rigid curvature symmetry to deformable curvature inhomogeneity, leading to functional abscission.

Figure 9

Figure 9. Near-critical elongational pathway leading to neck abscission. Several stages along a D-catenoid with border radius $\bar{R}=1.9$. Panels (a, b) correspond to D-catenoids on the left of the catenoidal curve in Figure 6, while (d), and (e) are on the right. At the waist, the Gaussian curvature has been normalized such that ${\mathcal{K}}_G=-1$. (a) D-catenoid of height $\bar{h}=1.5$. Gaussian curvature and mean curvature $H$ as a function of $\bar{z}$ (first column); local torque $\bar{m}$ and spontaneous curvature ${\bar{K}}_0$ as a function of $\bar{z}$ (second column); density of the bending energy as a function of $\bar{z}$ (third column). (c) Catenoidal shape such that the mean curvature $\bar{H}=0$.

4.3 Critical bifurcations at the metastable tipping point: necking stress and torque

Figure 10a evidences the axial force ${\bar{F}}_z$ encapsulating the critical organized dynamics. For both $\bar{R}=5$ and $\bar{R}=2$, a singularity emerges near the catenoidal region. In the supercritical regime $(\bar{R}=5\gg {\bar{R}}^{†})$, the axial force initially exhibits strong repulsion $({\bar{F}}_z\ll 0)$, indicating neck extension. This spontaneously extensional force relaxes as the system approaches the rigid catenoid configuration of minimal energy $({\mathrm{\Phi }}_R)$, but it intensifies again near the geometric singularity $(\bar{h}/\bar{R}=1)$. Beyond the singularity, the force becomes attractive $({\bar{F}}_z\gg 0)$, peaking sharply as it reflects the system’s effort to overcome bending resistance to elongate beyond the unitary aspect ratio ($E_b\gg \kappa$ for $\bar{h}/\bar{R}>1$; Figure 8). Additionally, Figure 10b shows the neck-shaping torque $\bar{m}$, which is initially constrictive well below the shape singularity ($\bar{m}>0$ for $\bar{h}/\bar{R}<1$) but becomes sharply elongational above it ($\bar{m}<0$ for $\bar{h}/\bar{R}>1$). Although spontaneous constrictive behaviors also appear near criticality $(\bar{R}=2\approx {\bar{R}}^{†})$, they persist longer as the system approaches the critical elongational state (for $\bar{h}/\bar{R}\to 1.33$), where the energy barrier decreases sharply ($E_b\approx \kappa$; Figure 9), facilitating access to the elongational abscission region beyond a tipping point. In this critical regime, ${\bar{F}}_z$ diminishes, signaling the system’s relaxation into a stable post-abscission configuration. In other words, the spontaneous process of critical abscission captures the delicate choreography of curvatures, forces (stress and torque), and bending energy near the critical $R^{†}$-catenoid. The regulated transition from constrictive attractive symmetry to repulsive asymmetry unfolds with striking precision, highlighting the mechanical and energetic pathways that govern the delicately regulated process of abscission.

Figure 10

Figure 10. (a) Axial force, $F_z$, as a function of $\bar{h}/\bar{R}$. The border radius is fixed to $\bar{R}=5$ and $\bar{R}=2$. A critical point close to the catenoidal region exists in both cases. (b) Local torque $\bar{m}$ on the waist of the neck as a function of $\bar{h}/\bar{R}$. The solid line is shown as a visual guide.

4.4 Biological implications

These findings regarding catenoidal necking under critical bifurcations provide fundamental insights into membrane remodeling processes relevant to various biological functions, e.g., cytokinesis, organelle fusion and fission, endocytosis, and vesicle traffic. The identification of inhomogeneous curvature pathways, with bifurcation points distributed along the membrane, highlights the mechanical constraints that govern neck stability during scissional shape transitions, such as ring constriction and elongational tube abscission. By demonstrating how spontaneous curvature accumulation at the catenoid waist drives mechanical instability, we offer a unifying theoretical framework to describe how membranes transition from metastable configurations to scission. Our analytical approach extends previous models of membrane elasticity by incorporating explicit necking criticality, providing a deeper mechanistic understanding of membrane-mediated biological processes.

4.5 Computational modeling

The inhomogeneous CH framework provides a new modeling perspective for simulation-based studies of membrane deformation, particularly in the context of necking, leading to spontaneous scission. Atomistic and coarse-grained simulations have extensively investigated how differential stress, spontaneous curvature, and lipid asymmetry shape membrane behavior, revealing key insights into bending moments and leaflet-specific mechanical properties (Amiral and Markus, 2020; Pöyry and Vattulainen, 2016). While these computational approaches capture microscopic details of lipid organization and stress distributions, our analytical model offers a mesoscopic, energy-based perspective on critical bifurcations in deformable catenoidal membranes. By identifying precise stability conditions and spontaneous curvature inhomogeneities that drive membrane remodeling, our results provide a theoretical foundation that can help interpret and guide future simulations investigating membrane scission mechanisms. A particularly relevant connection to simulation studies lies in the role of spontaneous curvature gradients and differential stress in stabilizing or destabilizing membrane structures. Prior computational work has demonstrated that differential stress can significantly impact bilayer bending rigidity (Amiral and Markus, 2020), which is analogous to how our model predicts the role of inhomogeneous spontaneous curvature in shaping the stability of catenoidal necks. This suggests that spontaneous curvature gradients could serve as a fundamental geometric mechanism for controlled scission, complementing computational studies that emphasize charged lipid redistribution and bilayer asymmetry (Pöyry and Vattulainen, 2016). By integrating these perspectives, our work not only reinforces existing simulation findings but also offers new directions for modeling membrane remodeling under biologically relevant conditions, particularly in the computational study of neck cytokinetic processes.

5 Conclusions

This paper presents a minimal model for understanding necking deformations in biological membranes at the mesoscopic scale using the Canham–Helfrich model with an inhomogeneously distributed spontaneous curvature term, ${\bar{K}}_0$. The model couples the membrane shape equation with the equation for ${\bar{K}}_0$, predicting the elastic forces required for membrane equilibrium and the distribution of spontaneous curvature along the membrane. We revisit the catenoid case, considering both rigid minimal energy configurations $(K=0)$ and deformable perturbed states $(\delta K\ne 0)$, solving the variational problem of curvature–elasticity. The shape-conformal equilibrium reduces to the Helmholtz equation for the inhomogeneous spontaneous curvature field $K_0$, with the Gaussian curvature, ${\mathcal{K}}_G$, acting as the supporting term that injects energy from the neck boundaries. Alternatively, the equilibrium equation can be derived from the translational symmetry of the rigid catenoids (Santiago and Monroy, 2023). Both approaches yield equivalent results, but our analysis highlights the crucial role of geometry in adapting the optimal pathway for functional abscission. We discuss the geometrically critical catenoid, which separates two bifurcating branches of mechanical behavior for ${\bar{K}}_0$. Close to the critical catenoid, both ${\bar{K}}_0$ and the local torque, $\bar{m}$, are intense and decrease as one moves away from it. This critical point corresponds to a singularity in the bending energy. For abscissional catenoids with very thin, tube-like waists (in the critical regime), ${\bar{K}}_0$ approaches 0, emphasizing the tight interplay between membrane energy and curvature to lead functional abscission.

In the second part, we explore deformed shapes near the catenoid (D-catenoids), which are able to adapt optimal abscissional pathways. By fixing the boundary radius $(\bar{R})$ and varying the neck length $(\bar{h})$, we transition from shapes with negative mean curvature $(\bar{K}<0)$ to those with positive mean curvature $(\bar{K}>0)$, intersecting the catenoid of minimal energy at a specific point (the bifurcating catenoidal curve). In the region where $\bar{K}<0$, ${\bar{K}}_0$ is positive with a local minimum at the waist; it weakens as it approaches the catenoid, becomes nearly 0 in the catenoidal region before turning negative with increased intensity at the waist of the D-catenoid. A similar pattern occurs with the local torque, which does not become 0 near the catenoidal bifurcating region. The bending energy is high in the $\bar{K}<0$ region, decreases to 0 in the catenoidal region, and increases again for $\bar{K}>0$. If the boundary radius is fixed near the critical catenoid, both ${\bar{K}}_0$ and the local torque $\bar{m}$ are intense and decrease as one moves away from the critical catenoid. The bending energy follows a similar bifurcating trend, leading to successful abscission or frustrated constriction. Theoretically, solutions along the catenoid curve belong to one of two branches separated by the critical catenoid. However, even if the transition does not occur along the catenoid curve—such as by fixing the boundary radius and modifying the waist’s radius—a critical point still exists. Very close to this point, the axial force required to maintain equilibrium becomes extremely large.

Our theoretical predictions suggest that the inhomogeneous Canham–Helfrich field, extended to include adaptive spontaneous curvature, captures not a smooth transition but a sharply defined “tipping point” for spontaneous necking abscission. This critical singularity marks the sudden shift from actively forced constriction to spontaneously functional abscission, representing a self-organized criticality with the critical catenoid manifold as a geometric attractor. In physiological membrane necking contexts or in artificial systems, such as synthetic cells, lipid nanotubes, and tethered vesicles, the deformation scales analyzed in our model closely align with those observed, from the initial constrictions through deformational elongations to terminal scission. The stability constraints we establish based on spontaneous curvature gradients and mechanical tension offer predictions that can be tested in controlled experiments using micropipette aspiration, membrane pulling with optical tweezers, and force traction techniques.

6 Outlook

Future work could explore the detailed effects of inhomogeneous Canham–Helfrich necking forces and the self-organizing properties of the dynamical system. More sophisticated models incorporating intrinsic membrane order from compositional interactions and other sources of mechanical inhomogeneity (e.g., bending rigidity) could provide a deeper theoretical understanding of these self-organizing critical transitions. The inhomogeneous CH framework offers a powerful tool for designing biomimetic membrane structures in synthetic biology, where curvature responses can be precisely tuned by controlling lipid and protein interactions. By modeling the energy costs and mechanisms involved in membrane bending, our approach may enable the engineering of synthetic cells (Vecchio Domitilla et al., 2016). Through cost-benefit analysis (Stachowiak et al., 2013), dynamic cellular processes can be efficiently mimicked, providing valuable insights into the design of responsive membrane systems for various biotechnological applications. Our inhomogeneous CH model may also provide insights into curvature-driven instabilities in real cells, with potential applications in disease modeling, such as mitochondrial membrane dysfunctions (Griffin et al., 2006) and related neurodegenerative disorders (Itoh et al., 2013). Our findings on catenoidal membrane necking through critical bifurcations provide a predictive framework that may enhance our understanding of abnormal mitosis, particularly in the context of cytokinetic failure and its implications for disease modeling (Musacchio and Salmon, 2007). Given that defective cytokinesis can lead to aneuploidy and tumorigenesis, the identification of critical membrane instabilities and spontaneous scission pathways provides potential insights into the physical constraints governing successful cell division. Our analysis may contribute to understanding how membrane remodeling errors influence de novo DNA damage formation during mitotic failure, potentially informing new approaches for studying and mitigating cancer-related abnormalities in cell division. Inhomogeneous CH models could further guide experimental efforts to detect membrane-driving singularities, shedding light not only on the normal functioning of natural cells but also on the spontaneous emergence of complexity in synthetic biological systems and active soft matter models. From a biomedical perspective, understanding how membrane shape criticality leads to necking transitions could aid in designing synthetic membranes that replicate functional processes. This is particularly relevant for the development of artificial vesicles for drug delivery and biomimetic materials for controlled membrane fusion and fission. Our findings on inhomogeneous necking may assess therapeutic strategies targeting membrane remodeling in diseases where endocytosis, cytokinesis, or other membrane dynamics are dysregulated, such as cancer and viral infections.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.

Author contributions

AA-M: Investigation, Methodology, Software, Visualization, Writing – original draft. FM: Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. JS: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by several funding agencies: the Spanish Ministry of Science and Innovation (MICINN)–Agencia Estatal de Investigación (AEI) through grants TED2021-132296BC52 and PID2019-108391RB-I00 and the Comunidad de Madrid (CAM) through grants S2018/NMT-4389 and Y2018/BIO-5207.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amiral, H., and Markus, D. (2020). Spontaneous curvature, differential stress, and bending modulus of asymmetric lipid membranes. Biophysical Journal 118, 624–642. doi:10.1016/j.bpj.2019.11.3398

PubMed Abstract | CrossRef Full Text | Google Scholar

Antonny, B., Burd, C., De Camilli, P., Chen, E., Daumke, O., Faelber, K., et al. (2016). Membrane fission by dynamin: what we know and what we need to know. EMBO J 35, 2270–2284. doi:10.15252/embj.201694613

PubMed Abstract | CrossRef Full Text | Google Scholar

Banani, S. F., Rice, A. M., Peeples, W. B., Lin, Y., Jain, S., Parker, R., et al. (2016). Compositional control of Phase-separated cellular Bodies. Cell 166, 651–663. doi:10.1016/j.cell.2016.06.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Barrio, R., Alarcón, T., and Hernandez-Machado, A. (2020). The dynamics of shapes of vesicle membranes with time dependent spontaneous curvature. PLoS One 15 (1), e0227562. doi:10.1371/journal.pone.0227562

PubMed Abstract | CrossRef Full Text | Google Scholar

Beltrán-Heredia, E., Almendro-Vedia, V. G., Monroy, F., and Cao, F. (2017). Modeling the mechanics of cell division: influence of spontaneous membrane curvature, surface tension, and Osmotic pressure. Front. Physiol. 8, 312. doi:10.3389/fphys.2017.00312

PubMed Abstract | CrossRef Full Text | Google Scholar

Bisson-Filho, A. W., Hsu, Y. P., Squyres, G. R., Kuru, E., Wu, F., Jukes, C., et al. (2017). Treadmilling by FtsZ filaments drives peptidoglycan synthesis and bacterial cell division. Science 355, 739–743. doi:10.1126/science.aak9973

PubMed Abstract | CrossRef Full Text | Google Scholar

Blain, J. C., and Szostak, J. W. (2014). Progress toward synthetic cells. Annu. Rev Biochem. 83, 615–640. doi:10.1146/annurev-biochem-080411-124036

PubMed Abstract | CrossRef Full Text | Google Scholar

Burton, K., and Taylor, D. L. (1997). Traction forces of cytokinesis measured with optically modified elastic substrata. Nature 385, 450–454. doi:10.1038/385450a0

PubMed Abstract | CrossRef Full Text | Google Scholar

CampeloF, , McMahonH, T., and Kozlov, M. M. (2008). The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys. J. 95, 2325–2339. doi:10.1529/biophysj.108.133173

PubMed Abstract | CrossRef Full Text | Google Scholar

Canham, P. B. (1970). The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theoret. Biol. 26, 61–81. doi:10.1016/s0022-5193(70)80032-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Capovilla, R., and Guven, J. (2002). Stresses in lipid membranes. J. Phys. A Math. Gen. 35, 6233–6247. doi:10.1088/0305-4470/35/30/302

CrossRef Full Text | Google Scholar

Capovilla, R., Guven, J., and Santiago, J. A. (2002). Lipid membranes with an edge. Phys. Rev. E 66, 021607. doi:10.1103/physreve.66.021607

PubMed Abstract | CrossRef Full Text | Google Scholar

Carlton, J. G., Jones, H., and Eggert, U. S. (2020). Membrane and organelle dynamics during cell division. Nat Rev Mol Cell Biol 21, 151–166. doi:10.1038/s41580-019-0208-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Chabanon, M., and Rangamani, P. (2018). Gaussian curvature directs the distribution of spontaneous curvature on bilayer membrane necks. Soft Matter 14, 2281–2294. doi:10.1039/c8sm00035b

PubMed Abstract | CrossRef Full Text | Google Scholar

Chan, K. Y., Yan, C. C. S., Roan, H. Y., Hsu, S. C., Tseng, T. L., Hsiao, C. D., et al. (2022). Skin cells undergo asynthetic fission to expand body surfaces in zebrafish. Nature 605, 119–125. doi:10.1038/s41586-022-04641-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooke, R. (1995). The actomyosin engine. FASEB J. 9 (8), 636–642. doi:10.1096/fasebj.9.8.7768355

PubMed Abstract | CrossRef Full Text | Google Scholar

Deserno, M. (2015). Fluid lipid membranes: from differential geometry to curvature stresses. Chemistry and Physics of Lipids 185, 11–45. doi:10.1016/j.chemphyslip.2014.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Durand, L. (1981). Stability and oscillations of a soap film: an analytic treatment. Am. J. Phys. 49, 334–343. doi:10.1119/1.12506

CrossRef Full Text | Google Scholar

Erickson, H. P. (2009). Modeling the physics of FtsZ assembly and force generation. PNAS 106 (23), 9238–9243. doi:10.1073/pnas.0902258106

PubMed Abstract | CrossRef Full Text | Google Scholar

Eyckmans, J., Boudou, T., Yu, X., and Chen, C. S. (2011). A Hitchhiker’s guide to mechanobiology. Dev. Cell 21, 35–47. doi:10.1016/j.devcel.2011.06.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferguson, S. M., Camilli, De, and Dynamin, P. (2012). A membrane-remodeling GTPase. Nat. Rev. Mol. Cell Biol. 13, 75–88. doi:10.1038/nrm3266

PubMed Abstract | CrossRef Full Text | Google Scholar

Fletcher, D. A., and Mullins, R. D. (2010). Cell mechanics and the cytoskeleton. Nature 463 (7280), 485–492. doi:10.1038/nature08908

PubMed Abstract | CrossRef Full Text | Google Scholar

Fournier, J. B. (2007). On the stress and torque tensors in fluid membranes. Soft Matter 3, 883. doi:10.1039/b701952a

PubMed Abstract | CrossRef Full Text | Google Scholar

Frolov, V. A., Cho, M. S., Bronk, P., Reese, T. S., and Zimmerberg, J. (2000). Multiple local contact sites are induced by GPI-linked influenza hemagglutinin during hemifusion and flickering pore formation. Traffic 1 (8), 622–630. doi:10.1034/j.1600-0854.2000.010806.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Griffin, E. E., Detmer, S. A., and Chan, D. C. (2006). Molecular mechanism of mitochondrial membrane fusion. Biochimica et Biophysica Acta (BBA)-Molecular Cell Research 1763 (5-6), 482–489. doi:10.1016/j.bbamcr.2006.02.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Guillamat, P., Ignés-Mullol, J., and Sagués, F. (2016). Control of active liquid crystals with a magnetic field. Proc. Natl Acad. Sci. 113 (20), 5498–5502. doi:10.1073/pnas.1600339113

PubMed Abstract | CrossRef Full Text | Google Scholar

Guven, J. (2004). Membrane geometry with auxiliary variables and quadratic constraints. J. Phys. A Math. Gen. 37, L313–L319. doi:10.1088/0305-4470/37/28/l02

CrossRef Full Text | Google Scholar

Helfrich, W. (1973). Elastic properties of lipid bilayers-theory and possible experiments. Z. Naturforsch C 28, 693–703. doi:10.1515/znc-1973-11-1209

PubMed Abstract | CrossRef Full Text | Google Scholar

Hinshaw, J. E., and Schmid, S. L. (1995). Dynamin self-assembles into rings suggesting a mechanism for coated vesicle budding. Nature 374, 190–192. doi:10.1038/374190a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Horger, I., Campelo, F., Hernández-Machado, A., and Tarazona, P. (2010). Constricting force of filamentary protein rings evaluated from experimental result. Physical Review E 81 (3 Pt 1), 031922. doi:10.1103/PhysRevE.81.031922

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutchison, C. A., Chuang, R. Y., Noskov, V. N., Assad-Garcia, N., Deerinck, T. J., Ellisman, M. H., et al. (2016). Design and synthesis of a minimal bacterial genome. Science 351, 6280. doi:10.1126/science.aad6253

PubMed Abstract | CrossRef Full Text | Google Scholar

Itoh, K., Nakamura, K., Iijima, M., and Sesaki, H. (2013). Mitochondrial dynamics in neurodegeneration. Trends in cell biology 23 (2), 64–71. doi:10.1016/j.tcb.2012.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Jia, L. L., Pei, S., Pelcovits, R. A., and Powers, T. R. (2021). Axisymmetric membranes with edges under external force: buckling, minimal surfaces, and tethers. Soft Matter 17, 7268–7286. doi:10.1039/d1sm00827g

PubMed Abstract | CrossRef Full Text | Google Scholar

Jülicher, F., and Seifert, U. (1994). Shape equations for axisymmetric vesicles: a clarification. Phys. Rev. E 49, 4728–4731. doi:10.1103/physreve.49.4728

PubMed Abstract | CrossRef Full Text | Google Scholar

Kozlov, M. M., Campelo, F., Liska, N., Chernomordik, L. V., Marrink, S. J., and McMahon, H. T. (2014). Mechanisms shaping cell membranes. Curr. Opin. Cell Biol. 29, 53–60. doi:10.1016/j.ceb.2014.03.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Kruse, K., Berthoz, R., Barberi, L., Reymann, A.-C., and Riveline, D. (2024). Actomyosin clusters as active units shaping living matter. Current Biology 34 (20), R1045–R1058. doi:10.1016/j.cub.2024.08.043

PubMed Abstract | CrossRef Full Text | Google Scholar

López-Montero, I., López-Navajas, P., Mingorance, J., Velez, M., Vicente, M., and Monroy, F. (2013). Membrane reconstitution of FtsZ-ZipA complex inside giant spherical vesicles made of E. coli lipids: large membrane dilation and analysis of membrane plasticity. Biochimica et Biophysica Acta - Biomembranes 1828 (2), 687–698. doi:10.1016/j.bbamem.2012.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

López-Montero, I., Mateos-Gil, P., Sferrazza, M., Navajas, P. L., Rivas, G., Vélez, M., et al. (2012). Active membrane viscoelasticity by the bacterial FtsZ-division protein. Langmuir 13 28 (10), 4744–4753. doi:10.1021/la204742b

PubMed Abstract | CrossRef Full Text | Google Scholar

Margolin, W. (2005). FtsZ and the divisionof prokaryotic cells and organelles. Nat Rev Mol Cel Biol 6, 862–871. doi:10.1038/nrm1745

PubMed Abstract | CrossRef Full Text | Google Scholar

Marino, A., and Antonio, D. S. (2009). Relaxation dynamics of fluid membranes. Physical Review E 79, 031915. doi:10.1103/physreve.79.031915

CrossRef Full Text | Google Scholar

McIntosh, J. R., Molodtsov, M. I., and Ataullakhanov, F. I. (2012). Biophysics of mitosis. Quarterly Reviews of Biophysics 45 (2), 147–207. doi:10.1017/s0033583512000017

PubMed Abstract | CrossRef Full Text | Google Scholar

McMahon, H. T., and Gallop, J. L. (2005). Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature 438, 590–596. doi:10.1038/nature04396

PubMed Abstract | CrossRef Full Text | Google Scholar

Mingorance, J., Rivas, G., Vélez, M., Gómez-Puertas, P., and Vicente, M. (2010). Strong FtsZ is with the force: mechanisms to constrict bacteria. Trends Microbiol 18 (8), 348–356. doi:10.1016/j.tim.2010.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchison, T., and Salmon, E. (2001). Mitosis: a history of division. Nat Cell Biol 3, E17–E21. doi:10.1038/35050656

PubMed Abstract | CrossRef Full Text | Google Scholar

Moeendarbary, E., and Harris, A. R. (2014). Cell mechanics: principles, practices, and prospects. Wiley Interdisciplinary Reviews. Systems Biology and Medicine 6 (5), 371–388. doi:10.1002/wsbm.1275

PubMed Abstract | CrossRef Full Text | Google Scholar

Morgan, D. O. (2007). The cell cycle: principles of control. London: New Science Press.

Google Scholar

Murrell, M., Oakes, P., Lenz, M., and Gardel, M. L. (2015). Forcing cells into shape: the mechanics of actomyosin contractility. Nat Rev Mol Cell Biol 16, 486–498. doi:10.1038/nrm4012

PubMed Abstract | CrossRef Full Text | Google Scholar

Musacchio, A., and Salmon, E. (2007). The spindle-assembly checkpoint in space and time. Nat Rev Mol Cell Biol 8, 379–393. doi:10.1038/nrm2163

PubMed Abstract | CrossRef Full Text | Google Scholar

Osawa, M., Anderson, D. E., and Erickson, H. P. (2008). Reconstitution of contractile FtsZ rings in Liposomes. Science 320, 792–794. doi:10.1126/science.1154520

PubMed Abstract | CrossRef Full Text | Google Scholar

Palacci, J., Sacanna, S., Steinberg, A. P., Pine, D. J., and Chaikin, P. M. (2013). Living crystals of light-activated colloidal surfers. Science 339, 936–940. doi:10.1126/science.1230020

PubMed Abstract | CrossRef Full Text | Google Scholar

Pavin, N., and Tolić, I. M. (2016). Self-Organization and forces in the mitotic spindle. Annual Review of Biophysics 45, 279–298. doi:10.1146/annurev-biophys-062215-010934

PubMed Abstract | CrossRef Full Text | Google Scholar

Pöyry, S., and Vattulainen, I. (2016). Role of charged lipids in membrane structures—Insight given by simulations. Biochimica et Biophysica Acta (BBA)-Biomembranes 1858 (10), 2322–2333. doi:10.1016/j.bbamem.2016.03.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Prosser, S., and Pelletier, L. (2017). Mitotic spindle assembly in animal cells: a fine balancing act. Nat Rev Mol Cell Biol 18, 187–201. doi:10.1038/nrm.2016.162

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramaswamy, S. (2010). The mechanics and Statistics of active matter. Annual Review of Condensed Matter Physics 1 (1), 323–345. doi:10.1146/annurev-conmatphys-070909-104101

CrossRef Full Text | Google Scholar

Ramirez-Diaz, D. A., Merino-Salomón, A., Meyer, F., Heymann, M., Rivas, G., Bramkamp, M., et al. (2021). FtsZ induces membrane deformations via torsional stress upon GTP hydrolysis. Nat Commun 12, 3310. doi:10.1038/s41467-021-23387-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Reinhard, L. (2014). Coupling of bending and stretching deformations in vesicle membranes. Advances in Colloid and Interface Science 208, 14–24. doi:10.1016/j.cis.2014.02.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenthal, C. (2017). Force sensing in cytokinesis. Nat Cell Biol 19, 600. doi:10.1038/ncb3548

PubMed Abstract | CrossRef Full Text | Google Scholar

Sagan, H. (1992). Introduction to the calculus of variations. Courier Dover Publications.

Google Scholar

Salinas-Almaguer, S., Mell, M., Almendro-Vedia, V. G., Calero, M., Robledo-Sánchez, K. C. M., Ruiz-Suarez, C., et al. (2022). Membrane rigidity regulates E. coli proliferation rates. Sci Rep 12, 933. doi:10.1038/s41598-022-04970-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Santiago, J. A., and Monroy, F. (2020). Mechanics of nematic membranes: Euler–Lagrange equations, Noether charges, stress, torque and boundary conditions of the surface Frank’s nematic field. J. Phys. A Math. Theor. 53, 165201. doi:10.1088/1751-8121/ab7cff

CrossRef Full Text | Google Scholar

Santiago, J. A., and Monroy, F. (2023). Inhomogeneous Canham–Helfrich abscission in catenoid necks under critical membrane mosaicity. Membranes 13, 796. doi:10.3390/membranes13090796

PubMed Abstract | CrossRef Full Text | Google Scholar

Seguin, B., and Fried, E. (2014). Microphysical derivation of the Canham–Helfrich free-energy density. J. Math. Biol. 68, 647–665. doi:10.1007/s00285-013-0647-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Spivak, M. (1979). A Comprehensive introduction to differential geometry. 2nd ed. Houston, TX, USA: Publish or Perish Inc.

Google Scholar

Stachowiak, J. C., Brodsky, F. M., and Miller, E. A. (2013). A cost-benefit analysis of the physical mechanisms of membrane curvature. Nat Cell Biol 15 (9), 1019–1027. doi:10.1038/ncb2832

PubMed Abstract | CrossRef Full Text | Google Scholar

Szostak, J., Bartel, D., and Luisi, P. (2001). Synthesizing life. Nature 409, 387–390. doi:10.1038/35053176

PubMed Abstract | CrossRef Full Text | Google Scholar

Thanedar, S., and Margolin, W. (2004). FtsZ exhibits rapid movement and oscillation waves in helix-like patterns in Escherichia coli. Curr. Biol. 14, 1167–1173. doi:10.1016/j.cub.2004.06.048

PubMed Abstract | CrossRef Full Text | Google Scholar

Vecchio Domitilla, D., Dy, A. J., and Yili, Q. (2016). Control theory meets synthetic biology. J. R. Soc. Interface 13, 20160380. doi:10.1098/rsif.2016.0380

PubMed Abstract | CrossRef Full Text | Google Scholar

Walzel, F., Requier, A., Boschi, K., Farago, J., Fuchs, P., Thalmann, F., et al. (2022). Perturbing the catenoid: stability and mechanical properties of nonaxisymmetric minimal surfaces. Phys. Rev. E 106, 014803. doi:10.1103/physreve.106.014803

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J. H.-C., and Thampatty, B. P. (2006). An introductory review of cell mechanobiology. Biomechanics and Modeling in Mechanobiology 5 (1), 1–16. doi:10.1007/s10237-005-0012-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Westermann, B. (2010). Mitochondrial fusion and fission in cell life and death. Nat Rev Mol Cell Biol 11, 872–884. doi:10.1038/nrm3013

PubMed Abstract | CrossRef Full Text | Google Scholar

Yano, M., Yamamoto, Y., and Shimizu, H. (1982). An actomyosin motor. Nature 299, 557–559. doi:10.1038/299557a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, R., Lee, D. M., Jimah, J. R., Gerassimov, N., Yang, C., Kim, S., et al. (2020). Dynamin regulates the dynamics and mechanical strength of the actin cytoskeleton as a multifilament actin-bundling protein. Nat Cell Biol 22, 674–688. doi:10.1038/s41556-020-0519-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhong-Can, O. Y., and Helfrich, W. (1989). Bending energy of vesicle membranes: general expressions for the first, second, and third variation of the shape energy and applications to spheres and cylinders. Phys. Rev. A 39, 5280–5288. doi:10.1103/physreva.39.5280

PubMed Abstract | CrossRef Full Text | Google Scholar