A perspective on coarse-graining methodologies for biomolecules: resolving self-assembly over extended spatiotemporal scales

The process of self-assembly of biomolecules underlies the formation of macromolecular assemblies, biomolecular materials and protein folding, and thereby is critical in many disciplines and related applications. This process typically spans numerous spatiotemporal scales and hence, is well suited for scientific interrogation via coarse-grained (CG) models used in conjunction with a suitable computational approach. This perspective provides a discussion on different coarse-graining approaches which have been used to develop CG models that resolve the process of self-assembly of biomolecules.

1 Introduction

The self-assembly process in biomolecular systems is ubiquitous and plays a key role in the formation of macromolecular assemblies, biomolecular materials and protein folding. As a consequence, self-assembly in biomolecular systems is of importance to a diverse range of disciplines and applications. The concentration of biomolecules must be at a critical value for their assembly. The chemistry of the molecules and the resultant physical forces determine the pathways adopted during their assembly and the final equilibrium characteristics of the aggregates. Hence, the self-assembly process involves a large range of spatiotemporal scales. Due to limitations in resolution of experimental techniques, computational approaches are particularly well suited to resolve the self-assembly process starting from biomolecules dispersed in solution to the formation of an equilibrium biomolecular aggregate or material. However, on account of the enormous number of degrees of freedom (DOFs, or singular DOF), adopting atomistic representation of the molecules in the system to study their assembly using computational techniques is only viable for very small systems. For larger systems, the assembly of biomolecules can be resolved via the use of reduced models to represent the molecules in conjunction with suitable computational techniques. One of the ways to generate such reduced models of biomolecules is via coarse-graining (Papoian, 2016; Allen and Tildesley, 2017) which is the focus of this perspective.

The philosophy of coarse-graining is to represent a group of atoms by pseudo atoms or coarse-grained (CG) beads to smooth over atomistic details and the corresponding potential energy landscape, thereby significantly increasing the computational efficiency. CG models have become very popular and are used extensively in the domain of Soft Materials and Biophysics. As a consequence, there exists a rich body of work that has developed and used CG models for these two domains and others. Hence, it is not feasible to discuss all the coarse-graining approaches and CG models which are relevant to these domains. Therefore, the scope of this perspective is more narrow. The goal of this perspective is to survey different coarse-graining approaches which have been used to generate reduced models of biomolecules to examine their self-assembly and, if possible, packing within the aggregates. In addition, there is some discussion of approaches and models used to examine the folding of proteins as this can also be construed as self-assembly. The CG models discussed are typically used in conjunction with particle dynamics based computational approaches. This perspective will not cover discussions of mesoscale simulation methods which can also be used to examine self-assembly, which have been discussed in numerous excellent reviews (Aydin et al., 2020; Deaton et al., 2021). This perspective further distinguishes itself from many other outstanding reviews of CG modeling (Peter and Kremer, 2009; Noid, 2013; Potestio et al., 2014; Jin et al., 2022) by focusing on CG approaches and models that have been used to specifically examine self-assembly of biomolecules and their packing within aggregates.

The perspective will be organized into five sections including Section 1 which is the Introduction. Section 2 will discuss the different philosophies underlying coarse-graining schemes, namely, the bottom-up and the top-down coarse-graining approaches. The discussion of approaches and models in the subsection on Bottom-Up Coarse-graining Approaches will be organized into correlation function based and variational approaches. Given the rapidly growing role of machine learning on the development of CG models, Section 3 will discuss machine learning-driven bottom-up CG models designed to resolve molecular assembly. Section 4 will discuss how solvent is modeled in CG models. Sections 2–4 will discuss the strengths and weaknesses associated with each approach or model in the context of three metrics: reproducibility of structural characteristics, thermodynamic properties and transferability. The final section, Section 5, will conclude the discussion with a summary of current approaches.

2 Philosophies of coarse-graining methodologies

The methodologies for developing coarse-grained force fields for biomolecules can be classified into two categories: bottom-up and top-down approaches. These approaches along with their application to resolve the self-assembly of biomolecules and, if possible, their organization within the aggregates are detailed in this section. Figure 1 shows an outline of these approaches.

Figure 1

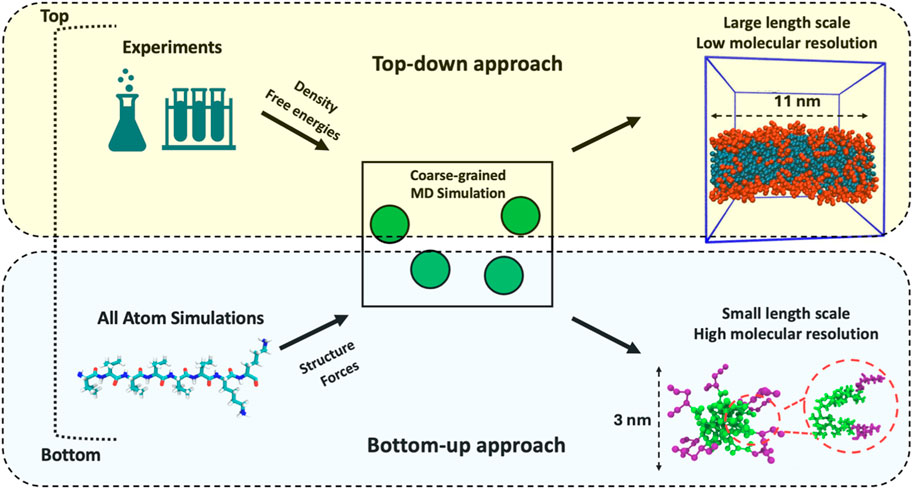
Figure 1. Top-down and bottom-up approaches employed to model assembly of biomolecules. The flowchart shows the assembly of V₆K₂ peptides. The bottom-up approach yields small micelles that provide good resolution of the local peptide-peptide interactions within the assembly. On the other hand, the top-down approach yields a larger assembly (nanorod). The local peptide-peptide interactions cannot be reliably investigated in this system.

2.1 Bottom-up coarse-graining approaches

Bottom-up coarse-graining methods aim to develop reduced models which reproduce targeted atomistic level characteristics of molecules. In this class of methods, a number of neighboring atoms in a molecule are grouped to form a CG bead based upon the target properties of interest. These properties include structural or thermodynamic properties of the molecules. The process adopted by bottom-up coarse-graining methods is to begin from a fine-grained, chemically detailed atomistic representation of the molecules, identify a coarse-graining scheme which reduces the DOFs and develop a CG model which accurately reproduces the target properties. The CG model encompasses both bonded and nonbonded potentials. The physical interactions and chemical structure are used as metrics to determine the agreement between the coarse-grained and fine-grained representations of the molecule.

2.1.1 Correlation function-based methods

Correlation function-based approaches encompass a class of techniques that develop CG models such that correlation functions obtained using CG trajectories agree with corresponding measurements obtained using all atom (AA) trajectories. An example of a correlation function is a radial distribution function (RDF). Most correlation function-based methods rely on the Henderson uniqueness theorem which states that “only one pair potential [is] able to exactly reproduce a given RDF” (Brini et al., 2013). The assumption is that a RDF can capture multibody correlations and effective pairwise interactions at low density or concentration. Hence, these methods aim at reproducing a target RDF based on the atomistic representation of the molecules.

One such method is the Boltzmann inversion (BI) (Müller-Plathe, 2002; Reith et al., 2003) technique which provides a strategy to extract the interaction energy between two particles as a function of a probability distribution function (PDF). A PDF describes the probability of finding a certain dependent variable of interest at a specified value of the independent variable. The RDF, which is defined as the probability of finding two particles at distance r from each other, is interpretable as a PDF. Beyond the RDF, a PDF could be used to represent various types of interactions, such as the distance between two particles forming a bond, the angle between three particles, the dihedral angle between four particles, or radial distribution between two nonbonded particles. All of these quantities need to be sampled extensively to form a statistically relevant PDF.

$E\left(r\right)=-K_{b}T\mathit{ln}\left(G\left(r\right)\right)$

Where $K_b$ is the Boltzmann constant, $T$ is the absolute temperature, and $G\left(r\right)$ is the RDF. Therefore, inverting the RDF and scaling it by a factor of $K_b*T$ gives a potential function that defines the energetics of a parameter. Because the RDF is inverted when generating $E\left(r\right)$, the maximum of the RDF becomes the minimum of $E\left(r\right)$. From a physical perspective, the most frequently occurring value of a parameter is assumed to be its most energetically favorable value. For example, in a molecular simulation, the most frequent bond length occurring between two bonded particles (for example, 3 Å) is the most energetically favorable bond length between these two particles. Any deviation from a bond length of 3 Å for this particular bond results in a higher bond energy, which corresponds to a decrease in the value of the RDF. Any change in the absolute temperature ($T$) will impact the shape of $E\left(r\right)$, but will not affect the parameter value [the bond length (r) described here] where the energy minimum exists.

BI has been used to resolve bonded interactions (namely, bonds, angles and dihedrals) in polymeric systems (Baschnagel et al., 2000; Villa et al., 2009a; Betancourt and Omovie, 2009; Xia et al., 2010). The method has been successful in determining potentials for interactions in the CG models which are isolated. In addition, BI has had some success in determining nonbonded potentials in systems with dilute CG sites (Tschöp et al., 1998; Louis et al., 2000), such as pure liquid or single-component systems (Moore et al., 2014). However, the method suffers from issues related to transferability of nonbonded potentials when applied to multicomponent systems (Reith et al., 2003).

Most condensed matter systems are not dilute. In multicomponent systems, the conformation of the molecules and the resulting configurations of the aggregate will be dominated by multibody interactions. However, the equation above depends only on the structure, and hence potentials calculated this way are inherently tuned to the specifics of the AA reference sample. Therefore, the CG potentials themselves are biased to the sampled AA reference conditions, including conformations of individual molecules and multibody configurations. As a result, when CG simulations using these potentials vary significantly from the AA reference conditions (e.g., in the number of molecules or their equilibrium arrangement) the RDF from an AA-mapped CG trajectory (CG RDF) will deviate from the RDF obtained from the reference AA representation (AA RDF). For example, a Boltzmann inverted potential may yield a CG RDF that would not be in good agreement with the corresponding AA RDF due to the presence of aggregates and their impact on the overall packing of the molecular system, and the corresponding change to nonbonded interactions. It is common with BI potentials to see cases in which the peaks of the CG RDF differ from those in the AA RDF in number, location, and magnitude. In general this is because the CG model lacks important multibody information which is not captured in the PDF representation. These inconsistencies often result in incorrect values of the end-to-end distance and radius of gyration for a CG representation of a biomolecule. Thus, an iterative scheme–Iterative Boltzmann Inversion (IBI)–is devised to match the AA and CG distributions and resolve some of these issues.

In the IBI method, the Boltzmann inverted potential is iteratively corrected using the difference in the potential of mean force (PMF) of the AA and CG simulations (Müller-Plathe, 2002; Reith et al., 2003)]. This method is known to improve the correspondence between the CG model and its AA reference.

The IBI method proceeds as follows: an MD simulation is run using the potential energy function for the ith step ($V_i^{CG}\left(r\right)$). Potential energy data generated from trajectories of a CG MD simulation is used to derive a PDF for the ith step ($g_i\left(r\right)$). This PDF is then compared to the reference AA PDF ($g_{ref}\left(r\right)$), and $V_i^{CG}\left(r\right)$ is updated to generate the potential function for the (i+1)th step. Thus the iteration scheme is given by the following equation:

$V_{i+1}^{\text{CG}}\left(r\right)=V_i^{\text{CG}}\left(r\right)+k_{B}T\ln \left[\frac{g_i\left(r\right)}{g_{\text{ref}}\left(r\right)}\right]$

The process then repeats itself starting with $V_{i+1}^{CG}\left(r\right)$, which is used to generate $V_{i+2}^{CG}\left(r\right)$. The process is initialized using a CG potential, V₀^CG(r), derived from the PDF generated using CG-mapped trajectories from an AA MD simulation.

The IBI method has been frequently used to resolve bonded potentials for complex liquids and polymers (Májek and Elber, 2009; Srinivas et al., 2011; Terakawa and Takada, 2011; Hadley and McCabe, 2012; Banerjee et al., 2018). For example, IBI (Bezkorovaynaya et al., 2012) has been used to derive PMFs for the DOFs of the small peptide ALA₃, which contains three amino acids in a sequence represented by seven CG beads. In this study, each amino acid side chain was represented as a single CG bead. In lipid bilayers (Hadley and McCabe, 2010a; Hadley and McCabe, 2010b; Wang and Deserno, 2010), IBI has been used to generate nonbonded potentials which have been employed to capture the chemical specificity of the polar head beads (Shelley et al., 2001).

The popularity of the IBI method is based upon treating each potential interaction and its corresponding distance independently, without explicitly addressing correlations with other interactions. The implementation of IBI requires two assumptions (Bezkorovaynaya et al., 2012). The model assumes that the total potential energy of the system is the summation of independent bonded and non-bonded components. In addition, the model assumes that the PDF describing the possible molecular conformations can be separated into its bond length, angle, and dihedral components, which implies that these DOFs are independent of one another. However, these assumptions are problematic in the case of many biomolecules, including peptides. The problem with the first assumption is that in addition to the potential energy of the bonded and non-bonded components, the potential energy provided by the solvent is very important in determining the conformation a peptide adopts, and must be taken into consideration in explicit solvent models. Therefore, corrective steps, such as explicit solvent pressure corrections and tracking of correlation between two interdependent DOFs, are needed to minimize the difference between a DOF’s PDFs computed using AA and CG trajectories. Further, the target of IBI (e.g., a RDF) may vary with different system sizes and thermodynamic variables (e.g., concentration of biomolecules or temperature of the system). Consequently, the derived potential would be non-transferable (Reith et al., 2003) across the same class of systems. Additionally, correlation function based methods like IBI depend on extensive sampling of the underlying interactions. For example, the IBI algorithm requires the system to be sampled with sufficient frequency to have a large data set for the AA particle-particle interactions in order to derive accurate CG particle-particle potentials. However, earlier studies (Villa et al., 2009b) have noted that RDFs in dilute peptide systems converge too slowly for IBI to be useful. Also, the IBI method is not based on principles of statistical mechanics, and thereby, cannot be used to systematically refine CG models with the goal of yielding thermodynamic quantities. Finally, the pair distribution function will encompass configurational degeneracy as reported by many studies (Fu et al., 2012; Potestio, 2013; Khot et al., 2019; Stillinger and Torquato, 2019; Wang et al., 2020). As a consequence, RDFs from the developed CG models can be similar. Refinements have been made to the IBI method to address the issues.

The IBI method has been extended to make the CG models transferable across specific thermodynamic variables. The standard IBI method yields CG models that are state dependent as their target properties are those associated with the AA representation of a system simulated at a particular temperature. In order to develop CG potentials that are valid over a range of temperatures, a different approach to sampling trajectories from AA MD simulations is required. To that end, the Multi-state IBI (Moore et al., 2014) method samples trajectories from multiple AA MD simulations, each running at a different temperature. Each of the AA MD simulations samples different regions of the potential energy surface. The aim is to identify a section of the surface where all the regions overlap. The potential associated with this region would be representative of the underlying interactions at multiple thermodynamic state points. The method was validated using n-alkanes. Atomistic simulations of propane and dodecane at different compositions and temperatures were set up to sample various states. The states that were in good agreement with experimental results were given a high weighting factor. The resulting potential is the weighted average of the Boltzmann inverted potentials of all AA simulations. The RDFs associated with the nonbonded interactions of the molecules were in agreement with AA distributions across a range of temperatures. In addition, the weights (for each AA MD simulation) were tuned to model structural properties like chain order parameters and tilt. Thus, the Multi-state IBI method enables the extension of CG potentials across various thermodynamic states, and yields results in reasonable agreement with atomistic structural properties.

The IBI method has been extended (Ganguly et al., 2012) to enable transferring potentials across different concentration ranges. This approach is relevant for biomolecular simulations as solute-solvent interactions (e.g., protein-water interactions) which vary significantly with concentration. The new method uses the Kirkwood−Buff (KB) solution theory in conjunction with IBI, and is therefore called KB-IBI. The theory equates the integral of a RDF (over volume) to a thermodynamic property. This integral is assumed to be a good measure of the interaction strength between two types of CG beads, and reproduces local liquid structure and solvation free-energies for multi-component systems. The KB-IBI method was validated using the urea-water system to measure the solvent-solvent interactions at various concentrations of urea. The developed CG potentials were found to be transferable over 2 M concentrations of urea. The method was also extended to capture solute-solvent (Ganguly and van der Vegt, 2013) interactions in multicomponent aqueous mixtures. In addition, the KB-IBI method was used to examine the dynamics of benzene in urea-water solutions, and reported the free-energies of benzene clusters to be in good agreement with corresponding results from AA MD simulations.

Another extension to the IBI method called coordination or cumulative-IBI (C-IBI) accounted for the proper solvation thermodynamics along with the replication of the pair-wise solution structure (de Oliveira et al., 2016). The C-IBI method used the estimate of coordination, $C\left(r\right)$, as the target function of interest rather than the RDF, $g\left(r\right)$, while proceeding through the iterative protocol as per the IBI method. The equation for $C\left(r\right)$ is provided below:

$C_{ij}\left(r\right)=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}}{g}_{ij}\left(r^{\prime }\right){r^{\prime }}^{2}d{r}^{\prime }$

Where $i$ and $j$ are the indices for each pair of particles. The initial guess of this method employs conventional (non-iterated) BI, however the iterative protocol is modified as follows:

${\mathrm{V}}_n^{C-\text{IBI}}\left(r\right)={\mathrm{V}}_{n-1}^{C-\text{IBI}}\left(r\right)+k_{\mathrm{B}}T\ln \left[\frac{C_{ij}^{n-1}\left(r\right)}{C_{ij}^{target}\left(r\right)}\right].$

The C-IBI method was tested by analyzing urea and water, both individually and in a solvent mixture. The pair-wise coordination calculation was determined to provide a good estimate of the solvent thermodynamics.

The inverse Monte Carlo (IMC) method, alternatively known as the reverse Monte Carlo method or the inverse Newton’s method, stems from the idea that for a set of temperatures and densities, two pair potentials with the same RDF can be shifted from each other by a constant (Lyubartsev and Laaksonen, 1995; Lyubartsev and Laaksonen, 1997). In this method, the effective potential interactions are iteratively refined to match target RDFs with greater precision. The IMC method was first used as a technique to iteratively generate molecular configurations whose radial distribution functions matched those calculated from neutron or x-ray scattering experiments (McGreevy and Pusztai, 1988). In the original development of the IMC method, initially $n$ atoms are randomly distributed in a simulation box with periodic boundary conditions. The density of the initial configuration corresponds to experimentally reported values. The experimental RDF is compared to the RDF associated with the initial configuration of the atoms. An atom is moved at random and if the resulting difference between the experimental structure factor at the new position and the structure factor of the initial configuration is smaller than the old difference, the move is accepted. If the difference is greater, the probability of the accuracy of the move is calculated and determines whether the new position is accepted or rejected. The algorithm underlying the method was subsequently altered to address the complexity of biomolecular systems. The revised algorithm as well as the process of determining and refining the initial atomistic configurations is described below. For the initial approximation, the value of the potential is calculated by the following equation:

$V_{\alpha }^{\left(0\right)}=-k_{B}T\ast \mathit{ln}\left(g_{\alpha }\right)$

Where ${V\left(0\right)}_{\alpha }$ is a suitable starting potential, often the PMF, $k_B$ is the Boltzman constant, T is the temperature, and $g_{\alpha }$ is the associated RDF. Initially, the potential is correlated to the RDF to yield the following relation:

$〈S_{\alpha }〉=\frac{g_{\alpha }{N}_p{A}_{\alpha }}{V}$

Where $S_{\alpha }$ is the number of particles that have the given value of the RDF ($g_{\alpha }$), $N_p$ is the number of pairs in the system, $A_{\alpha }$ is the volume of the bin, and $V$ is the total volume of the system. As the system is iteratively refined, the expression below is used to represent changes to the interactions after each accepted move:

$\Delta 〈S〉=A\Delta V$

This approach is often used to determine non-bonded interactions within the system. With increasing complexity, the initial estimate of the interaction requires refinement as the initial guess will be poor (Murtola et al., 2007). The value of $\Delta S$ can be multiplied by a factor of $r$, where $0<r<1$, to ensure the change is small enough to agree with the assumed linear approximation.

While there are many similarities between IBI and IMC, IMC has a faster convergence due to the potential update process. IBI uses an empirical update process which takes longer to converge. However, the computational cost per iteration of IMC is significantly higher. IMC utilizes thermodynamic constraints (Rühle et al., 2009) where the correction of the potential takes into consideration that the RDF could vary at all radial distances for any variation of the potential at a single point (Brini et al., 2013).

Iterative approaches, such as IMC and IBI, are useful for dense systems. As both methods depend upon an initial estimate of the RDF, an accurate initial estimate can be made via extensive sampling of the AA reference system. This would then allow for smoother peaks and more accurate analysis of the potentials. In the case of dilute systems, there are insufficient statistics for the analysis of non-bonded potentials between the CG beads relevant for interactions between biomolecules. Hence, these methods are less effective than alternate, non-iterative methods.

The IMC method was used to develop a CG model of interactions between DNA, the system ions (Cl⁺ and K⁻), and an arginine protein side-chain. The pair potentials were reconstructed using the original atomistic RDFs and the aforementioned procedure. The resulting simulation showed the CG RDFs, obtained using the IMC method, differed from the reference AA RDFs by 10%. In the CG model, explicit ions were used along with an implicit representation of the solvent (Lyubartsev et al., 2015).

The IMC method has also been used to develop a highly coarse-grained model for a 100 nm phospholipid/cholesterol bilayer with the goal of capturing accurate structural characteristics of dipalmitoylphosphatidylcholine (DPPC), a commonly studied phospholipid. The original formulation of the IMC technique yielded unphysical values for the thermodynamic properties. The IMC protocol was modified via the addition of thermodynamic constraints such as fixing the area compressibilities using experimental values. The effective interactions of the CG model were modeled through the corrected IMC protocol to reproduce corresponding interactions in the AA representation of the system (Murtola et al., 2007).

The high computational cost of the IMC method due to sampling every possible configuration has motivated the development of other correlation function-based approaches. Some of these new developments are based upon integral equations which can estimate multibody correlations. For example, an integral equation-based analytical approach which yields the effective CG interactions for polymers (Sambriski et al., 2006; Sambriski and Guenza, 2007; Clark et al., 2013). The efficiency of the parameterization process can be improved by using an inverted integral equation as an initial estimate for the IBI method.

2.1.2 Variational methods

The multibody PMF can be approximated in CG models by minimizing a relevant functional. Given the key role that forces play in the dynamics of molecules and thereby, the thermodynamics of systems, one such functional is force. Another functional that has been investigated is the relative entropy. Current approaches have examined the minimization of these functionals via the Multiscale Coarse-graining (MS-CG) and Relative Entropy Minimization (REM) methods.

The Multiscale Coarse-graining (MS-CG) (Izvekov and Voth, 2005a; Izvekov and Voth, 2005b; Izvekov and Voth, 2006) method is an extension of the Force Matching (FM) method (Izvekov et al., 2004) where multibody AA forces are projected onto the CG-mapped representation of a molecule. The difference in the CG force and the AA forces are minimized using least squares. This process results in a system of linear equations. By selecting an adequate number of frames from the AA trajectory, the system of linear equations is overdetermined and solved to yield an approximate PMF. The potential is a result of the average of PMFs calculated using multiple blocks of frames from the trajectory.

${\chi }^2={\displaystyle \sum _m^M}{\displaystyle \sum _n^N}{\left|F_{mn}^{\text{ref}}-F_{mn}^{\text{CG}}\right|}^2$

Where M is the number of MD frames, N is the number of CG beads. F^ref_mn is the force in the reference AA simulation, acting on the nth CG bead in the mth configuration, and F^CG_mn is the corresponding CG force.

The MS-CG method was tested on a dimyristoylphosphatidylcholine (DMPC) lipid bilayer using an intermediate resolution for the lipid molecule encompassing approximately 3–6 heavy atoms per CG bead. The density profile across the bilayer, radial distribution with solvent and other physical properties were observed to be in good agreement with corresponding results from AA simulations (Izvekov and Voth, 2005b).

The MS-CG method was extended to investigate equilibrium properties of proteins (Zhou et al., 2007). An alpha helical polyalanine and a β-hairpin V₅PGV₅ protein were chosen to compare the method with traditional PMF measurements. In order to validate the method across various mapping schemes, the alpha helical protein was modeled with 2 beads per amino acid, whereas the β-hairpin protein was modeled with 4 beads per amino acid. The resultant forces were compared to the derivative of the PMF (the spatial derivative of the PMF is the force at the corresponding distance). The energy wells for particular interactions were observed to be exaggerated due to multi-body effects. The inclusion of van der Waals, hydrogen bonding and electrostatic interactions into one interaction potential could potentially yield deeper energy wells. However, the potentials yielded accurate RDFs (in agreement with those corresponding to AA distributions) after long simulations.

The MS-CG method was extended to study the dynamics of protein folding using the same two proteins, the α-helical polyalanine and the β-hairpin V₅PGV₅ (Thorpe et al., 2008). Folded conformations were obtained from initially unfolded conformations. The model was validated by backmapping the CG representation to an AA representation of the molecule. The protein energy landscape for both the scales was determined to be in good agreement. In addition, the CG energy landscape was biased towards folding which helped accelerate the dynamics underlying the formation of the final folded structure.

The MS-CG method was extended to model arbitrary sequences of proteins (Hills et al., 2010) which required a generic mapping scheme for all amino acids. Chemical specificity was introduced by preserving the anisotropic packing of the AA model and polarity of the side chain residues. These requirements were fulfilled with a sidechain centric mapping scheme (namely, backbone residues: 1 CG bead; sidechain residues: 1–4 CG beads). The chemical diversity of all amino acids was simplified into five types of beads: polar, apolar, positively charged, negatively charged and alpha carbon (backbone bead). A set of simulations sampled all possible CG bead pairs. The temperature in the AA simulations was increased to rapidly sample various possible conformations. Consequently, the derived CG potentials were independent of sequence and thereby, transferable across protein sequences.

The MS-CG method captures multi-body effects in an AA system due to the manner in which the forces are projected onto a CG site. All forces in an AA system, associated to a specific CG bead, are propagated to the CG scale under the MS-CG protocol. Therefore, multi-body effects in the AA system are transferred to the CG system. These effects vary as a function of the system size and other thermodynamic variables. As a consequence, the resultant potentials are non-transferable for conditions other than those under which the potentials were developed. This constraint was addressed by the Effective Force Coarse-Graining (EF-CG) method (Wang et al., 2009) which was based on some assumptions that are applicable only to symmetrical molecules. The EF-CG scheme limited the force projection between two beads to the radial direction under the assumption that the neglected DOFs canceled out in a symmetrical molecule (namely, rotation and vibration). Since the EF-CG method matches the forces between two CG beads (in the radial direction), the multi-body effects are ignored. This method was used to develop a single-site CG model for neopentane which yielded a CG RDF in good agreement with the AA RDF. For a two-site CG model for methanol encompassing one symmetric CG bead and one asymmetric CG bead, the results are slightly skewed for the asymmetric bead. However, the potentials were transferable across different concentrations of methanol (Wang et al., 2009).

The REM method (Shell, 2008) is based upon minimization of the relative entropy between CG and AA probability distributions. The relative entropy quantifies the overlap between two molecular ensembles in the configurational phase space. In doing so, the discrepancies between the CG and AA properties are also measured. The equation for relative entropy $S_{rel}$ is given by

$S_{rel}=\sum p_T\left(i\right)\mathit{ln}\frac{p_T\left(i\right)}{p_M\left(i\right)}$

Where the summation is over all possible system configurations. $p\left(i\right)$ represents the probability of the configuration $i$, $T$ represents the target configuration, and $M$ represents the model configuration. If the target system is the AA representation and the model system is the CG representation, the equation for relative entropy becomes

$S_{rel}=\sum p_{AA}\left(i\right)\mathit{ln}\frac{p_{AA}\left(i\right)}{p_{CG}\left(i\right)}+S_{map}$

Where $S_{map}$ is the mapping entropy. The relative entropy has the following characteristics: 1) the value will always be positive, 2) the minimum value corresponds to the optimal configuration of the system, and 3) the equation is directional or asymmetric, which implies that the probabilities of the AA and CG system cannot be reversed in the equation.

The CG model parameters are variationally determined with analytical functions used for the CG potentials obtained via this method. For example, a pure Lennard-Jones (LJ) system was compared against the SPC/E water target system by measuring the relative entropy. This allowed the direct comparison between water and a simple fluid to determine the overlap between the references across different state points (Shell, 2008). The pure LJ system had effective parameters that were reproduced based on the properties of water at the state point being analyzed. The REM method was applied to the system, and the variation across the LJ parameters, ${ϵ}_{eff}$ and ${\sigma }_{eff}$, were determined to be 15% and 2%, respectively.

CG models which are consistent with their corresponding AA model must be able to capture the cross-correlations between the various DOFs. However, the CG model resulting from the MS-CG method may not be able to recreate the AA distributions for each DOF (Evans, 1990; Noid et al., 2008; Rudzinski and Noid, 2012). The iterative Yvon-Born-Greenberg (YBG) framework (Cho and Chu, 2009; Lu et al., 2013) addresses this difficulty by refining the CG models resulting from the MS-CG method. Including AA structural correlations in the force-based models required revising the approach for parameterizing the CG model. The generalized YBG (g-YBG) approach (Cho and Chu, 2009; DeMille et al., 2011) was developed to provide optimized interaction parameters for CG models while considering structural correlation functions.

The use of bottom-up CG models which capture multibody PMFs and resolve the process of large-scale self-assembly of biomolecules has been limited. This process is key to modeling the formation of biomolecular aggregates and materials while simultaneously providing insight into the packing and organization of the molecules within the aggregates. CG models (Villa et al., 2009a; Villa et al., 2009b) have been developed to examine their ability to resolve the assembly of dipeptide Diphenylalanine using both explicit and implicit solvent formulation. The nonbonded potentials were derived using PMF calculations between pairs of peptides by constraining the distance between their centers of mass. The bonded potentials were derived using IBI. An implicit solvent CG model (Ozgur and Sayar, 2020) of a peptide using BI for the bonded interactions and standard functions for the nonbonded interactions captured the secondary structure of the peptide and resolved their assembly into tetramers. The assembly of polyalanine strands into a beta-sheet like structure was resolved using a CG model developed via the REM approach (Carmichael and Shell, 2012). A bottom-up CG model (Haxton et al., 2015) with anisotropic potentials was developed to resolve the assembly of peptoids into a monolayer at the water-air interface. The spacing between the peptoids in the monolayer were observed to be in agreement with x-ray scattering measurements. A coarse-graining approach which captured multibody PMFs and the structure of the AA reference was used to develop CG models of aliphatic peptides, aromatic peptides and helical peptoids (Banerjee et al., 2022; Banerjee and Dutt, 2023a; Hooten et al., 2023). These models were able to resolve the assembly of the molecules while capturing their packing and organization within the aggregates (Figure 2). Using suitable backmapping protocols yielded the AA representation of individual molecules within assemblies (Banerjee et al., 2022; Hooten et al., 2023). In addition, these models (Banerjee et al., 2022; Banerjee and Dutt, 2023a; Hooten et al., 2023) enabled the study of large-scale self-assembly of biomolecules which resulted in the formation of aggregates in accordance with experimental observations.

Figure 2

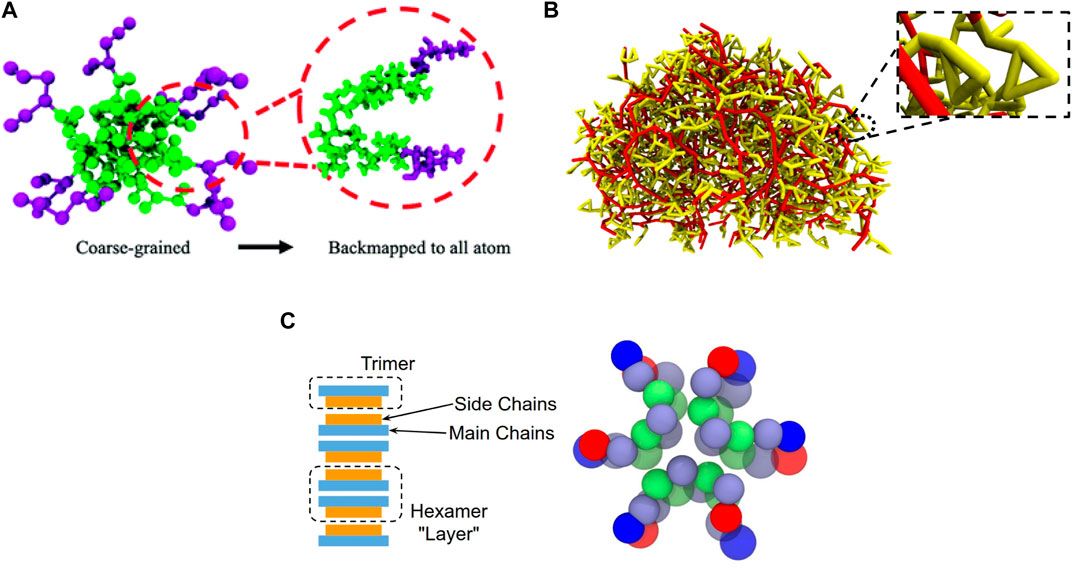
Figure 2. (A) Self-assembled micelle encompassing amphiphilic peptide with aliphatic residues obtained via CG models and backmapped to all atom representation, reproduced from (Banerjee et al., 2022) with permission from the Royal Society of Chemistry. (B) All atom representation of self-assembled hemispherical micelle encompassing helical peptoids, reproduced from (Banerjee and Dutt, 2023a). (C) Packing of aromatic tripeptides within an aggregate obtained using a CG model, adapted with permission from (Hooten et al., 2023). Copyright 2023 American Chemical Society.

Bottom-up coarse-graining approaches have been successful in capturing multibody PMFs and structural details of the AA reference. These CG models have been developed using target properties of an AA reference. The models have successfully resolved the assembly of biomolecules along with their packing and organization within aggregates. However, there exist other applications where it is important for the CG model to capture target macroscopic/thermodynamic properties of the system. These models can be developed using top-down coarse-graining approaches. These approaches largely neglect the fine-grained chemistry of the molecules and are based upon coarse-graining schemes which are able to reproduce target macroscopic properties of the system.

2.2 Top-down coarse-graining approaches

Top-down coarse-graining approaches have been developed to enable the study of dynamical processes and characteristics of molecular systems spanning large spatiotemporal scales. For example, the assembly of biomolecules and associated properties of the aggregates. These approaches yield models designed to reproduce target thermodynamic or macroscopic properties, such as density and surface tension obtained from experimental or theoretical measurements. Target properties are reproduced through the use of suitable parameterization of the nonbonded interactions. However, these approaches are unable to yield models that capture the chemical structure of the biomolecules which is related to bonded interactions. Top-down approaches can be categorized via the resolution or degree of coarse-graining of the resultant models, which determines their computational cost and efficiency. Highly coarse-grained models can resolve self-assembly over extended spatio-temporal scales at a low computational cost (Honeycutt and Thirumalai, 1990) due to significant reduction in the DOFs of a biomolecule. Whereas these models are simpler (Drouffe et al., 1991), they do not capture the detailed chemical structure of a molecule. Intermediate CG models (3–4 heavy atoms per CG bead) can provide insight into the structural and thermodynamic details of biomolecular assemblies (Bereau and Deserno, 2009). However, the computational costs and complexity of parameterization of these models is higher.

2.2.1 Coarse-grained models with low resolution

CG models with low resolutions are suitable for addressing scientific questions that are limited to the assembly or the assembly pathway of the molecules without emphasis on their chemical structure or conformation. This level of coarse-graining enables the study of biomolecular assembly (Condon and Jayaraman, 2018) with diminished emphasis on chemical details. Studies on protein folding have used simplified representations of the protein backbone (Honeycutt and Thirumalai, 1990) by limiting the parameters that define the conformation. Large samples of protein conformations were obtained by systematically varying the backbone parameters. Simulations pertaining to the different parameters were run simultaneously to identify the most stable structure on the basis of its energy. CG beads were assigned one of the three effective chemical characteristics: hydrophobic, hydrophilic and neutral. The strength of the nonbonded pair potential was determined by the effective chemistry of the beads. This brute force approach of optimizing parameters by sampling numerous conformations of a protein sequence was enabled by the low resolution of the CG model.

Considering one amino acid as a single CG bead significantly reduces the roughness of the protein folding energy landscape. This idea was extended (Baumketner et al., 2003) to study a constrained folding mechanism in a hydrophilic cavity. A ball and stick model was used, where each amino acid was represented by one CG bead centered at the alpha carbon position. These beads were connected by fixed bonds, forming a chain of spherically symmetric amino acid residues. Each CG bead was categorized into one of the three types based on the effective chemistry of the amino acid, namely, mutually attractive hydrophobic, repulsive hydrophilic and neutral. The study identified the conditions which enhanced the rate of folding as a function of temperature and cavity size. A modified protein was developed to reduce the energetic frustration between potential conformations by neglecting potentially accessible local energy minima, thereby accelerating the folding process.

Another study (Das et al., 2005) built upon existing models by incorporating details of the sequence and energetic frustration to appropriately shape the energy landscape via non-native interactions and energetic heterogeneity. These modifications distinguish the new model from prior models with the sole minimum energy requirement for the native structure (Honeycutt and Thirumalai, 1990). The study demonstrated the importance of tight packing for proper sampling of folding. Distributions of the distance between bead pairs were sampled to accurately describe interactions. The nonbonded potential was described as a function of three parameters: σ (shape of the residue), ε (energy at σ) and Δ (repulsive or attractive interactions). The parameter σ, which provides details of the sequence, was extracted from a distribution of distances between the alpha carbons in a database encompassing over 4,000 native structures of proteins. ε was determined by the following iterative process:

1. A set of decoy structures with different energies were defined.

2. One of the structures was considered as native, and the energy difference between the chosen structure and the set of decoys were evaluated.

3. The associated parameters for the chosen structure were used to run multiple heat and quench unfolding/refolding MD simulations.

4. If the native structure was recovered (that is, the root mean square between the chosen structure and the experimentally observed crystal structure was less than 1 nm), the parameter set was determined to be optimal. Otherwise, the process was repeated with another structure. This resulted in a protein folding landscape that was in good agreement with corresponding measurements using experiments.

Other studies have developed models with highly coarse-grained resolution that consist of generic descriptions for particular biomolecules and have parameters which can be tuned to mimic a wide range of systems. These types of tunable models (Drouffe et al., 1991; Cooke et al., 2005) enabled the comparison of macroscopic properties of various physiological systems using essentially the same model. For example, the thickness of various lipid bilayers was investigated with the same CG model, upon tuning a single parameter. In these models, each molecule was represented by a few CG beads (Drouffe et al., 1991; Cooke et al., 2005). Simple pair potentials were used to accelerate the self-assembly process. The thermodynamic properties of the bilayer model were aligned to many physiological lipid bilayer systems by tuning the model parameters. Although local interactions were ignored for computational efficiency, macroscopic properties like bilayer rigidity and thickness were accurately modeled. The bending rigidity (Cooke et al., 2005) of the bilayer was tuned by varying the interaction strength and range (i.e., ε and σ). Beyond capturing structural properties, the models needed to be responsive towards temperature to resolve bilayer-to-vesicle transitions. One model (Drouffe et al., 1991) introduced the hydrophobic effect in the interaction potential, mimicking lipid-water repulsions. Another model (Cooke et al., 2005) captured a phase diagram of lipid assemblies as a function of temperature and an interaction parameter. The assemblies were identified by their corresponding phase behavior (namely, gel, fluid or unstable). Extensions to an existing model (Cooke et al., 2005) have been used to examine the phase separation in a binary component lipid vesicle based upon different fluid-to-gel transition temperatures (Aydin and Dutt, 2014). This study was further extended to explore the spatial reorganization of charged lipids on the surface of a binary component vesicle using a nanoparticle with a charged patch (Aydin and Dutt, 2016). The electrostatic interactions were captured by using a Yukawa potential to implicitly represent the counterion concentration.

Another study developed a CG model (Brannigan et al., 2005) which tuned the properties of lipid bilayers by varying the chain stiffness of the lipid molecules. Each lipid was represented by five CG beads, where one bead was hydrophilic, three beads represented the hydrophobic tail, and one bead represented the interface between hydrophobic and hydrophilic moieties. The hydrophobic effect was effectively captured via strong attractive interactions between the interfacial beads. The stiffness of the lipid molecules was tuned by varying the force constant of the three body angle potentials. The force constant was systematically varied between limits that resulted in permissible values of the area per molecule (i.e., maximum value of 0.7 nm²). This tunable model could mimic bilayers that have a tendency to form pores and highly ordered packing corresponding respectively to low and high chain stiffness. The bending rigidity of bilayers were validated against corresponding experimental results. Flexible lipid membranes mimicked physical properties of membranes encompassing digalactosyldiacylglycerol (DGDG) which has a low gel-to-fluid transition temperature. Whereas stiffer lipid membranes mimicked properties of membranes encompassing DMPC which has a higher gel-to-fluid transition temperature. The model yielded results for other macroscopic properties (namely, bilayer thickness and compressibility modulus) that were in agreement with experiments.

CG models with low resolution have also been used to resolve the nucleation, growth (Zhang and Muthukumar, 2009), kinetics and temperature dependence (Wu and Shea, 2011) of the aggregation of proteins. In some cases, parameters were systematically varied to observe changes in the aggregation process and outcomes. A study (Pellarin et al., 2007) of amyloid fibril formation that has toxic effects on the human kidney investigated the pathways for self-assembly due to their potential to yield insight for novel therapeutic strategies. A key parameter (namely, the beta-aggregation propensity) was varied to determine its correlation with the assembly pathways. Changes in the beta-aggregation propensity of a polypeptide modulated the number of accessible fibril elongation pathways. Such types of model systems that are based on direct coupling between a parameter and a global property demonstrates the unique advantage of top-down coarse-graining approaches. Thus, despite ignoring several DOFs, the resolution of the model effectively preserves essential details of the assembly process along with the final structure of the fibril.

The assembly of biomolecules has also been examined by using lattice-based models (Patro and Przybycien, 1996). These models drastically reduce the computational cost for simulating large assemblies (Zhang and Muthukumar, 2009) (such as nano fibrils), and are considered as “toy” models that capture essential features of the assembly process. Processes like nucleation and kinetics have been reported by studies using lattice-based models (Wu and Shea, 2011). However, usage of these models were limited to specific properties of the aggregate, such as the cross-sectional surface properties of a protein aggregate (Patro and Przybycien, 1996). Each protein molecule was represented as a hexagon, where each side was either hydrophobic or hydrophilic. The potentials were developed using the free energy of transfer of a protein from dispersed to aggregated phase. Another example is the Hydrophobic-Polar lattice model (Dill et al., 1995), where each amino acid in a polymer sequence was coarse-grained as a single hydrophobic or polar bead and linked together to form a 2D or 3D lattice. This representation of the polymer sequence allowed for modeling of longer amino acid sequences over larger time scales by limiting the number of possible angles between bonded beads as well as the number of possible conformations adopted by the sequence. This approach to modeling polymer sequences simplified calculations of entropic, energetic, and free-energy contributions. However, these models are unable to resolve the effect of the peptide backbone and AA conformation of the amino acid residues (Dill et al., 1995).

The protein folding problem has been investigated by employing a model (Kolinski and Skolnick, 1994) which was used in two lattice-based hierarchical simulations. This model generated the three dimensional structure of a protein using its primary structure. The evolution from primary to tertiary structure provided insights concerning the folding mechanism and intermediates. The lattice-based hierarchical simulation provided these insights by limiting the number of possible spatial and angular configurations of the protein sequence, which greatly simplified thermodynamic and energetic calculations related to the folding mechanism. Initially, a coarser, flexible, lattice model designed to fold the protein into a family of possible tertiary structures beginning from the unconstrained primary sequence was set up. The generated three dimensional structure was subject to a finer lattice model which created defined patterns of hydrogen bonding and protein side chain packing. An AA MD simulation used the constraints resulting from the lattice-based simulation to limit the possible configurations it could generate. This model was used to simulate the folding of the B domain of Staphylococcal Protein A, a monomeric 120-residue version of E-coli ROP dimer, and the 46-residue protein crambin. Folding patterns with a substantial amount of accuracy and reproducibility were reported.

The mushroom and brush regimes for polymers have been studied using ultra-coarse-grained resolution models with limited structural details. A study (Crozier and Stevens, 2003) of counterion condensation on grafted polyelectrolytes (i.e., ssDNA and dsDNA) modeled each DNA monomer as one charged CG bead. The condensation of counter ions on polymer chains were observed to be a function of the chain length. Another study (Bright et al., 2001) examined polymer chains under confinement by placing tethered polymer chains between two walls. Purely repulsive potentials were used to model the excluded volume effects, and random fluctuations were induced to mimic solvent effects. Chain length, charge distribution and sequence were varied to study their effect on polymer conformation. These models provide the flexibility to modulate polymer properties to enable the study of immediate changes in their conformation.

CG models with low resolution can be applied to systems that are representative of the general characteristics of biomolecules and their assembly. These models can reproduce a subset of experimental observables and therefore have limitations on their utility. Since chemical details are ignored, accuracy of structural properties is limited to the excluded volume of each molecule within an assembly. In order to study the local organization of chemical fragments, and associated structure-activity properties, a relatively finer level of coarse-graining resolution is required.

2.2.2 Coarse-grained models with intermediate resolution

A realistic representation of a biomolecule requires greater chemical specificity and therefore, a finer level of coarse-graining by representing the molecule using a higher number of CG beads. An intermediate level of coarse-graining, where 3–4 heavy atoms are grouped into a CG bead preserves key structural characteristics. This level of coarse-graining would represent every residue (for example, an amino acid in a peptide chain) with a higher number of CG beads. Since there would be a greater number of CG bead pairs, the number of unknown parameters (for example, interaction strength or bead size) would be significantly higher. This challenge calls for rigorous parameterization involving several targets to fit the unknown model parameters. In order to achieve transferability, the chosen targets are typically experimental observations of macroscopic properties. An appropriate target is chosen for different fragments of the biomolecules. Examples of such targets include surface tension for moieties that are located at the interface with water (Shinoda et al., 2007); density for single component systems, and hydration free energy (Shinoda et al., 2007) for moieties that are miscible in water.

For some CG models with intermediate resolution, the nonbonded interactions are modeled by the Lennard-Jones potential which provides the interaction energy as a function of the distance between centers of mass (COM) of two particles. Interactions between a pair of particles are considered until a threshold distance, also known as a cutoff, is reached. Beyond the cutoff distance, the interaction between the pair of particles is neglected. For every unique interaction, one needs to determine the value of σ and ε against an appropriate target. σ is the distance between the COM of two CG beads at the energy minimum, and ε is the depth of the potential well. In some cases, the potential development process (Shinoda et al., 2007) is simplified by reducing the number of unknown parameters. For example, σ can be set to the arithmetic mean of the radii of two CG beads. Alternatively, certain mapping schemes (Souza et al., 2021) prescribe the same value of σ for the majority of CG chemical moieties. The errors arising from this approximation are corrected by determining precise values of ε. An appropriate combination of parameters would accurately define interactions between CG beads, leading to thermodynamic properties that are in good agreement with corresponding results from experiments.

The Coulomb’s equation for electrostatic potential energy is extensively used to compute long range electrostatics. These interactions are a function of the charge on each CG bead and the relative dielectric constant. The value of the relative dielectric constant is set to ensure a realistic dielectric profile. For example, the Martini model (Yesylevskyy et al., 2010) adopts a different dielectric constant for non-polarizable (ε = 15) and polarizable water (ε = 2.5).

CG models using an intermediate resolution adopt mapping schemes that attempt to reproduce local structure along with thermodynamic properties. In most of the models, the structure of a molecule is provided by bonds, angles and dihedrals. The intramolecular interactions can be implemented in different ways: the bonded interaction can be rigidly fixed about an equilibrium position; the interaction can be modeled by a harmonic potential that enables minor fluctuations, or the interactions can be implemented as a tabulated potential that would preserve majority of the atomistic structural details.

Several models with intermediate resolution have been developed over the past few decades. Each model has attempted to resolve chemical details within large biomolecular assemblies. A discussion of the respective mapping schemes and parameterization techniques to understand how each model is used is provided below.

A mapping scheme can be either specific to a biomolecule or generalized for a class of biomolecules (Souza et al., 2021). The latter scheme is transferable, and is used extensively for large scale CG MD simulations. The Martini (Souza et al., 2021) coarse-graining scheme generalizes the chemistry of lipids, protein, nucleic acids, carbohydrates and biopolymers. The distinct chemical moieties are assigned bead types that are representative of their polarity and charge. Also, hydrogen bonding is factored into the bead assignment process. The mapping scheme groups four heavy atoms into one CG bead. For aromatic residues, a finer resolution is chosen (2–3 heavy atoms per CG bead). The Martini scheme adopts a hybrid approach: the bonded interactions are resolved by comparison to atomistic simulations, and the nonbonded interactions are resolved by targeting experimental properties such as free energy of hydration or vaporization and partitioning free energy between oil and aqueous phases. The popularity of this model can be associated with characterizing a wide range of biomolecules into specific bead types. This model is transferable, and is employed for studying a diverse range of biophysical phenomena. Self-assembly of lipids into bilayers and vesicles is computationally efficient and reproducible in the Martini framework (Sharma et al., 2015). The self-organization of polyelectrolytic dendron-grafted amphiphiles (Figure 3A) within a lipid vesicle bilayer and its implications on the stability of the vesicle under different pH has been demonstrated using the Martini model (Banerjee et al., 2021; Banerjee and Dutt, 2023b). Peptide aggregation (Figures 3B, C) is accurately captured as a function of the concentration (Guo et al., 2012; Mushnoori et al., 2018; Mushnoori et al., 2023). This success can be attributed to use of a more detailed representation of the side chain residues and their chemical specificity. Hence, the Martini model has been used to study aggregation of a wide range of peptide sequences (Guo et al., 2012; Mansbach and Ferguson, 2017; Mushnoori et al., 2018; Mushnoori et al., 2023).

Figure 3

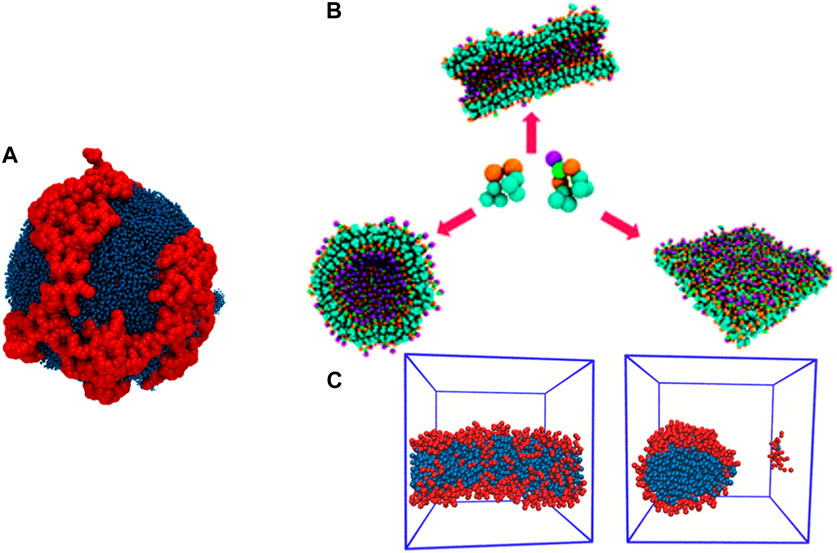
Figure 3. (A) Self-organization of PAMAM dendron-grafted amphiphiles in a vesicle bilayer at neutral pH, reproduced from (Banerjee et al., 2021) with permission from the Royal Society of Chemistry. (B) Polymorphism in morphology of nanostructures resulting from co-assembly of aromatic di- and tri-peptides, reproduced from (Mushnoori et al., 2018) with permission from the Royal Society of Chemistry. (C) Self-assembled nanorod encompassing amphiphilic peptide with aliphatic residues, reproduced from (Mushnoori et al., 2023).

Biopolymers have also been successfully modeled using the Martini framework. Polyethylene Glycol (PEG) is a polymer that is commonly used in processes such as precipitation, liquid-liquid extraction, and chromatography among others. CG MD simulations of PEG have elucidated its physicochemical properties as well as its interaction with various proteins in solution (Grünewald et al., 2021). PEG polymers of various chain lengths were studied to determine the effect of the chain length on its hydrodynamic radius and radius of gyration (Lee et al., 2009). In this study, each oxygen atom in PEG was coarse-grained into a single bead along with one of the neighboring carbon atoms.

Peptoids are peptidomimetics where the side chains are attached to Nitrogen atoms and form N-substituted glycines. They demonstrate a rich variety of secondary structures due to their lack of backbone chirality and Hydrogen bond donors. Hence, peptoids are of increasing interest for a wide range of applications in biomedicine such as antimicrobials, artificial lung surfactants, antibody markers and growth factors. Martini-compatible CG models (Gao and Tartakovsky, 2019; Zhao et al., 2020) have been developed for some peptoid sequences. One of these models demonstrated the assembly of the sequence into small aggregates which was in agreement with corresponding results using AA MD simulations (Zhao et al., 2020).

Dendrimers are another class of biopolymers where hyperbranched polymer chains, called dendrons, branch out from a multifunctional core. Dendrimers are often used in nanotechnology and biomedicine as functional groups, such as affinity ligands, radio ligands, or therapeutic compounds, can be attached to the extremities of the dendron branches (Dong et al., 2014). The binding of dendrons to lipid membranes (within the MARTINI framework) has been investigated (Li et al., 2018) for antifouling applications. Polyamidoamine (PAMAM) dendrimers are used for delivery of nucleic acid based therapeutics due to their response to changes in pH. This motivated the study of the impact of pH on the physical characteristics of PAMAM dendrimers (Chong et al., 2016). PAMAM dendrons have also been probed for their ability to remove heavy metal ions from solution (Chong and Dutt, 2015).

However, the Martini model is limited in its ability to capture protein-protein interactions. This limitation is attributed to constraints of the coarse-graining scheme which fixes the secondary structure of the protein. Hence, the model cannot be extended to systems where the secondary structure is expected to change (protein folding/unfolding) during the course of a simulation. In addition, protein-protein interactions have been reported to be over-exaggerated which has resulted in irreversible aggregation (Javanainen et al., 2017).

The PaLaCe model (Pasi et al., 2013) was developed to enable the secondary structure of a protein to change during the simulation, and thereby, resolve protein mechanics and structure-function properties. This feature is attributed to the two tier mapping scheme. The first tier isolates nonbonded interactions, where one bead is assigned to the backbone of an amino acid, and 1 or 2 beads are assigned to the side chain group (depending on its size). The second tier assigns explicit CG beads to the backbone for detailed representation of the bonded interactions. Specifically, alpha carbons, carbonyl carbons and nitrogens are each represented by a CG bead. The backbone oxygen and amide hydrogen are relatively placed as per the second tier beads. The explicit consideration of hydrogen bonds has the advantage of not constraining the secondary structure or cis/trans isomerization while neglecting the torsional coupling between large CG beads. The parameterization of the model requires a large dataset of experimentally resolved native structures in the PDB database. As the size of the dataset enables extensive sampling, the parameters are transferable across various protein sequences. The interaction energies are obtained from a probability distribution between atoms in the experimental structures, and require using the BI method on the conformational probability distribution of the structures of proteins in the PDB database. The BI method provides an initial guess for the potential which may not be appropriate for modeling folded states. Thus, an IBI protocol is employed to iteratively correct and refine the potential. A weighting factor (multiplied to the correction term) reduces the jaggedness of the final potential. The model was used to measure the mechanical properties of an immunoglobulin-like domain of Titin which were validated with corresponding measurements from experiments and AA simulations.

The united residue model (UNRES) (Li and Zhang, 2009) coarse-grains each amino acid residue as either one or two CG sites, which greatly minimizes the number of computations required to determine the global energy minimum of the CG amino acid. After computing this global energy minimum, the CG model is back-mapped to its corresponding AA representation. Back-mapping is performed by selecting the AA conformation, which corresponds to the CG model, with the optimal conformation of the hydrogen bonds. There are both on-lattice and off-lattice implementations to UNRES. The on-lattice approach discretizes the possible configurations by limiting the possible spatial configuration of the beads. In the off-lattice approach, the spatial configuration is a function of continuous variables. Therefore, the off-lattice approach provides more accurate results by sampling a larger configurational space. However, this approach requires significantly more computational power to attain the energy-minimized structure.

The optimized potential for efficient structure prediction (OPEP) (Maupetit et al., 2007) model was developed to study protein folding and aggregation. The backbone is resolved in complete atomistic detail and each side chain residue is represented with a single CG bead. To distinguish between different side chain residues, the associated van der Waal radius is varied. The bonded potentials are derived from the AA AMBER (Case et al., 2005) force field. The nonbonded potentials include contributions from van der Waals interactions and hydrogen bonding. The OPEP parameters are derived from a large dataset of decoy structures. These structures are obtained by running MD or Monte Carlo simulations or from the PDB database. They are classified into three categories which are given by native, native-like and highly unstable non-native structures. A genetic algorithm is employed to optimize model parameters on the basis of two conditions:

1. The native structure should have the lowest amount of energy

2. The energy of native-like structures should be higher than the native structure but lower than the non-native structures.

The model has been implemented to study amyloid fibril formation, where the relative compositions of different protein conformations is identified. However, due to the atomistic description of the backbone, the model cannot be used to study systems spanning large spatio-temporal scales. In addition, chemical specificity of protein sequences is limited due to the highly coarse-grained description of the side chains.

A top-down CG model was developed in conjunction with a discontinuous molecular dynamics (DMD) algorithm to efficiently study the assembly of proteins using computer simulations (Smith and Hall, 2001; Alder and Wainwright, 2004; Nguyen and Hall, 2006). The DMD method uses hard sphere CG beads in conjunction with square-well potentials that result in faster energy calculations. In continuous potentials, the repulsive component of a pair interaction involves rapid changes in the force. Since these forces are expensive to compute, square-well potentials provide a computationally efficient alternative. These potentials can model interactions with two types of calculations which include predicting the next event (i.e., collision) and determining velocities of CG beads after the event. Via the original formulation of DMD, the PRotein Intermediate Resolution ModEl (PRIME) is used to examine the self-assembly of proteins. The simulation encompasses the following steps:

1. The first event is predicted on the basis of current particle position and velocities.

2. The process moves forward in time until the event occurs.

3. The velocities and change in energy is evaluated after the event.

4. Steps 1–3 are repeated for the next event.

A DMD simulation progresses from event to event which permits the use of a large, variable time step. This feature accelerates the resolution of the self-assembly process. All systems are defined by three events: excluded volume events (namely, two hard spheres collide or repel); bond events (namely, fluctuations in a bond), and square-well events (i.e., association and dissociation of CG beads). Square-well events determine the status of all nonbonded interactions on the basis of the underlying kinetic energy. The kinetic energy of two beads is measured to determine whether the beads are associated/dissociated after an event. Energy and momentum are conserved in all events.

The mapping scheme for the PRIME model lays emphasis on the backbone, with three beads dedicated to the backbone of an amino acid, and one bead dedicated to the corresponding side chain residue. As a consequence, the model primarily captures hydrogen bonding along the backbone. The mapping scheme enables the efficient modeling of the self-assembly of random coil polyalanines into alpha helices (Smith and Hall, 2001). These structures are stabilized by the hydrogen bonding interactions along the backbone. Since the side chains are represented by one bead, the size of the side chains are varied to examine the effect of steric repulsions. The side chain-side chain steric repulsions are observed to hinder the formation of an alpha helix.

PRIME was extended to study the spontaneous formation of fibrils using polyalanines (namely, random coil peptides) at different concentrations and temperatures. At lower concentrations and temperatures, the peptides self-assemble into alpha helices. At higher concentrations, the peptides locally assemble into beta-sheets which align to form large fibrils. These fibrils are obtained above a critical temperature. The study also compares several structural properties to experiments. For example, the number of sheets formed, the degree of intra- and inter-sheet separation, and the alignment within each beta-sheet. The role of the side chains were explored by varying the size of the associated CG bead. Amorphous aggregates with larger side chain beads were observed in lieu of ordered fibrils. In another study (Nguyen et al., 2004), solvent effects are incorporated into the model by varying the relative strength of hydrophobic interactions between the side chain groups and hydrogen bonding within the backbone.

CG models have also been used to study the formation of membraneless organelles by intrinsically disordered proteins (IDPs). Dignon et al. (2018) developed a CG model that captures the phase transition of IDPs between a dilute and condensed phase. The condensed phase samples a large assembly of IDPs that provides an estimate of the properties of membraneless organelles. Each amino acid in the IDP is represented by a single bead. One of their approaches to derive the nonbonded potentials is using the hydrophobicity scale (HPS) model. The hydrophobicities of all amino acids are scaled between 0 and 1 to derive the nonbonded parameters. They are refined to match the predicted radius of gyration of the IDPs to corresponding values from experiments. The authors report a phase diagram that shows the equilibrium concentration of IDPs in condensed and dilute phases as a function of temperature. To improve the sequence specificity of the model, the same group introduced the HPS-Urry model where they use the Urry hydrophobicity scale. Here, the model can better capture the effect of sequence mutations such as an Arginine to a Lysine. The authors attribute the success of the approach in capturing phase transition behavior to their choice of nonbonded interaction parameters. These parameters are derived from the Urry hydrophobicity scale that specifically considers polypeptides transitioning from a dilute to concentrated phase (Regy et al., 2021). Another group developed a CG model that focuses on replicating the IDP ensembles from SAXS data (Baul et al., 2019). They built the Self-Organised Polymer IDP (SOP-IDP) by training their model on IDPs of varying sequence composition and length. The authors focus on replicating the conformational ensemble of IDPs as that may correlate with their biological function in biomolecular condensates. Finally, the established associated memory, water-mediated, structure and energy model (AWSEM) has been adapted for IDPs and termed AWSEM-IDP (Wu et al., 2018). This model aims at simultaneously reproducing the local chemical structure and the overall conformational ensembles of the IDP. It is noted that the AWSEM-IDP and SOP-IDP use finer coarse-grained representations in comparison to the single bead representations used by the HPS models. Majority of these works acknowledge that the accuracy of CG models will improve with the increased availability of experimental data.

A rebalanced Martini model (Benayad et al., 2021) has been used to simulate liquid droplet formation of the RNA-binding protein fused in sarcoma (FUS) low-complexity domain (LCD). A phase diagram for condensation of FUS-LCD was determined by scaling the strength of the nonbonded interactions in the Martini model. This approach yields densities observed in experiments for the dilute and dense phases. In the multiscale CG model called Mpipi (Joseph et al., 2021a) each amino or nucleic acid was represented by a unique bead using simulation and experimental data. The parameterization was developed using AA simulations and bioinformatics data to capture the pi-pi and cation-pi/pi-pi interactions along with the dominant attractive interactions attributed to specific amino acids. This model reproduced experimental trends in liquid-liquid phase separation (LLPS) for mutations of specific proteins such as FUS. Other CG models of biomolecular condensates have also used a single bead to represent each amino acid (Das et al., 2018; Dignon et al., 2018). The inclusion of explicit water and salt along with the use of a reparameterized version of the HPS protein force field (Garaizar and Espinosa, 2021) reproduced the experimental values of protein concentration and percentage of water in FUS-LCD droplets at physiological conditions. The Cocomo residue-based CG model (Valdes-Garcia et al., 2023) combined bonded interactions with short- and long-range nonbonded interactions, and predicted experimental results on LLPS systems. Minimal CG models employing patchy particles (Joseph et al., 2021b) have demonstrated RNA to enhance the stability of RNA binding protein condensates as it increases the connectivity between the molecules in the condensate. In this model, the RNA was represented by a self-avoiding polymer and the RNA binding protein as a patchy particle.

A key challenge of top-down approaches is the description of bonded interactions. In the case of proteins, many models are biased towards a certain secondary structure (Castillo et al., 2013). Thus, hybrid methods that combine bottom-up and top-down approaches are critical for preserving both the structure and thermodynamics. All atom simulations were used to derive peptide backbone dihedral potentials in conjunction with a top-down method (Seo et al., 2012). The derived potential permits changes in the secondary structure during protein aggregation. A specific atomistic target generates potentials that are sufficiently flexible so as to permit conformational changes along the backbone.

3 Machine learning-driven coarse-graining methodologies for multicomponent self-assembly of biomolecules

Machine learning has had an immediate impact in many fields of computation by automating the task of developing highly accurate models of phenomena of interest. Techniques for extrapolating model parameters from experimental or quantum data have been of interest in the MD and CG communities for many years. This is true particularly, though not only, in the subfield of bottom-up CG force field development (Müller-Plathe, 2002; Reith et al., 2003; Izvekov and Voth, 2005a; Izvekov and Voth, 2005b; Izvekov and Voth, 2006). The data-intensive nature of molecular modeling produces a situation in which there are many opportunities in the process of model development to exploit the high accuracy of ML models.

Among CG MD models of self-assembly in biophysical systems, a small number of studies have applied ML directly to the definition or parameterization of the models themselves (Ruff et al., 2015; Ge et al., 2023; Sahrmann et al., 2023). Other studies have applied ML effectively as a tool to efficiently explore the combinatorial design spaces comprising short peptides (Shmilovich et al., 2020; van Teijlingen and Tuttle, 2021; Batra et al., 2022).

3.1 ML in model parameterization

The CAMELOT bottom-up architecture (Ruff et al., 2015) uses a traditional additive force field in which the Lennard-Jones parameters of the CG model are resolved using Gaussian process Bayesian optimization (GPBO). GPBO is applied to minimize an objective function based on the error of CG pairwise particle distributions compared to AA reference samples, with clear analogy to traditional correlation function-based CG techniques. The resulting force field is applied in conjunction with Langevin dynamics to hybrid systems of colloidal particles representing large globular polypeptide sequences which interact with polyglutamine tracts, inducing the latter to form linear aggregates. A schematic showing the CG mapping architecture may be seen in Figure 4. These aggregates have been found to compare favorably with experiment.

Figure 4

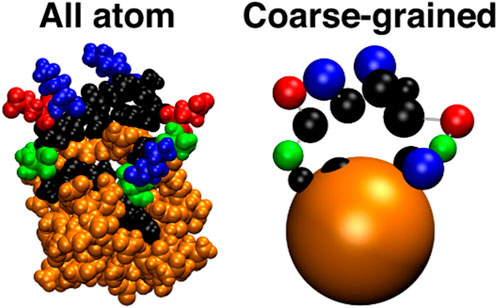
Figure 4. All atom and coarse-grained representations of N17-Q40 peptide, reproduced from (Ruff et al., 2015). In the CG model, the 17-residue N-terminal sequence (N17) is represented with one bead per residue, while the 40-residue polyglutamine sequence (Q40) is represented as a single colloid bead.

The self-assembly of diphenylalanine in aqueous ionic solvent was investigated (Ge et al., 2023) using a mixed resolution model in which the parameters coupling the two resolutions are optimized using a random forest (RF) architecture. In this mixed model, United atom representations of diphenylalanine interact with Martini CG beads representing a solvent composed of water and 1-butyl-3-methylimidazoliumtetrafluoroborate [(BMIM)+(BF4)−]. The study uses an iterative workflow in which test simulations of the mixed-model are run using trial values for the resolution coupling parameters. The test simulation results are compared to AA reference trajectories via RDFs and hydrogen bond counts. At each iteration, an RF model is trained on the results of the structural comparisons, and is used to generate a new set of trial parameters.

A variational derivative relative entropy minimization (VD-REM) methodology (Sahrmann et al., 2023) was adopted in which CG potentials are iteratively resolved using a gradient descent algorithm. Under this methodology, a simple correlation function-based CG mapping of 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) lipids in aqueous solution fails to exhibit the target behavior of bilayer formation. The authors add virtual site beads to incorporate these effects. Gradient boost models are used to construct a predictor for the conditional expectation of the potential energy derivatives, which are used to optimize virtual site interaction parameters.

3.2 ML in self-assembly workflows

ML techniques have also shown value as tools to facilitate the prediction or identification of highly valuable candidate systems from combinatorial biopolymer aggregation design spaces. Active learning workflows (Shmilovich et al., 2020; van Teijlingen and Tuttle, 2021; Batra et al., 2022) have been developed with the particular goal of CG MD self-assembly. Typically, a ML kernel is used to predict some property of interest for members of a large design space, say the set of all pentapeptides. The sequence is simulated via CG MD simulations and the results of the simulation provide feedback to the ML model for selection of the next candidate. Another study (Mushnoori et al., 2024) presents a workflow where a ML model is used to automatically categorize the structures resulting from an ensemble MD (Kasson and Jha, 2018) study. These studies demonstrate reasonable ML strategies for effectively exploring the large biomolecular design spaces which are of interest in self-assembly.

3.3 Discussion

A typical CG MD model development timeline could roughly be separated into a design cycle comprising these steps: model design; model parameterization; simulation; and sampling and analysis.

Model design includes the selection of molecular representation and force field. The model itself is often thought of in terms of intramolecular interactions, intermolecular/nonbonded interactions, and solvent effects. Parameterization is the process of numerically defining the model as it will be used to generate the simulation, usually based on empirical data (cf. top-down modeling) or on the results of a smaller-scale simulation (cf. bottom-up modeling). The parameterized model is used to run simulations from which samples are extracted and analyzed.

Based on our review of the literature, the application of ML techniques to parameterization of CG MD models of biomolecular self-assembly has been published only rarely, and typically to parameterize a physics-based model. Somewhat more common are studies in which ML is used in the analysis of simulations, or in the refinement of the models themselves as is done in iterative workflows.

We found no instances in the self-assembly literature in which ML techniques were used either in fundamental design of the dynamical model in terms of its molecular representation and force field architecture or in the execution of the simulation.

3.4 Notable advances in related fields

While the literature on ML-defined MD models of self-assembly may be limited, there has been useful progress made in the field of MD models of protein folding, where ML has been used to develop CG MD force fields capable of sampling realistic conformations in peptides and proteins. In one study (Wang et al., 2019), the bottom-up modeling strategy of force matching is reformulated as a deep learning problem, and AA data is used to train a model which learns CG free energy functions. Energy functions derived in this manner are used to simulate folding in systems of alanine dipeptide and chignolin, with positive results. In another study (Navarro et al., 2023), a neural network model is trained on experimental static protein structures to produce potential energy functions which are further refined via an iterative simulation workflow. This approach is applied to folding simulations of several proteins including chignolin and Trp-cage.

A recent review (Durumeric et al., 2023) presents these studies and others employing ML in the development of CG MD models which produce realistic folds of peptides and proteins in simulation. The particular successes of folding models built on deep learning are reasonably attributed to their ability to encode a large amount of multibody information into a high-dimensional parameter space, such as is commonly seen in modern neural networks.

Methods for model development in protein folding may also have value in multimolecular assembly. However, since folding is concerned with a single molecule at a time, there is still the unsolved problem of recalibrating the model for the interaction of multiple chains. In physics-based model development, there is typically a tradeoff between the stability of individual molecular conformation and the flexibility needed to assume realistic packing when multiple molecules come into contact. In other words, models which are biased to reproduce a single statistically-defined picture of a molecule are not necessarily transferable to the task of self-assembly, and it remains to be seen whether ML architectures could provide new capabilities or advantages on this front.

A number of other studies have investigated other ML architectures for CG biomolecular simulations which could be applied to problems of particular interest in self-assembly. For one example, graph-based CG (GBCG) (Webb et al., 2019) is a technique by which the graph definition of a macromolecule may be automatically processed into a hierarchy of progressively coarser representations. This approach provides a framework for systematically tuning structure-based CG representation. This is of particular interest since choice of molecular representation has been shown to influence the aggregation behavior of models with identical parameterization routines (Hooten et al., 2023).

4 Representation of solvent in coarse-grained models

There are two types of representation of the solvent in CG models: implicit solvent and explicit solvent representations. In the former (Nguyen and Hall, 2006; Aydin and Dutt, 2014; Chong and Dutt, 2015; Aydin and Dutt, 2016; Chong et al., 2016), the solvent is treated as a continuum with certain dielectric and interfacial properties (Zhang et al., 2017). The energetic effect of the solvent is accounted for in the parameters of the potentials. A primary advantage of this type of model is that the number of DOFs in the simulation is greatly reduced and the energy-minimized conformation of the solute is easier to achieve. This greatly reduces the computational resources required to run the simulation and allows for simulations spanning longer intervals of time. The disadvantage of using an implicit solvent representation is to forgo the physical interactions of the solute with the solvent and the important effects that these interactions have on the properties of the system. For example, ignoring hydrogen bonds between the solute and solvent molecules results in stronger intramolecular hydrogen bonds between the solute molecules, which potentially biases the results of the simulation. There has been some effort (Condon and Jayaraman, 2018) in including the effects of Hydrogen bonding in CG models which use an implicit solvent representation. Some studies (Yu and Dutt, 2020) have examined the introduction of hydrodynamic forces on the process of self-assembly by using implicit solvent CG models in conjunction with Molecular Dynamics-Lattice Boltzmann method. In explicit solvent representation (Guo et al., 2012; Mansbach and Ferguson, 2017; Mushnoori et al., 2018; Banerjee et al., 2021; Banerjee and Dutt, 2023a; Mushnoori et al., 2023), the physical effect of the solvent is considered in the model which increases the accuracy of the simulation results. However, since solvent molecules typically make up around 90% of the molecules in the system, the number of DOF for the system greatly increases. In comparison to implicit solvent models, the computational resources required to run explicit solvent models is significantly higher for the same time interval.

5 Conclusion

The self-assembly of biomolecules is prevalent in numerous disciplines and associated applications. The self-assembly process typically spans a wide range of spatiotemporal scales, and is well-suited for investigation by computational approaches using suitable reduced models, for example, CG models. The objective of this perspective is to survey coarse-graining approaches which have been used to develop CG models that resolve the self-assembly of biomolecules. To that end, the bottom-up and top-down philosophies underlying coarse-graining methodologies have been summarized. In addition, various coarse-graining methodologies within the scope of each philosophy have been discussed in some detail along with examples of their use towards the resolution of the self-assembly process. Further, recent efforts in developing CG self-assembly models via machine learning-driven algorithms have also been discussed. Throughout the discussion, the performance of the coarse-graining approaches and the resultant CG models have been critiqued using three metrics: reproducibility of structural characteristics, thermodynamic properties and transferability. Further improvement to the coarse-graining approaches are warranted to improve the performance of the CG models with respect to these metrics.

Correspondence between the dynamics in the CG representation and the dynamics in the reference is challenging for the process of self-assembly. During this process, local fluctuations in molecular concentrations are expected on account of the aggregation of the molecules. With existing coarse-graining approaches, it is not clear how the fluctuations in concentration impacts the correspondence of the CG dynamics with the dynamics of the reference system. Hence, the representation of the dynamics by these CG models and their correspondence to reference systems warrants further investigation.

In summary, there have been advances in developing CG models for resolving the self-assembly of biomolecules. Yet, significant challenges related to reproducibility of structural, thermodynamic properties, dynamics and transferability remain. These challenges must be addressed in order to improve predictions of biomolecular assembly.

Author contributions

AB: Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. MH: Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. NS: Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. RW: Investigation, Writing–original draft, Writing–review and editing. JS: Investigation, Writing–original draft. MD: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. National Science Foundation CAREER DMR-1654325, DMREF DMR-2118860, and 1835449 awards.

Acknowledgments

MD gratefully acknowledges financial support from National Science Foundation CAREER DMR-1654325, DMREF DMR-2118860, and 1835449 awards.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alder, B. J., and Wainwright, T. E. (2004). Studies in molecular dynamics. I. General method. J. Chem. Phys. 31 (2), 459–466. doi:10.1063/1.1730376

CrossRef Full Text | Google Scholar

Allen, M. P., and Tildesley, D. J. (2017). Computer simulation of liquids. Second edition. Oxford, United Kingdom: Oxford University Press.

Google Scholar

Aydin, F., Chu, X., and Dutt, M. (2020). Multiscale simulation methods: molecular dynamics and dissipative. Therm. Behav. Appl. Carbon-Based Nanomater. Theory, Methods Appl. 105. doi:10.1016/B978-0-12-817682-5.00005-2

CrossRef Full Text | Google Scholar

Aydin, F., and Dutt, M. (2014). Bioinspired vesicles encompassing two-tail phospholipids: self-assembly and phase segregation via implicit solvent coarse-grained molecular dynamics. J. Phys. Chem. B 118 (29), 8614–8623. doi:10.1021/jp503376r

PubMed Abstract | CrossRef Full Text | Google Scholar

Aydin, F., and Dutt, M. (2016). Surface reconfiguration of binary lipid vesicles via electrostatically induced nanoparticle adsorption. J. Phys. Chem. B 120 (27), 6646–6656. doi:10.1021/acs.jpcb.6b02334

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, A., and Dutt, M. (2023a). A hybrid approach for coarse-graining helical peptoids: solvation, secondary structure, and assembly. J. Chem. Phys. 158 (11), 114105. doi:10.1063/5.0138510

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, A., and Dutt, M. (2023b). Self-organization of mobile, polyelectrolytic dendrons on stable, amphiphile-based spherical surfaces. Langmuir 39 (9), 3439–3449. doi:10.1021/acs.langmuir.2c03386

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, A., Lu, C. Y., and Dutt, M. (2022). A hybrid coarse-grained model for structure, solvation and assembly of lipid-like peptides. Phys. Chem. Chem. Phys. 24 (3), 1553–1568. doi:10.1039/D1CP04205J

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, A., Tam, A., and Dutt, M. (2021). Dendronized vesicles: formation, self-organization of dendron-grafted amphiphiles and stability. Nanoscale Adv. 3 (3), 725–737. doi:10.1039/D0NA00773K

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, P., Roy, S., and Nair, N. (2018). Coarse-grained molecular dynamics force-field for polyacrylamide in infinite dilution derived from iterative Boltzmann inversion and MARTINI force-field. J. Phys. Chem. B 122 (4), 1516–1524. doi:10.1021/acs.jpcb.7b09019

PubMed Abstract | CrossRef Full Text | Google Scholar

Baschnagel, J., Binder, K., Doruker, P., Gusev, A. A., Hahn, O., Kremer, K., et al. (2000). “Bridging the gap between atomistic and coarse-grained models of polymers: status and perspectives,” in Viscoelasticity, atomistic models, statistical chemistry; advances in polymer science (Berlin, Heidelberg: Springer), 41–156.

CrossRef Full Text | Google Scholar

Batra, R., Loeffler, T. D., Chan, H., Srinivasan, S., Cui, H., Korendovych, I. V., et al. (2022). Machine learning overcomes human bias in the discovery of self-assembling peptides. Nat. Chem. 14 (12), 1427–1435. doi:10.1038/s41557-022-01055-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Baul, U., Chakraborty, D., Mugnai, M. L., Straub, J. E., and Thirumalai, D. (2019). Sequence effects on size, shape, and structural heterogeneity in intrinsically disordered proteins. J. Phys. Chem. B 123 (16), 3462–3474. doi:10.1021/acs.jpcb.9b02575

PubMed Abstract | CrossRef Full Text | Google Scholar

Baumketner, A., Jewett, A., and Shea, J. E. (2003). Effects of confinement in chaperonin assisted protein folding: rate enhancement by decreasing the roughness of the folding energy landscape. J. Mol. Biol. 332 (3), 701–713. doi:10.1016/S0022-2836(03)00929-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Benayad, Z., Von Bülow, S., Stelzl, L. S., and Hummer, G. (2021). Simulation of FUS protein condensates with an adapted coarse-grained model. J. Chem. Theory Comput. 17 (1), 525–537. doi:10.1021/acs.jctc.0c01064

PubMed Abstract | CrossRef Full Text | Google Scholar

Bereau, T., and Deserno, M. (2009). Generic coarse-grained model for protein folding and aggregation. J. Chem. Phys. 130 (23), 235106. doi:10.1063/1.3152842

PubMed Abstract | CrossRef Full Text | Google Scholar

Betancourt, M. R., and Omovie, S. J. (2009). Pairwise energies for polypeptide coarse-grained models derived from atomic force fields. J. Chem. Phys. 130 (19), 195103. doi:10.1063/1.3137045

PubMed Abstract | CrossRef Full Text | Google Scholar

Bezkorovaynaya, O., Lukyanov, A., Kremer, K., and Peter, C. (2012). Multiscale simulation of small peptides: consistent conformational sampling in atomistic and coarse-grained models. J. Comput. Chem. 33 (9), 937–949. doi:10.1002/jcc.22915

PubMed Abstract | CrossRef Full Text | Google Scholar

Brannigan, G., Philips, P. F., and Brown, F. L. H. (2005). Flexible lipid bilayers in implicit solvent. Phys. Rev. E 72 (1), 011915. doi:10.1103/PhysRevE.72.011915

PubMed Abstract | CrossRef Full Text | Google Scholar

Bright, J. N., Stevens, M. J., Hoh, J., and Woolf, T. B. (2001). Characterizing the function of unstructured proteins: simulations of charged polymers under confinement. J. Chem. Phys. 115 (10), 4909–4918. doi:10.1063/1.1392361

CrossRef Full Text | Google Scholar

Brini, E., Algaer, E. A., Ganguly, P., Li, C., Rodríguez-Ropero, F., and Vegt, N. F. A. van der. (2013). Systematic coarse-graining methods for Soft matter simulations – a review. Soft Matter 9 (7), 2108–2119. doi:10.1039/C2SM27201F

CrossRef Full Text | Google Scholar

Carmichael, S. P., and Shell, M. S. (2012). A new multiscale algorithm and its application to coarse-grained peptide models for self-assembly. J. Phys. Chem. B 116 (29), 8383–8393. doi:10.1021/jp2114994

PubMed Abstract | CrossRef Full Text | Google Scholar

Case, D. A., Cheatham, T. E., Darden, T., Gohlke, H., Luo, R., Merz, K. M., et al. (2005). The amber biomolecular simulation programs. J. Comput. Chem. 26 (16), 1668–1688. doi:10.1002/jcc.20290

PubMed Abstract | CrossRef Full Text | Google Scholar

Castillo, N., Monticelli, L., Barnoud, J., and Tieleman, D. P. (2013). Free energy of WALP23 dimer association in DMPC, DPPC, and DOPC bilayers. Chem. Phys. Lipids 169, 95–105. doi:10.1016/j.chemphyslip.2013.02.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Cho, H. M., and Chu, J.-W. (2009). Inversion of radial distribution functions to pair forces by solving the yvon–born–green equation iteratively. J. Chem. Phys. 131 (13), 134107. doi:10.1063/1.3238547

PubMed Abstract | CrossRef Full Text | Google Scholar

Chong, L., Aydin, F., and Dutt, M. (2016). Implicit solvent coarse-grained model of polyamidoamine dendrimers: role of generation and pH. J. Comput. Chem. 37 (10), 920–926. doi:10.1002/jcc.24277

PubMed Abstract | CrossRef Full Text | Google Scholar

Chong, L., and Dutt, M. (2015). Design of PAMAM-COO dendron-grafted surfaces to promote Pb(II) ion adsorption. Phys. Chem. Chem. Phys. 17 (16), 10615–10623. doi:10.1039/C5CP00309A

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, A. J., McCarty, J., and Guenza, M. G. (2013). Effective potentials for representing polymers in melts as chains of interacting Soft particles. J. Chem. Phys. 139 (12), 124906. doi:10.1063/1.4821818

PubMed Abstract | CrossRef Full Text | Google Scholar

Condon, J. E., and Jayaraman, A. (2018). Development of a coarse-grained model of collagen-like peptide (CLP) for studies of CLP triple helix melting. J. Phys. Chem. B 122 (6), 1929–1939. doi:10.1021/acs.jpcb.7b10916

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooke, I. R., Kremer, K., and Deserno, M. (2005). Tunable generic model for fluid bilayer membranes. Phys. Rev. E 72 (1), 011506. doi:10.1103/PhysRevE.72.011506

PubMed Abstract | CrossRef Full Text | Google Scholar

Crozier, P. S., and Stevens, M. J. (2003). Simulations of single grafted polyelectrolyte chains: ssDNA and dsDNA. J. Chem. Phys. 118 (8), 3855–3860. doi:10.1063/1.1540098

CrossRef Full Text | Google Scholar

Das, P., Matysiak, S., and Clementi, C. (2005). Balancing energy and entropy: a minimalist model for the characterization of protein folding landscapes. Proc. Natl. Acad. Sci. 102 (29), 10141–10146. doi:10.1073/pnas.0409471102

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, S., Amin, A. N., Lin, Y.-H., and Chan, H. S. (2018). Coarse-grained residue-based models of disordered protein condensates: utility and limitations of simple charge pattern parameters. Phys. Chem. Chem. Phys. 20 (45), 28558–28574. doi:10.1039/C8CP05095C

PubMed Abstract | CrossRef Full Text | Google Scholar

Deaton, T. A., Aydin, F., Li, N. K., Chu, X., Dutt, M., and Yingling, Y. G. (2021). “Dissipative particle dynamics approaches to modeling the self-assembly and morphology of neutral and ionic block copolymers in solution,” in Foundations of molecular modeling and simulation. Editors E. J. Maginn, and J. Errington (Singapore: Springer Singapore), 75–100. doi:10.1007/978-981-33-6639-8_4

CrossRef Full Text | Google Scholar

DeMille, R. C., Cheatham, T. E. I., and Molinero, V. (2011). A coarse-grained model of DNA with explicit solvation by water and ions. J. Phys. Chem. B 115 (1), 132–142. doi:10.1021/jp107028n

PubMed Abstract | CrossRef Full Text | Google Scholar

de Oliveira, T. E., Netz, P. A., Kremer, K., Junghans, C., and Mukherji, D. (2016). C –IBI: targeting cumulative coordination within an iterative protocol to derive coarse-grained models of (multi-component) complex fluids. J. Chem. Phys. 144 (17), 174106. doi:10.1063/1.4947253

PubMed Abstract | CrossRef Full Text | Google Scholar

Dignon, G. L., Zheng, W., Kim, Y. C., Best, R. B., and Mittal, J. (2018). Sequence determinants of protein phase behavior from a coarse-grained model. PLOS Comput. Biol. 14 (1), e1005941. doi:10.1371/journal.pcbi.1005941

PubMed Abstract | CrossRef Full Text | Google Scholar

Dill, K. A., Bromberg, S., Yue, K., Chan, H. S., Ftebig, K. M., Yee, D. P., et al. (1995). Principles of protein folding — a perspective from simple exact models. Protein Sci. 4 (4), 561–602. doi:10.1002/pro.5560040401

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, R., Zhou, Y., and Zhu, X. (2014). Supramolecular dendritic polymers: from synthesis to applications. Acc. Chem. Res. 47 (7), 2006–2016. doi:10.1021/ar500057e

PubMed Abstract | CrossRef Full Text | Google Scholar

Drouffe, J.-M., Maggs, A. C., and Leibler, S. (1991). Computer simulations of self-assembled membranes. Science 254 (5036), 1353–1356. doi:10.1126/science.1962193

PubMed Abstract | CrossRef Full Text | Google Scholar

Durumeric, A. E. P., Charron, N. E., Templeton, C., Musil, F., Bonneau, K., Pasos-Trejo, A. S., et al. (2023). Machine learned coarse-grained protein force-fields: are we there yet? Curr. Opin. Struct. Biol. 79, 102533. doi:10.1016/j.sbi.2023.102533

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, R. (1990). Comment on reverse Monte Carlo simulation. Mol. Simul. 4 (6), 409–411. doi:10.1080/08927029008022403

CrossRef Full Text | Google Scholar

Fu, C.-C., Kulkarni, P. M., Scott Shell, M., and Gary Leal, L. (2012). A test of systematic coarse-graining of molecular dynamics simulations: thermodynamic properties. J. Chem. Phys. 137 (16), 164106. doi:10.1063/1.4759463

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganguly, P., Mukherji, D., Junghans, C., and van der Vegt, N. F. A. (2012). Kirkwood–buff coarse-grained force fields for aqueous solutions. J. Chem. Theory Comput. 8 (5), 1802–1807. doi:10.1021/ct3000958

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganguly, P., and van der Vegt, N. F. A. (2013). Representability and transferability of kirkwood–buff iterative Boltzmann inversion models for multicomponent aqueous systems. J. Chem. Theory Comput. 9 (12), 5247–5256. doi:10.1021/ct400242r

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, P., and Tartakovsky, A. (2019). MARTINI-based coarse-grained model for poly(alpha-peptoid)s. arXiv. doi:10.48550/arXiv.1903.01975

CrossRef Full Text | Google Scholar

Garaizar, A., and Espinosa, J. R. (2021). Salt dependent phase behavior of intrinsically disordered proteins from a coarse-grained model with explicit water and ions. J. Chem. Phys. 155 (12), 125103. doi:10.1063/5.0062687

PubMed Abstract | CrossRef Full Text | Google Scholar

Ge, Y., Wang, X., Zhu, Q., Yang, Y., Dong, H., and Ma, J. (2023). Machine learning-guided adaptive parametrization for coupling terms in a mixed united-atom/coarse-grained model for diphenylalanine self-assembly in aqueous ionic liquids. J. Chem. Theory Comput. 19 (19), 6718–6732. doi:10.1021/acs.jctc.3c00809

PubMed Abstract | CrossRef Full Text | Google Scholar

Grünewald, F., Kroon, P. C., Souza, P. C. T., and Marrink, S. J. (2021). “Protocol for simulations of PEGylated proteins with Martini 3,” in Structural genomics: general applications. Editors Y. W. Chen, and C.-P. B. Yiu (New York, NY: Springer US), 315–335. doi:10.1007/978-1-0716-0892-0_18

CrossRef Full Text | Google Scholar

Guo, C., Luo, Y., Zhou, R., and Wei, G. (2012). Probing the self-assembly mechanism of diphenylalanine-based peptide nanovesicles and nanotubes. ACS Nano 6 (5), 3907–3918. doi:10.1021/nn300015g

PubMed Abstract | CrossRef Full Text | Google Scholar

Hadley, K. R., and McCabe, C. (2010a). A coarse-grained model for amorphous and crystalline fatty acids. J. Chem. Phys. 132 (13), 134505. doi:10.1063/1.3360146

PubMed Abstract | CrossRef Full Text | Google Scholar

Hadley, K. R., and McCabe, C. (2010b). A structurally relevant coarse-grained model for cholesterol. Biophysical J. 99 (9), 2896–2905. doi:10.1016/j.bpj.2010.08.044

PubMed Abstract | CrossRef Full Text | Google Scholar

Hadley, K. R., and McCabe, C. (2012). A simulation study of the self-assembly of coarse-grained skin lipids. Soft Matter 8 (17), 4802–4814. doi:10.1039/C2SM07204A

PubMed Abstract | CrossRef Full Text | Google Scholar

Haxton, T. K., Mannige, R. V., Zuckermann, R. N., and Whitelam, S. (2015). Modeling sequence-specific polymers using anisotropic coarse-grained sites allows quantitative comparison with experiment. J. Chem. Theory Comput. 11 (1), 303–315. doi:10.1021/ct5010559

PubMed Abstract | CrossRef Full Text | Google Scholar

Hills, R. D., Lu, L., and Voth, G. A. (2010). Multiscale coarse-graining of the protein energy landscape. PLOS Comput. Biol. 6 (6), e1000827. doi:10.1371/journal.pcbi.1000827

PubMed Abstract | CrossRef Full Text | Google Scholar

Honeycutt, J. D., and Thirumalai, D. (1990). Metastability of the folded states of globular proteins. Proc. Natl. Acad. Sci. U.S.A. 87 (9), 3526–3529. doi:10.1073/pnas.87.9.3526

PubMed Abstract | CrossRef Full Text | Google Scholar

Hooten, M., Banerjee, A., and Dutt, M. (2023). Multiscale, multiresolution coarse-grained model via a hybrid approach: solvation, structure, and self-assembly of aromatic tripeptides. J. Chem. Theory Comput. 20, 1689–1703. doi:10.1021/acs.jctc.3c00458

PubMed Abstract | CrossRef Full Text | Google Scholar

Izvekov, S., Parrinello, M., Burnham, C. J., and Voth, G. A. (2004). Effective force fields for condensed phase systems from ab initio molecular dynamics simulation: a new method for force-matching. J. Chem. Phys. 120 (23), 10896–10913. doi:10.1063/1.1739396

PubMed Abstract | CrossRef Full Text | Google Scholar

Izvekov, S., and Voth, G. A. (2005a). Multiscale coarse graining of liquid-state systems. J. Chem. Phys. 123 (13), 134105. doi:10.1063/1.2038787

PubMed Abstract | CrossRef Full Text | Google Scholar

Izvekov, S., and Voth, G. A. (2005b). A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B 109 (7), 2469–2473. doi:10.1021/jp044629q

PubMed Abstract | CrossRef Full Text | Google Scholar

Izvekov, S., and Voth, G. A. (2006). Multiscale coarse-graining of mixed phospholipid/cholesterol bilayers. J. Chem. Theory Comput. 2 (3), 637–648. doi:10.1021/ct050300c

PubMed Abstract | CrossRef Full Text | Google Scholar

Javanainen, M., Martinez-Seara, H., and Vattulainen, I. (2017). Excessive aggregation of membrane proteins in the Martini model. PLOS ONE 12 (11), e0187936. doi:10.1371/journal.pone.0187936

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, J., Pak, A. J., Durumeric, A. E. P., Loose, T. D., and Voth, G. A. (2022). Bottom-up coarse-graining: principles and perspectives. J. Chem. Theory Comput. 18 (10), 5759–5791. doi:10.1021/acs.jctc.2c00643

PubMed Abstract | CrossRef Full Text | Google Scholar

Joseph, J. A., Espinosa, J. R., Sanchez-Burgos, I., Garaizar, A., Frenkel, D., and Collepardo-Guevara, R. (2021b). Thermodynamics and kinetics of phase separation of protein-RNA mixtures by a minimal model. Biophysical J. 120 (7), 1219–1230. doi:10.1016/j.bpj.2021.01.031

CrossRef Full Text | Google Scholar

Joseph, J. A., Reinhardt, A., Aguirre, A., Chew, P. Y., Russell, K. O., Espinosa, J. R., et al. (2021a). Physics-driven coarse-grained model for biomolecular phase separation with near-quantitative accuracy. Nat. Comput. Sci. 1 (11), 732–743. doi:10.1038/s43588-021-00155-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Kasson, P. M., and Jha, S. (2018). Adaptive ensemble simulations of biomolecules. Curr. Opin. Struct. Biol. 52, 87–94. doi:10.1016/j.sbi.2018.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Khot, A., Shiring, S. B., and Savoie, B. M. (2019). Evidence of information limitations in coarse-grained models. J. Chem. Phys. 151 (24), 244105. doi:10.1063/1.5129398

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolinski, A., and Skolnick, J. (1994). Monte Carlo simulations of protein folding. I. Lattice model and interaction scheme. Proteins Struct. Funct. Bioinforma. 18 (4), 338–352. doi:10.1002/prot.340180405

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, H., de Vries, A. H., Marrink, S.-J., and Pastor, R. W. (2009). A coarse-grained model for polyethylene oxide and polyethylene glycol: conformation and hydrodynamics. J. Phys. Chem. B 113 (40), 13186–13194. doi:10.1021/jp9058966

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Jin, K., Mushnoori, S. C., and Dutt, M. (2018). Mechanisms underlying interactions between PAMAM dendron-grafted surfaces with DPPC membranes. RSC Adv. 8 (44), 24982–24992. doi:10.1039/C8RA03742F

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., and Zhang, Y. (2009). REMO: a new protocol to refine full atomic protein models from C-alpha traces by optimizing hydrogen-bonding networks. Proteins Struct. Funct. Bioinforma. 76 (3), 665–676. doi:10.1002/prot.22380

PubMed Abstract | CrossRef Full Text | Google Scholar

Louis, A. A., Bolhuis, P. G., Hansen, J. P., and Meijer, E. J. (2000). Can polymer coils Be modeled as ``Soft colloids. Phys. Rev. Lett. 85 (12), 2522–2525. doi:10.1103/PhysRevLett.85.2522

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, L., Dama, J. F., and Voth, G. A. (2013). Fitting coarse-grained distribution functions through an iterative force-matching method. J. Chem. Phys. 139 (12), 121906. doi:10.1063/1.4811667

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyubartsev, A. P., and Laaksonen, A. (1995). Calculation of effective interaction potentials from radial distribution functions: a reverse Monte Carlo approach. Phys. Rev. E 52 (4), 3730–3737. doi:10.1103/PhysRevE.52.3730

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyubartsev, A. P., and Laaksonen, A. (1997). Osmotic and activity coefficients from effective potentials for hydrated ions. Phys. Rev. E 55 (5), 5689–5696. doi:10.1103/PhysRevE.55.5689

CrossRef Full Text | Google Scholar

Lyubartsev, A. P., Naômé, A., Vercauteren, D. P., and Laaksonen, A. (2015). Systematic hierarchical coarse-graining with the inverse Monte Carlo method. J. Chem. Phys. 143 (24), 243120. doi:10.1063/1.4934095

PubMed Abstract | CrossRef Full Text | Google Scholar

Májek, P., and Elber, R. (2009). A coarse-grained potential for fold recognition and molecular dynamics simulations of proteins. Proteins Struct. Funct. Bioinforma. 76 (4), 822–836. doi:10.1002/prot.22388

CrossRef Full Text | Google Scholar

Mansbach, R. A., and Ferguson, A. L. (2017). Coarse-grained molecular simulation of the hierarchical self-assembly of π-conjugated optoelectronic peptides. J. Phys. Chem. B 121 (7), 1684–1706. doi:10.1021/acs.jpcb.6b10165

PubMed Abstract | CrossRef Full Text | Google Scholar

Maupetit, J., Tuffery, P., and Derreumaux, P. (2007). A coarse-grained protein force field for folding and structure prediction. Proteins Struct. Funct. Bioinforma. 69 (2), 394–408. doi:10.1002/prot.21505

PubMed Abstract | CrossRef Full Text | Google Scholar

McGreevy, R. L., and Pusztai, L. (1988). Reverse Monte Carlo simulation: a new technique for the determination of disordered structures. Mol. Simul. 1 (6), 359–367. doi:10.1080/08927028808080958

CrossRef Full Text | Google Scholar

Moore, T. C., Iacovella, C. R., and McCabe, C. (2014). Derivation of coarse-grained potentials via multistate iterative Boltzmann inversion. J. Chem. Phys. 140 (22), 224104. doi:10.1063/1.4880555

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller-Plathe, F. (2002). Coarse-graining in polymer simulation: from the atomistic to the mesoscopic scale and back. ChemPhysChem 3 (9), 754–769. doi:10.1002/1439-7641(20020916)3:9<754::AID-CPHC754>3.0.CO;2-U

CrossRef Full Text | Google Scholar

Murtola, T., Falck, E., Karttunen, M., and Vattulainen, I. (2007). Coarse-grained model for phospholipid/cholesterol bilayer employing inverse Monte Carlo with thermodynamic constraints. J. Chem. Phys. 126 (7), 075101. doi:10.1063/1.2646614

PubMed Abstract | CrossRef Full Text | Google Scholar

Mushnoori, S., Lu, C. Y., Schmidt, K., and Dutt, M. (2023). A coarse-grained molecular dynamics study of phase behavior in Co-assembled lipomimetic oligopeptides. J. Mol. Graph. Model. 125, 108624. doi:10.1016/j.jmgm.2023.108624

PubMed Abstract | CrossRef Full Text | Google Scholar

Mushnoori, S., Schmidt, K., Nanda, V., and Dutt, M. (2018). Designing phenylalanine-based hybrid biological materials: controlling morphology via molecular composition. Org. Biomol. Chem. 16 (14), 2499–2507. doi:10.1039/c8ob00130h

PubMed Abstract | CrossRef Full Text | Google Scholar

Mushnoori, S. C., Zang, E., Banerjee, A., Hooten, M., Merzky, A., Turilli, M., et al. (2024). Pipelines for automating compliance-based elimination and extension (pace 2): a systematic framework for high-throughput biomolecular materials simulation workflows. J. Phys. Mat. 7 (1), 015006. doi:10.1088/2515-7639/ad08d0

CrossRef Full Text | Google Scholar

Navarro, C., Majewski, M., and De Fabritiis, G. (2023). Top-down machine learning of coarse-grained protein force fields. J. Chem. Theory Comput. 19 (21), 7518–7526. doi:10.1021/acs.jctc.3c00638

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, H. D., and Hall, C. K. (2006). Spontaneous fibril formation by polyalanines; discontinuous molecular dynamics simulations. J. Am. Chem. Soc. 128 (6), 1890–1901. doi:10.1021/ja0539140

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, H. D., Marchut, A. J., and Hall, C. K. (2004). Solvent effects on the conformational transition of a model polyalanine peptide. Protein Sci. 13 (11), 2909–2924. doi:10.1110/ps.04701304

PubMed Abstract | CrossRef Full Text | Google Scholar

Noid, W. G. (2013). Perspective: coarse-grained models for biomolecular systems. J. Chem. Phys. 139 (9), 090901. doi:10.1063/1.4818908

PubMed Abstract | CrossRef Full Text | Google Scholar

Noid, W. G., Liu, P., Wang, Y., Chu, J.-W., Ayton, G. S., Izvekov, S., et al. (2008). The multiscale coarse-graining method. II. Numerical implementation for coarse-grained molecular models. J. Chem. Phys. 128 (24), 244115. doi:10.1063/1.2938857

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozgur, B., and Sayar, M. (2020). Representation of the conformational ensemble of peptides in coarse grained simulations. J. Chem. Phys. 153 (5), 054108. doi:10.1063/5.0012391

PubMed Abstract | CrossRef Full Text | Google Scholar

G. A. Papoian (2016). Coarse-grained modeling of biomolecules (Boca Raton: CRC Press). doi:10.1201/9781315374284

CrossRef Full Text | Google Scholar

Pasi, M., Lavery, R., and Ceres, N. (2013). PaLaCe: a coarse-grain protein model for studying mechanical properties. J. Chem. Theory Comput. 9 (1), 785–793. doi:10.1021/ct3007925

PubMed Abstract | CrossRef Full Text | Google Scholar

Patro, S. Y., and Przybycien, T. M. (1996). Simulations of reversible protein aggregate and crystal structure. Biophysical J. 70 (6), 2888–2902. doi:10.1016/S0006-3495(96)79859-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Pellarin, R., Guarnera, E., and Caflisch, A. (2007). Pathways and intermediates of amyloid fibril formation. J. Mol. Biol. 374 (4), 917–924. doi:10.1016/j.jmb.2007.09.090

PubMed Abstract | CrossRef Full Text | Google Scholar

Peter, C., and Kremer, K. (2009). Multiscale simulation of Soft matter systems–from the atomistic to the coarse-grained level and back. Soft Matter 5 (22), 4357–4366. doi:10.1039/b912027k

CrossRef Full Text | Google Scholar

Potestio, R. (2013). Is henderson’s theorem practically useful? JUnQ 3, 13–15.

Google Scholar

Potestio, R., Peter, C., and Kremer, K. (2014). Computer simulations of Soft matter: linking the scales. Entropy 16 (8), 4199–4245. doi:10.3390/e16084199

CrossRef Full Text | Google Scholar

Regy, R. M., Thompson, J., Kim, Y. C., and Mittal, J. (2021). Improved coarse-grained model for studying sequence dependent phase separation of disordered proteins. Protein Sci. 30 (7), 1371–1379. doi:10.1002/pro.4094

PubMed Abstract | CrossRef Full Text | Google Scholar

Reith, D., Pütz, M., and Müller-Plathe, F. (2003). Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 24 (13), 1624–1636. doi:10.1002/jcc.10307

PubMed Abstract | CrossRef Full Text | Google Scholar

Rudzinski, J. F., and Noid, W. G. (2012). The role of many-body correlations in determining potentials for coarse-grained models of equilibrium structure. J. Phys. Chem. B 116 (29), 8621–8635. doi:10.1021/jp3002004

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruff, K. M., Harmon, T. S., and Pappu, R. V. (2015). CAMELOT: a machine learning approach for coarse-grained simulations of aggregation of block-copolymeric protein sequences. J. Chem. Phys. 143 (24), 243123. doi:10.1063/1.4935066

PubMed Abstract | CrossRef Full Text | Google Scholar

Rühle, V., Junghans, C., Lukyanov, A., Kremer, K., and Andrienko, D. (2009). Versatile object-oriented toolkit for coarse-graining applications. J. Chem. Theory Comput. 5 (12), 3211–3223. doi:10.1021/ct900369w

PubMed Abstract | CrossRef Full Text | Google Scholar

Sahrmann, P. G., Loose, T. D., Durumeric, A. E. P., and Voth, G. A. (2023). Utilizing machine learning to greatly expand the range and accuracy of bottom-up coarse-grained models through virtual particles. J. Chem. Theory Comput. 19 (14), 4402–4413. doi:10.1021/acs.jctc.2c01183

PubMed Abstract | CrossRef Full Text | Google Scholar

Sambriski, E. J., and Guenza, M. G. (2007). Theoretical coarse-graining approach to bridge length scales in diblock copolymer liquids. Phys. Rev. E 76 (5), 051801. doi:10.1103/PhysRevE.76.051801

PubMed Abstract | CrossRef Full Text | Google Scholar

Sambriski, E. J., Yatsenko, G., Nemirovskaya, M. A., and Guenza, M. G. (2006). Analytical coarse-grained description for polymer melts. J. Chem. Phys. 125 (23), 234902. doi:10.1063/1.2404669

PubMed Abstract | CrossRef Full Text | Google Scholar

Seo, M., Rauscher, S., Pomès, R., and Tieleman, D. P. (2012). Improving internal peptide dynamics in the coarse-grained MARTINI model: toward large-scale simulations of amyloid- and elastin-like peptides. J. Chem. Theory Comput. 8 (5), 1774–1785. doi:10.1021/ct200876v

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharma, S., Kim, B. N., Stansfeld, P. J., Sansom, M. S. P., and Lindau, M. (2015). A coarse grained model for a lipid membrane with physiological composition and leaflet asymmetry. PLOS ONE 10 (12), e0144814. doi:10.1371/journal.pone.0144814

PubMed Abstract | CrossRef Full Text | Google Scholar

Shell, M. S. (2008). The relative entropy is fundamental to multiscale and inverse thermodynamic problems. J. Chem. Phys. 129 (14), 144108. doi:10.1063/1.2992060

PubMed Abstract | CrossRef Full Text | Google Scholar

Shelley, J. C., Shelley, M. Y., Reeder, R. C., Bandyopadhyay, S., and Klein, M. L. (2001). A coarse grain model for phospholipid simulations. J. Phys. Chem. B 105 (19), 4464–4470. doi:10.1021/jp010238p

CrossRef Full Text | Google Scholar

Shinoda, W., DeVane, R., and Klein, M. L. (2007). Multi-property fitting and parameterization of a coarse grained model for aqueous surfactants. Mol. Simul. 33 (1–2), 27–36. doi:10.1080/08927020601054050

CrossRef Full Text | Google Scholar

Shmilovich, K., Mansbach, R. A., Sidky, H., Dunne, O. E., Panda, S. S., Tovar, J. D., et al. (2020). Discovery of self-assembling π-conjugated peptides by active learning-directed coarse-grained molecular simulation. J. Phys. Chem. B 124 (19), 3873–3891. doi:10.1021/acs.jpcb.0c00708

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, A. V., and Hall, C. K. (2001). α-Helix formation: discontinuous molecular dynamics on an intermediate-resolution protein model. Proteins Struct. Funct. Bioinforma. 44 (3), 344–360. doi:10.1002/prot.1100

CrossRef Full Text | Google Scholar

Souza, P. C. T., Alessandri, R., Barnoud, J., Thallmair, S., Faustino, I., Grünewald, F., et al. (2021). Martini 3: a general purpose force field for coarse-grained molecular dynamics. Nat. Methods 18 (4), 382–388. doi:10.1038/s41592-021-01098-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Srinivas, G., Cheng, X., and Smith, J. C. (2011). A solvent-free coarse grain model for crystalline and amorphous cellulose fibrils. J. Chem. Theory Comput. 7 (8), 2539–2548. doi:10.1021/ct200181t

PubMed Abstract | CrossRef Full Text | Google Scholar

Stillinger, F. H., and Torquato, S. (2019). Structural degeneracy in pair distance distributions. J. Chem. Phys. 150 (20), 204125. doi:10.1063/1.5096894

PubMed Abstract | CrossRef Full Text | Google Scholar

Terakawa, T., and Takada, S. (2011). Multiscale ensemble modeling of intrinsically disordered proteins: P53 N-terminal domain. Biophysical J. 101 (6), 1450–1458. doi:10.1016/j.bpj.2011.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorpe, I. F., Zhou, J., and Voth, G. A. (2008). Peptide folding using multiscale coarse-grained models. J. Phys. Chem. B 112 (41), 13079–13090. doi:10.1021/jp8015968

PubMed Abstract | CrossRef Full Text | Google Scholar

Tschöp, W., Kremer, K., Batoulis, J., Bürger, T., and Hahn, O. (1998). Simulation of polymer melts. I. Coarse-graining procedure for polycarbonates. Acta Polym. 49 (2–3), 61–74. doi:10.1002/(sici)1521-4044(199802)49:2/3<61::aid-apol61>3.0.co;2-v

CrossRef Full Text | Google Scholar

Valdes-Garcia, G., Heo, L., Lapidus, L. J., and Feig, M. (2023). Modeling concentration-dependent phase separation processes involving peptides and RNA via residue-based coarse-graining. J. Chem. Theory Comput. 19 (2), 669–678. doi:10.1021/acs.jctc.2c00856

CrossRef Full Text | Google Scholar

van Teijlingen, A., and Tuttle, T. (2021). Beyond tripeptides two-step active machine learning for very large data sets. J. Chem. Theory Comput. 17 (5), 3221–3232. doi:10.1021/acs.jctc.1c00159

PubMed Abstract | CrossRef Full Text | Google Scholar

Villa, A., Peter, C., and Vegt, N. F. A. (2009a). Self-assembling dipeptides: conformational sampling in solvent-free coarse-grained simulation. Phys. Chem. Chem. Phys. 11 (12), 2077–2086. doi:10.1039/B818144F

PubMed Abstract | CrossRef Full Text | Google Scholar

Villa, A., Vegt, N. F. A., and Peter, C. (2009b). Self-Assembling dipeptides: including solvent degrees of freedom in a coarse-grained model. Phys. Chem. Chem. Phys. 11 (12), 2068–2076. doi:10.1039/B818146M

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Stillinger, F. H., and Torquato, S. (2020). Sensitivity of pair statistics on pair potentials in many-body systems. J. Chem. Phys. 153 (12), 124106. doi:10.1063/5.0021475

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Olsson, S., Wehmeyer, C., Pérez, A., Charron, N. E., de Fabritiis, G., et al. (2019). Machine learning of coarse-grained molecular dynamics force fields. ACS Cent. Sci. 5 (5), 755–767. doi:10.1021/acscentsci.8b00913

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Noid, W. G., Liu, P., and Voth, G. A. (2009). Effective force coarse-graining. Phys. Chem. Chem. Phys. 11 (12), 2002–2015. doi:10.1039/B819182D

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z.-J., and Deserno, M. (2010). A systematically coarse-grained solvent-free model for quantitative phospholipid bilayer simulations. J. Phys. Chem. B 114 (34), 11207–11220. doi:10.1021/jp102543j

PubMed Abstract | CrossRef Full Text | Google Scholar

Webb, M. A., Delannoy, J.-Y., and de Pablo, J. J. (2019). Graph-based approach to systematic molecular coarse-graining. J. Chem. Theory Comput. 15 (2), 1199–1208. doi:10.1021/acs.jctc.8b00920

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, C., and Shea, J.-E. (2011). Coarse-grained models for protein aggregation. Curr. Opin. Struct. Biol. 21 (2), 209–220. doi:10.1016/j.sbi.2011.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, H., Wolynes, P. G., and Papoian, G. A. (2018). AWSEM-IDP: a coarse-grained force field for intrinsically disordered proteins. J. Phys. Chem. B 122 (49), 11115–11125. doi:10.1021/acs.jpcb.8b05791

PubMed Abstract | CrossRef Full Text | Google Scholar

Xia, Z., Gardner, D. P., Gutell, R. R., and Ren, P. (2010). Coarse-grained model for simulation of RNA three-dimensional structures. J. Phys. Chem. B 114 (42), 13497–13506. doi:10.1021/jp104926t

PubMed Abstract | CrossRef Full Text | Google Scholar

Yesylevskyy, S. O., Schäfer, L. V., Sengupta, D., and Marrink, S. J. (2010). Polarizable water model for the coarse-grained MARTINI force field. PLOS Comput. Biol. 6 (6), e1000810. doi:10.1371/journal.pcbi.1000810

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, X., and Dutt, M. (2020). Implementation of dynamic coupling in hybrid molecular dynamics–lattice Boltzmann approach: modeling aggregation of amphiphiles. Comput. Phys. Commun. 257, 107287. doi:10.1016/j.cpc.2020.107287

CrossRef Full Text | Google Scholar

Zhang, J., and Muthukumar, M. (2009). Simulations of nucleation and elongation of amyloid fibrils. J. Chem. Phys. 130 (3), 035102. doi:10.1063/1.3050295

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Zhang, H., Wu, T., Wang, Q., and van der Spoel, D. (2017). Comparison of implicit and explicit solvent models for the calculation of solvation free energy in organic solvents. J. Chem. Theory Comput. 13 (3), 1034–1043. doi:10.1021/acs.jctc.7b00169

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, M., Sampath, J., Alamdari, S., Shen, G., Chen, C.-L., Mundy, C. J., et al. (2020). MARTINI-compatible coarse-grained model for the mesoscale simulation of peptoids. J. Phys. Chem. B 124 (36), 7745–7764. doi:10.1021/acs.jpcb.0c04567

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, J., Thorpe, I. F., Izvekov, S., and Voth, G. A. (2007). Coarse-grained peptide modeling using a systematic multiscale approach. Biophysical J. 92 (12), 4289–4303. doi:10.1529/biophysj.106.094425

PubMed Abstract | CrossRef Full Text | Google Scholar