
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Soft Matter , 30 June 2023
Sec. Polymers
Volume 3 - 2023 | https://doi.org/10.3389/frsfm.2023.1208777
This article is part of the Research Topic Dynamic and reconfigurable polymer networks View all 6 articles
The kinetics of crystallization and crystal-crystal transformations in ethylene vitrimers are studied by time-domain NMR. These vitrimers previously exhibited polymorphic transition of crystal structures, which are shown here to be distinguishable by NMR via their dipolar line widths based upon different proton densities and fast internal motions. The conditions under which the polymorphs are formed and interconvert are identified via time-resolved NMR experiments, with a focus on recrystallization after full and partial melting. DSC experiments are used to clarify an unexpected superheating effect, which challenges the determination of actual melting points. We further identify a strong memory effect in isothermal (re)crystallization. Implications of the dynamic nature of the vitrimers in relation to the kinetics of crystallization are discussed. We find that internal perfecting of crystals, enabled by the vitrimeric exchange process, can have a large effect on the DSC-detected melting enthalpy without change in overall crystallinity.
Covalent adaptable networks (CANs) are polymer networks crosslinked using dynamic covalent bonds (Kloxin and Bowman, 2013). Their ability to be reprocessed and recycled have made them prime candidates for the next-generation of sustainable plastics. Vitrimers are a sub-category of CANs where the network strands are crosslinked by associative covalent bonds (Montarnal et al., 2011; Guerre et al., 2020; Van Zee and Nicolaÿ, 2020; Zheng et al., 2021). These bonds undergo exchange reactions such that the overall crosslink density of the networks is conserved during the exchange. The bond exchange adds a degree of freedom on the molecular scale, that has a strong impact on macroscopic properties. A core question in the study of vitrimers has been to understand how parameters like molecular weight, molecular weight dispersity, junction chemistry, backbone chemistry, temperature, and crosslink density impact macroscopic properties such as viscosity, stress relaxation, creep, reprocessability, and self-healing ability (Denissen et al., 2015; Denissen et al., 2017; Röttger et al., 2017; El-Zaatari et al., 2020; Hubbard et al., 2021; Ishibashi et al., 2021; Porath and Evans, 2021; Ricarte and Shanbhag, 2021; Hubbard et al., 2022; Krishnan et al., 2022; Luo et al., 2022; Porath et al., 2022).
In recent years, using the knowledge generated from numerous fundamental studies, functional vitrimers have been developed for wide-ranging applications such as solid polymer electrolytes, durable coatings, shape-memory materials, and additive manufacturing (Jing and Evans, 2019; Yan et al., 2020; Chen et al., 2021; Ma et al., 2021; Niu et al., 2021; Rossegger et al., 2021; Gu et al., 2022; Lin et al., 2022; Van Lijsebetten et al., 2022) Despite the advances in vitrimers design and processing, a good understanding of how an exchange event that takes place on an Angstrom scale influences macroscopic events such as crystallization, rheological flow and self-assembly is lacking. Little work has focused on how adding dynamic bonds will affect the ability of polymer chains to crystallize (Soman et al., 2022a; Kuenstler and Bowman, 2023), which is a key attribute of polyolefins and many commercial plastics.
Most work on vitrimers has used rheology or dynamic mechanical analysis to study the moduli and flow properties of the networks (Yan et al., 2020; Chen et al., 2021; Ma et al., 2021; Niu et al., 2021; Gu et al., 2022; Lin et al., 2022; Van Lijsebetten et al., 2022). Some work has also utilized dielectric spectroscopy to probe segmental scale dynamics (Soman et al., 2022b; Pascual-Jose et al., 2023). While these methods can probe materials which are crystallizing, they are not routinely used to understand such processes and to infer quantities such as percent crystallinity or the degree of crystal perfection (Ezquerra et al., 1994; Wurm et al., 2005; Soccio et al., 2007) Solid-state NMR spectroscopy provides a plethora of techniques which can provide a great deal of insight regarding crystallization physics in soft materials (Chen and Kurosu, 2007). This holds in particular for proton NMR, possibly performed on cost-efficient low-field low-resolution instruments, which allows for a quick mobility-based determination of the absolute crystallinity (in terms of proton signal fraction, equaling mass fraction), provides access to domain sizes via spin diffusion, and importantly, has sufficient sensitivity to allow for time-resolved experiments with a resolution of less than a minute (Tanaka and Nishi, 1986; Maus et al., 2006; Schäler et al., 2015).
Work along these lines is relevant beyond the field of vitrimers, as crystallization in networks, in particular highly crosslinked ones, is little researched and understood in general (Golitsyn et al., 2019). The cited paper reports on one of the few systematic studies of model networks with short but defined network chain length, where the normally highly crystallinity of polyethylene oxide (PEO) linear polymers (typically 80% or higher) is significantly reduced in end-linked networks with chains of less than a few kDa. Tightly crosslinked thermosets are mostly amorphous, as are the covalent equivalents of the samples studied herein (Soman et al., 2022a). A peculiar exception seems to be urea/formaldehyde resins, which can reach crystallinities in the 50% range (Wibowo and Park, 2020). This, however, seems to be a special case where for the given small-molecule-based resin formulation, crystallization of linear stretches and crosslinking compete already during curing.
To sum up our recent work relevant for the given follow-up study, the role of dynamic bond exchange on crystallization in networks has been investigated in ethylene vitrimers (Soman et al., 2022a). They are comprised of monodisperse telechelic alkane diols (CH2)n (OH)2, with n being 10–12 in this work, crosslinked by boric acid, B(OH)3, samples with exact linker spacing were synthesized. The samples are denoted C10 and C12, respectively. In comparison to analogous, permanently crosslinked networks, which do not show any evidence of crystallization, ethylene vitrimers did crystallize with local packing motifs analogous to those of polyethylene (PE). At room temperature, crystallization was previously followed over 40 days, and the melting temperature of the crystals continuously increased by ∼25°C and the apparent crystallinity as reflected in the DSC-detected melting enthalpy increased by almost a factor of two. While the absolute crystallinity was not yet quantified, wide-angle X-ray scattering (WAXS) suggested rather high crystallinity indicated by the virtual absence of an amorphous halo and high thermal conductivity. WAXS further revealed an unexpected crystal–crystal transition which indicated a second crystal polymorph. It is interesting to note that these changes in properties take place in quiescent samples. We attributed the initial crystallization and the subsequent evolution in properties to the dynamic bonds. Local rearrangements of the network strands facilitated by bond exchange are hypothesized to allow crystal perfection or an increase in crystallinity, and to enable a crystal-crystal transformation into a more stable polymorph. Even more recent work by Kuenstler and Bowman (2023) have also investigated crystallization in dynamic networks, where different catalysts allowed for control of bond exchange kinetics. A similar long-time evolution in Tm was observed, and the actual Tm values were found to be inversely correlated with the exchange kinetics.
Here we investigate in more detail the crystallization of the recently reported high-crosslink-density ethylene vitrimer (Soman and Evans, 2021; Soman et al., 2022a; Soman et al., 2022b; Lv et al., 2023). We focus on the kinetics of isothermal crystallization as well as the annealing/recrystallization kinetics of two different samples with C10 and C12 spacer length. Along the lines of earlier work on the confined crystallization of pharmaceuticals (Sonnenberger et al., 2016), we are able to distinguish two different crystal polymorphs by simple 1H NMR via their dipolar line width, allowing us to monitor the interconversion in real time. Interestingly, we could identify an unexpected superheating effect, which challenges the determination of the melting points reported previously for our samples, as well as a prominent memory effect on crystallization.
The samples investigated in this work are prepared via the condensation of alkane diols with boric acid. The synthetic procedure follows exactly from our prior work (Soman et al., 2022a). The previously investigated and carefully dried C10 and C12 ethylene vitrimers were prepared in sealed glass tubes flushed with Argon for NMR measurements. We refer to our previous publication for details (Soman and Evans, 2021). The structure of the dynamic networks is shown as in inset in Figure 1A, where we have compiled the terminal relaxation times of these samples. The rheological measurements were already done in the context of our first publication, from which the Arrhenius slopes were determined, but the relaxation times of C10 and C12 were not explicitly published there. The data shows that the networks relax on a 0.1—1 s timescale in the temperature range relevant for the present study. This will be relevant for the discussion below.
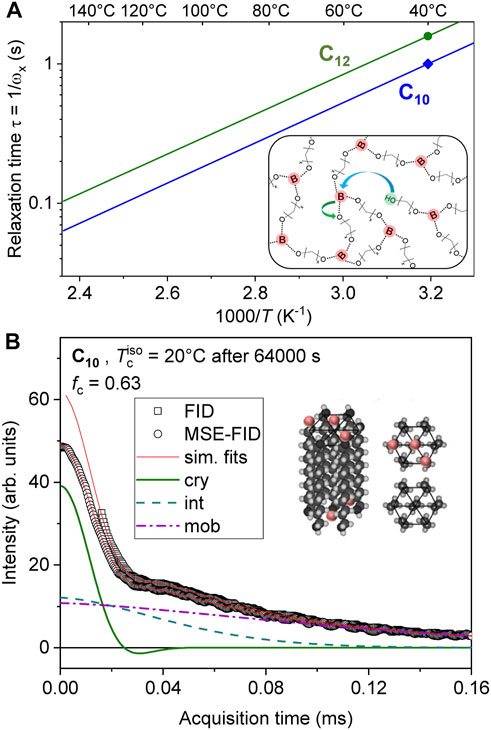
FIGURE 1. (A) Arrhenius plot of vitrimer relaxation times calculated as the inverse of the rheological crossover frequency of samples C10 and C12 measured at 40°C along with extrapolations based upon shift factors. The inset in A has been reproduced from Soman and Evans (2021) with permission from the Royal Society of Chemistry. The inset shows the network structure. (B) Simultaneous three-component fit of 1H FIDs, detected during isothermal crystallization at 20°C, both directly after the excitation pulse and after an MSE to avoid the dead time. The fits provide the crystalline fraction (fc) and second moments of the corresponding crystalline lineshapes (M2), as well as T2 relaxation times characterizing the restricted mobility of the intermediate and amorphous fractions. The inset in B has been reproduced from Soman et al. (2022a) with permission from the Royal Society of Chemistry.
For comparison with the crystallization behavior of our vitrimers, NMR crystallization studies were also conducted on a sample of poly (octadecyl methacrylate), PODMA, with an approximate number-averaged degree of polymerization DPn ≈ 27, which was previously studied by X-ray scattering and DSC (Hempel et al., 2006). The original sample from that study was provided by the authors.
Samples (2–5 mg) were melted into hermetically sealed pans in an Argon glovebox. Crystallization proceeded in the glovebox at ambient temperature. A TA Instruments DSC 25 was used to control the heating and cooling rates as described in the text.
Samples were prepared for X-ray analysis by sealing between two Kapton sheets using epoxy and a spacer. A Xenocs GeniX3D Cu Kα source generated 1.54
NMR experiments were conducted on a Bruker minispec mq20 instrument at a Larmor frequency of about 20 MHz. Pulse lengths were in a range of 2.5 and 5 μs for flip angles of 90° and 180°, respectively. A recycle delay of 1 s was sufficient for full T1 relaxation of both semicrystalline and amorphous/molten samples. The free induction decay (FID) of the proton signal is measured both directly and after a magic-sandwich echo (MSE-FID) to address the dead-time problem (Maus et al., 2006; Schäler et al., 2015). The latter suffers some intensity loss, which means that we fit the two datasets (restricted to an acquisition time interval of 200 m) simultaneously to a three-component model accounting for the crystalline (index c), amorphous (a), and interfacial (i) regions (Schäler et al., 2015):
The MSE leads to a small reduction of the amplitude prefactors, which are the only fitting parameters that are allowed to vary between FID and MSE-FID signals. Sample fits are shown in Figure 1B. Most importantly, these fits provide the crystalline fraction
The β exponents for the intermediate and mobile amorphous components are stretching parameters reflecting on the one hand dynamic heterogeneity, and on the other hand a partial Gaussian character typical for dipolar dephasing originating from the dominance of residual dipolar couplings in the short network chains (a discussion is given below). This explains why the β values were always ranging between 1 and 2. The T2i was around and below 0.1 ms in the network melt down to 0.03 ms for fully crystallized samples, while T2m was around 0.2 ms, staying the same or even increasing somewhat during crystallization. For the given short network chains, T2 values are in the range of 0.1–0.2 m, which means that the mobile and intermediate components together reflect inhomogeneities of the network structure. As network chains become part of the crystal, dangling defects with longer T2 are left over, thus it increases in some cases.
Our NMR-based crystallinity determination, applied to monitor isothermal crystallization of both samples in Figures 2A, B confirms the initial WAXS-based observation that the samples reach high crystallinity of ∼90% within a reasonably short time. This is an astonishingly high crystallinity for polymer samples that are quiescently kept at room temperature, in particular considering the disordered network structure and the short chains. The boric acid ester linkers are thus expected to be part of an ordered fold surface or to form intracrystalline layers, along the lines of recent studies of linear precision polymers (Trigg et al., 2017; Marxsen et al., 2021). To reach such high crystallinity, long-chain polymers are usually annealed at higher temperatures or shear aligned, and have to feature fast chain mobility in the crystals (Schulz et al., 2022). For highly crosslinked networks, it is in fact a peculiarity, as mentioned in the Introduction.
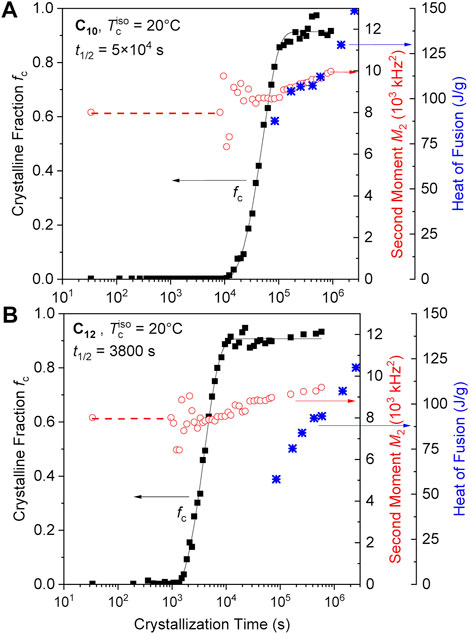
FIGURE 2. Crystalline fraction (fc), second moments of the crystalline lineshapes (M2) and heat of fusion (the latter taken from Soman et al., 2022a) plotted as a function of annealing time at 20°C for the (A) C10 and (B) C12 ethylene vitrimers. The red dashed line indicates the time range where M2 was fixed since stable fitting of a finite crystalline fraction was impossible. The black solid lines are fits to the Avrami function, from which we take the crystallization half time.
The crystallization kinetics fc(t) were evaluated by fits to the Avrami function (black solid lines in Figures 2A, B), which revealed Avrami exponents in the range between about 1 and 2. Since the variations were non-systematic across all our data (see also Figure 5 below), arising from uncertainties (noise) in the data at short times (where the initial upturn most sensitively encodes the Avrami exponent) and possible secondary crystallization at longer times, we refrain from reporting and discussing the fitted exponents, but just report crystallization half times t1/2. These are reliably determined in all cases, as the Avrami fit merely provides a robust interpolation in the data range covering intermediate crystallinities. The values are 830 and 63 min for C10 and C12, respectively, with the large difference mainly attributed to the different undercooling at 20°C. In both samples, the second moment M2 continues to grow during crystallization, indicating a gradual densification or a suppression of fast small-angle motions or conformational fluctuations. We thus interpret the observation in terms of an increase in crystal perfection, which, notably, takes place without further significant increase in crystallinity. The previously reported long-time increase in enthalpy of melting (Soman et al., 2022a), which is also shown in the figure, must in this new light be attributed to the increasing crystal perfection observed from NMR rather than percent crystallinity.
The crystallization of the networks was also tracked by WAXS over a 150 days crystallization period (Figures 3A, B). After 1 day of crystallization, the WAXS patterns already indicate a high crystallinity as inferred from the absence of an underlying amorphous halo which is observed in the scan of the amorphous network (0 min scan). In addition to the high crystallinity, the FWHM of the peaks does not show significant variation after the first day indicating a stable crystal size. At room temperature, the C10 eventually undergoes a spontaneous transformation from hexagonal to orthorhombic but not within the first 30 days. In the C12 network, the crystal structure appears to be hexagonal over the entire 150 days window and only transitions to orthorhombic at elevated temperatures of 65°C (to be discussed later).
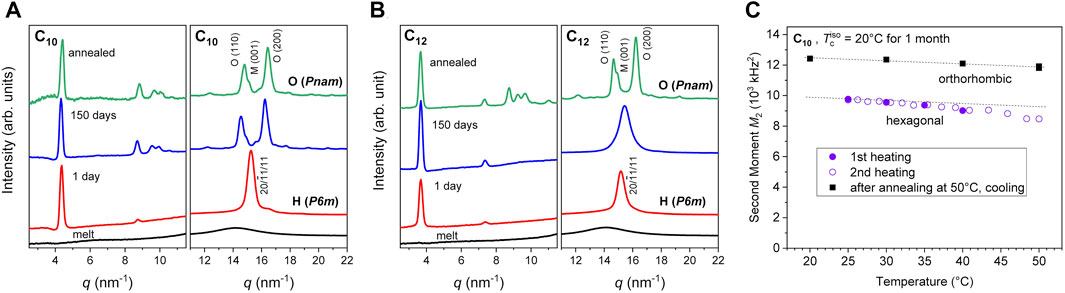
FIGURE 3. Time evolution of SAXS/WAXS spectra in the (A) C10 and (B) C12 networks at 23°C revealing the transformations from hexagonal to orthorhombic unit cells which occur with time (in the C10 network) or heating to 65°C (in the C12 network). Plots reproduced from Soman et al. (2022a) with permission from the Royal Society of Chemistry. (C) Second moment of the crystalline lineshape for the two relevant crystal structures as a function of temperature, recorded upon heating or cooling at 1°C/min. The parallel dashed lines indicate the typical weak decay due to thermal expansion of the lattice; the stronger and reversible decrease in the hexagonal phase indicates increased dynamics, e.g., increasing concentration of fluctuating conformational defects or librational motions.
The M2 values for hexagonal and orthorhombic crystals are distinct, and the NMR measurements reveal only hexagonal crystals in the first month, consistent with the prior WAXS data. This is evidenced by the comparison of M2 values for a C10 sample crystallized isothermally at 20 °C during heating and cooling with a rate of 1°C/min in Figure 3C. The first heating scan to 40°C reveals a slight decrease of M2 in a range below 104 kHz2 (accompanied by only a slight decrease in crystallinity from about 0.92 to 0.86). The sample was then cooled again to room temperature, upon which the variation of M2 is fully reversible, as evidenced by the second-heating data. Crystallinity actually diminishes above 48°C, and annealing at 50°C leads to a recrystallization into the orthorhombic phase (details to be discussed below in the context of Figure 6A). Importantly, this is directly reflected in the considerably larger M2 value of around 1.2 × 104 kHz2, which is now typical for similar crystal structures such as those of PE or aliphatic polyesters (Schäler et al., 2013). The orthorhombic crystallinity in the shown T range varies between 79% and 85%. The T-dependence of its M2 is even weaker, and depends mostly on thermal expansion. The stronger dependence and lower values of the initial hexagonal phase may be related to enhanced dynamics such as increasing amplitude of local librations or conformational fluctuations (Schäler et al., 2013). It is noted that the M2 values for the two phases are too close to allow for a separation of the fractions of either phase by fitting in samples where they coexist. However, in-between values can be interpreted qualitatively in terms of coexistence.
Our previous report of increasing Tm with crystallization time corresponded to samples heated at a rate of 20°C/min in the DSC (Soman et al., 2022a). As shown below, in our NMR experiments employing much slower heating (about 1°C/min owing to slower heat transfer), we consistently found both samples C10 and C12 to melt at considerably lower temperatures. We have therefore examined the time evolution of the DSC-based Tm of sample C10 using different heating rates spanning from 1°C to 20°C/min. The DSC traces are shown in the Appendix (Figure A1). In all cases an increase is observed with essentially the same slope (Figure 4). Surprisingly, the value of Tm decreases significantly with slower heating rates, a phenomenon also observed in conventional linear PE (Hellmuth and Wunderlich, 1965). This puts the previous Tm results (Soman et al., 2022a), taken to be not too far from equilibrium, into perspective. In that study, the increase in Tm was attributed to increasing crystallinity due to the change in the enthalpy of melting. Here, it is shown that increasing perfection rather leads to the increase in Tm. The higher apparent Tm values at 20°C/min are thus attributed to the superheating of crystals, which refers to the ability to be heated above the equilibrium melting temperature (Hellmuth and Wunderlich, 1965). For polyethylene and polyoxymethylene used in that study, the superheating effect amounted to a ∼4°C–5°C shift for a range of heating rates from 0.6°C to 20°C/min. The effect is much larger in ethylene vitrimers.
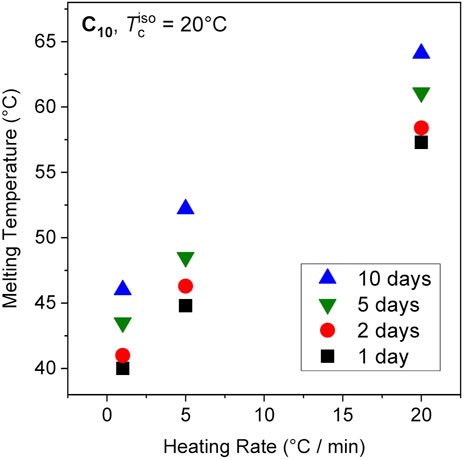
FIGURE 4. Melting temperatures of the C10 network as a function of crystallization time with different heating rates.
In the present work, we deduce from Figure 4 that while the vitrimeric rearrangements and enhanced crystal perfection result in systems which are more stable and melt at higher Tm, the superheating effect, apparent from the large differences between the different heating rates, is affected only little. We hypothesize that the melting kinetics are governed by the timescale of vitrimeric rearrangements, which could be slower in the organized environment between the crystalline alkyl sheets. Note that the total time for a heating cycle ranges from 5—100 min depending on the ramp rate, and the rheological crossover time in the melt state is ∼0.1 s (Figure 1A), indicating ample time for relaxation events and bond exchange to modify the samples during this ramp.
As noted in the Introduction, Kuenstler and Bowman (2023) found that dithioether/thioester-based vitrimers with crystallizable C10 alkyl-dithiol linkers also show a long-time increase in Tm, the absolute value which is of the order of 20°C, thus much lower than in our case. Tm was higher for systems with faster bond-exchange kinetics. The annealing time dependence of Tm was not studied explicitly. The effect was attributed to potential lamellar thickening—which was not measured. This explanation must be reconciled with a system in which the direction-disordered linear dithioether-thioester-dithioether network chain moieties, which feature dynamic exchange at the central thioester bond, may or may not be part of the lamellae, the thickness of which may be further bound by the crosslinks at the termini. Alternatively, only the extended C10 cores of the dithioether units could crystallize in PE-type fashion similar to polymers with alkyl sidechains. This could easily be addressed by NMR studies of this system.
A comparable system with pendant (rather than telechelic) short-alkyl chains, namely, atactic poly (n-octadecyl methacrylate) was studied by Beiner and coworkers (Hempel et al., 2006). For this sample, a similar long-term increase of Tm was observed. In that case, the C18 side-chains form interdigitated layered nanodomains separated by the disordered main chains, which feature a hexagonal crystalline packing with a similar WAXS peak at about 15 nm−1 as in our samples, see Figure 3. The perfecting of the structure over time was detected by a slow increase of both Tm as well as the heat of melting, similar to our vitrimer system. It was suggested that the core parts of the C18 chains crystallize first, forming initially thin lamellar crystals that then thicken to eventually comprise a larger part of the C18 chains.
We were able to obtain one of these samples and thus conduct an isothermal crystallization run with NMR observation, to be compared with the DSC-based kinetics of Hempel et al. (2006). The results are shown in Figure A2 of the Appendix. Notably, we reproduced the DSC-based kinetics almost quantitatively, with the added value of a reliable absolute-scale crystallinity fraction fc that actually almost reaches its maximum, corresponding to nearly full crystallinity of the C18 chains. Importantly, the slow long-time logarithmic increase of fc is also observed, yet accompanied by a nearly constant and comparably low value of M2 of about 5,300 kHz2. This confirms the suggestion of Hempel et al. (2006) to explain the long-term changes of their system in terms of an increase in actual crystallinity along the C18 stems. This is in contrast to our observations on the vitrimer samples. These are thus special in that the initially formed crystalline structure remains (as indicated by largely invariant sharp SAXS/WAXS peaks, see Figure 3) and perfects internally, as a result of slow vitrimeric rearrangement in the interlayers containing the boric ester groups. Finally, the low M2 value of PODMA, and the larger values along with an increase upon annealing from around 8,000–10,000 kHz2 for our vitrimers (see Figure 2) illustrate that the hexagonal packing of alkane chains allows for considerable variations in small-angle motions and conformational (dis)order, which in turn have a surprisingly strong effect on the heat of melting.
As observed in the SAXS/WAXS data of Figure 3, the C12 sample can transition from hexagonal to orthorhombic when annealed at 65°C. This transition was tracked using NMR on a C12 network first crystallized for 1 day followed by heating to 50°C in 1700 s (rate of ∼1°C/min) as shown in Figure 5A, where we used the lower temperature so as to be able to compare with isothermal crystallization at the same temperature. This procedure leads to a minor partial melting, and then recrystallization into a denser phase (orthorhombic) but with almost the same crystallinity and a higher perfection. Notably, the M2 values decrease first on heating from 20°C to 50°C (see also Figure 2C), suggesting fast (but effectively small-angle) segmental fluctuations with increasing amplitude. Then, they steadily increase to the level expected for the orthorhombic crystal. The increase of M2 can be interpreted in terms of increasing crystalline perfection, or simply by a converted fraction. Taking the latter perspective, a conversion half time of 500 min is estimated.
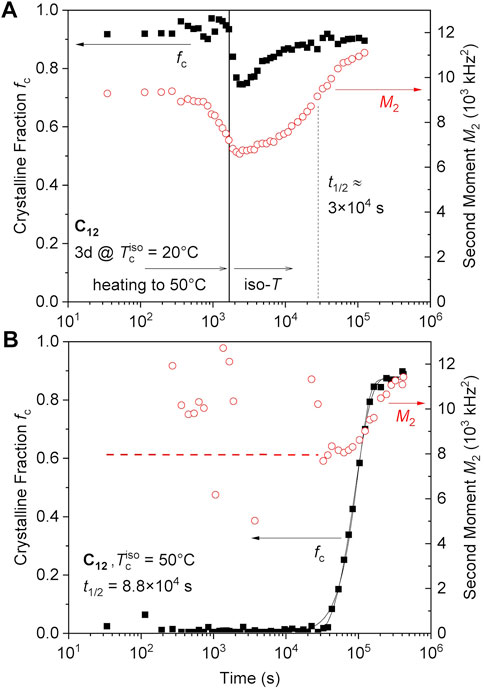
FIGURE 5. (A) C12 sample undergoes a crystal-crystal transition when annealed at 50°C after isothermal crystallization at RT for 1 day. The data left of the vertical line are taken during heating with about 1°C/min. (B) The C12 network directly cooled from the melt (150°C) transitions to the orthorhombic phase during isothermal crystallization at 50°C. The two black solid lines are Avrami fits excluding or assuming an onset time t0 of 2.8 × 104 s. The two scenarios, providing Avrami exponents of 2.6 or 1.6, respectively, cannot be distinguished on the basis of the data/fitting quality.
This can be compared with the isothermal crystallization of the same network, that is, cooled directly from the melt to 50°C, revealing a half time of about 1,500 min (Figure 5B). This temperature is apparently below the equilibrium melting point of the hexagonal phase, but is above the annealing temperature required to form the orthorhombic phase. The hexagonal phase forms first (M2 of around 8,000 kHz2), and then gradually converts to the orthorhombic phase during the crystallization (M2 > 11 kHz2). The crystallinity still reaches fc ∼ 0.9. The orthorhombic phase does not seem to directly nucleate and we note that this denser phase is effectively at a lower degree of undercooling than the hexagonal phase.
Polymer crystals are known to have memory effects which can take long times to anneal out and fully erase thermal and processing history (Cheng et al., 1986; Bastiaansen et al., 1990; Hamad et al., 2015; Sangroniz et al., 2020). The C10 network was first examined by crystallizing for 3 days or 1 month, followed by heating to 50°C (Figure 6). This temperature is above the melting point of the hexagonal phase initially formed on crystallization at lower temperatures (see Figure 4), and no crystallization directly into the orthorhombic phase was observed with several days at 50°C after cooling from the melt. As expected, both 20°C pre-crystallized samples show essentially complete melting upon heating to 50°C, yet this is now followed by recrystallization directly into the orthorhombic phase (as evidenced by the high and constant M2). The 3-day sample (Figure 6A) shows a notable induction period, while the 1-month sample has an even stronger memory effect (Figure 6B) with an apparently shorter induction period and shorter overall crystallization half time. The orthorhombic phase apparently does not nucleate well (or not all) and requires some “memory” facilitating its formation.
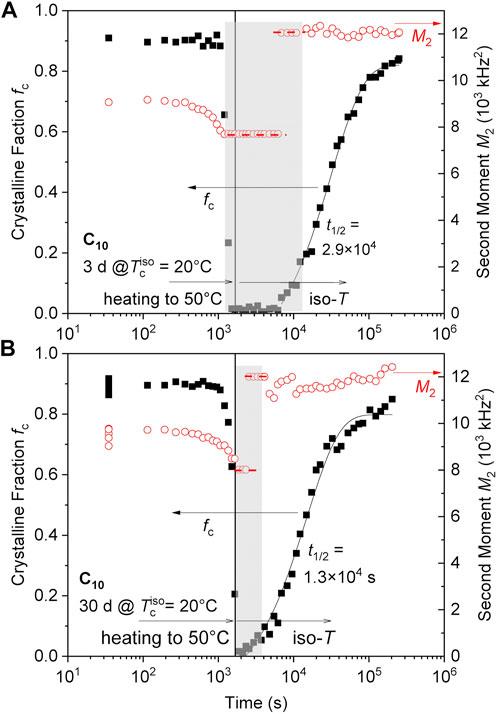
FIGURE 6. Memory effect on isothermal recrystallization at 50°C observed upon annealing of C10 a sample crystallized isothermally at 20°C for (A) 3 days and (B) 1 month. The latter has a stronger memory effect and thus faster crystallization (including a shorter apparent “induction time”). The data left of the vertical lines are taken during heating with about 1°C/min. Note that isothermal crystallization at 50°C after cooling from the virgin melt is not observed on the given timescale.
The C12 networks were also examined for memory effects, but heating to 50°C is not sufficient to induce the same phenomena as in the C10 networks, as isothermal crystallization from the virgin melt and formation of (or transition into) the orthorhombic phase is already observed at this temperature (see Figure 5A, B). We have thus focused on higher temperatures, where a sample crystallized at 20°C for 1.5 months showing the hexagonal modification melts completely at 65°C and recrystallizes directly into the orthorhombic phase after a lag time of about 1.5 h (Figure 7A). Qualitatively the same behavior was observed for a sample crystallized at 20°C for 20 days after heating to 60°C, where crystallization sets in already after about 20 min (data not shown). In contrast, a virgin melt cooled to the same temperatures did not crystallize.
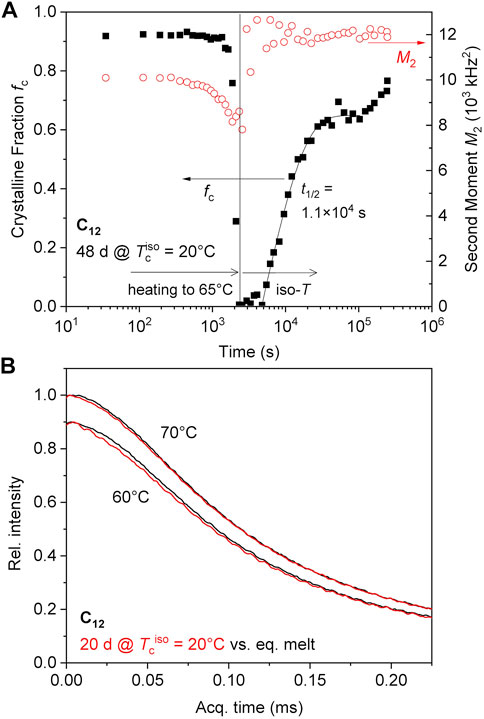
FIGURE 7. (A) Memory effect of C12 on isothermal recrystallization at 65°C; the data left of the vertical line are taken during heating with about 1°C/min. (B) MSE-FIDs at 60°C and 70°C; the latter was taken after 40 min Hold time at 60 °C. The intensity data at 60°C is scaled by a factor of 0.9 for visual separation.
As to the origin of this memory effect, one may consider an adapted network mesh topology providing a “melt memory” with pre-arranged chains. This option is, however, unlikely, as the memory is stable for hours, while the terminal (flow) time of the vitrimers, as governed by the bond-exchange process, is well below the second scale (see Figure 1A). To test this hypothesis, or check for the possible remainder of a small crystalline fraction, we compare in Figure 7B two (MSE-)FIDs of melt states at 60°C and 70°C for a sample crystallized for 20 days with and without memory (the latter taken after complete melting at 150°C for about 15 min). For this experiment, the pre-crystallized sample was held at 60°C for 40 min, during which time crystallization set in visibly. It was then further heated to 70°C and held. The shown data are averages of the FIDs taken during the induction times, where the signals did not change visibly and where no stable fitting of a finite crystallinity was possible.
Nevertheless, the direct comparison at 60°C with the data of the equilibrated melt shows that the signal from the samples “with memory” is always decaying somewhat more quickly, the data being compatible with a crystallinity degree on the percent level. The effect is very small but still visible at 70°C, while at 80°C (with data taken after another 40 min holding at 70°C) showed signals that are identical to those of the equilibrated melt within the noise. Thus, the memory is most likely related to the existence of a very small fraction of high-melting crystallites, possibly such ones for which the perfectioning has progressed more. We note that it is expected that the observed differences pertain not just to a minute fraction of crystalline signal but a somewhat decreased T2 relaxation time of a part of the sample (i.e., the intermediate fraction in our three-component fit), arising from some degree of immobilization of the chains surrounding the small crystallites.
We can now also rationalize the observations that the late-stage kinetics for memory-aided crystallization are not well captured by the Avrami fits, see the solid lines in Figures 6, 7A. In all these cases, and in contrast to crystallizations from the virgin melt (Figure 2; Figure 5), a more sluggish increase is evident at long times. For the case of C12 (Figure 7A), it was even necessary to exclude the late-stage data in order to fit the data satisfactorily (in the other cases, the Avrami exponents were more ill-defined, being dependent on the number of fitted data points). For a memory effect related to a small fraction of remaining crystallites, their sparsity and inhomogeneous spatial distribution may well be held responsible for such observations.
We finally add some comments on the shape of the melt-state FIDs, which could hold information on a “melt memory”. It is approximately Gaussian, as expected for very short network chains featuring rather large residual dipolar coupling constants arising from the strongly anisotropic motions of the short end-fixed chains (Saalwächter and Heuer, 2006). In other words, the transverse relaxation process (normally characterized by a T2 relaxation time) is rather pure dipolar dephasing, where an orientational (“powder”) average combined with multiple multi-spin couplings leads to the well-known Gaussian shape. In case of a homogeneous system, is described by I(t) = exp{(9/40)Dres2t2}, where Dres is the residual dipolar coupling, which is inversely proportional to the length of the network strands (Saalwächter and Heuer, 2006). Since in our case Dres is large due to the short strands (corresponding to a high crosslink density typical for thermosets), direct analysis of the FID, which is normally precluded by field inhomogeneities and additional contributions of segmental dynamics, becomes possible. Topological structures such as loops would contribute lower Dres and the relaxation function would become modified/stretched, yet again, no differences are apparent between the cases with and without memory.
Another relevant piece of information in this context is a nearly exponential long-T2 tail, for which fitting (not shown) provides a relative fraction of less than 10%. This corresponds to network defects, whose rather low amplitude confirms the high conversion of the networks with its mostly three-functional crosslinks. More in-depth analyses into the network structure and a more stable fitting are possible by using multiple-quantum (MQ) NMR, along the lines of our previous work (Saalwächter and Heuer, 2006). Results along these lines are deferred to a future publication, where we focus on stoichiometrically imbalanced, defect-containing samples.
The crystallization of ethylene vitrimers was investigated by time-domain NMR to probe the kinetics, perfection, and polymorphic transitions of these systems. NMR analysis confirms that the crystallinity is very high, of order 90%, in agreement with prior WAXS data. A notable and significant long-time increase of Tm upon annealing was shown to not be related to an increase in crystallinity (reaching its final level comparably quickly) but rather to an increased crystal perfection, enabled by a reorganization of the dynamic bonds on the surface of the crystalline alkyl layers. The dynamic bonds thus become part of a layered crystal structure, as also evidenced by a sharp SAXS peak reflecting the boric ester layer spacing.
These results may be of general relevance for systems in which alkyl nanodomains can crystallize. Both in a recent study of somewhat more complex C10-based vitrimers (Kuenstler and Bowman, 2023) and in a linear methacrylate polymer with C18 side-chains (Hempel et al., 2006), similar Tm increases were reported. In the latter case, the melting enthalpy change over time was also studied by DSC, and shown to increase along with Tm, in the same way as in our ethylene vitrimers (Soman et al., 2022a). By comparing long-time crystallization isotherms measured by NMR on both systems, we could here show that this increase has different reasons in the two cases. While absolute crystallinity is indeed further increasing slowly over time in the C18 side-chain system (and attributed to a thickening of lamellae that initially do not embody the full C18 chain), the increase in melting enthalpy in the vitrimer case is not related to increased crystallinity but is rather related to perfecting of the crystal structure, specifically the layers containing the crosslinks. This could be understood in terms of a reduction of internal surface energy. This emphasizes on the one hand the relevance of our NMR investigations, providing a robust measure of the degree of crystallinity, and on the other hand that vitrimeric rearrangements are centrally relevant for the perfection of the crystal structure.
NMR also allows us to follow the polymorphic transition from hexagonal to orthorhombic based on the dipolar second moment M2 of the crystalline lineshape, originating from slightly different proton densities and variable fast local motions, being detected in terms of differences in transverse relaxation times. Notably, for the case of hexagonally packed alkyl chains, the variations of the measured M2, reflecting fast internal motions and thus the perfection of the crystals, were found to correlate with changes in melting enthalpy. These relations are of fundamental relevance and deserve further systematic studies. We further identified a strong superheating effect, where higher heating rates lead to significantly higher apparent Tm values as the samples are heated beyond their equilibrium melting temperature. The related sluggish melting kinetics may be tied to a slower dynamic bond exchange in the crystalline interlayers. This finding suggests that it is generally difficult in the given system, as well as in related ones (Hempel et al., 2006; Kuenster and Bowman, 2023), to measure—and draw conclusions from—the actual melting temperature of the given structure.
The vitrimers are finally shown to exhibit strong memory effects, where our NMR observations are compatible with a small remaining high-melting fraction of well-optimized crystals that can nucleate the crystallization directly into the orthorhombic phase. In summary, our study has provided key new insights into the role of dynamic bonds on crystallization in dense networks, that would typically not crystallize despite being made up of monodisperse building blocks. Future work is directed towards introducing controlled defects and studying their impact on terminal flow and on semicrystalline structure formation.
The datasets generated and analyzed for this study as they appear in the figures of this article can be found in the Zenodo repository: https://doi.org/10.5281/zenodo.8008831.
Synthesis of vitrimers, X-ray scattering, rheology, and calorimetry were performed by BS. All NMR experiments, fitting, and analyses were performed by KS. All authors contributed to the writing of the article and approved the submitted version.
This work was partially supported by the National Science Foundation through award CBET-2029928 (BS and CE). Partial funding was also provided by the Deutsche Forschungsgemeinschaft (DFG) in the framework of the SFB-TRR 102 (project-ID 189853844), project A1 (KS).
We acknowledge the use of the facilities at the Materials Research Laboratory at the University of Illinois, Urbana-Champaign. We also thank Mario Beiner (Fraunhofer IMWS, Halle, Germany) for providing the PODMA sample.
Author KS declared that he was an editorial board member of Frontiers at the time of submission. This had no impact on the peer review process and the final decision.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Bastiaansen, C., Meyer, H., and Lemstra, P. (1990). Memory effects in polyethylenes: Influence of processing and crystallization history. Polymer 31, 1435–1440. doi:10.1016/0032-3861(90)90147-q
Chen, F., Cheng, Q., Gao, F., Zhong, J., Shen, L., Lin, C., et al. (2021). The effect of latent plasticity on the shape recovery of a shape memory vitrimer. Eur. Polym. J. 147, 110304. doi:10.1016/j.eurpolymj.2021.110304
Chen, Q., and Kurosu, H. (2007). Solid-state NMR studies on semicrystalline polymers. Annu. Rep. NMR Spectrosc. 61, 247–281. doi:10.1016/S0066-4103(07)61104-1
Cheng, S. Z., Cao, M., and Wunderlich, B. (1986). Glass transition and melting behavior of poly (oxy-1, 4-phenyleneoxy-1, 4-phenylenecarbonyl-1, 4-phenylene)(PEEK). Macromolecules 19, 1868–1876. doi:10.1021/ma00161a015
Denissen, W., Droesbeke, M., Nicolaÿ, R., Leibler, L., Winne, J. M., and Du Prez, F. E. (2017). Chemical control of the viscoelastic properties of vinylogous urethane vitrimers. Nat. Commun. 8, 14857. doi:10.1038/ncomms14857
Denissen, W., Rivero, G., Nicolaÿ, R., Leibler, L., Winne, J. M., and Du Prez, F. E. (2015). Vinylogous urethane vitrimers. Adv. Funct. Mater. 25, 2451–2457. doi:10.1002/adfm.201404553
El-Zaatari, B. M., Ishibashi, J. S., and Kalow, J. A. (2020). Cross-linker control of vitrimer flow. Polym. Chem. 11, 5339–5345. doi:10.1039/d0py00233j
Ezquerra, T. A., Majszczyk, J., Baltà-Calleja, F. J., López-Cabarcos, E., Gardner, K., and Hsiao, B. (1994). Molecular dynamics of the α relaxation during crystallization of a glassy polymer: A real-time dielectric spectroscopy study. Phys. Rev. B 50, 6023–6031. doi:10.1103/physrevb.50.6023
Golitsyn, Y., Pulst, M., Samiullah, M. H., Busse, K., Kressler, J., and Reichert, D. (2019). Crystallization in PEG networks: The importance of network topology and chain tilt in crystals. Polymer 165, 72–82. doi:10.1016/j.polymer.2019.01.018
Gu, W., Li, F., Liu, T., Gong, S., Gao, Q., Li, J., et al. (2022). Recyclable, self-healing solid polymer electrolytes by soy protein-based dynamic network. Adv. Sci. 9, 2103623. doi:10.1002/advs.202103623
Guerre, M., Taplan, C., Winne, J. M., and Du Prez, F. E. (2020). Vitrimers: Directing chemical reactivity to control material properties. Chem. Sci. 11, 4855–4870. doi:10.1039/d0sc01069c
Hamad, F. G., Colby, R. H., and Milner, S. T. (2015). Lifetime of flow-induced precursors in isotactic polypropylene. Macromolecules 48, 7286–7299. doi:10.1021/acs.macromol.5b01408
Hellmuth, E., and Wunderlich, B. (1965). Superheating of linear high-polymer polyethylene crystals. J. Appl. Phys. 36, 3039–3044. doi:10.1063/1.1702924
Hempel, E., Budde, H., Höring, S., and Beiner, M. (2006). On the crystallization behavior of frustrated alkyl groups in poly(n-octadecyl methacrylate). J. Non-Crystalline Solids 352, 5013–5020. doi:10.1016/j.jnoncrysol.2006.01.131
Hubbard, A. M., Ren, Y., Konkolewicz, D., Sarvestani, A., Picu, C. R., Kedziora, G. S., et al. (2021). Vitrimer transition temperature identification: Coupling various thermomechanical methodologies. ACS Appl. Polym. Mater. 3, 1756–1766. doi:10.1021/acsapm.0c01290
Hubbard, A. M., Ren, Y., Picu, C. R., Sarvestani, A., Konkolewicz, D., Roy, A. K., et al. (2022). Creep mechanics of epoxy vitrimer materials. ACS Appl. Polym. Mater. 4, 4254–4263. doi:10.1021/acsapm.2c00230
Ishibashi, J. S., Pierce, I. C., Chang, A. B., Zografos, A., El-Zaatari, B. M., Fang, Y., et al. (2021). Mechanical and structural consequences of associative dynamic cross-linking in acrylic diblock copolymers. Macromolecules 54, 3972–3986. doi:10.1021/acs.macromol.0c02744
Jing, B. B., and Evans, C. M. (2019). Catalyst-free dynamic networks for recyclable, self-healing solid polymer electrolytes. J. Am. Chem. Soc. 141, 18932–18937. doi:10.1021/jacs.9b09811
Kloxin, C. J., and Bowman, C. N. (2013). Covalent adaptable networks: Smart, reconfigurable and responsive network systems. Chem. Soc. Rev. 42, 7161–7173. doi:10.1039/c3cs60046g
Krishnan, B. P., Saalwaechter, K., Adjedje, V. K., and Binder, W. H. (2022). Design, synthesis and characterization of vitrimers with low topology freezing transition temperature. Polymers 14, 2456. doi:10.3390/polym14122456
Kuenstler, A. S., and Bowman, C. N. (2023). Catalytic control of crystallization in dynamic networks. ACS Macro Lett. 12, 133–139. doi:10.1021/acsmacrolett.2c00703
Lin, Y., Chen, Y., Yu, Z., Huang, Z., Lai, J.-C., Tok, J. B.-H., et al. (2022). Reprocessable and recyclable polymer network electrolytes via incorporation of dynamic covalent bonds. Chem. Mater. 34, 2393–2399. doi:10.1021/acs.chemmater.1c04396
Luo, J., Demchuk, Z., Zhao, X., Saito, T., Tian, M., Sokolov, A. P., et al. (2022). Elastic vitrimers: Beyond thermoplastic and thermoset elastomers. Matter 5, 1391–1422. doi:10.1016/j.matt.2022.04.007
Lv, G., Li, X., Jensen, E., Soman, B., Tsao, Y.-H., Evans, C. M., et al. (2023). Dynamic covalent bonds in vitrimers enable 1.0 W/(m K) intrinsic thermal conductivity. Macromolecules 56, 1554–1561. doi:10.1021/acs.macromol.2c02264
Ma, J., Porath, L. E., Haque, M. F., Sett, S., Rabbi, K. F., Nam, S., et al. (2021). Ultra-thin self-healing vitrimer coatings for durable hydrophobicity. Nat. Commun. 12, 5210. doi:10.1038/s41467-021-25508-4
Marxsen, S. F., Häußler, M., Mecking, S., and Alamo, R. G. (2021). Unlayered–layered crystal transition in recyclable long-spaced aliphatic Polyesters. ACS Appl. Polym. Mater. 3, 5243–5256. doi:10.1021/acsapm.1c01025
Maus, A., Hertlein, C., and Saalwächter, K. (2006). A robust proton NMR method to investigate hard/soft ratios, crystallinity, and component mobility in polymers. Macromol. Chem. Phys. 207, 1150–1158. doi:10.1002/macp.200600169
Montarnal, D., Capelot, M., Tournilhac, F., and Leibler, L. (2011). Silica-like malleable materials from permanent organic networks. Science 334, 965–968. doi:10.1126/science.1212648
Niu, W., Zhang, Z., Chen, Q., Cao, P.-F., and Advincula, R. C. (2021). Highly recyclable, mechanically isotropic and healable 3D-printed elastomers via polyurea vitrimers. ACS Mater. Lett. 3, 1095–1103. doi:10.1021/acsmaterialslett.1c00132
Pascual-Jose, B., De La Flor, S., Serra, A., and Ribes-Greus, A. (2023). Analysis of poly (thiourethane) covalent adaptable network through broadband dielectric spectroscopy. ACS Appl. Polym. Mater. 5, 1125–1134. doi:10.1021/acsapm.2c01543
Porath, L. E., and Evans, C. M. (2021). Importance of broad temperature windows and multiple rheological approaches for probing viscoelasticity and entropic elasticity in vitrimers. Macromolecules 54, 4782–4791. doi:10.1021/acs.macromol.0c02800
Porath, L., Huang, J., Ramlawi, N., Derkaloustian, M., Ewoldt, R. H., and Evans, C. M. (2022). Relaxation of vitrimers with kinetically distinct mixed dynamic bonds. Macromolecules 55, 4450–4458. doi:10.1021/acs.macromol.1c02613
Ricarte, R. G., and Shanbhag, S. (2021). Unentangled vitrimer melts: Interplay between chain relaxation and cross-link exchange controls linear rheology. Macromolecules 54, 3304–3320. doi:10.1021/acs.macromol.0c02530
Rossegger, E., Höller, R., Reisinger, D., Fleisch, M., Strasser, J., Wieser, V., et al. (2021). High resolution additive manufacturing with acrylate based vitrimers using organic phosphates as transesterification catalyst. Polymer 221, 123631. doi:10.1016/j.polymer.2021.123631
Röttger, M., Domenech, T., Van Der Weegen, R., Breuillac, A., Nicolaÿ, R., and Leibler, L. (2017). High-performance vitrimers from commodity thermoplastics through dioxaborolane metathesis. Science 356, 62–65. doi:10.1126/science.aah5281
Saalwächter, K., and Heuer, A. (2006). Chain dynamics in elastomers as investigated by proton multiple-quantum NMR. Macromolecules 39, 3291–3303. doi:10.1021/ma052567b
Sangroniz, L., Cavallo, D., and Müller, A. J. (2020). Self-nucleation effects on polymer crystallization. Macromolecules 53, 4581–4604. doi:10.1021/acs.macromol.0c00223
Schäler, K., Roos, M., Micke, P., Golitsyn, Y., Seidlitz, A., Thurn-Albrecht, T., et al. (2015). Basic principles of static proton low-resolution spin diffusion NMR in nanophase-separated materials with mobility contrast. Solid State Nucl. Magn. Reson. 72, 50–63. doi:10.1016/j.ssnmr.2015.09.001
Schäler, K., Achilles, A., Bärenwald, R., Hackel, C., and Saalwächter, K. (2013). Dynamics in crystallites of poly (ε-caprolactone) as investigated by solid-state NMR. Macromolecules 46, 7818–7825. doi:10.1021/ma401532v
Schulz, M., Schäfer, M., Saalwächter, K., and Thurn-Albrecht, T. (2022). Competition between crystal growth and intracrystalline chain diffusion determines the lamellar thickness in semicrystalline polymers. Nat. Commun. 13, 119. doi:10.1038/s41467-021-27752-0
Soccio, M., Nogales, A., Lotti, N., Munari, A., and Ezquerra, T. A. (2007). Evidence of early stage precursors of polymer crystals by dielectric spectroscopy. Phys. Rev. Lett. 98, 037801. doi:10.1103/physrevlett.98.037801
Soman, B., and Evans, C. M. (2021). Effect of precise linker length, bond density, and broad temperature window on the rheological properties of ethylene vitrimers. Soft Matter 17, 3569–3577. doi:10.1039/d0sm01544j
Soman, B., Go, Y. K., Shen, C., Leal, C., and Evans, C. M. (2022a). Impact of dynamic covalent chemistry and precise linker length on crystallization kinetics and morphology in ethylene vitrimers. Soft Matter 18, 293–303. doi:10.1039/d1sm01288f
Soman, B., Schweizer, K. S., and Evans, C. M. (2022b). Fragile glass formation and non-arrhenius upturns in ethylene vitrimers revealed by dielectric spectroscopy. Macromolecules 56, 166–176. doi:10.1021/acs.macromol.2c01657
Sonnenberger, N., Anders, N., Golitsyn, Y., Steinhart, M., Enke, D., Saalwächter, K., et al. (2016). Pharmaceutical nanocrystals confined in porous host systems–interfacial effects and amorphous interphases. Chem. Commun. 52, 4466–4469. doi:10.1039/c6cc00962j
Tanaka, H., and Nishi, T. (1986). Study of crystallization process of polymer from melt by a real-time pulsed NMR measurement. J. Chem. Phys. 85, 6197–6209. doi:10.1063/1.451850
Trigg, E. B., Stevens, M. J., and Winey, K. I. (2017). Chain folding produces a multilayered morphology in a precise polymer: Simulations and experiments. J. Am. Chem. Soc. 139, 3747–3755. doi:10.1021/jacs.6b12817
Van Lijsebetten, F., Engelen, S., Bauters, E., Van Vooren, W., Smulders, M. M., and Du Prez, F. E. (2022). Recyclable vitrimer epoxy coatings for durable protection. Eur. Polym. J. 176, 111426. doi:10.1016/j.eurpolymj.2022.111426
Van Zee, N. J., and Nicolaÿ, R. (2020). Vitrimers: Permanently crosslinked polymers with dynamic network topology. Prog. Polym. Sci. 104, 101233. doi:10.1016/j.progpolymsci.2020.101233
Wibowo, E. S., and Park, B.-D. (2020). Determination of crystallinity of thermosetting urea-formaldehyde resins using deconvolution method. Macromol. Res. 28, 615–624. doi:10.1007/s13233-020-8076-2
Wurm, A., Soliman, R., Goossens, J., Bras, W., and Schick, C. (2005). Evidence of pre-crystalline-order in super-cooled polymer melts revealed from simultaneous dielectric spectroscopy and SAXS. J. non-crystalline solids 351, 2773–2779. doi:10.1016/j.jnoncrysol.2005.04.072
Yan, P., Zhao, W., Zhang, B., Jiang, L., Petcher, S., Smith, J. A., et al. (2020). Inverse vulcanized polymers with shape memory, enhanced mechanical properties, and vitrimer behavior. Angew. Chem. Int. Ed. 59, 13371–13378. doi:10.1002/anie.202004311
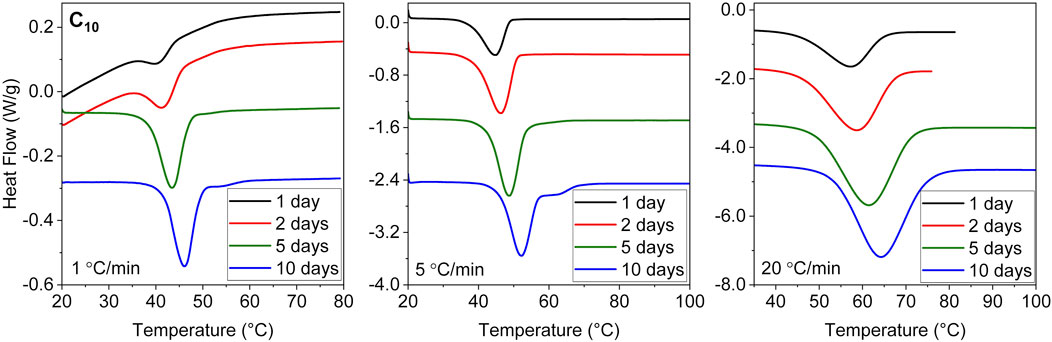
FIGURE A1. DSC heating traces of C10 crystallized isothermally at 20 °C for different durations (1–10 days), using different heating rates of 1 (left), 5 (middle) and 20°C/min (right).
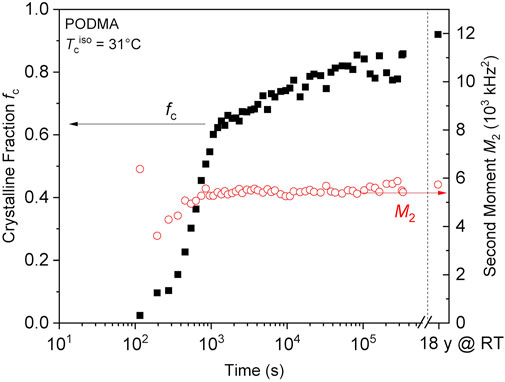
FIGURE A2. Crystalline fraction (fc) and second moment of the crystalline lineshapes (M2) of PODMA (see Hempel et al., 2006) plotted as a function of annealing time at 31°C after melting at about 60°C. The longest-time data points after the axis break (dashed vertical line) were taken on the as-received sample that was stored at room temperature for about 18 years before heating to 31°C. Notably, the NMR-based absolute crystallinity reaches about 80%, being more than twice as large as the values deduced from earlier DSC measurements. This suggests that the reference heat of melting based on pure n-octadecane as used by Hempel et al. (2006) was not appropriate; the side-chain crystallites thus suffer destabilization, possibly as a result of increased motional freedom as revealed by the comparably low value of the average M2. The final crystallinity is close to the fraction of protons in the crystallizable C18 chains, being 0.88.
Keywords: covalent adaptable networks, polymer crystallization, crystallization kinetics, polymorphism, memory effect, superheating
Citation: Saalwächter K, Soman B and Evans CM (2023) Crystallinity and perfection in ethylene vitrimers probed by combined calorimetry, scattering, and time-domain NMR. Front. Soft. Matter 3:1208777. doi: 10.3389/frsfm.2023.1208777
Received: 19 April 2023; Accepted: 12 June 2023;
Published: 30 June 2023.
Edited by:
Finizia Auriemma, University of Naples Federico II, ItalyReviewed by:
GengXin Liu, Donghua University, ChinaCopyright © 2023 Saalwächter, Soman and Evans. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kay Saalwächter, a2F5LnNhYWx3YWVjaHRlckBwaHlzaWsudW5pLWhhbGxlLmRl; Christopher M. Evans, Y21lMzY1QGlsbGlub2lzLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.