
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
MINI REVIEW article
Front. Soft Matter, 01 June 2023
Sec. Liquid Crystals
Volume 3 - 2023 | https://doi.org/10.3389/frsfm.2023.1193904
We study the effects of nanoparticles (NPs) on thermotropic nematic liquid crystals (LCs) in relatively dilute NP–LC mixtures. We are interested in the fundamental generic mechanisms that quantitatively and qualitatively affect the phase behavior of LCs. A simple molecular field analysis shows that a phase transition will likely occur upon entry into the ordered phase. Moreover, the interaction between nematogenic NPs and LCs could force a sergeant–soldier-like behavior, in which only the phase behavior of one component is affected despite the symmetric appearance of the coupling term. When NPs are anisotropic, their influence on LC phase behavior can be qualitatively different depending on the anchoring, even in the absence of the disorder. We illustrate numerically that a random-field-type disorder might impose either short-range, quasi-long-range, or even long-range order, which might survive.
Mixing soft materials with appropriate nanoparticles (NPs) can yield effective materials exhibiting new or anomalously enhanced properties (Balazs et al., 1979; Hamley, 2003). If soft materials exhibit a kind of orientational or translational order, the richness of the resulting qualitatively different effective materials explodes. Liquid crystalline (LC) materials are an excellent example. They combine a unique combination of liquid character, order, softness, and optical transparency (de Gennes, 1995; Kleman and Lavrentovich, 2003; Oswald and Pieranski, 2019). The liquid character enables relatively simple preparation of mixtures. Order in LC matrices can give rise to long-range forces among immersed NPs (Poulin et al., 1979; Pires et al., 2007). Softness can enable relatively strong responses in the LC matrix in the presence of adequate NPs (Lelidis et al., 1993; Li et al., 2006; Palffy-Muhoray, 2007). Furthermore, optical transparency enables relatively simple observation of NP-driven changes (Poulin et al., 1979; Pires et al., 2007). It should be noted that long-range forces among NPs could trigger the self-assembling of NPs, which can open different structural pathways (Hegmann et al., 2007; Bisoyi and Kumar, 2011; Lagerwall and Scalia, 2012; Lagerwall and Scalia, 2017).
Nematic (de Gennes, 1995; Kleman and Lavrentovich, 2003; Oswald and Pieranski, 2019) orientational order represents the simplest LC phase structure. It is described by the nematic molecular field. In bulk nematic equilibrium, the molecular field is uniaxial and spatially homogeneously aligned along a single symmetry-breaking orientation. Local uniaxial order is commonly described in terms of the nematic director field
Appropriate NPs could influence the nematic order via different generic mechanisms if inserted into nematic LCs. Important controlling parameters are the concentration of NPs, geometrical shape (Bellini et al., 2000; Kyrou et al., 2018; Kyrou et al., 2020; Skarabot et al., 2022), NP surface treatment (Nobili and Durand, 1992; Lavric et al., 2013a; Oswald and Pieranski, 2019; Kyrou et al., 2020), material characteristics of NPs (Mertelj et al., 2013; Kumar, 2014; Moghadas et al., 2015; Poursamad and Hallaji, 2017; Emdadi et al., 2018a; Emdadi et al., 2018b; Drozd-Rzoska et al., 2019; Jahanbakhsh et al., 2019; Poursamad and Emdadi, 2019; Lahiri et al., 2020; Bury et al., 2022; Ma et al., 2022; Sumandra et al., 2022), and LC material properties (de Gennes, 1995; Kleman and Lavrentovich, 2003; Oswald and Pieranski, 2019). Furthermore, NPs could effectively impose qualitatively different disorders on the LC order (Harris et al., 1973; Cleaver et al., 1996; Crawford and Žumer, 1996; Radzihovsky and Toner, 1997; Popa-Nita and Kralj, 2006). Most studies focusing on the impact of the disorder are performed in LC-aerosil mixtures, which can exhibit at least three qualitatively different disorder characteristics (Jin and Finotello, 2001; Bellini et al., 2002; Leon et al., 2004; Rotunno et al., 2005; Buscaglia et al., 2006; Cordoyiannis et al., 2006; Relaix et al., 2011). Furthermore, NPs could enforce LC matrix topological defects (TDs) (Mermin, 1979; Kurik and Lavrentovich, 1988) in the nematic orientational order. TDs correspond to topologically protected, elastically distorted regions in the orientational order. Nematic LCs could host either point or line defects (Schopohl and Sluckin, 1987; Kurik and Lavrentovich, 1988; Lavrentovich, 1998; Kralj and Virga, 2001). Generally, TDs can strongly interact with NPs, opening the door to predetermined and controlled superstructures stabilized by TD–NP interactions (Kikuchi et al., 2002; Yoshida et al., 2009; Karatairi et al., 2010; Liu et al., 2010; Rozic et al., 2011; Coursault et al., 2012; Wang et al., 2012; Lavric et al., 2013a; Lavric et al., 2013b; Liu et al., 2018).
This paper considers different NP-driven generic mechanisms via which NPs impact nematic thermotropic behavior.
Mixtures of nematic LCs and NPs can exhibit complex configurations. In the following, we present some qualitatively different scenarios and discuss generic mechanisms.
Supplementary Appendix SB illustrates a simple mean-field Maier–Saupe analysis that reveals the type of coupling terms in a mixture of two nematic mesogens. It yields the following free energy density expression:
Here,
Let us suppose that the first and second components represent LC molecules and NPs, respectively, and the volume concentration of NPs is given by
This term resembles the structure of the so-called Flory–Huggins free energy contribution (Onsager, 1949; Flory, 1956; Doi, 1981):
where
In most LCs, the second term, “switched-on” in the nematic, is relatively strong. Consequently, on cooling an isotropic mixture to the nematic phase, phase separation is generally likely to occur (Anderson et al., 2001). Figure 1 illustrates a typical phase separation in a mixture of nematic and spherical NPs (i.e.,

FIGURE 1. Typical phase separation pattern on entering the nematic LC phase in a nematic-NP mixture. In the case shown, NPs are spherical. Regions are exhibiting i) relatively strong nematic and ii) essentially isotropic (or paranematic) order, which are i) poor and ii) rich in NP content, respectively.
Let us suppose that the mixture remains homogeneous. A simple Maier–Saupe-type analysis (Humphries et al., 1972) presented in Supplementary Appendix SB suggests that in a mixture of two nematogenic components, a free energy density
which does not affect the qualitative order-disorder behavior of individual components. For simplicity, we assume that both components have identical condensation material constants with the exceptions of bulk phase transition temperatures of isolated components and w > 0 (i.e., this term tends to increase the degree of order in both components). We assume that an isolated ith component exhibits an isotropic-nematic phase transition at
where
where
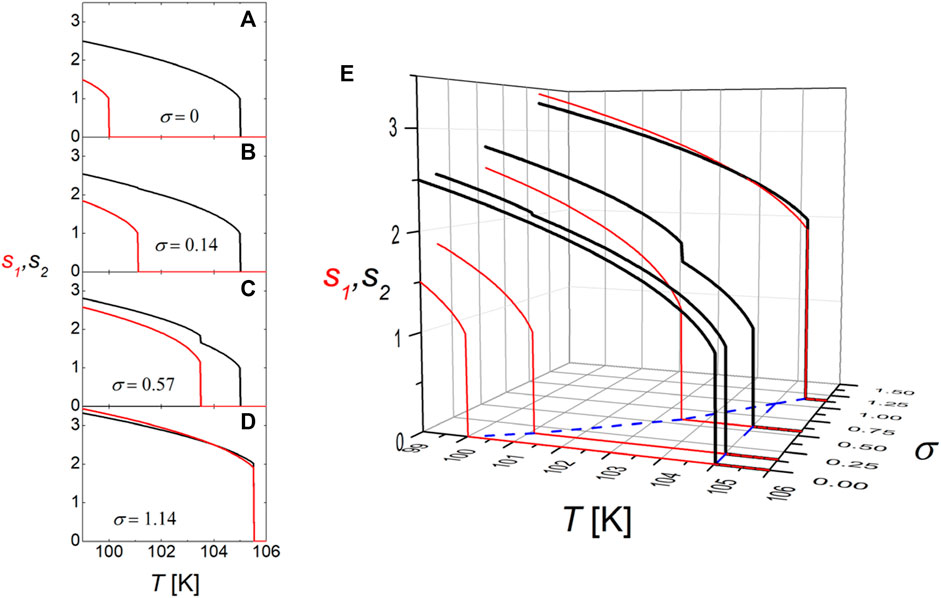
FIGURE 2. “Sergeant–soldier” behavior. For the dimensionless coupling strength
Next, we consider a dilute mixture where the second component consists of anisotropic particles. For illustration, we assume that the free energy F consists of LC condensation, LC nematic elastic, and NP–LC interfacial free energy contributions, where details are given in Supplementary Appendix SA. Of our interest is the impact of NPs on the LC order–disorder phase transition. We assume that NPs relatively weakly disrupt the nematic director field, as illustrated in Figure 3. In the nematic phase,
where
where
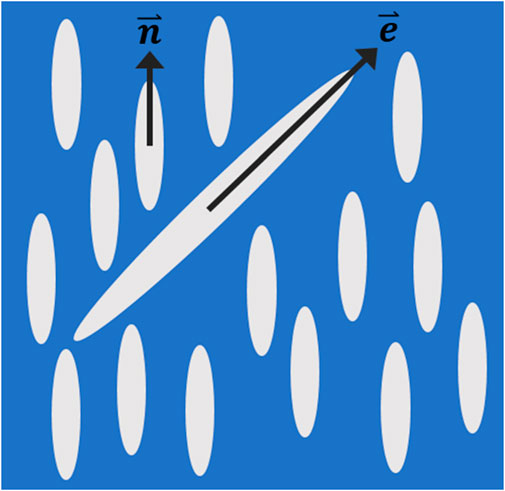
FIGURE 3. Dilute nematic LC—anisotropic NP mixture, where NPs relatively weakly interact with the nematic LC host. Consequently, the nematic LC orientational order, described by the nematic director field
In the limit
where
The phase behavior of this effective system is as follows. Typical nematic order parameter temperature variations are depicted in Figure 4. For
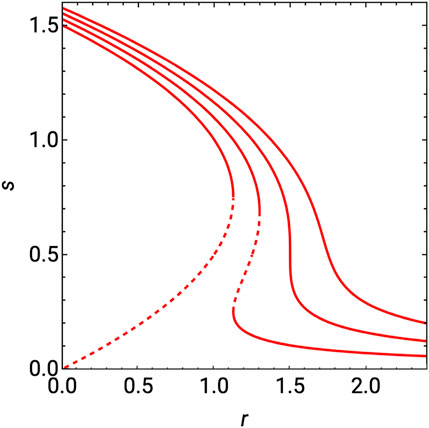
FIGURE 4. Nematic LC order
If
In the following, we discuss cases where NPs introduce a certain degree of randomness. The I–N phase transition is extremely susceptible to disorder due to the existence of Goldstone modes in the nematic director field in the nematic phase (Kleman and Lavrentovich, 2003; Palffy-Muhoray, 2007). These are the consequences of continuous symmetry breaking, via which bulk nematic equilibrium is established. According to the Imry–Ma theorem (Larkin, 1970; Imry and Ma, 1975), even infinitesimally weak random-field-type disorder is sufficient to break the long-range order (LRO) of the pure bulk phase, which is reached via continuous symmetry breaking. The resulting phase should possess short-range order (SRO), and the resulting domain-type pattern is predicted to be dominated by a single characteristic domain size
A convenient model to study the impact of NP-imposed randomness on the I–N phase transition is the Lebwohl–Lasher lattice model (Lebwohl and Lasher, 1972). Its key ingredients are presented in Supplementary Appendix SC. Using it, we probe the impact of NP-imposed random-type behavior on the LC order–disorder phase transition in the orientational order. Despite its simplicity, this approach well captures the essential features of LCs. In modeling, we vary the concentration p of sites by imposing a randomly selected orientation with finite disorder strength W. In typical studies focusing on a system’s range of orientational order, one commonly measures or calculates the orientational order correlation function G(r). This correlation function measures how orientational correlations decay with relative distance r. However, several studies (Denholm and Sluckin, 1993; Cvetko et al., 2009; Ranjkesh et al., 2014) reveal that G(r) dependence relatively poorly distinguishes between SRO and QLRO. Numerically, it is computationally more effective to extract the range of order using finite-size analysis (Eppenga and Frenkel, 1984; Ranjkesh et al., 2014). Namely, according to the central limit theorem, one expects that
where
Our simulations used this finite-scaling approach to determine the range of order on the varying concentration of NPs, their imposed anchoring strength W, and temperature. Furthermore, in the presence of disorder, one expects history-dependent behavior. For this reason, we probed systems’ behavior for three different histories, which we refer to as i) annealed history (AH), ii) temperature-quenched history (TQH), and (iii) field-quenched history (FQH). In AH, we gradually decreased temperature stepwise and calculated the structure at a given T by using as the initial “seed” structure the fixed-point configuration calculated at the previous T. In QH, we calculated the structure at a given T by originating from the isotropic phase. Finally, in FQH, the “seed” structure was spatially homogeneously aligned along a single symmetry-breaking direction. In Figures 5, 6, we plot
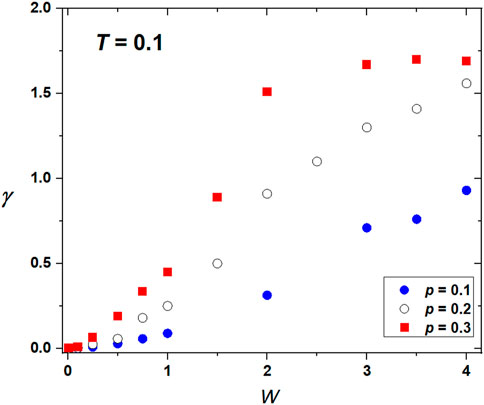
FIGURE 5. Variation of
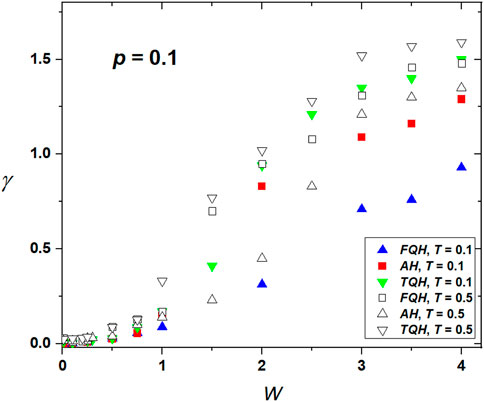
FIGURE 6. Variation of
We illustrated several mechanisms via which NPs could quantitatively or qualitatively modify the phase behavior of the bulk nematic LC phase. The simplicity of nematic ordering explodes into a rich palette of behaviors enabled by varying control parameters. In the study, we addressed only a few of them: concentration of NPs, nature and strength of NP–LC interactions, and anisotropy of NPs. The diversity of phenomena becomes even wider if the ferromagnetic, ferroelectric, or multiferroic properties of NPs are included. The ferromagnetic nanoparticles dispersed within the liquid crystals provide a new way to develop magneto-optic devices (Ji et al., 2019) that can also be used for THz filtering and modulation, in which sensing applications are becoming increasingly widespread (Abina et al., 2022).
In this paper, we focused only on phase behavior. It should be noted that structural behavior could be even richer. For instance, recent technological advances enable the stabilization of nematic structures incorporating diverse configurations of TDs, i.e., lattices of disclinations (Culbreath et al., 2011; Ackerman et al., 2012a; Ackerman et al., 2012b; Evans et al., 2013; Murray et al., 2014; Glazar et al., 2015; Guo et al., 2016; Peng et al., 2017; Wang et al., 2017; Yu et al., 2019; Sohn et al., 2020; Guo et al., 2021) or other assemblies (Harkai et al., 2020). Such structures could be further modified by appropriate NPs, which could make them more robust or introduce additional functionalities in the system. For example, conductive NPs assembled within a line defect can form a conductive wire (Coursault et al., 2012). Furthermore, recent experiments demonstrated (Harkai et al., 2020) that one could efficiently switch among competing line-defect structures using external fields. If these well-controllable defects would drag trapped NPs with them, one could construct rewritable networks of NPs, which could open doors to diverse applications.
AH, SK, AA, and AZ contributed to the conception and design of the study. AR organized and performed the experimental part. AH wrote the first draft of the manuscript. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The authors acknowledge support from the Slovenian Research Agency grants P1-0099, P2-0348, and J1-2457.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsfm.2023.1193904/full#supplementary-material
Abina, A., Puc, U., and Zidanšek, A. (2022). Challenges and opportunities of terahertz technology in construction and demolition waste management. J. Environ. Manage 315, 115118. doi:10.1016/j.jenvman.2022.115118
Ackerman, P. J., Qi, Z., Lin, Y., Twombly, C. W., Laviada, M. J., Lansac, Y., et al. (2012). Laser-directed hierarchical assembly of liquid crystal defects and control of optical phase singularities. Sci. Rep. 2, 414. doi:10.1038/srep00414
Ackerman, P. J., Qi, Z., and Smalyukh, . Optical generation of crystalline, quasicrystalline, and arbitrary arrays of torons in confined cholesteric liquid crystals for patterning of optical vortices in laser beams. Phys. Rev. E. 2012;86, 021703, doi:10.1103/physreve.86.0217032, 1).
Anderson, V. J., Terentjev, E. M., Meeker, S. P., Crain, J., and Poon, W. C. K. (2001). Cellular solid behaviour of liquid crystal colloids - 1. Phase separation and morphology. Eur. Phys. J. E 4 (1), 11–20. doi:10.1007/pl00013680
Balazs, A. C., Emrick, T., and Russell, T. P. (1979). Nanoparticle polymer composites: Where two small worlds meet. Science 314 (5802), 1107–1110. doi:10.1126/science.1130557
Bellini, T., Buscaglia, M., Chiccoli, C., Mantegazza, F., Pasini, P., and Zannoni, C. (2002). Nematics with quenched disorder: How long will it take to heal? Phys. Rev. Lett. 88 (24), 245506. doi:10.1103/physrevlett.88.245506
Bellini, T., Buscaglia, M., Chiccoli, C., Mantegazza, F., Pasini, P., and Zannoni, C. (2000). Nematics with quenched disorder: What is left when long range order is disrupted? Phys. Rev. Lett. 85 (5), 1008–1011. doi:10.1103/physrevlett.85.1008
Bisoyi, H. K., and Kumar, S. (2011). Liquid-crystal nanoscience: An emerging avenue of soft self-assembly. Chem. Soc. Rev. 40 (1), 306–319. doi:10.1039/b901793n
Bury, P., Vevericik, M., Cernobila, F., Tomasovicova, N., Zakut’anska, K., Kopcansky, P., et al. (2022). Role of magnetic nanoparticles size and concentration on structural changes and corresponding magneto-optical behavior of nematic liquid crystals. Nanomaterials 12 (14), 2463. doi:10.3390/nano12142463
Buscaglia, M., Bellini, T., Chiccoli, C., Mantegazza, F., Pasini, P., Rotunno, M., et al. Memory effects in nematics with quenched disorder. Phys. Rev. E. 2006;74, 011706, doi:10.1103/physreve.74.0117061, 1).
Chakrabarti, J. (1998). Simulation evidence of critical behavior of isotropic-nematic phase transition in a porous medium. Phys. Rev. Lett. 81 (2), 385–388. doi:10.1103/physrevlett.81.385
Cleaver, D. J., Kralj, S., Sluckin, T. J., and Allen, M. P. (1996). “The random anisotropy nematic spin model,” in Liquid crystals in complex geometries: Formed by polymer and porous networks G. P. Crawford, and S. Žumer (Oxford: Oxford University Press).
Cordoyiannis, G., Kralj, S., Nounesis, G., Zumer, S., and Kutnjak, Z., Soft-stiff regime crossover for an aerosil network dispersed in liquid crystals. Phys. Rev. E. 2006;73, 031707, doi:10.1103/physreve.73.0317073, 1).
Coursault, D., Grand, J., Zappone, B., Ayeb, H., Levi, G., Felidj, N., et al. (2012). Linear self-assembly of nanoparticles within liquid crystal defect arrays. Adv. Mater. 24 (11), 1461–1465. doi:10.1002/adma.201103791
Crawford, G. P., and Žumer, S. (1996). Liquid crystals in complex geometries formed by polymer and porous networks. London: Taylor & Francis.
Culbreath, C., Glazar, N., and Yokoyama, H. (2011). Note: Automated maskless micro-multidomain photoalignment. Rev. Sci. Instrum. 82 (12), 126107. doi:10.1063/1.3669528
Cvetko, M., Ambrožič, M., and Kralj, S. (2009). Memory effects in randomly perturbed systems exhibiting continuous symmetry breaking. Liq. Cryst. 36 (1), 33–41. doi:10.1080/02678290802638431
Denholm, D. R., and Sluckin, T. J. (1993). Monte Carlo studies of two-dimensional random-anisotropy magnets. Phys. Rev. B 48 (2), 901–912. doi:10.1103/physrevb.48.901
Doi, M. (1981). Molecular-Dynamics and rheological properties of concentrated-solutions of rodlike polymers in isotropic and liquid-crystalline phases. J. Polym. Sci. PART B-POLYMER Phys. 19 (2), 229–243. doi:10.1002/pol.1981.180190205
Drozd-Rzoska, A., Starzonek, S., Rzoska Sylwester, J., and Kralj, S. (2019). Nanoparticle-controlled glassy dynamics in nematogen-based nanocolloids. Phys. Rev. E 99 (5), 052703. doi:10.1103/physreve.99.052703
Emdadi, M., Poursamad, J. B., Sahrai, M., and Moghadas, F. (2018). Investigation of nematic liquid crystals doped with spherical multiferroic nanoparticles in the presence of a magnetic field. Braz. J. Phys. 48 (5), 433–441. doi:10.1007/s13538-018-0590-8
Emdadi, M., Poursamad, J. B., Sahrai, M., and Moghaddas, F. (2018). Behaviour of nematic liquid crystals doped with ferroelectric nanoparticles in the presence of an electric field. Mol. Phys. 116 (12), 1650–1658. doi:10.1080/00268976.2018.1441462
Eppenga, R., and Frenkel, D. (1984). Monte-carlo study of the isotropic and nematic phases of infinitely thin hard platelets. Mol. Phys. 52 (6), 1303–1334. doi:10.1080/00268978400101951
Evans, J. S., Ackerman, P. J., Broer, D. J., van de Lagemaat, J., and Smalyukh, (2013). Optical generation, templating, and polymerization of three-dimensional arrays of liquid-crystal defects decorated by plasmonic nanoparticles. Phys. Rev. E 87 (3), 032503. doi:10.1103/physreve.87.032503
Feldman, D. E. (2000). Quasi-long-range order in nematics confined in random porous media. Phys. Rev. Lett. 84 (21), 4886–4889. doi:10.1103/physrevlett.84.4886
Flory, P. J. (1956). Phase equilibria in solutions of rod-like particles. Proc. R. Soc. Lond A 234, 73–89.
Glazar, N., Culbreath, C., Li, Y., and Yokoyama, H. (2015). Switchable liquid-crystal phase-shift mask for super-resolution photolithography based on Pancharatnam-Berry phase. Appl. Phys. EXPRESS 8 (11), 116501. doi:10.7567/apex.8.116501
Guo, Y., Jiang, M., Afghah, S., Peng, C., Selinger, R. L. B., Lavrentovich, O. D., et al. (2021). Photopatterned designer disclination networks in nematic liquid crystals. Adv. Opt. Mater 9 (16), 2100181. doi:10.1002/adom.202100181
Guo, Y., Jiang, M., Peng, C., Sun, K., Yaroshchuk, O., Lavrentovich, O., et al. (2016). High-Resolution and high-throughput plasmonic photopatterning of complex molecular orientations in liquid crystals. Adv. Mater. 28 (12), 2353–2358. doi:10.1002/adma.201506002
Hamley, I. W. (2003). Nanotechnology with soft materials. Angew. Chemie-International Ed. 42 (15), 1692–1712. doi:10.1002/anie.200200546
Harkai, S., Murray, B. S., Rosenblatt, C., and Kralj, S. (2020). Electric field driven reconfigurable multistable topological defect patterns. Phys. Rev. Res. 2 (1), 013176. doi:10.1103/physrevresearch.2.013176
Harris, R., Plischke, M., and Zuckermann, M. J. (1973). New model for amorphous magnetism. Phys. Rev. Lett.31 (3), 160–162. doi:10.1103/physrevlett.31.160
Hegmann, T., Qi, H., and Marx, V. M. (2007). Nanoparticles in liquid crystals: Synthesis, self-assembly, defect formation and potential applications. J. Inorg. Organomet. Polym. Mater 17 (3), 483–508. doi:10.1007/s10904-007-9140-5
Holbl, A., Pal, K., Slavinec, M., and Kralj, S. (2022). Slave-master mechanism of thermotropic liquid crystal phase transitional behavior. Phys. B-CONDENSED MATTER 642, 414142. doi:10.1016/j.physb.2022.414142
Humphries, R. L., James, P. G., and Luckhurst, G. R. (1972). Molecular field treatment of nematic liquid-crystals. J. Chem. Society-Faraday Trans. II 68 (6), 1031. doi:10.1039/f29726801031
Imry, Y., and Ma, S. (1975). Random-field instability of the ordered state of continuous symmetry. Phys. Rev. Lett. 35 (21), 1399–1401. doi:10.1103/physrevlett.35.1399
Jahanbakhsh, F., Poursamad, J. B., Ara, M. H. M., Lorenz, A., Khoshsima, H., and Darabi, M. (2019). Dispersion of multiferroic BiFeO3 nanoparticles in nematic liquid crystals. Appl. Phys. A-Materials Sci. Process. 125 (12), 877. doi:10.1007/s00339-019-3153-0
Ji, Y., Fan, F., Xu, S., Yu, J., and Chang, S. (2019). Manipulation enhancement of terahertz liquid crystal phase shifter magnetically induced by ferromagnetic nanoparticles. Nanoscale 11 (11), 4933–4941. doi:10.1039/c8nr09259a
Jin, T., and Finotello, D. (2001). Aerosil dispersed in a liquid crystal: Magnetic order and random silica disorder. Phys. Rev. Lett. 86 (5), 818–821. doi:10.1103/physrevlett.86.818
Karatairi, E., Rozic, B., Kutnjak, Z., Tzitzios, V., Nounesis, G., Cordoyiannis, G., et al. Nanoparticle-induced widening of the temperature range of liquid-crystalline blue phases. Phys. Rev. E. 2010;81, 041703, doi:10.1103/physreve.81.0417034, 1).
Kikuchi, H., Yokota, M., Hisakado, Y., Yang, H., and Kajiyama, T. (2002). Polymer-stabilized liquid crystal blue phases. Nat. Mater 1 (1), 64–68. doi:10.1038/nmat712
Kleman, M., and Lavrentovich, O. D. (2003). Soft matter physics: An introduction. New York: Springer Science & Business Media.
Kralj, S., and Virga, E. G. (2001). Universal fine structure of nematic hedgehogs. J. Phys. A Math. Gen. 34 (4), 829–838. doi:10.1088/0305-4470/34/4/309
Kumar, S. (2014). Discotic liquid crystal-nanoparticle hybrid systems. NPG Asia Mater 6, e82. doi:10.1038/am.2013.75
Kurik, M. V., and Lavrentovich, O. D. (1988). Defects in liquid-crystals - homotopy-theory and experimental investigations. Uspekhi Fiz. Nauk. 154 (3), 381–431. doi:10.3367/ufnr.0154.198803b.0381
Kyrou, C., Kralj, S., Panagopoulou, M., Raptis, Y., Nounesis, G., and Lelidis, I. (2018). Impact of spherical nanoparticles on nematic order parameters. Phys. Rev. E 97 (4), 042701. doi:10.1103/physreve.97.042701
Kyrou, C., Tsiourvas, D., Kralj, S., and Lelidis, I. (2020). Effect of superhydrophobic nanoplatelets on the phase behaviour of liquid crystals. J. Mol. Liq. 298, 111984. doi:10.1016/j.molliq.2019.111984
Lagerwall, J. P., and Scalia, G. (2017). “Liquid crystals with nano and microparticles,” in 2 volumes) (series in soft condensed matter book 7) (Florida: CRC Press).
Lagerwall, J. P. F., and Scalia, G. (2012). A new era for liquid crystal research: Applications of liquid crystals in soft matter nano-bio- and microtechnology. Curr. Appl. Phys. 12 (6), 1387–1412. doi:10.1016/j.cap.2012.03.019
Lahiri, T., Pushkar, S. K., and Poddar, P. (2020). Theoretical study on the effect of electric field for carbon nanotubes dispersed in nematic liquid crystal. Phys. B-Condensed Matter 588, 412177. doi:10.1016/j.physb.2020.412177
Larkin, A. I. (1970). Effect of inhomogeneities on structure of mixed state of superconductors. Sov. Phys. JETP-USSR 31 (4), 784.
Lavrentovich, O. D. (1998). Topological defects in dispersed words and worlds around liquid crystals, or liquid crystal drops. Liq. Cryst. 24 (1), 117–126. doi:10.1080/026782998207640
Lavric, M., Cordoyiannis, G., Kralj, S., Tzitzios, V., Nounesis, G., and Kutnjak, Z. (2013). Effect of anisotropic MoS2 nanoparticles on the blue phase range of a chiral liquid crystal. Appl. Opt. 52 (22), E47–E52. doi:10.1364/ao.52.000e47
Lavric, M., Tzitzios, V., Kralj, S., Cordoyiannis, G., Lelidis, I., Nounesis, G., et al. (2013). The effect of graphene on liquid-crystalline blue phases. Appl. Phys. Lett. 103 (14), 143116. doi:10.1063/1.4824424
Lebwohl, P. A., and Lasher, G. (1972). Nematic-liquid-Crystal order—a Monte Carlo calculation. Phys. Rev. A Coll. Park) 6 (1), 426–429. doi:10.1103/physreva.6.426
Lelidis, I., Nobili, M., and Durand, G. (1993). Electric-field-Induced change of the order-parameter in a nematic liquid-crystal. Phys. Rev. E 48 (5), 3818–3821. doi:10.1103/physreve.48.3818
Leon, N., Korb, J. P., Bonalde, I., and Levitz, P. (2004). Universal nuclear spin relaxation and long-range order in nematics strongly confined in mass fractal silica gels. Phys. Rev. Lett. 92 (19), 195504. doi:10.1103/physrevlett.92.195504
Li, F., Buchnev, O., Il Cheon, C., Glushchenko, A., Reshetnyak, V., Reznikov, Y., et al. (2006). Orientational coupling amplification in ferroelectric nematic colloids. Phys. Rev. Lett. 97 (14), 147801. doi:10.1103/physrevlett.97.147801
Liu, F., Ma, G., and Zhao, D. (2018). Nickel nanoparticle-stabilized room-temperature blue-phase liquid crystals. Nanotechnology 29 (28), 285703. doi:10.1088/1361-6528/aabaa4
Liu, Q., Cui, Y., Gardner, D., Li, X., He, S., and Smalyukh, (2010). Self-alignment of plasmonic gold nanorods in reconfigurable anisotropic fluids for tunable bulk metamaterial applications. Nano Lett. 10 (4), 1347–1353. doi:10.1021/nl9042104
Ma, Z., Gao, Y., and Cao, H. (2022). The effect of chemically modified multi-walled carbon nanotubes on the electro-optical properties of a twisted nematic liquid crystal display mode. Cryst. (Basel) 12 (10), 1482. doi:10.3390/cryst12101482
Mermin, N. D. (1979). The topological theory of defects in ordered media. Rev. Mod. Phys. 51 (3), 591–648. doi:10.1103/revmodphys.51.591
Mertelj, A., Lisjak, D., Drofenik, M., and Copic, M. (2013). Ferromagnetism in suspensions of magnetic platelets in liquid crystal. Nature 504 (7479), 237–241. doi:10.1038/nature12863
Moghadas, F., Khoshsima, H., and Olyaeefar, B. (2015). High diffraction efficiency in permanent optical memories based on Methyl Red doped liquid crystal. Opt. Quantum Electron 47 (2), 225–233. doi:10.1007/s11082-014-9906-2
Murray, B. S., Pelcovits, R. A., and Rosenblatt, C. (2014). Creating arbitrary arrays of two-dimensional topological defects. Phys. Rev. E 90 (5), 052501. doi:10.1103/physreve.90.052501
Nobili, D., and Durand, G. (1992). Disorientation-induced disordering at a nematic-liquid-crystal-solid interface. Phys. Rev. A 46 (10), R6174–R6177. doi:10.1103/physreva.46.r6174
Onsager, L. (1949). The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 51 (4), 627–659. Available from:. doi:10.1111/j.1749-6632.1949.tb27296.x
Oswald, P., and Pieranski, P. (2019). Nematic and cholesteric liquid crystals concepts and physical properties illustrated by experiments. Florida: CRC Press.
Palffy-Muhoray, P. (2007). The diverse world of liquid crystals. Phys. Today 60 (9), 54–60. doi:10.1063/1.2784685
Peng, C., Guo, Y., Turiv, T., Jiang, M., Wei, Q. H., and Lavrentovich, O. D. (2017). Patterning of lyotropic chromonic liquid crystals by photoalignment with photonic metamasks. Adv. Mater. 29 (21), 1606112. doi:10.1002/adma.201606112
Pires, D., Fleury, J. B., and Galerne, Y. (2007). Colloid particles in the interaction field of a disclination line in a nematic phase. Phys. Rev. Lett. 98 (24), 247801. doi:10.1103/physrevlett.98.247801
Popa-Nita, V., and Kralj, S. (2006). Random anisotropy nematic model: Nematic-non-nematic mixture. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 73 (4), 041705–041708. doi:10.1103/physreve.73.041705
Poulin, P., Stark, H., Lubensky, T. C., and Weitz, D. A. (1979). Novel colloidal interactions in anisotropic fluids. Science 275 (5307), 1770–1773. doi:10.1126/science.275.5307.1770
Poursamad, J. B., and Emdadi, M. (2019). Optical nonlinearity of liquid crystals in the presence of chained ferroelectric nanoparticles. Acta Phys. Pol. A 136 (6), 861–865. doi:10.12693/aphyspola.136.861
Poursamad, J. B., and Hallaji, T. (2017). Freedericksz transition in smectic-A liquid crystals doped by ferroelectric nanoparticles. Phys. B-Condensed Matter 504, 112–115. doi:10.1016/j.physb.2016.10.022
Radzihovsky, L., and Toner, J. (1997). Nematic-to-smectic-A transition in aerogel. Phys. Rev. Lett. 79 (21), 4214–4217. doi:10.1103/physrevlett.79.4214
Ranjkesh, A., Ambrozic, M., Kralj, S., and Sluckin, T. J. (2014). Computational studies of history dependence in nematic liquid crystals in random environments. Phys. Rev. E 89 (2), 022504. doi:10.1103/physreve.89.022504
Relaix, S., Leheny, R. L., Reven, L., and Sutton, M., Memory effect in composites of liquid crystal and silica aerosil. Phys. Rev. E. 2011;84, 061705, doi:10.1103/physreve.84.061705
Rotunno, M., Buscaglia, M., Chiccoli, C., Mantegazza, F., Pasini, P., Bellini, T., et al. (2005). Nematics with quenched disorder: Pinning out the origin of memory. Phys. Rev. Lett. 94 (9), 097802. doi:10.1103/physrevlett.94.097802
Rozic, B., Tzitzios, V., Karatairi, E., Tkalec, U., Nounesis, G., Kutnjak, Z., et al. (2011). Theoretical and experimental study of the nanoparticle-driven blue phase stabilisation. Eur. Phys. J. E 34 (2), 17. doi:10.1140/epje/i2011-11017-8
Schopohl, N., and Sluckin, T. J. (1987). Defect core structure in nematic liquid-crystals. Phys. Rev. Lett. 59 (22), 2582–2584. doi:10.1103/physrevlett.59.2582
Skarabot, M., Mottram, N. J., Kaur, S., Imrie, C. T., Forsyth, E., Storey, J. M. D., et al. (2022). Flexoelectric polarization in a nematic liquid crystal enhanced by dopants with different molecular shape polarities. ACS Omega 7 (11), 9785–9795. doi:10.1021/acsomega.2c00023
Skarabot, M., Ryzhkova, A. V., and Musevic, I. (2018). Interactions of single nanoparticles in nematic liquid crystal. J. Mol. Liq. 267, 384–389. doi:10.1016/j.molliq.2018.01.068
Sohn, H. R. O., Liu, C. D., Voinescu, R., Chen, Z., and Smalyukh, (2020). Optically enriched and guided dynamics of active skyrmions. Opt. Express 28 (5), 6306–6319. doi:10.1364/oe.382845
Sumandra, S. B., Mahendra, B., Nugroho, F., and Yusuf, Y. (2022). Alignment of carbon nanotubes under the influences of nematic liquid crystals and electric fields - an analytical study. Int. J. Comput. Mater Sci. Eng. 11 (02). doi:10.1142/s2047684121500330
van der Schoot, P., Popa-Nita, V., and Kralj, S. (2008). Alignment of carbon nanotubes in nematic liquid crystals. J. Phys. Chem. B 112 (15), 4512–4518. doi:10.1021/jp712173n
Wang, L., He, W., Xiao, X., Meng, F., Zhang, Y., Yang, P., et al. (2012). Hysteresis-free blue phase liquid-crystal-stabilized by ZnS nanoparticles. Small 8 (14), 2189–2193. doi:10.1002/smll.201200052
Wang, M., Li, Y., and Yokoyama, H. (2017). Artificial web of disclination lines in nematic liquid crystals. Nat. Commun. 8, 388. doi:10.1038/s41467-017-00548-x
Yoshida, H., Tanaka, Y., Kawamoto, K., Kubo, H., Tsuda, T., Fujii, A., et al. (2009). Nanoparticle-stabilized cholesteric blue phases. Appl. Phys. EXPRESS 2 (12), 121501. doi:10.1143/apex.2.121501
Keywords: nanoparticles, phase behavior, surface interactions, disorder, sergeant–soldier behavior
Citation: Hölbl A, Ranjkesh A, Abina A, Kralj S and Zidanšek A (2023) Phase behavior of nematic-nanoparticle mixtures. Front. Soft. Matter 3:1193904. doi: 10.3389/frsfm.2023.1193904
Received: 25 March 2023; Accepted: 10 May 2023;
Published: 01 June 2023.
Edited by:
Yanlei Yu, Fudan University, ChinaReviewed by:
Ingo Dierking, The University of Manchester, United KingdomCopyright © 2023 Hölbl, Ranjkesh, Abina, Kralj and Zidanšek. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Aleksander Zidanšek, YWxla3NhbmRlci56aWRhbnNla0BpanMuc2k=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.