M. Kruteva
A.-C. Genix
O. Holderer
J. Oberdisse- 1Jülich Centre for Neutron Science (JCNS-1 and IBI-8), Forschungszentrum Jülich GmbH, Jülich, Germany
- 2Laboratoire Charles Coulomb (L2C), CNRS, University of Montpellier, Montpellier, France
- 3Jülich Centre for Neutron Science (JCNS) at Heinz Maier-Leibnitz Zentrum (MLZ), Forschungszentrum Jülich GmbH, Garching, Germany
The characterization of polymer nanocomposites on molecular length scales and timescales is a challenging task, which is also indispensable for the understanding of macroscopic material's properties. Neutron scattering is one of the techniques which are very well-suited for studying the structure and molecular motion in such soft matter systems. X-rays can also be used for the same purpose, however, with higher energy and thus a different focus on dynamics, where they are better suited for nanoparticle motion. In this mini-review, we aim at highlighting recent results in the field of polymer nanocomposites, including nanoparticle structure in various experimental systems, from model to industrial, and polymer and particle dynamics. This allows establishing the link between microscopic and macroscopic properties, in particular rheology.
1 Introduction
Any child will tell us that in order to know what is inside any material, one needs to cut it into pieces if possible and have a look. Most scientists would probably agree that although considerably more technically involved, most microscopy methods fall into this category. On the other hand, scattering approaches are usually non-destructive, and by finely observing changes in wave vector and energy of X-rays or neutrons shining through samples, it is possible to conclude on the microstructure and dynamics on the nanoscale. For polymer nanocomposites, both approaches have been used and sometimes combined to access information on either the polymer chains or the filler nanoparticles (Bailey and Winey (2020); Genix and Oberdisse (2015); Senses et al. (2022a)). In this mini-review, we focus on a few recent approaches to filler microstructure by small-angle scattering (of X-rays, SAXS or neutrons, and SANS, respectively) in the first subsection and on the dynamical properties of polymer chains, either in bulk or at interfaces, in the second subsection, using quasi-elastic neutron scattering (QENS), sometimes complemented by broadband dielectric spectroscopy (BDS).
2 Filler and chain microstructures by small-angle scattering
Since the very early applications of polymer nanocomposites, it is well-known that the incorporation of hard nanoparticles into soft polymer reinforces the latter (Heinrich et al., 2002; Robertson and Hardman, 2021). If the polymer is a melt, then the direct effect of reinforcement is to increase the viscosity (Einstein 1911), although in some cases the inverse may be observed (Mackay et al., 2003), due to the subtle correspondence of microscopic length scales. If the polymer is entangled or crosslinked, then the reinforcement effect is expressed via the relative increase in the plateau modulus, called the reinforcement factor (Oberdisse 2002). From here, a large variety of situations may be explored, depending on the dispersion state of the NPs. At high dilution and good dispersion, hydrodynamic reinforcement of the viscosity as calculated by Einstein originally for suspensions applies to melts (Smallwood 1944). The aggregate formation may be included based on its internal density or compacity (Baeza et al., 2013; Genix and Oberdisse, 2017), and NP or aggregate interactions can then be treated by adding quadratic terms to the structure factor (Batchelor and Green, 1972; Guth 1945). Percolation, finally, is usually described by power law divergences (Heinrich and Klüppel, 2002). In any event, it is clear that there is a strong impact of the spatial arrangement of the nanoparticles, i.e., of their aggregation, network formation, and internal density, on the final mechanical properties.
Scattering experiments provide a direct link to the main features of NP dispersion, like repulsive peaks or low-q upturns indicating aggregation. For crowded NP environments as encountered in many applications, the analysis of scattering is difficult due to the presence of interparticle interactions. Model fitting or simulations may give access to average structural quantities, like characteristic sizes, aggregation numbers, distribution of interparticle spacings, or pore sizes. Scattering experiments are typically preceded by easier-to-access lab-based characterization such as differential scanning calorimetry (DSC), SAXS, NMR, or rheology, especially neutron scattering then requires additional thoughts about possible contrast variation by the exchange of hydrogen with deuterium in parts of the system, thus enabling to highlight different components of a multicomponent system.
The fundamental scattering contribution to the NP–polymer contrast is the form factor of the primary particles, which should be measured independently. If NPs are monodisperse and spherical, one may describe the interparticle structure factor in a separate way (Lindner and Zemb, 2002), focusing on dispersion. If not, more involved calculations may lead to the same goal (Genix and Oberdisse, 2017). Two different approaches to understand the structure factor have been proposed in the recent past. Beaucage et al. have worked out a pseudo-thermodynamic description, which relates the decrease in the intensity at intermediate scattering vectors to the virial coefficient, repulsion, and thus quality of dispersion (Jin et al. (2017); Mulderig et al. (2017)). This approach has been followed further to relate structural features from scattering to dynamical, in particular the rheological ones (Rishi et al. (2018)). There is an alternative way of describing the same intensity decrease by lower compressibility caused by hard-sphere repulsion and thus relate it to quantitatively aggregate size and mass (Baeza et al., 2013). In a purely geometric model, where polydisperse hard-sphere NPs fill a simulation box, Musino et al. have applied a reverse Monte Carlo algorithm in order to find particle configurations compatible with the experimental scattering (Musino et al., 2020a; 2018). This led to the determination of the aggregate mass distribution functions, up to the identification of big percolating aggregates responsible for the strong increase of the mechanical storage modulus above a threshold concentration. Recently, interparticle spacings have been deduced from the scattering based on the same approach (Genix et al., 2022). It is interesting to note that in industrially relevant systems, in particular with SBR, ZnO particles are often used in small amounts as catalysts and accelerators. They can usually be neglected in SANS due to the low contrast and concentrations but strongly contribute to SAXS. Staropoli et al. (2020) have succeeded in extracting the corresponding partial structure factors of silica and ZnO NPs by combining two probes, neutrons, and X-rays.
NP–polymer interactions may have strong effects on particle dispersion. Three main polymer-mediated states have been predicted by the polymer reference interaction site model (PRISM) (Hooper and Schweizer, 2005): aggregated NPs with NP−NP contact, dispersed NPs sterically stabilized by adsorbed polymer layers, and polymer-bridged NPs. In the presence of strong interfacial attraction, the latter state leads to network formation and possibly phase separation, in agreement with the observation of a low-q upturn at high loading by SAXS measurements (Zhou et al., 2020). For attractive interactions, a decrease in density of the polymer close to the NP surface has also been measured by small-angle scattering (Genix et al., 2019). This confirms the analysis of Jouault (2016) based on aggregated silica. To the best of our knowledge, measurements reported in Genix et al. (2019) are the only static signature of the existence of an interfacial layer unperturbed by NP interactions. By combining SAXS and SANS, Jimenez et al. (2019) have followed desorption and thus reduction of the bound layer thickness upon annealing at high temperatures above Tg. The dynamic features of the interfacial layer have been described in detail in the literature (Baeza et al., 2016; Carroll et al., 2017; Cheng et al., 2017). They are all consistent with a slowdown of the segmental relaxation over 1–5 nm from the particle surfaces, with a corresponding effect on macroscopic mechanical properties (Genix et al. (2018)).
In turn, spatial organization of the filler NPs also has a direct impact on the polymer structure. The chain conformation in polymer nanocomposites has been the focus of many groups over the past 20 years (Genix et al., 2012; Nakatani et al., 2001; Nusser et al., 2010; Sen et al., 2007). Such experiments are straightforward to carry out on papers using the well-known zero-average contrast condition (Cotton and Hardouin (1997)) but usually failed in being unambiguous, mostly due to incomplete matching of unknown origins. Yet, a consensus has emerged over the past few years that chain conformation is mostly unaffected by the presence of filler particles (Crawford et al., 2013) and that the origin of the polluting signal could be due to statistical effects of local H-D fluctuations (Banc et al., 2015). Sun et al. (2021) have used ZAC to measure the anisotropic chain deformation, arguing that on the timescale of observation, they do not see any strain amplification which might explain the reinforcement effect. The hydrodynamic effect on single NP may be responsible, but further investigations of the particle structure are needed to clarify if the latter exists in the sample. In blends of short and long (homopolymer) chains with attractive interactions with silica NPs, taking again the advantage of the H-D contrast under a contrast-matched NP condition, it has recently been shown that there is an isotopic enrichment close to the NP surface, inducing the presence of a contrasted polymer shell, see Figure 1. Such structures driven by both entropic and enthalpic forces cause an intensity maximum at the NP scale while also contributing to the low-q intensity upturn Genix et al. (2021). In the same direction, prior studies combining small-angle scattering and PRISM demonstrated that polymer−polymer concentration fluctuations correlate with the NP ones in PNCs with attractive interactions (Hall et al., 2009; Zhou et al., 2020). A filler-induced polymer peak is found at the NP scale, and it is due to the exclusion of polymer chains from the space occupied by NPs: the imprinting of the NP order on the adsorbed polymer layers is detected.
3 Dynamical properties of polymers in the bulk and at nanoparticle interfaces
The structural (non-invasive) characterization by diffraction techniques such as SAXS and SANS, as well as the motion of the nanocomposite components, is of tremendous importance in manufacturing, mechanical stability, or aging. On the other hand, neutron spectroscopic techniques commonly referred to as quasi-elastic neutron scattering (QENS) such as neutron spin-echo (NSE) spectroscopy (Richter et al. (2005); Hoffmann (2014)) or backscattering spectroscopy (BS) (Frick (2006)) are focused on the polymer chain dynamics and provide insights into microscopic dynamic properties on molecular length scales and sub-microsecond timescales closely linked to macroscopic rheological properties.
The main use of NSE is extending the static correlation function from SANS into the time domain, providing the coherent dynamic intermediate scattering function S (q, t), the temporal and spatial correlation between different scattering entities. The domain of BS is the incoherent dynamic structure factor S (q, ω) (i.e., the self-correlation), mainly of the strongly incoherently scattering protons of the sample. The strength of neutron scattering is thereby the spatial resolution of the dynamics on molecular length scales. On the other hand, the range in the frequency domain is usually smaller than, for e.g., that in rheology or dielectric spectroscopy.
Since the beginning of high-resolution spectroscopy with neutrons, the link between rheology and microscopic motion has been established, first with linear polymer chains (Ewen et al. (1997)) and then with the increasing of the system. This local view of polymer chain and segmental relaxation complements the macroscopic measurements of the loss modulus G(ω)″ and therefore helps understand the rheological properties.
To describe polymer chain dynamics involving diffusion of the chain center-of-mass, two approaches are typically used. First, the Rouse model is based on the Langevin equation of segmental or monomer unit motion taking into account the entropic forces between the neighboring chains, stochastic forces, and friction with surrounding media (Rouse 1953). In the Rouse model, interactions between the segments of the other chains are not considered. In the second model, based on reptation, the inter-chain interactions lead to the confinement of the polymer chain in a tube built by the neighboring chains. It was shown that for the relatively short chains (M
Neutron scattering methods allow addressing a number of crucial phenomena in nanocomposites related to the confined polymer dynamics (Richter and Kruteva, 2019), as well as to the presence of possibly attractive particle interfaces, thus highlighting the role of chemical surface modification. In general, the local segmental dynamics were found to be unchanged in one-component nanocomposites (OCNC) consisting of nanoparticles grafted with polymer chains without additional (free) matrix polymers (Mark et al. (2017)). OCNC contain a single-polymer phase in form of chains grafted on the nanoparticle surface by covalent bonding in the case of silica (Hübner et al., 2010) or by ligand exchange in the case of metallic nanoparticles (Ehlert et al., 2014). Dynamic confinement could be observed in OCNC by combining different neutron spectroscopic techniques, backscattering spectroscopy for the single-chain dynamic structure factor on very local length scales at the surface of silica nanoparticles, and NSE spectroscopy for the coherent structure factor of the grafted polymer chains, showing a restriction of the mode spectrum of the polymer chain fluctuations (Mark et al. (2017)). Interestingly, the local dynamics of the segments of grafted chains in OCNC do not change for the loosely grafted chains (low grafting density), but it is different from the free chain motion in the corresponding bulk under dense grafting conditions (Sharma et al., 2022). Moreover, the role of the molecular weight of the grafted polymer chains on the local segmental dynamics in OCNC has been investigated in detail (Sharma et al., 2022).
The dynamics of polymer surface layers have been broadly discussed in the literature over the last decades. In particular, for PEO melts filled with silica particles, NMR studies inferred a number of different phases of mobility for the polymer chains such as a so-called glassy layer with about 1 nm thickness that is independent of the matrix molecular weight and does not change with temperature, a fraction with intermediate relaxation times to which network-like properties were ascribed and a bulk-like highly mobile fraction (Kim et al., 2012; Berriot et al., 2002). A neutron scattering study performed on similar systems showed that the PEO chains are locally highly mobile (Glomann et al.,2013). Recent dielectric measurements on silica-based PNCs with matrix poly(vinyl acetate) (PVAc) and poly(2-vinyl pyridine) (P2VP) also support the absence of an immobilized polymer layer implying significant intra-layer mobility (Cheng et al., 2016). In this context, some of us have also contributed to the first observation of segmental relaxation in PNCs using incoherent scattering probed by neutron spin-echo spectroscopy (Musino et al., 2020b). These experiments show a weak impact of the nanoparticles on the polymer dynamics, in agreement with low-field NMR results in which no impact of the grafting density on the probed dynamics was observed (Baeza et al. (2015)).
An interesting overall reduction of diffusion and heterogeneous non-Gaussian behavior caused by inter-chain interactions at high NP loading was found (Schneider et al., 2013). In general, global diffusivity of long chains in a PNC is too slow to be resolved by neutron scattering techniques. This information is available through elastic recoil detection experiments that measure global chain diffusion. The results for both weak and strong polymer-nanoparticle interactions were found to scale simply with the ratio of bottleneck size between NPs and radius of gyration (Gam et al., 2011). Based on the high-resolution NSE and BS spectroscopies complemented with coarse-grained simulations, Salatto et al. (2021) investigated the dynamics of the bound rubber layer in carbon black PNCs in detail. The results indicate the existence of entanglements and interdigitation of the bound rubber chains with neighboring free chains in the matrix, leading to a well-developed and adhesive interphase (Figure 2).
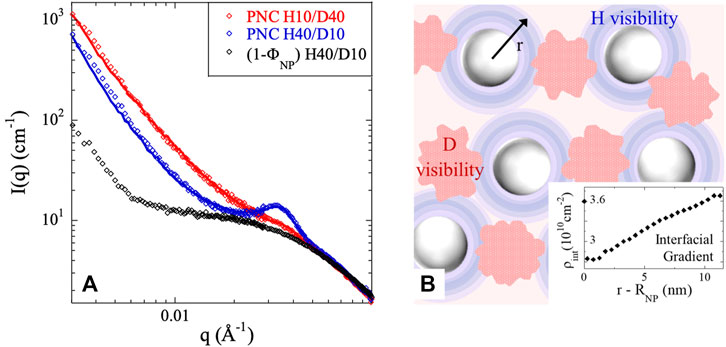
FIGURE 1. (A) Scattered SANS intensity of PNCs with asymmetric poly(vinyl acetate) blends (H10/D40 and H40/D10), where 10 and 40 strands for the hydrogenated H and deuterated D chain mass (in kg/mol) and contrast-matched silica NPs of ca 10 nm radius (ΦNP = 9%v). Pure matrix scattering is shown for comparison (black symbols). Fits superimposed to the data (solid lines) result from specifically developed numerical evaluation methods of the SANS intensity considering two types of spatial fluctuations of the H and D chains in PNC, beyond the random-phase approximation. (B) Schematic picture of the resulting spatial distribution with simultaneous bulk (red) and interfacial (blue) segregation of the short D and long H chains in PNC H40/D10. The isotopic density profile within the blue shell has been characterized by reverse Monte Carlo simulations, revealing the existence of a 10-nm-thick interfacial layer. Bulk segregation was only sufficient to describe the PNC H10/D40 data, highlighting the importance of chain-mass asymmetry in PNC blends. Reprinted with permission from Genix et al. (2021) (Copyright 2021, American Chemical Society).
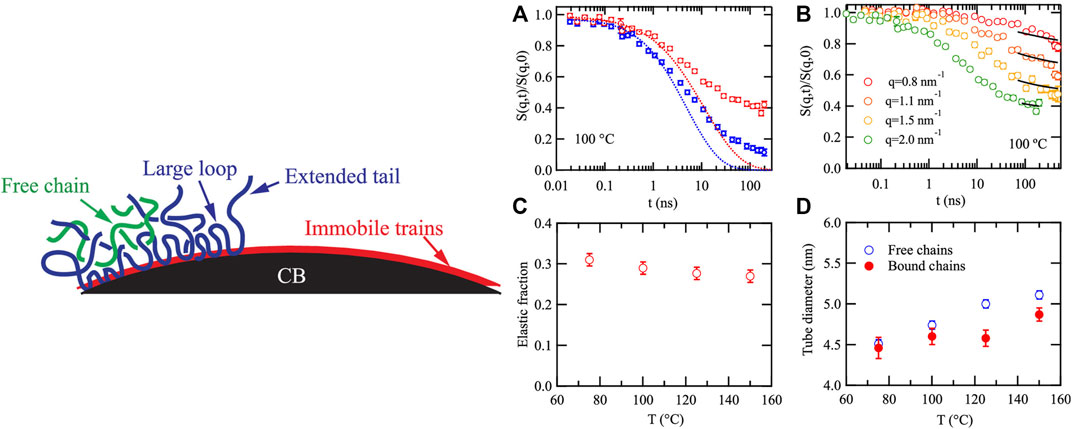
FIGURE 2. Schematic drawing of a carbon-black-reinforced rubber (car tire) with different topological environments of polymer chains around it (left). Segmental dynamics as measured with NSE of bound (red) and free (blue) chain segments (right, panel (A)), with the fraction of immobile chains deduced from NSE experiments (panel (C)). Panel (B) shows the intermediate scattering function of the carbon-black-bound polymer chains. (D) Evolution of the tube diameter for bound and free chains. Reprinted with permission from Salatto et al. (2021) (Copyright 2021, American Chemical Society).
Finally, the dynamics of PEG functionalized gold nanoparticles have been studied with MD simulations and Bayesian analysis, the latter helping to find the maximum information inherent in the intermediate scattering function (De Francesco et al., 2019), guiding to the best possible modeling without overinterpretation.
Finally, all-polymer nanocomposites, for example, comprise mixtures of single-chain nanoparticles (SCNPs), “coated” or embedded in a matrix of linear polymer chains (Arbe et al., 2016). In these systems, NSE revealed that the matrix chain dynamics deviate significantly from the expected reptation behavior, exploring a much larger tube volume, due to disentanglements in the nanocomposite. The effect of the surrounding linear polymer chains on the structure of the SCNPs as a function of the mass of the chains has been studied using contrast matching and extensive modeling, describing quantitatively the scattering over the accessible q-range (Oberdisse et al., 2019).
4 Discussion: Tuning of mechanical properties
The question of the relationship between microscopic structure of PNCs and their macroscopic properties has been tackled for decades. The mechanical reinforcement, one of the most important effects in PNCs, is broadly used, particularly, in the tire industry, because it allows increasing and tailoring the a priori weak pure polymer into strongly resistant materials capable of simultaneously lowering fuel consumption, sticking to the road, withstanding strong mechanical forces, and being long-lasting, and if possible cheap. All these properties are both length scale- and timescale-dependent, and each needs to be studied in its domain of relevance.
Thermally activated shear stiffening for the grafted chain in a polymer matrix was observed by Wu et al. (2022). The thermal stiffening effect can be used in devices that require high modulus and high viscosity under the oscillating shear application. Viscosity reduction was observed by scattering methods on fluidification of the nanocomposites through the addition of small NPs (Senses et al., 2022b).
The attempts to relate the macroscopic properties of PNCs to the microscopic details of polymer chain dynamics were undertaken by Salatto et al. They used industrially relevant materials filled with carbon black to focus on a molecular understanding of basic mechanisms that are important for reinforcement in rubbers. Among several factors contributing to mechanical reinforcement, a polymer-mediated NP network is considered to be the most important in polymer PNCs (Yavitt et al., 2021). As shown by XPCS, which is mostly focused on NP dynamics, the NP dynamics can be decoupled from the dynamical processes underlying stress relaxation. However sophisticated the experimental approaches discussed in this review may be, it is important to keep in mind that scattering allows deducing both structure and dynamics only in an indirect way. Therefore, it is crucial to proceed in a step-by-step construction of results, usually going from the statics to the more complex dynamics. As a famous example in polymer nanocomposites, one may think of samples produced in milling processes like solid-state mixing. Such samples are usually anisotropic, as one can immediately see in the two-dimensional representation of the static scattered intensity. Obviously, the dynamics take place on the landscape of the existing sample structure, and its anisotropy needs to be discussed in the light of the underlying nanoparticle arrangement.
5 Conclusion
With this short overview, we intend to highlight recent progress and the necessary steps for future success in understanding polymer nanocomposites. It is clear that meaningful scattering experiments need to be well-designed, for e.g., start from a precise measurement of the nanoparticle size and shape in order to arrange them in space or understand their interfacial layers. One needs to build on well-defined scattering contrasts and take coupling between form and structure factors, like higher-order oscillations, into account. Only if physical constraints are respected, for instance, excluded NP volume or the conserved quantity of matter, or scattering length, it will be possible to analyze scattering data correctly, allowing progress and eventually triggering new discoveries. Along the same lines, dynamics can be investigated by QENS making use of spatial resolution, with a considerably higher impact if the static structures are well-known and allow to relate dynamical processes to intrinsic length scales of the samples.
Including the increased complexity of the measurements into proper polymer models is one of the future challenges, where most likely also molecular dynamics simulations will strongly contribute to complementing real experiments with computer experiments, where details might be accessible or otherwise hidden in the complex sample. Generally, a thorough understanding helps for a targeted design of material’s properties, with the aim, goal, and challenge of linking scattering experiments with applications, for e.g., rubber tires for certain temperature and friction conditions.
To summarize, polymer nanocomposites cover a very broad field, from pure academic and well-defined one-component systems to industrial polymeric materials. Neutron scattering allows to shed light on microscopic structural and dynamic properties of such systems in all stages of purity, helping to understand the relationship between fundamental polymer physics concepts in these more and more complex systems to macroscopic material properties relevant to manufacturing and practical applications of such materials. Some recent advances from neutron diffraction and spectroscopy have been highlighted in this mini-review which provide interesting and valuable insights into this class of materials.
Author contributions
Conception and idea, MK, AC-G, JO, and OH. Writing of the manuscript, MK, AC-G, JO, and OH.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Arbe, A., Pomposo, J. A., Asenjo-Sanz, I., Bhowmik, D., Ivanova, O., Kohlbrecher, J., et al. (2016). Single chain dynamic structure factor of linear polymers in an all-polymer nano-composite. Macromolecules 49, 2354–2364. doi:10.1021/acs.macromol.5b02519
Baeza, G. P., Dessi, C., Costanzo, S., Zhao, D., Gong, S., Alegria, A., et al. (2016). Network dynamics in nanofilled polymers. Nat. Commun. 7, 11368–11376. doi:10.1038/ncomms11368
Baeza, G. P., Genix, A. C., Degrandcourt, C., Petitjean, L., Gummel, J., Couty, M., et al. (2013). Multiscale filler structure in simplified industrial nanocomposite silica/sbr systems studied by saxs and tem. Macromolecules 46, 317–329. doi:10.1021/ma302248p
Baeza, G. P., Oberdisse, J., Alegria, A., Saalwächter, K., Couty, M., and Genix, A. C. (2015). Depercolation of aggregates upon polymer grafting in simplified industrial nanocomposites studied with dielectric spectroscopy. Polymer 73, 131–138. doi:10.1016/j.polymer.2015.07.045
Bailey, E. J., and Winey, K. I. (2020). Dynamics of polymer segments, polymer chains, and nanoparticles in polymer nanocomposite melts: A review. Prog. Polym. Sci. 105, 101242. doi:10.1016/j.progpolymsci.2020.101242
Banc, A., Genix, A. C., Dupas, C., Sztucki, M., Schweins, R., Appavou, M. S., et al. (2015). Origin of small-angle scattering from contrast-matched nanoparticles: A study of chain and filler structure in polymer nanocomposites. Macromolecules 48, 6596–6605. doi:10.1021/acs.macromol.5b01424
Batchelor, G., and Green, J. T. (1972). The hydrodynamic interaction of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 56, 375–400. doi:10.1017/s0022112072002927
Berriot, J., Montes, H., Lequeux, F., Long, D., and Sotta, P. (2002). Evidence for the shift of the glass transition near the particles in silica-filled elastomers. Macromolecules 35, 9756–9762. doi:10.1021/ma0212700
Carroll, B., Cheng, S., and Sokolov, A. P. (2017). Analyzing the interfacial layer properties in polymer nanocomposites by broadband dielectric spectroscopy. Macromolecules 50, 6149–6163. doi:10.1021/acs.macromol.7b00825
Cheng, S., Carroll, B., Bocharova, V., Carrillo, J. M., Sumpter, B. G., and Sokolov, A. P. (2017). Focus: Structure and dynamics of the interfacial layer in polymer nanocomposites with attractive interactions. J. Chem. Phys. 146, 203201. doi:10.1063/1.4978504
Cheng, S., Holt, A. P., Wang, H., Fan, F., Bocharova, V., Martin, H., et al. (2016). Unexpected molecular weight effect in polymer nanocomposites. Phys. Rev. Lett. 116, 038302. doi:10.1103/physrevlett.116.038302
Cotton, J., and Hardouin, F. (1997). Chain conformation of liquid-crystalline polymers studied by small-angle neutron scattering. Prog. Polym. Sci. 22, 795–828. doi:10.1016/s0079-6700(97)00007-5
Crawford, M., Smalley, R., Cohen, G., Hogan, B., Wood, B., Kumar, S., et al. (2013). Chain conformation in polymer nanocomposites with uniformly dispersed nanoparticles. Phys. Rev. Lett. 110, 196001. doi:10.1103/physrevlett.110.196001
De Francesco, A., Scaccia, L., Lennox, R. B., Guarini, E., Bafile, U., Falus, P., et al. (2019). Model-free description of polymer-coated gold nanoparticle dynamics in aqueous solutions obtained by bayesian analysis of neutron spin echo data. Phys. Rev. E 99, 052504. doi:10.1103/physreve.99.052504
Ehlert, S., Taheri, S. M., Pirner, D., Drechsler, M., Schmidt, H. W., and Förster, S. (2014). Polymer ligand exchange to control stabilization and compatibilization of nanocrystals. ACS Nano 8, 6114–6122. doi:10.1021/nn5014512
Einstein, A. (1911). Eine neue bestimmung der molekuldimensionen. Ann. Phys. 34, 591–592. doi:10.1002/andp.19113390313
Ewen, B., Mours, M., Richter, D., Shiga, T., and Winter, H. (1997). Neutron spin echo spectroscopy viscoelasticity rheology, 134. Cham: Springer Science & Business Media.
Frick, B. (2006). “Neutron backscattering spectroscopy,” in Neutron and X-ray spectroscopy (Cham: Springer), 483–527.
Gam, S., Meth, J. S., Zane, S. G., Chi, C., Wood, B. A., Seitz, M. E., et al. (2011). Macromolecular diffusion in a crowded polymer nanocomposite. Macromolecules 44, 3494–3501. doi:10.1021/ma102463q
Genix, A. C., Bocharova, V., Carroll, B., Dieudonné-George, P., Chauveau, E., Sokolov, A. P., et al. (2022). How tuning interfaces impacts dynamics and structure of polymer nanocomposites simultaneously. submitted.
Genix, A. C., Bocharova, V., Carroll, B., Dieudonné-George, P., Sztucki, M., Schweins, R., et al. (2021). Direct structural evidence for interfacial gradients in asymmetric polymer nanocomposite blends. ACS Appl. Mat. Interfaces 13, 36262–36274. doi:10.1021/acsami.1c06971
Genix, A. C., Bocharova, V., Carroll, B., Lehmann, M., Saito, T., Krueger, S., et al. (2019). Understanding the static interfacial polymer layer by exploring the dispersion states of nanocomposites. ACS Appl. Mat. Interfaces 11, 17863–17872. doi:10.1021/acsami.9b04553
Genix, A. C., Bocharova, V., Kisliuk, A., Carroll, B., Zhao, S., Oberdisse, J., et al. (2018). Enhancing the mechanical properties of glassy nanocomposites by tuning polymer molecular weight. ACS Appl. Mat. Interfaces 10, 33601–33610. doi:10.1021/acsami.8b13109
Genix, A. C., and Oberdisse, J. (2017). Determination of the local density of polydisperse nanoparticle assemblies. Soft Matter 13, 8144–8155. doi:10.1039/c7sm01640a
Genix, A. C., and Oberdisse, J. (2015). Structure and dynamics of polymer nanocomposites studied by x-ray and neutron scattering techniques. Curr. Opin. Colloid & Interface Sci. 20, 293–303. doi:10.1016/j.cocis.2015.10.002
Genix, A. C., Tatou, M., Imaz, A., Forcada, J., Schweins, R., Grillo, I., et al. (2012). Modeling of intermediate structures and chain conformation in silica–latex nanocomposites observed by sans during annealing. Macromolecules 45, 1663–1675. doi:10.1021/ma202308c
Glomann, T., Schneider, G., Allgaier, J., Radulescu, A., Lohstroh, W., Farago, B., et al. (2013). Microscopic dynamics of polyethylene glycol chains interacting with silica nanoparticles. Phys. Rev. Lett. 110, 178001. doi:10.1103/physrevlett.110.178001
Hall, L. M., Anderson, B. J., Zukoski, C. F., and Schweizer, K. S. (2009). Concentration fluctuations, local order, and the collective structure of polymer nanocomposites. Macromolecules 42, 8435–8442. doi:10.1021/ma901523w
Heinrich, G., and Klüppel, M. (2002). Recent advances in the theory of filler networking in elastomers. Fill. elastomers drug Deliv. Syst. 2002, 1–44. doi:10.1007/3-540-45362-8_1
Heinrich, G., Klüppel, M., and Vilgis, T. A. (2002). Reinforcement of elastomers. Curr. Opin. solid state Mater. Sci. 6, 195–203. doi:10.1016/s1359-0286(02)00030-x
Hoffmann, I. (2014). Neutrons for the study of dynamics in soft matter systems. Colloid Polym. Sci. 292, 2053–2069. doi:10.1007/s00396-014-3330-9
Hooper, J. B., and Schweizer, K. S. (2005). Contact aggregation, bridging, and steric stabilization in dense polymer- particle mixtures. Macromolecules 38, 8858–8869. doi:10.1021/ma051318k
Hübner, E., Allgaier, J., Meyer, M., Stellbrink, J., Pyckhout-Hintzen, W., and Richter, D. (2010). Synthesis of polymer/silica hybrid nanoparticles using anionic polymerization techniques. Macromolecules 43, 856–867. doi:10.1021/ma902213p
Jimenez, A. M., Zhao, D., Misquitta, K., Jestin, J., and Kumar, S. K. (2019). Exchange lifetimes of the bound polymer layer on silica nanoparticles. ACS Macro Lett. 8, 166–171. doi:10.1021/acsmacrolett.8b00877
Jin, Y., Beaucage, G., Vogtt, K., Jiang, H., Kuppa, V., Kim, J., et al. (2017). A pseudo-thermodynamic description of dispersion for nanocomposites. Polymer 129, 32–43. doi:10.1016/j.polymer.2017.09.040
Jouault, N. (2016). Intra- and interchain correlations in polymer nanocomposites: A small-angle neutron scattering extrapolation method. ACS Macro Lett. 5, 1095–1099. doi:10.1021/acsmacrolett.6b00500
Kim, S. Y., Meyer, H. W., Saalwächter, K., and Zukoski, C. F. (2012). Polymer dynamics in peg-silica nanocomposites: Effects of polymer molecular weight, temperature and solvent dilution. Macromolecules 45, 4225–4237. doi:10.1021/ma300439k
Kremer F., and Schönhals A. (Editors) (2003). Broadband dielectric spectroscopy (Cham: Springer Berlin Heidelberg). doi:10.1007/978-3-642-56120-7
Lindner, P., and Zemb, T. (2002). Neutrons. X-Rays and light: Scattering methods applied to soft condensed matter. London: Elsevier Science.
Mackay, M. E., Dao, T. T., Tuteja, A., Ho, D. L., Van Horn, B., Kim, H. C., et al. (2003). Nanoscale effects leading to non-einstein-like decrease in viscosity. Nat. Mat. 2, 762–766. doi:10.1038/nmat999
Mark, C., Holderer, O., Allgaier, J., Hübner, E., Pyckhout-Hintzen, W., Zamponi, M., et al. (2017). Polymer chain conformation and dynamical confinement in a model one-component nanocomposite. Phys. Rev. Lett. 119, 047801. doi:10.1103/physrevlett.119.047801
Mulderig, A., Beaucage, G., Vogtt, K., Jiang, H., Jin, Y., Clapp, L., et al. (2017). Structural emergence in particle dispersions. Langmuir 33, 14029–14037. doi:10.1021/acs.langmuir.7b03033
Musino, D., Genix, A. C., Chaussée, T., Guy, L., Meissner, N., Kozak, R., et al. (2018). Aggregate formation of surface-modified nanoparticles in solvents and polymer nanocomposites. Langmuir 34, 3010–3020. doi:10.1021/acs.langmuir.7b03932
Musino, D., Genix, A. C., Chauveau, E., Bizien, T., and Oberdisse, J. (2020a). Structural identification of percolation of nanoparticles. Nanoscale 12, 3907–3915. doi:10.1039/c9nr09395h
Musino, D., Oberdisse, J., Farago, B., Alegria, A., and Genix, A. C. (2020b). Resolving segmental polymer dynamics in nanocomposites by incoherent neutron spin–echo spectroscopy. ACS Macro Lett. 9, 910–916. doi:10.1021/acsmacrolett.0c00369
Nakatani, A., Chen, W., Schmidt, R., Gordon, G., and Han, C. C. (2001). Chain dimensions in polysilicate-filled poly (dimethyl siloxane). Polymer 42, 3713–3722. doi:10.1016/s0032-3861(00)00771-0
Nusser, K., Neueder, S., Schneider, G. J., Meyer, M., Pyckhout-Hintzen, W., Willner, L., et al. (2010). Conformations of silica- poly (ethylene- propylene) nanocomposites. Macromolecules 43, 9837–9847. doi:10.1021/ma101898c
Oberdisse, J., Gonzalez-Burgos, M., Mendia, A., Arbe, A., Moreno, A. J., Pomposo, J. A., et al. (2019). Effect of molecular crowding on conformation and interactions of single-chain nanoparticles. MACROMOLECULES 52, 4295–4305. doi:10.1021/acs.macromol.9b00506
Oberdisse, J. (2002). Structure and rheological properties of latex- silica nanocomposite films: Stress- strain isotherms. Macromolecules 35, 9441–9450. doi:10.1021/ma020635d
Pasini, S., Holderer, O., Kozielewski, T., Richter, D., and Monkenbusch, M. (2019). J-nse-phoenix, a neutron spin-echo spectrometer with optimized superconducting precession coils at the mlz in garching. Rev. Sci. Instrum. 90, 043107. doi:10.1063/1.5084303
Richter, D., and Kruteva, M. (2019). Polymer dynamics under confinement. Soft Matter 15, 7316–7349. doi:10.1039/C9SM01141B
Richter, D., Monkenbusch, M., Arbe, A., and Colmenero, J. (2005). “Neutron spin echo in polymer systems,” in Advances in polymer science (Cham: Springer), 1–221.
Rishi, K., Beaucage, G., Kuppa, V., Mulderig, A., Narayanan, V., McGlasson, A., et al. (2018). Impact of an emergent hierarchical filler network on nanocomposite dynamics. Macromolecules 51, 7893–7904. doi:10.1021/acs.macromol.8b01510
Robertson, C. G., and Hardman, N. J. (2021). Nature of carbon black reinforcement of rubber: Perspective on the original polymer nanocomposite. Polymers 13, 538. doi:10.3390/polym13040538
Rouse, P. E. (1953). A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 21, 1272–1280. doi:10.1063/1.1699180
Salatto, D., Carrillo, J. M. Y., Endoh, M. K., Taniguchi, T., Yavitt, B. M., Masui, T., et al. (2021). Structural and dynamical roles of bound polymer chains in rubber reinforcement. Macromolecules 54, 11032–11046. doi:10.1021/acs.macromol.1c01239
Schneider, G. J., Nusser, K., Neueder, S., Brodeck, M., Willner, L., Farago, B., et al. (2013). Anomalous chain diffusion in unentangled model polymer nanocomposites. Soft Matter 9, 4336–4348. doi:10.1039/c3sm27886g
Sen, S., Xie, Y., Kumar, S. K., Yang, H., Bansal, A., Ho, D. L., et al. (2007). Chain conformations and bound-layer correlations in polymer nanocomposites. Phys. Rev. Lett. 98, 128302. doi:10.1103/physrevlett.98.128302
Senses, E., Kitchens, C. L., and Faraone, A. (2022a). Viscosity reduction in polymer nanocomposites: Insights from dynamic neutron and x-ray scattering. J. Polym. Sci. 60 (2022), 1130–1150. doi:10.1002/pol.20210320
Senses, E., Kitchens, C. L., and Faraone, A. (2022b). Viscosity reduction in polymer nanocomposites: Insights from dynamic neutron and X-ray scattering. J. Polym. Sci. (2020). 60, 1130–1150. doi:10.1002/pol.20210320
Sharma, A., Kruteva, M., Zamponi, M., Ehlert, S., Richter, D., and Förster, S. (2022). Influence of molecular weight on the distribution of segmental relaxation in polymer grafted nanoparticles. Phys. Rev. Mat. 6, L012601. doi:10.1103/PhysRevMaterials.6.L012601
Smallwood, H. M. (1944). Limiting law of the reinforcement of rubber. J. Appl. Phys. 15, 758–766. doi:10.1063/1.1707385
Staropoli, M., Gerstner, D., Radulescu, A., Sztucki, M., Duez, B., Westermann, S., et al. (2020). Decoupling the contributions of zno and silica in the characterization of industrially-mixed filled rubbers by combining small angle neutron and x-ray scattering. Polymers 12, 502. doi:10.3390/polym12030502
Sun, R., Melton, M., Safaie, N., Ferrier, R. C., Cheng, S., Liu, Y., et al. (2021). Molecular view on mechanical reinforcement in polymer nanocomposites. Phys. Rev. Lett. 126, 117801. doi:10.1103/physrevlett.126.117801
Unruh, T., Neuhaus, J., and Petry, W. (2007). The high-resolution time-of-flight spectrometer toftof. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 580, 1414–1422. doi:10.1016/j.nima.2007.07.015
Wu, D., Ge, Y., Li, R., Feng, Y., and Akcora, P. (2022). Thermally activated shear stiffening in polymer-grafted nanoparticle composites for high-temperature adhesives. ACS Appl. Polym. Mat. 4, 2819–2827. doi:10.1021/ACSAPM.2C00097
Wuttke, J., Budwig, M. A. D., Kämmerling, H., Kayser, F. J., Kleines, H., Ossovyi, V., et al. (2012). Spheres, jülich’s high-flux neutron backscattering spectrometer at frm ii. Rev. Sci. Instrum. 83, 075109. doi:10.1063/1.4732806
Yavitt, B. M., Salatto, D., Zhou, Y., Huang, Z., Endoh, M., Wiegart, L., et al. (2021). Collective nanoparticle dynamics associated with bridging network formation in model polymer nanocomposites. ACS Nano 15, 11501–11513. doi:10.1021/acsnano.1c01283
Zhou, Y., Yavitt, B. M., Zhou, Z., Bocharova, V., Salatto, D., Endoh, M. K., et al. (2020). Bridging-controlled network microstructure and long-wavelength fluctuations in silica–poly (2-vinylpyridine) nanocomposites: Experimental results and theoretical analysis. Macromolecules 53, 6984–6994. doi:10.1021/acs.macromol.0c01391
Keywords: neutron scattering, neutron spin echo, rheology, nanocomposites, X-ray scattering
Citation: Kruteva M, Genix A-C, Holderer O and Oberdisse J (2022) Recent scattering approaches to structure and dynamics of polymer nanocomposites. Front. Soft. Matter 2:992563. doi: 10.3389/frsfm.2022.992563
Received: 12 July 2022; Accepted: 23 August 2022;
Published: 13 September 2022.
Edited by:
Paul Sotta, UMR5223 Ingenierie des Materiaux polymeres, FranceReviewed by:
Naisheng Jiang, University of Science and Technology Beijing, ChinaCopyright © 2022 Kruteva, Genix, Holderer and Oberdisse. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: O. Holderer, by5ob2xkZXJlckBmei1qdWVsaWNoLmRl