- 1Materials Modeling Research Group (MMRG), Department of Chemical Engineering, McGill University, Montréal, QC, Canada
- 2HydrateTech, Department of Chemical Engineering, McGill University, Montréal, QC, Canada
This review presents theory and simulation of liquid crystal phase ordering in biological fibrous materials, solutions, and composites in the presence of elastic fields, second phase inclusions, and transport phenomena, including complex shear-extensional flow and mass transfer. Liquid crystal self-assembly through phase ordering on elastic deformable membranes is first applied to characterize the mechanisms that control the structures in plant cell walls, highlighting how curvophobic and curvophilic effects introduce new structuring fields beyond hard-core repulsion. Then chiral nematic self-assembly is simulated in a mesophase containing fibrillar colloidal inclusions (liquid crystal-fibre composites) to demonstrate how the inclusion positional order generates defects and disclinations as shown in the plant cell wall. Coupling phase ordering to tuned transport phenomena is shown how and why it leads to self-organization such as paranematic states of dilute acidic aqueous collagen solutions. Further directed dehydration of well-organized paranematic collagen leads to defect free cholesteric films only when directed dehydration is synchronized with chirality formation. In addition, the ubiquitous surface nanowrinkling of cholesterics is captured with surface anchoring. In these four representative systems, the new mechanisms that enhance the well-known exclude volume interactions are identified quantified and validated with experimental data. Future directions to create new advanced multifunctional materials based on principles of self-assembly and self-organization are identified by leveraging the new couplings between material structure, geometry, and transport phenomena.
1 Introduction
Rod-like lyotropic polymer and colloidal liquid crystals are viscoelastic multifunctional materials that undergo phase ordering transitions with increasing concentration mainly due to hardcore excluded volume interactions, giving rise to mesophases with intermediate degrees of orientational and positional order (Tsuji and Rey, 1997; Lhuillier and Rey, 2004; Donald et al., 2006; Mottram and Newton, 2014; Zhao et al., 2017). The simplest phase ordering transition is the isotropic-to-nematic N transition, predicted by the Onsager model (Lekkerkerker and Vroege, 1993; Selinger, 2016), where the isotropic I phase undergoes an orientational ordering transition characterized by the emergence of molecular or fibrillar alignment (non-zero scalar order parameter S) along an anisotropic axis or director n; this vector is of unit length (n ⋅n = 1) (Donald et al., 2006). In the uniaxial nematic phase (Donald et al., 2006), the characterizing non-conserved order parameter (NCOP) is a symmetric traceless uniaxial tensor Q = S (nn − I/3), where S controls fast time scales and short nano-length scales, and n is the slow variable associated with micron range length scales and unique direction of material property anisotropy (transverse isotropy) (Tsuji and Rey, 1997; Liu and Calderer, 2000; Rey, 2009). Since the uniaxial N phase has no positional order (P0), anisotropic viscosity is possible and since orientation gradients due to spatial gradients of n (∇n ≠ 0) store energy, these materials are also elastic. The elasticity is known as Frank elasticity and the elastic modes are splay, bend, and twist (Barbero and Evangelista, 2000).
The presence of chemical, geometric and electrostatic chirality gives rise to chiral nematic N* phases, widely observed in in vitro bio macromolecular solutions [DNA, collagen, in in vivo secretions (silk, sperm)], and in liquid crystal solid analogues as collagen in bone, cellulose in plant cell walls, and chitin in insects, which are the focus on this review (Neville and Caveney, 1969; Neville, 1993; Belamie et al., 2006; Bouligand, 2008; Rey, 2010; Rey and Herrera-Valencia, 2012; Lagerwall et al., 2014; Rey et al., 2014; Sharma et al., 2014; Canejo et al., 2017; Mitov, 2017; Priemel et al., 2017; Almeida et al., 2018; Harrington et al., 2018; Khadem et al., 2020; Casado et al., 2021; Harrington and Fratzl, 2021). In these anisotropic viscoelastic materials, chirality introduces spatial periodicity along the helix axis h and an intrinsic periodic length scale or pitch P0, and hence at the simplest level they can behave as highly viscous along the h direction. For relative long pitch (mm-range) biaxiality can be neglected and the Q-tensor is uniaxial and spatially periodic along the helix direction. The scalar helicity of the N* is H = 4π/P0 = Q: (∇ ×Q)/(Q: Q), defined by the curl of Q (Khadem et al., 2020).
Figure 1 shows a schematic of the isotropic phase 1), uniaxial nematic N 2) and cholesteric N* 3) local organization and the non-conserved tensor order parameter Q for each case, neglecting fluctuations and assuming that S is the equilibrium value (Donald et al., 2006). The point to emphasize when going from left to right in Figure 1, is that the symmetry breaking increases and the number of distinguishing directions increase from zero to two (n, h).
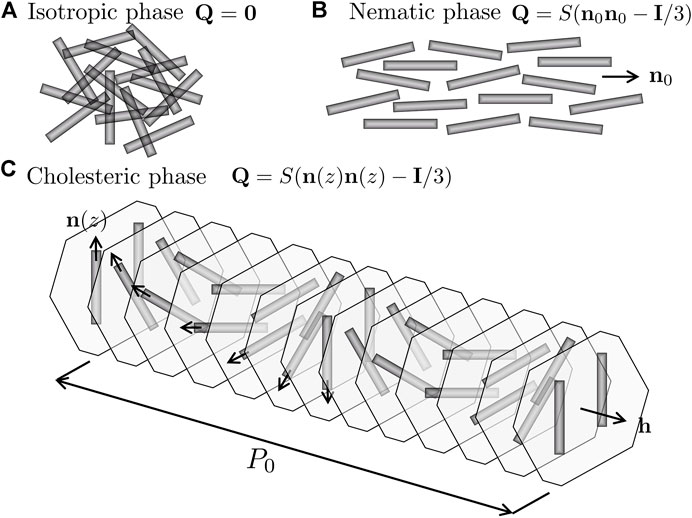
FIGURE 1. Schematics of (A) isotropic, (B) uniaxial nematic, and (C) chiral nematic liquid crystal organization of rod-like fibrillar materials and their uniaxial tensor order parameter Q. The isotropic state is a viscous liquid, the uniaxial nematic N and chiral nematic N* are anisotropic viscoelastic materials. The uniaxial nematic is distinguished by a uniaxial director n0. The chiral nematic Q-tensor is periodic in the helix h direction. The pitch P0 of a biological cholesteric liquid crystal is usually in the micron-range.
Representative examples that reflect the abundance and ubiquity of LC order in biological-related materials in vivo and in vitro solutions, as well as frozen-in in the case of biological analogues are given (Rey, 2010; Mitov, 2017). We note that biological analogues are fibrillar composite solids displaying mainly the cholesteric organization, known as the Bouligand architecture (Ritchie, 2014; Suksangpanya et al., 2017; Yang et al., 2017; Natarajan and Gilman, 2018). The fibrous composite Bouligand plywood architecture has a number of advanced functionalities including water sensing (Rofouie et al., 2015) and optimal mechanical fibre reinforcement abilities under uniform planar stress loading normal to the helix direction. In the former case, certain coniferous plants exhibit quantitative blue-to-green color changes according to material water content; the connection with structural colour has been reviewed (Vignolini et al., 2013). In the latter case the reinforcement efficiency of a Bouligand architecture is constant at 0.375 while for a simple nematic order is varies between 0 and 1 (Aguilar Gutierrez and Rey, 2016b). A comprehensive toolbox for structure reconstruction and pitch determinations for the Bouligand and related cornea-like organizations from 2D cross-sectional micrographs has been developed using differential geometry and automatized by visualization software (Gutierrez and Rey, 2014a; Gutierrez and Rey, 2014b; Gutierrez and Rey, 2016). Hence the interest of focusing on biological LCs materials is to use LC science to contribute to the development of biological material science and to use the biological systems as a source of inspiration to new biomimetic and green material engineering processes.
Following the widely accepted terminology for equilibrium self-assembly in closed systems and dissipative self-organization in open systems, we find many important fundamental and practical processes in LC material science and physics where phase ordering occurs under minimization of energy (closed system) or it is coupled to transport of mass, thermal energy and/or linear momentum (open system). These two phenomena are highlighted in Figure 2, which also gives the organization of this review, as discussed in what follows. On the left of Figure 2, we find phase ordering in closed systems and two representative examples of increased complexity: 1) 2D Nematic N phase ordering in curved deformable elastic membranes (Murugesan and Rey, 2010a; Murugesan and Rey, 2010b) and 2) Cholesteric N* phase ordering in LC-colloid composites (filled cholesterics with second phase inclusions) (Rey et al., 2016). On the right of Figure 2, we find phase ordering in open systems and two representative examples of biomimetic practical utility: 3) Paranematic PN phase ordering under co-existing shear and extensional kinematics (Rey and Murugesan, 2011), and 4) Cholesteric N* phase ordering under directed water evaporation in dilute aqueous acidic triple-helix collagen solutions (Murugesan et al., 2011).
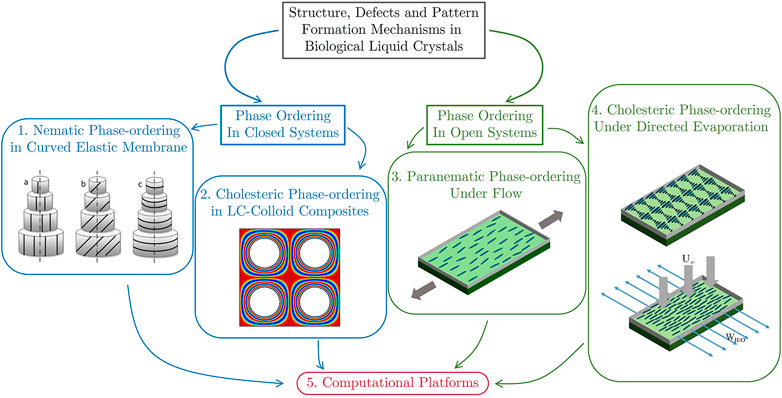
FIGURE 2. Organization of this review paper. Structure and pattern formation in biological liquid crystal through phase ordering in close (self-assembly on the left) and open (self-organization on the right) systems. (1) Nematic phase ordering on elastic deformable membranes (cellulose fibrils in plant cell walls); (2) cholesteric phase ordering in the presence of second phase inclusions (defects in plant cell walls); (3) Paranematic phase ordering under shear/extensional flow of dilute collagen; (4) Cholesteric phase ordering under directed dehydration. Lastly in (5) we present computational platforms for self-assembly and self-organization in liquid crystals. (1) is adapted from dissertation (Murugesan, 2012). (2) is republished with permission of Royal Society of Chemistry, from (Rey, 2010); permission conveyed through Copyright Clearance Center, Inc. (3) is reprinted with permission from Aguilar Gutierrez and Rey, (2016a). Copyright (2016) American Chemical Society. (4) is republished with permission of Royal Society of Chemistry, from (Gutierrez and Rey, 2017); permission conveyed through Copyright Clearance Center, Inc.
1.1 Nematic Phase Ordering in Curved Elastic Membranes
The nematic and chiral nematic phase ordering in a closed system is well understood, characterized and presented in many monographs. In particular nucleation and growth, defect generation mechanisms, and effect of electromagnetic fields (Selinger, 2016; Rey, 2010). More recently, driven by questions arising from biological material synthesis, such as plant cell walls with a basic fibrous composite architecture, models that capture the interaction between orientational ordering and elastic membrane curvature are being developed and refined (Murugesan and Rey, 2010a; Murugesan and Rey, 2010b; Rey et al., 2016; Rey and Murugesan, 2011; Murugesan et al., 2011; Murugesan and Rey, 2010c). Even with the simplest tubular elastic membranes with zero Gaussian curvature (K = 0) the director field n that emerges from PO can display many possible modes, including helical and ring-like orientation of fibrils, leading to new curvophobic and curvophilic mechanisms in 2D nematic ordering on curved elastic membranes. In this paper, we will highlight and summarize the new mechanism and validate it with observations and measurements from plant-based cellulosic materials.
1.2 Cholesteric N* Phase Ordering in LC-Colloid Composites (Filled Cholesterics)
Following the closed system phase ordering approach and again motivated from plant-based facts, we focus on colloidal particle-cholesteric liquid crystals and establish what defect organization emerges as a function of the local particle arrangements, such as triangular and square. This organizational mechanism is known as Zimmers’ rule (Murugesan et al., 2013; Phillips et al., 2011a; Phillips et al., 2011b; Rey et al., 2011; Shams et al., 2015; Soule and Rey, 2012). Since in the N* various singular and non-singular disclinations are possible, the number and type of these defect provides semi- quantitative information on the degree of anisotropy in elastic material properties. Equally significant, the defects in the phase ordering model in the presence of colloidal inclusion (pit canals of plants) provide proof and certainty that many solid analogues displaying the Bouligand architecture are formed through a liquid crystalline phase.
1.3 Paranematic Phase Ordering Under Shear and Extensional Kinematics
Cholesteric rheology is highly complex due to the addition of chirality, exhibiting uncoiling, orientational wave- propagation, disclination nucleation which generate films and bulk materials with many unavoidable defects when applications require defect-free monodomains (Rey, 1996a; Rey, 1996b; Rey, 2000b; Rey, 2002b; Rey, 2002c; Cui et al., 2006; Marenduzzo et al., 2006; Marenduzzo et al., 2004; Cui and Wang, 2011; Venhaus et al., 2013; Noroozi et al., 2014; Echeverria et al., 2015; Echeverria et al., 2017). One approach to achieve monodomains is to process the precursor materials in the dilute regime using the principle of flow-induced-orientation (FIO), widely used in polymer processing (Aguilar Gutierrez and Rey, 2016a). In actual film processing, the presence of shear and extensional deformation rates are always present. In this section, we show how to select the intensity and type of flow deformation mix that leads to a well-organized paranematic (PN) organization with a preselected director n and scalar order parameter. The state is paranematic because the equilibrium concentration used to flow-process the dilute solution is below the Onsager threshold and if the deformation rate introduced by the flow is removed, Q eventually relaxes to the zero tensor state: Q = 0.
1.4 Cholesteric Phase Ordering Under Directed Evaporation
Directed evaporation, especially of isotropic or colloidal droplet phases generates phase ordering of various defect content. Hence starting from a paranematic well-oriented phase with an order parameter S close to the target one, one can in principle obtain defect-free films with directed evaporation, where the mass transfer drives the order in a controlled way (Gutierrez and Rey, 2017). Hence if we look at the open system examples, we find evaporation examples such as in (Chu et al., 2018; Pospisil et al., 2020).
In the next sections of this review, we focus on the salient features of nematic and cholesteric phase ordering under close and open conditions and in bulk and membrane geometries. The emphasis is on highlighting mechanisms and applications in these phase ordering processes, while mathematical derivations (included in the references) are kept at a minimum. We follow the numbering of Figure 2.
2 Self-Assembly and Self-Organization in Biological Liquid Crystalline Materials
2.1 Closed System Phase Ordering Models, Predictions and Validations
2.1.1 Nematic Phase Ordering in Curved Elastic Membranes
The plant cell wall (PCW) is nature’s most abundant biological fibrous composite. In order to demonstrate the universality of nematic phase ordering mechanisms in nature, we focus on the uniqueness of PCW and base on 2D phase ordering on elastic membranes (Murugesan and Rey, 2010a; Rey et al., 2016). Recent work on 2D isotropic-nematic transition includes the recent work of Zonta and Soule (Zonta and Soulé, 2019).
To operate as a supporting mechanical structure and at the same time allow for cell growth through expansion, plant cells are encompassed by a stiff, multilayered, viscoelastic-viscoplastic composite wall (Brett, 1985). In terms of geometric dimensionality, the typical thickness of plant cell walls generally varies from 0.1 to 0.3 µm, about one hundred times thinner than the size of the plant cell itself. It is made of sequentially deposited layers of different thicknesses, chemical composition and structural organization. At the appropriate scale, the PCW can be considered as a reinforced biological fibre-laden composite membrane consisting of well-aligned cellulose microfibrils (CMFs) of high tensile strength coated with hemicellulose and embedded in a matrix of polysaccharides (pectin/lignin) and structural glycoproteins (Neville, 1993). Different plant species synthesize cell walls with a wide range of mechanical properties by tuning the arrangement of these four material components (cellulose, lignin, hemicellulose and pectin) in the cell wall and/or cellular structure.
Thus understanding the process through which the CMFs are oriented in a specific direction is crucial in unravelling the mechanisms underlying nature’s material synthesis. Figure 3 shows the basic plant cell wall textures, and the microfibrils observed microfibril angles in PCW’s, where the CMFs are oriented in strategic directions to generate commonly observed textures such as line, helix, ring, crossed helix and helicoid (Emons and Mulder, 2000). In the line (ring) mode, the CMF’s are aligned parallel (perpendicular) to the major axis of the cell. In the helical mode, the CMF’s are oriented obliquely to the major axis of the cell and in the ring mode they are in the azimuthal direction. In the helicoid, the CMF gradually rotates and in the crossed helix the rotation is discontinuous Here we discuss (a)-(b) only.
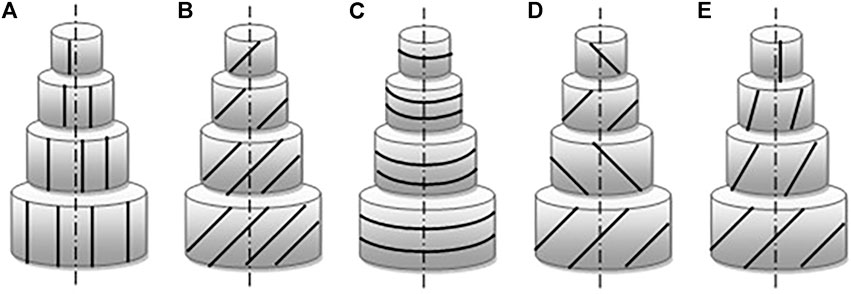
FIGURE 3. Basic plant cell wall textures: (A) line, (B) helix, (C) ring, (D) crossed helix and (E) helicoid. The black lines indicate the CMFs and the dashed line represents the major axis of the cell. Adapted from dissertation (Murugesan, 2012).
The Onsager 3D isotropic-nematic model predicts that when the rod volume fraction ϕ is less than ϕI = 3.34D/L, the phase is isotropic and when it is larger than ϕn = 4.48D/L, it is nematic (Donald et al., 2006). External fields such as magnetic, shear and extensional flow fields can shift these predictions, such that in the dilute regime the isotropic phase is ordered and oriented by the external field. This field-induced phase is denoted paranematic phase, such that when the external field is turned off, the paranematic phase relaxes to the isotropic state. To predict plant cell textures, we introduce the concept of curvature-induced paranematic ordering and consider the nematic tensor order parameter Q as two-dimensional since the fibrils are tangential to the curved elastic substrate. The elastic substrate is described by the classical membrane Helfrich elasticity due to bending (changes in mean curvature) and torsion (changes in deviatoric curvature) elastic modes. The total free energy minimization process that drives the alignment of molecules on a 2D surface is called “planar self-assembly.” We only consider dilute CFM concentration regimes that correspond to isotropic states on flat surfaces but become nematic under curved membranes. Nematic LCs exhibit anchoring energy at surfaces, which in the simplest case involve Q: kk couplings contributions. Here k is the surface unit normal. The next higher order contribution associated with a surface is Q: ∇sk; b = −∇sk = H (e1e1 + e2e2) + D (e1e1 − e2e2), where b is the symmetric curvature tensor. H(D) is the mean (deviatoric) surface curvature given by 2H = κ1 + κ2; 2D = κ1 − κ2; κ1 > κ2 and {ei} are the principal curvatures directions. Since we only consider surface ordering, the proper biaxial 2D tensor is Q = S (nn − Is/2). The schematic of the proposed curvature-driven planar self-assembly model is presented in Figure 4. Cell walls with unidirectional CMF alignment can be considered as a two dimensional fibre reinforced membrane. An integrated mechanical model for curvature driven planar self-assembly of rigid rods on an arbitrarily curved fluid membrane through novel surface phenomena such as curvophobic and curvophilic effects, has been applied to predict the uniaxial modes in plant cell walls. Curvophilic (curvophobic) effects seeks to align the CMFs along high (zero) curvature directions. The ratio of these two effects introduces an internal length scale l.
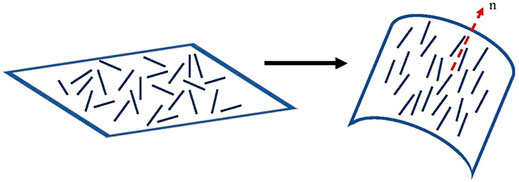
FIGURE 4. Schematic of curvature-induced 2D nematic LC self-assembly on elastic membranes. At dilute CMF concentrations below Onsager’s critical limit, the isotropic Q = 0 state observed on a flat membrane (left) may lead to a nematic state Q > 0 (right) due to curvature-mediated interactions that include couplings between Q and the membrane curvature tensor b.
The total free energy of the fibre-laden membrane system per unit area
When the free energy of the ensemble is minimized on a given cylinder of radius R (H = D = −1/R), the equilibrium fibre alignment angle cos α = (n ⋅e1) and order parameter S = 2Q: nn are obtained as a function of dimensionless radius R* = R/l of the cylindrical membrane. Figure 5 depicts the fibre orientation modes in terms of cosine of equilibrium fibre orientation angle with respect to the azimuthal coordinate (cos α) and equilibrium fibre order in terms of scalar order parameter (S), obtained by minimizing Eq. 1 with typical parameters’ values. At low dimensionless membrane radius, for 0 < R* < 0.1847, the curvophilic free energy is negligible and the curvophobic free energy is minimized, thus the fibres are aligned in the axial direction resulting in the line mode. At intermediate membrane radius, for 0.1847 < R* < 0.3867, the competition between the fibre interactions and curvophilic free energy aligns the fibres at an angle between 0 and 90°, resulting in the helical mode. At high membrane radius, for R* > 0.3867, the curvophobic free energy is negligible and the curvophilic free energy is minimized, thus the fibres are aligned in the azimuthal direction resulting in the ring mode. At low membrane radius, the fibres are more uniformly aligned in the axial direction. As the membrane radius increases, the fibre order S decreases until a local minimum (cusp) is reached, due to the cancellation of free energy contributions from curvophobic and curvophilic interactions. At the onset of the ring mode, the fibre order S starts increasing until a local maximum is reached promoted by curvophilic interactions. At high membrane radii, the fibre order vanishes.
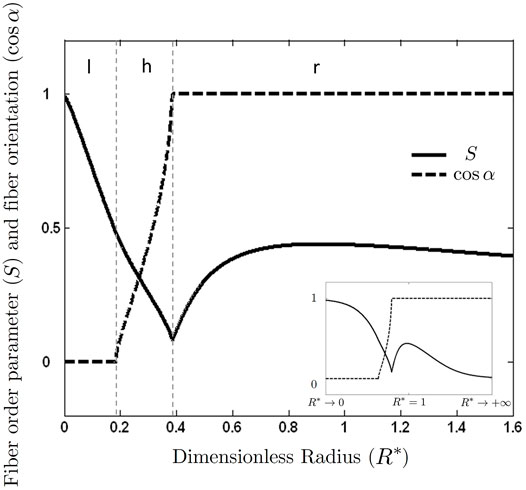
FIGURE 5. Fibre orientation cos α = (n ⋅e1) for cylindrical membranes of circular cross-section. The three possible modes are: line mode (l), helical mode (h), ring mode (r) that correspond to alignment along the cylinder axis, oblique to the axis and in the azimuthal direction, respectively. The order parameter S exhibits a typical V-shape and the orientation a step-like response as the radius increases. The inset semi-log plot shows the decrease of S towards zero as R* → ∞ (Murugesan et al., 2015). Republished with permission of Royal Society of Chemistry, from (Murugesan et al., 2011); permission conveyed through Copyright Clearance Center, Inc.
Despite the fact that the present 2D phase ordering model does not take into account temporal variation of cellulose microfibril concentration during different stages of cell wall deposition, the predicted fibre orientation (Figure 5) is in good qualitative agreement with the experimental observations for the orientation of cellulose microfibrils in cell walls of tracheids of conifers based on field emission scanning microscopy (Abe and Funada, 2005). Future opportunities in this area include self-assembly in evolving surface shapes.
2.1.2 Cholesteric N* Phase Ordering in LC-Colloid Composites
Cholesteric (N*) phase ordering is widely observed in solid analogues. A representative case is the extracellular domain of a plant cell in which chiral self-assembly takes place in a 3D space that is rich in secondary inclusions such as pit canals and other plant cells themselves. The presence of these second phases has an impact on the self-organization of defects such as the type (singular or non-singular cores), topological charge (±1/2, ±1, … ), number density and possible positional order of disclinations. To affect the director field n, the inclusion’s characteristic size L should be greater than the extrapolation length or ratio between bulk Frank orientational elasticity K and the anchoring surface energy W: L > K/W. For curved inclusions such as cylindrical fibres with mean curvature −1/R, the strong anchoring introduces radial, oblique or azimuthal surface orientation that propagates into the bulk and interacts with orientation fields from neighboring inclusions leading to defects. For nematics and cholesterics the defect charge C in a LC matrix that contains N inclusions is C = −(N −2)/2, where the minus sign corresponds to tangential anchoring conditions. The inclusion of these secondary phases induces confinement of the cholesteric material between them, and the resulting frustration in the mesophase is relieved through nucleation of defects and distortion of the pitch of the mesophase as shown in Figure 6A. There is strong evidence that the solid helicoidal plywood architecture is formed through LC self-assembly by the existence of specific defect patterns observed in the presence of these secondary phases in the domain of self-assembly (Reis et al., 1992).
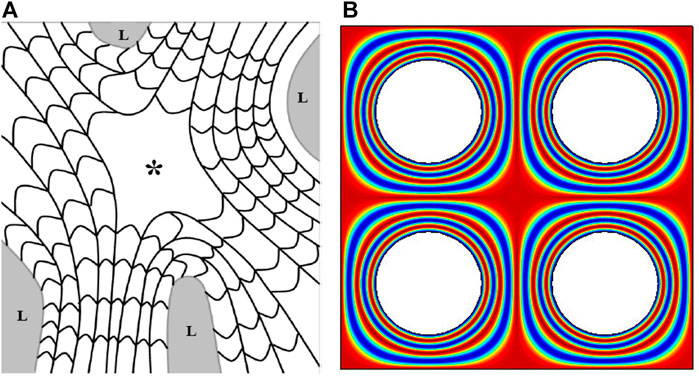
FIGURE 6. Helicoidal plywoods in plant cell walls with secondary phases. (A) Adaptation of helicoidal plywood to embedded pit canals (L inside the gray circles) by dilation of layers (shown by width changes in arc-patterns) and bending of layers (bending of arced patterns) and a − 1 saddle defect (denoted by *) in a natural helicoidal plywood due to inclusion of four (L) lumens in walnut (Gutierrez and Rey, 2017). (B) A self-assembly simulation of a −1 saddle defect. For filled LCs, a defect of strength −(N −2)/2 is expected (Rey et al., 2016). For the four (L) lumens, N = 4 and the plywood has a –1 saddle defect (*). Republished with permission of Royal Society of Chemistry, from (Rey, 2010); permission conveyed through Copyright Clearance Center, Inc.
Figure 6B shows a 2D visualization of the director field during N* (out-of-plane nz-component) phase ordering computed by minimizing the total free energy in a rectangular domain with four inclusions. In this case the free energy has local (Landau-de Gennes), elastic (Frank elasticity), and chiral contributions: F = Ffibre(Q) + Felastic (∇Q) + Fchiral (∇ ×Q). At the center of the N = 4 arrangement, there is a non-singular − 1 saddle defect as in the biological analogue. The colored ring spacing is related to the pitch P0. Matching the main features of the experimental texture one is then able to extract the concentration of rods (terms in Ffibre(Q)), the elastic anisotropy [terms in Felastic (∇Q)] and pitch effects [terms in Fchiral (∇ ×Q)] and check for consistency with characteristic values of biological LCP. This representative example shows how the liquid crystal modeling platform provides quantitative information of biological self-assembled structures.
2.2 Open System Phase Ordering Models, Predictions and Validations
2.2.1 Paranematic Phase Ordering Under Shear and Extensional Kinematics
Coupling phase ordering and transport phenomena lead to new self-organization mechanism by interactions between the spatio-temporal behavior of Q with symmetry- breaking fields, such as flow (Rey, 1995a; Rey, 1995b; Rey, 1995c; Rey and Tsuji, 1998; Pujolle-Robic et al., 2002; Forest et al., 2004a; Forest et al., 2004b; Hess and Ilg, 2005; Ji et al., 2006; Mendil-Jakani et al., 2009; Golmohammadi and Rey, 2010a; Golmohammadi and Rey, 2010b; Xu et al., 2011), heat (Huisman and Fasolino, 2007; Abukhdeir et al., 2008; Abukhdeir and Rey, 2009; Yang et al., 2009; Abukhdeir, 2016) and mass fluxes (Rey, 1997; Rey, 2000a; Bedolla Pantoja et al., 2019). For example, in (Rey, 1995a; Rey, 1995b), it is shown that subjecting isotropic phases to extensional flows is rich in symmetry breaking bifurcations, since the equivalence condition
is satisfied for rotational and reflectional transformation matrix T, here f is the system of nematodynamic equations, v is the solution vector in terms of eigenvectors of Q, Pe is the Péclet number, and ϕ is the rod concentration.
In the present representative open system, we discuss the injection of momentum by shear and extension flow into isotropic states of dilute collagen solutions to created paranematic states. The phase diagram of aqueous acidic triple helix collagen solutions has been formulated using phase ordering processes that include Onsager hard core interaction, electrostatic repulsion, chirality and attractive interactions of the Maier-Saupe type (Khadem and Rey, 2019a; Khadem and Rey, 2019b; Khadem and Rey, 2021). The predictions are in excellent agreement with experimental data (Gobeaux et al., 2007). A significant effect of these additional interactions is to bend the biphasic I-N* region in an acidic-collagen concentration diagram towards higher collagen concentrations than Onsager’s predictions (Donald et al., 2006). Since processing macroscopic defect-free collagen films is not generally possible, film casting flows of dilute isotropic triple helix collagen solutions are used (Rey, 2010). These flows usually contain mixtures of vorticity and deformation rates and flow-align the rods according to the balance of nematodynamic torques and thermodynamic torques. An approach that sheds important quantitative information is to perform characterization studies based on the four-roll mill apparatus, which provides all the possible flow configurations, from pure vortex to simple shear, and to uniaxial extensional flow. The equations of Q-tensor nematodynamics were solved using experimental parametric data for collagen solutions. The key issue was to determine how the different couplings between vorticity and order parameter (W ⋅Q), and deformation rate and order parameter (A ⋅Q) generate orientation (n) and order (S), to create a collagen paranematic phase that relaxes back to isotropic (Q = 0) if the flow is removed. One important output of the study is what is the optimal vorticity-deformation rate mixture and their intensities to target well oriented samples with sufficient scalar order parameter. Figure 7 in terms of director angle with respect to the flow direction and scalar order parameter S. The ellipsoids represent Q + I/3, the colour intensity is the Deborah (
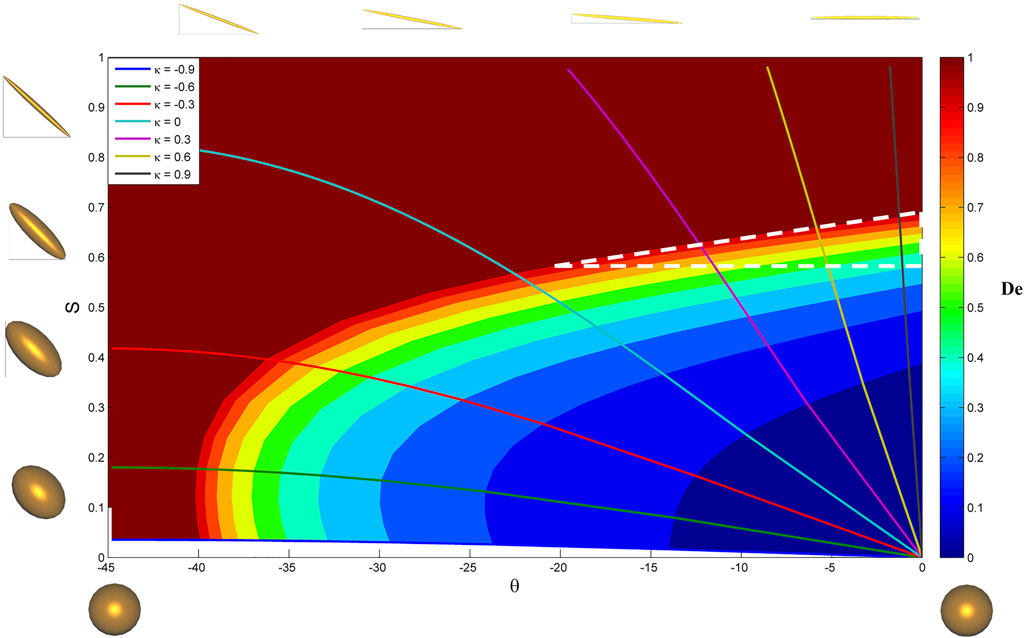
FIGURE 7. Computed flow induced structuring in terms of the scalar order parameter S and the director angle θ with respect to the flows’ direction. The color intensity is the Deborah number De and the colour curved lines correspond to the flow type
As expect extensional flow (κ = ±1) is required as it is the strongest orienting field with De less than 0.7 corresponding to deformation rates of the order of 700 s−1. Pure vorticity (κ = −1) does not create phase ordering and S = 0. These results expand results of shear flow effects on the I-N transition and highlight the importance of extensional (potential) flow. Since the generated paranematic PN phase is characterized by an order parameter SPN(De, κ) (y-axis in Figure 7), one can then estimate the equivalent equilibrium value in terms of concentration, pitch and pH: SPN(De, κ) = Seq (ϕ, P0, pH, …).
2.2.2 Cholesteric Phase Ordering Under Directed Evaporation
The coupling of phase ordering and phase separation has been widely studied in various mesophase-solvent-nanoparticle blends and self-selected textures and defects in spinodal and nucleation and growth modes have been characterized and validated (Das and Rey, 2004; Das and Rey, 2005; Das and Rey, 2006; Matsuyama, 2008; Soule and Rey, 2012; Milette et al., 2013; Soulé and Rey, 2013; Gurevich et al., 2014; Soule and Rey, 2019; Khadem and Rey, 2021). In contrast with this case, in open systems loss of solvent, as in dehydration, is dictated or coupled to external sinks and not to equilibrium thermodynamic driving forces. As in the case of undercooling in solidification, when the temperature is below the thermodynamic liquidus value and instability sets in, we will see below a representative corresponding soft matter example of dehydration of collagen solutions, when the externally controlled evaporation creates a water concentration profile below its equilibrium value (Kirkwood and Fuller, 2009; Gutierrez and Rey, 2017).
In this section we start with the dehydration analysis of the PN material produced in the previously discussed step (Section 2.2.1). After imposing shear/extensional flow to an isotropic aqueous acidic triple collagen solution to create a PN state, one can then use directed evaporation of the PN phase to create a stable, defect-free cholesteric N* phase (Figure 8):
where
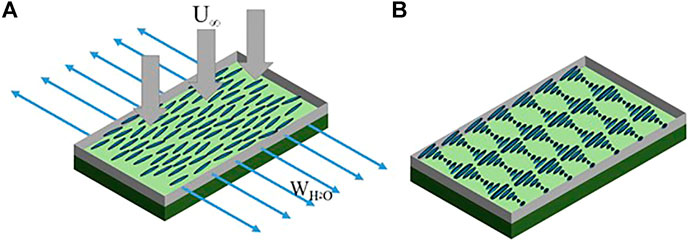
FIGURE 8. Schematic representation of the drying process used by Kirkwood and Fuller (Kirkwood and Fuller, 2009) to produce defect-free collagen films (A) and a well aligned cholesteric helix after drying (B). In this case water leaves the film along the horizontal direction and the helix forms along the water flux. Republished with permission of Royal Society of Chemistry, from (Gutierrez and Rey, 2017); permission conveyed through Copyright Clearance Center, Inc.
The optimal design and operation match the scalar order parameter produced by the shear/extensional flow with the order parameter of the final equilibrium cholesteric dehydrated films: SPN(De, κ) ≈ Seq (ϕ, P0, pH, …) = SCh(ϕ, P0, pH, …), so that there is minimal adjustment in order throughout the drying process. Simultaneously, the helix (h, P0) forms by the torques generated by the water concentration gradients, to eventually achieve a perfectly aligned helix with uniform pitch. The synchronicity in a film of size L, is obtained when the ratio of the collagen rotational time scale 1/(6Dr) water diffusion time scale L2/D achieves an optimal value (Π = Πop):
This novel phase ordering/mass transfer coupling is shown in Figure 9. The figure shows the integrated phase ordering/directed evaporation cycle in an open system self-organization process. The yellow central arrow indicates how starting with concentration fluctuations we create order (S), torques and helicity (P0). Fluctuation in concentration (mass transfer) creates nematic order (S) which creates torques to form the helix (h). Mass transfer is controlled by water diffusion constant D (right box) and phase ordering by the collagen rotational diffusion Dr (left box).
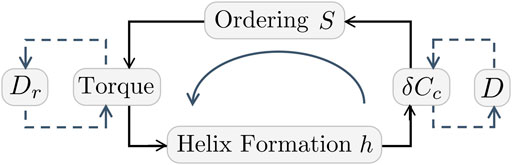
FIGURE 9. Integrated phase ordering/directed evaporation cycle in an open system self-organization process. The arrow indicates how starting with concentration fluctuations we create order, torques and helicity. Fluctuation in concentration (mass transfer) creates nematic order (S) which creates torques to form the helix (h) Mass transfer is controlled by water diffusion constant D (right box) and phase ordering by the collagen rotational diffusion Dr (left box). Redrew with permission of Royal Society of Chemistry, from (Gutierrez and Rey, 2017) for higher figure resolution; permission conveyed through Copyright Clearance Center, Inc.
Using an integrated mass transfer and Q-tensor nematodynamics with moving boundaries representative results of self-organization were obtained for almost perfectly synchronized (Π = Πc, left figure in Figure 10) and largely unsynchronized (Π < Πc, right figure in Figure 10) phase ordering/evaporation. The PN-to-N* transformation under mass transfer coupling to phase ordering offers new routes to material processing not available to phase ordering-phase separation closed system process since driving forces are related to the rate of entropy production and not to equilibrium free energy. Additional process variables that can be explored to target surface wrinkling functionalities are airflow intensity, directionality and flow type (tangential shear, stagnation flows).
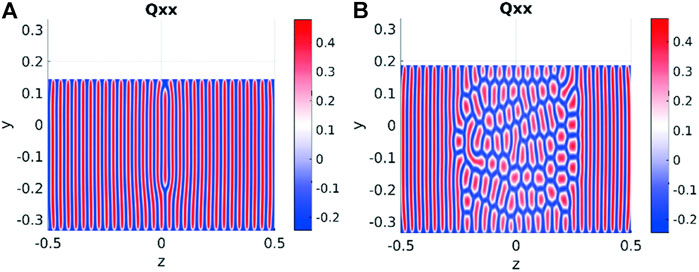
FIGURE 10. (A) Nearly synchronized (Π ≈ Πop) phase ordering/mass transfer produces an almost defect-free film, and 1 disclination is present; (B) Fast evaporation (Π < Πop) creates a central defect network with many disclinations and rod-polygon shape textures. Republished with permission of Royal Society of Chemistry, from (Gutierrez and Rey, 2017); permission conveyed through Copyright Clearance Center, Inc.
At the end of the drying process the collagen film surface has characteristic nano-wrinkles, which are ubiquitous in many cholesteric free surfaces (Terris et al., 1992; Fernandes et al., 2013; Rofouie et al., 2014; Rofouie et al., 2017a; Rofouie et al., 2017b; Almeida et al., 2018; Wang et al., 2019; Wang et al., 2020a). The wavelength is usually of the order of the pitch P0. The amplitude of these wrinkles is in the nano-scale and not in the micron scale, as when driven by Frank elasticity in micron range confinements. The origin of these nano-wrinkles is the nematic liquid crystal capillary pressure pc:
where ξ is the Cahn-Hoffman capillary vector, γ is the surface tension, and W is the quadratic the anchoring coefficient (Cheong and Rey, 2002a; Cheong and Rey, 2002b; Cheong and Rey, 2002c; Rey, 2002a; Rey, 2004a; Rey, 2004b; Rey, 2005; Rey, 2006; Wincure and Rey, 2007). Performing the surface gradient of the capillary vector one finds that the easy shape condition leads to:
The brackets in the numerator of Eq. 6 can be shown to represent a 1-D splay-bend director distortion and is the source of a periodic director capillary pressure.
Figure 11 shows a representative calculation of the surface relief profile for W/γ0 = 0.002 to 0.004.
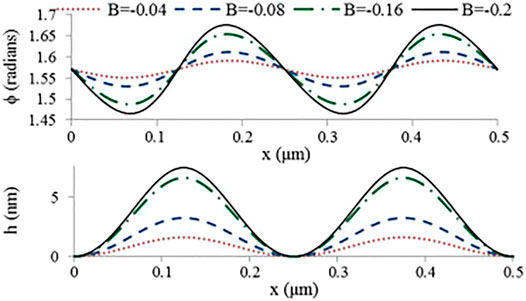
FIGURE 11. Surface relief of a cholesteric surface displaying characteristic nanowrinkling with a wavelength equal to the pitch P0. Here B = W/γ0 is the scaled anchoring coefficient. Reprinted from Rofouie et al. (2014), Copyright (2014), with permission from Elsevier.
A key finding of this surface pattern formation model is that the amplitude hmax and wavelength λ does scale linearly with the P0 as observed in experiments:
Extensions of this model to higher order anchoring functions predict two-wavelength patterns (Wang et al., 2020a) and two dimensional director fields are expected to generate egg cartons (Wang et al., 2021). Coupling the liquid crystal shape equation with interfacial mass transfer leads to new Marangoni flows (Rey, 1999; Yue et al., 2005; Herminghaus et al., 2014; Choi and Takezoe, 2016) that can be explored in the presence of wrinkling. Introducing these nanoscale effects to wetting and film phenomena (Kondic and Cummings, 2021) in liquid crystals may provide new routes to multiscale pattern formation.
3 Computational Platforms
We end this review with a discussion of some computational platforms that are used in liquid crystal self-assembly and self-organization that may also be applied to areas such as active liquid crystal matter (Forest et al., 2013; Yang et al., 2016; Wang, 2021; Zhang et al., 2021). Some of the challenges arise because of the multiscale 19 nature of the tensor order parameter, the presence of orientational boundary layers, nucleation and annihilation of disclinations under flow, need to resolve disclination cores, the presence of interfaces and contact lines, nucleation-growth-impingement of colloidal drops, presence of faceted particles, 3D disclination line textures, complex 3D director fields, and more. For example, to simulate real liquid crystal polymer textured flows with Q-tensor nematodynamics, the energy ratio R and Ericksen number Er need to be specified (Grecov and Rey, 2003):
Here the energy ratio is expressed in terms of geometric (gap used in a rheometer) and defect radius length scales. So, unless high-performance computing and adaptive methods are used no resolution of defect nucleation, and defect annihilation is possible, as required by experiments (Zhu and Farrell, 2002). Even in the absence of flow, it was shown that to resolve defects in monomeric LCs a mesh smaller than 3 nm is needed (Chen et al., 2021). The platforms include:
(a) Geometric modeling. i) It has been used to resolve the arc-patterns observed in cross-sectional projections of cholesteric and orthogonal plywood. The projected director field is converted to planar curves whose curvature provides information on the pitch of the material using the inverse problem techniques. ii) Characterization of nanowrinkling can be assisted by computation of higher order moments of the surface relief distribution using accurate integration methods. iii) Interfacial and membrane geometries (Gutierrez and Rey, 2018; Wang et al., 2020b) can be better resolved by decoupling shape from curvedness instead of the usual mean and Gaussian curvature that comingle these two quantities. Recasting the equilibrium and dissipative shape equations in terms of shape and curvedness and their rates provides an additional phase space where trajectories detect the birth, death and transformations of shapes.
(b) Phase field modeling (Yang et al., 2006; Yang et al., 2013; Zhao et al., 2016; Qiu et al., 2021). i) It has been used to simulate near equilibrium and flow phenomena, using stable variational-informed schemes that provide consistent description of the Q-tensor, composition and accurately resolve interfacial physics (Zhao et al., 2016; Qiu et al., 2021). ii) Phase ordering and phase separation in liquid crystal nanocomposites (Gurevich et al., 2014; Gurevich et al., 2017) leading to dendritic patterns have been resolved accurately using adaptive schemes that resolve nematic order, concentration, as well as nanoparticle positional ordering.
(c) AI-based modeling. i) Neural networks have been used to predict various material properties with high accuracy, based on direct optical images (Sigaki et al., 2019; Sigaki et al., 2020). ii) The nearly intractable problem of nucleation, growth and impingement at a large population level has been resolved using AI techniques, to show that the limits of direct numerical simulation can be largely extended (Khadem and Rey, 2021).
(d) Defect detection and tensor visualization methods. Singular and non-singular defects nucleate, annihilate, and act as defect sources. For singular defects the normalized biaxiality index is a useful index to detect disclinations since cores are biaxial (Zhu and Farrell, 2002; Jankun-Kelly et al., 2009; Fu and Abukhdeir, 2014).
(e) Optical methods. Resolving textures and defects using FDTD methods (Han and Rey, 1995; Hwang and Rey, 2005; Hwang et al., 2007) is a useful tool in characterization methods, such rheo-optics, when one can follow the action of deformation rates on Q-tensor response (Hwang et al., 2007).
(f) Bifurcation methods and flow solvers. Liquid cyrstals are rarely flow-aligning under shearing conditions and usually display solution multiplicities, periodic and oscillatory modes, and flow-induced transitions that require the use of bifurcation methods, and adaptive schemes for torque balances (Farhoudi and Rey, 1993; Han and Rey, 1993a; Han and Rey, 1993b; Han and Rey, 1994; Singh and Rey, 1998; de Andrade Lima and Rey, 2004; Forest et al., 2004b; Fox et al., 2020; Chillingworth et al., 2021).
4 Conclusion, Summary and Outlook
Table 1 summarizes the key finding and identifies opportunities for future work in liquid crystal self-assembly and self-organization, as follows. Liquid crystal phase ordering describes many processes and structures observed in nature and can be described and quantified by non-conserved order parameter models such as the Q-tensor equations for self-assembly. Here defect generation and identification, provide an important tool to describe processes that started with liquid crystalline precursors and end with solid liquid crystal analogues. A material system that offers fertile inspirational ground is the plant cell wall where the orientation of cellulose microfibrils displays typical nematic and cholesteric architectures. Here we demonstrated that a 2D phase ordering process on an elastic membrane serves as a good model for self-assembly. By reducing the physical and phase space dimensionality to 2D we find couplings that guide the fibres towards and away from principal curvatures, augmenting the number of mechanisms beyond the excluded volume interactions that create nematic phases. In the presence of second phases, colloidal particles, inclusions, liquid crystal organization accommodates to the geometric constraints by creating defects of various kinds with positional order that reflect the inserted particles arrangements. Consistency between Q-tensor models a variety of actual systems including plant cell walls and synthetic materials like carbon-carbon composites and polymer dispersed liquid crystals has been presented. Future directions include shape-changing inclusions with translational and rotational degrees of freedom.
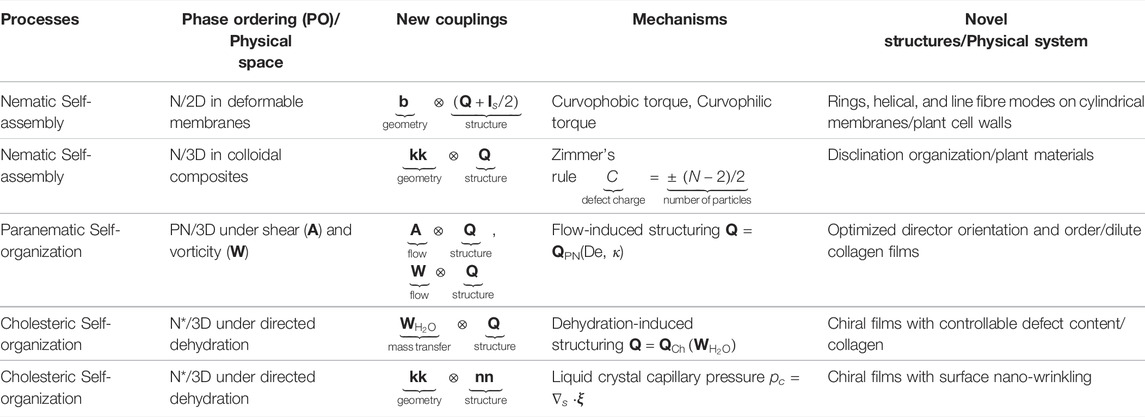
TABLE 1. Summary of self-organization and self-assembly in open and closed systems, with paranematic, nematic and cholesteric order in complex physical spaces, observed experimentally and predicted by theory and simulation.
In the presence of transport processes including heat, mass, and momentum, couplings with conserved order parameters provide new mechanisms of self-organization (Park et al., 2021). The film processing of aqueous acidic triple helix collagen for tissue engineering applications is an example where sequential transport processes, flow and then directed dehydration, can create an essentially defect-free cholesteric thin (typically in the micron range) film. Subjecting a dilute isotropic collagen solution to a shear/extensional flow produces a paranematic phase that can be dehydrated at a rate that retains the flow-induced order but that creates a moving front that converts the nearly uniform director to a helix. Future directions include the use of transient flows and film casting flows as well as different evaporation processes and confinement (Srinivasarao, 2021).
In closing, liquid crystal-based self-assembly and self-organization research is a driving force for new biomimetic principles for green manufacturing of advanced and multifunctional materials and devices, as recent publications show.
Author Contributions
ZW, PS, and AR contributed to conception of the study. ZW prepared the figures and bibliography. AR wrote the first draft of the manuscript. ZW, PS and AR revised the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work is supported by the Natural Science and Engineering Research Council of Canada (NSERC) (Grant number: 223086).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
AR and PS are thankful for financial support from the Natural Science and Engineering Research Council of Canada (NSERC), and to Compute Canada and CLUMEQ for support and access to high performance computing. AR is thankful to McGill University for financial support through the James McGill Professor appointment. ZW is grateful to the Faculty of Engineering for support through the MEDA scholarship program. AR wishes to acknowledge the fundamental contributions of Gino de Luca, Ahmad Sayyed Khadem, Oscar Aguilar Gutierrez, Yogesh Murugesan, Oscar Matus Rivas, E.E. Herrera Valencia, Ziheng Wang, Pardis Rofouie, Yun Yan, Gaurav Gupta, Dana Grecov, Won Hee Han, Philip K. Chan, Ezequiel Soule, Nasser Mohieddin Abukhdeir, Susanta K Da, Samir Mushrif, Paul M. Phillips, Mojdeh Golmohammadi, Luiz R. P de Andrade Lima, Alireza Shams, Dae Kun Hwang, Benjamin Wincure, Ae-Gyeong Cheong, Hang Hu, Mohan Srinivasarao, Linda Reven, and Raffaele Mezzenga.
References
Abe, H., and Funada, R. (2005). Review - the Orientation of Cellulose Microfibrils in the Cell Walls of Tracheids in Conifers. Iawa J. 26, 161–174. doi:10.1163/22941932-90000108
Abukhdeir, N. M., and Rey, A. D. (2009). Nonisothermal Model for the Direct Isotropic/Smectic-A Liquid-Crystalline Transition. Langmuir 25, 11923–11929. doi:10.1021/la9015965
Abukhdeir, N. M., Soulé, E. R., and Rey, A. D. (2008). Non-Isothermal Model for Nematic Spherulite Growth. Langmuir 24, 13605–13613. doi:10.1021/la8022216
Abukhdeir, N. M. (2016). Nematic Phase Transition and Texture Dynamics. Liq. Cryst. 43, 2300–2319. doi:10.1080/02678292.2016.1239772
Aguilar Gutierrez, O. F., and Rey, A. D. (2016a). Theory and Simulation of Cholesteric Film Formation Flows of Dilute Collagen Solutions. Langmuir 32, 11799–11812. doi:10.1021/acs.langmuir.6b03443
Aguilar Gutierrez, O. F., and Rey, A. D. (2016b). Characterization Methodology for Biological Plywoods Based on Characteristic Cross-Section Patterns. J. Renew. mater 4, 241–250. doi:10.7569/jrm.2016.634119
Almeida, A. P. C., Canejo, J. P., Fernandes, S. N., Echeverria, C., Almeida, P. L., and Godinho, M. H. (2018). Cellulose-based Biomimetics and Their Applications. Adv. Mat. 30, 1703655. doi:10.1002/adma.201703655
Barbero, G., and Evangelista, L. R. (2000). An Elementary Course on the Continuum Theory for Nematic Liquid Crystals, 3. Singapore: World Scientific Publishing Company.
Bedolla Pantoja, M. A., Yang, Y., and Abbott, N. L. (2019). Toluene-induced Phase Transitions in Blue Phase Liquid Crystals. Liq. Cryst. 46, 1925–1936. doi:10.1080/02678292.2019.1633432
Belamie, E., Mosser, G., Gobeaux, F., and Giraud-Guille, M. M. (2006). Possible Transient Liquid Crystal Phase during the Laying Out of Connective Tissues: α-chitin and Collagen as Models. J. Phys. Condens. Matter 18, S115–S129. doi:10.1088/0953-8984/18/13/s08
Bouligand, Y. (2008). Liquid Crystals and Biological Morphogenesis: Ancient and New Questions. Comptes Rendus Chim. 11, 281–296. doi:10.1016/j.crci.2007.10.001
Brett, C. T., and Hillman, J. R. (1985). Biochemistry of Plant Cell Walls Cambridge, UK: Cambridge University Press.
Canejo, J. P., Monge, N., Echeverria, C., Fernandes, S. N., and Godinho, M. H. (2017). Cellulosic Liquid Crystals for Films and Fibers. Liq. Cryst. Rev. 5, 86–110. doi:10.1080/21680396.2017.1394923
Casado, U., Mucci, V. L., and Aranguren, M. I. (2021). Cellulose Nanocrystals Suspensions: Liquid Crystal Anisotropy, Rheology and Films Iridescence. Carbohydr. Polym. 261, 117848. doi:10.1016/j.carbpol.2021.117848
Chen, Y., Korculanin, O., Narayanan, S., Buitenhuis, J., Rogers, S. A., Leheny, R. L., et al. (2021). Probing Nonlinear Velocity Profiles of Shear-Thinning, Nematic Platelet Dispersions in Couette Flow Using X-Ray Photon Correlation Spectroscopy. Phys. fluids 33, 063102. doi:10.1063/5.0050942
Cheong, A.-G., and Rey, A. D. (2002a). Cahn-Hoffman Capillarity Vector Thermodynamics for Curved Liquid Crystal Interfaces with Applications to Fiber Instabilities. J. Chem. Phys. 117, 5062–5071. doi:10.1063/1.1498821
Cheong, A. G., and Rey, A. D. (2002b). Cahn-hoffman Capillarity Vector Thermodynamics for Liquid Crystal Interfaces. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 66, 021704. doi:10.1103/PhysRevE.66.021704
Cheong, A.-G., and Rey, A. D. (2002c). Capillary Instabilities in a Thin Nematic Liquid Crystalline Fiber Embedded in a Viscous Matrix. Continuum Mech. Thermodyn. 14, 263–279. doi:10.1007/s001610200093
Chillingworth, D., Forest, M. G., Lauterbach, R., and Wulff, C. (2021). Existence and Stability of Kayaking Orbits for Nematic Liquid Crystals in Simple Shear Flow. Arch. Ration. Mech. Anal. 242, 1229–1287. doi:10.1007/s00205-021-01703-x
Choi, H., and Takezoe, H. (2016). Circular Flow Formation Triggered by Marangoni Convection in Nematic Liquid Crystal Films with a Free Surface. Soft Matter 12, 481–485. doi:10.1039/c5sm02098k
Chu, G., Vilensky, R., Vasilyev, G., Martin, P., Zhang, R., and Zussman, E. (2018). Structure Evolution and Drying Dynamics in Sliding Cholesteric Cellulose Nanocrystals. J. Phys. Chem. Lett. 9, 1845–1851. doi:10.1021/acs.jpclett.8b00670
Cui, Z., Wang, Q., and Wang, Q. (2011). Permeation Flows in Cholesteric Liquid Crystal Polymers under Oscillatory Shear. Discrete and Continuous Dyn. Systems-B 15, 45–60. doi:10.3934/dcdsb.2011.15.45
Cui, Z., Calderer, M. C., and Wang, Q. (2006). Mesoscale Structures in Flows of Weakly Sheared Cholesteric Liquid Crystal Polymers. Discrete and Continuous Dyn. Systems-B 6, 291. doi:10.3934/dcdsb.2006.6.291
Das, S. K., and Rey, A. D. (2004). Texture Formation under Phase Ordering and Phase Separation in Polymer-Liquid Crystal Mixtures. J. Chem. Phys. 121, 9733–9743. doi:10.1063/1.1804494
Das, S. K., and Rey, A. D. (2005). Colloidal Crystal Formation via Polymer-Liquid-Crystal Demixing. Europhys. Lett. 70, 621–627. doi:10.1209/epl/i2005-10034-2
Das, S. K., and Rey, A. D. (2006). Magnetic Field-Induced Shape Transitions in Multiphase Polymer-Liquid Crystal Blends. Macromol. Theory Simul. 15, 469–486. doi:10.1002/mats.200600024
de Andrade Lima, L. R. P., and Rey, A. D. (2004). Poiseuille Flow of Discotic Nematic Liquid Crystals' Onion Textures. J. Newt. fluid Mech. 119, 71–81. doi:10.1016/j.jnnfm.2003.01.001
Donald, A. M., Windle, A. H., and Hanna, S. (2006). Liquid Crystalline Polymers. Cambridge, UK: Cambridge University Press.
Echeverria, C., Almeida, P. L., Feio, G., Figueirinhas, J. L., Rey, A. D., and Godinho, M. H. (2015). Rheo-nmr Study of Water-Based Cellulose Liquid Crystal System at High Shear Rates. Polymer 65, 18–25. doi:10.1016/j.polymer.2015.03.050
Echeverria, C., Almeida, P. L., Aguilar Gutierrez, O. F., Rey, A. D., and Godinho, M. H. (2017). Two Negative Minima of the First Normal Stress Difference in a Cellulose-Based Cholesteric Liquid Crystal: Helix Uncoiling. J. Polym. Sci. Part B Polym. Phys. 55, 821–830. doi:10.1002/polb.24332
Emons, A. M. C., and Mulder, B. M. (2000). How the Deposition of Cellulose Microfibrils Builds Cell Wall Architecture. Trends plant Sci. 5, 35–40. doi:10.1016/s1360-1385(99)01507-1
Farhoudi, Y., and Rey, A. D. (1993). Shear Flows of Nematic Polymers. I. Orienting Modes, Bifurcations, and Steady State Rheological Predictions. J. Rheology 37, 289–314. doi:10.1122/1.550444
Fernandes, S. N., Geng, Y., Vignolini, S., Glover, B. J., Trindade, A. C., Canejo, J. P., et al. (2013). Structural Color and Iridescence in Transparent Sheared Cellulosic Films. Macromol. Chem. Phys. 214, 25–32. doi:10.1002/macp.201200351
Forest, M. G., Wang, Q., and Zhou, R. (2004a). The Flow-phase Diagram of Doi-Hess Theory for Sheared Nematic Polymers Ii: Finite Shear Rates. Rheol. Acta 44, 80–93. doi:10.1007/s00397-004-0380-9
Forest, M. G., Wang, Q., and Zhou, R. (2004b). The Weak Shear Kinetic Phase Diagram for Nematic Polymers. Rheol. acta 43, 17–37. doi:10.1007/s00397-003-0317-8
Forest, M. G., Wang, Q., and Zhou, R. (2013). Kinetic Theory and Simulations of Active Polar Liquid Crystalline Polymers. Soft Matter 9, 5207–5222. doi:10.1039/c3sm27736d
Fox, R. J., Forest, M. G., Picken, S. J., and Dingemans, T. J. (2020). Observation of Transition Cascades in Sheared Liquid Crystalline Polymers. Soft Matter 16, 3891–3901. doi:10.1039/d0sm00275e
Fu, F., and Abukhdeir, N. M. (2014). A Topologically-Informed Hyperstreamline Seeding Method for Alignment Tensor Fields. IEEE Trans. Vis. Comput. Graph 21, 413–419. doi:10.1109/TVCG.2014.2363828
Gobeaux, F., Belamie, E., Mosser, G., Davidson, P., Panine, P., and Giraud-Guille, M.-M. (2007). Cooperative Ordering of Collagen Triple Helices in the Dense State. Langmuir 23, 6411–6417. doi:10.1021/la070093z
Golmohammadi, M., and Rey, A. D. (2010a). Structural Modeling of Carbonaceous Mesophase Amphotropic Mixtures under Uniaxial Extensional Flow. J. Chem. Phys. 133, 034903. doi:10.1063/1.3455505
Golmohammadi, M., and Rey, A. D. (2010b). Structure and Phase Transitions of Carbonaceous Mesophase Binary Mixtures under Uniaxial Extensional Flow. J. Newt. fluid Mech. 165, 698–711. doi:10.1016/j.jnnfm.2010.03.006
Grecov, D., and Rey, A. D. (2003). Shear-induced Textural Transitions in Flow-Aligning Liquid Crystal Polymers. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 68, 061704. doi:10.1103/PhysRevE.68.061704
Gurevich, S., Soule, E., Rey, A., Reven, L., and Provatas, N. (2014). Self-assembly via Branching Morphologies in Nematic Liquid-Crystal Nanocomposites. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 90, 020501. doi:10.1103/PhysRevE.90.020501
Gurevich, S., Provatas, N., and Rey, A. (2017). Nanoscale Interfacial Defect Shedding in a Growing Nematic Droplet. Phys. Rev. E 96, 022707. doi:10.1103/PhysRevE.96.022707
Gutierrez, O. F. A., and Rey, A. D. (2014a). Chiral Graded Structures in Biological Plywoods and in the Beetle Cuticle. Colloid Interface Sci. Commun. 3, 18–22. doi:10.1016/j.colcom.2015.04.001
Gutierrez, O. F. A., and Rey, A. D. (2014b). Structure Characterisation Method for Ideal and Non-ideal Twisted Plywoods. Soft Matter 10, 9446–9453. doi:10.1039/c4sm01803f
Gutierrez, O. F. A., and Rey, A. D. (2016). Geometric Reconstruction of Biological Orthogonal Plywoods. Soft matter 12, 1184–1191. doi:10.1039/c5sm02214b
Gutierrez, O. F. A., and Rey, A. D. (2017). Biological Plywood Film Formation from Para-Nematic Liquid Crystalline Organization. Soft matter 13, 8076–8088. doi:10.1039/c7sm01865g
Gutierrez, O. F. A., and Rey, A. D. (2018). Extracting Shape from Curvature Evolution in Moving Surfaces. Soft Matter 14, 1465–1473. doi:10.1039/c7sm02409f
Han, W. H., and Rey, A. D. (1993a). Stationary Bifurcations and Tricriticality in a Creeping Nematic Polymer Flow. J. Newt. fluid Mech. 50, 1–28. doi:10.1016/0377-0257(93)85013-z
Han, W. H., and Rey, A. D. (1993b). Supercritical Bifurcations in Simple Shear Flow of a Non-aligning Nematic: Reactive Parameter and Director Anchoring Effects. J. Newt. fluid Mech. 48, 181–210. doi:10.1016/0377-0257(93)80070-r
Han, W. H., and Rey, A. D. (1994). Orientation Symmetry Breakings in Shearing Liquid Crystals. Phys. Rev. E 50, 1688–1691. doi:10.1103/physreve.50.1688
Han, W. H., and Rey, A. D. (1995). Theory and Simulation of Optical Banded Textures of Nematic Polymers during Shear Flow. Macromolecules 28, 8401–8405. doi:10.1021/ma00128a059
Harrington, M. J., and Fratzl, P. (2021). Natural Load-Bearing Protein Materials. Prog. Mater. Sci. 120, 100767. doi:10.1016/j.pmatsci.2020.100767
Harrington, M. J., Jehle, F., and Priemel, T. (2018). Mussel Byssus Structure‐Function and Fabrication as Inspiration for Biotechnological Production of Advanced Materials. Biotechnol. J. 13, 1800133. doi:10.1002/biot.201800133
Herminghaus, S., Maass, C. C., Krüger, C., Thutupalli, S., Goehring, L., and Bahr, C. (2014). Interfacial Mechanisms in Active Emulsions. Soft matter 10, 7008–7022. doi:10.1039/c4sm00550c
Hess, S., and Ilg, P. (2005). On the Theory of the Shear-Induced Isotropic-To-Nematic Phase Transition of Side Chain Liquid-Crystalline Polymers. Rheol. Acta 44, 465–477. doi:10.1007/s00397-004-0426-z
Huisman, B. A., and Fasolino, A. (2007). Influence of Latent Heat and Thermal Diffusion on the Growth of Nematic Liquid Crystal Nuclei. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 76, 021706. doi:10.1103/PhysRevE.76.021706
Hwang, D. K., and Rey, A. D. (2005). Computational Modeling of the Propagation of Light through Liquid Crystals Containing Twist Disclinations Based on the Finite-Difference Time-Domain Method. Appl. Opt. 44, 4513–4522. doi:10.1364/ao.44.004513
Hwang, D. K., Han, W. H., and Rey, A. D. (2007). Computational Rheooptics of Liquid Crystal Polymers. J. Newt. fluid Mech. 143, 10–21. doi:10.1016/j.jnnfm.2006.11.006
Jankun-Kelly, T. J., Zhang, S., Callan-Jones, A. C., Pelcovits, R. A., Slavin, V. A., and Laidlaw, D. H. (2009). “Tensor Visualization and Defect Detection for Nematic Liquid Crystals Using Shape Characteristics,” in Visualization and Processing of Tensor Fields (Springer), 213–238. doi:10.1007/978-3-540-88378-4_11
Ji, G., Wang, Q., Zhang, P., and Zhou, H. (2006). Study of Phase Transition in Homogeneous, Rigid Extended Nematics and Magnetic Suspensions Using an Order-Reduction Method. Phys. Fluids 18, 123103. doi:10.1063/1.2408484
Khadem, S. A., and Rey, A. D. (2019a). Theoretical Platform for Liquid-Crystalline Self-Assembly of Collagen-Based Biomaterials. Front. Phys. 7, 88. doi:10.3389/fphy.2019.00088
Khadem, S. A., and Rey, A. D. (2019b). Thermodynamic Modelling of Acidic Collagenous Solutions: from Free Energy Contributions to Phase Diagrams. Soft matter 15, 1833–1846. doi:10.1039/c8sm02140f
Khadem, S. A., and Rey, A. D. (2021). Nucleation and Growth of Cholesteric Collagen Tactoids: A Time-Series Statistical Analysis Based on Integration of Direct Numerical Simulation (Dns) and Long Short-Term Memory Recurrent Neural Network (Lstm-rnn). J. Colloid Interface Sci. 582, 859–873. doi:10.1016/j.jcis.2020.08.052
Khadem, S. A., Bagnani, M., Mezzenga, R., and Rey, A. D. (2020). Relaxation Dynamics in Bio-Colloidal Cholesteric Liquid Crystals Confined to Cylindrical Geometry. Nat. Commun. 11, 4616–4710. doi:10.1038/s41467-020-18421-9
Kirkwood, J. E., and Fuller, G. G. (2009). Liquid Crystalline Collagen: a Self-Assembled Morphology for the Orientation of Mammalian Cells. Langmuir 25, 3200–3206. doi:10.1021/la803736x
Kondic, L., and Cummings, L. J. (2021). Instabilities of Nematic Liquid Crystal Films. Curr. Opin. Colloid & Interface Sci. 55, 101478. doi:10.1016/j.cocis.2021.101478
Lagerwall, J. P. F., Schütz, C., Salajkova, M., Noh, J., Hyun Park, J., Scalia, G., et al. (2014). Cellulose Nanocrystal-Based Materials: from Liquid Crystal Self-Assembly and Glass Formation to Multifunctional Thin Films. NPG Asia Mater 6, e80. doi:10.1038/am.2013.69
Lekkerkerker, H., and Vroege, G. (1993). Lyotropic Colloidal and Macromolecular Liquid Crystals. Philosophical Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 344, 419–440.
Lhuillier, D., and Rey, A. D. (2004). Liquid-crystalline Nematic Polymers Revisited. J. Newt. fluid Mech. 120, 85–92. doi:10.1016/j.jnnfm.2004.01.016
Liu, C., and Calderer, M. C. (2000). Liquid Crystal Flow: Dynamic and Static Configurations. SIAM J. Appl. Math. 60, 1925–1949. doi:10.1137/s0036139998336249
Marenduzzo, D., Orlandini, E., and Yeomans, J. M. (2004). Permeative Flows in Cholesteric Liquid Crystals. Phys. Rev. Lett. 92, 188301. doi:10.1103/physrevlett.92.188301
Marenduzzo, D., Orlandini, E., and Yeomans, J. M. (2006). Permeative Flows in Cholesterics: Shear and Poiseuille Flows. J. Chem. Phys. 124, 204906. doi:10.1063/1.2198816
Matsuyama, A. (2008). Morphology of Spinodal Decompositions in Liquid Crystal-Colloid Mixtures. J. Chem. Phys. 128, 224907. doi:10.1063/1.2936831
Mendil-Jakani, H., Baroni, P., and Noirez, L. (2009). Shear-induced Isotropic to Nematic Transition of Liquid-Crystal Polymers: Identification of Gap Thickness and Slipping Effects. Langmuir 25, 5248–5252. doi:10.1021/la803848h
Milette, J., Toader, V., Soulé, E. R., Lennox, R. B., Rey, A. D., and Reven, L. (2013). A Molecular and Thermodynamic View of the Assembly of Gold Nanoparticles in Nematic Liquid Crystal. Langmuir 29, 1258–1263. doi:10.1021/la304189n
Mitov, M. (2017). Cholesteric Liquid Crystals in Living Matter. Soft Matter 13, 4176–4209. doi:10.1039/c7sm00384f
Mottram, N. J., and Newton, C. J. P. (2014). Introduction to Q-Tensor Theory. arXiv preprint arXiv:1409.3542.
Murugesan, Y. K., and Rey, A. D. (2010a). Modeling Textural Processes during Self-Assembly of Plant-Based Chiral-Nematic Liquid Crystals. Polymers 2, 766–785. doi:10.3390/polym2040766
Murugesan, Y. K., and Rey, A. D. (2010b). Structure and Rheology of Fiber-Laden Membranes via Integration of Nematodynamics and Membranodynamics. J. Newt. fluid Mech. 165, 32–44. doi:10.1016/j.jnnfm.2009.08.009
Murugesan, Y. K., and Rey, A. D. (2010c). Thermodynamic Model of Structure and Shape in Rigid Polymer-Laden Membranes. Macromol. Theory Simul. 19, 113–126. doi:10.1002/mats.200900044
Murugesan, Y. K., Pasini, D., and Rey, A. D. (2011). Microfibril Organization Modes in Plant Cell Walls of Variable Curvature: a Model System for Two Dimensional Anisotropic Soft Matter. Soft Matter 7, 7078–7093. doi:10.1039/c1sm05363a
Murugesan, Y. K., Pasini, D., and Rey, A. D. (2013). Defect Textures in Polygonal Arrangements of Cylindrical Inclusions in Cholesteric Liquid Crystal Matrices. Soft Matter 9, 1054–1065. doi:10.1039/c2sm26365c
Murugesan, Y. K., Pasini, D., and Rey, A. D. (2015). Self-assembly Mechanisms in Plant Cell Wall Components. J. Renew. mater 3, 56–72. doi:10.7569/jrm.2014.634124
Murugesan, Y. K. (2012). Anisotropic Soft Matter Models for Plant Cell Walls. Ph.D. Thesis. Montreal, QC: McGill University.
Natarajan, B., and Gilman, J. W. (2018). Bioinspired Bouligand Cellulose Nanocrystal Composites: a Review of Mechanical Properties. Phil. Trans. R. Soc. A 376, 20170050. doi:10.1098/rsta.2017.0050
Neville, A. C., and Caveney, S. (1969). Scarabaeid Beetle Exocuticle as an Optical Analogue of Cholesteric Liquid Crystals. Biol. Rev. 44, 531–562. doi:10.1111/j.1469-185x.1969.tb00611.x
Neville, A. C. (1993). Biology of Fibrous Composites: Development beyond the Cell Membrane. New York, NY: Cambridge University Press.
Noroozi, N., Grecov, D., and Shafiei-Sabet, S. (2014). Estimation of Viscosity Coefficients and Rheological Functions of Nanocrystalline Cellulose Aqueous Suspensions. Liq. Cryst. 41, 56–66. doi:10.1080/02678292.2013.834081
Park, S. M., Bagnani, M., Yun, H. S., Han, M. J., Mezzenga, R., and Yoon, D. K. (2021). Hierarchically Fabricated Amyloid Fibers via Evaporation-Induced Self-Assembly. ACS Nano 15, 20261–20266. doi:10.1021/acsnano.1c08374
Phillips, P. M., Mei, N., Reven, L., and Rey, A. (2011a). Faceted Particles Embedded in a Nematic Liquid Crystal Matrix: Textures, Stability and Filament Formation. Soft Matter 7, 8592–8604. doi:10.1039/c1sm05870c
Phillips, P. M., Mei, N., Soulé, E. R., Reven, L., and Rey, A. D. (2011b). Textures in Polygonal Arrangements of Square Nanoparticles in Nematic Liquid Crystal Matrices. Langmuir 27, 13335–13341. doi:10.1021/la203226g
Pospisil, M. J., Noor, M. M., Amit, S. K., Neufeld, C. W., Saha, P., Davis, V. A., et al. (2020). Chiral Structure Formation during Casting of Cellulose Nanocrystalline Films. Langmuir 36, 4975–4984. doi:10.1021/acs.langmuir.0c00508
Priemel, T., Degtyar, E., Dean, M. N., and Harrington, M. J. (2017). Rapid Self-Assembly of Complex Biomolecular Architectures during Mussel Byssus Biofabrication. Nat. Commun. 8, 14539–14612. doi:10.1038/ncomms14539
Pujolle-Robic, C., Olmsted, P. D., and Noirez, L. (2002). Transient and Stationary Flow Behaviour of Side Chain Liquid-Crystalline Polymers: Evidence of a Shear-Induced Isotropic-To-Nematic Phase Transition. Europhys. Lett. 59, 364–369. doi:10.1209/epl/i2002-00203-9
Qiu, M., Feng, J. J., and Loudet, J. C. (2021). Phase-field Model for Elastocapillary Flows of Liquid Crystals. Phys. Rev. E 103, 022706. doi:10.1103/PhysRevE.103.022706
Reis, D., Roland, J., Mosiniak, M., Darzens, D., and Vian, B. (1992). The Sustained and Warped Helicoidal Pattern of a Xylan-Cellulose Composite: the Stony Endocarp Model. Protoplasma 166, 21–34. doi:10.1007/BF01320139
Rey, A. D., and Herrera-Valencia, E. E. (2012). Liquid Crystal Models of Biological Materials and Silk Spinning. Biopolymers 97, 374–396. doi:10.1002/bip.21723
Rey, A. D., and Murugesan, Y. K. (2011). Mechanical Model for Fiber-Laden Membranes. Contin. Mech. Thermodyn. 23, 45–61. doi:10.1007/s00161-010-0160-y
Rey, A. D., and Tsuji, T. (1998). Recent Advances in Theoretical Liquid Crystal Rheology. Macromol. Theory Simul. 7, 623–639. doi:10.1002/(sici)1521-3919(19981101)7:6<623:aid-mats623>3.0.co;2-e
Rey, A. D., Golmohammadi, M., and Herrera Valencia, E. E. (2011). A Model for Mesophase Wetting Thresholds of Sheets, Fibers and Fiber Bundles. Soft Matter 7, 5002–5009. doi:10.1039/c1sm05113j
Rey, A. D., Herrera-Valencia, E., and Murugesan, Y. K. (2014). Structure and Dynamics of Biological Liquid Crystals. Liq. Cryst. 41, 430–451. doi:10.1080/02678292.2013.845698
Rey-Bellet, P., Pasini, D., and Murugesan, Y. K. (2016). Parcours et mémoires. Biomimetics 36, 151–188. doi:10.3917/psys.163.0151
Rey, A. D. (1995a). Bifurcational Analysis of the Isotropic-Discotic Nematic Phase Transition in the Presence of Extensional Flow. Liq. Cryst. 19, 325–331. doi:10.1080/02678299508031988
Rey, A. D. (1995b). Bifurcational Analysis of the Isotropic-Nematic Phase Transition of Rigid Rod Polymers Subjected to Biaxial Stretching Flow. Macromol. Theory Simul. 4, 857–872. doi:10.1002/mats.1995.040040501
Rey, A. D. (1995c). Macroscopic Theory of Orientation Transitions in the Extensional Flow of Side-Chain Nematic Polymers. Rheola Acta 34, 119–131. doi:10.1007/bf00398431
Rey, A. D. (1996a). Flow Alignment in the Helix Uncoiling of Sheared Cholesteric Liquid Crystals. Phys. Rev. E 53, 4198–4201. doi:10.1103/physreve.53.4198
Rey, A. D. (1996b). Structural Transformations and Viscoelastic Response of Sheared Fingerprint Cholesteric Textures. J. Newt. fluid Mech. 64, 207–227. doi:10.1016/0377-0257(96)01434-6
Rey, A. D. (1997). Theory and Simulation of Gas Diffusion in Cholesteric Liquid Crystal Films. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A. Mol. Cryst. Liq. Cryst. 293, 87–109. doi:10.1080/10587259708042767
Rey, A. D. (1999). Marangoni Flow in Liquid Crystal Interfaces. J. Chem. Phys. 110, 9769–9770. doi:10.1063/1.478943
Rey, A. D. (2000a). Pitch Contributions to the Cholesteric−Isotropic Interfacial Tension. Macromolecules 33, 9468–9470. doi:10.1021/ma0001685
Rey, A. D. (2000b). Theory of Linear Viscoelasticity of Cholesteric Liquid Crystals. J. Rheology 44, 855–869. doi:10.1122/1.551112
Rey, A. D. (2002a). Capillary Thermodynamics of Nematic Polymer Interfaces. Macromol. Theory Simul. 11, 944–952. doi:10.1002/1521-3919(200211)11:9<944:aid-mats944>3.0.co;2-d
Rey, A. D. (2002b). Generalized Cholesteric Permeation Flows. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 65, 022701. doi:10.1103/PhysRevE.65.022701
Rey, A. D. (2002c). Simple Shear and Small Amplitude Oscillatory Rectilinear Shear Permeation Flows of Cholesteric Liquid Crystals. J. Rheology 46, 225–240. doi:10.1122/1.1428317
Rey, A. D. (2004a). Interfacial Thermodynamics of Polymeric Mesophases. Macromol. Theory Simul. 13, 686–696. doi:10.1002/mats.200400030
Rey, A. D. (2004b). Thermodynamics of Soft Anisotropic Interfaces. J. Chem. Phys. 120, 2010–2019. doi:10.1063/1.1635357
Rey, A. D. (2005). Mechanics of Soft-Solid-Liquid-Crystal Interfaces. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 72, 011706. doi:10.1103/PhysRevE.72.011706
Rey, A. D. (2006). Mechanical Model for Anisotropic Curved Interfaces with Applications to Surfactant-Laden Liquid−Liquid Crystal Interfaces. Langmuir 22, 219–228. doi:10.1021/la051974d
Rey, A. D. (2010). Liquid Crystal Models of Biological Materials and Processes. Soft Matter 6, 3402–3429. doi:10.1039/b921576j
Rofouie, P., Pasini, D., and Rey, A. D. (2014). Nanostructured Free Surfaces in Plant-Based Plywoods Driven by Chiral Capillarity. Colloids Interface Sci. Commun. 1, 23–26. doi:10.1016/j.colcom.2014.06.003
Rofouie, P., Pasini, D., and Rey, A. D. (2015). Tunable Nano-Wrinkling of Chiral Surfaces: Structure and Diffraction Optics. J. Chem. Phys. 143, 114701. doi:10.1063/1.4929337
Rofouie, P., Pasini, D., and Rey, A. D. (2017a). Multiple-Wavelength Surface Patterns in Models of Biological Chiral Liquid Crystal Membranes. Soft Matter 13, 541–545. doi:10.1039/c6sm02619b
Rofouie, P., Pasini, D., and Rey, A. D. (2017b). Morphology of Elastic Nematic Liquid Crystal Membranes. Soft Matter 13, 5366–5380. doi:10.1039/c7sm00977a
Selinger, J. V. (2016). Introduction to the Theory of Soft Matter: From Ideal Gases to Liquid Crystals. Cham, Switzerland: Springer.
Shams, A., Yao, X., Park, J. O., Srinivasarao, M., and Rey, A. D. (2015). Disclination Elastica Model of Loop Collision and Growth in Confined Nematic Liquid Crystals. Soft Matter 11, 5455–5464. doi:10.1039/c5sm00708a
Sharma, V., Crne, M., Park, J. O., and Srinivasarao, M. (2014). Bouligand Structures Underlie Circularly Polarized Iridescence of Scarab Beetles: A Closer View. Mater. Today Proc. 1, 161–171. doi:10.1016/j.matpr.2014.09.019
Sigaki, H. Y. D., de Souza, R. F., de Souza, R. T., Zola, R. S., and Ribeiro, H. V. (2019). Estimating Physical Properties from Liquid Crystal Textures via Machine Learning and Complexity-Entropy Methods. Phys. Rev. E 99, 013311. doi:10.1103/PhysRevE.99.013311
Sigaki, H. Y. D., Lenzi, E. K., Zola, R. S., Perc, M., and Ribeiro, H. V. (2020). Learning Physical Properties of Liquid Crystals with Deep Convolutional Neural Networks. Sci. Rep. 10, 7664–7710. doi:10.1038/s41598-020-63662-9
Singh, A. P., and Rey, A. D. (1998). Microstructure Constitutive Equation for Discotic Nematic Liquid Crystalline Materials. Rheol. acta 37, 30–45. doi:10.1007/s003970050088
Soule, E. R., and Rey, A. D. (2012). Modelling Complex Liquid Crystal Mixtures: from Polymer Dispersed Mesophase to Nematic Nanocolloids. Mol. Simul. 38, 735–750. doi:10.1080/08927022.2012.669478
Soulé, E. R., and Rey, A. D. (2013). Oscillating Fronts Produced by Spinodal Decomposition of Metastable Ordered Phases. Soft Matter 9, 10335–10342. doi:10.1039/c3sm51669e
Soule, E. R., and Rey, A. D. (2019). Chapter 2. Phase Diagrams, Phase Separation Mechanisms and Morphologies in Liquid Crystalline Materials: Principles and Theoretical Foundations. Polymer-modified Liq. Cryst. 8, 19–36. doi:10.1039/9781788013321-00019
Srinivasarao, M. (2021). Spontaneous Emergence of Chirality. Liq. Cryst., 311–346. doi:10.1002/9781119850809.ch5
Suksangpanya, N., Yaraghi, N. A., Kisailus, D., and Zavattieri, P. (2017). Twisting Cracks in Bouligand Structures. J. Mech. Behav. Biomed. Mater 76, 38–57. doi:10.1016/j.jmbbm.2017.06.010
Terris, B. D., Twieg, R. J., Nguyen, C., Sigaud, G., and Nguyen, H. T. (1992). Force Microscopy of Chiral Liquid-Crystal Surfaces. Europhys. Lett. 19, 85–90. doi:10.1209/0295-5075/19/2/005
Tsuji, T., and Rey, A. D. (1997). Effect of Long Range Order on Sheared Liquid Crystalline Materials Part 1: Compatibility between Tumbling Behavior and Fixed Anchoring. J. Newt. fluid Mech. 73, 127–152. doi:10.1016/s0377-0257(97)00037-2
Venhaus, D. G., Conatser, K. S., and Green, M. J. (2013). Dynamics of Chiral Liquid Crystals under Applied Shear. Liq. Cryst. 40, 846–853. doi:10.1080/02678292.2013.779037
Vignolini, S., Moyroud, E., Glover, B. J., and Steiner, U. (2013). Analysing Photonic Structures in Plants. J. R. Soc. Interface. 10, 20130394. doi:10.1098/rsif.2013.0394
Wang, Z., Rofouie, P., and Rey, A. (2019). Surface Anchoring Effects on the Formation of Two-Wavelength Surface Patterns in Chiral Liquid Crystals. Crystals 9, 190. doi:10.3390/cryst9040190
Wang, Z., Servio, P., and Rey, A. D. (2020a). Mechanogeometry of Nanowrinkling in Cholesteric Liquid Crystal Surfaces. Phys. Rev. E 101, 062705. doi:10.1103/PhysRevE.101.062705
Wang, Z., Servio, P., and Rey, A. (2020b). Rate of Entropy Production in Evolving Interfaces and Membranes under Astigmatic Kinematics: Shape Evolution in Geometric-Dissipation Landscapes. Entropy 22, 909. doi:10.3390/e22090909
Wang, Z., Servio, P., and Rey, A. (2021). Biaxial Nanowrinkling in Cholesteric Surfaces: Egg Carton Surfaces through Chiral Anchoring. Colloid Interface Sci. Commun. 41, 100372. doi:10.1016/j.colcom.2021.100372
Wang, Q. (2021). “Generalized Onsager Principle and it Applications,” in Frontiers and Progress of Current Soft Matter Research (Springer), 101–132. doi:10.1007/978-981-15-9297-3_3
Wincure, B., and Rey, A. D. (2007). Growth and Structure of Nematic Spherulites under Shallow Thermal Quenches. Contin. Mech. Thermodyn. 19, 37–58. doi:10.1007/s00161-007-0043-z
Xu, K., Forest, M. G., Gregory Forest, M., and Yang, X. (2011). Shearing the I-N Phase Transition of Liquid Crystalline Polymers: Long-Time Memory of Defect Initial Data. Discrete & Continuous Dyn. Systems-B 15, 457–473. doi:10.3934/dcdsb.2011.15.457
Yang, X., Feng, J. J., Liu, C., and Shen, J. (2006). Numerical Simulations of Jet Pinching-Off and Drop Formation Using an Energetic Variational Phase-Field Method. J. Comput. Phys. 218, 417–428. doi:10.1016/j.jcp.2006.02.021
Yang, X., Forest, M. G., Mullins, W., and Wang, Q. (2009). Quench Sensitivity to Defects and Shear Banding in Nematic Polymer Film Flows. J. Newt. fluid Mech. 159, 115–129. doi:10.1016/j.jnnfm.2009.02.005
Yang, X., Gregory Forest, M., Li, H., Liu, C., Shen, J., Wang, Q., et al. (2013). Modeling and Simulations of Drop Pinch-Off from Liquid Crystal Filaments and the Leaky Liquid Crystal Faucet Immersed in Viscous Fluids. J. Comput. Phys. 236, 1–14. doi:10.1016/j.jcp.2012.10.042
Yang, X., Li, J., Forest, M., and Wang, Q. (2016). Hydrodynamic Theories for Flows of Active Liquid Crystals and the Generalized Onsager Principle. Entropy 18, 202. doi:10.3390/e18060202
Yang, R., Zaheri, A., Gao, W., Hayashi, C., and Espinosa, H. D. (2017). Afm Identification of Beetle Exocuticle: Bouligand Structure and Nanofiber Anisotropic Elastic Properties. Adv. Funct. Mat. 27, 1603993. doi:10.1002/adfm.201603993
Yue, P., Feng, J. J., Liu, C., and Shen, J. (2005). Interfacial Forces and Marangoni Flow on a Nematic Drop Retracting in an Isotropic Fluid. J. colloid interface Sci. 290, 281–288. doi:10.1016/j.jcis.2005.04.018
Zhang, R., Mozaffari, A., and de Pablo, J. J. (2021). Autonomous Materials Systems from Active Liquid Crystals. Nat. Rev. Mater 6, 437–453. doi:10.1038/s41578-020-00272-x
Zhao, J., Yang, X., Shen, J., and Wang, Q. (2016). A Decoupled Energy Stable Scheme for a Hydrodynamic Phase-Field Model of Mixtures of Nematic Liquid Crystals and Viscous Fluids. J. Comput. Phys. 305, 539–556. doi:10.1016/j.jcp.2015.09.044
Zhao, J., Yang, X., Gong, Y., and Wang, Q. (2017). A Novel Linear Second Order Unconditionally Energy Stable Scheme for a Hydrodynamic Q-Tensor Model of Liquid Crystals. Comput. Methods Appl. Mech. Eng. 318, 803–825. doi:10.1016/j.cma.2017.01.031
Zhu, Y.-M., and Farrell, P. A. (2002). A Vector Grouping Algorithm for Liquid Crystal Tensor Field Visualization. Liq. Cryst. 29, 1259–1264. doi:10.1080/713935624
Keywords: liquid crystal, self-assembly, self-organization, pattern formation, nematic, paranematic, cholesteric
Citation: Wang Z, Servio P and Rey AD (2022) Structure and Pattern Formation in Biological Liquid Crystals: Insights From Theory and Simulation of Self-Assembly and Self-Organization. Front. Soft. Matter 2:904069. doi: 10.3389/frsfm.2022.904069
Received: 25 March 2022; Accepted: 02 May 2022;
Published: 02 June 2022.
Edited by:
Tommy Nylander, Lund University, SwedenReviewed by:
Yuri Gerelli, Marche Polytechnic University, ItalyYoungki Kim, Pohang University of Science and Technology, South Korea
Copyright © 2022 Wang, Servio and Rey. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alejandro D. Rey, YWxlamFuZHJvLnJleUBtY2dpbGwuY2E=
 Ziheng Wang1,2
Ziheng Wang1,2 Alejandro D. Rey
Alejandro D. Rey