A perspective on the Langmuir adsorption model applied to molecular liquid crystals containing ions and nanoparticles

Electrical properties of molecular liquid crystals doped with nanomaterials have been extensively studied over the past two decades. In general, nanoparticles in liquid crystals can play a dual role acting as either ion capturing agents or ion generating objects. An interplay between ions and nanomaterials in liquid crystals can result in a great variety of nontrivial ionic effects. This perspective discusses the Langmuir adsorption model applied to describe ionic phenomena in molecular liquid crystals doped with nanoparticles. The applicability and limitations of this model are emphasized. Within a range of its applicability, the Langmuir adsorption model can be used to obtain a wealth of information about nanoparticle-induced ionic effects in molecular liquid crystals. In addition, this model also offers important improvements to standard experimental procedures for evaluation of electrical properties of advanced liquid crystal materials.

Introduction

The future progress of liquid crystal science and technology relies on the development of advanced mesogenic materials exhibiting multifunctional properties. A very promising approach to produce such materials involves merging liquid crystals and nanotechnology (Lagerwall and Scalia, 2016; Dierking, 2019; Lee and Kumar, 2021). Nanomaterials dispersed in liquid crystals can significantly modify the properties of a liquid crystal host (Lagerwall and Scalia, 2016; Dierking, 2019; Lee and Kumar, 2021). Very often a combination of liquid crystals and nanoparticles leads to new functionalities of the composite materials thus opening a door to new and exciting applications (Lagerwall and Scalia, 2016; Dierking, 2019; Lee and Kumar, 2021). This exciting possibility to produce advanced liquid crystal materials was a driving force behind very active research into the properties of liquid crystal materials doped with nanoparticles. Recently published reviews provide detailed discussion of the properties of liquid crystals doped with carbon-based (Yadav and Singh, 2016; Kumar et al., 2022a), semiconductor and dielectric (Mirzaei et al., 2012; Prakash et al., 2020; Kumar et al., 2022b), metal (Chen et al., 2020; Gonçalves et al., 2021), magnetic (Mertelj and Lisjak, 2017), and ferroelectric (Garbovskiy and Glushchenko, 2017) nanoobjects.

An increasing body of literature (Mirzaei et al., 2012; Lagerwall and Scalia, 2016; Yadav and Singh, 2016; Garbovskiy and Glushchenko, 2017; Mertelj and Lisjak, 2017; Dierking, 2019; Chen et al., 2020; Prakash et al., 2020; Gonçalves et al., 2021; Lee and Kumar, 2021; Kumar et al., 2022a; Kumar et al., 2022b) and references therein] indicates a high promise of liquid crystals doped with nanomaterials as novel materials for existing and emerging applications including liquid crystal displays (Wang and Lin, 2021; Xiong et al., 2021), tunable waveguides (d’Alessandro and Asquini, 2021), dynamic lenses (Lin et al., 2017), diffractive elements (Morris et al., 2021), spatial light modulators (Otón et al., 2018), reconfigurable microwave (Camley et al., 2018; Jakoby et al., 2020) and plasmonic devices (Jeng, 2020), to name a few. Because the aforementioned devices are driven by electric fields, an understanding of electrical properties of liquid crystals doped with nanoparticles is critical to assessing their suitability for a given application. In fact, ionic conductivity of molecular liquid crystals containing nanoobjects can limit possible applications of such materials because of the electric field screening and Joule heating effects caused by ions (Neyts and Beunis, 2014; Garbovskiy, 2021). For example, in the case of liquid crystal displays the electric field screening effect can lead to image sticking, image flickering, and overall slow electro-optical response whereas the Joule heating effect can result in excessive power consumption (Neyts and Beunis, 2014; Garbovskiy, 2021).

According to numerous experimental reports, nanoparticles dispersed in molecular liquid crystals can affect their electrical properties in different ways [(Garbovskiy and Glushchenko, 2015; Garbovskiy, 2021) and references therein]. Nanodopants can capture ions thus reducing their volume concentration and leading to a decrease in the electrical conductivity. There are also papers reporting the ion-releasing behavior of nanoparticles in molecular liquid crystals [(Garbovskiy and Glushchenko, 2015; Garbovskiy, 2021) and references therein]. In other words, nanomaterials mixed with liquid crystals increase the total concentration of mobile ions and electrical conductivity. This dual, ion-capturing and ion-releasing, role of nanoparticles in molecular liquid crystals calls for a quantitative explanation.

Recently, an elementary model utilizing the Langmuir formalism and the possibility of ionic contamination of nanoparticles was proposed to explain nanoparticle-induced ionic effects in molecular liquid crystals (Garbovskiy, 2021). The proposed model was successfully applied to available experimental data reviewed in papers (Garbovskiy, 2018a; Garbovskiy, 2021). One of the objectives of this perspective is the discussion of this model and its capabilities to predict possible outcomes of experiments with a hope that some readers could use it in their research.

Another objective of this paper is related to the applicability of the Langmuir adsorption model. Even though agreement between the model and experiments was more than satisfactory, its justification is still not complete. The Langmuir adsorption model was developed for neutral particles and its applicability to electrically charged particles is not obvious and requires explanation. Some arguments in favor of its applicability to describe the adsorption of ionic species in molecular liquid crystals can be found in publications (Garbovskiy, 2018a; Garbovskiy, 2021). In this paper, an additional strong argument in support of the Langmuir adsorption model applied to molecular liquid crystals containing ions and nanoparticles is given.

The Langmuir adsorption model and ionic contamination of nanoparticles

In general, nanoparticles prior to dispersing them in molecular liquid crystals can be contaminated with ions. To account for this possibility, the ionic contamination is quantified by means of the contamination factor ${\nu }_{NP}$ defined as a ratio of the number of adsorption sites on the surface of nanoparticles occupied by ionic contaminants to the total number of adsorption sites (Garbovskiy, 2016). To simplify the discussion, consider ions of one type. In this case, once nanoparticles are dispersed in liquid crystals, both ion-releasing and ion-capturing processes take place according to Eq. 1:

$\frac{dn}{dt}=-k_a^{NP}{n}_{NP}{A}_{NP}{\sigma }_S^{NP}n\left(1-{\Theta }_{NP}\right)+k_d^{NP}{n}_{NP}{A}_{NP}{\sigma }_S^{NP}{\Theta }_{NP}(1)$

where $n$ is the volume concentration of ions; $t$ is time; $k_a^{NP}$ is the adsorption rate constant quantifying the ion-capturing process; $k_d^{NP}$ is the desorption rate constant describing the ion-releasing process; $n_{NP}$ is the volume concentration of nanoparticles; $A_{NP}$ is the surface area of one nanoparticle; ${\sigma }_S^{NP}$ is the surface density of all adsorption sites on the surface of one nanoparticle; ${\Theta }_{NP}$ is the fractional surface coverage of nanoparticles.

The conservation law of the total number of ions is given by Equation 2:

$n_0+n_{NP}{A}_{NP}{\sigma }_S^{NP}{\nu }_{NP}=n+n_{NP}{A}_{NP}{\sigma }_S^{NP}{\Theta }_{NP}(2)$

where $n_0$ is the initial concentration of ions in liquid crystals, and ${\nu }_{NP}$ is already defined contamination factor of nanoparticles.

If pure (without ionic contamination) nanoparticles are dispersed in molecular liquid crystals, the only possible outcome is the ion-capturing regime (dashed-dotted curve) shown in Figure 1A. In this case the concentration of mobile ions gradually decreases as more nanoparticles are added to liquid crystals. The ionic contamination of nanoparticles results in non-trivial ionic effects. Depending on interplay between parameters describing the system, three regimes are possible, namely, the ion capturing regime (solid curve, Figure 1A), ion releasing regime (dashed curve, Figure 1A), and no change regime (dotted curve, Figure 1A) (Garbovskiy, 2018b). It should be noted that the ionic contamination of nanoparticles is a key factor enabling the possibility of different regimes shown in Figure 1.

FIGURE 1

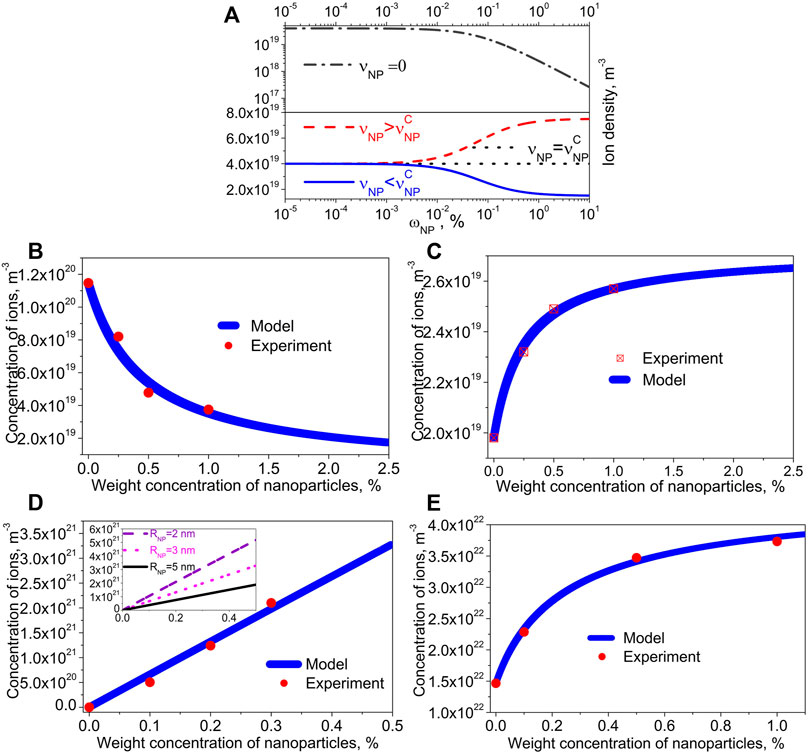
FIGURE 1. (A) The dependence of the bulk ion density on the weight concentration of nanoparticles ${\omega }_{NP}$. (B) and (C) The dependence of the concentration of ions in liquid crystals doped with Ti O ₂ nanoparticles on the weight concentration of nanodopants. Experimental datapoints are from (Shcherbinin and Konshina, 2017a). (D) The concentration of ‘slow’ ions in liquid crystals doped with CdSe/ZnS quantum dots as a function of the weight concentration of nanodopants. Experimental datapoints are from (Shcherbinin and Konshina, 2017b). (E) The dependence of the concentration of ions in liquid crystals doped with Cu₇PS₆ nanoparticles on the weight concentration of nanodopants. Experimental datapoints are from (Kovalchuk et al., 2017). Reproduced from (Garbovskiy, 2018b), under the Creative Commons Attribution License.

Within the framework of the proposed elementary model, the ionic contamination of nanoparticles is quantified by means of the contamination factor ${\nu }_{NP}$. If its value is greater than a critical value ${\nu }_{\mathrm{N}\mathrm{P}}^C$ (${\nu }_{NP}>{\nu }_{\mathrm{N}\mathrm{P}}^C$), ions carried by nanoparticles are released into the liquid crystal bulk thus leading to the ion releasing regime. As a result, an increase in the concentration of nanoparticles ${\omega }_{NP}$ causes a corresponding increase in the concentration of mobile ions until a saturation level is reached (dashed curve, Figure 1A). If ${\nu }_{NP}<{\nu }_{\mathrm{N}\mathrm{P}}^C$, nanoparticles can capture mobile ions leading to the ion-capturing regime characterized by decrease in the concentration of ions as a function of ${\omega }_{NP}$ (solid curve, Figure 1A). If ${\nu }_{NP}={\nu }_{\mathrm{N}\mathrm{P}}^C$, the number of ions trapped by nanoparticles is equal to the number of ions released into liquid crystals (no change regime, dotted curve, Figure 1A). The critical contamination factor is defined as ${\nu }_{\mathrm{N}\mathrm{P}}^C=n_0{K}_{NP}/\left(1+n_0{K}_{NP}\right)$, where $K_{NP}=\raisebox{1ex}{$k_a^{NP}$}\!\left/ \!\raisebox{-1ex}{$k_d^{NP}$}\right.$ (Garbovskiy, 2016). Because it depends on the initial concentration of ions in liquid crystals $n_0$, contaminated nanomaterials dispersed in low resistivity liquid crystals can lead to the ion capturing effect (Figure 1B,) whereas the same nanomaterials mixed with high resistivity liquid crystals can result in the ion releasing effect (Figure 1C). Experimental results shown in Figures 1B,C were reported for $Ti{O}_2$ nanoparticles dispersed in nematic liquid crystals ZkK1282 (Shcherbinin and Konshina, 2017a). Additional examples of ion releasing effects observed in nematic liquid crystals ZhK1289 doped with CdSe/ZnS quantum dots (Shcherbinin and Konshina, 2017b) and nematic 6CB doped with superionic nanoparticles Cu₇PS₆ (Kovalchuk et al., 2017) are shown in Figures 1D,E.

An elementary model represented by Eqs 1, 2 was able to describe a wide range of existing experimental reports. A detailed analysis of the reported experimental results can be found in recent reviews (Garbovskiy, 2018a; Garbovskiy, 2021). If needed, this model can also be easily generalized to account for the presence of ions of several types (Garbovskiy, 2017a). By considering temperature dependence of the ion releasing/ion capturing rate constants, temperature-induced ionic effects in liquid crystals doped with nanoparticles can be analysed (Garbovskiy, 2017b; Garbovskiy, 2017c).

In the case of relatively thin cells interactions between ions and substrates of the liquid crystal cell become very important and should not be ignored. The combined effect of nanoparticles and alignment layers on the concentration of ions can be treated in a similar way, as was discussed in recent papers (Garbovskiy, 2017a; Garbovskiy, 2017d). As a result, both steady-state and time-dependent ionic effects in cells filled with molecular liquid crystals doped with nanoparticles can be described (Garbovskiy, 2018c).

Discussion: Applicability of the model and its limits

An agreement between a rather elementary model (1), (2) and existing experimental results calls for possible explanations. At a first glance, Eqs 1, 2 do not agree with a classical model of colloidal particles in electrolyte. A surface of colloidal particle immersed in electrolyte gets charged due to specific ion adsorption and/or dissociation of the surface groups (Israelachvili, 1992). The immobilized surface charges attract ions of the opposite sign resulting in the formation of electric double layers. In the case of multiple charges adsorbed on a surface of colloidal particle, Eqs 1, 2 should be modified by considering the dependence of the ion capturing/ion releasing rate constants on the surface potential. Because the surface potential depends on the concentration of ions, it should be found by solving the Poisson-Boltzmann equation (Barbero and Evangelista, 2006; Batalioto et al., 2017). This approach is perfectly valid assuming sufficient number of ions is available for the formation of electric double layer. Surprisingly, this assumption is violated in the case of molecular liquid crystals doped with nanoparticles as explained below.

Molecular liquid crystals are characterized by a relatively small concentration of mobile ions (10¹⁶–10²¹ m⁻³) (Neyts and Beunis, 2014; Garbovskiy, 2021). As a result, under certain conditions the concentration of colloidal particles can become comparable to the concentration of ions in liquid crystals. This effect becomes very important if the size of colloidal particles gets smaller as shown in Figure 2A. This figure shows a number of ions available per one colloidal particle ($N_{ION}/N_{NP}$) as a function of the radius $R_{NP}$ of a spherical particle. The weight concentration of particles is set to 0.01 and a low resistivity liquid crystal is assumed (the volume concentration of ions is 10²⁰ m⁻³). In the case of microparticles thousands of ions are available per single particle (Figure 2A). This region of particle sizes corresponds to a classical model of colloidal particle in electrolyte. However, as the radius of particles gets smaller, the number of ions available per single particle decreases, and, at certain size, can become equal to or even smaller than 1. This transition from a region with abundant number of ions (>>1) to a region with insufficient number if ions (≤1) per single particle takes place when we approach the nanoscopic scale. In the case shown in Figure 2A once the radius of particles becomes smaller than 20 nm, the number of ions per one nanoparticle becomes smaller than 1. As a result, in this region of particle sizes (essentially, nanoscale domain) ion-capturing and ion-releasing processes can be described by applying the Langmuir adsorption model given by Eqs 1, 2.

FIGURE 2

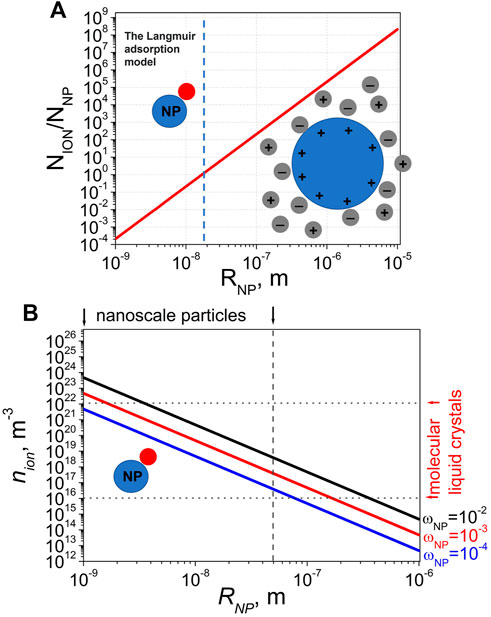
FIGURE 2. (A) The number of ions per one colloidal particle in molecular liquid crystals as a function of the particle radius. (B) The concentration of mobile ions in molecular liquid crystals as a function of the particle radius assuming a one ion per one colloidal particle condition ($\frac{N_{ION}}{N_{NP}}=1$). This concentration is computed for three values of weight concentration of nanoparticles (10⁻²; 10⁻³; 10⁻⁴).

The condition $\frac{N_{ION}}{N_{NP}}=1$ can be used to define an approximate boundary between the region of particle sizes corresponding to the Langmuir adsorption model and the classical model of colloidal particle region (Figure 2B). As can be seen from Figure 2B, typical molecular liquid crystals doped with nanoscale objects belong to the Langmuir adsorption model region. As a result, the proposed Eqs 1, 2 can be reasonably applied to analyse existing experimental data and predict possible outcomes of future experiments. It should be noted that additional arguments supporting the Langmuir adsorption model were also given in papers (Garbovskiy, 2016; Garbovskiy, 2017a).

Conclusion

Nanoparticles in molecular liquid crystals play a dual role. They can capture ions leading to reduced values of the direct current electrical conductivity. Nanomaterials can also behave as a new source of ion generation in liquid crystals. In any practical situation, the realization of the ion capturing or ion releasing effect depends on an interplay between physical parameters characterizing materials under test including initial concentration of ions in liquid crystals, ionic contamination of nanoparticles, and temperature-dependent ion capturing and ion releasing rate constants.

Surprisingly, the Langmuir adsorption model can be applied to analyse nanoparticle-induced ionic effects in molecular liquid crystals. A relatively low concentration of mobile ions in molecular liquid crystals combined with a small (nanoscale) size of dispersed particles can result in situations when the number of ions available per one nanoparticle is smaller than 1 (Figure 2). For given concentrations of mobile ions and nanoparticles in molecular liquid crystals the size of dispersed colloidal particles determines the transition to the Langmuir adsorption model (Figure 2). Such transition occurs if the number of ions available per one nanoparticle is simply not sufficient for the formation of electric double layer. This argument can explain a good agreement between the Langmuir adsorption model and numerous experimental results (Garbovskiy, 2021). Figure 2 also calls for a need to develop an improved model capable of describing the transition region between the classical model of colloidal particle in electrolyte and the Langmuir adsorption model. It should be stressed that the electric double layer is a key concept of colloidal science and electrochemistry (Israelachvili, 1992; Wu, 2022). It is also of great relevance to liquid crystals (Kleman and Lavrentovich, 2003). For example, the properties and morphology of liquid crystal droplets in an aqueous medium strongly depend on the formation of electric double layers (Dubtsov et al., 2018). Molecular liquid crystals doped with nanoparticles could become a playground for exploring alterations in the electric double layer structure thus opening doors to new applications.

The Langmuir adsorption model has important practical and scientific implications. A proper analysis of nanoparticle-induced ionic effects in molecular liquid crystals can be done only if interactions between ions and substrates of a liquid crystal cell are taken into consideration. As a rule, substrate-induced ionic effects are very strong if thin cells are used in experiments whereas the use of thicker cells (assuming the alignment quality of liquid crystal is not altered) allows to reduce or even eliminate the ionic effects caused by the substrates. An interplay between ionic effects caused by nanoparticles and substrates can result in non-trivial dependences of the electrical conductivity on the concentration of nanodopants and on the cell thickness. To differentiate between such ionic effects, existing experimental procedures should be improved. In the simplest case, for a given concentration of nanoparticles in molecular liquid crystals, measuring cells of several cell thickness can be utilized. A description of an experimental realization of this approach can be found in recent publication (Kovalchuk et al., 2022).

Future experimental, theoretical, and computational research will definitely improve our understanding of ionic effects in molecular liquid crystals doped with nanomaterials thus making possible to achieve a full control over ionic processes in such materials.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YG conceived the idea, analyzed the data, and wrote the paper.

Funding

This research was supported by the 2022–2023 CSU—AAUP Faculty Research Grant and Faculty Development Grant.

Acknowledgments

The author would like to acknowledge the support provided by the School of Engineering, Science and Technology at Central Connecticut State University.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barbero, G., and Evangelista, L. R. (2006). Adsorption phenomena and anchoring energy in nematic liquid crystals, 48. Boca Raton, FL, USA: Taylor & Francis.

Google Scholar

Batalioto, F., Figueiredo Neto, A. M., and Barbero, G. (2017). Ion trapping on silica nanoparticles: Effect on the ζ-potential. J. Appl. Phys. 122 (16), 164303. doi:10.1063/1.4994639

CrossRef Full Text | Google Scholar

Camley, R., Celinski, Z., Garbovskiy, Y., and Glushchenko, A. (2018). Liquid crystals for signal processing applications in the microwave and millimeter wave frequency ranges. Liq. Cryst. Rev. 6 (1), 17–52. doi:10.1080/21680396.2018.1509385

CrossRef Full Text | Google Scholar

Chen, Y., Ai, B., and Wong, Z. J. (2020). Soft optical metamaterials. Nano Converg. 7, 18–17. doi:10.1186/s40580-020-00226-7

PubMed Abstract | CrossRef Full Text | Google Scholar

d’Alessandro, A., and Asquini, R. (2021). Light propagation in confined nematic liquid crystals and device applications. Appl. Sci. (Basel). 11, 8713. doi:10.3390/app11188713

CrossRef Full Text | Google Scholar

Dierking, I. (2019). From colloids in liquid crystals to colloidal liquid crystals. Liq. Cryst. 46, 2057–2074. doi:10.1080/02678292.2019.1641755

CrossRef Full Text | Google Scholar

Dubtsov, A. V., Pasechnik, S. V., Shmeliova, D. V., Saidgaziev, A. S., Gongadze, E., Iglic, A., et al. (2018). Liquid crystalline droplets in aqueous environments: Electrostatic effects. Soft Matter 14, 9619–9630. doi:10.1039/c8sm01529e

PubMed Abstract | CrossRef Full Text | Google Scholar

Garbovskiy, Y., and Glushchenko, I. (2015). Nano-objects and ions in liquid crystals: Ion trapping effect and related phenomena. Crystals 5, 501–533. doi:10.3390/cryst5040501

CrossRef Full Text | Google Scholar

Garbovskiy, Y. (2017c). Ions in liquid crystals doped with nanoparticles: Conventional and counterintuitive temperature effects. Liq. Cryst. 44, 1402–1408. doi:10.1080/02678292.2017.1280856

CrossRef Full Text | Google Scholar

Garbovskiy, Y. (2018a). Nanomaterials in liquid crystals as ion-generating and ion-capturing objects. Crystals 8, 264. doi:10.3390/cryst8070264

CrossRef Full Text | Google Scholar

Garbovskiy, Y. (2017b). Nanoparticle enabled thermal control of ions in liquid crystals. Liq. Cryst. 44, 948–955. doi:10.1080/02678292.2016.1254827

CrossRef Full Text | Google Scholar

Garbovskiy, Y. (2018b). Nanoparticle—Enabled ion trapping and ion generation in liquid crystals. Adv. Condens. Matter Phys. 2018, 1–8. doi:10.1155/2018/8914891

CrossRef Full Text | Google Scholar

Garbovskiy, Y. (2016). Switching between purification and contamination regimes governed by the ionic purity of nanoparticles dispersed in liquid crystals. Appl. Phys. Lett. 108, 121104. doi:10.1063/1.4944779

CrossRef Full Text | Google Scholar

Garbovskiy, Y. (2021). Conventional and unconventional ionic phenomena in tunable soft materials made of liquid crystals and nanoparticles. Nano Ex. 2, 012004. doi:10.1088/2632-959x/abe652

CrossRef Full Text | Google Scholar

Garbovskiy, Y., and Glushchenko, A. (2017). Ferroelectric nanoparticles in liquid crystals: Recent progress and current challenges. Nanomaterials 7, 361. doi:10.3390/nano7110361

PubMed Abstract | CrossRef Full Text | Google Scholar

Garbovskiy, Y. (2017d). Ion capturing/ion releasing films and nanoparticles in liquid crystal devices. Appl. Phys. Lett. 110, 041103. doi:10.1063/1.4974453

CrossRef Full Text | Google Scholar

Garbovskiy, Y. (2017a). Ions and size effects in nanoparticle/liquid crystal colloids sandwiched between two substrates. The case of two types of fully ionized species. Chem. Phys. Lett. 679, 77–85. doi:10.1016/j.cplett.2017.04.075

CrossRef Full Text | Google Scholar

Garbovskiy, Y. (2018c). Kinetics of ion-capturing/ion-releasing processes in liquid crystal devices utilizing contaminated nanoparticles and alignment films. Nanomaterials 8 (2), 59. doi:10.3390/nano8020059

PubMed Abstract | CrossRef Full Text | Google Scholar

Gonçalves, D. P. N., Prévôt, M. E., Üstünel, Ş., Ogolla, T., Nemati, A., Shadpour, S., et al. (2021). Recent progress at the interface between nanomaterial chirality and liquid crystals. Liq. Cryst. Rev. 9 (1), 1–34. doi:10.1080/21680396.2021.1930596

CrossRef Full Text | Google Scholar

Israelachvili, J. (1992). Intermolecular and surface forces. 2nd ed. New York: Academic Press, 450.

Google Scholar

Jakoby, R., Gaebler, A., and Weickhmann, C. (2020). Microwave liquid crystal enabling technology for electronically steerable antennas in SATCOM and 5G millimeter-wave systems. Crystals 10, 514. doi:10.3390/cryst10060514

CrossRef Full Text | Google Scholar

Jeng, S. C. (2020). Applications of Tamm plasmon-liquid crystal devices. Liq. Cryst. 47, 1223–1231. doi:10.1080/02678292.2020.1733114

CrossRef Full Text | Google Scholar

Kleman, M., and Lavrentovich, O. D. (2003). Soft matter physics: An introduction (partially ordered systems). New York: Springer.

Google Scholar

Kovalchuk, O. V., Studenyak, I. P., Izai, V. Y., Rubak, A. S., Pogodin, O. I., Kopcansky, P., et al. (2017). Saturation effect for dependence of the electrical conductivity of planar oriented nematic liquid crystal 6CB on the concentration of Cu7PS6 nanoparticles. Semicond. Phys. Quantum Electron. Optoelectron. 20, 437–441. doi:10.15407/spqeo20.04.437

CrossRef Full Text | Google Scholar

Kovalchuk, O. V., Kovalchuk, T. M., Tomašovičová, N., Timko, M., Zakutanska, K., Miakota, D., et al. (2022). Dielectric and electrical properties of nematic liquid crystals 6CB doped with iron oxide nanoparticles. The combined effect of nanodopant concentration and cell thickness. J. Mol. Liq. 366 (15), 120305. doi:10.1016/j.molliq.2022.120305

CrossRef Full Text | Google Scholar

Kumar, A., Meena, H., Prakash, J., Wang, L., and Singh, G.Priyam (2022b). Recent advances on semiconducting nanomaterials–ferroelectric liquid crystals nanocomposites. J. Phys. Condens. Matter 34, 013004. doi:10.1088/1361-648x/ac2ace

CrossRef Full Text | Google Scholar

Kumar, A., Pratap Singh, D., and Singh, G. (2022a). Recent progress and future perspectives on carbon-nanomaterial-dispersed liquid crystal composites. J. Phys. D. Appl. Phys. 55, 083002. doi:10.1088/1361-6463/ac2ced

CrossRef Full Text | Google Scholar

J. P. F. Lagerwall, and G. Scalia (Editors) (2016). Liquid crystals with nano and microparticles (Singapore: World Scientific), 2.

Google Scholar

Lee, W., and Kumar, S. (2021). Unconventional liquid crystals and their applications. Berlin, Boston: De Gruyter.

Google Scholar

Lin, Y. H., Wang, Y. J., and Reshetnyak, V. (2017). Liquid crystal lenses with tunable focal length. Liq. Cryst. Rev. 5 (2), 111–143. doi:10.1080/21680396.2018.1440256

CrossRef Full Text | Google Scholar

Mertelj, A., and Lisjak, D. (2017). Ferromagnetic nematic liquid crystals. Liq. Cryst. Rev. 5, 51–33. doi:10.1080/21680396.2017.1304835

CrossRef Full Text | Google Scholar

Mirzaei, J., Reznikov, M., and Hegmann, T. (2012). Quantum dots as liquid crystal dopants. J. Mat. Chem. 22223, 22350–22365. doi:10.1039/c2jm33274d

CrossRef Full Text | Google Scholar

Morris, R., Jones, C., and Nagaraj, M. (2021). Liquid crystal devices for beam steering applications. Micromachines 12, 247. doi:10.3390/mi12030247

PubMed Abstract | CrossRef Full Text | Google Scholar

Neyts, K., and Beunis, F. (2014). “Chapter 11, Ion transport in liquid crystals,” in Handbook of liquid crystals: Physical properties and phase behavior of liquid crystals (Germany: Wiley VCH), 2, 357–382.

Google Scholar

Otón, J. M., Otón, E., and Quintana Xand Geday, M. A. (2018). Liquid-crystal phase-only devices. J. Mol. Liq. 267, 469–483. doi:10.1016/j.molliq.2017.10.148

CrossRef Full Text | Google Scholar

Prakash, J., Khan, S., Chauhan, S., and Biradar, A. M. (2020). Metaloxide-nanoparticles and liquid crystal composites: A review of recent progress. J. Mol. Liq. 297, 112052. doi:10.1016/j.molliq.2019.112052

CrossRef Full Text | Google Scholar

Shcherbinin, D. P., and Konshina, E. A. (2017a). Impact of titanium dioxide nanoparticles on purification and contamination of nematic liquid crystals. Beilstein J. Nanotechnol. 8, 2766–2770. doi:10.3762/bjnano.8.275

PubMed Abstract | CrossRef Full Text | Google Scholar

Shcherbinin, D. P., and Konshina, E. A. (2017b). Ionic impurities in nematic liquid crystal doped with quantum dots CdSe/ZnS. Liq. Cryst. 44, 648–655. doi:10.1080/02678292.2016.1227483

CrossRef Full Text | Google Scholar

Wang, Y. J., and Lin, Y. H. (2021). Liquid crystal technology for vergence-accommodation conflicts in augmented reality and virtual reality systems: A review. Liq. Cryst. Rev. 9 (1), 35–64. doi:10.1080/21680396.2021.1948927

CrossRef Full Text | Google Scholar

Wu, J. (2022). Understanding the electric double-layer structure, capacitance, and charging dynamics. Chem. Rev. 122 (12), 10821–10859. doi:10.1021/acs.chemrev.2c00097

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiong, J., Hsiang, E. L., He, Z., Zhan, T., and Wu, S. T. (2021). Augmented reality and virtual reality displays: Emerging technologies and future perspectives. Light. Sci. Appl. 10, 216. doi:10.1038/s41377-021-00658-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Yadav, S. P., and Singh, S. (2016). Carbon nanotube dispersion in nematic liquid crystals: An overview. Prog. Mat. Sci. 80, 38–76. doi:10.1016/j.pmatsci.2015.12.002

CrossRef Full Text | Google Scholar