Effects of network connectivity on viscoelastic relaxation in transient networks using experimental approach

The effect of network connectivity on viscoelastic relaxation in transient networks with well-defined structures (Tetra-PEG slime) was experimentally evaluated and compared to bond dissociation kinetics. To control the connectivity and discuss the pure effect precisely, we mixed the precursors in off-stoichiometric ratio. With decreasing network connectivity, the viscoelastic relaxation time accelerated and became shorter than the bond dissociation time. With increasing polymer concentration, the connectivity at which the viscoelastic relaxation time matched the dissociation time shifted to the high-connectivity region. The dependence of viscoelastic relaxation on connectivity can be adequately explained within the framework of the lifetime of a backbone. The backbone has numerous breakage points in low-connectivity region nearby the gelation point, resulting in a shorter lifetime than the dissociation time. However, the Rubinstein-Semenov model based on backbone relaxation does not predict the concentration dependence, suggesting that the formation of the network in the dilute/semi-dilute region deviates from a random branching process. These findings provide a crucial foundation for the molecular comprehension of transient network materials.

Introduction

Transient networks are three-dimensional networks formed by reversible crosslinks. Due to the temporal nature of these crosslinks, transient networks show significant viscoelasticity. Viscoelasticity of transient networks is not only determined by the lifetime of the strand (τ_d) but also by equilibrium network structures, including concentration, strand length, and connectivity (Annable and Ettelaie, 1994; Annable et al., 1996; Uneyama et al., 2012; Parada and Zhao, 2018; Katashima et al., 2022).

However, the intricate relationship between network connectivity and other structural parameters remains obscure for two reasons. The primary reason includes the nature of the crosslinks that are formed by the equilibrium reaction between particular end groups. For instance, crosslinks are created by a one-to-one binding system.

$\begin{array}{c}\mathrm{A}+\mathrm{B}\rightleftharpoons \mathrm{C}\end{array}(1)$

Here, the equilibrium constant, K, is written as follows:

$\begin{array}{c}K=\frac{\left[\mathrm{C}\right]}{\left[\mathrm{A}\right]\left[\mathrm{B}\right]}\end{array}(2)$

where, [X] is the molar concentration of the substance, X (= A, B, and C). Additionally, the bond formation kinetics can be expressed as follows:

$\begin{array}{c}\frac{\mathrm{d}\left[\mathrm{C}\right]}{\mathrm{d}t}=k_{\mathrm{a}}\left({\left[\mathrm{A}\right]}_0-\left[\mathrm{C}\right]\right)\left({\left[\mathrm{B}\right]}_0-\left[\mathrm{C}\right]\right)-k_{\mathrm{d}}\left[\mathrm{C}\right]\end{array}(3)$

Here, k_a is the association rate constant, k_d is the dissociation rate constant, and [A]₀ and [B]₀ are the initial concentrations of A and B, respectively. In the equilibrium state, where the binding and dissociation are balanced (d [C]/dt = 0), the equilibrium network connectivity, p = 2 [C]/([A]₀ + [B]₀), is described as follows:

$\begin{array}{c}p=\left\{1+\frac{1}{\left({\left[\mathrm{A}\right]}_0+{\left[\mathrm{B}\right]}_0\right)K}\right\}-{[{\left\{1+\frac{1}{\left({\left[\mathrm{A}\right]}_0+{\left[\mathrm{B}\right]}_0\right)K}\right\}}^2-1]}^{\frac{1}{2}}\end{array}(4)$

According to Eq. 4, p is dependent on K and the concentration of crosslinking agents, indicating a strong relationship between p and other network parameters such as concentration and strand length. Several studies have focused on adjusting K by altering the chemical species or pH of a solvent (Yesilyurt et al., 2016; Marco-Dufort et al., 2020). However, the change in hydrophobicity is frequently accompanied by the tuning of chemical species (Matsumoto et al., 2012). Due to a significant change in K, the latter method cannot precisely control K near the pKa value. Consequently, none of the methods can achieve continuous and robust control over p.

The second issue involves static and dynamic heterogeneities in transitory networks (Katashima, 2021). Static heterogeneity refers to the spatially heterogeneous distribution of polymer segments in a state of equilibrium, such as the polydispersity of network strand lengths, functionality, and aggregation structures. Conversely, dynamic heterogeneity has been reported in conventional transient networks due to the network component’s slow dynamics compared to the unimer and micelle components’ rapid dynamics. These heterogeneous structures are uncontrollable and cannot be assessed quantitatively, preventing us from comprehending the relationships between viscoelasticity and network structures.

To address the controllability of such polymer networks, we constructed a model system with a regular network structure by connecting two types of branched polymers that are mutually reactive and studied the relationship between property and structure (Sakai et al., 2008; Sakai, 2014; Sakai, 2020; Fujiyabu et al., 2019; Sakumichi et al., 2021). Recently, we extended this model system to create a model transient network by employing dynamic covalent bonds between phenylboronic acid and diols as the link between branched polymers, Tetra-PEG slime (Katashima et al., 2022). Tetra-PEG slime is composed of four-armed precursors with a narrow distribution, which form regular structures with uniform strand length and functionality. In addition, using symmetric precursors with the same mobility reduces the dynamic heterogeneity compared to the conventional system.

In this study, we report the dependence of viscoelastic relaxation time on network connectivity using Tetra-PEG slime. We mixed two precursors in stoichiometrically imbalanced proportions to tune the network connectivity independent of other structural parameters (Figure 1). This method enabled us to evaluate the pure effects of network connectivity while maintaining polymer concentration, strand length, chemical species, and solvent quality. Accordingly, these findings will aid in comprehending the molecular mechanism of viscoelasticity in transient networks.

FIGURE 1

FIGURE 1. Schematic illustration of tuning the network connectivity, where two precursors are mixed at either a stoichiometrically balanced (s = 0.5) or imbalanced ratio (s ≠ 0.5).

Materials and methods

Sample preparation

Tetra-PEG-FPBA and Tetra-PEG-GDL with the same poly (ethylene glycol) (PEG) backbones (M_w = 1.0 × 10⁴ and 2.0 × 10⁴ g mol⁻¹) were separately dissolved in a phosphate buffer (pH7.4, 200 mM). The polymer syntheses are described in detail in the Supplementary Material. The concentration of the prepolymers was adjusted to 40, 60, 80, 100, and 160 g L⁻¹. As shown in Table 1, the two polymer solutions were mixed at various stoichiometrically imbalanced proportions to systematically control the network connectivity. After mixing, each reaction was given 12 h at 25°C to complete.

TABLE 1

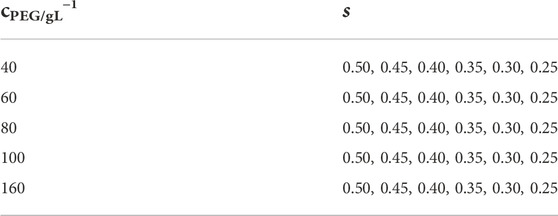
TABLE 1. Sets of polymer concentrations (c_PEG) and molar mixing fraction of Tetra-PEG-FPBA to total prepolymers (s).

Binding assays by surface plasmon resonance

The association/dissociation kinetics of phenylboronic acid and diol were analyzed using the surface plasmon resonance (SPR) technique on a Biacore T200 instrument (Cytiva). The amine coupling method was used to immobilize the diol group on Series S PEG-modified Sensor Chip (Cytiva). N-Hydroxysuccinimide and ethyl (dimethylaminopropyl)carbodiimide were initially used to activate the sensor chip. Subsequently, diol was captured on the sensor chip by passing the diol-containing solution over the sensor chip resulting in its covalent attachment. SPR sensorgrams were generated by injecting compounds into a sensor chip decorated with a diol in a running buffer containing 200 mM phosphate buffer (pH7.4) at a flow rate of 30 μl min⁻¹ at 25°C. Injecting 100 µl of a solution containing 1 M ethanolamine blocked the activated groups on the sensor’s surface. The binding kinetics of phenylboronic acid (analyte) to diol were determined by injecting different concentrations of analyte (250–1,000 μM) into the sensor chip at a flow rate of 30 μl min⁻¹. Herein, we used the monofunctional FPBA-modified PEG (M_w = 5,000 g mol⁻¹) as the analyte molecule. The synthesis of PEG-FPBA with a single function has been outlined in a previous publication (Katashima et al., 2022). PB (pH7.4–8.0, 200 mM) was utilized for the measurements. The contact time and dissociation time were 1 and 5 min, respectively.

Small amplitude oscillatory shear measurement

For the small amplitude oscillatory shear measurement (SAOS), Tetra-PEG slime samples were placed on the measuring plate of a rheometer (MCR301; Anton Paar, Graz, Austria) utilizing a cone plate fixture with a 25 mm diameter and a 4° cone angle. The angular frequency dependence (0.1–100 rad s⁻¹) of the storage (G′) and loss (G″) moduli was measured at 25°C. Additionally, the oscillatory shear strain amplitudes were within the linear viscoelasticity range.

Results and discussion

Overview of SAOS measurements

Figure 2 illustrates the dependence of the storage and loss moduli (G′, G″) for the Tetra-PEG slime (c_PEG = 100 g L⁻¹, M = 10,000 g mol⁻¹) with different off-stoichiometric mixing ratios (s = 0.25–0.50). G′ exhibited the plateau at high frequencies and the power law G' ∼ ω² at low frequencies for all samples, whereas G″ demonstrated the symmetric power law behaviors exhibited by G" ∼ ω and G" ∼ ω⁻¹ at high and low frequencies, respectively. These viscoelastic properties correspond well to the prediction of the Maxwellian model (solid lines in figures), which is described as follows:

$\begin{array}{c}{G}^{\prime }=∆G\frac{{\omega }^2{\tau }^2}{1+{\omega }^2{\tau }^2}\end{array}(5)$

$\begin{array}{c}{G}^{″}=∆G\frac{\omega \tau }{1+{\omega }^2{\tau }^2}\end{array}(6)$

Here, ΔG and τ represent the plateau modulus and the terminal relaxation time, respectively. Despite network connectivity, the correspondence with the Maxwellian model suggests that viscoelastic relaxation occurs via a unique process.

FIGURE 2

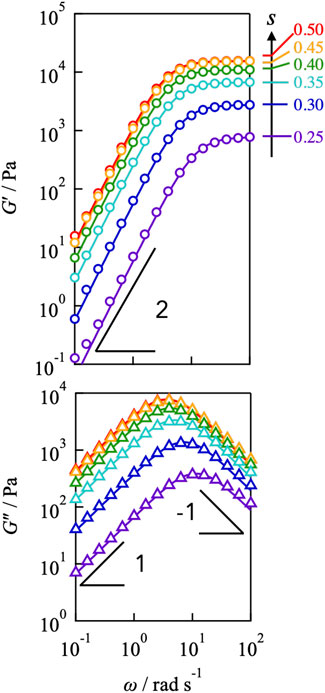
FIGURE 2. Frequency dependence of storage (top) and loss (bottom) moduli for Tetra-PEG slimes with various stoichiometrically imbalanced ratios (c_PEG = 100 g L⁻¹, M = 10,000 g mol⁻¹). The measured temperatures were 25°C. Solid lines represent the prediction of the Maxwellian model.

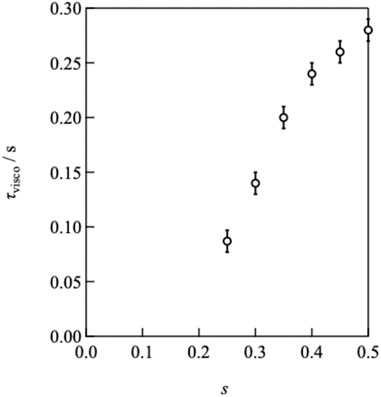
By decreasing the value of s from 0.50, the plateau modulus decreased, reflecting the decrease in the number density of the elastically active strands. In contrast, the peak of G″ shifted to higher frequencies as s decreased, indicating that the relaxation time accelerated, as depicted in Figure 3. The connectivity dependence of the viscoelastic relaxation time indicates that classical transient network models have failed (Green and Tobolsky, 1946). In the original model, viscoelastic relaxation is merely dictated by the strand lifetime.

FIGURE 3

FIGURE 3. τ_visco as a function of the stoichiometrically imbalanced ratio (s).

Binding analysis by SPR

We conducted surface plasmon resonance measurements to examine the connection between binding/dissociation kinetics and viscoelasticity. Figure 4A depicts a typical sensorgram of the SPR. Upon injection of monofunctional FPBA-modified PEG, the SPR signal increased and plateaued between 0 and 60 s. Injecting pure solvent to flush the system caused the signal to degrade after the injection. The SPR signal reflects the change in surface mass resulting from analyte adsorption. The plateau region between t = 5 and 60 s represents the equilibrium between binding and dissociation. FPBA and GDL form a one-to-one binding reaction, according to previous reports (Hall, 2006; Cambre and Sumerlin, 2011; Nishiyabu et al., 2011; Guo et al., 2012; Naito et al., 2012; Bull et al., 2013; Yoshinaga et al., 2017, 2021, 2022). The equilibrium constant was determined using the Benesi-Hildebrand plot (Benesi and Hildebrand, 1949), where the SPR signal at the equilibrium state (R_eq) is represented by the following equation.

$\begin{array}{c}\frac{1}{R_{\mathrm{e}\mathrm{q}}}=\frac{1}{\epsilon K{C}_{\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{a}\mathrm{n}\mathrm{d},0}}\frac{1}{C_{\mathrm{a}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{y}\mathrm{t}\mathrm{e},0}}+\frac{1}{\epsilon C_{\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{a}\mathrm{n}\mathrm{d},0}}\end{array}(7)$

Here, ε is the molar coefficient to the SPR signal of the complex, and C_analyte,0 and C_ligand,0 are the initial analyte and ligand concentrations, respectively. Figure 4B shows the values of R_eq⁻¹ as a function of C_analyte,0⁻¹, and the linear relationship was observed. According to Eq. 7, the slope and intercept agree with (εKC_ligand,0) ⁻¹ and (εC_ligand,0) ⁻¹, respectively, leading to K = 208 at 25°C in phosphate buffer (pH7.4). The estimated value of K is consistent with the previous report evaluated by other methods, (Soundararajan et al., 1989; Tong et al., 2001; Springsteen and Wang., 2002; Parada and Zhao, 2018) indicating that the SPR measurements are reliable.

FIGURE 4

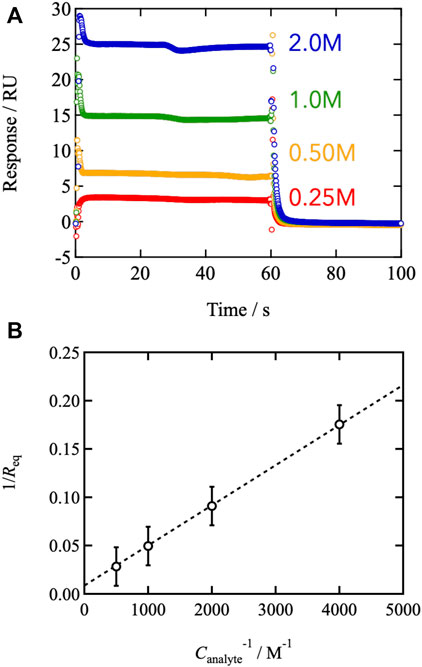
FIGURE 4. (A) Representative sensorgrams of the SPR measurements. The measured temperature was 25°C. The pH of the injected buffer was 7.4. The analyte (mono-functional FPBA) concentrations were tuned from 0.25 to 2.0 M (B) 1/R_eq against the inverse of the analyte concentration (Benesi-Hildebrand plot).

From K, the network connectivity at the equilibrium state (p) can be obtained. In this study, we mixed the FPBA- and GDL-modified precursors with stoichiometrically imbalanced ratios (s) to tune the connectivity while maintaining other structural parameters. This is the case that [A]₀/([A]₀ + [B]₀) = s in Eq. 4. Here, A and B correspond to FPBA and GDL, respectively. As a result, we can write p as follows:

$\begin{array}{c}p=\left\{1+\frac{1}{C_{\mathrm{e}\mathrm{n}\mathrm{d}}K}\right\}-{\left[{\left\{1+\frac{1}{C_{\mathrm{e}\mathrm{n}\mathrm{d}}K}\right\}}^2-4s\left(1-s\right)\right]}^{\frac{1}{2}}\end{array}(8)$

Here, C_end is the molar concentration of total reactive end groups (=[A]₀ + [B]₀). Figure 5 shows the estimated connectivity as a function of stoichiometrically imbalanced ratio with various polymer concentrations. As s approaches 0.5, p increases, and the end group concentration increases. In this figure, the solid lines are provided as a reference to represent permanent networks, where the end reaction is ideally connected. Notably, the value of p for all the Tetra-PEG slimes is less than 0.6, even when s reaches 0.5. The lower value of p of Tetra-PEG slimes than that of permanent network system is attributed to the low equilibrium constant and network formation in the dilute-concentration region. In the transient networks, the connectivity state is an equilibrium between binding and dissociation depending on the reactive end concentration. This differs significantly from the case of gels, wherein covalent bonds are formed kinetically even at low concentrations.

FIGURE 5

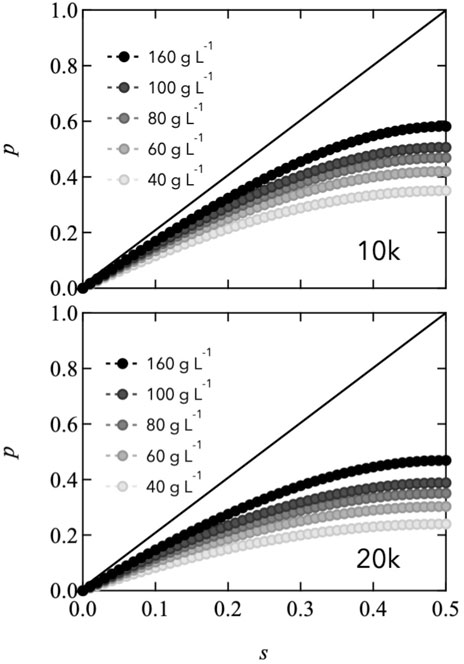
FIGURE 5. Estimated connectivity (p) as a function of the stoichiometrically imbalanced ratio (s) at various polymer concentrations (Top: 10,000 g mol⁻¹, Bottom: 20,000 g mol⁻¹). Solid lines represent ideal permanent networks as a reference.

Relationships between viscoelastic relaxation and network connectivity

Figure 6 illustrates the p-dependence of τ at different concentrations and strand lengths, showing that τ increased as p increased for every sample. The solid and dashed lines in the figure represent the power law fitting results. Evidently, the p-dependence of τ became more pronounced as c decreased. A similar dependence was observed between M_w = 10,000 and 20,000 g mol⁻¹, but the absolute values were distinct. Notably, in conventional transient network systems such as (polyvinyl alcohol)-borax slime, hydrophobically ethoxylated urethane urea, and so on, p cannot be controlled independently of the polymer concentration and network strand length. Therefore, Figure 6 is the first example of the p-dependence of the relaxation time excluding the effects of the polymer concentration and network strand length.

FIGURE 6

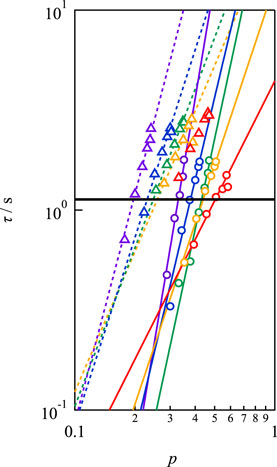
FIGURE 6. Double logarithmic plot of viscoelastic relaxation time against network connectivity. Circles and triangles represent the data of M_w = 10,000 and 20,000 g mol⁻¹, respectively. (Purple: 40 g L⁻¹, blue: 60 g L⁻¹, green: 80 g L⁻¹, yellow: 100 g L⁻¹, red: 160 g L⁻¹). The solid line represents the bond lifetime estimated by SPR (τ_d).

Notably, all the frequency-dependent data were measured in the linear viscoelastic regime with no strain dependence (representative data are shown in Supplementary Figure S1), and the activation energy estimated from the temperature dependence of the viscoelastic relaxation time was constant, regardless of the connectivity (Supplementary Figure S2). These experimental results strongly suggest that the effect of additional stress on the bonds is negligible and does not contribute to an acceleration of the relaxation.

In Figure 6, the solid line represents the dissociation time as estimated by SPR (τ_d). τ_d was experimentally determined to be 1.13 s at pH7.4 by fitting the SPR data after 60s to a single exponential function, which assumes that dissociation proceeds through a first-order reaction (Katashima et al., 2022). The viscoelastic relaxation time is faster than the bond lifetime for low p values, and the condition of τ/τ_d < 1 moves to higher p with increasing concentration.

The connectivity dependence can be explained in terms of the “backbone,” which is the primary stress-supporting strand. Notably, the backbone is not equivalent to the percolation network, which consists of numerous dangling chains that are elastically ineffective. In regions with a high degree of connectivity, the backbone flourishes and nearly all of the bonds belong to the backbone. Due to the other bonds, the backbone can survive the dissociation of one of the bonds. Therefore, the increment of p determines the durability of the backbone (top panel in Figure 7). However, when the connectivity decreases near the gelation point, the backbone is formed by super-bridging chains in which bonds are connected linearly via reversible bonds. In this case, the dissociation of the bond is crucial in determining the lifespan of the backbone (bottom panel in Figure 7). For instance, the backbone can be approximated as an N-bonded linear chain. Here, the lifetime of a single bond is τ_d. According to first-order kinetics, the probability [P_bond(t)] that the bond still exists after a certain period of time (t) can be expressed as

$\begin{array}{c}{P}_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}}\left(t\right)=\exp \left(-\frac{t}{{\tau }_{\mathrm{d}}}\right)\end{array}(9)$

FIGURE 7

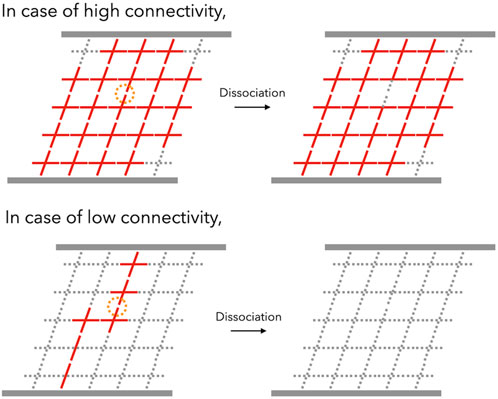
FIGURE 7. Schematic illustration of viscoelastic relaxation in transient networks in the case of high-connectivity (top) and low-connectivity (bottom) networks. With high connectivity, one dissociation event (represented by an orange circle) does not kill the backbone (red networks), whereas the backbone of the low-connectivity network can be killed by one dissociation event.

On the other hand, because the backbone has N dissociable points, the possibility that the “backbone” still survives after a period of time, [P_backbone(t)], can be expressed as

$\begin{array}{c}{P}_{\mathrm{b}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{e}}\left(t\right)=\exp \left(-N\frac{t}{{\tau }_{\mathrm{d}}}\right)\end{array}(10)$

Eq. 10 indicates that the lifetime of the backbone inversely decreases with increasing the number of reversible bonds in the backbone from the dissociation time.

According to the conventional theoretical studies of Rubinstein and Semenov, the mean-field approximation and Gaussian random branching structure predicted that the viscoelastic relaxation time increases with increasing p (Rubinstein and Semenov, 1998). The p-dependence of the viscoelastic relaxation time quantitatively agrees with the experimental results. Alternatively, the Rubinstein-Semenov model did not predict that the backbone lifetime is independent of the concentration without the connectivity effect, and the value of p where viscoelastic relaxation time corresponds to the bond lifetime depends on the polymer concentration. These deviations are attributed to the failure of the mean-field approximation. In low polymer concentrations such as dilute and semi-dilute regions with limited reactive neighbors, the intramolecular reaction dominantly occurs to form a percolation network with a lower fractal dimension than the prediction of the mean-field theories (∼2.5) (Sakai et al., 2016). Under such a condition, the cluster-cluster aggregation process is dominant, where the sparse aggregation clusters easily grow (Katashima et al., 2019) and branching is formed after percolation. Therefore, the backbone prepared in low concentrations easily forms branching after percolation at lower p, resulting in the moving of condition τ/τ_d < 1 moves to higher p with increasing concentration.

Conclusion

We experimentally estimated the effects of network connectivity (p) on viscoelastic relaxation in a model transient network (Tetra-PEG slime) through the imbalanced mixing of two mutually tetra-armed prepolymers. Our key findings are as follows: 1) the viscoelastic relaxation time was accelerated by decreasing p and became shorter than the bond dissociation time estimated by SPR; 2) the p-dependence was influenced by network strand length and polymer concentration; 3) the relaxation time near the gelation threshold became shorter than the dissociation time: and 4) the τ/τ_d < 1 condition moves to high connectivity region increasing the polymer concentration. This is well explained by the durability of the “backbone” which is the essential network supporting the stress. In close proximity to the gelation threshold, the backbone resembles a linear chain with breakage points, resulting in a shorter lifetime than the dissociation. However, the conventional models do not predict the concentration dependence, indicating that the network formation in the semi-dilute region is far from a random branching process. These findings will provide a solid foundation for discussion in order to understand the molecular picture of viscoelasticity in transient networks.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, TK; methodology, TK, MN, and SN; formal analysis, TK, RK, and RO; investigation, TK; writing—original draft preparation, TK; writing—review and editing, TK, MN, SN, KM, KT, U-IC, and TS. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Japan Society for the Promotion of Science (JSPS) through the Grants-in-Aid for Early-Career Scientists to TK (grant number: 20K15338), Transformative Research Area Grant to TS (grant number: 20H05733), and Scientific Research (A) to TS (grant number: 21H04688). This work was also supported by the Japan Science and Technology Agency (JST) to MN (COI grant number JPMJCE1305), TS (CREST grant number: JPMJCR 1992), and U-IC. (COI grant number: JPMJCE1304). This research was partially supported by Platform Project for Supporting Drug Discovery and Life Science Research (Basis for Supporting Innovative Drug Discovery and Life Science Research [BINDS]) from AMED under Grant Number JP21a.m.0101094 (to TK).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsfm.2022.1059156/full#supplementary-material

References

Annable, T., Buscall, R., and Ettelaie, R. (1996). Network formation and its consequences for the physical behaviour of associating polymers in solution. Colloids Surf. A Physicochem. Eng. Asp. 112, 97–116.

CrossRef Full Text | Google Scholar

Annable, T., and Ettelaie, R. (1994). Thermodynamics of phase separation in mixtures of associating polymers and homopolymers in solution. Macromolecules 27, 5616–5622.

CrossRef Full Text | Google Scholar

Benesi, H. A., and Hildebrand, J. H. (1949). A spectrophotometric investigation of the interaction of iodine with aromatic hydrocarbons. J. Am. Chem. Soc. 71, 2703–2707. doi:10.1021/ja01176a030

CrossRef Full Text | Google Scholar

Bull, S. D., Davidson, M. G., van den Elsen, J. M. H., Fossey, J. S., Jenkins, A. T. A., Jiang, Y.-B., et al. (2013). Exploiting the reversible covalent bonding of boronic acids: Recognition, sensing, and assembly. Acc. Chem. Res. 46, 312–326. doi:10.1021/ar300130w

PubMed Abstract | CrossRef Full Text | Google Scholar

Cambre, J. N., and Sumerlin, B. S. (2011). Biomedical applications of boronic acid polymers. Polymer 52, 4631–4643. doi:10.1016/j.polymer.2011.07.057

CrossRef Full Text | Google Scholar

Fujiyabu, T., Yoshikawa, Y., Chung, U., and Sakai, T. (2019). Structure-property relationship of a model network containing solvent. Sci. Technol. Adv. Mater 20, 608–621.

PubMed Abstract | CrossRef Full Text | Google Scholar

Green, M. S., and Tobolsky, A. V. (1946). A new approach to the theory of relaxing polymeric media. J. Chem. Phys. 14, 80–92. doi:10.1063/1.1724109

CrossRef Full Text | Google Scholar

Guo, Z., Shin, I., and Yoon, J. (2012). Recognition and sensing of various species using boronic acid derivatives. Chem. Commun. 48, 5956–5967. doi:10.1039/c2cc31985c

PubMed Abstract | CrossRef Full Text | Google Scholar

Hall, D. G. (2006). Boronic acids: Preparation, applications in organic synthesis and medicine. Weinheim, Germany: Wiley VCH.

Google Scholar

Katashima, T., Kudo, R., Naito, M., Nagatoishi, S., Miyata, K., Chung, U.-I., et al. (2022). Experimental comparison of bond lifetime and viscoelastic relaxation in transient networks with well-controlled structures. ACS Macro Lett. 11, 753–759. doi:10.1021/acsmacrolett.2c00152

PubMed Abstract | CrossRef Full Text | Google Scholar

Katashima, T. (2021). Rheological studies on polymer networks with static and dynamic crosslinks. Polym. J. 53, 1073–1082. doi:10.1038/s41428-021-00505-y

CrossRef Full Text | Google Scholar

Katashima, T., Sakurai, H., Chung, U.-I., and Sakai, T. (2019). Dilution effect on the cluster growth near the gelation threshold. J. Soc. Rheol. Jpn. 47, 61–66. doi:10.1678/rheology.47.61

CrossRef Full Text | Google Scholar

Marco-Dufort, B., Iten, R., and Tibbitt, M. W. (2020). Linking molecular behavior to macroscopic properties in ideal dynamic covalent networks. J. Am. Chem. Soc. 142, 15371–15385. doi:10.1021/jacs.0c06192

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsumoto, A., Ishii, T., Nishida, J., Matsumoto, H., Kataoka, K., and Miyahara, Y. (2012). A synthetic approach toward a self-regulated insulin delivery system. Angew. Chem. Int. Ed. Engl. 124, 2166–2170. doi:10.1002/ange.201106252

CrossRef Full Text | Google Scholar

Naito, M., Ishii, T., Matsumoto, A., Miyata, K., Miyahara, Y., and Kataoka, K. (2012). A phenylboronate-functionalized polyion complex micelle for ATP-triggered release of siRNA. Angew. Chem. Int. Ed. Engl. 51, 10909–10913. doi:10.1002/ange.201203360

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishiyabu, R., Kubo, Y., James, T. D., and Fossey, J. S. (2011). Boronic acid building blocks: Tools for self assembly. Chem. Commun. 47, 1124–1150. doi:10.1039/c0cc02921a

PubMed Abstract | CrossRef Full Text | Google Scholar

Parada, G. A., and Zhao, X. (2018). Ideal reversible polymer networks. Soft Matter 14, 5186–5196. doi:10.1039/c8sm00646f

PubMed Abstract | CrossRef Full Text | Google Scholar

Rubinstein, M., and Semenov, A. N. (1998). Thermoreversible gelation in solutions of associating polymers. 2. Linear dynamics. Macromolecules 31, 1386–1397. doi:10.1021/ma970617+

CrossRef Full Text | Google Scholar

Sakai, T. (2014). Experimental verification of homogeneity in polymer gels. Polym. J. 46, 517–523. doi:10.1038/pj.2014.28

CrossRef Full Text | Google Scholar

Sakai, T., Katashima, T., Matsushita, T., and Chung, U. (2016). Sol-gel transition behavior near critical concentration and connectivity. Polym. J. 48, 629–634. doi:10.1038/pj.2015.124

CrossRef Full Text | Google Scholar

Sakai, T., Matsunaga, T., Yamamoto, Y., Ito, C., Yoshida, R., Suzuki, S., et al. (2008). Design and fabrication of a high-strength hydrogel with ideally homogeneous network structure from tetrahedron-like macromonomers. Macromolecules 41, 5379–5384. doi:10.1021/ma800476x

CrossRef Full Text | Google Scholar

Sakai, T. (2020). Physics of polymer gels. Weinheim, Germany: Wiley VCH.

Google Scholar

Sakumichi, N., Yoshikawa, Y., and Sakai, T. (2021). Linear elasticity of polymer gels in terms of negative energy elasticity. Polym. J. 53, 1293–1303.

CrossRef Full Text | Google Scholar

Soundararajan, S., Badawi, M., Kohlrust, C. M., and Hagernan, J. H. (1989). Boronic acids for affinity chromatography: Spectral methods for determinations of ionization and diol-binding constants. Anal. Biochem. 178, 125–134. doi:10.1016/0003-2697(89)90367-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Springsteen, G., and Wang, B. (2002). A detailed examination of boronic acid–diol complexation. Tetrahedron 58, 5291–5300. doi:10.1016/s0040-4020(02)00489-1

CrossRef Full Text | Google Scholar

Tong, A. J., Yamauchi, A., Hayashita, T., Zhang, Z. Y., Smith, B. D., and Teramae, N. (2001). Boronic acid fluorophore/β-cyclodextrin complex sensors for selective sugar recognition in water. Anal. Chem. 73, 1530–1536. doi:10.1021/ac001363k

PubMed Abstract | CrossRef Full Text | Google Scholar

Uneyama, T., Suzuki, S., and Watanabe, H. (2012). Concentration dependence of rheological properties of telechelic associative polymer solutions. Phys. Rev. E 86, 031802. doi:10.1103/physreve.86.031802

PubMed Abstract | CrossRef Full Text | Google Scholar

Yesilyurt, V., Webber, M. J., Appel, E. A., Godwin, C., Langer, R., and Anderson, D. G. (2016). Injectable self-healing glucose-responsive hydrogels with pH-regulated mechanical properties. Adv. Mat. 28, 86–91. doi:10.1002/adma.201502902

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoshinaga, N., Ishii, T., Naito, M., Endo, T., Uchida, S., Cabral, H., et al. (2017). Polyplex micelles with phenylboronate/gluconamide cross-linking in the core exerting promoted gene transfection through spatiotemporal responsivity to intracellular pH and ATP concentration. J. Am. Chem. Soc. 139, 18567–18575. doi:10.1021/jacs.7b08816

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoshinaga, N., Uchida, S., Dirisala, A., Naito, M., Koji, K., Osada, K., et al. (2022). Bridging mRNA and polycation using RNA oligonucleotide derivatives improves the robustness of polyplex micelles for efficient mRNA delivery. Adv. Healthc. Mat. 11, e2102016. doi:10.1002/adhm.202102016

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoshinaga, N., Uchida, S., Dirisala, A., Naito, M., Osada, K., Cabral, H., et al. (2021). mRNA loading into ATP-responsive polyplex micelles with optimal density of phenylboronate ester crosslinking to balance robustness in the biological milieu and intracellular translational efficiency. J. Control. Release 330, 317–328. doi:10.1016/j.jconrel.2020.12.033

PubMed Abstract | CrossRef Full Text | Google Scholar