Evaluating CPU, GPU, and FPGA performance in the context of modal reverberation: a comparative analysis

The vibration of acoustic systems can be represented through modal decomposition, reducing the problem to a set of harmonic oscillators. This study investigates the real-time performance of CPUs, GPUs, and FPGAs in implementing such models, focusing on the synthesis of large-scale modal reverberation. By leveraging their respective architectures, these processors are assessed for their ability to manage the high computational demands of modal synthesis. GPUs and FPGAs, known for their parallel processing capabilities, are evaluated alongside recent multi-core CPUs, which increasingly approach similar performance levels in handling such tasks. Through a series of platform-specific optimisations, this paper examines the maximum achievable mode count, latency, and processing efficiency for each platform in various real-time scenarios. Results indicate that while GPUs offer superior scalability, FPGAs achieve unparalleled latency performance, making them suitable for specific low-latency applications. CPUs, conversely, demonstrate unexpectedly high performance in smaller-scale applications. This work provides insight into the practical application of each processor type within real-time digital signal processing and suggests pathways for future research in hardware-based audio DSP.

1 Introduction

Modal methods are a foundational technique in computer-aided sound synthesis, representing some of the earliest examples of real-time physical models altogether. Modal projections, akin to Galerkin-like and spectral techniques (Boyd, 2001; Meirovitch, 2010), began in earnest as a viable digital synthesis technique with the works by J.M. Adrien and associates at IRCAM (Adrien, 1991) and with projects such as Mosaic and Modalys (Eckel, 1995). Such early success was partly due to the naturally parallel structure of the modal decomposition. In linear, time-invariant systems, multiple independent solutions coexist, each contributing to a system’s global response to a given input. Such physical independence can be naturally exploited at the computational level through parallelisation. In a typical workflow, the input is first projected onto the modes, which are then updated in parallel, and their contribution is summed, yielding the global system’s response. Modal techniques form the core current synthesis techniques, and share common features with other synthesis methods such as the Udwadia-Kalaba method (Debut and Antunes, 2020), the Functional Transformation Method (Rabenstein and Trautmann, 2003), and current machine-learning approaches (Schlecht et al., 2022). They have been extended to treat typical nonlinearities arising in physical models, such as contact friction nonlinearities (Russo et al., 2022) and intermittent contact (van Walstijn et al., 2016; Ducceschi et al., 2023).

One common area of application, and one which has gained much prominence in recent years, is modal reverberation. In this case, the simulated system is not a musical instrument per se but a large resonator fed with incoming dry audio. These systems are characterised by a considerable modal density, with thousands of overlapping modes contributing to forming the system’s response. Rooms and acoustic enclosures are prominent cases (Pierce, 2019). Plates and springs, introduced initially as means to sustain sound through more portable devices, are further examples (Valimaki et al., 2012). In the context of artificial reverberation, an additional distinction can be made based on the specific method used to derive the modal parameters—whether it is model-based or signal-based (Abel et al., 2014). In the former, the modes are readily derived from an input model of the target system, such as springs (McQuillan and van Walstijn, 2021; van Walstijn, 2020) and plates (Ducceschi and Webb, 2016). In signal-based modal synthesis, the modal parameters are first identified through a suitable algorithm either in the time or in the frequency domain (Avitabile, 2017), and the resulting system’s response is then synthesised via a parallel biquad filter structure. Examples of such applications abound, particularly in room acoustics, where the modal identification is carried out both in the time domain (Kereliuk et al., 2018; Rau et al., 2021) using modifications of the ESPRIT algorithm (Roy and Kailath, 1989), as well as in the frequency domain via nonlinear optimisation (Maestre et al., 2017; 2016; Bank and Ramos, 2011).

Due to their parallel nature, modal synthesis algorithms present a promising approach for certain processors that offer high parallel computing capabilities, such as Field-Programmable Gate Arrays (FPGAs) and Graphics Processing Units (GPUs). This paper aims to explore the feasibility of executing modal physical modelling algorithms in real-time on these platforms as a potential alternative to Central Processing Units (CPUs). Specifically, a metal plate with simply-supported boundaries is considered, for which the modal parameters can be directly obtained in closed-form from a model PDE (Partial Differential Equation) (Ducceschi and Webb, 2016; Willemsen et al., 2017; Russo et al., 2023). This algorithm is used to synthesise the maximum possible number of modes across various CPUs, FPGAs, and GPUs, involving a wide range of platform-specific optimisations, which are detailed herein. The findings indicate that the latest generations of CPUs increasingly exhibit performance levels competitive with those of high-end FPGAs and GPUs.

The structure of the paper is as follows: an overview of previous research on executing real-time audio DSP algorithms on GPUs and FPGAs is provided initially. This is followed by a presentation of the modal synthesis algorithm, along with a comprehensive description of the platform-specific optimisations implemented for various CPUs, FPGAs, and GPUs. The performance of this algorithm on each platform is then reported, leading to a discussion of these results and suggestions for potential future research directions.

2 Real-time audio DSP on GPUs and FPGAs

This section provides an overview of GPU and FPGA usage in real-time audio DSP, with an emphasis on key historical developments in both platforms and their applications in audio processing and synthesis.

2.1 GPUs

In recent years, GPUs have been extensively employed in machine learning training and real-time inference applications. Real-time audio synthesis and effects processing on GPUs, however, remains a niche area of research, with notable progress emerging since the introduction of CUDA and unified shader pipelines in 2006. Early work in this domain, such as Savioja et al. (2010), demonstrated the feasibility of synthesising one million sinusoids at audio rates, albeit through computing multiple adjacent time samples in parallel to accommodate the GPU clock rates available at the time.

With hardware advances, running certain audio synthesis and filtering tasks with inter-sample dependencies became possible. Renney et al. (2020) test real-time feasibility of more modern Nvidia and AMD GPUs. Work such as the NESS project (Bilbao et al., 2019) utilised GPUs for high-quality, physically accurate audio synthesis, though generally slower than real-time. There have been commercial products released to end users utilizing commodity GPUs. GPU Audio, Inc.¹ has developed a SDK for partners to integrate or develop GPU-based plugins. Some features such as parallel GPU-accelerated convolution in the Vienna Symphonic Library plugin are available to end-users. Several years prior, CUDA acceleration was availble in Acusticaudio s. r.l’s Nebula 3,² though this functionality was later removed. Finally, in prior work, Skare and Abel (2019) demonstrated the ability to run a modal filter bank based on phasor filters at audio rates that could accept MIDI input to synthesise percussion sounds.

2.2 FPGAs

FPGAs have gained prominence as a platform for real-time audio Digital Signal Processing (DSP) within both industry and academic environments. Their low-level architecture enables them to achieve unmatched real-time performance in terms of audio latency and exceptionally high sampling rates (Popoff et al., 2022). The reconfigurable nature of FPGAs allows for maximised optimisation tailored to specific applications, with adaptable levels of parallelisation and pipelining to attain the optimal performance that the system can support.

Early contributions to audio processing on Field-Programmable Gate Arrays (FPGAs) emerged in the 2000s, primarily focusing on the manual implementation of specific applications or algorithms using Hardware Description Languages (HDLs) such as VHDL or Verilog on FPGA-only boards. For instance, Motuk et al. (2007) provides a notable example, aiming to implement Finite-Difference Time-Domain (FDTD) models. Similarly, other projects have concentrated on digital drum kits (Jadhao and Singh Patel, 2020), audio effect generators (Chhetri et al., 2015; Dragoi et al., 2021), among others. More recent developments, with the integration of System on Chip (SoC)³ capabilities in contemporary FPGA platforms, have facilitated fully standalone applications capable of managing both audio control and processing, thus enabling a hardware⁴/software co-design approach (Cannon et al., 2022; Deulkar and Kolhare, 2020; Vaca et al., 2019). Within industry, companies such as Novation,⁵ Antelope Audio,⁶ UDO Audio,⁷ futur3soundz,⁸ and Audinate⁹ offer products that incorporate FPGA technology.

When it comes to implementing audio DSP algorithms on an FPGA, various approaches can be taken. As mentioned above, the most common and “obvious” one is to write HDL code “by hand.” This solution is only accessible to hardware engineers with highly specialised skills and is therefore out of reach to most DSP and software engineers. Environments such as Matlab Simulink¹⁰ enables the assembly of pre-designed DSP blocks to implement specific applications. While this solution is good for basic prototyping, it remains limited, especially when it comes to using custom algorithms. MathWorks’ HDL Coder¹¹ is another solution which allows for the programming of FPGAs at a high-level using Matlab. While it has been successfully used in a couple of projects in academia for real-time audio DSP applications (Vannoy, 2020), it mostly targets rapid prototyping to the detriment of optimisation and computational efficiency. Verstraelen et al. (2014) proposed a programmable parallel machine on FPGA targeting audio applications, but this project is not active anymore.

More recently, High-Level Synthesis (HLS) (Lahti et al., 2018) has proven to balance ease of programming and performance. In this context, the open source Syfala project,¹² which relies on the vitis_hls tool provided by Xilinx/AMD, has been aiming at providing an optimised “audio DSP to FPGA compiler” taking both C/C++ or Faust (Orlarey et al., 2009) code as an input (Popoff et al., 2022). Syfala can target various Xilinx/AMD FPGA boards and provide a broad range of side features such as various sister boards for control and multichannel audio applications (Popoff et al., 2024), Open Sound Control (OSC), MIDI, etc. control, hardware acceleration on dedicated Linux (Cochard et al., 2024), etc. When using C/C++, Syfala heavily relies on HLS pragmas for optimisation and code must respect various standards in order to be as efficient as possible.¹³

3 Modal synthesis and reverberation

Before proceeding, it is worth recalling the mathematics of modal reverberation. The purpose of this section is to describe the modal algorithms and introduce notation. As mentioned in the introduction, in model-based modal reverberation, the modal parameters are either assumed to be known (Ducceschi and Webb, 2016; Russo et al., 2023) or are obtained through a numerical eigenvalue problem (van Walstijn, 2020; McQuillan and van Walstijn, 2021). Here, as the focus is on the performance of modal algorithms, the former approach is chosen for a thin metallic plate with a simply-supported boundary. This serves as a first approximation to plate reverb units such as the EMT140 (Arcas and Chaigne, 2010; Valimaki et al., 2012). To that end, consider the following model describing the flexural vibration of a thin plate (Bilbao et al., 2006):

$\frac{{\partial }^{2}u\left(\mathbf{x},t\right)}{\partial t^2}={\alpha }^2\mathrm{\Delta }u\left(\mathbf{x},t\right)-{\kappa }^4\mathrm{\Delta }\mathrm{\Delta }u\left(\mathbf{x},t\right)-2\sigma \frac{\partial u\left(\mathbf{x},t\right)}{\partial t}+\delta \left(\mathbf{x}-{\mathbf{x}}_f\right)f\left(t\right).(1)$

In the above, $u=u(\mathbf{x},t):\mathcal{D}\times {\mathbb{R}}_0^{+}\to \mathbb{R}$ represents the flexural displacement of the metallic sheet over a rectangular domain $\mathcal{D}≔[0,L_x]\times [0,L_y]$. $\mathrm{\Delta }$ and $\mathrm{\Delta }\mathrm{\Delta }$ are, respectively, the Laplace and the biharmonic operators. In Cartesian coordinates, these are:

$\mathrm{\Delta }≔\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2},\mathrm{\Delta }\mathrm{\Delta }≔{\left(\mathrm{\Delta }\right)}^2.$

Furthermore, in (Equation 1), $\alpha ≔{(T_0/\rho h)}^{1/2}$ is a tension term, with $T_0$ being the applied tension per unit length along the edges, $\rho$ being the metal density and $h$ being the thickness of the plate (of the order of half a millimetre for steel reverb units). $\kappa ≔{(D/\rho h)}^{1/4}$ is a stiffness constant, with $D≔E{h}^3/12(1-{\nu }^2)$ being a rigidity constant, $E$ being Young’s modulus and $\nu$ being Poisson’s ratio. The constant $\sigma$ is a loss factor, $f(t)$ is the incoming dry audio, and ${\mathbf{x}}_f=(x_f,y_f)$ is the input location on the plate.

A particular solution to (Equation 1) is obtained by first solving the eigenvalue problem defined on the lossless system, that is:

${\omega }^{2}U=-{\alpha }^2\mathrm{\Delta }U+{\kappa }^4\mathrm{\Delta }\mathrm{\Delta }U,(2)$

together with the boundary conditions $U=\mathrm{\Delta }U=0$ along the boundary $\partial \mathcal{D}$, for a modal shape $U=U(x,y)$. A particular solution is given by:

$U_{p,q}\left(x,y\right)≔\frac{2}{\sqrt{L_x{L}_y}}\sin \left(\frac{p\pi x}{L_x}\right)\sin \left(\frac{q\pi y}{L_y}\right),(3)$

such that (Equation 2) is solved by:

${\omega }_{p,q}^2≔{\alpha }^2{\gamma }_{p,q}^2+{\kappa }^4{\gamma }_{p,q}^4$

for real-valued modal wavenumbers ${\gamma }_{p,q}≔\sqrt{{\left(p\pi /L_x\right)}^2+{\left(q\pi /L_y\right)}^2}$ and positive modal indices $(p,q)\in \mathbb{N}$. One may then sort the particular solutions according to increasing frequency, using a single sorting index $m$. Thus, ${\omega }_1<{\omega }_2\le {\omega }_3<\dots \le {\omega }_m\le \dots \le {\omega }_M$, where $M$ represents the total amount of modes retained in the model. The associated mode shapes are $U_m(x,y)$, as per (Equation 3). The modal equation for the $m^{\text{th}}$ mode is then:

${\ddot{u}}_m\left(t\right)=-{\omega }_m^2{u}_m\left(t\right)-2{\sigma }_m{\dot{u}}_m\left(t\right)+U_m\left(x_f,y_f\right)f\left(t\right),(4)$

where the loss factor ${\sigma }_m$ is now mode-dependent and can be given in terms of the 60 dB decay time ${\tau }_m$ as ${\sigma }_m≔3\log (10)/{\tau }_m$. $u_m(t)$ is the time-dependent modal coordinate for mode $m$. Note that, in (Equation 4), total time derivates are now denoted with overdots.

The global solution at location ${\mathbf{x}}_o≔(x_o,y_o)$ is then reconstructed as:

$u\left({\mathbf{x}}_o,t\right)={\displaystyle \sum _{m=1}^M}{U}_m\left(x_o,y_o\right)u_m\left(t\right).(5)$

A schematic representation of the typical workflow in model-based modal synthesis is offered in Figure 1. Pictures of the first few modal shapes are given in Figure 2.

Figure 1

Figure 1. Workflow of model-based modal synthesis. An incoming dry audio signal is projected onto $M$ modal shapes, yielding the input modal weights. The modal equations are in the form of a bank of $M$ parallel oscillators, and the global output is then reconstructed through a reduced sum.

Figure 2

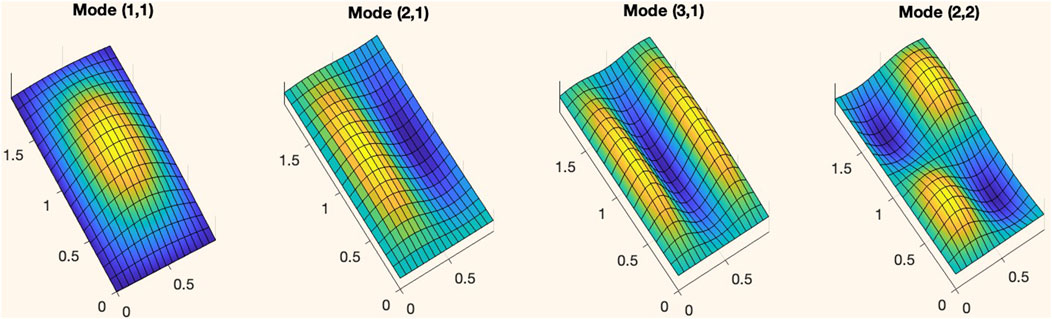
Figure 2. The first four modal shapes $U_p$ for a rectangular plate with $L_x=1$, $L_y=2$, typical dimensions for plate reverb units such as the EMT140. The shapes are sorted according to increasing frequency, and modal indices $p,q$ are as given.

Before proceeding, it is worth solving (Equation 4) in the frequency domain, after substituting $u_m=e^{st}{\widehat{u}}_m$, $f=e^{st}\widehat{f}$ for complex amplitudes ${\widehat{u}}_m$, $\widehat{f}$. This gives the transfer function:

${\widehat{H}}_m\left(s\right)≔\frac{{\widehat{u}}_m}{\widehat{f}}=\frac{U_m\left(x_f,y_f\right)}{s^2+{\omega }_m^2+2{\sigma }_{m}s}.(6)$

3.1 Discrete-time update

A time-stepping algorithm is constructed by approximating the continuous solution $u_m(t)$ with a time series $u_m[n]$, defined at $t_n≔Tn$, where $T$ is the sampling interval (i.e., the multiplicative inverse of the sample rate), and $n\in \mathbb{N}$ is the sampling index. A discrete-time transfer function, discretising ${\widehat{H}}_m(s)$ in (Equation 8), is usually obtained using two main approaches. The first is through the integration of (Equation 4) using a basic Störmer-Verlet algorithm as done, e.g., in Ducceschi and Webb (2016); the second is via an exact integrator such as the one given in Cieśliński (2011). The two discrete-time transfer functions follow as.

${\mathfrak{H}}_m^{SV}\left(z\right)≔\frac{T^2{U}_m\left(x_f,y_f\right)}{z\left(1+{\sigma }_{m}T\right)-2+T^2{\omega }_m^2+z^{-1}\left(1-{\sigma }_{m}T\right)},(\mathrm{7a})$

${\mathfrak{H}}_m^{EX}\left(z\right)≔\frac{T^2{e}^{-{\sigma }_{m}T}{U}_m\left(x_f,y_f\right)}{z-2\cos \left({\omega }_{m}T\right)e^{-{\sigma }_{m}T}+z^{-1}{e}^{-2{\sigma }_{m}T}}.(\mathrm{7b})$

The online computational burden of the two discretisations is the same once the constant coefficients are computed before runtime. (Equation 7b) is preferred in general as it does not introduce artificial frequency warping. Furthermore, it is unconditionally stable as opposed to (Equation 7a) for which one must choose ${\omega }_m<2/T$ for stability.

Regardless of the particular form of the transfer function, the prototype algorithm has the form:

$u_m\left[n+1\right]=c_1\times u_m\left[n\right]+c_2\times u_m\left[n-1\right]+c_3\times f\left[n\right],m=1,\dots ,M,(8)$

requiring three multiplies and two adds per mode, besides swapping two state arrays after the update. The reduced sum in (Equation 5) is used to compute the output at the output point as:

$\text{output}\left[n\right]={\displaystyle \sum _{m=1}^M}{\text{weights}}_m\times u_m\left[n\right].(9)$

3.2 Algorithm architecture

Algorithm 1 shows the standard layout of the computation for a modal processor. At each time step, the modal state array uNext is updated using two previous states, u and uPrev, and arrays of coefficients, and the input sample is also added to each modal equation, as per Equation 8. A dot product is subsequently performed over this updated state with an array of weights to generate the output sample for the given time step, as shown in Equation 9. The state arrays are then interchanged prior to initiating the next time iteration.

Algorithm 1

Algorithm 1. Standard algorithm for Modal Processing.

To produce full-bandwidth audio, the simulation is conducted at 48 kHz—equivalent to 48,000 time steps, divided into buffers, to yield one second of output. A typical buffer size is 256 samples. The computational cost, therefore, depends on the number of modes employed, which determines the size of the state arrays. Observing that each element of the state array is updated independently, the algorithm can be reformulated as in Equation 2. Rather than looping over time first, the process can loop over the modes of the state, updating each mode across a buffer of time steps. The final output samples are then computed incrementally, and the state of each mode is updated by writing individual values at each time iteration.

Algorithm 2

Algorithm 2. Modified algorithm with swapped loops.

4 Implementations

The performance and parallelisation methods that these two approaches offer are now discussed.

4.1 Central processing unit

In single-threaded CPU execution, the standard algorithm 1) achieves optimal performance when both the state update and dot product are consolidated within a single FOR loop. Compilers such as Clang can fully vectorise this operation under the -Ofast setting. The state arrays may be interchanged through a simple pointer swap, incurring minimal computational cost. In contrast, the modified algorithm 2) shows approximately tenfold (x10) slower performance in its unoptimised form. Specifically, the compiler fails to auto-vectorize the FOR loop operations, and each element of the state arrays must be read and written individually to perform the state swap. This memory transfer, coupled with inefficient caching, results in a reduction in overall performance.

To maximise CPU performance, multi-threading is employed to exploit the multi-core architecture. Parallelisation on a limited number of cores is implemented by partitioning the state arrays into discrete sections. For example, with eight threads, each thread processes one-eighth of the modal state, performing the dot product over its designated data segment. Upon completing their respective tasks, the partial sums from the eight threads are aggregated to produce the final output sample. Thread-launch overhead is minimised by allowing each thread to compute a buffer of timesteps, writing the data to a temporary array before synchronising across threads.

This approach, implemented with C++ stdthreads, is effective across buffer sizes from 128 to 1,024 without impacting performance. Initial offline testing was conducted on a simulation of 48,000 timesteps, corresponding to one second of audio simulation at 48 kHz. The primary performance metric was the maximum number of modes that could be computed within a runtime limit of 0.8 s, deemed the threshold for usability in a real-time system. Tests were conducted on a range of Apple Silicon machines—M1, M2 Pro, and M2 Max processors—using configurations of 1, 2, 4, and eight execution threads. The results are presented in Table 1.

Table 1

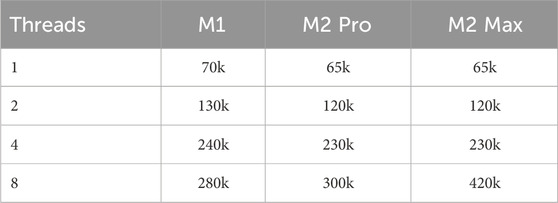
Table 1. Number of modes computed in an average of 0.8 s of run-time on the CPU over 48000 time-steps.

4.2 Graphics processing unit

Although GPUs have long been used for general-purpose computing, the introduction of Nvidia’s CUDA platform in 2007 significantly expanded accessibility due to its simplified programming API. Prior to this, GPGPU code was developed using complex shader languages, which presented a steep learning curve. CUDA introduced a straightforward API with C/C++ extensions, rapidly establishing itself as the default platform for GPU parallel computation code in scientific applications.GPUs are designed on a markedly different model from standard CPUs, which typically contain a limited number of cores, multiple levels of cache, and access to a centralised pool of global memory. In contrast, GPUs consist of thousands of compute cores, organised into Streaming Multiprocessors (SMs) and support multiple memory environments, including local, shared, and global memory. This architecture enables the simultaneous execution of numerous threads, thereby providing substantial parallel computational capabilities. Figure 3 illustrates the threading mechanism, wherein blocks of threads are grouped and executed on an SM. Kirk and Wen-Mei (2016) provides a comprehensive overview of CUDA hardware, programming, and optimisation.

Figure 3

Figure 3. CUDA thread model. Nvidia Corp.

The effective utilisation of this computational capability depends on the specific algorithm in use. Optimal GPU performance requires issuing thousands of threads, each executing a kernel on data-independent memory, along with an efficient ratio of computation to memory access. To surpass CPU performance, especially in large-scale simulations, millions of threads must be issued to fully harness the GPU’s available computational resources. Potential speedup factors and runtime constraints are application-dependent, though studies such as Bakhoda et al. (2009) comment on real-world performance and optimisation strategies across domains.

4.2.1 Metrics

Latency and throughput are measured as follows. For a GPU implementation, latency refers to the “loop computation” time required for the GPU to synthesise up to $M$ modes, await the completion of this computation, and then sum the results into a mono audio channel. Transfer of input filter parameters to the GPU and transfer of output audio data from the GPU are included in total time. Thus, the total latency corresponds to the wall-clock time necessary to compute one second of audio. In some experiments, audio is processed in chunks with buffer sizes aligned to those requested by real-time digital audio workstation processes, which may also enable adjustments in the scope of sub-problems. For cases involving multiple buffers, median, tail, and maximum latencies are reported, with the stipulation that a real-time system must not exceed the allowed time for processing a callback (sample rate divided by buffer size), allowing for some overhead.

Throughput is determined by the maximum number of modes a system can synthesise to generate one second of audio within 800 milliseconds, with the remaining 200 milliseconds reserved as a buffer. This metric aligns with the previously described CPU implementation.

4.2.2 Implementation

The initial approach for the CUDA implementation was to use the standard algorithm. This requires 3 separate kernels: one to update the state, another to perform the dot product, and then a final thread to load the result into the output memory array. However, this leads to very poor performance, even when using the optimised cuBlas library for the dot product operation. The array sizes are simply not large enough for the dot product function to operate efficiently.

The modified algorithm can potentially perform better as it can be implemented in a single kernel that removes the need for a dot product. However, each thread will be competing to access and write to the output memory as it updates over time-steps. This will inevitably lead to race conditions accessing that data. For the parallel code to function correctly, it is necessary to employ an atomic function to read, modify, and subsequently write to the output array within each thread. CUDA provides this functionality with atomicAdd (), which ensures that only a single thread can modify the value at any given moment. The resulting kernel is presented in Listing 1. Further optimisations are given in the following sections.

Listing 1. CUDA Kernel for Modifed Algorithm with atomicAdd() to avoid race conditions.

__global__ void updateState (float* uNext, float* u, float* uPrev, float* c1, float* c2, float* c3, float* wouts, float* input, float* output, int b)

{

  int m = blockIdx.u*Blocksize + threadIdx.u;

  for (int t = 0; t < buffer_size; ++t)

  {

    uNext [m] = u [m]*c1 [m] + uPrev [m]*c2 [m] + c3 [m]*input [t];

    float outpart = uNext [m]*wouts [m];

    int index = b*buffer_size + t;

    atomicAdd (&(output [index]), outpart);

    uPrev [m] = u [m];

    u [m] = uNext [m];

   }

 }

4.2.3 Test setups for optimised GPU strategies

In subsequent sections, we compare per-platform optimisations applied to synthesis kernels implemented in CUDA and Metal. The systems under test are documented in Table 2.

Table 2

Table 2. Test systems for GPU experiments.

4.2.4 Banked memory writes plus tree-sum stage

The computation continues with each thread tasked to compute one mode and to write a 256- or 512-sample audio buffer. These writes are organised such that 32 threads within a warp¹⁴ compute the same time sample $t_k$ and write in unison to adjacent memory locations. Careful consideration of memory access patterns helps to avoid bank conflicts and contention, thereby enabling higher memory throughput. This process yields numberOfModes channels of audio, with one mode per channel, that must be summed to produce a monaural output. Summation is performed within each warp and then across warps to achieve the final monaural signal. Within a warp, an efficient primitive, such as __shfl_down_sync (), may be used to conduct a tree-sum reduction, collapsing 32 channels to one in five pairwise steps. This operation results in one partially summed channel per thread group, which can be finalised on either the GPU or CPU. A demonstration of the two-stage tree-sum approach is presented below in Listing 2, as an extension of Listing 1.

Listing 2. Modified kernel with specialisation of summation within each warp as “submixes.”

 //For simplicity, assume number of filters is a multiple of 32.

 __global__ void updateState (float* uNext, float* u, float* uPrev, float* c1,

  float* c2, float* c3, float* wouts, float* input, float* output, int b)

{

  int m = blockIdx.x * blockDim.x + threadIdx.x;

  int warpId = threadIdx.x/32;

  // Threads within a warp each compute a filter independently.

  // Arrange data so memory writes are aligned.

  for (int t = 0; t < BUFFER_SIZE; ++t)

  {

   uNext [m] = u [m]*c1 [m] + uPrev [m]*c2 [m] + c3 [m]*input [t];

   float outpart = uNext [m]*wouts [m];

   int index = t*THREADGROUP_SIZE + m;

   output [index] + = outpart;

   uPrev [m] = u [m];

   u [m] = uNext [m];

  }

  // Sum the audio channels within the warp to mono.

  for (int t = 0; t < BUFFER_SIZE; ++t) {

   float thread_value = output [t*THREADGROUP_SIZE + m];

   for (int offset = 16; offset >0; offset/ = 2) {

    thread_value + = __shfl_down_sync (0xffffffff, thread_value, offset);

   }

   // First thread in warp writes result.

   if (m

   output [t] = thread_value;

   }

  }

  // We now transfer only the first audio channel from the device.

  // Filter state |uPrev| for each filter must be sent to the host

  // or persisted to global memory.

 }

This multi-stage summation approach has minimal effect when handling a small number of modes but increases the maximum synthesisable mode count by over 2.5 times compared to a single-threaded CPU summation stage. This increase is attributable to both parallelisation and reduced I/O costs. With this approach, data transfer overhead (host-to-device transfer of parameters plus device-to-host transfer of the output signals) is 12% of the total wall clock time and second-stage summation of the per-warp signals on the CPU 17%. Further optimisations of the summation stage include summing across warps on the GPU or employing multi-threading and vectorisation on the CPU side.

4.2.5 Hybrid CPU/GPU approach

Metrics presented in this section synthesise all filters on the GPU, however we note that further performance gains might be obtained by using the CPU and GPU in parallel.

During the synthesis of modes on a GPU, the CPU remains idle. Depending on the GPU hardware, execution may encounter a bottleneck where filter updates saturate the FPU units with multiplications. If a single buffer of latency is acceptable in a real-time application, it may be possible to leverage the idle hardware by pipelining the mode computation and summation operations, thus enabling additional parallelism. For instance, audio may be synthesised as a sequence of buffer computations $B_1\dots B_k$. While synthesising modes for buffer $C_k$, post-processing, including summation to mono, may be performed for buffer $C_{k-1}$. This approach allows the execution time of the faster computational task to be effectively “hidden.”

4.2.6 Caching

On Nvidia discrete GPUs, the 32 threads’ buffers of 256 or 512 samples may fit in fast shared memory local to a thread block. Our implementation explicitly requests to store data in this memory and is written to avoid bank conflicts. GPU kernels that must use larger but slower global memory may automatically benefit from caches, however we confirmed maximum throughput was achieved by keeping our working set in shared memory.

On the CUDA system, these optimisations enable the synthesis of a signal comprising over 600,000 modes at 48 kHz in real time, meeting the feasibility threshold of a real-time factor below 1.0 for synthesising one second of audio. Results for this platform in isolation are presented at the end of this section in Table 3.

Table 3

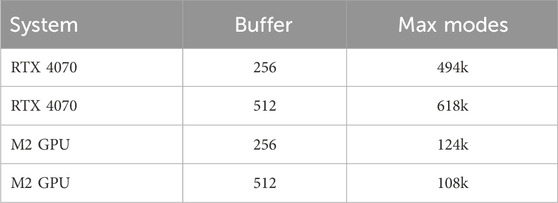
Table 3. Number of modes computed in 0.8 s of run-time on each GPU system over 48000 time-steps, processed in sets of $|$buffer$|$ samples.

4.2.7 Discrete GPU latency analysis

It is observed that there is significantly greater variance in latency when synthesising modes on the GPU compared to the CPU, while the FPGA system provides even more stable latency metrics. We analyze this practical consideration for the GPU platform. An experiment was conducted in which audio was processed in a series of 256- or 512-sample buffers, simulating a real-time system typical of audio production. Table 4 presents the median, 95th percentile, and maximum computational latency observed across each buffer processed on the GPU system. If any of these values, along with overhead, exceeds the host audio driver’s deadline for providing a result, a buffer underrun will occur, resulting in audio dropout in a real-time system. Latency compensation or pipelining may mitigate such issues in practical applications.

Table 4

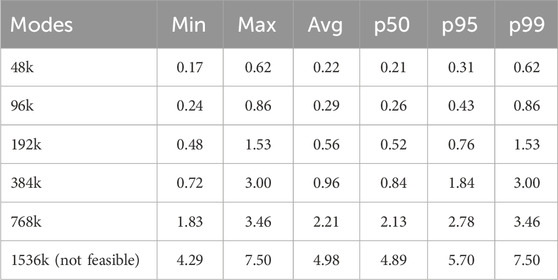
Table 4. Latency statistics for processing 256-sample buffers, using CUDA system, for increasing number of modes, in milliseconds.

4.2.8 Shared memory system

The aforementioned GPU results were measured on PCs with CUDA-compatible GPUs and APIs. Modern Apple platforms contain an on-die GPU and in-package memory, which the CPU and GPU each write to directly. There may be some locking and synchronisation overhead, but a transfer from one memory to another is avoided. As an experiment, the simulation was run on an Apple M2 system, using Metal GPU compute shader code to perform the mode computation and subsequent sum to one channel. Results are displayed in Table 5. To emphasize, reported statistics for CUDA platforms include explicit host/device data transfers; there is no corresponding explicit data transfer step in the Metal kernel, but both platforms’ performance statistics include any overhead for relevant API calls and synchronisation. Due to the GPU platforms’ variance in latency between calls, we present buffer processing times here. Maximum system throughput is presented in the immediately following section, for comparison with the CPU and FPGA platforms.

Table 5

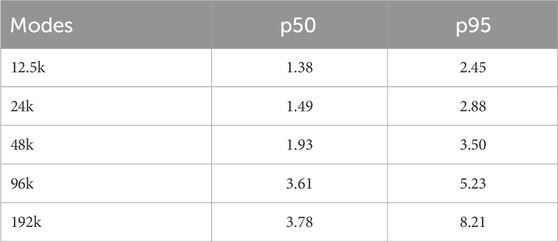
Table 5. Median and tail latency processing times for buffers of 256 samples, shared memory architecture.

4.2.9 Results and observations

With optimisations, the maximum number of modes that may be synthesised for a 1-s signal of audio in under 800 milliseconds of compute time was again determined, reserving 200 milliseconds for overhead in the calling code, operating system, or GPU driver. Times reported include data transfer to and from the GPU kernel and all required API calls. Data was processed in buffers sized similarly to those requested by real-world digital audio workstation hosts; this also allowed efficient use of GPU memory caches and thread-local memory on the CUDA platform.

4.3 Field-programmable gate array

FPGAs are well-suited for implementing modal processors due to their parallelisation capabilities. In this context, High-Level Synthesis (HLS), specifically the Syfala toolchain (see §2.2), was selected to conduct experiments on AMD-Xilinx FPGAs. The choice of these tools permitted the use of a similar C++ code input as employed in the CPU/GPU experiments while also enabling the utilisation of C-Simulation (CSIM) to verify that the output results matched those of the C++ reference code.

Additionally, the Syfala toolchain allowed us to quickly and fully implement the algorithm on different FPGA development boards, and test its output in a reliable real-time context of execution. In that regard, having a hand-tuned HDL implementation for this specific algorithm would have probably allowed us to reach better overall performances, but would have certainly been much more challenging and time-consuming to implement and stabilize.

4.3.1 Metrics

In the context of an FPGA implementation, latency is measured by taking the critical path of the implemented DSP “circuit,” which will be the number of clock cycles that its longest branch takes to get a value from input to output. Another crucial metric comes into play when implementing a specific algorithm: its size, i.e., the area it occupies on the Programmable Logic (PL). The first requirement is that the algorithm’s usage of logic resources stays below the number of available logic cells (or slices) that the FPGA chip physically possesses. Those cells are usually divided into different categories.

$•$ Digital Signal Processing (DSP) slices, mainly used for multiply-accumulate operations;

$•$ Flip Flops (FF), which are individual single clock-driven logic registers;

$•$ Look-up Tables (LUT) which are used for logic operations, multiplexers, etc.;

$•$ Block RAM (BRAM), which can be used for storing static arrays, implementing FIFOs, etc.;

If the estimation or implementation reports generated by Vitis HLS indicate that any of those cell categories is over-used, the synthesis/implementation process will eventually fail to produce an FPGA bitstream.

4.3.2 Implementation details

All experiments have been conducted with AMD-Xilinx Vitis HLS 2024.1 and tested on incrementally-sized AMD-Xilinx FPGA chips as listed in Table 6, in order to be able to benefit from a higher number of logic resources each time a maximum of modes and/or logic resources was reached for a specific chip.

Table 6

Table 6. Hardware resources in a number of slices of the different FPGAs used for our experiments.

A full implementation and validation process (including sound testing) was conducted for FPGA development boards in our possession, including the xc7z010clg400-1, xc7z020clg400-1, and xczu3eg-sfvc784-1-e FPGAs. For the others, only “estimate reports” were available, which do not always guarantee that the implementation will eventually fit on the FPGA, especially if resource utilisation is getting close to saturation. Consequently, in order to obtain a safer margin, experiments reporting a resource utilisation of more than 80% on one or several logic cell categories were discarded for those specific chips.

Regarding latency, all experiments were configured to run with a 48 kHz sample rate and a 122.88 MHz FPGA clock rate, which was chosen in order to match the traditional 256fs or 384fs based rates used for operating with audio codecs. Higher clock-rates, such as 184.32 MHz or 245.76 MHz were also experimented, but resulted in errors and timing violations throughout the HLS process, which we were not able to fully resolve yet. Consequently, the maximum latency for the processing of a single sample was in this context of 2,560 clock cycles. Buffer sizes from 24 to 1,024 samples were used in order to keep the latency per sample below maximum.

Listing 3. Vitis HLS implementation of modified algorithm.

 static float u [modesNumber];

 static float uPrev [modesNumber];

 static float uNext [modesNumber];

 int c = 0;

 for (int m = 0; m < modesNumber; m++) {

  #pragma HLS pipeline

  float c1 = coeffs [c++];

  float c2 = coeffs [c++];

  float c3 = coeffs [c++];

  float modes_out = coeffs [c++];

  for (int n = 0; n < BUFFER_NSAMPLES; ++n) {

   #pragma HLS unroll

   uNext [m] = c1 *u [m]

    + c2 * uPrev [m]

    + c3 * input [n];

   uPrev [m] = u [m];

   u [m] = uNext [m];

   output [n] + = uNext [m] * modes_out;

  }

 }

Initialisation of coefficient arrays c1, c2, c3 and modes_out was done on the ARM CPU (which is on the same System on Chip as the FPGA), stored in DDR memory and shared with the PL through the ARM Advanced Microcontroller Bus Architecture (AMBA), using the Advanced eXtensible Interface (AXI4) protocol. This allowed to prevent logic resource saturation when the number of modes became too important for all coefficients to be directly stored and read in the PL Block-RAMs or LUT-RAMs. Furthermore, it also allowed freeing DSP slices for expensive operations (such as cosine, exponential and square-root functions) that would have been used only once but permanently implemented on the PL. These coefficients were stored in an interleaved way, so they could be retrieved from the DSP kernel with a single burst request occurring for each mode iteration, somewhat limiting the impact on latency. There were no other read/write accesses to DDR memory. The intermediate storage arrays (u [N], uPrev [N], and uNext [N]) were, on the other hand, directly allocated in the programmable logic (PL), in either Block-RAMs or LUT-RAMs. Finally, as shown in Listing 3, DSP computation loops were “inverted,” resulting in a positive performance impact by reducing interdependencies between logic cells and enabling the parallel processing of a buffer of samples rather than an array of coefficients. Such an approach would have been challenging to implement on smaller FPGA chips due to limited resources. To enforce this strategy, the pipeline and unroll HLS pragmas were applied to each loop.

4.3.3 Code verification

In order to properly ensure that the DSP kernel is valid and produces - from the same inputs - the same outputs as the original C++ reference code, Vitis HLS’ C-Simulation (CSIM) feature was used. Vitis HLS maintains the order of operations performed in the C code when synthesizing float and double types to ensure that the results are the same as the C simulation, unless optimisations are explicitly requested. To quantify numerical accuracy, we compared the FPGA-generated outputs on a Digilent Zybo Z7-20 with the C++ reference implementation across 48,000 samples. The results showed a mean absolute error of 1.85 $\times 10^{-6}$, a maximum absolute error of 9.4 $\times 10^{-6}$, and a signal-to-noise ratio (SNR) of 87.25 dB. These minor discrepancies stem from floating-point implementation variations, which are not likely to have a perceptible impact on the resulting audio.

4.3.4 Results and observations

In this configuration, the addition of a single mode increased latency by approximately 10 clock cycles. Increasing the buffer size provided a means to offset this latency penalty by enabling parallelisation; however, this also led to a substantial rise in the utilisation of logic resources, as these were duplicated for the processing of each sample. The final results of our experiments and simulations, in terms of maximum number of modes for each targeted FPGA chip, are detailed in Table 7.

Table 7

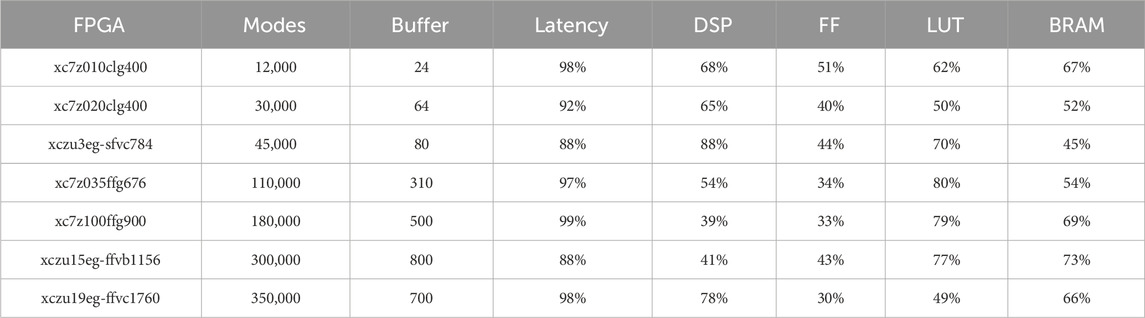
Table 7. Maximum number of synthesised modes in real-time on different FPGAs and corresponding resource usage. Latency corresponds here to the time it takes to generate a sample to meet real-time conditions. If latency exceeds 100%, then the program can not be executed in real-time.

5 Discussion and future directions

CPUs, GPUs, and FPGAs function in a very different way and potentially in very different contexts. In that regard, it is not necessarily straightforward to provide an objective comparison between them.

An important consideration here is that this study has focused on achieving real-time performance for the largest modal model across various processors without accounting for the potential parallel operation of other system elements. In other words, the utility of running such computationally intensive algorithms may be limited if other processes—such as a Digital Audio Workstation (DAW), graphical interface, or physical user interface—are not running concurrently. While this limitation may be less pronounced when using GPUs or FPGAs, typically employed as “hardware accelerators” alongside a CPU, preserving capacity on a standalone CPU for additional tasks is critical, particularly as an Operating System (OS) is likely to be running.

One of the main observations that can be made from the results presented in the previous sections is that recent CPUs do provide unexpectedly good performances in the context of modal synthesis, potentially competing with processors providing a higher level of parallelisation, such as FPGAs and GPUs. That being said, and despite the aforementioned limitations in terms of data transfer between the GPU and its associated CPU, GPUs do provide the best performances compared to CPUs and FPGAs, allowing for more than 600k modes to be synthesised in real-time and leaving the associated CPU free to carry out other tasks. It is also worth noting that the multi-threaded CPU and GPU approaches may each realize tens of thousands of modes in a context where the use of the resources is not mutually exclusive. In that regard, future work might explore a hybrid system that divides work among the two simultaneously.

FPGAs appear to yield “less impressive” results within the context of modal synthesis, compounded by the high potential cost of larger FPGA models, such as the xczu19eg-ffvc1760, which are likely considerably more expensive than the CPUs and GPUs evaluated in this study. However, one metric not addressed here, where FPGAs demonstrate superiority, is audio latency. Despite the focus on computational efficiency in the configurations presented in §4.3.4, it is feasible to eliminate buffering on an FPGA, thereby achieving outstanding latency performance compared to other processors.

An additional consideration is that the current study employs HLS for FPGA programming to provide a more balanced comparison between FPGAs, GPUs, and CPUs. Rewriting the modal synthesis algorithm entirely in a hardware description language, using fixed-point rather than floating-point arithmetic may yield improved performance over the results presented here. A compromise approach could involve the use of optimised floating-point hardware operators, such as those provided by FloPoCo (De Dinechin and Pasca, 2011).

6 Conclusion

This study has evaluated the performance of three principal processor types—CPUs, GPUs, and FPGAs—in the context of modal synthesis and processing. For smaller-scale models, CPUs emerge as the most practical platform owing to their widespread availability, adaptability, and flexibility, particularly in recent models with enhanced computational capabilities. When greater computational power is required, GPUs can serve as effective accelerators alongside CPUs, providing a scalable solution for larger model processing in many personal computers, where high-performance GPUs are now commonly installed. Although FPGAs are less accessible and typically not integrated into standard PCs, they offer unmatched audio latency performance, which may be advantageous in specific real-time audio processing applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RM: Writing–original draft, Writing–review and editing. MD: Writing–original draft, Writing–review and editing. PC: Writing–original draft, Writing–review and editing. TS: Writing–original draft, Writing–review and editing. CW: Writing–original draft, Writing–review and editing. RR: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation programme Grant agreement No. 950084 NEMUS.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://gpu.audio/

²https://www.acustica-audio.com/

³SoC: System on Chip.

⁴The term “hardware programming” is commonly used in the context of FPGA programming.

⁵https://novationmusic.com/en/synths/summit

⁶https://en.antelopeaudio.com/

⁷https://www.udo-audio.com/\#introduction

⁸https://www.futur3soundz.com/

⁹https://www.audinate.com/

¹⁰https://www.mathworks.com/products/simulink.html

¹¹https://www.mathworks.com/products/hdl-coder.html

¹²https://inria-emeraude.github.io/syfala/

¹³https://inria-emeraude.github.io/syfala/tutorials/cpp-tutorial-advanced/

¹⁴A CUDA warp is a collection of threads concurrently executing the same code on different pieces of data.

References

Abel, J. S., Coffin, S., and Spratt, K. (2014). Human–made rock mixes feature tight relations between spectrum and loudness (JAES volume 62 issue 10 pp. 643-653; october 2014). J. Audio Eng. Soc. 62, 643–653. doi:10.17743/jaes.2014.0039

CrossRef Full Text | Google Scholar

Adrien, J.-M. (1991). “The missing link: modal synthesis,” in Representations of musical signals (Cambridge, MA, USA: MIT Press), 269–298.

Google Scholar

Arcas, K., and Chaigne, A. (2010). On the quality of plate reverberation. Appl. Acoust. 71, 147–156. doi:10.1016/j.apacoust.2009.07.013

CrossRef Full Text | Google Scholar

Avitabile, P. (2017). Modal testing: a practitioner’s guide. Hoboken, New Jersey: John Wiley & Sons.

Google Scholar

Bakhoda, A., Yuan, G. L., Fung, W. W., Wong, H., and Aamodt, T. M. (2009). “Analyzing cuda workloads using a detailed gpu simulator,” in 2009 IEEE international symposium on performance analysis of systems and software (IEEE), 163–174.

Google Scholar

Bank, B., and Ramos, G. (2011). Improved pole positioning for parallel filters based on spectral smoothing and multiband warping. IEEE Signal Process. Lett. 18, 299–302. doi:10.1109/lsp.2011.2124456

CrossRef Full Text | Google Scholar

Bilbao, S., Arcas, K., and Chaigne, A. (2006). A physical model for plate reverberation. In 2006 IEEE international conference on acoustics speech and signal processing proceedings. vol. 5, V–V

Google Scholar

Bilbao, S., Desvages, C., Ducceschi, M., Hamilton, B., Harrison-Harsley, R., Torin, A., et al. (2019). The ness project: physical modeling, algorithms and sound synthesis. Computer Music Journal. Cambridge, MA: MIT Press.

Google Scholar

Boyd, J. P. (2001). Chebyshev and Fourier spectral methods. Mineola, New York, USA: Dover.

Google Scholar

Cannon, D., Fang, T., and Saniie, J. (2022). “Modular delay audio effect system on FPGA,” in Proceedings of the 2022 IEEE international conference on electro information technology (eIT) (Mankato, USA), 248–251.

Google Scholar

Chhetri, S. R., Poudel, B., Ghimire, S., Shresthamali, S., and Sharma, D. K. (2015). Implementation of audio effect generator in FPGA. Nepal J. Sci. Technol. 15, 89–98. doi:10.3126/njst.v15i1.12022

CrossRef Full Text | Google Scholar

Cieśliński, J. L. (2011). On the exact discretization of the classical harmonic oscillator equation. J. Differ. Equations Appl. 17, 1673–1694. doi:10.1080/10236191003730563

CrossRef Full Text | Google Scholar

Cochard, P., Popoff, M., Michon, R., and Risset, T. (2024). “Programming FPGA platforms for real-time audio signal processing in C++,” in Proceedings of the 2024 sound and music computing conference (SMC-24) (Porto, Portugal).

Google Scholar

Debut, V., and Antunes, J. (2020). Physical synthesis of six-string guitar plucks using the Udwadia-Kalaba modal formulation. J. Acoust. Soc. Am. 148, 575–587. doi:10.1121/10.0001635

PubMed Abstract | CrossRef Full Text | Google Scholar

De Dinechin, F., and Pasca, B. (2011). Designing custom arithmetic data paths with flopoco. IEEE Des. & Test Comput. 28, 18–27. doi:10.1109/mdt.2011.44

CrossRef Full Text | Google Scholar

Deulkar, A. S., and Kolhare, N. R. (2020). “FPGA implementation of audio and video processing based on Zedboard,” in Proceedings of the 2020 international conference on smart innovations in design, environment, management, planning and computing (ICSIDEMPC) (Aurangabad, India: IEEE, 305–310.

CrossRef Full Text | Google Scholar

Dragoi, C., Anghel, C., Stanciu, C., and Paleologu, C. (2021). “Efficient FPGA implementation of classic audio effects,” in Proceedings of the 2021 13th international Conference on electronics, Computers and artificial intelligence (ECAI) (pitesti, Romania: ieee).

Google Scholar

Ducceschi, M., Bilbao, S., and Webb, C. (2023). “Real-time modal synthesis of nonlinearly interconnected networks,” in Proceedings of the 26th international conference on digital audio effects (DAFx) (Copenhagen, Denmark), 53–60.

Google Scholar

Ducceschi, M., and Webb, C. (2016). “Plate reverberation: towards the development of a real-time physical model for the working musician,” in Procedings of the 22nd international congress on acoustics ICA 2016.

Google Scholar

Eckel, G. (1995). Sound synthesis by physical modelling with modalys. Proc. ISMA’ 95, 478–482.

Google Scholar

Jadhao, K. M., and Singh Patel, G. (2020). “Hardware architecture of digital drum kit using FPGA,” in Proceedings of the 2020 IEEE international Conference on advent Trends in multidisciplinary Research and innovation (ICATMRI) (buldhana, India: ieee), 1–4.

Google Scholar

Kereliuk, C., Herman, W., Little Ferry, N., Wedelich, R., and Gillespie, D. J. (2018). “Modal analysis of room impulse responses using subband esprit,” in Proceedings of the 21st international Conference on digital audio effects (DAFx) (aveiro, Portugal).

Google Scholar

Kirk, D. B., and Wen-Mei, W. H. (2016). Programming massively parallel processors: a hands-on approach. Burlington, MA: Morgan kaufmann.

Google Scholar

Lahti, S., Sjövall, P., Vanne, J., and Hämäläinen, T. D. (2018). Are we there yet? a study on the state of high-level synthesis. IEEE Trans. Computer-Aided Des. Integr. Circuits Syst. 38, 898–911. doi:10.1109/TCAD.2018.2834439

CrossRef Full Text | Google Scholar

Maestre, E., Abel, J., Smith, J., and Scavone, G. (2017). “Constrained pole optimization for modal reverberation,” in Proceedings of the 20th international conference on digital audio effects (DAFx) (Edinburgh, UK), 381–388.

Google Scholar

Maestre, E., Scavone, G. P., and Smith, J. O. (2016). Design of recursive digital filters in parallel form by linearly constrained pole optimization. IEEE Signal Process. Lett. 23, 1547–1550. doi:10.1109/lsp.2016.2605626

CrossRef Full Text | Google Scholar

McQuillan, J., and van Walstijn, M. (2021). “Modal spring reverb based on discretisation of the thin helical spring model,” in Proceedings of the 24th international conference on digital audio effects (DAFx) (Vienna, Austria), 191–198.

Google Scholar

Meirovitch, L. (2010). Fundamentals of vibrations. Long Grove, Illinois, USA: Waveland Press.

Google Scholar

Motuk, E., Woods, R., Bilbao, S., and McAllister, J. (2007). Design methodology for real-time FPGA-based sound synthesis. IEEE Trans. Signal Process. 55, 5833–5845. doi:10.1109/tsp.2007.898785

CrossRef Full Text | Google Scholar

Orlarey, Y., Fober, D., and Letz, S. (2009). Faust: an efficient functional approach to DSP programming. Paris, France: New Computational Paradigms for Computer Music, 65–96.

Google Scholar

Pierce, A. D. (2019). Acoustics: an introduction to its physical principles and applications. Cham, Switzerland: Springer Nature.

CrossRef Full Text | Google Scholar

Popoff, M., Michon, R., and Risset, T. (2024). “Enabling affordable and scalable audio spatialization with multichannel audio expansion boards for FPGA,” in Proceedings of the 2024 Sound and music computing conference (porto, Portugal).

Google Scholar

Popoff, M., Michon, R., Risset, T., Orlarey, Y., and Letz, S. (2022). “Towards an FPGA-based compilation flow for ultra-low latency audio signal processing,” in Proceedings of the 2022 Sound and music Computing conference SMC-22 saint-étienne, France.

Google Scholar

Rabenstein, R., and Trautmann, L. (2003). Digital sound synthesis of string instruments with the functional transformation method. Signal Process. 83, 1673–1688. doi:10.1016/s0165-1684(03)00083-5

CrossRef Full Text | Google Scholar

Rau, M., Abel, J. S., James, D., Smith, I., and Julius, O. (2021). Electric-to-acoustic pickup processing for string instruments: an experimental study of the guitar with a hexaphonic pickup. J. Acoust. Soc. Am. 150, 385–397. doi:10.1121/10.0005540

PubMed Abstract | CrossRef Full Text | Google Scholar

Renney, H., Mitchell, T., and Gaster, B. R. (2020). “There and back again: the practicality of gpu accelerated digital audio,” in Nime, 202–207.

Google Scholar

Roy, R., and Kailath, T. (1989). Esprit-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. speech, signal Process. 37, 984–995. doi:10.1109/29.32276

CrossRef Full Text | Google Scholar

Russo, R., Ducceschi, M., and Bilbao, S. (2022). “Efficient simulation of the bowed string in modal form,” in Proceedings of the 25th international conference on digital audio effects (DAFx) (Vienna, Austria), 122–129.

Google Scholar

Russo, R., Ducceschi, M., Bilbao, S., and Hamilton, M. (2023). “Efficient simulation of acoustic physical models with nonlinear dissipation,” in Proceedings of the sound and music computing conference (Stockholm, Sweden), 125–131.

Google Scholar

Savioja, L., Välimäki, V., and Smith III, J. O. (2010). “Real-time additive synthesis with one million sinusoids using a gpu,” in Audio engineering society convention, 128. London: Audio Engineering Society.

Google Scholar

Schlecht, S., Parker, J., Schäfer, M., and Rabenstein, R. (2022). “Physical modeling using recurrent neural networks with fast convolutional layers,” in Proceedings of the 25th international conference on digital audio effects (DAFx) (Vienna, Austria), 138–145.

Google Scholar

Skare, T., and Abel, J. (2019). “Real-time modal synthesis of crash cymbals with nonlinear approximations, using a gpu,” in Proceedings of the 22nd international Conference on digital audio effects (DAFx) (birmingham, UK).

Google Scholar

Vaca, K., Jefferies, M. M., and Yang, X. (2019). “An open audio processing platform with Zync FPGA,” in Proceedings of the 2019 IEEE international Symposium on Measurement and Control in robotics (ISMCR) (houston, Texas).

Google Scholar

Valimaki, V., Parker, J. D., Savioja, L., Smith, J. O., and Abel, J. S. (2012). Fifty years of artificial reverberation. IEEE Trans. Audio, Speech, Lang. Process. 20, 1421–1448. doi:10.1109/tasl.2012.2189567

CrossRef Full Text | Google Scholar

Vannoy, T. C. (2020). Enabling rapid prototyping of audio signal processing systems using system-on-chip field programmable gate arrays. Masters Thesis

Google Scholar

van Walstijn, M. (2020). “Numerical calculation of modal spring reverb parameters,” in Proceedings of the 23rd international conference on digital audio effects (DAFx) (Vienna, Austria).

Google Scholar

van Walstijn, M., Bridges, J., and Mehes, S. (2016). “A real-time synthesis oriented tanpura model,” in Proceedings of the 19th international conference on digital audio effects (DAFx) (Brno, Czech Republic).

Google Scholar

Verstraelen, M., Kuper, J., and Smit, G. J. M. (2014). “Declaratively programmable ultra-low latency audio effects processing on FPGA,” in Proceedings of the 17th international Conference on digital audio effects (DAFx) (erlangen, Germany).

Google Scholar

Willemsen, S., Serafin, S., and Jensen, J. R. (2017). “Virtual analog simulation and extensions of plate reverberation,” in Proceedings of the Sound and music computing conference (espoo, Finland), 314–319.

Google Scholar