Water vapor density field estimation using commercial microwave link attenuation combined with temperature measurements

Accurate water vapor density (WVD) measurement is critical for weather models, health risk management, and industrial management among many other applications. A number of machine-learning based algorithms (e.g. support vector machine) for estimating water vapor density at a reference weather station using the received signal level values measured at a commercial microwave link has been proposed in the past, and also was expanded to include a combination of three commercial microwave links with temperature measurements to achieve a higher estimation accuracy (with respect to the root mean square error at a given location). In this paper, we leverage on the preliminary potential presented, and propose enhanced machine learning models that utilize a larger number of CMLs combined with temperature data inside a given area to estimate a reference weather station humidity measurements. We then show how the presented approach can be expanded to estimate the water vapor density field - taking into consideration the elevation via the humidity-elevation profile. The models were evaluated using data from 32 weather stations and 505 CMLs in Germany, with performance assessed through root mean square error (RMSE) and correlation coefficients (CC). The enhanced models achieved a mean RMSE of 0.587 g/m³ for WVD field estimation, outperforming prior approaches as well as can be used as "virtual weather stations" - to estimate the water vapor density values in locations where no actual weather stations exist.

1 Introduction

Water vapor density (WVD) (aka humidity) spatiotemporal distribution data at high resolution is important for accurate weather forecasting; it is currently based on numerical weather prediction models (Gutman and Benjamin, 2001). WVD measurements are also beneficial for health risk management (Gao et al., 2014), agricultural management (Ferrante and Mariani, 2018), and other industries (Hoffmann and Koehl, 2014). Generally, WVD is measured at a specific spatial point over time, such as by weather stations (WS). WVD at multiple locations and heights can also be measured by radiosondes, but these devices are more cumbersome to use and may only provide measurement at the path of the instrument at the time of its passing; they are thus not common. Satellites provide better spatiotemporal resolutions but have greater errors of measurement and cannot always differentiate between the different atmospheric layers. Water vapor attenuates microwave and mmWave signals propagating through the atmosphere. Commercial microwave links (CMLs) are widely used as the infrastructure for wireless communication networks (WCNs), such as the back-haul of current and future cellular and smart-city communication networks. In David et al. (2009), it was shown that WVD can be estimated using such CML attenuation data by using the theoretical relationship between water vapor and channel attenuation. This method has been improved over the years, and Rubin et al. (2023) presented a more accurate approach for estimating the spatial WVD using CML.

In Song et al. (2021), a support vector machine (SVM)-learning model was used to estimate the WVD at a reference WS location using the received signal level (RSL) of CMLs at frequencies of 15 GHz, 18 GHz, and 23 GHz. This achieved relatively accurate results compared with reference WS humidity observations (WS-HO). This model was trained using prior RSL measurements from the CMLs and WS-HO. In Bragin et al. (2023), we leveraged that approach to show that using three CMLs (operating at frequencies approximately 23 GHz) significantly improved the WVD estimation at a reference WS with respect to the root mean square error (RMSE). Furthermore, we also showed that the addition of temperature measurement information (available from thermometers located at the WS) as an input to model estimations improved the results even further, reducing the overall RMSE to a value of 0.767 $g/m^3$, compared to 1.81 $g/m^3$ achieved by the approach suggested by Song et al. (2021), adapted for use in our scenario.

We here leverage the model first presented in Song et al. (2021) and expanded by us in Bragin et al. (2023) to present an approach that can make use of a much larger number of CMLs in combination with temperature data in order to achieve better accuracy. We test our proposed approach on a large area, giving us the possibility to use and compare its performance with 32 dedicated WSs. We then further show how to incorporate information regarding ground elevation and present a combined model capable of estimating a WVD field at multiple locations and elevations without being restricted to the original WS locations. This is done by utilizing multiple CML attenuation observations, temperature measurements, and the humidity-elevation profile, which we learn separately via a dedicated side model. This approach resulted in WVD estimates with an average RMSE of 0.587 $g/m^3$ compared to the reference WSs, outperforming our previously presented model, while producing a full WVD field which can be used to extract the WVD at locations where no WS was available for training—a limiting factor of previous models.

The rest of this paper is organized as follows. In Section 2, we present the full WVD estimation approach and describe the available data and its pre-processing. In Section 3, we demonstrate the use of our approach on a real-world experimental setup. Section 4 includes a discussion regarding the results and concludes this study.

2 Materials and methods

In this section, we first present in detail the three models that incorporate our WVD estimation approach (Sections 2.1–2.3), following by a description of the available data and the pre-processing stages performed on it (Section 2.4).

The three models are:

• WSHEM (2.1): a WS humidity estimation machine learning model that uses multiple CML attenuation with or without additional side information (i.e., the temperature and/or the measured timestamp) to estimate the WVD at a reference WS.

• WVDEP (2.2): a WVD–elevation profile model to determine the humidity–elevation profile.

• WVDEM (2.3): a WVD enhanced-estimation model. This is the fully enhanced approach that combines the WSHEM and WVDEP models to achieve high accuracy WVD spatial field estimation.

2.1 WS humidity estimation model (WSHEM)

This model is based on machine learning tools to estimate the WS-HO at each WS location. A support vector machine (SVM) regression model inspired by Song et al. (2021) was performed. SVM is a general function comprised of a sum of weighted kernel functions. The input of the SVM is a vector of parameters. Training the SVM is essentially fitting a hyperplane to a mapping of the input parameters and a given output. The fitted hyperplane and mapping are then used to predict an output for a given input. Further details regarding the SVM approach can be found in Vapnik (2013). The SVM regression was implemented using the Scikit-learn Python library Pedregosa et al. (2011). We set the SVM properties and hyperparameters as follows. (i) Radial basis function kernel with normalization (gamma coefficient) was used, with $1/N_f$ where $N_f$ is the number of features (length of model input vector). (ii) The SVM regularization parameter (C) was set to 1. (iii) All other hyperparameters were set to their default values.

The loss function was the $ϵ$-insensitive loss function as detailed in Vapnik (2013) and was set to 0.1.

The WSHEM is trained per WS using past measurements (see Section 2.4). That is, each WS is associated with a specific and different WSHEM instance. In the sequence, we use the following notations to address and differentiate between the different types and instances of the model:

$WSHE{M}_i^{\square }(j)$

where $j$ represents the index of each specific WS, and $i$ represents the number of CMLs used as input to the model. When more than a single CML is used, they are selected such that the closest CML to the respective WS will be chosen first. In the square superscript $\square$, the letter/s $T$, $H$, or $TH$ will be added in cases where, in addition to the CML data, the temperature, timestamp of the measurements (hour of the day), or both (respectively) are used as input to the model.

The rationale behind adding time as an input parameter is that sometimes the humidity exhibits a repetitive diurnal pattern (Rubin et al., 2022). This theoretically may provide additional information to the estimation model. Temperature and humidity are linked, as the higher the temperature, the higher the atmospheric WVD saturation (Koutsoyiannis, 2012); temperature could thus provide additional information to the estimation model. In Fencl et al. (2021), temperature measurements were in fact used alongside CML attenuation to improve WVD estimation model accuracy.

The WSHEM model that makes use of a single CML that is closest to the WS (i.e., ${\text{WSHEM}}_1(j)$) and the three closest CMLs (i.e., ${\text{WSHEM}}_3(j)$) are considered as the base models and will be used as the basis for comparison with the enhanced approach. We detailed a limited experimental result using those two basic models with a single WS in Bragin et al. (2023).

The WSHEM models use the CML attenuation time series without calibration or baseline removal in order to relate fluctuations in attenuation to WS-HO rather than absolute values. Fast and temporary changes to the baseline attenuation not related to humidity are dealt with at the pre-processing of the data, as will be detailed below. Aside from these temporally localized events, we assume that the baseline attenuation of the functional CMLs does not vary significantly throughout the time of the gathered data and especially not between the training and testing periods.

2.2 WVD-elevation profile

The WVD in a given area is correlated with the altitude of the area above sea level (ASL) as atmospheric water vapor generally decreases with altitude Ruckstuhl et al. (2007). That is, given a number of WS-HO measurements collected by different locations and elevations within a given area at the same time, it is possible to extrapolate the behavior of the WVD with respect to the changes in ground height. The WVD-elevation profile might change during the day (Rubin et al., 2022).

Therefore, in order to improve the capabilities of the proposed enhanced approach and to allow it to produce a full WVD field, we propose to use the WVD-elevation profile. We estimate the time-dependent WVD-elevation profile for the 24 h of a day, which is therefore actually comprised of 24 WVD-elevation profiles, one for each hour, as the WVD-elevation profile might change between the hours. We also estimate the WVD-elevation profile for all the hours together (without discrepancy between the hours). The estimation is done by first taking the median value of every WS-HO for each WS at each hour of the day for the time dependent case and at all hours together for the time-independent case. Then, a linear function is fitted to the median WS-HO as a function of the WS elevation ASL by minimizing the minimum square error (MSE), similar to the method presented in Rubin et al. (2022). We will thus have two WVDEP models: one is time-dependent (comprising 24 WVD-elevation profiles, one for each hour) and the other is time-independent (one general profile). At each given hour, the time dependent WVD-elevation profile uses the respective hour’s WVD-elevation profile, which is a fitted linear curve to the median WS-HO at that hour as a function of the WS’s elevation ASL.

Figure 1A shows an example of the daily WS-HO median plotted as a function of the WS elevation, with the resulting fitted linear curve.

Figure 1

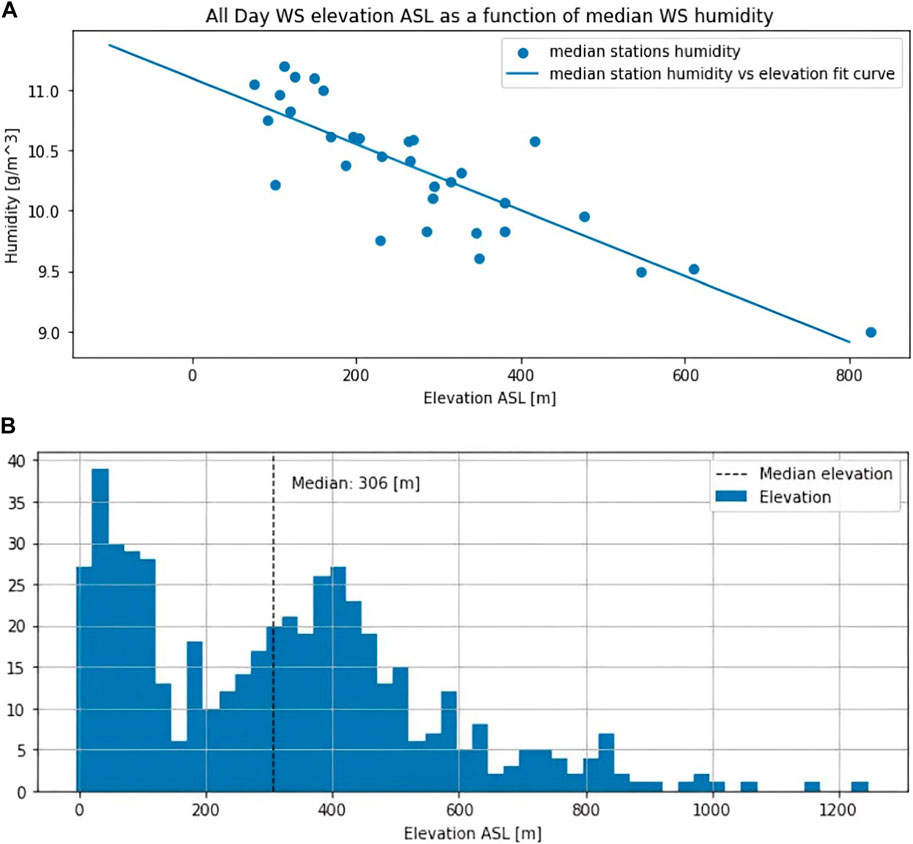
Figure 1. WS and CML elevations. (A) Median WS humidity measurement as a function of WS elevation in blue dots. Each dot represents a WS with a total of 32 WSs. The blue line is a fitted linear to the data. The data used are the first 70% of the available data at all hours of the day (training data: approximately 42 days). (B) CML elevation ASL histogram and median CML elevation. CML elevation is the mean elevation of both its points.

Note that the target data are the median WS humidity (per hour or total) over the training period and not the measurements themselves.

2.3 WVD estimation model (WVDEM)

Given the estimated hourly WVD-elevation profile (WVDEP) and an ensemble of trained WSHEMs (one for each WS), it is possible to estimate the WVD field at any point in space in the given area at a required time—the WVD spatiotemporal field.

The WVDEM algorithm goes as follows.

 0. A well-performing WSHEM ensemble is chosen with an optimal number of CMLs and side information.

 1. An hour, coordinate, and elevation are given for the WVD’s estimation.

 2. The distances to all the WSs are calculated using the haversine formula (Chopde and Nichat, 2013) as well as the elevation difference to all the WSs.

 3. All WS-HO estimations (given by the WSHEM) are adjusted to the elevation of interest using the estimated WVD-elevation profile.

 4. The elevation-adjusted WSHEM estimations are averaged.

The elevation adjustment for the WS-HO estimations is similar to the method in Rubin et al. (2022), using the slope of the WVD-elevation profile according to:

$WVD\left(h,WS\right)=m\left(h-h_{WS}\right)+WVD\left(WS\right),$

where $h$ is the elevation ASL of interest at which the WVD is estimated, $h_{WS}$ is the WS elevation, $WVD(h,WS)$ is the WVD estimation at elevation $h$ ASL at the WS lateral coordinates, $WVD(WS)$ is the WVD (or its estimation) at a WS coordinate at the WS elevation ASL, and $m$ is the slope of the WVD elevation profile (at a given hour).

The averaging of the elevation-adjusted WSHEM estimations can be a simple mean or a weighted average with weights inversely proportional to the distance between every WSHEM corresponding WS and the given coordinate (stage 3 in the above algorithm).

Thus, the estimated WVD field given by the WVDEM is calculated as follows:

$WVD\left(lon,lat,h\right)={\displaystyle \sum _{i=1}^N}\frac{w_k\left(n\right)WVD\left(h,WS\left(n\right)\right)}{N},$

where $WVD(lon,lat,h)$ is the WVDEM WVD estimation at longitude $lon$, latitude $lat$, and elevation $h$ ASL, $w_k(n)$ is the averaging weight of type $k$ of WS $n$ out of $N$ WSs. $WS(n)$ is the $n$^th WS of N, and $WVD(h,WS(n))$ is the WVD estimation at elevation $h$ ASL at $WS(n)$ lateral coordinates.

In Rubin et al. (2023), a version of the inverse weighting method (IDW) with a maximal radius of influence was used to average several CML attenuation-based humidity estimations. Here, we use a version that does not have a maximal radius of influence. The IDW weighing method is as follows:

$w_1\left(n\right)=\frac{\frac{1}{d_n}}{{\displaystyle \underset{i=1}{\overset{N}{\mathrm{\Sigma }}}}\frac{1}{d_i}},(1)$

where $n$ is the number of the WS-corresponding WSHEM estimations that are used, and $w_1(n)$ is the weight of each WSHEM estimation that is included in the average. N is the total number of WSHEMs (and WSs), and $d_n$ is the distance between the coordinate of interest and WS number $n$.

Another weighing method is possible. A linear weighing method (LD) is:

$w_2\left(n\right)=\frac{d_{\mathit{max}}+d_{\mathit{min}}-d_n}{{\displaystyle \underset{i=1}{\overset{N}{\mathrm{\Sigma }}}}{d}_{\mathit{max}}+d_{\mathit{min}}-d_i},(2)$

where $d_{\mathit{max}}$ is the distance from the coordinate to the farthest WS, $d_{\mathit{min}}$ is the distance from the coordinate to the closest WS, and $w_2(n)$ is the weight of each WSHEM estimation that is included in the average.

These weight functions give the least weight to the farthest WSHEM estimation (corresponding to the farthest WS) and the most to the closest. In $w_2(n)$, the change is linear. The sum of all the WSHEM weights is 1.

The WVD estimation model (WVDEM) is tested on one of the WS each time while using the WSHEM corresponding to all other WSs without the test WS’s corresponding WSHEM. A WVDEM is noted similarly to the WSHEM in the following manner:

$WVDE{M}_i^{\square }(j)$

where $j$ represents the index of each specific test WS, unlike WSHEMs that are named after their corresponding WS. The WVDEM uses all the WSHEMs aside from WSHEM(j) (as it is tested on WS “j” humidity observations). $i$ represents the number of CML used by the WSHEMs. In the square superscript $\square$, the letter/s $T$, $H$, or $TH$ will be added in cases where, in addition to CML data, the temperature, timestamp of the measurements (hour of the day), or both (respectively) are used as input to the WSHEM.

The WVDEM can use the WS-HOs instead of the WSHEM estimations. In such a case, the model instances will be noted as $WVDE{M}_{HO}^{\square }(j)$. If no elevation adjustment is used in the WVDEM, it will be marked with an asterisk in the subscript, as in $WVDE{M}_{*HO}^{\square }(j)$. If a weighted average is used by the WVDEM, then it will be noted as $WVDE{M}_i^{\square }(j,weighing\text{\_}method)$ where the weighing method could be either IDW or LD in the cases of inverse distance and linear distance weighing, respectively. The default is mean average.

2.4 Available data and pre-possessing

The data used in this study are based on measurements collected by WSs and CMLs in Germany during May and June 2018, as used and detailed in Rubin et al. (2022) and Bragin et al. (2023).

The received signal level (RSL) quantization level is 0.3 dB, and the transmitted signal level (TSL) quantization level is 1 dB. RSL and TSL were measured instantaneously every minute.

The WS measurements used in the paper were measured at the end of each hour (at 1-h intervals).

To correspond to the values observed by the WS and to increase accuracy, the RSL and TSL were averaged at the last 10 min of each hour. Since they were measured every minute, the mean average of the ten last RSL and TSL measurements of each hour are used. In every case where CML attenuation is now mentioned, it refers to the hour’s last 10 min average attenuation.

The CML total attenuation (A) in dB is given by:

$A=TSL-RSL.$

There are 3,862 CMLs ranging in frequency from 6.46 GHz to 38.85 GHz. The CMLs work at discrete frequencies. Not all frequencies at this range are being used by the CMLs, and there are small and major frequency gaps. Specifically, there are no CMLs in the frequency ranges of:

19.57 GHz–22 GHz,

22.3 GHz–23.08 GHz,

23.32 GHz–24.86 GHz.

At approximately 22.24 GHz, water vapor induced attenuation has a local maximum (Van Vleck, 1947), and it is expected that the effect of CML attenuation by water vapor will be maximal around this frequency. Therefore, for this work, we chose to mainly focus on the 505 functional CMLs that operate at a frequency range of 22–23.32 GHz (with the above frequency gap in between). Note that in Bragin et al. (2023), we only used CMLs with frequency of 23.086 GHz. The longer the CML, the stronger the water vapor attenuation due to the path length of the electromagnetic waves through the atmospheric water vapor.

Some of the other attenuation measurement factors such as measurement and quantization noise are not affected by the CML length. This means that the longer the CML, the better the SNR for the water vapor attenuation signal. The length of the CMLs used ranges from 2.4 km to 15.9 km, with a median length of 8.3 km.

The CML elevation refers to the mean elevation of both its points. The WVD changes with elevation (Rubin et al., 2022) and may also be affected at lower elevations by different land covers (Jin et al., 2022) and other local deviations from the larger scale humidity.

The humidity–elevation profile may change during the day with the diurnal weather pattern (Rubin et al., 2022).

The change of the median humidity with elevation can be seen in Figure 1A, where the median WS humidity measurement as a function of the WS elevation is plotted as in Section 2.2.

For a CML attenuation-based humidity estimation model, it is beneficial to have CMLs from varying elevations to minimize outlier local deviations from the general weather pattern. The CMLs used cover a wide range of elevations (Figure 1B) and are distributed quite uniformly across Germany (Figure 2B).

Figure 2

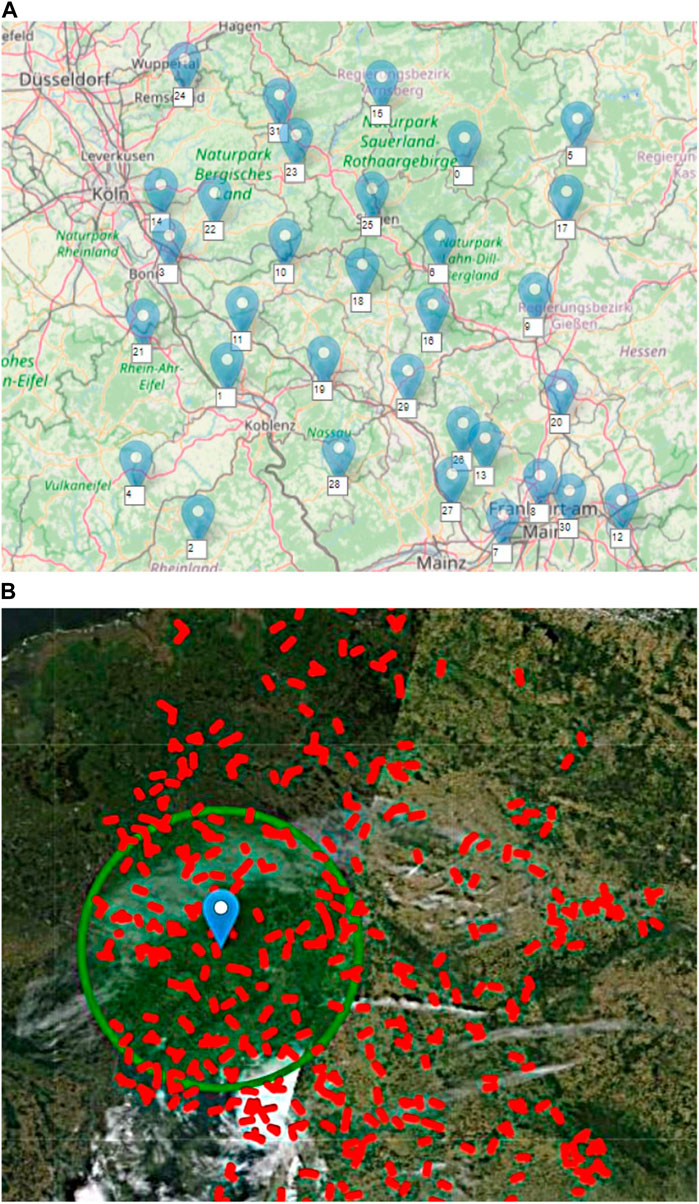
Figure 2. WS and CML maps. The data is the same as in Rubin et al. (2022). (A) WS (blue markers) and surrounding area. The total area is approximately 150 × 200 km. The white text box marks the WS number. (B) Map of available functional CMLs (red lines) and center of the WS group (blue marker). The 130 CMLs used by $WSHE{M}_{130}(18)$, located approximately at the center of the WS group, are in the green circle with a radius of approximately 133 km.

The WVD and temperature measurements were taken at 32 WSs located in western Germany (unlike the CMLs which are from all over Germany). The region is approximately at longitude 48–51.3 N and latitude 5-9 E (size of 1̃50 km 132 × 200 km) (Figure 2A).

Some WS-HOs had physically unlikely values, most likely due to instrument error. Therefore, WVD measurements outside the range of $0-51g/m^3$ were deleted. 51 g/m³ is the WVD at 40° Celsius at 100% relative humidity and 40° Celsius was not exceeded at the WSs temperature measurements. This was not done in our previous preliminary paper (Bragin et al., 2023).

The WS-HO standard deviation mean value is 2.590 $g/m^3$, so there is variability (mean WS-HO standard deviation) in the data such that learning is possible (as opposed to data with little variability where simply a constant value can be set as an estimator).

The variation between the different WSs humidity observations’ standard deviation is 0.128 $g/m^3$ and indicates that the weather patterns do not change much between WSs. The difference between the WS mean humidity observation is more noticeable as the mean WS mean HO is 9.880 $g/m^3$ and the WS mean HO range is 8.797–10.603 $g/m^3$, with the WS mean HO standard deviation at 0.409 $g/m^3$. This along with the humidity–elevation profile (Figure 1B) indicates that it is most likely because of the difference between the various WS elevations and local conditions.

Another indication that the different WSs experience the same humidity pattern is in Figure 3A, showing the correlation between WS 12 and the other WSs as a function of their distance from each other. WS 12 was chosen as it is on the fringe of the WSs group, as in Figure 2A.

Figure 3

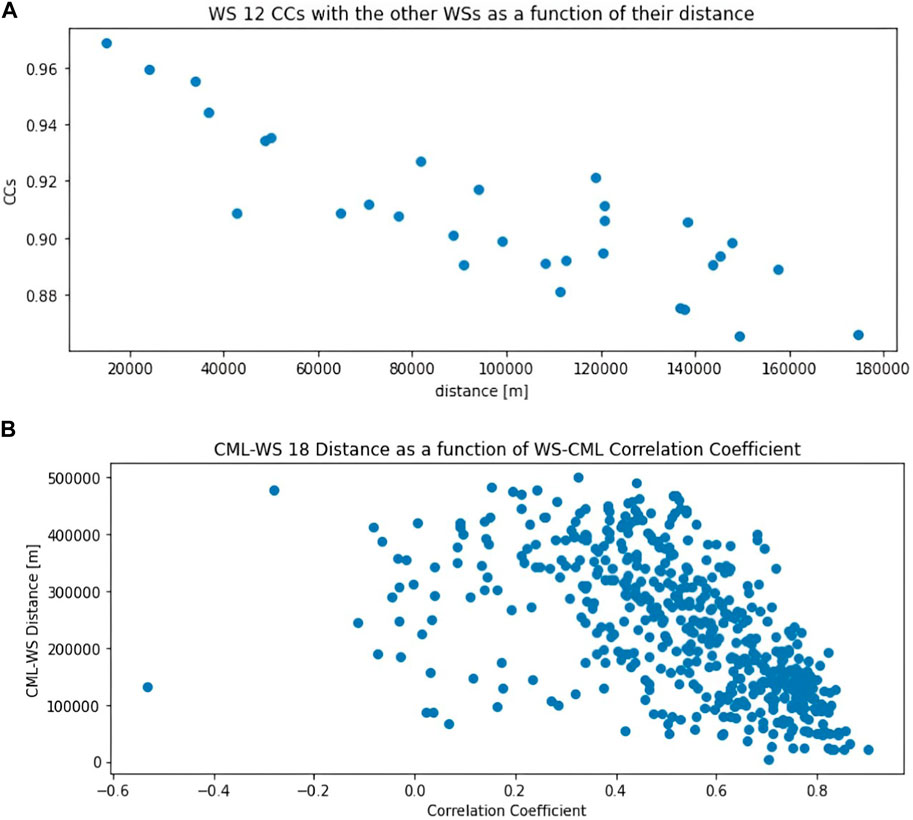
Figure 3. Correlation coefficients of the WSs with other WSs and with the CMLs. (A) Correlation coefficients of WS 12 against the other WSs as a function of their distance. (B) Correlation coefficients of the 505 available CMLs and WS 18 as a function of the distance between them. Note that the farther the CML from the station, the lower the likely correlation will be.

Figure 3A shows that all the WSs have very high correlation between them, with a minimum of 0.87 for the farthest WS.

Note that the correlation coefficient (CC) generally goes down as the distance between the WSs increases.

The distances from every WS to all the available CMLs centers were calculated.

The averaged CML attenuation data (one value per hour) were aligned with the WS-HO and temperature observations time series.

Even after averaging the last 10 min of every hour, many CMLs had extreme attenuations that are most likely caused by malfunctions or obstructions (that could also be meteorological). Initially in Bragin et al. (2023), these extreme attenuations were addressed by omitting attenuation values outside the 0.001 to 99.99 percentile range. This study takes a different, more robust approach.

In cases where the malfunctions were continuous such that the attenuation time series statistics were altered significantly, the CMLs were considered dysfunctional and were omitted from the database. They were removed by individually observing each attenuation time series. This resulted in the loss of less than 10% of the CMLs and the aforementioned 505 available functional CMLs. Examples of such dysfunctional CMLs are in Figure 4A.

Figure 4

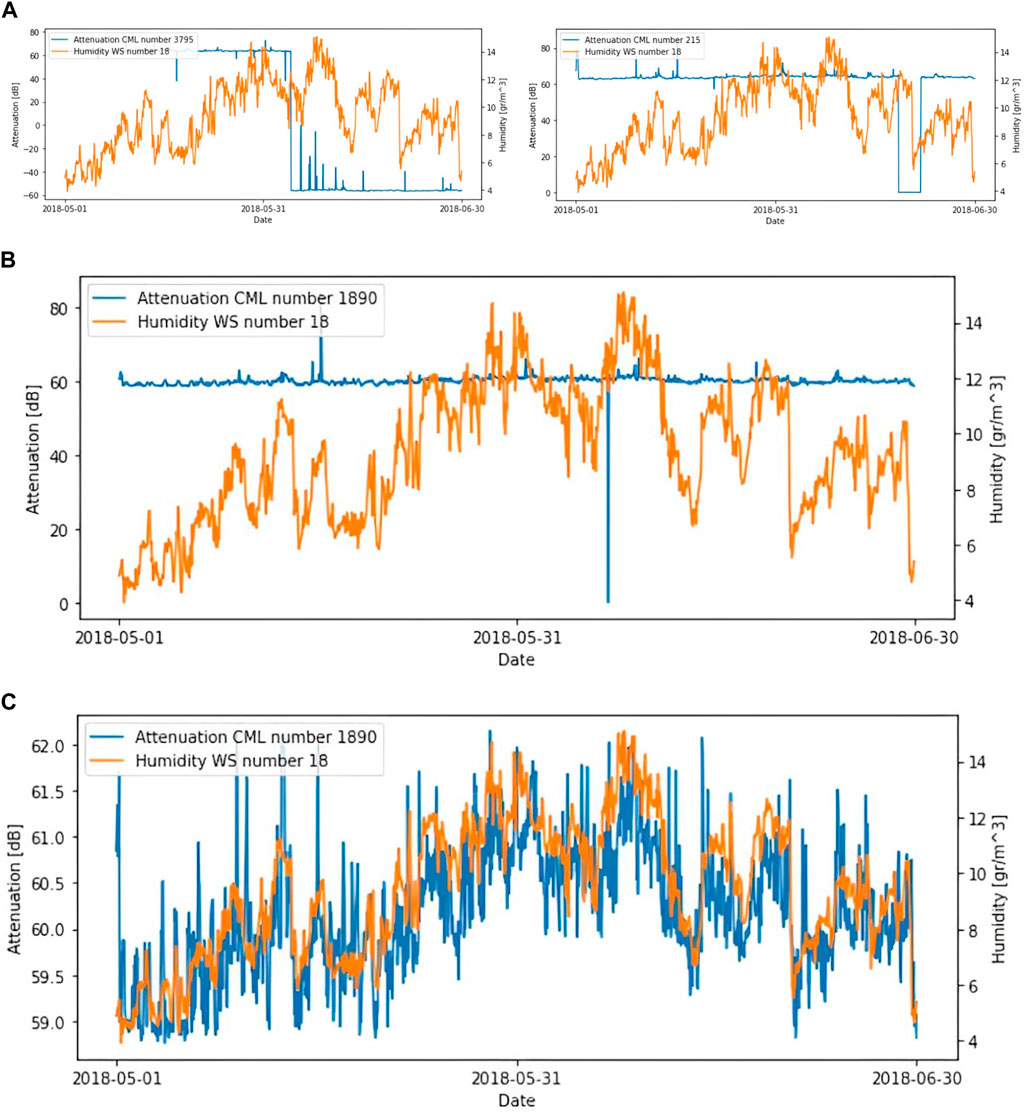
Figure 4. Example of a CML attenuation time series with outlier extreme attenuations before (B) and after (C) IQR outlier detection and interpolation is represented in blue. An example of WS 18 HO for comparison is represented in orange. (A) Examples of CML attenuation time series with major malfunctions are represented in blue. An example of WS 18 HO for comparison is represented in orange.

For the other CMLs, where extreme attenuations were anecdotal, the extreme outlier attenuations were interpolated to be the nearest previous non-outlier attenuation value.

Outlier attenuations are marked using the interquartile range algorithm as per Fredianto and Putri (2023) and Baek et al. (2022). The interquartile range (IQR) is defined as:

$IQR=Q_3-Q_1,$

where $Q_3$ and $Q_1$ are the third and first quartiles of attenuation, respectively. Outlier attenuations are those whose values exceed $1.5IQR$ above $Q_3$ (i.e.,$>Q_3+1.5IQR$) or below $1.5IQR$ below $Q_1$ (i.e., $<Q_1-1.5IQR$). An example of a CML attenuation time series before and after IQR algorithm outlier detection and interpolation is shown in Figures 4B and C.

The IQR method is preferable to the previous method of outlier detection using a fixed percentile threshold (as used in our previous paper, Bragin et al., 2023), particularly because it is more robust to extreme values and better suited for skewed distributions. By focusing on the middle 50% of the data, the IQR method reduces the influence of outliers, leading to a more reliable detection process (Seo, 2006).

In our previous paper, outliers were deleted along with their associated timestamps rather than being interpolated. This approach resulted in significant information loss, especially as the number of CMLs increased, since any timestamp with an outlier in any of the CMLs was entirely removed.

The WS aligned time series after the above processing had a length of 1,455 points ± 2 points (aside from the WS 1 aligned time series with a length of 1,356).

For each time-series, the last 30% of the data points were used as the test set for evaluating the humidity estimation models while the rest was used for training (i.e., from 8 weeks of data, the last 17 days were used as test data). This temporal separation for train and test datasets ensures that during training, the model is not exposed to future conditions for which the estimation will be performed, so no bias from close by time periods or data points is introduced into the model—which would be the case if random train-set selection was made. This prevents the training from being over-optimistic and thus enhances the training procedures performed (de Bruin et al., 2021). The statistics of the train set and test set WS measurements are very similar aside from one difference: the mean WS-HO standard deviation is 2.880 $\frac{g}{m^3}$ for the train period while it is 1.783 $\frac{g}{m^3}$ for the test period. This indicates some change to the weather pattern between the periods.

The CCs between the CMLs’ attenuation and the WS-HO time series largely decrease as the distance between CML and WS increases. In Figure 3B, the CCs between the 505 available CMLs and WS 18 are presented as a function of the distance from CML to WS. Since we established from the WSs-HOs statistics and Figure 3A that the different WSs largely measure the same weather patterns, Figure 3B is a good indicator for other WSs, especially since WS 18 is at the center of the WSs group (Figure 2A).

From the usual decrease in CC value with distance between the CML and the WS, a good “rule of thumb” we used was to use the closest CMLs to a WS to train a WSHEM.

3 Results

The estimation models are fed with the CML attenuation time-series (one time stamp at a time) without any removal of the base line attenuation, such as done in Rubin et al. (2022). We expect the models to be able to establish the correct relationship between the total attenuation values and the WS-HO based on the fluctuations rather than the absolute values. In accordance with previous research on similar topics (Rubin et al., 2022; Song et al., 2021; Andersson et al., 2007; Bragin et al., 2023), the performance of the various models will be measured using the RMSE and CC metrics.

3.1 WS-HO estimation basic model

For the basic model $(WSHE{M}_1)$, we used the closest CML to each WS. Table 1 presents the mean and standard deviation of the distance of the CMLs from their corresponding WSs in the case of one CML and the mean and standard deviation of the distance to the farthest CML for multiple CMLs. The standard deviation of the CMLs’ distance from their corresponding WS is of the same order of magnitude as the mean distance in the case of one CML. This large variation in CML distance from the WS might induce some more variation in the WSHEMs RMSE and CC, as change in local conditions is more influential in such cases. High RMSE and CC variation is indeed observed in $WSHE{M}_1$, as can be seen in Table 2, which presents the 1-, 3-, and 130-CML WSHEM WSs-HO estimation statistics.

Table 1

Table 1. Radii of 1, 3 and 130 CMLs.

Table 2

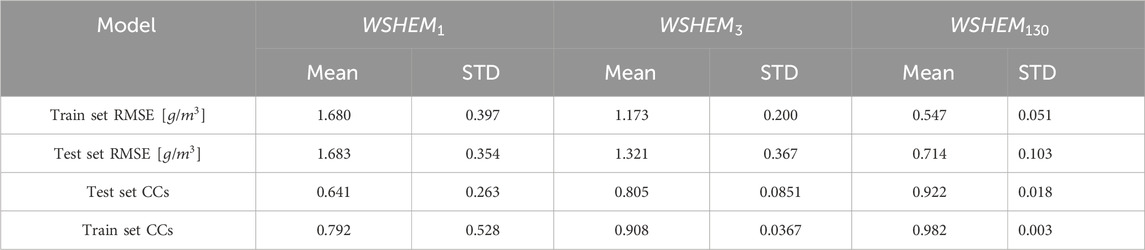
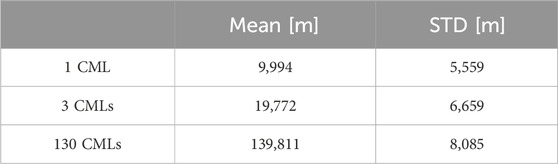
Table 2. Mean and standard deviation (STD) of the 32 WS-HO estimation models based on 1, 3, and 130 CML SVM.

As in Table 2, the mean test set RMSE of the basic model is 1.683 $g/m^3$, while in Song et al. (2021), the test set RMSE was 1.89 (at 23 GHz) and in Bragin et al. (2023) it was 1.81 $g/m^3$ for the single CML model compared to a single WS. Note that in Table 2, the mean RMSE of 32 $WSHE{M}_1$ referring to 32 WSs is shown instead of a single WS, as in previous studies. Figure 5A depicts $WSHE{M}_1(18)$ estimations compared to the WS-HO for WS 18 time-series (for the test data).

Figure 5

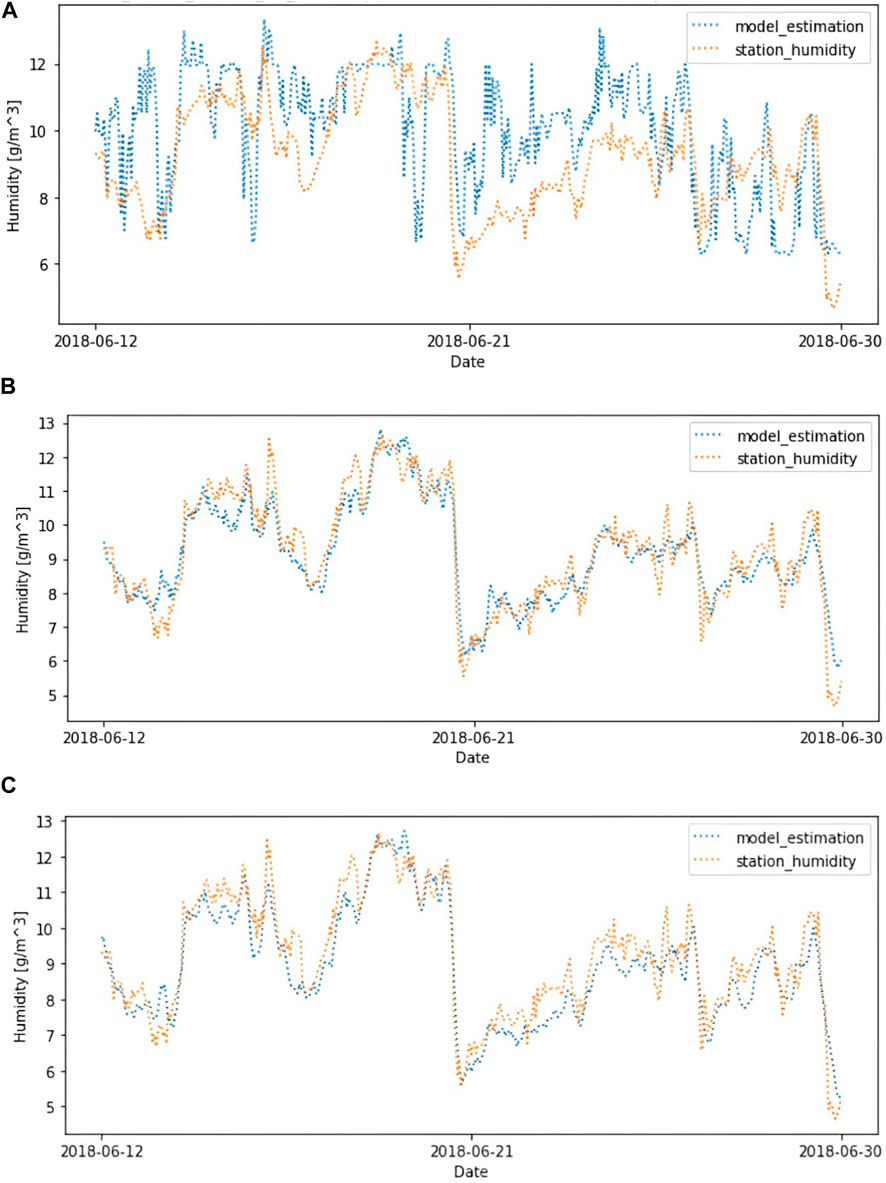
Figure 5. WS 18 WSHEM estimations (blue) and WS 18 -HO time-series (orange) for 17 days of test data for the basic model $WSHE{M}_1(18)$ (A) and for the 130-CML and temperature WSHEM $WSHE{M}_{130}^T(18)$ (B). In (C), $WVDE{M}_{130}^T(18)$ estimations are represented in blue, and WS 18 -HO time-series, in orange. For WS 18, $WSHE{M}_1(18)$ had an RMSE of 1.683 $g/m^3$, and for $WSHE{M}_{130}^T(18)$, an RMSE of 0.634 $g/m^3$. $WVDE{M}_{130}^T(18)$ test set RMSE is 0.587 $g/m^3$.

Thus, despite the differences mentioned in Bragin et al. (2023) between the data used here and in Song et al. (2021), the basic models here in these references performed similarly. This indicates that the performance of the more advanced models can be compared to both basic models.

3.2 WS-HO estimation advanced models

The first improvement of the basic WSHEM $(WSHE{M}_1)$ was achieved by incorporating additional CML attenuation data (from closest to farthest) to the SVM, which showed significant improvement to the accuracy of the WVD estimates (and as such, the RMSE when compared to $WSHE{M}_1$ was smaller). In Bragin et al. (2023), we introduced a model that uses three CMLs ($WSHE{M}_3(18)$), and its RMSE was 0.896 $g/m^3$. However when tested on all 32 WSs, the mean RMSE was 1.321 $g/m^3$, as can be seen in Table 2, where $WSHE{M}_3$ statistics are shown. High result variations were also observed in this case. A possible contributing cause might again be the large variation in farthest CML distance compared to the mean farthest CML distance (Table 1) combined with a small number of indicators of three CMLs. This makes isolating the larger WVD pattern from the varying local conditions harder for the WSHEM.

There is reason to believe that the more CMLs available to the estimation model, the better its performance.

Even in cases where the additional CML attenuation data are uncorrelated to the WS-HO, one might expect that the model would learn to ignore the irrelevant data source.

However, the experimental setup has shown that the models do have a maximal number of CMLs that can be used without decreasing model error and thus reduce performance.

The optimal amount of CMLs used in an WS-HO estimation model is calculated by iteratively incorporating more CMLs until the point where model performance decreases—that is, training the WSHEMs for all WSs at an increasing number of CMLs until the mean RMSE stops improving (and at some point, even gets slightly worse).

This computation was done again only with an increasing radius around each WS inside of all the CMLs are used.

The mean test and train set RMSEs and their standard deviation confidence intervals for each number of CMLs (or CMLs containing radius) can be seen in Figure 6.

Figure 6

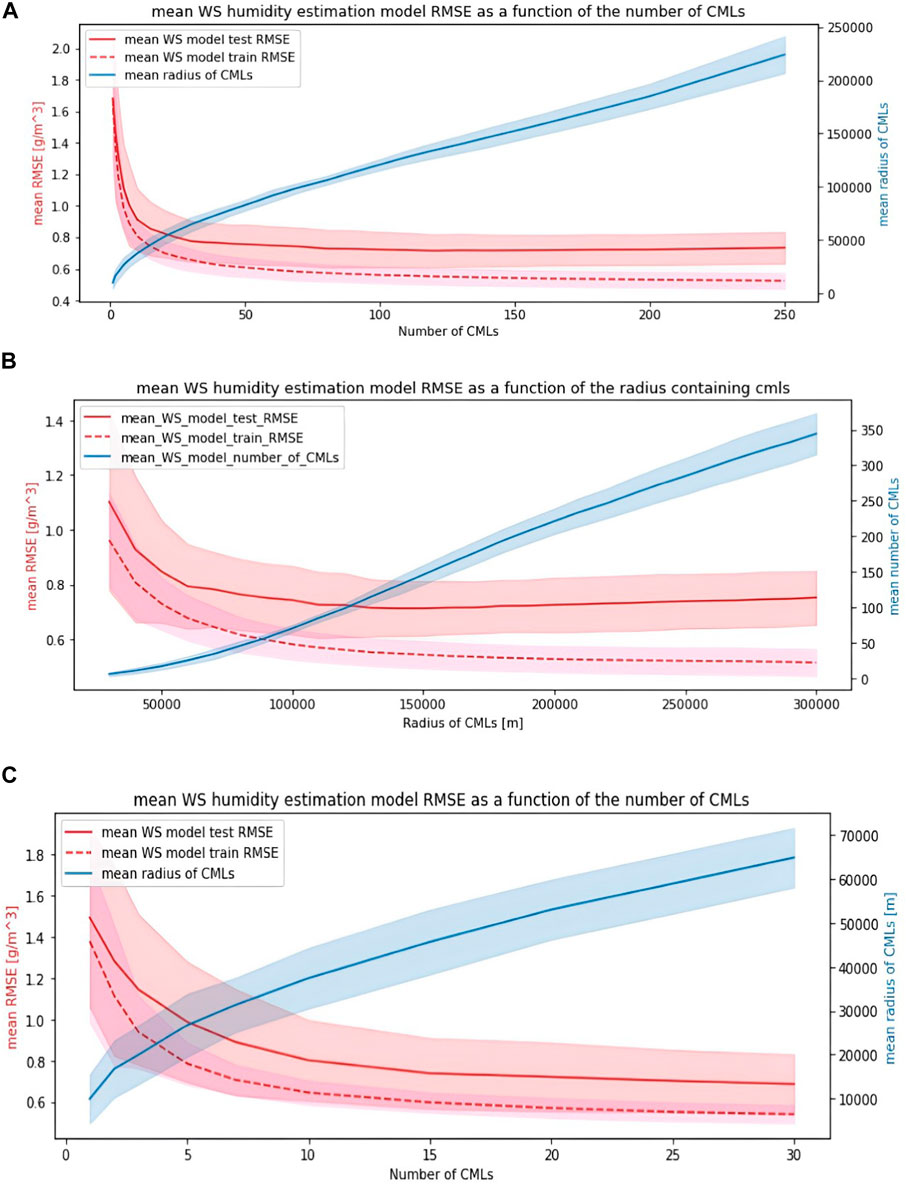
Figure 6. Mean SVM-based WSHEM RMSE, with red lines for test (continuous line) and training (broken line) sets and corresponding translucent red areas representing standard deviation confidence intervals. Mean CML containing radius is represented in blue, along with its standard deviation confidence interval (blue translucent area), both as a function of the number of CMLs used by the models. Without temperature in (A) with temperature in (C). Mean SVM-based WSHEM RMSE, with red lines for test (continuous line) and training (broken line) sets and corresponding translucent red areas representing standard deviation confidence intervals. The mean number of CMLs is represented in blue, along with standard deviation confidence interval (blue translucent area), both as a function of the radius containing the CMLs used by the models (B).

Both Figures 6A and B show that WSHEM reaches near optimal mean RMSE at approximately 50 CMLs and optimal results at 130 CMLs (with little improvement in the mean RMSE between the two numbers of CMLs used). For research purposes, the optimal number of 130 CMLs is used.

Table 2 presents the 1-, 3-, and 130-CML SVM WSHEMs, $WSHE{M}_1$, $WSHE{M}_3$, and $WSHE{M}_{130}$ statistics.

Table 2 shows major improvement in both mean RMSE and CCs for both test and training sets compared to the basic single CML SVM based $WSHE{M}_1$ and 3-CML SVM based $WSHE{M}_3$.

$WSHE{M}_{130}$ mean RMSE is 0.714 $g/m^3$, while $WSHE{M}_1$ mean RMSE is 1.683 $g/m^3$—over twice smaller.

Adding the hour of day as an additional input parameter was tested. For the 3-CML model, adding time, on average, very slightly improved results over our previous study (Bragin et al., 2023), where adding time slightly degraded model accuracy. This is possible since the data process was improved and the model was tested on more WSs. The 3-CML and time SVM model $WSHE{M}_3^H$ statistics are in Table 3.

Table 3

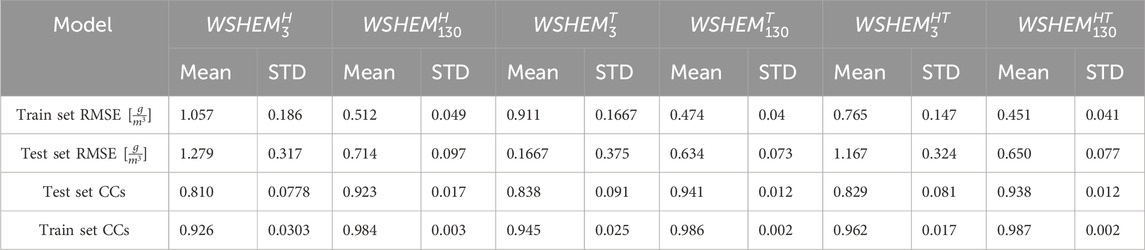
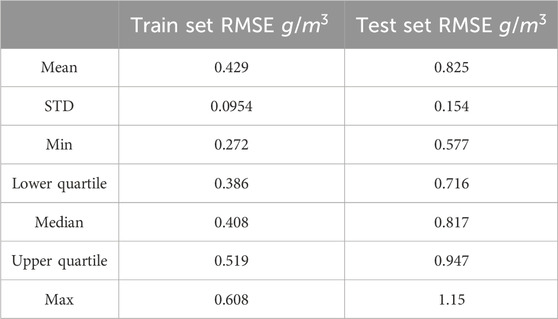
Table 3. Mean and standard deviation (STD) of the 32 WS-HO estimation models based on 3 and 130 CMLs with time and/or temperature SVM.

Adding the hour of day as an additional input parameter to the 130-CML model slightly lowered the minimum and maximum RMSE measured but also slightly increased the upper quartiles RMSE as well as the median RMSE. Test-set RMSE decreased more noticeably.

Adding time also slightly increased the CCs, especially for the training set compared to the WSHEMs without time as a parameter.

The test-set CCs did not improve meaningfully with the addition of time as a parameter.

This effect on model performance can be seen in Table 3. The insignificant improvement in test-set CCs and negative effects on RMSE instigated by the addition of the time parameter for the 130-CML WSHEM and the negligible improvement for the 3-CML WSHEM serves as an indicator not to use the addition of time as a parameter for the next stages of the algorithm.

As opposed to adding the time of day as an additional input parameter, adding the temperature observations (as measured by the WS) slightly increased the accuracy of the WSHEMs and thus decreased the RMSE and increased CCs across the board for both the 3-CML and 130-CML WSHEM. The results can be seen in Table 3, which also presents 130-CML and 3-CML both with WS temperature measurement WSHEM ($WSHE{M}_3^T$ and $WSHE{M}_{130}^T$) statistics respectively. Obviously, the $WSHE{M}_{130}^T$ ensemble still performs better than $WSHE{M}_3^T$ and any previous model. Figure 5B depicts $WSHE{M}_{130}^T(18)$ estimations compared to the WS-HO for time series of WS 18 (for the test data).

To ensure that both the CML attenuation and WS temperature measurements contributed significant data to the WSHEM, as opposed to just the temperature measurement being the main indicator for humidity and the CML attenuation an insignificant data source in comparison, the multi-CML and WS temperature measurement SVM WSHEMs were trained on an increasing number of CMLs and corresponding WS temperature measurements. The mean test and train set RMSE as well as their standard deviation confidence intervals for each number of CMLs can be seen in Figure 6C.

Figure 6C shows that Both the CML attenuation and the WS temperature measurements contribute to the model’s performance, as the addition of more CMLs improves the WSHEM's performance.

To test that indeed the addition of time as a parameter is not beneficial in any meaningful way, it is again tested with the addition of WS temperature as a parameter (along with the 130 and 3 closest CMLs to each WS). $WSHE{M}_3^{TH}$ and $WSHE{M}_{130}^{TH}$ were tested, and Table 3 presents their statistics; the addition of time to temperature as a parameter did not improve the test set’s WSHEM performance and even degraded it slightly.

However, for the training set, the addition of time as a parameter led to better fitting of the model to the data (and lower RMSE and higher CCs). A possible cause for this phenomenon is that the diurnal humidity pattern changes from the training to the test period. This possibility is reinforced by the change between the mean WS-HO standard deviation in the training and test periods. Nonetheless, the lack in performance improvement by the addition of time as a parameter reinforces the decision to not use time as an input parameter.

The 130-CML and WS temperature measurement SVM $WSHE{M}_{130}^T$ has the best performance on average followed by the 130-CML and SVM $WSHE{M}_{130}$.

3.3 WVD-elevation profile results

In Rubin et al. (2022), the WVDEP was trained in the 2 weeks prior to the testing period, and it was assumed that the diurnal WVD-elevation profile would not change significantly between the training and test periods. Here, we assume the same, only that the training period is the prior 42 days (the entire training period). The linear curve fitted in Figure 1A is for the median WS-HOs for all the hours together. The fitted linear approximation for the WVD elevation profile in that case is:

$WVD=-0.00274h+11.1,$

where $h$ is the elevation above sea level (ASL) in meters and the WVD is in $g/m^3$.

The fitted linear train set RMSE is 0.298 $g/m^3$, and the test set RMSE is 0.809 $g/m^3$.

The same fit was done also for the median WS-HOs for every hour of the day. The slope of the line is the only significant parameter, as we use elevation differences to adjust humidity based on elevation.

The slope of the fitted linear curves for the hourly median WS-HO, as a function of elevation, ranged from −0.00165 $g/m^4$to −0.00373 $g/m^4$.

The fitted curves statistics can be seen in Table 4.

Table 4

Table 4. Hourly WVD-elevation profile RMSE statistics.

The difference between the training and test set RMSE might indicate that there is some variation in the WVD-elevation profile from the training to the test period. However, we use the fitted linear curves under the premise that the change in WVD-elevation profile from the training to the test period is not large enough to make the WVD-elevation profile irrelevant. The basis for the premise is that, according to Figure 1A, the median WS-HO range for the WS elevation range used is approximately 2.5 $\frac{g}{m^3}$ while the test set error for the WVD-elevation models is mostly below 1 $\frac{g}{m^3}$.

Table 4 shows some variation between the different hours’ WVD-elevation profile test set RMSE, indicating that the profile does change somewhat between the hours and strengthens the conjecture that the diurnal pattern changes from the training to the test period.

3.4 WVD estimation model results

The WVD estimation models (WVDEM) use an average (weighted or not) of the elevation-adjusted WSHEM estimations. It is tested on one WS at a time while using the WSHEMs corresponding to all other stations without the corresponding WSHEM of the test WS. The WVDEM is tested over the test period data detailed in Section 2.4.

WS 1 WSHEM was not used since the WS 1 aligned time series had a length shorter by about 7% from the rest of the WSs’ aligned time series. The shorter time-series would shorten the number of available data points for the other test stations estimations and might skew the results. Note that WS 1 was used as a test WS.

We first establish a base-line performance for the WVD estimations by using the WS-HO instead of the WSHEM estimations ($WVDE{M}_{HO}$).

This removes the error component imposed by the inaccuracy of the WS-HO WSHEM estimations. The WVDEM test results using the mean averaged WS-HOs without and with elevation adjustment are in Table 5.

Table 5

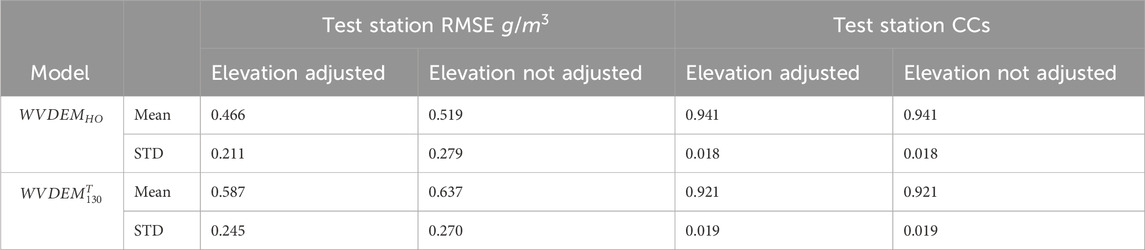
Table 5. 32 test WSs mean and standard deviation (STD) of mean average WS-HO and 130-CML and temperature WSHEM-based WVDEM with ($WVDE{M}_{HO}$, $WVDE{M}_{130}^T$) and without $(WVDE{M}_{*HO},WVDE{M}_{*130}^T)$ elevation adjustment.

From Table 5, the use of the learned WVD-elevation profile decreased the WVDEM RMSE, even though the WVD-elevation profile had a substantially larger RMSE for the test period data than the training data (as in Table 4).

This shows that despite possible changes of the WVD-elevation profile from the training to the test period, it is still relevant to the latter.

Table 6 shows the WVDEM test results using the IDW weighted average (Equation 1) and linear distance weighted average (Equation 2) WS-HOs with elevation adjustment. It is apparent that the change of the weighing method of the average to give less weight to more distance WSHEMs increased the RMSE of the WVD estimations but also slightly increased the correlation coefficients. The increase in correlation is expected as, generally, the closer WSs are to each other, the higher they are correlated—as mentioned above and depicted in Figure 3A. In accordance with this phenomenon, the above weighing methods give more weight to closer WSs. However, the increase in RMSE was not expected and may be a result of some bias.

Table 6

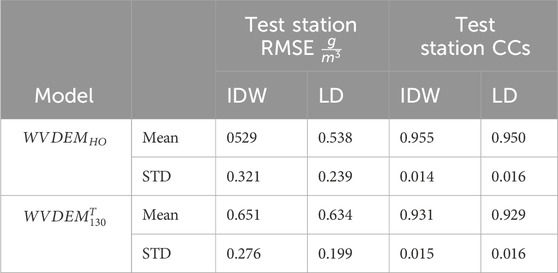
Table 6. 32 test WS mean and standard deviations (STD) of IDW and linear distance averages’ elevation-adjusted WS-HO-based WVDEM and 130-CML and temperature WSHEM based WVDEM ($WVDE{M}_{HO}(IDW)$, $WVDE{M}_{130}^T(IDW)$, $WVDE{M}_{HO}(LD)$, and $WVDE{M}_{130}^T(LD)$) test WS statistics.

Next, instead of the WS-HOs, the WSHEM estimations are used for the WVD estimations. Recall that the WSHEMs estimate their corresponding WS-HOs.

The WVDEM test results using the mean (not weighted) average, elevation-adjusted 31 130-CML with and without WS temperature measurement SVM WSHEMs ($WVDE{M}_{130}$ and $WVDE{M}_{130}^T$) are shown in Table 7.

Table 7

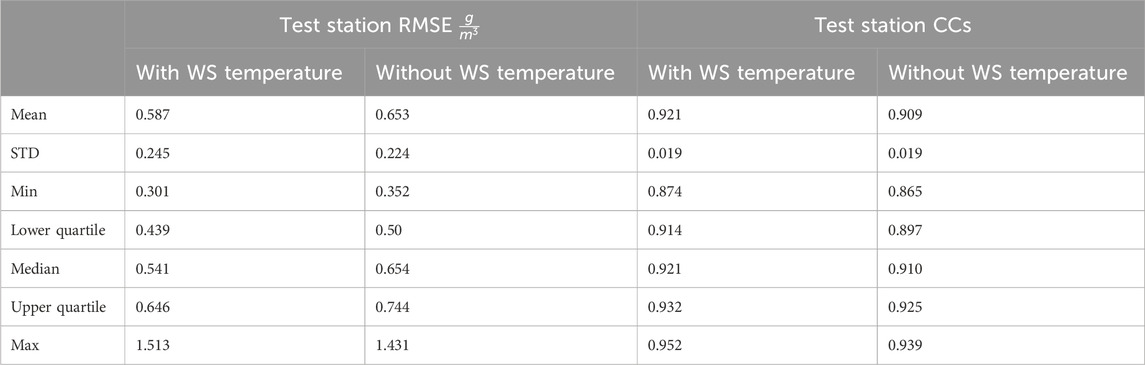
Table 7. 32 test WSs’ mean and standard deviation (STD) of mean average 130-CML with and without WS temperature SVM elevation-adjusted WSHEMS-based WVDEM test WS statistics ($WVDE{M}_{130}$ vs. $WVDE{M}_{130}^T$).

The increase in RMSE and decrease in correlation compared to the WS-HO being used for the WVDEM (Table 5) is expected as, instead of using the WS-HO, its estimation is used (given by the WSHEMs). However, in both cases the mean RMSE over the test WSs is lower than the mean RMSE of $WSHE{M}_{130}$ and $WSHE{M}_{130}^T$ compared to their respective WSs, and we consider it a low RMSE.

To test again the benefit of the WSHEM estimation adjustments based on the WVD-elevation profile, the WVDEM was tested without the elevation adjustments using the SVM 130-CML and WS temperature WSHEMS. The WVD with $(WVDE{M}_{130}^T)$ and without $(WVDE{M}_{*130}^T)$ elevation adjustment test results are shown in Table 5.

This table shows again a higher mean RMSE and worse overall performance than when elevation adjustment is not used and thus shows that elevation adjustments are indeed beneficial.

Indeed, a notable effect was on WS 13, the highest WS with an elevation of 826 [m] ASL, whose RMSE (the maximum RMSE) increased to 1.651 $g/m^3$ from 0.364 $g/m^3$. As mentioned before, the averaging of the WSHEM elevation adjusted estimations in the WVDEM can also be weighted.

The WVDEM—using the SVM 130-CML and WS temperature WSHEM—test statistics with IDW averaging and linear weighted averaging are shown in Table 6.

Again, the use of the weighted averages increased the RMSE but also the CCs (compared to Table 5 with elevation adjustment). This indicates that some bias was introduced into the WVDEM model estimation.

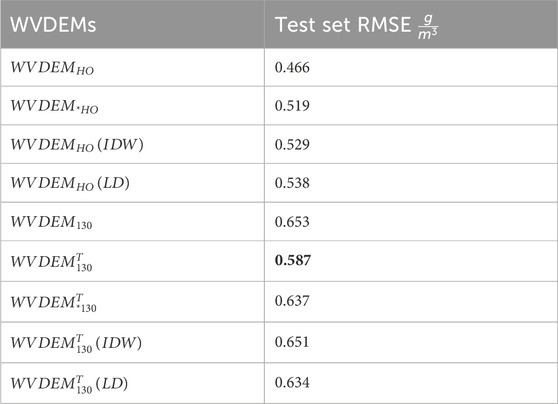
The WVDEMs that were tested and their respective test set mean RMSE are in Table 8.

Table 8

Table 8. WVDEM test set mean RMSE.

The WVDEM based on mean average, elevation adjusted, 31 WSHEMS that use attenuation data from CMLs with $(WVDE{M}_{130}^T)$ and without $(WVDE{M}_{130})$ WS temperature measurements achieved a low average mean RMSE of 0.587 $g/m^3$ and 0.653 $g/m^3$, respectively, and is generalized for locations not restricted to the WSs and their ground elevations. An example of $WVDE{M}_{130}^{T}18$ estimation compared to WS 18 HO can be seen in Figure 5C. This means that the WVDEM can estimate the WVD field in the research area with good accuracy.

4 Discussion and conclusion

This study presents an algorithm for estimating the WVD field using CML attenuations and WS temperature readings, termed $WVDE{M}_{130}^T$. The algorithm uses two models: one, an ensemble of WS-HO estimation models $(WSHE{M}_{130}^T)$ and the other, an hour-dependent WVD-elevation profile model (WVDEP). Several variations of this algorithm were shown, with the main difference between them being the number of CMLs used and different additions (or lack thereof) of side information such as time and temperature. Nonetheless, the $WVDE{M}_{130}^T$ RMSE was the lowest, so much so that, on average, it was lower than $WSHE{M}_{130}^T$ when compared with each instance’s respective WS without having its estimations restricted to the WS location.

The WSHEM models were first introduced by us in Bragin et al. (2023) and are expanded upon in this paper. The incorporation of more than one CML attenuation datum as input to the WSHEMs drastically improved the accuracy of the WVD time-series estimates for RMSE and CCs compared to the respective WS-HO time-series. This increase in accuracy probably occurs due to additional data of the non-WVD factors that cause (some) of the CML channel attenuation, which might be differently spatial-temporal dependent than WVD; this in turn enables the model to isolate and learn the WVD-based attenuation effects better.

The 130-CML SVM-based $WSHE{M}_{130}$ and $WSHE{M}_{130}^T$ had very good performance; however, when more than 130 CMLs are used or when CMLs from over 150 km are used, WSHEM performance started to degrade slightly.

It might be assumed that the more CMLs available to the estimation model, the better its performance.

Even in cases where the additional CML attenuation data are uncorrelated to the WS-HO, it might be expected that the model would learn to ignore the irrelevant data source.

However, the experimental setup has shown that the models do have a maximal number of CMLs that can be used without decreasing model error beyond which there is reduced performance.

A possible reason for this could be model overfitting.

When the amount of data are unlimited, an increase in input parameters could not degrade the model performance but only improve it if the new inputs contain relevant information.

Practically, the amount of available data are limited, and even the addition of too much relevant, well WS-HO-correlated, CML attenuation as inputs might degrade the estimation model’s performance because the more inputs the model has, the more complex it must be.

Given a fixed amount of time (or data) for training, the model can only be so complex before the available amount of training data will not suffice to tune all its parameters, which would result in overfitting (Ying, 2019).

However, it is not certain that this is the case as SVMs are known to be robust to overfitting, especially in cases where the number of features is much smaller than the length of the database, as in the case of WSHEM (Hua et al., 2005).

Another possible reason for the degradation of the WSHEM results beyond a certain number of CML attenuation as input features is that very far CMLs might not always correlate very well with the WSs (as faraway areas may experience different weather patterns). This correlation might also change from time to time, depending on the weather patterns. Recall that the increase in the number of CMLs is from nearest to farthest. Thus, the phenomenon of the degraded test period WSHEM performance occurs when CMLs at distances of 150 Km and more are used. These could have been in a humidity pattern more closely resembling that in the WS area during the training period and not during the test period. This would confuse the model as it would give weight to inputs that are misleading.

Similar cases are the suspected change in the diurnal humidity pattern and WVD-elevation profile from the training to the test period. In any case, depending on the amount of available data and distance from the WS, there most likely exists a CML number that could be used to establish a well-performing WSHEM. Thus, even though the cause of the WSHEM degradation of performance with an increasing number of CMLs beyond a certain point should be further investigated, it does not prevent the use of the WSHEM algorithm given an established CML number for use.

The addition of time of day as a parameter for estimation seemed reasonable since previous research identified diurnal patterns in WS-HO and CML attenuation data (Rubin et al., 2022). The 3-CML model indeed showed very slight and not meaningful improvement. However, the 130-CML model’s performance decreased on average when time was added as an input to it. At the WSs where the model’s performance increased (marginally) with the addition of time, the performance was even better with the addition of temperature measurements.

It is possible that the humidity diurnal pattern is not very stable throughout the time of the gathered data. Specifically, it changes from the train to the test period. This suspected change is supported by the aforementioned change of the mean WS-HO standard deviation between the train and test periods (Section 2.4).

This explains the improved performance of the WSHEMs at the training period (more relevant data) and their performance degradation in the testing period (diurnal pattern change) compared to the WSHEMs that did not use time as a parameter.

The change of the diurnal humidity pattern from the training to the test period would also explain some of the increase in variation of the RMSE of the hourly WVD-elevation profile between the periods (Table 4).

Nonetheless, the correct implementation of the time of day as an additional input should be investigated in future research.

In contrast, the addition of WS temperature time-series observations as an additional input did increase estimation accuracy. This enhanced accuracy can be attributed to the fact that temperature is a parameter in determining the saturation of humidity in the air (Koutsoyiannis, 2012).

The negative effect of time as a WSHEM input is more noticeable when both time and WS temperature are used as inputs in conjunction with CML attenuation, probably because the temperature parameter decreased the model error enough for the time parameter’s induced error to be more noticeable on average.

It should be noted that it is the combination of both CML attenuation and WS temperature that improve WSHEM performance as opposed to just the temperature measurements being the main indicator for humidity and the CML attenuation a comparatively insignificant data source. This is evident from Figure 6Cshows that Both the CML attenuation and the WS temperature measurements contribute to the model’s performance, as the addition of more CMLs improves the WSHEM's performance.

The best WSHEM performance was achieved using SVM regression machine learning model whose inputs were the corresponding WS temperature measurements and the attenuation data from its nearest 130 CMLs $(WSHE{M}_{130}^T)$. The mean test set RMSE of these WSHEMs was 0.634 $g/m^3$, almost three times smaller than the base, single CML WSHEMs $(WSHE{M}_1)$.

The addition of more meteorological side-data such as pressure, wind speed, and wind direction should be interesting to investigate.

In addition to adding multiple CMLs and side-information, in Bragin et al. (2023) we also tested another machine learning method: the Xgboost regressor.

This method performed well when used with 3-CML but fell short in comparison to the SVM at a larger number of CMLs. It proved difficult to scale the model and tune its parameters and not reach overfitting with the limited amount of available data. Nonetheless, more machine learning methods, including the Xgboost, and their implementation should be further studied for the basis of WSHEMs.

The learned hourly WVD-elevation profile showed very little variation in RMSE during the training period and a higher variation of RMSE during the testing period. Furthermore, the mean RMSE increased significantly from the training to testing periods.

This might suggest that the diurnal humidity pattern and WVD-elevation profile could have changed between the training and testing periods. Again, the suspected change is supported by the aforementioned change of the mean WS-HO standard deviation between the train and test periods (Section 2.4). This merits further research. To use the learned hourly WVD-elevation profile to estimate the WVD, it is necessary that those changes are not significant enough to make the WVD-profile irrelevant. This is indeed the case, with its use in the WVD estimation improving results more than without it. Nonetheless, the more accurate the hourly WVD-elevation profile, the more accurate the interpolation of the WSHEM estimations with it to estimate the WVD field.

More ways to estimate the WVD-elevation profile more accurately should be researched (using non-linear models, for instance). Perhaps even using the WSHEM estimations instead of the WS-HO to interpolate a WVD-elevation profile at each time period could be useful and should also be investigated.

It could also be beneficial to study the coherence of the WVD-elevation profile and the diurnal humidity pattern. Nonetheless, despite the reduction of accuracy of the WVD-elevation profile in the testing period, it was still useful.

The WVDEM is an interpolation of an ensemble of WSHEM estimations together with a learned hourly WVD-elevation profile in an area whose weather pattern does not vary much from one place to another.

The interpolation was first done using the WS-HOs instead of the WSHEM estimations to establish a base for performance of the WVD estimation and its different variations.

This baseline showed that the WVD-elevation profile was beneficial in the testing period. It also showed that using a mean average was better than the weighted averages.

These variations were also checked again when WSHEM was used.

The WVDEM based on the mean averaged, elevation-adjusted SVM 130-CML with WS temperature $WVDE{M}_{130}^T$ had the best result of a mean test WS RMSE of 0.587 $g/m^3$.

When 130-CML without WS temperature WSHEM was used, the mean test WS RMSE was higher at 0.653 $g/m^3$. This was expected as those WSHEMs were less accurate than those using the WS temperature measurements. When the learned humidity elevation profile was not used to adjust the WSHEM estimations before averaging, the mean test WS RMSE was worse. Again, this shows that it was beneficial to adjust for elevation.

From Figure 3A, it is safe to assume that, generally, the greater the distance between two WSs, the less correlated they are.

If this is true, it is safe to assume that it would also be true for WSHEM as it estimates the WS-HO.

Therefore, it might seem beneficial to give more weight to closer WSHEM estimations in the averaging phase of WVDEM.

When more weight was given to closer WSHEMs or WS-HO either with IDW weighing or linear distance weights, the WVDEM RMSE increased but CCs increased as well. The increase in correlation was expected but the increase in mean RMSE was not. It seems that the distance-dependent weighting methods induced some bias. A possible reason might be that the reduction in accuracy due to distance-caused correlation reduction is much smaller than the variability in the WSHEM accuracy of the mesoscale humidity pattern due to local conditions. This can give less weight, on average, to farther WSHEMs that are more accurate and indicative to WVD than closer WSHEMs.

Therefore, some WSs may have a bias from the mesoscale humidity pattern in their WS-HO due to local conditions (which translate to a bias for their respective WSHEMs). The bias source could be a nearby humidity source such as a water pool or dense vegetation that increases the measured humidity at a nearby WS. The difference in baseline humidity between two WSs where one is biased due to a humidity source (after elevation difference adjustment) could be greater then what would be expected only from their CC.

This biased humidity can be given more weight on average when a distance-based weighting method is used since the spatial distribution of WSs is not perfectly uniform (Figure 2A) and leads to the above results.

This phenomenon requires further investigation.

It also unknown, and requires further investigation, how the spatial distribution and density of the WSs, and by extension the WSHEMs, affect WVDEM accuracy, especially when different weighing methods are used.

The WVDEM algorithm can be used in a practical manner by having a portable WS that stays in one place for enough time to train a WSHEM and then be moved to another place to create another WSHEM, and so on. After several WSHEMS are trained along a humidity-elevation profile, the WVDEM can be used.

Another way the methods presented here should be investigated is by reversing the WVDEM algorithm. First, the $WVDE{M}_{HO}$ (WS-HO based WVDEM) should be used at various location and elevations to establish an accurate estimation of the WVD at these locations. Then these WVD estimations should be used as ground truth to train WSHEMs for the selected locations, thus creating more virtual WSs.

It should be noted that the amount of time required to train a WSHEM for it to be reliable for the different seasons and general weather patterns should be researched as well. In this study, the amount of data were limited as was their timeframe.

Another point to consider is the limited area of interest in the study—on the mesoscale (10–1,000 km). The weather patterns (and specifically, humidity pattern) of this scale are influenced by different land cover, humidity sources, topography, and synoptic-scale weather patterns.

Therefore, the boundaries of the effective area and elevation for accurate estimation of the WVD field and relevance of the WVD-elevation profile should also be inspected, especially when changes of land cover, topography, and humidity source prevalence occur. The effective elevation boundary is probably affected by the inversion layer height (and its diurnal pattern) where the humidity elevation profile might change (Haikin et al., 2015; Garratt, 1994).

This work is a preliminary example of a machine learning tool used for opportunistic water-vapor sensing that benefits from additional sources of data such as multiple CMLs and temperature observations. Although the preliminary results presented here are very encouraging, there are some points that require further research.

Specifically, it would be worthwhile to investigate how this enhanced model copes with WVD estimation in meteorologically challenging geographical locations such as the surrounding areas of Jerusalem, Israel, as such areas often experience unique WVD spatial profiles. Jerusalem, for instance, has a Mediterranean climate but is very close to the arid Judean desert. Moreover, Jerusalem and its surrounding areas are very hilly and thus have a lot of variability in ground elevation (Alpert et al., 2024). Such conditions might affect the high accuracy of the WVDEM, WVDEP, and WSHEMs, as demonstrated in this study. For instance, it might be necessary to not use nearby WSHEMs for the WVDEM if they are from different climate areas (even though they are “close”). Additionally, where seasonal weather patterns change significantly from season to season, there might be a need to train the model for each season by itself. Areas that experience very large shifts in boundary layer altitude or that are sometimes below or above the boundary layer may need to use completely different WVDEP models. The model’s performance in rainy seasons and other strong, frequent, meteorological events also requires investigation. Such events can have a lasting effect on the CML baseline attenuation (Ostrometzky and Messer, 2017; Harel et al., 2015). For instance, the CML antennas can remain wet well after the rain stops and add to CML baseline attenuation. This might cause a slow change (compared to the usual changes in attenuation) to the base-line attenuation as the antenna dries, which can be missed by current pre-processing methods. Other phenomena, such as gradual hardware degradation, could also lead to similar inaccuracies as they may invalidate the assumption that the baseline attenuation is constant. Possible ways to deal with slow change to baseline attenuation could be machine learning models with memory such as RNN, and dynamic baseline attenuation estimation and removal as part of pre-processing [similar to the method suggested in Ostrometzky and Messer, (2017)]. In practice, the issues of malfunctioning CMLs, CMLs that are scraped, and new CMLs need to be addressed with more flexible machine learning models and constant learning.

Data availability statement

The data analyzed in this study are subject to the following licenses/restrictions. The dataset was shared for the purpose of this research only. The raw data include commercial company equipment details that should not be shared. Requests to access these datasets should be directed to aXRheWJyYWdpbkBnbWFpbC5jb20=.

Author contributions

IB: conceptualization, formal analysis, investigation, methodology, software, validation, visualization, writing–original draft, and writing–review and editing. YR: conceptualization, data curation, investigation, methodology, project administration, resources, supervision, visualization, and writing–review and editing. PA: conceptualization, investigation, methodology, project administration, supervision, and writing–review and editing. JO: conceptualization, investigation, methodology, project administration, supervision, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This publication is supported in part by the European Union under Grant 101037193 ENTITLED I-CHANGE.

Acknowledgments

The authors would like to thank Dr. Christian Chwala for collecting and sharing the CML data used in this work. They would also like to thank Prof. Hagit Messer and the CellenMon Lab team for their advice and fruitful discussion. This publication is supported in part by the European Union under Grant 101037193.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alpert, P., Rubin, Y., Campos, G. D., Romantso, K., Haikin, N., Stupp, A., et al. (2024). Challenges in climate change impact and risks in Jerusalem by the I-CHANGE Jerusalem Living Lab citizens science. Tech. Rep. doi:10.5194/egusphere-egu24-455

CrossRef Full Text | Google Scholar

Andersson, E., Hólm, E., Bauer, P., Beljaars, A., Kelly, G., McNally, A., et al. (2007). Analysis and forecast impact of the main humidity observing systems. Q. J. R. Meteorological Soc. A J. Atmos. Sci. Appl. meteorology Phys. Oceanogr. 133, 1473–1485. doi:10.1002/qj.112

CrossRef Full Text | Google Scholar

Baek, I.-H., Bart, F., Elschner, R., Meier, F., Hellmann, D., Maassen, A., et al. (2022). “Time adaptive probabilistic shaping for combined optical/thz links,” in Photonic networks; 23th ITG-symposium (VDE), 1–8.

Google Scholar

Bragin, I., Rubin, Y., Alpert, P., and Ostrometzky, J. (2023). “Improved water vapor density estimation with commercial microwave links attenuation and temperature,” in 2023 IEEE international conference on acoustics, speech, and signal processing workshops (ICASSPW) (IEEE), 1–5.

CrossRef Full Text | Google Scholar

Chopde, N. R., and Nichat, M. (2013). Landmark based shortest path detection by using a* and haversine formula. Int. J. Innovative Res. Comput. Commun. Eng. 1, 298–302.

Google Scholar

David, N., Alpert, P., and Messer, H. (2009). Technical Note: novel method for water vapour monitoring using wireless communication networks measurements. Atmos. Chem. Phys. 9, 2413–2418. doi:10.5194/acp-9-2413-2009

CrossRef Full Text | Google Scholar

de Bruin, G. J., Veenman, C. J., van den Herik, H. J., and Takes, F. W. (2021). “Experimental evaluation of train and test split strategies in link prediction,” in Complex networks and their applications IX: volume 2, proceedings of the ninth international conference on complex networks and their applications COMPLEX NETWORKS 2020 (Springer), 79–91.

Google Scholar

Fencl, M., Dohnal, M., and Bareš, V. (2021). Retrieving water vapor from an e-band microwave link with an empirical model not requiring in situ calibration. Earth Space Sci. 8, e2021EA001911. doi:10.1029/2021ea001911

CrossRef Full Text | Google Scholar

Ferrante, A., and Mariani, L. (2018). Agronomic management for enhancing plant tolerance to abiotic stresses: high and low values of temperature, light intensity, and relative humidity. Horticulturae 4, 21. doi:10.3390/horticulturae4030021

CrossRef Full Text | Google Scholar

Fredianto, F., and Putri, D. A. P. (2023). “Comparison of the interquartile range algorithm and local outlier factor on australian weather data sets,” in AIP Conference Proceedings (America: AIP Publishing), doi:10.1063/5.0141897

CrossRef Full Text | Google Scholar

Gao, J., Sun, Y., Lu, Y., and Li, L. (2014). Impact of ambient humidity on child health: a systematic review. PloS one 9, e112508. doi:10.1371/journal.pone.0112508

PubMed Abstract | CrossRef Full Text | Google Scholar

Garratt, J. R. (1994). Review: the atmospheric boundary layer. Earth-Science Rev. 37, 89–134. doi:10.1016/0012-8252(94)90026-4

CrossRef Full Text | Google Scholar

Gutman, S. I., and Benjamin, S. G. (2001). The role of ground-based gps meteorological observations in numerical weather prediction. GPS solutions 4, 16–24. doi:10.1007/pl00012860

CrossRef Full Text | Google Scholar

Haikin, N., Galanti, E., Reisin, T., Mahrer, Y., and Alpert, P. (2015). Inner structure of atmospheric inversion layers over haifa bay in the eastern mediterranean. Boundary-Layer Meteorol. 156, 471–487. doi:10.1007/s10546-015-0038-4

CrossRef Full Text | Google Scholar

Harel, O., David, N., Alpert, P., and Messer, H. (2015). The potential of microwave communication networks to detect dew—experimental study. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 8, 4396–4404. doi:10.1109/jstars.2015.2465909

CrossRef Full Text | Google Scholar

Hoffmann, S., and Koehl, M. (2014). Effect of humidity and temperature on the potential-induced degradation. Prog. Photovoltaics Res. Appl. 22, 173–179. doi:10.1002/pip.2238

CrossRef Full Text | Google Scholar

Hua, J., Xiong, Z., Lowey, J., Suh, E., and Dougherty, E. R. (2005). Optimal number of features as a function of sample size for various classification rules. Bioinformatics 21, 1509–1515. doi:10.1093/bioinformatics/bti171

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, J., Yin, S., and Yin, H. (2022). Impact of land use/land cover types on surface humidity in northern China in the early 21st century. J. Arid Land 14, 705–718. doi:10.1007/s40333-022-0055-3

CrossRef Full Text | Google Scholar

Koutsoyiannis, D. (2012). Clausius–clapeyron equation and saturation vapour pressure: simple theory reconciled with practice. Eur. J. Phys. 33, 295–305. doi:10.1088/0143-0807/33/2/295

CrossRef Full Text | Google Scholar

Ostrometzky, J., and Messer, H. (2017). Dynamic determination of the baseline level in microwave links for rain monitoring from minimum attenuation values. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 11, 24–33. doi:10.1109/jstars.2017.2752902

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830.

Google Scholar

Rubin, Y., Rostkier-Edelstein, D., Chwala, C., and Alpert, P. (2022). Challenges in diurnal humidity analysis from cellular microwave links (cml) over Germany. Remote Sens. 14, 2353. doi:10.3390/rs14102353

CrossRef Full Text | Google Scholar

Rubin, Y., Sohn, S., and Alpert, P. (2023). High-resolution humidity observations based on commercial microwave links (cml) data—case of tel aviv metropolitan area. Remote Sens. 15, 345. doi:10.3390/rs15020345

CrossRef Full Text | Google Scholar

Ruckstuhl, C., Philipona, R., Morland, J., and Ohmura, A. (2007). Observed relationship between surface specific humidity, integrated water vapor, and longwave downward radiation at different altitudes. J. Geophys. Res. Atmos. 112. doi:10.1029/2006jd007850

CrossRef Full Text | Google Scholar

Seo, S. (2006). A review and comparison of methods for detecting outliers in univariate data sets. America: University of Pittsburgh. Ph.D. thesis.

Google Scholar

Song, K., Liu, X., Gao, T., and Zhang, P. (2021). Estimating water vapor using signals from microwave links below 25 ghz. Remote Sens. 13, 1409. doi:10.3390/rs13081409

CrossRef Full Text | Google Scholar

Van Vleck, J. (1947). The absorption of microwaves by uncondensed water vapor. Phys. Rev. 71, 425–433. doi:10.1103/physrev.71.425

CrossRef Full Text | Google Scholar

Vapnik, V. (2013). The nature of statistical learning theory. Springer science and business media.

Google Scholar

Ying, X. (2019). An overview of overfitting and its solutions. In J. Phys, Conf. Ser., Journal of physics: Conference series UK: IOP Publishing, 1168, 022022, doi:10.1088/1742-6596/1168/2/022022

CrossRef Full Text | Google Scholar

Nomenclature

ASL above sea level

CC correlation coefficient

CML commercial microwave links

IQR interquartile range

MSE minimum squared error

RMSE root mean square error

RSL received signal level

SVM support vector machine

TSL transmitted signal level

WS weather station

WSHEM WS humidity estimation machine learning model

WS-HO weather station humidity observations

WVD water vapor density

WVDEM WVD estimation model

WVDEP WVD-elevation profile model