Approximation properties relative to continuous scale space for hybrid discretisations of Gaussian derivative operators

This paper presents an analysis of properties of two hybrid discretisation methods for Gaussian derivatives, based on convolutions with either the normalised sampled Gaussian kernel or the integrated Gaussian kernel followed by central differences. The motivation for studying these discretisation methods is that in situations when multiple spatial derivatives of different orders are needed at the same scale level, they can be computed significantly more efficiently, compared to more direct derivative approximations based on explicit convolutions with either sampled Gaussian derivative kernels or integrated Gaussian derivative kernels. We characterise the properties of these hybrid discretisation methods in terms of quantitative performance measures, concerning the amount of spatial smoothing that they imply, as well as the relative consistency of the scale estimates obtained from scale-invariant feature detectors with automatic scale selection, with an emphasis on the behaviour for very small values of the scale parameter, which may differ significantly from corresponding results obtained from the fully continuous scale-space theory, as well as between different types of discretisation methods. The presented results are intended as a guide, when designing as well as interpreting the experimental results of scale-space algorithms that operate at very fine scale levels.

1 Introduction

When analysing image data by automated methods, a fundamental constraint originates from the fact that natural images may contain different types of structures at different spatial scales. For this reason, the notion of scale-space representation (Iijima, 1962; Witkin, 1983; Koenderink, 1984; Koenderink and van Doorn, 1987; Koenderink and van Doorn, 1992; Lindeberg, 1993b; Lindeberg, 1994; Lindeberg, 2011; Florack, 1997; Weickert et al., 1999; ter Haar Romeny, 2003) has been developed to process the image data at multiple scales, in such a way that different types of image features can be obtained depending on the spatial extent of the image operators. Specifically, according to both theoretical and empirical findings in the area of scale-space theory, Gaussian derivative responses, or approximations thereof, can be used as a powerful basis for expressing a rich variety of feature detectors, in terms of provably scale-covariant or scale-invariant image operations, that can in an automated manner handle variabilities in scale, caused by varying the distance between the observed objects and the camera (Lindeberg, 1998b; 1998b; Lindeberg, 2013a; Lindeberg, 2013b; Lindeberg, 2015; Lindeberg, 2021b; Bretzner and Lindeberg, 1998; Chomat et al., 2000; Lowe, 2004; Bay et al., 2008). More recently, Gaussian derivative operators have also been used as a basis, to formulate parameterised mathematical primitives, to be used as the layers in deep networks (Jacobsen et al., 2016; Worrall and Welling, 2019; Lindeberg, 2020; 2022; Pintea et al., 2021; Sangalli et al., 2022; Penaud-Polge et al., 2022; Yang et al., 2023; Gavilima-Pilataxi and Ibarra-Fiallo, 2023).

When to implement the underlying Gaussian derivative operators in scale-space theory in practice, special attention does, however, need to be taken concerning the fact that most of the scale-space formulations are based on continuous signals or images (see Appendix A in the Supplementary Material for a conceptual background), while real-world signals and images are discrete (Lindeberg, 1990; Lindeberg, 1993b; Lindeberg, 2024b). Thus, when discretising the composed effect of the underlying Gaussian smoothing operation and the following derivative computations, it is essential to ensure that the desirable properties of the theoretically well-founded scale-space representations are to a sufficiently good degree of approximation transferred to the discrete implementation. Simultaneously, the amount of necessary computations needed for the implementation may often constitute a limiting factor, when to choose an appropriate discretisation method for expressing the actual algorithms, that are to operate on the discrete data to be analysed.

While one may argue that at sufficiently coarse scale levels, it ought to be the case that the choice of discretisation method should not significantly affect the quality of the output of a scale-space algorithm, at very fine scale levels, on the other hand, the properties of a discretised implementation of notions from scale-space theory may depend strongly on the actual choice of a discretisation method.

The subject of this article, is to perform a more detailed analysis of a class of hybrid discretisation methods, based on convolution with either the normalised sampled Gaussian kernel or the integrated Gaussian kernel, followed by computations of discrete derivative approximations by central difference operators, and specifically characterise the degree of approximation of continuous expressions in scale-space theory, that these discretisation give rise to, see Figure 1 for examples of graphs of equivalent convolution kernels corresponding to these discretisation methods. This class of discretisation methods was outlined among extensions to future work in Section 6.1 in (Lindeberg, 2024b), and was also complemented with a description about their theoretical properties in Footnote 13 in (Lindeberg, 2024b). There were, however, no further in-depth characterisations of the approximation properties of these discretisations, with regard to what results they lead to in relation to corresponding results from the continuous scale-space theory.

Figure 1

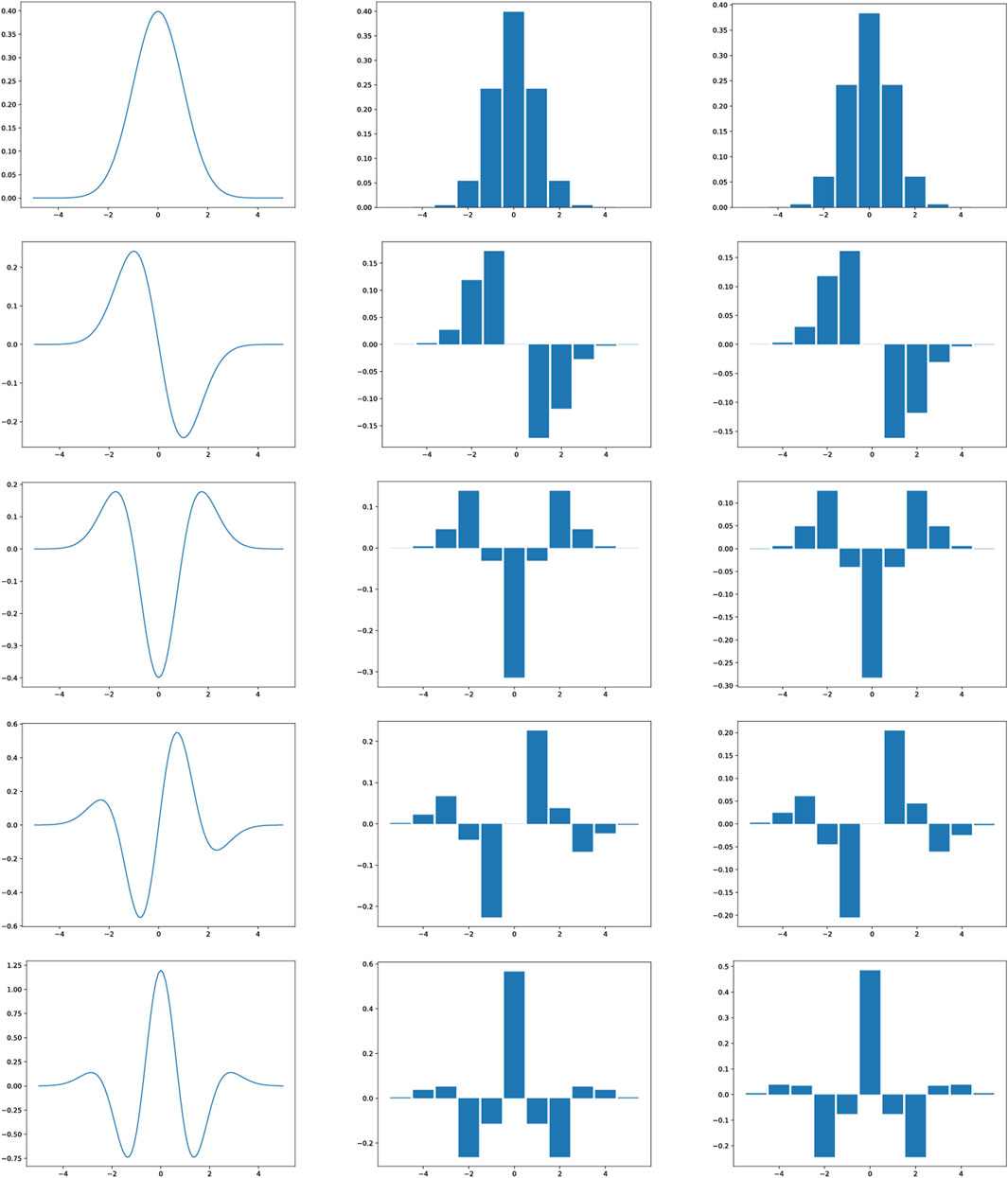
Figure 1. Graphs of the main types of Gaussian smoothing kernels as well as of the equivalent convolution kernels for the hybrid discretisations of Gaussian derivative operators considered specially in this paper, here at the scale $\sigma =1$, with the raw smoothing kernels in the top row and the order of spatial differentiation increasing downwards up to order 4: (left column) continuous Gaussian kernel and continuous Gaussian derivatives, (middle column) normalised sampled Gaussian kernel and central differences applied to the normalised sampled Gaussian kernel, (right column) integrated Gaussian kernel and central differences applied to the integrated Gaussian kernel. Note that the scaling of the vertical axis may vary between the different subfigures (Horizontal axes: the 1-D spatial coordinate $x\in [-\mathrm{5,5}]$.). (Graphs of the regular sampled Gaussian derivative kernels, the regular integrated Gaussian derivative kernels and the discrete analogues of Gaussian derivatives up to order 4 are shown in Figure 1 in (Lindeberg, 2024b).

The main goal of this paper is to address this topic in terms of a set of quantitative performance measures, intended to be of general applicability for different types of visual tasks. Specifically, we will perform comparisons to the other main types of discretisation methods considered in (Lindeberg, 2024b), based on either (i) explicit convolutions with sampled Gaussian derivative kernels, (ii) explicit convolutions with integrated Gaussian derivative kernels, or (iii) convolution with the discrete analogue of the Gaussian kernel, followed by computations of discrete derivative approximations by central difference operators.

A main rationale for studying this class of hybrid discretisations is that, in situations when multiple Gaussian derivative responses of different orders are needed at the same scale level, these hybrid discretisations imply substantially lower amounts of computations, compared to explicit convolutions with either sampled Gaussian derivative kernels or integrated Gaussian derivative kernels for each order of differentiation. The reason for this better computational efficiency, which also holds for the discretisation approach based on convolution with the discrete analogue of the Gaussian kernel followed by central differences, is that the spatial smoothing part of the operation, which is performed over a substantially larger number of input data than the small-support central difference operators, can be shared between the different orders of differentiation.

A further rationale for studying these hybrid discretisations is that in certain applications, such as the use of Gaussian derivative operators in deep learning architectures (Jacobsen et al., 2016; Lindeberg, 2021a; 2022; Pintea et al., 2021; Sangalli et al., 2022; Penaud-Polge et al., 2022; Gavilima-Pilataxi and Ibarra-Fiallo, 2023), the modified Bessel functions of integer order, as used as the underlying mathematical primitives in the discrete analogue of the Gaussian kernel, may, however, not be fully available in the framework used for implementing the image processing operations. For this reason, the hybrid discretisations may, for efficiency reasons, constitute an interesting alternative to using discretisations in terms of either sampled Gaussian derivative kernels or integrated Gaussian derivative kernels, when to implement certain tasks, such as learning of the scale levels by backpropagation, which usually require full availability of the underlying mathematical primitives in the scale-parameterised filter family with regard to the deep learning framework, to be able to propagate the gradients between the layers in the deep learning architecture.

Deliberately, the scope of this paper is therefore to complement the in-depth treatment of discretisations of the Gaussian smoothing operation and the Gaussian derivative operators, and as a specific complement to the outline of the hybrid discretisations in the future work section in (Lindeberg, 2024b).

We will therefore not consider other theoretically well-founded discretisations of scale-space operations (Wang, 1999; Lim and Stiehl, 2003; Tschirsich and Kuijper, 2015; Slavík and Stehlík, 2015; Rey-Otero and Delbracio, 2016). Nor will we consider alternative approaches in terms of pyramid representations (Burt and Adelson, 1983; Crowley and Stern, 1984; Simoncelli et al., 1992; Simoncelli and Freeman, 1995; Lindeberg and Bretzner, 2003; Crowley and Riff, 2003; Lowe, 2004), Fourier-based implementations, splines (Unser et al., 1991; 1993; Wang and Lee, 1998; Bouma et al., 2007; Bekkers, 2020; Zheng et al., 2022), recursive filters (Deriche, 1992; Young and van Vliet, 1995; van Vliet et al., 1998; Geusebroek et al., 2003; Farnebäck and Westin, 2006; Charalampidis, 2016), or specific wavelet theory (Mallat, 1989; Mallat, 1989; Mallat, 1999; Mallat 2016; Daubechies, 1992; Meyer, 1992; Teolis, 1998; Debnath and Shah, 2002).

Instead, we will focus on a selection of five specific methods, for implementing Gaussian derivative operations in terms of purely discrete convolution operations, and then with the emphasis on the behaviour for very small values of the scale parameter. This focus on very fine scale levels is particularly motivated from requirements regarding deep learning, where deep learning architectures often prefer to base their decisions on very fine-scale information, and specifically below the rule of thumb in classical computer vision, of not going trying to go to scale levels below a standard deviation $\sigma =\sqrt{s}$ of the Gaussian derivative kernels below, say $1/\sqrt{2}$ or 1, in units of the grid spacing.

2 Methods

The notion of scale-space representation is very general, and applies to wide classes of signals. Based on the separability property when computing Gaussian derivative responses in arbitrary dimensions (see Appendices B.1–B.2 in the Supplementary Material), we will in this section focus on discretisations of 1-D Gaussian derivative kernels. By separable extension over multiple dimensions, this methodology can then be applied to signals, images and video over arbitrary numbers of dimensions.

2.1 Discretisation methods for 1-D Gaussian derivative operators

Given the definition of a scale-space representation of a one-dimensional continuous signal (Iijima, 1962; Witkin, 1983; Koenderink, 1984; Koenderink and van Doorn, 1987; 1992; Lindeberg, 1993b; 1994; 2011; Florack, 1997; Sporring et al., 1997; Weickert et al., 1999; ter Haar Romeny, 2003), the 1-D Gaussian kernel is defined according to (for $x\in \mathbb{R}$):

$g\left(x;s\right)=\frac{1}{\sqrt{2\pi s}}{e}^{-x^2/2s},(1)$

where the parameter $s\in {\mathbb{R}}_{+}$ is referred to as the scale parameter, and any 1-D Gaussian derivative kernel for spatial differentiation order $\alpha$ is defined according to

$g_{x^{\alpha }}\left(x;s\right)={\partial }_{x^{\alpha }}g\left(x;s\right),(2)$

with the associated computation of Gaussian derivative responses from any 1-D input signal $f(x)$, in turn, defined according to

$L_{x^{\alpha }}\left(x;s\right)={\int }_{u\in \mathbb{R}}{g}_{x^{\alpha }}\left(u;s\right)f\left(x-u\right)du.(3)$

Let us first consider the following ways of approximating the Gaussian convolution operation for discrete data, based on convolutions with either (for $n\in \mathbb{Z})$:

• The sampled Gaussian kernel defined from the continuous Gaussian kernel (Equation 1) according to (see also Appendix B.3 in the Supplementary Material).

$T_{\text{sampl}}\left(n;s\right)=g\left(n;s\right),(4)$

• The normalised sampled Gaussian kernel defined from the sampled Gaussian kernel (Equation 4) according to (see also Appendix B.4 in the Supplementary Material).

$T_{\text{normsampl}}\left(n;s\right)=\frac{g\left(n;s\right)}{\sum _{m\in \mathbb{Z}}g\left(m;s\right)},(5)$

• The integrated Gaussian kernel defined according to (Lindeberg, 1993b; Equation 3.89) (see also Appendix B.5 in the Supplementary Material).

$T_{\text{int}}\left(n;s\right)={\int }_{x=n-1/2}^{n+1/2}g\left(x;s\right)dx,(6)$

• Or the discrete analogue of the Gaussian kernel defined according to (Lindeberg, 1990; Equation 19) (see also Appendix B.6 in the Supplementary Material).

$T_{\text{disc}}\left(n;s\right)=e^{-s}{I}_n\left(s\right),(7)$

where $I_n(s)$ denotes the modified Bessel functions of integer order (Abramowitz and Stegun, 1964).

Then, we consider the following previously studied methods for discretising the computation of Gaussian derivative operators, in terms of either:

• Convolutions with sampled Gaussian derivative kernels from the continuous Gaussian derivative kernel (Equation 2) according to (see also Appendix B.7 in the Supplementary Material).

$T_{\text{sampl},x^{\alpha }}\left(n;s\right)=g_{x^{\alpha }}\left(n;s\right),(8)$

• Convolutions with integrated Gaussian derivative kernels according to (Lindeberg, 2024b; Equation 54) (see also Appendix B.8 in the Supplementary Material).

$T_{\text{int},x^{\alpha }}\left(n;s\right)={\int }_{x=n-1/2}^{n+1/2}{g}_{x^{\alpha }}\left(x;s\right)dx,(9)$

• The genuinely discrete approach corresponding to convolution with the discrete analogue of the Gaussian kernel $T_{\text{disc}}(n;s)$ according to Equation 7 followed by central difference operators ${\delta }_{x^{\alpha }}$, thus corresponding to the equivalent discrete approximation kernel (Lindeberg, 1993a; Equation 58) (see also Appendix B.9 in the Supplementary Material).

$T_{\text{disc},x^{\alpha }}\left(n;s\right)=\left({\delta }_{x^{\alpha }}{T}_{\text{disc}}\right)\left(n;s\right).(10)$

Here, the central difference operators are for orders 1 and 2 defined according to

${\delta }_x=\left(-\frac{1}{2},0,+\frac{1}{2}\right),(11)$

${\delta }_{xx}=\left(+1,-2,+1\right),(12)$

and for higher values of $\alpha$ according to:

${\delta }_{x^{\alpha }}=\left\{\begin{array}{cc}{\delta }_x{\left({\delta }_{xx}\right)}^i\hfill & \text{if\hspace{0.17em}}\alpha =1+2i\text{,}\hfill \\ {\left({\delta }_{xx}\right)}^i\hfill & \text{if\hspace{0.17em}}\alpha =2i\text{,}\hfill \end{array}\right.(13)$

for integer $i$, where the special cases $\alpha =3$ and $\alpha =4$ then correspond to the difference operators

${\delta }_{xxx}=\left(-\frac{1}{2},+\mathrm{1,0},-1,+\frac{1}{2}\right),(14)$

${\delta }_{xxxx}=\left(+1,-4,+6,-4,+1\right).(15)$

In addition to the above, already studied discretisation methods in (Lindeberg, 2024b), we will here specifically consider the properties of the following hybrid methods, in terms of either:

• The hybrid approach corresponding to convolution with the normalised sampled Gaussian kernel $T_{\text{normsampl}}(n;s)$ according to Equation 5 followed by central difference operators ${\delta }_{x^{\alpha }}$ according to Equation 13, thus corresponding to the equivalent discrete approximation kernel (Lindeberg, 2024b; Equation 116) (see also Appendix B.10 in the Supplementary Material).

$T_{\text{hybr}-\text{sampl},x^{\alpha }}\left(n;s\right)=\left({\delta }_{x^{\alpha }}{T}_{\text{normsampl}}\right)\left(n;s\right),(16)$

• The hybrid approach corresponding to convolution with the integrated Gaussian kernel $T_{\text{int}}(n;s)$ according to Equation 6 followed by central difference operators ${\delta }_{x^{\alpha }}$ according to Equation 13, thus corresponding to the equivalent discrete approximation kernel (Lindeberg, 2024b; Equation 117) (see also Appendix B.11 in the Supplementary Material).

$T_{\text{hybr}-\text{int},x^{\alpha }}\left(n;s\right)=\left({\delta }_{x^{\alpha }}{T}_{\text{int}}\right)\left(n;s\right).(17)$

A motivation for introducing these hybrid discretisation methods (Equation 16) and (Equation 17), based on convolutions with the normalised sampled Gaussian kernel (Equation 5) or the integrated Gaussian kernel (Equation 6) followed by central difference operators of the form (Equation 13), is that these discretisation methods have substantially better computational efficiency, compared to explicit convolutions with either the sampled Gaussian derivative kernels (Equation 8) or the integrated Gaussian derivative kernels (Equation 9), in situations when spatial derivatives of multiple orders $\alpha$ are needed at the same scale level.

The reason for this is that the same spatial smoothing stage can then be shared between the computations of discrete derivative approximations for the different orders of spatial differentiation, thus implying that these hybrid methods will be as computationally efficient as the genuinely discrete approach, based on convolution with the discrete analogue of the Gaussian kernel (Equation 7) followed by central differences of the form (Equation 13), and corresponding to equivalent convolution kernels of the form (Equation 10).

2.1.1 Quantitative measures of approximation properties relative to continuous scale space

To measure how well the above discretisation methods for the Gaussian derivative operators reflect properties of the underlying continuous Gaussian derivatives, we will consider quantifications in terms of the following the spatial spread measure, defined from spatial variance $V$ of the absolute value of each equivalent discrete derivative approximation kernel (Lindeberg, 2024b; Equation 80):

$\sqrt{V\left(|T_{x^{\alpha }}\left(\cdot ;s\right)|\right)},(18)$

where the variance $V(h(\cdot ))$ of a non-negative continuous 1-D function $h(x)$ is defined as

$V\left(h\left(\cdot \right)\right)=\frac{{\int }_{x\in \mathbb{R}}{x}^{2}h\left(x\right)dx}{{\int }_{x\in \mathbb{R}}h\left(x\right)dx}-{\left(\frac{{\int }_{x\in \mathbb{R}}xh\left(x\right)dx}{{\int }_{x\in \mathbb{R}}h\left(x\right)dx}\right)}^2.(19)$

To furthermore more explicitly quantify the deviation from the corresponding fully continuous spatial spread measures $\sqrt{V(|g_{x^{\alpha }}(\cdot ;s)|)}$, we also consider the following measures of the offsets of the spatial spread measures (Lindeberg, 2024b; Equation 81):

$O_{\alpha }\left(s\right)=\sqrt{V\left(|T_{x^{\alpha }}\left(\cdot ;s\right)|\right)}-\sqrt{V\left(|g_{x^{\alpha }}\left(\cdot ;s\right)|\right)},(20)$

where the variance $V(h(\cdot ))$ of a non-negative discrete function $h(n)$ is defined as

$V\left(h\left(\cdot \right)\right)=\frac{\sum _{n\in \mathbb{Z}}{n}^{2}h\left(n\right)}{\sum _{n\in \mathbb{Z}}h\left(n\right)}-{\left(\frac{\sum _{n\in \mathbb{Z}}nh\left(n\right)}{\sum _{n\in \mathbb{Z}}h\left(n\right)}\right)}^2.(21)$

2.2 Methodology for characterising the resulting consistency properties over scale in terms of the accuracy of the scale estimates obtained from integrations with scale selection algorithms

To perform a further evaluation of the hybrid discretisation method to consistently process input data over multiple scales, we will characterise the abilities of these methods in a context of feature detection with automatic scale selection (Lindeberg, 1998b; Lindeberg, 2021b), where hypotheses about local appropriate scale levels are determined from local extrema over scale of scale-normalised derivative responses.

For this purpose, we follow a similar methodology as used in (Lindeberg, 2024b; Section 4). Thus, with the theory in Section 2.1 now applied to 2-D image data, by separable application of the 1-D theory along each image dimension, we consider scale-normalised derivative operators defined according to (Lindeberg, 1998b; Lindeberg, 1998a) (for $(x,y)\in {\mathbb{R}}^2$ and $s\in {\mathbb{R}}_{+}$):

${\partial }_{\xi }=s^{\gamma /2}{\partial }_x,{\partial }_{\eta }=s^{\gamma /2}{\partial }_y,(22)$

with $\gamma >0$ being a scale normalisation power, that is chosen specially adapted for each feature detection task.

2.2.1 Scale-invariant feature detectors with automatic scale selection

Specifically, we will evaluate the performance of the following types of scale-invariant feature detectors, defined from the spatial derivatives $L_x(x,y;s)$, $L_y(x,y;s)$, $L_{xx}(x,y;s)$, $L_{xy}(x,y;s)$ and $L_{yy}(x,y;s)$ up to order 2 of the 2-D scale-space representation $L(x,y;s)$ of any 2-D image $f(x,y)$ at scale $s$, obtained by convolution with 2-D Gaussian kernels $g_{2D}(x,y;s)$ for different values of $s$, thereby defined from 2-D extensions of the 1-D Gaussian derivative responses according to Equation 3:

• Interest point detection from scale-space extrema (extrema over both space $(x,y)$ and scale $s$) of the scale-normalised Laplacian operator (Lindeberg, 1998b; Equation 30) according to Equation 22.

${\nabla }_{\text{norm}}^{2}L=s\left(L_{xx}+L_{yy}\right),(23)$

or the scale-normalised determinant of the Hessian operator (Lindeberg, 1998b; Equation 31).

$\det {\mathcal{H}}_{\text{norm}}L=s^2\left(L_{xx}{L}_{yy}-L_{xy}^2\right),(24)$

where we here choose the scale normalisation parameter $\gamma =1$, such that the selected scale level for a Gaussian blob of size $s_0\in {\mathbb{R}}_{+}$

$f_{\text{blob},s_0}\left(x,y\right)=g_{2D}\left(x,y;s_0\right)=\frac{1}{2\pi s_0}{e}^{-\frac{x^2+y^2}{2s_0}}(25)$

will for both Laplacian and determinant of the Hessian interest point detection be equal to the size of the blob (Lindeberg, 1998b; Equation 36 and Equation 37):

$\left(\widehat{x},\widehat{y};\widehat{s}\right)={\arg \hspace{0.17em}\min }_{\left(x,y;s\right)}\left({\nabla }_{\text{norm}}^{2}L\right)\left(x,y;s\right)=\left(\mathrm{0,0};s_0\right),(26)$

$\left(\widehat{x},\widehat{y};\widehat{s}\right)={\text{arg}\hspace{0.17em}\text{max}}_{\left(x,y;s\right)}\left(\det {\mathcal{H}}_{\text{norm}}L\right)\left(x,y;s\right)=\left(\mathrm{0,0};s_0\right),(27)$

• Edge detection from combined:

• Maxima of the gradient magnitude in the spatial gradient direction $e_v$, reformulated such that the second-order directional derivative in the gradient direction $L_{vv}$ is zero and the third-order directional derivative in the gradient direction $L_{\mathit{vvv}}$ is negative (Lindeberg, 1998a; Equation 8), and

• Maxima over scale of the scale-normalised gradient magnitude $L_{v,\text{norm}}$ according to (Lindeberg, 1998a; Equation 15)

$L_{v,\text{norm}}=s^{\gamma /2}\sqrt{L_x^2+L_y^2},(28)$

where we here set the scale normalisation parameter $\gamma$ to (Lindeberg, 1998a; Equation 23).

${\gamma }_{\text{edge}}=\frac{1}{2},(29)$

such that the selected scale level $\widehat{s}$ for an idealised model of a diffuse edge (Lindeberg, 1998a; Equation 18).

$f_{\text{edge},s_0}\left(x,y\right)={\int }_{u=-\infty }^x{g}_{1D}\left(u;s_0\right)du={\int }_{u=-\infty }^x\frac{1}{\sqrt{2\pi s_0}}{e}^{-\frac{u^2}{2s_0}}du(30)$

will be equal to the amount of diffuseness $s_0\in {\mathbb{R}}_{+}$ of that diffuse edge

$\widehat{s}={\text{arg}\hspace{0.17em}\text{max}}_s{L}_{v,\text{norm}}\left(\mathrm{0,0};s\right)=s_0,(31)$

• Ridge detection from combined

$•$ zero-crossings of the first-order directional derivative $L_p$ in the first principal curvature direction $e_p$ of the Hessian matrix, such that $L_p=0$ (Lindeberg, 1998a; Equations 42), and

• Minima over scale of the scale-normalised ridge strength in terms the scale-normalised second-order derivative $L_{pp,\text{norm}}$ in the direction $e_p$ according to (Lindeberg, 1998a; Equation 47):

$L_{pp,\text{norm}}=s^{\gamma }{L}_{pp}=s^{\gamma }\left(L_{xx}+L_{yy}-\sqrt{{\left(L_{xx}-L_{yy}\right)}^2+4L_{xy}^2}\right),(32)$

where we here choose the scale normalisation parameter $\gamma$ as (Lindeberg, 1998a; Equation 56).

${\gamma }_{\text{ridge}}=\frac{3}{4},(33)$

such that the selected scale level $\widehat{s}$ for a Gaussian ridge model of the form

$f_{\text{ridge},s_0}\left(x,y\right)=g_{1D}\left(x;s_0\right)=\frac{1}{\sqrt{2\pi s_0}}{e}^{-\frac{x^2}{2s_0}}(34)$

will be equal to the width $s_0\in {\mathbb{R}}_{+}$ of that idealised ridge model

$\widehat{s}={\text{arg}\hspace{0.17em}\text{max}}_s{L}_{pp,\text{norm}}\left(\mathrm{0,0};s\right)=s_0.(35)$

A common property of all these scale-invariant feature detectors is, thus, that the selected scale levels $\widehat{s}$ obtained from local extrema over scale will reflect characteristic¹ scales $s_0$ in the input data (Lindeberg, 2021b). By evaluating discretisation methods of Gaussian derivatives with respect to such scale selection properties, we therefore have a way of formulating a well-defined proxy task, for evaluating how well the different types of discretisation methods lead to appropriate consistency properties over scales for the numerical implementations of Gaussian derivative operators.

Supplementary Figures 5–8 in Appendix D in the Supplementary Material provide visualisations of the conceptual steps involved when defining these scale estimates $\widehat{s}$.

2.2.2 Quantitative measures for characterising the accuracy of the scale estimates obtained from the scale selection methodology

To quantify the performance of the different discretisation methods with regard to the above scale selection tasks, we will

• Compute the selected scale levels $\widehat{\sigma }=\sqrt{\widehat{s}}$ according to Equations 26, 27, Equation 31 and Equation 35 for appropriate values of the scale normalisation power γ with γ = 1 for the interest point detection tasks and γ according to Equation 29 and Equation 33 for the edge detection and ridge detection tasks, for different values of the characteristic scale $s_0$ in the image data, measured in dimension length ${\sigma }_0=\sqrt{s_0}$, and

• Quantify the deviations from the reference in terms of the relative error measure (Lindeberg, 2024b; Equation 107).

$E_{\text{scaleest,rel}}\left(\sigma \right)=\frac{\widehat{\sigma }}{{\widehat{\sigma }}_{\text{ref}}}-1,(36)$

under variations of the characteristic scale $s_0$ in the input image, where the deviations between the selected scale levels $\widehat{\sigma }=\sqrt{\widehat{s}}$ and the reference value ${\sigma }_0=\sqrt{s_0}$ are to be interpreted as the results of discretisation errors.

When generating discrete model signals for the different discrete approximation methods, we use as conceptually close discretisation methods for the input model signals (Gaussian blobs according to Equation 25 for interest point detection, diffuse edges according to Equation 30 for edge detection, or Gaussian ridges according to Equation 34 for ridge detection) as for the discrete approximations of Gaussian derivatives, according to Appendix C in the Supplementary Material.

3 Results

3.1 Characterisation of the effective amount of spatial smoothing in discrete approximations of Gaussian derivatives in terms of spatial spread measures

Figures 2, 3 show the graphs of computing the spatial spread measure $\sqrt{V(|T_{x^{\alpha }}(\cdot ;s)|)}$ according to Equations 18, 19, 21 as well as the offset measure $O_{\alpha }(s)$ according to Equation 20 over an interval of finer scale values $\sigma =\sqrt{s}\in [0.1,2]$, for each one of the different discretisation methods described in Section 2.1.

Figure 2

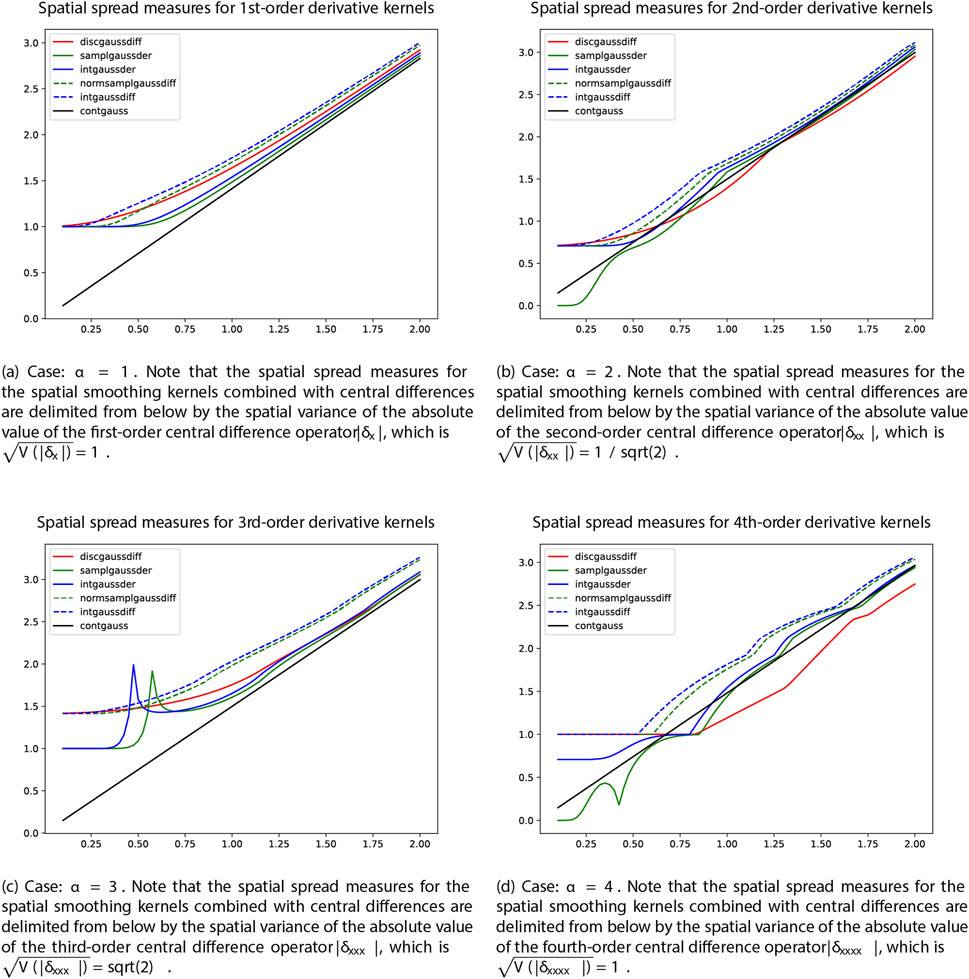
Figure 2. Graphs of the spatial spread measure $\sqrt{V(|T_{x^{\alpha }}(\cdot ;s)|)}$ according to Equation 18 for different discrete approximations of Gaussian derivative kernels of order $\alpha$: (i) for either discrete analogues of Gaussian derivative kernels $T_{\text{disc},x^{\alpha }}(n;s)$ according to Equation 10, corresponding to convolutions with the discrete analogue of the Gaussian kernel $T_{\text{disc}}(n;s)$ according to Equation 7 followed by central differences according to Equation 13, (ii) sampled Gaussian derivative kernels $T_{\text{sampl},x^{\alpha }}(n;s)$ according to Equation 8, (iii) integrated Gaussian derivative kernels $T_{\text{int},x^{\alpha }}(n;s)$ according to Equation 9, (iv) the hybrid discretisation kernel $T_{\text{hybr}-\text{sampl},x^{\alpha }}(n;s)$ according to Equation 16, corresponding to convolution with the normalised sampled Gaussian kernel $T_{\text{normsampl}}(n;s)$ according to Equation 5 followed by central differences according to Equation 13, and (v) the hybrid discretisation kernel $T_{\text{hybr}-\text{int},x^{\alpha }}(n;s)$ according to Equation 17, corresponding to convolution with the integrated Gaussian kernel $T_{\text{int}}(n;s)$ according to Equation 6 followed by central differences according to Equation 13. (Horizontal axes: Scale parameter in units of $\sigma =\sqrt{s}\in [0.1,2]$). (A) case α = 1, (B) case α = 2, (C) case α = 3, (D) case α = 4.

Figure 3

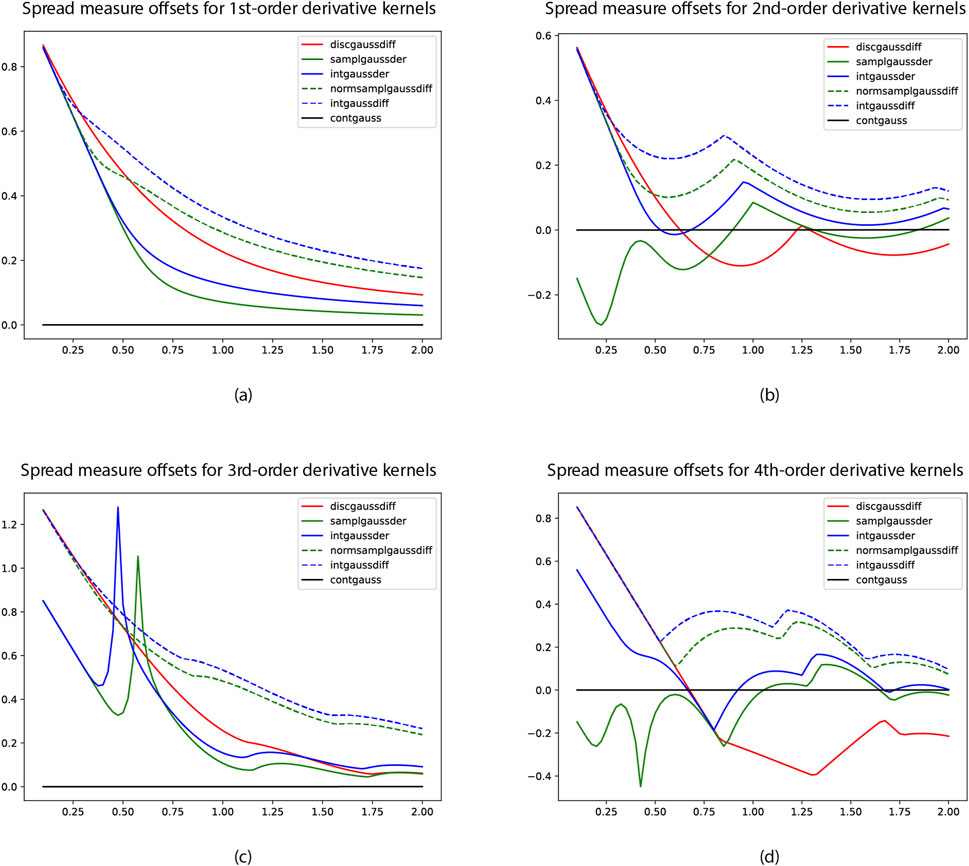
Figure 3. Graphs of the spatial spread measure offset $O_{\alpha }(s)$, relative to the spatial spread of a continuous Gaussian kernel, according to Equation 20, for different discrete approximations of Gaussian derivative kernels of order $\alpha$: (i) for either discrete analogues of Gaussian derivative kernels $T_{\text{disc},x^{\alpha }}(n;s)$ according to Equation 10, corresponding to convolutions with the discrete analogue of the Gaussian kernel $T_{\text{disc}}(n;s)$ according to Equation 7 followed by central differences according to Equation 13, (ii) sampled Gaussian derivative kernels $T_{\text{sampl},x^{\alpha }}(n;s)$ according to Equation 8, (iii) integrated Gaussian derivative kernels $T_{\text{int},x^{\alpha }}(n;s)$ according to Equation 9, (iv) the hybrid discretisation kernel $T_{\text{hybr}-\text{sampl},x^{\alpha }}(n;s)$ according to Equation 16, corresponding to convolution with the normalised sampled Gaussian kernel $T_{\text{normsampl}}(n;s)$ according to Equation 5 followed by central differences according to Equation 13, and (v) the hybrid discretisation kernel $T_{\text{hybr}-\text{int},x^{\alpha }}(n;s)$ according to Equation 17, corresponding to convolution with the integrated Gaussian kernel $T_{\text{int}}(n;s)$ according to Equation 6 followed by central differences according to Equation 13. (Horizontal axes: Scale parameter in units of $\sigma =\sqrt{s}\in [0.1,2]$.) (A) Case: $\alpha =1$, (B) Case: $\alpha =2$, (C) Case: $\alpha =3$, (D) Case: $\alpha =4$.

As can be seen from these graphs:

• The agreement with the underlying fully continuous spread measures for the continuous Gaussian derivative kernels is substantially better for the genuinely sampled or integrated Gaussian derivative kernels than for the hybrid discretisations based on combining either the normalised sampled Gaussian kernel or the integrated Gaussian kernel with central difference operators according to Equations 11–14.

In situations when multiple derivatives of different orders $\alpha$ are to be computed at the same scale levels, the hybrid discretisation methods are, however, as previously mentioned, computationally much more efficient, implying that the introduction of the hybrid discretisations implies a trade-off between the accuracy in terms of the overall amount of spatial smoothing of the equivalent discrete filters and the computational efficiency of the implementation.

• The agreement with the underlying fully continuous spread measures for the continuous Gaussian derivative kernels is substantially better for the genuinely discrete analogue of Gaussian derivative operators, obtained by first convolving the input data with the discrete analogue of the Gaussian kernel and then applying central difference operators to the spatially smoothed input data, compared to using any of the hybrid discretisations.

If, for efficiency reasons, a discretisation method is to be chosen, based on combining a first stage of spatial smoothing with a following application of central difference operators, the approach based on using spatial smoothing with the discrete analogue of the Gaussian kernel, in most of the cases, leads to better agreement with the underlying continuous theory, compared to using either the normalised sampled Gaussian kernel or the integrated Gaussian kernel in the first stage of spatial smoothing.

As previously stated, the hybrid discretisation methods may, however, anyway be warranted in situations where the underlying modified Bessel functions $I_n(s)$ are not fully available in the computational environment, where the discrete filtering operations are to be implemented, such as when performing learning of the scale levels in deep networks based on Gaussian derivative operators.

A further general implication of these results is that, depending on what discretisation method is chosen for discretising the computation of Gaussian derivative responses at fine scales, different values of the spatial scale parameter $s$ will be needed, to obtain a comparable amount of spatial smoothing of the input data for the different discretisation methods.

3.2 Characterisation of the approximation properties relative to continuous scale space in terms of the scale levels selected by scale selection algorithms

We will next characterise the approximation properties of the scale estimates for the different benchmark tasks outlined in Section 2.2.1 with regard to the quantitative measures defined in Section 2.2.2.

For generating the input data, we used 50 logarithmically scale values ${\sigma }_0\in [1/\mathrm{3,3}]$. When performing the scale selection step, we searched over a range of 80 logarithmically scale levels ${\sigma }_0\in [0.1,5]$, and accumulated the variability over scale at the image center for each differential feature detector, and additionally performed parabolic interpolation over the logarithmic scale values, to localise the scale estimates to higher accuracy. This very dense sampling of the scale levels is far beyond what is usually needed in actual image processing or computer vision algorithms, but was chosen here in order to essentially eliminate the effects of discrete sampling issues in the scale direction.

Figure 4A shows a graph of the scale estimates obtained for the second-order Laplacian interest point detector based on Equation 23 in this way, with the corresponding relative scale errors in Figure 4C. Supplementary Figures 9A, 9C in Appendix E in the Supplementary Material show corresponding results for the non-linear determinant of the Hessian interest point detector based on Equation 24.

Figure 4

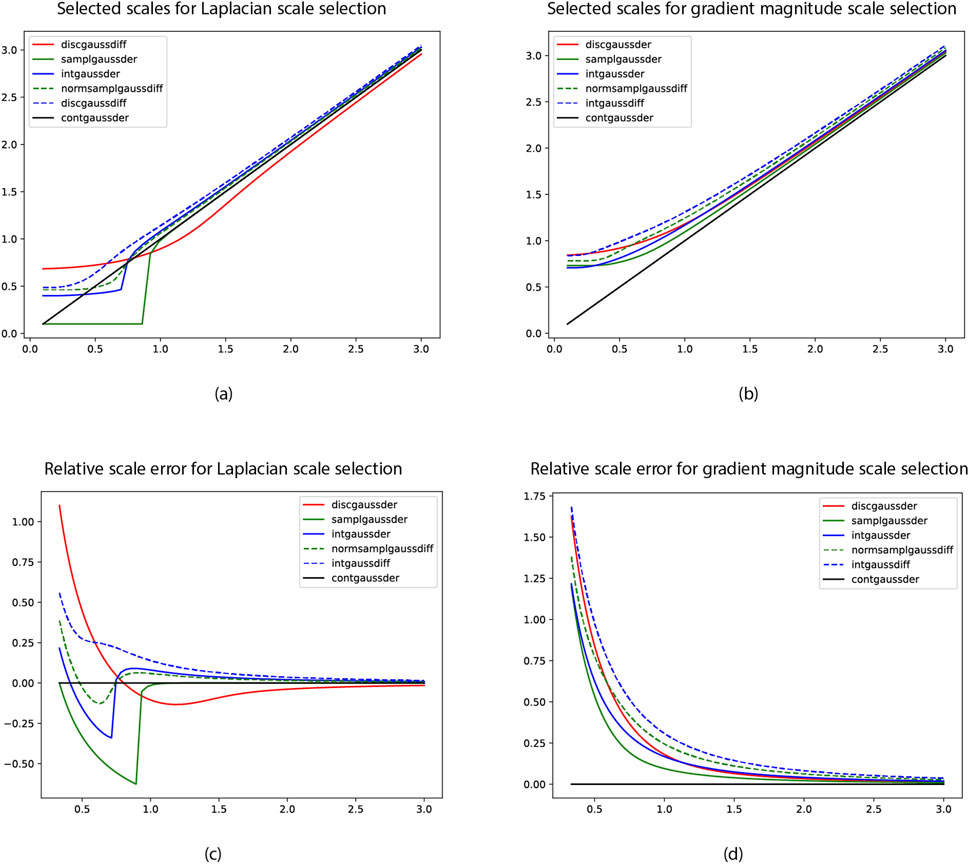
Figure 4. Graphs of the selected scales $\widehat{\sigma }=\sqrt{\widehat{s}}$ as well as the relative scale estimation error $E_{\text{scaleest,rel}}(\sigma )$, according to Equation 36, when (left column) applying scale selection from local extrema over scale of the scale-normalised Laplacian response according to Equation 23 to a set of Gaussian blobs of different size ${\sigma }_{\text{ref}}={\sigma }_0$, for different discrete approximations of the Gaussian derivative kernels or (right column) when applying scale selection from local extrema over scale of the scale-normalised gradient magnitude response according to Equation 28 to a set of diffuse step edges of different width ${\sigma }_{\text{ref}}={\sigma }_0$, for either (i) discrete analogues of Gaussian derivative kernels $T_{\text{disc},x^{\alpha }}(n;s)$ according to Equation 10, (ii) sampled Gaussian derivative kernels $T_{\text{sampl},x^{\alpha }}(n;s)$ according to Equation 8, (iii) integrated Gaussian derivative kernels $T_{\text{int},x^{\alpha }}(n;s)$ according to Equation 9, (iv) the hybrid discretisation method corresponding the equivalent convolution kernels $T_{\text{hybr}-\text{sampl},x^{\alpha }}(n;s)$ according to Equation 16 or (v) the hybrid discretisation method corresponding the equivalent convolution kernels $T_{\text{hybr}-\text{int},x^{\alpha }}(n;s)$ according to Equation 17. (Horizontal axes: Reference scale ${\sigma }_{\text{ref}}={\sigma }_0\in [1/\mathrm{3,3}]$.) (A) Selected scales $\widehat{\sigma }$, (B) Selected scales $\widehat{\sigma }$, (C) Relative scale estimation error $E_{scaleest,rel}\left(\sigma \right)$, (D) Relative scale estimation error $E_{scaleest,rel}\left(\sigma \right)$.

As can be seen from these graphs, the consistency errors in the scale estimates obtained for the hybrid discretisation methods, based on either the normalised Gaussian kernel or the integrated Gaussian kernel with central differences, are for larger values of the scale parameter higher than the corresponding consistency errors in the regular discretisation methods based on either sampled Gaussian derivatives or integrated Gaussian derivatives. For smaller values of the scale parameter, there is, however, a range of scale values, where the consistency errors are lower for the hybrid discretisation methods than for underlying corresponding regular discretisation methods.

Notably, the consistency errors for the discretisation methods involving central differences are also generally lower for the genuinely discrete method, based on convolution with the discrete analogue of the Gaussian kernel followed by central differences, than for the hybrid methods.

Figure 4B shows the selected scale levels for the first-order gradient-magnitude-based edge detection operation based on Equation 28, with the corresponding relative error measures shown in Figure 4D. As can be seen from these graphs, the consistency errors are notably higher for the hybrid discretisation approaches, compared to their underlying regular methods. In these experiments, the consistency errors are also higher for the hybrid discretisation methods than for the genuinely discrete approach, based on discrete analogues of Gaussian derivatives.

Finally, Supplementary Figures 9B, 9D in Appendix E in the Supplementary Material show corresponding results for the second-order principal-curvature-based ridge detector based on Equation 32, which are structurally similar to the previous results for the second-order Laplacian and determinant of the Hessian interest point detectors.

4 Summary and discussion

In this paper, we have extended the in-depth treatment of different discretisations of Gaussian derivative operators in terms of explicit convolution operations in (Lindeberg, 2024b) to two more discretisation methods, based on hybrid combinations of either convolutions with normalised sampled Gaussian kernels or convolutions with integrated Gaussian kernels with central difference operators.

The results from the treatment show that it is possible to characterise general properties of these hybrid discretisation methods in terms of the effective amount of spatial smoothing that they imply. Specifically, for very small values of the scale parameter, the results obtained after the spatial discretisation may differ significantly from the results obtained from the fully continuous scale-space theory, as well as between the different types of discretisation methods.

The results from this treatment are intended to be generically applicable in situations, when scale-space operations are to be applied at scale levels below the otherwise rule of thumb in classical computer vision, of not going below a certain minimum scale level, corresponding to a standard deviation of the Gaussian kernel of the order of $1/\sqrt{2}$ or 1. We argue that the presented quantitative performance characterisations should have a predictive ability, for how the different types of discrete derivative approximation methods could have comparative advantages in other multi-scale settings.

One direct application domain for these results is when implementing deep networks in terms of Gaussian derivatives, where empirical evidence indicates that deep networks often tend to benefit from using finer scale levels than as indicated by the previous rule of thumb in classical computer vision, and which we will address in future work.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author. Python code, that implements the discretization methods for Gaussian smoothing and Gaussian derivatives described in this paper, is available in the pyscsp package, available at GitHub: https://github.com/tonylindeberg/pyscsp as well as through PyPi: “pip install pyscsp”.

Author contributions

TL: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Validation, Visualization, Writing–original draft, Writing–review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Swedish Research Council under contract 2022-02969.

Acknowledgments

A preprint of this article has been deposited at arXiv:2405.05095 (Lindeberg, 2024a).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsip.2024.1447841/full#supplementary-material

Footnotes

¹The notion of “characteristic scale” refers to a scale that reflects a characteristic length in the image data, in a similar way as the notion of characteristic length is used in the areas of physics. See Appendix A.3.1 in the Supplementary Material for further details.

References

Abramowitz, M., and Stegun, I. A. (1964). in Handbook of mathematical functions. Applied mathematics series. 55 edn. (National bureau of standards, US government printing office).

Google Scholar

Bay, H., Ess, A., Tuytelaars, T., and van Gool, L. (2008). Speeded-up robust features (SURF). Comput. Vis. Image Underst. 110, 346–359. doi:10.1016/j.cviu.2007.09.014

CrossRef Full Text | Google Scholar

Bekkers, E. J. (2020). B-spline CNNs on Lie groups. Int. Conf. Learn. Repr. (ICLR 2020). Available at: https://openreview.net/forum?id=H1gBhkBFDH.

Google Scholar

Bouma, H., Vilanova, A., Bescós, J. O., ter Haar Romeny, B., and Gerritsen, F. A. (2007). Fast and accurate Gaussian derivatives based on B-splines. Scale Space and Var. Meth. in Com. Vis. Springer LNCS, 4485, 406–417. doi:10.1007/978-3-540-72823-8_35

CrossRef Full Text | Google Scholar

Bretzner, L., and Lindeberg, T. (1998). Feature tracking with automatic selection of spatial scales. Comput. Vis. Image Underst. 71, 385–392. doi:10.1006/cviu.1998.0650

CrossRef Full Text | Google Scholar

Burt, P. J., and Adelson, E. H. (1983). The Laplacian pyramid as a compact image code. IEEE Trans. Comm. 9, 532–540.

PubMed Abstract | Google Scholar

Charalampidis, D. (2016). Recursive implementation of the Gaussian filter using truncated cosine functions. IEEE Trans. Signal Process. 64, 3554–3565. doi:10.1109/tsp.2016.2549985

CrossRef Full Text | Google Scholar

Chomat, O., de Verdiere, V., Hall, D., and Crowley, J. (2000). Local scale selection for Gaussian based description techniques. Eur. Conf. Comput. Vis. (ECCV 2000) Springer LNCS vol. 1842:117–133.

Google Scholar

Crowley, J. L., and Riff, O. (2003). Fast computation of scale normalised Gaussian receptive fields. Scale Space Meth. in Comp. Visi. Springer LNCS vol. 2695, 584–598. doi:10.1007/3-540-44935-3_41

CrossRef Full Text | Google Scholar

Crowley, J. L., and Stern, R. M. (1984). Fast computation of the difference of low pass transform. IEEE Trans. Pattern Anal. Mach. Intell. 6, 212–222. doi:10.1109/tpami.1984.4767504

PubMed Abstract | CrossRef Full Text | Google Scholar

Daubechies, I. (1992). Ten lectures on wavelets. Philadelphia: SIAM.

Google Scholar

Debnath, L., and Shah, F. A. (2002). Wavelet transforms and their applications. Springer.

Google Scholar

Deriche, R. (1992). “Recursively implementing the Gaussian and its derivatives,” in Proc. International conference on image processing (ICIP’92), 263–267.

Google Scholar

Farnebäck, G., and Westin, C.-F. (2006). Improving Deriche-style recursive Gaussian filters. J. Math. Imaging Vis. 26, 293–299. doi:10.1007/s10851-006-8464-z

CrossRef Full Text | Google Scholar

Florack, L. M. J. (1997). Image structure. Springer. doi:10.1007/978-3-642-60893-3_1

CrossRef Full Text | Google Scholar

Gavilima-Pilataxi, H., and Ibarra-Fiallo, J. (2023). “Multi-channel Gaussian derivative neural networks for crowd analysis,” in Proc. International Conference on Pattern Recognition Systems (ICPRS 2023), Guayaquil, Ecuador, 04-07 July 2023 (IEEE), 1–7.

CrossRef Full Text | Google Scholar

Geusebroek, J.-M., Smeulders, A. W. M., and van de Weijer, J. (2003). Fast anisotropic Gauss filtering. IEEE Trans. Image Process. 12, 938–943. doi:10.1109/tip.2003.812429

PubMed Abstract | CrossRef Full Text | Google Scholar

Iijima, T. (1962). Basic theory on normalization of pattern (in case of typical one-dimensional pattern). Bulletin of the Electrotechnical Laboratory 26, 368–388.

Google Scholar

Jacobsen, J.-J., van Gemert, J., Lou, Z., and Smeulders, A. W. M. (2016). Structured receptive fields in CNNs. Proc. Comput. Vis. Patt. Recogn. (CVPR 2016), 2610–2619. doi:10.1109/cvpr.2016.286

CrossRef Full Text | Google Scholar

Koenderink, J. J. (1984). The structure of images. Biol. Cybern. 50, 363–370. doi:10.1007/bf00336961

PubMed Abstract | CrossRef Full Text | Google Scholar

Koenderink, J. J., and van Doorn, A. J. (1987). Representation of local geometry in the visual system. Biol. Cybern. 55, 367–375. doi:10.1007/bf00318371

PubMed Abstract | CrossRef Full Text | Google Scholar

Koenderink, J. J., and van Doorn, A. J. (1992). Generic neighborhood operators. IEEE Trans. Pattern Anal. Mach. Intell. 14, 597–605. doi:10.1109/34.141551

CrossRef Full Text | Google Scholar

Lim, J.-Y., and Stiehl, H. S. (2003). A generalized discrete scale-space formulation for 2-D and 3-D signals. Proc. Scale-Space Meth. Comput. Vis. (Scale-Space’03) vol. 2695, 132–147. doi:10.1007/3-540-44935-3_10

CrossRef Full Text | Google Scholar

Lindeberg, T. (1990). Scale-space for discrete signals. IEEE Trans. Pattern Anal. Mach. Intell. 12, 234–254. doi:10.1109/34.49051

CrossRef Full Text | Google Scholar

Lindeberg, T. (1993a). Discrete derivative approximations with scale-space properties: a basis for low-level feature extraction. Jour. of Math. Imag. and Visi. 3 (1), 349–376.

CrossRef Full Text | Google Scholar

Lindeberg, T. (1993b). Scale-space theory in computer vision. Springer.

Google Scholar

Lindeberg, T. (1994). Scale-space theory: a basic tool for analysing structures at different scales 21. Jour. of. Appl. Stat. 225–270.

CrossRef Full Text | Google Scholar

Lindeberg, T. (1998a). Edge detection and ridge detection with automatic scale selection. Int. J. Comput. Vis. 30, 117–154.

Google Scholar

Lindeberg, T. (1998b). Feature detection with automatic scale selection. Int. J. Comput. Vis. 30, 77–116.

Google Scholar

Lindeberg, T. (2011). Generalized Gaussian scale-space axiomatics comprising linear scale-space, affine scale-space and spatio-temporal scale-space. J. Math. Imag. Vis. 40, 36–81. doi:10.1007/s10851-010-0242-2

CrossRef Full Text | Google Scholar

Lindeberg, T. (2013a). “Generalized axiomatic scale-space theory,” in Adv. Imaging Phys. Editor P. Hawkes (Elsevier) 178, 1–96. doi:10.1016/b978-0-12-407701-0.00001-7

CrossRef Full Text | Google Scholar

Lindeberg, T. (2013b). Scale selection properties of generalized scale-space interest point detectors. J. Math. Imag. Vis. 46, 177–210. doi:10.1007/s10851-012-0378-3

CrossRef Full Text | Google Scholar

Lindeberg, T. (2015). Image matching using generalized scale-space interest points. Jour. of Math. Imag. and Vis. 52, 3–36.

CrossRef Full Text | Google Scholar

Lindeberg, T. (2020). Provably scale-covariant continuous hierarchical networks based on scale-normalized differential expressions coupled in cascade. J. Math. Imag. Vis. 62, 120–148. doi:10.1007/s10851-019-00915-x

CrossRef Full Text | Google Scholar

Lindeberg, T. (2021a). Scale-covariant and scale-invariant Gaussian derivative networks. J. Math. Imag. Vis. 12679, 223–242. doi:10.1007/s10851-021-01057-9

CrossRef Full Text | Google Scholar

Lindeberg, T. (2021b). “Scale selection,” in Computer vision. Editor K. Ikeuchi, 1110–1123. doi:10.1007/978-3-030-03243-2_242-1

CrossRef Full Text | Google Scholar

Lindeberg, T. (2022). Scale-covariant and scale-invariant Gaussian derivative networks. J. Math. Imaging Vis. 64, 223–242. doi:10.1007/s10851-021-01057-9

CrossRef Full Text | Google Scholar

Lindeberg, T. (2024a). Approximation properties relative to continuous scale space for hybrid discretizations of Gaussian derivative operators. arXiv Prepr. arXiv:2405.05095. doi:10.48550/arXiv.2405.05095

CrossRef Full Text | Google Scholar

Lindeberg, T. (2024b). Discrete approximations of Gaussian smoothing and Gaussian derivatives. J. Math. Imaging Vis. 66, 759–800. doi:10.1007/s10851-024-01196-9

CrossRef Full Text | Google Scholar

Lindeberg, T., and Bretzner, L. (2003). Real-time scale selection in hybrid multi-scale representations. Proc. Scale-Space Meth. Comput. Vis. (Scale-Space’03), Springer LNCS. vol. 2695, 148–163. doi:10.1007/3-540-44935-3_11

CrossRef Full Text | Google Scholar

Lowe, D. G. (2004). Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 60, 91–110. doi:10.1023/b:visi.0000029664.99615.94

CrossRef Full Text | Google Scholar

Mallat, S. (1989a). Multifrequency channel decompositions of images and wavelet models. IEEE Trans. Acoust. 37, 2091–2110. doi:10.1109/29.45554

CrossRef Full Text | Google Scholar

Mallat, S. (2016). Understanding deep convolutional networks. Phil. Trans. R. Soc. A 374, 20150203. doi:10.1098/rsta.2015.0203

PubMed Abstract | CrossRef Full Text | Google Scholar

Mallat, S. G. (1989b). A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 11, 674–693. doi:10.1109/34.192463

CrossRef Full Text | Google Scholar

Mallat, S. G. (1999). A wavelet tour of signal processing. Academic Press.

Google Scholar

Meyer, Y. (1992). Wavelets and operators, 1. Cambridge University Press, 256–365. doi:10.1017/cbo9780511662294.012

CrossRef Full Text | Google Scholar

Penaud-Polge, V., Velasco-Forero, S., and Angulo, J. (2022). “Fully trainable Gaussian derivative convolutional layer,” in International Conference on Image Processing (ICIP 2022), Bordeaux, France, 16-19 October 2022 (IEEE), 2421–2425.

CrossRef Full Text | Google Scholar

Pintea, S. L., Tömen, N., Goes, S. F., Loog, M., and van Gemert, J. C. (2021). Resolution learning in deep convolutional networks using scale-space theory. IEEE Trans. Image Process. 30, 8342–8353. doi:10.1109/tip.2021.3115001

PubMed Abstract | CrossRef Full Text | Google Scholar

Rey-Otero, I., and Delbracio, M. (2016). Computing an exact Gaussian scale-space. Image Process. Online 6, 8–26. doi:10.5201/ipol.2016.117

CrossRef Full Text | Google Scholar

Sangalli, M., Blusseau, S., Velasco-Forero, S., and Angulo, J. (2022). “Scale equivariant U-net,” in Proc. British machine vision conference (BMVC 2022), 763.

Google Scholar

Simoncelli, E. P., and Freeman, W. T. (1995). “The steerable pyramid: a flexible architecture for multi-scale derivative computation,” in Proc. International Conference on Image Processing (ICIP’95), Washington, USA, 23-26 October 1995 (IEEE), 444–447. doi:10.1109/icip.1995.537667

CrossRef Full Text | Google Scholar

Simoncelli, E. P., Freeman, W. T., Adelson, E. H., and Heeger, D. J. (1992). Shiftable multi-scale transforms. IEEE Trans. Inf. Theory 38, 587–607. doi:10.1109/18.119725

CrossRef Full Text | Google Scholar

Slavík, A., and Stehlík, P. (2015). Dynamic diffusion-type equations on discrete-space domains. J. Math. Analysis Appl. 427, 525–545. doi:10.1016/j.jmaa.2015.02.056

CrossRef Full Text | Google Scholar

Teolis, A. (1998). Computational signal Processing with wavelets Birkhäuser.

Google Scholar

ter Haar Romeny, B. (2003). Front-end vision and multi-scale image analysis Springer.

Google Scholar

Tschirsich, M., and Kuijper, A. (2015). Notes on discrete Gaussian scale space. J. Math. Imag. Vis. 51, 106–123.

CrossRef Full Text | Google Scholar

Unser, M., Aldroubi, A., and Eden, M. (1991). Fast B-spline transforms for continuous image representation and interpolation. IEEE Trans. Pattern Anal. Mach. Intell. 13, 277–285. doi:10.1109/34.75515

CrossRef Full Text | Google Scholar

Unser, M., Aldroubi, A., and Eden, M. (1993). B-spline signal processing. I. Theory. IEEE Trans. Signal Process. 41, 821–833. doi:10.1109/78.193220

CrossRef Full Text | Google Scholar

van Vliet, L. J., Young, I. T., and Verbeek, P. W. (1998). Recursive Gaussian derivative filters. Int. Conf. Pattern Recognit. 1, 509–514. doi:10.1109/icpr.1998.711192

CrossRef Full Text | Google Scholar

Wang, Y.-P. (1999). Image representations using multiscale differential operators. IEEE Trans. Image Process. 8, 1757–1771. doi:10.1109/83.806621

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y.-P., and Lee, S. L. (1998). Scale-space derived from B-splines. IEEE Trans. on patt. analy. and machi. intelli. 20, 1040–1055.

Google Scholar

Weickert, J., Ishikawa, S., and Imiya, A. (1999). Linear scale-space has first been proposed in Japan. J. Math. Imag. Vis. 10, 237–252. doi:10.1023/a:1008344623873

CrossRef Full Text | Google Scholar

Witkin, A. P. (1983). Scale-space filtering. Proc. 8th Int. Joint Conf. Art. Intell., 1019–1022.

Google Scholar

Worrall, D., and Welling, M. (2019). Deep scale-spaces: equivariance over scale. Advances in Neural Information Processing Systems (NeurIPS 2019), 7366–7378.

Google Scholar

Yang, Y., Dasmahapatra, S., and Mahmoodi, S. (2023). Scale-equivariant UNet for histopathology image segmentation. arXiv Prepr. arXiv:2304.04595. doi:10.48550/arXiv.2304.04595

CrossRef Full Text | Google Scholar

Young, I. T., and van Vliet, L. J. (1995). Recursive implementation of the Gaussian filter. Signal Process. 44, 139–151. doi:10.1016/0165-1684(95)00020-e

CrossRef Full Text | Google Scholar

Zheng, Q., Gong, M., You, X., and Tao, D. (2022). A unified B-spline framework for scale-invariant keypoint detection. Int. J. Comput. Vis. 130, 777–799. doi:10.1007/s11263-021-01568-3

CrossRef Full Text | Google Scholar