- 1Beijing Institute of Radio Measurement, Beijing, China
- 2State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, China
Airborne forward-looking radar (AFLR) has been more and more impoatant due to its wide application in the military and civilian fields, such as automatic driving, sea surveillance, airport surveillance and guidance. Recently, sparse deconvolution technique has been paid much attention in AFLR. However, the azimuth resolution performance gradually decreases with the complexity of the imaging scene. In this paper, a data-driven airborne Bayesian forward-looking superresolution imaging algorithm based on generalized gaussian distribution (GGD- Bayesian) for complex imaging scene is proposed. The generalized gaussian distribution is utilized to describe the sparsity information of the imaging scene, which is quite essential to adaptively fit different imaging scenes. Moreover, the mathematical model for forward-looking imaging was established under the maximum a posteriori (MAP) criterion based on the Bayesian framework. To solve the above optimization problem, quasi-Newton algorithm is derived and used. The main contribution of the paper is the automatic selection for the sparsity parameter in the process of forward-looking imaging. The performance assessment with simulated data has demonstrated the effectiveness of our proposed GGD- Bayesian algorithm under complex scenarios.
1 Introduction
Forward-looking radar (FLR) are increasingly receiving a lot of attention in many military and civilian fields due to its advantages over optical sensing tools, such as search and rescue, sea surveillance, airport surveillance and guidance (Curlander and McDonough, 1991; Cumming and Wang, 2005; Richards, 2005; Skolnik, 2008). Traditional Doppler beam sharpening (DBS) (Long et al., 2011; Chen et al., 2017) and synthetic aperture radar (SAR) (Moreira and Huang, 1994; MoreiraPrats-Iraola et al., 2013; Li et al., 2016; Sun et al., 2022; Lu et al., 2023; Huang et al., 2017) usually work on the strip mode or the squint mode, and the observation area are on the side or squint side of the flying trajectory. The Doppler history caused by the relative movement between the platform and imaging scene is the key point for DBS or SAR imaging. Constrained by the Doppler imaging principles, however, neither of these two methods can perform high-resolution imaging for the area in front of the flight direction, resulting in a forward-looking blind zone. In addition, under the forward-looking imaging model, the observation area that are symmetrical about the trajectory have the same range history, resulting in the Doppler ambiguity for the left and right sides of the trajectory. The constant pursuit of azimuth resolution performance is the driving force for the development of forward-looking imaging techniques.
In order to acquire the fine details of the observation scene for FLR, high range resolution can be guaranteed by exploiting the wide bandwidth signals and pulse compression technology. According to Radar hand book, the azimuth resolution is mainly inversely proportional to the antenna aperture size, and it can expressed as
where
Forward-looking superresolution imaging technique (Richards, 1988; Kusama et al., 1990; Dropkin and Ly, 1997) become a research hotspot in recent years, which can break through the inherent limitation of the real antenna and can obtain higher azimuth resolution than the real beam. Previous researchers have proposed that the AFLR echoes can be expressed as a convolution relationship between the antenna pattern and the scatterers in the imaging scene. Theoretically, deconvolution methods can be used to increase the azimuth resolution. The deconvolution problem is ill-posed due to the low-pass characteristics of the real antenna in the highly noise-sensitive case.
To mitigate the ill-posedness of the forward-looking deconvolution problem, the truncated singular value decomposition method (TSVD) is introduced by Huang and Tuo et al. (Huang et al., 2015; Tuo et al., 2021), which can enhance the azimuth quality by discarding some smaller singular values. Then, Yang and Zhang et al. introduce the IAA method (Zhang et al., 2018a; Zhang et al., 2018b) into the forward-looking imaging. The regularization method (Chen et al., 2015; Li et al., 2019; Zhang et al., 2019) is a good tool to transform the ill-posed problem to the nearby well-conditioned problem, and this operation can be achieved by selecting different regularization constraints on the least square algorithm. Regularization can relax the forward-looking deconvolution problem and acquire better performance. Moreover, Yang and Zhang et al. proposes the total variation (TV) (Zhang et al., 2020a; Zhang et al., 2020b) based method to describe the scene information, which performs well for the in preserving the contour of the target. To make full use of the prior information of the forward-looking imaging scene, Yang, Chen and Li et al. propose the Bayesian framework (Yang et al., 2020; Chen et al., 2022; Li et al., 2022) based forward-looking methods, which converts forward-looking into the optimization estimation. The key point of these methods is to well establish the imaging scene model.
In this paper, on the basis of the forward-looking imaging model established previously (Richards, 1988; Kusama et al., 1990; Dropkin and Ly, 1997; Chen et al., 2015; Huang et al., 2015; Zhang et al., 2018a; Zhang et al., 2018b; Li et al., 2019; Zhang et al., 2019; Zhang et al., 2020a; Zhang et al., 2020b; Yang et al., 2020; Tuo et al., 2021; Chen et al., 2022; Li et al., 2022), a data-driven airborne Bayesian superresolution imaging method via generalized gaussian distribution (GGD- Bayesian) for complex imaging scene is proposed. The main contribution of the paper is the forward-looking method for the automatic selection of the sparsity parameter. Moreover, the proposed method performs parameter updating during each iteration, which means that it is robust to different situations. The key ingredient of the proposed GGD-Bayesian method is the use of the quasi-Newton algorithm.
The arrangement of this paper is organized as follows. Section 2 introduces the Doppler convolution model for the FLR. In Section 3, the data-driven airborne Bayesian forward-looking imaging model via Generalized Gaussian Distribution is introduced in detail. In Section 4, simulations by different methods are conducted to verify the performance of the GGD-Bayesian method. Section 5 provides a brief conclusion of this paper.
2 Forward-looking imaging model
2.1 Instantaneous range history model
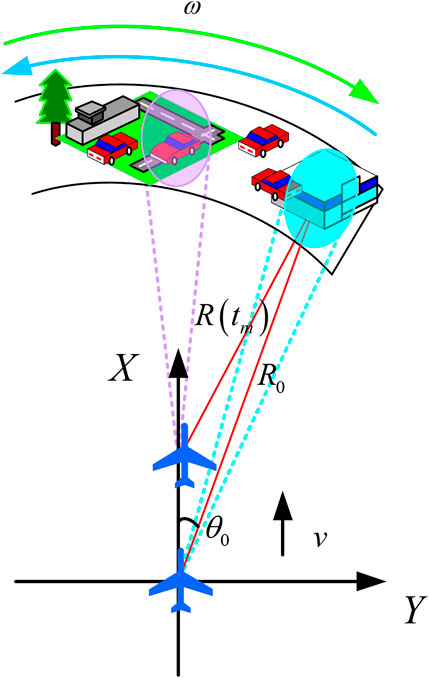
Figure 1 shows the AFLR imaging geometric model. In the reference Cartesian coordinate defined by
The instantaneous range history can be given as
where
Performing higher-order Taylor series expansion on Eq. 2, we can obtain the following form
where
2.2 Decoupling effect model between range and azimuth
Assume that the AFLR transmits a linear-frequency-modulation (LFM) pulse signal, which is given as
where
After demodulation we can get
where
After range pulse compression and range cell migration correction (RCMC), the echoed signal can be expressed as
where
From Eq. 9, it can be found that the coupling effect between the range and the azimuth make it different to choose enough pulses. Therefore, the range walk must be eliminated.
Keystone Transform (KT) can be used to compensate the linear range walk (Li et al., 2008; Li et al., 2022), and the range migration can be corrected as
2.3 AFLR Doppler deconvolution model
Then we can further transform Eq. 10 as
where
From above equation, it can be found that the echoed signal in one range cell is the convolution between the antenna pattern and the scattering coefficient (Zhang et al., 2020a; Zhang et al., 2020b; Yang et al., 2020; Chen et al., 2022), which is given as
where
Considering the effect of noise, Eq. 13 can be rewritten as
where
From the previous derivation (Zhang et al., 2020b; Yang et al., 2020; Chen et al., 2022; Li et al., 2022), the Doppler convolution model can be written into the matrix form
where
3 Data-driven airborne bayesian forward-looking superresolution imaging based on generalized Gaussian distribution
In order to improve the performance of Doppler deconvolution, it is very important to extract prior information. More recently, sparsity information has been used for FLR imaging (Chen et al., 2015; Zhang et al., 2018b; Li et al., 2019). However, the direct use of sparsity is limited because the scatterers may not be sparse in the single-beam space.
To solve this problem, we propose a multiple beam space model (Chen et al., 2022). The single-beam echo is spliced to form a high-dimensional space in the azimuth direction. When the number of scattering points in the forward-looking scene is limited, the imaging scene can be regarded as sparse. The sparsity of the scene is further enhanced by the beam-merging operations. To fully describethe sparsity of the scatters, Bayesian method based on the maximum a posteriori (MAP) criterion is adopted. From our previous derivation (Chen et al., 2022), the echoed signal in the high-dimensional space can be given as
For one range bin, Eq. 18 can be further expressed as
where
From above analysis, the distribution functions of imaging scene of one range bin may include the Gaussian distribution, Laplace distribution, and other distributions in expanded beam space. Therefore, the generalized Gaussian distribution (GGD) (Bishop, 2006; El-Darymli et al., 2015) is introduced to describe the sparsity property of the forward-looking imaging scene, which is given as
where
where
Since
In order to simplify the derivation process, the mean can be compensated. Then, we can get the following express
Under the condition of independent identically distributed (i.i.d.), the probability density function (PDF) of the imaging scene can be written as
Based on Bayesian framework, the maximum a posterior (MAP) estimation of the forward-looking imaging scene can be given as
Where
After some simplification, the forward-looking imaging problem can be illustrated as the following form
where
To solve Eq. 28, we make the following approximation
where
Substituting Eq. 29 into Eq. 28, we can get
To obtain the optimization solution, we can get the gradient of
where
Moreover, we can obtain the iterative solution with the quasi-Newton method, which can be written as
where
As is seen from the above derivation, we can see that the regularization parameter is very important. Detailed regularization parameter estimation information can be found in (Cetin et al., 2014; Xu et al., 2015).
Suppose
4 Experimental data processing
Simulations are conducted in this section. We compare the performance of real beam, TSVD, iterative shrinkage threshold algorithm (ISTA), IAA, and Bayesian method with the proposed method.
4.1 Point targets experimental results
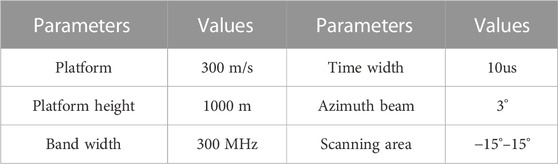
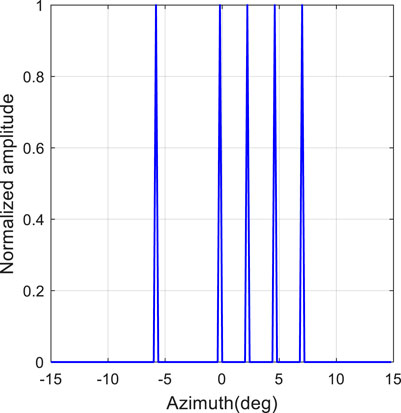
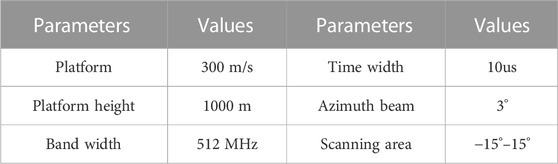
In order to verify that the method proposed has superior performance. In this section, five-point targets are considered. All of them have the same amplitude values. The comparisons between real beam, TSVD, ISTA, IAA, Bayesian and the proposed Bayesian method are given. Simulation parameters are shown in Table 1.
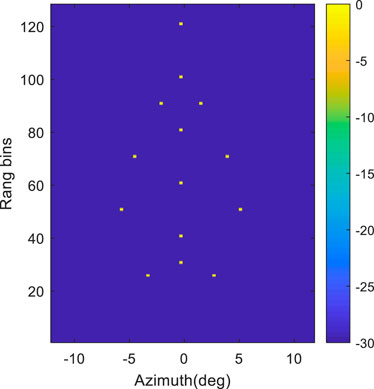
Figure 2 shows the true original scene. In this experiment, the white Gaussian noise is set as 20 dB. The real part and the imagery part histogram statistical results for the imaging scene are shown in Figure 3.
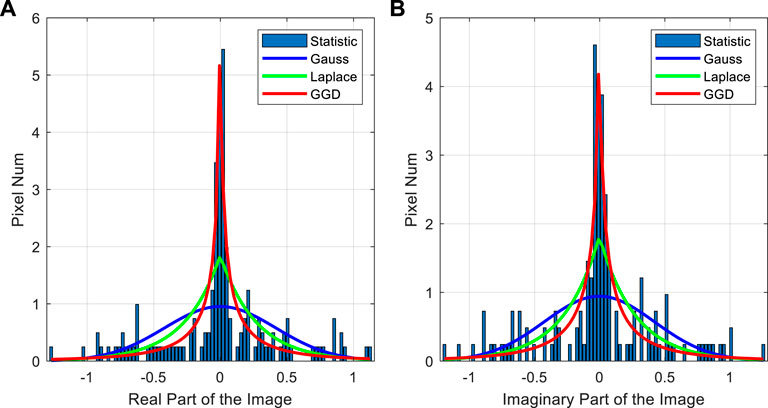
FIGURE 3. The Sparse statistical characteristics of forward-looking image. (A) Real part of the image. (B) Imaginary part of the image.
From Figure 3, we can see that the Laplace prior can be used to describe the static property of the imaging scene. However, the Laplace model matching performance is worse than GGD model. The sparsity of the echo signal is well described in the GGD model. The imaging results with different methods is given in Figure 4.
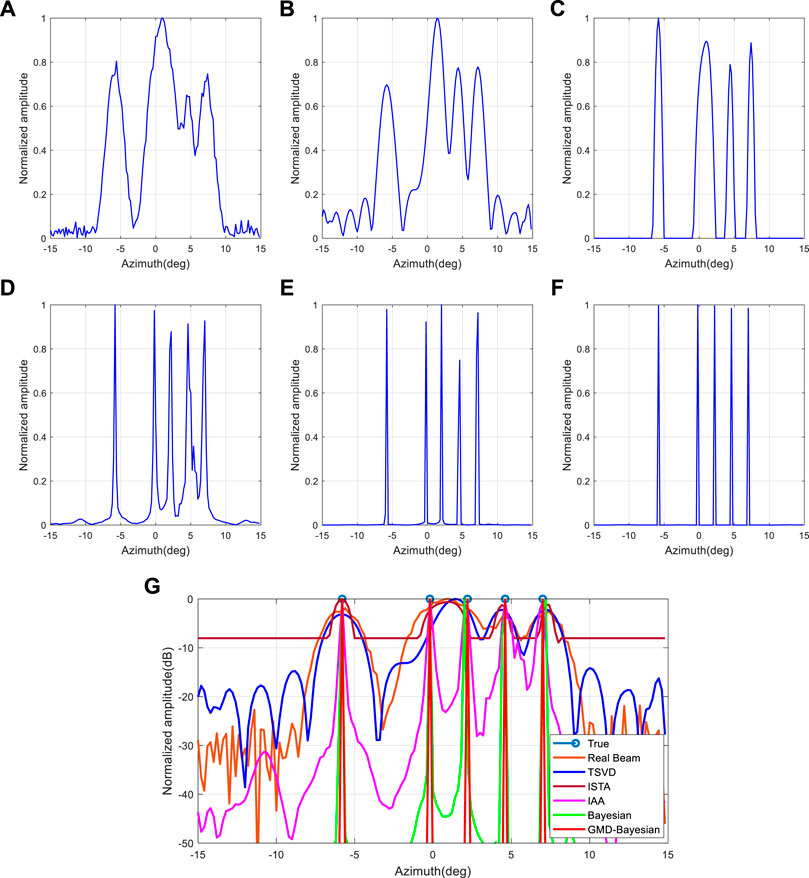
FIGURE 4. Angular super-resolution results. (A) Real beam imaging method; (B) TSVD method; (C) ISTA Method; (D) IAA method; (E) Bayesian method. (F) Proposed GGD-Bayesian method; (G) Comparison results of angular super-resolution.
From Figures 4A, B, we can see that the real beam and TSVD methods has obvious signal aliasing, and they are hard to recover the two close targets. Figure 4C shows the results of the ISTA method, and ISAT method has lower sidelobes. Although the resolution has been improved, it is still hard to distinguish the two close targets. The result of IAA method is shown in Figure 4D. It can be seen that the two closely spaced targets are well separated, and the targets outline is sharpened. However, the IAA method suffers from high sidelobes. Figure 4E gives the Bayesian based forward-looking imaging results. The imaging results are clear, but there is a certain degree of attenuation in the signal amplitude, which reduce the image quality. Obviously, the proposed GGD-Bayesian method in Figure 4E performs the best among all the forward-looking imaging methods. Moreover, the GGD-Bayesian method can eliminate the signal aliasing phenomenon and suppress the noise amplification. The forward-looking comparison results under different methods are illustrated in Figure 4G, which further verify the effectiveness of the proposed GGD-Bayesian algorithm.
4.2 Simple surface-target experimental results
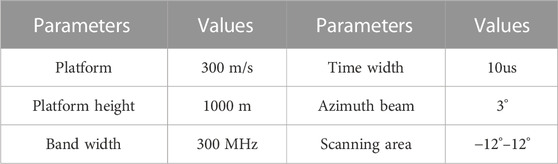
Point target simulation is demonstrated the performance of the proposed GGD-Bayesian method from above results. A simple surface target scene is constructed in this simulation. Simulation parameters are shown in Table 2. Figure 5 gives the true original scene. Then, the SNR is set as 10dBand 20 dB to the echo, respectively. For the sake of consistency, all the forward-looking results are normalized with the same color scale.
In Figures 6A–F, the SNR is set as 10 dB. From Figure 6, we can see that the real beam method has obvious signal aliasing phenomenon. The TSVD method suffer is seriously affected by noise, which may be caused by the difficulty in selecting proper singular values at low SNR. The ISTA method has maintains the integrity of the imaging information, but some residual images appear around the target. The imaging results based on IAA method is shown in Figure 6D. We can see that the targets outline is sharpened, and the imaging information maintains intact. However, there are many residual sidelobes around the target. Figures 6E, F show the imaging results of Bayesian and the proposed GGD-Bayesian method. Both of them perform well, and the proposed GGD-Bayesian method performs the best. From Figure 6, we can see that proposed GGD-Bayesian method not only enhance the forward-looking imaging resolution, but also suppress the noise.
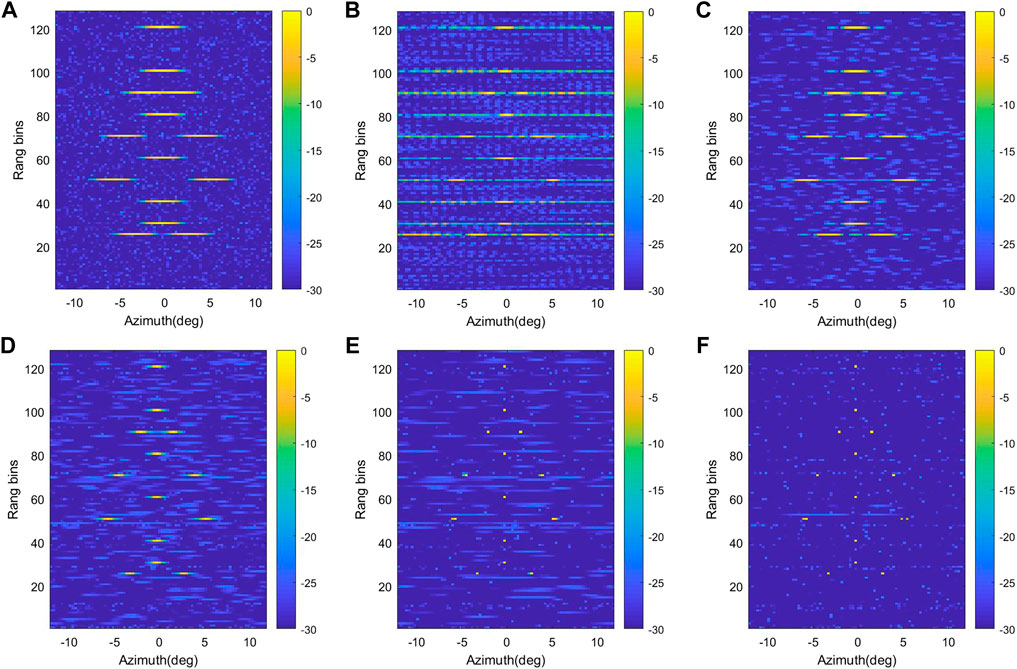
FIGURE 6. FLR super-resolution imaging results with SNR = 10 dB. (A) Real beam imaging method; (B) TSVD method; (C) ISTA method; (D). IAA method (E) Bayesian method; (F) Proposed GGD-Bayesian method.
The forward-looking results under different methods with 20 dB signal-to-noise ratio is shown if Figure 7. Similar to Figure 6, the real beam method has low azimuth resolution in Figure 7A. From Figures 7B, C, we can see that the TSVD and ISTA method can be used to increase the azimuth resolution. However, the resolution improvement is limited, there are many residual shadows. The IAA method performs well to improve the azimuth resolution. However, there are many residual sidelobes around the target in Figure 7D. Though the Bayesian method has better performance than IAA as shown in Figures 7D, E, the proposed GGD-Bayesian method has the best beam sharpening ability and noise suppression ability among all the methods.
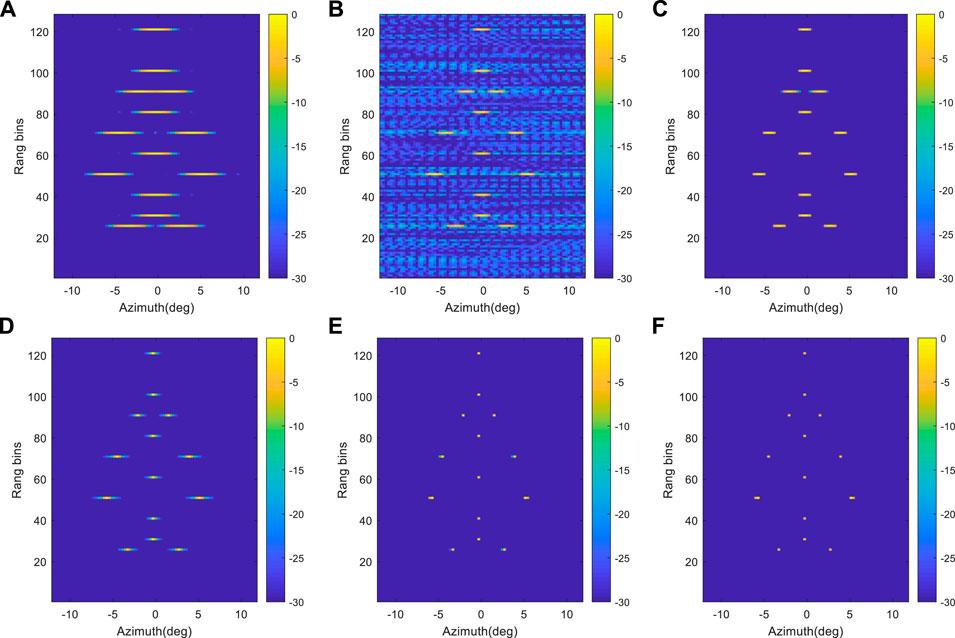
FIGURE 7. FLR super-resolution imaging results with SNR = 20 dB. (A) Real beam imaging method; (B) TSVD method; (C) ISTA method; (D). IAA method (E) Bayesian method; (F) Proposed GGD-Bayesian method.
4.3 Complex surface-target experimental results
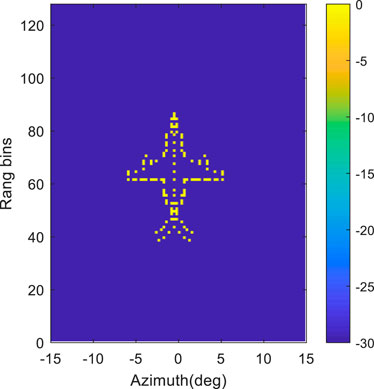
To further verify the performance of the proposed method, a more complex airplane model is considered in this section. The SNR is about 20 dB in this experiment. The airplane model is shown in Figure 8. Simulation parameters are shown in Table 3.
As shown in Figure 9, the complex surface-targets using real beam, TSVD, ISTA, IAA, Bayesian and the proposed GGD-Bayesian method is first analyzed.
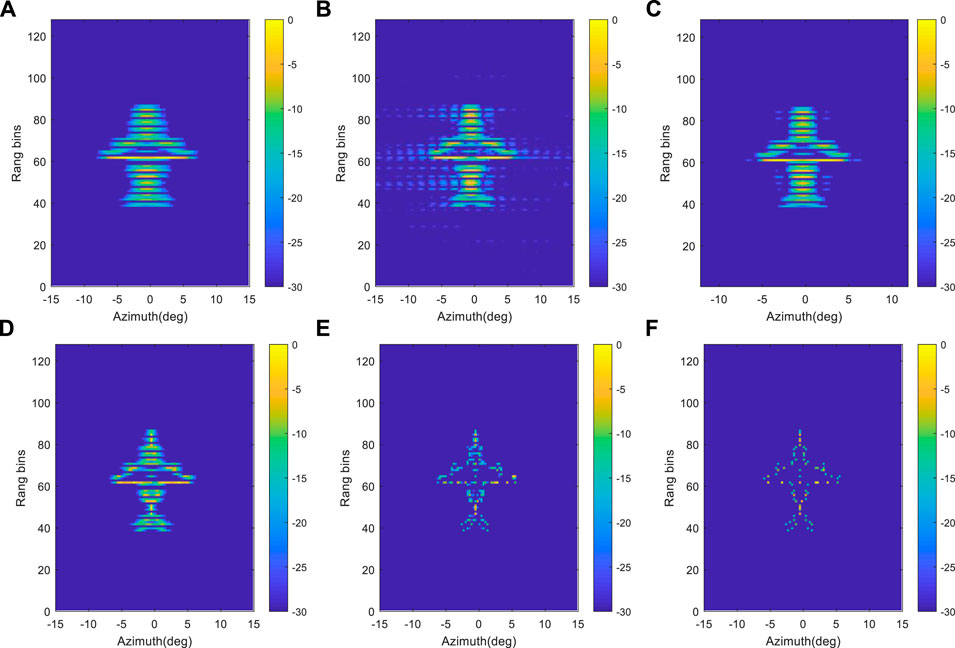
FIGURE 9. FLR super-resolution imaging results with SNR = 20 dB. (A) Real beam imaging method; (B) TSVD method; (C) ISTA method; (D). IAA method (E) Bayesian method; (F) Proposed GGD-Bayesian method.
In Figure 9A, the forward-looking imaging result based on real beam is blurred, which means that the azimuth resolution is poor. As illustrated in Figures 10B–D, the imaging results based on ISAT, TSVD and IAA methods performs better than the real beam method. However, there are still some shadows and sidelobes in the images. The Bayesian method can realize better resolution than IAA, and it can image the outline of targets, but more detailed information is still blurred. In contrast, more detailed airplane information has be recovered in the proposed GGD-Bayesian algorithm, and few shadows can be found. In addition, we can find more detailed information (i.e., the aircraft engine) in Figure 9F. The forward-looking imaging resolution is greatly improved, the aircraft target is clear. Like above experiments, the results of the proposed GGD-Bayesian method have higher azimuth super-resolution ability and better noise suppression ability than those of other methods.
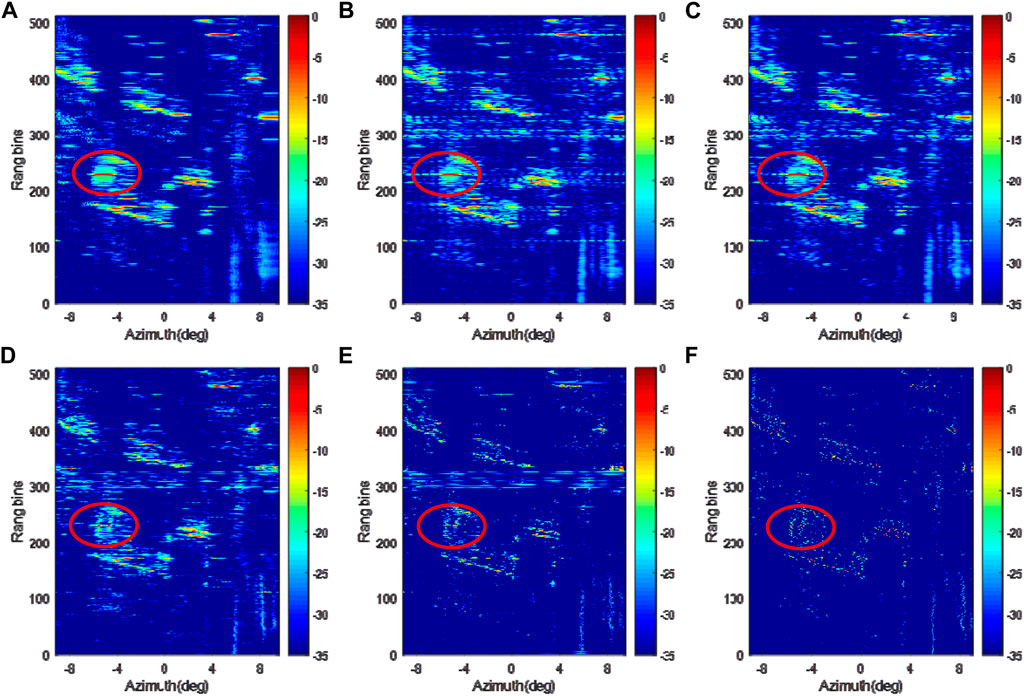
FIGURE 10. FLR super-resolution imaging results. (A) Real beam imaging method; (B) TSVD method; (C) ISTA method; (D). IAA method (E) Bayesian method; (F) Proposed GGD-Bayesian method.
4.4 Real data experimental results
In this section, the real data collected with a airborne Radar is used to demonstrate the effectiveness of the proposed GGD-Bayesian algorithm. The forward-looking area covers −9° to 9 in the azimuth direction. The experiment was undertaken at Yixian, Hebei Province. This scenario includes two typical areas characterized by adjacent houses and roads, respectively.
As shown in Figure 10A, the real beam image suffers from low resolution. The TSVD and ISTA imaging results can be used to improve the azimuth resolution, as shown in Figures 10B, C. In contrast, the IAA, Bayesian and GGD- Bayesian method provides higher resolution. Moreover, the proposed GGD-Bayesian method has the best performance. The house and roads are more distinguishable in Figure 10E. In addition, for the houses, the sharpening ability provided by GGD-Bayesian method outperforms the existing super-resolution methods.
Based on above experiments, we can conclude that the proposed GGD-Bayesian method can greatly improve the azimuth resolution and suppress the noise.
5 Conclusion
Forward-looking imaging has attracted more and more attention with the advantages of automatic driving and precision guidance. This paper proposes an efficient data-driven airborne forward-looking superresolution imaging algorithm based on Generalized Gaussian Distribution. In the proposed GGD-Bayesian method, the sparsity information of the imaging scene is described and constructed with the generalized Gaussian distribution, which is quite essential to adaptively fit different imaging scenes. The main contribution of the paper is the automatic selection for the sparsity parameter in the process of forward-looking imaging. This operation can ensure robustness to different situations. Through the results of simulated data processing, it is proved that the proposed method has better noise suppression and azimuth resolution improvement than traditional methods. In the future, we will focus on reducing the computational complexity of the algorithm with enhanced forward-looking performance.
In the future, we will focus on the forward-looking performance enhancement with complex trajectory for the airplane applications. (Huang et al., 2017).
Data availability statement
The original contributions presented in the study are included in the article/supplementary material further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Acknowledgments
The authors would like to thank the reviewers for their constructive comments that helped in improving this paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author HC declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Cetin, M., Stojanovic, I., Onhon, O., Varshney, K., Samadi, S., Karl, W. C., et al. (2014). Sparsity-driven synthetic aperture radar imaging: Reconstruction autofocusing moving targets and compressed sensing. IEEE Signal Process. Mag. 31 (4), 27–40. doi:10.1109/msp.2014.2312834
Chen, H., Li, M., Wang, Z., Lu, Y., Cao, R., Zhang, P., et al. (2017). Cross-range resolution enhancement for DBS imaging in a scan modeusing aperture-extrapolated sparse representation. IEEE Geosci. Remote Sens. Lett. 14 (9), 1459–1463. doi:10.1109/lgrs.2017.2710082
Chen, H., Li, Y., Gao, W., Zhang, W., Sun, H., Guo, L., et al. (2022). Bayesian forward-looking superresolution imaging using Doppler deconvolution in expanded beam space for high-speed platform. IEEE Trans. Geosci. Remote Sens. 60, 1–13. doi:10.1109/tgrs.2021.3107717
Chen, H. M., Li, M., Wang, Z. Y., Lu, Y. L., Zhang, P., and Wu, Y. (2015). Sparse super-resolution imaging for airborne single channel forward-looking radar in expanded beam space via lp regularisation. Electron. Lett. 51 (11), 863–865. doi:10.1049/el.2014.3978
Cumming, I. G., and Wang, F. H. (2005). Digital processing of synthetic aperture radar data: Algorithm and implementation. Norwood, MA, USA: Artech House.
Curlander, J. C., and McDonough, R. N. (1991). Synthetic aperture radar, 396. New York, NY, USA: Wiley.
Dropkin, H., and Ly, C. (1997). Superresolution for scanning antenna. Proceedings of the 1997 IEEE National Radar Conference, Syracuse, NY, USA, May 1997 306–308.
El-Darymli, K., Mcguire, P., Gill, E. W., Power, D., and Moloney, C. (2015). Characterization and statistical modeling of phase in single-channel synthetic aperture radar imagery. IEEE Trans. Aerosp. Electron. Syst. 51 (3), 2071–2092. doi:10.1109/taes.2015.140711
Huang, P., Liao, G., Yang, Z., Xia, X.-G., Ma, J., and Zheng, J. (2017). Ground maneuvering target imaging and high-order motion parameter estimation based on second-order keystone and generalized Hough-HAF transform. IEEE Trans. Geosci. Remote Sens. 55 (1), 320–335. doi:10.1109/tgrs.2016.2606436
Huang, Y., Zha, Y., Wang, Y., and Yang, J. (2015). Forward looking radar imaging by truncated singular value decomposition and its application for adverse weather aircraft landing. Sensors 15 (6), 14397–14414. doi:10.3390/s150614397
Kusama, K., Arai, I., Motomura, K., Tsunoda, M., and Wu, X. (1990). “Compression of radar beam by deconvolution,” in Noise and clutter rejection in radars and imaging sensors (Amsterdam, Netherlands: Elsevier Science Publishers).
Li, G., Xia, X.-G., and Peng, Y. N. (2008). Doppler keystone transform: An approach suitable for parallel implementation of SAR moving target imaging. IEEE Geosci. Remote Sens. Lett. 5 (4), 573–577. doi:10.1109/lgrs.2008.2000621
Li, W., Li, M., Zuo, L., Chen, H., and Wu, Y. (2022). Real aperture radar forward-looking imaging based on variational bayesian in presence of outliers. IEEE Trans. Geosci. Remote Sens. 60, 1–13. doi:10.1109/tgrs.2022.3203807
Li, Z., Xing, M., Liang, Y., Gao, Y., Chen, J., Huai, Y., et al. (2016). A frequency-domain imaging algorithm for highly squinted SAR mounted on maneuvering platforms with non-linear trajectory. IEEE Trans. Geosci. Remote Sens. 54 (7), 4023–4038. doi:10.1109/tgrs.2016.2535391
Long, T., Lu, Z., Ding, Z., and Liu, L. (2011). A DBS Doppler centroid estimation algorithm based on entropy minimization. IEEE Trans. Geosci. Remote Sens. 49 (10), 3703–3712. doi:10.1109/tgrs.2011.2142316
Lu, J., Zhang, L., Wei, S., and Li, Y. (2023). Resolution enhancement for forwarding looking multi-channel SAR imagery with exploiting space–time sparsity. IEEE Trans. Geosci. Remote Sens. 61, 1–17. doi:10.1109/tgrs.2022.3232392
Moreira, A., and Huang, Y. (1994). Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation. IEEE Trans. Geosci. Remote Sens. 32 (5), 1029–1040. doi:10.1109/36.312891
MoreiraPrats-Iraola, P., Younis, M., Krieger, G., Hajnsek, I., and Papathanassiou, K. P. (2013). A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 1 (1), 6–43. doi:10.1109/mgrs.2013.2248301
Richards, M. A. (1988). Iterative noncoherent angular superresolution. Proceedings of the 1988 IEEE National Radar Conference, Ann Arbor, MI, USA, April 1988, 100–105.
Sun, G. C., Liu, Y., Xiang, J., Liu, W., Xing, M., and Chen, J. (2022). Spaceborne synthetic aperture radar imaging algorithms: An overview. IEEE Geosci. Remote Sens. Mag. 10 (1), 161–184. doi:10.1109/mgrs.2021.3097894
Tuo, X., Zhang, Y., Huang, Y., and Yang, J. (2021). Fast sparse-TSVD superresolution method of real aperture radar forward-looking imaging. IEEE Trans. Geosci. Remote Sens. 59 (8), 6609–6620. doi:10.1109/tgrs.2020.3027053
Xu, G., Xing, M., Xia, X., Zhang, L., Liu, Y., and Bao, Z. (2015). Sparse regularization of interferometric phase and amplitude for InSAR image formation based on Bayesian representation. IEEE Trans. Geosci. Remote Sens. 53 (4), 2123–2136. doi:10.1109/tgrs.2014.2355592
Yang, J., Kang, Y., Zhang, Y., Huang, Y., and Zhang, Y. (2020). A Bayesian angular superresolution method with lognormal constraint for sea-surface target. IEEE Access 8, 13419–13428. doi:10.1109/access.2020.2965973
Li, Y., Liu, J., Jiang, X., and Huang, X. (2019). Angular superresol for signal model in coherent scanning radars. IEEE Trans. Aerosp. Electron.vol.55, no. 6, pp. 3103–3116. doi:10.1109/taes.2019.2900133
Zhang, Q., Pei, J., Yi, Q., Li, W., Zhang, Y., Huang, Y., et al. (2020). Tv-sparse super-resolution method for radar forward-looking imaging. IEEE Trans. Geosci. Remote Sens. 58 (9), 6534–6549. doi:10.1109/tgrs.2020.2977719
Zhang, Q., Zhang, Y., Huang, Y., and Zhang, Y. (2019). Azimuth superresolutionof forward-looking radar imaging which relies on linearized Bregman. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 12 (7), 2032–2043. doi:10.1109/jstars.2019.2912993
Zhang, Y., Jakobsson, A., Yin, Z., Huang, Y., and Yang, J. (2018). Wideband sparse reconstruction for scanning radar. IEEE Trans. Geosci. Remote Sens. 56 (10), 1–14. doi:10.1109/tgrs.2018.2830100
Zhang, Y., Tuo, X., Huang, Y., and Yang, J. (2020). A TV forward-looking super-resolution imaging method based on TSVD strategy for scanning radar. IEEE Trans. Geosci. Remote Sens. 58 (7), 4517–4528. doi:10.1109/tgrs.2019.2958085
Zhang, Y., Zhang, Y., Li, W., Huang, Y., and Yang, J. (2018). Super-resolution surface mapping for scanning radar: Inverse filtering based on the fast iterative adaptive approachfiltering based on the fast iterative adaptive approach. IEEE Trans. Geosci. Remote Sens. 56 (1), 127–144. doi:10.1109/tgrs.2017.2743263
Keywords: radar, radar imaging, forward-looking imaging, Doppler deconvolution, superresolution (sr)
Citation: Chen H, Wang Z, Zhang Y, Jin X, Gao W and Yu J (2023) Data-driven airborne bayesian forward-looking superresolution imaging based on generalized Gaussian distribution. Front. Sig. Proc. 3:1093203. doi: 10.3389/frsip.2023.1093203
Received: 08 November 2022; Accepted: 28 April 2023;
Published: 11 May 2023.
Edited by:
Guolong Cui, University of Electronic Science and Technology of China, ChinaReviewed by:
Shuwen Xu, Xidian University, ChinaYin Zhang, University of Electronic Science and Technology of China, China
Copyright © 2023 Chen, Wang, Zhang, Jin, Gao and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zeyu Wang, emV5dXdhbmdAYnVwdC5lZHUuY24=
 Hongmeng Chen
Hongmeng Chen Zeyu Wang2*
Zeyu Wang2*