Deep Reinforcement Learning-Based Optimization for RIS-Based UAV-NOMA Downlink Networks (Invited Paper)

This study investigates the application of deep deterministic policy gradient (DDPG) to reconfigurable intelligent surface (RIS)-based unmanned aerial vehicles (UAV)-assisted non-orthogonal multiple access (NOMA) downlink networks. The deployment of UAV equipped with a RIS is important, as the UAV increases the flexibility of the RIS significantly, especially for the case of users who have no line-of-sight (LoS) path to the base station (BS). Therefore, the aim of this study is to maximize the sum-rate by jointly optimizing the power allocation of the BS, the phase shifting of the RIS, and the horizontal position of the UAV. The formulated problem is non-convex, the DDPG algorithm is utilized to solve it. The computer simulation results are provided to show the superior performance of the proposed DDPG-based algorithm.

1 Introduction

Reconfigurable intelligent surfaces (RIS) have been recognized as one of the promising technologies for sixth-generation (6G) wireless communications (Zhang et al., 2019) since they have shown excellent features with better spectrum-, energy-, and cost-efficiency (Zhao, 2019). RIS can be viewed as a low-cost antenna array consisting of a large number of programmable reflecting elements (Wu and Zhang, 2019). A variety of proven techniques, such as massive multiple-input multiple-output (massive-MIMO) and cooperative communications, only focus on how the transceiver can adapt to the channel environment, while RIS have the capability to control the wireless communication propagation environment (Chen et al., 2019). A typical scenario to apply RIS is when the direct links from the base station (BS) to users are blocked by buildings or mountains, which means RIS can create extra propagation paths to guarantee the quality of service (QoS).

Inspired by the superiorities of non-orthogonal multiple access (NOMA) such as high spectrum efficiency (Ding et al., 2017), this study combines NOMA with the IRS. Ding et al. (2020) have illustrated the better performance of combining RIS with NOMA than it has with the conventional orthogonal multiple access (OMA). On the other hand, as another promising 6G technique (Chowdhury et al., 2020), unmanned aerial vehicles (UAV) have been widely applied in NOMA systems, such as UAV-MEC-NOMA, UAV-RIS-NOMA, etc. Lu et al. (2022) proposed a scheme that maximizes the average security computation capacity of a NOMA-based UAV-MEC network when a flying eavesdropper exists. To the best of our knowledge, most RIS-related works consider fixed RIS deployment scenarios (Ding et al., 2020; Fang et al., 2020; Zuo et al., 2020). This study introduces UAV to a RIS-NOMA system, which enhances the flexibility of RIS significantly. Our prior works (Jiao et al., 2020) jointly optimized beamforming and phase shift with pre-optimized UAV position and derived the closed-form of the optimal beamforming for a 2-user RIS-UAV-NOMA downlink system. Most RIS-related works consider only fixed channel environments. However, the time-varying multi-user scenario is closer to the real wireless communication systems. Conventional optimization methods, such as convex optimization, are difficult to solve non-convex joint optimization problems with highly coupled variables.

To date, artificial intelligence (AI), such as deep learning (DL) and deep reinforcement learning (DRL)-based methods have been successfully applied to a variety of wireless communication problems (Cui et al., 2019; Ding, 2020). On the other hand, unlike DL which needs a huge number of training labels, DRL-based methods allow wireless communication systems to learn by interacting with the environment. Hence, DRL is more appropriate for this study, as training labels are very hard to obtain in real-time wireless communication systems. There are generally two types of reinforcement learning, one is value-based and the other is policy-based. Q-learning, as one of the representatives of the value-based reinforcement learning method, chooses action from the state-action table by using the ϵ-greedy policy. In terms of policy-based reinforcement learning, policy gradient (PG) has the capability to solve problems with continuous action. However, PG easily convergences to a local optimal. Deep Q Network (DQN) is proposed by integrating deep neural networks and Q-learning, which can solve high-dimensional discrete action problems (Lillicrap et al., 2015). However, DQN cannot straightforwardly be used in continuous space because it finds the action that maximizes the Q-function, which demands an iterative optimization process at each step. This is hard to realize when the action is continuous (Lillicrap et al., 2015). However, the deep deterministic policy gradient (DDPG) is applicable to the cases with the high-dimension continuous action space since DDPG outputs actions with a deterministic policy. Considering that this study aims to optimize a wireless communication problem with continuous actions, DDPG is applied.

This study investigates the application of the DRL-based methods to the multi-user RIS-UAV-NOMA downlink system. The DDPG algorithm is introduced into the DRL framework to optimize the power allocation of the BS, the phase shifting of the RIS, and the horizontal position of the UAV simultaneously. Computer simulation results are provided to demonstrate the proposed algorithm's robustness and superior performance on the sum rate.

2 System Model and Problem Formulation

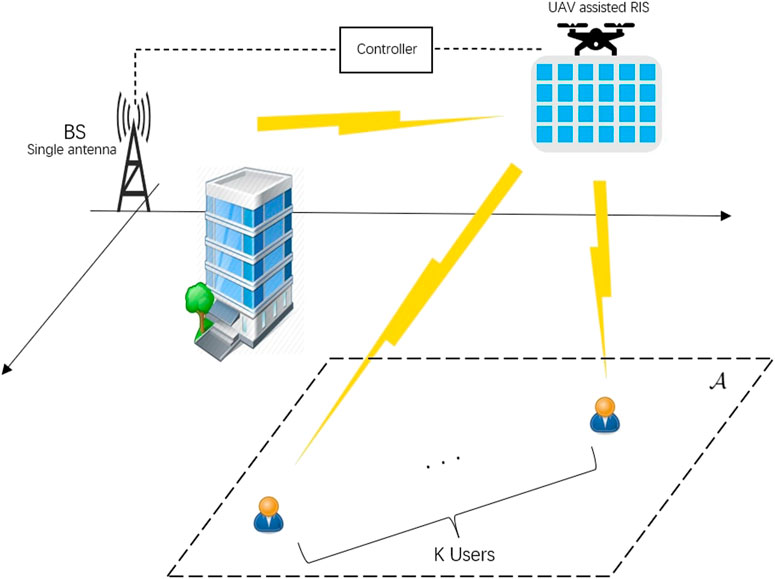
Consider an RIS-UAV-NOMA network as shown in Figure 1. It is assumed that each node is equipped with a single antenna. The base station (BS) serves K users (denote the users set by $\mathcal{K}$) who are randomly distributed in a certain area $\mathcal{A}$. Assume that downlink users’ direct links to the BS are blocked, for example, by buildings and mountains. Hence, the UAV-equipped RIS is deployed to create reflection links between the users and the BS, where the RIS is equipped with N passive phase shift elements. Assume that the UAV flies at a fixed altitude over area $\mathcal{A}$ autonomously, and starts at a fixed charge point. The channels are assumed as the Rician fading channel because the UAV-to-ground links are line-of-sight (LoS) (Wang et al., 2019), and the channel state information (CSI) is assumed to be known perfectly (that is, CSI estimation errors are not considered) at the BS and the UAV-equipped RIS, where the energy consumption and flight duration issues of the UAV (Sun and Wu, 2013) are neglected. Observe that due to the used DDPG method, the proposed algorithm is applicable to the case, where the channels are time-varying between time slots, but remain constant within one time-slot. Denote the channel vectors between the BS and the RIS by $\mathit{g}\in {\mathbb{C}}^{N\times 1}$ and the channel vectors between the RIS and the kth user by ${\mathit{h}}_{rk}\in {\mathbb{C}}^{N\times 1}$, respectively. The small scale fading and the path loss are both considered. According to the NOMA principle, the BS transmits the superposition coding to all users. Hence, the received signal at each user is given by

$y_k={\mathit{h}}_{rk}^H\mathbf{\Phi }\mathit{g}\sum _{i=1}^K{\rho }_i{s}_i+n_k,k=1,\dots ,K,(1)$

where $\mathrm{\Phi }=\mathrm{diag}(e^{j{\theta }_1},e^{j{\theta }_2},\dots ,e^{j{\theta }_N})$ is the RIS diagonal phase shift matrix, θ_n ∈ [0, 2π] is the phase shift of the nth element, ρ_i ∈ [0, 1] is the BS transmitted power allocation coefficient and ${\sum }_{i=1}^K{\rho }_i=1$, s_i is the transmitted signal for the ith user that satisfying $\mathbb{E}[s_i^2]=1$, and n_k is the noise which follows $\mathcal{C}\mathcal{N}(0,{\sigma }^2)$. Since the UAV is deployed, we use v(x, y) to denote the RIS-UAV horizontal position and h_I for its height. The BS is located at the original point (0,0) and the BS height is h_B. u_k(x_k, y_k), k = 1, … , K denotes the horizontal position of the kth user. Hence, the distance between the BS and the RIS can be derived as $d_{BI}=\sqrt{x^2+y^2+{(h_B-h_I)}^2}$ and the distance between the RIS and the kth user is $d_{I{u}_k}=\sqrt{{(x-x_k)}^2+{(y-y_k)}^2+h_I^2}$. Considering the path loss, the channel gain for the kth user can be rewritten as:

${\mathit{h}}_k=\frac{{\mathit{h}}_{rk}^H\mathbf{\Phi }\mathit{g}}{{\left(d_{BI}{d}_{I{u}_k}\right)}^{\alpha }},(2)$

where the α is the path loss coefficient.

FIGURE 1

FIGURE 1. UAV-based RIS-assisted NOMA downlink system.

To implement the successive interference cancellation (SIC) for NOMA users, the channels’ quality should be obtained first. Assume that the weakest user (who has the worst channel) is the 1st user and the strongest user (who has the best channel) is the Kth user. According to the SIC principle, the jth (1 ≤ j ≤ K) user needs to decode the signals of all j − 1 weaker users so that the jth user can remove those signals from the superposed received signal. Therefore, the signal-to-interference-plus-noise ratio (SINR) for the jth user to decode the tth (t ≤ j − 1 ≤ K) user’s signal is as follows:

${\text{SINR}}_{t\to j}=\frac{{|{\mathit{h}}_j|}^2{P}_{\mathit{max}}{\rho }_t}{{\sum }_{i=t+1}^K{|{\mathit{h}}_j|}^2{P}_{\mathit{max}}{\rho }_i+{\sigma }^2}.(3)$

Afterwards, the user j can decode its own signal by simply treating the signal of all the rest users as interference. The SINR for the jth user to decode its own signal is given by

${\text{SINR}}_{j\to j}=\frac{{|{\mathit{h}}_j|}^2{P}_{\mathit{max}}{\rho }_j}{{\sum }_{i=j+1}^K{|{\mathit{h}}_j|}^2{P}_{\mathit{max}}{\rho }_i+{\sigma }^2},(4)$

where P_max is the maximum transmit power. Observe that the data rate for each user to decode its own signal can be calculated by Eq. 4 and R = log(1 + SINR). Denote the minimum target data rate by R_min. To make sure SIC can be successfully implemented, the data rate of the jth user decoding the tth user’s signal is required no smaller than the data rate of the tth user decoding its own signal, which means R_t→j ≥ R_t→t ≥ R_min, ∀t < j. The problem formulation will be described next in detail.

Our aim is to maximize the sum-rate by jointly optimizing the power allocation ρ_i at the BS, the phase-shifting Φ of the RIS and the horizontal position v(x, y) of the UAV. Hence, the optimization problem can be formulated as follows:

$\left(P1\right):{\max }_{\left\{\rho ,\mathrm{\Phi },v\right\}}\sum _{t=1}^K{R}_{t\to t},(\mathrm{5a})$

$\text{s.t.}{R}_{t\to t}\ge R_{\mathit{min}},\forall t\in \mathcal{K},(\mathrm{5b})$

$R_{t\to j}\ge R_{t\to t}\forall t,j\in \mathcal{K},t>j,(\mathrm{5c})$

$\sum _{k=1}^K{\rho }_k\le 1,(\mathrm{5d})$

$v\left(x,y\right)\in \mathcal{A},(5e)$

$0\le {\theta }_n\le 2\pi ,n=1,\dots ,N.(\mathrm{5f})$

Constraint (Eq. 5b) is to guarantee the QoS for all users, and (Eq. 5c) ensures that the SIC processing can be implemented successfully. Constraint (Eq. 5d) is the BS total transmission power constraint and (Eq. 5e) is to restrict the UAV to flight within a certain feasible area. The last constraint (Eq. 5f) is the angle constraint for each element of the RIS. The problem (P1) is non-convex and it is hard to find a global optimal solution due to the coupled variables {ρ, Φ, v}. Hence, in this study, we propose a robust DRL-based framework to solve the problem (P1).

3 Deep Reinforcement Learning-Based Optimization

In this section, the DDPG algorithm is first briefly introduced. Afterward, actions, states, and rewards are defined, respectively. Finally, we discuss how can the DDPG framework be applied to solve the formulated problem and what is the working procedure of DDPG.

3.1 Introduction to Deep Deterministic Policy Gradient

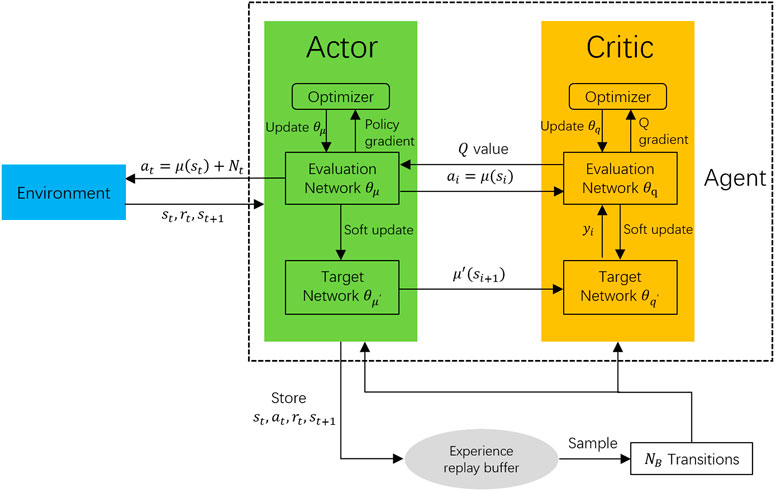
DDPG is a model-free, off-policy actor-critic algorithm by applying the deep function approximators. Generally speaking, similar to DQN, the aim of DDPG is to find an action that maximizes the output Q value according to the current state. However, unlike the DQN algorithm can only be used for discontinuous action scenario, DDPG allows agent learns policies in a high-dimension, continuous action space (Lillicrap et al., 2015). On the other hand, although the policy gradient method is suitable for continuous action, it is unsatisfactory in the wireless communication context (Feng et al., 2020) because of its drawback of slow convergence. Specifically, DDPG has the following four neural networks that need to be trained.

• An evaluation actor network μ(s|θ_μ). θ_μ denotes its parameters. It outputs actions a_t by taking state s_t as its input.

• A target actor network μ′(s|θ_μ′). This neural network is parametrized by θ_μ′. The input is the previous state of s_t−1, but the output action is used to update the parameters of the evaluation critic network.

• An evaluation critic network Q(s, a|θ_q). θ_q denotes its parameters. It inputs the current state s_t and action a_t and outputs the Q value.

• A target critic network Q′(s, a|θ_q′). This neural network is parametrized by θ_q′. The input is previous state s_t−1 and the corresponding actions from the target actor network, and the output is the target Q value.

3.2 DDPG Working Procedure

Before the training starts, there are two important mechanisms to be clarified:

1) Exploration: In order to make the agent obtain better exploration, randomly generated noise is added to the output action of the evaluation actor network

${\mu }^{\prime }\left(s_t\right)=\mu \left(s_t;{\theta }_{\mu }\right)+\mathcal{N},(6)$

where $\mathcal{N}$ is the Gaussian noise which has the same dimension with the output action.

2) Experience replay: To avoid the correlation between different samples being too strong, similar to DQN, DDPG also uses experience replay. In detail, an experience replay buffer $\mathcal{D}$ with capacity $\mathcal{C}$ is created to store multiple transitions (s_t, a_t, r_t, s_t+1), and then these past experiences will be randomly selected with a fixed quantity to train the networks. The selected experiences set is called mini-batch with batch size N_B.

In DDPG, the training stage starts when the experience replay buffer is full. N_B transitions (s_t, a_t, r_t, s_t+1) are selected as a mini-batch to train the four neural networks. As mentioned earlier, the goal of the DDPG algorithm is to find an action that can maximize the Q value (i.e., the output of Q(s_t, a_t|θ_q) where a_t = μ(s_t|θ_μ)). Therefore, to train the evaluation actor network the following objective function needs to be maximized:

$J\left({\theta }_{\mu }\right)=Q\left(s_t,a_t=\mu \left(s_t|{\theta }_{\mu }\right)|{\theta }_q\right).(7)$

To maximize the objective function above, gradient ascent with chain rule is applied:

${\nabla }_{{\theta }_{\mu }}J=\frac{1}{N_B}\sum _{t=1}^{N_B}\left({\nabla }_{a}Q\left(s_t,\mu \left(s_t|{\theta }_{\mu }\right)|{\theta }_q\right){\nabla }_{{\theta }_{\mu }}\mu \left(s_t|{\theta }_{\mu }\right)\right).(8)$

It is more complicated for critic network training. First, the target Q value is obtained by inputting the output of the target actor network according to state s_t+1:

$y_t=r_t+\lambda Q^{\prime }\left(s_{t+1},{\mu }^{\prime }\left(s_{t+1}|{\theta }_{{\mu }^{\prime }}\right)|{\theta }_{q^{\prime }}\right),(9)$

where λ is the discount factor. Second, the Q value calculated by evaluation critic network is obtained according to s_t and a_t, i.e., Q(s_t, a_t|θ_q). Finally, the evaluation critic network is updated by minimizing the loss function

$L\left({\theta }_q\right)=\frac{1}{N_B}\sum _{t=1}^{N_B}{\left(y_t-Q\left(s_t,a_t|{\theta }_q\right)\right)}^2.(10)$

For target actor network and target critic network updating, DDPG uses soft updating (Lillicrap et al., 2015) to avoid the unstable and divergence trend that appears in Q-learning.

${\theta }^{\prime }\leftarrow \tau \theta +\left(1-\tau \right){\theta }^{\prime },(11)$

where τ ≪ 1 is the soft updating coefficient. Observe that this updating strategy means updating the target network’s parameters by slowly tracking the learned evaluation network. The framework of DDPG is illustrated in Figure 2.

FIGURE 2

FIGURE 2. Framework of DDPG.

3.3 The DRL Processing

In the communication system model Figure 1, we define the time-varying channels as the environment and treat the RIS-UAV as the agent. The rest of the corresponding elements are defined as follows.

• State space: The state of the time step t is defined as

$\begin{array}{ll}\hfill s_t=& \left[R_1^{\left(t-1\right)},\dots ,R_K^{\left(t-1\right)},{\theta }_1^{\left(t-1\right)},\dots ,{\theta }_N^{\left(t-1\right)},\right.\hfill \\ \hfill & \left.{\rho }_1^{\left(t-1\right)},\dots ,{\rho }_k^{\left(t-1\right)},x^{\left(t-1\right)},y^{\left(t-1\right)}\right],\hfill \end{array}(12)$

where $\{R_1^{(t-1)},\dots ,R_K^{(t-1)}\}$ are all users’ data rate at time t − 1, $\{{\theta }_1^{(t-1)},\dots ,{\theta }_N^{(t-1)}\}$ denotes the angle of the RIS phase shift, $\{{\rho }_1^{(t-1)},\dots ,{\rho }_k^{(t-1)}\}$ denotes the power allocation to each user’s signal and {x^(t−1), y^(t−1)} represents the UAV’s horizontal position.

• Action space: According to optimization-needed variables, the action of the time step t is defined as

$a_t=\left[\begin{array}{c}\hfill {\theta }_1^{\left(t\right)},\dots ,{\theta }_N^{\left(t\right)},{\rho }_1^{\left(t\right)},\dots ,{\rho }_k^{\left(t\right)},x^{\left(t\right)},y^{\left(t\right)}\hfill \end{array}\right].(13)$

At the time step t, the agent inputs the state s_t to obtain the corresponding action a_t according to the current environment. Then the agent obtains the new phase shift Φ, power allocation ρ_i, i = 1, … , k, and horizontal position v.

• Reward: Because the objective is to maximize downlink users’ sum-rate, intuitively we use the sum-rate as the reward, which is consistent with the aim of DDPG to maximize the cumulated reward.

$r_t=R_{\mathit{sum}}^{\left(t\right)}=\sum _{k=1}^K{R}_k^{\left(t\right)},k=1,\dots ,K.(14)$

3.4 Processing to Satisfy Constraints

To satisfy the constraints of the problem (P1), the following manipulations are carried out: To guarantee QoS constraint (Eq. 5b), the data rate $R_k^{(t)}$ of each user is to be calculated at each step t to check if it can achieve the minimum target rate. If all the calculated rates satisfy the constraint (Eq. 5b), this experience is to be stored into the replay buffer directly. In contrast, a punishment mechanism will be carried out (e.g., set r_t = 0) for those experiences that are not satisfactory (Eq. 5b) to avoid the agent taking bad actions. In order to ensure the SIC is successfully implemented (i.e., the constraint (Eq. 5c)), conventional optimization methods, such as convex optimization, have to do a large amount of mathematical processing. However, in the proposed algorithm, the constraint (Eq. 5c) can always be satisfied if the channel quality-dependent decoding order is re-decided after the action a_t is outputted at each step t (see Remark 1 and Proposition 1). Observe that, as aforementioned, the perfect CSI can be obtained by the BS and UAV.

Remark 1. Observe that channel vectors are randomly generated at the beginning of each episode. Hence the generated channels are fixed within one episode. However, recall the Eq. 2, the total channel is changing because of the different output phase shifts from the actor network at each step.

Proposition 1. The SIC constraint (Eq. 5c) will always be satisfied if the decoding order is decided by the current channels.

Proof. Recall Eq. 3, its numerator and denominator are divided by |h_j|² simultaneously (where the case for the weaker tth user shown in (Eq. 4) can be obtained similarly), then we have

${\text{SINR}}_{t\to j}=\frac{P_{\mathit{max}}{\rho }_t}{{\sum }_{i=t+1}^K{P}_{\mathit{max}}{\rho }_i+\frac{{\sigma }^2}{|h_j{|}^2}},(15)$

${\text{SINR}}_{t\to t}=\frac{P_{\mathit{max}}{\rho }_t}{{\sum }_{i=t+1}^K{P}_{\mathit{max}}{\rho }_i+\frac{{\sigma }^2}{|h_t{|}^2}}.(16)$

Under the given |h_j|≥|h_t|, we have SINR_t→j ≥ SINR_t→t that satisfies the SIC constraint. □

Therefore, the problem (P1) becomes:

$\left(P2\right):{\max }_{\left\{\rho ,\mathrm{\Phi },v\right\}}\sum _{t=1}^K{R}_{t\to t}(\mathrm{17a})$

$\text{s.t.}{R}_{t\to t}\ge R_{\min },\forall t\in \mathcal{K},(\mathrm{17b})$

$\left(5\text{d}\right)-\left(5\text{f}\right).(\mathrm{17c})$

For the constraint (Eq. 5d), We found that the output of the neural network is very likely to have negative values. To solve this, some functions (for example, exponential function) can be used to map the output values to the feasible range, and this trick is also valid for constraints (Eq. 5e) and (Eq. 5f). Based on all the aforementioned discussions, Algorithm 1 is summarized to show the proposed algorithm in detail.

Algorithm 1. Proposed DDPG-based algorithm.

4 Simulation Results

4.1 Channel Environment and Hyper Parameters

In this section, we carry out the proposed DDPG-based algorithm and present the results to analyze its performance. As Figure 1 shown, the BS is deployed at the origin point (0,0), the RIS-UAV starts at the point (50,0), and users are randomly distributed in the area $\mathcal{A}$ which is (45,45), (55,45), (55,55), and (45,55). In each episode, users’ positions are assumed fixed. As assumed previously, the channels between the BS and the RIS, and the channels between the RIS and users are all LoS. The Rician fading channel is used according to the following equation:

$\mathit{G}=\bar{\mathit{H}}\sqrt{\frac{\mathrm{\Omega }}{\mathrm{\Omega }+I_N}}+{\mathit{H}}_{\mathit{R}}\sqrt{\frac{1}{\mathrm{\Omega }+I_M}},(18)$

where $\bar{\mathit{H}}$ represents the deterministic component, H_R denotes the Rayleigh fading component and Ω is the Rician K-factor. In our simulations, we set Ω = 10. For the large scale fading, the path loss coefficient is α = 2. According to the channel assumption in Section I, the channels are randomly generated for each episode, but they are fixed within each episode. On the other hand, the altitude of the BS is h_B = 20 and the RIS-UAV is deployed at h_U = 30. For other parameters, we set noise power as σ² = −60dB.

4.2 Deep Neural Network Structure and Parameters

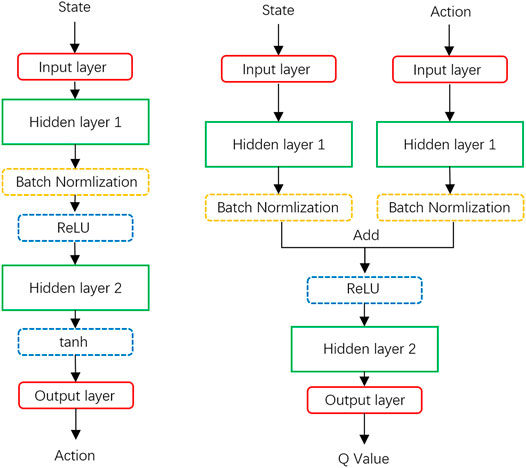
The whole framework for DDPG is shown as Figure 2 where the actor and critic use different structures, respectively. The depth of the neural network and the number of neurons (that is, the dimension of each layer) affect the learning efficiency and effect. In our experiments, for the actor network, we use two layers fully connected network (that is, two-layered DNN) for both of actor evaluation network and actor target network (see Figure 3 left). The dimensions of the input layer and the output layer are determined by the dimensions of state and action. Hence, the dimension of the input layer is set as N + 2(K + 1) and the dimension of the output layer is set as N + K + 2. On the other hand, the first layer uses the ReLU function as the activation function while the output layer uses tan(⋅) function to gain enough gradient, and the batch normalization is applied between two hidden layers. For the critic network, similarly, a two-layer fully connected network is used. However, the structure becomes the following: input the state data to one layer and input the action state to another layer, then add these two layers’ output together and follow the ReLU function as the input of the output layer (see Figure 3 right). As the setting of the Actor, there is a batch normalization layer behind the first hidden layer as well. The hyper-parameters are set as follows: learning rate for training evaluation network β = 0.001, discount factor λ = 0.95, learning rate for soft update τ = 0.005, experience replay buffer size $\mathcal{C}=50000$, number of episodes J = 1000, number of steps for each episode T = 500, size if sampled mini-Batch N_B = 16. In addition, the added noise in Eq. 6 for exploration is set as complex Gaussian noise with zero mean and 0.1 variance.

FIGURE 3

FIGURE 3. DNN framework for the actor network and critic network.

4.3 Simulation Results

In Figure 4 and Figure 5, the number of episodes versus accumulated reward is shown, respectively, under different RIS and user setups, where their first 100 episodes are the random data collection stage. The number of neurons for each hidden layer is 300. Figure 4 illustrates that the more RIS elements are used, the higher the accumulated reward can be obtained. In addition, comparing these three cases, the RIS = 4 case converges before 200 episodes, the RIS = 16 case converges before 400 episodes, and the RIS = 64 cases converges at around 800 episodes. For the same DDPG framework training, the fewer the number of RIS elements, the faster the convergence. Hence, increasing the number of neurons can improve the convergence speed, but more neurons lead to more calculations. Therefore, it is crucial that build a neural network depending on the actual situation. Figure 5 reveals what will happen when a BS serves a different number of users. It is clear that these five scenarios start at different levels at the random initialization stage, but converge at the same level after around 800 episodes. In consequence, in this system when the transmit power and the number of RIS elements are fixed, increasing the number of users does not guarantee the sum rate improvement, as the degrees of freedom available for resource allocation are limited in a downlink system(Sun et al., 2018). Hence, it is important to consider the tradeoff between the number of users and the data rate when designing the system. On the other hand, no matter how many RIS elements or users there are, the proposed algorithm is convergent and stable (In other words, it is robust to the number of RIS elements and users).

FIGURE 4

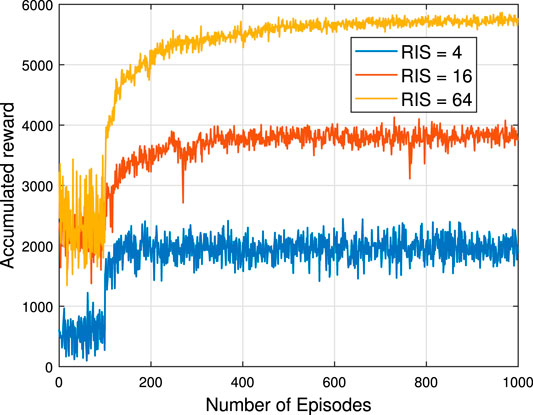
FIGURE 4. Number of episodes versus accumulated reward for different numbers of RIS elements P_t = 10dB, K = 4.

FIGURE 5

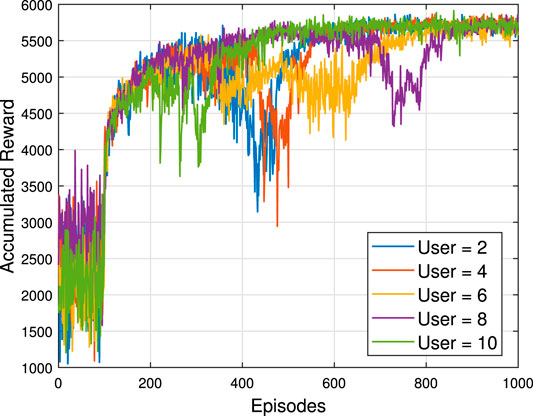
FIGURE 5. Number of episodes versus accumulated reward for different numbers of users P_t = 10dB, N = 64.

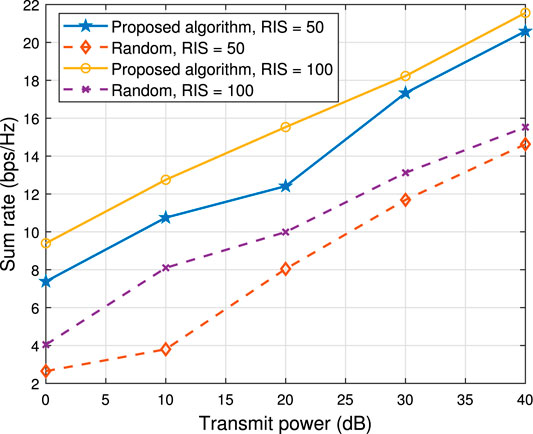
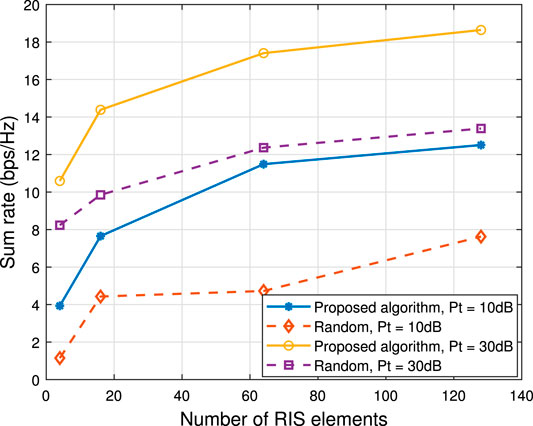
Figure 6 illustrates the sum rate versus maximum transmitted power P_t. Consider two cases of system parameters setup, one is RIS elements N = 50 and the other one is N = 100. As can be seen, the proposed algorithm outperforms the random case significantly for all considered power transmissions, even the optimized case for N = 50 is much better than the random case for N = 100.

FIGURE 6

FIGURE 6. Transmit power versus sum rate K = 4.

To further demonstrate the proposed algorithm’s performance, we carried out the algorithm for scenarios of a different number of RIS elements, as shown in Figure 7. It can be seen that the sum-rate increases with the increase of RIS elements quantity. Therefore, increasing RIS elements is a good way to enhance the sum rate. Nevertheless, the more RIS elements are equipped the larger the size of the training data is, which will need more neurons and increase the training duration. Too much training data and too many neurons will cause higher calculation complexities and make non-negligible output latency. Hence, the tradeoff between sum rate and complexity has to be considered in practical construction.

FIGURE 7

FIGURE 7. Number of RIS elements versus sum rate, K = 4.

5 Conclusion

This study investigated the sum rate maximizing problem in a RIS-UAV-NOMA downlink network. Power allocation of the BS, the RIS phase shift, and the UAV position are jointly optimized by applying the proposed DDPG-based algorithm efficiently. Rearranging the decoding order according to the current channel environment in each step is an efficient way to guarantee SIC implementation successfully. Computer simulations have shown that the proposed algorithm can be applied in the time-varying channel environment to enhance the sum-rate performance significantly, as well as is robust to the number of RIS elements and users.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SJ and ZD contributed to the conception and design of the study. SJ organized the database. SJ and XX performed the statistical analysis. SJ wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the UK EPSRC under grant number EP/P009719/2, and by H2020 H2020-MSCA-RISE-2020 under grant number 101006411.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, J., Liang, Y.-C., Pei, Y., and Guo, H. (2019). Intelligent Reflecting Surface: A Programmable Wireless Environment for Physical Layer Security. IEEE Access 7, 82599–82612. doi:10.1109/ACCESS.2019.2924034

CrossRef Full Text | Google Scholar

Chowdhury, M. Z., Shahjalal, M., Ahmed, S., and Jang, Y. M. (2020). 6G Wireless Communication Systems: Applications, Requirements, Technologies, Challenges, and Research Directions. IEEE Open J. Commun. Soc. 1, 957–975. doi:10.1109/ojcoms.2020.3010270

CrossRef Full Text | Google Scholar

Cui, J., Liu, Y., and Nallanathan, A. (2019). Multi-agent Reinforcement Learning-Based Resource Allocation for UAV Networks. IEEE Trans. Wirel. Commun. 19, 729–743.

Google Scholar

Ding, Z. (2020). Harvesting Devices’ Heterogeneous Energy Profiles and QoS Requirements in IoT: WPT-NOMA vs BAC-NOMA. arXiv Prepr. arXiv:2007.13665.

Google Scholar

Ding, Z., Liu, Y., Choi, J., Sun, Q., Elkashlan, M., Chih-Lin, I., et al. (2017). Application of Non-orthogonal Multiple Access in LTE and 5G Networks. IEEE Commun. Mag. 55, 185–191. doi:10.1109/MCOM.2017.1500657CM

CrossRef Full Text | Google Scholar

Ding, Z., Schober, R., and Poor, H. V. (2020). On the Impact of Phase Shifting Designs on IRS-NOMA. IEEE Wirel. Commun. Lett. 9, 1596–1600. doi:10.1109/LWC.2020.2991116

CrossRef Full Text | Google Scholar

Fang, F., Xu, Y., Pham, Q.-V., and Ding, Z. (2020). Energy-efficient Design of Irs-Noma Networks. IEEE Trans. Veh. Technol. 69, 14088–14092. doi:10.1109/tvt.2020.3024005

CrossRef Full Text | Google Scholar

Feng, K., Wang, Q., Li, X., and Wen, C.-K. (2020). Deep Reinforcement Learning Based Intelligent Reflecting Surface Optimization for MISO Communication Systems. IEEE Wirel. Commun. Lett. 9, 745–749. doi:10.1109/lwc.2020.2969167

CrossRef Full Text | Google Scholar

Jiao, S., Fang, F., Zhou, X., and Zhang, H. (2020). Joint Beamforming and Phase Shift Design in Downlink UAV Networks with IRS-Assisted NOMA. J. Commun. Inf. Netw. 5, 138–149.

CrossRef Full Text | Google Scholar

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., et al. (2015). Continuous Control with Deep Reinforcement Learning. arXiv Prepr. arXiv:1509.02971.

Google Scholar

Lu, W., Ding, Y., Gao, Y., Chen, Y., Zhao, N., Ding, Z., et al. (2022). Secure Noma-Based Uav-Mec Network towards a Flying Eavesdropper. IEEE Trans. Commun. 70, 3159703. doi:10.1109/tcomm.2022.3159703

CrossRef Full Text | Google Scholar

Sun, N., and Wu, J. (2013). “Minimum Error Transmissions with Imperfect Channel Information in High Mobility Systems,” in MILCOM 2013-2013 IEEE Military Communications Conference (San Diego, CA, USA: IEEE), 922–927. doi:10.1109/milcom.2013.160

CrossRef Full Text | Google Scholar

Sun, X., Yang, N., Yan, S., Ding, Z., Ng, D. W. K., Shen, C., et al. (2018). Joint Beamforming and Power Allocation in Downlink NOMA Multiuser Mimo Networks. IEEE Trans. Wirel. Commun. 17, 5367–5381. doi:10.1109/twc.2018.2842725

CrossRef Full Text | Google Scholar

Wang, Q., Zhang, W., Liu, Y., and Liu, Y. (2019). Multi-uav Dynamic Wireless Networking with Deep Reinforcement Learning. IEEE Commun. Lett. 23, 2243–2246. doi:10.1109/lcomm.2019.2940191

CrossRef Full Text | Google Scholar

Wu, Q., and Zhang, R. (2019). Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 18, 5394–5409. doi:10.1109/TWC.2019.2936025

CrossRef Full Text | Google Scholar

Zhang, Z., Xiao, Y., Ma, Z., Xiao, M., Ding, Z., Lei, X., et al. (2019). 6G Wireless Networks: Vision, Requirements, Architecture, and Key Technologies. IEEE Veh. Technol. Mag. 14, 28–41. doi:10.1109/MVT.2019.2921208

CrossRef Full Text | Google Scholar

Zhao, J. (2019). A Survey of Intelligent Reflecting Surfaces (IRSs): Towards 6G Wireless Communication Networks. arXiv Prepr. arXiv:1907.04789.

Google Scholar

Zuo, J., Liu, Y., Qin, Z., and Al-Dhahir, N. (2020). Resource Allocation in Intelligent Reflecting Surface Assisted Noma Systems. IEEE Trans. Commun. 68, 7170–7183. doi:10.1109/tcomm.2020.3016742

CrossRef Full Text | Google Scholar