
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Signal Process. , 27 April 2022
Sec. Image Processing
Volume 2 - 2022 | https://doi.org/10.3389/frsip.2022.885644
This article is part of the Research Topic Video Content Production and Delivery Over IP Networks and Distributed Computing Facilities View all 5 articles
 David Taubman1,2*
David Taubman1,2* Aous Naman1
Aous Naman1 Michael Smith3
Michael Smith3 Pierre-Anthony Lemieux4
Pierre-Anthony Lemieux4 Hassaan Saadat1,2
Hassaan Saadat1,2 Osamu Watanabe5
Osamu Watanabe5 Reji Mathew1
Reji Mathew1ITU-T Rec T.814 | IS 15444-15, known as High Throughput JPEG 2000, or simply HTJ2K, is Part-15 in the JPEG 2000 series of standards, published in 2019 by the ITU and ISO/IEC. JPEG 2000 Part-1 has long been used as a key component in the production, archival and distribution of video content, as the distribution format for Digital Cinema, and an Interoperable Master Format from which streaming video services are commonly derived. JPEG 2000 has one of the richest feature sets of any coding standard, including scalability, region-of-interest accessibility and non-iterative optimal rate control. HTJ2K addresses a long-standing limitation of the original JPEG 2000 family of standards: relatively low throughput on CPU and GPU platforms. HTJ2K introduces an alternative block coding algorithm that allows extremely high processing throughputs, while preserving all other aspects of the JPEG 2000 framework and offering truly reversible transcoding with the original block coded representation. This paper demonstrates the benefits that HTJ2K brings to video content production and delivery, including cloud-based processing workflows and low latency video content streaming over IP networks, considering CPU, GPU and FPGA-based platforms. For non-iterative optimal rate control, HTJ2K encoders with the highest throughputs and lowest hardware encoding footprints need a strategy for constraining the number of so-called HT-Sets that are generated ahead of the classic Post-Compression Rate-Distortion optimization (PCRD-opt) process. This paper describes such a strategy, known as CPLEX, that involves a second (virtual) rate-control process. The novel combination of this virtual (CPLEX) and actual (PCRD-opt) processes has many benefits, especially for hardware encoders, where memory size and memory bandwidth are key indicators of complexity.
JPEG 2000 provides a rich set of features, including high coding efficiency, scalability, region-of-interest accessibility, parallelism, the ability to achieve a target compressed size without iterative encoding and error resilience/resynchronisation capabilities. Quality scalability refers to the ability to extract reduced quality representations directly from the code-stream, while ensuring that the extracted representation has the same high coding efficiency as if the content were encoded directly at the corresponding reduced bit-rate. Resolution scalability refers to the ability to extract reduced resolution representations directly from the code-stream. Accessibility refers to the ability to extract a limited subset of the code-stream that is sufficient to reconstruct a given spatial region of interest over a defined set of components, such that the extracted bytes form an efficient representation of the region of interest, so long as the region is sufficiently large.
Most of these features derive from use of the EBCOT (Embedded Block Coding with Optimized Truncation) algorithm (Taubman, 2000), while use of the hierarchical Discrete Wavelet Transform (DWT) also plays an important role. Additionally, JPEG 2000 supports a huge range of image dimensions, data precisions and number of components (image planes), while extended technologies contained in Part-2 of the standard support non-linear tone curves for high dynamic range and even floating-point compression, along with transforms for multispectral, hyperspectral and volumetric compression. Both lossless and lossy compression are supported in the same framework, enabling quality scalable lossy-to-lossless coding. Part-9 of the standard (a.k.a. JPIP) adds tools for incremental dissemination of JPEG 2000 content that enable highly efficient and responsive interactive browsing of potentially enormous images, volumes and even video over low bandwidth reliable or unreliable networks, taking full advantage of all scalability and accessibility features of the coded content.
With this rich set of features and capabilities, JPEG 2000 has found application in many diverse fields, including geospatial imagery dissemination, defense and surveillance applications, medical imaging, and document and video archival. JPEG 2000 is also the standard for Digital Cinema and a primary mezzanine format used in the production, archival and dissemination of professional motion picture content.
In some of these applications, involving large frame dimensions or high frame rates, the relatively high computational cost of the embedded block coding algorithm in JPEG 2000 has become problematic, however. In particular, the JPEG 2000 block coder is based on bit-plane coding, at least formally executing three coding passes for each successive magnitude bit-plane within each block of subband samples. In some cases, the adverse impact of incremental coding on throughput can be offset by the parallelism offered by JPEG 2000. In particular, a typical image or video frame has thousands of code-blocks, any number of which can be encoded or decoded in concurrently, but this also increases the working memory footprint of an implementation.
To address this issue, Part-15 (ISO/IEC 15444-15, 2019) of the JPEG 2000 family of standards has been developed to augment the entire family with an alternate “High Throughput” (HT) block coding algorithm. This new part, known as High Throughput JPEG 2000 (HTJ2K), defines the HT algorithm and specifies how it can be used as a drop-in replacement for the original block coding algorithm (ISO/IEC 15444-1, 2000), identified in this document as the J2K1 block coder. In comparison to J2K1, the HT algorithm offers order-of-magnitude increases in throughput on common CPU and GPU platforms, while also enabling very high throughput hardware systems, including all-on-chip solutions (no external memory) on common FPGA platforms. These innovations allow high bandwidth media to be practically encoded and decoded with much less working memory and much lower latencies.
The HTJ2K standard has been developed with a strong focus on compatibility with the existing JPEG 2000 ecosystem. In particular, HT and J2K1 block bit-streams are reversibly interchangeable, meaning that content encoded using the original J2K1 algorithm can be transcoded to use the much faster HT representation without losing any information whatsoever, and HT block bit-streams can be transcoded back to the J2K1 representation, again without any mathematical loss. This feature allows existing JPEG 2000 based media repositories1 to be migrated to the HTJ2K format where desirable, without any risk of information loss, but there are many potential other benefits that arise from the reversible transcodability of the HT and J2K1 representations, as discussed briefly in Section 5.
This paper focuses specifically on the benefits HTJ2K brings to video content production and delivery, and how these benefits can be realized. Section 2 provides a brief overview of the HT algorithm and how it is integrated into the JPEG 2000 framework to form a media compression solution with most of the rich set of features described above. Section 3 is concerned with encoder rate control, showing how non-iterative precise rate control can be achieved in HTJ2K with high throughput and deterministic complexity, the latter being especially important for hardware deployments. Section 4 provides evidence for the high throughput and coding efficiency of HTJ2K, specifically focusing on professional video content and streaming applications, considering existing CPU and GPU solutions, as well as FPGA developments that are approaching maturity. Section 5 then discusses applications of HTJ2K, focusing on those relevant to professional video production and delivery, including the use of HTJ2K as a mezzanine format, the benefits of no-proxy remote editing strategies based on HTJ2K, and low latency video streaming over IP networks.
Both HT and J2K1 block coders encode quantized subband samples from a block within a given DWT subband. The original J2K1 algorithm processes magnitude bit-planes of the quantized samples one by one, starting from the coarsest bit-plane
The HT algorithm notionally processes exactly the same set of three coding passes per bit-plane, which are designated “Cleanup”, “SigProp” and “MagRef.” As in J2K1, the SigProp and MagRef passes encode a next finer magnitude bit for a data-dependent set of samples2. However, where the J2K1 Cleanup pass encodes a next finer magnitude bit only for those samples not refined by the preceding SigProp and MagRef passes, the HT Cleanup pass encodes all sample values to the precision associated with the relevant bit-plane
During code-stream formation, at most one Cleanup pass is included for a code-block, optionally followed by one SigProp and/or one MagRef coding pass, so that the redundancy exists only within the encoder itself and the decoder only needs to decode at most three coding passes (one of each type). This works because the JPEG 2000 packet headers that describe code-block contributions, explicitly encode the value of
While an HT encoder notionally produces coding passes, from which optimal truncation points are determined using the Post-Compression Rate-Distortion Optimization (PCRD-opt) algorithm (Taubman, 2000), efficient encoding strategies aim to generate only a limited collection of coding passes, which are sufficient to provide almost all interesting truncation points for a given target bit-rate. For hardware encoders, in particular, it is critical that the number of coding passes generated for each code-block is deterministically bounded. As we shall see, it turns out that six coding passes, are generally adequate, organized into two consecutive “HT Sets”, each consisting of a Cleanup pass, a SigProp pass and a MagRef pass, as shown in Figure 1.
The non-incremental nature of HT Cleanup passes is one important factor that contributes to the high throughput of HTJ2K, both for encoders and decoders, since it deterministically bounds the number of coding passes that must be performed, and indeed all of the passes can be performed concurrently. However, it does mean that the quality scalability feature of JPEG 2000 is largely lost, since HT block bit-streams have at most three coding passes, presenting only a very limited set of embedded truncation options for decoders and content streaming systems.
In fact, quality scalability is the only JPEG 2000 feature that is sacrificed by HTJ2K, but it is readily retrievable by reversibly transcoding some or all code-blocks back to the highly embedded J2K1 representation. HTJ2K code-streams can contain an arbitrary mixture of code-blocks encoded with J2K1 and HT technologies and HTJ2K code-streams are also fully compatible with all aspects of the JPIP standard (Part-9) mentioned earlier, for efficient remote browsing of imagery and even video assets. HTJ2K code-streams are also capable of embedding or preserving all of the quality layer boundaries and associated coding pass truncation point information associated with regular JPEG 2000 code-streams, regardless of whether the HT or J2K1 algorithm is used for encoding.
For video applications in the media/entertainment industry, however, quality scalability has not been used in practice. In particular, the Digital Cinema, Broadcast and IMF profiles of JPEG 2000 disallow the use of multiple quality layers.
For the sake of conciseness, we provide only a very brief overview here of the actual HT block coding algorithm. As mentioned earlier, JPEG 2000 block coder output is comprised of one or more so-called codeword segments. For the HT block coder, each HT Set involves one or two codeword segments: the Cleanup pass produces its own HT Cleanup segment, while the SigProp and MagRef refinement passes, if present, contribute to an HT Refinement segment. Figure 2 reveals the relationship between HT codeword segments and their constituent byte-streams.
The Cleanup pass produces three separate byte-streams, which are packed into the Cleanup codeword segment. In addition to the segment length,
The HT refinement passes are similar to those in J2K1, except that all refinement information is emitted as raw uncoded bits, and the information is reordered to allow vectorized and table-based accelerated encoding and decoding strategies that are not possible with J2K1.3
The HT Cleanup algorithm, however, is quite different to that in J2K1. Figure 3 reveals the core elements of the HT Cleanup pass encoder. Code-block samples indexed by
The residual values
1) the 4-bit significance pattern
2) some or all of the quad’s 4-bit EMB pattern
3) information about whether the unsigned residual
This information involves most of the quantities describing a quad that have significantly skewed statistics, yet it is sufficiently compact to be encoded jointly using variable length codewords that are at most 7 bits long. Constraining codewords to lengths of at most seven is quite critical to high throughput decoding implementations, since it allows CxtVLC decoding to proceed on a quad-by-quad basis using lookup tables of small size. However, since 7 bits are not sufficient to efficiently capture all combinations of the above quantities, a variable-to-variable length code is employed, which encodes only some of the EMB pattern bits in a data-dependent manner. Those EMB bits that are not encoded are packed along with the less significant bits of the
Finally, we note that the HT Cleanup encoder provides a method to efficiently encode quads that are entirely insignificant, using an adaptive run-length coding state machine (MEL coder), that is derived from the MELCODE in the JPEG-LS standard (ISO/IEC 14495-1, 1999). The MEL coding algorithm shares many features and a common heritage with multiplier-free arithmetic coding algorithms, including the MQ arithmetic coder used in J2K1, which may be traced back to the “skew coder” (Langdon, 1991). Importantly, the MEL code has a very small state machine that can be unwrapped to encode or decode multiple symbols concurrently, in optimized CPU or GPU deployments, while the algorithm is also very simple to implement in hardware.
In this way, the HT Cleanup encoder produces three bit-streams that are packed into byte-streams with a bit-stuffing procedure that allows error resilient decoding and resynchronization. Both software and hardware encoders benefit from the ability to produce these bit-streams in any order, allowing them to issue CxtVLC and zero or more variable-length coded bits from non-zero residuals
In addition to a deterministically limited number of coding passes and concurrency at the code-block, coding pass and sub-bit-stream levels, what makes the HT algorithm fast is the careful design of the individual coding tools mentioned above so that almost everything can be vectorized, and those elements that cannot be vectorized can be greatly accelerated using modest lookup tables.
Figure 4 illustrates the elements of an HTJ2K encoding system, along with the corresponding decoder. The only departures from a traditional JPEG 2000 codec are the HT block coding algorithm itself and the optional “complexity control” module. The PCRD-opt rate control procedure is used to discard generated coding passes so as to achieve a rate or distortion target, which may be global (whole code-stream) or local (small window of code-blocks), as is common in most JPEG 2000 encoders. The purpose of the complexity control module is to determine which coding passes should actually be generated by the HT encoder, noting that as little as one HT Cleanup pass may be sufficient, but a larger collection of coding passes presents more options to the PCRD-opt stage, allowing it to form code-stream content that meets its rate or distortion targets with high overall coding efficiency.
With the original J2K1 algorithm, complexity control is not always necessary, since the sequential processing of coding passes for any given code-block can be terminated at any time, although heuristics have been developed to make good decisions regarding early termination of the encoding process, e.g. (Taubman, 2002). With the HT algorithm, complexity control becomes more important, both for computational reasons and because each Cleanup pass redundantly encodes information contained in coarser coding passes, so that the memory consumed by coded passes ahead of the PCRD-opt stage can become problematic. Again, this is especially important for hardware encoders. The term FBCOT has been coined (Taubman et al., 2017) for the combination of high throughput (HT) non-incremental encoding with complexity control ahead of PCRD-opt to stress its connection with the original EBCOT algorithm on which JPEG 2000 is based, along with the importance of complexity control in the non-incremental setting required for fast execution. Complexity control is the primary subject of the next section.
In this section, we introduce a family of related strategies for the complexity control module in Figure 4. We will consistently refer to these as “CPLEX” complexity control, since they first appeared in Kakadu’s JPEG 2000 toolkit4 under that name, where they are controlled by its “Cplex” coding parameter attribute. The CPLEX algorithm’s purpose is to efficiently compute a good choice for the coarsest bit-plane
The CPLEX algorithm is driven by an overall length constraint
To avoid this risk, the CPLEX algorithm must choose the
To do this, the CPLEX algorithm implements a “virtual rate control loop” that is driven by conservative rate estimates. Specifically, for each code-block or collection of code-blocks belonging to a given subband
To combine the estimated length vectors from all subbands, it is necessary to first introduce bias factors
It is well-known that the solution to the optimal rate control problem involves quantizing the samples of each subband such that each sample is expected to produce roughly the same contribution to the overall distortion (Pearlman, 1991). Thus, we expect the solution to the optimal rate control problem to involve truncating the subband samples of subband
where
We can think of
To make the QP decision efficiently, the estimated length vectors
Then, the global length vector
While space does not permit us to provide details of the length estimation process itself, the important thing to note is that the length estimates
The simplest way to perform CPLEX-based encoding is to transform and quantize all subband samples in an entire image or video frame, collecting the length estimate vectors
Where encoding latency or working memory are tightly constrained, essentially the same approach can be employed incrementally over small “flush-sets,” as shown in Figure 5. Code-block dimensions are selected such that each subband has the same number of stripes of horizontally adjacent code-blocks, which means that the number of subband rows in each stripe decreases exponentially with depth in the DWT hierarchy. Each “flush-set” consists of one stripe of code-blocks from each subband, and both the CPLEX “virtual rate control” and PCRD-opt “actual rate control” operations are performed independently within flush-sets. In this case, block encoding for a stripe can begin as soon as its CPLEX decision (QP value) has been made, which can happen once all subband samples within the flush-set have been collected. Block encoding then proceeds in parallel with the arrival of the next stripe in each subband, while final PCRD-opt rate control and incremental code-stream flushing are performed for the preceding flush-set.
The encoding latency for such an approach is roughly three flush-set heights plus any additional latency associated with the pipelined DWT transform. The main disadvantage of such low latency encoding strategies is that relatively few vertical levels of wavelet decomposition can be supported, and the PCRD-opt rate control algorithm only has a limited window into the image, over which to optimize the way in which the coded length constraint is achieved.
Although low latency encoding is naturally compatible with low memory footprints, allowing the development of all-on-chip (no external memory) hardware encoding solutions, it is a mistake to assume that memory requirements are directly related to latency. In particular, it is possible to increase the window over which the PCRD-opt algorithm forms its rate control decisions, without increasing the window over which CPLEX estimates and block encoding are performed. That is, the virtual CPLEX rate control process and the actual PCRD-opt rate control process can be run at different time scales, because the two processes are entirely decoupled. This is illustrated in Figure 6. The benefit of this is that statistical multiplexing efficiency can be increased significantly, with a consequent increase in latency, but without a large increase in working memory footprint, because the block encoder outputs that are consumed by the PCRD-opt algorithm are in the compressed domain.
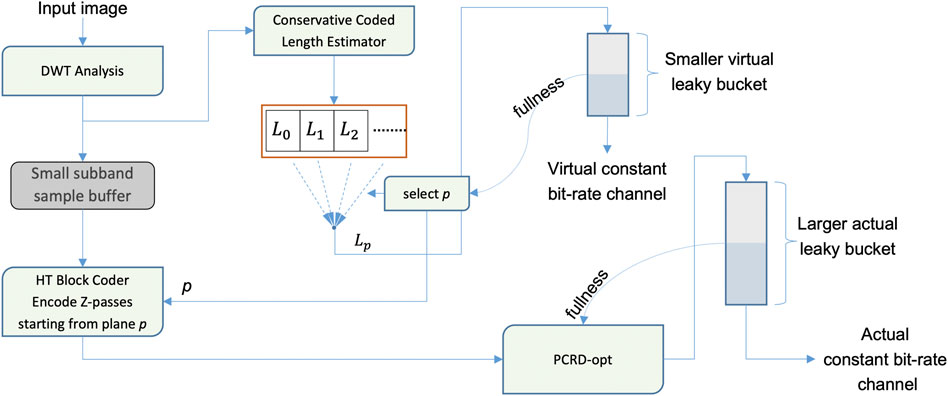
FIGURE 6. Decoupled virtual (CPLEX) and actual (PCRD-opt) rate control processes for memory efficient video encoding.
We can think of the CPLEX-based HTJ2K encoding procedures described above as “deterministic” in the sense that the CPLEX virtual rate allocation process is deferred until all associated quantized subband samples have become available. An alternate approach, however, is to perform CPLEX rate allocation incrementally with a full frame length constraint
The idea is illustrated in Figure 7. One potentially very short “active stripe” of subband samples is maintained for each subband
Although the forecast length records
The simplest way to form length forecasts
For video encoding, an alternative to spatial forecasting is temporal forecasting, where forecast records for as-yet unseen subband samples are derived from the reliable length records formed in a preceding frame. Again, temporal forecasting has its own weaknesses, in the event of sudden frame changes or very large frame-to-frame motions. However, it is not hard to develop hybrid forecasting strategies that combine spatial and temporal forecasts, using reliable estimates from the current frame to estimate the reliability of temporal forecasts and adapt the way in which spatial and temporal forecasts are combined. Since length records are very small in comparison to the subband data that they represent, these strategies are all compatible with low memory software and hardware deployment. In fact, a spatio-temporal forecasting strategy may be the preferred CPLEX-based encoding solution for hardware platforms with external memory, since the reliable length estimates allow memory bandwidth to be deterministically constrained, while external memory allows PCRD-opt decisions to be deferred until the end of each frame.
To demonstrate the robustness of low-memory CPLEX-based video encoding, we encode a short 4K video sequence with dramatic spatial and temporal variations in scene complexity using the Kakadu compression tool “kdu_compress” with three different complexity control strategies, with results presented in Figure 8.5 The HT-FULL trace in the figure corresponds to the strategy described in (Taubman, 2002) that has been widely used for regular JPEG 2000 video compression, where each code-block sequentially generates all possible coding passes, from coarse to fine, until the ratio between incremental distortion reduction and coded length increase becomes smaller than the smallest global PCRD-opt distortion-length slope threshold seen in the last two frames. This method does not encode a deterministic number of coding passes, so is not suitable for high throughput hardware, and generally encodes many more passes than necessary. The CPLEX-SPATIAL and CPLEX-SPACE-TIME traces both involve the encoding of exactly Z = 6 coding passes for every code-block based on the CPLEX algorithm, with each stripe consisting of one row of code-blocks only, for minimal working memory consumption–the first uses spatial forecasting alone, while the second uses spatio-temporal forecasting.
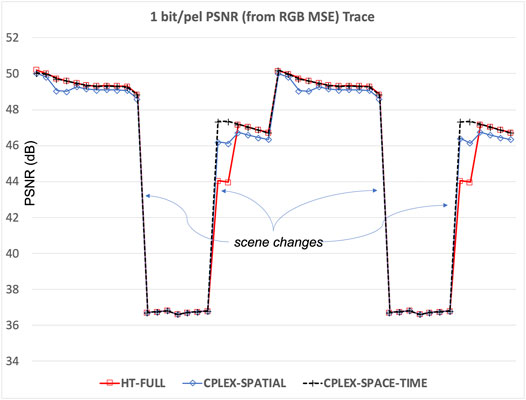
FIGURE 8. Robustness of low memory CPLEX-based video encoding with spatio-temporal forecasting, illustrated using a temporal trace of the frame-by-frame decompressed PSNR resulting from three different complexity constrained encoding strategies.
Interestingly, the much more complex HT-FULL strategy does not perform as well as the deterministic 6-pass encoding methods, due to huge variations in scene complexity between some pairs of frames. The spatial-only forecasting strategy performs well, but suffers a little when coding some frames whose upper half is mostly covered by “fog” and extremely compressible. Due to its superior robustness and deterministic low encoding complexity, all video encoding results presented in this paper other than low-latency encoding results, are obtained using the forecasting method presented here with spatio-temporal forecasting.
We note that all of the results presented here and elsewhere in this paper involve deterministic non-iterative PCRD-opt based rate control, targeting a fixed number of coded bytes per frame. This is important for rate constrained communication channels, such as IP networks, where the objective is to obtain the maximum possible compressed image quality, subject to the available network bandwidth. Of course, variable bit-rate (VBR) variants of PCRD-opt (and indeed the CPLEX algorithm) are possible, allowing even lower average reconstructed frame distortions for a given average data rate, but such approaches are less suitable for high quality communication over dedicated IP networks. For the results presented in Figure 8, rate-control is performed at the frame level, which requires sufficient working memory to store one or more entire frames of compressed data. In Sections 4.3 and 4.5, however, we consider evaluate efficiency and describe hardware systems suitable for constant bit-rate video compression with much less working memory and sub-frame end-to-end latencies.
In this section, we provide a selection of experimental results to demonstrate both the coding efficiency and high throughput of HTJ2K. Many more experimental results may be found at http://www.htj2k.com. A short, called Meridian, produced using a modern ACES production workflow with high-quality visual effects and post-production techniques was released by Netflix under the “Creative Commons” license and is available from https://opencontent.netflix.com/. Small thumbnails from every 1000-frames of the full 17,345-frame sequence are shown in Table 1. Different forms of the Meridian short were used for the compression tests reported in Sections 4.1 and 4.2 below, as well as Section 5.1.
Speed testing was performed on a MacBook Pro (15-inch, 2018) with 2.9Ghz 6-core Intel i9-8950HK CPU with 16 GB of RAM, using BlackMagic DaVinci Resolve 17.4.4, Apple Compressor 4.5.4 and the Kakadu v8.2.1 applications “kdu_vcom_fast” and “kdu_vex_fast.” BlackMagic DaVinci Resolve6 and Apple Compressor7 are commonly used software applications for high quality editing, mastering and compression within the professional media industry. The Kakadu kdu_vcom_fast and kdu_vex_fast applications are example applications included with the Kakadu SDK8 that perform JPEG2000 encoding and decoding respectively. The test clip spans 1 min from the Meridian short in 3,840 × 2,160 24 4:2:2 10bit BT709 format. Encoding and decoding speed testing results are shown in Figure 9. These results show that HTJ2K has comparable encoding and decoding speed to ProRes HQ, while HTJ2K is much faster than J2K1.
When performing high-performance speed testing, the time spent reading and writing uncompressed and compressed data to/from disk can itself become a bottleneck. Typical real-time capture applications store uncompressed imagery in memory that can be accessed directly by the encoder, while real-time playback applications store decoded data in memory not on disk. The BlackMagic Resolve and Apple Compressor speed results included reading/writing a Quicktime V210 10bit 4:2:2 uncompressed file (∼32 GB), while the Kakadu speed results included reading/writing a YUV 16bit 4:2:2 uncompressed file (∼48 GB). With HTJ2K decoding at 68.6 frames per second, Kakadu’s “kdu_vex_fast” results in decoded data being written to disk at 68.6 frames/second × (3,840 × 2,160 pixels/frame) × 2 samples/pixel × 2 Bytes/sample = 2,275, 983, 360 Bytes/second ∼2.12 GB/s, which is close to the upper limits of the sustained write-rate of the NVM PCIe 3.0 1.0 TB SSD included within the 2018 Macbook Pro. If no output file argument (-o) is used with the Kakadu “kdu_vex_fast” application, it decodes the input file to memory instead of disk. Decoding the same HTJ2K file in this way takes 11.1 s, which corresponds to 129.7 frames per second and is almost twice as fast as when writing the decoded image data to disk.
Rate Distortion performance of HTJ2K, J2K1 and ProRes HQ was compared by first compressing 1 min of Meridian with ProRes HQ using Apple Compressor 4.5.4, and then computing the actual data rate of the output ProRes HQ file, which was determined to be 758 Mbs. HTJ2K and J2K1 streams with the same bit-rate are then generated using Kakadu v8.2.1 “kdu_v_compress,” with a constant coded length constraint for each frame. The PSNR and SSIM results are shown in Figure 10. These results show that HTJ2K outperforms ProRes HQ by a similar margin to that by which J2K1 outperforms HTJ2K.
FFMPEG 5.0 was used to calculate these PSNR and SSIM results, which includes the “PSNR Average” and “SSIM All” metrics that are shown in Figure 10. The “PSNR Average” calculation for 4:2:2 content is computed as
where
and MSE_Y, MSE_Cb, MSE_Cr are the mean square error of the luma and chroma components at their native sampling resolution. “SSIM All” is computed with a weighted average in a similar way, as
JPEG 2000 was designed to support incremental low latency compression. In fact, it is possible to achieve extremely low end-to-end latencies, down to a few tens of lines of an image or video frame, without partitioning frames into independent sub-images or tiles. At very low latencies, however, the number of code-blocks available for concurrent processing necessarily reduces, which can make it hard or even impossible to achieve very high throughputs with the original JPEG 2000 block coding algorithm, even in hardware. HTJ2K provides the solution to this problem, by delivering a block coding algorithm with both much lower complexity and much higher levels of internal concurrency.
Figure 11 reveals the rate-distortion performance of HTJ2K as a function of end-to-end latency, corresponding to configurations involving two levels of vertical wavelet transformation with the LeGall 5/3 transform kernels and three levels of vertical wavelet transformation with the Cohen-Daubechies-Foveaux (CDF) 9/7 transform kernels. The results presented here are obtained using the CPLEX-based encoding strategy described in Section 3.1, generating Z = 6 coding passes (two HT Sets) for each code-block. We follow the encoding paradigm introduced in Figure 5, with flush-set heights of 8 and 16 video lines, for the cases with two and three vertical transform levels, respectively, while five levels of wavelet transformation are employed in the horizontal direction. The experiments are performed using the Kakadu tools9 “kdu_compress” and “kdu_expand” with the following encoding options:
1. Corder = PCRL Cblk = {41,024} Qstep = 0.0001 Clevels = 5 Cdecomp = B(-:-:-),B(-:-:-),H(-) Cprecincts = {88,192},{48,192},{28,192} Scbr = {1,10} Catk = 2 Kkernels:I2 = I5X3 Cmodes = HT Cplex = {6,EST,0.25,-1} –no_weights
2. Corder = PCRL Cblk = {8,512} Qstep = 0.0001 Clevels = 5 Cdecomp = B(-:-:-),B(-:-:-),B(-:-:-),H(-) Cprecincts = {16,8192},{88,192},{48,192},{28,192} Scbr = {1,18} Cmodes = HT Cplex = {6,EST,0.25,-1} –no_weights
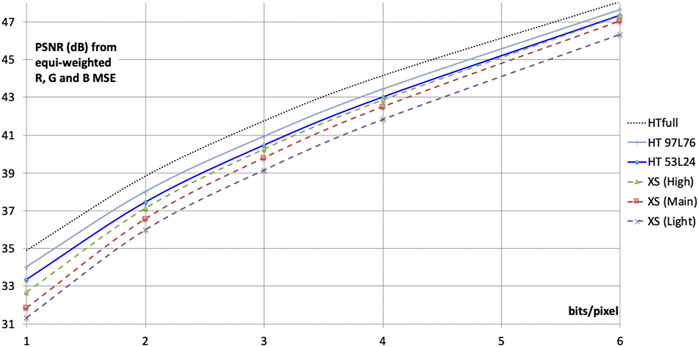
FIGURE 11. Rate-distortion performance of HTJ2K over 10 RGB 4:4:4 test images in low latency configurations, with fundamental end-to-end latencies of 24 lines (HT 53L24 has two levels of vertical 5/3 DWT) and 76 lines (HT 97L76 has three levels of vertical 9/7 DWT), compared with JPEG-XS and with full-frame (i.e., not low-latency) HTJ2K (5 levels of 9/7 DWT). Fundamental latencies exclude computation time, which may increase the end-to-end latency by up to 50% in a typical hardware implementation. According to Annex E of ISO/IEC 21122-2:2018, the Light, Main and High profiles of JPEG-XS have 2, 10 and 20 video lines of latency respectively.
PSNR results presented for this study are averaged over a diverse set of ten 444 RGB test frames from the test set maintained by the JPEG standards working group. The images are: ARRI_AlexaDrums (3840 × 2160, 12bit P3, frame 0); ARRI_AlexaHelicopterView (3840 × 2160, 12bit P3, frame 0); EBU_PendulusWide (3840 × 2160, 10bit BT709, frame 1); VQEG_CrowdRun (3840 × 2160, 8bit BT709, frame 7,111); VQEG_ParkJoy (3840 × 2160, 8bit BT709, frame 15,523); RICHTER_Screen_Content (3840 × 2160, 8bit sRGB, frame 1); APPLE_BasketBallScreen (2560 × 1440, 8bit sRGB, frame 0); BLENDER_Sintel2 (4096 × 1744, 10bit sRGB, frame 4,606); BIKE (2048 × 2,560, 8bit sRGB); and WOMAN (2048 × 2,560, 8bit sRGB). PSNR is the rate control optimization objective used for both the presented HTJ2K encoding results, and also for the reference JPEG-XS encoding results, that are obtained by exercising the public JPEG-XS reference software (ISO/IEC 21122-5, 2020) over its Main, High and Light profiles. Edwards performed a similar comparison between low-latency codecs HTJ2K, JPEG-XS and VC-2 using 4:2:2 content (Edwards and Smith, 2021).
The HT block coding algorithm and all other aspects of HTJ2K compression and decompression systems, as shown in Figure 4, are amenable to high-throughput implementation on GPUs. GPU-based HTJ2K decoding and quantization-based encoding results have previously been presented in (Naman and Taubman, 2019) and (Naman and Taubman, 2020); those results were obtained with code that has been heavily optimized to perform decoding and encoding for a particular configuration of HTJ2K codestream, in order to demonstrate what can be achieved.
In this section, we focus on a full GPU-based encoding solution, incorporating global CPLEX-based complexity control, following the approach in Section 3.1, with PCRD-opt rate control. We note that the encoding implementation described here has yet to be fully optimized, but provides nonetheless a strong indication of the potential for very high throughput full GPU-based encoding solutions with non-iterative rate control. We also discuss possible usage scenarios for GPU-based HTJ2K compression and decompression in general.
For HTJ2K encoding, a typical scenario involves transferring raw image data to the GPU, encoding the data on the GPU and then transferring the compressed code-stream back to the CPU to complete codestream assembly. The raw data is transferred to the GPU through the PCI-Express (PCIe) interface. The current generation of CPU and GPU hardware support 16 lane bidirectional PCIe 4.0; for a GPU, this translates to approximately 24 GB/s of usable bandwidth in each direction. For 16K video frames (15360 × 8640), it is possible to transfer 30 frames per second of 4:4:4 full RGB content at 16-bit per channel; for 8K and 4K video, transfer rates of 120 and 480 frames per second are possible, respectively. The amount of compressed data transferred back to the host (or CPU) is significantly smaller than the raw data transferred to the GPU; additionally, compressed data transfers can exploit the bidirectionality of the PCIe interface, and in practice have negligible effect on the achievable throughput of the system. Next generation of hardware should support the PCIe 5.0 standard, which doubles the bandwidth of PCIe 4.0; in fact, current 12th generation Intel CPUs (codenamed Alder Lake) already support this standard, and it is expected that some GPUs released before the end of this year will support it.
For HTJ2K decoding, a typical scenario involves transferring compressed code-streams to the GPU, which decodes them; then, decoded frames can either be transferred to the frame buffer of the GPU for display or transferred back to the host (CPU) for further processing.
All results presented here are obtained using a floating-point 9/7 CDF wavelet transform for lossy compression, and the integer 5/3 LeGall wavelet transform for lossless compression. We employ seven levels of decomposition and 64 × 64 code-blocks. We present results for encoding a 4K 4:4:4 12 bit video frame from the ARRI_AlexaDrums JPEG video test sequence10. For lossy compression, we show results at a bit-rate of 2 bits/pixel, which yields a PSNR of around 45 dB. 16K content is obtained by concatenating 16 copies of each 4K frame on a 4 × 4 grid.
Qstep results refer to quantization-based encoding, where each subband is quantized with a quantization step size derived from a common base step size based on the synthesis energy gains
The presented results are obtained using code developed for the nVidia CUDA platform. Results are obtained for the GT1030 and GTX1660Ti GPUs, which are members of previous generation of GPUs offered by nVidia. The GT1030 is considered a low-end device, while the GTX 1660Ti is a mid-range card with a manufacturer recommended price of around 300 USD when it was first released in early 2019. In the current (preliminary) implementation, the colour transform is actually performed by the CPU, rather than the GPU–this will change in the future. Data is then transferred to the GPU, which employs a variety of kernels before transferring code-stream data back to the host.
In Table 2 we provide the time consumed by some of the key encoding steps. The “DWT” step includes the time consumed by DWT for all decomposition levels. The DWT step also includes wavelet coefficient quantization, since performing quantization concurrently with the DWT reduces memory bandwidth consumption. The “Cleanup” time includes the time taken to produce all MagSgn, VLC, and MEL byte-streams. While producing the MagSgn byte-stream, the MagSgn kernel saves one 32-bit state variable for each quad; this state variable contains the data needed for VLC and MEL coding. It also contains all needed data for the HT SigProp and HT MagRef passes that follows the HT Cleanup pass. The MagSgn kernel also collects statistics for distortion-length convex hull analysis of that code-block, which is required by the PCRD-opt rate control procedure. “SPP/MRP” is the time taken to perform the SigProp and MagRef passes, which are performed in one kernel. The “TX to Host” time is the time taken to transfer code-stream back to the host, which is currently performed by a CUDA kernel as opposed to using a GPU driver call. The total time includes other kernels, such as the CPLEX algorithm evaluation kernels and the convex hull analysis kernel; it also includes some gaps where the GPU is idling waiting for the completion of unknown internal events.
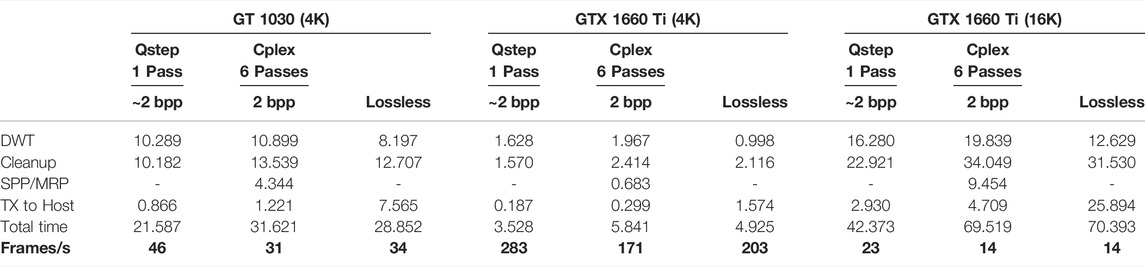
TABLE 2. Time (in milliseconds) consumed by different CUDA kernels for encoding 4K and 16K video frames. The “Total time” includes the time needed by additional kernels, not discussed here. The bottom row shows achievable frame rate.
To employ the CPLEX algorithm, we collect statistics for quantized wavelet coefficients during the DWT step; this is followed by a kernel that employs the CPLEX algorithm to determine the first bit-plane
These results indicate that previous generation mid-range GPUs are able to perform full HTJ2K encoding with rate control, at a rate that is approximately half the maximum transfer bandwidth of their PCIe 3.0 express bus. Our future work will explore the full potential of an optimized encoding solution across a wider range of GPU platforms, including current and next generation PCIe five capable devices.
This project describes a full HTJ2K hardware encoding solution, whose development is approaching maturity. The first stage of this development activity focuses on all-on-chip FPGA encoders with no external memory, targeting video formats from 4K to 16 K. As in Section 4.4, we use the term “full HTJ2K encoding solution” to refer to a system equipped with PCRD-opt and complexity control machinery, so that precise non-iterative rate control is available together with deterministic high throughput.
The most precious resource for an all-on-chip encoder is on-chip memory, which is conserved by employing the low-latency CPLEX-based encoding framework of Figure 5. Memory requirements are constrained by: 1) working with short flush-sets, spanning as few as 8 video lines; 2) limiting the number of vertical levels of wavelet decomposition, while allowing a larger number of horizontal decomposition levels; and 3) executing the PCRD-opt rate control procedure after all code-blocks in a flush-set have been produced and emitting the corresponding portion of the code-stream. This is the same framework employed for the low-latency encoding experiments in Section 4.3, but our chief concern is memory rather than latency.
The encoder uses memory in four primary ways. Each stage of vertical wavelet transformation utilizes a small number of “DWT line buffers” for a vertical lifting state machine; five line buffers are required for the CDF 9/7 wavelet transform of JPEG 2000 Part-1, while three line buffers are sufficient if only the LeGall 5/3 wavelet transform is implemented11. “Collector memory” is required to collect quantized subband samples so that they can be processed by the HT block encoder. The HT encoder is actually able to process code-block samples sequentially line-pair by line-pair, without first buffering entire code-blocks in memory, but our collectors fully buffer short, wide code-blocks prior to encoding, so that the CPLEX algorithm can generate encoding parameters that avoid the risk of overflowing the memory pools allocated for block encoder products. “Encoder pool” memory captures the six coding passes produced by the HT block encoders, allowing selected passes to be retrieved after the PCRD-opt stage has determined optimal truncation points for the flush-set. Encoder pools are managed in banks, with at least one bank to absorb encoder products that are being generated within one flush-set, while a second bank holds content from a previous flush-set that is accessed by the PCRD-opt algorithm and code-stream generation machinery. The fourth way in which memory is used in the encoder is for a “drain buffer,” that receives generated codestream data and drains it to a network packet generator that emits a stream of RTP packets over an IP network at a constant data rate.
The last three types of memory can be flexibly dimensioned to achieve different trade-offs between memory consumption, coding efficiency and latency. Our basic architectures correspond to the “HT 53L24” and “HT 97L76” configurations shown in Figure 11, for which end-to-end latencies are already extremely low. However, increasing latency by adding additional encoder pool memory and drain buffer memory is desirable, since it allows the PCRD-opt algorithm to optimize the allocation of data to code-blocks over a larger extent within the original image or video frame. Importantly, encoder pools and the drain buffer hold compressed data, rather than original frame samples or wavelet subband samples; as a result, it is relatively inexpensive to extend the latency and broaden the optimization horizon of an all-on-chip HTJ2K encoder.
At this stage, we are able to provide substantial insight into the resource consumption, operating frequencies and capabilities of our full HTJ2K encoding hardware that is under development. The most critical modules have been fully designed and synthesized, while others have been designed down to the register-transfer-level. For modules that have not been fully synthesized, resources are derived using a comprehensive yet conservative estimation methodology. The modular architecture is supported by a software-based composer that can be used to form and analyze encoding designs with a wide range of capabilities. Out of these, we choose to report here the number of LUTs12, DSP slices, flip-flops and Block RAM resources required on Xilinx Series 7 platforms13 for basic 4K/60 and 8K/60 video encoding solutions.
A basic 4K video encoder, supporting the “HT 53L24” encoding configuration of Figure 11, can be assembled with just under 40K LUTs, around 45K flip-flops, 111 36kbit Block RAM modules and around 135 Xilinx DSP48E1 slices. To put this into perspective, these correspond to just under 30%, 17%, 31% and 19%, respectively, of the LUTs, flip-flops, Block RAM and DSP resources available on a Xilinx Artix-7 XC7A200T FPGA. At 60 frames/second, with standard 4K CTA pixel- and line-rates14, the encoder’s front-end operates at 297 MHz, processing two pixels per clock-cycle, while encoding, rate control and code-stream formation operate at a back-end clock rate of approximately 205 MHz.
An 8K video encoder, supporting the “HT 97L76” encoding configuration of Figure 11, can be assembled with around 115 K LUTs, around 135 K flip-flops, 374 36 kbit Block RAM modules and around 500 Xilinx DSP48E1 slices. For comparison purposes, these correspond to approximately 86%, 50%, 102% and 67% of a Xilinx Artix-7 XC7A200T platform, but will comfortably fit on most of the larger Kintex-7 platforms and all Virtex-7 FPGAs. To achieve 60 frame/second encoding, with standard 8K CTA pixel- and line-rates15, the encoder’s front-end operates at 297 MHz, processing eight pixels per clock-cycle, while encoding, rate control and code-stream formation operate at a back-end clock rate of approximately 262 MHz. All critical elements of the design have been synthesized and verified at these clock frequencies even on the Artix-7 XC7A200T with speed-grade 2, although the larger and faster Kintex devices are likely to be required to comfortably meet timing constraints once the entire solution is instantiated.
The preliminary designs documented above provide sufficient encoder pool and drain buffer memory to support minimal latency encoding, suitable for overall compressed bit-rates of up to 3 bits/pixel. In particular, 4K/60 over 1 Gbps IP networks and 8K/60 over 5 Gigabit ethernet or 6 Gbps SDI links are a particular focus. Memory can easily be increased to support optimized rate control at higher compressed bit-rates. Moreover, as mentioned above, it is relatively inexpensive to increase the PCRD-opt rate allocation horizon, along with latency, by adding memory to the encoder pool and drain buffer, since these hold only compressed data.
Regarding the HT block encoder itself, we note that 51% of all LUTs in the basic 4K design and 57% of all LUTs in the basic 8K design are devoted to concurrently generating 6 HT coding passes for each code-block and arranging for the 10 resulting byte-streams (2 MagSgn, 2 VLC, 2 MEL, 2 SigProp and 2 MagRef byte-streams) to be recorded within the relevant encoder pool memories.
A further 18% of all LUTs and 11% of all DSP resources in the basic 4K design are associated with the PCRD-opt rate control algorithm, including calculation of the impact of each coding pass on reconstructed frame distortion (with optional visual weighting), rate-distortion convex hull analysis of the seven truncation options available for each code-block and iterative determination of an optimal distortion-length slope threshold for each flush-set. For the 8K design, these tasks also represent approximately 18% of all LUTs, but only about 7% of the DSP resources of the overall encoder.
The CPLEX complexity constraint machinery consumes approximately 10% of all LUTs and 20% of DSP resources in the 4K encoder, but less than 7% of the LUTs and 8% of DSP resources in the 8K encoding solution. The algorithm implemented in hardware is identical to that implemented in the Kakadu software tools used to generate the results of Section 4.3. These figures suggest that the CPLEX “virtual rate control” machinery is less expensive than the corresponding PCRD-opt true rate control machinery, especially at larger frame sizes, where both CPLEX and PCRD-opt together consume around 25% of the overall encoder’s logic resources.
As noted earlier, the relatively low throughput of JPEG 2000 on CPUs and GPUs has limited its reach in M&E workflows. This has been exacerbated by the steady increase of image size driven by improvements in camera sensors and displays: 4K workflows, which use 8 MP images sampled at 16 bit per channel and 24 frames per second, are now common, with workflows using 32 MP (8K) images on the horizon.
By addressing this shortcoming, HTJ2K allows current JPEG 2000 infrastructure to immediately benefit from the reduction in compute cost offered by HTJ2K and allows JPEG 2000 to extend its reach across M&E workflows–thereby significantly simplifying operations, improving quality, and reducing R&D costs.
Table 3 provides an example of the throughput and coding efficiencies that can be expected from HTJ2K in comparison to J2K1, for professional M&E content. These results demonstrate that HTJ2K can achieve faster-than-real-time decoding of large images, lossless and lossy alike, without the need for specialized computing platforms. In fact, HTJ2K’s advantage over J2K1 grows with the size of the compressed images, since HTJ2K improves the throughput of the entropy coder whose relative contribution to the overall compute costs increases with amount of coded data.

TABLE 3. Comparison of J2K1 and HTJ2K compressed sizes and decoding throughput over a 10 s portion of the Meridian short in 3,840 × 2,160 4:4:4 SDR BT.709 format. The content is encoded first using JPEG 2000 Part-1 (J2K1) and then losslessly transcoded to HTJ2K code-streams, using the HT block coding algorithm exclusively (i.e., there is no mixing of J2K1 and HT encoding options in the transcoded result). The table reports the increase in compressed size associated with the much faster HTJ2K representation of exactly the same information as the J2K1 original, as well as the decoding throughputs that are achieved using the Kakadu “kdu_vex_fast” application, on a MacBook Pro 15-inch 2018 platform with 2.9 GHz Intel Core i9 (6-core) processor, 16 GB RAM and 1 TB SSD. Note that the labels “HTJ2K Lossy 400 Mb” and “HTJ2K Lossy 800 Mb” are indicative only; the actual HTJ2K bit-rates are larger by the amount indicated in the last column. Encoding throughput speedup factors for HTJ2K over J2K1 are substantially similar.
This allows JPEG 2000 to be used in applications that require interactive viewing and editing of large images on everyday PC, server and mobile devices. Such applications include:
Mathematically lossless coding of archival images. Images generated from the production process are routinely exchanged and stored using baseband file formats such as TIFF, DPX and OpenEXR. While such formats preserve the creative intent in its totality, they also result in very large files (approximately 8 TB for a 2-h movie) and correspondingly long transfer time to, from and within storage, whether in the cloud or on-premises. Uploading a 2-h movie to the S3 service of Amazon AWS at 2 Gbps requires approximately 9 h using a baseband file format. HT typically cuts this time by 50%. The 4.5 h saved can instead be turned into additional production time, which is particularly precious as delivery deadlines loom.
Lossy coding for high-quality mezzanine images. For many M&E workflows, it is customary to lightly encode the images generated from production, trading a visually transparent coding loss for an order of magnitude reduction in file size. The resulting mezzanine images can be used for editing and transcoding to emission formats. HT brings JPEG 2000 to the party with other codecs in this space, such as ProRes and AVC-I, which allow real-time editing and browsing of image sequences on PCs and mobile devices.
The interactive browsing of the large images used in M&E workflows has always been a challenge. For example, a typical lossless UHD image sequence sampled at 24 frames per second and 16 bits per color requires a 5 Gbps storage channel, which exceeds all but the fastest local storage options. A common approach is to create a separate low-resolution proxy of the sequence, often using a different codec. This approach has several limitations: latency is required to create the proxies, multiple proxies are required to match varying storage channel bandwidth, and both image and metadata fidelity are compromised.
The resolution scalability features inherent to JPEG 2000, and preserved by HTJ2K, allow the creation of proxies to be avoided. This can readily be achieved by storing images in resolution major order and reading from them only the number of bytes available to the storage channel at a given time. This approach is applicable to remote viewing over networks as well as local browsing over slower storage channels. HTJ2K further simplifies this approach by allowing the resulting images to be processed on even lower-power client platforms.
A preliminary demonstration of this strategy is available at https://demo.noproxy.cloud/, where the HTJ2K decoder is implemented in JavaScript16 within the web-browser and the image sequence is stored in MXF and accessed over plain HTTP.
As described in Section 2.1, it is possible to transcode HTJ2K to/from J2K1 mathematically losslessly, regardless of whether the coding is irreversible (lossy) or reversible (lossless). This allows workflows to mix-and-match HTJ2K and J2K1 to fit their needs. As illustrated in Figure 12, a system (a) can use HTJ2K internally for throughput performance and for interchange with an HTJ2K-capable external system (d), but transcode to J2K1 for compatibility with external legacy systems (b) and (c). Similarly, it can store images in J2K1 for long-term storage (e), where the additional coding efficiency might be cost-effective, but otherwise store images in HTJ2K (f).
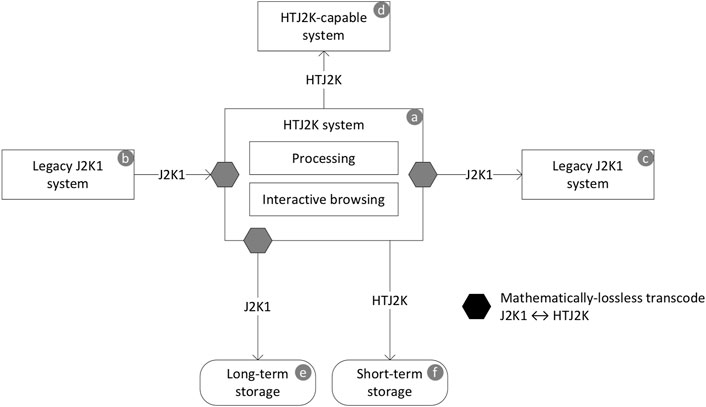
FIGURE 12. The ability to transcode HTJ2K to/from J2K1 mathematically losslessly allows an HTJ2K workflow to retaining compatibility with legacy J2K1 systems.
HT can immediately result in significantly lower compute costs per image compared to J2K1 on popular cloud platforms such as AWS and Azure, where monetary costs are proportional to compute costs. The resulting monetary savings can be used, for example, to purchase additional compute resources or to purchase carbon offsets to achieve carbon neutrality.
The wide availability of cost-effective and flexibly switched IP network infrastructure makes it particularly attractive for the transport of professional video content, both during content acquisition (contribution) and post-production, including live editing workflows. As discussed earlier, HTJ2K is well matched to such streaming applications, achieving both high coding efficiency and exceptionally high throughputs at the transport data rates offered by modern IP networks. The results provided in Section 4.3, indicate that HTJ2K provides an attractive solution for 4K/60 video streaming over Gigabit ethernet based IP networks, for which the usable compressed bit-rate is in the range 1.7–2 bits/pixel. By extrapolation, HTJ2K provides an attractive solution for 8K/60 video streaming over 5 Gigabit ethernet and 16K/30 video streaming over 10 Gigabit ethernet.
Since HTJ2K is part of the JPEG 2000 family, IP streaming solutions can be based around the RTP payload formats for JPEG 2000 developed by the Internet Engineering Task Force (IETF): (IETF RFC 5371, 2008); and (IETF RFC 5372, 2008). These formats provide sufficient payload header information (8 bytes) to associate RTP packets with corresponding J2K packets and assign RTP packet priorities based on the significance of the coded content within those J2K packets. This correspondence can potentially be used to resynchronize a decoder in the event of network packet loss, so as to decode as much usable content as possible for any given frame. However, the mechanism for doing this relies upon a decoder being able to map absolute byte offsets within a frame’s compressed codestream to J2K packets, which is only possible with the inclusion of random access (PLM or PLT) marker segments within the codestream headers. This is unfortunate, firstly because these random access marker segments are not themselves resilient to packet loss, and secondly because PLM and PLT marker segments must precede the coded data, but cannot be generated until after the content has been encoded, so they are not compatible with low latency or low memory encoding solutions.
We propose to overcome these weaknesses of the existing RTP streaming formats for JPEG 2000 by using a similar 8-byte RTP payload header that encodes the semantic identity of the first J2K packet found within the RTP packet, rather than its absolute location within the codestream. Specifically, for all packets other than those containing the codestream main header, it is sufficient to include: 1) a 4-bit “sync” field that indicates the existence and type of any resynchronization point within the packet; 2) a 12-bit packet offset (“poff”) field that indicates the byte offset, relative to the start of the RTP packet, at which the resynchronization point occurs, which is necessarily the first byte of a J2K packet; and 3) a 32-bit precinct-id (“pid”) field that uniquely identifies that J2K packet within the codestream. For the “sync” field we propose to use 3 bits to identify the J2K packet progression order that applies from the synchronization point, with two special values (e.g., 0 and 1) to indicate the lack of any synchronization point and the first packet in the codestream, respectively. For fourth bit of “sync” can be used to indicate whether or not the tile associated with the resynchronization point has coding parameters that differ from those found in the main codestream header and its first tile-part header, which a decoder can use to deduce whether or not it has received sufficient additional tile-part headers to use the resynchronization point.
In most streaming applications, and especially with HTJ2K content, we expect only to have one quality layer, so there is only one J2K packet per J2K precinct, and the “pid” field is then a unique precinct identifier. An excellent choice for the value of this field is the unique precinct identifier defined in the JPIP standard (ISO/IEC 15444-9, 2005), which fits within 32 bits for all video frame sizes one expects to encounter in practice. For the general case of codestreams with multiple quality layers, usable resynchronization points can occur at non-initial packets of a J2K precinct only when one of the following two progression orders is used: 1) layer-resolution-component-position; and 2) resolution-layer-component-position. These progression orders are not useful for very low-latency or low memory footprint streaming applications, but the proposed RTP payload format could be adapted to support them by using 24 bits of the “pid” field as a unique precinct identifier and the eight remaining bits to encode the quality layer index of the relevant J2K packet, only when the “sync” field identifies one of these two progression orders.
We finish this section by pointing out that the payload format enhancements above are not strictly required for RTP streaming of HTJ2K content over IP networks. The enhancements are valuable, however, in that they can allow a decoder to skip over lost RTP packets, while still decoding most content available for a codestream. This property could also be exploited by a network agent to generate derived RTP streams that deliberately omit packets associated with the highest one or two video resolution levels, or perhaps packets associated with spatial regions of a frame that are of no interest to a recipient of the derived stream, thereby taking advantage of the rich scalability and region-of-interest accessibility attributes of JPEG 2000 and HTJ2K codestreams.
HTJ2K is an extremely valuable addition to the JPEG 2000 family of standards, enriching the entire family with the ability to operate at extremely high throughputs, and enabling practical high speed video streaming solutions at low latencies and/or with very small memory footprints.
By building on JPEG 2000 and addressing its primary shortcoming, HTJ2K leverages existing code, infrastructure, and expertise, minimizing technical risks and deployment costs. As evidence, there are now multiple independent implementations of HTJ2K, the majority of which are open-source. Examples include: OpenJPH17; OpenHTJS18; OpenHTJ2K19; MatHTJ2K20; Grok21; OpenJPEG22; the Kakadu SDK used for experimental results in this paper; and the formal HTJ2K reference software23 (ISO/IEC 15444-5, 2021).
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
DT is the primary developer of the HT block coding algorithm, the FBCOT compression principle and the CPLEX algorithm for complexity constrained encoding. AN was involved with the original development of the HT algorithm; he is author of the OpenJPH implementation of HTJ2K, and developer of the GPU implementations described in Section 4.4. MS is co-editor of the HTJ2K standard; he produced the experimental results in Sections 4.1 and 4.2 and has been actively contributing to standards and tools to support the deployment of HTJ2K in professional video production, archiving and distribution. P-AL was the chief editor of the HTJ2K standard and has been very active in developing supporting standards and professional tools for HTJ2K, including championing MXF file support for HTJ2K within SMPTE and the open source community. HS is the chief hardware developer working on FPGA-based HTJ2K solutions described in Section 4.5. OW made many contributions to the HTJ2K standard’s development and is a co-editor of the standard; he is also author of the HTJ2K implementations MatHTJ2K and OpenHTJ2K identified in this paper. RM was involved with the original development of the HT block coding algorithm, along with evaluation and early implementations of what became the HTJ2K standard.
DT and HS were employed by Kakadu Software Pty Ltd. MS was employed by Wavelet Consulting LLC. P-AL was employed by Sandflow Consulting LLC.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsip.2022.885644/full#supplementary-material
Edwards, T., and Smith, M. D. (2021). High Throughput JPEG 2000 for Broadcast and IP-Based Applications. SMPTE Mot. Imag. J. 130, 22–35. doi:10.5594/jmi.2021.3066183
IETF RFC 5371 (2008). RTP Payload Format for JPEG 2000 Video Streams. Internet Engineering Task Force.
IETF RFC 5372 (2008). Payload Format for JPEG 2000 Video: Extensions for Scalability and Main Header Recovery. Internet Engineering Task Force.
ISO/IEC 14495-1 (1999). Information Technology - JPEG-LS - Lossless and Near-Lossless Compression of Continuous-Tone Still Images. Geneva: International Standards Organization.
ISO/IEC 15444-1 (2000). Information Technology — JPEG 2000 Image Coding System: Core Coding System. Geneva: International Standards Organization.
ISO/IEC 15444-15 (2019). Information Technology — JPEG 2000 Image Coding System — High-Throughput JPEG 2000. Geneva: International Standards Organization.
ISO/IEC 15444-5 (2021). Information Technology — JPEG 2000 Image Coding System — Part 5: Reference Software. Geneva: International Standards Organization.
ISO/IEC 15444-9 (2005). Information Technology — JPEG 2000 Image Coding System: Interactivity Tools, APIs and Protocols. Geneva: International Standards Organization.
ISO/IEC 21122-5 (2020). Information Technology — JPEG XS Low-Latency Lightweight Image Coding System — Part 5: Reference Software. Geneva: International Standards Organization.
Langdon, G. (1991). Probabilistic and Q-Coder Algorithms for Binary Source Adaptation. Data Compression Conference. Utah: Snowbird.
Naman, A., and Taubman, D. (2019). Decoding High-Throughput JPEG2000 (HTJ2K) on a GPU. Taipei, Taiwan: IEEE International Conference on Image Processing ICIP.
Naman, A., and Taubman, D. (2020). Encoding High-Throughput Jpeg2000 (Htj2k) Images on A GPU. Taipei, Taiwan: IEEE International Conference on Image Processing ICIP.
Pearlman, W. (1991). “Performance Bounds for Subband Coding,” in Subband Image Coding. Editor J. Woods (Kluwer). doi:10.1007/978-1-4757-2119-5_1
Taubman, D. (2000). High Performance Scalable Image Compression with EBCOT. IEEE Trans. Image Process. 9, 1158–1170. doi:10.1109/83.847830
Taubman, D., Naman, A., and Mathew, R. (2017). FBCOT: A Fast Block Coding Option for JPEG 2000. San Diego: SPIE Optics & Photonics: Applications of Digital Imaging.
Taubman, D. S., and Marcellin, M. W. (2002). JPEG2000 : Image Compression Fundamentals, Standards, and Practice. New York: Springer.
Taubman, D. (2002). Software Architectures for JPEG2000. Greece: Proc. IEEE Int. Conf. DSP. Santorini.S
1One example of a large media repository is Library of Congress–National Audio Visual Conversation Center (NAVCC) which holds 10.825 Petabytes of JPEG2000 Part-1 MXF files in its archives, as of February 2022; this information is based on private communication with James Synder, Senior Systems Administrator Library of Congress - National Audio Visual Conversation Center (NAVCC).
2The fact that J2K1 and HT block bit-streams can be reversibly transcoded derives from the fact that the data-dependent decisions regarding which samples should be refined within the SigProp and MagRef passes are exactly the same for both algorithms. If HT used a different set of coding passes, or only one pass per bit-plane, this reversible transcoding property would be lost, along with some rate-distortion optimisation benefits associated with sub-bit-plane coding passes.
3The J2K1 algorithm provides so-called “Bypass” options that allow the SigProp and MagRef refinement passes also to emit raw uncoded bits, bypassing the arithmetic coder. This has relatively limited impact on coding efficiency, considering that the data-dependent selection of samples to process in these passes leaves the binary refinement digits with substantially unskewed probability distributions. However, the ordering conventions for these bits in J2K1 limits the throughput enhancement that can be achieved with its Bypass option.
4See http://www.kakadusoftware.com for more information on Kakadu and downloadable tools, which are used for many of the experimental results presented in this paper.
5The sequence itself has been constructed by stitching together content cropped from highly diverse challenging photographic images, and may be found in the Supplementary Material for this paper.
6https://www.blackmagicdesign.com/products/davinciresolve/.
7https://www.apple.com/final-cut-pro/compressor/.
9These can be downloaded from https://kakadusoftware.com/documentation-downloads/downloads.
10Frame 0 of this sequence is part of the test set described in Section 4.3.
11A reversible integer version of the 5/3 transform is defined in Part-1 of the JPEG 2000 standard, but we work with the irreversible (truly linear) 5/3 transform that requires the syntactical extensions of JPEG 2000 Part-2.
12Xilinx Series 7 FPGAs have four 6-input LUTs and eight flip-flops in each configurable logic block (CLB).
13See https://www.xilinx.com/support/documentation/selection-guides/7-series-product-selection-guide.pdf.
143,840 × 2,160 frames are contained within a window with
157,680 × 4,320 frames are contained within a window with
16The decoder uses the OpenJPH open source implementation at https://github.com/aous72/OpenJPH, compiled to WebAssemblyd.
17https://github.com/aous72/OpenJPH.
18https://www.npmjs.com/package/openht.
19https://github.com/osamu620/OpenHTJ2K.
20https://github.com/osamu620/MatHTJ2K.
21https://github.com/GrokImageCompression/grok.
Keywords: HTJ2K, video coding, video streaming, mezzanine codecs, scalable coding
Citation: Taubman D, Naman A, Smith M, Lemieux P-A, Saadat H, Watanabe O and Mathew R (2022) High Throughput JPEG 2000 for Video Content Production and Delivery Over IP Networks. Front. Sig. Proc. 2:885644. doi: 10.3389/frsip.2022.885644
Received: 28 February 2022; Accepted: 29 March 2022;
Published: 27 April 2022.
Edited by:
Matteo Naccari, Audinate, United KingdomReviewed by:
Norishige Fukushima, Nagoya Institute of Technology, JapanCopyright © 2022 Taubman, Naman, Smith, Lemieux, Saadat, Watanabe and Mathew. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David Taubman, ZC50YXVibWFuQHVuc3cuZWR1LmF1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.