Survey on Deep Learning-Based Point Cloud Compression

Point clouds are becoming essential in key applications with advances in capture technologies leading to large volumes of data. Compression is thus essential for storage and transmission. In this work, the state of the art for geometry and attribute compression methods with a focus on deep learning based approaches is reviewed. The challenges faced when compressing geometry and attributes are considered, with an analysis of the current approaches to address them, their limitations and the relations between deep learning and traditional ones. Current open questions in point cloud compression, existing solutions and perspectives are identified and discussed. Finally, the link between existing point cloud compression research and research problems to relevant areas of adjacent fields, such as rendering in computer graphics, mesh compression and point cloud quality assessment, is highlighted.

1 Introduction

Recent advances have increased the accuracy and availability of 3D capture technologies making point clouds an essential data structure for transmission and storage of 3D data. 3D point clouds are crucial to a large range of applications such as virtual reality (Bruder et al., 2014), mixed reality (Fukuda, 2018), autonomous driving (Yue et al., 2018), construction (Wang and Kim, 2019), cultural heritage (Tommasi et al., 2016), etc. In such applications, compression is necessary as large scale point clouds can have large numbers of points.

Point clouds are sets of points with x, y, z coordinates and associated attributes such as colors, normals and reflectance. Point clouds can be split into two components: the geometry, the position of each individual point, and the attributes, additional information attached to each of these points. A point cloud with a temporal dimension is referred to as a dynamic point cloud, and without a temporal dimension as a static point cloud.

The Moving Picture Experts Group (MPEG) has promoted two standards (Schwarz et al., 2018): MPEG Geometry-based Point Cloud Compression (G-PCC) and MPEG Video-based Point Cloud Compression (V-PCC). These two standards have reached the Final Draft International Standard stage. G-PCC makes use of native 3D data structures such as the octree to compress point clouds while V-PCC adopts a projection-based approach based on existing video compression technologies. In addition, the Joint Photographic Experts Group (JPEG) has issued a call for evidence (JPEG, 2020) on PCC.

Common capturing techniques for point clouds include camera arrays (Sterzentsenko et al., 2018), LiDAR sensing (Goyer and Watson, 1963) and RGBD cameras (Besl, 1989). It is important to consider capturing techniques as the resulting point clouds will exhibit specific characteristics which can be exploited for compression. Among these characteristics, the geometry resolution and the number of points are key for point cloud compression algorithms. The ratio between the number of points and the geometry resolution is the surface sampling density of the point cloud.

For example, camera arrays tend to produce point clouds that are dense, regularly sampled and amenable to 2D projections. RGBD cameras produce point clouds that can be represented on a 2D image with depth and color components; the resulting point clouds are dense, regularly sampled and susceptible to occlusions. Spinning LiDAR sensors are commonly used for autonomous driving, they tend to produce point clouds that can be approximately represented on a 2D image with depth and reflectance components. Such LiDAR point clouds are sparse and unevenly sampled in euclidean space but more dense and evenly sampled in spherical space which is an approximation of the sensing mechanism. In Figure 1, we show point clouds captured with aerial LiDAR (“Dourado Site”), camera arrays (“soldier” and “phil”) and fused terrestrial LiDARs (“Arco Valentino”).

FIGURE 1

FIGURE 1. Point clouds visualizations. From left to right, “Dourado Site” (Zuffo, 2018), “soldier” (d’Eon et al., 2017), “phil” (Loop et al., 2016) and “Arco Valentino” (GTI-UPM, 2016).

The target application must also be considered. In the case of human visualization, a point cloud combined with a rendering method is a simplified model for a plenoptic function (Landy and Movshon, 1991) which results in six degrees of freedom. Therefore, we aim to maximize the perceived visual quality given a rate constraint. For autonomous driving, we instead aim to maximize the performance of the autonomous driving function given a rate constraint. Note that it is actually possible to improve quality with lower bitrate in the case of point clouds. For example, sparse samplings of surfaces are more costly to code compared to dense samplings (watertight at a given resolution). In addition, compared to dense samplings, sparse samplings can result in inferior renderings and for autonomous driving, in safety issues due to occupancy false negatives (not sampled).

This can be explained by the sampling process. The actual state of each voxel can actually be considered as ternary instead of binary with unseen, empty and near surface states (Curless and Levoy, 1996). As as result, deciding the occupancy of unseen voxels is important when performing compression as a dense surface is less costly to code than a sparsely sampled surface. In particular, compression methods based on surface models and deep learning tend to complete missing points from surfaces in sparser point clouds.

Existing literature reviews provide an overview of MPEG standardization efforts (Schwarz et al., 2018; Graziosi et al., 2020; Cao et al., 2021), a classification taxonomy (Pereira et al., 2020) and an analysis based on the coding dimensionality (Cao et al., 2019). In this review, we will provide a general overview of PCC approaches with a focus on deep learning-based methods.

Point clouds can be divided into two components: the geometry and the attributes. The geometry is represented by points at given positions and the attributes attach information to each of these points. These two components can be coded separately, although it is necessary to transfer attributes if we code the geometry in a lossy manner as shown in Figure 2.

FIGURE 2

FIGURE 2. Point Cloud Compression by separating geometry and attribute compression.

For geometry, one of the main difficulties is the sparsity of the signal. Geometry can be considered as a binary signal on a regular voxel grid. We define sparsity as the ratio between the number of points and the number of voxels. In addition, we introduce the concepts of global and local sparsity when evaluating point cloud sparsity at different Level of Details (LoDs). A point cloud at its original LoD has certain precision and coarser LoDs are obtained by reducing this precision usually via quantization. Local sparsity refers to sparsity localized at finer LoDs and global sparsity to sparsity localized at coarser LoDs. Note that local and global sparsity are not mutually exclusive. The localization of sparsity in specific LoDs has been exploited for better entropy modeling of octree occupancy codes at different LoDs (Jiang et al., 2012). Such LoDs can be defined in duality with an octree representation by assuming the voxel grid dimensions are a common power of two. Then, quantization by a power of two and duplicate removal is identical to octree pruning. Following this, coarser LoDs are typically denser than finer LoDs for locally sparse point clouds which is important as performance of compression approaches depends on sparsity characteristics.

For attributes, the sparsity of the geometry which forms the support for the attributes is also one of the difficulties. An additional difficulty is the irregularity of the support: while geometry is a sparse signal on a regular support, attributes form a signal on an irregular support that may also be locally sparse, globally sparse or both. Irregularity can thus be defined as the absence of a regular support structure such as the regular grid sampling of images. Essentially, regular supports can be defined as the cartesian product of one or multiple regularly sampled intervals coresponding to different dimensions (horizontal, vertical, temporal, ...).

In the case of text, audio, images and video, the attributes lie on a regular grid, and the geometry, which represents a negligible amount of information. In the case of point clouds, we can consider that the information lies on a sparse subset of a regular grid and coding this sparse subset (the point positions, the geometry) is expensive. In addition, the information now lies on a sparse, irregular domain with irregular neighborhoods making attribute compression more difficult.

2 Point Cloud Compression

We consider geometry and attribute compression separately and for each of them, we separate approaches tailored to LiDAR point clouds as they tend to have very specific structures.

2.1 G-PCC and V-PCC Standards

The MPEG G-PCC standard (MPEG, 2021c) features numerous techniques in order to handle different types of point clouds. It separates geometry coding and attribute coding following the scheme in Figure 2. Geometry can be coded using two modes: octree coding and predictive geometry coding. Octree coding is a general compression approach while predictive geometry coding targets LiDAR point clouds. In addition, compression of LiDAR point clouds using a sequential structure (MPEG, 2021b) and compression of point cloud sequences with inter prediction (MPEG, 2021a) are being investigated as exploratory experiments.

The MPEG V-PCC standard aims to compress point cloud sequences using video coding techniques. The point cloud is divided into patches, they are then packed into a 2D grid and the geometry and attributes are compressed separately with video codecs (ITU-T, 2019). Preprocessing and postprocessing operations such as smoothing, padding and interpolation are applied to improve reconstruction quality.

2.2 Geometry Compression

Geometry compression can be considered as the compression of a sparse binary occupancy signal over a regular voxel grid. One of the main difficulties in compressing geometry is the sparsity of the signal which can be global, local or both.

By definition, global sparsity occurs when large volumes of space are entirely empty, e.g. when the point cloud is a scene composed of multiple objects. It can also be a result of the sampling process which samples only the surfaces of real world volumes resulting in the inside of the volumes being empty. Local sparsity can occur when the sampling density, the number of points per unit of volume, is low compared to the considered precision or voxel size. For example, this can happen in fused LiDAR point clouds of monuments and buildings as LiDAR sensors provide high precision captures with a sampling density that can be comparatively low and/or non uniform.

The structure of the point cloud is also primordial. Spinning LiDAR point clouds (Li and Ibanez-Guzman, 2020) are both globally and locally sparse in 3D space but with a model of the sensor, such as the spherical coordinate system, it becomes more regular, uniformly distributed and dense.

2.2.1 Regular Point Clouds

2.2.1.1 Octree

Regular point clouds are quite dense allowing compression with a large range of operations. Among these operations, the simplest is a hierarchical voxel grid representation with the octree data structure. The geometry can be locally simplified by fitting a primitive such as planes, triangles, etc. Transform coding and dimensionality reduction are also possible by changing the voxel grid basis to another basis, for example, with projection to 2D or 1D spaces.

The most common geometry compression algorithm is octree coding (Schnabel and Klein, 2006). 3D space is recursively divided into eight equal subvolumes until the desired LoD is achieved. This is equivalent to encoding an occupancy map, i.e. a binary signal on a voxel grid, in a multiresolution manner. When a containing volume is empty, all its subvolumes are empty. Therefore, only the occupancy of valid voxels, whose parents are occupied, needs to be encoded. This explains the octree-voxel duality as each level of an octree can be associated with a voxel grid as shown in Figure 3.

FIGURE 3

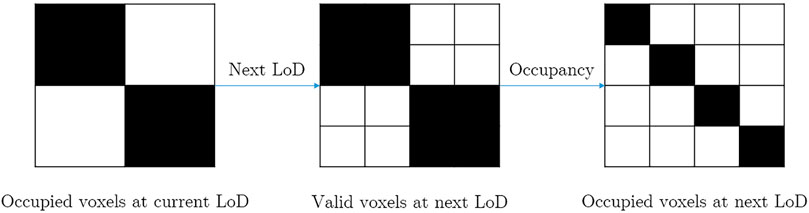
FIGURE 3. Simplified 2D view of an octree construction. Octrees can be seen as hierarchical binary voxel grids. An occupied voxel has at least one point within its volume and a valid voxel is possibly occupied while invalid voxels must be empty. Only valid voxels need to be coded at each LoD.

For each octree node, coding can be done bitwise (per voxel) but also bytewise (per octree node). When coding occupancy bits bytewise, it is possible to reorder bits to improve compression performance. Specifically, approaches using tangent planes to guide reordering have been explored in the literature (Schnabel and Klein, 2006; Huang et al., 2008; Jiang et al., 2012). In addition, an octree node can have between one and eight occupied voxels. The number of occupied voxels can be encoded to serve as a context for encoding occupancies (Schnabel and Klein, 2006). For context based entropy modeling, the estimated occupancy probabilities can also be conditioned on the previously coded occupancies in the current octree node (MPEG, 2021c). The structure of an octree node requires that at least one of eight occupancy bits is occupied (256 − 1 = 255 combinations) and the voxel grid interpretation enables the use of regular neighborhoods as contexts.

Taking advantage of the hierarchical nature of the octree, it is possible to use information from the parent node to code voxel occupancies at the current LoD Garcia and de Queiroz (2018). Such hierarchical contexts improve the compression performance compared to using no context. Furthermore, the neighbors of the parent node are also used as context in G-PCC neighbor-dependent entropy context (MPEG, 2021c). Based on the duality between each octree level and a voxel grid, a regular neighborhood can be used to construct a voxel-based context using both current and parent level(s).

2.2.1.2 Transforms and Dimensionality Reduction

Point clouds can be represented using 2D surfaces fitted to the point cloud. In addition, the points can also be projected onto 2D surfaces either using predefined surfaces (such as axis aligned planes) or fitted surfaces. Reducing the dimensionality to a single dimension makes the point cloud into a point sequence.

For dense point clouds, assuming that points are sampled from surfaces is common. Therefore, local point distributions can be modeled using surface models such as planes (Dricot and Ascenso, 2019b), triangles (Dricot and Ascenso, 2019a), Bézier patches (Cohen et al., 2017), etc. Surfaces can also be modeled implicitly with Bézier volumes (Krivokuća et al., 2020) as the level set of a volumetric function. Sim et al. (2005) also represent point clouds as a tree of spheres.

The dimensionality of point cloud compression can also be reduced using projection methods. For example, geometry can be compressed with dyadic decomposition Freitas et al. (2020); instead of an octree, a binary tree of 2D binary images is encoded. A simplified approach based on a single projection has also been studied (Tzamarias et al., 2021). In Kaya et al. (2021), the point cloud is partially reconstructed from two depthmaps and the missed points are encoded separately. Projections can also be performed adaptively at a local level. For example, it is possible to project points on a 2D plane and encode a height field on this 2D plane (Ochotta and Saupe, 2004). Similarly, the MPEG Video-based Point Cloud Compression standard (V-PCC) projects the point cloud geometry to a 2D grid and performs compression with video compression technologies (ITU-T, 2019). Li et al. (2021) improve upon V-PCC with occupancy-map-based rate distortion optimization and partition, Xiong et al. (2021) uses occupancy map information for fast decision of coding units and fast mode decision. Similar to V-PCC, Zhu et al. (2021) also propose a view-dependent video coding approach but focus on quality of experience for streaming and show competitive results in their subjective quality experiments. We notice that modeling point clouds with surface models is the same as projecting the points onto 2D surfaces with an height field that is zero everywhere i.e. the third dimension is entirely discarded.

The dimensionality can be further reduced by considering point clouds as sequences of points. Given a sequence of points and a prediction method, it is interesting to ask what is the optimal ordering for compression. However, this is difficult to compute due to the combinatorial natural of problem. A proxy criterion for the reordering is a formulation as the Traveling Salesman problem which is considered in Zhu et al. (2017) with binary tree based block partitioning.

Graph transforms have also been applied to geometry compression. When applying the graph transform for attribute compression, the geometry forms a support on which a graph and a corresponding basis can be built. In such approaches, the graph and a corresponding basis are built from a support and a graph transform is applied to a function lying on this support. However, the difficulty for geometry compression is that the geometry is the support itself or the voxel grid is the support for binary occupancy. In the first case, the support is not available at the decoder and, in the second case, the dimensionality is too high. This conundrum can be resolved by encoding a lower resolution point cloud (base layer) and upsampling it via surface reconstruction (upsampled base layer) (de Oliveira Rente et al., 2019). This upsampled base layer can then be used as a support and the original geometry becomes an attribute on this support which resembles residual coding.

2.2.2 LiDAR Point Clouds

LiDAR point clouds are typically sparse in 3D space and can exhibit non uniform density due to their specific structures. Due to the scanning mechanism, spinning LiDAR point clouds are usually denser near the sensor and sparser far from the sensor. Such structures can be exploited for compression as these point clouds typically lie on a lower dimensional manifold in 3D space.

Point clouds captured with LiDAR sensors can often be represented as a sequence. LASzip (Isenburg, 2013) is a lossless, order-preserving codec specialized for LiDAR point clouds treating them as sequences and using metadata related to the LiDAR scanning mechanism (ASPRS, 2019). In the special case of spinning LiDAR sensors, Song et al. (2021) separate the point cloud into ground, object and noise layers. Typically, most points belong to the ground, and they form circular patterns which can be efficiently compressed. The point cloud formed by objects is usually globally sparse: the objects form clusters of points sparsely located in the scene.

LiDAR point clouds can be transformed to depth images by approximating the LiDAR sensor mechanism with quantized spherical angular coordinates. However, this transformation is often lossy on most LiDAR sensors albeit some new sensors make it lossless (Pacala, 2018) by outputting a range image directly. The distortion introduced by this transformation will be acceptable or unacceptable depending on the application. In Ahn et al. (2015), range images are compressed with predictive coding in hybrid coordinate systems: spherical, cylindrical and 3D space. Using mode selection, the range is predicted either directly, via the elevation or using a planar estimation. In Sun et al. (2019), the range image is segmented into ground and objects, followed by predictive and residual coding for compression.

LiDAR point cloud packets can be directly compressed in some cases. The point cloud in this format has a natural 2D arrangement with the laser index and rotation. Full LiDAR point cloud frames are produced at 10 Hz, while packets are typically produced at frequencies greater than 1000 Hz. As a result, directly compressing LiDAR packets is more appealing for low-latency scenarios than full frames. Such packets can then be compressed using image compression techniques (Tu et al., 2016). In addition, Tu et al. (2017) propose the use of Simultaneous Localization And Mapping (SLAM) to predict and compress dynamic LiDAR point clouds.

In three dimensions, the structure of the LiDAR sensor can be used as a prior for octree coding. Specifically, sensor information such as the number of lasers, the position and angle of each laser and the angular resolution of each laser per frame can be encoded and exploited to improve compression. Only valid voxels, or plausible voxels according to the acquisition model, must be encoded when the acquisition process is known. This has been implemented as the angular coding mode in G-PCC (MPEG, 2021c).

2.3 Attribute Compression

The geometry forms a support for the attributes. In classical compression problems on images, videos, audios have attributes supported on regular grids. This results in regular neighborhoods for each sample leading to regular inputs for context modeling. The main difference between point cloud compression and these well studied compression problems is that the geometry, i.e. the support of the attributes, is sparse and irregular instead of being a regular grid. We show that the different point cloud attribute compression approaches actually all attempt to address sparsity, irregularity or both at once. Hence, sparsity and irregularity of this support are key challenges for point cloud attribute compression.

In Zhang et al. (2014), sparsity and irregularity are also referred to as unstructured (absence of a grid structure) and addressed with a graph transform. de Queiroz and Chou (2016) specifically aim to address irregularity and Cohen et al. (2016) focus on sparsity after irregularity has been addressed with a graph transform (Zhang et al., 2014). We also note that for some types of point clouds such as LiDAR point clouds, the point cloud structure, e.g. acquisition structure, can be used to reduce sparsity and irregularity.

2.3.1 Regular Point Clouds

Point cloud attributes can be compressed using a graph transform (Zhang et al., 2014). We can construct a graph based on the point cloud geometry to define a fourier transform on graphs. This addresses the sparsity and irregularity issue as we are now in the graph frequency domain instead of the spatial domain. However, building such graphs and defining the specific transform for compression is a complex problem. Cohen et al. (2016) focus on sparse point clouds and propose a method to compact attributes and generating efficient graphs for compression de Queiroz and Chou (2017) partition the point cloud into blocks and perform transform coding on point cloud attributes. Specifically, they propose a Gaussian Process Transform which is a variant of the Karhunen-Loève Transform (KLT) that assumes points are samples of a 3D zero-mean Gaussian Process. Such approaches resolve the irregularity by working in the spectral domain defined by a graph transform.

The Region-Adaptive Hierarchical Transform (RAHT) (de Queiroz and Chou, 2016) is akin to an adaptive variation of a Haar wavelet for point cloud attribute compression. In addition, it has been found that reordering of the RAHT coefficients significantly improves the performance of the run-length Golomb-Rice coding compared to other entropy coding schemes (Sandri et al., 2018). Souto et al. (2021) improve upon this RAHT with Set Partitioning in Hierarchical Trees (Said and Pearlman, 1996). Chou et al. (2020) generalize the RAHT with volumetric functions defined on a B-spline wavelet basis. They show that the RAHT can be interpreted as a volumetric B-Spline of first order and that higher order volumetric B-Splines eliminate blocking artifacts. In this case, the irregularity is resolved by considering the point cloud in an octree structure. Indeed, the geometric structure is irregular but the hierarchical relations are regular.

Sandri et al. (2019) propose a number of extensions to the RAHT in order to compress plenoptic point cloud attributes. In plenoptic point clouds, the color of a point varies with the viewing direction. In particular, they find out that the combination of the RAHT and the KLT performs best: this method is referred to as RAHT-KLT. Krivokuća and Guillemot (2020) compress plenoptic point clouds using a combination of clustering and separate encoding of diffuse and specular components using the RAHT-KLT. Krivokuća et al. (2021) extend this approach to incomplete plenoptic point clouds (6-D) where a point may not have attributes for some viewpoints as it is not visible. This extends the RAHT to plenoptic point clouds whose plenoptic component is irregular. That is, for a given point, some viewpoints may not be valid and may not have attributes resulting in a 6-D structure.

G-PCC also proposes an attribute compression scheme based on prediction and lifting operations (MPEG, 2021c). Multiple LoDs are constructed and predictors are built based on the attributes of nearest neighbors. This shows that attribute compression schemes need not follow the same structure as geometry compression albeit doing so may provide some complexity advantages (single pass). Indeed, by assuming that geometry is fully available when decoding attributes, any type of division, segmentation can be performed using this information. Attributes tend to be spatially correlated, hence a subset of point attributes can form a good basis for estimating remaining attributes. Similarly to RAHT, while the geometry is irregular, here a regular hierarchical structure is built.

Mekuria et al. (2017) propose a complete point cloud codec for both geometry and attribute compression. It is also known as the “MPEG Anchor” as it was used as a comparison basis in early stages of the MPEG standardization process for point cloud compression. Attributes are projected to a 2D image and compressed using the JPEG codec. Zhang et al. (2017) cluster the point cloud with mean-shift clustering and compress the attributes by projecting them on a 2D plane and performing a 2D Discrete Cosine Transform (DCT). Gu et al. (2017) also explore the use of a 1D DCT to compress point cloud attributes. First, they group the points by blocks and order them by their Morton codes (Morton, 1966). Then, the 1D DCT is applied and entropy coded. In these approaches, the attributes are mapped on a 2D or 1D regular grid in a spatially contiguous manner. As a result, the irregularity of the geometry is resolved or at least reduced.

Hou et al. (2017) make use of sparse representations via a virtual adaptive sampling. Indeed, point cloud attributes have an irregular structure, reducing a block of voxels (voxel grid) to the subset of occupied voxels can be viewed as a virtual adaptive sampling process. Gu et al. (2020) improve upon this approach with inter-block prediction and run-length encoding. Shen et al. (2020) also make use of this virtual adaptive sampling formulation and propose learning a multi-scale structured dictionary.

V-PCC (MPEG, 2020b) compresses attributes from 2D projections and video coding. The attributes are mapped to a 2D image, the image is then smoothed using different methods and compressed using video compression method (ITU-T, 2019). The smoothing aims to maximize rate-distortion performance by completing values of empty pixels. Similarly, He et al. (2020) propose an approach based on spherical projections to project both geometry and attributes upon a 2D image. The attribute image can then be compressed using image compression techniques.

In de Queiroz et al. (2021), the authors propose a model description for volumetric point clouds that is independent of lighting and camera viewpoint. This generalizes the concept of plenoptic point clouds as the point cloud is no longer a simplified model for the plenoptic function Landy and Movshon (1991). Instead, the visual aspect of the point cloud can vary depending on the characteristics of the scene. This is related to the Bidirectional Scattering Distribution Function (BSDF) (Bartell et al., 1981) which models how light is reflected or transmitted by a given surface. In perspective, by rendering point clouds with surfaces or volumes, it is possible to apply rendering techniques developed for meshes such as Physically Based Rendering Greenberg (1999) approaches. This is an important consideration for attribute compression as it changes the nature and structure of the attributes being compressed.

2.3.2 LiDAR Point Clouds

LASzip (Isenburg, 2013) is a specialized codec for LiDAR point clouds. The point cloud is considered as a sequence and the attributes are compressed using delta coding, predictive coding and context-based entropy coding. Specifically, the LAS format (ASPRS, 2019) contains the number of returns and the return number for an emitted laser pulse. This information is used to perform context-based entropy coding and improve delta coding by selecting reference values that are more likely to be similar to the current value.

He et al. (2020) use equirectangular projection to produce a 2D image from a LiDAR point cloud. Then, the authors test different image compression algorithms on color and reflectance images. Similarly, Houshiar and Nüchter (2015) compressed color images using the PNG format.

Yin et al. (2021) improve the predicting transform of G-PCC by exploiting normals. Specifically, the normals of two points are used to improve G-PCC mode selection. This demonstrates that attributes can be conditioned on the geometry by their position on the local characteristics of the geometry such as normals.

3 Deep Learning Based Point Cloud Compression

In Figure 4, we present a taxonomy of learning-based approaches for point cloud compression. A point cloud is composed of two components, geometry and attributes and can include motion (dynamic) or not (static). The components can be compressed separately or jointly and in a lossy or lossless manner.

FIGURE 4

FIGURE 4. A taxonomy of Learning-based Point Cloud Compression.

We also differentiate approaches based on their encoding domain. Voxel based approaches are typically more suited to dense point clouds and point-based approaches to sparse point clouds. Indeed, while the complexity of voxel based approaches depends on the dimension of the voxel grid (precision), the complexity of point based approaches depends on the number of points.

It is also important to consider prior information. The most common source of structure in point clouds is usually the sensor. Spinning LiDAR sensors can be approximately modeled using a spherical coordinate system, point clouds from camera arrays have a representation as multiple 2D images, RGBD cameras produce a point cloud that can be stored on a single 2D image etc. Taking this prior information into account can yield significant compression gains but requires specific processing for each type of prior.

3.1 Geometry Compression

3.1.1 Lossy Compression

By considering point clouds as a binary signal on a voxel grid, we can use Convolutional Neural Networks (CNNs) for point cloud geometry compression. Specifically, CNN based autoencoder architectures aim to transform the input into a lower dimensional latent space and reconstruct an output identical to the input. This can be interpreted from the point of view of transform coding with an analysis f_a and synthesis transform f_s as shown in Figure 5. The quantization part is also essential in that it must be differentiable in order to train the neural network. It is shown in Ballé et al. (2017) that additive uniform noise models quantization well during training and is differentiable. Additionally, the distribution of the latent space is modeled as part of the network and the resulting entropy enables rate distortion optimization of the network for specified rate distortion tradeoffs. The probabilities predicted by the entropy model can then be used by an arithmetic coder in order to encode and decode the latent space.

FIGURE 5

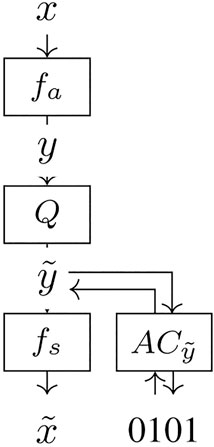
FIGURE 5. Simple autoencoder architecture for compression. f_a is an analysis transform, f_s a synthesis transform, Q refers to quantization and AC to arithmetic coding with its associated entropy model.

Quach et al. (2019) introduce the use of CNNs for point cloud geometry compression and in (Quach et al., 2020b) the proposed approach significantly outperform MPEG G-PCC (MPEG, 2021c) as shown in Figure 6. The decoding of a point cloud can be cast as a binary classification problem in a voxel grid. However, point clouds tend to be extremely sparse and this causes a class imbalance problem; this problem is resolved with the use of the focal loss (Lin et al., 2017). Quach et al. (2021) investigate differentiable loss functions and their correlation with perceived visual quality. Also, Guarda et al. (2020b) propose a neighborhood adaptive loss function as an alternative to the focal loss.

FIGURE 6

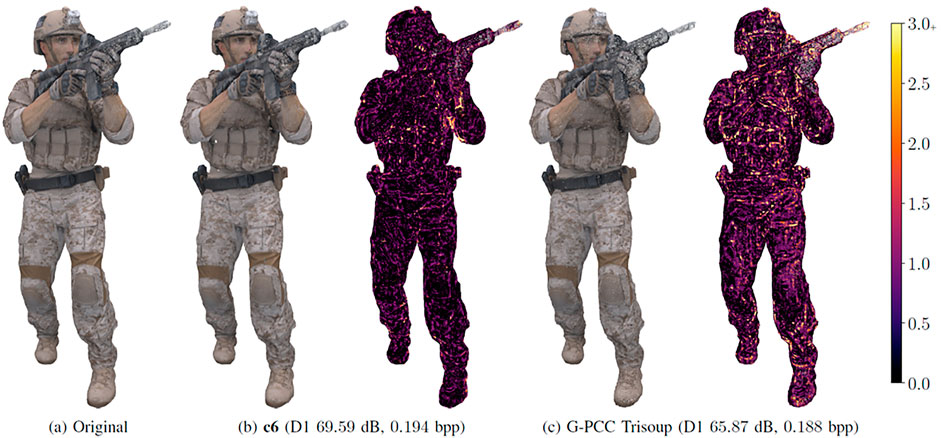
FIGURE 6. Comparison between geometry compression codecs in (Quach et al., 2020b) and MPEG G-PCC v10.0 (MPEG, 2021c). Learning-based approaches can achieve significantly lower distortions at equivalent bitrates.

A drawback of CNNs on voxel grids is the significant temporal and spatial complexity. This can be alleviated by using block partitioning (Guarda et al., 2019; Wang et al., 2019; Quach et al., 2020b). Wang et al. (2020) go further along this path by making use of sparse convolutions (Choy et al., 2019) which reduces the temporal and spatial complexities even further. However, the disadvantage is that compression performance on sparse point clouds is degraded. Furthermore, Killea et al. (2021) propose the use of lightweight 1D+2D separable convolutions for point cloud geometry compression resulting in less operations and network parameters with almost equivalent performance to their baseline model.

Overall, more elaborate neural network architectures are explored in Wang et al. (2019, 2020) and the impact of deeper neural network architectures is measured in Quach et al. (2020b). Wang et al. (2020) propose a multiscale approach using sparse convolutions. This approach is extended in Wang et al. (2021) by making use of both the previous LoD and the current LoD by progressively building the current LoD. In particular, the authors study different levels of progressivity: n-stage with a sequential dependency chain, eight-stage which unpacks a voxel into eight subvoxels one by one and 3-stage which unpacks a voxel dimension-wise into two, four and finally eight voxels. The authors also make use of the lossless-lossy compression scheme to adapt their method to point clouds with different levels of density.

Since the decoding can be cast as a classification problem (Quach et al., 2019), the compression performance can be improved significantly with adaptive thresholding approaches. Indeed, the density of the training dataset and the test dataset may vary. This can cause a mismatch between the distribution of predicted occupancy probabilities and the actual occupancies. This mismatch can be corrected with adaptive thresholding. For example, Wang et al. (2019) encode the number of points as a threshold so that the reconstruction has the same number of points as the original. Quach et al. (2020b) encode a threshold that is optimal given a specific distortion metric. Guarda et al. (2020a) perform mode selection on models trained for different densities in order to achieve adaptive behavior.

The key observation is that CNNs for point cloud geometry compression tend to be biased towards a particular density depending on the training dataset and loss function parameters (Quach et al., 2020b). Adaptive thresholding can correct this bias and can be based on factors such as the number of points and the distortion metric. Using mode selection on models targeting different densities is another way of making a density adaptive solution. The neighborhood adaptive loss function also removes the need to adjust focal loss parameters.

Commonly, one neural network is trained for each Rate-Distortion (RD) tradeoff. In that way, each network is optimized for a RD tradeoff at the cost of additional training time. Different approaches have been proposed to reduce the training time. Quach et al. (2020b) propose a sequential training scheme that significantly reduce the training time by progressively finetuning a model trained on a first RD tradeoff to subsequent RD tradeoffs. Guarda et al. (2020c) propose the use of implicit-explicit quantization of the latent space which reduces the number of models to be trained. Implicit quantization controls the RD tradeoff with a scalar RD tradeoff parameter in the loss function when training. On the other hand, explicit quantization controls the RD tradeoff by varying the quantization step on the latent space. Surprisingly, the performance of implicit-explicit quantization is higher compared to implicit-only quantization.

In (Lazzarotto et al., 2021), CNNs are used for block prediction. More precisely, the blocks are predicted from already decoded neighboring blocks. Lazzarotto and Ebrahimi (2021) perform residual coding and encode a residual between a ground-truth block and a degraded block compressed with G-PCC. (Akhtar et al., 2020) perform super-resolution using CNNs which improves the reconstruction quality significantly without any additional coding cost.

3.1.2 Lossless Compression

Lossless compression algorithms can be extended using deep learning based entropy models. These entropy models predict occupancy probabilities which are then fed into an entropy coder. Different types of contexts can be used to make such predictions.

In the context of octree coding, parent node information can be used as context. Huang et al. (2020) improve the coding of an octree by proposing a neural network based entropy model for octree codes. Specifically, this neural network takes the location and information from the parent node to predict occupancy probabilities. Biswas et al. (2020) extend this to dynamic point clouds and propose the use of continuous convolutions to improve probability predictions using already decoded frames. However, such a context only provides limited information.

By introducing a sequential dependency in the voxel grid, one can use voxels at the current LoD as context. Nguyen et al. (2021) proposes a deep CNN with masked convolutions called VoxelDNN for lossless compression of point cloud geometry. The neural network predicts the occupancy probability of each voxel, and the probabilities are then fed to an arithmetic coder. The rate-optimized octree partitioning improves performance on sparser regions. The compression performance is further improved with data augmentation and context extension techniques (Nguyen et al., 2021a). The drawback of such approaches is that the sequential dependency increases complexity significantly. Nguyen et al. (2021b) reduce the temporal complexity significantly with a multiscale approach. It reduces the complexity by estimating the probabilities in parallel with a multiscale approach which reduces the sequential dependency when estimating occupancy probabilities.

Also, we can entirely remove the sequential dependencies by predicting the voxel occupancy using only the parent LoD. Que et al. (2021) propose a neural network which takes a voxel grid context from the parent LoD to predict occupancy probabilities. These probabilities are then used for entropy coding. In addition, they predict an offset for each point in order to further refine coordinates. Although such approaches have a reasonable complexity, they do not take into account already decoded voxels at the current LoD which limits compression performance.

Kaya and Tabus (2021) propose an approach that makes use of the current LoD while reducing complexity. Such approaches typically exhibit a sequential dependency in the current LoD. To alleviate this issue, the authors propose to process the current LoD by slice. In this way, the probabilities can be estimated slice by slice instead of voxel per voxel. The resulting parallelization significantly reduces complexity while preserving most of the context in the current LoD.

3.1.3 Point-Based Approaches

Point-based approaches process the point cloud as a set of points instead of a binary occupancy signal over a voxel grid. Yan et al. (2019) proposed the use of a PointNet-like (Charles et al., 2017) autoencoder architecture for point cloud geometry compression. Wen et al. (2020) proposes a similar scheme improved with curvature-based adaptive octree partitioning and clustering. Gao et al. (2021) propose a more elaborate neural network architecture with a novel neural graph sampling module. Wiesmann et al. (2021) propose a point-based neural network for LiDAR point cloud compression. The authors propose a convolutional autoencoder architecture based on the KPConv (Thomas et al., 2019) and a novel deconvolution operator to compress point cloud geometry.

3.1.4 LiDAR Specific Approaches

With some sensors, the LiDAR point cloud frame is constructed from packets. A packet is arranged as 2D data with respect to the laser ID and emission. Tu et al. (2019a) exploit this 2D structure to compress point cloud geometry with a convolutional Long Short-Term Memory (LSTM) neural network (Hochreiter and Schmidhuber, 1997; Shi et al., 2015) and residual coding; this is an extension of Tu et al. (2017). Tu et al. (2019b) take inspiration from video coding and divide dynamic point cloud frames into I-frames and B-frames (ITU-T, 2019). The B-frames are predicted with U-net (Ronneberger et al., 2015) based flow computation and interpolation extending work in Tu et al. (2016).

Assuming that LiDAR point clouds can be represented as a 2D range image, Sun et al. (2020) also take inspiration from video coding and propose the use of a convolutional LSTM neural network to compress the range images.

3.2 Deep Learning Based Attribute Compression

One key difficulty for point cloud attribute compression is the irregularity of the geometry. Indeed, the geometry forms the support of the attributes. Hence, irregular geometry results in irregular neighborhoods which in turn make context modeling and prediction schemes difficult. Existing works attempt to resolve this irregularity by substituting the support.

First, it is possible to assume that the point cloud is a sampling of a 2D manifold and that it has a 2D parameterization that allows attributes to be projected onto a 2D image. This is similar to the concept of UV texture maps (Catmull, 1974) in Computer Graphics except that here we seek to recover such a parameterization from a point cloud. In this context, Quach et al. (2020a) propose a folding based approach for point cloud compression illustrated in Figure 7. FoldingNet (Yang et al., 2017) reconstructs a point cloud by folding a 2D plane using an autoencoder neural network. Building upon this, Quach et al. (2020a) parameterize a point cloud as a 2D manifold and project the attributes in 2D space. The attributes can then be compressed using any image compression method.

FIGURE 7

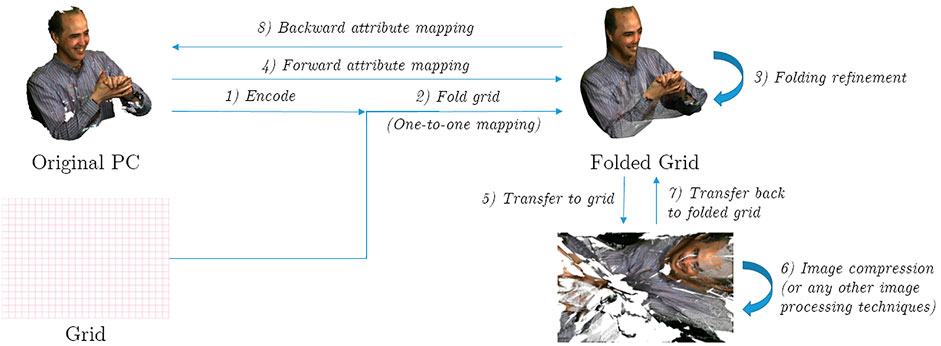
FIGURE 7. Folding-based attribute compression (Quach et al., 2020a). Attributes are transferred to a 2D grid using a neural network followed by image compression.

Alternatively, attributes can be directly mapped onto a voxel grid. Alexiou et al. (2020) extend convolutional neural networks used for geometry compression to attribute compression. Specifically, they propose joint compression of geometry and attributes defined on a voxel grid.

Another approach is to design neural networks that embrace this irregularity. This can be done with point-based neural networks and convolutions expressed directly on points (point convolutions). Sheng et al. (2021) propose a point-based neural network for point cloud attribute compression. In particular, they propose a second-order point convolution which improves upon the general point convolution. Biswas et al. (2020) also make use of point convolutions for inter-frame coding of intensities for intensity prediction in dynamic LiDAR point clouds.

Isik et al. (2021) compress point cloud attributes by representing them with volumetric functions. This is strongly related to Chou et al. (2020) where attributes are encoded using volumetric functions parameterized with a B-spline basis. In Isik et al. (2021), volumetric functions are parameterized with coordinate based networks instead and the latent vectors of a hierarchy of volumetric functions are compressed with RAHT.

Overall, existing works handle the irregularity of the support, the geometry, by mapping attributes onto a 2D plane, using CNNs to compress attributes on a voxel grid or using point convolutions to directly define convolutions on the points.

4 Discussion and Perspectives

4.1 Geometry Compression

In Table 1, we show an overview of geometry compression approaches for point clouds. Methods are divided into traditional and deep learning based. Different data structures employed for geometry compression: octree, surface models, sequence, graphs, voxel grids, range images etc.

TABLE 1

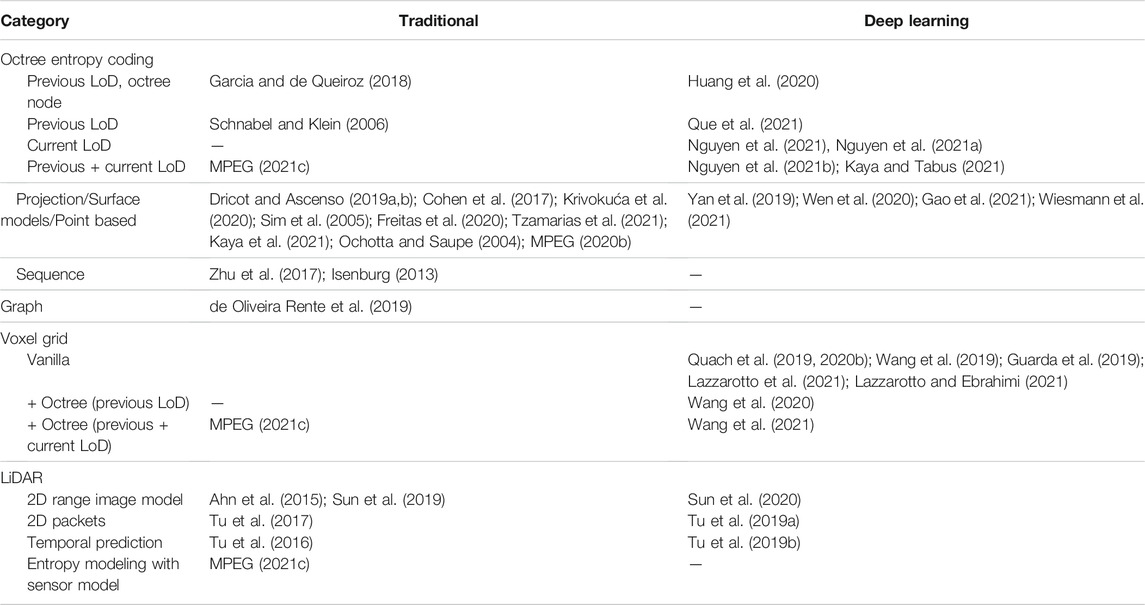
TABLE 1. Approaches to point cloud geometry compression divided into traditional and deep learning based methods.

For lossless octree coding, we can differentiate approaches depending on whether they exploit the previous LoD, the current LoD or both as a context. Using only the octree node information of the previous LoD presents a complexity advantage in that the information can be retrieved easily. Using the previous LoD (in a voxel grid sense) allows for parallel probability estimations on the current LoD that are more precise than when restrained to the octree node in the previous LoD. When employing the current LoD, a sequential constraint is necessary in that we can only use already decoded occupancies as a context. This results in a more precise entropy model at the cost of complexity. It is also possible to combine both the previous and the current LoD. The first advantage is that the previous LoD can provide coarse occupancy information for areas of the current LoD that are not yet decoded. The second advantage is that the sequential constraint can be loosened to form a hybrid approach that balances coding performance and complexity.

Projection and surface models transforms the data into another space which typically has a lower dimensionality or a different structure. Typical surface models include planes, triangles etc... Point based deep learning approaches can be thought of as projection based approaches in that the points are represented by a codeword in a latent space of lower dimensionality. The point cloud information is aggregated by a pooling operation which can be a max-pooling, an adaptive pooling operation or other types of pooling. Here, we refer to adaptive pooling as a pooling which aggregates information from points in a way that depends on the neighborhood structure. This is typical in point based convolution operators (Thomas et al., 2019).

Point clouds can also be compressed as a sequence of points. This can be interesting as it allows for formulating point cloud compression as a variant of the Traveling Salesman Problem (TSP) (Zhu et al., 2017). In addition, for LiDAR point clouds, a natural 1D structure exists and compression these points clouds as a sequence preserves this natural structure (Isenburg, 2013).

Voxel-based deep learning based methods are the most common approaches for geometry compression. Specifically, CNN autoencoders have been used to compress point cloud geometry as a binary signal over a regular voxel grid. We notice that an octree level can be represented by a voxel grid and that the two representations are interchangeable. In particular, the octree encodes binary voxel grids at multiple LoDs while eliminating sparsity of the binary signal and reducing the redundancy between LoDs; if the parent voxel is empty, all its children are empty and need not be encoded. In addition, block prediction and residual coding have also been explored using CNN architectures. In general, such networks predict a field of probabilities. Since the decoding is a classification problem (Quach et al., 2019), these approaches can be employed as both lossy (thresholding) and lossless (thresholding + residual or entropy coding) codecs.

The loss function is a crucial factor when training neural networks for geometry compression. While for lossless compression, the binary cross-entropy is suitable as it is directly related to the bitrate. For lossy compression, it is important that the loss function is suitable to the application. For example, loss functions correlated with perceived visual quality (Quach et al., 2021) would be relevant for applications with human visualisation. A limitation of current approaches is the use of simple loss functions such as the binary cross-entropy which may not adequately model perceived visual quality. An open question is how to best design such loss functions for the best rate-distortion performance.

de Oliveira Rente et al. (2019) codes geometry by starting from a low resolution point cloud, performing surface reconstruction on this low resolution point cloud and then coding a residual between this surface reconstruction and the original point cloud. As Lazzarotto and Ebrahimi (2021) has explored point cloud residual coding with neural networks, the intersection of deep learning based residual coding and surface reconstruction can be an interesting avenue of research.

LiDAR point clouds tend to have very specific structures that typically lie in one or two dimensions rather three dimensions. As such, specialized approaches have been developed to compress LiDAR point clouds. LiDAR point clouds can be compressed as 2D range images, as 2D LiDAR packets but also applying specific temporal prediction techniques such as SLAM or flow estimation. This is applicable both for learning-based (Tu et al., 2019b,a) and handcrafted methods (Tu et al., 2016, 2017).

4.1.1 Compression Performance

MPEG (2021d) performed a comparison in the performance of different state of the art point cloud compression approaches. Overall, CNN based approaches (Guarda et al., 2020a; Quach et al., 2020b; Nguyen et al., 2021a; Kaya and Tabus, 2021; Wang et al., 2021) outperform the G-PCC codec with the drawback of additional computational complexity. CNN based methods seem to perform better on denser point clouds. Indeed, a difference is observed between 10-bit dense (watertight) point clouds (longdress, redandblack, loot, soldier) from d’Eon et al. (2017) and sparser 12-bit point clouds (house without roof, statue klimt) which require downscaling the voxel grid in order to make the point cloud denser and obtain competitive compression performance. Also, CNN based methods using sparse convolution (Wang et al., 2021) achieve state of the art compression performance with lower computational complexity compared to dense convolutions. As described in (MPEG, 2021d), the runtime on GPU is faster to the G-PCC runtime on CPU. However, on a CPU it is still significantly slower (3.65 times slower for encoding and 37.1 times slower for decoding).

4.2 Attribute Compression

Traditional approaches handle the irregularity of the geometry by making use of the octree structure to build a multiscale decomposition of the attributes (de Queiroz and Chou, 2016). Also, we can build a graph and use the Graph Fourier Transforms (GFTs) or similar transforms to compress attributes (Zhang et al., 2014). In addition, attributes can be mapped onto a 2D grid and then compressed using image compression methods (Mekuria et al., 2017); and similarly, points can be ordered into a sequence and compressed as such (Gu et al., 2017). Another type of approach is to modelize the irregularity of the geometry with a virtual adaptive sampling process (Hou et al., 2017). Essentially, we modelize the attributes as a 3D field over a voxel grid and this field is sampled at occupied voxels.

4.2.1 3D Approaches

Deep learning based methods handle the irregularity of the geometry by using a 3D regular space (voxel grid) (Alexiou et al., 2020), by mapping attributes onto a 2D grid (Quach et al., 2020a) or with the use of point convolutions to define CNNs that operate directly on the points (Sheng et al., 2021). Note that such point convolutions can often be seen as graph convolutions with the topology of the graph built from the point cloud geometry and its neighborhood structure.

The essence of attribute compression is handling the irregularity of the geometry. One approach is to map attributes into n-dimensional regular grids where we usually have 1 ≤ n ≤ 3. In addition to this mapping, with the virtual adaptive sampling hypothesis, we can extrapolate attribute values to non-occupied voxels to simplify the problem to compression of a 3D regularly sampled field (instead of irregularly sampled). Another approach is to embrace the irregularity of the geometry and make use of the same octree structure that is commonly used for compression of the geometry.

In Table 2, we can see that deep learning based point cloud attribute compression is still relatively unexplored. Current deep learning based approaches are not competitive with G-PCC or V-PCC (MPEG, 2021c; 2020b). One of the key difficulties is how to handle the irregularity of the geometry and from Table 2 we can see a few interesting points.

TABLE 2

TABLE 2. Approaches to point cloud attribute compression divided into traditional and deep learning based methods.

Alexiou et al. (2020) has explored the use of CNNs on voxel grids for point cloud attribute compression. However, the combination between such approaches and the virtual adaptive sampling hypothesis explored in numerous works (Hou et al., 2017; Gu et al., 2020; Shen et al., 2020) for learning sparse dictionaries has not been explored. Indeed, we can interpret point cloud attributes as a color field defined everywhere on a voxel grid but only sampled at occupied locations. Then, these attributes could be compressed by first extrapolating the color field values everywhere on the voxel grid and compressing the resulting regularly sampled color field.

Octree-based approaches, such as the RAHT (de Queiroz and Chou, 2016), are an interesting basis for deep learning based approaches. Specifically, sparse convolutions (Choy et al., 2019) may be a possible avenue to express convolutions on an octree structure as is done for geometry compression in Wang et al. (2020). As there is a duality between octree and voxel grids, the same question about extrapolation applies. It is an open question whether good convolutional transforms can be learned to compress attributes that lie on an irregular geometry and thus have irregular neighborhoods. In addition, inspired by RAHT, Isik et al. (2021) propose a deep learning attribute compression approach based on volumetric functions parameterized by coordinate based neural networks. They adopt a hierarchical structure of latent vectors which are compressed with RAHT.

Compressing attributes as volumetric functions is similar in spirit to virtual adaptive sampling and extrapolation. All three of these approaches remove the irregularity by assuming that the attributes are samples of an attribute field defined over 3D space (a volumetric function) which can be seen as a virtual adaptive sampling process. In other words, this is also extrapolating missing values from the available samples. The final result is that the attributes are now defined over the entire 3D space removing the sparsity and irregularity which may arise from the geometry.

4.2.2 Dimensionality Reduction

Point cloud attribute compression is difficult due to the irregularity and sparsity of the support. It is possible to attenuate the irregularity with projections to lower dimensions which makes the support denser and more regular. In addition, techniques to remove the irregularity and sparsity in the 3D domain are actually applicable in all dimensions. This is interesting as point clouds are known to exhibit certain structures. For example, LiDAR point clouds have a 1D structure and most point clouds have a 2D manifold or surface structure.

Numerous approaches have explored the use of 2D images for point cloud attribute compression (Mekuria et al., 2017; Zhang et al., 2017; MPEG, 2020b). Specifically, Quach et al. (2020a) has explored a deep learning based approach for mapping attributes from each point to a 2D image using a FoldingNet (Yang et al., 2017). This presents the advantage of enabling the use of any image processing or image compression method. However, the complexity is high and the mapping can introduce distortion. Similar to 3D approaches, extrapolation for empty pixels in the image domain improves rate-distortion performance. Mekuria et al. (2017) has proposed a simple mapping procedure that makes use of Morton ordering and MPEG (2020b) a more advanced procedure that segments the point cloud according to their normals and performs bin packing to store them in a 2D image. To the best of our knowledge, the combination of such handcrafted mappings and deep learning based image compression methods (Ballé et al., 2017) has not been explored yet and may be promising.

Point cloud attributes can also be compressed as a sequence of points. This is especially suitable for spinning LiDAR point clouds which have a clear 1D structure. In Isenburg (2013), both LiDAR point cloud geometry and attributes such as reflectance are compressed as a sequence. Currently, while research is considering compression with 2D structures (Tu et al., 2019a), deep learning based approaches have not been explored for 1D structures yet.

Dimensionality reduction for point cloud attribute compression essentially exploits the spatial structure to alleviate irregularity and sparsity. How to find a new geometry (support) and a mapping from the original geometry to the new geometry that results in the best rate-distortion performance remains an open question. A limitation of existing approaches is that the new geometry and its mapping are fixed and not optimized for rate-distortion.

4.2.3 Graph Based Approaches

Graph based approaches have been used to compress point cloud attributes with the GFT (Zhang et al., 2014; Cohen et al., 2016; de Queiroz and Chou, 2017). Point based approaches can be considered as a special case of graph based approaches where the graph is defined by the point cloud geometry. In Sheng et al. (2021), point convolutions are proposed for the compression of attributes. Such convolutions have been shown to perform well for tasks such as classification and segmentation but the compression performance is currently lacking compared to traditional approaches such as the G-PCC implementation of RAHT (MPEG, 2021c). Point based neural networks are interesting as the complexity of these approaches depends on the number of points and not on the number of voxels. The drawback is that we are not working on a regular voxel grid anymore which makes the design of such networks more difficult. As such, a currently open question is how to build high performance point convolutional neural networks for attribute compression?

4.2.4 Compression Performance

Currently, deep learning based attribute compression approaches (Alexiou et al., 2020; Quach et al., 2020a; Isik et al., 2021; Sheng et al., 2021) are not yet competitive with the latest G-PCC codec. However, it is shown in Isik et al. (2021) and Sheng et al. (2021) that these approaches are actually competitive with RAHT which is used in G-PCC but improved with additional coding tools such as predictive RAHT, context adaptive arithmetic coding and joint entropy coding of color as discussed in Isik et al. (2021). In addition, Quach et al. (2020a) actually show performance close to earlier versions of G-PCC at the cost of high complexity which is also the case of Isik et al. (2021).

4.3 LoD Decomposition and Compression

For both geometry and attribute compression, it is interesting to consider the point cloud decomposed into multiple LoDs. Specifically, with LoDs based on octree decomposition, we can consider sparsity for a given LoD as the number of occupied voxels divided by the number of valid voxels at this LoD. Then, we can consider point clouds whose coarse LoDs are sparse as globally sparse: it can be the case in a point cloud composed of multiple objects. And we can consider point clouds whose finer LoDs are sparse as locally sparse: this typically happens in LiDAR point clouds or when the geometry resolution is too high compared to the number of points. This is important as certain methods are known to work better on dense point clouds (such as CNN based methods) than sparse ones.

In addition, decomposing the point cloud into multiple LoDs also allows us to mix differents compression methods. A common scheme is to perform block partitioning before applying compression methods that are more computationally expensive. This can be seen as compressing a set of block coordinates, which is by definition a point cloud, and then compressing a point cloud for each block. Such decompositions can be performed according to LoDs which makes it possible to code sparse LoDs separately (with different methods) from dense LoDs. A very common situation is that the first LoDs are dense and the last few LoDs are sparse; this typically happens when point cloud geometry is described with a precision that is high compared to the number of points or when the sampling is not uniform (such as with LiDAR point clouds).

An interesting property of such decompositions is that it is always possible to use a lossless geometry compression approach followed by a lossy one. For example, when using block partitioning, the compression of block coordinates can be performed with not only octree coding but any kind of lossless point cloud geometry compression method. This is particularly useful combined with the observation that point clouds can be sparse at different LoDs and that certain compression methods are known to work better with certain densities. Considering a LoD-based point decomposition, it is thus interesting to consider compression schemes that select the most suitable compression method for each LoD based on their density. In addition, the geometric distortion introduced by such lossless-lossy schemes is bounded by the volume of losslessly coded voxels.

At a given LoD, the relation between compression algorithm, point cloud characteristics at a given LoD and compression performance remains an open question. How to best select and combine compression algorithms to adapt to different point cloud characteristics is also mostly unexplored. A limitation of the current state of the art is that algorithms tend to be specialized or manually tuned towards specific characteristics: dense, sparse, spinning LiDAR, etc.

4.4 Joint Compression of Geometry and Attributes in Relation With Rendering

We provide a general overview of the surrounding of point cloud compression in Figure 8. We define the notion of 3D scene in a general manner as including real world 3D scenes, meshes, voxels etc. A 3D scene can be modelled (or acquired, sampled...) into a point cloud and prior to rendering, point clouds must be interpreted as they are only sets of coordinates. Common interpretations of a point include screen-aligned squares with a given window-space size (“point” primitive), cubes, spheres etc. In addition, surface reconstruction can also be performed to build a mesh from a point cloud. Note that point clouds are only one way to compress 3D scenes and their visualizations.

FIGURE 8

FIGURE 8. 3D scenes (real world, mesh, point clouds, voxels) can be compressed with point clouds. Depending on the context, different types of distortion may be evaluated: point cloud distortion, 3D scene distortion (e.g. mesh distortion) or visualization distortion. For visualization distortion, rendering is especially important and may be optimized as aprt of the point cloud codec.

As shown in Figure 2, separating geometry and attributes compression simplifies point cloud compression by dividing it into two independent components. However, jointly compressing both geometry and attributes may be important when considering the problem more globally as illustrated in Figure 8. Indeed, for numerous applications (visualization, machine vision) geometry and attributes may impact performance in an interdependent manner. In Computer Graphics, the well-known bump mapping technique simulates wrinkled surfaces with a simplified geometry by adding perturbations to the attributes (Blinn, 1978). In the case of meshes, perturbations are added to the surface normals which results in an apparently wrinkled surface due to lighting calculations. For point clouds, the same could be achieved by perturbating the point colors.

As a result, an open research question is how to design compression techniques that compress point cloud geometry and attributes while maximizing perceived visual quality subject to a rate constraint? This differs from existing approaches, which take geometry and attributes into account separately and evaluate their quality separately.

4.5 LoD Decomposition and Rendering: Points and Voxels

We have previously treated the topic of rendering and its importance to point cloud compression and quality assessment. Also, we have analyzed the topic of point cloud compression with approaches based on LoD decompositions. Decompositions can be interpreted in two manners: point based or volumetric.

In a point based view, the decomposition can be interpreted as as decomposing the point coordinates. With an octree decomposition, we decompose the coordinates in base two; then, the octree can be interpreted as a prefix tree (Briandais, 1959) on the Morton codes (Morton, 1966) of the coordinates.

On the other hand, we can interpret this decomposition in a volumetric manner. A voxel is occupied if it contains at least one point within its volume; otherwise, it is empty. When the point cloud is represented at a lower LoD, the voxels become larger. With a point based interpretation, a problem of octree based compression is that the point cloud becomes sparser at lower LoDs. The volumetric interpretation offers an alternative in that the geometry becomes coarser at lower LoDs but not sparser. As a result, octree based compression with a volumetric interpretation does not result in sparse renderings. A possible implementation is to render each voxel as a cube of corresponding volume.

Such coarse but dense geometry for point cloud compression is interesting as the bounded geometric error allows preservation of watertightness which is beneficial for rendering quality. How to best exploit such characteristics of compression algorithms for rendering remains an open question and is currently unexplored in the literature.

4.6 Sparsity for Geometry Compression

One of the key problems with point cloud compression is sparsity. Sparsity can be defined as the ratio between the number of captured points and the number of voxels which is directly related to the geometry precision, also defined as geometry bitdepth. The capturing process is the main driver behind sparsity: point clouds captured with camera arrays are typically dense because the sampling density is spatially uniform. On the other hand, LiDAR point clouds have non-uniform density: denser near the sensor and sparser far from the sensor. However, they exhibit near uniform density in the spherical coordinate system which explains non-uniformity in the 3D space.

In such point clouds, the number of points can be low compared to the precision of the point coordinates. To obtain a dense point cloud, it is necessary to use a geometry precision that is suitable to the number of captured points. This is an important consideration as some compression methods may perform better at some density/sparsity levels. For example, deep learning based convolutional geometry compression approaches tend to perform better on dense point clouds.

Decomposing point clouds into LoDs is also useful to analyze point cloud sparsity. In particular, the location of sparse LoDs is important to differentiate global from local sparsity. Global sparsity is typically handled by performing block partitioning which removes global sparsity by focusing compression algorithms onto occupied blocks. Handling local sparsity is currently an open problem. One approach is to remove local sparsity by removing the sparse local LoDs resulting in a dense point cloud which is easier to compress. Another approach is to compress these sparse LoDs separately by first using a lossless compression methods on the first LoDs and another compression method suitable for sparse point clouds on the later LoDs.

Also, we have observed that on local sparse LoDs, existing methods are not able to exceed 2 dB per bit per input point per LoD (D1 PSNR) which is equivalent to the RD performance of a scalar quantizer. This suggests that sparse local LoDs may not be compressible beyond this limit in some cases. Whether these local sparse LoDs are akin to acquisition noise and are not compressible beyond this limit remains an open question. If this is true, compressing dense LoDs and these sparse LoDs separately may be essential to sparse point cloud compression.

4.7 Point Cloud Quality Assessment

Commonly used distortion measures include the point-to-point (D1), the point-to-plane metric (D2) and other metrics based on nearest neighbors (MPEG, 2020a). These distortion metrics may not be suitable for all applications such as LiDAR point clouds for autonomous driving which may require application-specific distortion metrics. For instance, Feng et al. (2020) evaluate the performance of their LiDAR point cloud compression method with registration translation error, object detection accuracy and segmentation error. Such metrics may be more relevant than generic metrics as these are common operations on such point clouds.

In addition, interpreting LiDAR point clouds in a volumetric manner could potentially improve safety. Indeed, with volumetric octree compression point clouds could be compressed with only false positives. This could be useful for collision avoidance in the context of autonomous driving. As a result, a distorted point cloud with distance-bounded distortion and only false positives could actually improve collision avoidance. However, if such a distortion is too severe, an autonomous vehicle could fail to find a valid route to its destination by overestimating the size of obstacles.

Another related factor is the accuracy and the precision of the LiDAR sensor. When considering LiDAR point clouds in a voxelized manner, we may want to consider a certain space around each occupied voxel as occupied to account for sensor uncertainty. This may be interesting for collision avoidance as marking a safety margin as occupied would also make the point cloud denser and thus easier to compress. Overall, how to design an objective metric that correlates best with autonomous driving performance remains an open question.

Furthermore, deep learning based point cloud quality assessment approaches are being explored (Chetouani et al., 2021a,b; Liu et al., 2020). We note that it presents the same challenges as geometry and attribute compression simultaneously. We consider the following open question: how to design an objective metric that correlates best with perceived visual quality? We notice that rendering must be considered as the point cloud cannot be viewed otherwise. Generally, it is important to consider what is the distortion of interest: point cloud distortion, 3D scene distortion, or distortion of the 3D scene visualization (Figure 8)?

4.8 Relation to Mesh Compression

Meshes can be constructed from point clouds using Poisson surface reconstruction (Kazhdan et al., 2006) and point clouds can be sampled from meshes. Surfaces can be represented explicitly with polygons but also implicitly as Truncated Signed Distance Functions (TSDFs). As such, meshes can be compressed under a TSDF representation and deep learning based convolutional compression techniques for point clouds (Quach et al., 2019) and for meshes (Tang et al., 2020) are strongly related. The key difference lies in the signal representation which can be binary (point clouds) or a distance field (point cloud or surface). Surface reconstruction from TSDFs can be performed with methods such as Marching Cubes Lorensen and Cline (1987). It remains an open question how exchange of ideas between techniques of point cloud and mesh compression could further progress in both fields.

5 Conclusion

Point clouds are increasingly common, with numerous applications and the large amounts of data are a challenge for transmission and storage. Compression is thus crucial but also complex as point cloud compression lies at the intersection of signal processing, data compression, computer graphics and even deep learning for state of the art approaches. The signal characteristics make point cloud compression significantly different from traditionally compressed media such as images and video. Indeed, the geometry can be seen as a sparse binary signal on a voxel grid or as a set of points and the attributes then lie on this sparse, irregular geometry posing challenges for point cloud compression.

In recent works, deep learning based approaches have exhibited outstanding performance on geometry compression and have become comparable to state of the art approaches on attribute compression. However, many challenges remain and exchange of ideas between traditional and deep learning based methods have led to fast progress in the field. In this work, we put a focus on deep learning approaches and highlight their relation to traditional methods. Specifically, we highlight different categories of geometry and attribute compression approaches with relations between deep learning and traditional approaches. We discuss the importance of LoD decomposition for compression, the limitation of separating geometry and attribute compression and the importance of rendering in the context of compression. Then, we discuss the specific challenges posed by sparsity for geometry compression, the importance of point cloud quality assessment and how its challenges mirror those of compression. Finally, we discuss how point cloud compression relates to mesh compression and point out their intersection.

We note that approaches for compressing point cloud geometry have improved significantly by exploiting the duality between octree and voxel grid and the LoD decomposition resulting from octrees. Currently, deep learning approaches using sparse convolutions offer state of the art performance and competitive complexity (with GPU) compared to G-PCC (with CPU). However, the characteristics of point cloud geometry can vary significantly resulting in numerous parameters that need to be tuned for a codec to work uniformly well across various point clouds. We believe that geometry compression approaches need to combine both hand-crafted and learning based approaches in order to achieve compression performance, reasonable complexity and adaptability to different point cloud characteristics (e.g. density).

In comparison, learning based attribute compression approaches has been the subject of less research compared to geometry compression. Current learning based approaches struggle to compete the state of the art and often come at high complexity cost. We believe that research into the different methods to construct regular or almost regular neighborhoods for the attributes is essential for learning based attribute compression. For example, using an octree provides a hierarchical regular neighborhood (one parent for each octree node) and mapping the attributes to 2D grid can provide an almost regular neighborhood. The attributes are spatially correlated and this can be verified visually. As such, a key question is how can learning based approaches best exploit this spatial correlation for compression? Using which representation?

Author Contributions

The Author Contributions section is mandatory for all articles, including articles by sole authors. If an appropriate statement is not provided on submission, a standard one will be inserted during the production process. The Author Contributions statement must describe the contributions of individual authors referred to by their initials and, in doing so, all authors agree to be accountable for the content of the work. Please see here for full authorship criteria.

Funding

This work was funded by the ANR ReVeRy national fund (REVERY ANR-17-CE23-0020).

Conflict of Interest

Authors JP and DT were employed by the company InterDigital.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahn, J., Lee, K., Sim, J., and Kim, C. (2015). Large-Scale 3D Point Cloud Compression Using Adaptive Radial Distance Prediction in Hybrid Coordinate Domains. IEEE J. Sel. Top. Signal. Process. 9, 422–434. doi:10.1109/JSTSP.2014.2370752

Akhtar, A., Gao, W., Zhang, X., Li, L., Li, Z., and Liu, S. (2020). “Point Cloud Geometry Prediction Across Spatial Scale Using Deep Learning,” in 2020 IEEE International Conference on Visual Communications and Image Processing (VCIP) (IEEE), 70–73. doi:10.1109/VCIP49819.2020.9301804

Alexiou, E., Tung, K., and Ebrahimi, T. (2020). “Towards Neural Network Approaches for Point Cloud Compression,” in Applications of Digital Image Processing XLIII (International Society for Optics and Photonics), 1151008. doi:10.1117/12.2569115

ASPRS (2019). LAS Specification, Version 1.4 – R15. American Society for Photogrammetry & Remote Sensing.

Ballé, J., Laparra, V., and Simoncelli, E. P. (2017). “End-to-end Optimized Image Compression,” in 2017 5th International Conference on Learning Representations (ICLR) (IEEE).

Bartell, F. O., Dereniak, E. L., and Wolfe, W. L. (1981). “The Theory and Measurement of Bidirectional Reflectance Distribution Function (Brdf) and Bidirectional Transmittance Distribution Function (BTDF),” in Radiation Scattering in Optical Systems (Huntsville, United States: SPIE), 154–160. doi:10.1117/12.959611

Besl, P. J. (1989). “Active Optical Range Imaging Sensors,” in Advances in Machine Vision. Editor J. L. C. Sanz (New York, NY: Springer Series in Perception Engineering), 1–63. doi:10.1007/978-1-4612-4532-2_1

Biswas, S., Liu, J., Wong, K., Wang, S., and Urtasun, R. (2020). MuSCLE: Multi Sweep Compression of LiDAR Using Deep Entropy Models. Adv. Neural Inf. Process. Syst. 33, 1.

Blinn, J. F. (1978). “Simulation of Wrinkled Surfaces,” in Proceedings of the 5th Annual Conference on Computer Graphics and Interactive Techniques (New York, NY: Association for Computing Machinery), 286–292. doi:10.1145/800248.507101

Briandais, R. D. L. (1959). “File Searching Using Variable Length Keys,” in IRE-AIEE-ACM Computer Conference (San Francisco, California, United States: ACM). doi:10.1145/1457838.1457895

Bruder, G., Steinicke, F., and Nüchter, A. (2014). “Poster: Immersive point Cloud Virtual Environments,” in 2014 IEEE Symposium on 3D User Interfaces (3DUI) (IEEE), 161–162. doi:10.1109/3DUI.2014.6798870

Cao, C., Preda, M., and Zaharia, T. (2019). “3D Point Cloud Compression,” in The 24th International Conference on 3D Web Technology (UCLA, CA: ACM), 1–9. doi:10.1145/3329714.3338130

Cao, C., Preda, M., Zakharchenko, V., Jang, E. S., and Zaharia, T. (2021). Compression of Sparse and Dense Dynamic Point Clouds-Methods and Standards. Proc. IEEE 109, 1537–1558. doi:10.1109/JPROC.2021.3085957

Catmull, E. E. (1974). A Subdivision Algorithm for Computer Display of Curved Surfaces. Salt Lake City, United States: Ph.D. thesis, The University of Utah.

Charles, R. Q., Su, H., Kaichun, M., and Guibas, L. J. (2017). “PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (IEEE), 77–85. doi:10.1109/CVPR.2017.16

Chenxi Tu, C., Takeuchi, E., Miyajima, C., and Takeda, K. (2016). “Compressing Continuous Point Cloud Data Using Image Compression Methods,” in 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC) (IEEE), 1712–1719. doi:10.1109/ITSC.2016.7795789

Chetouani, A., Quach, M., Valenzise, G., and Dufaux, F. (2021a). “Convolutional Neural Network for 3D Point Cloud Quality Assessment with Reference,” in IEEE International Workshop on Multimedia Signal Processing (MMSP’2021) (IEEE).

Chetouani, A., Quach, M., Valenzise, G., and Dufaux, F. (2021b). “Deep Learning-Based Quality Assessment of 3d Point Clouds Without Reference,” in 2021 IEEE International Conference on Multimedia Expo Workshops (ICMEW) (IEEE), 1–6. doi:10.1109/ICMEW53276.2021.9455967

Chou, P. A., Koroteev, M., and Krivokuca, M. (2020). A Volumetric Approach to Point Cloud Compression-Part I: Attribute Compression. IEEE Trans. Image Process. 29, 2203–2216. doi:10.1109/TIP.2019.2908095

Choy, C., Gwak, J., and Savarese, S. (2019). “4D Spatio-Temporal ConvNets: Minkowski Convolutional Neural Networks,” in 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (Long Beach, CA: IEEE), 3070–3079. doi:10.1109/CVPR.2019.00319

Cohen, R. A., Krivokuca, M., Feng, C., Taguchi, Y., Ochimizu, H., Tian, D., et al. (2017). “Compression of 3-D point Clouds Using Hierarchical Patch Fitting,” in 2017 IEEE International Conference on Image Processing (ICIP) (IEEE), 4033–4037. doi:10.1109/ICIP.2017.8297040

Cohen, R. A., Tian, D., and Vetro, A. (2016). “Attribute Compression for Sparse Point Clouds Using Graph Transforms,” in 2016 IEEE International Conference on Image Processing (ICIP) (IEEE), 1374–1378. doi:10.1109/ICIP.2016.7532583

Curless, B., and Levoy, M. (1996). “A Volumetric Method for Building Complex Models from Range Images,” in Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques - SIGGRAPH ’96 (New Orleans, LA, United States: ACM Press), 303–312. doi:10.1145/237170.237269

de Oliveira Rente, P., Brites, C., Ascenso, J., and Pereira, F. (2019). Graph-Based Static 3D Point Clouds Geometry Coding. IEEE Trans. Multimedia 21, 284–299. doi:10.1109/TMM.2018.2859591

de Queiroz, R. L., and Chou, P. A. (2016). Compression of 3D Point Clouds Using a Region-Adaptive Hierarchical Transform. IEEE Trans. Image Process. 25, 3947–3956. doi:10.1109/TIP.2016.2575005

de Queiroz, R. L., and Chou, P. A. (2017). Transform Coding for Point Clouds Using a Gaussian Process Model. IEEE Trans. Image Process. 26, 3507–3517. doi:10.1109/TIP.2017.2699922

de Queiroz, R. L., Dorea, C., Freitas, D. R., Krivokuca, M., and Sandri, G. P. (2021). Model-Centric Volumetric Point Cloud Attributes. arXiv [Preprint]. Available at: https://arxiv.org/abs/2106.15539.

de Queiroz, R., Souto, A., Figueiredo, V., and Chou, P. (2021). Set Partitioning in Hierarchical Trees for Point Cloud Attribute Compression. doi:10.36227/techrxiv.15032901.v1

d’Eon, E., Harrison, B., Myers, T., and Chou, P. A. (2017). “8i Voxelized Full Bodies - A Voxelized Point Cloud Dataset,” in ISO/IEC JTC1/SC29 Joint WG11/WG1 (MPEG/JPEG) Input Document WG11M40059/WG1M74006 (Geneva: ISO).

Dricot, A., and Ascenso, J. (2019a). “Adaptive Multi-Level Triangle Soup for Geometry-Based Point Cloud Coding,” in 2019 IEEE 21st International Workshop on Multimedia Signal Processing (MMSP) (IEEE), 1–6. doi:10.1109/MMSP.2019.8901791

Dricot, A., and Ascenso, J. (2019b). “Hybrid Octree-Plane Point Cloud Geometry Coding,” in 2019 27th European Signal Processing Conference (EUSIPCO), 1–5. doi:10.23919/EUSIPCO.2019.8902800

Feng, Y., Liu, S., and Zhu, Y. (2020). Real-Time Spatio-Temporal LiDAR Point Cloud Compression. arXiv [Preprint]. Available at: https://arxiv.org/abs/2008.06972.

Freitas, D. R., Peixoto, E., de Queiroz, R. L., and Medeiros, E. (2020). “Lossy Point Cloud Geometry Compression via Dyadic Decomposition,” in 2020 IEEE International Conference on Image Processing (ICIP) (IEEE), 2731–2735. doi:10.1109/icip40778.2020.9190910

Fukuda, T. (2018). “Point Cloud Stream on Spatial Mixed Reality - toward Telepresence in Architectural Field,” in Computing for a Better Tomorrow - Proceedings of the 36th eCAADe Conference - Volume 2. Editors A. Kepczynska-Walczak, and S. Bialkowski (Lodz, Poland: Lodz University of Technology), 727–734.

Gao, L., Fan, T., Wan, J., Xu, Y., Sun, J., and Ma, Z. (2021). “Point Cloud Geometry Compression via Neural Graph Sampling,” in 2021 IEEE International Conference on Image Processing (ICIP) (IEEE), 3373–3377. doi:10.1109/ICIP42928.2021.9506631

Garcia, D. C., and de Queiroz, R. L. (2018). “Intra-Frame Context-Based Octree Coding for Point-Cloud Geometry,” in 2018 25th IEEE International Conference on Image Processing (ICIP) (IEEE), 1807–1811. doi:10.1109/ICIP.2018.8451802

Goyer, G. G., and Watson, R. (1963). The Laser and its Application to Meteorology. Bull. Am. Meteorol. Soc. 44, 564–570. doi:10.1175/1520-0477-44.9.564

Graziosi, D., Nakagami, O., Kuma, S., Zaghetto, A., Suzuki, T., and Tabatabai, A. (2020). An Overview of Ongoing point Cloud Compression Standardization Activities: Video-Based (V-PCC) and Geometry-Based (G-PCC). Sip 9, 1. doi:10.1017/ATSIP.2020.12

Greenberg, D. P. (1999). A Framework for Realistic Image Synthesis. Commun. ACM 42, 44–53. doi:10.1145/310930.310970

GTI-UPM (2016). JPEG Pleno Database: GTI-UPM Point-cloud Data Set. Available at: http://plenodb.jpeg.org/pc/upm.

Gu, S., Hou, J., Zeng, H., Chen, J., Zhu, J., and Ma, K.-K. (2017). “Compression of 3D point Clouds Using 1D Discrete Cosine Transform,” in 2017 International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS) (IEEE), 196–200. doi:10.1109/ISPACS.2017.8266472

Gu, S., Hou, J., Zeng, H., Yuan, H., and Ma, K.-K. (2020). 3D Point Cloud Attribute Compression Using Geometry-Guided Sparse Representation. IEEE Trans. Image Process. 29, 796–808. doi:10.1109/TIP.2019.2936738

Guarda, A. F. R., Rodrigues, N. M. M., and Pereira, F. (2021a). Adaptive Deep Learning-Based Point Cloud Geometry Coding. IEEE J. Sel. Top. Signal. Process. 15, 415–430. doi:10.1109/JSTSP.2020.3047520

Guarda, A. F. R., Rodrigues, N. M. M., and Pereira, F. (2020c). “Deep Learning-Based Point Cloud Geometry Coding: RD Control through Implicit and Explicit Quantization,” in 2020 IEEE International Conference on Multimedia Expo Workshops (ICMEW) (IEEE), 1–6. doi:10.1109/ICMEW46912.2020.9106022

Guarda, A. F. R., Rodrigues, N. M. M., and Pereira, F. (2021b). Neighborhood Adaptive Loss Function for Deep Learning-Based Point Cloud Coding with Implicit and Explicit Quantization. IEEE MultiMedia 28, 107–116. doi:10.1109/MMUL.2020.3046691

Guarda, A. F. R., Rodrigues, N. M. M., and Pereira, F. (2019). “Point Cloud Coding: Adopting a Deep Learning-Based Approach,” in 2019 Picture Coding Symposium (PCS) (IEEE), 1–5. doi:10.1109/PCS48520.2019.8954537

He, Y., Li, G., Shao, Y., Wang, J., Chen, Y., and Liu, S. (2020). “A point Cloud Compression Framework via Spherical Projection,” in 2020 IEEE International Conference on Visual Communications and Image Processing (VCIP) (IEEE), 62–65. doi:10.1109/VCIP49819.2020.9301809

Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735

Hou, J., Chau, L.-P., He, Y., and Chou, P. A. (2017). “Sparse Representation for Colors of 3D point Cloud via Virtual Adaptive Sampling,” in 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (IEEE), 2926–2930. doi:10.1109/ICASSP.2017.7952692

Houshiar, H., and Nüchter, A. (2015). “3D point Cloud Compression Using Conventional Image Compression for Efficient Data Transmission,” in 2015 XXV International Conference on Information, Communication and Automation Technologies (ICAT) (IEEE), 1–8. doi:10.1109/ICAT.2015.7340499

Huang, L., Wang, S., Wong, K., Liu, J., and Urtasun, R. (2020). “OctSqueeze: Octree-Structured Entropy Model for LiDAR Compression,” in 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (IEEE), 1310–1320. doi:10.1109/CVPR42600.2020.00139

Isenburg, M. (2013). LASzip. Photogramm Eng. Remote Sensing 79, 209–217. doi:10.14358/pers.79.2.209

Isik, B., Chou, P. A., Hwang, S. J., Johnston, N., and Toderici, G. (2021). LVAC: Learned Volumetric Attribute Compression for Point Clouds Using Coordinate Based Networks. arXiv [Preprint]. Available at: https://arxiv.org/abs/2111.08988.

ITU-T (2019). ITU-T Recommendation H.265. High efficiency video coding (HEVC).

Jae-Young Sim, J.-Y., Chang-Su Kim, C.-S., and Sang-Uk Lee, S.-U. (2005). Lossless Compression of 3-D point Data in QSplat Representation. IEEE Trans. Multimedia 7, 1191–1195. doi:10.1109/TMM.2005.858410

Jiang, W., Tian, J., Cai, K., Zhang, F., and Luo, T. (2012). “Tangent-plane-continuity Maximization Based 3D point Compression,” in 2012 19th IEEE International Conference on Image Processing (IEEE), 1277–1280. doi:10.1109/ICIP.2012.6467100

JPEG (2020). “Final Call for Evidence on JPEG Pleno Point Cloud Coding,” in ISO/IEC JTC1/SC29/WG1 JPEG Output Document N88014 (ISO).

Kaya, E. C., Schwarz, S., and Tabus, I. (2021). Refining the Bounding Volumes for Lossless Compression of Voxelized point Clouds Geometry. arXiv [Preprint]. Available at: https://arxiv.org/abs/2106.00828.

Kaya, E. C., and Tabus, I. (2021). Neural Network Modeling of Probabilities for Coding the Octree Representation of Point Clouds. arXiv [Preprint]. Available at: https://arxiv.org/abs/2106.06482.

Kazhdan, M., Bolitho, M., and Hoppe, H. (2006). “Poisson Surface Reconstruction,” in Proceedings of the Fourth Eurographics Symposium on Geometry Processing (Goslar, Germany: Eurographics Association), 61–70.

Killea, R., Li, Y., Bastani, S., and McLachlan, P. (2021). DeepCompress: Efficient Point Cloud Geometry Compression. arXiv [Preprint]. Available at: https://arxiv.org/abs/2106.01504.

Krivokuca, M., Chou, P. A., and Koroteev, M. (2020). A Volumetric Approach to Point Cloud Compression-Part II: Geometry Compression. IEEE Trans. Image Process. 29, 2217–2229. doi:10.1109/TIP.2019.2957853

Krivokuća, M., and Guillemot, C. (2020). “Colour Compression of Plenoptic point Clouds Using Raht-Klt with Prior Colour Clustering and Specular/diffuse Component Separation,” in IEEE International Conference on Acoustics, Speech, and Signal Processing (IEEE). doi:10.1109/icassp40776.2020.9053862

Krivokuca, M., Miandji, E., Guillemot, C., and Chou, P. (2021). Compression of Plenoptic Point Cloud Attributes Using 6-D Point Clouds and 6-D Transforms. IEEE Trans. Multimedia 1, 1. doi:10.1109/TMM.2021.3129341

Landy, M., and Movshon, J. A. (1991). “The Plenoptic Function and the Elements of Early Vision,” in Computational Models of Visual Processing (MIT Press), 3–20.

Lazzarotto, D., Alexiou, E., and Ebrahimi, T. (2021). “On Block Prediction for Learning-Based Point Cloud Compression,” in 2021 IEEE International Conference on Image Processing (ICIP) (IEEE), 3378–3382. doi:10.1109/ICIP42928.2021.9506429

Lazzarotto, D., and Ebrahimi, T. (2021). “Learning Residual Coding for point Clouds,” in Applications of Digital Image Processing XLIV (San Diego, California, United States: International Society for Optics and Photonics), 118420S. doi:10.1117/12.2597814

Li, L., Li, Z., Liu, S., and Li, H. (2021). Occupancy-Map-Based Rate Distortion Optimization and Partition for Video-Based Point Cloud Compression. IEEE Trans. Circuits Syst. Video Technol. 31, 326–338. doi:10.1109/TCSVT.2020.2966118

Li, Y., and Ibanez-Guzman, J. (2020). Lidar for Autonomous Driving: The Principles, Challenges, and Trends for Automotive Lidar and Perception Systems. IEEE Signal. Process. Mag. 37, 50–61. doi:10.1109/MSP.2020.2973615

Lin, T.-Y., Goyal, P., Girshick, R., He, K., and Dollár, P. (2017). “Focal Loss for Dense Object Detection,” in 2017 IEEE International Conference on Computer Vision (ICCV) (IEEE), 2999–3007. doi:10.1109/ICCV.2017.324

Liu, Y., Yang, Q., Xu, Y., and Yang, L. (2020). Point Cloud Quality Assessment: Large-Scale Dataset Construction and Learning-Based No-Reference Approach. arXiv [Preprint]. Available at: https://arxiv.org/abs/2012.11895.

Loop, C., Cai, Q., Escolano, S. O., and Chou, P. A. (2016). “Microsoft Voxelized Upper Bodies - A Voxelized point Cloud Dataset,” in ISO/IEC JTC1/SC29 Joint WG11/WG1 (MPEG/JPEG) Input Document m38673/M72012 (Geneva, Switzerland: ISO).

Lorensen, W. E., and Cline, H. E. (1987). Marching Cubes: A High Resolution 3D Surface Construction Algorithm. SIGGRAPH Comput. Graph. 21, 163–169. doi:10.1145/37402.37422

Mekuria, R., Blom, K., and Cesar, P. (2017). Design, Implementation, and Evaluation of a Point Cloud Codec for Tele-Immersive Video. IEEE Trans. Circuits Syst. Video Technol. 27, 828–842. doi:10.1109/tcsvt.2016.2543039

Morton, G. M. (1966). A Computer Oriented Geodetic Data Base and a New Technique in File Sequencing. Springer.

MPEG (2020a). “Common Test Conditions for PCC,” in ISO/IEC JTC1/SC29/WG11 MPEG Output Document N19324 (Alpbach, Austria: ISO).

MPEG (2021a). “Description of Exploration Experiment 13.2 on Inter Prediction,” in ISO/IEC JTC 1/SC 29/WG 7 MPEG Output Document N0155 (ISO).

MPEG (2021b). “EE 13.53 Low Latency Low Complexity LIDAR Codec (LL-LC²),” in ISO/IEC JTC 1/SC 29/WG 7 MPEG Output Document N0165 (ISO).

MPEG (2021c). “G-PCC Codec Description V12,” in ISO/IEC JTC 1/SC 29/WG 7 MPEG Output Document N00151 (ISO).

MPEG (2021d). “Performance Analysis of Currently AI-Based Available Solutions for PCC,” in ISO/IEC JTC 1/SC 29/WG 7 MPEG Output Document N00233 (ISO).

MPEG (2020b). “V-PCC Codec Description,” in ISO/IEC JTC 1/SC 29/WG 7 MPEG Output Document N00100 (ISO).

Nguyen, D. T., Quach, M., Valenzise, G., and Duhamel, P. (2021). "Learning-based Lossless Compression of 3D point Cloud Geometry," in ICASSP 2021 - 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, Ontario, Canada, 4220–4224. doi:10.1109/ICASSP39728.2021.9414763

Nguyen, D. T., Quach, M., Valenzise, G., and Duhamel, P. (2021a). Lossless Coding of Point Cloud Geometry Using a Deep Generative Model. ICASSP IEEE Int. Conf. Acoust. Speech Signal Process. 31 (12), 4617–4629. doi:10.1109/TCSVT.2021.3100279

Nguyen, D. T., Quach, M., Valenzise, G., and Duhamel, P. (2021b). Multiscale Deep Context Modeling for Lossless point Cloud Geometry Compression. IEEE Int. Conf. Multimed. Expo Workshops 2021, 1–6. doi:10.1109/ICMEW53276.2021.9455990

Ochotta, T., and Saupe, D. (2004). Compression of Point-Based 3D Models by Shape-Adaptive Wavelet Coding of Multi-Height Fields. Zurich, Switzerland: The Eurographics Association. doi:10.2312/SPBG/SPBG04/103-112

Pacala, A. (2018). Lidar as a Camera - Digital Lidar’s Implications for Computer Vision. Available at: https://ouster.com/blog/the-camera-is-in-the-lidar.

Pereira, F., Dricot, A., Ascenso, J., and Brites, C. (2020). Point Cloud Coding: A Privileged View Driven by a Classification Taxonomy. Signal. Processing: Image Commun. 85, 115862. doi:10.1016/j.image.2020.115862

Quach, M., Chetouani, A., Valenzise, G., and Dufaux, F. (2021). A Deep Perceptual Metric for 3D point Clouds. Electron. Imaging 2021 (9), 257-1.

Quach, M., Valenzise, G., and Dufaux, F. (2020a). “Folding-Based Compression of Point Cloud Attributes,” in 2020 IEEE International Conference on Image Processing (ICIP) (IEEE), 3309–3313. doi:10.1109/ICIP40778.2020.9191180

Quach, M., Valenzise, G., and Dufaux, F. (2020b). “Improved Deep Point Cloud Geometry Compression,” in 2020 IEEE 22nd International Workshop on Multimedia Signal Processing (MMSP) (IEEE), 1–6. doi:10.1109/MMSP48831.2020.9287077

Quach, M., Valenzise, G., and Dufaux, F. (2019). “Learning Convolutional Transforms for Lossy Point Cloud Geometry Compression,” in 2019 IEEE International Conference on Image Processing (ICCIP) (IEEE), 4320–4324. doi:10.1109/ICIP.2019.8803413

Que, Z., Lu, G., and Xu, D. (2021). VoxelContext-Net: An Octree Based Framework for Point Cloud Compression. arXiv [Preprint]. Available at: https://arxiv.org/abs/2105.02158.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net: Convolutional Networks for Biomedical Image Segmentation. arXiv [Preprint]. Available at: https://arxiv.org/abs/1505.04597.

Said, A., and Pearlman, W. A. (1996). A New, Fast, and Efficient Image Codec Based on Set Partitioning in Hierarchical Trees. IEEE Trans. Circuits Syst. Video Technol. 6, 243–250. doi:10.1109/76.499834

Sandri, G., de Queiroz, R. L., and Chou, P. A. (2018). Comments on ”Compression of 3D Point Clouds Using a Region-Adaptive Hierarchical Transform”. arXiv [Preprint]. Available at: https://arxiv.org/abs/1805.09146.

Sandri, G., de Queiroz, R. L., and Chou, P. A. (2019). Compression of Plenoptic Point Clouds. IEEE Trans. Image Process. 28, 1419–1427. doi:10.1109/TIP.2018.2877486

Schnabel, R., and Klein, R. (2006). “Octree-based Point-cloud Compression,” in Proceedings of the 3rd Eurographics / IEEE VGTC Conference on Point-Based Graphics (Aire-la-Ville, Switzerland: Eurographics Association), 111–121. doi:10.2312/SPBG/SPBG06/111-120

Schwarz, S., Preda, M., Baroncini, V., Budagavi, M., Cesar, P., Chou, P. A., et al. (2019). Emerging MPEG Standards for Point Cloud Compression. IEEE J. Emerg. Sel. Top. Circuits Syst. 9, 133–148. doi:10.1109/JETCAS.2018.2885981

Shen, Y., Dai, W., Li, C., Zou, J., and Xiong, H. (2020). Multi-Scale Structured Dictionary Learning for 3-D Point Cloud Attribute Compression. IEEE Trans. Circuits Syst. Video Tech. 1, 1. doi:10.1109/TCSVT.2020.3026046

Sheng, X., Li, L., Liu, D., Xiong, Z., Li, Z., and Wu, F. (2021). Deep-PCAC: An End-To-End Deep Lossy Compression Framework for Point Cloud Attributes. IEEE Trans. Multimedia 1, 1. doi:10.1109/TMM.2021.3086711

Shi, X., Chen, Z., Wang, H., Yeung, D.-Y., Wong, W.-k., and Woo, W.-c. (2015). Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. arXiv [Preprint]. Available at: https://arxiv.org/abs/1506.04214.

Song, Z., Zhao, L., Zhou, J., Wang, H., and Li, T. (2021). Learning Hybrid Semantic Affinity for Point Cloud Segmentation. IEEE Trans. Circuits Syst. Video Technol. 1, 1. doi:10.1109/tcsvt.2021.3132047

Sterzentsenko, V., Karakottas, A., Papachristou, A., Zioulis, N., Doumanoglou, A., Zarpalas, D., et al. (2018). “A Low-Cost, Flexible and Portable Volumetric Capturing System,” in 2018 14th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS) (IEEE), 200–207. doi:10.1109/SITIS.2018.00038

Sun, X., Ma, H., Sun, Y., and Liu, M. (2019). A Novel Point Cloud Compression Algorithm Based on Clustering. IEEE Robot. Autom. Lett. 4, 2132–2139. doi:10.1109/LRA.2019.2900747

Sun, X., Wang, S., Wang, M., Wang, Z., and Liu, M. (2020). A Novel Coding Architecture for LiDAR Point Cloud Sequence. IEEE Robot. Autom. Lett. 5, 5637–5644. doi:10.1109/LRA.2020.3010207

Tang, D., Singh, S., Chou, P. A., Häne, C., Dou, M., Fanello, S., et al. (2020). “Deep Implicit Volume Compression,” in 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (IEEE), 1290–1300. doi:10.1109/cvpr42600.2020.00137

Thomas, H., Qi, C. R., Deschaud, J.-E., Marcotegui, B., Goulette, F., and Guibas, L. J. (2019). “KPConv: Flexible and Deformable Convolution for Point Clouds,” in In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 6411–6420.

Tommasi, C., Achille, C., and Fassi, F. (2016). “From Point Cloud to Bim: A Modelling Challenge in the Cultural Heritage Field,” in ISPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences XLI-B5 (IEEE), 429–436. doi:10.5194/isprsarchives-XLI-B5-429-2016

Tu, C., Takeuchi, E., Carballo, A., and Takeda, K. (2019a). “Point Cloud Compression for 3D LiDAR Sensor Using Recurrent Neural Network with Residual Blocks,” in 2019 International Conference on Robotics and Automation (ICRA) (IEEE), 3274–3280. doi:10.1109/ICRA.2019.8794264

Tu, C., Takeuchi, E., Carballo, A., and Takeda, K. (2019b). Real-Time Streaming Point Cloud Compression for 3D LiDAR Sensor Using U-Net. IEEE Access 7, 113616–113625. doi:10.1109/ACCESS.2019.2935253

Tu, C., Takeuchi, E., Miyajima, C., and Takeda, K. (2017). “Continuous Point Cloud Data Compression Using SLAM Based Prediction,” in 2017 IEEE Intelligent Vehicles Symposium (IV) (IEEE), 1744–1751. doi:10.1109/IVS.2017.7995959

Tzamarias, D. E. O., Chow, K., Blanes, I., and Serra-Sagristà, J. (2021). “Compression of point Cloud Geometry through a Single Projection,” in 2021 Data Compression Conference (DCC) (IEEE), 63–72. doi:10.1109/DCC50243.2021.00014

Wang, J., Ding, D., Li, Z., Feng, X., Cao, C., and Ma, Z. (2021). Sparse Tensor-Based Multiscale Representation for Point Cloud Geometry Compression. arXiv [Preprint]. Available at: https://arxiv.org/abs/2111.10633.

Wang, J., Ding, D., Li, Z., and Ma, Z. (2020). Multiscale Point Cloud Geometry Compression. arXiv [Preprint]. Available at: https://arxiv.org/abs/2011.03799.

Wang, J., Zhu, H., Ma, Z., Chen, T., Liu, H., and Shen, Q. (2019). Learned Point Cloud Geometry Compression. arXiv [Preprint]. Available at: https://arxiv.org/abs/1909.12037.

Wang, Q., and Kim, M.-K. (2019). Applications of 3D point Cloud Data in the Construction Industry: A Fifteen-Year Review from 2004 to 2018. Adv. Eng. Inform. 39, 306–319. doi:10.1016/j.aei.2019.02.007

Wen, X., Wang, X., Hou, J., Ma, L., Zhou, Y., and Jiang, J. (2020). “Lossy Geometry Compression of 3d Point Cloud Data via an Adaptive Octree-Guided Network,” in 2020 IEEE International Conference on Multimedia and Expo (ICME) (IEEE), 1–6. doi:10.1109/ICME46284.2020.9102866

Wiesmann, L., Milioto, A., Chen, X., Stachniss, C., and Behley, J. (2021). Deep Compression for Dense Point Cloud Maps. IEEE Robot. Autom. Lett. 6, 2060–2067. doi:10.1109/LRA.2021.3059633

Xiong, J., Gao, H., Wang, M., Li, H., and Lin, W. (2021). Occupancy Map Guided Fast Video-Based Dynamic Point Cloud Coding. IEEE Trans. Circuits Syst. Video Technol. 1, 1. doi:10.1109/TCSVT.2021.3063501

Yan Huang, Y., Jingliang Peng, J., Kuo, C.-C. J., and Gopi, M. (2008). A Generic Scheme for Progressive Point Cloud Coding. IEEE Trans. Vis. Comput. Graphics 14, 440–453. doi:10.1109/TVCG.2007.70441

Yan, W., Shao, Y., Liu, S., Li, T. H., Li, Z., and Li, G. (2019). Deep AutoEncoder-Based Lossy Geometry Compression for Point Clouds. arXiv [Preprint]. Available at: https://arxiv.org/abs/1905.03691.

Yang, Y., Feng, C., Shen, Y., and Tian, D. (2017). “FoldingNet: Point Cloud Auto-Encoder via Deep Grid Deformation,” in 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (IEEE).

Yin, Q., Ren, Q., Zhao, L., Wang, W., and Chen, J. (2021). Lossless Point Cloud Attribute Compression with Normal-based Intra Prediction. arXiv [Preprint]. Available at: https://arxiv.org/abs/2106.12236.

Yue, X., Wu, B., Seshia, S. A., Keutzer, K., and Sangiovanni-Vincentelli, A. L. (2018). “A LiDAR Point Cloud Generator,” in Proceedings of the 2018 ACM on International Conference on Multimedia Retrieval (New York, NY: Association for Computing Machinery), 458–464. doi:10.1145/3206025.3206080

Zhang, C., Florêncio, D., and Loop, C. (2014). “Point Cloud Attribute Compression with Graph Transform,” in 2014 IEEE International Conference on Image Processing (ICIP) (IEEE), 2066–2070. doi:10.1109/ICIP.2014.7025414

Zhang, X., Wan, W., and An, X. (2017). Clustering and DCT Based Color Point Cloud Compression. J. Sign Process. Syst. 86, 41–49. doi:10.1007/s11265-015-1095-0

Zhu, W., Ma, Z., Xu, Y., Li, L., and Li, Z. (2021). View-Dependent Dynamic Point Cloud Compression. IEEE Trans. Circuits Syst. Video Technol. 31, 765–781. doi:10.1109/TCSVT.2020.2985911

Zhu, W., Xu, Y., Li, L., and Li, Z. (2017). “Lossless point Cloud Geometry Compression via Binary Tree Partition and Intra Prediction,” in 2017 IEEE 19th International Workshop on Multimedia Signal Processing (MMSP) (IEEE), 1–6. doi:10.1109/mmsp.2017.8122226

Zuffo, M. (2018). EmergIMG — Downloads - USPAULOPC. Available at: http://uspaulopc.di.ubi.pt/.

REVERY ANR-17-CE23-0020