Persymmetric Adaptive Union Subspace Detection

This paper addresses the detection of a signal belonging to several possible subspace models, namely, a union of subspaces (UoS), where the active subspace that generated the observed signal is unknown. By incorporating the persymmetric structure of received data, we propose three UoS detectors based on GLRT, Rao, and Wald criteria to alleviate the requirement of training data. In addition, the detection statistic and classification bound for the proposed detectors are derived. Monte-Carlo simulations demonstrate the detection and classification performance of the proposed detectors over the conventional detector in training-limited scenarios.

1 Introduction

Adaptive detection (Liu et al., 2021; Rong et al., 2021) of signals usually assumes a homogeneous environment, namely, the clutter in the cell under test is independent and identically distributed with the training data from adjacent cells. However, it is difficult to satisfy the homogeneity of the noise in practice due to power fluctuations. Among the possible non-homogeneous models, the partially homogeneous environment (PHE) is proven effective and widely used in radar signal detection (Pulsone and Raghavan, 1999; Bandiera et al., 2007), especially for the generalized likelihood ratio test (GLRT) and two-step GLRT (Conte et al., 2001), the adaptive cosine estimator (Kraut and Scharf, 1999), and the Rao and Wald tests (Gao et al., 2020). The PHE assumes the noise in the cell under test and the training data sharing the same covariance matrix but different power levels.

The detectors above only take rank-one signal into consideration, i.e., the nominal steering vector is in accordance with the actual steering vector. However, the actual array radar has model errors (De Maio, 2005; Yu et al., 2019) such as antenna pointing error, array element position error, and channel mismatch. In practical application, if the model error is not considered, the detection performance may be reduced greatly. Scharf and Friedlander (1994) and Kraut et al. (2001) assume that the target signal comes from a multi-rank subspace to illustrate the indeterminacy of the target steering vector. Besides, more specific subspace detectors for various detecting environments have been proposed (Liu et al., 2014; Gao et al., 2018; Mao et al., 2019). However, the data in many real-world scenarios tend to be generated by processes that switch/operate in different modes (Lodhi and Bajwa, 2018). In such instances, data generated through each mode of the process can be modeled as lying on a subspace, in which case the entire data generated during the process as a whole can be best described as coming from a union of subspaces. In recent years, UoS detection has been attracting many researchers’ attention (Joneidi et al., 2015; Wimalajeewa et al., 2015). Based on the UoS model, Lodhi and Bajwa (2018) derived the bounds on the performances of UoS detector in terms of geometry of subspaces.

Although effective, the methods mentioned above fail to detect signals without sufficient training data. Real scenarios are generally training-limited due to the limitations of the environment and the radar system itself (Aubry et al., 2021; Aubry et al., 2018). The persymmetric structure of the covariance matrix is considered to alleviate the requirement of training data. Persymmetric structure means that the noise covariance matrix is Hermitian about its principal diagonal and persymmetric about its cross diagonal, which often exists in a uniformly distributed linear array or uniformly pulse trains. Many methods considered the persymmetric structure in the design of detectors. For homogeneous environments, such typical detectors are persymmetric ACE (Gao et al., 2015), persymmetric AMF (Pailloux et al., 2011), persymmetric invariant test (Ciuonzo et al., 2016), persymmetric Rao and Wald tests (Wang et al., 2016), persymmetric subspace Rao (Gao et al., 2019), and persymmetric subspace tunable detection method (Liu et al., 2018). For PHE, many detectors have been proposed in Hao et al. (2012), Liu et al. (2014), and Mao et al. (2019).

To the best of the authors’ knowledge, the design of persymmetric union subspace signal detection in PHE has not been developed yet. In this paper, we address the detection of a signal belonging to several possible subspace models, namely, a union of subspaces in PHE. Not only did the active subspace of UoS generate the observed signal, but also the power scale is unknown. Based on GLRT, Rao, and Wald criteria, we exploit the persymmetric structure of received data in the design of detection, thus proposing three UoS detectors to alleviate the amount of training data. Besides, the detection statistic and classification bound for the proposed detectors are derived. Numerical results demonstrate the detection and classification performance of the proposed detectors in training-limited scenarios.

Notations: Vector and matrix are denoted by boldface lower case and upper case letters, respectively. (⋅)*, (⋅)^T, and (⋅)^H denote complex conjugate, transpose, and complex conjugate transpose, respectively. The notation ∼ denotes “be distributed as.” |⋅| represents the determinant of a matrix, and tr(⋅) represents the trace of a matrix.

2 Problem Formulation

In this section, we formulate the problem model of UoS detection. There are N pulses over a coherent processing interval (CPI). In this paper, we assume that the target signal $\mathbf{s}\in {\mathbb{C}}^{N\times 1}$ comes from a union of subspaces. Let K₀ different subspaces S_k, k = 1, … , K₀ represent different characteristics of the target signal. Then, the target s can be expressed by s = H_kα_k, k = 1, … , K₀, where ${\mathbf{H}}_k\in {\mathbb{C}}^{N\times q}$ denotes the kth subspace matrix, and α_k the corresponding coordinate.

The collected test data are modeled as $\mathbf{x}\in {\mathbb{C}}^{N\times 1}$. If a target signal is detected, the test data can be expressed by x = s + n, where $\mathbf{n}\sim \mathcal{C}\mathcal{N}(\mathbf{0},{\sigma }^2\mathbf{M})$ represents the clutter in a non-homogeneous environment, where σ² denotes the power scaling factor, and M the covariance matrix of clutter. Thus, the UoS signal detection problem can be formulated by

$\begin{array}{cc}\hfill & H_0:\left\{\begin{array}{cc}\hfill & \mathbf{x}=\mathbf{n},\hfill \\ \hfill & {\mathbf{x}}_p={\mathbf{n}}_p,p=1,\dots ,N_0;\hfill \end{array}\right.\hfill \\ \hfill & H_k:\left\{\begin{array}{cc}\hfill & \mathbf{x}=\mathbf{s}+\mathbf{n},\mathbf{s}\in {\mathbf{S}}_k,k=1,\dots ,K_0\hfill \\ \hfill & {\mathbf{x}}_p={\mathbf{n}}_p,p=1,\dots ,N_0;\hfill \end{array}\right.\hfill \end{array}(1)$

where x_p, p = 1, … , N₀ denotes the training data collected from adjacent range cells of the test data, which contain clutter ${\mathbf{n}}_p\sim \mathcal{C}\mathcal{N}(\mathbf{0},\mathbf{M})$, p = 1, … , N₀ only. Moreover, the detection problem can be formulated as two hypotheses: the null hypothesis H₀ indicating that there is no target signal in the observation, and an alternative hypothesis H_k (Lodhi and Bajwa, 2018) representing that a UoS signal is detected. In traditional signal detection, the target signal can be seen as belonging to a low-dimensional subspace. In contrast, our purpose is to detect the UoS signal, so we assume the case of the target signal s belonging to a union of low-dimensional subspaces: $\mathbf{s}\in {\cup }_{k=1}^{K_0}{\mathbf{S}}_k$, and this is referred to as the detection stage. After detecting the UoS signal, we deal with the problem of active subspace detection, whose goal is to identify the subspace S_k to which s belongs, and this stage is referred to as the classification stage.

3 The Proposed Persymmetric UoS Detectors

In this section, we exploit the persymmetric structure to propose three UoS detectors, by resorting to GLRT, Rao, and Wald criteria.

First, a unitary matrix is used to transform the collected data and the assumed UoS matrix, where the unitary matrix is denoted as

$\mathbf{T}=\left\{\begin{array}{c}\frac{1}{\sqrt{2}}\left[\begin{array}{cc}\hfill {\mathbf{I}}_{N/2}\hfill & \hfill {\mathbf{J}}_{N/2}\hfill \\ \hfill j{\mathbf{I}}_{N/2}\hfill & \hfill -j{\mathbf{J}}_{N/2}\hfill \end{array}\right]\text{for\hspace{0.17em}}N\text{\hspace{0.17em}even},\hfill \\ \frac{1}{\sqrt{2}}\left[\begin{array}{ccc}\hfill {\mathbf{I}}_{\left(N-1\right)/2}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{J}}_{\left(N-1\right)/2}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \sqrt{2}\hfill & \hfill \mathbf{0}\hfill \\ \hfill j{\mathbf{I}}_{\left(N-1\right)/2}\hfill & \hfill \mathbf{0}\hfill & \hfill -j{\mathbf{J}}_{\left(N-1\right)/2}\hfill \end{array}\right]\text{for\hspace{0.17em}}N\text{\hspace{0.17em}odd}.\hfill \end{array}\right.(2)$

where J denotes the permutation matrix.

The transforming process can be formulated by

$\begin{array}{cc}\hfill & \tilde{\mathbf{x}}=\mathbf{T}\mathbf{x},{\tilde{\mathbf{x}}}_p=\mathbf{T}{\mathbf{x}}_p,{\tilde{\mathbf{H}}}_k={\mathbf{T}\mathbf{H}}_k,\hfill \\ \hfill & \tilde{\mathbf{n}}=\mathbf{T}\mathbf{n},{\tilde{\mathbf{n}}}_p=\mathbf{T}{\mathbf{n}}_p,\mathbf{R}=\mathbf{T}\mathbf{M}{\mathbf{T}}^H.\hfill \end{array}(3)$

It is worth noting that R denotes a real symmetric matrix. Thus, the detection problem in Eq. 1 is rewritten as:

$\begin{array}{cc}\hfill & H_0:\left\{\begin{array}{cc}\hfill & \tilde{\mathbf{x}}=\tilde{\mathbf{n}},\hfill \\ \hfill & {\tilde{\mathbf{x}}}_p={\tilde{\mathbf{n}}}_p,p=1,\dots ,N_0;\hfill \end{array}\right.\hfill \\ \hfill & H_k:\left\{\begin{array}{cc}\hfill & \tilde{\mathbf{x}}=\tilde{\mathbf{s}}+\tilde{\mathbf{n}},\tilde{\mathbf{s}}\in {\tilde{\mathbf{S}}}_k,k=1,\dots ,K_0\hfill \\ \hfill & {\tilde{\mathbf{x}}}_p={\tilde{\mathbf{n}}}_p,p=1,\dots ,N_0;\hfill \end{array}\right.\hfill \end{array}(4)$

3.1 P-UoS-GLRT Detector Design

The GLRT detector can be formulated by

$\frac{\underset{{\sigma }^2}{\max }\underset{{\mathit{\alpha }}_k}{\max }{f}_1\left(\tilde{\mathbf{x}}\right)}{\underset{{\sigma }^2}{\max }{f}_0\left(\tilde{\mathbf{x}}\right)}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\gamma ,(5)$

where $f_1(\tilde{\mathbf{x}})$ denotes the probability density function (pdf) of $\tilde{\mathbf{x}}$ under the alternative hypothesis, and $f_0(\tilde{\mathbf{x}})$ represents the pdf of $\tilde{\mathbf{x}}$ under hypothesis H₀. These two statistics can be expressed as follows:

$f_1\left(\tilde{\mathbf{x}}\right)=\frac{1}{{\pi }^N{\sigma }^{2N}|\mathbf{R}|}\text{exp}\left[-{\left(\tilde{\mathbf{x}}-{\tilde{\mathbf{H}}}_k{\mathit{\alpha }}_k\right)}^H{\mathbf{R}}^{-1}\left(\tilde{\mathbf{x}}-{\tilde{\mathbf{H}}}_k{\mathit{\alpha }}_k\right)/{\sigma }^2\right](6)$

$f_0\left(\tilde{\mathbf{x}}\right)=\frac{1}{{\pi }^N{\sigma }^{2N}|\mathbf{R}|}\text{exp}\left[-{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}/{\sigma }^2\right](7)$

To obtain the MLE (maximum likelihood estimation) of α_k, we can resort to the derivative of $f_1(\tilde{\mathbf{x}})$. Take the derivative of $f_1(\tilde{\mathbf{x}})$ with respect to α_k, and set the derivative equal to zero, then the estimation of α_k is obtained:

${\widehat{\mathit{\alpha }}}_k=\arg \underset{{\mathit{\alpha }}_k}{\max }{f}_1\left(\tilde{\mathbf{x}}\right)={\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}(8)$

To solve the problem shown in Eq. 5, the MLE of σ² is supposed to be obtained as follows:

${\widehat{\sigma }}_1^2=\left[{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}-{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k{\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}\right]/N(9)$

${\widehat{\sigma }}_0^2=\left({\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}\right)/N(10)$

Substitute Eqs 8–10 into the GLRT detector Eq. 5 to obtain the rewritten expression of GLRT:

$\frac{{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}-{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k{\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\gamma (11)$

Obtain the MLE of R by using the training data and transform it into a symmetric one:

$\widehat{\mathbf{R}}=\frac{1}{N_0}\sum _{p=1}^{N_0}{\mathbf{x}}_p{\mathbf{x}}_p^H(12)$

${\widehat{\mathbf{R}}}_p={\mathbf{T}}^H\widehat{\mathbf{R}}\mathbf{T}(13)$

Replace R in Eq. 11 with ${\widehat{\mathbf{R}}}_p$, obtaining

$\frac{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}-{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\tilde{\mathbf{H}}}_k{\left({\tilde{\mathbf{H}}}_k^H{\widehat{\mathbf{R}}}_p^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\gamma (14)$

Let ${\mathbf{P}}_{{\tilde{\mathbf{H}}}_k}={\tilde{\mathbf{H}}}_k{({\tilde{\mathbf{H}}}_k^H{\widehat{\mathbf{R}}}_p^{-1}{\tilde{\mathbf{H}}}_k)}^{-1}{\tilde{\mathbf{H}}}_k^H{\widehat{\mathbf{R}}}_p^{-1}$ denote the projection matrix of ${\tilde{\mathbf{H}}}_k$. Then, Eq. 14 can be rewritten as

$\frac{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}-{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\mathbf{P}}_{{\tilde{\mathbf{H}}}_k}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\gamma (15)$

Let $\widehat{k}$ be the index of the maximum value of the GLRT test Eq. 15, then the P-UoS-GLRT detector can be formulated by

$\frac{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}-{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\mathbf{P}}_{{\tilde{\mathbf{H}}}_{\widehat{k}}}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\gamma (16)$

In order to examine the performance of classification, we have to resort to classification probability bounds, as the exact expressions could not be acquired directly, and the target should be identified in a specific subspace in the UoS. Let $g(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_k)={\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\mathbf{P}}_{{\tilde{\mathbf{H}}}_k}\tilde{\mathbf{x}}$, $h(\tilde{\mathbf{x}})={\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}$, then the classification probability bound of the P-UoS-GLRT test can be expressed by

$\begin{array}{cc}\hfill P_{H_k}\left({\tilde{H}}_k\right)\ge \max & \left\{0,P_{S_k}\left(\frac{h\left(\tilde{\mathbf{x}}\right)}{h\left(\tilde{\mathbf{x}}\right)-g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_k\right)}>\gamma \right)\right.\hfill \\ \hfill & \left.+\sum _{j=1,j\ne k}^{K_0}{P}_{S_k}\left(\frac{h\left(\tilde{\mathbf{x}}\right)-g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_k\right)}{h\left(\tilde{\mathbf{x}}\right)-g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_j\right)}>1\right)-\left(K_0-1\right)\right\}\hfill \end{array}(17)$

3.2 P-UoS-Rao Detector Design

Assume that the unknown parameters $\mathit{\theta }={[{\mathit{\theta }}_r^T,{\theta }_s]}^T$, where θ_r = α_k stands for the corresponding coordinate, θ_s = σ² represents the power scaling factor which is deterministic but known, and R is known. Thus, the Rao test is formulated by

${\left.\frac{\partial \text{ln}{f}_1\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)}{\partial {\mathit{\theta }}_r}\right|}_{\mathit{\theta }={\widehat{\mathit{\theta }}}_0}^T{\left[{\mathbf{J}}^{-1}\left({\widehat{\mathit{\theta }}}_0\right)\right]}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}{\left.\frac{\partial \text{ln}{f}_1\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)}{\partial {\mathit{\theta }}_r^{*}}\right|}_{\mathit{\theta }={\widehat{\mathit{\theta }}}_0}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\xi ,(18)$

where J(θ) is a Fisher information matrix which is given by

$\mathbf{J}\left(\mathit{\theta }\right)=\left[\begin{array}{cc}\hfill {\mathbf{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\hfill & \hfill {\mathbf{J}}_{{\mathit{\theta }}_r,{\theta }_s}\hfill \\ \hfill {\mathbf{J}}_{{\theta }_s,{\mathit{\theta }}_r}\hfill & \hfill {\mathbf{J}}_{{\theta }_s,{\theta }_s}\hfill \end{array}\right],(19)$

and

${\left[{\mathbf{J}}^{-1}\left(\mathit{\theta }\right)\right]}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}={\left[{\mathbf{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\left(\mathit{\theta }\right)-{\mathbf{J}}_{{\mathit{\theta }}_r,{\theta }_s}\left(\mathit{\theta }\right){\mathbf{J}}_{{\theta }_s,{\theta }_s}^{-1}\left(\mathit{\theta }\right){\mathbf{J}}_{{\theta }_s,{\mathit{\theta }}_r}\left(\mathit{\theta }\right)\right]}^{-1}(20)$

${\widehat{\mathit{\theta }}}_0={\left[{\widehat{\mathit{\theta }}}_{r,0}^T,{\widehat{\theta }}_{s,0}\right]}^T$ denotes the MLE of θ under null hypothesis H₀. The pdf of $\tilde{\mathbf{x}}$ under the alternative hypothesis is given by

$f_1\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)=\frac{1}{{\left(\pi {\sigma }^2\right)}^N|\mathbf{R}|}\text{exp}\left[-\frac{{\left(\tilde{\mathbf{x}}-{\tilde{\mathbf{H}}}_k{\mathit{\alpha }}_k\right)}^H{\mathbf{R}}^{-1}\left(\tilde{\mathbf{x}}-{\tilde{\mathbf{H}}}_k{\mathit{\alpha }}_k\right)}{{\sigma }^2}\right].(21)$

The Fisher information matrix is expressed as follows:

$\mathbf{J}\left(\mathit{\theta }\right)=\text{E}\left\{\left[\frac{\partial \text{ln}{f}_1\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)}{\partial {\mathit{\theta }}^{*}}\right]\left[\frac{\partial \text{ln}{f}_1\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)}{\partial {\mathit{\theta }}^T}\right]\right\}.(22)$

It is straightforward to obtain the derivative

$\frac{\partial \text{ln}{f}_1\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)}{\partial {\mathit{\theta }}_r}=\frac{2}{{\sigma }^2}{\left[{\left(\tilde{\mathbf{x}}-{\tilde{\mathbf{H}}}_k{\mathit{\alpha }}_k\right)}^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right]}^T,(23)$

$\frac{\partial \text{ln}{f}_1\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)}{\partial {\mathit{\theta }}_r^{*}}=\frac{2}{{\sigma }^2}\left[{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\left(\tilde{\mathbf{x}}-{\tilde{\mathbf{H}}}_k{\mathit{\alpha }}_k\right)\right].(24)$

Thus, the ${\mathbf{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}(\mathit{\theta })$ under H₀ can be obtained as follows:

${\mathbf{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\left({\mathit{\theta }}_0\right)=\frac{4}{{\sigma }^2}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k.(25)$

Since ${\mathbf{J}}_{{\mathit{\theta }}_r,{\theta }_s}(\mathit{\theta })$ is a null matrix, we can obtain

${\left[{\mathbf{J}}^{-1}\left({\mathit{\theta }}_0\right)\right]}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}={\mathbf{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}^{-1}\left({\mathit{\theta }}_0\right)=\frac{{\sigma }^2}{4}{\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}(26)$

Substituting Eqs. 23, 24, and 26 into the Rao test Eq. 18, the rewritten expression of Rao can be formulated as

$\frac{{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k{\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}}{{\sigma }^2}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\lambda (27)$

Next, the MLE of σ² under H₀ is obtained as follows:

${\widehat{\theta }}_{s,0}={\widehat{\sigma }}_0^2=\arg \underset{{\sigma }^2}{\max }{f}_0\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)={\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}/N(28)$

where $f_0(\tilde{\mathbf{x}}|\mathit{\theta })$ denotes the pdf of $\tilde{\mathbf{x}}$ under H₀, which can be expressed by

$f_0\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)=\frac{1}{{\pi }^N{\sigma }^{2N}|\mathbf{R}|}\exp \left(-\frac{{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}}{{\sigma }^2}\right)(29)$

Substituting it into Eq. 27, the Rao test can be rewritten as

$\frac{{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k{\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\lambda (30)$

Replacing R by its symmetric MLE ${\widehat{\mathbf{R}}}_p$, the P-UoS-Rao detector can be formulated as

$\frac{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\tilde{\mathbf{H}}}_k{\left({\tilde{\mathbf{H}}}_k^H{\widehat{\mathbf{R}}}_p^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\lambda ,(31)$

which equals

$\frac{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\mathbf{P}}_{{\tilde{\mathbf{H}}}_k}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\lambda (32)$

Let $\widehat{k}$ be the index of the maximum value of the Rao test Eq. 32, then the P-UoS-Rao detector can be formulated by

$\frac{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\mathbf{P}}_{{\tilde{\mathbf{H}}}_{\widehat{k}}}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\lambda (33)$

Finally, the classification probability bound of the P-UoS-Rao detector can be derived as

$\begin{array}{cc}\hfill P_{H_k}\left({\tilde{H}}_k\right)\ge \max & \left\{0,P_{S_k}\left(\frac{g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_k\right)}{h\left(\tilde{\mathbf{x}}\right)}>\gamma \right)\right.\hfill \\ \hfill & \left.+\sum _{j=1,j\ne k}^{K_0}{P}_{S_k}\left(\frac{g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_k\right)}{g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_j\right)}>1\right)-\left(K_0-1\right)\right\}\hfill \end{array}(34)$

3.3 P-UoS-Wald Detector Design

The Wald test is formulated by

${\left({\widehat{\mathit{\theta }}}_{r,1}-{\mathit{\theta }}_{r,0}\right)}^H{\left\{{\left[{\mathbf{J}}^{-1}\left({\widehat{\mathit{\theta }}}_1\right)\right]}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\right\}}^{-1}\left({\widehat{\mathit{\theta }}}_{r,1}-{\mathit{\theta }}_{r,0}\right)\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\xi .(35)$

where θ_r,1 denotes the coordinate α_k under the alternative hypothesis.

From $f_1(\tilde{\mathbf{x}}|\mathit{\theta })$ denoted in Eq. 21, we can obtain the MLE of θ_r,1,

$\begin{array}{cc}\hfill {\widehat{\mathit{\theta }}}_{r,1}& =\arg \underset{{\mathit{\alpha }}_k}{\max }{f}_1\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)\hfill \\ \hfill & ={\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}},\hfill \end{array}(36)$

and θ_r,0 = 0_q×1. According to Eq. 22, ${\mathbf{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}(\widehat{\mathit{\theta }})$ under the alternative hypothesis is given by

${\mathbf{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}\left({\widehat{\mathit{\theta }}}_1\right)=\frac{4}{{\sigma }^2}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k.(37)$

Since ${\mathbf{J}}_{{\mathit{\theta }}_r,{\theta }_s}({\widehat{\mathit{\theta }}}_1)$ is a null matrix, it is straightforward that

${\left[{\mathbf{J}}^{-1}\left({\widehat{\mathit{\theta }}}_1\right)\right]}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}={\mathbf{J}}_{{\mathit{\theta }}_r,{\mathit{\theta }}_r}^{-1}\left({\widehat{\mathit{\theta }}}_1\right)=\frac{{\sigma }^2}{4}{\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}.(38)$

Substituting Eqs. 36, 38 into the Wald test Eq. 35, the rewritten expression of Wald can be formulated by

$\frac{{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k{\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}}{{\sigma }^2}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\xi (39)$

The MLE of σ² under the alternative hypothesis is expressed as follows:

$\begin{array}{cc}\hfill {\widehat{\theta }}_{s,1}& ={\widehat{\sigma }}_1^2\hfill \\ \hfill & =\arg \underset{{\sigma }^2}{\max }{f}_1\left(\tilde{\mathbf{x}}|\mathit{\theta }\right)\hfill \\ \hfill & =\frac{1}{N}\left[{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}-{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k{\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}\right]\hfill \end{array}(40)$

Moreover, by replacing σ² in Eq. 39 by ${\widehat{\theta }}_{s,1}$, Eq. 39 could be rewritten as

$\frac{{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k{\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}-{\tilde{\mathbf{x}}}^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k{\left({\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}{\tilde{\mathbf{H}}}_k\right)}^{-1}{\tilde{\mathbf{H}}}_k^H{\mathbf{R}}^{-1}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\xi (41)$

Substitute Eq. 13 into Eq. 41, then obtain the P-UoS-Wald detector

$\frac{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\mathbf{P}}_{{\tilde{\mathbf{H}}}_k}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}-{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\mathbf{P}}_{{\tilde{\mathbf{H}}}_k}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\xi (42)$

Let $\widehat{k}$ be the index of the maximum value of the Wald test Eq. 42, then the P-UoS-Wald detector can be formulated by

$\frac{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\mathbf{P}}_{{\tilde{\mathbf{H}}}_{\widehat{k}}}\tilde{\mathbf{x}}}{{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}\tilde{\mathbf{x}}-{\tilde{\mathbf{x}}}^H{\widehat{\mathbf{R}}}_p^{-1}{\mathbf{P}}_{{\tilde{\mathbf{H}}}_{\widehat{k}}}\tilde{\mathbf{x}}}\begin{array}{c}\hfill H_k\hfill \\ \hfill \gtrless \hfill \\ \hfill H_0\hfill \end{array}\xi (43)$

Finally, the classification probability bound of P-UoS-Wald can be derived by

$\begin{array}{cc}\hfill P_{H_k}\left({\tilde{H}}_k\right)& \ge \max \left\{0,P_{S_k}\left(\frac{g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_k\right)}{h\left(\tilde{\mathbf{x}}\right)-g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_k\right)}>\gamma \right)\right.\hfill \\ \hfill & \left.+\sum _{j=1,j\ne k}^{K_0}{P}_{S_k}\left(\frac{g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_k\right)\left(h\left(\tilde{\mathbf{x}}\right)-g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_j\right)\right)}{g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_j\right)\left(h\left(\tilde{\mathbf{x}}\right)-g\left(\tilde{\mathbf{x}},{\tilde{\mathbf{H}}}_k\right)\right)}>1\right)-\left(K_0-1\right)\right\}\hfill \end{array}(44)$

4 Numerical Result

In this section, numerical results are provided to illustrate the detection and classification performance of the proposed detectors named P-UoS-GLRT, P-UoS-Rao, and P-UoS-Wald over the traditional ones [UoS-GLRT, UoS-Rao, and UoS-Wald (Pan et al., 2021)].

We use 10⁴ Monte Carlo trials to evaluate the threshold and the probability of detection and classification. If not otherwise specified, we set N = 8, ρ = 0.9, σ² = 0.7, SNR = 10dB, the Doppler frequency f_d = [0.09, 0.1], and the number of training data N₀ = 10, 16, 32, respectively, throughout this paper. For each false alarm probability P_FA, the statistics of detectors in each trial of the Monte Carlo experiment can be obtained. Arrange these statistics in descending order, then the threshold is the last statistic that occupies the preceding false alarm probability of all statistics. The detection probability and classification probability can be obtained by comparing the statistics obtained by using the observation with the threshold.

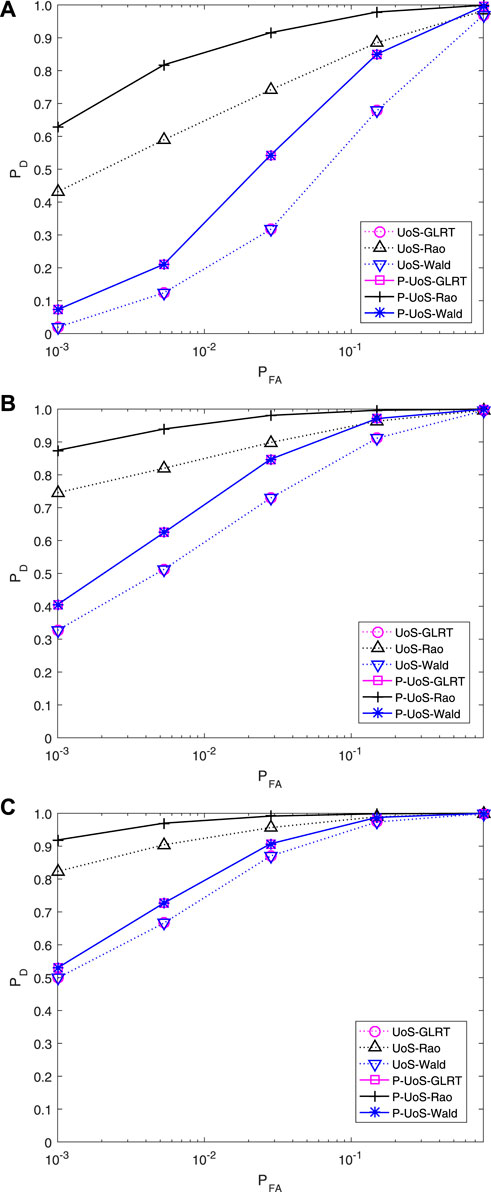
Figure 1 shows the detection performance of the proposed detectors and the traditional ones. It could be seen that as P_FA grows, the detection probability of detectors is improved remarkably, among which Rao has the highest detection probability and the GLRT detector shows the same performance with Wald. Moreover, with the increase in the number of samples, the detection performance is improved to some extent. As we can see in Figure 1C, among the proposed detectors, P-UoS-Rao has the best detection performance, followed by P-UoS-Rao and P-UoS-Wald, but all these three detectors perform better than their corresponding traditional ones. However, when the number of training data turns small, as is shown in Figures 1A,B, the detection probability of traditional detectors degrades greatly because of the lack of training data. However, the proposed persymmetric ones still keep high detection probability, exceeding the traditional ones greatly. Thus, the proposed persymmetric detectors have better detection performance in general environment, also in training-limited scenarios.

FIGURE 1

FIGURE 1. Probability of detection comparison for N = 8. (A) N₀ = 10 (B) N₀ = 16 (C) N₀ = 32.

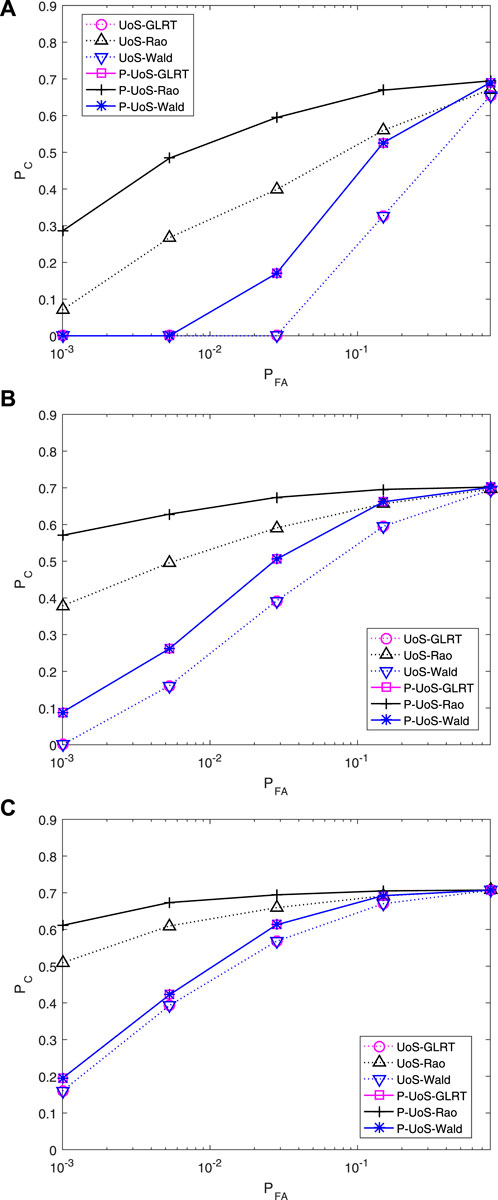
Similar results are shown in Figure 2. Figure 2 plots the classification performance of the proposed detectors and the traditional ones. As we can see, the Rao detector has the highest classification probability, followed by the GLRT detector and the Wald detector. Figure 2C shows that P-UoS-Rao outperforms P-UoS-GLRT and P-UoS-Wald, and these three detectors all perform better over their corresponding traditional ones. By comparing Figures 2A,B, we can conclude that the proposed persymmetric detectors have higher classification probability, in both training-sufficient and training-limited scenarios.

FIGURE 2

FIGURE 2. Probability of classification comparison for N = 8. (A) N₀ = 10 (B) N₀ = 16 (C) N₀ = 32.

To better simulate the real detection scenario, the interference model containing clutter and noise is supposed to be considered. In the numerical experiment, we set CNR = 20dB and SNR = 20dB and evaluate the detection and classification performance of the proposed detectors, compared with the traditional ones. Figure 3 shows the detection probability of the proposed detectors and the traditional ones. Numerical results illustrate that the proposed persymmetric detectors outperform the traditional ones in signal detection both in the training-sufficient and in the training-limited scenarios. Among them, P-UoS-Rao has the best detection performance, followed by P-UoS-GLRT and P-UoS-Wald, which is consistent with Figure 1. Figure 4 shows the classification probability of the proposed detectors. Moreover, the same simulation results with Figure 2 can be obtained; that is, the classification probability of the proposed persymmetric UoS detectors is higher than the traditional ones, both with sufficient training data and with limited training data.

FIGURE 3

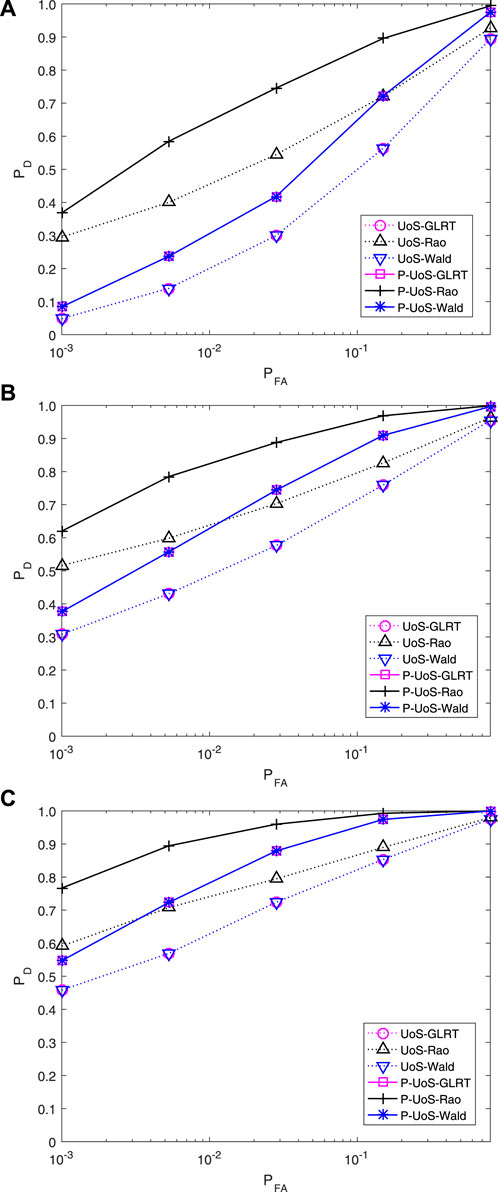
FIGURE 3. Probability of detection comparison for N = 8 with regard to CNR = 20 dB. (A) N₀ = 10 (B) N₀ = 16 (C) N₀ = 32.

FIGURE 4

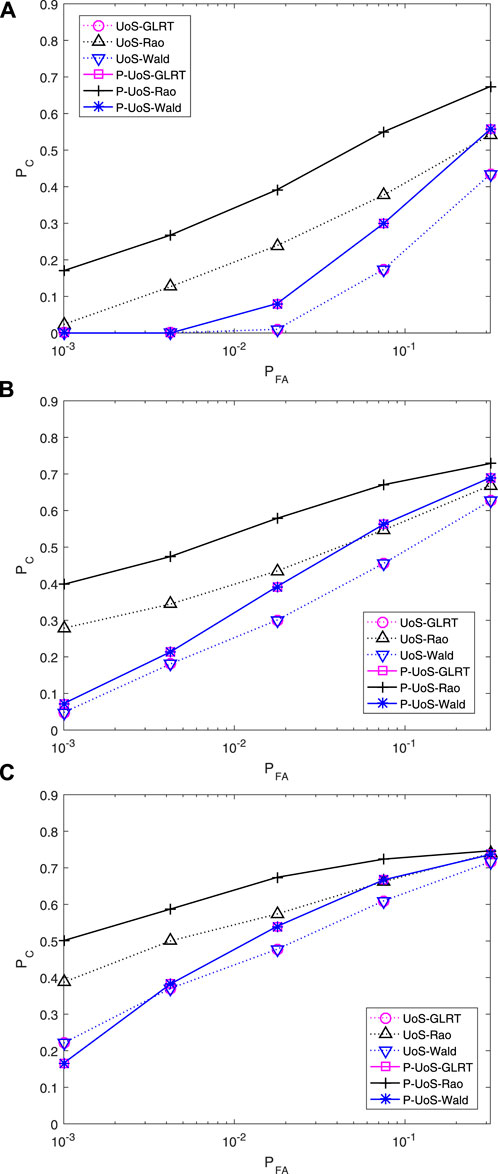
FIGURE 4. Probability of classification comparison for N = 8 with regard to CNR = 20 dB. (A) N₀ = 10 (B) N₀ = 16 (C) N₀ = 32.

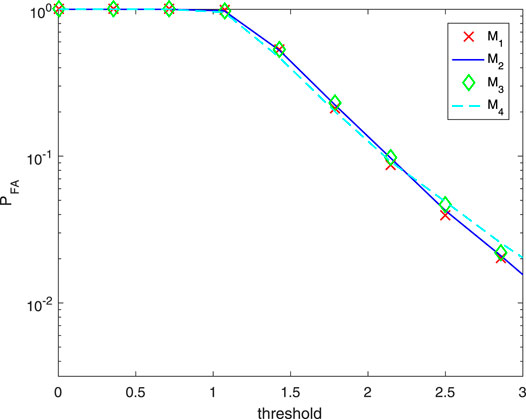
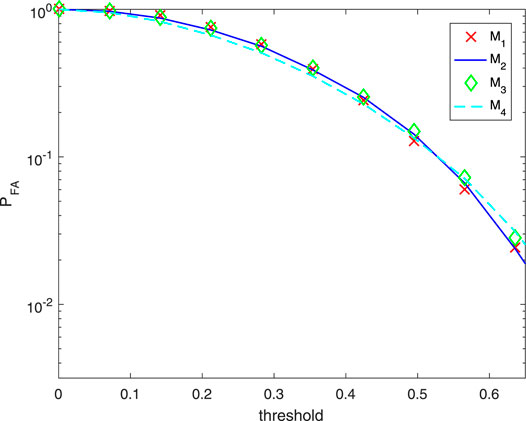
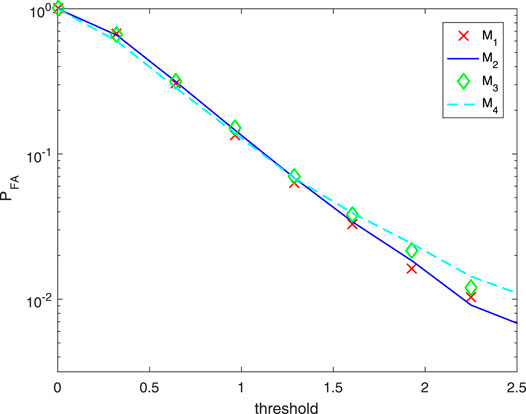
Figures 5–7 show the CFAR property of the proposed detectors P-UoS-GLRT, P-UoS-Rao, and P-UoS-Wald, respectively. Each experiment of these three are under four kinds of interference covariance matrix with different clutters, among which M₁ represents 0.1^|i−j|, M₂ denotes 0.5^|i−j|, M₃ denotes 0.9^|i−j|, and M₄ stands for $0.5^{{(i-j)}^2}{e}^{-j2\pi \cdot 0.2(i-j)}+0.9^{-{(i-j)}^2}+{\delta }_{i,j}$. It can be seen that the P_FA under each of the four kinds of interference covariance matrix approximately coincides with others, for all these three persymmetric UoS detectors. This demonstrates that the proposed detectors have an approximate CFAR property.

FIGURE 5

FIGURE 5. CFAR property of the P-UoS-GLRT detector.

FIGURE 6

FIGURE 6. CFAR property of the P-UoS-Rao detector.

FIGURE 7

FIGURE 7. CFAR property of the P-UoS-Wald detector.

5 Conclusion

In this paper, we dealt with the detection of a signal that belonged to a union of subspaces in PHE. Not only did the active subspace of UoS generate the observed signal, but also the power scale is unknown. Based on the GLRT, Rao, and Wald criteria, we used the persymmetric structure of received data to design three UoS detectors to alleviate the amount of training data. Besides, the detection statistic and classification bound for the proposed detectors were derived. Numerical results demonstrated the detection and classification performance of the proposed detectors over its competitor, especially in training-limited scenarios.

Data Availability Statement

The raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study.

Author Contributions

LP completed the simulation and main body of the paper. YG provided the idea and some writing part of the paper. ZY, YL, and MF completed some writing part and revision of the paper.

Funding

This work was supported by the China Postdoctoral Science Foundation under Grant 2020T130493 and 2019M653561, by the National Defense Science and Technology Foundation of China under Grant 2019-JCJQ-JJ-060, by the Aeronautical Foundation of China under Grant 20180181001, by the Aerospace Science and Technology Fund under Grant SAST 2018-098, and by the Natural Science Foundation of Shaanxi Province under Grant 2019JM-032.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aubry, A., De Maio, A., and Pallotta, L. (2018). A Geometric Approach to Covariance Matrix Estimation and its Applications to Radar Problems. IEEE Trans. Signal. Process. 66, 907–922. doi:10.1109/TSP.2017.2757913

CrossRef Full Text | Google Scholar

Aubry, A., Maio, A. D., Marano, S., and Rosamilia, M. (2021). Structured Covariance Matrix Estimation with Missing-Data for Radar Applications via Expectation-Maximization. IEEE Trans. Signal Process 69, 5920–5934. doi:10.1109/TSP.2021.3111587

CrossRef Full Text | Google Scholar

Bandiera, F., De Maio, A., Greco, A. S., and Ricci, G. (2007). Adaptive Radar Detection of Distributed Targets in Homogeneous and Partially Homogeneous Noise Plus Subspace Interference. IEEE Trans. Signal. Process. 55, 1223–1237. doi:10.1109/tsp.2006.888065

CrossRef Full Text | Google Scholar

Ciuonzo, D., Orlando, D., and Pallotta, L. (2016). On the Maximal Invariant Statistic for Adaptive Radar Detection in Partially Homogeneous Disturbance with Persymmetric Covariance. IEEE Signal. Process. Lett. 23, 1830–1834. doi:10.1109/LSP.2016.2618619

CrossRef Full Text | Google Scholar

Conte, E., De Maio, A., and Ricci, G. (2001). GLRT-based Adaptive Detection Algorithms for Range-Spread Targets. IEEE Trans. Signal. Process. 49, 1336–1348. doi:10.1109/78.928688

CrossRef Full Text | Google Scholar

De Maio, A. (2005). Robust Adaptive Radar Detection in the Presence of Steering Vector Mismatches. IEEE Trans. Aerosp. Electron. Syst. 41, 1322–1337. doi:10.1109/TAES.2005.1561887

CrossRef Full Text | Google Scholar

Gao, Y., Ji, H., and Liu, W. (2019). Persymmetric Adaptive Subspace Detectors for Range-Spread Targets. Digital Signal. Process. 89, 116–123. doi:10.1016/j.dsp.2019.03.007

CrossRef Full Text | Google Scholar

Gao, Y., Li, H., and Himed, B. (2018). Adaptive Subspace Tests for Multichannel Signal Detection in Auto-Regressive Disturbance. IEEE Trans. Signal. Process. 66, 5577–5587. doi:10.1109/TSP.2018.2869123

CrossRef Full Text | Google Scholar

Gao, Y., Liao, G., Zhu, S., and Yang, D. (2015). Generalised Persymmetric Parametric Adaptive Coherence Estimator for Multichannel Adaptive Signal Detection. IET Radar, Sonar & Navigation 9, 550–558. doi:10.1049/iet-rsn.2014.0101

CrossRef Full Text | Google Scholar

Gao, Y., Mao, L., Ji, H., and Pan, L. (2020). “Persymmetric Subspace Rao and Wald Tests for Distributed Target in Partially Homogeneous Environment,” in 2020 IEEE 11th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hangzhou, China, June 8, 2020, 1–5. doi:10.1109/SAM48682.2020.9104407

CrossRef Full Text | Google Scholar

Hao, C., Orlando, D., Ma, X., and Hou, C. (2012). Persymmetric Rao and Wald Tests for Partially Homogeneous Environment. IEEE Signal. Process. Lett. 19, 587–590. doi:10.1109/LSP.2012.2207891

CrossRef Full Text | Google Scholar

Joneidi, M., Ahmadi, P., Sadeghi, M., and Rahnavard, N. (2015). Union of Low-Rank Subspaces Detector. IET Signal. Process. 10, 55–62. doi:10.1049/iet-spr.2015.0009

CrossRef Full Text | Google Scholar

Kraut, S., Scharf, L. L., and McWhorter, L. T. (2001). Adaptive Subspace Detectors. IEEE Trans. Signal. Process. 49, 1–16. doi:10.1109/78.890324

CrossRef Full Text | Google Scholar

Kraut, S., and Scharf, L. L. (1999). The CFAR Adaptive Subspace Detector Is a Scale-Invariant GLRT. IEEE Trans. Signal. Process. 47, 2538–2541. doi:10.1109/78.782198

CrossRef Full Text | Google Scholar

Liu, J., Liu, W., Gao, Y., Zhou, S., and Xia, X.-G. (2018). Persymmetric Adaptive Detection of Subspace Signals: Algorithms and Performance Analysis. IEEE Trans. Signal. Process. 66, 6124–6136. doi:10.1109/TSP.2018.2875416

CrossRef Full Text | Google Scholar

Liu, W., Liu, J., Hao, C., Gao, Y., and Wang, Y. L. (2021). Multichannel Adaptive Signal Detection: Basic Theory and Literature Review. Sciece China. Inf. Sci. doi:10.1007/s11432-020-3211-8

CrossRef Full Text | Google Scholar

Liu, W., Xie, W., Liu, J., and Wang, Y. (2014). Adaptive Double Subspace Signal Detection in Gaussian Background-Part I: Homogeneous Environments. IEEE Trans. Signal. Process. 62, 2345–2357. doi:10.1109/TSP.2014.2309556

CrossRef Full Text | Google Scholar

Lodhi, M. A., and Bajwa, W. U. (2018). Detection Theory for union of Subspaces. IEEE Trans. Signal. Process. 66, 6347–6362. doi:10.1109/TSP.2018.2875897

CrossRef Full Text | Google Scholar

Mao, L., Gao, Y., Yan, S., and Xu, L. (2019). Persymmetric Subspace Detection in Structured Interference and Non-homogeneous Disturbance. IEEE Signal. Process. Lett. 26, 928–932. doi:10.1109/LSP.2019.2913332

CrossRef Full Text | Google Scholar

Pailloux, G., Forster, P., Ovarlez, J.-P., and Pascal, F. (2011). Persymmetric Adaptive Radar Detectors. IEEE Trans. Aerosp. Electron. Syst. 47, 2376–2390. doi:10.1109/TAES.2011.6034639

CrossRef Full Text | Google Scholar

Pan, L., Gao, Y., Li, J., and Xin, Z. (2021). “Union of Subspaces Signal Detection and Classification Based on Rao and Wald Test,” in International Conference on Frontiers of Electronics, Information and Computation Technologies, Changsha, China, May 21, 2021, 1–6.

Google Scholar

Pulsone, N. B., and Raghavan, R. S. (1999). Analysis of an Adaptive CFAR Detector in Non-gaussian Interference. IEEE Trans. Aerosp. Electron. Syst. 35, 903–916. doi:10.1109/7.784060

CrossRef Full Text | Google Scholar

Rong, Y., Aubry, A., De Maio, A., and Tang, M. (2021). Adaptive Radar Detection in Low-Rank Heterogeneous Clutter via Invariance Theory. IEEE Trans. Signal. Process. 69, 1492–1506. doi:10.1109/TSP.2021.3058447

CrossRef Full Text | Google Scholar

Scharf, L. L., and Friedlander, B. (1994). Matched Subspace Detectors. IEEE Trans. Signal. Process. 42, 2146–2157. doi:10.1109/78.301849

CrossRef Full Text | Google Scholar

Wang, Z., Li, M., Chen, H., Lu, Y., Cao, R., Zhang, P., et al. (2016). Persymmetric Detectors of Distributed Targets in Partially Homogeneous Disturbance. Signal. Process. 128, 382–388. doi:10.1016/j.sigpro.2016.05.010

CrossRef Full Text | Google Scholar

Wimalajeewa, T., Eldar, Y. C., and Varshney, P. K. (2015). Subspace Recovery from Structured union of Subspaces. IEEE Trans. Inform. Theor. 61, 2101–2114. doi:10.1109/TIT.2015.2403260

CrossRef Full Text | Google Scholar

Yu, X., Cui, G., Kong, L., Li, J., and Gui, G. (2019). Constrained Waveform Design for Colocated MIMO Radar with Uncertain Steering Matrices. IEEE Trans. Aerosp. Electron. Syst. 55, 356–370. doi:10.1109/TAES.2018.2852200

CrossRef Full Text | Google Scholar