- 1Department of Chemical and Biological Engineering, University of Colorado Boulder, Boulder, CO, United States
- 2Department of Mechanical Engineering, Stanford University, Stanford, CA, United States
Diffusiophoresis involves the movement of colloidal-scale entities in response to concentration gradients of a solute. It is broadly categorized into two types: passive and active diffusiophoresis. In passive diffusiophoresis, external concentration gradients drive the motion, while in active diffusiophoresis, the colloidal entity itself assists in generating the gradients. In this perspective, we delve into the fundamental processes underlying passive and active diffusiophoresis and emphasize how prevalent both kinds of diffusiophoresis are in colloidal and natural systems. In particular, we highlight the colloidal focusing feature in passive diffusiophoresis and discuss how it underpins the variety of experimental observations and applications such as low-cost zetasizers, water filtration, and biological pattern formation. For active diffusiophoresis, we emphasize the dependence of particle trajectory on its shape and surface heterogeneity, and discuss how this dictates the applications such as drug delivery, removal of microplastics, and self-repairing materials. Finally, we offer insights and ideas regarding future opportunities in diffusiophoresis.
1 Introduction
The term ‘diffusiophoresis’ is a combination of the words ‘diffusion’ and ‘phoresis’ and requires two components: a particle and a diffusing species. The diffusing species is typically dissolved in a solvent, and thus, we refer to it as a solute. During diffusiophoresis, the particle moves along the concentration gradients of the solute. Although it may seem counterintuitive, the particle often (though not always) moves towards areas of higher concentration of the solute with which it is interacting. The concept of diffusiophoresis was first documented in 1947 by Derjaguin et al. (Derjaguin et al., 1947). In the 1980s and 90s, Anderson and co-workers (Anderson et al., 1982; Anderson and Prieve, 1984; Prieve et al., 1984; Ebel et al., 1988; Anderson, 1989) derived expressions for the mobility of diffusiophoretic particles in electrolytic and non-electrolytic solute gradients. Over the last two decades, the experimental research on diffusiophoresis has grown significantly. Broadly, this research can be divided into two main categories: passive diffusiophoresis and active diffusiophoresis. Passive diffusiophoresis involves particles moving in response to external concentration gradients of the solute. This is most commonly achieved in microfluidic devices where several studies have reported colloidal focusing (Abécassis et al., 2008; Shi et al., 2016; Shin et al., 2016; 2017c; Ault et al., 2017), i.e., the tendency of colloids to concentrate in a particular region. In contrast, active diffusiophoresis refers to phenomena where the particle assists in creating solute concentration gradients, which has led to significant interest in developing autonomous micromachines (Palacci et al., 2013; Aubret et al., 2018).
Recent research on diffusiophoresis has demonstrated that it is crucial for a broad range of phenomena, such as exclusion zone formation near membranes (Florea et al., 2014), removal of contaminants during laundry (Shin et al., 2018), formation of patterns on vertebrate skins (Alessio and Gupta, 2023a), and possibly even migration patterns in humans Alessio and Gupta (2023b). In fact chemotaxis, i.e., movement of microorganisms upon sensing gradients in chemoattractants, is essentially a subclass for diffusiophoresis, and is mathematically identical to diffusiophoresis (Alessio and Gupta, 2023a; Alessio and Gupta, 2023b; Chu et al., 2021). From an application standpoint, diffusiophoresis has been used for creating living crystals (Palacci et al., 2013), micromotor machines (Aubret et al., 2018), membrane-less water filters (Shin et al., 2017c) and low-cost zetasizers (Shin et al., 2017a). Therefore, given the breadth of the applications of this process from interfacial phenomena to colloidal physics and biophysical systems, this perspective seeks to share ideas on how diffusiophoresis can advance fundamental research in colloidal physics and enable new technologies in biomedicine and lab-on-a-chip.
In Section 2, we provide a brief summary of the fundamentals and applications of passive diffusiophoresis. In Section 3, we highlight the impact of particle shape and surface heterogeneity on active diffusiophoresis and discuss some of the promising applications. Finally, we suggest upcoming trends and outline future opportunities in Section 4.
2 Passive diffusiophoresis: A colloidal focusing mechanism
Definition: Passive diffusiophoresis is the movement of colloidal particles in response to external concentration gradients. Figure 1 summarizes fundamental features of passive diffusiophoresis and recent developments in the field.

FIGURE 1. Fundamentals and applications of passive diffusiophoresis. (A) A schematic of a diffusiophoretic particle being propelled at velocity vDP by an osmotic pressure gradient near its surface resulting from an external chemical gradient. Other interaction potentials, such as electrostatic, may also impact this process. (B) Dead-end pore experiments and simulations demonstrating the role of diffusiophoresis and diffusioosmosis in tandem; reproduced with permission from Alessio et al. (2021), under license number RNP/23/O CT/071087, and Alessio et al. (2022), under CC BY. (C) Experiments and simulations of colloidal banding due to diffusiophoresis; reproduced with permission from Shi et al. (2016), under license number RNP/23/O CT/071088, Banerjee and Squires (2019), under CC BY-NC 4.0, and Raj et al. (2023b), under license ID 1406995-1. (D) Simulations of diffusiophoretic-enhanced Turing patterns where colloidal focusing is observed in the presence of reaction-diffusion instability-induced chemical concentration patterns. (E) Active transport of functionally unrelated cargo along spatio-temporal patterns of E. coli MinDE proteins, adapted with permission from Ramm et al. (2021) under CC BY 4.0. (F) The sharpness of the color gradients of the intricate hexagonal and stripe patterns on a male Ornate Boxfish (Aracana ornata) can be observed and explained through diffusiophoresis-enhanced Turing patterns, adapted with permission from Alessio and Gupta (2023a), under CC BY-NC 4.0. (G) Rinsing a stained fabric with fresh water naturally establishes a surfactant gradient within the deep pore space, with negligible convection, providing a pathway for removal of colloidal soil particles diffusiophoretically, reproduced with permission from Shin et al. (2018) under license number RNP/23/O CT/071089. (H) Membrane-less water filtration technology using diffusiophoretic motion of colloidal particles along concentration gradients of dissolved CO2, reporduced with permission from Shin et al. (2017c) under CC BY 4.0.
Physical explanation: Diffusiophoresis, in its simplest form, can be understood through excess osmotic pressure. Due to the interaction potential between the particle and the solute, the external solute concentration gradient and consequently the osmotic pressure gradient are enhanced near the particle surface. In the frame of reference of the particle, the fluid will have a tendency to move against the osmotic pressure gradients. However, since the fluid is stationary, the particle will move in the direction of osmotic pressure gradient, or towards higher solute concentrations; see Figure 1A. While the particle typically moves towards higher concentration of solute, it is possible that this direction can be reversed, for instance if there is electrostatic interaction between the solute and the particle (Velegol et al., 2016).
Mobility relationships: The derivation for diffusiophoretic mobility for a spherical particle has been covered extensively by Anderson et al. (1982), Prieve et al. (1984) and Keh and Wei (2000). Briefly, in these calculations, solute conservation equations and Stokes flow equations are solved simultaneously. Since the particles are small, the velocity of the particle is calculated by invoking a force-free condition such that the phoretic force is balanced by the Stokes drag. The calculations can be significantly simplified in the limit of shallow concentration gradient, small interaction potential and thin interaction limit. Several derivations exist for both electrolytic and non-electrolytic solutes. Recent work in the area focuses on diffusiophoresis in concentrated electrolytes (Prieve et al., 2019), multiple electrolytes (Chiang and Velegol, 2014; Gupta et al., 2019), dependence of mobility on solute concentration (Gupta et al., 2020; Lee et al., 2023b), multivalent electrolytes (Wilson et al., 2020), particle shape (Doan et al., 2023) and composite particles (Li and Keh, 2016; Mondal et al., 2023).
Observation in experiments: The most striking feature of passive diffusiophoresis is the “focusing” effect where a region of high colloid concentration is observed. This, in effect, is as if diffusiophoresis imparts a “negative diffusion” coefficient to colloids (Murray, 2003). This effect was observed by Staffeld and Quinn (1989), and has been repeatedly observed in various settings in recent literature (Shi et al., 2016; Shin et al., 2016; 2017c; Ault et al., 2017). Physically, this is understood from the fact that due to diffusiophoresis, particles have a tendency to migrate towards region of high solute concentration. However, their diffusion is significantly weaker due to their large size (compared to the solute) and thus they collect and move with the front of the diffusing solute and focus. We specifically highlight the work of Shi et al. (2016) who showed that the focusing can be controlled through an acid-base reaction; see Figure 1C left-panel.
Diffusiophoresis and diffusioosmosis in tandem: Theoretical calculations based on diffusiophoresis alone for the setup described above significantly over-predict the focusing effect (Alessio et al., 2021), i.e., the experimentally observed focusing is weaker than theoretical predictions. Alessio et al. (2022) demonstrated that this is because of the diffusioosmotic flow generated by the sidewalls of the microfluidic channel and found that effective diffusivity of the particle is enhanced due to this flow, akin to Taylor dispersion (Figure 1B). They showed that this increased dispersion dampens the focusing and quantitatively recovered the experimental trends. The effect of diffusiophoresis and diffusioosmosis in tandem, combined with geometric and flow considerations, can be employed to trap or eject particles (Kar et al., 2015; Shin et al., 2020; Singh et al., 2020; Singh et al., 2022a; Singh et al., 2022b).
Beyond one-dimensional gradients: The studies described above have largely focused on one-dimensional external gradients. This is due to the fact that appreciable two- and three-dimensional solute gradients are challenging to sustain because solutes diffuse quickly compared to the colloids they propel. Banerjee et al. (2016) proposed and demonstrated a creative mechanism for maintaining solute gradients in two dimensions by deliberately placing gel beacons which can act as solute sources or sinks, soaking them with solution, and flushing the arrangement with deionized water and colloids to observe long-lasting particle banding (Banerjee and Squires, 2019); see Figure 1C right-panel. Colloidal focusing via diffusiophoresis is still seen in these geometries, and the design principle is applied to more complicated situations such as particulate navigation in porous media (Tan et al., 2021). Recently, Raj et al. (2023b) extended this approach computationally by optimizing the spatial arrangement of arbitrary collections of sources and sinks for maximizing colloid concentration (Figure 1C right panel).
Diffusiophoresis-enhanced Turing patterns: An underexplored topic in diffusiophoresis literature is the use of reaction-diffusion instabilities. Alan Turing theorized in 1952 (Turing, 1952) that instabilities arising from non-linearities in chemical reaction pathways can be sufficient for sustained pattern formation and biological development from an initially homogeneous state. The fundamental mechanisms for biological pattern formation and the role of Turing instabilities to this day are still under scrutiny (Maini et al., 2012) and mechanisms such as motility-induced phase separation and chemotaxis are thought to be essential contributors (Cates and Tailleur, 2015; Zhao et al., 2023), though Turing patterns serve as an excellent starting point for analyzing spatial heterogeneity of chemical and biological materials (Figure 1D). Ramm et al. (2021) showed in experiments with pattern-forming Escherichia coli MinDE protein that unrelated DNA origami-streptavidin nanostructures, when dispersed over the already-patterned E. coli were organized via diffusiophoresis into mirroring patterns. This was the first-ever direct observation of diffusiophoresis in a cell biology context. The authors also discussed the focusing effect of diffusiophoresis wherein the patterns became sharper with larger cargo size (Figure 1E). Following this, Alessio and Gupta (2023a) developed a theory for this phenomenon and coined the term Diffusiophoresis-Enhanced Turing Patterns. The authors showed that diffusiophoretic focusing explains mysterious features such as sharpening and double-spotting of the chromatophores in vertebrae such as the Ornate Boxfish and the Jewel Moray Eel (Figure 1F) and can qualitatively recover the experimental results of Ramm et al. (2021). Inspired by the similarity between colloids and chemotaxis by the ubiquity of diffusiophoretic motion of biological microorganisms and colloids along gradients of chemical concentration, Alessio and Gupta (2023b) argued that humans also migrate towards concentration gradients of opportunities (economy, social connections, safety, etc.). Due to the focusing effect of diffusiophoresis, they were able to create hotspots in human population densities that mimic cities.
Applications: As is clear from the above discussion, the key feature of diffusiophoresis is the tendency to focus colloids. Since high concentration provides an easy method to track colloidal fronts, diffusiophoresis has been suggested to create a low-cost Zetasizer (Shin et al., 2017a). Finally, given that diffusiophoresis can collect the particles to a particular region, it can also deplete the particles from a region, which enables it to clear contaminant from a fabric (Shin et al. (2018), see Figure 1G), and develop a membrane-less water filtration device (Shin et al. (2017c), see Figure 1H).
3 Active diffusiophoresis: The “chemical” mode of swimming
Definition: Active diffusiophoresis, also referred to as self-diffusiophoresis, is the movement of a particle in response to the concentration gradient of a solute it creates. Therefore, the particle plays an “active” role in its own propulsion. The most common approach to achieve active diffusiophoresis is to coat the particle surface with a catalytic patch (Golestanian et al., 2007), which subsequently creates concentration gradients due to a surface reaction. We refer to this mode of propulsion as “chemical” swimming (this could also include active droplets which are driven by surfactant concentration gradients which subsquently result in Marangoni forces (Dwivedi et al., 2022), but are not the focus of this perspective). This is distinct from the “mechanical” mode of swimming, where a particle propels by changing their shape with time, such as surface distortions (Stone and Samuel, 1996).
Physical explanation: The mechanism of active diffusiophoresis is similar to passive diffusiophoresis, i.e., osmotic pressure gradients help drive the motion. However, in self-diffusiophoresis, since the particle creates the gradient itself, asymmetry in particle geometry or catalytic patch is required to induce motion (Figure 2A). Therefore, the propulsion direction in active diffusiophoresis is dependent on the local orientation of particles, unlike passive diffusiophoresis. This feature can give rise to life-like collective behavior (Palacci et al., 2013).
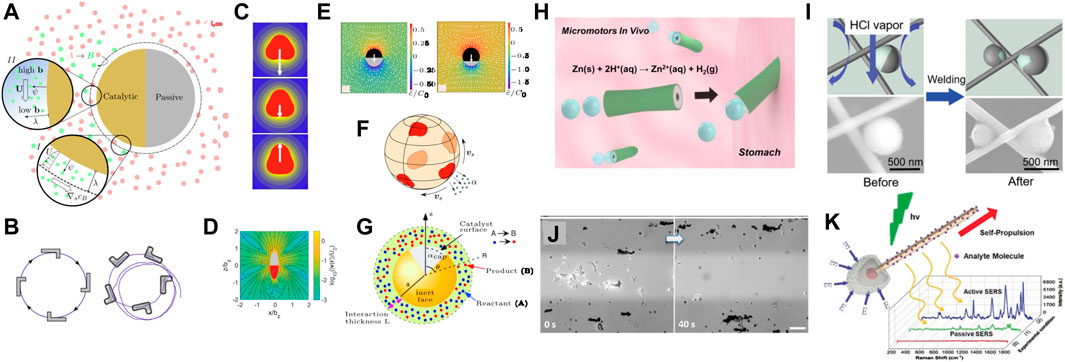
FIGURE 2. Fundamentals and applications of active diffusiophoresis. (A) A schematic of a self-diffusiophoretic particle being propelled due to catalytic surface reactions. The velocity can be estimated using a phoretic slip velocity or through a volumetric body force. (B) Active bent rod particles have been experimentally observed and theoretically predicted to move in two-dimensional circular trajectories, right-panel reproduced with permission from Kümmel et al. (2013) under license no. RNP/23/O CT/071090. (C) Shape dependence has also been theoretically studied by near-spherical particles by Shklyaev et al. (2014), where it was seen that particle-fluid interaction and particle motion depend on sphericity, reproduced with permission under license no. 5646630647202. (D) Poehnl et al. (2020) derived the flow field around chemically active prolate spheroids and observed that the spheroids eccentricity affects the surrounding flow field, reproduced with permission under CC BY 3.0. (E) The propulsion of spherical microparticles depends on catalytic coverage. Maximum propulsion is realized for hemispherical catalytic caps, reproduced with permission from Popescu et al. (2018) under CC BY 4.0. (F) Variations in the shape and size of catalytic and hydrodynamic surface patches lead to linear and helical trajectories of spherical microswimmers, reproduced with permission from Lisicki et al. (2018) under license ID 1406140-1. (G) The effect of catalytic coverage and, additionally, the interaction length scale at arbitrary interaction lengths also affect propulsion speeds, reproduced with permission from Sharifi-Mood et al. (2013) under license no. 5646680704849. (H) Catalytic micro-rods for in vivo targeted drug delivery in mice stomach reproduced with permission from Gao et al. (2015) under ACS editor’s choice usage agreement. (I) Photocatalytic Janus particles for the fabrication of self-repairing materials and for micro-welding, reproduced with permission from Wang et al. (2019b) under license no. 5646681386495. (J) removal of microplastics from environmental water samples, reprinted with permission from Wang et al. (2019a). Copyright 2019 American Chemical Society. (K) Match-like micro-nano motors have also been used for more effective biochemical sensing via surface-enhanced Raman spectroscopy, reprinted from Wang et al. (2018) under license no. 5646690570147.
Mobility relationships: The most common setup for self-diffusiophoresis is a spherical particle coated with a catalytic patch. The velocity (both translational and rotational) of the particle is typically calculated through one of two distinct approaches. In the first, the solute transport equation with a phoretic flux and a surface flux boundary condition is coupled to Stokes flow equations and solved by invoking the zero net force and torque conditions (Michelin and Lauga, 2014). In the second, a phoretic slip velocity is assumed on the particle surface and then the reciprocal theorem is invoked to obtain the translational and rotational velocity using the same zero net force and torque conditions (Stone and Samuel, 1996; Golestanian et al., 2007; Poehnl and Uspal, 2021; Ganguly and Gupta, 2023). The first approach is cumbersome but is more accurate because it can resolve the velocity as a function of interaction potential, interaction length scale, and Péclet number. On the other hand, the second approach is more popular but suffers from the limitation that it is only valid in the thin interaction limit and requires a lumped mobility parameter to estimate the phoretic slip velocity (Figure 2A). In Ganguly et al. (2023), authors extended the second approach to develop a universal mobility relationship with a volumetric body force (Figure 2A) for spherical particles that reduces to relevant limits for both active and passive diffusiophoretic systems.
Shape and surface heterogeneity effects: One of the exciting features of self-diffusiophoresis is that the trajectories are orientation dependent and hence shape and surface heterogeneity serve as useful parameters to control trajectories. In Ganguly and Gupta (2023), authors focused on the geometry of a slender bent-rod. This geometry is particularly interesting because it can be described entirely by two dimensionless parameters: the length asymmetry of the two arms and the angle between the arms. The authors showed that the two-dimensional motion of a self-diffusiophoretic bent rod will always be circular, consistent with experimental reports (Kümmel et al. (2013); Figure 2B). Perhaps most importantly, the authors showed that even if the catalytic activity is uniform across the bent rod, the particle can self-propel entirely due to its geometric anisotropy. This was also observed in Shklyaev et al. (2014) where the authors described “chemical sailing” of nearly spherical particles. Specifically, the authors emphasize that even if the catalytic activity is uniform, the particles can swim entirely due to geometric anisotropy (Figure 2C). Poehnl et al. (2020) developed an analytical solution for a spheroidal swimmer (Figure 2D) and Poehnl and Uspal (2021) investigated a helical swimmer. For the latter, the authors developed a slender body theory, which is a useful method to investigate shape effects in active diffusiophoresis (Schnitzer and Yariv, 2015; Yariv, 2019; Katsamba et al., 2020). The realization of curvilinear trajectories in active-diffusiophoresis is not only limited to non-spherical particles. Such curvilinear motion could also be induced through surface heterogeneity (Sharifi-Mood et al., 2013; Lisicki et al., 2018; Raman et al., 2023). In fact, Lisicki et al. (2018) observed that both linear and helical trajectories can be obtained by controlling the placement of catalytic and hydrodynamic patches on a sphere (Figure 2F). Finally, the aforementioned features may be combined with interaction lengthscales to further change the mobility, as discussed in Sharifi-Mood et al. (2013).
Life-like or machine-like behavior due to collective motion: The applications of active diffusiophoresis may be broadly categorized into two different categories. In the first category, the focus is on collective behavior of particles. For instance, Palacci et al. (2013) showed how collective motion can create “living crystals” which assemble upon activation of surface reaction and disperse upon deactivation. In Aubret et al. (2018), it was shown that a similar setup can be used to create spinning microgears which can be activated and deactivated upon demand. The collective motion of active diffusiophoretic particles can thus be employed to create life-like or machine-like functionality.
Functionality due to autonomous motion of a single particle: In the second category of applications, the focus is instead on the autonomous motion of individual particles and how we can “steer” them on demand. There are several experimental studies exploring how these steerable microparticles could be used for biomedical applications such as targeted drug delivery (Gao et al., 2015; Peng et al., 2015; Luo et al., 2020). Specifically, Gao et al. (2015) conducted in vivo experiments using catalytic micro-rods fueled by gastric juices in the stomach of mice; see Figure 2H. They found that catalytic actuation led to enhanced delivery and retention of drugs within the mucosal layer in the stomach. Beyond biomedical applications, self-diffusiophoresis is being employed in technologies related to environmental remediation, fabrication of functional materials, and chemical sensing. Das et al. (2015) studied how boundaries could be leveraged to steer active Janus particles, which Wang et al. (2019b) utilized to photocatalytically drive particles and weld junctions of Ag-nanowire networks; see Figure 2I. Similarly, Wang et al. (2019a) used photocatlytic active particles for removing microplastics from environmental water samples, see Figure 2J. Deng et al. (2022) reviewed recent work on behavior of active colloids in the vicinity of air-water interfaces, which is important to develop robust environmental remediation systems. Another application of self-diffusiophoretic particles is in chemical sensing, where catalytically driven particles chemically detect ricin and other toxins for bio-defense (Esteban-Fernández de Ávila et al., 2016), or enhance the effectiveness of existing biochemical sensing techniques such as SERS (Wang et al., 2018); see Figure 2K.
4 Future opportunities
Through this perspective, we sought to provide an overview of the crucial features of both passive and active diffusiophoresis. In particular, we emphasized that colloidal focusing underpins passive diffusiophoresis and enables a range of different applications. In contrast, in active diffusiophoresis, the particle shape and surface heterogeneity give rise to intriguing trajectories which are employed for autonomous swimming or collective behavior applications. Going forward, in our view, these are some of the future opportunities in the area of diffusiophoresis:
Electrochemical concentration gradients in passive diffusiophoresis: The concentration gradients typically employed in passive diffusiophoresis typically are externally imposed. However, employing electrochemical reactions to generate concentration gradients and subsequently using them as a driving force for diffusiophoresis remains relatively underexplored. Some recent studies have begun to investigate this phenomenon, referred to as electrodiffusiophoresis (Jarvey et al., 2022; Jarvey et al., 2023; Rath et al., 2021; Wang et al., 2022a; b). We believe this broad area provides opportunity for combining colloidal physics with electrochemistry and could be useful for directed assembly of colloids or removing deposited colloids on electrodes.
Porous media and charged confinement in passive diffusiophoresis: The majority of the work on passive diffusiophoresis focuses on unconfined geometries. Some preliminary experimental studies and theoretical investigations (Sambamoorthy and Chu, 2023) focus on confinement due to biofilms (Somasundar et al., 2023) or hydrogels (Doan et al., 2021). A few studies do consider diffusiophoresis in a charged cavity (Keh and Anderson, 1985; Zydney, 1995; Lee and Keh, 2014; Chiu and Keh, 2018), but future theoretical studies could focus on charged confinement in a capillary-like geometry, where double layers from the surface may interact with the double layers around the particles (Henrique et al., 2023; Henrique et al., 2022b; Henrique et al., 2022a), and diffusioosmosis may also play a role. This is particularly important for diffusiophoresis of nanoparticles that may allow enhanced transport in nanoporous materials.
Shape and fluid flow effects in passive diffusiophoresis: Though shape has played a central role in active diffusiophoresis, it has been rarely investigated in passive diffusiophoresis. The recent work by Doan et al. (2023) et al. for ellipsoids shows the importance of particle orientation on trajectories. In addition, only a few studies have investigated background flow (Alessio et al., 2022; Alessio et al., 2021; Shin et al., 2016; Shin et al., 2017a; Shin et al., 2017b; Shin et al., 2020; Staffeld and Quinn, 1989) and recent studies have shown that it can significantly impact colloidal focusing (Chu et al., 2022; Chu et al., 2020). Therefore, future fundamental investigations can focus on particle shape and background flow. The knowledge from these studies will be particularly relevant for lab-on-a-chip applications.
Chemical swimming with other modes of swimming: Active diffusiophoresis provides a convenient way to control trajectories using shape and surface heterogeneity. However, these trajectories can be further controlled by combining two different modes of swimming. In Raj et al. (2023a), the authors investigated the combination of chemical and mechanical modes of swimming simultaneously, and noted that even reciprocal strokes yield nonreciprocal displacement when both modes are employed simultaneously. Similar investigations with other modes of activation such as electric fields and magnetic fields could provide improved control over particle trajectories (Lee et al., 2023a).
Combination of active and passive diffusiophoresis: Combining the two modes provides an exciting opportunity to exploit the two features described, i.e., diffusiophoretic focusing and orientation-dependent motion. This might enable a finer control on life-like crystal formation due to active control, for instance, to only occur in a certain region where particles focus due to passive control.
Applications: In addition to the applications described earlier, diffusiophoresis presents several opportunities for future applications. Similar to its role in laundry (Shin et al., 2018), diffusiophoresis can be used for cleaning membranes or removing particles from electrodes. Additionally, by triggering reaction-diffusion instabilities (Alessio and Gupta, 2023a), Turing patterns may allow one to sense external chemical concentration. Another possibility for sensing applications is to use passive and active diffusiophoresis simultaneously to create shape-shifting patterns in real-time for detection of harmful chemicals.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
AGa: Conceptualization, Writing–original draft, Writing–review and editing, Data curation. BA: Conceptualization, Data curation, Writing–original draft, Writing–review and editing. AGu: Conceptualization, Writing–original draft, Writing–review and editing, Supervision.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. AG thanks the National Science Foundation (CBET - 2238412) CAREER award for financial support. Acknowledgement is made to the donors of the American Chemical Society Petroleum Research Fund for partial support of this research.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abécassis, B., Cottin-Bizonne, C., Ybert, C., Ajdari, A., and Bocquet, L. (2008). Boosting migration of large particles by solute contrasts. Nat. Mater. 7, 785–789. doi:10.1038/nmat2254
Alessio, B. M., and Gupta, A. (2023a). Diffusiophoresis-enhanced turing patterns. Sci. Adv. 9, eadj2457. doi:10.1126/sciadv.adj2457
Alessio, B. M., and Gupta, A. (2023b). The ubiquity of diffusiophoresis: exploring human population dynamics while including concentration gradient-driven advection. Available at: https://arxiv.org/catchup?smonth=9&sday=27&group=grp_&archive=cond-mat&num=2000&order=reverse&method=without&syear=2023 (Accessed September 27, 2023).
Alessio, B. M., Shim, S., Gupta, A., and Stone, H. A. (2022). Diffusioosmosis-driven dispersion of colloids: a taylor dispersion analysis with experimental validation. J. Fluid Mech. 942, A23. doi:10.1017/jfm.2022.321
Alessio, B. M., Shim, S., Mintah, E., Gupta, A., and Stone, H. A. (2021). Diffusiophoresis and diffusioosmosis in tandem: two-dimensional particle motion in the presence of multiple electrolytes. Phys. Rev. Fluids 6, 054201. doi:10.1103/physrevfluids.6.054201
Anderson, J., Lowell, M., and Prieve, D. (1982). Motion of a particle generated by chemical gradients Part 1. Non-electrolytes. J. Fluid Mech. 117, 107–121. doi:10.1017/s0022112082001542
Anderson, J. L. (1989). Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 21, 61–99. doi:10.1146/annurev.fl.21.010189.000425
Anderson, J. L., and Prieve, D. C. (1984). Diffusiophoresis: migration of colloidal particles in gradients of solute concentration. Sep. Purif. Methods 13, 67–103. doi:10.1080/03602548408068407
Aubret, A., Youssef, M., Sacanna, S., and Palacci, J. (2018). Targeted assembly and synchronization of self-spinning microgears. Nat. Phys. 14, 1114–1118. doi:10.1038/s41567-018-0227-4
Ault, J. T., Warren, P. B., Shin, S., and Stone, H. A. (2017). Diffusiophoresis in one-dimensional solute gradients. Soft Matter 13, 9015–9023. doi:10.1039/c7sm01588g
Banerjee, A., and Squires, T. M. (2019). Long-range, selective, on-demand suspension interactions: combining and triggering soluto-inertial beacons. Sci. Adv. 5, eaax1893. doi:10.1126/sciadv.aax1893
Banerjee, A., Williams, I., Azevedo, R. N., Helgeson, M. E., and Squires, T. M. (2016). Soluto-inertial phenomena: designing long-range, long-lasting, surface-specific interactions in suspensions. Proc. Natl. Acad. Sci. 113, 8612–8617. doi:10.1073/pnas.1604743113
Cates, M. E., and Tailleur, J. (2015). Motility-induced phase separation. Annu. Rev. Condens. Matter Phys. 6, 219–244. doi:10.1146/annurev-conmatphys-031214-014710
Chiang, T.-Y., and Velegol, D. (2014). Multi-ion diffusiophoresis. J. Colloid Interface Sci. 424, 120–123. doi:10.1016/j.jcis.2014.03.003
Chiu, Y. C., and Keh, H. J. (2018). Diffusiophoresis of a charged porous particle in a charged cavity. J. Phys. Chem. B 122, 9803–9814. doi:10.1021/acs.jpcb.8b06967
Chu, H. C., Garoff, S., Tilton, R. D., and Khair, A. S. (2020). Advective-diffusive spreading of diffusiophoretic colloids under transient solute gradients. Soft Matter 16, 238–246. doi:10.1039/c9sm01938c
Chu, H. C., Garoff, S., Tilton, R. D., and Khair, A. S. (2021). Macrotransport theory for diffusiophoretic colloids and chemotactic microorganisms. J. Fluid Mech. 917, A52. doi:10.1017/jfm.2021.322
Chu, H. C., Garoff, S., Tilton, R. D., and Khair, A. S. (2022). Tuning chemotactic and diffusiophoretic spreading via hydrodynamic flows. Soft Matter 18, 1896–1910. doi:10.1039/d2sm00139j
Das, S., Garg, A., Campbell, A. I., Howse, J., Sen, A., Velegol, D., et al. (2015). Boundaries can steer active janus spheres. Nat. Commun. 6, 8999. doi:10.1038/ncomms9999
Deng, J., Molaei, M., Chisholm, N. G., Yao, T., Read, A., and Stebe, K. J. (2022). Active colloids on fluid interfaces. Curr. Opin. Colloid and Interface Sci. 61, 101629. doi:10.1016/j.cocis.2022.101629
Derjaguin, B., Sidorenkov, G., Zubashchenkov, E., and Kiseleva, E. (1947). Kinetic phenomena in boundary films of liquids. Kolloidn. zh 9. doi:10.1016/0079-6816(93)90023-o
Doan, V. S., Chun, S., Feng, J., and Shin, S. (2021). Confinement-dependent diffusiophoretic transport of nanoparticles in collagen hydrogels. Nano Lett. 21, 7625–7630. doi:10.1021/acs.nanolett.1c02251
Doan, V. S., Kim, D.-O., Snoeyink, C., Sun, Y., and Shin, S. (2023). Shape-and orientation-dependent diffusiophoresis of colloidal ellipsoids. Phys. Rev. E 107, L052602. doi:10.1103/physreve.107.l052602
Dwivedi, P., Pillai, D., and Mangal, R. (2022). Self-propelled swimming droplets. Curr. Opin. Colloid and Interface Sci. 61, 101614. doi:10.1016/j.cocis.2022.101614
Ebel, J., Anderson, J. L., and Prieve, D. (1988). Diffusiophoresis of latex particles in electrolyte gradients. Langmuir 4, 396–406. doi:10.1021/la00080a024
Esteban-Fernández de Ávila, B., Loper-Ramirez, M. A., Báez, D. F., Jodra, A., Singh, V. V., Kaufman, K., et al. (2016). Aptamer-modified graphene-based catalytic micromotors: off–on fluorescent detection of ricin. ACS Sensors 1, 217–221. doi:10.1021/acssensors.5b00300
Florea, D., Musa, S., Huyghe, J. M., and Wyss, H. M. (2014). Long-range repulsion of colloids driven by ion exchange and diffusiophoresis. Proc. Natl. Acad. Sci. 111, 6554–6559. doi:10.1073/pnas.1322857111
Ganguly, A., and Gupta, A. (2023). Going in circles: slender body analysis of a self-propelling bent rod. Phys. Rev. Fluids 8, 014103. doi:10.1103/physrevfluids.8.014103
Ganguly, A., Roychowdhury, S., and Gupta, A. (2023). Universal mobility relationship for phoretic and self-phoretic particles with arbitrary interaction potentials. submitted.
Gao, W., Dong, R., Thamphiwatana, S., Li, J., Gao, W., Zhang, L., et al. (2015). Artificial micromotors in the mouse’s stomach: a step toward in vivo use of synthetic motors. ACS Nano 9, 117–123. doi:10.1021/nn507097k
Golestanian, R., Liverpool, T., and Ajdari, A. (2007). Designing phoretic micro-and nano-swimmers. New J. Phys. 9, 126. doi:10.1088/1367-2630/9/5/126
Gupta, A., Rallabandi, B., and Stone, H. A. (2019). Diffusiophoretic and diffusioosmotic velocities for mixtures of valence-asymmetric electrolytes. Phys. Rev. Fluids 4, 043702. doi:10.1103/physrevfluids.4.043702
Gupta, A., Shim, S., and Stone, H. A. (2020). Diffusiophoresis: from dilute to concentrated electrolytes. Soft Matter 16, 6975–6984. doi:10.1039/d0sm00899k
Henrique, F., Zuk, P. J., and Gupta, A. (2022a). Charging dynamics of electrical double layers inside a cylindrical pore: predicting the effects of arbitrary pore size. Soft Matter 18, 198–213. doi:10.1039/d1sm01239h
Henrique, F., Zuk, P. J., and Gupta, A. (2022b). Impact of asymmetries in valences and diffusivities on the transport of a binary electrolyte in a charged cylindrical pore. Electrochimica Acta 433, 141220. doi:10.1016/j.electacta.2022.141220
Henrique, F., Zuk, P. J., and Gupta, A. (2023). Kirchhoff’s laws for electric-double-layer charging in arbitrary porous networks. Available at: https://arxiv.org/pdf/2308.13100.pdf.
Jarvey, N., Henrique, F., and Gupta, A. (2022). Ion transport in an electrochemical cell: a theoretical framework to couple dynamics of double layers and redox reactions for multicomponent electrolyte solutions. J. Electrochem. Soc. 169, 093506. doi:10.1149/1945-7111/ac908e
Jarvey, N., Henrique, F., and Gupta, A. (2023). Asymmetric rectified electric and concentration fields in multicomponent electrolytes with surface reactions. Soft Matter 19, 6032–6045. doi:10.1039/D3SM00823A
Kar, A., Chiang, T.-Y., Ortiz Rivera, I., Sen, A., and Velegol, D. (2015). Enhanced transport into and out of dead-end pores. ACS Nano 9, 746–753. doi:10.1021/nn506216b
Katsamba, P., Michelin, S., and Montenegro-Johnson, T. D. (2020). Slender phoretic theory of chemically active filaments. J. Fluid Mech. 898, A24. doi:10.1017/jfm.2020.410
Keh, H.-J., and Anderson, J. (1985). Boundary effects on electrophoretic motion of colloidal spheres. J. Fluid Mech. 153, 417–439. doi:10.1017/s002211208500132x
Keh, H. J., and Wei, Y. K. (2000). Diffusiophoretic mobility of spherical particles at low potential and arbitrary double-layer thickness. Langmuir 16, 5289–5294. doi:10.1021/la991373k
Kümmel, F., Ten Hagen, B., Wittkowski, R., Buttinoni, I., Eichhorn, R., Volpe, G., et al. (2013). Circular motion of asymmetric self-propelling particles. Phys. Rev. Lett. 110, 198302. doi:10.1103/physrevlett.110.198302
Lee, J. G., Thome, C. P., Cruse, Z. A., Ganguly, A., Gupta, A., and Shields, C. W. (2023a). Magnetically locked Janus particle clusters with orientation-dependent motion in AC electric fields. Nanoscale 15, 16268–16276. doi:10.1039/D3NR03744D
Lee, S., Lee, J., and Ault, J. T. (2023b). The role of variable zeta potential on diffusiophoretic and diffusioosmotic transport. Colloids Surfaces A Physicochem. Eng. Aspects 659, 130775. doi:10.1016/j.colsurfa.2022.130775
Lee, T. C., and Keh, H. J. (2014). Electrophoretic motion of a charged particle in a charged cavity. Eur. J. Mechanics-B/Fluids 48, 183–192. doi:10.1016/j.euromechflu.2014.06.004
Li, W. C., and Keh, H. J. (2016). Diffusiophoretic mobility of charge-regulating porous particles. Electrophoresis 37, 2139–2146. doi:10.1002/elps.201600091
Lisicki, M., Reigh, S. Y., and Lauga, E. (2018). Autophoretic motion in three dimensions. Soft Matter 14, 3304–3314. doi:10.1039/c8sm00194d
Luo, M., Li, S., Wan, J., Yang, C., Chen, B., and Guan, J. (2020). Enhanced propulsion of urease-powered micromotors by multilayered assembly of ureases on Janus magnetic microparticles. Langmuir 36. doi:10.1021/acs.langmuir.9b03315
Maini, P. K., Woolley, T. E., Baker, R. E., Gaffney, E. A., and Lee, S. S. (2012). Turing’s model for biological pattern formation and the robustness problem. Interface Focus 2, 487–496. doi:10.1098/rsfs.2011.0113
Michelin, S., and Lauga, E. (2014). Phoretic self-propulsion at finite Péclet numbers. J. Fluid Mech. 747, 572–604. doi:10.1017/jfm.2014.158
Mondal, B., Bhattacharyya, S., Majhi, S., and Ohshima, H. (2023). Diffusiophoresis of a soft particle incorporating ion partitioning and hydrophobic core. Phys. Fluids 35. doi:10.1063/5.0156467
Murray, J. D., (2003). Mathematical biology: II: spatial models and biomedical applications, vol. 3. Cham: Springer.
Palacci, J., Sacanna, S., Steinberg, A. P., Pine, D. J., and Chaikin, P. M. (2013). Living crystals of light-activated colloidal surfers. Science 339, 936–940. doi:10.1126/science.1230020
Peng, F., Tu, Y., Van Hest, J. C., and Wilson, D. A. (2015). Self-guided supramolecular cargo-loaded nanomotors with chemotactic behavior towards cells. Angew. Chem. Int. Ed. 54, 11662–11665. doi:10.1002/anie.201504186
Poehnl, R., Popescu, M. N., and Uspal, W. E. (2020). Axisymmetric spheroidal squirmers and self-diffusiophoretic particles. J. Phys. Condens. Matter 32, 164001. doi:10.1088/1361-648x/ab5edd
Poehnl, R., and Uspal, W. (2021). Phoretic self-propulsion of helical active particles. J. Fluid Mech. 927, A46. doi:10.1017/jfm.2021.801
Popescu, M., Uspal, W., Eskandari, Z., Tasinkevych, M., and Dietrich, S. (2018). Effective squirmer models for self-phoretic chemically active spherical colloids. Eur. Phys. J. E 41, 1–24. doi:10.1140/epje/i2018-11753-1
Prieve, D., Anderson, J., Ebel, J., and Lowell, M. (1984). Motion of a particle generated by chemical gradients. Part 2. Electrolytes. J. Fluid Mech. 148, 247–269. doi:10.1017/s0022112084002330
Prieve, D. C., Malone, S. M., Khair, A. S., Stout, R. F., and Kanj, M. Y. (2019). Diffusiophoresis of charged colloidal particles in the limit of very high salinity. Proc. Natl. Acad. Sci. 116, 18257–18262. doi:10.1073/pnas.1701391115
Raj, R. R., Ganguly, A., Becker, C., Shields IV, C. W., and Gupta, A. (2023a). Motion of an active bent-rod with an articulating hinge: exploring mechanical and chemical modes of swimming. Front. Phys. Sec. Fluid Dynamics 11. doi:10.3389/fphy.2023.1307691
Raj, R. R., Shields, C. W., and Gupta, A. (2023b). Two-dimensional diffusiophoretic colloidal banding: optimizing the spatial and temporal design of solute sinks and sources. Soft Matter 19, 892–904. doi:10.1039/d2sm01549h
Raman, H., Das, S., Sharma, H., Singh, K., Gupta, S., and Mangal, R. (2023). Dynamics of active SiO2–Pt Janus colloids in dilute poly (ethylene oxide) solutions. ACS Phys. Chem. Au 3, 279–289. doi:10.1021/acsphyschemau.2c00056
Ramm, B., Goychuk, A., Khmelinskaia, A., Blumhardt, P., Eto, H., Ganzinger, K. A., et al. (2021). A diffusiophoretic mechanism for ATP-driven transport without motor proteins. Nat. Phys. 17, 850–858. doi:10.1038/s41567-021-01213-3
Rath, M., Weaver, J., Wang, M., and Woehl, T. (2021). pH-mediated aggregation-to-separation transition for colloids near electrodes in oscillatory electric fields. Langmuir 37, 9346–9355. doi:10.1021/acs.langmuir.1c00671
Sambamoorthy, S., and Chu, H. C. (2023). Diffusiophoresis of a spherical particle in porous media. Soft Matter 19, 1131–1143. doi:10.1039/d2sm01620f
Schnitzer, O., and Yariv, E. (2015). Osmotic self-propulsion of slender particles. Phys. Fluids 27. doi:10.1063/1.4914417
Sharifi-Mood, N., Koplik, J., and Maldarelli, C. (2013). Diffusiophoretic self-propulsion of colloids driven by a surface reaction: the sub-micron particle regime for exponential and van der Waals interactions. Phys. Fluids 25. doi:10.1063/1.4772978
Shi, N., Nery-Azevedo, R., Abdel-Fattah, A. I., and Squires, T. M. (2016). Diffusiophoretic focusing of suspended colloids. Phys. Rev. Lett. 117, 258001. doi:10.1103/physrevlett.117.258001
Shin, S., Ault, J. T., Feng, J., Warren, P. B., and Stone, H. A. (2017a). Low-cost zeta potentiometry using solute gradients. Adv. Mater. 29, 1701516. doi:10.1002/adma.201701516
Shin, S., Ault, J. T., Toda-Peters, K., and Shen, A. Q. (2020). Particle trapping in merging flow junctions by fluid-solute-colloid-boundary interactions. Phys. Rev. Fluids 5, 024304. doi:10.1103/physrevfluids.5.024304
Shin, S., Ault, J. T., Warren, P. B., and Stone, H. A. (2017b). Accumulation of colloidal particles in flow junctions induced by fluid flow and diffusiophoresis. Phys. Rev. X 7, 041038. doi:10.1103/physrevx.7.041038
Shin, S., Shardt, O., Warren, P. B., and Stone, H. A. (2017c). Membraneless water filtration using CO2. Nat. Commun. 8, 15181. doi:10.1038/ncomms15181
Shin, S., Um, E., Sabass, B., Ault, J. T., Rahimi, M., Warren, P. B., et al. (2016). Size-dependent control of colloid transport via solute gradients in dead-end channels. Proc. Natl. Acad. Sci. 113, 257–261. doi:10.1073/pnas.1511484112
Shin, S., Warren, P. B., and Stone, H. A. (2018). Cleaning by surfactant gradients: particulate removal from porous materials and the significance of rinsing in laundry detergency. Phys. Rev. Appl. 9, 034012. doi:10.1103/physrevapplied.9.034012
Shklyaev, S., Brady, J. F., and Córdova-Figueroa, U. M. (2014). Non-spherical osmotic motor: chemical sailing. J. Fluid Mech. 748, 488–520. doi:10.1017/jfm.2014.177
Singh, N., Vladisavljević, G. T., Nadal, F., Cottin-Bizonne, C., Pirat, C., and Bolognesi, G. (2020). Reversible trapping of colloids in microgrooved channels via diffusiophoresis under steady-state solute gradients. Phys. Rev. Lett. 125 (24), 248002.
Singh, N., Vladisavljević, G. T., Nadal, F., Cottin-Bizonne, C., Pirat, C., and Bolognesi, G. (2022a). Enhanced accumulation of colloidal particles in microgrooved channels via diffusiophoresis and steady-state electrolyte flows. Langmuir. 38 (46), 14053–14062.
Singh, N., Chakra, A., Vladisavljević, G. T., Cottin-Bizonne, C., Pirat, C., and Bolognesi, G. (2022b). Composite Norland Optical Adhesive (NOA)/silicon flow focusing devices for colloidal particle manipulation and synthesis. Colloids Surf. A: Physicochem. Eng. 652, 129808.
Somasundar, A., Qin, B., Shim, S., Bassler, B. L., and Stone, H. A. (2023). Diffusiophoretic particle penetration into bacterial biofilms. ACS Appl. Mater. Interfaces 15, 33263–33272. doi:10.1021/acsami.3c03190
Staffeld, P. O., and Quinn, J. A. (1989). Diffusion-induced banding of colloid particles via diffusiophoresis: 1. Electrolytes. J. Colloid Interface Sci. 130, 69–87. doi:10.1016/0021-9797(89)90079-9
Stone, H. A., and Samuel, A. D. (1996). Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 77, 4102–4104. doi:10.1103/physrevlett.77.4102
Tan, H., Banerjee, A., Shi, N., Tang, X., Abdel-Fattah, A., and Squires, T. M. (2021). A two-step strategy for delivering particles to targets hidden within microfabricated porous media. Sci. Adv. 7, eabh0638. doi:10.1126/sciadv.abh0638
Turing, A. M. (1952). The chemical basis of morphogenesis. Philosophical Trans. R. Soc. Lond. 327. doi:10.1007/BF02459572
Velegol, D., Garg, A., Guha, R., Kar, A., and Kumar, M. (2016). Origins of concentration gradients for diffusiophoresis. Soft Matter 12, 4686–4703. doi:10.1039/c6sm00052e
Wang, K., Behdani, B., and Silvera Batista, C. A. (2022a). Visualization of concentration gradients and colloidal dynamics under electrodiffusiophoresis. Langmuir 38, 5663–5673. doi:10.1021/acs.langmuir.2c00252
Wang, K., Leville, S., Behdani, B., and Batista, C. A. S. (2022b). Long-range transport and directed assembly of charged colloids under aperiodic electrodiffusiophoresis. Soft Matter 18, 5949–5959. doi:10.1039/d2sm00631f
Wang, L., Kaeppler, A., Fischer, D., and Simmchen, J. (2019a). Photocatalytic TiO2 micromotors for removal of microplastics and suspended matter. ACS Appl. Mater. Interfaces 11, 32937–32944. doi:10.1021/acsami.9b06128
Wang, Y., Duan, W., Zhou, C., Liu, Q., Gu, J., Ye, H., et al. (2019b). Phoretic liquid metal micro/nanomotors as intelligent filler for targeted microwelding. Adv. Mater. 31, 1905067. doi:10.1002/adma.201905067
Wang, Y., Zhou, C., Wang, W., Xu, D., Zeng, F., Zhan, C., et al. (2018). Photocatalytically powered matchlike nanomotor for light-guided active SERS sensing. Angew. Chem. 130, 13294–13297. doi:10.1002/ange.201807033
Wilson, J. L., Shim, S., Yu, Y. E., Gupta, A., and Stone, H. A. (2020). Diffusiophoresis in multivalent electrolytes. Langmuir 36, 7014–7020. doi:10.1021/acs.langmuir.9b03333
Yariv, E. (2019). Self-diffusiophoresis of slender catalytic colloids. Langmuir 36, 6903–6915. doi:10.1021/acs.langmuir.9b02393
Zhao, H., Košmrlj, A., and Datta, S. S. (2023). Chemotactic motility-induced phase separation. Phys. Rev. Lett. 131, 118301. doi:10.1103/physrevlett.131.118301
Keywords: colloids, Turing patterns, microfluidics, microbot, propulsion, differential equations, biomedical
Citation: Ganguly A, Alessio BM and Gupta A (2023) Diffusiophoresis: a novel transport mechanism - fundamentals, applications, and future opportunities. Front. Sens. 4:1322906. doi: 10.3389/fsens.2023.1322906
Received: 17 October 2023; Accepted: 13 November 2023;
Published: 30 November 2023.
Edited by:
Chang-Soo Lee, Chungnam National University, Republic of KoreaReviewed by:
Jesse Ault, Brown University, United StatesCopyright © 2023 Ganguly, Alessio and Gupta. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ankur Gupta, YW5rdXIuZ3VwdGFAY29sb3JhZG8uZWR1
 Arkava Ganguly
Arkava Ganguly Benjamin M. Alessio
Benjamin M. Alessio Ankur Gupta
Ankur Gupta