Dual-Parameter Sensing With a Single Supermode Interferometer

Optical fiber interferometers have intrinsic sensitivity to temperature, thus, in sensing applications; they need a reference temperature sensor or a mechanism to control the temperature. Here, we demonstrate that a single multicore fiber interferometer can monitor two parameters simultaneously; more particularly, refractive index, and temperature. The interferometer is easy to manufacture; a short segment of an optical fiber with seven coupled cores is fusion spliced at the distal end of a conventional single mode optical fiber. In the coupled-core fiber, two supermodes beat; this makes the reflection spectrum of the device to exhibit a well-defined series of maxima and minima. The refractive index of a sample in contact with multicore fiber alters the amplitude of the interference pattern and temperature induces a shift to such a pattern. The changes of the interference pattern are easy to monitor and decode with a low-resolution spectrometer. As an application of our dual-parameter sensor, the thermo-optic coefficient of a sample was measured.

Introduction

Optical fibers are made of materials that have an intrinsic sensitivity to temperature. Consequently, they have been widely used for point and distributed temperature sensing; see for example (Huang et al., 2021) for a brief summary of such applications. However, the temperature sensitivity is an issue when one devises an optical fiber interferometer to sense other physical parameters, as for example, the refractive index of a sample. Thus, for such application, it is necessary to control the temperature during the measurements or to compensate its effect on the interferometer. Another alternative is to monitor temperature and refractive index simultaneously. In this manner, one knows at which temperature the refractive index was measured. In an ideal case, it would be desirable that the same interferometer monitors temperature and refractive index with high accuracy. In addition, the interferometer should be compact, easy to fabricate, and its interrogation should be as simple as possible. We believe that no such ideal dual-parameter optical fiber interferometric sensor currently exists.

The optical fiber sensor community has long been striving to achieve compact and functional dual-parameter fiber optic sensing devices. In (Pevec and Donlagić, 2019), for example, a variety of sensing architectures that can monitor two parameters are reviewed. The vast majority of such schemes need two sensors; one is used as a reference, or two different platforms to monitor two magnitudes, usually temperature, and the target parameter. However, the fabrication of a sensing device that has a reference, or that is composed by two platforms, tend to be complex as it may entail several steps or elaborated procedures. Hence, they may be impractical for real-world applications.

So far, several sensors based on a single platform that are capable of monitoring refractive index and temperature have been proposed in the literature. These include long-period gratings (Hu et al., 2012; Huang et al., 2013; Du et al., 2019;Pang et al., 2020; Shang et al., 2020), tilted fiber Bragg gratings (Wong et al., 2011; Jiang et al., 2017), and Fabry-Perot interferometers with a single cavity (Wang and Wang, 2012; Tan et al., 2014; André et al., 2016; Wu et al., 2019; Flores-Bravo et al., 2021b). Optical fibers coated with a thin gold layer have also been proposed for index and temperature sensing (Xiao et al., 2014; Velázquez-González et al., 2017; Alonso-Murias et al., 2019; Zhang et al., 2021b). The chief disadvantage of grating-based sensors is their low sensitivity in the important refractive index range around 1.33 and their expensive interrogation. The drawbacks of sensors based on cavities or metal-coated fibers include poor reproducibility or issues related with their reusability.

Single optical fiber interferometers have also been proposed for simultaneous sensing of index and temperature. Such interferometer can be built with conventional optical fibers (Xiong et al., 2014; Wang et al., 2016; Yu et al., 2016), polarization-maintaining fibers (Kim and Han, 2011; Zhao et al., 2017), or multicore fibers (Zhang et al., 2017; Madrigal et al., 2019). The inconvenience of such interferometers is the need of multi-step or manual fabrication processes, which usually lead to low reproducibility. Structures composed by a segment of multimode fiber spliced to single mode fiber (Kim et al., 2012; Xue et al., 2013; Zhao et al., 2015; Musa et al., 2018) have been demonstrated for index and temperature measurements as well. The disadvantage in these cases is the lack of control on the number of modes that are excited in the multimode optical fiber. Such lack of control on the mode interference may lead to inaccurate refractive index measurements.

In this work, we report advances on our previously reported index-temperature multicore fiber interferometer (Flores-Bravo et al., 2021a). We have investigated analytically and experimentally the performance of our dual-parameter sensor in a broader refractive index range. Moreover, the signal process reported here is simpler with the advantage that the accuracy of the sensor is improved. A simple expression is provided to calibrate the sensor and its potential to measure the thermo-optic coefficient of a sample is also demonstrated.

Theoretical Considerations

The cross section of the multicore fiber (MCF) used to fabricate our interferometer; its structure and interrogation are shown in Figure 1. The MCF has been described in more detail in (Amorebieta et al., 2019; Flores-Bravo et al., 2021a). To assemble the interferometer, the multicore fiber was fusion spliced at the distal end of a conventional single mode fiber (SMF). After that, the MCF was cleaved at a length L. As demonstrated in (Flores-Bravo et al., 2021a), the length of the MCF is not critical in the sensitivity of the interferometer when it is used for refractive index and temperature sensing. Thus, we chose L = 3.7 cm. In our device, the cleaved end of the MCF works as a reflector that is sensitive to the refractive index of a sample.

FIGURE 1

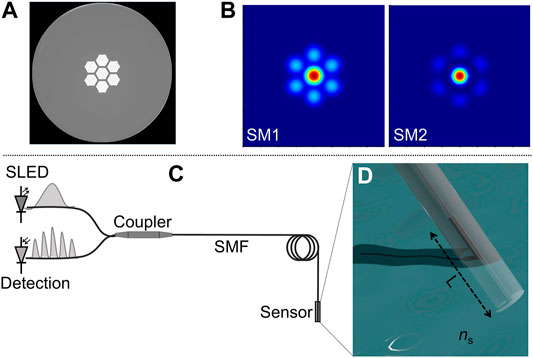
FIGURE 1. (A) Cross section of the multicore fiber used in the experiments. (B) Profile of the two supermodes (SM) excited in the MCF. (C) Schematic representation of the interrogation system; the injected and reflected light from the device are illustrated with a broad and multiple peak “spectrum”, respectively. (D) Illustration of the sensor immersed in a sample with refractive index of ns; L is the length of the MCF segment.

The working mechanism of the SMF-MCF structure has also been discussed in (Flores-Bravo et al., 2021a) with certain detail. The fundamental SMF mode excites two supermodes in the MCF whose profiles are shown in Figure 1B. The propagation constants of the two supermodes can be denoted as ${\beta }_1$ and ${\beta }_2$. The difference between them can be expressed as $\text{Δ}\beta =2\pi \Delta n_{ef}/\lambda$, where $\Delta n_{ef}= n_{e1}-n_{e2}$, the latter are the effective refractive indices of the two supermodes excited in the MCF and λ is the wavelength of the excitation light source. The wavelength dependence of $\Delta n_{ef}$ of the MCF shown in Figure 1A can be found in (Flores-Bravo et al., 2021a).

The intensity of the reflected spectrum of our MCF interferometer can be expressed as:

$I_r\left(\lambda , n_s\right) = I_s\left(\lambda \right)R_F\left(n_s\right)\left(I_1+I_2\right)\left[1+V\mathrm{c}\mathrm{o}\mathrm{s}\left(2\mathrm{\Delta }\mathrm{\varphi }\right)\right](1)$

In Eq. 1, $I_s\left(\lambda \right)$ denotes the profile of the light source, $I_1$ and $I_2$ denote the intensities of the supermodes that are excited in the MCF and the phase difference between them is $\text{Δ}\varphi =2\pi \mathrm{\Delta }{n}_{ef}L/\lambda$. In Eq. 1, $R_F\left(n_s\right)={\left[(n_c-n_s)/(n_c+n_s)\right]}^2$ is the Fresnel reflection coefficient where $n_c$ is the refractive index of the MCF core, which is known or can be chosen, and $n_s$ the refractive index of the sample we want to measure. $V=2\sqrt{I_1{I}_2}/(I_1+I_2)$; it is known as the visibility of the interference pattern; a parameter that is easy to measure.

When the external medium is air, the Fresnel reflection coefficient can be denoted as $R_1$. In this case, the maximum of the reflection spectrum ($I_{mx}$) given in Eq. 1 is $I_{mx}=I_0{R}_1(I_1+I_2)(1+V)$; where $I_0$ is the maximum of $I_s\left(\lambda \right)$. To avoid the effect of power fluctuations of the light source on the performance of our sensor, Eq. 1 can be divided by $I_{mx}$, a value that is easy to measure experimentally. Thus, the normalized reflection of our MCF interferometer can be expressed as

$R\left(\lambda , n_s\right) = \left[I_s\left(\lambda \right)R_F\left(n_s\right)/\left(I_0{R}_1\right)\right]\cdot \left[1+\mathrm{V}\mathrm{c}\mathrm{o}\mathrm{s}\left(2\mathrm{\Delta }\mathrm{\varphi }\right)\right]/\left(1+V \right)(2)$

From Eq. 2, it can be noted that the reflection spectrum of our MCF interferometer has two well-defined components. The first term on the right hand side of Eq. 2 depends exclusively on the refractive index of the sample, while the second term depends on the supermodes excited in the MCF. As it was mentioned before, the MCF is sensitive to temperature. Thus, the second term on the right hand side of Eq. 2 depends exclusively on temperature. Therefore, when the MCF interferometer is exposed to simultaneous changes of refractive index and temperature, it is expected that the interference pattern shifts and its amplitude changes. Hence, the key to measure index and temperature simultaneously depends on how the changes of the interference pattern are decoded. In our previous work (Flores-Bravo et al., 2021a), the fast Fourier transform was used to decode such changes. The disadvantage of the analysis in the Fourier domain is its low precision with the interference pattern has a long period, i.e., when the segment of MCF is short.

Here, a simpler signal deconvolution is used that works well for short MCF interferometers. For calibration purposes, we will take the reflection spectrum of the MCF interferometer when the external medium is air as a reference. This reference will be taken at a fixed temperature, at 25°C for example. We will see that this will simplify the calibration of the MCF interferometer as a refractive index and temperature sensor.

In Figure 2, we show the calculated interference patterns of an MCF interferometer at different values of $n_s$. For the calculations, it was assumed that V = 0.95, as this visibility is observed experimentally, L = 3.7 cm; the refractive index of MCF core ($n_c$) was considered to be 1.451. The refractive indices of the sample medium were between 1 and 1.440. The spectral distribution of the light source was considered to be Gaussian; $I_s\left(\lambda \right)=P_{s}exp\left[-{\left(\lambda -{\lambda }_0\right)}^2/\left(2\text{Δ}{\lambda }^2\right)\right]$. In the latter expression, the optical power, the peak wavelength, and the spectral width of the light source are denoted, respectively, as $P_s$, ${\lambda }_0,$ and $\text{Δ}\lambda$. In the simulations we considered the following values for the light source, ${\lambda }_0$ = 1,548 nm and $\text{Δ}\lambda$ = 39 nm. These values correspond to the superluminescent light emitting diode (SLED) we used in our experiments. The temperature was assumed to be constant in all cases shown in Figure 2.

FIGURE 2

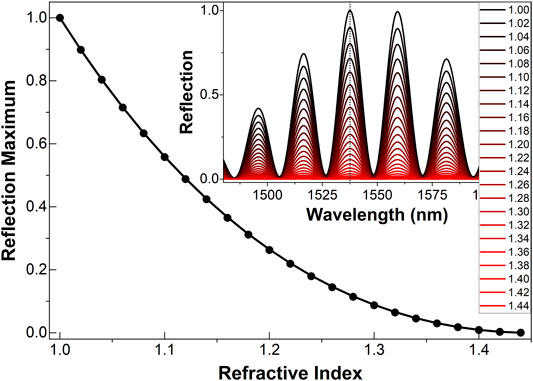
FIGURE 2. Calculated maxima of the interference patterns (dots) shown in the inset graph as a function of the refractive index. The continuous line is a fitting to the data. The list of values shown in the table are values of n_s. The dotted vertical line shown the maxima of the interference patterns.

The normalized absolute maximum of each interference pattern displayed in the inset graph of Figure 2 as a function of refractive index is shown in the figure with the continuous solid line. The maximum drops from 1 to nearly 0 when the refractive index of the sample is approximately equal to the index of the MCF core; this means that the measuring refractive index range of our MCF interferometer is between air and refractive indices lower that the index of the MCF core. Note in Figure 2 that for any value of $n_s$ between 1 and 1.440, the wavelength position of the interference pattern does not change. This is due to the fact that the temperature was assumed to be constant.

Let us now analyze the effect of temperature on the MCF interferometer and on the sample. The temperature range considered here was between 0 and 60°C approximately. At lower temperatures, a liquid sample may freeze, and at higher temperatures, it may boil or evaporate. In such a narrow temperature range, the index of the MCF core varies linearly with temperature; $n_c=n_0+{\gamma }_f\Delta T$, where $n_0$ is the index of the MCF core at a temperature $T_0$, ${\gamma }_f$ is the thermo-optic coefficient of the material the core is made of, and $\Delta T=T-T_0$, where $T$ is any temperature in the aforementioned range. The refractive index of the sample has a similar expression; the only difference is the sample’s index at a temperature $T_0$ and the value of its thermo-optic coefficient.

According to the literature, see for example (Adamovsky et al., 2012), the thermo-optic coefficient of germanium-doped silica is ${\gamma }_f\approx 2.37x{10}^{-5}$°C⁻¹. Thus, a small change in temperature will induce a minute change of $\Delta n_{ef}$, hence, of $\Delta \varphi$. Consequently, the interference pattern will shift linearly with temperature. In fact, this property has been exploited to develop MCF temperature sensors (Antonio-Lopez et al., 2014; Amorebieta et al., 2019). In such works, the temperature sensitivity of an MCF interferometer was found to be around 22 pm/°C for temperatures above 0°C and below 100°C.

It is important to point out that a shift of the interference pattern does not alter its maximum value, particularly, when the shift is small. For example, a temperature change of 45°C to our MCF interferometer will induce a shift to the reflection spectrum of around 1 nm. Hence, temperature cannot perturb the refractive index measurements as they are linked to the maxima of the reflection spectra and not to the maximum at a particular wavelength.

Next, we will show experimental results that were carried out at a constant temperature and when both, the refractive index of a sample and temperature changed in a controlled manner.

Experimental Results and Discussion

A 3.7 cm-long MCF interferometer was fabricated and calibrated as a refractive index sensor at a constant temperature. For the calibration, liquids with known refractive index from Cargille laboratories were used. Four liquids with indices of 1.295, 1.343, 1.382, and 1.440 (at λ = 1,550 nm) were chosen. As Cargille indices are calibrated at 25°C, we carried out the measurements at such a temperature in a commercial temperature calibrator (Fluke, model 9,103). Before immersing the MCF facet into the Cargille liquids, it was cleaned with ethyl alcohol and dried with air. As mentioned before, the reflection spectrum of the MCF in air at 25°C was taken as a reference.

Figure 3 shows the reflection spectra that were observed when the facet of the MCF interferometer was in air or immersed in the aforementioned calibrated refractive index liquids. All the spectra were divided by the absolute maximum of the reflection spectrum that was measured when the MCF was in air. The maximum of the reflection spectrum measured at each refractive index is also shown in Figure 3. The fitting to the experimental data (discrete squares in the figure) was carried out with the following expression:

$n_s = n_c\left(1-\sqrt{R_1{R}_m} \right)/\left(1+\sqrt{R_1{R}_m} \right)(3)$

FIGURE 3

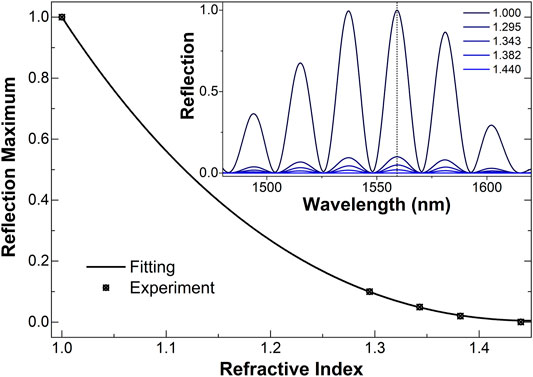
FIGURE 3. Measured maxima of the interference patterns shown in the inset graph as a function of refractive index. The solid line is a fitting to the experimental data which was calculated with Eq. 3. The dotted vertical line shows the maxima of the interference patterns.

In Eq. 3, $R_m$ is the maximum of the normalized interference pattern observed for each value of $n_s$; $R_1$ can be calculated with the Fresnel equation (mentioned above) provided that the index of air and $n_c$ are known. The refractive index of air can be found in the literature; a value of 1.0002739 is usually used, see for example (Kim and Su, 2004).

It is important to point out that most manufacturers of commercial optical fibers tend to keep secret the exact composition of materials they used to fabricate their fibers. For this reason, the exact value of $n_c$ may not be known. Hence, the calibration of index sensors based on commercial optical fibers may not be accurate. In our case, an ad hoc MCF was used to fabricate the interferometer. The cores of the MCF were made of germanium-doped silica where $n_c=1.451$ at λ = 1,550 nm.

With the MCF interferometer and the methodology here proposed, the refractive index of a sample only depends on the measurement of a single parameter; see Eq. 3, which is the maximum of a well-defined interference pattern. The latter can be easily measured experimentally at high speed and with high precision. This ensures accurate refractive index measurement. However, before measuring the refractive index of a sample, the MCF facet must be properly cleaned and dried. Dust particles or residues of a sample remaining on the MCF face can falsify the refractive index measurement. Cleaning of an optical fiber facet is straightforward and it is a common practice in the telecommunications industry. Presently, different fiber optic cleaning products are commercially available; same that can be used to clean the MCF interferometer.

Once the aforementioned calibration was carried out, we proceeded with an experiment in which the refractive index of a sample and temperature changed simultaneously in a controlled manner. For this experiment, the tip of the MCF interferometer was immersed in a Cargille liquid with $n_s=1.295$. Then, the MCF and the liquid were placed inside the temperature calibrator mentioned above. The temperature of the calibrator was varied from 0 to 60°C in steps of 5°C. In each step, we waited 10 min before collecting the interference patterns. In this manner, we ensured that the MCF interferometer and the Cargille liquid were at a stable temperature.

In Figure 4, we show some observed interference patterns at different temperatures. It is important to point out that all the patterns were divided by the maximum of the reflection of the MCF interferometer when it was in air and at 25°C. The changes in the interference pattern are evident. The shift of the interference patterns is due to refractive index changes of the MCF core caused by temperature. Changes of the maximum of the interference pattern are due to refractive index variations of the sample, which are also caused by temperature.

FIGURE 4

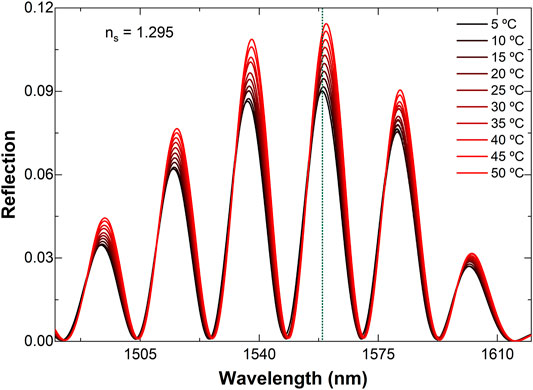
FIGURE 4. Interference patterns observed when the MCF interferometer immersed in a liquid with an index of 1.295 was exposed to different temperatures. The dotted vertical line is to show the shift of the interference patterns.

To calculate temperature from the spectra shown in Figure 4, we found the wavelength positions of the maxima. The shift of the patterns were calculated with respect to that at 25°C. The shift at different temperatures is plotted in the top graph of Figure 5. The slope of the fitting line of the interference pattern shifts versus temperature graph is the temperature sensitivity of our 3.7 cm-long MCF interferometer. It was found to be 21.57 ± 0.452 pm/°C, which is the same temperature sensitivity of an MCF interferometer calibrated in air (Amorebieta et al., 2019; Flores-Bravo et al., 2021a). This means that the presence of a liquid on the MCF face does not alter the temperature measurements and sensitivity of the interferometer, which in good agreement with what is predicted in Eq. 2.

FIGURE 5

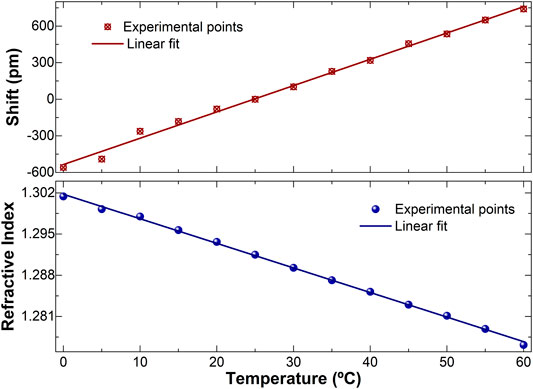
FIGURE 5. Shift of the interference pattern (top graph) and refractive index as a function of temperature (bottom graph) calculated from the spectra shown in Figure 4. The experimental points of the bottom graph were calculated with Eq. 3.

To calculate the refractive index of the sample at different temperatures from Figure 4, we used the calibration procedure discussed in Figure 3 and Eq. 3. The calculated indices as a function of temperature are shown in the bottom graph of Figure 5. The index of the sample decreased with temperature because the thermo-optic coefficient (${\gamma }_s$) of Cargille liquids is negative. The slope of the fitting line is the value of ${\gamma }_s$, which was found to be ${\gamma }_s= -4.175\text{x}{10}^{-4}\pm 4.423\text{x}{10}^{-6}$°C⁻¹. In the data sheet of the referred Cargille liquid, a thermo-optic coefficient of ${\gamma }_s= -3.33\text{x}{10}^{-4}$ is provided, however, such a coefficient was measured at λ = 589.3 nm. In our case, the light source had a peak wavelength of 1,548 nm. Thus, we believe that our MCF interferometer can be useful to measure the thermo-optic coefficient of a sample.

It is important to point out that several refractive index sensors, in which the Fresnel reflection is monitored or measured, have been reported so far, see for example (Kim and Su, 2004; Su and Huang, 2007; Zhao et al., 2009; Shlyagin et al., 2013; Martinez-Manuel et al., 2019; Brientin et al., 2021; Xu et al., 2021). However, these sensors cannot provide any information of temperature. Ergo, they are legitimized to be used only when temperature is known or controlled. Refractive index sensors based on different interferometers have also been demonstrated (Zhao et al., 2019; Hu et al., 2020; Zhang et al., 2021a), but such interferometers cannot discriminate refractive index and temperature as in many cases refractive index induces a shift of the interference pattern.

Conclusion

In this work, we have reported on a compact and simple multicore fiber interferometer that has the capability to measure two parameters (refractive index and temperature) simultaneously. The multicore fiber used in our experiments had seven identical coupled cores embedded in a common cladding. To fabricate the device, tools, and equipment (optical fiber cleaver, fusion splicer, etc.) widely used in the telecommunications industry were employed. Thus, the fabrication of the MCF interferometers is inexpensive and reproducible.

In the interferometer reported here, two supermodes beat in the MCF segment; such beating gives rise to a reflection spectrum with a well-defined series of maxima and minima. The wavelength positions of such maxima changed with temperature in a predictable manner. It was found that the refractive index of the external medium did not perturb the wavelength positions of the interference pattern. This allowed us to monitor temperature with the interferometer. On the other hand, samples with different refractive indices in direct contact with the MCF facet modified the amplitude of the interference pattern while the wavelength positions of such a pattern were unaltered. We have demonstrated that the maximum of the interference pattern can be correlated with the refractive index of a sample. Therefore, our MCF interferometer can be used as a refractometer and as a thermometer at the same time.

The potential of the device here reported to measure the thermo-optic coefficient of a liquid was demonstrated. It is also feasible to measure the thermo-optic coefficient of gels, polymers or other materials that do not absorb light in the emission wavelength range of the excitation light source. The MCF interferometer can also be used to monitor other parameters along with temperature. The MCF facet can be coated with materials or layers whose refractive index change when they are exposed to physical or chemical parameters or gases. The advantage of our MCF interferometer is that with a simple signal processing it can provide information about the target parameter and temperature.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is part of the project No. PGC 2018-101997-B-I00 funded by the MCIN/AEI/10.13039/501100011033/ and FEDER, Una manera de hacer Europa.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to J. E. Antonio-Lopez, A. Schülzgen, and R. Amezcua-Correa from the College of Optics and Photonics, University of Central Florida, Orlando, U.S., for providing the multicore fiber described here.

References

Adamovsky, G., Lyuksyutov, S. F., Mackey, J. R., Floyd, B. M., Abeywickrema, U., Fedin, I., et al. (2012). Peculiarities of Thermo-Optic Coefficient under Different Temperature Regimes in Optical Fibers Containing Fiber Bragg Gratings. Opt. Commun. 285, 766–773. doi:10.1016/j.optcom.2011.10.084

CrossRef Full Text | Google Scholar

Alonso-Murias, M. d. C., Velazquez-Gonzalez, J. S., and Monzon-Hernandez, D. (2019). SPR Fiber Tip Sensor for the Simultaneous Measurement of Refractive Index, Temperature, and Level of a Liquid. J. Lightwave Technol. 37, 4808–4814. doi:10.1109/jlt.2019.2921302

CrossRef Full Text | Google Scholar

Amorebieta, J., Durana, G., Ortega-Gomez, A., Fernandez, R., Velasco, J., Saez de Ocariz, I., et al. (2019). Packaged Multi-Core Fiber Interferometer for High-Temperature Sensing. J. Lightwave Technol. 37, 2328–2334. doi:10.1109/jlt.2019.2903595

CrossRef Full Text | Google Scholar

André, R. M., Warren-Smith, S. C., Becker, M., Dellith, J., Rothhardt, M., Zibaii, M. I., et al. (2016). Simultaneous Measurement of Temperature and Refractive index Using Focused Ion Beam Milled Fabry-Perot Cavities in Optical Fiber Micro-tips. Opt. Express 24, 14053–14065. doi:10.1364/OE.24.014053

PubMed Abstract | CrossRef Full Text | Google Scholar

Antonio-Lopez, J. E., Eznaveh, Z. S., Likamwa, P., Schülzgen, A., and Amezcua-Correa, R. (2014). Multicore Fiber Sensor for High-Temperature Applications up to 1000°C. Opt. Lett. 39, 4309–4312. doi:10.1364/ol.39.004309

PubMed Abstract | CrossRef Full Text | Google Scholar

Brientin, A., Leduc, D., Gaillard, V., Girard, M., and Lupi, C. (2021). Numerical and Experimental Study of a Multimode Optical Fiber Sensor Based on Fresnel Reflection at the Fiber Tip for Refractive index Measurement. Opt. Laser Tech. 143, 107315. doi:10.1016/j.optlastec.2021.107315

CrossRef Full Text | Google Scholar

Du, C., Wang, Q., Hu, S., and Zhao, Y. (2019). Simultaneous Measurement of Refractive index and Temperature Based on a Long Period Fiber Grating Inscribed in a Photonic crystal Fiber with an Electric-Arc Discharge. Instrumentation Sci. Tech. 47, 185–194. doi:10.1080/10739149.2018.1508033

CrossRef Full Text | Google Scholar

Flores-Bravo, J. A., Fernandez, R., Antonio-Lopez, J. E., Zubia, J., Schulzgen, A., Amezcua Correa, R., et al. (2021a). Simultaneous Sensing of Refractive Index and Temperature with a Supermode Interferometer. J. Lightwave Tech. 1, 1. doi:10.1109/JLT.2021.3113863

CrossRef Full Text | Google Scholar

Flores-Bravo, J. A., Illarramendi, M. A., Zubia, J., and Villatoro, J. (2021b). Optical Fiber Interferometer for Temperature-independent Refractive index Measuring over a Broad Range. Opt. Laser Tech. 139, 106977. doi:10.1016/j.optlastec.2021.106977

CrossRef Full Text | Google Scholar

Hu, Y., Lin, Q., Yan, F., Xiao, L., Ni, L., Liang, W., et al. (2020). Simultaneous Measurement of the Refractive Index and Temperature Based on a Hybrid Fiber Interferometer. IEEE Sensors J. 20, 13411–13417. doi:10.1109/jsen.2020.3006089

CrossRef Full Text | Google Scholar

Huang, J., Albero Blanquer, L., Gervillie, C., and Tarascon, J.-M. (2021). Distributed Fiber Optic Sensing to Assess In-Live Temperature Imaging inside Batteries: Rayleigh and FBGs. J. Electrochem. Soc. 168, 6. doi:10.1149/1945-7111/ac03f0

CrossRef Full Text | Google Scholar

Huang, J., Lan, X., Kaur, A., Wang, H., Yuan, L., and Xiao, H. (2013). Optical Sensors Reflection-Based Phase-Shifted Long Period Fiber Grating for Simultaneous Measurement of Temperature and Refractive index. Opt. Eng. 52, 014404. doi:10.1117/1.oe.52.1.014404

CrossRef Full Text | Google Scholar

Jiang, B., Zhou, K., Wang, C., Zhao, Y., Zhao, J., and Zhang, L. (2017). Temperature-calibrated High-Precision Refractometer Using a Tilted Fiber Bragg Grating. Opt. Express 25, 25910–25918. doi:10.1364/oe.25.025910

PubMed Abstract | CrossRef Full Text | Google Scholar

Juan Hu, D. J., Lim, J. L., Jiang, M., Wang, Y., Luan, F., Ping Shum, P., et al. (2012). Long Period Grating Cascaded to Photonic crystal Fiber Modal Interferometer for Simultaneous Measurement of Temperature and Refractive index. Opt. Lett. 37, 2283–2285. doi:10.1364/ol.37.002283

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, C.-B., and Su, C. B. (2004). Measurement of the Refractive index of Liquids at 1.3 and 1.5 Micron Using a Fibre Optic Fresnel Ratio Meter. Meas. Sci. Technol. 15, 1683–1686. doi:10.1088/0957-0233/15/9/002

CrossRef Full Text | Google Scholar

Kim, H.-J., and Han, Y.-G. (2011). Polarization-dependent In-Line Mach–Zehnder Interferometer for Discrimination of Temperature and Ambient index Sensitivities. J. lightwave Technol. 30, 1037–1041. doi:10.1109/JLT.2011.2167597

CrossRef Full Text | Google Scholar

Kim, Y. H., Park, S. J., Jeon, S.-W., Ju, S., Park, C.-S., Han, W.-T., et al. (2012). Thermo-optic Coefficient Measurement of Liquids Based on Simultaneous Temperature and Refractive index Sensing Capability of a Two-Mode Fiber Interferometric Probe. Opt. Express 20, 23744–23754. doi:10.1364/oe.20.023744

PubMed Abstract | CrossRef Full Text | Google Scholar

Madrigal, J., Barrera, D., and Sales, S. (2019). Refractive index and Temperature Sensing Using Inter-core Crosstalk in Multicore Fibers. J. Lightwave Technol. 37, 4703–4709. doi:10.1109/jlt.2019.2917629

CrossRef Full Text | Google Scholar

Martínez-Manuel, R., Bautista-Morales, M. d. R., López-Cortés, D., Pineda-Arellano, C. A., Shlyagin, M. G., and Esteban, Ó. (2019). Multi-point Fiber Refractometer Using Fresnel Reflection and a Coherent Optical Frequency-Domain Multiplexing Technique. Appl. Opt. 58, 684–689. doi:10.1364/ao.58.000684

PubMed Abstract | CrossRef Full Text | Google Scholar

Musa, S. M. A., Baharin, N. F., Azmi, A. I., Ibrahim, R. K. R., Abdullah, A. S., Mohd Noor, M. Y., et al. (2018). Double-clad Fiber Michelson Interferometer for Measurement of Temperature and Refractive index. Microw Opt. Technol. Lett. 60, 822–827. doi:10.1002/mop.31056

CrossRef Full Text | Google Scholar

Pang, B., Gu, Z., Ling, Q., Wu, W., and Zhou, Y. (2020). Simultaneous Measurement of Temperature and Surrounding Refractive index by Superimposed Coated Long Period Fiber Grating and Fiber Bragg Grating Sensor Based on Mode Barrier Region. Optik 220, 165136. doi:10.1016/j.ijleo.2020.165136

CrossRef Full Text | Google Scholar

Pevec, S., and Donlagić, D. (2019). Multiparameter Fiber-Optic Sensors: A Review. Opt. Eng. 58, 072009. doi:10.1117/1.oe.58.7.072009

CrossRef Full Text | Google Scholar

Shang, B., Miao, Y., Zhang, H., and Zu, L. (2020). Structural Modulated Ultralong Period Microfiber Grating for the Simultaneous Measurement of the Refractive Index and Temperature in a Low-Refractive-Index Range. IEEE Sensors J. 20, 1329–1335. doi:10.1109/jsen.2019.2947298

CrossRef Full Text | Google Scholar

Shlyagin, M. G., Martínez Manuel, R., and Esteban, Ó. (2013). Optical-fiber Self-Referred Refractometer Based on Fresnel Reflection at the Fiber Tip. Sensors Actuators B: Chem. 178, 263–269. doi:10.1016/j.snb.2012.12.092

CrossRef Full Text | Google Scholar

Su, H., and Huang, X. G. (2007). Fresnel-reflection-based Fiber Sensor for On-Line Measurement of Solute Concentration in Solutions. Sensors Actuators B: Chem. 126, 579–582. doi:10.1016/j.snb.2007.04.008

CrossRef Full Text | Google Scholar

Tan, X. L., Geng, Y. F., Li, X. J., Deng, Y. L., Yin, Z., and Gao, R. (2014). UV-curable Polymer Microhemisphere-Based Fiber-Optic Fabry-Perot Interferometer for Simultaneous Measurement of Refractive Index and Temperature. IEEE Photon. J. 6, 1–8. doi:10.1109/jphot.2014.2332460

CrossRef Full Text | Google Scholar

Velázquez-González, J. S., Monzón-Hernández, D., Moreno-Hernández, D., Martínez-Piñón, F., and Hernández-Romano, I. (2017). Simultaneous Measurement of Refractive index and Temperature Using a SPR-Based Fiber Optic Sensor. Sensors Actuators B: Chem. 242, 912–920. doi:10.1016/j.snb.2016.09.164

CrossRef Full Text | Google Scholar

Wang, H., Meng, H., Xiong, R., Wang, Q., Huang, B., Zhang, X., et al. (2016). Simultaneous Measurement of Refractive index and Temperature Based on Asymmetric Structures Modal Interference. Opt. Commun. 364, 191–194. doi:10.1016/j.optcom.2015.11.015

CrossRef Full Text | Google Scholar

Wang, T., and Wang, M. (2012). Fabry-Pérot Fiber Sensor for Simultaneous Measurement of Refractive Index and Temperature Based on an In-Fiber Ellipsoidal Cavity. IEEE Photon. Technol. Lett. 24, 1733–1736. doi:10.1109/lpt.2012.2212184

CrossRef Full Text | Google Scholar

Wong, A. C. L., Chung, W. H., Tam, H.-Y., and Lu, C. (2011). Single Tilted Bragg Reflector Fiber Laser for Simultaneous Sensing of Refractive index and Temperature. Opt. Express 19, 409–414. doi:10.1364/oe.19.000409

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Li, H., Yan, G., Meng, F., and Zhu, L. (2019). Simultaneous Measurement of Refractive index and Temperature Based on Asymmetrical Fabry‐Perot Interferometer. Microw Opt. Technol. Lett. 61, 2190–2195. doi:10.1002/mop.31879

CrossRef Full Text | Google Scholar

Xiao, F., Michel, D., Li, G., Xu, A., and Alameh, K. (2014). Simultaneous Measurement of Refractive index and Temperature Based on Surface Plasmon Resonance Sensors. J. Lightwave Technol. 32, 4169–4173. doi:10.1109/jlt.2014.2348999

CrossRef Full Text | Google Scholar

Xiong, R., Meng, H., Yao, Q., Huang, B., Liu, Y., Xue, H., et al. (2014). Simultaneous Measurement of Refractive index and Temperature Based on Modal Interference. IEEE Sensors J. 14, 2524–2528. doi:10.1109/jsen.2014.2310463

CrossRef Full Text | Google Scholar

Xu, W., Zhuo, Y., Song, D., Han, X., Xu, J., and Long, F. (2021). Development of a Novel Label-free All-Fiber Optofluidic Biosensor Based on Fresnel Reflection and its Applications. Analytica Chim. Acta 1181, 338910. doi:10.1016/j.aca.2021.338910

CrossRef Full Text | Google Scholar

Xue, H., Meng, H., Wang, W., Xiong, R., Yao, Q., and Huang, B. (2013). Single-mode-multimode Fiber Structure Based Sensor for Simultaneous Measurement of Refractive index and Temperature. IEEE Sensors J. 13, 4220–4223. doi:10.1109/jsen.2013.2264460

CrossRef Full Text | Google Scholar

Yong Zhao, Y., Lu Cai, L., and Xue-Gang Li, X.-G. (2015). High Sensitive Modal Interferometer for Temperature and Refractive index Measurement. IEEE Photon. Technol. Lett. 27, 1341–1344. doi:10.1109/lpt.2015.2421349

CrossRef Full Text | Google Scholar

Yu, X., Chen, X., Bu, D., Zhang, J., and Liu, S. (2016). In-fiber Modal Interferometer for Simultaneous Measurement of Refractive index and Temperature. IEEE Photon. Technol. Lett. 28, 189–192. doi:10.1109/lpt.2015.2489559

CrossRef Full Text | Google Scholar

Zhang, C., Ning, T., Li, J., Pei, L., Li, C., and Lin, H. (2017). Refractive index Sensor Based on Tapered Multicore Fiber. Opt. Fiber Tech. 33, 71–76. doi:10.1016/j.yofte.2016.11.008

CrossRef Full Text | Google Scholar

Zhang, W., Wu, X., Zhang, G., Shi, J., Zuo, C., Fang, S., et al. (2021a). Simultaneous Measurement of Refractive index and Temperature or Temperature and Axial Strain Based on an Inline Mach-Zehnder Interferometer with TCF-TF-TCF Structure. Appl. Opt. 60, 1522–1528. doi:10.1364/ao.417124

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Chen, H., Wang, M., Liu, Y., Fan, X., Chen, Q., et al. (2021b). Simultaneous Measurement of Refractive index and Temperature of Seawater Based on Surface Plasmon Resonance in a Dual D-type Photonic crystal Fiber. Mater. Res. Express 8, 242. doi:10.1088/2053-1591/ac1ae7

CrossRef Full Text | Google Scholar

Zhao, J. R., Huang, X. G., and Chen, J. H. (2009). A Fresnel-Reflection-Based Fiber Sensor for Simultaneous Measurement of Liquid Concentration and Temperature. J. Appl. Phys. 106, 083103. doi:10.1063/1.3239851

CrossRef Full Text | Google Scholar

Zhao, R.-A., Lang, T., Chen, J., and Hu, J. (2017). Polarization-maintaining Fiber Sensor for Simultaneous Measurement of the Temperature and Refractive index. Opt. Eng. 56, 057113. doi:10.1117/1.oe.56.5.057113

CrossRef Full Text | Google Scholar

Zhao, X., Dong, M., Zhang, Y., Luo, F., and Zhu, L. (2019). Simultaneous Measurement of Strain, Temperature and Refractive index Based on a Fiber Bragg Grating and an In-Line Mach-Zehnder Interferometer. Opt. Commun. 435, 61–67. doi:10.1016/j.optcom.2018.11.022

CrossRef Full Text | Google Scholar