
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
PERSPECTIVE article
Front. Sens. , 02 February 2022
Sec. Physical Sensors
Volume 2 - 2021 | https://doi.org/10.3389/fsens.2021.805351
This article is part of the Research Topic Emerging Technologies and Applications in Distributed Optical Fiber Sensors View all 4 articles
Nanoparticle-doped optical fibers, investigated first as fiber lasers and fiber amplifiers, have gained tremendous interest over the past few years as fiber sensors. One of the main interests of such fibers relies on the ability to develop a distributed sensor, allowing real-time measurement with multiplexed architecture. To go beyond the actual proof of concept, we discuss in this perspective paper three main challenges to tackle: understanding light propagation in heterogeneous materials, controlling nanoparticle formation in glass, and engineering nanoparticle characteristics. Identified as the main directions to follow, they will contribute to promote nanoparticle-doped fiber sensors in the next few years.
Nanoparticles in optical fibers were first reported in 1998 (Tick, 1998). At that time, such fibers were investigated to develop new fiber lasers and fiber amplifiers (Veber et al., 2019; Kasik et al., 2016). The motivation was to embed luminescent ions (e.g., rare earth or transition metal ions) within nanoparticles whose composition, different from the silica matrix, would allow obtaining new luminescent properties. Based on this approach, proof of concepts were reported but with limited interest were compared to conventional (i.e., without nanoparticles) fiber lasers and fiber amplifiers. Such limitation arises from the presence of nanoparticles inducing light scattering (optical loss increases). Then for years, light scattering was considered an issue to tackle. Consequently, the main doxa was to reduce the nanoparticle size.
Very recently, in 2018, an article reported for the first time the interest of the nanoparticle-induced light scattering to develop a fiber sensor (Sypabekova et al., 2018). In this pioneering work, a distributed fiber optic refractive index sensor was reported, based on the analysis of the backscattered light using the optical backscatter reflectometer (OBR) system. Then this concept was applied to temperature, strain, 3D shape, and dosimetry sensors (Tosi et al., 2020b; Olivero et al., 2021). One of the main interests of this concept is to extend OBR from one-dimensional to two- or three-dimensional measurements. Indeed, a major weakness of OBR is that this method is not suitable for multiplexing onto multiple conventional fibers. A switch can be used to connect multiple channels, but the measurement is relatively slow. The fiber can be bent, but special care must be taken to the bending radius to avoid detrimental optical loss. This impacts the distribution of the sensing points. A new method has been proposed to overcome this scenario, named “scattering-level multiplexing” (SLMux) (Beisenova et al., 2019b; Tosi et al., 2020a). This concept relies on the use of nanoparticle-doped fibers, the sensing fibers spliced to standard single-mode fibers (SMFs), used as extenders. Different lengths of fiber extenders allow displacing the position of each sensor. As the backscattering power of the nanoparticle-doped fiber is 30 or 40 dB larger than that of the SMF, it is possible to demodulate each sensing fiber. Another promising approach has been proposed for mechanical perturbation assessment based on the transmission reflection analysis (Silveira et al., 2020; Leal-Junior et al., 2020). Thanks to the use of the enhanced backscattering optical fiber, spatial resolution of this inexpensive technique is reduced to about few mm while it is about 1 m with the standard silica fiber. Finally, fiber Bragg gratings (FBGs) and intrinsic Fabry–Pérot interferometers have been inscribed on an enhanced backscattering optical fiber by using a femtosecond laser (Molardi et al., 2019; Paixão et al., 2020). The FBG has been reported to be stable at least up to 700°C.
The most common process used to prepare nanoparticle-doped optical fibers is based on the drawing of a preform prepared with the modified chemical vapor deposition (MCVD) (Blanc et al., 2011). This process is widely applied in the industry to prepare specialty optical fibers based on silica. It is based on the deposition of porous glassy layers inside a rotating silica tube. The composition of this porous layer is mainly SiO2, generally doped with germanium to increase the refractive index. Nanoparticles can be obtained by incorporating elements such as alkaline earth ions (Mg, Ca, and Sr) during the solution doping step. Average size and density of nanoparticles in the preform mainly depend on the concentration in the doping solution. Then the porous layer is sintered, and the tube is collapsed at high temperature (
Despite the success of already reported nanoparticle-doped fiber based sensors, there is still a need to improve our knowledge to push forward this technology. We have identified three main challenges to tackle related to the fabrication process. As this technology is based on backscattered light, it is important to understand the influence of the characteristics of nanoparticles (size, size distribution, density, and refractive index) on light scattering, more specifically on light backscattering. Then the next challenge is to prepare a fiber with optimized nanoparticles based on light scattering considerations. To reach this goal, we will discuss two routes: the first one deals with the nucleation/growth process and the second one is related to the drawing step.
The main characteristic of an optical fiber with a nanoparticle-doped core is the enhanced backscattering. This property of scattering, combined with the standard size of the fiber, which permits comfortable splicing, makes the nanoparticle-doped fibers an excellent platform for distributed fiber sensors, in particular for the implementation of the parallel Scattering Level Multiplexing (SLMux) paradigm (Tosi et al., 2021). The presence of nanoparticles creates a strong scattering gain, more than 40 dB, with respect to the usual Rayleigh scattering of standard telecom fibers SMF-28. On the other hand, the high scattering contributes to enhance the scattering-dependent losses which can be significantly high, with peak values of 300 dB/m. To understand this behavior, it is necessary to identify the correct model to describe the system. Since the nanoparticles presents an average diameter that can go from 40 to 100 nm, less than 1/10 of the operating wavelength of 1.55 μm, the scattering of the nanoparticle-doped fiber can be modeled as Rayleigh scattering of spherical particles presenting a refractive index np surrounded by a medium with a refractive index ng. The scattering power Ps of a fiber section normalized to the incoming signal intensity I0, representing the scattering cross section Csca, can be written as follows (Cox et al., 2002):
where N is the density of nanoparticles over the volume V of the selected fiber section, d is the average diameter of the nanoparticles, and λ is the working wavelength 1.55 μm. From Eq 1, it is possible to imply that the increase in the scattering power can be tailored by three factors: the increase in the particle density, the increase in the particle size, and the increase in the index contrast between particles and the surrounding medium. The most effective of these three factors is the size of the nanoparticles which impacts with an exponent of 6 over the scattering power. Simulated and experimental results agree with the model of Rayleigh scattering given by spherical particles (Beisenova et al., 2019a; Blanc et al., 2011).
The experimental backscattering traces, taken with Luna OBR 4600, depict a different behavior according to the nature and the distribution of the nanoparticles. Figures 1A,B show the backscattering trace of two different fibers presenting nanoparticles with different average size, precisely 80 nm for the fiber of Figure 1A and 55 nm for the fiber of Figure 1B. These fibers were prepared by using two MgCl2 concentrations in the doping solution: 0.1 (Figure 1B) and 1 mol/L (Figure 1A). In the first case, the losses along the fiber are 301 dB/m, ten times larger with respect to the ones along the second fiber. From Eq 1, changing the average diameter from 55 to 80 nm leads to an increase by one order of magnitude of the scattered power, in accordance with the measured value.
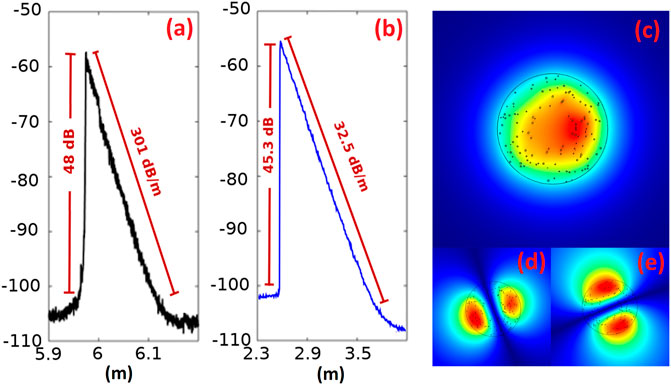
FIGURE 1. (A) Backscattering trace of the nanoparticle-doped fiber presenting nanoparticle with an average diameter of 80 nm; (B) backscattering trace of the nanoparticle-doped fiber presenting nanoparticle with an average diameter of 55 nm; (C) LP01-like mode of a nanoparticle-doped fiber with a nanoparticle pattern similar to the one analyzed in (A), the core overlap Γ is 0.827; (D) and (E) LP11-like modes of the same fiber, the core overlaps are, respectively, Γ = 0.447 and Γ = 0.273.
Another interesting property, derived from the presence of nanoparticles, is the mode localization effect (Abaie et al., 2017), which can be useful to tailor the modal properties of the guided modes. In Figures 1C–E, are shown, respectively, the LP01-like fundamental mode and the two LP11-like higher order modes. According to the simulation results, the LP01-like is well-confined, presenting a core overlap of 0.827. Since the fiber of the simulation presents an index contrast between core and cladding of 2 × 10–3, the fiber should be a strictly single mode at the operating wavelength of 1.55 μm. Nevertheless, the presence of nanoparticles fosters the onset of an LP11-like mode. In particular, the LP11-like of Figure 1D shows a mode overlap of 0.447, while the LP11-like of Figure 1E shows a mode overlap of 0.273. The evident difference between the overlaps implies that the LP11-like modes are no more degenerated, with one of them guided and the other one not guided.
As the backscattered light strongly depends on the characteristics of the nanoparticles, there is a crucial need to understand their formation through the phase separation mechanism. These nanoparticles are formed during the optical fiber making process which can be divided into two main steps: preform formation and proper fiber making through a drawing process. During both of these steps, the material is heated at a high temperature (about 2,000–2,100°C). At these temperatures, the viscosity of the material is lowered, allowing diffusion to occur within it. Depending on the miscibility of the potential present phases, an unmixing of the material can happen forming distinct phases. This phase separation is the key phenomenon for the nanoparticle formation.
The moment when the first germs of the new phase separating from the glass matrix are formed is called nucleation. This phenomenon has been extensively studied since J. W. Gibbs’ work about phase equilibrium (Gibbs, 1878). The study of this phenomenon leads to a theory called the classical nucleation theory in which the current statement has been given by Becker and Döring (1935). This theory gives the work Wc needed to form a germ of a critical size rc sufficient enough to be stable and start growing as a new phase:
where γ and ΔGV represent the surface tension and the variation of the volumic Gibbs free enthalpy for the germ formation, respectively.
In the classical nucleation theory, the formed germ is considered to have the same properties as the macroscopic phase forming, including its composition. But this is not what is observed for small particles whose composition deviates from the one of the macroscopic phase, depending on the particle radius. This has been shown in metallic systems (Bonvalet et al., 2014), in silicate liquids (Sen and Mukerji, 1999) and more recently in oxide glasses optical fiber systems (Blanc et al., 2019). It has to be emphasized that such results require a very specific characterization tool, allowing measuring the composition at the nanometer scale as the atom probe tomography (Blanc et al., 2019).
Several theories have been developed to explain this composition variability with the particle size, such as the phase field approach, based on the work by J. W. Cahn and J. E. Hilliard (Cahn and Hilliard, 1958; Cahn, 1959; Cahn and Hilliard, 1959). A more recent one, known as the general Gibbs approach, has been developed by J. W. P. Schmelzer (Gutzow and Schmelzer, 1995). In this approach, constraints on the germ composition are released, allowing it to change as the germ grows. This results in a new form of the germ formation work as follows:
with nα = ∑njα the total number of particles in the germ and {xα} and {xβ} all the independent molar fractions of the constituents of the two phases. Then the critical conditions can be rewritten as follows:
where cα = ∑njα/Vα is the total volume concentration of the constituents j in the new forming phase α and the ambient phase β. rc and Wc then depend on the phase composition. In the generalized Gibbs approach, the critical germ corresponds to the minimum of Wc for all the possible compositions of the phase α. Then this composition verifies the following equation:
The logarithmic derivative of the critical nucleation work regarding the molar fraction of the constituent j in the phase α gives the following equation:
We can see that cα is independent from xjα and with rc described before:
which for a given radius R gives the following equation:
which leads to the following equation:
The latter equation highlights which are the key parameters controlling the growing germ properties: chemical potentials of the different constituents in the different phases μ and the surface tension γ. On the one hand, chemical potentials can be investigated through the CALculation of PHAse Diagrams (CALPHAD methods). Based on thermodynamic databases, such methods perform predictive calculation about thermodynamic and kinetic properties of multicomponent systems. On the other hand, surface tension is a difficult-to-access parameter. Measurements of this parameter in silicate liquids have hardly been done and only for very simple systems (Lyon, 1944). As an alternative approach, an adaptive potential has been developed to study phase separation by molecular dynamics simulations (Bidault et al., 2015). The composition change versus the size of the particles is observed with these simulations, in accordance with measurements made by atom probe tomography (Blanc et al., 2019). However, if the trend is concerned, the size of the nanoparticles and the temperatures of the molecular dynamics simulations are definitively different from the experimental values. This highlights the need for research in these fields in order to get exploitable data allowing the modelization and then synthesis of size- and composition-controlled nanoparticles inside the optical fiber core.
The final characteristics of the nanoparticles not only depend on the thermal history. The fiber drawing process is an important step to control the morphology of the nanoparticles. For conventional fibers, the drawing step corresponds to a homothetic transformation of the preform to the fiber. The external diameter is divided by two orders of magnitude, but the ratio of core and cladding diameters is constant. In the case of the nanoparticle-doped fiber, nanoparticle size does not decrease homothetically. A 100-nm spherical nanoparticle in the preform does not lead to a 1-nm spherical nanoparticle in the fiber. Actually, nanoparticle morphology can change vastly during the fiber drawing process. In particular, nanoparticles can elongate (Vermillac et al., 2017b; Fuertes et al., 2021). This phenomenon provides us a way to regulate their size distribution by inducing breakups of the elongated particle threads. Figure 2 shows a neck-down region of the preform being drawn to the fiber at 1800°C. Nanoparticles were obtained by adding 0.7 mol/L of LaCl3 in the doping solution. As clearly shown on the left SEM image, before drawing, nanoparticles exhibit a round shape and are distributed uniformly inside the preform core, where the mean size is 235 nm. Passing through the heating zone, the preform starts to deform and elongate. This part is the neck-down region; after this region, the diameter of the preform is highly reduced down to 125 μm, the diameter of the final fiber. The core has a diameter of 10 μm, and nanoparticles inside the fiber are also elongated and even break up after the neck-down region, as shown on the right SEM image of Figure 2. This phenomenon is a competition between two competing forces: the viscous stress and the surface tension, where the former tends to break up the particle and the latter tends to maintain the spherical shape of the particle. By decreasing the temperature, the viscous stress is enhanced and ergo accelerates the particle elongation and breakup processes. Another approach which can be used to control the size of the nanoparticles is to increase the drawing temperature. It has been reported that by heating up to 100 or 200°C above the usual drawing temperature allows reducing the size of the nanoparticles (Fuertes et al., 2021). Here, the dissolution mechanism would occur. Then the drawing process is a promising way to engineer the size distribution and the morphology of the nanoparticles.

FIGURE 2. Neck-down region of the fiber drawing process and SEM images of longitudinal sections of the preform (left) and fiber (right). Nanoparticles in the fiber are elongated along the drawing axis.
First reported in 2018, the use of nanoparticle-doped optical fibers as sensors has rapidly grown in interest. However, this new generation of optical fiber sensors is still at its infancy. Until now, such fibers are based on silica glass. However, this concept can be extended to other glasses such as chalcogenide (Ballato et al., 2017) or polymer fiber. We have identified and discussed three main challenges to tackle to push forward this technology in this article. There is a clear need to improve our knowledge on the light–nanoparticle interaction to engineer backscattered light with the aim to guide the fabrication process to reach the right characteristics of the nanoparticles. However, the control of the characteristics of the nanoparticles is far from being simple. Advanced model and numerical simulations must be developed to understand the nucleation/growth of phase-separated particles. A very promising route to control such characteristics relies on the drawing step which can allow controlling the size and the shape. Solutions to those bottlenecks will strongly contribute to develop nanoparticle-doped fiber sensors and will extend the actual short-distance range applications to long-distance ones.
The data analyzed in this study is subject to the following licenses/restrictions: data can only be processed with our consent. Requests to access these datasets should be directed to Wilfried Blanc, CNRS, wilfried.blanc@inphyni.cnrs.fr.
ZL, TR, CM, and WB wrote the draft of the article. All authors read and approved it for publication.
This study is partly supported by the project NanoSlim (ANR-17-CE08-0002) and project Distributed Measurement of Bite Force by Fiber-Optic Sensorized Dental Guard (Nazarbayev University, code: 021220FD1851).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abaie, B., Mobini, E., Karbasi, S., Hawkins, T., Ballato, J., and Mafi, A. (2017). Random Lasing in an anderson Localizing Optical Fiber. Light Sci. Appl. 6, e17041. doi:10.1038/lsa.2017.41
Ballato, J., Ebendorff-Heidepriem, H., Zhao, J., Petit, L., and Troles, J. (2017). Glass and Process Development for the Next Generation of Optical Fibers: A Review. Fibers 5, 11. doi:10.3390/fib5010011
Becker, R., and Döring, W. (1935). Kinetische Behandlung der Keimbildung in übersättigten Dämpfen. Ann. Phys. 416, 719–752. doi:10.1002/andp.19354160806
Beisenova, A., Issatayeva, A., Korganbayev, S., Molardi, C., Blanc, W., and Tosi, D. (2019a). Simultaneous Distributed Sensing on Multiple Mgo-Doped High Scattering Fibers by Means of Scattering-Level Multiplexing. J. Lightwave Technol. 37, 3413–3421. doi:10.1109/jlt.2019.2916991
Beisenova, A., Issatayeva, A., Sovetov, S., Korganbayev, S., Jelbuldina, M., Ashikbayeva, Z., et al. (2019b). Multi-fiber Distributed thermal Profiling of Minimally Invasive thermal Ablation with Scattering-Level Multiplexing in Mgo-Doped Fibers. Biomed. Opt. Express 10, 1282–1296. doi:10.1364/boe.10.001282
Bidault, X., Chaussedent, S., and Blanc, W. (2015). A Simple Transferable Adaptive Potential to Study Phase Separation in Large-Scale xMgO-(1-x)SiO2 Binary Glasses. J. Chem. Phys. 143, 154501. doi:10.1063/1.4932984
Blanc, W., Martin, I., Francois-Saint-Cyr, H., Bidault, X., Chaussedent, S., Hombourger, C., et al. (2019). Compositional Changes at the Early Stages of Nanoparticles Growth in Glasses. J. Phys. Chem. C 123, 29008–29014. doi:10.1021/acs.jpcc.9b08577
Blanc, W., Mauroy, V., Nguyen, L., Shivakiran Bhaktha, B. N., Sebbah, P., Pal, B. P., et al. (2011). Fabrication of Rare Earth-Doped Transparent Glass Ceramic Optical Fibers by Modified Chemical Vapor Deposition. J. Am. Ceram. Soc. 94, 2315–2318. doi:10.1111/j.1551-2916.2011.04672.x
Bonvalet, M., Philippe, T., Sauvage, X., and Blavette, D. (2014). The Influence of Size on the Composition of Nano-Precipitates in Coherent Precipitation. Philosophical Mag. 94, 2956–2966. doi:10.1080/14786435.2014.941029
Cahn, J. W. (1959). Free Energy of a Nonuniform System. Ii. Thermodynamic Basis. J. Chem. Phys. 30, 1121–1124. doi:10.1063/1.1730145
Cahn, J. W., and Hilliard, J. E. (1959). Free Energy of a Nonuniform System. III. Nucleation in a Two‐Component Incompressible Fluid. J. Chem. Phys. 31, 688–699. doi:10.1063/1.1730447
Cahn, J. W., and Hilliard, J. E. (1958). Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 28, 258–267. doi:10.1063/1.1744102
Cox, A. J., DeWeerd, A. J., and Linden, J. (2002). An experiment to Measure Mie and Rayleigh Total Scattering Cross Sections. Am. J. Phys. 70, 620–625. doi:10.1119/1.1466815
Fuertes, V., Grégoire, N., Labranche, P., Gagnon, S., Wang, R., Ledemi, Y., et al. (2021). Engineering Nanoparticle Features to Tune Rayleigh Scattering in Nanoparticles-Doped Optical Fibers. Sci. Rep. 11. doi:10.1038/s41598-021-88572-2
Gibbs, J. W. (1878). On the Equilibrium of Heterogeneous Substances. Am. J. Sci. s3-16, 441–458. 1820-1879. doi:10.2475/ajs.s3-16.96.441
Kasik, I., Peterka, P., Mrazek, J., and Honzatko, P. (2016). Silica Optical Fibers Doped with Nanoparticles for Fiber Lasers and Broadband Sources. Cnano 12, 277–290. doi:10.2174/1573413711666150624170638
Leal-Junior, A. G., Ribeiro, D., Avellar, L. M., Silveira, M., Díaz, C. A. R., Frizera-Neto, A., et al. (2020). Wearable and Fully-Portable Smart Garment for Mechanical Perturbation Detection with Nanoparticles Optical Fibers. IEEE Sensors J. 21, 2995–3003.
Lyon, K. C. (1944). Calculation of Surface Tensions of Glasses*. J. Am. Ceram. Soc. 27, 186–189. doi:10.1111/j.1151-2916.1944.tb14889.x
Molardi, C., Paixão, T., Beisenova, A., Min, R., Antunes, P., Marques, C., et al. (2019). Fiber Bragg Grating (Fbg) Sensors in a High-Scattering Optical Fiber Doped with Mgo Nanoparticles for Polarization-dependent Temperature Sensing. Appl. Sci. 9, 3107. doi:10.3390/app9153107
Olivero, M., Mirigaldi, A., Serafini, V., Vallan, A., Perrone, G., Blanc, W., et al. (2021). Distributed X-ray Dosimetry with Optical Fibers by Optical Frequency Domain Interferometry. IEEE Trans. Instrum. Meas. 70, 1–9. doi:10.1109/tim.2021.3075518
Paixão, T., Pereira, L., Min, R., Molardi, C., Blanc, W., Tosi, D., et al. (2020). Bragg Gratings and Fabry-Perot Interferometers on an Er-Mgo-Doped Optical Fiber. Opt. Laser Technology 123, 105946. doi:10.1016/j.optlastec.2019.105946
Sen, S., and Mukerji, T. (1999). A Generalized Classical Nucleation Theory for Rough Interfaces: Application in the Analysis of Homogeneous Nucleation in Silicate Liquids. J. Non-Crystalline Sol. 246, 229–239. doi:10.1016/s0022-3093(99)00093-9
Silveira, M., Frizera, A., Leal-Junior, A., Ribeiro, D., Marques, C., Blanc, W., et al. (2020). Transmission-Reflection Analysis in High Scattering Optical Fibers: A Comparison with Single-Mode Optical Fiber. Opt. Fiber Technology 58, 102303. doi:10.1016/j.yofte.2020.102303
Sypabekova, M., Korganbayev, S., Blanc, W., Ayupova, T., Bekmurzayeva, A., Shaimerdenova, M., et al. (2018). Fiber Optic Refractive index Sensors through Spectral Detection of Rayleigh Backscattering in a Chemically Etched Mgo-Based Nanoparticle-Doped Fiber. Opt. Lett. 43, 5945–5948. doi:10.1364/ol.43.005945
Tick, P. A. (1998). Are Low-Loss Glass-Ceramic Optical Waveguides Possible? Opt. Lett. 23, 1904–1905. doi:10.1364/ol.23.001904
Tosi, D., Molardi, C., Blanc, W., Paixão, T., Antunes, P., and Marques, C. (2020a). Performance Analysis of Scattering-Level Multiplexing (Slmux) in Distributed Fiber-Optic Backscatter Reflectometry Physical Sensors. Sensors 20, 2595. doi:10.3390/s20092595
Tosi, D., Molardi, C., and Blanc, W. (2021). Rayleigh Scattering Characterization of a Low-Loss Mgo-Based Nanoparticle-Doped Optical Fiber for Distributed Sensing. Opt. Laser Technology 133, 106523. doi:10.1016/j.optlastec.2020.106523
Tosi, D., Molardi, C., Sypabekova, M., and Blanc, W. (2020b). Enhanced Backscattering Optical Fiber Distributed Sensors: Tutorial and Review. IEEE Sensors J. 21, 12667–12678. doi:10.1109/JSEN.2020.3010572
Veber, A., Lu, Z., Vermillac, M., Pigeonneau, F., Blanc, W., and Petit, L. (2019). Nano-structured Optical Fibers Made of Glass-Ceramics, and Phase Separated and Metallic Particle-Containing Glasses. Fibers 7, 105. doi:10.3390/fib7120105
Vermillac, M., Fneich, H., Lupi, J.-F., Tissot, J.-B., Kucera, C., Vennéguès, P., et al. (2017a). Use of Thulium-Doped LaF3 Nanoparticles to Lower the Phonon Energy of the Thulium's Environment in Silica-Based Optical Fibres. Opt. Mater. 68, 24–28. doi:10.1016/j.optmat.2016.11.042
Keywords: optical fiber, nanoparticles, light scattering, drawing, phase separation
Citation: Lu Z, Robine T, Molardi C, Pigeonneau F, Tosi D and Blanc W (2022) Toward Engineered Nanoparticle-Doped Optical Fibers for Sensor Applications. Front. Sens. 2:805351. doi: 10.3389/fsens.2021.805351
Received: 30 October 2021; Accepted: 06 December 2021;
Published: 02 February 2022.
Edited by:
Patrice Megret, University of Mons, BelgiumReviewed by:
Carlos Marques, University of Aveiro, PortugalCopyright © 2022 Lu, Robine , Molardi, Pigeonneau, Tosi and Blanc. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wilfried Blanc, wilfried.blanc@inphyni.cnrs.fr
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.