Effect of underactuated parallelogram shape-shifting for environmental adaptation movement of a three modular in-pipe robot

This paper presents an in-pipe robot with three underactuated parallelogram crawler modules, which can automatically shift its body shape when encountering obstacles. The shape-shifting movement is achieved by only a single actuator through a simple differential mechanism by only combining a pair of spur gears. It can lead to downsizing, cost reduction, and simplification of control for adaptation to obstacles. The parallelogram shape does not change the total belt circumference length, thus, a new mechanism to maintain the belt tension is not necessary. Moreover, the proposed crawler can form the anterior-posterior symmetric parallelogram relative to the moving direction, which generates high adaptability in both forward and backward directions. However, whether the locomotion or shape-shifting is driven depends on the gear ratio of the differential mechanism because their movements are only switched mechanically. Therefore, to clarify the requirements of the gear ratio for the passive adaptation, two outputs of each crawler mechanism (torques of the flippers and front pulley) are quasi-statically analyzed, and how the environmental and design parameters influence the robot performance are verified by real experiments. From the experiments, although the robot could not adapt to the stepped pipe in vertical section, it successfully shifted its crawler’s shape to parallelogram in horizontal section only with our simulated output ratio.

1 Introduction

Maintenance of pipelines is one of the recent consequential missions for urban society. For efficient replacement of aging pipelines, how to know damaged and deteriorated points is the key process. However, it is time-consuming, costly, and dangerous if the inspection is performed manually. To solve this problem, self-propelled in-pipe inspection robots are collecting attention. Previously, many types of the in-pipe robot have been already researched and developed (Hirose et al., 1999; Rome et al., 1999; Streich and Adria, 2004; Birkenhofer et al., 2005; Fjerdingen et al., 2009; Schempf et al., 2010; Dertien et al., 2011; 2014; Kakogawa and Ma, 2012; Nishimura et al., 2012; Debenest et al., 2014; Pfotzer et al., 2014; 2015; Inazawa et al., 2021; Liu et al., 2022).

Among them, articulated robot is one of the most adaptable strucre for narrow (less than 4 in inner diameter) and winding pipelines Dertien et al. (2011, 2014); Debenest et al. (2014); Fjerdingen et al. (2009), and we have been also tackling on this projects (Kakogawa and Ma, 2018; Kakogawa et al., 2019; 2022b; a). If the adaptive pipe size is not a big issue (more than 4 in inner diameter), in-pipe robots with three independent driving modules have been also reported as a reliable structure (Roh and Choi, 2005; Roh et al., 2009; Kim et al., 2010; Park et al., 2010; Kwon and Yi, 2012; Suryavanshi et al., 2020; Tugeumwolachot et al., 2022). They revealed that the robot can travel through straight pipes and also steer at three-dimensional T-branches by only adjusting the speed difference among the modules.

Most three modular in-pipe robot is equipped with three actuators for moving forward and backward, and one passive compliant contractile mechanism that presses the modules radially to the inner pipe wall. This contractile mechanism needs to keep expanding the crawler to the wall. Therefore, when encountering obstacles or entering into smaller diameter pipes, large propulsive force is necessary. As assistance of the shrinkage, the mechanism with additional actuators has been reported (Park et al., 2010). However, it causes a critical increase in the total size of the robot. The robot cannot be equipped with many actuators for switching movements or sensors for contact detection in limited space such as in-pipe. In those cases, a method that maximizes the functionality of the motor itself is required.

Therefore, we herein proposed a new in-pipe robot with three underactuated parallelogram crawler modules. The crawler module can shift its body shape to parallelogram to adapt to obstacles without any additional actuators and sensors. Two kinds of movement (traveling and shape-shifting) are switched by using a simple differential mechanism and utilizing the external forces from the obstacle. However, the two behaviors change depending on the gear ratio of the differential mechanism.

To design the gear ratio, we focuse on the required output ratio of the pulley and the flipper in the normal driving and parallelogram modes. And, they are analyzed based on quasi-statics. The influences of the roll angle of the robot, the initial resistance of the crawler, the slope angle of the pipe, and the frictional coefficient are also examined. Experiments in a tilted stepped pipe are conducted to verify the performance of the developed in-pipe robot depending on the different gear ratio. Our previous works have already proposed the same idea (Kakogawa and Ma, 2013; Kakogawa et al., 2014). However, this paper explains how to design the gear ratio of the differential mechanism more in detail and the experiments with more conditions are performed to verify the validity of the proposed robot.

Originally, a realistic model that accurately includes the three modules is necessary. However, in reality, the characteristics of the environment (especially the friction coefficient of the pipe’s inner wall) are indeterminate, and in the friction losses of the sliding parts of the three links and the individual differences of the motor characteristics cannot be ignored. Therefore, building a too accurate model would be almost meaningless. We performed a quasi-static analysis to obtain a rough estimate of the gear tooth ratio. It should be noted here that the torque required to overcome the obstacle was not obtained, but only the output ratio of the differential mechanism. In this case, if the output ratio is well designed and the torque generated by the actuator is sufficiently large, the operation can be switched without control depending on the external environment. This paper proposes a design method for this purpose.

2 Mechanical structure of the proposed in-pipe robot and the principle of the underactuated movement

2.1 Basic structure

Figure 1A shows the overview of the developed in-pipe robot. Its specifications are: ϕ136 mm—ϕ202 mm of the adaptive diameter, 235 mm of the axial length, 1.8 kg of the total weight, and 0.069 m/s of the moving speed. A geared motor (DCX16S GB kL 12 V and GPX19 C) with 231:1 reduction (Maxon group ag, Sachseln, Switzerland) was used for each crawler module. This robot is composed of a contractile mechanism and three crawler modules arranged radially at intervals of 120° with respect to the robot’s center axis.

A pantograph and a coil spring as shown in Figure 1B are installed for the expansion and contraction of the contractile mechanism. Two pantograph mechanisms and two coil springs are used for one crawler module. The slider that moves horizontally with respect to the robot center axis pushes the linkage of the pantograph mechanism with a spring, and the force generated by this pushes the joints A and B in the center of the crawler. The direction of the spring force is changed from the horizontal direction to the radial direction of the pipe.

FIGURE 1

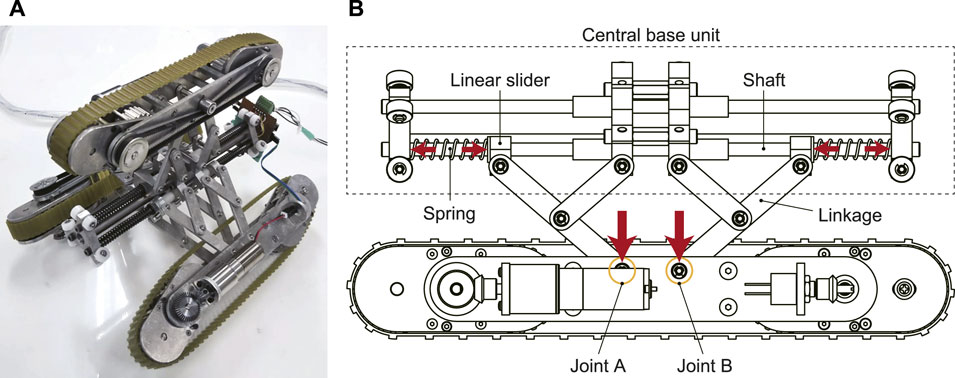
FIGURE 1. A mechanical model of our proposed in-pipe robot with underactuated parallelogram modules [(A): overview picture, (B): pantograph contractile mechanism].

2.2 Underactuated parallelogram crawler module

The contractile mechanism always presses each module against the inner wall of the pipe with a spring, thus it is difficult to shrink the robot body when an obstacle is encountered or the diameter of the pipe is reduced. Therefore, in this study, we developed a new shape-shifting mechanism called “underactuated parallelogram crawler” and installed it in three modules to address this problem. In general, active flipper arms and shape-shifting functions have often been deployed independently to solve such obstacle adaptation problems. However, in an environment that is restricted in space, such as in pipelines, adding actuators is a major barrier to downsizing. In this research, the power for moving forward and backward is utilized for shifting the crawler shape by an underactuated mechanism.

There are three reasons why a parallelogram shape is adopted for the crawler mechanism.

1. When the crawler shape is shifted to a parallelogram, the mainframe of the crawler is lifted, and a force can be generated in the direction to shrink the contractile mechanism.

2. Even if the crawler shape is shifted to a parallelogram, the total belt circumference length is constant, thus, there is no need to add a new mechanism to maintain the belt tension.

3. Usually, in-pipe robots need to have the same function not only when moving forward but also when moving backward. A parallelogram can achieve anterior-posterior symmetric shape as illustrated in Figure 2. By using this symmetric shape-shifting function, even if it is difficult to pivot-turn, it can achieve the same transformation in the reverse direction by simply moving backward without changing the robot orientation.

FIGURE 2

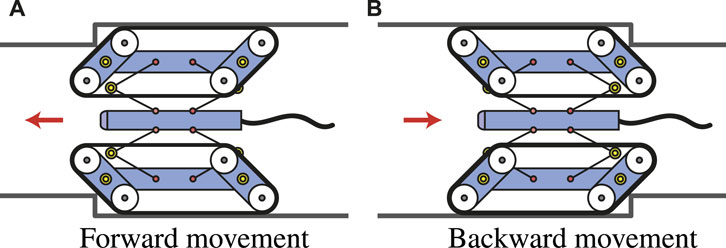
FIGURE 2. Similar mobility for anterior-posterior symmetric transformation [(A): forward movement, (B): backward movement].

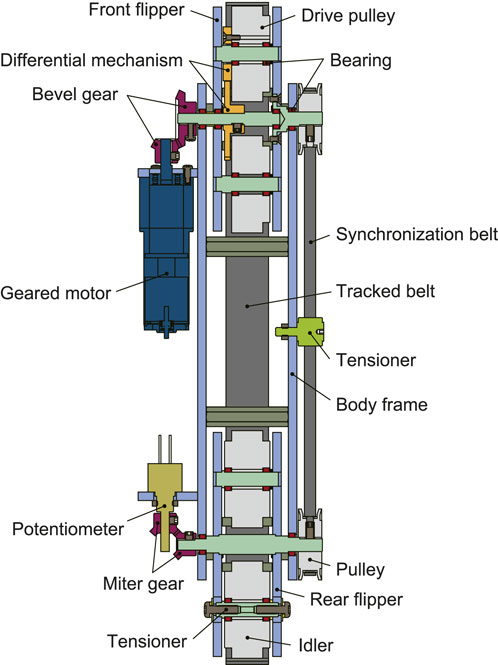
Figure 3 shows the cross-sectional view of a single underactuated parallelogram crawler. First, the motor is fixed to the outside of the crawler frame, and the power is transmitted to the differential mechanism in the front flipper via the bevel gear. With this differential mechanism, the power is transmitted to the drive pulley at the tip and the rotation of the flippers at the same time. The detailed principle is described later in the next subsection.

FIGURE 3

FIGURE 3. A CAD model of an underactuated parallelogram crawler module (cross-sectional view).

It is necessary to synchronize the rotation of the front and rear flippers to make the crawler parallelogram. In the real world, a parallel link mechanism is often used to synchronize the front and rear rotations, as seen in crank-bars of steam locomotives. However, during the normal driving in our case, the front and rear flippers are aligned in a straight line. For this reason, the flipper must be rotated from a singular posture, and the forward and backward movements are not uniquely determined (Ye et al., 2012). To solve this problem, the output of the front flipper is also transmitted to the rear flipper via a timing belt attached to the opposite side of the motor. As a result, the axes of the front and rear flippers are synchronized. Optionally, a potentiometer can be attached to the rear flipper to estimate the rotation angle of the flippers.

In conventional underactuated crawler robots, a reduction gear such as a planetary gear mechanism is often used to generate the differential movement (underactuated movement) (Lan et al., 2007; Kim et al., 2010; Quan and Ma, 2011; Wang et al., 2016). However, a large reduction gear cannot be used because the inner space of the pipe is limited. Therefore, in this study, a simple differential mechanism using a couple of spur gears is adopted (Li et al., 2010).

2.3 Pseudo multiple degrees of freedom by utilizing external forces

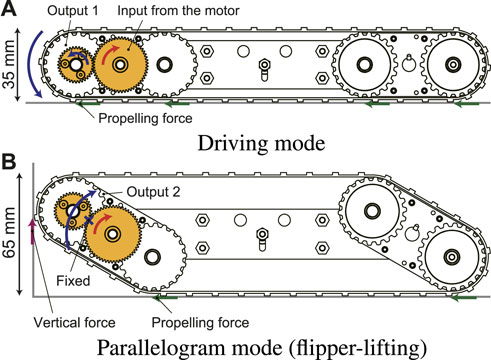
Figure 4 shows the principle of the proposed underactuated parallelogram crawler as well as two modes of the normal driving and parallelogram. In the normal driving mode (Figure 4A), the front and rear flippers are horizontal because the crawler module is pressed against the inner wall of the pipe by the pantograph mechanism. In this state, the power is transmitted to the drive pulley at the front tip, and the crawler can move forward and backward.

FIGURE 4

FIGURE 4. The two modes of the differential mechanism [(A): driving mode, (B): parallelogram mode].

On the other hand, when the crawler is in contact with an obstacle and the robot movement is intercepted, the drive pulley cannot be rotated around its own axis. As a result, it revolutes around the input gear and the crawler shape is shifted to a parallelogram as shown in Figure 4B.

In addition, since the pulley’s drive force is always generated even in contact with the obstacle, a vertically upward force is applied to the contact point of the crawler front portion. This force has an effect of assisting the rotation of the flipper. The flippers can be lifted without using a high reduction ratio thanks to this assistance. In other words, if the force acting on the crawler’s contact point can generate a moment in the direction of assisting the rotation of the flipper, the desired operation can be performed even at a low reduction ratio. Therefore, the number of gears can be greatly reduced compared with conventional underactuated crawler robots. This will lead to downsizing and lightweight.

Many existing crawler robots used in outdoor environments often improve obstacle-adaptability by preparing a tilt angle of the tracked-belt. However, since the size is limited in pipelines, a method of shifting the robot’s shape depending on the environment is more effective. Furthermore, when an unexpected external force is applied to the crawler during the travel, it can be mitigated using the rotation of the flipper. This can reduce the impact on the motor (Quan and Ma, 2011).

When the crawler contacts with the obstacle, the flippers rotate inward, and the shape is shifted to a parallelogram. However, if the resistance continues to be applied to the tracked-belt, the flippers keep rotating infinitely in the opposite direction to that of travel. Eventually, the robot cannot overcome the obstacle. To solve this, when the flipper is rotated to 30°, stopper pins are attached to prevent further rotation (Figure 5). If the motor continues to rotate in this state, the crawler can move forward by driving the tracked-belt while maintaining the parallelogram.

FIGURE 5

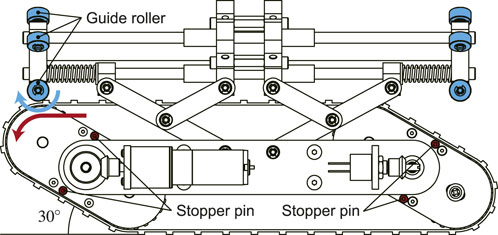
FIGURE 5. Stopper pins used to limit the rotational angle of the flippers and guide rollers to guarantee smooth motion of the tracked belt.

When the contractile mechanism shrinks while keeping a parallelogram shape of the crawler, the tracked-belt contacts with the central portion of the robot. Thus, a large resistance is generated that interrupts the robot movement. To reduce this resistance, guide rollers are attached to the front and rear tips of the robot as shown in Figure 5.

3 Quasi-static model

Since the underactuated mechanism divides one input into two outputs simultaneously, the distribution ratio of the two outputs greatly affects the performance. This differential phenomenon is often expressed using a branch tube as shown in Figure 6 (Lan et al., 2007). In normal driving mode, only the drive pulley rotates and the flipper must be stationary. In other words, the actual torque transmitted to the drive pulley τ_act.p must be larger than τ_req.p. In the same manner, the actual torque transmitted to the flipper τ_act.f must be less than τ_req.f. On the other hand, in parallelogram mode, the drive pulley should stop and the flipper must rotate. Therefore, τ_act.p must be smaller than τ_req.p, and τ_act.f must be greater than τ_req.f.

FIGURE 6

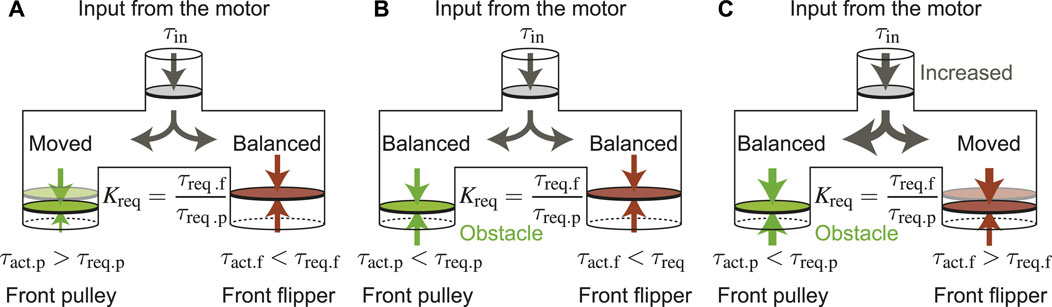
FIGURE 6. Branch pipe models for torque distribution: (A) Driving mode, (B) Between driving mode and parallelogram mode, (C) Parallelogram mode.

Here, the ratio between the torque required to rotate the drive pulley and the one required to lift the flipper and the actual output ratio are defined as follows, respectively.

$K_{\text{req}}={\tau }_{\text{req.f}}/{\tau }_{\text{req.p}}(1)$

$K_{\text{act}}={\tau }_{\text{act.f}}/{\tau }_{\text{act.p}}(2)$

in the driving mode, both of the following two conditions should be satisfied.

${\tau }_{\text{act.f}}<{\tau }_{\text{req.f}}(3)$

${\tau }_{\text{act.p}}>{\tau }_{\text{req.p}}(4)$

in the parallelogram mode, the following two conditions should be satisfied in a similar way.

${\tau }_{\text{act.f}}>{\tau }_{\text{req.f}}(5)$

${\tau }_{\text{act.p}}<{\tau }_{\text{req.p}}(6)$

therefore, K_act should meet the following conditions.

$\left\{\begin{array}{cc}{K}_{\text{act}}<K_{\text{req}}\hfill & \left(\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{d}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\right)\hfill \\ K_{\text{act}}>K_{\text{req}}\hfill & \left(\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\right)\hfill \end{array}\right.(7)$

Since τ_req.p and τ_req.f change depending on the environment the crawler encounters, these values are derived based on static models as shown in Figure 7A–C, respectively.

The static model is simplified by dividing the crawler into three rigid bodies: a front flipper, a rear flipper, and a body frame. To generalize, the crawler moves on the inner wall of the pipe tilted by α, and the front flipper is in contact with the step. The rotation axes of the front and rear flippers are at the respective centers and are fixed to both ends of the main body frame. In addition, since the axes of these flippers are synchronized by the timing belt, the torque required to rotate the rear flipper τ_req.r interact with the front flipper as inner torque. The motor input torque τ_req.f is applied to the front flipper, and its reaction is applied to the body frame.

FIGURE 7

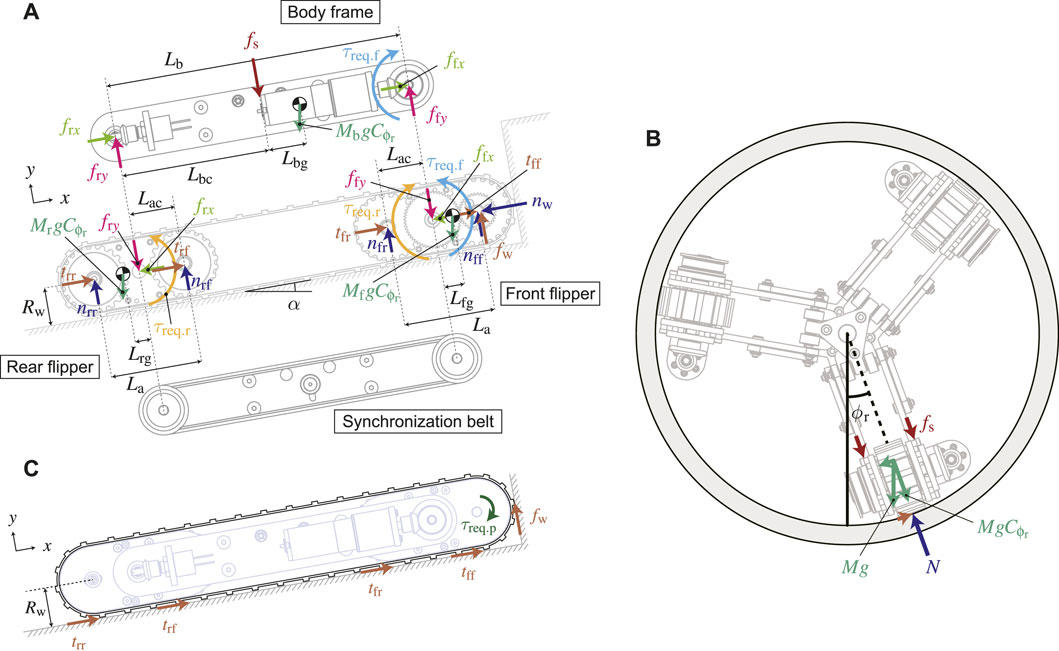
FIGURE 7. Possible external forces acting on the underactuated parallelogram crawler [(A): forces of each rigid body, (B): forces of the tracked belt, (C): forces in the cross-sectional view].

Since the three crawler modules are arranged radially as shown in Figure 7B, the direction of gravity applied to the modules changes depending on the roll-posture of the robot. Therefore, each gravitational force acting in the radial direction of the pipe is calculated by $M_{\text{f}}g{C}_{{\varphi }_{\text{r}}}$, $M_{\text{b}}g{C}_{{\varphi }_{\text{r}}}$, and $M_{\text{r}}g{C}_{{\varphi }_{\text{r}}}$, respectively.

3.1 Torque for lifting the flippers

From Figure 7A, the torque required to lift the flipper can be obtained from the balance of external forces and moments acting on the three rigid bodies (front flipper, rear flipper, and body frame). This is because the required torque means a boundary value to break down the force balance. Considering the balance of forces in the x and y-axes and the moment around the rotation axis of the flipper, the static balance equations of the front flipper can be obtained by

$t_{\text{ff}}+t_{\text{fr}}-f_{\text{f}x}-n_{\text{w}}-M_{\text{f}}g{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }=0(8)$

$N_{\text{ff}}+n_{\text{fr}}-f_{\text{f}y}+f_{\text{w}}-M_{\text{f}}g{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }=0(9)$

$\begin{array}{ll}\hfill & t_{\text{ff}}{R}_{\text{w}}+t_{\text{fr}}{R}_{\text{w}}+n_{\text{ff}}{L}_{\text{ac}}-n_{\text{fr}}{L}_{\text{ac}}+f_{\text{w}}{L}_{\text{ac}}\hfill \\ \hfill & +{\tau }_{\text{req.f}}-{\tau }_{\text{req.r}}-M_{\text{f}}g{C}_{{\varphi }_{\text{r}}}{L}_{\text{fg}}{C}_{\alpha }=0\hfill \end{array}(10)$

in the same way, the static balance equations of the body frame can be derived by

$f_{\text{f}x}+f_{\text{r}x}-M_{\text{b}}g{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }=0(11)$

$f_{\text{f}y}+f_{\text{r}y}-M_{\text{b}}g{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }-f_{\text{s}}=0(12)$

$f_{\text{f}y}{L}_{\text{bc}}-f_{\text{r}y}{L}_{\text{bc}}-{\tau }_{\text{req.f}}-M_{\text{b}}g{C}_{{\varphi }_{\text{r}}}{L}_{\text{bg}}{C}_{\alpha }=0(13)$

the static balance equations of the rear flipper are obtained by

$t_{\text{rf}}+t_{\text{rr}}-f_{\text{r}x}-M_{\text{r}}g{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }=0(14)$

$n_{\text{rf}}+n_{\text{rr}}-f_{\text{r}y}-M_{\text{r}}g{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }=0(15)$

$t_{\text{rf}}{R}_{\text{w}}+t_{\text{rr}}{R}_{\text{w}}+n_{\text{rf}}{L}_{\text{ac}}-n_{\text{rr}}{L}_{\text{ac}}+{\tau }_{\text{req.r}}-M_{\text{r}}g{C}_{{\varphi }_{\text{r}}}{L}_{\text{rg}}{C}_{\alpha }=0(16)$

They are basic equations for force and moment balance, thus, the applied external forces vary depending on the situation where the crawler is placed. Different torque conditions in two situations, the normal driving mode and the parallelogram mode, are obtained, respectively.

3.1.1 Torque for lifting the flippers in the normal driving mode

In the normal driving mode, the tip of the crawler does not touch the obstacle. Therefore, f_w = n_w = 0 is obtained. Assuming that the flipper is slightly raised, t_ff = t_rf = n_ff = n_rf = 0. Substituting them into the above Eqs 8–10, the equations of equilibrium for the front flipper can be derived below:

$t_{\text{fr}}-f_{\text{f}x}-M_{\text{f}}g{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }=0(17)$

$n_{\text{fr}}-f_{\text{f}y}-M_{\text{f}}g{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }=0(18)$

$t_{\text{fr}}{R}_{\text{w}}-n_{\text{fr}}{L}_{\text{ac}}+{\tau }_{\text{req.f}}-{\tau }_{\text{req.r}}-M_{\text{f}}g{C}_{{\varphi }_{\text{r}}}{L}_{\text{fg}}{C}_{\alpha }=0(19)$

in a similar way, substituting the above conditions into Eqs 14–16, the equations of equilibrium for the rear flipper can be obtained.

$t_{\text{rr}}-f_{\text{r}x}-M_{\text{r}}g{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }=0(20)$

$n_{\text{rr}}-f_{\text{r}y}-M_{\text{r}}g{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }=0(21)$

$t_{\text{rr}}{R}_{\text{w}}-n_{\text{rr}}{L}_{\text{ac}}+{\tau }_{\text{req.r}}-M_{\text{r}}g{C}_{{\varphi }_{\text{r}}}{L}_{\text{rg}}{C}_{\alpha }=0(22)$

the equations of equilibrium for the body frame are the same as Eqs 11–13.

From Eqs 11, 17, 20, the sum of the tangential force of the crawler is

$t_{\text{fr}}+t_{\text{rr}}=Mg{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }(23)$

from Eqs 12, 18, 21, the sum of the normal forces is

$n_{\text{fr}}+n_{\text{rr}}=Mg{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }+f_{\text{s}}(24)$

Now, substituting Eqs 23, 24 into the sum of Eqs 19, 22, the torque to lift both front and rear flippers in the normal driving mode τ_req.f can be calculated as follows:

$\begin{array}{ll}\hfill {\tau }_{\text{req.f}}& =L_{\text{ac}}\left(Mg{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }+f_{\text{s}}\right)-Mg{C}_{{\varphi }_{\text{r}}}{R}_{\text{w}}{S}_{\alpha }\hfill \\ \hfill & +\left(M_{\text{f}}{L}_{\text{fg}}-M_{\text{r}}{L}_{\text{rg}}\right)g{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }+{\tau }_{\text{i}}.\hfill \end{array}(25)$

The first term depends on the gravitational force and the spring force of the contractile mechanism, meaning that these forces need to be overcome to lift the flippers. The second term depends on the inclination angle of the inner wall of the pipe α. The larger this angle is, the smaller the torque required to lift the flipper, thus, the sign is negative. The third term depends on the position of the center of gravity of the front and rear flippers. The farther the position of the center of gravity is from the rotational axis of the arm, the more susceptible it is to that effect. In an actual robot, there is an initial resistance that is generated by the mechanical frictions such as the forces applied to the bearings and shafts due to the tension of the belt, and the inertia, etc., which influence each other in a complicated manner. Therefore, this initial resistance is collectively defined as τ_i here.

3.1.2 Torque for lifting the flippers in the parallelogram mode

In the parallelogram mode, it is assumed that the flippers are slightly lifted, thus, t_ff = t_rf = n_ff = n_rf = 0 can be obtained. However, the tip of the crawler is in contact with the obstacle. Therefore, f_w ≠ n_w ≠ 0, and the equations for the force-moment balance of the front flipper are given below:

$t_{\text{fr}}-f_{\text{f}x}-n_{\text{w}}-M_{\text{f}}g{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }=0(26)$

$n_{\text{fr}}-f_{\text{f}y}-f_{\text{w}}-M_{\text{f}}g{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }=0(27)$

$t_{\text{fr}}{R}_{\text{w}}-n_{\text{fr}}{L}_{\text{ac}}+f_{\text{w}}{L}_{\text{ac}}+{\tau }_{\text{req.f}}-{\tau }_{\text{req.r}}-M_{\text{f}}g{C}_{{\varphi }_{\text{r}}}{L}_{\text{fg}}{C}_{\alpha }=0(28)$

The equations of equillibrium for the rear flipper are the same as Eqs 20–22 as well as that for the body frame are the same as Eqs 11–13. From Eqs 11, 20, 26, the sum of the tangential force of the crawler is derived by

$t_{\text{fr}}+t_{\text{rr}}=Mg{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }+n_{\text{w}}(29)$

from Eqs 12, 21, 27, the sum of the normal forces applying on the crawler is

$n_{\text{fr}}+n_{\text{rr}}=Mg{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }+f_{\text{s}}-f_{\text{w}}(30)$

When the crawler contacts an obstacle and cannot move forward further, the tracked-belt slips. Since sliding friction force generates at this moment, the following relationship can be derived using the sliding friction coefficient μ_s:

$t_{\text{fr}}={\mu }_{\text{s}}{n}_{\text{fr}}(31)$

$t_{\text{rr}}={\mu }_{\text{s}}{n}_{\text{rr}}(32)$

$f_{\text{w}}={\mu }_{\text{s}}{n}_{\text{w}}(33)$

substituting Eqs 29, 30, 33 into the sum of Eqs 22, 28, τ_req.f can be calculated by

$\begin{array}{ll}\hfill {\tau }_{\text{req.f}}& =L_{\text{ac}}\left(Mg{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }+f_{\text{s}}\right)-Mg{C}_{{\varphi }_{\text{r}}}{R}_{\text{w}}{S}_{\alpha }+\left(M_{\text{f}}{L}_{\text{fg}}\right.\hfill \\ \hfill & +\left.M_{\text{r}}{L}_{\text{rg}}\right)g{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }-n_{\text{w}}\left\{2{\mu }_{\text{s}}{L}_{\text{a}}+R_{\text{w}}\left(1+{\mu }_{\text{s}}\right)\right\}+{\tau }_{\text{i}}\hfill \end{array}(34)$

from Eqs 29–33, the normal force that disturbs the crawler movement n_w is obtained by

$n_{\text{w}}=\frac{{\mu }_{\text{s}}\left(Mg{C}_{{\varphi }_{\text{r}}}{C}_{\alpha }+f_{\text{s}}\right)-Mg{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }}{{\mu }_{\text{s}}^2+1}(35)$

In a similar way as Eq. 25, the first term in Eq. 34 depends on the gravitational force and the spring force of the contractile mechanism. The second term depends on the inclination angle of the inner wall of the pipe α, and the larger this angle is, the torque necessary to lift the flippers reduces. The third term also depends on the position of the center of gravity of the front and rear flippers, similar to Eq. 25. The fourth term depends on the upward force applying between the crawler and the obstacle f_w, and this force assists the rotation of the flippers. τ_i is also defined as the initial resistance.

3.2 Torque for rotating the pulley of the tracked-belt

The torque for rotating the pulley at the tip τ_req.p is generated from the torque for rotating the front flipper τ_req.f transmitted via the spur gear. It can be assumed that this torque is balanced with the forces applying along the crawler’s belt as shown in Figure 7C. Considering the initial resistance τ_i in the same manner, τ_req.p is given by

${\tau }_{\text{req.p}}=R_{\text{w}}\left(t_{\text{ff}}+t_{\text{fr}}+t_{\text{rf}}+t_{\text{rr}}+f_{\text{w}}\right)+{\tau }_{\text{i}}(36)$

as mentioned in the section of the torques for lifting the flipper in the normal driving mode and the parallelogram mode, the torque for rotating the pulley at the tip τ_req.p varies between two modes. Therefore, they are derived in each mode as follows.

3.2.1 Torque for rotating the pulley in the normal driving mode

In the normal driving mode, f_w = n_w = 0 because the tip of the crawler does not contact the obstacle. Therefore, τ_req.p can be obtained by removing f_w from Eq. 36.

${\tau }_{\text{req.p}}=R_{\text{w}}\left(t_{\text{ff}}+t_{\text{fr}}+t_{\text{rf}}+t_{\text{rr}}\right)+{\tau }_{\text{i}}(37)$

eliminating n_w from the sum of Eqs 8, 11, 14 and substituting them into Eq. 37, τ_req.p can be obtained by

${\tau }_{\text{req.p}}=R_{\text{w}}Mg{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }+{\tau }_{\text{i}}(38)$

3.2.2 Torque for rotating the pulley in the parallelogram mode

On the other hand, in the parallelogram mode, the tip of the crawler contacts the obstacle, and the front and rear flippers are lifted. Therefore, f_w ≠ n_w ≠ 0 and t_ff = t_rf = 0. As a result, τ_req.p is given by

${\tau }_{\text{req.p}}=R_{\text{w}}\left(t_{\text{fr}}+t_{\text{rr}}+f_{\text{w}}\right)+{\tau }_{\text{i}}(39)$

substituting Eqs 29, 33 into Eq. 39, the torque for rotating the pulley in the parallelogram mode τ_req.p can be derived by

${\tau }_{\text{req.p}}=R_{\text{w}}\left\{Mg{C}_{{\varphi }_{\text{r}}}{S}_{\alpha }+\left({\mu }_{\text{s}}+1\right)n_{\text{w}}\right\}+{\tau }_{\text{i}}(40)$

n_w can be obtained from Eq. 35.

4 Gear ratio design

τ_req.p, τ_req.f obtained by the static analysis, and their output ratio K are given by Eqs 25, 38 in the normal driving mode and Eq. 34, 40 in the parallelogram mode. The parameters of each rigid body used in the analysis are: M_f [kg] = 0.13, M_b [kg] = 0.20, M_r [kg] = 0.12, g [m/s²] = 9.8, R_w [mm] = 20, L_a [mm] = 46, and L_b [mm] = 150. Since the rear flipper of the crawler and the mainframe have a symmetrical structure, L_bg = L_rg = 0 is assumed. Also, the center of gravity of the front flipper is moved only by the gear of the tip pulley, and this influence is small, thus, L_fg = 0. For the sliding friction coefficient μ_s, 0.4 of the general polyurethane belt used for crawlers and vinyl chloride used for pipes is used.

For the initial resistance τ_i, the value when the real crawler was idling with no load, which is calculated by the following equation using the motor current i at no-load rotation, torque constant K_τ, and reduction ratio K_ratio.

${\tau }_{\text{i}}=K_{\text{ratio}}{K}_{\tau }i(41)$

the current value is the measured value i = 0.054 A, the torque constant is K_τ = 8.83 Nmm/A from the motor specifications, and the reduction ratio is the actual value K_ratio = 231 is used. Based on them, τ_i = 106.4 Nmm is obtained.

4.1 Influence of the expanding force of the contractile mechanism f_s and determination of the spring stiffness

When the crawler module is located on the upper inner wall of the pipe, the contractile mechanism needs to press the crawler with a larger force against gravity. Therefore, the influence of the expanding pressing force f_s of the contractile mechanism is calculated under the conditions of α = 0 and ϕ_r = 180°. Figure 8A, B show the effects of f_s in the normal driving mode and that of f_s in the parallelogram mode, respectively. When f_s is 4.4 N or less, τ_req.p and τ_req.f are both less than τ_i. This means that the crawler moves away from the inner surface of the pipe, in other words, f_s should be at least 4.4 N.

FIGURE 8

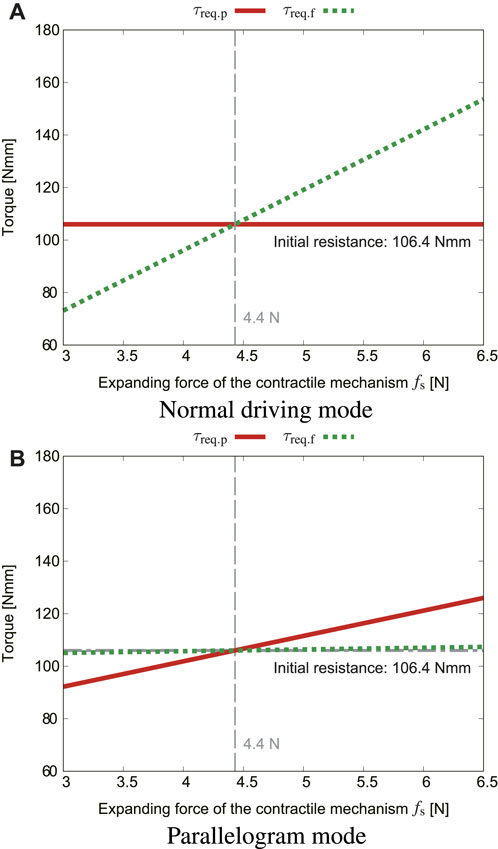
FIGURE 8. Effects of the expanding force f_s, where μ_s = 0.4, α = 0, ϕ_r = 180° [(A): normal driving mode, (B): parallelogram mode].

The expansion force of the contractile mechanism is influenced by the spring force s_p. The relationship between those two forces can be obtained by the following equation with the tangent function, referring to the literature (Kwon and Yi, 2012).

$f_{\text{s}}=2s_{\text{p}}\tan \psi (42)$

in our case, the actual natural length of the spring is 55 mm, and it shrinks to 53 mm when the robot enters the straight pipe. Therefore, the spring force is given by s_p = K_s(55 − 53) (k denotes the spring stiffness). In the straight pipe, ψ = 70°, and K_s = 0.5 N/mm was selected because f_s is approximately 5.5 N, which satisfies the condition of 4.4 N or higher.

4.2 Influence of the robot roll angle ϕ_r

Figure 9A shows how the roll angle of the robot ϕ_r influences τ_req.p, τ_req.f, and output ratio K_req in the normal driving mode. For f_s, the above-mentioned value of 5.5 N was substituted. In a similar way, Figure 9B shows how ϕ_r influences τ_req.p, τ_req.f, and output ratio K_req in the parallelogram mode. In order to make the robot perform the ideal motion, the actual output ratio K_act should be smaller than K_req in the normal driving mode but greater than that in the parallelogram mode according to Eq. 7. Combining these two graphs, the output ratio should be within the range of 0.98 < K_act < 1.23 to fit with all roll angles range ϕ_r. When K_act < 0.98, even if the robot contacts with an obstacle, the flipper cannot be lifted and keeps slipping. When 1.36 > K_act, the flipper is lifted even in the normal driving mode.

FIGURE 9

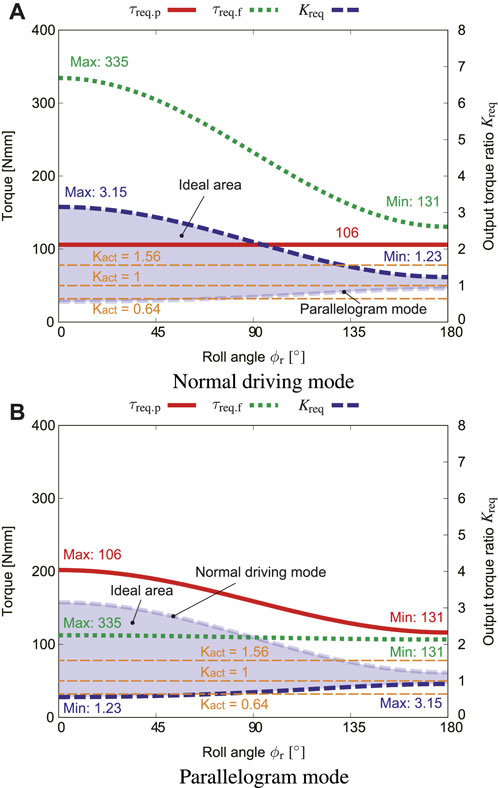
FIGURE 9. Effect of the roll angle ϕ_r, where μ_s = 0.4, f_s = 5.5 N, α = 0 [(A): normal driving mode, (B): parallelogram mode].

4.3 Influence of the initial resistance τ_i

Figure 10A plots how the initial resistance τ_i influences τ_req.p, τ_req.f, and output ratio K_req in the normal driving mode. From Figure 9, the rolling angle at the most severe condition (K_req range is the narrowest) ϕ_r = 180° was used. Figure 10B shows how τ_i influences τ_req.p, τ_req.f, and output ratio K_req in the parallelogram mode.

The results revealed that the initial resistance τ_i should be small to increase the range of K_req. On the other hand, as the initial resistance increases, the values of K both approach one, thus the range of K_req is very narrow. If structures that cause a large initial resistance are installed, the output ratio must be set to one, which leads to a decrease in the option of the reduction ratio.

FIGURE 10

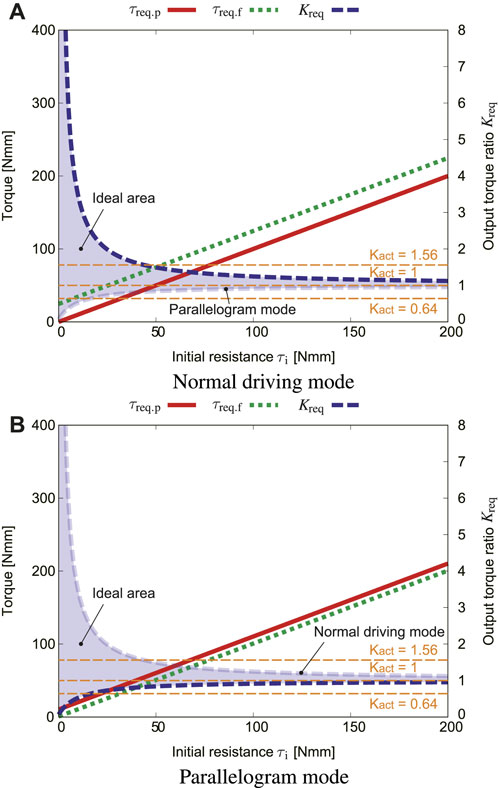
FIGURE 10. Effect of the initial friction τ_i, where μ_s = 0.4, f_s = 5.5 N, α = 0, ϕ_r = 180° [(A): normal driving mode, (B): parallelogram mode].

4.4 Influence of the pipe slope angle α

Figure 11A shows how the pipe slope angle α influences τ_req.p, τ_req.f, and output ratio K_req in the normal driving mode. In the normal driving mode, τ_req.p is maximum where α = 90°, which corresponds to the vertical pipe. The torque τ_req.f for lifting the flipper is inversely proportional to α. This means that as α increases, gravity helps the flippers rotate.

FIGURE 11

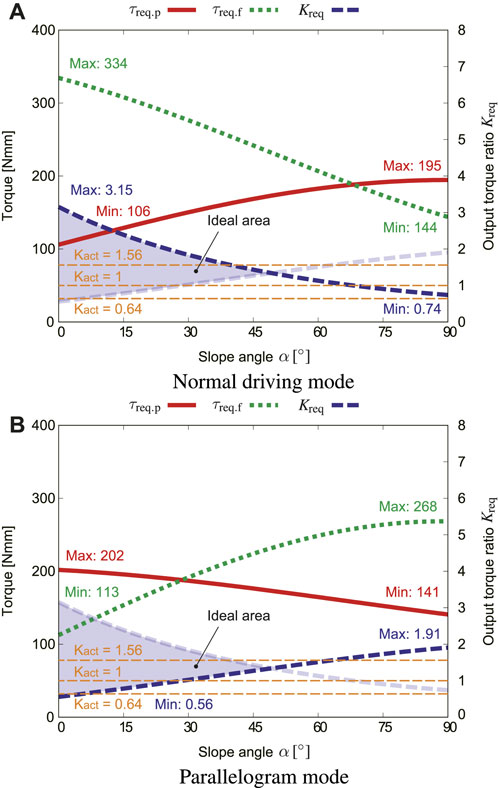
FIGURE 11. Effect of the slope angle α, where μ_s = 0.4, f_s = 5.5 N, ϕ_r = 0 [(A): normal driving mode, (B): parallelogram mode].

Figure 11B shows how α influences τ_req.p, τ_req.f, and output ratio K_req in the parallelogram mode. Since Eq. 34 is a function that includes both sin α and cos α, τ_req.f is maximum near α = 60°. The two K_req curves intersect at about α = 47°. This means that if α exceeds 47°, the flipper will be lifted even in the normal driving mode. However, in reality, when the flipper is lifted, the contractile mechanism is also shrunk, then f_s increases, and the flipper stops rotating and restarts the movement.

The ideal range of K_act gradually narrows as α increases. In this study, the actual output ratio is set to three variations: K_act = 1.56, K_act = 1, and K_act = 0.64 to fit with as wide range of α as possible. This is the value where the gear teeth number ratio is 56 : 36, 46 : 46, and 36 : 56, respectively. The output ratio K_act = 1.56 exceeds K_req at around ϕ_r = 135° as illustrated in Figure 9. This means that the flipper may be rotated when the crawler is flipped and located at the top inner surface of the pipe. However, this will not influence the forward and backward movement of the robot, because it can move even with the parallelogram shape.

4.5 Influence of the sliding frictional coefficient μ_s

The sliding friction coefficient μ_s is not taken into account in the normal driving mode. Therefore, only the influence of μ_s in the parallelogram mode is described here. Figure 12 shows how μ_s influences τ_req.p, τ_req.f, and output ratio K_req in the parallelogram mode. The torque for lifting the flipper τ_req.f has a negative value when μ_s exceeds around 0.8. This means that if μ_s is sufficient, the torque for rotating the flipper is not needed, and the crawler can shift its shape by only using the pulley rotation. When the sliding friction coefficient μ_s is less than around 0.2, K_act needs to be larger than 1.56, and the flipper cannot be lifted at this state because the crawler slips. The larger the sliding friction coefficient μ_s, the wider the ideal range of K_act. With this condition, the crawler can perform the adaptive movement to the environment even with a small output ratio.

FIGURE 12

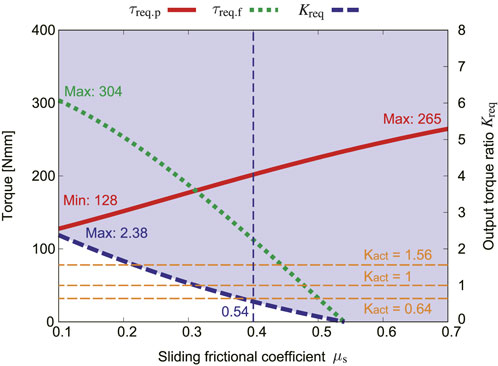
FIGURE 12. Effect of the sliding frictional coefficient μ_s in the parallelogram mode, where f_s = 5.5 N, ϕ_r = 0, α = 0.

The rated torque of the geared motor used for the proposed robot is 1,230 Nmm. The maximum value of the torque required to rotate the flipper τ_req.f is 335 Nmm according to Figures 9, 11. This satisfies the requirement. However, considering further safety factor, the torque of the motor is amplified twice by the bevel gear.

5 Experiments

5.1 Experimental setup

Adaptability of the proposed robot with underactuated parallelogaram modules was tested in a straight stepped pipe as shown in Figure 13. A standard constricted pipe called decreser was connected with two straight pipes with different diamiter; 202 mm (8 in) and 154 mm (6 in). The influence of the pipe slope angle α can be also examined by using a slope adjustment mechanism.

FIGURE 13

FIGURE 13. Experimental setup of a straight stepped pipe with a slope adjustment mechanism.

To verify the performance with different gear ratio (output ratio K_act), three types of teeth number conbination: K_act = 1.56, K_act = 1, and K_act = 0.64 are prepared as depicted in Figure 14.

Each teeth number of two spur gears needs to satisfy the following condition:

$N_{\text{f}}+N_{\text{p}}=\frac{2D}{N_{\mathrm{m}\mathrm{o}\mathrm{d}}}(43)$

where N_f, N_p, D, and N_mod denote the teeth number of the input (flipper) and output (pulley) gears, distance between two gear centers, and the gear module (the ratio of the reference diameter of the gear divided by the number of teeth), respectively. In our case, D = 23 mm and N_mod = 0.5, thus, the sum of N_f and N_p should keep 92.

FIGURE 14

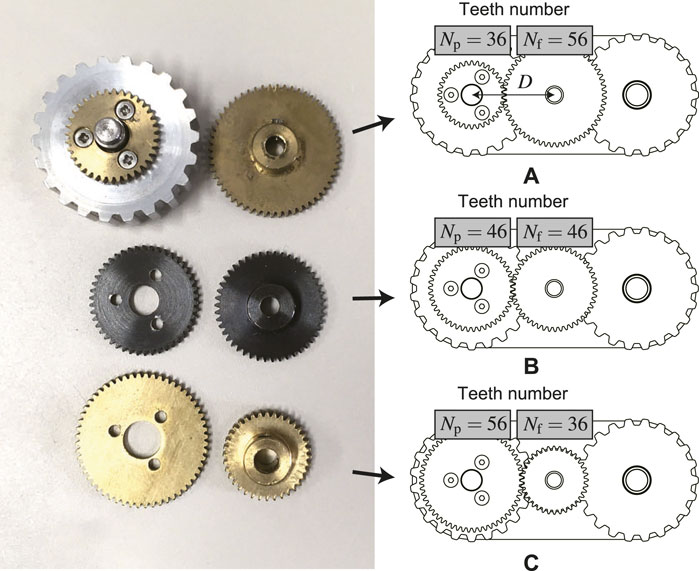
FIGURE 14. Three types of gear ratio: (A) Speed multiplication K_act = 1.56, (B) No speed change K_act = 1, (C) Speed reduction K_act = 0.64.

Three motor drivers combining an ESCON 50/5 (Maxon group ag, Sachseln, Switzerland) and a microcontroller were fabricated for smooth experimentation, and control commands were given to each of them to keep the rotation speed at 40 rpm via CAN communication. The control commands were given via a graphical user interface (GUI) created with Visual Studio C#.

5.2 Experimental results

The experiment was conducted three times each with the following five combinations: α = 0 & ϕ_r = 0, α = 0 & ϕ_r = 180°, α = 45° & ϕ_r = 0, α = 45° & ϕ_r = 180°, and α = 90°. Upper table in Table 1 lists the success number in each trial where K_s = 0.5 N/mm.

From the experiment, it was found that the robot had the best step-adaptability when the output ratio was K_act = 0.64. It indicates that it is better to distribute the torque to the pulley than to the flipper. This result differs from the analysis in the previous section. However, the crawler module was able to deform into a parallelogram shape upon contacting the step in all results. The front half of the robot then slid to a stop as it entered the next narrow pipe (6 in). In all cases, the reason for the inability to travel to the narrow pipe was that the propulsive force of the crawler module was not sufficient to shurink the contractile mechanism.

TABLE 1

TABLE 1. Experimental results where K_s = 0.5 N/mm (upper) and K_s = 0.3 N/mm (lower).

On the other hand, experiments were also conducted for K_s = 0.3 N/mm, which had been excluded because the analysis resulted the difficulty of adaptation to the step. The results of the experiment are listed in the lower table of Table 1. Overall, the results with K_act = 0.64 tended to be better, and in all cases the crawler module was able to shift its shape into a parallelogram. However, the performance at K_act = 1.56 was slightly better than that in the experiments with K_s = 0.3 N/mm.

Overall, the results with K_act = 0.64 tended to be better, and in all cases the crawler module was able to shift its shape into a parallelogram. However, the performance at K_act = 1.56 was slightly better than that in the experiments with K_s = 0.3 N/mm.

Some problems were found as a result of the experiments in the stepped pipe. For example, even when the robot adapted from a large-diameter to a small-diameter pipe, it sometimes did not return to its initial pose after returning from a small-diameter to a large-diameter pipe. Pressing the three crawler modules against the wall by a spring force large enough for the mass of the central part of the robot could solve this problem. However, the weight of the central part of the robot must be drastically reduced and the motor power must be increased due to the increased spring force.

On the other hands, even if the robot did not return to the original pose, it can be solved by controlling only each crawler module individually. For example, if only the contractile mechanism of the lower module shrinks, only that module will shift to parallelogram shape when only the lower one is driven and the other two upper modules are not. After repeating this operation several times, the pose will return to its original state (straightened). This is a disadvantage of the underactuated mechanism, but it is also an advantage of requiring fewer motors.

6 Conclusion

This paper proposes an environmental adaptation in-pipe robot with underactuated parallelogram crawlers. Without using additional motors and sensors, each crawler module can shift its body shape to a parallelogram to adapt to obstacles. The shape-shifting movement is generated by a simple differential mechanism of a pair of spur gears. However, whether the crawler moves forward or shifts the body shape depends on the gear ratio of the differential mechanism. To design the gear ratio, the required output ratio of the pulley to rotate and the flipper to lift up in the normal driving and parallelogram modes was analyzed quasi-statically. The influences of the roll angle of the robot, the initial resistance of the crawler, the slope angle of the pipe, and the frictional coefficient were also simulated. To examine the adaptability performance depending on the gear ratio, experiments in a tilted stepped pipe with a developed in-pipe robot were performed.

The robot successfully shifted its crawler’s shape to parallelogram only with our simulated output ratio, which implies that our quasi-static analysis is valid. In addition to the shape-shifting, the propulsive force for the contraction of the contractile mechanism and friction coefficient of the tracked belt were also found to be important for the adaptation to the stepped pipe. However, in tilted pipe experiments, the robot could not overcome the step, while it could climb the straight section against the gravity. This is because the unexpected uneven posture of the contractile mechanism was generated. One possible solution could be changing the stiffness of the contractile mechanism, but the gear ratio should be also redesigned again to match with this. Expanding the distance between two pantographs at each crawler module may make the contractile mechanism stiff against the external force. This would also solve the uneven posture problem.

Data availability statement

The datasets presented in this article are not readily available because Raw data cannot be published and shared. Requests to access the datasets should be directed to kakogawa@fc.ritsumei.ac.jp.

Author contributions

AK designed and built the robot and wrote the paper. SM advised him on research and writing papers. All authors contributed to the article and approved the submitted version.

Acknowledgments

We would like to express our sincere thanks to Mr. Ferdinand Fukui Peper and Mr. Yosuke Imamura, graduate students, who helped us with the experiments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Birkenhofer, C., Hoffmeister, M., Zollner, J., and Dillmann, R. (2005). “Compliant motion of a multi-segmented inspection robot,” in Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, August 2005 (IEEE), 2632–2637.

CrossRef Full Text | Google Scholar

Debenest, P., Guarnieri, M., and Hirose, S. (2014). “Pipetron series-robots for pipe inspection,” in Proceedings of the 2014 3rd international conference on applied robotics for the power industry, Foz do Iguacu, Brazil, October 2014 (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Dertien, E., Foumashi, M. M., Pulles, K., and Stramigioli, S. (2014). “Design of a robot for in-pipe inspection using omnidirectional wheels and active stabilization,” in Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, June 2014 (IEEE), 5121–5126.

CrossRef Full Text | Google Scholar

Dertien, E., Stramigioli, S., and Pulles, K. (2011). “Development of an inspection robot for small diameter gas distribution mains,” in Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, May 2011 (IEEE), 5044–5049.

CrossRef Full Text | Google Scholar

Fjerdingen, S. A., Liljebäck, P., and Transeth, A. A. (2009). “A snake-like robot for internal inspection of complex pipe structures (piko),” in Proceedings of the 2009 IEEE/RSJ international conference on intelligent robots and systems, St. Louis, MO, USA, October 2009 (IEEE), 5665–5671.

CrossRef Full Text | Google Scholar

Hirose, S., Ohno, H., Mitsui, T., and Suyama, K. (1999). “Design of in-pipe inspection vehicles for/spl phi/25,/spl phi/50,/spl phi/150 pipes,” in Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, May 1999 (IEEE), 2309–2314.

Google Scholar

Inazawa, M., Takemori, T., Tanaka, M., and Matsuno, F. (2021). Unified approach to the motion design for a snake robot negotiating complicated pipe structures. Front. Robotics AI 8, 629368. doi:10.3389/frobt.2021.629368

CrossRef Full Text | Google Scholar

Kakogawa, A., Hirose, C., and Ma, S. (2022a). “A standards-based pipeline route drawing system using a towed sensing unit,” in Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, October 2022 (IEEE), 7167–7173.

CrossRef Full Text | Google Scholar

Kakogawa, A., Komurasaki, Y., and Ma, S. (2019). Shadow-based operation assistant for a pipeline-inspection robot using a variance value of the image histogram. J. Robotics Mechatronics 31, 772–780. doi:10.20965/jrm.2019.p0772

CrossRef Full Text | Google Scholar

Kakogawa, A., and Ma, S. (2018). Design of a multilink-articulated wheeled pipeline inspection robot using only passive elastic joints. Adv. Robot. 32, 37–50. doi:10.1080/01691864.2017.1393348

CrossRef Full Text | Google Scholar

Kakogawa, A., and Ma, S. (2013). “Design of an underactuated parallelogram crawler module for an in-pipe robot,” in Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, December 2013 (IEEE), 1324–1329.

CrossRef Full Text | Google Scholar

Kakogawa, A., Ma, S., and Hirose, S. (2014). “An in-pipe robot with underactuated parallelogram crawler modules,” in Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, June 2014 (IEEE), 1687–1692.

CrossRef Full Text | Google Scholar

Kakogawa, A., and Ma, S. (2012). Stiffness design of springs for a screw drive in-pipe robot to pass through curved pipes and vertical straight pipes. Adv. Robot. 26, 253–276. doi:10.1163/156855311x614554

CrossRef Full Text | Google Scholar

Kakogawa, A., Murata, K., and Ma, S. (2022b). Automatic T-branch travel of an articulated wheeled in-pipe inspection robot using joint angle response to environmental changes. IEEE Trans. Industrial Electron. 70, 7041–7050. doi:10.1109/tie.2022.3201301

CrossRef Full Text | Google Scholar

Kim, B.-S., Vu, Q.-H., Song, J.-B., and Yim, C.-H. (2010a). Novel design of a small field robot with multi-active crawlers capable of autonomous stair climbing. J. Mech. Sci. Technol. 24, 343–350. doi:10.1007/s12206-009-1108-7

CrossRef Full Text | Google Scholar

Kim, J.-H., Sharma, G., and Iyengar, S. S. (2010b). “Famper: A fully autonomous mobile robot for pipeline exploration,” in Proceedings of the 2010 IEEE International Conference on Industrial Technology, Via del Mar, Chile, March 2010 (IEEE), 517–523.

CrossRef Full Text | Google Scholar

Kwon, Y.-S., and Yi, B.-J. (2012). Design and motion planning of a two-module collaborative indoor pipeline inspection robot. IEEE Trans. Robotics 28, 681–696. doi:10.1109/tro.2012.2183049

CrossRef Full Text | Google Scholar

Lan, G., Ma, S., Inoue, K., and Hamamatsu, Y. (2007). Development of a novel crawler mechanism with polymorphic locomotion. Adv. Robot. 21, 421–440. doi:10.1163/156855307780132045

CrossRef Full Text | Google Scholar

Li, Z., Ma, S., Li, B., Wang, M., and Wang, Y. (2010). “Design and basic experiments of a transformable wheel-track robot with self-adaptive mobile mechanism,” in Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, October 2010 (IEEE), 1334–1339.

Google Scholar

Liu, Y., Bi, Q., Dai, X., Song, R., Zhao, J., and Li, Y. (2022). Ticbot: development of a tensegrity-based in-pipe crawling robot. IEEE Trans. Industrial Electron. 70, 8184–8193. doi:10.1109/tie.2022.3224131

CrossRef Full Text | Google Scholar

Nishimura, T., Kakogawa, A., and Ma, S. (2012). “Pathway selection mechanism of a screw drive in-pipe robot in t-branches,” in Proceedings of the 2012 IEEE international conference on automation science and engineering (CASE), Seoul, Korea (South), August 2012 (IEEE), 612–617.

CrossRef Full Text | Google Scholar

Park, J., Hyun, D., Cho, W.-H., Kim, T.-H., and Yang, H.-S. (2010). Normal-force control for an in-pipe robot according to the inclination of pipelines. IEEE Trans. Industrial Electron. 58, 5304–5310. doi:10.1109/tie.2010.2095392

CrossRef Full Text | Google Scholar

Pfotzer, L., Ruehl, S., Heppner, G., Roennau, A., and Dillmann, R. (2014). “Kairo 3: A modular reconfigurable robot for search and rescue field missions,” in Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO 2014), Bali, Indonesia, December 2014 (IEEE), 205–210.

CrossRef Full Text | Google Scholar

Pfotzer, L., Staehler, M., Hermann, A., Roennau, A., and Dillmann, R. (2015). “Kairo 3: moving over stairs & unknown obstacles with reconfigurable snake-like robots,” in Proceedings of the 2015 European Conference on Mobile Robots (ECMR), Lincoln, UK, September 2015 (IEEE), 1–6.

Google Scholar

Quan, Q., and Ma, S. (2011). Development of a modular crawler for tracked robots. Adv. Robot. 25, 1839–1849. doi:10.1163/016918611x584712

CrossRef Full Text | Google Scholar

Roh, S.-g., and Choi, H. R. (2005). Differential-drive in-pipe robot for moving inside urban gas pipelines. IEEE Trans. robotics 21, 1–17. doi:10.1109/tro.2004.838000

CrossRef Full Text | Google Scholar

Roh, S.-g., Kim, D. W., Lee, J.-S., Moon, H., and Choi, H. R. (2009). In-pipe robot based on selective drive mechanism. Int. J. Control, Automation Syst. 7, 105–112. doi:10.1007/s12555-009-0113-z

CrossRef Full Text | Google Scholar

Rome, E., Hertzberg, J., Kirchner, F., Licht, U., and Christaller, T. (1999). Towards autonomous sewer robots: the makro project. Urban Water 1, 57–70. doi:10.1016/s1462-0758(99)00012-6

CrossRef Full Text | Google Scholar

Schempf, H., Mutschler, E., Gavaert, A., Skoptsov, G., and Crowley, W. (2010). Visual and nondestructive evaluation inspection of live gas mains using the explorer^tm family of pipe robots. J. Field Robotics 27, 217–249. doi:10.1002/rob.20330

CrossRef Full Text | Google Scholar

Streich, H., and Adria, O. (2004). “Software approach for the autonomous inspection robot makro,” in Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA '04. 2004, New Orleans, LA, USA, May 2004, 3411–3416.

CrossRef Full Text | Google Scholar

Suryavanshi, K., Vadapalli, R., Vucha, R., Sarkar, A., and Krishna, K. M. (2020). “Omnidirectional tractable three module robot,” in Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, August 2020 (IEEE), 9315–9321.

CrossRef Full Text | Google Scholar

Tugeumwolachot, T., Seki, H., Tsuji, T., and Hiramitsu, T. (2022). “Development of a multi-dof cutting tool with a foldable supporter for compact in-pipe robot,” in Proceedings of the 2022 International Conference on Mechatronics and Automation, Guilin, Guangxi, China, August 2022 (IEEE), 587–592.

CrossRef Full Text | Google Scholar

Wang, Q., Quan, Q., Deng, Z., and Hou, X. (2016). An underactuated robotic arm based on differential gears for capturing moving targets: analysis and design. J. Mech. Robotics 8. doi:10.1115/1.4032811

CrossRef Full Text | Google Scholar

Ye, C., Lv, G., Ma, S., and Ni, H. (2012). “Development of a variable parallelogram tracked mobile robot,” in Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, December 2012 (IEEE), 2156–2160.

CrossRef Full Text | Google Scholar

Nomenclature