- 1Department of Electrical Engineering and Information Technology, University of Naples Federico II, Naples, Italy
- 2Scuola Superiore Meridionale, Naples, Italy
- 3Department of Mathematics and Applications “R. Caccioppoli”, University of Naples Federico II, Naples, Italy
Introduction: Geometric pattern formation is crucial in many tasks involving large-scale multi-agent systems. Examples include mobile agents performing surveillance, swarms of drones or robots, and smart transportation systems. Currently, most control strategies proposed to achieve pattern formation in network systems either show good performance but require expensive sensors and communication devices, or have lesser sensor requirements but behave more poorly.
Methods and result: In this paper, we provide a distributed displacement-based control law that allows large groups of agents to achieve triangular and square lattices, with low sensor requirements and without needing communication between the agents. Also, a simple, yet powerful, adaptation law is proposed to automatically tune the control gains in order to reduce the design effort, while improving robustness and flexibility.
Results: We show the validity and robustness of our approach via numerical simulations and experiments, comparing it, where possible, with other approaches from the existing literature.
1 Introduction
Many robotic applications require—or may benefit from—one or more groups of multiple agents to perform a joint task (Shi and Yan, 2021); this is, for example, the case of surveillance (Lopes and Lima, 2021), exploration (Kegeleirs et al., 2021), herding (Auletta et al., 2022) or transportation (Gardi et al., 2022). When the number of agents becomes extremely large, the task becomes a swarm robotics problem (Brambilla et al., 2013; Heinrich et al., 2022). Typically, in these problems, it is assumed that the agents are relatively simple, and thus have limited communication and sensing capabilities, and limited computational resources; see, for example the robotic swarms described in Hauert et al. (2009); Rubenstein et al. (2014); Gardi et al. (2022). Sometimes, to cope with such big ensembles, macroscopic methods exploiting partial differential equations can be also suitable (Biswal et al., 2021; Maffettone et al., 2023a, b).
In swarm robotics, typical tasks of interest include aggregation, flocking, navigation, spatial organisation, collaborative manipulation, and task allocation (Brambilla et al., 2013; Bayindir, 2016). Among these, an important subclass of spatial organisation problems is geometric pattern formation, where the goal is for the agents to self-organize their relative positions into some desired structure or pattern, e.g., arranging themselves to form multiple adjacent triangles or on a lattice. Pattern formation is crucial in many applications (Oh et al., 2017), including sensor networks deployment (Kim et al., 2014; Zhao et al., 2019), cooperative transportation and construction (Rubenstein et al., 2013; Mooney and Johnson, 2014; Gardi et al., 2022), and 2D or 3D exploration and mapping (Kegeleirs et al., 2021) or area coverage (Wang and Rubenstein, 2020). Moreover, the formation of patterns is common in many biological systems where agents, such as cells or microorganisms, form organized geometric structures, e.g., Tan et al. (2022).
There are two main difficulties associated with achieving pattern formation. Firstly, as there are no leader agents, the pattern must emerge by exploiting a control strategy that is the same for all agents, distributed and local (i.e., each agent can only use information about “nearby” agents). Secondly, the number of agents is large and may change over time; therefore, the control strategy must also be scalable to varying sizes of the swarm and robust to uncertainties due to its possible variations.
This sets the problem of achieving pattern formation apart from the more classical formation control problems (Oh et al., 2015) where agents are typically fewer and have pre-assigned roles within the formation. Moreover, note that geometric formations can also emerge as a by-product of flocking algorithms as those described in Olfati-Saber (2006); Wang G. et al. (2022). Nevertheless in such cases often the focus of the control strategy is to achieve coordinated motion rather than desired regular formations to emerge.
To classify existing solutions to pattern formation, we employ the same taxonomy used in Oh et al. (2015), and later extended in Sakurama and Sugie (2021), which is based on the type of information available to the agents. Namely, existing strategies can be classified as being (i) position-based when it is assumed agents know their position and orientation and those of their neighbours, in a global reference frame; (ii) displacement-based when agents can only sense their own orientation with respect to a global reference direction (e.g., North) and the relative positions of their neighbours; (iii) distance-based when agents can measure the relative positions of their neighbours with respect to their local reference frame. In terms of sensor requirements, position-based solutions are the most demanding, requiring global positioning sensors, typically GPS, and communication devices, such as WiFi or LoRa. Differently, displacement-based methods require only a distance sensor (e.g., LiDAR) and a compass, although the latter can be replaced by a coordinated initialisation procedure of all local reference frames (Cortés, 2009). Finally, distance-based algorithms are the least demanding, needing only the availability of some distance sensors.
A pressing open challenge in pattern formation problems is that of devising new local and distributed control strategies that can combine low sensor requirements with consistently high performance. This is crucial in swarm robotics, where it can be generally cumbersome, or prohibitively expensive, to equip all agents with GPS sensors and communication capabilities, e.g., Rubenstein et al. (2014).
2 Related work and main contributions
Next, we give a brief overview of the existing literature before expounding our main contributions. Notice that most of these control strategies are based on the use of virtual forces (see Khatib, 1985), an approach inspired by Physics, where each agent is subject to virtual forces [e.g., Lennard-Jones and Morse functions (Brambilla et al., 2013; D’Orsogna et al., 2006)] from neighbouring agents, obstacles, and the environment.
2.1 Position-based approaches
In Pinciroli et al. (2008), a position-based algorithm was proposed to achieve 2D triangular lattices in a constellation of satellites in a 3D space. This strategy combines global attraction towards a reference point with local interaction among the agents to control both the global shape and the internal lattice structure of the swarm. In Casteigts et al. (2012), a position-based approach was presented that combines the common radial virtual force [also used in Spears et al. (2004), Hettiarachchi and Spears (2005), Torquato (2009)] with a normal force. In this way, a network of connections is built such that each agent has at least two neighbours; then, a set of geometric rules is used to decide whether any or both of these forces are applied between any pair of agents. Importantly, this approach requires the acquisition of positions from two-hop neighbours. In Zhao et al. (2019), a position-based strategy is presented to achieve triangular and square patterns, as well as lines and circles, both in 2D and 3D; the control strategy features global attraction towards a reference point and re-scaling of distances between neighbours, with the virtual forces changing according to the goal pattern. Therein, a qualitative comparison is also provided with the distance-based strategy from Spears et al. (2004), showing more precise configurations and a shorter convergence time, due to the position-based nature of the solution. Finally, a simple position-based algorithm for triangular patterns, based on virtual forces and requiring communication between the agents, is proposed in Trotta et al. (2018) to have unmanned aerial vehicles perform area coverage.
2.2 Displacement-based approaches
In Li et al. (2009), a displacement-based approach is presented based on the use of a geometric control law similar to the one proposed in Lee and Chong (2008). The aim is to obtain triangular lattices but small persisting oscillations of the agents are present at steady state, as the robots are assumed to have a constant non-zero speed. In Balch and Hybinette (2000a, b), an approach is discussed inspired by covalent bonds in crystals, where each agent has multiple attachment points for its neighbours. Only starting conditions close to the desired pattern are tested, as the focus is on navigation in environments with obstacles. In Song and O’Kane (2014) the desired lattice is encoded by a graph, where the vertices denote possible roles the agents may play in the lattice and edges denote rigid transformations between the local frames or reference of pairs of neighbours. All agents communicate with each other and are assigned a label (or identification number) through which they are organised hierarchically to form triangular, square, hexagonal or octagon-square patterns. Formation control is similarly addressed in Coppola et al. (2019). The algorithm proposed therein is made of a higher level policy to assign positions in a square lattice to the agents, and a lower level control, based on virtual forces, to have the agents reach these positions. The algorithm can be readily applied to the formation of square geometric patterns, but not to triangular ones. Notably, the reported convergence time is relatively long and increase with the number of agents. Finally, a solution to progressively deploy a swarm on a predetermined set of points is presented in Li et al. (2019). The algorithm can be used to perform both formation control and geometric lattice formation, even though the orientation of the formation cannot be controlled. Moreover, this strategy requires local communication between the agents and the knowledge of a common graph associated to the formation.
2.3 Distance-based approaches
A popular distance-based approach for the formation of triangular and square lattices, named physicomimetics, was proposed in Spears and Gordon (1999) and later further investigated in Spears et al. (2004); Hettiarachchi and Spears (2005). In these studies, triangular lattices are achieved with long-range attraction and short-range repulsion virtual forces only, while square lattices are obtained through a selective rescaling of the distances between some of the agents. The main drawback of the physicomimetics strategy (Spears and Gordon, 1999; Spears et al., 2004; Hettiarachchi and Spears, 2005; Sailesh et al., 2014) is that it can produce the formation of multiple aggregations of agents, each respecting the desired pattern, but with different orientations. Another problem, described in Spears et al. (2004), is that, for some values of the parameters, multiple agents can converge towards the same position and collide.
Similar approaches are also used to obtain triangular lattices when using flocking algorithms (Olfati-Saber, 2006; Wang et al., 2022b, a). An extension to achieve the formation of hexagonal lattices was proposed in Sailesh et al. (2014), but with the requirement of an ad hoc correction procedure to prevent agents from remaining stuck in the centre of a hexagon.
In Torquato (2009), an approach exploiting Lennard-Jones-like virtual forces is numerically optimised to locally stabilise a hexagonal lattice. When applied to mobile agents, the interaction law is time-varying and requires synchronous clocks among the agents. A stability proof for the formation of triangular (or 3D lattices) under the effect of virtual forces control algorithm, was recently published in Giusti et al. (2023). In Lee and Chong (2008), a different distance-based control strategy, derived from geometric arguments, was proposed to achieve the formation of triangular lattices. An analytical proof of convergence was given to the desired lattice exploiting Lyapunov methods. Robustness to agents’ failure and the capability of detecting and repairing holes and gaps in the lattice are obtained via an ad hoc procedure and verified numerically. A 3D extension was later presented in Lee et al. (2010).
2.4 Main contributions
Our main contributions can be listed as follows.
1. We introduce a novel distributed displacement-based local control strategy to solve geometric pattern formation problems in swarm robotics that requires no communication among the agents or any need for labelling them. In particular, to achieve triangular and square lattices, we employ two virtual forces controlling the norm and the angle of the agents’ relative position, respectively.
2. We show that the strategy performs significantly better than distance-based algorithms (Spears et al., 2004) when achieving square lattices, in terms of precision and robustness.
3. We propose an adaptive strategy to select the control gains automatically in order for the agents to organize themselves and switch from one desired pattern to another, without the need of off-line tuning of the control gains.
4. We present an exhaustive numerical and experimental validation of the proposed strategy showing its effectiveness even in the presence of actuator constraints and other more realistic effects.
When compared to the control strategies in the existing literature, our approach (i) is able to achieve both triangular and square lattices rather than just triangular ones [e.g., as in Lee and Chong (2008), Casteigts et al. (2012)] (ii) yields more precise and robust square lattices with respect to distance-based algorithms (e.g., Spears et al., 2004; Sailesh et al., 2014), with only a minimal increase in sensor requirements (a compass); and (iii) does not require the more costly sensors and communication devices used for position-based strategies (e.g., Zhao et al., 2019), nor labelling of the agents (Song and O’Kane, 2014; Coppola et al., 2019).
3 Mathematical preliminaries
Notation. We denote by ‖⋅‖ the Euclidean norm. Given a set
3.1 Planar swarms
Definition 1. (Swarm). A (planar) swarm
Moreover,
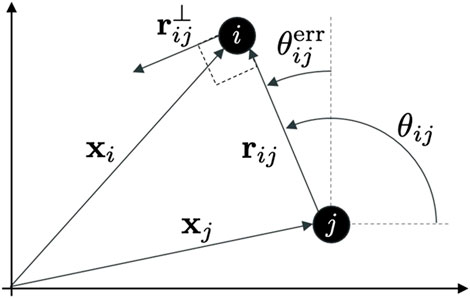
FIGURE 1. Schematic diagram of two agents, i and j, showing the key variables used in the paper to describe the agents’ position and their geometrical relationship.
Definition 2. (Neighbourhood). Given a swarm and a sensing radius
Definition 3. (Adjacency set). Given a swarm and some finite
Notice that if Rmax ≤ Rs then
Definition 4. (Links). A link is a pair
Clearly, it is possible to associate to the swarm a time-varying graph
Finally, given any two links (i, j) and (h, k), we denote with
3.2 Lattice and performance metrics
Definition 5. (Lattice). Given some L ∈ {4, 6} and
In Definition 5, L = 4, and L = 6 correspond to square and triangular lattices,2 respectively, as portrayed in Figure 2. We say that a swarm self-organises into a (L, R)-lattice if (i) each agent has at most L links, and (ii)
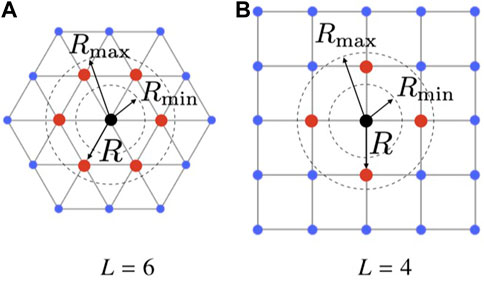
FIGURE 2. (L, R)-lattice formations. (A) shows a triangular lattice (L =6), and (B) shows a square lattice (L =4). Red dots are agents in the adjacency set
Definition 6. (Regularity metric). Given a swarm and a desired (L, R)-lattice, the regularity metric eθ(t) ∈ [0, 1] is
where, omitting the dependence on time,
The regularity metric eθ, derived from Spears et al. (2004), quantifies the incoherence in the orientation of the links in the swarm. In particular, eθ = 0 when all the pairs of links form angles that are multiples of 2π/L (which is desirable to achieve the (L, R)-lattice), while eθ = 1 when all pairs of links have the maximum possible orientation error, equal to π/L. (eθ ≈ 0.5 generally corresponds to the agents being arranged randomly.)
Definition 7. (Compactness metric). Given a swarm and a desired (L, R)-lattice, the compactness metric eL(t) ∈ [0, (N − 1 − L)/L] is
The compactness metric eL measures the average difference between the number of neighbours each agent has and the one they are ought to have if they were arranged in a (L, R)-lattice. According to this definition, eL reaches its maximum value, eL, max = (N − 1 − L)/L, when all agents are concentrated in a small region, and links exist between all pairs of agents, while eL = 1 when all the agents are scattered loosely in the plane, and no links exist between them, and, eL = 0 when all the agents have L links (typically we will require that eL is below some acceptable threshold, see Section 5.1.1). It is important to remark that, if the number N of agents is finite, eL can never be equal to zero, because the agents on the boundary of the group will always have less than L links (Figure 2). This effect gets less relevant as N increases. Note that a similar metric was also independently defined in Song and O’Kane. (2014). We remark that the compactness metric inherently penalizes the presence of holes in the configuration and the emergence of detached swarms, as those scenarios are characterized by larger boundaries.
For the sake of brevity, in what follows we will omit dependence on time when that is clear from the context.
4 Control design
4.1 Problem formulation
Consider a planar swarm
where xi(t) was given in Definition 1 and
We want to design a distributed feedback control law
1. robust to failures of agents and to noise;
2. flexible, allowing dynamic reorganisation of the agents into different patterns;
3. scalable, allowing the number of agents N to change dynamically.
We will assess the effectiveness of the proposed strategy by using the performance metrics eθ and eL introduced above (see Definition 6 and Definition 7).
4.2 Distributed control law
To solve this problem we propose a distributed displacement-based control law of the form
where ur,i and un,i are the radial and normal control inputs, respectively. The two inputs have different purposes and each comprises several virtual forces. The radial input ur,i is the sum of attracting/repelling actions between the agents, with the purpose of aggregating them into a compact swarm, while avoiding collisions. The normal input un,i is also the sum of multiple actions, used to adjust the angles of the relative positions of the agents.
Note that the control strategy in (7) is displacement-based because it only requires each agent i (i) to be able to measure the relative positions of the agents close to it (in the sets
4.3 Radial interaction control
The radial control input ur,i in (7) is defined as the sum of several virtual forces, one for each agent in
where
where
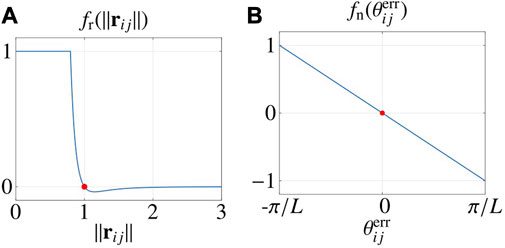
FIGURE 3. Interaction functions. (A) shows the radial function and (B) shows the normal interaction function. Red dots highlight zeros of the functions. Parameters are taken from Table 2.
4.4 Normal interaction
For any link (i, j), we define the angular error
Then, the normal control input un,i in (7) is chosen-as
where
fn is portrayed in Figure 3B.
5 Numerical validation
In this section, we assess the performance and the robustness of our proposed control algorithm (7) through an extensive simulation campaign. The experimental validation of the strategy is later reported in Section 7. First in Section 5.2, using a numerical optimisation procedure, we tune the control gains Gr,i and Gn,i in (8), (11), as the performance of the controlled swarm strongly depends on these values. Then in Section 5.3, we assess the robustness of the control law with respect to (i) agents’ failure, (ii) noise, (iii) flexibility to pattern changes, and (iv) scalability. Finally in Section 5.4, we present a comparative analysis of our distributed control strategy and other approaches previously presented in the literature. The simulations and experiments performed in this and the next Sections are summarised in Table 1.
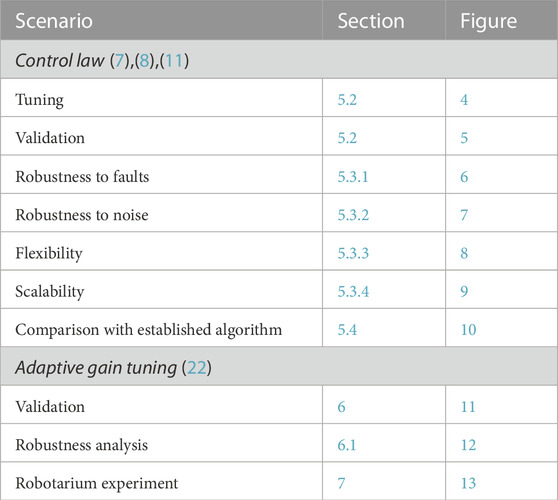
TABLE 1. List of simulations and experiments reported in this paper with indication of the section and figures were the results are presented.
5.1 Simulation setup
We consider a swarm consisting of N = 100 agents (unless specified differently). To represent the fact that the agents are deployed from a unique source (as typically done in the literature, see e.g., Spears et al. (2004), their initial positions are drawn randomly with uniform distribution from a disk of radius r = 2 centred at the origin4, 5.
Initially, for the sake of simplicity and to avoid the possibility of some agents becoming disconnected from the group, we assume that Rs in (1) is large enough so that
i.e., any agent can sense the relative position of all others. Later, in Section 5.3, we will drop this assumption and show the validity of our control strategy also for smaller values of Rs. All simulation trials are conducted in Matlab6, integrating the agents’ dynamics using the forward Euler method with a fixed time step Δt > 0. Moreover, the speed of the agents is limited to Vmax > 0. The values of the parameters used in the simulations are reported in Table 2.
5.1.1 Performance evaluation
To assess the performance of the controlled swarm, we exploit the metrics eθ and eL given in Definition 6 and Definition 7. Namely, we select empirically the thresholds
We give an analogous definition for the steady state of eL (using
Finally, to asses how quickly the pattern is formed, we define.
5.2 Tuning of the control gains
For the sake of simplicity, in this section we assume that Gr,i = Gr and Gn,i = Gn, for all
The results are reported in Figure 4 for the triangular (L = 6) and the square (L = 4) lattices; in the former case, the pair
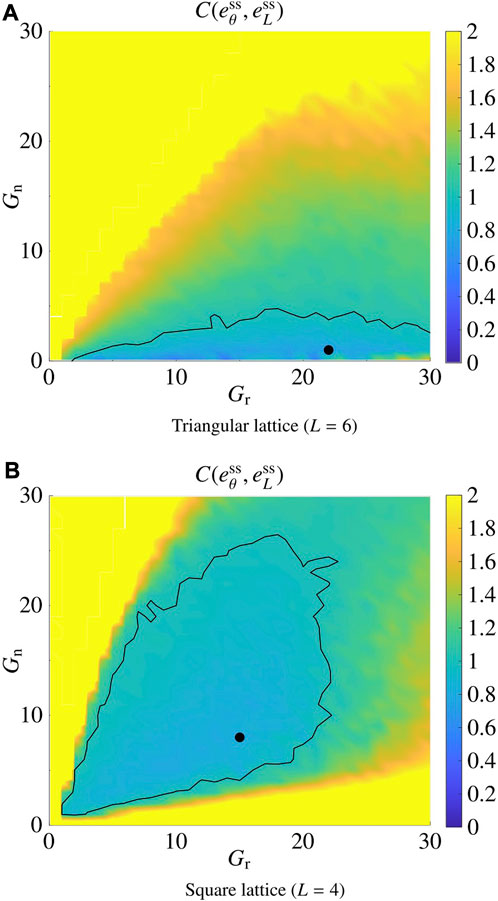
FIGURE 4. Tuning of the control gains Gr and Gn. (A) shows the result for the triangular lattice (L =6), and (B) shows the result for the square lattice (L =4). The black dots correspond to
In Figure 5, we report four snapshots at different time instants of two representative simulations, together with the metrics eθ(t) and eL(t), for the cases of a triangular and a square lattice, respectively. The control gains were set to the optimal values
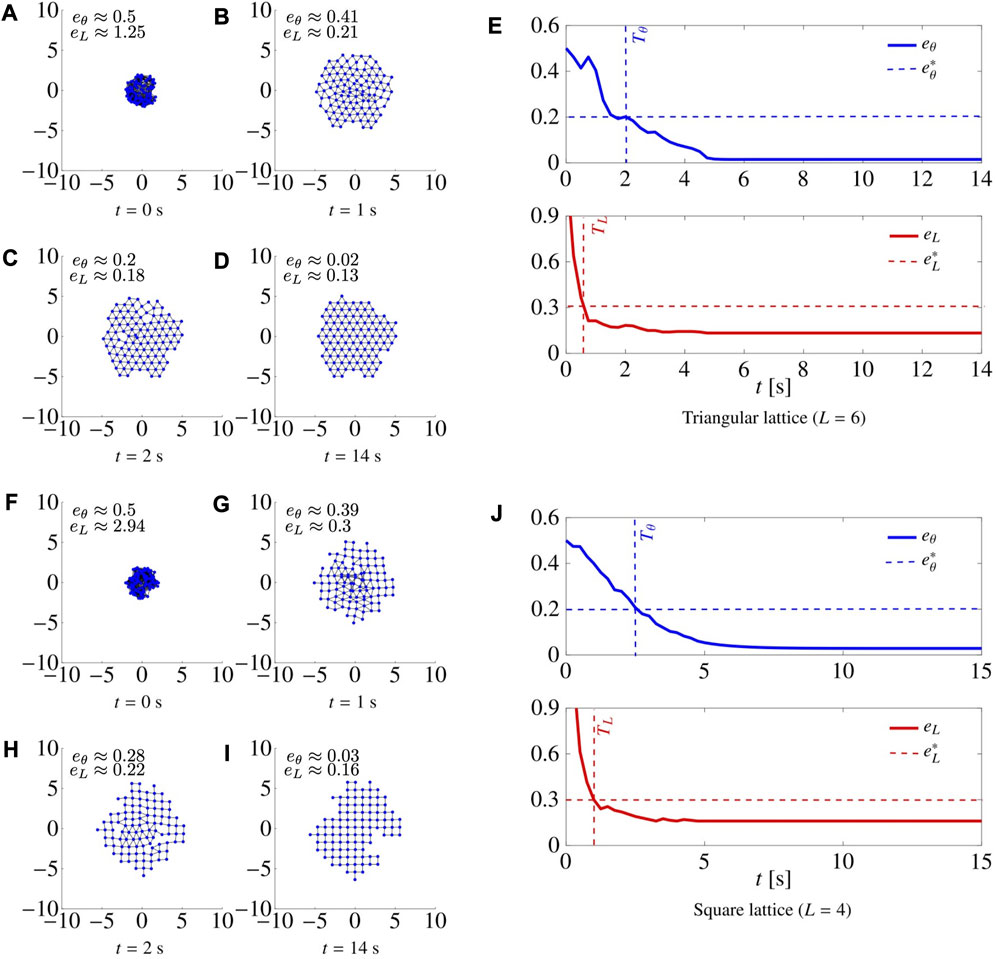
FIGURE 5. Snapshots at different time instants of a swarm of N =100 agents being controlled to form a triangular lattice (A–D) and a square lattice (F–I). For each snapshot, we also report the values of eθ and eL. (E–J) show the time evolution of the metrics eθ and eL for L =6 and L =4, respectively. When L =6, we set
5.3 Robustness analysis
In this section, we investigate numerically the properties that we required in Section 4.1, that is robustness to faults and noise, flexibility, and scalability.
5.3.1 Robustness to faults
We ran a series of simulations in which we removed a percentage of the agents at a certain time instant, and assessed the capability of the swarm to recover the desired pattern. For the sake of brevity, we report only one of them as a representative example in Figure 6, where, with L = 4, 30% of the agents were removed at random at time t = 30 s. We notice that, as the agents are removed, eL(t) and eθ(t) suddenly increase, but, after a short time, they converge again to values below the thresholds, recovering the desired pattern, despite the formation of small holes in the pattern at steady-state that increase
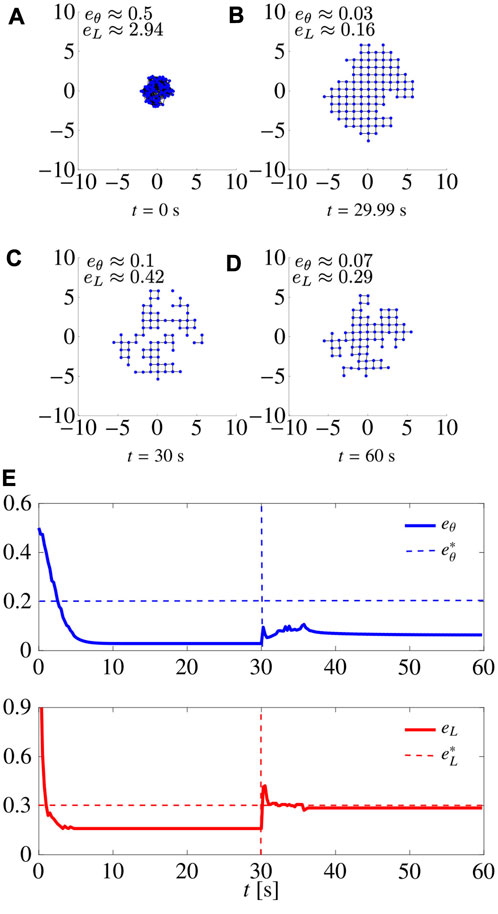
FIGURE 6. Robustness to agents’ removal. (A–D) show snapshots at different time instants of a swarm agents achieving a square lattice. Initially, there are N =100 agents with 30 agents being removed at t =30 s. (E) shows the time evolution of the metrics; dashed vertical lines denote the time instant when agents are removed. Here L =4, and
5.3.2 Robustness to noise
We assessed the robustness to noise both on actuation and on sensing, in two separate tests. In the first case, we assumed that the dynamics (6) of each agent is affected by additive white Gaussian noise with standard deviation σa. In the second case, we assumed that, for each agent, both the distance measurements ‖rij‖ in (8) and the angular measurements
In particular, we set L = 4 and varied either σa or σm in intervals of interest with small increments. For each value of σa and σm, we ran M = 30 trials, starting from random initial conditions, and report the average values of
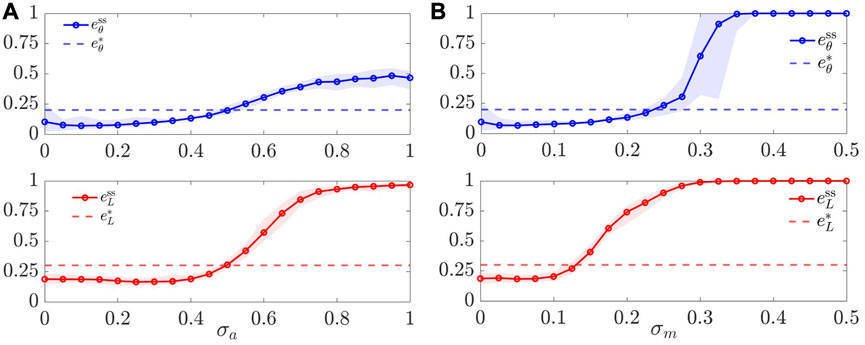
FIGURE 7. Robustness to noise. Value of the metrics
We obtained qualitatively similar results when we assumed the presence of noise on the compass measurements of the agents (obtained by adding Gaussian noise on the variables
5.3.3 Flexibility
In Figure 8, we report a simulation where L was initially set equal to 4 (square lattice), changed to 6 (triangular lattice) at time t = 30 s, and finally changed back to 4 at t = 60 s. The control gains are set to
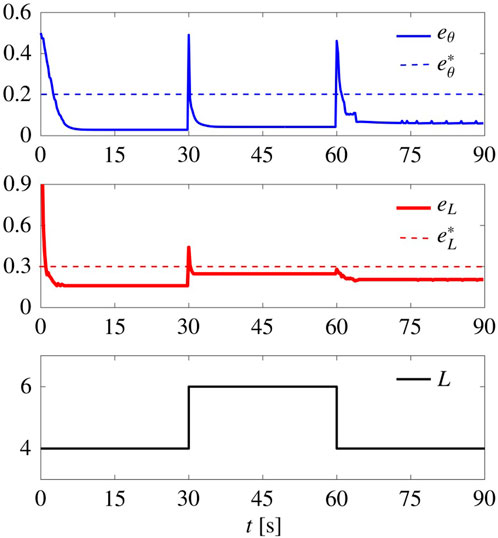
FIGURE 8. Flexibility to spatial reorganisation. Time evolution of the metrics
5.3.4 Scalability
We relaxed the assumption that (13) holds and characterised
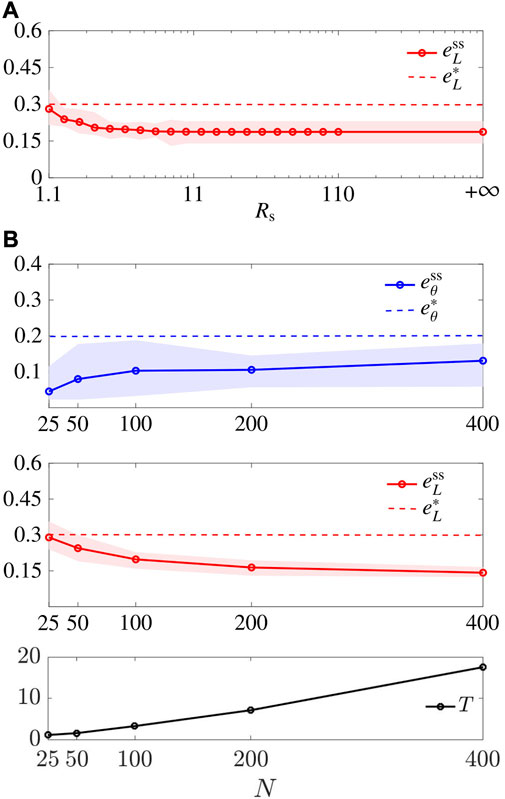
FIGURE 9. Scalability. (A) shows
5.4 Comparison with other established algorithm
As done in related literature (Zhao et al., 2019) (yet for a position-based solution) we compared our control law (7) to the so-called “gravitational virtual forces strategy” (see the Appendix) (Spears et al., 2004), that represent an established solution to geometric pattern formation problems. In Spears et al. (2004), a second order damped dynamics is considered for the agents. Hence, for the sake of comparison, we reduced the model therein to the first order model in (6), by assuming that the viscous friction force is significantly larger than the inertial one.
To select the gravitational gain G and the saturation value Fmax in the control law from Spears et al. (2004), we applied the same tuning procedure described in Section 5.2. In particular, we considered (G, Fmax) ∈ {0, 0.5, …, 10}×{0, 1, …, 40}, and performed 30 trials for each pair of parameters, obtaining as optimal pair for the square lattice
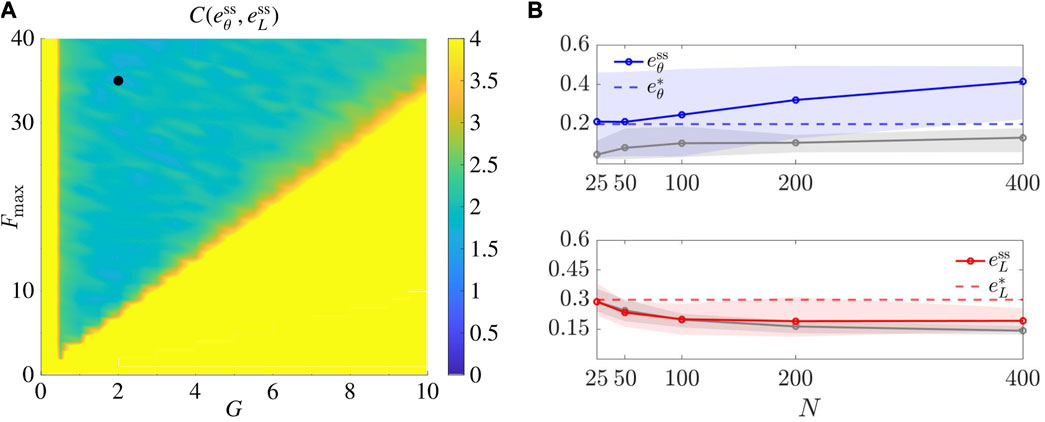
FIGURE 10. Representative application of the algorithm from Spears et al. (2004) (see Appendix). (A) shows the tuning of parameters G and Fmax for the square lattice (L =4). The black dot denotes the optimal pair
Then, we performed the same scalability test in Section 5.3.4 and report the results in Figure 10B. Remarkably, by comparing these results with ours, we see that our proposed control strategy performs better, obtaining much smaller values of
6 Adaptive tuning of control gains
Tuning the control gains (here Gr,i and Gn,i) can in general be a tedious and time-consuming procedure. Therefore, to avoid it, we propose the use of a simple, yet effective adaptive control law, that might also improve the robustness and flexibility of the swarm. Specifically, for the sake of simplicity, Gr,i is set to a constant value Gr for all the swarm, while each agent computes its gain Gn,i independently, using only local information. Letting eθ,i ∈ [0, 1] be the average angular error for agent i, given by
Gn,i is varied according to the law.
where α > 0 is an adaptation gain and
In Figure 11, we report the time evolution of eL, eθ, and of
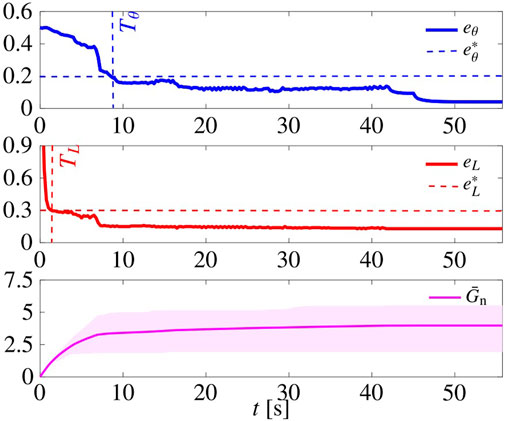
FIGURE 11. Pattern formation using the adaptive tuning law (22). Initial conditions are the same as those of the simulation in Figure 5. The shaded magenta area is delimited by
6.1 Robustness analysis
Next, we test robustness to faults, flexibility, and scalability for the adaptive law (22), similarly to what we did in Section 5.3.
We ran a series of agent removal tests, as described in Section 5.3.1. For the sake of brevity, we report the results of one of such tests with L = 4 in Figures 12A–E. At t = 30 s, 30% of the agents are removed; yet, after a short time the swarm reaggregates to recover the desired lattice.
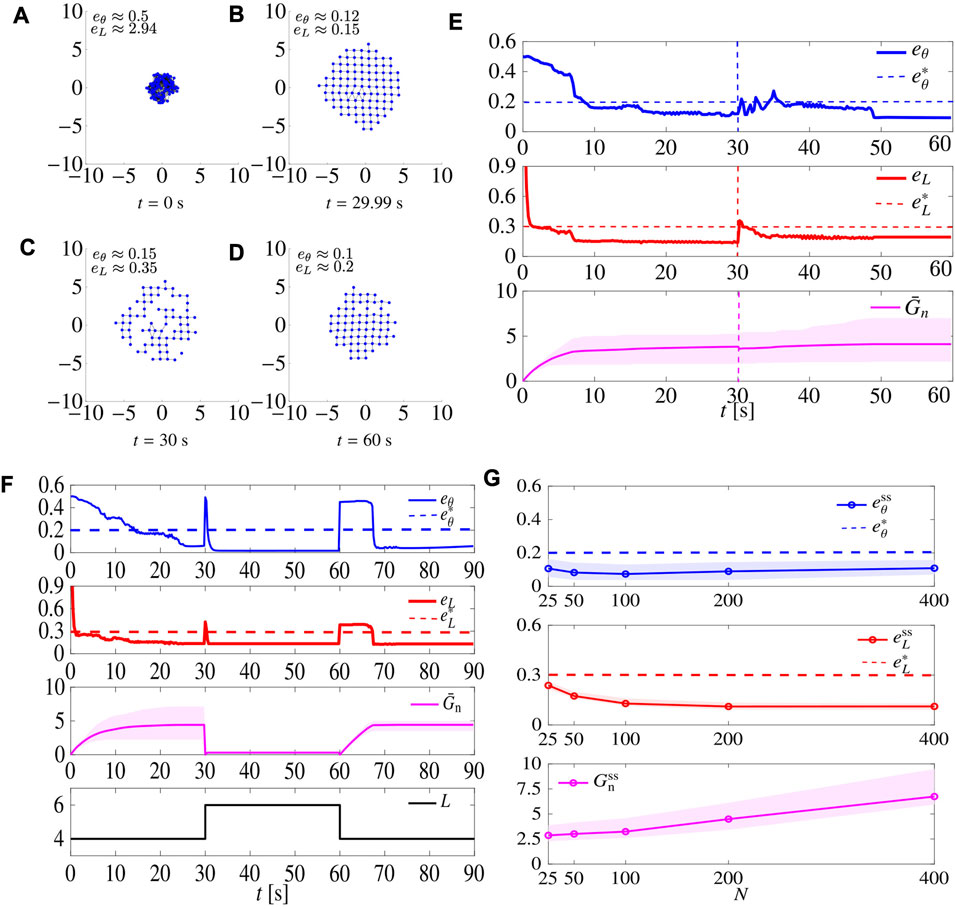
FIGURE 12. Robustness tests using the adaptive tuning law (22). Panels (A–E) show the results of the simulations when starting from 100 agents, 30 agents are removed at t =30 s. Initial conditions are the same as those of the simulation in Figure 6. (A–D) show snapshots of the agents’ configurations at different time instants. (E) shows the time evolution of the metrics eθ and eL, and of the adaptive gain Gn (the shaded magenta area is delimited by
We then repeated the test in Section 5.3.3, with the difference that this time we set Gr = 18.5 (that is the average between the optimal gain for square and triangular patterns), and set Gn,i according to law (22), resetting all Gn,i to 0 when L is changed. The results are shown in Figure 12F. When compared to the non-adaptive case (Figure 8), here
Finally, we repeated the test in Section 5.3.4, setting again the sensing radius Rs to 3 R and assessing performance while varying the size N of the swarm; results are shown in Figure 12G. First, we notice that the larger the swarm is, the larger the steady state value of
7 Robotarium experiments
To further validate our control algorithm, we tested it in a real robotic scenario, using the open access Robotarium platform; see Pickem et al. (2017); Wilson et al. (2020) for further details. The experimental setup features 20 differential drive robots (GRITSBot Pickem et al., 2015), that can move in a 3.2 m × 2 m rectangular arena. The robots have a diameter of about 11 cm, a maximum (linear) speed of 20 cm/s, and a maximum rotational speed of about 3.6 rad/s. To cope with the limited size of the arena, distances
As a paradigmatic example, we performed a flexibility test (similarly to what done in Section 5.3.3 and reported in Figure 8). During the first 33 s, the agents reach an aggregated initial condition. Then we set L = 4 for t ∈ [33, 165), L = 6 for t ∈ [165, 297), and L = 4 for t ∈ [297, 429], ending the simulation. We used the static control law (7)–(8) and (11), and to comply with the limited size of the arena, we scaled the control gains to the values Gr = 0.8 and Gn = 0.4, selected empirically.
The resulting movie is available online (https://github.com/diBernardoGroup/SwarmSimPublic/tree/SwarmSimV1/Media), while representative snapshots are reported in Figure 13, with the time evolution of the metrics. The metrics qualitatively reproduce the behaviour obtained in simulation (see Figure 8). In particular, we obtain
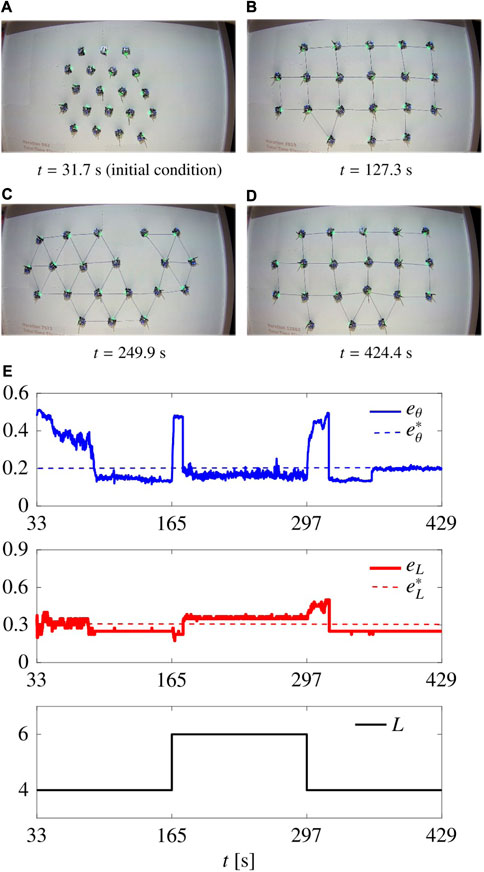
FIGURE 13. Flexibility test in Robotarium. (A–D) show the swarm at different time instants. (E) shows the time evolution of the metrics and the parameter L. The gains are set as
8 Conclusion
We presented a distributed control law to solve pattern formation for the case of square and triangular lattices, based on the use of virtual forces. Our control strategy is distributed, only requires distance sensors and a compass, and does not need communication between the agents. We showed via exhaustive simulations and experiments that the strategy is effective in achieving triangular and square lattices. As a benchmark, we also compared it with the well established distance-based strategy in Spears et al. (2004), observing better performance particularly when the goal is that of achieving square lattices. Additionally, we showed that the control law is robust to failures of the agents and to noise, it is flexible to changes in the desired lattice and scalable with respect to the number of agents. We also presented a simple yet effective gain adaptation law to automatically tune the gains so as to be able to switch the goal pattern in real-time.
In the future, we plan to study analytically the stability and convergence of the control law; results in the case of triangular lattices, also for higher dimensions, were recently presented in Giusti et al. (2023). Other possible future extensions include the ability to obtain other patterns (e.g. hexagonal ones, or non-regular tilings), move in 3D environments and the synthesis of a more sophisticated adaptive law, or a reinforcement learning strategy, able to tune all the control gains at the same time.
Data availability statement
The software platform used to produce the results presented in the paper is SWARMSIMV1, which is available here: https://github.com/diBernardoGroup/SwarmSimPublic/tree/SwarmSimV1.
Author contributions
AG and GM with support from DF and MC carried out the modeling, control design, numerical and experimental validation of the proposed techniques, AG and GM with support from MC and DF analysed the data and wrote the numerical code used for all simulations, MdB with support from DF designed the research. All authors contributed to the article and approved the submitted version.
Acknowledgments
The authors wish to acknowledge the University of Naples Federico II and the Scuola Superiore Meridionale for supporting their research activity. This work was in part supported by the Research Project “SHARESPACE” funded by the European Union (EU HORIZON-CL4-2022-HUMAN-01-14. SHARESPACE. GA 101092889 - http://sharespace.eu), by the the research projects PON INCIPIT, INSIST and PRIN 2017 “Advanced Network Control of Future Smart Grids” (http://vectors.dieti.unina.it) funded by the Italian Ministry for University and Research, and by the University of Naples Federico II—“Finanziamento della Ricerca di Ateneo (FRA)— Linea B” through “BIOMASS”.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1Formally,
2Regular tilings exist only for L ∈ {3, 4, 6}. The case L = 2 corresponds more trivially to a line, rather than a planar structure. The case L = 3, corresponding to hexagonal tilings, where vertices appear in two different spatial configurations (one with edges at angles π/2, 7/6 π, 11/6 π, and one with edges at angles π/6, 5/6 π, 3/2 π—plus an optional offset). Hence, the control strategy we propose here would need to be extended to select one or the other of the possible hexagonal configurations.
3First order models like (6) are often used in the literature Lee and Chong (2008); Lee et al. (2010); Casteigts et al. (2012); Zhao et al. (2019). In some other works Spears et al. (2004); Sailesh et al. (2014) a second order model is used, given by
4That is, denoting with U([a, b]) the uniform distribution on the interval [a, b], the initial position of each agent in polar coordinates xi(0):= (di, ϕi) is obtained by independently sampling
5We also considered different deployment strategies (e.g., agents starting uniformly distributed from a larger disk or several disjoint disks) and verified that the results are qualitatively similar.
6Simulations are performed using SwarmSimV1, a software platform we developed to simulate swarms of mobile agents. The code is available at https://github.com/diBernardoGroup/SwarmSimPublic/tree/SwarmSimV1.
References
Auletta, F., Fiore, D., Richardson, M. J., and di Bernardo, M. (2022). Herding stochastic autonomous agents via local control rules and online target selection strategies. Aut. Robots 46, 469–481. doi:10.1007/s10514-021-10033-6
Balch, T., and Hybinette, M. (2000a). “Behavior-based coordination of large-scale robot formations,” in Proceedings of the 4th International Conference on MultiAgent Systems (ICMAS), 363–364. doi:10.1109/ICMAS.2000.858476
Balch, T., and Hybinette, M. (2000b). “Social potentials for scalable multi-robot formations,” in Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2000), 73–80. doi:10.1109/ROBOT.2000.8440421
Bayindir, L. (2016). A review of swarm robotics tasks. Neurocomputing 172, 292–321. doi:10.1016/j.neucom.2015.05.116
Biswal, S., Elamvazhuthi, K., and Berman, S. (2021). Decentralized control of multiagent systems using local density feedback. IEEE Trans. Automatic Control 67, 3920–3932. doi:10.1109/tac.2021.3109520
Brambilla, M., Ferrante, E., Birattari, M., and Dorigo, M. (2013). Swarm robotics: A review from the swarm engineering perspective. Swarm Intell. 7, 1–41. doi:10.1007/s11721-012-0075-2
Casteigts, A., Albert, J., Chaumette, S., Nayak, A., and Stojmenovic, I. (2012). Biconnecting a network of mobile robots using virtual angular forces. Comput. Commun. 35, 1038–1046. doi:10.1016/j.comcom.2011.09.008
Coppola, M., Guo, J., Gill, E., and de Croon, G. C. (2019). Provable self-organizing pattern formation by a swarm of robots with limited knowledge. Swarm Intell. 13, 59–94. doi:10.1007/s11721-019-00163-0
Cortés, J. (2009). Global and robust formation-shape stabilization of relative sensing networks. Automatica 45, 2754–2762. doi:10.1016/j.automatica.2009.09.019
D’Orsogna, M. R., Chuang, Y. L., Bertozzi, A. L., and Chayes, L. S. (2006). Self-propelled particles with soft-core interactions: patterns, stability, and collapse. Phys. Rev. Lett. 96, 104302. doi:10.1103/PhysRevLett.96.104302
Engel, P., Michel, L., and Senechal, M. (2004). Tech. rep. Institut des Hautes Etudes Scientifique. Lattice Geometry.
Gardi, G., Ceron, S., Wang, W., Petersen, K., and Sitti, M. (2022). Microrobot collectives with reconfigurable morphologies, behaviors, and functions. Nat. Commun. (13), 1–14. doi:10.1038/s41467-022-29882-5
Giusti, A., Coraggio, M., and di Bernardo, M. (2023). Local convergence of multi-agent systems toward rigid lattices. IEEE Control Syst. Lett. 7, 2869–2874. doi:10.1109/LCSYS.2023.3289060
Hauert, S., Zufferey, J. C., and Floreano, D. (2009). Evolved swarming without positioning information: an application in aerial communication relay. Aut. Robots 26, 21–32. doi:10.1007/s10514-008-9104-9
Heinrich, M. K., Wahby, M., Dorigo, M., and Hamann, H. (2022). “Swarm robotics,” in Cognitive robotics. chap. 5. 77–98. doi:10.7551/mitpress/13780.003.0009
Hettiarachchi, S., and Spears, W. M. (2005). “Moving swarm formations through obstacle fields,” in Proceedings of the 2005 International Conference on Artificial Intelligence (ICAI’05).97–103
Kegeleirs, M., Grisetti, G., and Birattari, M. (2021). Swarm SLAM: challenges and perspectives. Front. Robotics AI (8), 1–6. doi:10.3389/frobt.2021.618268
Khatib, O. (1985). “Real-time obstacle avoidance for manipulators and mobile robots,” in Proceedings of the IEEE International Conferencce on Robotics and Automation (ICRA), 500–505. doi:10.1109/ROBOT.1985.108724785
Kim, S., Oh, H., Suk, J., and Tsourdos, A. (2014). Coordinated trajectory planning for efficient communication relay using multiple UAVs. Control Eng. Pract. 29, 42–49. doi:10.1016/j.conengprac.2014.04.003
Latora, V., Nicosia, V., and Russo, G. (2017). Complex networks: Principles, methods and applications. Cambridge University Press. doi:10.1093/comnet/cnx062
Lee, G., and Chong, N. Y. (2008). A geometric approach to deploying robot swarms. Ann. Math. Artif. Intell. 52, 257–280. doi:10.1007/s10472-009-9125-x
Lee, G., Nishimura, Y., Tatara, K., and Chong, N. Y. (2010). “Three dimensional deployment of robot swarms,” in Proceedings of the EEE/RSJ 2010 International Conference on Intelligent Robots and Systems (IROS 2010), 5073–5078. doi:10.1109/IROS.2010.5652055
Li, G., St-Onge, D., Pinciroli, C., Gasparri, A., Garone, E., and Beltrame, G. (2019). Decentralized progressive shape formation with robot swarms. Aut. Robots 43, 1505–1521. doi:10.1007/s10514-018-9807-5
Li, X., Ercan, M. F., and Fung, Y. F. (2009). “A triangular formation strategy for collective behaviors of robot swarm,” in Proceedings of the 2009 International Conference on Computational Science and Its Applications (ICCSA 2009), 897–911. doi:10.1007/978-3-642-02454-2_70
Lopes, H. J., and Lima, D. A. (2021). Evolutionary Tabu Inverted Ant Cellular Automata with Elitist Inertia for swarm robotics as surrogate method in surveillance task using e-Puck architecture. Robotics Aut. Syst. 144, 103840. doi:10.1016/j.robot.2021.103840
Maffettone, G. C., Boldini, A., Di Bernardo, M., and Porfiri, M. (2023a). Continuification control of large-scale multiagent systems in a ring. IEEE Control Syst. Lett. 7, 841–846. doi:10.1109/LCSYS.2022.3226619
Maffettone, G. C., Porfiri, M., and Di Bernardo, M. (2023b). Continuification control of large-scale multiagent systems under limited sensing and structural perturbations. IEEE Control Syst. Lett. 7, 2425–2430. doi:10.1109/LCSYS.2023.3286773
Mooney, J. G., and Johnson, E. N. (2014). A comparison of automatic nap-of-the-earth guidance strategies for helicopters. J. Field Robotics 31, 637–653. doi:10.1002/rob.21514
Oh, H., Ramezan Shirazi, A., Sun, C., and Jin, Y. (2017). Bio-inspired self-organising multi-robot pattern formation: A review. Robotics Aut. Syst. 91, 83–100. doi:10.1016/j.robot.2016.12.006
Oh, K. K., Park, M. C., and Ahn, H. S. (2015). A survey of multi-agent formation control. Automatica 53, 424–440. doi:10.1016/j.automatica.2014.10.022
Olfati-Saber, R. (2006). Flocking for multi-agent dynamic systems: algorithms and theory. IEEE Trans. Automatic Control 51, 401–420. doi:10.1109/TAC.2005.864190
Pickem, D., Glotfelter, P., Wang, L., Mote, M., Ames, A., Feron, E., et al. (2017). “The robotarium: A remotely accessible swarm robotics research testbed,” in Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), 1699–1706. doi:10.1109/ICRA.2017.7989200
Pickem, D., Lee, M., and Egerstedt, M. (2015). “The GRITSBot in its natural habitat - a multi-robot testbed,” in Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2015), 4062–4067. doi:10.1109/ICRA.2015.7139767
Pinciroli, C., Birattari, M., Tuci, E., Dorigo, M., Zapatero, M. D. R., Vinko, T., et al. (2008). “Self-organizing and scalable shape formation for a swarm of pico satellites,” in Proceedings of the 2008 NASA/ESA Conference on Adaptive Hardware and Systems (AHS), 57–61. doi:10.1109/AHS.2008.41
Rubenstein, M., Cabrera, A., Werfel, J., Habibi, G., McLurkin, J., and Nagpal, R. (2013). “Collective transport of complex objects by simple robots,” in Proceedings of the 2013 International Conference on Autonomous Agents and Multi-agent Systems, 47–54. doi:10.5555/2484920.2484932
Rubenstein, M., Cornejo, A., and Nagpal, R. (2014). Programmable self-assembly in a thousand-robot swarm. Science 345, 795–799. doi:10.1126/science.1254295
Sailesh, P., William, L., and James, M. (2014). Hexagonal lattice formation in multi-robot systems. Distrib. Aut. Robot. Syst. 104, 307–320. doi:10.1007/978-3-642-55146-82_2
Sakurama, K., and Sugie, T. (2021). Generalized coordination of multi-robot systems. Found. Trends Syst. Control 9, 1–170. doi:10.1561/2600000025
Shi, P., and Yan, B. (2021). A survey on intelligent control for multiagent systems. IEEE Trans. Syst. Man, Cybern. Syst. 51, 161–175. doi:10.1109/TSMC.2020.3042823
Song, Y., and O’Kane, J. M. (2014). “Decentralized formation of arbitrary multi-robot lattices,” in Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), 1118–1125. doi:10.1109/ICRA.2014.6906994
Spears, W. M., and Gordon, D. F. (1999). “Using artificial physics to control agents,” in Proceedings of the 1999 International Conference on Information Intelligence and Systems (ICIIS 1999) (IEEE), 281–288. doi:10.1109/ICIIS.1999.810278
Spears, W. M., Spears, D. F., Hamann, J. C., and Heil, R. (2004). Distributed, physics-based control of swarms of vehicles. Aut. Robots 17, 137–162. doi:10.1023/B:AURO.0000033970.96785.f2
Tan, T. H., Mietke, A., Li, J., Chen, Y., Higinbotham, H., Foster, P. J., et al. (2022). Odd dynamics of living chiral crystals. Nature 607, 287–293. doi:10.1038/s41586-022-04889-6
Torquato, S. (2009). Inverse optimization techniques for targeted self-assembly. Soft Matter 5, 1157–1173. doi:10.1039/b814211b
Trotta, A., Felice, M. D., Montori, F., Chowdhury, K. R., and Bononi, L. (2018). Joint coverage, connectivity, and charging strategies for distributed UAV networks. IEEE Trans. Robotics 34, 883–900. doi:10.1109/TRO.2018.2839087
Wang, G., Liu, M., Wang, F., and Chen, Y. (2022a). A novel and elliptical lattice design of flocking control for multi-agent ground vehicles. IEEE Control Syst. Lett. 7, 1159–1164. doi:10.1109/LCSYS.2022.3231628
Wang, H., and Rubenstein, M. (2020). Shape Formation in homogeneous swarms using local task swapping. IEEE Trans. Robotics 36, 597–612. doi:10.1109/tro.2020.2967656
Wang, X., Sun, J., Wu, Z., and Li, Z. (2022b). Robust integral of sign of error-based distributed flocking control of double-integrator multi-agent systems with a varying virtual leader. Int. J. Robust Nonlinear Control 32, 286–303. doi:10.1002/rnc.5823
Wilson, S., Glotfelter, P., Wang, L., Mayya, S., Notomista, G., Mote, M., et al. (2020). The robotarium: globally impactful opportunities, challenges, and lessons learned in remote-access, distributed control of multirobot systems. IEEE Control Syst. Mag. 40, 26–44. doi:10.1109/MCS.2019.2949973
Zhao, H., Wei, J., Huang, S., Zhou, L., and Tang, Q. (2019). Regular topology formation based on artificial forces for distributed mobile robotic networks. IEEE Trans. Mob. Comput. 18, 2415–2429. doi:10.1109/TMC.2018.2873015
Appendix
Let us first introduce some useful notation. Given a real-valued function x(t) and
In Spears and Gordon (1999); Spears et al. (2004); Sailesh et al. (2014), the agent dynamics is described by
where
where f is a gravitational-like virtual force, given by
In (25),
The control law given by (24) and (25) was showed to work for triangular lattices. To make it suitable for square patterns, a binary variable called spin is introduced for each agent, and the swarm is divided in two subsets, depending on the value of their spin. Then, agents with different spin aggregate at a distance of R, while agents with the same spin do so at a distance of
Keywords: multiagent systems, pattern formation, distributed control, swarm robotics, collective dynamics
Citation: Giusti A, Maffettone GC, Fiore D, Coraggio M and di Bernardo M (2023) Distributed control for geometric pattern formation of large-scale multirobot systems. Front. Robot. AI 10:1219931. doi: 10.3389/frobt.2023.1219931
Received: 09 May 2023; Accepted: 05 September 2023;
Published: 28 September 2023.
Edited by:
Roberto Casadei, University of Bologna, ItalyReviewed by:
Gianluca Aguzzi, University of Bologna, ItalyMatteo Luperto, University of Milan, Italy
Danilo Pianini, University of Bologna, Italy
Copyright © 2023 Giusti, Maffettone, Fiore, Coraggio and di Bernardo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mario di Bernardo, bWFyaW8uZGliZXJuYXJkb0B1bmluYS5pdA==
†These authors have contributed equally to this work and share first authorship
 Andrea Giusti
Andrea Giusti Gian Carlo Maffettone
Gian Carlo Maffettone Davide Fiore
Davide Fiore Marco Coraggio
Marco Coraggio Mario di Bernardo
Mario di Bernardo