
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Robot. AI, 25 February 2022
Sec. Soft Robotics
Volume 9 - 2022 | https://doi.org/10.3389/frobt.2022.849516
This article is part of the Research TopicSoft Robotics based on Liquid Crystal Elastomers (LCEs)View all 5 articles
 Xudong Liang*
Xudong Liang* Dongfeng Li
Dongfeng LiLiquid crystal elastomers (LCEs) are a rubbery network of polymers with ordered liquid crystal mesogens. The combination of rubber elasticity and the anisotropic liquid crystalline order gives exceptional mechanical properties, like soft elasticity, where near-constant stress accompanies large elastic deformation in the material. However, the soft elasticity in LCEs is often bounded by the intrinsic molecular interactions and structures, limiting the range of programmable mechanical properties and functionalities. Here, we demonstrate that the semi-soft elasticity of LCEs can be integrated into the framework of metamaterials to realize markedly programmabilities. Under uniaxial deformation, each state of the building blocks in metamaterials and the molecular composition of the nematic LCEs is associated with a distinctly different stress-strain relation that is fully elastic. Taking advantage of the tunable bending and stretching deformation enabled by the geometry of the building blocks and the semi-soft elasticity of the nematic LCE in the metamaterials, we can engineer the local stretch and stress at an unmet level of their counterpart composed by elastomers. Numerical simulations and analytical models are developed to relate the metamaterial geometries and the LCE soft elasticity to the mechanical responses. In addition, an elastic region with near-zero stiffness up to a stretch of 1.4 can be designed by connecting the compliant responses due to bending deformation and the soft elasticity in the LCE. We expect that the specialized mechanical tunability enabled by the LCE metamaterials can facilitate the development of advanced forms of mechanical metamaterials and impact the design of robotic systems.
Programming mechanical properties and functionalities are one of the most fundamental goals in material science, owing to its central role in applications (Surjadi et al., 2019). To design a material with a targeted set of properties and mechanical responses, people have endeavored to discover new materials, modify the material compositions, and optimize the material manufacturing process (Meyers and Chawla, 2008; Fleck et al., 2010). Great progress has been made in developing materials with the desired properties over the past centuries. However, intrinsic mechanical properties and the basic physical mechanisms often limit the capacity to design materials with desired responses (Surjadi et al., 2019). For example, the positive stiffness is required for stability of an unconstrained block of material in deformation based on thermodynamics (Wang and Lakes, 2005; Coulais et al., 2015); the stiffness-toughness conflict exists in regular polymer networks where the crosslinks stiffen the polymers but embrittle them (Lake and Thomas, 1967; Kim et al., 2021); the intimate coupling between strength and density is observed in most materials where high strength normally means large density (Schaedler et al., 2011; Yu et al., 2018).
Nature has provided numerous examples of well-defined architectures to bypass the general limitations in material design, achieving mechanical properties and functionalities differing from and surpassing constituent materials (Meyers et al., 2008; Launey et al., 2010). For example, the carps are known to have superior toughness against the penetration from predator’s tooth by developing the “Bouligand structure” in their scales, where fibrils of collagen are aligned in layers, with the fibril in each layer rotating by roughly 36° (Quan et al., 2020). Soft biological tissues composed of semiflexible filamentous proteins can undergo strain-stiffening, with a tenfold increase in shear moduli under strains as small as 20% (Gardel et al., 2004; Storm et al., 2005).
Inspired by the architectures in biological materials, recent advancements in manufacturing techniques have enabled material design via geometric arrangements of the underlying structures (Bertoldi et al., 2017; Kadic et al., 2019). Built upon the periodically arranged building blocks, mechanical metamaterial has been fabricated to mediate mechanical deformation, stress, and energy (Kochmann and Bertoldi, 2017). It also boasts the discoveries of functionalities not available in natural materials, such as auxeticity (Lakes, 1987), negative stiffness (Coulais et al., 2015), and non-monotonic energy dissipations (Liang and Crosby, 2020a). Traditionally, the design for properties exhibited in metamaterials relies on the structural responses in the periodic building blocks, where a linear elastic or a hyperelastic constitutive relation of the materials are adopted (Bertoldi et al., 2017; Pishvar and Harne, 2020). Recently, new characteristics have been realized in metamaterials by combining additional fields beyond elasticity. For example, the ability to alter mechanical memories with stable memories (Chen et al., 2021), or to generate reversible solid-solid phase transitions (Liang et al., 2022) is achieved by incorporating magnetic domains in metamaterials. However, these functionalities are still programmed through the building blocks’ geometries, focusing on the spatial heterogeneity in the structures.
The control of the structural responses of the building blocks has motivated the design of sophisticated layouts in the metamaterials while avoiding selecting materials with complex constitutive responses in previous studies. Although effective, such a paradigm might constrain the tunability of the mechanical properties and functionalities, leaving an ample design space unexplored for the material-based programmability. Synergetically combining the material-level constitutive behaviors and structural-level building block mechanical responses can open new avenues for programmable metamaterials. A recent study has demonstrated that coupling the constitutive materials’ viscoelasticity with the elastic snap-through instability in metamaterials can exhibit a programmable hysteric response with optimal dissipations at different loading rates (Dykstra et al., 2019).
In this paper, we integrate the soft elasticity in the liquid crystal elastomer (LCE) into the framework of metamaterials. By engraving the orthogonally aligned elliptical pores into an LCE sheet, we can create a metamaterial with networks of “plates” connected by thin “ligaments” that undergo programmable strain-softening to strain-stiffening responses (Liang and Crosby, 2020b). The nematic LCE in the metamaterials can enter the state of soft elasticity as the material is stretched vertically to the liquid crystal ordering direction, where the deformation is accommodated with near-constant stress as liquid crystal mesogens rotate (Küupfer and Finkelmann, 1994; Warner and Terentjev, 2007; Biggins et al., 2008). As a result, the nematic LCEs have a “stress-strain plateau” during liquid crystal mesogens’ rotation and stiffen as the molecules align to the stretching direction. Although the constitutive responses in LCEs rely on the molecular structures, the critical stretch to trigger the compliant and stiffening effect is controlled by the local deformation in the building blocks (Liang and Crosby, 2020b). By tuning the structural geometry and the molecular compositions of the metamaterials, we can design the structural responses in the building blocks and the soft elasticity of the LCEs in a coupled and controllable manner. This framework can extend the design space in the material-based tunability unavailable by controlling the geometry in the building blocks alone.
This paper studies the mechanical responses of metamaterials composed of liquid crystal elastomers with soft elasticity. The paper is structured as follows. We first describe the semi-soft elasticity constitutive model of the nematic LCEs stretched perpendicularly to the molecule’s ordering direction in Section 2. Finite element simulations that incorporate the semi-soft elasticity constitutive model into metamaterials with different geometries in the building blocks are presented in Section 3. The simulated mechanical responses reflect how the soft elasticity in LCEs and the pore shapes in the building block synergetically program the mechanical responses, particularly the strain-softening and strain-stiffening behaviors. In Section 4, we derive a reduced analytical model to understand the coupling between the material and the structural properties. The metamaterial is modeled as rigid rotating plates connected by elastic springs, in which the soft elasticity governs the material constitutive responses. We conclude with a few remarks on material-based tunability based on the metamaterial geometry and the soft elasticity, with a new strategy for programming material properties and functionalities.
Liquid crystal elastomers are rubbery polymer networks composed of molecules with liquid-like mobility and are capable of withstanding large deformation. By incorporating the spontaneous liquid-crystalline ordering into networks of the polymers, the nematic LCEs can reach a delicate balance between the stiffness of the liquid crystal molecules and the entropically driven elasticity of polymer chains (Warner and Terentjev, 2007). Compared to elastomers described by the classical rubber elasticity, the aligned liquid crystal mesogens in the nematic LCE induce the molecular shape anisotropy, modifying the elastic function in deformation (Bladon et al., 1993; Verwey and Warner, 1997a). Previous efforts have been made to extend the classical rubber elasticity to account for the nuances with liquid crystal orderings, known as the “neo-classical” theory for rubber elasticity (Warner and Terentjev, 2007; Biggins et al., 2008; Biggins et al., 2012; Sonnet and Virga, 2012). Here, we briefly introduce the “neo-classical” theory of nematic LCEs for the completeness of the current study. More systematic considerations can be found in Warner and Terentjev (2007). In addition, the viscoelasticity of the polymer network and the rate dependence of the mesogen director rotation can substantially affect the constitutive responses of the nematic LCE (Warner and Terentjev, 2007; Zhang et al., 2019). Here, we focus on the quasi-static responses of the LCE metamaterial and model the nematic LCE with the “neo-classical” theory.
The liquid crystal mesogens are aligned along the x-axis in fabrications, as indicated by the director n0 with the green arrows in Figure 1A. The presence of liquid crystal mesogens in the polymer networks leads to an anisotropic Gaussian distribution of the end-to-end vector of the polymer chain between the two crosslinks, R. The mean square end-to-end vector for the polymer chain follows,
where l = lij is the effective step length tensor for the nematic LCE; L is the arclength of the polymer chain, where L = Nb, with N being the number of monomers between two crosslinks and b being the step length of the monomer. The bracket <..> represents the averaging for N monomers in the polymer chain. In the undeformed nematic LCEs, the director n0 is along the x-axis, and the mean square sizes in the plane perpendicular to the n0 are identical. Therefore, the step length tensor at the undeformed state can be written as,
where ln and lp are the effective step lengths in the directions parallel and perpendicular, respectively, to the liquid crystal director n0. The anisotropic step lengths in Eq. 2 turn the spheroid formed by the polymer chain in elastomers into an ellipsoid in the LCEs (Herbert et al., 2021), as shown in Figure 1B. The ratio between the two effective step lengths, r = ln/lp, representing the anisotropy for the nematic LCE, can be further expressed with the nematic order of the liquid crystal ordering, Q,
where Q = 1 represents the perfect nematic ordering with the liquid crystal mesogens directed in one direction, and Q = 0 corresponds to randomly oriented mesogens (Warner and Terentjev, 2007; Sonnet and Virga, 2012).
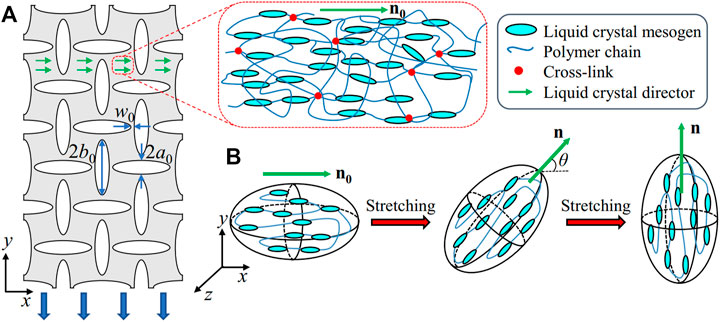
FIGURE 1. Schematics of the LCE metamaterials. (A) The metamaterials composed of the nematic LCE aligned along the x-axis, with engraved pores. The metamaterial is stretched along the y-axis, orthogonal to the liquid crystal ordering. The nematic LCE is a network of crosslinked polymer chains with aligned liquid crystal mesogens (indicated by the director n0). (B) The ellipsoid formed between the crosslinks in the LCE polymer chains due to the liquid crystalline ordering. With the vertical extension, the ellipsoid and the liquid crystal director rotate with an angle θ along the z-axis. The rotation is completed as the liquid crystal mesogens are aligned along the y-axis, with θ=π/2.
As the nematic LCEs aligned along the horizontal direction are stretched along the y-axis, the liquid crystal mesogens anchoring to the bulk rotate along the z-axis with an angle θ (Figure 1B). The step length tensor in the deformed state is now written as,
Considering the entropy changes of crosslinked polymer chains with liquid crystal mesogens in deformation, the free energy density of the nematic LCEs is (Bladon et al., 1993; Warner and Terentjev, 2007),
where F is the deformation gradient for the LCE and µ is the small-strain shear modulus of the nematic LCE. To account for variations in the anisotropy r due to compositional fluctuations in the liquid crystal ordering, an additional energy term that leads to “semi-softness” in rotation (Verwey and Warner, 1997b; Popov and Semenov, 1998) is introduced,
where α=<1/r > −1/<r> is the anisotropy fluctuation of the anisotropy of the nematic LCE, α > 0; n = cosθex + sinθey is the liquid crystal director at the deformed state, and I is the identity tensor. Therefore, the free energy density for LCEs is W=Wel + Wss (Verwey and Warner, 1997a; Warner and Terentjev, 2007).
Considering the metamaterials with an extension imposed along the y-axis (Figure 1A), we follow the model of stretching strips of nematic LCEs perpendicular to the director (Verwey et al., 1996; Verwey and Warner, 1997a; Warner and Terentjev, 2007) by integrating the step length tensor in Eq. 4 into the free energy density functions in Eqs 5, 6. The director of the liquid crystal n rotates to the optimal value that minimizes the free energy density W in stretching, and the nematic LCE is relaxed on the plane normal to the x-axis, with the nominal stress components Sxy= Sxx = 0. Therefore, the free energy density of the LCEs is a function of the stretch in the y-axis,
Here we distinguish the local stretch in the material with a bar as
From Eq. 8, we can obtain the critical stretch for the onset of rotation,
While sophisticated continuum constitutive models (Zhang et al., 2019) and computational micromechanics simulations (Zhou and Bhattacharya, 2021) for nematic LCEs have been proposed recently, we shall proceed with the simple phenomenological description of LCE with free energy density function in Eq. 7. The LCE metamaterials under the imposed uniaxial stretching deform in the thin ligament region, where the nematic LCEs are stretched along the y-axis and relaxed in the transverse dimension along the x-axis. Therefore, we only focus on the stress component along the y-axis, and the corresponding nominal stress follows,
In Figure 2, we compare the scaled nominal stress of the nematic LCEs with soft elasticity predicted by Eq. 9 with the traditional elastomers described by the Neo-Hookean model. By controlling the ratio for the anisotropy r and the fluctuations of the anisotropy α, we can program the stress-strain relations in nematic LCEs under the uniaxial extension perpendicular to the liquid crystal alignment direction n0. In Figure 2A, we plot scaled nominal stress with the fluctuation fixed at α = 0.1 and the anisotropy of the nematic LCEs increasing from r = 1.5 to r = 6. The mechanical responses in the nematic LCE are the same Neo-Hookean elastomers for r = 1, and the liquid crystal alignment along with the x-axis increases as r increases from 1. The neo-classical theory captures the semi-soft elastic responses in LCEs as the stress becomes near constant with increasing stretch. The materials behave like the traditional elastomers as the stretch is below
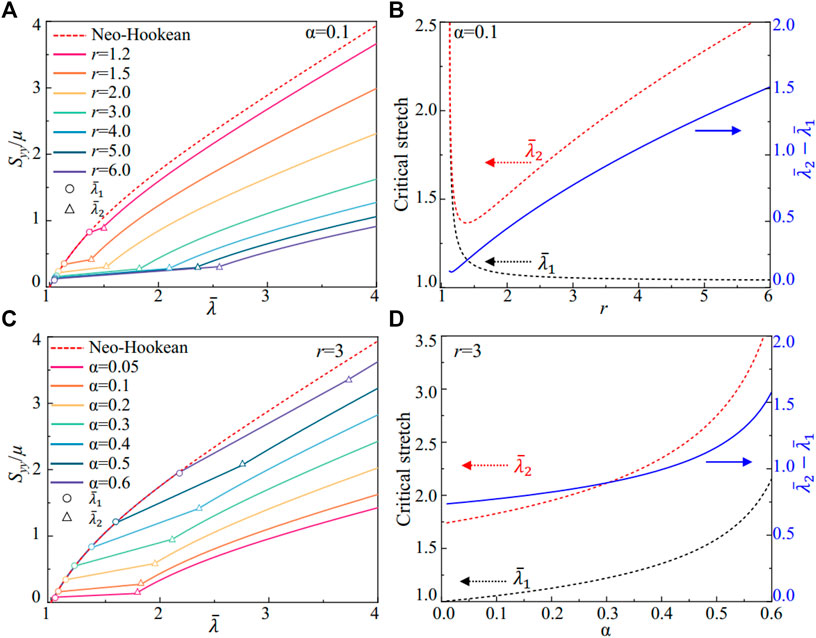
FIGURE 2. Constitutive responses of semi-soft elasticity of the nematic LCE. (A) The scaled nominal stress Syy/μ, and (B) the critical stretches for the soft elasticity in uniaxial extension with different liquid crystalline ordering r and a fixed fluctuation α=0.1. (C) The scaled nominal stress Syy/μ, and (D) the critical stretches for the soft elasticity in uniaxial extension with different liquid crystalline ordering fluctuations α and a fixed anisotropy r=3.
We can further design the softness responses via the fluctuation of the liquid crystal ordering in the nematic LCE. With a fixed anisotropy r = 3, the nematic LCE shows softness responses for different values of α (Figure 2C). As the fluctuation parameter α increases from 0, where there are no variations in the liquid crystal ordering, the stress in the LCE under the same local stretch
We conduct numerical simulations using finite element (FE) methods to fully explore the relationship between the metamaterial building blocks’ geometry and the nematic LCE’s constitutive responses, especially the connection between global deformation and the local soft elasticity. Quasi-static nonlinear analysis of the LCE metamaterials under uniaxial stretching is performed using the commercial FE software Abaqus. The constitutive responses of the nematic LCE are modeled with the Marlow model, where the uniaxial stress-stretch relation from Eq. 9 is used to define the strain energy potential in the simulations. In Figure 3, we compare the stress-strain relation defined by the Marlow model in the simulations of uniaxially stretched rectangular bars (solid symbols) to the one from Eq. 9 (solid lines). The deformation in the uniaxial stretching is homogeneous, ensuring that the local stretch in the nematic LCE is the same as the applied global stretch,
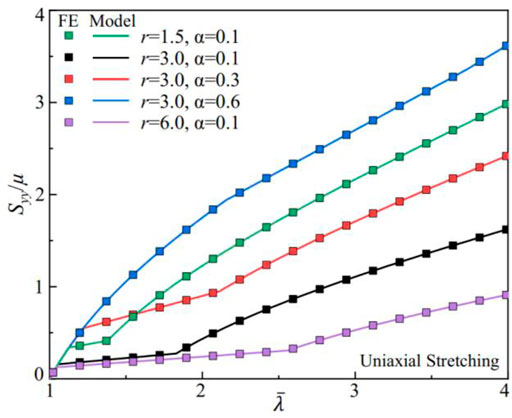
FIGURE 3. Stress-stretch relations of uniaxial stretching nematic LCEs. The solid lines are the predictions from the phenomenological model of soft elasticity in Eq. 9. The solid symbols are simulation results of the homogeneously stretched rectangular bars with the material model defined by the Marlow strain energy potential.
In the FE simulations, we study the configurations shown in Figure 1A by varying aspect ratio of the pores (ar = a0/b0), with a fixed width of the ligaments, w0 = 0.1L0, where L0 = a0+b0+w0 is the length of the building blocks. We have explored the mechanical responses of metamaterials composed of elastomers with different geometries, including the effect of the ligament width in previous studies (Liang and Crosby, 2020a; Liang and Crosby, 2020b). Here, we focus on the effect of the pore aspect ratio and its potential coupling with the soft elasticity in nematic LCEs. 2D plane-strain simulations (Abaqus element type CPE6H) are carried out. The simulations are built upon a single layer of three unit cells, which is selected to mirror the mechanical response of the overall structure (inset, Figure 4B). Symmetric boundary conditions about the y axis are applied to the left boundary, while the right is stress-free. In the metamaterials under uniaxial extension, the building blocks along the x-axis remain horizontal, with the right edge free from constraints. To mimic the uniaxial loading conditions in experiments, the bottom boundary is prescribed with a displacement, and the top boundary is constrained to be horizontal. As a result, the horizontal building blocks in the metamaterials remain horizontal, as shown with the deformed shapes in the inset of Figure 4B. In addition, the effect of the number of horizontal building blocks in the mechanical responses is considered minor compared to the uniaxial extension along the y-axis.
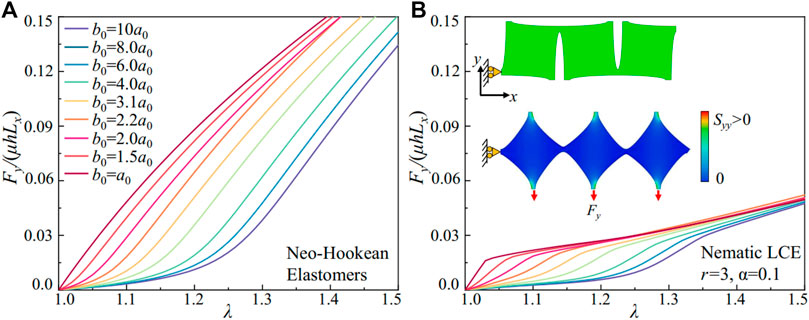
FIGURE 4. FE simulations of the metamaterials with different geometries. (A) The scaled stretching force Fy/µLxh in metamaterials composed of Neo-Hookean elastomers with pore aspect ratios ar ranging from 0.1 to 1. (B) The scaled stretching force Fy/µLxh in metamaterials composed of nematic LCEs (r = 3 and α = 0.1) with pore aspect ratio ar ranging from 0.1 to 1. Inset: FE models for the metamaterials at initial and deformed states.
We measure the scaled stretching force from simulations, Fy/µLxh, where Lx is the horizontal length and h is the thickness of the metamaterials under uniaxial extension. We compare the stress-strain relation for metamaterials composed of Neo-Hookean elastomers and the nematic LCE with soft elasticity in Figure 4. The metamaterials with elastomers show a transition from strain-stiffening to a weakly strain-softening as the pore aspect ratio ar increases from 0.1 to 1, as shown Figure 4A. For metamaterials with circular pores (ar∼1), the internal deformation is governed by the ligament stretching, leading to a stress-strain relation similar to the constituent elastomers with a negligible softening. For metamaterials with elliptical pores (ar∼0), the ligament undergoes a bending deformation first, inducing a compliant response with the effective shear modulus around 0.1µ. The subsequent ligament stretching stiffens the stress-strain curve, with a fivefold increase of the effective shear modulus to 0.5µ. The geometry of the pores in the building blocks of metamaterials is shown to program the mechanical responses. However, the design space is often limited, for example, by the finite size of the ligament and the maximum rotation angle in bending.
The metamaterials can bypass the limitations in geometries by incorporating the nematic LCEs with soft elasticity. In Figure 4B, we simulate the metamaterials composed of nematic LCEs (r = 3 and α = 0.1). The nematic LCE deforms with near-constant stresses as the stretch increases from 1.05 to 1.5 (Figure 2A). Integrating the building blocks with different pore shapes, the stiffness of the metamaterials with the same geometry decreases due to the rotation of the liquid crystal mesogens. However, the tunability for the mechanical properties in metamaterials is substantially increased, with an enlarged space in programming the strain-softening and strain-stiffening responses. For metamaterials with circular pores (ar∼1), as the nematic LCE in the ligament is stretched to the critical value for soft elasticity, a dramatic softening with a tenfold reduction in the effective shear modulus (0.5µ to 0.05µ) is observed. For metamaterials with elliptical pores (ar = 0.1), the stretch in the bending ligament can trigger the soft elasticity in the nematic LCE. Therefore, the metamaterial shows a compliant response with an effective shear modulus as low as 0.03µ, up to the stretch as large as 1.2. The transition from bending to stretching in the ligament leads to higher structural stiffness and larger local stretch, driving the nematic LCE to exit the soft elasticity with the stretch larger than
We can design the stress-strain relations in metamaterials via the soft elasticity of the nematic LCE. With a fixed liquid crystal ordering fluctuation of α = 0.1, the anisotropy in LCE can increase from r = 1, requiring a larger local stretch to rotate the liquid crystal mesogens. As a result, the constitutive responses in the nematic LCE depart from the Neo-Hookean elastomer, showing the soft elasticity that lasts for a wider region in the stretch and generates lower stress in deformation (Figure 2A). As shown in Figures 5A,B, the molecular liquid crystal ordering in the LCE can program the stress-strain relation in metamaterials with different pore shapes (elliptical in Figure 5A and circular in Figure 5B). A large range of stress-strain relations is created in the metamaterials with different liquid crystal orderings (r). In addition, all the stress-strain curves in the LCE metamaterials fall beneath the one generated by the metamaterial composed of the Neo-Hookean elastomers (dashed line), given the reduction in the stress due to the liquid crystal mesogens’ rotation. The stress-strain curves in the LCE metamaterials start to depart from the elastomeric metamaterials after reaching the critical stretch for the onset of soft elasticity
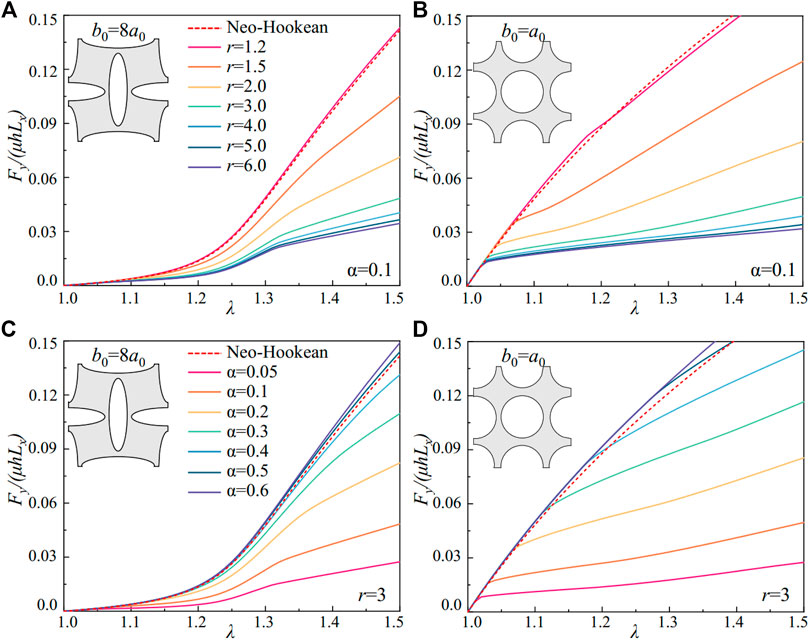
FIGURE 5. The scaled stretching force Fy/µLxh in LCE metamaterials under uniaxial extension. The nematic LCE with (A) a fixed fluctuation α = 0.1 and (C) a fixed liquid crystal ordering r = 3 in the metamaterials with elliptical pores (b0 = 8a0). The nematic LCE with (B) a fixed fluctuation α = 0.1 and (D) a fixed liquid crystal ordering r = 3 in the metamaterials with circular pores (b0 = a0).
The stress-strain relation in metamaterials also can be designed via the fluctuations of the liquid crystal ordering in the nematic LCE. With a fixed anisotropy of the nematic LCE at r = 3, the spread of the liquid crystal ordering distribution increases the energy barrier for the molecular rotation of liquid crystals, suppressing the soft elasticity. Similar to controlling the constitutive responses of the nematic LCE via the liquid crystal ordering with r, the metamaterials composed of the nematic LCE can generate highly tunable stress-strain relations for both elliptical (Figure 5C) and circular pores (Figure 5D). Furthermore, with the increase of α, the stress-strain relations can recover the one generated by the metamaterial with the Neo-Hookean elastomers (dashed line). Different from varying the anisotropy in the nematic LCE with r, the critical stretch for the onset of soft elasticity
The FE simulations demonstrated that the soft elasticity in the nematic LCE could couple with the structural design in the building blocks of metamaterials, programming the stress-strain relations in uniaxial extension. As a result, the molecular control of the constitutive responses of the materials and the structural design of the geometry in the building blocks are no longer independent components in the LCE metamaterials. Instead, the two components synergetically program the mechanical properties, leading to tunable strain-softening and strain-stiffening behaviors at the required deformation and the active control of the stress-strain relations without altering the constituent materials.
We develop an analytical model to understand how the metamaterial geometry and the nematic LCE soft elasticity affect the stress-strain relation under uniaxial extension. Since the soft elasticity in LCE is related to the local stretch in the metamaterials, we first propose a simplified kinematics analysis to describe the local deformation in the ligament.
As shown in Figure 6A, the maximum angle in bending is θc = arctan ((b0−a0)/L0), where the “plates” in the building blocks are rotated along the y-axis (Liang and Crosby, 2020a; Liang and Crosby, 2020b). The rotation angle θc is reached with a critical stretch λc = Lt/L0, where
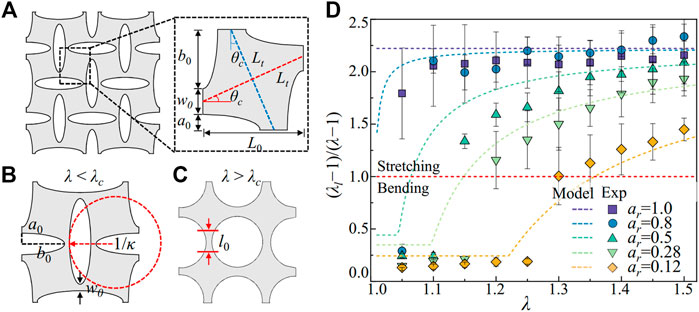
FIGURE 6. Analytical model for the local stretch in the metamaterial. (A) Deformation kinematics of the metamaterials under uniaxial extension. The ligament bending is reflected by the rotations in blue and red dashed lines, with a maximum bending angle θc. (B) Measurement of the local stretch in ligament bending through the changes of the radius of curvature κ. (C) Measurement of the local stretch in the ligament stretching through the length of the deformed ligament l0. (D) The ratio between the local and the global stretch (
For λ >λc, the maximum rotational angle is θc reached, and further stretching the metamaterials leads to elongation of the ligament with a length l0 = 0.5 (a0+b0), as shown in Figure 6C. For the building blocks with a length L0 deform with the stretch λ, the local stretch in the ligament is expressed as,
We compare the local stretch predicted by Eqs 10, 11 with previous experiments (Liang and Crosby, 2020a) in Figure 6D. The ratio between the local strain
To relate the local deformation to the force applied to the metamaterials, we substitute the local stretch predicted by Eqs 10, 11 in the constitutive model of the nematic LCE with soft elasticity in Eq. 9. Given the crosssection area of the ligament is proportional to its width w0, the scaled stretching force in the metamaterials is Fy/μL0h = Syyw0/μL0. In Figure 7A, we plot the stress-strain relation predicted by the analytical model of the nematic LCE with r = 3 and α = 0.1, with the same pore shapes adopted in the FE simulations in Figure 2B. Albeit simple, our analytical model qualitatively captures the mechanical responses in the metamaterial, especially the coupling between local stretch in the ligament and the soft elasticity in the nematic LCE. The predicted stresses are larger than the FE simulations, as the inhomogeneous stress distribution in the ligament’s crosssection is neglected in the model.
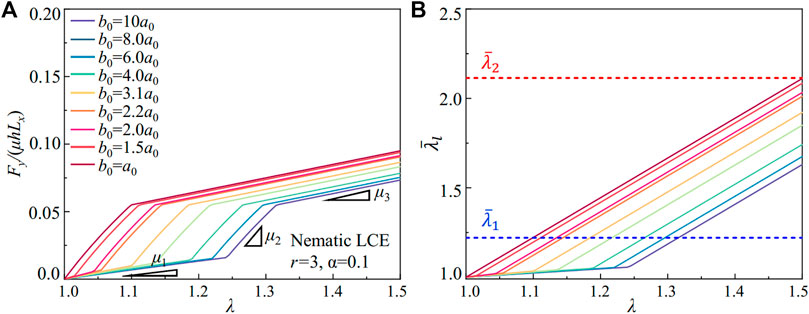
FIGURE 7. (A) The scaled stretching force Fy/µLxh predicted by the model for metamaterials with nematic LCEs (r = 3 and α = 0.1). (B) The local stretch in the ligament
The strain-softening response for the metamaterials with circular pores is predicted by considering the soft elasticity in the nematic LCE. As the pores become elliptical, the bending deformation in the ligament induces a local stretch smaller than the one for the onset of soft elasticity
The relation between the local stretch and the global stretch determines the strain-softening and strain-stiffening responses in the metamaterials. As the global stretch λc is applied to the metamaterials, the maximum local stretch for rotation is
Here, we consider the semi-soft elasticity with onset stretch
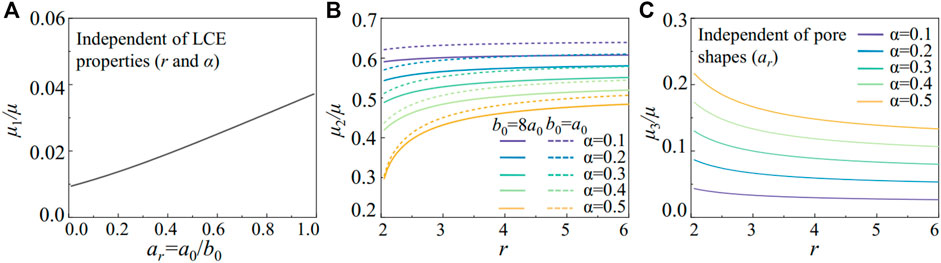
FIGURE 8. The effective shear moduli in the LCE metamaterials. (A) For the local stretch
The strain-stiffening responses happen as the ligament starts to stretch, where the local stretch in the nematic LCE changes from
The effective shear modulus follows μ2 = w0(Syy
In Figure 8B, we plot the effect of soft elasticity in the nematic LCE on effective shear modulus μ2 with a fixed ligament width w0 = 0.1L0. In the metamaterials with elliptical pores (b0 = 8a0), the aligned liquid crystals (increasing anisotropy r) in the nematic LCE lead to a larger μ2, resulting in a stronger stiffening effect in the metamaterials. The fluctuation of the liquid crystal ordering (increasing α) reduces μ2, as it increases the critical stretch
As the nematic LCE reaches the local stretch for soft elasticity, the metamaterials deform until the ligament reaches the critical local stretch
As shown in Eq. 15, the effective shear modulus is independent of the pore shapes, where 2w0/(a0+b0) = 2w0/(L0-w0). The effective shear modulus μ3 is only controlled by the ligament width and critical stretch
Finally, we can join the deformation induced by the ligament bending and the LCE soft elasticity with
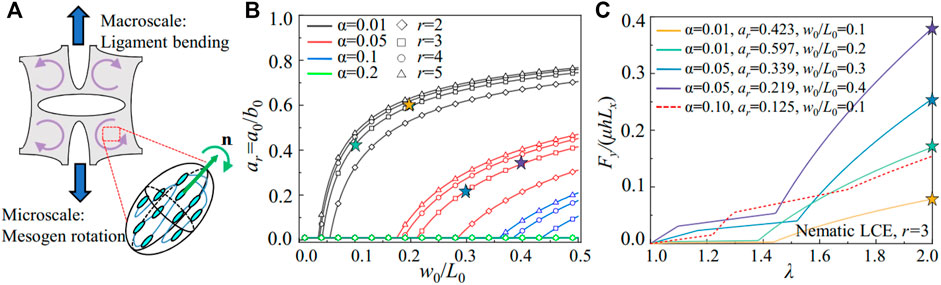
FIGURE 9. (A) Schematic of macroscale ligament bending and the microscale mesogen rotation. (B) The geometries of the metamaterials required for the continuous transition from the ligament bending to the soft elasticity in the nematic LCE, with different material properties. (C) The scaled stretching force Fy/µLxh in LCE metamaterials with the continuous transition of
In Figure 9B, we plot the critical geometric conditions (ar and w0/L0) based on Eq. 16 for different nematic LCE properties (r and α). Since the ligament bending deformation tends to attenuate the local stretch, a low fluctuation (small α) or a high anisotropy (large r) can reduce the critical stretch for the onset of soft elasticity that enables the continuous transition of the compliant responses between the ligament bending and soft elasticity. We compare the stress-strain curves for the LCE metamaterials with the anisotropy r = 3 with the continuous transition (marked by stars in Figure 9B) to the discontinuous one adopted from Figure 7A. As shown in Figure 9C, the LCE metamaterials with the continuous transition generate the compliant responses up to a stretch of 1.4 (solid lines), much larger than the discontinuous one (1.2 in the dashed line). In addition, the effective shear modulus (slope of the compliant region) is greatly reduced for the similar ligament width due to the soft elasticity in the nematic LCE. Particularly, for the nematic LCE with r = 3 and α = 0.01, the metamaterials with the geometric conditions ar = 0.423 and w0/L0 = 0.1 can generate an elastic response with near-zero stiffness. The subsequent stiffening responses in the metamaterials also strengthen as the nematic LCE exits the soft elasticity and generates large stress in the ligament with the local stretch concentration. The analytical model proposed here connects the deformation of the building blocks and the soft elasticity of the nematic LCE via the local stretch, guiding the program of the stress-strain relations in the metamaterials.
In conclusion, we demonstrate the material-based programmability enabled by metamaterials composed of nematic LCEs, especially the stress-strain relations with tunable strain-softening and strain-stiffening effects. Taking advantage of the tunable bending and stretching deformation enabled by the geometry of the building blocks and the semi-soft elasticity of the nematic LCE, we engineer the local stretch in the ligament of the metamaterials to program the stress-strain relation in the metamaterial under uniaxial extension. Starting from the molecular description of the soft elasticity, we relate the liquid crystal ordering to the constitutive model of the nematic LCE and integrate the semi-soft elasticity of LCE into the metamaterials. Numerical simulations have revealed that the attenuated local stretch due to the ligament bending and the soft elasticity in the nematic LCE induce a compliant response in the metamaterials, where the effective shear modulus is much lower than the constituent materials. The subsequent stretching deformation in the ligament and the exiting of the soft elasticity in the nematic LCE leads to the surge of the stress, leading to a stiffening response. To relate the softening and stiffening responses to the geometric and material parameters in the LCE metamaterials, we develop an analytical model that predicts the local stretch in the ligament and calculates the force in the LCE metamaterials. The metamaterials undergo a transition between strain-softening and strain-stiffening with different effective shear moduli, depending on the maximum local stretch in bending and the critical stretch for the onset of the soft elasticity. By designing a continuous transition from the ligament bending to the semi-soft elasticity in the LCE, we can program an elastic region with near-zero stiffness up to the stretch of 1.4. The highly programmable softening and stiffening behaviors offer a material-based control of the mechanical properties in the LCE metamaterials, inducing the stress-strain relations within the space prescribed by the Neo-Hookean elastomers with the same shear modulus. The LCE metamaterials provide a platform for material-based programmability, facilitating the development of advanced forms of mechanical metamaterials and impacting the design of robotic systems.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
XL developed the concept, derived the theoretical model, conducted numerical calculations, and wrote the manuscript. DL helped in the numerical calculations and edited the manuscript. All authors contributed to manuscript revision, development and approved the submitted version.
XL acknowledges the startup funding from Harbin Institute of Technology, Shenzhen (HITSZ) grant number 20210138. Financial support provided by Shenzhen Science and Technology Program (Grant No. KQTD20200820113045083) is also acknowledged.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The authors thank Professor Zhijian Wang (BUAA) for the insightful discussions.
Bai, R., and Bhattacharya, K. (2020). Photomechanical Coupling in Photoactive Nematic Elastomers. J. Mech. Phys. Sol. 144, 104115. doi:10.1016/j.jmps.2020.104115
Bertoldi, K., Vitelli, V., Christensen, J., and Van Hecke, M. (2017). Flexible Mechanical Metamaterials. Nat. Rev. Mater. 2, 1–11. doi:10.1038/natrevmats.2017.66
Biggins, J. S., Terentjev, E. M., and Warner, M. (2008). Semisoft Elastic Response of Nematic Elastomers to Complex Deformations. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 78, 041704. doi:10.1103/PhysRevE.78.041704
Biggins, J. S., Warner, M., and Bhattacharya, K. (2012). Elasticity of Polydomain Liquid crystal Elastomers. J. Mech. Phys. Sol. 60, 573–590. doi:10.1016/j.jmps.2012.01.008
Bladon, P., Terentjev, E. M., and Warner, M. (1993). Transitions and Instabilities in Liquid crystal Elastomers. Phys. Rev. E 47, R3838–R3840. doi:10.1103/physreve.47.r3838
Chen, T., Pauly, M., and Reis, P. M. (2021). A Reprogrammable Mechanical Metamaterial with Stable Memory. Nature 589, 386–390. doi:10.1038/s41586-020-03123-5
Coulais, C., Overvelde, J. T., Lubbers, L. A., Bertoldi, K., and Van Hecke, M. (2015). Discontinuous Buckling of Wide Beams and Metabeams. Phys. Rev. Lett. 115, 044301. doi:10.1103/PhysRevLett.115.044301
Dykstra, D. M., Busink, J., Ennis, B., and Coulais, C. (2019). Viscoelastic Snapping Metamaterials. J. Appl. Mech. 86, 1. doi:10.1115/1.4044036
Fleck, N. A., Deshpande, V. S., and Ashby, M. F. (2010). Micro-architectured Materials: Past, Present and Future. Proc. R. Soc. A. 466, 2495–2516. doi:10.1098/rspa.2010.0215
Gardel, M. L., Shin, J. H., Mackintosh, F. C., Mahadevan, L., Matsudaira, P., and Weitz, D. A. (2004). Elastic Behavior of Cross-Linked and Bundled Actin Networks. Science 304, 1301–1305. doi:10.1126/science.1095087
Herbert, K. M., Fowler, H. E., Mccracken, J. M., Schlafmann, K. R., Koch, J. A., and White, T. J. (2021). Synthesis and Alignment of Liquid Crystalline Elastomers. Nat. Rev. Mater. 7, 1–16. doi:10.1038/s41578-021-00359-z
Kadic, M., Milton, G. W., Van Hecke, M., and Wegener, M. (2019). 3D Metamaterials. Nat. Rev. Phys. 1, 198–210. doi:10.1038/s42254-018-0018-y
Kim, J., Zhang, G., Shi, M., and Suo, Z. (2021). Fracture, Fatigue, and Friction of Polymers in Which Entanglements Greatly Outnumber Cross-Links. Science 374, 212–216. doi:10.1126/science.abg6320
Kochmann, D. M., and Bertoldi, K. (2017). Exploiting Microstructural Instabilities in Solids and Structures: from Metamaterials to Structural Transitions. Appl. Mech. Rev. 69. doi:10.1115/1.4037966
Küupfer, J., and Finkelmann, H. (1994). Liquid crystal Elastomers: Influence of the Orientational Distribution of the Crosslinks on the Phase Behaviour and Reorientation Processes. Macromolecular Chem. Phys. 195, 1353–1367. doi:10.1002/macp.1994.021950419
Lake, G., and Thomas, A. (1967). The Strength of Highly Elastic Materials. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 300, 108–119. doi:10.1098/rspa.1967.0160
Lakes, R. (1987). Foam Structures with a Negative Poisson's Ratio. Science 235, 1038–1040. doi:10.1126/science.235.4792.1038
Launey, M. E., Buehler, M. J., and Ritchie, R. O. (2010). On the Mechanistic Origins of Toughness in Bone. Annu. Rev. Mater. Res. 40, 25–53. doi:10.1146/annurev-matsci-070909-104427
Liang, X., and Crosby, A. J. (2020a). Programming Impulsive Deformation with Mechanical Metamaterials. Phys. Rev. Lett. 125, 108002. doi:10.1103/physrevlett.125.108002
Liang, X., and Crosby, A. J. (2020b). Uniaxial Stretching Mechanics of Cellular Flexible Metamaterials. Extreme Mech. Lett. 35, 100637. doi:10.1016/j.eml.2020.100637
Liang, X., Fu, H., and Crosby, A. J. (2022). Phase-transforming Metamaterial with Magnetic Interactions. Proc. Natl. Acad. Sci. USA 119, e2118161119. doi:10.1073/pnas.2118161119
Meyers, M. A., and Chawla, K. K. (2008). Mechanical Behavior of Materials. United Kingdom: Cambridge University Press.
Meyers, M. A., Chen, P.-Y., Lin, A. Y.-M., and Seki, Y. (2008). Biological Materials: Structure and Mechanical Properties. Prog. Mater. Sci. 53, 1–206. doi:10.1016/j.pmatsci.2007.05.002
Pishvar, M., and Harne, R. L. (2020). Foundations for Soft, Smart Matter by Active Mechanical Metamaterials. Adv. Sci. 7, 2001384. doi:10.1002/advs.202001384
Popov, Y. O., and Semenov, A. N. (1998). Nematic Ordering in Anisotropic Elastomers: Effect of Frozen Anisotropy. Eur. Phys. J. B 6, 245–256. doi:10.1007/s100510050547
Quan, H., Yang, W., Lapeyriere, M., Schaible, E., Ritchie, R. O., and Meyers, M. A. (2020). Structure and Mechanical Adaptability of a Modern Elasmoid Fish Scale from the Common Carp. Matter 3, 842–863. doi:10.1016/j.matt.2020.05.011
Schaedler, T. A., Jacobsen, A. J., Torrents, A., Sorensen, A. E., Lian, J., Greer, J. R., et al. (2011). Ultralight Metallic Microlattices. Science 334, 962–965. doi:10.1126/science.1211649
Sonnet, A. M., and Virga, E. G. (2012). Dissipative Ordered Fluids: Theories for Liquid Crystals. Berlin, Germany: Springer Science & Business Media.
Storm, C., Pastore, J. J., Mackintosh, F. C., Lubensky, T. C., and Janmey, P. A. (2005). Nonlinear Elasticity in Biological Gels. Nature 435, 191–194. doi:10.1038/nature03521
Surjadi, J. U., Gao, L., Du, H., Li, X., Xiong, X., Fang, N. X., et al. (2019). Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 21, 1800864. doi:10.1002/adem.201800864
Verwey, G. C., and Warner, M. (1997a). Compositional Fluctuations and Semisoftness in Nematic Elastomers. Macromolecules 30, 4189–4195. doi:10.1021/ma961801i
Verwey, G. C., and Warner, M. (1997b). Nematic Elastomers Cross-Linked by Rigid Rod Linkers. Macromolecules 30, 4196–4204. doi:10.1021/ma961802a
Verwey, G. C., Warner, M., and Terentjev, E. M. (1996). Elastic Instability and Stripe Domains in Liquid Crystalline Elastomers. J. Phys. France 6, 1273–1290. doi:10.1051/jp2:1996130
Wang, Y. C., and Lakes, R. S. (2005). Composites with Inclusions of Negative Bulk Modulus: Extreme Damping and Negative Poisson's Ratio. J. Compos. Mater. 39, 1645–1657. doi:10.1177/0021998305051112
Warner, M., and Terentjev, E. M. (2007). Liquid crystal Elastomers. United Kingdom: Oxford University Press.
Yu, X., Zhou, J., Liang, H., Jiang, Z., and Wu, L. (2018). Mechanical Metamaterials Associated with Stiffness, Rigidity and Compressibility: A Brief Review. Prog. Mater. Sci. 94, 114–173. doi:10.1016/j.pmatsci.2017.12.003
Zhang, Y., Xuan, C., Jiang, Y., and Huo, Y. (2019). Continuum Mechanical Modeling of Liquid crystal Elastomers as Dissipative Ordered Solids. J. Mech. Phys. Sol. 126, 285–303. doi:10.1016/j.jmps.2019.02.018
Keywords: metamaterials, liquid crystal elastomer, soft elasticity, programmable materials, strain softening and stiffening
Citation: Liang X and Li D (2022) A Programmable Liquid Crystal Elastomer Metamaterials With Soft Elasticity. Front. Robot. AI 9:849516. doi: 10.3389/frobt.2022.849516
Received: 06 January 2022; Accepted: 02 February 2022;
Published: 25 February 2022.
Edited by:
Qiguang He, University of Pennsylvania, United StatesReviewed by:
Ruobing Bai, Northeastern University, United StatesCopyright © 2022 Liang and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xudong Liang, bGlhbmd4dWRvbmdAaGl0LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.