Learning Optimal Fin-Ray Finger Design for Soft Grasping

The development of soft hands is an important progress to empower robotic grasping with passive compliance while greatly decreasing the complexity of control. Despite the advances during the past decades, it is still not clear how to design optimal hands or fingers given the task requirements. In this paper, we propose a framework to learn the optimal design parameter for a fin-ray finger in order to achieve stable grasping. First, the pseudo-kinematics of the soft finger is learned in simulation. Second, the task constraints are encoded as a combination of desired grasping force and the empirical grasping quality function in terms of winding number. Finally, the effectiveness of the proposed approach is validated with experiments in simulation and using real-world examples as well.

1. Introduction

Soft robotics is one of the most fast-growing area in robotics. This is in part due to the breaking idea of building robots from highly compliant material similar as living organisms (Laschi et al., 2016). More importantly, soft robots allows for increased flexibility and adaptability for accomplishing complex tasks that is impossible for traditional rigid robots. Therefore, soft robots brings up the potential to push the boundaries of current robot abilities (Laschi et al., 2016). Previous work in this domain mostly focuses on the design of new types of soft robots (Lipson, 2014; Rus and Tolley, 2015; Hughes et al., 2016), including novel driving actuators (Polygerinos et al., 2015b; Zhao et al., 2016), bio-inspired structure and mechanism (Cutkosky and Kim, 2009; Lipson, 2014; Manti et al., 2015; Hughes et al., 2016), special design and control methods (Hiller and Lipson, 2011), and stretchable electronics (Rogers et al., 2010). Despite these achievements, the relation between given task at hand and the correct robot embodiment for the task remains a challenge. In another word, when designing the novel soft robots, there are few work taking the task constraints into account.

In this paper, we address the problem of optimal geometry design for a fin-ray finger given an object to be grasped. The task constraint is encapsulated as a grasp quality function, which is a combination of the object shape and the geometry of the deformed finger. The object feature is modeled using superquadratics, which allows for a variety of inputs such as the point cloud and object CAD models. The grasp quality function is chosen as the winding number that represents how well the soft finger is surrounding the object surface. Given a new object, the best grasp quality with different hands can be quickly predicted using the object and hand features. An overview of the proposed framework is shown in Figure 1. The main contribution of this paper is two-fold: (1) We first propose a framework to learn the optimal fin-ray finger design for soft grasping. This can possibly open a new direction for the design of soft hands considering the task to be done, which is important to move soft robots from lab to real world. (2) For soft grasping, we propose to use the winding number to empirically estimate the quality of the obtained grasp. This quality function is not limited to fin-ray finger, but also can be used for many other types of soft robots.

FIGURE 1

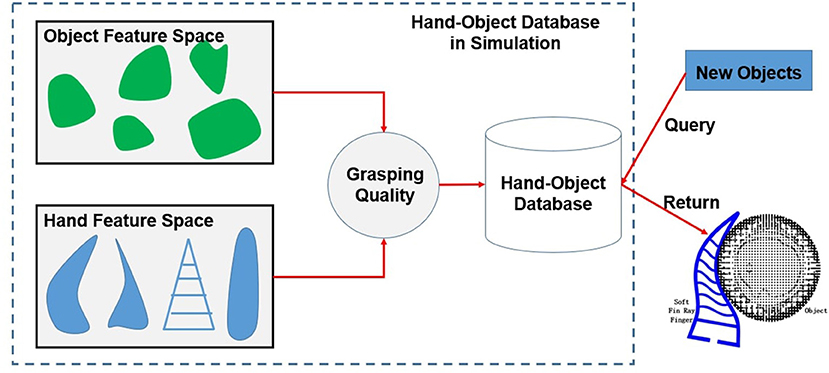
Figure 1. The pipeline of the proposed framework. The soft fin-ray hand and object feature are encoded and integrated with the grasp quality function in simulation. Given a new object, the best hand design parameters are obtained by querying the learned hand-object database.

The paper is organized as follows: section 2 provides a review of the related work, mainly focusing on the modeling of soft hands and the evaluation of soft grasping. Section 3 gives an approach to object and hand feature encoding, along with an empirical grasp quality function. Implementation details and experiments results are described in section 4, followed by a discussion of future directions and conclusion in section 5.

2. Related Work

Soft hand and soft grasping have been extensively studied during the past decades. The studies can be roughly divided into two sub-areas. The first one is trying to use new materials and structures to design various new hands and robots, which are different from previous robots that are built from rigid material including motors and links. Another direction is mainly focusing on the planning of compliant grasping with soft hands. The performance of the final grasping is usually demonstrated by the real-world grasping examples. There is no grasp quality function to guide the search for optimal grasps. The remaining part of this section will discuss the work on soft hand design and the performance of soft grasping, respectively.

2.1. Soft Hands Design and Modeling

Many researchers have attempted to use different materials, structures, sensors, and actuators to design novel robots and hands. Hannan and Walker (2003) developed a continuum style robot mimicking an elephant's trunk, where the kinematics is formulated using curvatures of the robot's shape. A universal gripper is developed based on jamming of granular material, with the goal to pick up unfamiliar object of widely varying shapes and surface properties (Brown et al., 2010; Amend et al., 2012). A wearable robotic glove is designed with soft actuators consisting of molded elastomeric chambers with fiber reinforcements that induce specific bending, twisting, and extending trajectories under fluid pressurization (Polygerinos et al., 2015a). The parameters are specifically selected to match the motion of human hands. Deimel and Brock (2016) describes the design and testing of an inexpensive, modular, under-actuated soft robot hand with pneumatically actuated fiber-reinforced elastomer fingers. The usage of various soft hands for exoskeletons is presented in Shahid et al. (2018). Internal sensing capability is further incorporated with a soft robot hand for robust proprioceptive grasping and object identification (Homberg et al., 2019). Abondance et al. (2020) presents a design of a prototype hand with dexterous soft fingers capable of moving object within the hand using several basic motion primitives.

There are some studies attempting to build the kinematic or kinetostatic models for soft robots and hands. The kinematics of constant curvature continuum robots is modeled and summarized in Webster and Jones (2010). A generic geometry-based framework is proposed to compute the deformation of soft robots within the range of linear material elasticity, namely linear stress–strain relation (Fang et al., 2020). The first-order dynamic modeling and control of soft robots is studied in George Thuruthel et al. (2020). For a fin-ray effect soft finger (Hosale and Kievid, 2010; Corporate, 2011; Pfaff et al., 2011), the kinetostatic model of a general multi-crossbeam finger is established (Shan and Birglen, 2020). A comprehensive survey on soft robotic gripper is given in Shintake et al. (2018) that categorize the soft gripping in three types: actuation, controlled stiffness, and controlled adhesion.

As discussed above, most of the previous work focus on the specific design of new soft hands and the analytical performance modeling of the designed hands. In this paper, one of the main motivations comes from the challenge that how to design a proper soft hand given the desired task requirement. To this end, two basic components are necessary: how to model the hand (in terms of kinematics, dynamics) and how to model the task requirements. In this paper, we choose to use the fin-ray finger as a testing example for our proposed framework, but also noticing that our approach is not limited to this specific type of fingers. Rather than using an analytic model to formulate the kinematics, the pseudo-kinematics of the finger is directly simulated using Ansys Workbench® due to its generality. For the task requirements, we choose stable grasping as the goal while some other more complex task requirements (e.g., object identification, dexterous manipulation) can be also considered. The performance of soft grasping is reviewed in the next part.

2.2. Quality of Soft Grasping

Unlike its counterpart of multi-fingered robotic hands where various metrics have been proposed to evaluate the quality of a given grasp, the grasping quality using a soft hand is usually much more difficult to evaluate. This is mainly due to the fact that the assumption of point contact is not valid in the case of soft grasping as mentioned in Shintake et al. (2018). The contact during soft grasping is continuously deformable in an infinity of possible shapes through interaction with objects. Several quality measures (Cloud Quality, Closure Index, and Net Force) are used in order to extract the grasp affordances for a soft hand (Bonilla et al., 2014). There are also some works that design the hand to simply mimic the structure or functionality of human hands (Deimel and Brock, 2016). Implicitly, in these cases the actual grasp quality is assumed to be the feasibility to achieve the human grasp taxonomy. Later, a co-design strategy is proposed to design the hand morphology with specific structure (Deimel et al., 2017). The grasp quality here is evaluated by a soft hand grasping simulator.

In this paper, we proposed to use the winding number to evaluate the quality of a soft grasp. Based on this quality function and the object shape geometry, the optimal finger design parameters can be selected. Compared with other grasping quality function, winding number inherently represents the total number of times that a curve travels around an object. This quality function is more generic and can be extend to many other soft robots with different kinematics.

3. Hand-Object Feature Encoding and Grasping Quality

As shown in Figure 1, the problem can be formulated as finding a mapping from a given task to a desired hand design, namely ${M}:{T}\to {H}(\varphi )$, where ${T}$ and ${H}$ represent the task requirement and hand design space, respectively. The task requirement in this paper is chosen as the quality of the final grasp and the hand design space depend on the design parameters of the hand ϕ.

3.1. Hand Feature Encoding

A soft fin-ray finger is chosen as an example in this paper (see Figure 2), where the design parameters ϕ include the thickness a and the spacing distance h. Note that some other more complex parameters (angle, morphology) are not considered here for simplicity.

FIGURE 2

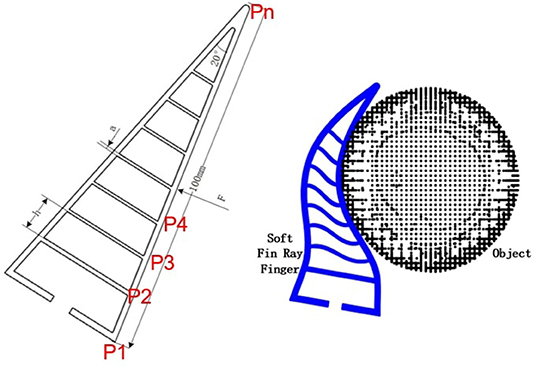
Figure 2. The fin-ray finger with its design parameters and its deformation during interaction with object.

During the hand object interaction, different selection of the design parameters will lead to different level of deformation and therefore different task performance. To compute these deformations, a dataset of the hand deformation is collected in simulation using Ansys Workbench®. The parameters a, h, and the applied force F are all chosen with fixed spacing and range. The material we used is TPU 95A with Young's modulus 26 MPa, yield strength 8.6 MPa, breaking strength 39 MPa, and Poisson ratio 0.48¹. Some of the results are shown in Figure 2. After the simulations, a dataset of N_h hand feature is collected as: ${{D}}_h={\left\{F_f^i,h^i,a^i,d^i,x_n^i,y_n^i,z_n^i\right\}}^{i=1..N_h}$, where superscript represents the order of the hands. $F_f^i$ represents the contact force between the hand and the object, and dⁱ represents the maximal deformation. $x_n^i,y_n^i,z_n^i$ represents the coordinates of the nodes Pn after deformation as shown in Figure 3. As discussed above, note that some other analytical methods can be also used here to compute the deformation as presented in Fang et al. (2020).

FIGURE 3

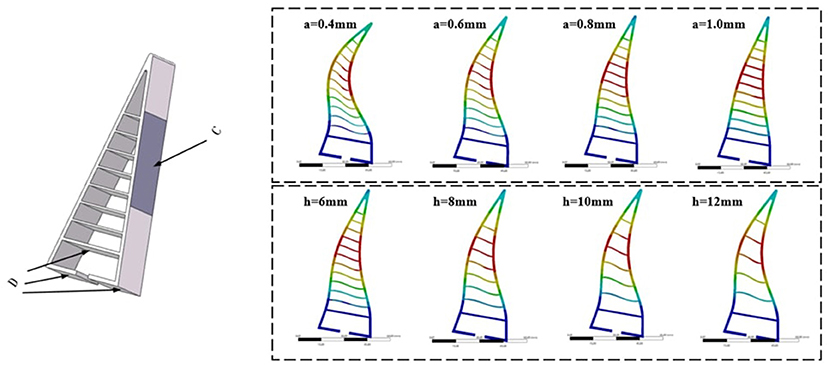
Figure 3. (Left) D represents the fixed constraints during simulation and C represents the area to apply forces. (Right) The resulting deformation with different design parameters.

3.2. Object Feature Encoding

A superquadratics model is used to represent the object shape (Jaklič et al., 2000), which is consisting of five parameters, namely a₁, a₂, a₃, e₁, e₂. In our case, we only consider a two-fingered grasping and the section that z = 0 is considered as the grasping plane. Therefore, e₁ and a₃ are not required. Together with the allowed grasping force F_o, the dataset of object feature can be encoded as: ${{D}}_o={\left\{F_o^i,a_1^i,a_2^i,e_1^i,e_2^i\right\}}^{i=1..N_o}$.

$\begin{array}{ll}{\left({\left(\frac{x}{a_1}\right)}^{\frac{2}{e_2}}+{\left(\frac{y}{a_2}\right)}^{\frac{2}{e_2}}\right)}^{\frac{e_1}{e_2}}+{\left(\frac{z}{a_3}\right)}^{\frac{2}{e_1}}=1& (1)\end{array}$

Note that in this paper, we will assume that the parameters of the object feature are known in advance. However, it is still possible to extract these parameters from either object point cloud or the CAD model (El Khoury et al., 2012; El-Khoury et al., 2013; Li et al., 2016).

3.3. Soft Grasping Quality

The task we consider here is stable soft grasping. To evaluate the quality of the grasp, a topological grasp quality measure is adopted, i.e., the winding number that counts the number of times that a curve wraps around a point (Pokorny et al., 2013; Li, 2016). In our case, this quality intuitively measures how well the fingers wrap around the approximated superquadratics. Mathematically, given a piecewise-linear curve that connects points, ${\text{p}}^1,{\text{p}}^2,{\text{p}}^i={\left[p_1^i,p_2^i\right]}^T\cdots ,{\text{p}}^n\in {ℝ}^2$, the winding number can be computed as (Hormann and Agathos, 2001), as illustrated in Figure 4,

$\begin{array}{l}w=\frac{1}{2\pi }{\displaystyle \sum _{i=0}^{n-1}\{}{\tan }^{-1}\left(\frac{{\text{p}}^{\text{i}+1}{}^{{}^T}({\text{p}}^{\text{i}+1}-{\text{p}}^{\text{i}})}{D_i}\right)\\ +{\tan }^{-1}\left(\frac{{\text{p}}^{\text{i}}{}^{{}^T}({\text{p}}^{\text{i}}-{\text{p}}^{\text{i}+1})}{D_i}\right)\}& (2)\end{array}$

where $D_i=p_1^i{p}_2^{i+1}-p_2^i{p}_1^{i+1}$. Note that the winding number changes sign if the curve change direction. For our cases, we use two fin-ray finger for soft grasping. Therefore, we define the quality of a soft grasp ${G}$ as,

$\begin{array}{ll}{w}_{{G}}=\left|w_l\right|+\left|w_r\right|& (3)\end{array}$

where w_l, w_r corresponds to the winding number of the left and right finger, respectively. Since these two fingers are symmetric, $w_{{G}}=2\left|w_l\right|$.

FIGURE 4

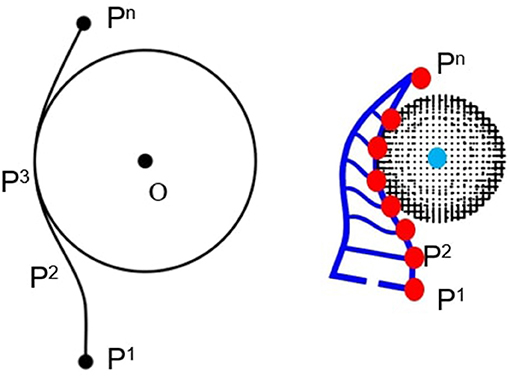
Figure 4. The illustration of winding number for soft grasping. The red dots represent the nodes of the beams, which are used for computing the winding number.

3.4. Desired Parameters Selection

Given a dataset of the hand feature ${{D}}_h$ and the object feature ${{D}}_o$, the pairwise grasping quality can be computed using Equation (3). $w_{{G}}^{i,j},i=1..N_h,j=1..N_o$ represents the grasping quality that grasping the jth object in ${{D}}_o$ using the ith hand in ${{D}}_h$. For jth object in the dataset, we can choose the best hand design as $\text{arg }{\text{min}}_i{w}^{i,j}$. The similarity of a new object and the object dataset is defined as:

$\begin{array}{ll}{{Q}}^{new}=min\{\alpha \Vert {\displaystyle F_o^i}-F_o^{new}\Vert +\beta {\displaystyle \sum _{k=1}^2}(\Vert a_k^i-a_k^{new}\Vert +\Vert e_k^i-e_k^{new}\Vert )\}& (4)\end{array}$

where α and β are the scaling parameters. Given a manually selected threshold σ, if ${{Q}}^{new}<\sigma$, this new object is considered as similar enough to the objects in the dataset and the hand design is selected accordingly. When ${{Q}}^{new}>\sigma$, the object to be grasped is considered as unknown before, the procedure to find the optimal design parameters is summarized in Algorithm 1.

4. Experiments and Results

In the experiments, we demonstrated the results both in simulation and with real-world objects.

4.1. Results in Simulation

For the examples with simulated object, 8 objects from the YCB object dataset are used (Calli et al., 2015), as shown in Figure 5. The approximated superquadratics for each object is learned through constrained optimization (Jaklič et al., 2000).

FIGURE 5

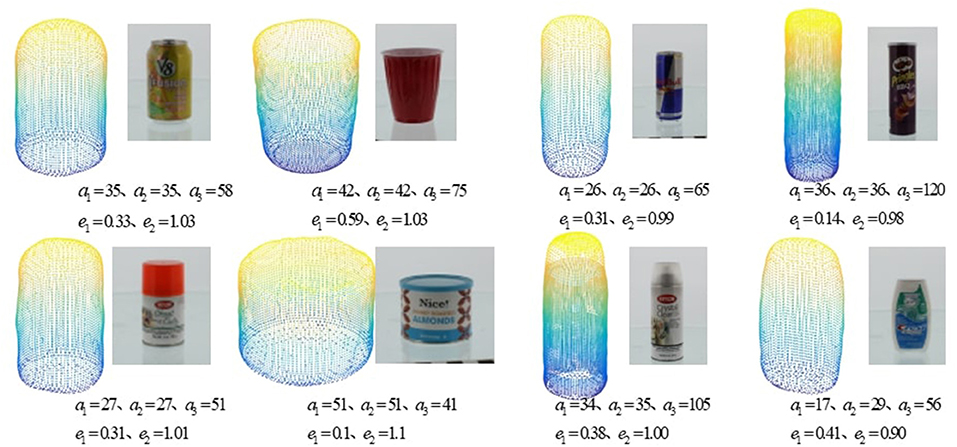
Figure 5. The YCB objects used in the experiments and their approximated superquadratics, including v8, red_cup,red_bull,pringles,krylon_short_cuts,honey_roasted_almonds,krylon_crystal_clear,crest_minty_fresh.

We take the first object v8 as an example and the desired force is set to 2N. The grasp qualities for different hand parameters is shown as follows (see Figure 6). The best grasp quality is 0.3621 and the corresponding parameters are a = 0.5mm and h = 11mm. For another object pringles, the desired force is set to 3N and the best hand design parameters (a = 0.7mm and h = 10mm) are shown in Figure 7. For another object cre_minty_fresh, the desired force is set to 3N and the best hand design parameters (a = 1.0mm and h = 11mm) are shown in Figure 8.

FIGURE 6

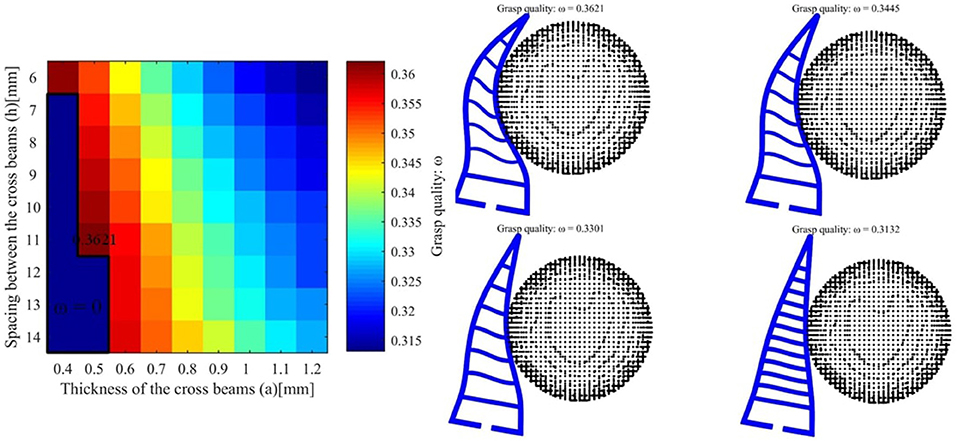
Figure 6. (Left) The grasping quality for object v8 with different hand design parameters. (Right) The hand object interaction for different final grasp qualities.

FIGURE 7

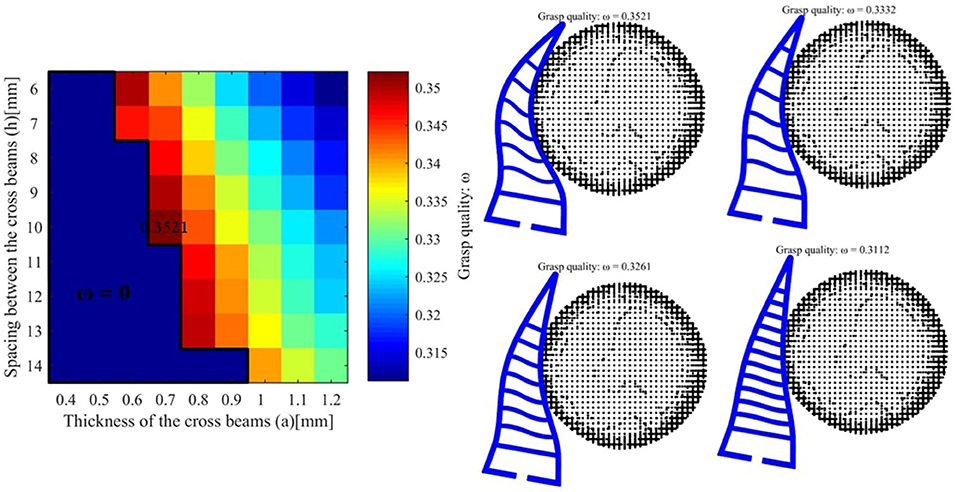
Figure 7. (Left) The grasping quality for object pringles with different hand design parameters. (Right) The hand object interaction for different final grasp qualities.

FIGURE 8

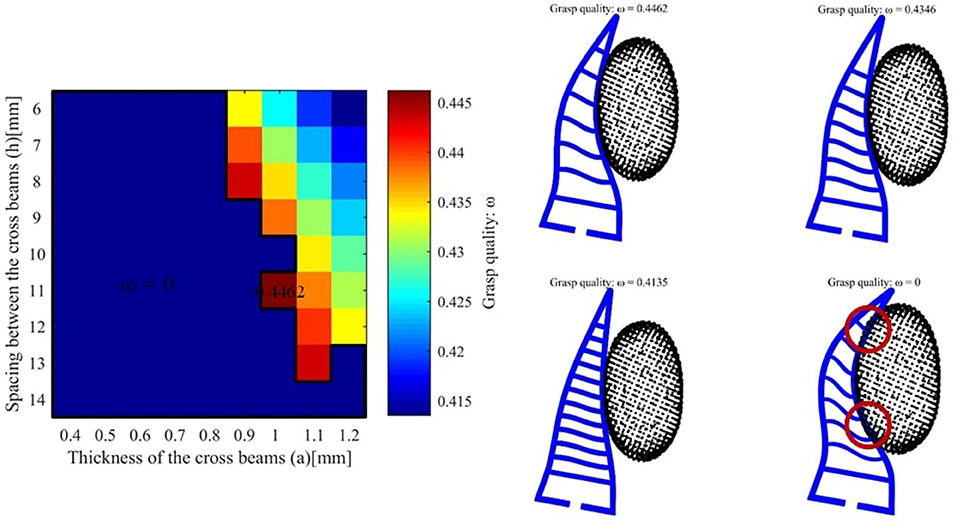
Figure 8. (Left) The grasping quality for object crest_minty_fresh with different hand design parameters. (Right) The hand object interaction for different final grasp qualities. The red circles stand for over-shot deformation and thus the quality is set to w = 0.

4.2. Results With Real-World Objects

The 3D-printed fin-ray finger used for grasping two real-world objects is shown in Figure 9. The true deformations for current examples are hard to measure. Therefore, we cannot directly compute the grasp quality in the real-world example. However, in the future work, we are planning to integrate tactile sensing with the soft finger, which allows us to estimate the grasp quality from previous experience (Li et al., 2014).

FIGURE 9

Figure 9. The 3D-printed fin-ray finger used for grasping two real-world objects.

5. Discussion and Conclusion

5.1. Discussion and Limitations

The functionality of soft hands is highly dependent on the inherent compliance from the structure and the material. Therefore, it is important to select the proper design parameters for a given task or a set of tasks. The complete searching space of the design parameters is usually embedded in a high dimension space. This paper only studies the case of a fin-ray finger where the design parameters are simplified as thickness of the beam and the spacing between beams. The performance of the soft grasping is evaluated using winding number, which can be computed in simulation. A much larger grasping dataset can be created in the future to enlarge the search space for different tasks.

ALGORITHM 1

Algorithm 1. The algorithm to find the optimal hand design parameters for a new object.

There are some limitations of the current proposed framework. First, the task constraints for soft grasping is quantified using winding number. This is a geometric metric and it does not reflect the information from sensors and actuators. It is possible to co-design the structure and control algorithm together by taking into account the external sensing information (Deimel et al., 2017; Homberg et al., 2019). Second, the design space is simplified as a two-dimensional vector space in this paper. However, the morphology of the soft hand is a much more complicated space. It will be interesting to study the mapping between this morphology space to the final task performance. For example, in the fin-ray finger design, the beams are located with constant distance in parallel. It will be very useful to extend the space of the design parameters, especially by leveraging the power of big data and deep learning. This is part of our planned future work.

5.2. Conclusion

In this paper, we proposed a framework to learn the optimal fin-ray finger design for soft grasping. The hand feature is learned in simulation to encode the deformation of the finger during interaction. The object feature is represented using superquadratics and a topological metric is used to quantify the final task performance. Given a new object, the desired hand parameters can be quickly selected using the hand and object feature representation, under the guidance of the grasp quality function. For the future work, more complex hand design space and task quality function will be studied by leaveraging the power of big data and deep learning.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

ZD designed the experiments and wrote the draft of this paper. ML served as adviser of this project and revised the draft accordingly. All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 51705371) and the Natural Science Foundation of Jiangsu Province (Grant No. BK20180235).

Conflict of Interest

ML was partly employed by the company Wuhan Cobot Technology.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^https://freddieflip.s3.us-west-2.amazonaws.com/uploads/sites/28/2018/03/28133640/Plural_Elasto95A_Data_Sheet-2.pdf

References

Abondance, S., Teeple, C. B., and Wood, R. J. (2020). A dexterous soft robotic hand for delicate in-hand manipulation. IEEE Robot. Autom. Lett. 5, 5502–5509. doi: 10.1109/LRA.2020.3007411

CrossRef Full Text | Google Scholar

Amend, J. R., Brown, E., Rodenberg, N., Jaeger, H. M., and Lipson, H. (2012). A positive pressure universal gripper based on the jamming of granular material. IEEE Trans. Robot. 28, 341–350. doi: 10.1109/TRO.2011.2171093

CrossRef Full Text | Google Scholar

Bonilla, M., Farnioli, E., Piazza, C., Catalano, M., Grioli, G., Garabini, M., et al. (2014). “Grasping with soft hands,” in 2014 IEEE-RAS International Conference on Humanoid Robots (Madrid), 581–587. doi: 10.1109/HUMANOIDS.2014.7041421

CrossRef Full Text | Google Scholar

Brown, E., Rodenberg, N., Amend, J., Mozeika, A., Steltz, E., Zakin, M. R., et al. (2010). Universal robotic gripper based on the jamming of granular material. Proc. Natl. Acad. Sci. U.S.A. 107, 18809–18814. doi: 10.1073/pnas.1003250107

CrossRef Full Text | Google Scholar

Calli, B., Singh, A., Walsman, A., Srinivasa, S., Abbeel, P., and Dollar, A. M. (2015). “The YCB object and model set: towards common benchmarks formanipulation research,” in 2015 international conference on advanced robotics (ICAR) (Istanbul), 510–517. doi: 10.1109/ICAR.2015.7251504

CrossRef Full Text | Google Scholar

Corporate, F. (2011). Bionictripod with fingripper. Available online at: https://www.festo.com/rep/en_corp/assets/pdf/Tripod_en.pdf

Google Scholar

Cutkosky, M. R., and Kim, S. (2009). Design and fabrication of multi-material structures for bioinspired robots. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 367, 1799–1813. doi: 10.1098/rsta.2009.0013

PubMed Abstract | CrossRef Full Text | Google Scholar

Deimel, R., and Brock, O. (2016). A novel type of compliant and underactuated robotic hand for dexterous grasping. Int. J. Robot. Res. 35, 161–185. doi: 10.1177/0278364915592961

CrossRef Full Text | Google Scholar

Deimel, R., Irmisch, P., Wall, V., and Brock, O. (2017). “Automated co-design of soft hand morphology and control strategy for grasping,” in 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (Vancouver, BC), 1213–1218. doi: 10.1109/IROS.2017.8202294

CrossRef Full Text | Google Scholar

El Khoury, S., Li, M., and Billard, A. (2012). “Bridging the gap: one shot grasp synthesis approach,” in 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (Vilamoura), 2027–2034. doi: 10.1109/IROS.2012.6385886

CrossRef Full Text | Google Scholar

El-Khoury, S., Li, M., and Billard, A. (2013). On the generation of a variety of grasps. Robot. Auton. Syst. 61, 1335–1349. doi: 10.1016/j.robot.2013.08.002

CrossRef Full Text | Google Scholar

Fang, G., Matte, C.-D., Scharff, R. B., Kwok, T.-H., and Wang, C. C. (2020). Kinematics of soft robots by geometric computing. IEEE Trans. Robot. 36, 1272–1286. doi: 10.1109/TRO.2020.2985583

CrossRef Full Text | Google Scholar

George Thuruthel, T., Renda, F., and Iida, F. (2020). First-order dynamic modeling and control of soft robots. Front. Robot. AI 7:95. doi: 10.3389/frobt.2020.00095

PubMed Abstract | CrossRef Full Text | Google Scholar

Hannan, M. W., and Walker, I. D. (2003). Kinematics and the implementation of an elephant's trunk manipulator and other continuum style robots. J. Robot. Syst. 20, 45–63. doi: 10.1002/rob.10070

PubMed Abstract | CrossRef Full Text | Google Scholar

Hiller, J., and Lipson, H. (2011). Automatic design and manufacture of soft robots. IEEE Trans. Robot. 28, 457–466. doi: 10.1109/TRO.2011.2172702

CrossRef Full Text | Google Scholar

Homberg, B. S., Katzschmann, R. K., Dogar, M. R., and Rus, D. (2019). Robust proprioceptive grasping with a soft robot hand. Auton. Robots 43, 681–696. doi: 10.1007/s10514-018-9754-1

CrossRef Full Text | Google Scholar

Hormann, K., and Agathos, A. (2001). The point in polygon problem for arbitrary polygons. Comput. Geomet. 20, 131–144. doi: 10.1016/S0925-7721(01)00012-8

CrossRef Full Text | Google Scholar

Hosale, M., and Kievid, C. (2010). Modulating territories, penetrating boundaries. Footprint 55–68. doi: 10.7480/FOOTPRINT.4.1.719

CrossRef Full Text | Google Scholar

Hughes, J., Culha, U., Giardina, F., Guenther, F., Rosendo, A., and Iida, F. (2016). Soft manipulators and grippers: a review. Front. Robot. AI 3:69. doi: 10.3389/frobt.2016.00069

CrossRef Full Text | Google Scholar

Jaklič, A., Leonardis, A., and Solina, F. (2000). “Superquadrics and their geometric properties,” in Segmentation and Recovery of Superquadrics (Springer), 13–39. doi: 10.1007/978-94-015-9456-1_2

CrossRef Full Text | Google Scholar

Laschi, C., Mazzolai, B., and Cianchetti, M. (2016). Soft robotics: technologies and systems pushing the boundaries of robot abilities. Sci. Robot. 1:eaah3690. doi: 10.1126/scirobotics.aah3690

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, M. (2016). “Learning partial power grasp with task-specific contact,” in 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), 337–343. doi: 10.1109/ROBIO.2016.7866345

CrossRef Full Text | Google Scholar

Li, M., Bekiroglu, Y., Kragic, D., and Billard, A. (2014). “Learning of grasp adaptation through experience and tactile sensing,” in 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, 3339–3346. doi: 10.1109/IROS.2014.6943027

CrossRef Full Text | Google Scholar

Li, M., Hang, K., Kragic, D., and Billard, A. (2016). Dexterous grasping under shape uncertainty. Robot. Auton. Syst. 75, 352–364. doi: 10.1016/j.robot.2015.09.008

CrossRef Full Text | Google Scholar

Lipson, H. (2014). Challenges and opportunities for design, simulation, and fabrication of soft robots. Soft Robot. 1, 21–27. doi: 10.1089/soro.2013.0007

CrossRef Full Text | Google Scholar

Manti, M., Hassan, T., Passetti, G., D'Elia, N., Laschi, C., and Cianchetti, M. (2015). A bioinspired soft robotic gripper for adaptable and effective grasping. Soft Robot. 2, 107–116. doi: 10.1089/soro.2015.0009

CrossRef Full Text | Google Scholar

Pfaff, O., Simeonov, S., Cirovic, I., and Stano, P. (2011). Application of fin ray effect approach for production process automation. Ann. DAAAM Proc. 22, 1247–1249.

Google Scholar

Pokorny, F. T., Stork, J. A., and Kragic, D. (2013). “Grasping objects with holes: a topological approach,” in 2013 IEEE International Conference on Robotics and Automation (Karlsruhe), 1100–1107. doi: 10.1109/ICRA.2013.6630710

CrossRef Full Text | Google Scholar

Polygerinos, P., Wang, Z., Galloway, K. C., Wood, R. J., and Walsh, C. J. (2015a). Soft robotic glove for combined assistance and at-home rehabilitation. Robot. Auton. Syst. 73, 135–143. doi: 10.1016/j.robot.2014.08.014

CrossRef Full Text | Google Scholar

Polygerinos, P., Wang, Z., Overvelde, J. T., Galloway, K. C., Wood, R. J., Bertoldi, K., et al. (2015b). Modeling of soft fiber-reinforced bending actuators. IEEE Trans. Robot. 31, 778–789. doi: 10.1109/TRO.2015.2428504

CrossRef Full Text | Google Scholar

Rogers, J. A., Someya, T., and Huang, Y. (2010). Materials and mechanics for stretchable electronics. Science 327, 1603–1607. doi: 10.1126/science.1182383

PubMed Abstract | CrossRef Full Text | Google Scholar

Rus, D., and Tolley, M. T. (2015). Design, fabrication and control of soft robots. Nature 521, 467–475. doi: 10.1038/nature14543

PubMed Abstract | CrossRef Full Text | Google Scholar

Shahid, T., Gouwanda, D., Nurzaman, S. G., et al. (2018). Moving toward soft robotics: a decade review of the design of hand exoskeletons. Biomimetics 3:17. doi: 10.3390/biomimetics3030017

PubMed Abstract | CrossRef Full Text | Google Scholar

Shan, X., and Birglen, L. (2020). Modeling and analysis o soft robotic fingers using the fin ray effect. Int. J. Robot. Res. 39:1686–1705. doi: 10.1177/0278364920913926

CrossRef Full Text | Google Scholar

Shintake, J., Cacucciolo, V., Floreano, D., and Shea, H. (2018). Soft robotic grippers. Adv. Mater. 30:1707035. doi: 10.1002/adma.201707035

CrossRef Full Text | Google Scholar

Webster R. J. III. and Jones B. A. (2010). Design and kinematic modeling of constant curvature continuum robots: a review. Int. J. Robot. Res. 29, 1661–1683. doi: 10.1177/0278364910368147

CrossRef Full Text | Google Scholar

Zhao, H., O'Brien, K., Li, S., and Shepherd, R. F. (2016). Optoelectronically innervated soft prosthetic hand via stretchable optical waveguides. Sci. Robot. 1:eaai7529. doi: 10.1126/scirobotics.aai7529

PubMed Abstract | CrossRef Full Text | Google Scholar