A Partitioning Algorithm for Extracting Movement Epochs from Robot-Derived Kinematic Data

Beed, Alexander T.; Peduzzi, Peter; Guarino, Peter; Wininger, Michael

doi:10.3389/frobt.2017.00057

METHODS article

Front. Robot. AI, 20 November 2017

Sec. Biomedical Robotics

Volume 4 - 2017 | https://doi.org/10.3389/frobt.2017.00057

A Partitioning Algorithm for Extracting Movement Epochs from Robot-Derived Kinematic Data

Alexander T. Beed^1,2

Peter Peduzzi^1,2

Peter Guarino^1,2,3 $Michael Wininger,,*\r\n$ Michael Wininger^1,2,4*

¹Department of Biostatistics, Yale School of Public Health, New Haven, CT, United States
²Cooperative Studies Program, Department of Veterans Affairs, West Haven, CT, United States
³Statistical Center for HIV/AIDS Research and Prevention, Fred Hutchinson Cancer Research Center, Seattle, WA, United States
⁴Department of Rehabilitation Sciences, University of Hartford, West Hartford, CT, United States

Point-to-point exercising of the upper-limb, as elicited through the presentation of visual targets on a computer screen, is a ubiquitous paradigm in the robot-assisted rehabilitation of motor-impaired individuals. Kinematic data collected from the robot’s sensors can be used to assess motor function; these data allow objective quantification of motor performance, an approach that shows promise both for guiding therapy and documenting patient progress. It is imperative that these datasets be fully understood and that tools be continually developed to support analysis and proper interpretation of robot-generated data. It is our experience that data collected from kinematic robots and partitioned according to target achievement may be prone to errors in analysis and interpretation because the movements of highly spastic individuals rarely stop within the target. Here, we propose that it is preferable to partition serial movement data based on local minima in velocity rather than target achievement; this design reflects the convention that movement epochs start and end at low or zero velocity, an assumption that is prevalent even in severely impaired individuals. Using a commercially available robot (MIT-Manus, Interactive Motion Technologies), we recorded movements from 16 moderate to severely impaired chronic stroke patients. Data partitioned according to target presentation typically interrupted movements in mid-motion: velocity at file start was 32.6 ± 26.4% of the overall velocity range. By re-apportioning, we obtained velocity at file start of 7.4 ± 9.5% of total range. Across 3,200 movements, 12.4 ± 10.4% of data points were re-allocated on average. Thus, our routine is capable of re-partitioning to more accurately reflect observed behavior. Our study is thus the first to identify and propose a solution to the problem of high relevance to the community of robot-aided rehabilitation specialists, i.e., sub-optimal partitioning according to target achievement. Through the algorithm described in this paper, we were able to re-partition the data so that movement epochs were properly demarcated at velocity minima, thus adhering to the fundamental assumptions of human motor behavior and facilitating analysis of patient performance on a per-movement basis.

Introduction

Description of the Problem

For healthy individuals, directional sensitivity is seen in small, but measurable differences in speed, accuracy, and precision of movements made across a range of targets (Schmidt et al., 1979; Georgopoulos et al., 1982, 1986; Bullock and Grossberg, 1988; Zelaznik et al., 1988; Mushiake et al., 1991; Schwartz, 1992, 1993; Bootsma et al., 1994; Scott et al., 1997; Shadmehr et al., 1998; Patton and Mussa-Ivaldi, 2004; Yarosh et al., 2004; Yamamoto et al., 2006; Richardson et al., 2008; Brown et al., 2010; Coderre et al., 2010; Hewitt et al., 2011; Scott and Dukelow, 2011; Turnham et al., 2012; Berniker et al., 2014; Muceli et al., 2014). For people with impaired neuromotor systems, performance discrepancies between targets can be profound and also highly variable (Mattingley et al., 1994; Ghika et al., 1998; Wu et al., 2001; Azouvi et al., 2002; Gauthier et al., 2008; Swayne et al., 2008; Dipietro et al., 2009; Thies et al., 2009). Thus, the ability to stop on-target depends on (1) the specific task demands, (2) their level of motor impairment, and (3) the position of the target in space. Given the propensity for highly impaired individuals to overshoot a target (Acosta et al., 2011; Hu et al., 2011; Merlo et al., 2013; Mani et al., 2013), it is problematic that data extracted from rehabilitation robots is commonly partitioned based on target presentation.

Typically, once the robot’s cursor is held within the target for a pre-defined window, the movement is presumed complete, and the next target is presented; this window is often a small fraction of a second and constant across all targets. For highly impaired individuals, who move slowly, erratically, or overshoot their target, mere target achievement may be an inappropriate criterion for partitioning movement units. Consider the example of a multi-point movement task, where patients are instructed to move around a wheel of targets (Figure 1A). Suppose the patient moves through one target but is unable to stop on-target and instead continues beyond the target before transitioning to the next targeted movement. The movement record will reset upon target achievement, with the last portions of the movement being truncated and inappropriately pre-pended to the file containing the next movement (Figure 1B). Thus, our goal is to re-organize data into epochs that reflect the complete movement unit and not necessarily what is windowed according to the robot’s programmed target presentation (Figure 1C).

FIGURE 1

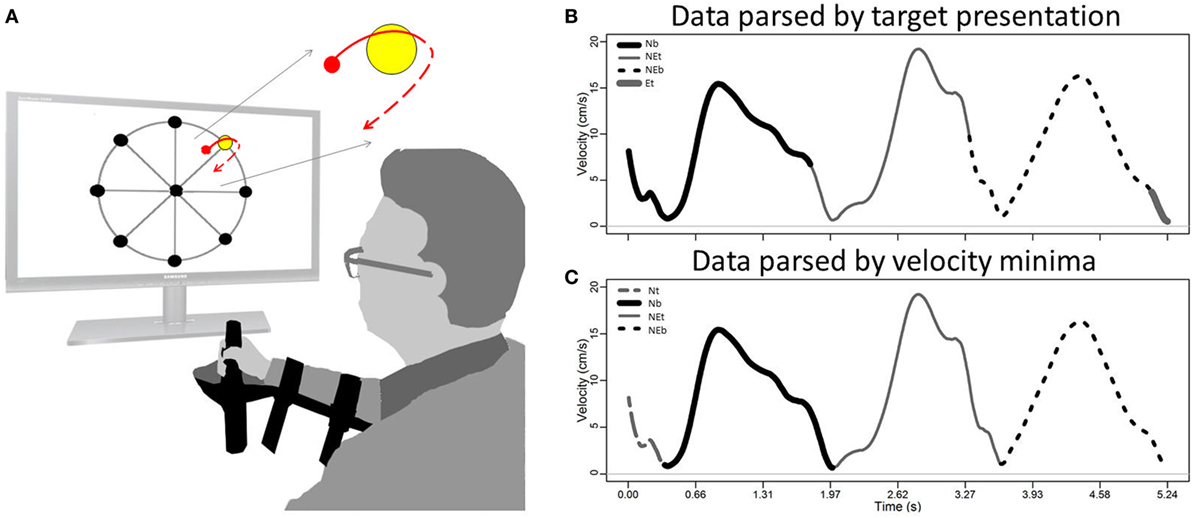
Figure 1. Schematic of subject performing a robot-driven multi-target task (A); and kinematic record (velocity versus time) of data collected through serial targets (B,C). Raw data obtained from the robot may not coincide with the subject’s transition between targets (B); the time-series may require conditioning so that each movement is bounded by a local minimum of velocity (C). Direction annotations in figure legends are Nt = North toward (from center target toward North target), Nb = North back (from North target back to center target), NEt = Northeast toward (toward the NE target), NEb = Northeast back, and Et = East toward; see Section “Patient Population and Protocol.”

Importance of the Problem

There is obvious benefit to automated partitioning of the continuous data stream by the robot. While we make no assumption about the intent of the robot manufacturer and it would be unusual for a technology to be described with the level of granularity that it’s process for file writing is full detailed, there are many products that suggest that they are, or could be, programmed to write out data based on target presentation (Hogan et al., 1995; Lockery et al., 2011; Csaba, 2013; Crainic et al., 2014) and note that this is so in our own device, for which four identical robots were purchased from the same entity, for use in a multi-site clinical trial. Furthermore, we assume that the end-user would prefer the data be partitioned into movement epochs, not strictly by target achievement; as seen in Figure 1, these two criteria may yield two different datasets. Obviously, there is need to partition the movement data collected from patients in a way that is intuitive and commensurate with how the task both performed (by the patient) and observed (by the clinician); a substantial portion of the robot’s utility is in providing accurate quantitative support to guiding therapy in real-time and supporting offline analysis. Moreover, considering that in adaptive robotics, early-session data are used to train the robot’s force-impedance settings for optimized re-training (Patton and Mussa-Ivaldi, 2004; Xu et al., 2011; Song et al., 2015), the ongoing inquiry into movement decomposition (modeling the speed profile as a series of log-normal curves) (Rohrer et al., 2002; Dipietro et al., 2009; Balasubramanian et al., 2012, 2015), or the robotic manipulandums prevalent in industrial applications (Gao and Zhang, 2015; Chen et al., 2016; He et al., 2017). These arenas are just a few examples of where boundary conditions are critically important parameters. Whereas initial and final position and velocity are typically integral to modeling and intelligent robotics, it is imperative that the data from the robots provide robustly partitioned movements, with reliable estimates of position and velocity at the time of movement start and end.

Key Assumption

In substantiation of this enterprise, there is a single primary assumption, i.e., movements start and end at a period of low or zero velocity. This has been demonstrated repeatedly to be true for healthy individuals (Flash and Hogan, 1985; Plamondon, 1991; Harris and Wolpert, 1998; Pattacini et al., 2010). More relevant to rehabilitation robotics, this framework has been shown to apply even in severely impaired individuals: movement onset and cessation is from rest or at low speed if transitioning in a movement re-direction; velocity profiles are typically single or multiple peaked (Trombly, 1993; Cirstea and Levin, 2000; Rohrer et al., 2002; Wininger et al., 2009). To wit, this principle is embedded in robot-based assistive technology (Patton and Mussa-Ivaldi, 2004; Kahn et al., 2006; Velliste et al., 2008; Mazzoleni et al., 2014). And while not an explicit requirement for our algorithm, we note that a bell-shaped velocity profile is typical of a healthy actor, and conformity to a bell-shaped template is an indication of motoric recovery (Trombly, 1993; Rohrer et al., 2002).

Methods

Patient Population and Protocol

The data used in this study represent a sample from a larger pool of data collected during the VA-ROBOTICS randomized clinical trial (Lo et al., 2009, 2010; Wu et al., 2016). Participants were seated in the study robot, the MIT-Manus system (InMotion Technologies, Cambridge, MA, USA), which utilized pre-programmed exercise regimens (Aisen et al., 1997). Inclusion and exclusion criteria for the main trial are described fully elsewhere (Lo et al., 2009), but are summarized as follows: inclusion on the basis of index stroke >6 months prior, 18 years of age or older, moderate-to-severe impairment (Fugl–Meyer score between 7 and 38 points, inclusive), cognitive and language acuity to understand the instructions, willingness to avoid new rehabilitation activities during the study, and provision of informed consent; exclusion included circumstances that prevented participation in or completion of the study, co-enrollment in a competing trial, and prior exposure to robotic therapy. No additional criteria were imposed for the purposes of this sub-study. Not all participants provided a complete recorded sample across the full target wheel in the point-to-point movement task; the participants analyzed here are thus a convenience sample of those who performed the same task at least once in their time in the trial. We analyzed movements performed in a cyclic point-to-point movement task where participants moved their affected arm within the transverse plane, in order to place a cursor within a target on a computer screen above the robot. The target moved in a predictable fashion around eight directions (N, NE, E, SE, S, SW, W, and NW); for each direction, there was a “toward” target (e.g., North toward) and “back” to center (North back) movement, yielding 16 movements per cycle. Participants recorded five cycles (80 total movements) per visit. The robot’s operating system was programmed to provide kinematic data in separate files on a per-movement basis, with the movement direction indicated in the file name. Data were sampled at 200 Hz and were not processed prior to file writing.

Data Acquisition and Processing

Raw planar position data (x- and y-position versus time) were conditioned via Tukey’s 3R smoother (Bryc and Peligrad, 1992), differentiated to instantaneous velocity, converted into a one-dimensional instantaneous velocity via Euclidean distance calculation, and smoothed again. The smoother used here is “3R” meaning that it computes a replacement value based on running medians of length 3; the process is repeated until convergence (Tukey, 2000). Data conversion into tab-delimited files was performed using a custom routine in Octave numerical computing environment (v3.2.4); all data processing and algorithmic activities were performed using custom routines in the R statistical software (v 3.3.1).

Algorithm

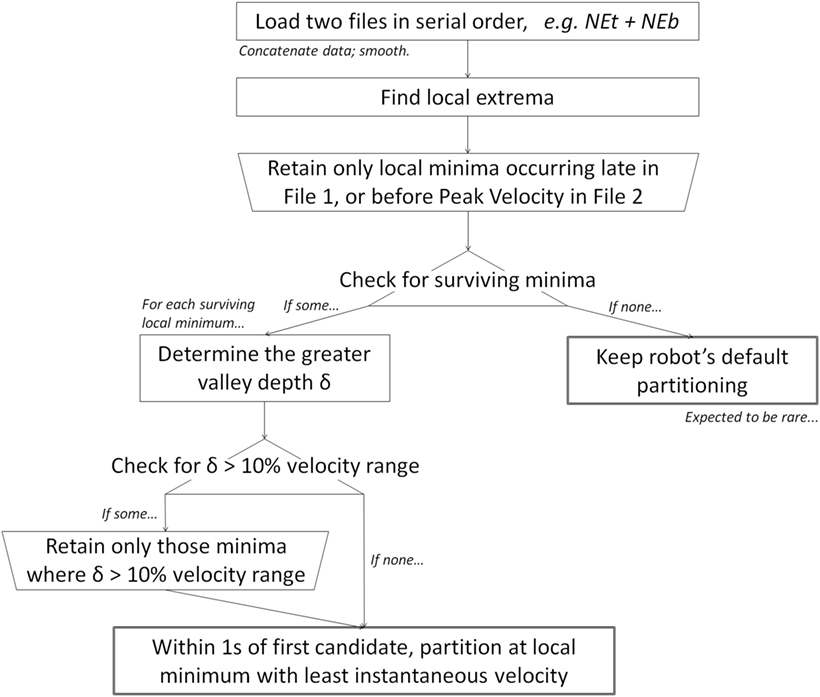
The objective of our algorithm is to identify landmarks in the kinematic record where the subject is most likely to be transitioning between targets. Our main assumption is that targeted movements begin and end at a local velocity minimum (Jeannerod, 1990; Culmer et al., 2009; Perfetti et al., 2011). Our two secondary assumptions are (1) patients’ true transition point is most likely to be found after the file terminus and not before; and (2) the local minimum associated with the true transition point is a deep valley offset by relatively large decrease and/or large increase in velocity.

Data files were loaded two-at-a-time, in serial order, i.e., Northeast toward + Northeast back (NEb), then NEb + East toward, etc. As a precaution against artifact, data were smoothed with an additional local polynomial regression fitting (LOESS) with a 0.5-s (100-sample) window.

Following the main assumption: local maxima M_j and minima m_k were extracted as ordered pairs of time and instantaneous velocity:

\begin{matrix} M_{j} = & 〈 t_{i}, v_{i} 〉 ∋^{'} \frac{a_{i + 1} - a_{i}}{t_{i + 1} - t_{i}} = - 2 : a_{i} = \frac{v_{i + 1} - v_{i}}{t_{i + 1} - t_{i}} j = 1 \dots J \\ m_{k} = & 〈 t_{i}, v_{i} 〉 ∋^{'} \frac{a_{i + 1} - a_{i}}{t_{i + 1} - t_{i}} = + 2 : a_{i} = \frac{v_{i + 1} - v_{i}}{t_{i + 1} - t_{i}} k = 1 \dots K . \end{matrix}

The plus-or-minus 2 reflects that this difference is taken over a signed value (value is either +1 or −1, so the difference between adjacent points across a transition will yield ±2).

Following secondary assumption 1: local minima were retained if they occurred late in the first file or prior to the peak velocity of the second file; “late” is defined as within 0.5 s (100 samples) of the first file terminus.

Following secondary assumption 2: for each local minimum in the velocity versus time portrait, the greater valley depth, δ, was calculated as the maximum of (i) the vertical distance, d₁, from nearest preceding local maximum versus (ii) the vertical distance, d₂, from nearest succeeding local maximum, i.e., δ = max(d₁, d₂), where

\begin{matrix} d_{1} = & v_{j} - v_{k} ∋^{'} | t_{k} - t_{j} | = \begin{matrix} m i n \\ j \in J \end{matrix} : t_{k} > t_{j} \\ d_{2} = & v_{j} - v_{k} ∋^{'} | t_{k} - t_{j} | = \begin{matrix} min \\ j \in J \end{matrix} : t_{j} > t_{k} \end{matrix}

where ⟨t_j, v_j⟩ = M_j and ⟨t_k, v_k⟩ = m_k. Any minima such that δ was greater than 10% of the total range of velocity across the two files were retained as candidate transition points (Figure 2). Given the prioritization of the main assumption, if there were no “substantial” minima, then the set of candidate minima was re-defined to include any local minima. Figure 2 highlights identification of d₁ and d₂ for one local minima (at time approximately t = 1.2 s), but per secondary assumption 1, the local minima at t = 1.5 and 1.9 s would both yield their own d₁ and d₂s.

FIGURE 2

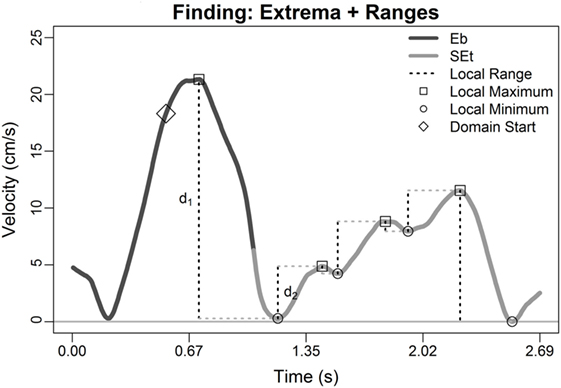
Figure 2. Illustration of Steps 1–3: two serial movement records are concatenated; all local extrema were extracted (circles and squares; Step 1) and retained if occurring later than 0.5-s before the terminus of file 1 (diamond) or before the peak velocity in file 2 (last square; Step 2), and local min–max ranges were calculated (Step 3, dashed lines). Direction annotations in figure legend is Eb = East back (from East target back to center target), and SEt = Southeast toward (from center target toward Southeast target); see Section “Patient Population and Protocol.”

Among all surviving candidate minima, the following rule was used to identify the transition point.

Within 1 s (200 samples) of the first candidate minimum, the single candidate with the least absolute instantaneous velocity was retained as the transition point. If multiple candidates shared the same instantaneous velocity value, then the earliest candidate was retained.

If there were no local minima whatsoever, the original file terminus was retained as the transition point.

We summarize our algorithm in Figure 3.

FIGURE 3

Figure 3. Flowchart summarizing partitioning algorithm.

Analysis

In order to measure both the extent to which target-partitioned files deviate from expectation, and also the effectiveness of our algorithm, we extracted several features from the raw- and re-conditioned data including average velocity and instantaneous velocity at movement onset and cessation. Additionally, given the template of an approximately bell-shaped velocity profile, we measured the goodness-of-fit of a second-order polynomial function to log-transformed velocity data via the coefficient of determination (R²). Lastly, we report on the number of samples relocated to a new file. All hypothesis tests were performed via a paired t-test on samples.

Results

Descriptive Statistics

A total of 16 participants met our inclusion criteria; several participants met these criteria on multiple days, yielding 40 datasets total. The participant pool at the time of study entry was 14 (88%) male, 65.8 ± 14.9 years of age, 63.4 ± 47.5 months poststroke, 23.9 ± 10.1 Fugl–Meyer scores.

Analysis

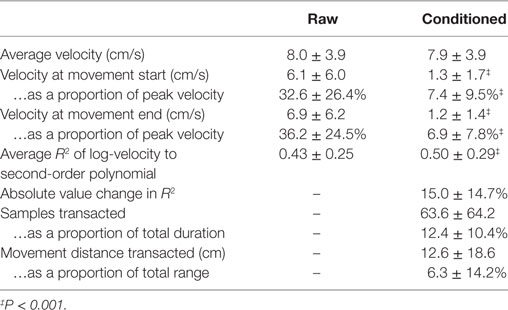
Results from our analysis of the data packaged by the robot (“raw”) and re-packaged by our algorithm (“conditioned”) are shown in Table 1.

TABLE 1

Table 1. Summary statistics for before and after file reapportionment.

Average velocity does not change following adjustment of the file boundaries (8.0 ± 3.9 versus 7.9 ± 3.9 cm/s, P > 0.05). Raw data files started and ended with high velocities: 6.1 ± 6.0 and 6.9 ± 6.2 cm/s, respectively, equivalent to 32–36% of the total velocity range. Following file reapportionment, start- and end-velocities were reduced to 1.3 ± 1.7 and 1.2 ± 1.4 cm/s, respectively, equivalent to 7% total velocity range.

The average improvement in fit to a bell-shaped profile was 16.3% (0.50 ± 0.29 versus 0.43 ± 0.25, difference greater than zero per paired t-test: P < 0.001); however, the absolute value of change was >30% (|ΔR²| = 0.15 ± 0.15), showing that some raw data, when partitioned by the robot, yielded deceivingly large R², when the movements, where not quite so bell-shaped. While the improvement of the fit to the bell-shape was interesting to us, we find the absolute value of change to be more compelling: a per-movement change of more than 30% suggests a remarkable susceptibility to error in assessing motor performance by this metric when the data are partitioned by target achievement as opposed to the nearest movement reversal. The high SD indicates that this effect is highly variable cycle-to-cycle and that the effect of re-partitioning does not incur uniform change on extracted features. We note the substantial transfer of data between files: 12.4 ± 10.4% of data were re-allocated to different files, corresponding to 6.3 ± 14.2% of total movement range.

In Figure 4, we show two complete exemplars before and after re-partitioning.

FIGURE 4

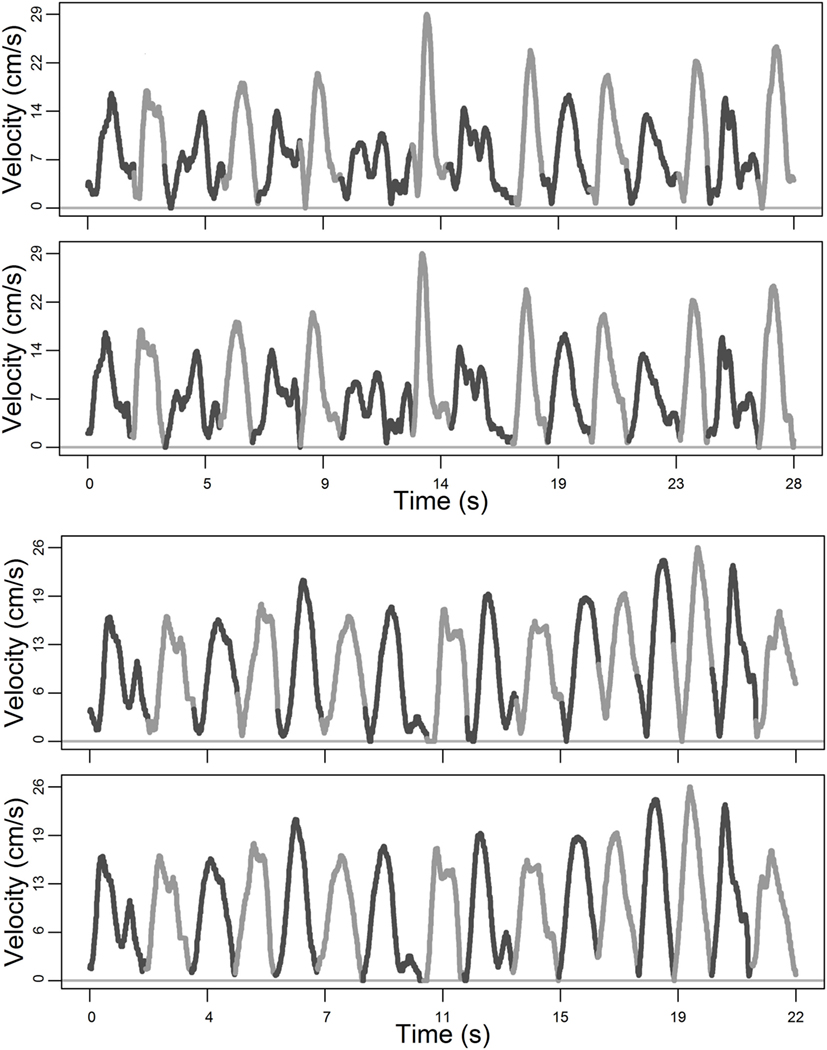
Figure 4. Exemplars of complete target cycles: 16 movements each. Top panels show movement cycles as partitioned by the robot; bottom panels show movement cycles conditioned post hoc: all boundaries coincide with local minima.

In Figure 5, we show two exemplars plotted in the plane of movement, i.e., x and y within the transverse plane, demonstrating conditioned data partitioned at movement reversals.

FIGURE 5

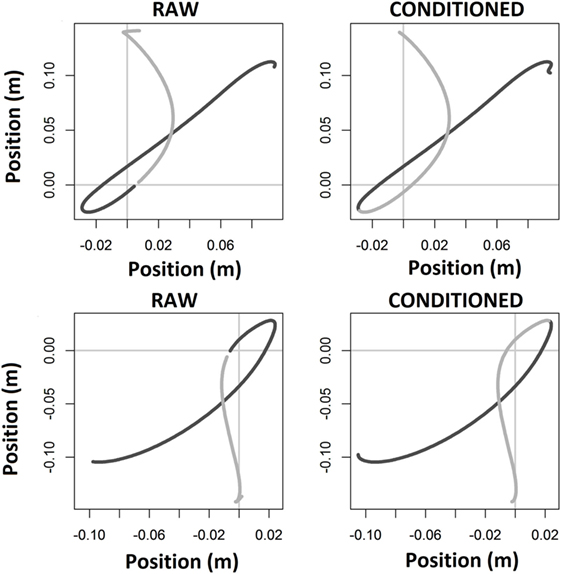
Figure 5. Exemplars in the plane of movement: data from two files are plotted. Raw data (left) show partitioning within the bounds of center target (data break near origin); conditioned data (right) show partitioning at movement reversals.

Discussion

Importance

There is increasing interest in understanding kinematic movements of the upper-limb in motor-impaired individuals (Averta et al., 2017); while not all studies involve targeted movements, target training is a ubiquitous paradigm in rehabilitation. Furthermore, identification of single movements by velocity threshold algorithms are widely used (Burdet et al., 2000; Yoon et al., 2001; Casellato et al., 2012). To our knowledge, we are the first to raise issue with the convention of imposing a constant time criterion over all movement directions, given that many patients exhibit directionally dependent movement characteristics and propensity to move slowly through a target overshoot. We show that data outputted by a popular, commercially available robot, measuring impaired persons, yield highly counter-intuitive file sets when partitioned according to target presentation does not yield data files partitioned near movement reversals. Despite the erratic nature of data collected from impaired individuals, we obtained robust results through a simple algorithm involving straightforward calculations with only three assumptions. This study is most relevant to those extracting kinematic data from rehabilitation robots situated in a clinic with moderately to severely impaired clientele: a fixed and brief time criterion for target achievement may coincide with movement reversals in highly skilled and healthy individuals, but we should expect that for most patients with neurological deficit, movement reversals will lag target achievement across some or all of the targets.

Advantages and Limitations

This method is intended to allow for enhanced accuracy in extracting data from biomedical robotic devices. In any scenario where it is desirable to analyze motor skill on a per-movement basis, this method will allow for high-fidelity partitioning of data from movement start to movement end, not per se from target presentation to target achievement. The main limitation of this method is that it requires three embedded assumptions about the velocity profile: onset and cessation of movement at velocity minima; transition of movement at the point of target achievement or after; and the local minimum will occur in a “deep valley” where at least one “valley wall” is tall (10% of total velocity). While the first two assumptions are intuitive and compatible with commonly held expectations of human motor performance, the third assumption is potentially problematic, as the optimal threshold may change, depending on the sampling rate, filter characteristics, and raw performance of the human actor. While within our own dataset, δ equivalent to 10% velocity range provided adequate threshold, we recognize that this is at best a rule-of-thumb and that threshold selection may be empiric from study to study. Nevertheless, we believe that this is a feature of the algorithm that is easy to modify ad hoc and does not impact interpretation of results.

Regarding our assumptions, it is instructive to contemplate scenarios where the assumptions come into jeopardy. Given the apparently universal precept that movement epochs begin and end with—at minimum—a change in movement direction, and more typically, a pause in motion, the assertion of a local minimum in velocity at the movement boundaries seems robust. There may be higher-dimensional movement tasks where high velocity in one dimension obscures a velocity minimum in another dimension, but this may be addressed by selective filtering for minima. On the other hand, there is the implicit expectation here that the target is always achieved. In cases where the target is not achieved, but the user changes direction anyways, this autonomous over-ride will not be detected: it’s the robot’s acquisition of target achievement that guides our algorithm. We believe this to be valid, since the robot-aided rehabilitation paradigm assumes that the user attends to the presented target until achievement, i.e., until such time that the robot presents a new target. Our secondary assumptions are not as straightforward: in particular, the designation of 0.5 s and 10% velocity range as thresholds for winnowing candidate minima was arbitrary, albeit informed from inspection of the data. Surely, there are plausible circumstances where these conditions may prove sub-optimal; we urge vigilance on the part of the investigator, and a willingness to take an empiric approach to threshold setting.

Implications

We do not necessarily suggest that the native data obtained from robots are flawed. However, given the evidence that this problem pervades other studies (Perfetti et al., 2011; Huang and Ahmed, 2014; Muceli et al., 2014), we believe that our findings may add impetus to revisit prior inquiries into directional-specific movement. It is beyond the scope of this paper to speculate on which scenarios may make this issue more likely. Investigators would be well-advised to check their data in all cases to verify their assumptions.

Future Work

Whereas the algorithm presented here is the first of its kind, it remains to be determined whether other approaches may provide yet improved results, particularly on more challenging datasets. Of further interest to the community would be establishing normative ranges for multi-target datasets so that further developments in this arena can be objectively measured against empirical benchmarks. We believe that this algorithm may provide additional tools to those wishing to study the directional dependency of movement exhibited by healthy and impaired actors. While it would be ideal to test the need for this algorithm in healthy persons, such exploration is beyond the scope of this article. However, we speculate that most healthy individuals, given a reasonable task (adequately sized target and adequate target achievement time within sub-maximal velocity range, etc.), would yield data that were suited for partitioning by target achievement: it would be expected that in most cases the actor would have no physiological impediment to stopping on-target.

Summary

In this work, we draw attention to the potential for error consequent from the partitioning of kinematic data obtained from rehabilitation robots: human actors start- and stop movements at low velocity, including severely impaired individuals; at the same time, impaired persons are unlikely to stop on-target. Thus, in target-tracking tasks, it is likely preferable to partition data at velocity minima. In our own dataset, we found that data partitioned according to target presentation exhibited features inconsistent with the basic assumptions of human motor control. Re-partitioning the data resulted in the re-assignment of >10% of data points, but a substantial restoration of boundary conditions to levels commensurate with expectation.

Conclusion

In this study, we identify a problem endemic to robotic tracking of targeted movements in impaired persons: the inappropriately parsed datasets when partitioned according to target presentation in the setting of a constant time target achievement criterion. We propose an algorithm for re-partitioning these data according to finding local minima of velocity near the file terminus, yielding new data series segmented naturalistically in conformance with the assumption that targeted movements begin and end with a movement reversal. We encourage others to consider incorporating a re-partitioning step in analysis of robot data, and in cases where re-partitioning is not undertaken, to justify that the data were partitioned properly by the robot.

Ethics Statement

The study protocol was approved by the institutional review boards at each participating site and the human rights committee at the coordinating center, listed as follows: VA Maryland Health Care System (Baltimore), North Florida/South Georgia Veterans Health System (Gainesville), VA Puget Sound Health Care System (Seattle), and VA Connecticut Healthcare System (West Haven). All participants gave written informed consent prior to study participation. The study was registered on ClinicalTrials.gov (ClinicalTrials.gov identifier, NCT 00372411). The contents do not represent the views of the U.S. Department of Veterans Affairs or the United States Government.

Author Contributions

This secondary study was initially conceived and conducted by MW and AB. Original trial design and operations was overseen by PG and PP. All authors were involved in the drafting and approving of this manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

This study was conducted by the United States (U.S.) Department of Veterans Affairs, Office of Research and Development, Cooperative Studies Program. Additional support for this analysis was through the Veterans Affairs Connecticut Research and Education Foundation.

References

Acosta, A. M., Dewald, H. A., and Dewald, J. P. A. (2011). Pilot study to test effectiveness of video game on reaching performance in stroke. J. Rehabil. Res. Dev. 48, 431–444. doi: 10.1682/JRRD.2010.04.0052

PubMed Abstract | CrossRef Full Text | Google Scholar

Aisen, M. L., Krebs, H. I., Hogan, N., McDowell, F., and Volpe, B. T. (1997). The effect of robot-assisted therapy and rehabilitative training on motor recovery following stroke. Arch. Neurol. 54, 443–446. doi:10.1001/archneur.1997.00550160075019

PubMed Abstract | CrossRef Full Text | Google Scholar

Averta, G., Della Santina, C., Battaglia, E., Felici, F., Bianchi, M., and Bicchi, A. (2017). Unvealing the principal modes of human upper limb movements through functional analysis. Front. Robot. AI. 4:37. doi:10.3389/frobt.2017.00037