A Neural Network-Based Approach for Trajectory Planning in Robot–Human Handover Tasks

Service robots and even industrial robots recently started sharing human workspace for creating new working settings where humans and robots work even hand by hand. On the one hand, this new scenario raises problems of safety, which are being solved by adding suitable sensor batteries to robot control systems, and on the other hand, it entails dealing with psychophysical aspects as well. Motion intention understanding and prediction comes more natural and effective if the controlled movement is biologically inspired. In order to generate biologically inspired movements in a robotic-assisted surgery scenario, where a robotic assistant shares the execution of tasks with, or hands over tools to a surgeon, we designed a trajectory planning system based on an artificial neural network architecture trained on human actions. After the design and training of the neural controller for motion planning, we checked the objective characteristics of the achieved biologically inspired motion as functional minimization (minimum jerk), two-third power law and bell-shaped velocity. The controller was also experimentally implemented by using a redundant serial robotic arm (LWR4+, Kuka, Germany), and it was actually perceived as “human-like” in the majority of cases by naive subjects. The implemented neural-based control strategy provided to be an effective scheme for human–robot interaction control, also by qualitative assessment.

Introduction

Humans can exploit robotic assistance in several professional activities, in which the robots act as coworker in a shared workspace. Robots offer increased precision and accuracy, can empower human strength and stamina, and relieve the human operator from tedious, hard, or dangerous tasks. This is what happens in industrial settings, such as in the automotive manufacturing, where the robot and human can cooperatively work on a common task. The possibility of safely sharing the same environment is guaranteed by the presence of monitoring sensors (Avanzini et al., 2014; Comparetti et al., 2014).

Human–robot cooperation in medical applications (Beretta et al., 2015a,b) can imply carrying objects together (De Momi et al., 2010) or performing object handover. Collaborative robots can be used to share responsibility of surgical tasks, such as those that have been used in orthopedic surgery for bone milling in knee arthroplasty procedures. Jakopec et al. (2003) presented a system with a back-drivable robot with controlled admittance, so that the bone milling was limited to preoperatively defined areas on patient preoperative images. Jacob et al. (2013) presented a speech- and gesture-based robotic scrub nurse for surgical instruments detection, picking, and delivery into the surgeon hands.

In order to facilitate the collaboration between human and robotic operators, several studies have focused on human–robot interaction analysis, which plays a fundamental role in robotic handover tasks. Strabala et al. (2012) proposed a coordination structure for human–robot seamless handovers that considers the physical and social–cognitive aspects of the interaction separately. There are unconscious processes that induce humans to perceive another agent as interaction partner. One of such mechanisms investigated by Sciutti et al. (2012) is related to the “motor resonance,” i.e., the automatic activation, during actions perception, of the perceiver’s motor system. In their review, the authors synthesize that, despite non-human-like behaving agents can elicit the same neurophysiological effects, motion interference and priming are influenced by the appearance and by the types of kinematic motion adopted by the robotic agent (Chaminade and Cheng, 2009). This observation leads to the assumption that humans would interact more naturally and effectively with robotic agents which evoke a higher “motor resonance” [e.g., in the “chameleon effect” (Chartrand and Bargh, 1999)].

Investigations on human multi-joint arm coordination in reaching movements in a plane have suggested that the end point follows a straight path with a bell-shaped velocity profile (Flash and Hogan, 1985). In this respect, Shibata et al. (1997) analyzed the handover process between two humans suggesting to set velocity bell profile to ensure the best acceptance of robots in human–robot cooperative tasks. Similarly, Huber et al. (2008) demonstrated that human reaction time is shorter when the robot trajectory follows a minimum-jerk profile. More recent studies tried to increase the handover efficacy improving the intention communication between the robot and the human (Cakmak et al., 2011a,b).

Resembling the biologically inspired strategies in robotic control also applies to arm redundancy management strategies. Motion control theories of synergies (Santello et al., 1998), alternatively seen as uncontrolled manifold (Scholz and Schöner, 1999), and minimization of the joint-torque change (Uno et al., 1989) or a mix between the absolute work of torques and the integrated squared joint acceleration (Berret et al., 2011), have been applied to serial robotic arms. Secco et al. (2001, 2004) solved the redundancy problem arising from the presence of three links by assuming that there is a constant ratio between the second and the third joint motion, and Secco and Magenes (2002) implemented a multilayer perceptron for dynamic control of a 3 degrees of freedom finger. Rigotti et al. (2001) replicated 3D human-like trajectories of human arms by computing the weights of a neural network (NN) system trained using actual motion data captured with a spatial localizer, without involving a mathematical model of either direct or inverse kinematics. More recently, Zanchettin et al. (2013) derived a simple relationship between the hand pose and the swivel angle in the acquired motion of the human arms and applied this theory to the control of a robotic arm.

In this paper, we investigate the effectiveness of a redundant robotic arm in imitating the human motor strategies during reaching tasks, which is part of the control strategy envisaged for a robotic surgeon assistant (e.g., a robotic scrub nurse). The problem has been simplified, and the robot has to replicate the human wrist motion (Cartesian position of the end effector), while handling objects to the coworker. Even if the robotic arm is redundant, we disregarded redundancy optimization in the kinematics methods, which will be investigated in future developments.

The aim of the paper is the implementation and performance assessment of a neural trajectory planning module able to generate biologically inspired motion planning so to ease the interaction of the robot and the human during handover task.

Materials and Methods

In order to develop our surgical robotic assistant, a human subject is instructing the robotic arm to replicate his/her kinematics strategies in performing reaching tasks for object handling. A NN is then trained to generalize such set of trajectories, given the starting and end points data as input information. The NN output is supposed to be the via-points of the reaching trajectory.

The “biologically inspired” generated trajectories (which we refer to as “human-like”) were then used for trajectory planning of a serial redundant robotic arm, acting as robotic scrub nurse in our envisaged collaboration scenario.

Experimental Data Acquisition and Processing

A subject (male, left-handed, 25 years old, 186 cm tall) was instructed to perform reaching motions in a natural manner, as if he was handling surgical instruments to the surgeon, from a starting point to a target position. This study was carried out in accordance with the recommendations of our institution with written informed consent from the subject in accordance with the Declaration of Helsinki. The following short (distance 30 cm) and long (distance 50 cm) reaching movements were performed (Figure 1):

– eight short movements in the horizontal plane (two perpendicular and two parallel to the long table axis, and four diagonal)

– eight long movements in the horizontal plane (two perpendicular and two parallel to the long table axis, and four diagonal)

– eight short movements upward (15 cm high, 30 cm long)

– eight short movements upward (30 cm high, 30 cm long)

– eight long movements upward (15 cm high, 50 cm long)

– eight long movements upward (30 cm high, 50 cm long).

FIGURE 1

Figure 1. Schematic drawing of the reaching motion acquisition experimental setup.

All movements started at zero velocity and ended at the target at zero velocity. The motion was captured using a Kinect camera (Kinect, Microsoft Corporation), whose accuracy depends on its distance from the measured object (Khoshelham and Elberink, 2012). According to Karan (2015), the accuracy of a Kinect camera spans from 6.5 to 10 cm without sensor calibration for depth distance between 2 and 3 m. The camera calibration method introduced by Zhang (2000) and Zhang (2011) allows reducing the error between the depth and the RGB sensors, leading to an overall error between 1.5 and 3 cm in the same depth range (2–3 m). In our setup, the Kinect sensor was attached to the ceiling, and the mean distance between the sensor and the subject was approximately 2.5 m.

Acquisition of the subject’s wrist position was performed using the OpenNi framework of the NITE package (Primesense™, Inc., NiTE Middleware) implemented as a Robot Operating System (ROS, Fuerte release) node. The NITE package allows the user to track the positions and orientation of the joints of multiple subjects. The recordings were performed at 30 Hz with an average duration of 2 s. All movements were performed twice, and, after data selection, 91 trajectories remained, as 5 were too noisy to be used. Before processing the data, a cubic smoothing spline using de Boor’s algorithm was applied to the data to smoothen the trajectories and reduce measurement noise (de Boor, 1978).

Neural Network Architecture

Our NN architecture is based on the assumption that a reaching motion kinematics can be completely described by the initial and final Cartesian position of the subject wrist (end effector). The NN architecture, fed with three inputs, namely, the coordinates of the desired ending point, computed the “biologically inspired” trajectory via-points, and the time required for its execution. The vector from start to end point was initially translated to [0, 0, 0]. When the trajectory was computed, it was translated back again to begin in the actual starting point.

Three separate Feedforward Perceptron Neural Networks (NNs) were used to learn the acquired trajectories: one for the x-axis, one for the y-axis, and one for the z-axis. Each network had one input, which was the x, y, or z coordinate of the target point. The topology of one of the three (identical) NNs can be seen in Figure 2. A fourth network was trained with the three coordinates of the end point and the time required as desired output. Each network was trained by supervised learning. Gradient backpropagation with Fletcher–Reeves restarts was applied to update the network weights and bias values (Fletcher and Reeves, 1964).

FIGURE 2

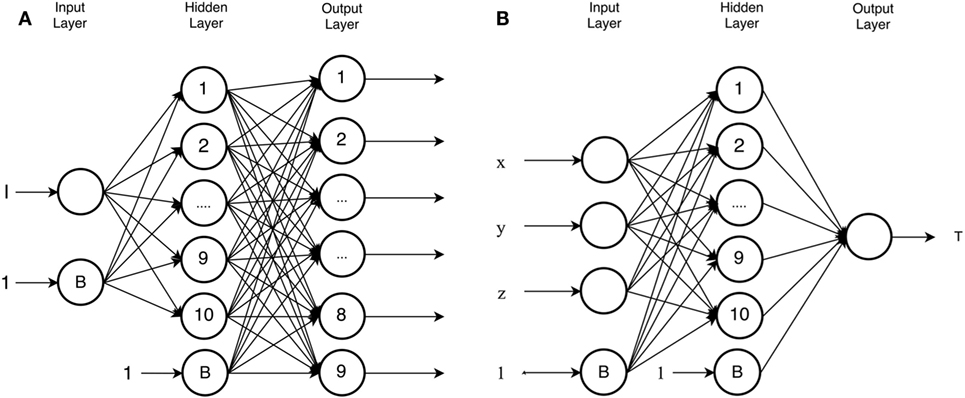
Figure 2. Topology of the neural networks. In (A), “I” is the target x, y, or z coordinate. The architecture for the three networks is the same: 1 input, 10 neurons in the hidden layer, and 10 via-points as output. The neurons between the layers are all interconnected and the hidden layer and the output layer have a bias input. The neural network estimating the time is given in (B) and has three inputs (x, y, and z of end point), 10 neurons in the hidden layer and generates the total time as output.

Each network returned nine via-points as output. This number of outputs is a trade-off between accuracy (more via-points mean the network is more accurate) and the number of acquisitions required to train the network (more via-points require more datasets to train the network). The acquired reaching trajectories were down sampled to 11 points: one final point (input), 9 via-points (output) plus the first additional point fixed to [0, 0, 0]. The number of neurons in the hidden layer was determined varying the number of neurons and assessing the generalization capabilities of the network. We defined 10 neurons as the best trade-off.

The target point, used as input, is added as a final point to the trajectory and everything is translated to the start point. A smooth trajectory is created by applying a natural cubic b-spline to approximate the via-points (de Boor, 1978). To ensure zero velocity and acceleration at the starting position and at the target position, the coordinates these two points were artificially triplicated in the same position.

In order to train the NN, the total acquired dataset was divided in:

– Training set (81 trajectories)

– Validation set (10 trajectories)

– Testing set (105 trajectories: 7 trajectories, which the subject repeated 15 times, were additionally acquired)

The training set was used to update the neurons weights. During training, the error on the validation set was monitored. Overfitting on the dataset makes the error on the validation increasing. If the error on the validation set kept on increasing for a predefined number of iterations, the NN returned to the weights for which it had the lowest validation error. When the NN converged to its final configuration, the testing set was used to assess its actual ability to generalize.

The testing set was obtained by defining seven additional targets. The targets were chosen to generate trajectories comparable to the trajectories the network was trained on: in-plane motions (traveled distance 40 cm) in multiple directions, and motions to a higher target in multiple directions. Two of the target points were in the horizontal plane, and five motions were directed toward a higher target. The subject made 15 reaching movements to each target, and these were captured using the above-mentioned setup with the Kinect. All trajectories were down sampled to 11 points and interpolated using the above-mentioned b-spline. For each target, the mean trajectory was calculated, computing the mean of the 15 splined trajectories. For each trajectory, the distance in terms of root mean square error (RMSE) with respect to the mean trajectory ($\overline{x}$, $\overline{y}$,and $\overline{z}$) was calculated for each via-point i (Eq. 1).

$\text{RMSE}=\sqrt{\frac{{\displaystyle \sum _{i=1}^N{(x_i-{\overline{x}}_i)}^2+{(y_i-{\overline{y}}_i)}^2+{(z_i-{\overline{z}}_i)}^2}}{N}}$ (1)

where N is the number of via-points (9). The RMSE gives a measure for the variability in the human–motion trajectories.

Seven target points were given as input for the NN. The RMSE of the NN-generated trajectories was compared with the RMSE of the human motions to see whether the error of the network was comparable with human motion variability.

The aforementioned network was trained using MATLAB’s 2015 NNs toolbox (Mathworks©).

Robot Control

A graphical interface was implemented to analyze the trajectories generated by the network both in Cartesian and joint spaces, considering the workspace and joint limits of the robot arm (LWR4+ from KUKA, Germany) used for the experiments (Figure 3). The inverse kinematic function used the algorithm of Shimizu et al. (2008). The redundancy of the robot arm was not employed, and the corresponding redundancy parameters were kept constant at appropriate values.

FIGURE 3

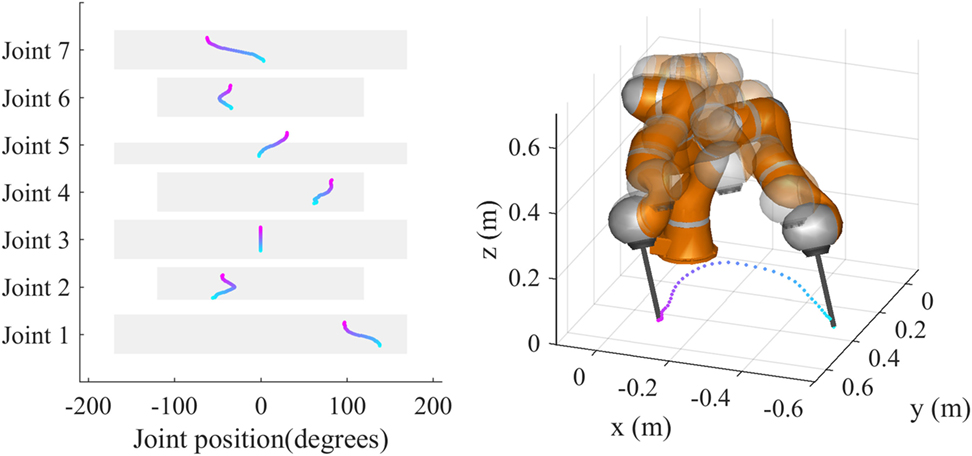
Figure 3. The graphical interface for trajectory simulation. On the right, the Cartesian trajectory computed by the trained NN can be seen. The left plot presents the joint space trajectories for all the seven joints, from the start point (cyan) to the destination (magenta). The width of the gray rectangles represents the available range of each joint, while their height represents normalized time (0–1).

The movements acquired by the Kinect were transformed into the Robot reference frame using the calibration algorithm based on the method by Zhang (2000). The mean calibration residual, computed as the mean error between the four corners of a checkerboard and the pose of the tool tip of the robot touching the same points, was 0.0152 m, a value compatible with the Kinect expected accuracy.

The software architecture developed for the experiments encompassed three parts: trajectory generator, kinematics, and communications, all written in C++ as OROCOS (Open Robotics Control Software, http://www.orocos.org/) components. Communication with the robot hardware controller was achieved through real-time Ethernet at 100 Hz. Given a valid Cartesian destination, the software generated a trajectory from the current pose of the robot to the destination and sent the corresponding joint positions to the robot. The current pose of the robot was used as starting point. The target point was then mapped into the robot reference frame, and the target position was fed into the NN. The trajectory duration was scaled to half-speed to ensure that the joint velocity limits were respected.

System Validation

All the movements, both acquired and generated by NN, laid mainly into a plane variably oriented in the space. We fitted a plane to the data by using the principal component analysis (PCA) to extract the principal components, and project the trajectory on the plane perpendicular to the first dominant component. In this way we mapped (x, y, z) → (u, v, 0). In biologically inspired trajectories, the tangential velocity is related to the curvature with a non-linear proportional law, and the ratio between the natural logarithms of the two is roughly equal to 2/3 (Lacquaniti et al., 1983; Wann et al., 1988). The tangential velocity v was computed using the first order adaptive windowing (FOAW) (Janabi-Sharifi et al., 2000), whereas the curvature C(t) was computed as:

$C(t)=\frac{1}{R(t)}$ (2)

with R curvature radius computed as:

$R(t)=\frac{{\left[{\left(\frac{du(t)}{dt}\right)}^2+{\left(\frac{dv(t)}{dt}\right)}^2\right]}^{\frac{3}{2}}}{\left|\frac{du(t)}{dt}\frac{d^{2}v(t)}{d{t}^2}-\frac{dv(t)}{dt}\frac{d^{2}u(t)}{d{t}^2}\right|}$ (3)

According to the 2/3rd power law, the relationship between curvature and velocity is given by:

$v(t,\beta )=K{\left(\frac{R(t)}{1+\alpha R(t)}\right)}^{1-\beta }$ (4)

where α, β, and K are positive parameters that have to be estimated from the trajectory. β is the 2/3 parameter that defines the power law, whereas α can be usually set to 0. The parameter K is generally estimated by successive approximations. Equation 4 as rewritten by Wann et al. (1988) is:

$\log v(t)=\log K+\frac{1}{3}\log R(t)$ (5)

In this way, the parameter K does not influence the relation between v and R, as it is only a constant factor added to a proportional relationship. The proportional relationship between the logarithm of the velocity and the logarithm of the radius of the curvature can be identified fitting a line on the points. The slope of the line characterizes how much the motion is similar to a human motion. It is, in fact, proven that a human motion produces a ratio of 1/3 between the logarithm of the velocity and the logarithm of the radius of the curvature.

Smoothness Index

The motion jerk defines the roughness of the movement: the lower the jerk, the smoother the trajectory. In order to compare trajectories with different lengths and duration a “smoothness” index (S-index) has been defined as (Teulings et al., 1997):

$S=\sqrt{\frac{T^5}{L^2}{\displaystyle \sum _{i=1}^N{\Vert \frac{d^3{u}_i}{d{t}^3}+\frac{d^3{v}_i}{d{t}^3}\Vert }^{2}dt}}$ (6)

where T is the total time for each trajectory and L the length of the trajectory. The motion is fitted on a 2-D plane with u and v having the same meaning as in Eq. 3, i being the i-th sample and N the overall number of samples. The duration time for the human trajectories is obtained from the acquisitions. The time for the NN-generated trajectories was defined by the NN itself. We compared then the S-index of the trajectories generated by the NN with the S-index of the acquired trajectories.

Experimental Protocol

Ten healthy naive subjects (four women, age between 21 and 29 years) were enrolled to participate to the experimental qualitative evaluation of the trajectories performed by the lightweight robot (LWR4+, Kuka). Written informed consent was obtained from each participant in the study.

The robot arm was covered, so that the subjects could evaluate the trajectory performed by the end effector only (see Figure 4), without considering joint kinematics. The subjects, seated at a distance of 3 m from the robot arm and wearing a soundproof headset in order not to be influenced by the robot motor noise, were instructed to classify the 20 randomly presented reaching trajectories as if they perceived them as “biologically inspired” or “non-biologically inspired.”

FIGURE 4

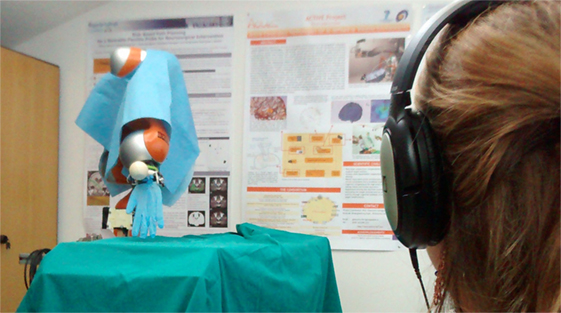
Figure 4. Experimental setup. The subject was seated at 3 m distance from the robot arm. The human-like and the non-human-like trajectories were performed in a random order (10 human-like and 10 non-human-like). The subject was instructed to determine whether the performed trajectory was human-like or non-human-like. A noise-reducing headset is used to prevent the subject from being influenced by the robot motor noise.

For the biologically inspired trajectories, the time duration was defined by the NN. The velocity profile was defined using the before-mentioned cubic spline (de Boor, 1978) approximating the points. For the non-biologically inspired trajectories, the maximum velocity (following a trapezoidal profile) of the robot was set as 0.3 m/s, while the maximum acceleration was 0.9 m/ s². Time duration was automatically defined by the length of the trajectory and the maximum velocity and acceleration defined. The motions were generated using the same starting and ending point for each couple (biologically and not biologically inspired) of trajectories. Examples of trajectory and velocity profiles for both motions are shown in Figure 5.

FIGURE 5

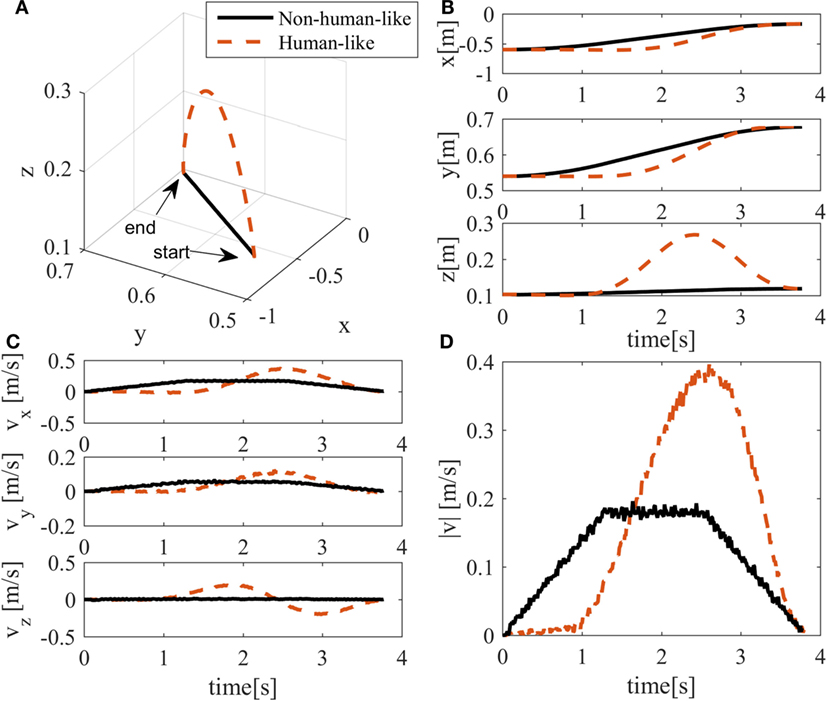
Figure 5. Trajectory characteristics for the experimental setup. Black solid lines represent the non-human-like trajectory, whereas orange dotted lines represent the neural network-generated human-like trajectory. In (A), the 3D-trajectory is shown. (B) shows the position for each axis in time. (C) shows the velocity in the three axes, whereas (D) shows the module of the velocity.

The percentage of correct and wrong classifications was assessed (in terms of true/false positive/negatives) and the overall classification accuracy estimated. Trajectories and velocity profiles performed by the robot end effector were also acquired at 100 Hz using ROS package.

Results

Simulation Results

Testing Trajectories

The characteristics of a human trajectory are shown in Figure 6 compared with those generated by the NN, given the target point as input. The network also generated the movement duration. For this trajectory, the time generated by the network was longer than the measured human trajectory duration.

FIGURE 6

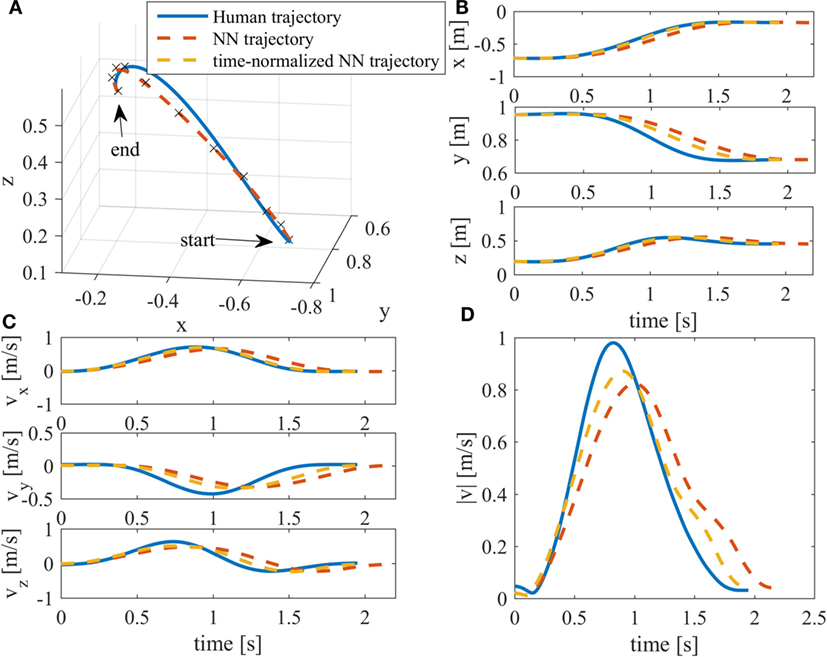
Figure 6. Human trajectory compared with the trajectory generated by the NN. The solid line represents the acquired trajectory, and the red-dashed line represents the neural network-generated trajectory. The 3D plot of the trajectories is given in (A) [the black crosses in plot (A) represent the via-points generated by the neural network] the positions in (B), the velocities in (C), and the velocity module is given in (D). It can be seen that there is a small error in the time generated by the network, the trajectory lasts longer. In order to assess the performance of the network disregarding lag, the normalized trajectory is also shown (yellow dotted line). The normalized trajectory represents the original trajectory more accurately. The RMSE computed for this trajectory is 3.2 cm.

The RMSE between the NN output and the subject acquired mean trajectories and between all the subjects reaching trajectories and the mean trajectory for each target point are reported in Table 1. Network RMSE performance is comparable with the subject’s motion variability around the mean trajectory.

TABLE 1

Table 1. RMSE of the seven testing trajectories and RMSE of the neural network trajectories with respect to the acquired mean trajectory.

2/3rd Power Law

Figure 7 shows the logarithmic plot of the velocity samples versus trajectory curvature computed for trajectories generated by the NN. Ideally, the slope of the interpolated line should be 1/3 [that means the motion is in accordance with the 2/3rd power law, see Eq. 5]. The slope of the fitted line in this case has been found to be 0.3127. The slopes and the related R² values of all the trajectories are reported in Table 2. Except the first two cases, the tested trajectories satisfied the biological trajectory criterion of the power 2/3.

FIGURE 7

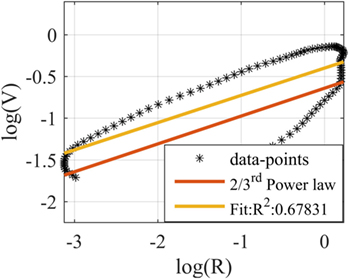
Figure 7. Logarithm of velocity (V) (meter per second) versus logarithm of curvature radius (R) (meter) for one of the seven trajectories generated by the NN. The two-third power law line is plotted in red and has a slope of 1/3. The yellow line is a fit of the data points. The slope of the fitted line is 0.3264. Similar results were obtained for the other testing trajectories, as can be seen in Table 2.

TABLE 2

Table 2. Fit characteristics of the neural network trajectories to 2/3rd power law.

Smoothness Index

S-index (Eq. 6) values are shown in Figure 8 as resulting from the testing trajectories. As it can be seen, the smoothness of the trajectories generated by the network trajectories shows values, which are compatible with the results expected from human trajectories, being below or close to their median smoothness. The biologically inspired smoothness index for the first two trajectories resulted to be higher than the smoothness index computed for the other trajectories. The first two trajectories are indeed shorter than the other five, but were performed in about the same time span. For these two trajectories, the network had a relatively lower smoothness index, because the network created a longer path about lasting approximately the same time and in consequence of this, for the Eq. 6, a smaller S-index is indeed expected.

FIGURE 8

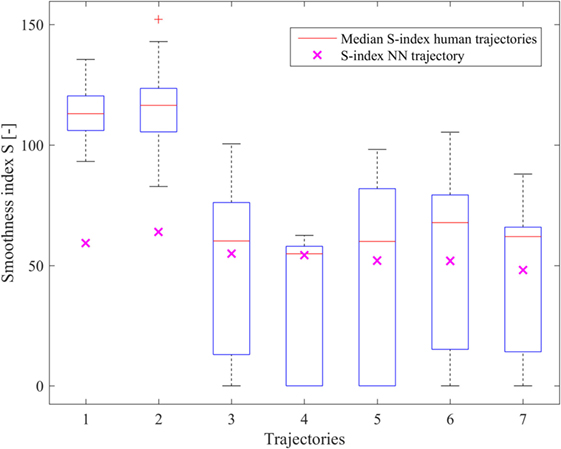
Figure 8. The smoothness index (S) for the seven groups of test trajectories. Each test trajectory was repeated 15 times by the subject. The variation in the smoothness index for the human motion is represented by the box plots. The lower bound of the box represents the 25th percentile, while the upper bound marks the 75th percentile. Outliers are marked with a “+.” Indicated with a purple cross is the smoothness index for the neural network-generated trajectories.

Qualitative Experimental Results

Table 3 represents the confusion matrix (percentages of true and false positives and negatives) for the test performed by the 10 naive subjects, who blindly evaluated whether the performed motion was biologically inspired or not. There was a great variability in subjects’ perception of the type of motion, being the false negative ratio 26% and the false positive one 31%; anyway, the overall accuracy index was quite high: 71.3%.

TABLE 3

Table 3. Confusion matrix for trajectory recognition.

Discussion

Robotic assistance applications have increased in recent years, being robot able nowadays to safely share the workspace with humans. The acceptance of robots as coworker has therefore gained outmost importance, being them less prone to error and fatigue and able to complement human work. This paper presents a neural controller approach generating “biologically inspired” type trajectories for a robotic scrub nurse in order to increase the effectiveness of human robot interaction, as per the assumption made by Chartrand and Bargh (1999). Bisio et al. (2014) previously demonstrated that the properties of the observed action influence coworker motor response in a sort of “motor contagion.” In the operating room, during interventions, surgeon assistants are asked to properly handle the right instrument at the proper time (trying even to anticipate the actual request), so that the surgeon can keep attention on the surgical field, while receiving the new instrument. Biologically inspired kinematics will allow a more natural interaction, maximizing the handover gesture efficacy. The approach followed in this paper is the “learning from imitation” by exploiting the generalization capability of artificial NN.

The NNs architecture here presented, which was trained with real human trajectories, has shown to be able to approximate human behavior. Given target points (start and end positions) in the workspace, the networks reproduced the path and the bell-shaped velocity profile of the human, which is expression of jerk minimization. Given the same targets, the network residual errors (around 3 cm) have the same order of magnitude of the subject’s variability in performing similar targeting gestures and also the same order of magnitude of the error of the tracking system used for motion capture.

The obtained kinematics could be considered “biologically inspired” since it fits some major motor control invariants. One is the ratio between the logarithm of the velocity and the logarithm of the curvature that is approximately 1/3 as mean value for the testing trajectories. Also, in the NN-generated trajectories, the smoothness well aligns with the median value achieved by human performing the same reaching movements. The errors with respect to the ideal behavior have different sources, among which the motion capture system accuracy, which is co-responsible of trajectories residual error. In fact, in order to train the network, we acquired the subject motion using a low-cost unobtrusive motion tracking system (Kinect, Microsoft). Such device allows acquiring the human joints kinematics using an open-source framework. Despite having the possibility of tracking the entire pose of the training scrub nurse, we considered only the position of the wrist, for the sake of simplicity- and accuracy-related issues. Accuracy can be easily improved with Kinect 2 (still not cumbersome at all and widely available at low cost) or with more expensive motion capture systems based on passive or active markers. The other not perfect result, i.e., the 2/3rd power law, can be related with the nature of trajectories, which are not oscillatory (circles, ellipses, Lissajous figures, etc.) as in the papers, which observed first the phenomenon (de’Sperati and Viviani, 1997). The boundary effects (also related to initial and final speed and curvature) can have indeed a strong influence on the results, which indeed do not depend on the human likeness of the trajectories.

The qualitative experimental evaluation was aimed at assessing the perception of naive users on the biologically inspired trajectories performed by a serial anthropometric arm. Previously, in order to measure subject action perception relationship, Bisio et al. (2014) measured the velocity of human motion performing gestures after observing a humanoid robot performing biologically and non-biologically inspired types of movements, while Huber et al. (2008) measured instead the subject interaction in terms of reaction time and in terms of their personal qualitative judgment of the trajectory biologically inspired characteristics.

Our experimental tests on motion perception showed that users, focusing their attention on the robot end-effector motion, could effectively perceive the network-generated trajectories as biologically inspired. Further analysis will be directed toward the assessment of human reaction time as consequence of the robot motion nature, in order to strengthen our hypothesis on the effectiveness of human robot cooperation. The residual confusion in the assessment by the observer can be attributed to the fixed orientation of the wrist and to the lack of visible joint kinematics (actually masked) that was not learned by the system. Future work will encompass both the wrist orientation learning and the optimization of the redundant robot null-space resembling human optimization strategies, such as the minimization of joint-torque change and synergies theories. Thus, the robot behavior will more closely resemble a biologically inspired motion, increasing the surgeon acceptance of the robotic coworker. Additional benefit of human-like motion planning is the fact that smoothness preserves life of robot motors as well.

Future developments will include also an improvement of trajectory description, by increasing the number of estimated via-points. This will be pursued by increasing the number of training trajectories as well as their variability in space and among different performers. Such a huge corpus of data, inherently increasing incrementally with subsequent works of the same or other authors, will be the starting point for a database for training and testing data made publicly available. A further application of the method is the robotic rehabilitation (e.g., for stroke patients) by creating haptic tunnels consistent with the human-like trajectories to correct for disrupted motor coordination and execution in real and virtual environments (Ziherl et al., 2009).

Conclusion

In this paper, a black box approach to biologically inspired robot trajectories design has been pursued and tested both on relevant mathematical indexes related to biological motion and on observers by a real implementation of trajectories on a service robot. We have shown that NNs are an effective solution for the implementation of a biologically inspired trajectory planner module that facilitates the psychophysical interaction of the robot and the human during handover tasks. Besides the surgical environment, which has been the target of this paper, this approach can be applicable in other human–robot shared work environments, such as chemical industry or automotive industry, improving the user acceptance of the robotic assistant. Future developments of the work will encompass the addition of an inverse kinematic module keeping into account also the redundancy management typical of biologically inspired joint control and further qualitative tests on other naive subjects and professionals, as well the use of a bigger number of training trajectories from more subjects in order to include in the NN weights also the inter-subject variability.

Author Contributions

EDM envisaged the experimental scenario, supervised the method development, the results analysis, and the manuscript drafting and revision. LK implemented the network setup and performed results analysis. He also contributed to manuscript drafting. MV designed the network, implemented the experimental setup with the lightweight robot, and performed results analysis. She also contributed to manuscript drafting. NE implemented the kinematics methods and supervised the robot control development. GF advised on human motor control invariants, gave suggestions for the methods, and revised the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

This work was partially funded by ICT 270460 project ACTIVE.

Supplementary Material

The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/frobt.2016.00034

References

Avanzini, G. B., Member, S., Ceriani, N. M., Member, S., Zanchettin, A. M., Rocco, P., et al. (2014). Safety control of industrial robots based on a distributed distance sensor. IEEE Trans. Control Syst. Technol. 22, 2127–2140.

Google Scholar

Beretta, E., De Momi, E., Rodriguez y Baena, F., and Ferrigno, G. (2015a). Adaptive hands-on control for reaching and targeting tasks in surgery. Int. J. Adv. Robot. Syst. 20, 50. doi: 10.5772/60130

CrossRef Full Text | Google Scholar

Beretta, E., Nessi, F., Ferrigno, G., Di Meco, F., Perin, A., Bello, L., et al. (2015b). Enhanced torque-based impedance control to assist brain targeting during open-skull neurosurgery: a feasibility study. Int. J. Med. Robot. doi:10.1002/rcs.1690

PubMed Abstract | CrossRef Full Text | Google Scholar

Berret, B., Chiovetto, E., Nori, F., and Pozzo, T. (2011). Evidence for composite cost functions in arm movement planning: an inverse optimal control approach. PLoS Comput. Biol. 7:e1002183. doi:10.1371/journal.pcbi.1002183

PubMed Abstract | CrossRef Full Text | Google Scholar

Bisio, A., Sciutti, A., Nori, F., Metta, G., Fadiga, L., Sandini, G., et al. (2014). Motor contagion during human-human and human-robot interaction. PLoS ONE 9:e106172. doi:10.1371/journal.pone.0106172

PubMed Abstract | CrossRef Full Text | Google Scholar

Cakmak, M., Srinivasa, S. S., Lee, M. K., Forlizzi, J., and Kiesler, S. (2011a). “Human preferences for robot-human hand-over configurations,” in IEEE International Conference on Intelligent Robots and Systems (San Francisco, CA: IEEE), 1986–1993.

Google Scholar

Cakmak, M., Srinivasa, S. S., Lee, M. K., Kiesler, S., and Forlizzi, J. (2011b). “Using spatial and temporal contrast for fluent robot-human hand-overs,” in HRI ’11 Proceedings of the 6th international conference on Human-robot interaction, (New York, NY, USA: ACM), 489–496.

Google Scholar

Chaminade, T., and Cheng, G. (2009). Social cognitive neuroscience and humanoid robotics. J. Physiol. Paris 103, 286–295. doi:10.1016/j.jphysparis.2009.08.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Chartrand, T. L., and Bargh, J. A. (1999). The chameleon effect: the perception-behavior link and social interaction. J. Pers. Soc. Psychol. 76, 893–910. doi:10.1037/0022-3514.76.6.893

PubMed Abstract | CrossRef Full Text | Google Scholar

Comparetti, M. D., Beretta, E., Kunze, M., De Momi, E., Raczkowsky, J., and Ferrigno, G. (2014). “Event-based device-behavior switching in surgical human-robot interaction,” in 2014 IEEE International Conference on Robotics and Automation, (Hong Kong: ICRA) 1877–1882.

Google Scholar

de Boor, C. (1978). A Practical Guide to Splines. New York: Springer-Verlag, 27.

Google Scholar

De Momi, E., and Ferrigno, G. (2010). Robotic and artificial intelligence for keyhole neurosurgery: the ROBOCAST project, a multi-modal autonomous path planner. Proc. Inst. Mech. Eng. H. 224(5), 715–727.

Google Scholar

de’Sperati, C., and Viviani, P. (1997) The relationship between curvature and velocity in two-dimensional smooth pursuit eye movements J. Neurosci. 17(10), 3932–3945.

Google Scholar

Flash, T., and Hogan, N. (1985). The coordination of arm movements: an experimentally confirmed mathematical model. J. Neurosci. 5, 1688–1703.

PubMed Abstract | Google Scholar

Fletcher, R., and Reeves, C. M. (1964). Function minimization by conjugate gradients. Comput. J. 7, 149–154. doi:10.1093/comjnl/7.2.149

CrossRef Full Text | Google Scholar

Huber, M., Rickert, M., Knoll, A., Brandt, T., and Glasauer, S. (2008). “Human-robot interaction in handing-over tasks,” in RO-MAN 2008 – The 17th IEEE International Symposium on Robot and Human Interactive Communication (Munich: IEEE), 107–112.

Google Scholar

Jacob, M. G., Li, Y.-T., Akingba, G. A., and Wachs, J. P. (2013). Collaboration with a robotic scrub nurse. Commun. ACM 56, 68. doi:10.1145/2447976.2447993

CrossRef Full Text | Google Scholar

Jakopec, M., Harris, S. J., Rodriguez y Baena, F., Gomes, P., and Davies, B. L. (2003). The Acrobot^® system for total knee replacement. Ind. Robot 30, 61–66. doi:10.1108/01439910310457724

CrossRef Full Text | Google Scholar

Janabi-Sharifi, F., Hayward, V., and Chen, C. S. J. (2000). Discrete-time adaptive windowing for velocity estimation. IEEE Trans. Control Syst. Technol. 8, 1003–1009. doi:10.1109/87.880606

CrossRef Full Text | Google Scholar

Karan, B. (2015). Calibration of kinect-type RGB-D sensors for robotic applications. FME Trans. 43.1, 47–54. doi:10.5937/fmet1501047K

CrossRef Full Text | Google Scholar

Khoshelham, K., and Elberink, S. O. (2012). Accuracy and resolution of kinect depth data for indoor mapping applications. Sensors 12, 1437–1454. doi:10.3390/s120201437

PubMed Abstract | CrossRef Full Text | Google Scholar

Lacquaniti, F., Terzuolo, C., and Viviani, P. (1983). The law relating the kinematic and figural aspects of drawing movements. Acta Psychol. 54, 115–130. doi:10.1016/0001-6918(83)90027-6

CrossRef Full Text | Google Scholar

Rigotti, C., Cerveri, P., Andreoni, G., Pedotti, A., and Ferrigno, G. (2001). Modeling and driving a reduced human mannequin through motion captured data: a neural network approach. IEEE Trans. Syst. Man Cybern. A 31, 187–193. doi:10.1109/3468.925658

CrossRef Full Text | Google Scholar

Santello, M., Flanders, M., and Soechting, J. F. (1998). Postural hand synergies for tool use. J. Neurosci. 18, 10105–10115.

PubMed Abstract | Google Scholar

Scholz, J. P., and Schöner, G. (1999). The uncontrolled manifold concept: identifying control variables for a functional task. Exp. Brain Res. 126, 289–306. doi:10.1007/s002210050738

PubMed Abstract | CrossRef Full Text | Google Scholar

Sciutti, A., Bisio, A., Nori, F., Metta, G., Fadiga, L., Pozzo, T., et al. (2012). Measuring human-robot interaction through motor resonance. Int. J. Soc. Robot. 4, 223–234. doi:10.1007/s12369-012-0143-1

CrossRef Full Text | Google Scholar

Secco, E. L., and Magenes, G. (2002). A feedforward neural network controlling the movement of a 3 DOF finger. IEEE SMC Trans. A, 32.3 437–445. doi:10.1109/TSMCA.2002.803101

CrossRef Full Text | Google Scholar

Secco, E. L., Visioli, A., and Magenes, G. (2001). A minimum jerk approach for the motion planning of a prosthetic finger. Proc. Int. Soc. Biomech. 21, 361–368. doi:10.1002/rob.20018

CrossRef Full Text | Google Scholar

Secco, E. L., Visioli, A., and Magenes, G. (2004). Minimum jerk motion planning for a prosthetic finger. J. Robot. Syst. 21, 361–368. doi:10.1002/rob.20018

CrossRef Full Text | Google Scholar

Shibata, S., Sahbi, B. M., Tanaka, K., and Shimizu, A. (1997). “An analysis of the process of handing over an object and its application to robot motions.” IEEE International Conference on Systems, Man, and Cybernetics, Computational Cybernetics and Simulation (Orlando, FL: IEEE), 64–69.

Google Scholar

Shimizu, M., Kakuya, H., Yoon, W.-K., Kitagaki, K., and Kosuge, K. (2008). Analytical inverse kinematic computation for 7-DOF redundant manipulators with joint limits and its application to redundancy resolution. IEEE Trans. Robot. 24, 1131–1142. doi:10.1109/TRO.2008.2003266

CrossRef Full Text | Google Scholar

Strabala, K., Lee, M. K., Dragan, A., Forlizzi, J., Srinavasa, S. S., Cakmak, M., et al. (2012). Towards seamless human-robot handovers. J. Hum. Robot Interact. 1, 112–132. doi:10.5898/jhri.v2i1.114

CrossRef Full Text | Google Scholar

Teulings, H. L., Contreras-Vidal, J. L., Stelmach, G. E., and Adler, C. H. (1997). Parkinsonism reduces coordination of fingers, wrist, and arm in fine motor control. Exp. Neurol. 146, 159–170. doi:10.1006/exnr.1997.6507

PubMed Abstract | CrossRef Full Text | Google Scholar

Uno, Y., Kawato, M., and Suzuki, R. (1989). Formation and control of optimal trajectory in human multijoint arm movement. Biol. Cybern. 61(2), 89–101 doi:10.1007/BF00204593

CrossRef Full Text | Google Scholar

Wann, J., Nimmo-Smith, I., and Wing, A. M. (1988). Relation between velocity and curvature in movement: equivalence and divergence between a power law and a minimum-jerk model. J. Exp. Psychol. Hum. Percept. Perform. 14(4), 622–637.

Google Scholar

Zanchettin, A. M., Bascetta, L., and Rocco, P. (2013). Achieving humanlike motion: resolving redundancy for anthropomorphic industrial manipulators. IEEE Robot. Autom. Mag. 20, 131–138. doi:10.1109/MRA.2013.2283650

CrossRef Full Text | Google Scholar

Zhang, Z. (2000). A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 22, 1330–1334. doi:10.1109/34.888718

CrossRef Full Text | Google Scholar

Zhang, C., and Zhang, Z. (2011). “Calibration between depth and color sensors for commodity depth cameras,” 2011 IEEE International Conference on Multimedia and Expo (Barcelona: IEEE) 1–6.

Google Scholar

Ziherl, J., Podobnik, J., Sikic, M., and Munih, M. (2009). Pick to place trajectories in human arm training environment. Technol Health Care 17(4), 323–35. doi:10.3233/THC-2009-0543

CrossRef Full Text | Google Scholar