Learning Controllers for Reactive and Proactive Behaviors in Human–Robot Collaboration

Designed to safely share the same workspace as humans and assist them in various tasks, the new collaborative robots are targeting manufacturing and service applications that once were considered unattainable. The large diversity of tasks to carry out, the unstructured environments, and the close interaction with humans call for collaborative robots to seamlessly adapt their behaviors, so as to cooperate with the users successfully under different and possibly new situations (characterized, for example, by positions of objects/landmarks in the environment or by the user pose). This paper investigates how controllers capable of reactive and proactive behaviors in collaborative tasks can be learned from demonstrations. The proposed approach exploits the temporal coherence and dynamic characteristics of the task observed during the training phase to build a probabilistic model that enables the robot to both react to the user actions and lead the task when needed. The method is an extension of the hidden semi-Markov model where the duration probability distribution is adapted according to the interaction with the user. This adaptive duration hidden semi-Markov model (ADHSMM) is used to retrieve a sequence of states governing a trajectory optimization that provides the reference and gain matrices to the robot controller. A proof-of-concept evaluation is first carried out in a pouring task. The proposed framework is then tested in a collaborative task using a 7-DOF backdrivable manipulator.

1. Introduction

The first generations of robots were mostly designed to handle heavy parts, do dangerous tasks, or execute operations at fast pace in a stand-alone manner. Nowadays, due to the advances in the fields of sensing and control, robots are designed to work alongside humans and assist them in a large variety of complex tasks, not only in manufacturing production lines but also in spaces such as houses, museums, and hospitals. In order for a robot to successfully collaborate with a human, it needs to physically interact with the user in a safe manner (Haddadin et al., 2012), understand the user’s intentions (Wang et al., 2013), and decide when it can lead the task or follow the human (Evrard et al., 2009), among other needs. Nevertheless, hardcoding an extensive repertoire of these collaborative behaviors for a robot becomes an intractable problem, and therefore robot learning arises as a promising solution to tackle the challenges posed by human–robot collaboration (HRC).

Various modalities of programing by demonstration (PbD), such as kinesthetic teaching and observational learning, make it natural to interact with these robots and teach them the skills and tasks we want them to perform (Billard et al., 2008). PbD is used in this paper to teach a robot about reactive and proactive behaviors for collaborative tasks. Here, reactive behaviors refer to actions that are conditioned on the interaction with the user, while proactive behaviors involve taking the lead of the task. These two types of behaviors allow the collaborative robot to assist users in a larger variety of tasks, in which the robot not only adapts its behavior according to the user actions but also takes advantage of the taught knowledge in a proactive manner. To achieve this goal, we propose to learn a model of the collaborative task with a modified version of the hidden semi-Markov model (Yu, 2010) where the duration probability distribution is adapted online according to the interaction, which permits to modify the temporal dynamics of the task as a function of the user actions.

The proposed method, hereinafter referred to as adaptive duration hidden semi-Markov model (ADHSMM), exploits the temporal coherence and dynamic features of the task to locally shape the states duration according to the interaction with the user. The ADHSMM is then used to retrieve a sequence of states in a trajectory optimization process providing a reference with associated gain matrices within an infinite horizon linear quadratic regulator (LQR). In summary, the novelties of this learning framework for collaborative behaviors are (i) encoding of reactive behaviors based on the user actions, (ii) proactive behaviors generation that exploits the temporal coherence of the task, and (iii) time-independent retrieval of reference trajectories and gain matrices governing the robot motion.

The rest of the paper is organized as follows: Section 2 reviews work related to our problem, whereas Section 3 presents the proposed framework for learning reactive and proactive collaborative behaviors. Section 4 describes a number of experiments that evaluate the proposed algorithm. Finally, conclusions and future routes of research are given in Section 5.

2. Related Work

HRC has been investigated from the early nineties, when purely control-based approaches were designed to endow collaborative robots with a follower role, while its user led the task (Kosuge et al., 1993). However, the key limitation in this approach is the need for a model of the task linked to an analysis of the possible robot movements, so that both the parameters and the structure of the controller can be designed accordingly (Kosuge and Kazamura, 1997). This, in turn, confines the set of actions that the robot can perform, because it merely follows a predefined plan with limited adaptation and interaction capabilities. These shortcomings are here overcome by exploiting PbD.

In the field of robot learning for HRC, several groups have focused on teaching robots collaborative tasks in which their role is purely reactive to the partner actions. Amor et al. (2013) proposed to learn separate models [based on probabilistic principal components analysis (PPCA) and hidden Markov models (HMM)] of two persons interacting during a collaborative task, encapsulating the adaption of their behaviors to the movements of the respective partner. One of these models was then transferred to the robot, so that it is able to autonomously respond to the behavior of the human partner. Maeda et al. (2014) proposed to use probabilistic interaction primitives (Paraschos et al., 2013) to learn collaborative movements that need to be coordinated with the user actions by exploiting the correlations between human and robot trajectories.

Collaborative reactive behaviors have also been learned to modify the temporal dynamics of a task. Maeda et al. (2015) included a phase variable representing the speed of the task execution, which eliminated the need of aligning demonstrations in time and allowed the robot to react faster. At a higher level task representation, Wilcox et al. (2012) proposed an adaptive algorithm for handling HRC tasks where the temporal behavior is adapted online based on the user preferences. Their method is built on dynamic scheduling of simple temporal problems and formulated as a non-linear program considering person-specific workflow patterns. In contrast to our learning framework, the aforementioned approaches only provide the robot with reactive behaviors, that is, without proactive behaviors learned during the demonstrations of the task.

Other works have exploited PbD to teach collaborative robots follower and leader roles.¹ Evrard et al. (2009) proposed to use Gaussian mixture models (GMM) and Gaussian mixture regression (GMR) to, respectively, encode and reproduce robot collaborative behaviors. Leading and following roles in a cooperative lifting task were demonstrated by teleoperation. GMM encapsulated the robot motion and the sensed forces, whereas GMR generated the reference force during reproduction. Medina et al. (2011) endowed a robot with a cognitive system providing segmentation, encoding and clustering of collaborative behavioral primitives. These were represented by a primitive graph and a primitive tree using HMM, which were incrementally updated during reproduction. One of the main differences with respect to Evrard et al. (2009) is that the robot starts behaving as a follower, and its role progressively becomes more proactive as it acquires more knowledge about the task.

Murata et al. (2014) used a dynamic neural network to predict future perception and action and to generate both reflex and voluntary behaviors. The former were generated with probabilistic estimation of subsequent actions when the human intention state was not utilized in the learning process. In contrast, the latter was produced with deterministic prediction of subsequent actions when human intention information was available. Note that reflex behaviors refer here to instinctive responses triggered by sensory stimuli, while voluntary behaviors correspond to actions that depend on the situation. Li et al. (2015) addressed the role allocation problem through a formulation based on game theory. A continuous role adaptation is achieved by modifying the contribution of the human and the robot in the minimization of a linear quadratic cost. This adaption depended on the level of disagreement between partners, which was estimated as the difference between desired and real interaction forces. Similarly, Kulvicius et al. (2013) used dynamic movement primitives in HRC where interaction forces were considered. The learning problem was treated as that of finding an acceleration-based predictive reaction for coupled agents, in response to force signals indicating disagreements due to obstacle avoidance or different paths to follow.

Our approach is similar to the foregoing works in the sense that it provides the robot with both reactive and proactive actions that are learned from demonstrations of the collaborative task. However, unlike Li et al. (2015) and Kulvicius et al. (2013), the behavior in the approach that we propose is not a function of the partners’ disagreement, but instead depends on the temporal patterns observed during the demonstration phase, and on the way the temporal dynamics is shaped by the interaction with the human partner. Our controller shares similarities with the approach presented by Li et al. (2015), with the difference that the role allocation is not directly affecting the robot control input, but is instead driven by a linear quadratic regulator. Additionally, our time-independent trajectory retrieval approach provides gain matrices that exploit the variability of the task and shape the robot compliance accordingly.

3. Proposed Approach

When two persons cooperatively carry out a task, each participant is not only required to perform the part of the task he/she is in charge of but also to adapt to the other’s actions and/or changes in the task plan. Therefore, in this collaborative scenario, learning and adaptation capabilities are imperative for success. Consequently, if collaborative robots need to assist humans, they need to be endowed with such capability in order to naturally interact with users. This interaction encompasses a large variety of behaviors that enable the robot to react and adapt to different situations arising during the execution of a specific task. In this Section, we present a PbD approach that allows the robot not only to learn the collaborative task but also to behave reactively or proactively according to the interaction with the user and the temporal coherence of the task.

The rest of this section first presents the adaptive duration hidden semi-Markov model (ADHSMM) that is used to both encode the task and extract the reactive and proactive behaviors by exploiting the temporal patterns observed during the demonstration phase. Second, a trajectory model for retrieving reference trajectories based on the learning model is explained.

3.1. Adaptive Duration Hidden Semi-Markov Model (ADHSMM)

A hidden Markov model (HMM) is characterized by an initial state distribution Π_i, a transition probability matrix a_i,j, and an emission distribution for each state in the model, commonly expressed as a Gaussian distribution with mean μ_i and covariance matrix Σ_i. In HMM, the self-transition probabilities a_i,i only allow a crude implicit modeling of the number of iterations that we can expect to stay in a given state i before moving to another state. Indeed, the probability of staying d consecutive time steps in a state i follows the geometric distribution [see, for example, Rabiner (1989)]

${\mathcal{P}}_i\left(d\right)=a_{i,i}^{d-1}\left(1-a_{i,i}\right),$ (1)

decreasing exponentially with time.

Variable duration modeling techniques such as the hidden semi-Markov model (HSMM) sets the self-transition probabilities a_i,i of the HMM to zero and replaces it with an explicit model (non-parametric or parametric) of the relative time during which one stays in each state, see, for example, Yu and Kobayashi (2006) and Zen et al. (2007b).

Since the state duration is always positive, its distribution should preferably be modeled by a function preserving this property. It is proposed to use a univariate normal distribution $\mathcal{N}\left({\mathrm{\mu }}_{{}_i}^{\mathcal{D}},{\Sigma }_{{}_i}^{\mathcal{D}}\right)$ with mean ${\mathrm{\mu }}_{{}_i}^{\mathcal{D}}$ and associated covariance matrix ${\Sigma }_{{}_i}^{\mathcal{D}}$ to model the logarithm of the duration, which is equivalent to the use of a lognormal distribution to fit the duration data. Indeed, if d is lognormally distributed, log(d) is normally distributed.

In the resulting HSMM, the probability to be in state i at time step t given the partial observation ζ_1:t = {ζ₁, ζ₂, …, ζ_t}, namely α_t,i ≜𝒫(s_t = i|ζ_1:t), can be recursively computed with [see, for example, Rabiner (1989)]

$\begin{array}{llll}\hfill & {\mathrm{\alpha }}_{t,i}={\displaystyle \sum _{d=1}^{d^{\max }}}{\displaystyle \sum _{j=1}^K}{\mathrm{\alpha }}_{t-d,j}{a}_{j,i}{\mathcal{N}}_{d,i}^{\mathcal{D}}{\displaystyle \prod _{s=t-d+1}^t}{\mathcal{N}}_{s,i},\text{\hspace{0.17em}and\hspace{0.17em}}{h}_{t,i}=\frac{{\mathrm{\alpha }}_{t,i}}{{\sum }_{k=1}^K{\mathrm{\alpha }}_{t,k}},& \hfill & \\ \hfill & \text{where\hspace{0.17em}}{\mathcal{N}}_{d,i}^{\mathcal{D}}=\mathcal{N}\left(\log \left(d\right)|{\mathrm{\mu }}_i^{\mathcal{D}},{\Sigma }_i^{\mathcal{D}}\right)\text{\hspace{0.17em}and\hspace{0.17em}}{\mathcal{N}}_{s,i}=\mathcal{N}\left({\mathrm{\zeta }}_s\mathrm{|}{\mathrm{\mu }}_i,{\Sigma }_i\right).\end{array}$ (2)

For t < d^max, the initialization is given by

$\begin{array}{llll}\hfill & {\mathrm{\alpha }}_{1,i}={\mathrm{\Pi }}_i{\mathcal{N}}_{1,i}^{\mathcal{D}}{\mathcal{N}}_{1,i},{\mathrm{\alpha }}_{2,i}={\mathrm{\Pi }}_i{\mathcal{N}}_{2,i}^{\mathcal{D}}{\displaystyle \prod _{s=1}^2}{\mathcal{N}}_{s,i}+{\displaystyle \sum _{j=1}^K}{\mathrm{\alpha }}_{1,j}{a}_{j,i}{\mathcal{N}}_{1,i}^{\mathcal{D}}{\mathcal{N}}_{2,i},& \hfill & \\ \hfill & {\mathrm{\alpha }}_{3,i}={\mathrm{\Pi }}_i{\mathcal{N}}_{3,i}^{\mathcal{D}}{\displaystyle \prod _{s=1}^3}{\mathcal{N}}_{s,i}+{\displaystyle \sum _{d=1}^2}{\displaystyle \sum _{j=1}^K}{\mathrm{\alpha }}_{3-d,j}{a}_{j,i}{\mathcal{N}}_{d,i}^{\mathcal{D}}{\displaystyle \prod _{s=4-d}^3}{\mathcal{N}}_{s,i},\end{array}$

etc., which corresponds to the update rule

$\begin{array}{l}\hfill {\mathrm{\alpha }}_{t,i}={\mathrm{\Pi }}_i{\mathcal{N}}_{t,i}^{\mathcal{D}}{\displaystyle \prod _{s=1}^t}{\mathcal{N}}_{s,i}+{\displaystyle \sum _{d=1}^{t-1}}{\displaystyle \sum _{j=1}^K}{\mathrm{\alpha }}_{t-d,j}{a}_{j,i}{\mathcal{N}}_{d,i}^{\mathcal{D}}{\displaystyle \prod _{s=t-d+1}^t}{\mathcal{N}}_{s,i}.\end{array}$ (3)

Note that the above iterations can be reformulated for efficient computation, see Yu and Kobayashi (2006) and Yu (2010) for details.

3.1.1. Conditional Estimation of Duration Probability

The explicit-duration formulation of HSMM assumes that the duration probability 𝒫_i(d) exclusively depends on how long the system stays in state i. Yamagishi and Kobayashi (2005) noted that such assumption can have drawbacks in some applications such as in speech synthesis where various speaking styles and/or emotions could influence the duration model. In such case, it looks relevant to consider adaptive duration probability. In Yamagishi and Kobayashi (2005) and Nose et al. (2007), the authors proposed to express the mean ${\mathrm{\mu }}_i^{\mathcal{D}}$ of the duration probability 𝒫_i(d) as an affine function of a style vector, whose parameters were estimated by a maximum likelihood linear regression (MLLR) method (Leggetter and Woodland, 1995). This approach also showed to improve human walking motion synthesis (Yamazaki et al., 2005).

We propose an adaptive duration hidden semi-Markov model (ADHSMM) in which the duration in every state depends on an external input u. Unlike Yamagishi and Kobayashi (2005) and Nose et al. (2007), we express the duration probability as 𝒫_i(log(d)|u), obtained from a Gaussian mixture model of K^𝒟 components encoding the joint distribution 𝒫_i(u, log(d)) for each state i of the HSMM. We thus obtain a GMM for each state, with parameters

$\begin{array}{l}{\mathrm{\pi }}_{i,j}^{\mathcal{D}},{\mathrm{\mu }}_{i,j}=\left[\begin{array}{c}{\mathrm{\mu }}_{i,j}^{\mathcal{U}}\\ {\mathrm{\mu }}_{i,j}^{\mathcal{D}}\end{array}\right],{\Sigma }_{i,j}=\left[\begin{array}{c}{\Sigma }_{i,j}^{\mathcal{U}}{\Sigma }_{i,j}^{\mathcal{U}\mathcal{D}}\\ {\Sigma }_{i,j}^{\mathcal{D}\mathcal{U}}{\Sigma }_{i,j}^{\mathcal{D}}\end{array}\right]\forall i\in \left\{1,\dots ,K\right\},j\in \left\{1,\dots ,K^{\mathcal{D}}\right\}.\end{array}$ (4)

In contrast to Yamagishi and Kobayashi (2005) and Nose et al. (2007) that only consider an affine relationship between ${\mathrm{\mu }}_i^{\mathcal{D}}$ and the input vector, our approach permits to encode more complex non-linear relationships between the duration of the state and the external parameter.

We also propose to define a maximum duration $d_i^{\max }$ for each state i that depends on the duration probability distribution 𝒫_i(log(d)|u). Indeed, the maximum allowed duration d^max does not necessarily need to be the same for each state i, see, for example, Mitchell et al. (1995). In the experiments, we used $d_i^{\max }=\exp \left({\mathrm{\mu }}_i^{\mathcal{D}}+2{\Sigma }_i^{{\mathcal{D}}^{\frac{1}{2}}}\right)$, which means that ~95% of the observed duration for the state i lie within 2 SDs.²

Therefore, we compute ${\mathcal{N}}_{d,i}^{\mathcal{D}}$ in equation (2) as ${\mathcal{P}}_i\left(\log \left(d\right)|{\mathit{\text{u}}}_t\right)\sim \mathcal{N}\left({\widehat{\mathrm{\mu }}}_{i,t}^{\mathcal{D}},{\widehat{\Sigma }}_{i,t}^{\mathcal{D}}\right)$ with

${\widehat{\mathrm{\mu }}}_{i,t}^{\mathcal{D}}={\displaystyle \sum _{j=1}^{K^{\mathcal{D}}}}{\mathrm{\gamma }}_{i,j}\left({\mathit{\text{u}}}_t\right){\tilde{\mathrm{\mu }}}_{i,j}^{\mathcal{D}}\left({\mathit{\text{u}}}_t\right),$ (5)

$\begin{array}{ll}\hfill {\widehat{\Sigma }}_{i,t}^{\mathcal{D}}& ={\displaystyle \sum _{j=1}^{K^{\mathcal{D}}}}{\mathrm{\gamma }}_{i,j}\left({\mathit{\text{u}}}_t\right)\left({\tilde{\Sigma }}_{i,j}^{\mathcal{D}}+{\tilde{\mathrm{\mu }}}_{i,j}^{\mathcal{D}}\left({\mathit{\text{u}}}_t\right)\left({\tilde{\mathrm{\mu }}}_{i,j}^{\mathcal{D}}\left({\mathit{\text{u}}}_t\right)\right){}^{\top }\right)-{\widehat{\mathrm{\mu }}}_{i,t}^{\mathcal{D}}{\left({\widehat{\mathrm{\mu }}}_{i,t}^{\mathcal{D}}\right)}^{\top },\end{array}$ (6)

$\text{where\hspace{0.17em}}{\tilde{\mathrm{\mu }}}_{i,j}^{\mathcal{D}}\left({\mathit{\text{u}}}_t\right)={\mathrm{\mu }}_{i,j}^{\mathcal{D}}+{\Sigma }_{i,j}^{\mathcal{D}\mathcal{U}}{{\Sigma }_{i,j}^{\mathcal{U}}}^{-1}\left({\mathit{\text{u}}}_t-{\mathrm{\mu }}_{i,j}^{\mathcal{U}}\right),$ (7)

${\tilde{\Sigma }}_{i,j}^{\mathcal{D}}={\Sigma }_{i,j}^{\mathcal{D}}-{\Sigma }_{i,j}^{\mathcal{D}\mathcal{U}}{\Sigma {}_{i,j}^{\mathcal{U}}}^{-1}{\Sigma }_{i,j}^{\mathcal{U}\mathcal{D}},$ (8)

${\mathrm{\gamma }}_{i,j}\left({\mathit{\text{u}}}_t\right)=\frac{{\mathrm{\pi }}_{i,j}^{\mathcal{D}}\mathcal{N}\left({\mathit{\text{u}}}_t\mathrm{|}{\mathrm{\mu }}_{i,j}^{\mathcal{U}},{\Sigma }_{i,j}^{\mathcal{U}}\right)}{{\sum }_k^{K^{\mathcal{D}}}{\mathrm{\pi }}_{i,k}^{\mathcal{D}}\mathcal{N}\left({\mathit{\text{u}}}_t\mathrm{|}{\mathrm{\mu }}_{i,k}^{\mathcal{U}},{\Sigma }_{i,k}^{\mathcal{U}}\right)}.$ (9)

When it comes to human–robot collaboration, the proposed formulation can be exploited for learning reactive and proactive behaviors. On the one hand, ADHSMM encodes the temporal patterns and sequential information observed during the demonstration phase through its duration probabilities and transition matrix. This feature allows the robot to behave proactively by taking leading actions in case the user does not follow the task plan as experienced in the training phase. On the other hand, ADHSMM also permits the robot to shape the task dynamics by modifying the states duration according to the interaction with the human, and therefore react to the user’s actions. These two types of behaviors are driven by the forward variable α_t in equation (2), which determines the influence of the ADHSMM states at each time step t considering the partial observation ζ_1:t, the transition matrix a_i,j, and the duration model 𝒫_i(log(d)|u_t) that takes into account the interaction with the user. The forward variable will next be used to generate trajectory distributions to control the robot during the collaborative task.

3.2. Trajectory Retrieval Using Dynamic Features

In the field of speech processing, it is common to exploit both static and dynamic features to reproduce smooth trajectories from HMMs (Furui, 1986; Tokuda et al., 1995; Zen et al., 2007a). This is achieved by encoding the distributions of both static and dynamic features (the dynamic features are often called delta coefficients). In speech processing, these parameters usually correspond to the evolution of mel-frequency cepstral coefficients characterizing the power spectrum of a sound, but the same approach can be used with any form of continuous signals. In robotics, this approach has rarely been exploited, at the exception of the work from Sugiura et al. (2011) employing it to represent object manipulation movements. We take advantage of this formulation for retrieving a reference trajectory with associated covariance that will govern the robot motions according to the behavior determined by the ADHSMM.

For the encoding of robot movements, velocity and acceleration can alternatively be used as dynamic features. By considering an Euler approximation, the velocity is computed as

${\dot{\mathit{\text{x}}}}_t=\frac{{\mathit{\text{x}}}_{t+1}-{\mathit{\text{x}}}_t}{\mathrm{\Delta }t},$ (10)

where x_t is a multivariate position vector. The acceleration is similarly computed as

${\ddot{\mathit{\text{x}}}}_t=\frac{{\dot{\mathit{\text{x}}}}_{t+1}-{\dot{\mathit{\text{x}}}}_t}{\mathrm{\Delta }t}=\frac{{\mathit{\text{x}}}_{t+2}-2{\mathit{\text{x}}}_{t+1}+{\mathit{\text{x}}}_t}{\mathrm{\Delta }{t}^2}.$ (11)

By using equations (10) and (11), the observation vector ζ_t will be used to represent the concatenated position, velocity, and acceleration vectors at time step t, namely³

${\mathrm{\zeta }}_t=\left[\begin{array}{c}\hfill {\mathit{\text{x}}}_t\hfill \\ \hfill {\dot{\mathit{\text{x}}}}_t\hfill \\ \hfill {\ddot{\mathit{\text{x}}}}_t\hfill \end{array}\right]=\left[\begin{array}{ccc}\mathit{\text{I}}& \hfill \mathbf{\text{0}}\hfill & \hfill \mathbf{\text{0}}\hfill \\ \hfill -\frac{1}{\mathrm{\Delta }t}\mathit{\text{I}}\hfill & \hfill \frac{1}{\mathrm{\Delta }t}\mathit{\text{I}}\hfill & \hfill \mathbf{\text{0}}\hfill \\ \hfill \frac{1}{\mathrm{\Delta }{t}^2}\mathit{\text{I}}\hfill & -\frac{2}{\mathrm{\Delta }{t}^2}\mathit{\text{I}}& \frac{1}{\mathrm{\Delta }{t}^2}\mathit{\text{I}}\end{array}\right]\left[\begin{array}{c}{\mathit{\text{x}}}_t\\ {\mathit{\text{x}}}_{t+1}\\ {\mathit{\text{x}}}_{t+2}\end{array}\right].$ (12)

ζ and x are then defined as large vectors concatenating ζ_t and x_t for all time steps, namely

$\mathrm{\zeta }=\left[\begin{array}{c}\hfill {\mathrm{\zeta }}_1\hfill \\ \hfill {\mathrm{\zeta }}_2\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathrm{\zeta }}_T\hfill \end{array}\right],\mathbf{x}=\left[\begin{array}{c}\hfill {\mathit{\text{x}}}_1\hfill \\ \hfill {\mathit{\text{x}}}_2\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathit{\text{x}}}_T\hfill \end{array}\right].$ (13)

Similar to the matrix operator in equation (12) defined for a single time step, a large sparse matrix Φ can be defined so that ζ = Φx, namely⁴

$\stackrel{\mathrm{\zeta }}{\overbrace{\left[\begin{array}{c}\hfill ⋮\hfill \\ \hfill {\mathit{\text{x}}}_t\hfill \\ \hfill {\dot{\mathit{\text{x}}}}_t\hfill \\ \hfill {\ddot{\mathit{\text{x}}}}_t\hfill \\ \hfill {\mathit{\text{x}}}_{t+1}\hfill \\ \hfill {\dot{\mathit{\text{x}}}}_{t+1}\hfill \\ \hfill {\ddot{\mathit{\text{x}}}}_{t+1}\hfill \\ \hfill ⋮\hfill \end{array}\right]}}=\stackrel{\mathrm{\Phi }}{\overbrace{\left[\begin{array}{cccccc}\hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill \\ \hfill \cdots \hfill & \hfill \mathit{\text{I}}\hfill & \hfill \mathbf{\text{0}}\hfill & \hfill \mathbf{\text{0}}\hfill & \hfill \cdots \hfill & \hfill \hfill \\ \hfill \cdots \hfill & \hfill -\frac{1}{\mathrm{\Delta }t}\mathit{\text{I}}\hfill & \hfill \frac{1}{\mathrm{\Delta }t}\mathit{\text{I}}\hfill & \hfill \mathbf{\text{0}}\hfill & \hfill \cdots \hfill & \hfill \hfill \\ \hfill \cdots \hfill & \hfill \frac{1}{\mathrm{\Delta }{t}^2}\mathit{\text{I}}\hfill & \hfill -\frac{2}{\mathrm{\Delta }{t}^2}\mathit{\text{I}}\hfill & \hfill \frac{1}{\mathrm{\Delta }{t}^2}\mathit{\text{I}}\hfill & \hfill \cdots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \cdots \hfill & \hfill \mathit{\text{I}}\hfill & \hfill \mathbf{\text{0}}\hfill & \hfill \mathbf{\text{0}}\hfill & \hfill \cdots \hfill \\ \hfill \hfill & \hfill \cdots \hfill & \hfill -\frac{1}{\mathrm{\Delta }t}\mathit{\text{I}}\hfill & \hfill \frac{1}{\mathrm{\Delta }t}\mathit{\text{I}}\hfill & \hfill \mathbf{\text{0}}\hfill & \hfill \cdots \hfill \\ \hfill \hfill & \hfill \cdots \hfill & \hfill \frac{1}{\mathrm{\Delta }{t}^2}\mathit{\text{I}}\hfill & \hfill -\frac{2}{\mathrm{\Delta }{t}^2}\mathit{\text{I}}\hfill & \hfill \frac{1}{\mathrm{\Delta }{t}^2}\mathit{\text{I}}\hfill & \hfill \cdots \hfill \\ \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \\ \hfill \hfill \end{array}\right]}}\stackrel{\mathit{\text{x}}}{\overbrace{\left[\begin{array}{c}\hfill ⋮\hfill \\ \hfill {\mathit{\text{x}}}_t\hfill \\ \hfill {\mathit{\text{x}}}_{t+1}\hfill \\ \hfill {\mathit{\text{x}}}_{t+2}\hfill \\ \hfill {\mathit{\text{x}}}_{t+3}\hfill \\ \hfill ⋮\hfill \end{array}\right]}}.$ (14)

During the demonstration phase of a collaborative task, the collected dataset ${\left\{{\mathrm{\zeta }}_t\right\}}_{t=1}^N$ with $N={\sum }_m^M{T}_m$ is composed of M trajectory samples, where the m-th trajectory sample has T_m datapoints. This dataset is encoded by an ADHSMM, which can also provide a given sequence of states s = {s₁, s₂, …, s_T} of T time steps, with discrete states s_t ∈ {1, …, K}. So, the likelihood of a movement ζ is given by

$\mathcal{P}\left(\mathrm{\zeta }\mathrm{|}\mathit{\text{s}}\right)={\displaystyle \prod _{t=1}^T}\mathcal{N}\left({\mathrm{\zeta }}_t\mathrm{|}{\mathrm{\mu }}_{s_t},{\Sigma }_{s_t}\right),$ (15)

where ${\mathrm{\mu }}_{s_t}$ and ${\Sigma }_{s_t}$ are the center and covariance of state s_t at time step t. This product can be rewritten as the conditional distribution

$\mathcal{P}\left(\mathrm{\zeta }\mathrm{|}\mathit{\text{s}}\right)=\mathcal{N}\left(\mathrm{\zeta }\mathrm{|}{\mathrm{\mu }}_{\mathit{\text{s}}},{\Sigma }_{\mathit{\text{s}}}\right),$ (16)

$\begin{array}{r}\text{with\hspace{0.17em}}{\mathrm{\mu }}_{\mathit{\text{s}}}=\left[\begin{array}{c}\hfill {\mathrm{\mu }}_{s_1}\hfill \\ \hfill {\mathrm{\mu }}_{s_2}\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathrm{\mu }}_{s_T}\hfill \end{array}\right]\text{\hspace{0.17em}and\hspace{0.17em}}{\Sigma }_{\mathit{\text{s}}}=\left[\begin{array}{cccc}\hfill {\Sigma }_{{{\text{s}}}_1}\hfill & \hfill \mathbf{\text{0}}\hfill & \hfill \cdots \hfill & \hfill \mathbf{\text{0}}\hfill \\ \hfill \mathbf{\text{0}}\hfill & \hfill {\Sigma }_{{{\text{s}}}_2}\hfill & \hfill \cdots \hfill & \hfill \mathbf{\text{0}}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \mathbf{\text{0}}\hfill & \hfill \mathbf{\text{0}}\hfill & \hfill \cdots \hfill & \hfill {\Sigma }_{s_T}\hfill \end{array}\right].\end{array}$

By using the relation ζ = Φx, we then seek during reproduction for a trajectory x maximizing equation (16), namely

$\widehat{\mathit{\text{x}}}=\arg \underset{\mathit{\text{x}}}{\max }\log \mathcal{P}\left(\mathrm{\Phi }\mathit{\text{x}}|\mathit{\text{s}}\right).$ (17)

The part of log 𝒫(Φx|s) dependent on x takes the quadratic error form

$\begin{array}{llll}\hfill c& ={\left({\mathrm{\mu }}_{\mathit{\text{s}}}-\mathrm{\zeta }\right)}^{\top }{\Sigma }_{\mathit{\text{s}}}^{-1}\left({\mathrm{\mu }}_{\mathit{\text{s}}}-\mathrm{\zeta }\right)& \hfill & \\ \hfill & ={\left({\mathrm{\mu }}_{\mathit{\text{s}}}-\mathrm{\Phi }\mathit{\text{x}}\right)}^{\top }{\Sigma }_{\mathit{\text{s}}}^{-1}\left({\mathrm{\mu }}_{\mathit{\text{s}}}-\mathrm{\Phi }\mathit{\text{x}}\right).\end{array}$ (18)

A solution can be found by differentiating the above objective function with respect to x and equating to 0, providing the trajectory (in vector form)

$\widehat{\mathit{\text{x}}}={\left({\mathrm{\Phi }}^{\top }{{\Sigma }_{\mathit{\text{s}}}}^{-1}\mathrm{\Phi }\right)}^{-1}{\mathrm{\Phi }}^{\top }{{\Sigma }_{\mathit{\text{s}}}}^{-1}{\mathrm{\mu }}_{\mathit{\text{s}}},$ (19)

with the covariance error of the weighted least squares estimate given by

${\widehat{\Sigma }}^{\mathit{\text{x}}}=\mathrm{\sigma }{\left({\mathrm{\Phi }}^{\top }{{\Sigma }_{\mathit{\text{s}}}}^{-1}\mathrm{\Phi }\right)}^{-1},$ (20)

where σ is a scale factor.⁵

The resulting Gaussian $\mathcal{N}\left(\widehat{\mathit{\text{x}}},{\widehat{\Sigma }}^{\mathit{\text{x}}}\right)$ forms a trajectory distribution that will be used to control the robot motion during the collaborative task. Specifically, once a reference trajectory $\widehat{\mathit{\text{x}}}$ has been obtained, the optimal controller for human–robot collaborative tasks proposed in Rozo et al. (2015) is used to track this reference. Such an optimal feedback controller allows the robot to plan a feedback control law tracking the desired state within a minimal intervention control principle. Formally, the problem is stated as finding the optimal input ν that minimizes the cost function

$J_t={\displaystyle \sum _{n=t}^{\infty }}(x_n-{\widehat{x}}_t){}^{\top }{\mathit{\text{Q}}}_t\left({\mathit{\text{x}}}_n-{\widehat{\mathit{\text{x}}}}_t\right)+{\mathrm{\nu }}_n^{\top }{\mathit{\text{R}}}_t{\mathrm{\nu }}_n,$ (21)

where the matrices Q_t and R_t are weighting matrices that determine the proportion in which the tracking errors and control inputs affect the minimization problem. Here, we take advantage of the variability observed during the demonstrations to adapt the error costs in equation (27) in an online manner by defining

${\mathit{\text{Q}}}_t={\left({\widehat{\Sigma }}_t^{\mathit{\text{x}}}\right)}^{-1},$ (22)

and by setting R_t in accordance to the application and motors used in the experiment (set as constant diagonal matrix in the experiments reported in this paper).

4. Experiments

This section introduces the two experimental settings that were used to test the performance of the proposed learning framework and to show its functionality in different scenarios. The first experiment, a pouring task, is used to illustrate our approach in a scenario where the robot reproduces a task in a stand-alone manner. The second experiment, a handover and transportation task in a human–robot collaboration setting, is aimed at showing how reactive and proactive behaviors can be learned and reproduced using our framework.

4.1. Pouring Task

Pouring is a challenging skill for a robot to learn (Rozo et al., 2013b). We want the robot to learn how to pour into a glass liquid from a bottle that can be filled up to different levels. Thus, the time it takes to rotate the bottle and pour the liquid should scale with the amount of liquid that the bottle contains. Therefore, the duration of the pouring movement executed by the robot should be modulated by the amount of liquid to be poured, making it a skill for which our approach can be employed.

The task is demonstrated through kinesthetic teaching in two distinct situations: full and almost-empty bottle. We use a 7-DOF torque-controlled WAM manipulator with a Barrett Hand, which employs a gravity compensation controller during the kinesthetic teaching phase (see Figure 1). The pouring movement is performed by using only the last two joints of the kinematic chain. Joint 7 provides a rotational degree of freedom in task space that allows for rotating the bottle from an upright position to a pouring configuration and back to the initial position, while joint 6 provides a compliant DOF that facilitates the kinesthetic teaching process (in practice, its variation is small across demonstrations). The remaining joints are kept at a constant value. The amount of fluid inside the bottle (not explicitly computed) is sensed by a force-torque sensor attached to the wrist of the manipulator. The force along the vertical axis of the robot’s base frame is recorded at the beginning of each demonstration. This force is used as the input u in the state duration model.⁶

FIGURE 1

Figure 1. Experimental setting of the pouring task. Kinesthetic teaching and reproduction are shown in the left and right pictures, respectively. The amount of fluid inside the bottle is sensed by a force-torque sensor attached to the wrist of the manipulator.

We collected three demonstrations of each situation, totaling six demonstrations (see Figures 2A,B). The observation vector is given by ${\mathrm{\zeta }}_t={\left[{\mathit{\text{q}}}_{6,t},{\dot{\mathit{\text{q}}}}_{6,t},{\mathit{\text{q}}}_{7,t},{\dot{\mathit{\text{q}}}}_{7,t}\right]}^{\top }$, where q_n,t and ${\dot{\mathit{\text{q}}}}_{n,t}$ are the observed angle of joint n and its first derivative at time step t. With this dataset, we trained an ADHSMM with K = 6 states (selected empirically) as an HSMM initialized with left-right topology. The state duration models were trained using a dataset ${\left\{{\mathrm{\xi }}_{i,m}\right\}}_{m=1}^{M_i}$ with ${\mathrm{\xi }}_{i,m}=\left[{\mathit{\text{u}}}_m^{\top },\log \left(d_{i,m}\right)\right]$, where u_m represents the force measured along the vertical axis of the robot base frame (changing for each demonstration sequence), log(d_i,m) is the log-transformed duration given by the number of consecutive time steps that the system stays in state i, and M_i is the number of datapoints in the demonstration sequences in which state i was visited. With this dataset, a Gaussian distribution was fitted (K^𝒟 = 1, selected empirically), estimating the joint probability of state duration and external input.⁷

FIGURE 2

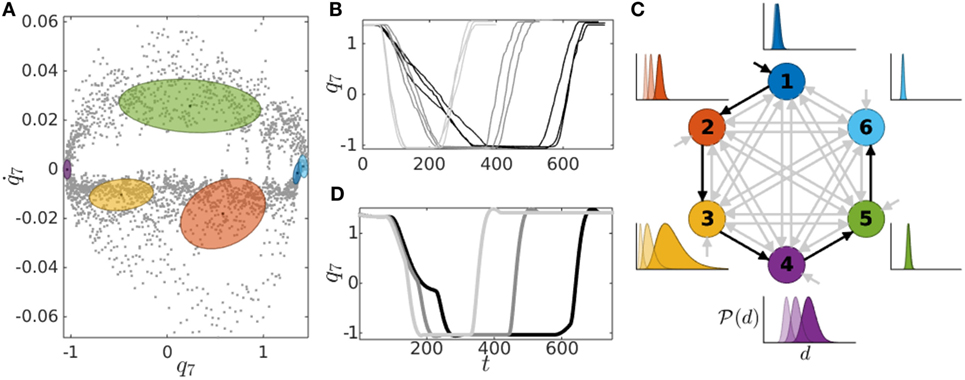
Figure 2. Model, demonstrations, and reproductions of the pouring skill. (A) The 6 states model projected on the space $\dot{\mathit{\text{q}}}$₇, q₇, and the demonstrations (dotted gray). Joint angles and velocities are in radian and radian per second, respectively. (B) Evolution in time of demonstrations for two different bottle weights (darker lines depict heavier bottle). (C) Reproductions of the skill, including the new situation of a half-full bottle. (D) State transition diagram and state duration probabilities (darker log-normals correspond to a heavier bottle, and therefore a longer duration).

The learned model was then used to regenerate the pouring movement for different bottle weights, showing that the robot is capable of reproducing the skill with a duration modulated by an external input. In order to evaluate the generalization capability of the approach, we considered the two demonstrated situations during reproduction (almost-empty and full bottle), as well as the new situation of a half-full bottle.

4.1.1. Results

Figure 2A shows the obtained model with the Gaussian kernels (plotted as iso-contour of 1 SD) successfully encoding the local correlations between q₇ and ${\dot{\mathit{\text{q}}}}_{\text{7}}$. Figure 2B shows the demonstrations over time, which illustrates the required movement duration for each type of input (darker lines correspond to a heavier bottle). This information is complemented by Figure 2D, which shows the state transition graph of the model, together with the duration distributions for the three different inputs that we considered. The duration distributions were retrieved using equations (5)–(9) with darker Gaussians corresponding to higher initial bottle weights. Figure 2D indicates that the duration of states 2–4 is strongly correlated with the input, since its mean increases when a heavier bottle is used. This reflects the demonstrations since states 2 and 3 cover the part of the movement responsible for the rotation of the bottle, while state 4 encodes the actual pouring, which should last longer when the bottle is fuller. The reproductions of the skill are shown in Figure 2C, where the value of q₇ over time is depicted (we omit q₆ since it is practically constant). This is the result of the trajectory retrieval and tracking process described in Section 3.2. We observe that the movements are correctly generated, in particular that the duration of the most relevant phases of the movement (rotating the bottle and pouring) increases as the input signal grows. Notably, the movement is correctly generalized to the situation of a half-full bottle, which was not demonstrated. Indeed, we can see that the duration of the rotation and pouring scales correctly with the bottle weight (longer than the almost-empty scenario, but shorter than with the full bottle).

The duration of each state during the reproductions is shown in Figure 3 by the rescaled forward variable h_t,i, which determines the influence of each state at every step in the movement.⁸ As previously observed, states 2–4 (i.e., orange, yellow, and purple states, respectively) are particularly influenced by the input, with their durations decreasing as a lighter bottle is used, resulting in an overall faster movement. The duration of the last part of the movement, encoded in states 5 and 6 (i.e., green and light blue), shows a much lower correlation with the input, since the demonstrator rotated the bottle back to the initial configuration at a similar rate in all the demonstrations, as a result of the bottle being empty after the pouring. These results clearly show how the proposed model is able to shape the temporal dynamics of the task as a function of an external input. This approach will be next exploited to learn reactive and proactive behaviors in a collaborative task. A video showing the results of this experiment is available at http://programming-by-demonstration.org/Frontiers2016/

FIGURE 3

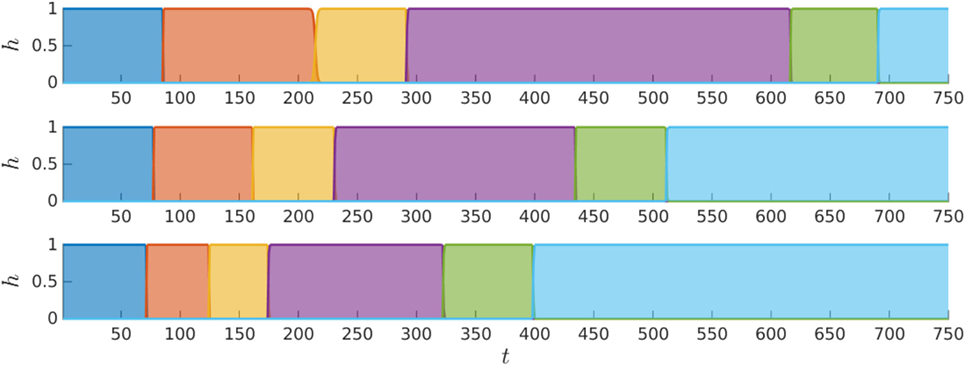
Figure 3. Evolution of the rescaled forward variable h_t,i, where each plot corresponds to a different initial bottle weight, which decreases from the uppermost to the lowermost plot.

4.2. Handover and Transportation Task

In order to show how the proposed approach can be exploited in HRC scenarios, we consider a collaborative task in which the robot role is to first reach for an object that is delivered by the user, and then transport it along a given path to attain a final location. The first part of the task should thus be conditioned by the human motion, namely, the state durations for this phase of the task should vary according to the user hand position measured when he/she is bringing the object to the location where the robot will grab it. The second part of the task occurs when the robot takes the object and transports it toward the final location. Here, the robot motion is expected to be independent from the human motion.

A Barrett WAM robot is used in this experiment. In the demonstration phase, the gravity-compensated robot is kinesthetically guided by the teacher while cooperatively achieving the task with a person, as shown in Figure 4. A human teacher first shows the robot how to approach the object location based on the user motion, and how to transport the object to the final location. The collaborator’s hand position is tracked with a marker-based NaturalPoint OptiTrack motion capture system, which is composed of 12 cameras working at a rate of 30 fps. The position of the robot is defined by Cartesian position x, while the external input u, conditioning state duration, corresponds to the human hand position x^ℋ.

FIGURE 4

Figure 4. Experimental setting of the handover and transportation task. The teacher on the left demonstrates the skill to the robot, while the person on the right is the collaborator. After learning, the robot reproduces the collaborative behavior as demonstrated by the teacher. Top: first phase of the demonstration in which the robot reaches for an object (a screwdriver in this setup) that is delivered by the user. The hand position is tracked using optical markers. Bottom: second phase of the demonstration showing the transportation of the object toward its final location (black area).

During the demonstration phase, the first part of the task was demonstrated by showing three different human motion velocities labeled as low, medium, and fast. We collected four demonstrations for each velocity level, totaling twelve demonstrations, and afterward trained a model of nine components (K = 9, selected empirically), under the assumption of a left-right topology. Each datapoint consists of the robot position x_t and velocity ${\dot{\mathit{\text{x}}}}_t$ at each time step t of the demonstration, therefore the observation vector is defined as ${\mathrm{\zeta }}_t=\left[{\mathit{\text{x}}}_t^{\top },{\dot{\mathit{\text{x}}}}_t^{\top }\right]$ in this experiment. We model the state duration using a GMM with K^𝒟 = 2 (selected empirically), trained by using the dataset ${\left\{{\mathrm{\xi }}_{i,m}\right\}}_{m=1}^{M_i}$ with ${\mathrm{\xi }}_{i,m}=\left[{\mathit{\text{u}}}_m^{\top },\log \left(d_{i,m}\right)\right]$, where u_m corresponds to the hand position x^ℋ recorded while the system is in state i, log(d_i,m) is the log-transformed duration given by the number of consecutive time steps that the system stays in state i, and M_i is the number of datapoints in the demonstration sequences in which state i was visited.⁹

4.2.1. Results

4.2.1.1. Reactive Behaviors

Figure 5 shows the model, demonstrations and reproductions of the collaborative task when the robot is acting in a reactive manner to the human input. In Figure 5A, we show a 3D view of the model in the workspace of the robot, as well as the human input during the demonstrations. The model successfully encodes the local correlations between the task-space variables. Figure 5B depicts the demonstrations provided to the robot through kinesthetic teaching, with lighter lines corresponding to a faster approach toward the human hand before the handover occurs. In Figure 5C, we show the skill reproductions for two different hand velocities. We can see that the movement is correctly regenerated in both situations. Finally, Figure 6 shows the forward variable in the two cases that we considered during the reproductions. First, we see that the sequence of states is correctly generated in both scenarios, matching what one would expect to be an accurate task-space trajectory of the end-effector for the considered skill. Note that, similar to the previous experiment, this was achieved by taking advantage of the probabilistic modeling of temporal variability employed by ADHSMM, through state transition and state duration probabilities. Second, we observe that the duration of the first three states is strongly correlated with the human hand motion since the duration shortens when the hand moves faster (first row), resulting in a faster approach of the end-effector to the human hand. The influence of the hand movement in the remaining states is negligible, as expected.

FIGURE 5

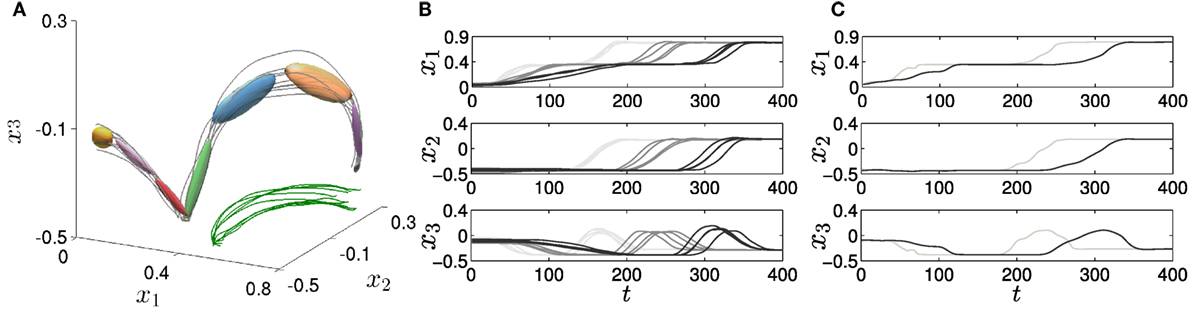
Figure 5. Model, demonstrations, and reproductions of the handover task in the reactive behavior scenario. (A) Task-space view of the model, robot end-effector, and human hand trajectories depicted in gray and green solid lines, respectively. (B) Evolution in time of the demonstrations. (C) Reproductions of the skill. Darker lines display slower human hand motion.

FIGURE 6

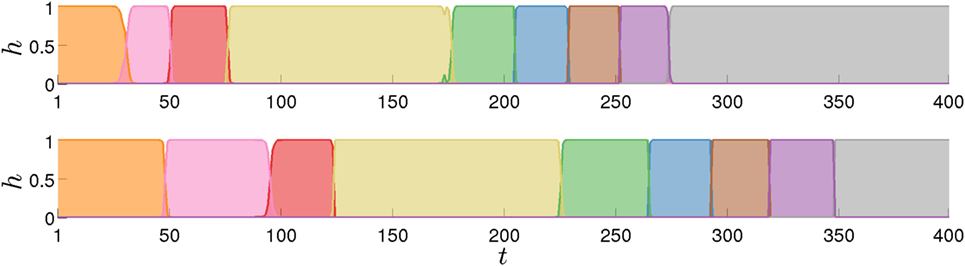
Figure 6. Evolution in time of the rescaled forward variable h_t,i during the handover task. The temporal dynamics of the task is autonomously adapted according to the interaction with the user.

These results show how the robot learned to react to the interaction with the user by modifying the temporal dynamics of the task accordingly. This modulation of durations becomes highly relevant when we consider that humans might not perform the task with the same dynamics across repetitions. More importantly, this adaptation of the temporal aspects of the skill could provide the robot with the capability of interacting with several partners exhibiting different motion dynamics.

4.2.1.2. Proactive Behaviors

In addition to human-adaptive reactive behaviors, the proposed approach can also be used to generate proactive behaviors that remain consistent with the expected temporal evolution of the task. To showcase this property, we portray a scenario where the human stops moving while reaching the object (Figure 7, top). This illustrates a situation in which a new person would be interacting with the robot and would not know enough about the task to lead the cooperation. Consequently, the behavior that one would like to observe in the robot would be that it provides clues about how previous users proceeded in similar situations. In the proposed approach, the robot will take the initiative to proceed with the movement after some time (in case this duration lasts unexpectedly longer than in past experiences) and will guide the user toward the next step of the task (Figure 7, middle). This occurs at most when the duration of state 1 exceeds its maximum value $d_1^{\max }$ and the model transits to state 2 (Figure 7, bottom). This mechanism can be exploited to let the robot help new users proceed with their roles in the collaboration by showing its intent in the cooperation, i.e., showing the way in which the task is believed to be continued (see Figure 7, before t = 100).¹⁰ A video showing the results of this experiment is available at http://programming-by-demonstration.org/Frontiers2016/

FIGURE 7

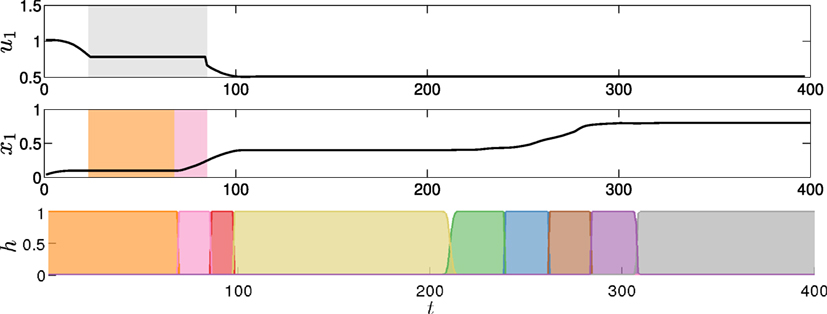
Figure 7. Evolution in time of the proactive behavior variables. Top: first dimension of the user hand position. The hand does not move during the period marked by the shaded area. Middle: dimension x₁ of the robot end-effector position in task space. The state transition (shaded areas) marks the start of the proactive behavior. Bottom: rescaled forward variable h_t,i.

This mechanism currently has some limitations. In the example, the robot had to stop only once before the user could understand what to do. If the user had not understood that his/her role was to hand the object to the robot, the cooperation would have failed because the robot would have finished the task without having the object in its hand. A possible way to increase the number of clues that the robot provides to the human before continuing the task on its own could be to add more states to the model to let the user better understand the intent of the movement. This would make the robot reach the handover pose in approximately the same time, but with a greater number of state transitions, i.e., discrete movements toward the target, providing the user with more information about the movement. Similarly, additional sensory information could be used to verify that a valid situation occurs before moving on to the next part of the task.

Finally, note that this type of proactive behavior allowing the robot to communicate its intent may be combined with approaches aimed at creating legible robot motions. This enables the collaborator to quickly and confidently infer the task goal (Dragan et al., 2015; Stulp et al., 2015), which may lead to more fluent collaborations.

5. Conclusion and Future Work

Human–robot collaboration requires robots not only to passively react to users’ movements and behaviors but also to exploit their knowledge about the collaborative task to improve their level of assistance, therefore achieving better assistance in the collaboration. This paper introduced an approach allowing collaborative robots to learn reactive and proactive behaviors from human demonstrations of a collaborative task. We showed that reactive behaviors could include the modulation of the temporal evolution of the task according to the interaction with the user, while proactive behaviors could be achieved by exploiting the temporal patterns observed during the learning phase.

These collaborative behaviors can be exploited to extend the robot capability to assisting tasks in which both interaction and temporal aspects are relevant. Indeed, the probabilistic nature of the proposed ADHSMM allows the robot to react to different human dynamics, which is beneficial for collaborating with different partners. The proposed proactive behavior allows the robot to take the lead of a task when it is appropriate (namely, according to the task dynamics previously experienced in the demonstrations), which can be exploited to communicate its intention to the user.

We plan to extend the proposed learning model to situations in which the transitions between the model states also depend on the interaction with the partner, which will allow the robot to learn more complex collaborative tasks. We will also explore how the optimization in the trajectory retrieval process can be integrated with the optimal controller used to drive the collaborative robot motion, so that only a single optimization step is carried out. Additionally, we plan to investigate how the robot could learn a larger repertory of behaviors in which not only the interaction with the user is considered, but where the situation and the environment are also taken into account, by combining the developed approach with our previous work on task-parameterized models (Rozo et al., 2013a).

Author Contributions

LR and SC developed the approach. LR and JS performed the experiments and analyzed the results. LR, SC, and JS wrote the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

This work was partially supported by the European Project DexROV (H2020-EU.3.2-635491).

Footnotes

1. ^A leader role can be considered as a type of proactive behavior since the robot exploits the knowledge of the task to take the lead during execution.
2. ^Note that the conditional duration probability is characterized by a mean and a variance lying in the log-transformed space of the duration data, therefore an exponential mapping is needed to define the maximum duration as time steps.
3. ^To simplify the notation, the number of derivatives will be set up to acceleration, but the results can easily be generalized to a higher or lower number of derivatives.
4. ^Note that a similar operator is defined to handle border conditions, and that Φ can automatically be constructed through the use of Kronecker products.
5. ^Equations (19) and (20) describe a trajectory distribution and can be computed efficiently with Cholesky and/or QR decompositions by exploiting the positive definite symmetric band structure of the matrices, see, for example, Strang (1986). With the Cholesky decomposition ${\Sigma }_{\mathit{\text{s}}}^{-1}={\mathit{\text{T}}}^{\top }\mathit{\text{T}}$, the objective function is maximized when $\mathit{\text{T}}\mathrm{\Phi }\mathit{\text{x}}=\mathit{\text{T}}{\mathrm{\mu }}_{\mathit{\text{s}}}$. With a QR decomposition TΦ = QR, the equation becomes QRx = Tμ_s with a solution efficiently computed with x = R−1 Q^⊤Tμ_s. When using Matlab, $\widehat{\mathit{\text{x}}}$ and $\widehat{\Sigma }\mathit{\text{x}}$ in equations (19) and (20) can, for example, be computed with the lscov function.
6. ^Note that, since this value is only measured once, the subscript t is removed from u_t in the description of this experiment.
7. ^The choice of using K^𝒟 = 1 instead of a GMM in this experiment is driven by the assumption of a linear relation between duration and bottle weight.
8. ^In this experiment, a time step lasts 0.04 s approximately.
9. ^In contrast to the pouring task that used K^𝒟 = 1, the use of K^𝒟 = 2 for the hand-over task allows the encoding of non-linear relationships with the input variable (hand position).
10. ^In this experiment, a time step approximately lasts 0.04 s.

References

Amor, H. B., Vogt, D., Ewerton, M., Berger, E., Jung, B., and Peters, J. (2013). “Learning responsive robot behavior by imitation,” in IEEE/RSJ Intl. Conf. on Intelligent Robots and Systems (IROS) (Tokyo: IEEE), 3257–3264.

Google Scholar

Billard, A., Calinon, S., Dillmann, R., and Schaal, S. (2008). “Robot programming by demonstration,” in Springer Handbook of Robotics, eds B. Siciliano and O. Khatib (New York, NY: Springer), 1371–1394.

Google Scholar

Dragan, A., Bauman, S., Forlizzi, J., and Srinivasa, S. (2015). “Effects of robot motion on human-robot collaboration,” in ACM/IEEE Intl. Conf. on Human-Robot Interaction (HRI) (Portland: ACM), 51–58.

Google Scholar

Evrard, P., Gribovskaya, E., Calinon, S., Billard, A., and Kheddar, A. (2009). “Teaching physical collaborative tasks: object-lifting case study with a humanoid,” in IEEE/RAS Intl. Conf. on Humanoid Robots (Humanoids) (Paris: IEEE), 399–404.

Google Scholar

Furui, S. (1986). Speaker-independent isolated word recognition using dynamic features of speech spectrum. IEEE Trans. Acoust. 34, 52–59. doi: 10.1109/TASSP.1986.1164788

CrossRef Full Text | Google Scholar

Haddadin, S., Haddadin, S., Khoury, A., Rokahr, T., Parusel, S., Burgkart, R., et al. (2012). On making robots understand safety: embedding injury knowledge into control. Int. J. Robot. Res. 31, 1578–1602. doi:10.1177/0278364912462256

CrossRef Full Text | Google Scholar

Kosuge, K., and Kazamura, N. (1997). “Control of a robot handling an object in cooperation with a human,” in IEEE Intl. Workshop on Robot and Human Communication (Sendai: IEEE), 142–147.

Google Scholar

Kosuge, K., Yoshida, H., and Fukuda, T. (1993). “Dynamic control for robot-human collaboration,” in IEEE Intl. Workshop on Robot and Human Communication (Tokyo: IEEE), 398–401.

Google Scholar

Kulvicius, T., Biehlc, M., Aein, M. J., Tamosiunaite, M., and Wörgötter, F. (2013). Interaction learning for dynamic movement primitives used in cooperative robotic tasks. Rob. Auton. Syst. 61, 1450–1459. doi:10.1016/j.robot.2013.07.009

CrossRef Full Text | Google Scholar

Leggetter, C., and Woodland, P. (1995). Maximum likelihood linear regression for speaker adaptation of continuous density hidden Markov models. Comput. Speech Lang. 9, 171–185. doi:10.1006/csla.1995.0010

CrossRef Full Text | Google Scholar

Li, Y., Tee, K. P., Chan, W. L., Yan, R., Chua, Y., and Limbu, D. K. (2015). Continuous role adaptation for human-robot shared control. IEEE Trans. Robot. 31, 672–681. doi:10.1109/TRO.2015.2419873

CrossRef Full Text | Google Scholar

Maeda, G., Ewerton, M., Lioutikov, R., Amor, H. B., Peters, J., and Neumann, G. (2014). “Learning interaction for collaborative tasks with probabilistic movement primitives,” in IEEE/RAS Intl. Conf. on Humanoid Robots (Humanoids) (Madrid: IEEE), 527–534.

Google Scholar

Maeda, G., Neumann, G., Ewerton, M., Lioutikov, R., and Peters, J. (2015). “A probabilistic framework for semi-autonomous robots based on interaction primitives with phase estimation,” in Intl. Symp. on Robotics Research (Sestri Levante: IEEE), 1–16.

Google Scholar

Medina, J., Lawitzky, M., Mortl, A., Lee, D., and Hirche, S. (2011). “An experience-driven robotic assistant acquiring human knowledge to improve haptic cooperation,” in IEEE/RSJ Intl. Conf. on Intelligent Robots and Systems (IROS) (San Francisco, CA: IEEE), 2416–2422.

Google Scholar

Mitchell, C., Harper, M., and Jamieson, L. (1995). On the complexity of explicit duration HMM’s. IEEE Trans. Speech Audio Process. 3, 213–217. doi:10.1109/89.388149

CrossRef Full Text | Google Scholar

Murata, S., Yamashita, Y., Arie, H., Ogata, T., Tani, J., and Sugano, S. (2014). “Generation of sensory reflex behavior versus intentional proactive behavior in robot learning of cooperative interactions with others,” in Joint IEEE Intl. Conf. on Development and Learning and Epigenetic Robotics (Genoa: IEEE), 242–248.

Google Scholar

Nose, T., Kato, Y., and Kobayashi, T. (2007). “Style estimation of speech based on multiple regression hidden semi-Markov model,” in INTERSPEECH (Antwerp: ISCA), 2285–2288.

Google Scholar

Paraschos, A., Daniel, C., Peters, J., and Neumann, G. (2013). “Probabilistic movement primitives,” in Neural Information Processing Systems (NIPS) (Lake Tahoe: Curran Associates, Inc.), 2616–2624.

Google Scholar

Rabiner, L. (1989). “A tutorial on hidden Markov models and selected applications in speech recognition,” in Proceedings of the IEEE (New York, NY: IEEE), 257–286.

Google Scholar

Rozo, L., Bruno, D., Calinon, S., and Caldwell, D. G. (2015). “Learning optimal controllers in human-robot cooperative transportation tasks with position and force constraints,” in IEEE/RSJ Intl. Conf. on Intelligent Robots and Systems (IROS) (Hamburg: IEEE), 1024–1030.

Google Scholar

Rozo, L., Calinon, S., Caldwell, D. G., Jiménez, P., and Torras, C. (2013a). “Learning collaborative impedance-based robot behaviors,” in AAAI Conf. on Artificial Intelligence (Bellevue: AAAI Press), 1422–1428.

Google Scholar

Rozo, L., Jiménez, P., and Torras, C. (2013b). “Force-based robot learning of pouring skills using parametric hidden Markov models,” in IEEE-RAS Intl. Workshop on Robot Motion and Control (RoMoCo) (Wasowo: IEEE), 227–232.

Google Scholar

Strang, G. (1986). Introduction to Applied Mathematics. Wellesley, MA: Wellesley-Cambridge Press.

Google Scholar

Stulp, F., Grizou, J., Busch, B., and Lopes, M. (2015). “Facilitating intention prediction for humans by optimizing robot motions,” in IEEE/RSJ Intl. Conf. on Intelligent Robots and Systems (IROS) (Hamburg: IEEE), 1249–1255.

Google Scholar

Sugiura, K., Iwahashi, N., Kashioka, H., and Nakamura, S. (2011). Learning, generation, and recognition of motions by reference-point-dependent probabilistic models. Adv. Robot. 25, 825–848. doi:10.1163/016918611X563328

CrossRef Full Text | Google Scholar

Tokuda, K., Masuko, T., Yamada, T., Kobayashi, T., and Imai, S. (1995). “An algorithm for speech parameter generation from continuous mixture HMMs with dynamic features,” in Proc. European Conference on Speech Communication and Technology (EUROSPEECH) (Madrid: ISCA), 757–760.

Google Scholar

Wang, Z., Mülling, K., Deisenroth, M., Amor, H. B., Vogt, D., Schölkopf, B., et al. (2013). Probabilistic movement modeling for intention inference in human-robot interaction. Int. J. Robot. Res. 32, 841–858. doi:10.1177/0278364913478447

CrossRef Full Text | Google Scholar

Wilcox, R., Nikolaidis, S., and Shah, J. (2012). “Optimization of temporal dynamics for adaptive human-robot interaction in assembly manufacturing,” in Robotics: Science and Systems (R:SS) (Sydney: MIT Press), 1–8.

Google Scholar

Yamagishi, J., and Kobayashi, T. (2005). “Adaptive training for hidden semi-Markov model,” in IEEE Intl. Conf. on Acoustics, Speech, and Signal Processing (ICASSP) (Philadelphia, PA: IEEE), 365–368.

Google Scholar

Yamazaki, T., Naotake, N., Yamagishi, J., and Kobayashi, T. (2005). “Human walking motion synthesis based on multiple regression hidden semi-Markov model,” in IEEE Intl. Conf. on Cyberworlds (CW) (Singapore: IEEE), 452–459.

Google Scholar

Yu, S. (2010). Hidden semi-Markov models. Artif. Intell. 174, 215–243. doi:10.1016/j.artint.2009.11.011

CrossRef Full Text | Google Scholar

Yu, S., and Kobayashi, T. (2006). Practical implementation of an efficient forward-backward algorithm for an explicit-duration hidden Markov model. IEEE Trans. Signal Process. 54, 1947–1951. doi:10.1109/TSP.2006.872540

CrossRef Full Text | Google Scholar

Zen, H., Tokuda, K., and Kitamura, T. (2007a). Reformulating the HMM as a trajectory model by imposing explicit relationships between static and dynamic feature vector sequences. Comput. Speech Lang. 21, 153–173. doi:10.1016/j.csl.2006.01.002

CrossRef Full Text | Google Scholar

Zen, H., Tokuda, K., Masuko, T., Kobayashi, T., and Kitamura, T. (2007b). A hidden semi-Markov model-based speech synthesis system. IEICE Trans. Inform. Syst. E90-D, 825–834. doi:10.1093/ietisy/e90-d.3.692

CrossRef Full Text | Google Scholar