Space as an Invention of Active Agents

The question of the nature of space around us has occupied thinkers since the dawn of humanity, with scientists and philosophers today implicitly assuming that space is something that exists objectively. Here, we show that this does not have to be the case: the notion of space could emerge when biological organisms seek an economic representation of their sensorimotor flow. The emergence of spatial notions does not necessitate the existence of real physical space, but only requires the presence of sensorimotor invariants called “compensable” sensory changes. We show mathematically and then in simulations that naive agents making no assumptions about the existence of space are able to learn these invariants and to build the abstract notion that physicists call rigid displacement, independent of what is being displaced. Rigid displacements may underly perception of space as an unchanging medium within which objects are described by their relative positions. Our findings suggest that the question of the nature of space, currently exclusive to philosophy and physics, should also be addressed from the standpoint of neuroscience and artificial intelligence.

1. Introduction

How do we know that there is space around us? Our brains sit inside the dark bony cavities formed by the skull, with myriads of sensorimotor signals coming in and going out. From this immense flow of spikes, our brains conclude that there is such thing as space, filled with such things as objects, and that there is such thing as body – a special type of object which brains have most control over. Taking this “tabula rasa” approach, it is not clear what constitutes space as something discoverable in the sensory information, or, in other words, how space manifests itself to a naive agent that has no information other than its undifferentiated sensory inputs and motor outputs.

Poincaré (1905) was among the first to recognize this problem and to attempt its mathematical formalization. He suggested that space can manifest itself through what he called “compensable changes”: such changes in the world, which the agent can nullify by its own action. For example, consider standing in front of a red ball. The light reflected from the ball is projected into the retina where it creates excitation of the sensory cells. If now the ball displaces 1 m away the input to the retina becomes different from what it was before. Yet, you can make the input to be the same as before if you walk 1 m in the same direction as the ball. It is through this ability to nullify the changes in the environment that we learn about space (Poincaré, 1905). This approach was further developed by Nicod (1929), who showed, among other things, that temporal sequences can be used to determine the topology of space. After Nicod, this line of research was for long time discontinued, until it was reinitiated in the field of artificial intelligence and robotics (Kuipers, 1978; Pierce and Kuipers, 1997). Nowadays, a whole body of work has accumulated describing how robotic agents can build models of themselves and their environments (Kaplan and Oudeyer, 2004; Klyubin et al., 2004, 2005; Gloye et al., 2005; Bongard et al., 2006; Hersch et al., 2008; Hoffmann et al., 2010; Gordon and Ahissar, 2011; Sigaud et al., 2011; Koos et al., 2013). However, the question of the acquisition of the spatial concepts as something independent of particular sensory coding remains rather poorly studied [however, see Philipona et al. (2003), Roschin et al. (2011), and Laflaquiere et al. (2012)].

In the current paper, we show how a naive agent can acquire spatial notions in the form of internalized (or “sensible,” cf., Nicod, 1929) rigid displacements. We show that being equipped with such notions the agent can solve spatial tasks that would be unsolvable in the metric of the original sensory inputs. Moreover, we show that notions indistinguishable from internalized rigid displacements can be built by an agent inhabiting a spaceless universe. We thus suggest that the notion of space we possess is a construct of our perceptual system, based on certain sensorimotor invariants, which, however, do not necessitate the objective existance of space.¹

2. Illustration of Principle

To illustrate the principle, consider first the sensory universe or “Merkwelt” (cf von Uexküll, 1957) of the one-dimensional agent in Figure 1. Note that in the present work, we are attempting a proof of concept showing that an agent interacting with the world could adduce the notion of space. For this reason, we will be assuming that the agent is equipped with sufficient memory and computational resources to perform the necessary manipulation of the sensorimotor information.

FIGURE 1

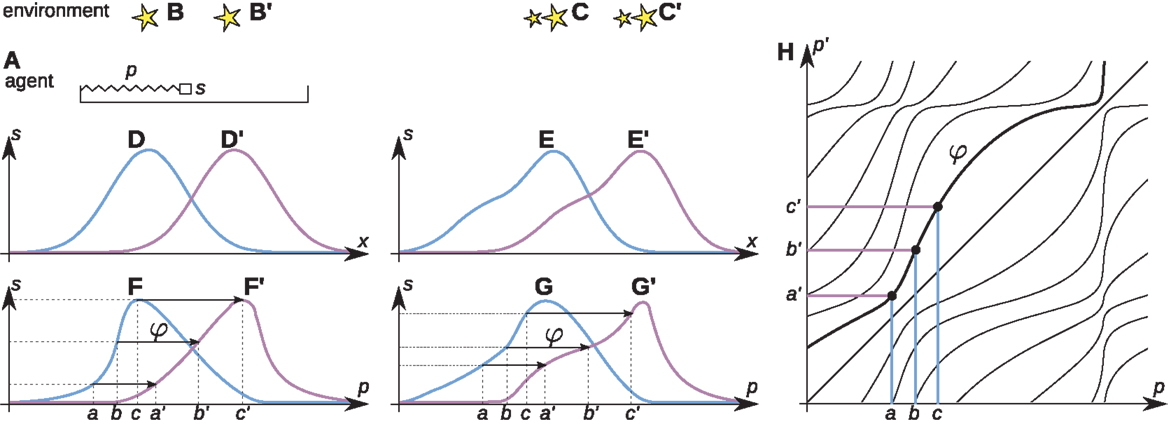
Figure 1. Algorithm of space acquisition illustrated with a simplified agent. The agent (A) has the form of a tray, inside which a photoreceptor s moves with the help of a muscle, scanning the environment (B) composed of scattered light sources. The length of the muscle is linked to the output of the proprioceptive cell p in a systematic, but unknown way. The output of the photoreceptor depends on its position x in real space (D). The agent learns the sensorimotor contingency (F) linking p and s. After a rigid displacement of the agent, or a corresponding displacement of the environment from (B) to (B′), the output of the photoreceptor changes from (D) to (D′) and a new sensorimotor contingency (F′) is established. For a sufficiently small rigid displacement, the outputs of the photoreceptor will overlap before and after the displacement. The agent makes a record of the corresponding proprioceptive values between the sensorimotor contingency (F,F′) (arrows from a, b, c to a′, b′, c′) and constructs the function p′ = φ(p) [(H), bold line]. Different functions φ [thin lines in (H)] correspond to different rigid displacements. If the agent faces a different environment (C) and makes a rigid displacement equivalent to its displacement to (C′), the outputs of the photoreceptor change from (E) to (E′) and the corresponding sensorimotor contingency changes from (G) to (G′). Yet, because of the existence of space, the same function φ links (G) to (G′). The tests in Figures 3–6 show that the functions φ constitute the basis of spatial knowledge. Reproduced with permission from Terekhov and O’Regan (2014) © 2016 IEEE.

Assume (though this is not known to the agent’s brain) that its body is composed of a single photoreceptive sensor that can move laterally inside its body using a “muscle” (Figure 1A). Assume a one-dimensional environment as in Figure 1B, and assume first that it is static. If the agent were to perform scanning actions with the muscle and were to plot photoreceptor output against the photoreceptor’s actual physical position, it would obtain a plot such as Figure 1D. But it cannot do this because it has no notion, let alone any measure, of physical position, and only has knowledge of proprioception. The agent can only plot photoreceptor output against proprioception, and so obtains a distorted plot as in Figure 1F. This “sensorimotor contingency” (MacKay, 1962; O’Regan and Noë, 2001) is all that the agent knows about. It does not know anything about the structure of its body and sensor, let alone that there is such a thing as space in which it is immersed. Indeed, the agent does not need such notions to understand its world, since its world is completely accounted for by its knowledge of the sensorimotor contingency it has established by scanning.

But now suppose that the environment can move relative to the agent, for example, taking Figures 1B,B′. The previously plotted sensorimotor contingency will no longer apply, and a different plot will be obtained (e.g., Figure 1F′). The agent goes from being able to completely predict the effects of its scanning actions on its sensory input, to no longer being able to do so.

However, there is a notable fact which applies. Although the agent does not know this, physicists looking from outside the agent would note that if the displacement relative to the environment is not too large, there will be some overlap between the physical locations scanned before and after the displacement. In this overlapping region, the sensor occupies the same positions relative to the environment as it occupied before the displacement occurred. Since sensory input depends only on the position of the photoreceptor relative to the environment, the agent will thus discover that for these positions the sensory input from the photoreceptor will be the same as before the displacement.

Registering such a coincidence is not uncommon for an agent with a single photoreceptor, but the same would happen for an agent with numerous receptors. For such a more complicated agent, the coincidence would be extremely noteworthy.

In an attempt to better “understand” its environment, the agent will thus naturally make a catalog of these coincidences (cf. arrows in Figures 1F,F′), and so establish a function φ linking the values of proprioception observed before a change to the corresponding values of proprioception after the change. Such a function for all values of proprioception is shown in Figure 1H.

Assume that over time, the environment displaces rigidly to various extents, with the agent located initially at various positions. Furthermore, assume that such displacements can happen for entirely different environments (e.g., Figure 1C). Since the sensorimotor contingencies themselves depend on all these factors, it might be expected that different functions φ would have to be cataloged for all these different cases. Yet, it is a remarkable fact that the set of functions φ is much simpler: for a given displacement of the environment, the agent will discover the same functions φ, even when this displacement starts from different initial positions, and even when the environment is different.

We shall see below that this remarkable simplicity of the functions φ provides the agent with the notion of space. But, first let us see where the simplicity derives from.

Each function φ links proprioceptive values before an environmental change to proprioceptive values after the change, in such a way that for the linked values the outputs of the photoreceptor match before and after the change. Seen from outside the agent, the physicist would know that this situation will occur if the agent’s photoreceptor occupies the same position relative to the environment before and after the environmental change. And this will happen if (1) the environment makes a rigid displacement, and if (2) the agent’s photoreceptor makes a rigid displacement equal to the rigid displacement of the environment. Thus, physicists looking at the agent would know that the functions φ actually measure, in proprioceptive coordinates, rigid physical displacements of the environment relative to the agent (or vice versa) (see Section 6).

Let us stress again that a priori there was no reason at all why the φ functions for different starting points should be the same for a given displacement, and the same for all environments. But now, we can understand why the set of functions φ is so simple: it is because a defining property of rigid displacements is that they are independent of their starting points, and independent of the properties of what is being displaced.

The functions φ can thus be seen as perceptual constructs equivalent to physical rigid displacements, or one could say, following Nicod (1929), that they are sensible rigid displacements, where sensible refers to the fact that they are defined within the Merkwelt of the agent.

3. Results

To illustrate that these sensible rigid displacements or functions φ really have the properties of real physical rigid displacements, we will use computer simulations with the more complex two-dimensional agent described in Figure 2. The details of the simulation are presented in the Methods (section 5). In Formalization (section 6), we show that the demonstration applies to an arbitrarily complicated agent, with certain restrictions.

FIGURE 2

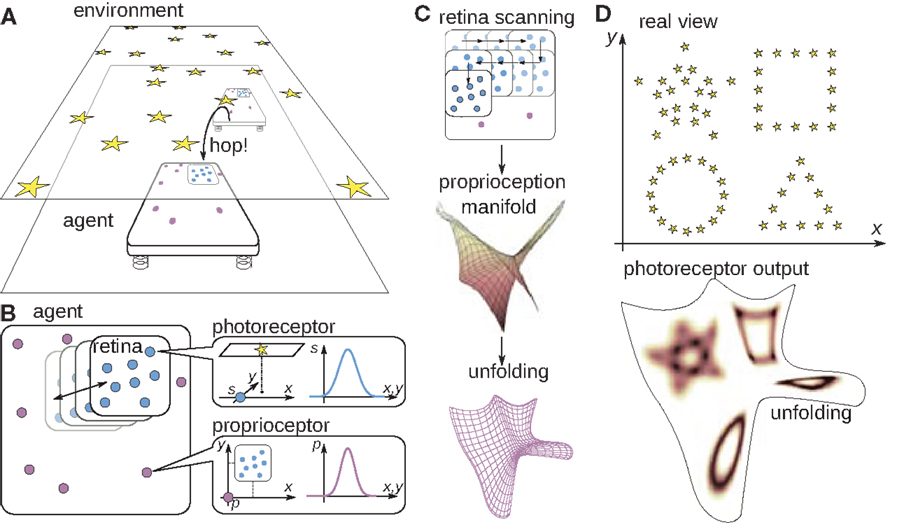
Figure 2. The tray-like two-dimensional agent. (A) The agent inhabits a plane where it can perform uncontrolled hops (or equivalently, the environment can shift through unknown distances), resulting in the translation of the agent’s body in an unknown direction through an unknown distance. Outside of the agent’s plane there is an environment made of light sources. The agent can sense the light sources with nine photoreceptors placed on its mobile retina (B), which can translate with the help of muscles, and whose position is sensed by eight pressure-sensitive proprioceptive cells scattered over the agent’s body. As the retina performs the scanning motion (C), the proprioceptors take values lying in a two-dimensional proprioceptive manifold inside the eight-dimensional space of the possible proprioceptive outputs. This manifold can be unfolded into a plane. (D) An example environment and the output of one photoreceptor over this unfolding as the agent performs scanning movements of the retina. This unfolding will be used hereafter in order to illustrate the outputs of the photoreceptors as the agent performs scanning movements of the retina.

In Figure 3, the two-dimensional simulated agent is first shown an environment that makes a certain displacement (or the agent makes an equivalent hop relative to the environment). The agent is then shown two other instances of the same displacement, but with two completely different environments. Even though in each case, the sensory experiences of the agent are different, and even though they change in different ways, the Figure shows that the same function φ can be used to account for these changes. This is what is to be expected from a notion of rigid displacement, which should not depend on the content of what is displaced.

FIGURE 3

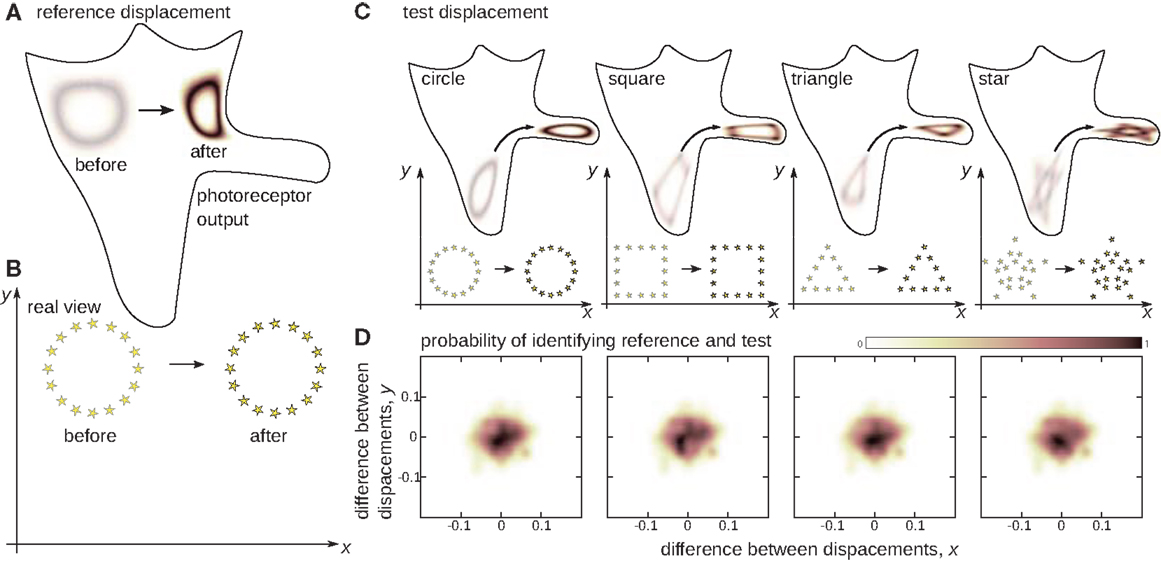
Figure 3. The notion of sensible rigid displacements. Seemingly different changes in sensory input will be associated if they correspond to the same displacement in real physical space. The 2D agent is presented with a reference displacement of the environment (B), which it scans before and after the displacement. The output of one of the photoreceptors over the unfolded proprioceptive manifold (Figure 2C) is presented in (A). Then the agent is presented with test displacements (C) from different initial positions and for different environments. Even though the test displacements may strongly alter the shape of the reference, the agent succeeds in associating test and reference if they correspond to the same physical displacement (D). This ability of the agent provides the basis of the notion of displacement independent of the environment.

Figure 4 shows further that, once equipped with the notion of sensible rigid displacement, the agent is well on its way toward understanding space. In particular, sensible rigid displacements endow the agent with the percept of space as an unchanging medium, which implies being able to distinguish between the sensory changes caused by the proper movements of the agent from those reflecting the deformation of the environment. Figure 4 shows how the simulated agent is able to distinguish between the two despite the fact that in the sensory input a rigid shift may look like a deformation (Figure 4C), while deformations may seem just like a minor displacement (Figure 4B).

FIGURE 4

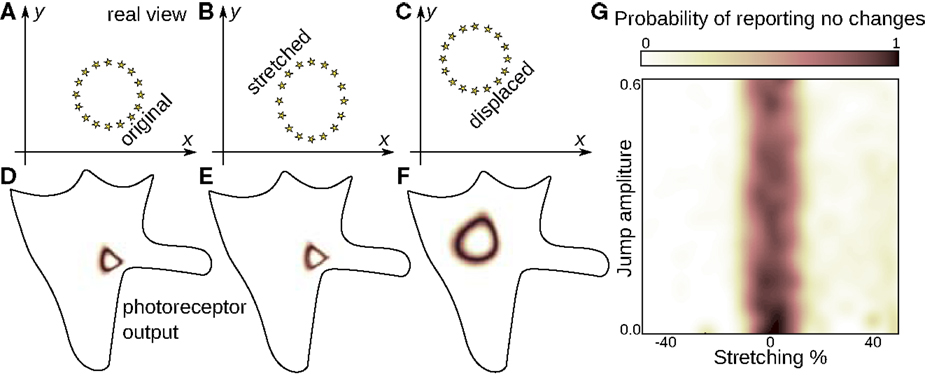
Figure 4. The notion of space as unchanging medium. The 2D agent can distinguish between the sensory changes provoked by its own movement and those resulting from the joint effect of its own motion and changes in the environment. The agent is presented with an environment (A) which it scans (D). Then the agent makes a jump and simultaneously the environment is stretched or shrunk along one axis by a certain amount (B), which can be zero (C). The agent is to judge whether the environment was the same before and after the jump. Note that the visual input in the modified environment (E) resembles the original (D) more than it does the unchanged environment (F). Yet, the agent can successfully identify the case when the environment does not change, and it can do this independently of the extent of the jumps (G). This ability of the agent underlies the notion of space as an unchanging medium through which the agent makes displacements.

Figure 5 shows that the agent can define the notion of relative position of A with respect to B. This notion is more abstract than displacement, as there exist numerous paths leading from B to A, while relative position is independent of the choice of a particular path. The notion of relative position allows the agent to “understand” that it is at the same “somewhere” independently of how it got there. To define the notion of relative position, the agent must be able to take different combinations of displacements having the same origin and destination, and consider them as equivalent.

FIGURE 5

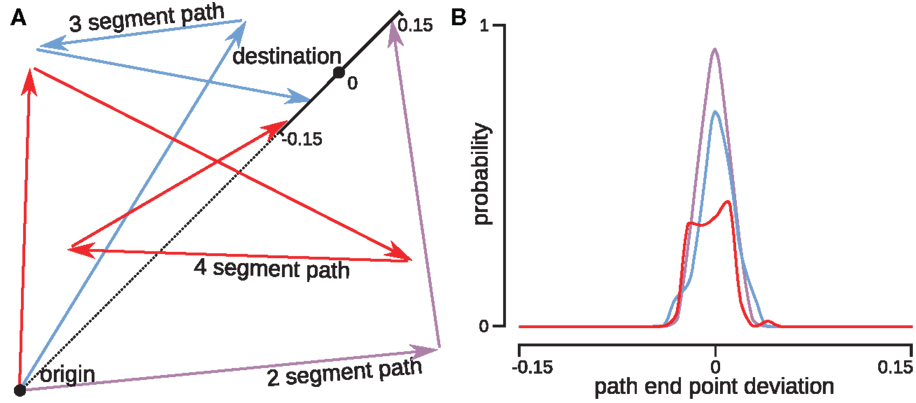
Figure 5. The notion of relative position, independent of the connecting path. The 2D agent can construct the notion of relative position of a destination point with respect to an origin by associating all possible paths connecting the origin to the destination. The agent was presented with a reference single-segment path. Then it was returned to the origin and moved along two-, three-, or four-segment paths with possibly different destination points at a distance in the range [−0.15, 0.15] from the destination of the reference path; all points were chosen on the same straight line (A). The surrounding environment was altered at every path presentation in order to ensure that the agent calculated the displacement instead of comparing the view at the destination points. The agent successfully associated together paths which arrived close to the original destination point. This association was more accurate for the 2-segment path, and became weaker as the number of path segments increased (B). This can be explained by accumulation of the integration error.

4. Discussion

We have shown that, without assuming a priori the existence of space, the agent invents the notions of sensible displacement, unchanging medium and relative position. These notions allow the agent to conceive of its environment in a way that we can assimilate to possessing the notion of space. The agent can now separate the properties of its sensed environment into properties a physicist would call spatial (position, orientation) and non-spatial (shape, color, etc). These are the properties whose changes the agent respectively can and cannot account for in terms of sensible rigid displacements. Several further points should be mentioned.

The method that the agent uses to “invent” its notion of space involves defining φ functions from matching sensory signals. As is the case for temporal coincidence, this can be understood as a strategy of associating causes that lead to the same consequences (Markram et al., 2011). This is a productive learning strategy in general and is easily implementable in neural hardware.

Note, however, that constructing sensible rigid displacements on the basis of matches is only possible if sensory changes caused by modifications in the environment can be compensated (i.e., equalized or canceled) by the agent’s own action. The conditions for this to be possible are (1) that the agent be able to act,² and (2) that appropriate compensatory changes can occur in the environment. The agent’s own actions are thus crucial for the acquisition of the notion of space. Of course, if the agent knows in advance that there is space, it may be able to reconstruct it without acting. But if the agent has limited action capacities, it will not invent space “correctly.” In particular, the simple two-dimensional agent we have considered has a retina that can translate, but cannot rotate. This agent will therefore classify relative position, but not orientation, as being a spatial property. Evidence from biology also shows the importance of action in the acquisition of spatial notions: an example is the classic result of Held and Hein (1963).

In addition to action, sufficient richness of the environment is essential for an agent to discover space. If for example displacement in a certain direction has no sensory consequences, or if they are ambiguous, then the agent will be unable to learn the corresponding sensible rigid displacements. Again this is coherent with biology, where it has been shown (Blakemore and Cooper, 1970) that kittens raised in visual environments composed of vertical stripes are blind to displacements of horizontally aligned objects and vice versa.

Another point worth mentioning is the fact that sensible rigid displacements are nothing but abstract constructs – they do not imply that something really moves: if the agent inhabited a different physical universe but where the sensorimotor regularities were the same, then it would develop the same construct of sensible rigid displacement. For example in Audio Agent (section 7), we describe an agent whose world consists only of sounds, but that develops sensible rigid displacements in pitch analogous to the spatial constructs of the agent in Figure 1.

A final point concerns the statistical approaches often used up to now to understand brain functioning (Zhaoping, 2006; Ganguli and Sompolinsky, 2012). Such approaches use statistical correlations to compress the data observed in sensory and motor activity. It is possible that these approaches may be adapted to capture the “algebraic” notion of mutual compensability between environment changes and an agent’s actions that is instantiated by the functions φ and that is essential for understanding the essence of space.

In conclusion, the three-dimensional space we perceive could be nothing but a construct, which simplifies the representation of information provided by our limited senses in response to our limited actions. In reality space – if it exists – may have a higher number of dimensions, most of which we perceive as non-spatial properties because of our inability to perform corresponding compensatory movements. Or, conversely, there may in fact be no physical space: our impression that space exists may be nothing but a gross oversimplification generated by our perceptual systems, with the real world only being very approximately describable as a collection of “objects” moving through an “unchanging medium.”

5. Methods

5.1. Agent

The two-dimensional agent from Figure 2 was simulated to illustrate the acquisition of spatial knowledge. The agent has a square body in a form of a tray, within which a square retina translates. We choose the measurement units so that the retina movements are confined to a unit square. The position x, y of the retina is registered by proprioceptors scattered over the body surface and having outputs

$p_j=\exp \left\{-\frac{{\left(d_j^p\right)}^2}{{\left({\mathrm{\sigma }}_j^p\right)}^2}\right\},$

where $d_j^p$ is the distance between the center of the retina and the location of the j-th proprioceptor, and ${\sigma }_j^p$ is its acuity.

The retina is covered with photoreceptors, measuring the intensity of the light coming from N_ℓ spot light sources located in a plane above the agent. The response of j-th photoreceptor is

$s_j={\displaystyle \sum _{i=1}^{N_{\ell }}}{I}_i\exp \left\{-\frac{{\left(d_{\mathit{ij}}^s\right)}^2}{{\left({\mathrm{\sigma }}_j^s\right)}^2}\right\},$

where $d_{\mathit{ij}}^s$ is the distance between the projection of the i-th light source onto the plane of the agent and the j-th photoreceptor; I_i is the intensity of the i-th light source, and ${\sigma }_j^s$ is the acuity of the j-th photoreceptor.

For the simulations presented in the paper we deliberately distributed the eight proprioceptors over the agent’s body in a non-uniform way so as to ensure a certain amount of distortion of the image in Figures 3–5. Their acuities ${\sigma }_j^p$ was set to 0.3 for all receptors. The positions of the nine photoreceptors were drawn randomly from a square with sides of length 0.3. The acuity of the receptors ${\sigma }_j^s$ took random values between 0.03 and 0.3. Due to the retinal mobility the agent’s “field of view” was a 1.0 × 1.0 square centered at what we call the agent’s position.

5.2. Learning Functions φ

The agent was placed into the environment with 200 light sources distributed randomly in 3 × 3 square, centered at the agent’s initial position (see Figure 6). The agent scanned the environment by moving the retina inside the body and tabulating the tuples of proprioceptive and photoreceptive inputs $\langle p_k,s_k\rangle$. The agent then jumped to a new position, which was within a 1.8 × 1.8 square centered at its initial position, and again scanned the environment and tabulated the tuples $\langle p_k^{\prime },s_k^{\prime }\rangle$. The agent then looked for the co-occurrences $s_k=s_{k\prime }^{\prime }$ and put the corresponding proprioceptive inputs into pairs $\langle p_k,p_{k\prime }^{\prime }\rangle$. The function φ was then defined as the set of all such pairs.

FIGURE 6

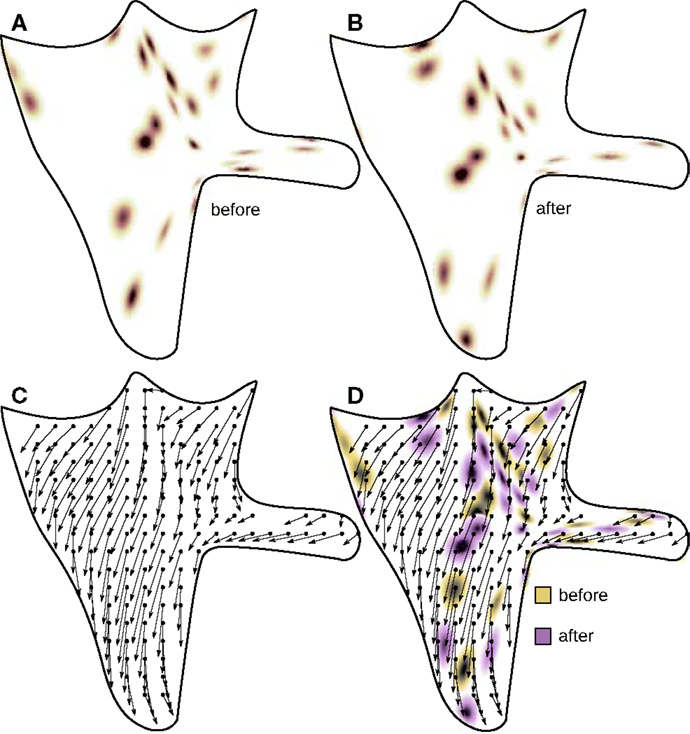
Figure 6. Acquisition of φ functions. The agent scans the environment composed of random light sources before (A) and after (B) a rigid displacement caused by the agent’s jump. The corresponding function φ is illustrated in (C) with the arrows connecting points of coinciding photoreceptor outputs before (the origin of the arrow) and after the jump (the end of the arrow). (D) illustrates the meaning of the function φ, which is the field of the proprioceptive changes necessary to compensate changes in photoreceptors induced by the rigid motion (jump).

Exclusively for the sake of code optimization when “scanning” the environment the retina moved over a regular 201 × 201 grid. The outputs of the photoreceptors were considered as matching if for every photoreceptor the difference of the outputs before and after the jump was less than 0.005. The corresponding values of proprioception before and after the jump were taken to form the function φ. If the value of every proprioceptor in one pair differed by less than 0.01 from the value of proprioceptor in the other pair, then one of the pairs was discarded. The destination points of the agent’s jumps also belonged to a regular grid centered at the agent’s initial position and having a step size of 0.02. In total, we obtained 8281 different functions φ.

It must be emphasized here that though we used only rigid displacements of the environment for learning the φ functions, the result would have been essentially the same if arbitrary deformations of the environment were allowed. For instance, in our pilot simulations, we allowed the environment to shift and then deform along one of the axes, and then computed the corresponding φ functions. We found that the φ functions for such non-rigid changes of the environment contained less than 3% of what a pure rigid displacement would contain and depended heavily upon the particular environment used. Thus, introducing a simple criterion, like retaining only those φ functions with a certain number of points, and running the simulations for both rigid and non-rigid changes would produce essentially the same functions φ as running the simulations for rigid displacements only.

5.3. Sensible Rigid Displacement

The agent was facing 40 light sources distributed uniformly along a circle with 0.1 radius. The center of the circle was chosen randomly within a 1.0 × 1.0 square centered at the agent. In the reference displacement, all stars moved as a whole to a new random position, which was also within a 1.0 × 1.0 square. The agent determined the function φ corresponding to the reference displacement. Then the agent was shown one of four objects shown in Figure 3: the same circle, a square (composed of 40 lights), a triangle (39 lights), or a star (40 lights). The square and triangle had sides of length 0.2, and the star had a ray length 0.3. The objects underwent a random test displacement with initial and final positions within a 1.0 × 1.0 square. In order to save simulation time, we only considered displacements which differed from the reference by no more than 0.1 for each axis. The agent determined the functions $\tilde{\phi }$ for each of the tests and computed the distance between φ and $\tilde{\phi }$ as

$\mathrm{\rho }\left(\mathrm{\phi },\stackrel{\sim }{\mathrm{\phi }}\right)={\displaystyle \sum _{k\prime ,\tilde{k}\prime :p_k={\tilde{p}}_{\tilde{k}}}}\parallel p_{k\prime }^{\prime }-{\tilde{p}}_{\tilde{k}\prime }^{\prime }\parallel ,$ (1)

where ||⋅|| is a euclidean distance in the proprioception space. The agent identified two displacements as the same if the error was below a threshold which was chosen so that 90% of displacements of size less than 0.005 were considered identical. The procedure was repeated 1,000 times.

5.4. Unchanging Medium

The agent was facing 40 light sources distributed uniformly over a circle with radius 0.1. The center of the circle was chosen randomly in a 0.4 × 0.4 square centered at the agent. The agent scanned the environment and tabulated the tuples $\langle p_k,s_k\rangle$. Then the agent made a jump to a random point located in a 0.6 × 0.6 square and simultaneously the circle was randomly stretched or shrunk by up to 50% along a fixed axis. Only those jump destinations were considered for which the agent could “see” the entire circle. The agent scanned the environment again and tabulated new tuples $\langle p_k^{\prime },s_k^{\prime }\rangle$. The agent then searched for a function φ which gave the best fit of the photoreceptors after the jump based on their values before the jump. In particular, the following error was computed:

$\mathrm{\epsilon }={\displaystyle \sum _{k=1}^{N_k}}\parallel s_k-s_{k\prime }^{\prime }\parallel ,$

where k′ was such that $\mathrm{\phi }\left(p_k\right)=p_{k\prime }^{\prime }$. If the error was below the threshold, the agent assumed that the environment did not change during the jump. The threshold value of the error was chosen in such a way that the agent answered correctly in 90% of cases when the deformation of the circle was below 0.5%. Figure 2 shows the result of simulations computed on the basis of 10,000 repetitions of the test.

5.5. Relative Position

The agent was facing an environment filled with 200 light sources with random locations and intensities. It was displaced from its original position to the destination point, which had coordinates (0.6, 0.6) relative to the agent’s initial position. The agent determined the reference function φ_ref, which gave the best account of the displacement-induced changes of the photoreceptor outputs. Then the environment was replaced with a new randomly generated environment, and the agent was moved along a path composed of several segments. At every intermediate point along the path, the agent determined the function φ_j accounting for the changes in photoreceptor values. The agent then computed the composition function φ_comp = φ_n ∘ ⋯ ∘ φ₁, where n is the number of path segments. For any two functions φ and $\stackrel{\sim }{\mathrm{\phi }}$ defined by sets of pairs $\langle p_k,p_{k\prime }^{\prime }\rangle$ and $\langle {\tilde{p}}_{\tilde{k}},p_{\tilde{k}\prime }^{\prime }\rangle$ the composition $\tilde{\phi }$ ∘ φ was defined as a set of pairs $\langle p_k,p_{\tilde{k}\prime }^{\prime }\rangle$, such that $p_{k\prime }^{\prime }={\tilde{p}}_{\tilde{k}}$. The distance between φ_ref and φ_comp was computed using formula 1. The test and reference paths were assumed to correspond to the same relative position if the distance was below the same threshold as for the sensible rigid displacements. The procedure was repeated 1,000 times for two-, three-, and four-segment paths. Each intermediate point of the path was within the 0.9 × 0.9 square centered at the original position. In order to reduce simulation time the final points of all paths lay on the same line and were not more than 0.1 away from the origin.

6. Formalization

Here, we consider a general agent immersed in real physical space. Later, we will abandon the assumption of the existence of physcial space and give the conditions for the emergence of perceptual “space-like” constructs independently of whether they correspond to any real physical space.

Let s be the vector of the agent’s exteroceptor outputs. The exteroceptors are connected to a body, assumed to be rigid, whose position and orientation is described by a spatial coordinate defined by the vector x. For every environment ℰ, the outputs of the exteroceptors are defined by a function

$s={\mathrm{\sigma }}_{\mathcal{E}}\left(x\right).$ (2)

We assume that this function has the property that if the environment ℰ makes a rigid motion and becomes ℰ′, then there exists a rigid transformation T of entire space such that

$s\prime ={\mathrm{\sigma }}_{\mathcal{E}\prime }\left(x\right)={\mathrm{\sigma }}_{\mathcal{E}}\left(T\left(x\right)\right).$ (3)

Proprioception p reports the position of the exteroceptors in the agent’s body. For a given position of the agent 𝒳 we assume there is a function π_𝒳 such that

$p={\mathrm{\pi }}_{\mathcal{X}}\left(x\right).$ (4)

Again, the function π_𝒳 has the property that the agent’s displacement to a position 𝒳′ can be accounted for by the rigid transformation 𝒯 of entire space:

$p\prime ={\mathrm{\pi }}_{\mathcal{X}\prime }\left(x\right)={\mathrm{\pi }}_{\mathcal{X}}\left(\mathcal{T}\left(x\right)\right).$ (5)

Assuming that proprioception unambigously defines the position of the exteroceptors in space

$x={\mathrm{\pi }}_{\mathcal{X}}^{-1}\left(p\right)$

and

$s=\left({\mathrm{\sigma }}_{\mathcal{E}}\circ {\mathrm{\pi }}_{\mathcal{X}}^{-1}\right)\left(p\right)$

where the function $\left({\mathrm{\sigma }}_{\mathcal{E}}\circ {\mathrm{\pi }}_{\mathcal{X}}^{-1}\right)$ is the sensorimotor contingency learned by the agent for every position 𝒳 of itself and of the environment ℰ.

When the agent or the environment moves, a new sensorimotor contingency is established

$s\prime =\left({\mathrm{\sigma }}_{\mathcal{E}\prime }\circ {\mathrm{\pi }}_{\mathcal{X}\prime }^{-1}\right)\left(p\prime \right)=\left({\mathrm{\sigma }}_{\mathcal{E}}\circ T\circ \mathcal{T}-1\circ {\mathrm{\pi }}_{\mathcal{X}}^{-1}\right)\left(p\prime \right).$

The agent learns the function φ linking the values p and p′ such that s = s′, or

$\left({\mathrm{\sigma }}_{\mathcal{E}}\circ {\mathrm{\pi }}_{\mathcal{X}}^{-1}\right)\left(p\right)=\left({\mathrm{\sigma }}_{\mathcal{E}}\circ T\circ {\mathcal{T}}^{-1}\circ {\mathrm{\pi }}_{\mathcal{X}}^{-1}\right)\left(p\prime \right).$

The function φ is not always defined uniquely since the mapping σ_ℰ can be non-invertible. It can be inverted in the domain of its arguments if the environment is sufficiently rich, i.e., if the vector of exteroceptor outputs is different at every position of the exteroceptors within the range admitted by the proprioceptors. In this case

$\mathrm{\phi }={\mathrm{\pi }}_{\mathcal{X}}\circ \mathcal{T}\circ T^{-1}\circ {\mathrm{\pi }}_{\mathcal{X}}^{-1}.$ (6)

It can be seen from the expression for the function φ that it simply gives a proprioceptive account of the relative rigid displacement 𝒯 ∘ T⁻¹ of the environment and the agent. The functions φ are thus the agent’s extensible rigid displacements, which are associated with the environment’s rigid motion from ℰ to ℰ′ and the agent’s rigid motion from 𝒳 to 𝒳′. As is clear from equation 6, the function φ only depends on the transformations T and 𝒯. In physical space, these transformations depend only on the displacements themselves and are independent of the initial positions of the agent and the environment, and of the content of the environment. Moreover, since the transformations T and 𝒯 form Lie groups, the functions φ also inherit some group properties. For any two φ functions,

${\mathrm{\phi }}_1={\mathrm{\pi }}_{\mathcal{X}}\circ \mathcal{T}\circ T_1^{-1}\circ {\mathrm{\pi }}_{\mathcal{X}}^{-1}\text{and}{\mathrm{\phi }}_2={\mathrm{\pi }}_{\mathcal{X}}\circ {\mathcal{T}}_2\circ T_2^{-1}\circ {\mathrm{\pi }}_{\mathcal{X}}^{-1}.$

there exists a function φ₃ such that

${\mathrm{\phi }}_1\circ {\mathrm{\phi }}_2={\mathrm{\pi }}_{\mathcal{X}}\circ {\mathcal{T}}_1\circ T_1^{-1}\circ {\mathcal{T}}_2\circ T_2^{-1}\circ {\mathrm{\pi }}_{\mathcal{X}}^{-1}={\mathrm{\pi }}_{\mathcal{X}}\circ {\mathcal{T}}_3\circ T_3^{-1}\circ {\mathrm{\pi }}_{\mathcal{X}}^{-1}={\mathrm{\phi }}_3$

where 𝒯₃ and T₃ are transformations describing the total displacements of agent and of the environment, for which 𝒯₃ ∘ ${\mathcal{T}}_3^{-1}$ = 𝒯₁ ∘ ${\mathcal{T}}_1^{-1}$ ∘ 𝒯₂ ∘ ${\mathcal{T}}_2^{-1}$.

The functions φ do not form a group. This is because they are defined only on a subset of proprioceptive values, for which the exteroceptor outputs overlap before and after the shift. It may happen that the domain of definition of the function φ₃ is larger than that of φ₁ ∘ φ₂ and hence the composition φ₁ ∘ φ₂ is not one of the functions φ.

Up until this point we have assumed the existence of real physical space. Now, we would like to abandon this assumption, and only retain the conditions which allow the construction of the function φ. This gives us a list of requirements for the existence of “space-like” constructs. (1) There must be a variable x and functions σ_ℰ and π_𝒳 such that the outputs of the extero- and proprioceptors can be described by the equations (2) and (4), and the function π must be invertible. The agent must be able to “act,” i.e., induce changes in the variable x. (2) Moreover, there must exist (and be sufficiently often) changes of the environment ℰ → ℰ′ and/or of the agent 𝒳 → 𝒳′such that the equations (3) and (5) hold. The corresponding transformations T and/or 𝒯 must be applicable to all environments ℰ and external states of the agent 𝒳, and they must form a group with respect to the composition operator.

Note that the requirement (2) does not presume that there are no other types of changes of the environment and/or of the agent. The agent will identify only the changes possessing such a property as sensible rigid displacements and will obtain the functions φ that correspond to them.

Also note again that here we do not assume the existence of space. We only make certain assumptions regarding the structure of the sensory inputs that the agent can receive.

The agent presented in Figure 2 of the main text will only recognize translations as the spatial changes, because it can only translate its retina, and hence for this agent the variable x only includes the position of the retina in space, not its orientation.

One can imagine an agent that can stretch its retina in addition to translations and rotations. For such an agent, the variable x will include position, orientation, and stretching of the retina. If this agent can stretch its entire body, or if the environment has a tendency for such deformations, then stretching will be classified as a sensible rigid displacement similarly to translations and rotations.

One can also imagine an agent whose sensory inputs do not depend on physical spatial properties, but satisfy the requirements described above. Such an agent will develop a false notion of space, where it is not present. The description of such an agent is given below.

7. Audio Agent

Here, we show that an agent can develop incorrect spatial knowledge, i.e., that does not correspond to physical space, if the conditions presented in the previous section are satisfied. The agent, inspired by Jean Nicod, inhabits the world of sounds (Figure 7). Its environment is a continuously lasting sine wave, or a chord (Figure 7A). The agent consists of a hair-cell, which oscillates in response to the acoustic waves (Figure 7B). The amplitude of this oscillation is measured by an exteroceptor s. The response is maximal if the frequency f of one of the sine waves coincides with the eigenfrequency of the hair-cell.

FIGURE 7

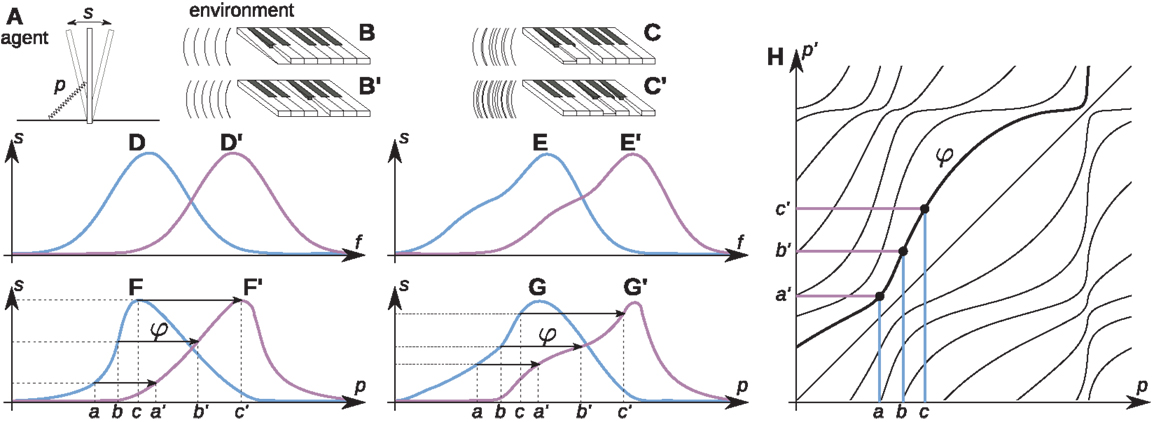
Figure 7. A simple audio agent. The agent (A) consists of a rod attached to a support, oscillating in response to the acoustic waves (B). The agent measures the intensity of this oscillation with an “exteroceptor” s. By exercising its muscle the agent can change the stiffness of the spring at the support and thus the eigenfrequency f of the rod, measured with the proprioceptor p. For an acoustic wave generated by a single note (A) the exteroceptor response s depends on the eigenfrequency f as shown in (D). However, the agent measures the proprioceptive response p and not the eigenfrequency, and so only has access to the sensorimotor contingency (F). The change of the note from (B) to (B′) results in a shift in the characteristics (D) to (D′) and in the establishment of a new sensorimotor contingency (F′). The agent can learn the functions φ (H) by taking note of the coincidences in the exteroceptor output s. If a pair of notes is played (C,C′) with the dependencies (E,E′), new sensorimotor contingencies are obtained by the agent (G,G′), yet the same functions φ link them together. Reproduced with permission from Terekhov and O’Regan (2014) © 2016 IEEE.

The agent can “scan” the environment by changing the stiffness at the cell’s attachment point and thus its eigenfrequency, which is measured by the proprioceptor p. For the environment B, the dependency between the amplitude and the cell’s eigenfrequency has the shape illustrated in Figure 7D. We assume that for any other note (like B′), the dependency between the amplitude and the cell’s eigenfrequency remains the same, but shifted (Figure 7D′).

The agent does not know these facts. It only knows the dependency between exteroception s and proprioception p, which constitutes the sensorimotor contingency (Figure 7F) corresponding to the environment B. For a new note (B′), a new sensorimotor contingency F′ is established. Yet, as before, the agent notices that the outputs of the exteroceptor s coincide for certain values of p. It makes note of these coincidences and defines the functions φ corresponding to all changes of the notes (Figure 7H).

The same procedure applies if the agent faces a chord of two (C and C′) or more notes. Instead of changes in the pitch of a note, we now have transposition of the whole chord. The agent can discover that the same set of functions φ works for notes and for chords.

Although this agent is unable to move in space and although it only perceives continuous sound waves, it can nevertheless build the basic notions of space. However, these notions are “incorrect,” in the sense that they do not correspond to actual physical space, but to the set of note pitches. The sensible rigid displacements for this agent correspond to transpositions of the chords. The unchanging medium is the musical scale, and the relative position of one chord with respect to an identical but transposed chord is just the interval through which the chord has been transposed. For such an agent, a musical piece is somehow similar to what a silent film is for us: it is a sequence of objects (notes), appearing, moving around (changing pitch), and disappearing.

Using the formalism introduced above, we can say that for this agent, the spatial variable is frequency, f. For any given environment ℰ, which in this case is constituted by simultaneously played notes, the output of the exteroceptor s depends only on the eigenfrequency of the hair-cell, which can be measured using the same variable f. This means that the function σ_ℰ(f) exists. The rigid shift of the environment ℰ to ℰ′, which is the chord transposition, results just in frequency scaling: σ_ℰ′(f) = σ_ℰ(kf). Evidently, these transformations form a group. Proprioception p signals the stiffness of the hair-cell, which is functionally related to its eigenfrequency, and hence the invertible function π(f) also exists. As our auditory agent is unable to perform anything similar to rigid displacements, the function π does not depend on anything equivalent to the state 𝒳 of our original simple agent (Figure 1).

The existence of the functions σ_ℰ(f) and π(f) fulfills the requirement (1) from the previous section. We can assume that music being played is just a piano exercise and hence the chords are often followed by their transposed versions. In this case there exist (and are sufficiently often) changes of the environment ℰ → ℰ′, which correspond to a simple shift of all played notes by the same musical interval. These shifts evidently form a group, and hence the requirement (2) is also fulfilled. The fulfilment of these two requirements suffices for the existence of sensible rigid displacements and thus for basic spatial knowledge, described above.

Author Contributions

AT and JO conceived and planned the study. AT coded computational experiments. AT and JO wrote the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank A. Laflaquière and G. Le Clec’H for fruitful discussions and suggestions improving the quality of the manuscript. Section 2, Figure 1 together with its caption and Figure 7 contain materials reprinted, with permission, from Terekhov, A.V. and O’Regan, J. K. (2014). Learning abstract perceptual notions: the example of space. In: Development and Learning and Epigenetic Robotics (ICDL-Epirob), 2014 Joint IEEE International Conferences on. p. 368–373. © 2016 IEEE.

Funding

The work was financed by ERC Advanced Grant Number 323674 “Feel” to JO.

Footnotes

1. ^While the present article concerns the notion of space, it would be extremely interesting to attempt a similar approach for the emergence of the notion of time. However at present we have no clear idea of how to do this. In the present article we have attempted to reduce assumptions about time to a minimum.
2. ^In the particular case of our agent the action involves moving the sensor within the agent’s body. This ensures that the agent has a reliable measure of the motion that it is producing, with, in particular, a one-to-one relation between muscle changes and physical changes. Our algorithm would have to be improved in order to allow cases where the agent moved its body using, for example, legs whose repeated action creates motion, since here there is no longer a one-to-one link between leg muscle command and physical change in space.

References

Blakemore, C., and Cooper, G. F. (1970). Development of the brain depends on the visual environment. Nature 228, 477–478. doi: 10.1038/228477a0

CrossRef Full Text | Google Scholar

Bongard, J., Zykov, V., and Lipson, H. (2006). Resilient machines through continuous self-modeling. Science 314, 1118–1121. doi:10.1126/science.1133687

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganguli, S., and Sompolinsky, H. (2012). Compressed sensing, sparsity, and dimensionality in neuronal information processing and data analysis. Annu. Rev. Neurosci. 35, 485–508. doi:10.1146/annurev-neuro-062111-150410

PubMed Abstract | CrossRef Full Text | Google Scholar

Gloye, A., Wiesel, F., Tenchio, O., and Simon, M. (2005). Reinforcing the driving quality of soccer playing robots by anticipation. Inf. Technol. 47, 250–257. doi:10.1524/itit.2005.47.5_2005.250

CrossRef Full Text | Google Scholar

Gordon, G., and Ahissar, E. (2011). “Reinforcement active learning hierarchical loops,” in Neural Networks (IJCNN), The 2011 International Joint Conference on (IEEE), (San Jose, CA: IEEE), 3008–3015.

Google Scholar

Held, R., and Hein, A. (1963). Movement-produced stimulation in the development of visually guided behavior. J. Comp. Physiol. Psychol. 56, 872–876. doi:10.1037/h0040546

CrossRef Full Text | Google Scholar

Hersch, M., Sauser, E. L., and Billard, A. (2008). Online learning of the body schema. Int. J. HR 5, 161–181. doi:10.1142/S0219843608001376

CrossRef Full Text | Google Scholar

Hoffmann, M., Marques, H. G., Hernandez Arieta, A., Sumioka, H., Lungarella, M., and Pfeifer, R. (2010). Body schema in robotics: a review. IEEE Trans. Auton. Ment. Dev. 2, 304–324. doi:10.1109/TAMD.2010.2086454

CrossRef Full Text | Google Scholar

Kaplan, F., and Oudeyer, P.-Y. (2004). “Maximizing learning progress: an internal reward system for development,” in Embodied Artificial Intelligence (Springer), 259–270.

Google Scholar

Klyubin, A. S., Polani, D., and Nehaniv, C. L. (2005). “Empowerment: a universal agent-centric measure of control,” in Evolutionary Computation, 2005. The 2005 IEEE Congress, Vol. 1 (Edinburgh: IEEE), 128–135.

Google Scholar

Klyubin, E. S., Polani, D., and Nehaniv, C. L. (2004). “Tracking information flow through the environment: simple cases of stigmergy,” in Artificial Life IX: Proceedings of the Ninth International Conference on the Simulation and Synthesis of Living Systems (Boston: The MIT Press), 563–568.

Google Scholar

Koos, S., Cully, A., and Mouret, J.-B. (2013). Fast damage recovery in robotics with the t-resilience algorithm. Int. J. Rob. Res. 32, 1700–1723. doi:10.1177/0278364913499192

CrossRef Full Text | Google Scholar

Kuipers, B. (1978). Modeling spatial knowledge. Cogn. Sci. 2, 129–153. doi:10.1207/s15516709cog0202_3

CrossRef Full Text | Google Scholar

Laflaquiere, A., Argentieri, S., Breysse, O., Genet, S., and Gas, B. (2012). “A non-linear approach to space dimension perception by a naive agent,” in Intelligent Robots and Systems (IROS), 2012 IEEE/RSJ International Conference (Vilamoura: IEEE), 3253–3259.

Google Scholar

MacKay, D. M. (1962). “Aspects of the theory of artificial intelligence,” in The Proceedings of the First International Symposium on Biosimulation Locarno, June 29 – July 5, 1960, eds C. A. Muses and W. S. McCulloch (New York: Springer US), 83–104. doi:10.1007/978-1-4899-6584-4_5

CrossRef Full Text | Google Scholar

Markram, H., Gerstner, W., and Sjöström, P. J. (2011). A history of spike-timing-dependent plasticity. Front. Syn. Neurosci. 3:4. doi:10.3389/fnsyn.2011.00004

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicod, J. (1929). The Foundations of Geometry and Induction. London: Kegan Paul, Trench, Trubner & Co., Ltd.

Google Scholar

O’Regan, J. K., and Noë, A. (2001). A sensorimotor account of vision and visual consciousness. Behav. Brain. Sci. 24, 939–972. doi:10.1017/S0140525X01000115

PubMed Abstract | CrossRef Full Text | Google Scholar

Philipona, D., O’Regan, J., and Nadal, J.-P. (2003). Is there something out there? inferring space from sensorimotor dependencies. Neural Comput. 15, 2029–2049. doi:10.1162/089976603322297278

PubMed Abstract | CrossRef Full Text | Google Scholar

Pierce, D., and Kuipers, B. J. (1997). Map learning with uninterpreted sensors and effectors. Artif. Intell. 92, 169–227. doi:10.1016/S0004-3702(96)00051-3

CrossRef Full Text | Google Scholar

Poincaré, H. (1905). Science and Hypothesis. New York, NY: The Walter Scott Publishing Co., Ltd.

Google Scholar

Roschin, V. Y., Frolov, A. A., Burnod, Y., and Maier, M. A. (2011). A neural network model for the acquisition of a spatial body scheme through sensorimotor interaction. Neural Comput. 23, 1821–1834. doi:10.1162/NECO_a_00138

PubMed Abstract | CrossRef Full Text | Google Scholar

Sigaud, O., Salaün, C., and Padois, V. (2011). On-line regression algorithms for learning mechanical models of robots: a survey. Rob. Auton. Syst. 59, 1115–1129. doi:10.1016/j.robot.2011.07.006

CrossRef Full Text | Google Scholar

Terekhov, A. V., and O’Regan, J. K. (2014). “Learning abstract perceptual notions: the example of space,” in Development and Learning and Epigenetic Robotics (ICDL-Epirob), 2014 Joint IEEE International Conferences on, p. 368–373.

Google Scholar

von Uexküll, J. (1957). “A stroll through the worlds of animals and men: a picture book of invisible worlds,” in Instinctive Behavior: The Development of a Modern Concept, ed. C. H. Schiller (New York: International Universities Press, Inc), 5–80.

Google Scholar

Zhaoping, L. (2006). Theoretical understanding of the early visual processes by data compression and data selection. Network 17, 301–334. doi:10.1080/09548980600931995

PubMed Abstract | CrossRef Full Text | Google Scholar