Robust Structure and Motion Factorization of Non-Rigid Objects

Structure from motion is an import theme in computer vision. Although great progress has been made both in theory and applications, most of the algorithms only work for static scenes and rigid objects. In recent years, structure and motion recovery of non-rigid objects and dynamic scenes have received a lot of attention. In this paper, the state-of-the-art techniques for structure and motion factorization of non-rigid objects are reviewed and discussed. First, an introduction of the structure from motion problem is presented, followed by a general formulation of non-rigid structure from motion. Second, an augmented affined factorization framework, by using homogeneous representation, is presented to solve the registration issue in the presence of outlying and missing data. Third, based on the observation that the reprojection residuals of outliers are significantly larger than those of inliers, a robust factorization strategy with outlier rejection is proposed by means of the reprojection residuals, followed by some comparative experimental evaluations. Finally, some future research topics in non-rigid structure from motion are discussed.

1. Introduction

Structure from motion (SfM) refers to the process of extracting three-dimensional structure of the scene as well as camera motions by analyzing an image sequence. SfM is an important theme in computer vision, and great progress has been made both in theory and in practice during the last three decades. Successful applications include robot navigation, augmented reality, industrial inspection, medical image analysis, digital entertainment, and many more.

The classical method for 3D reconstruction is stereo vision using two or three images (Hartley and Zisserman, 2004), where the 3D structure is calculated via triangulations from the correspondences between these images. For a sequence of many images, the typical approach is the structure and motion factorization algorithm, which was first proposed by Tomasi and Kanade (1992). The factorization method is based on a bilinear formulation that decomposes image measurements directly into the structure and motion components. By assuming the tracking matrix of an image sequence is available, the algorithm deals uniformly with the data from all images; thus, its solution is more stable and accurate than the stereo vision method (Quan, 1996; Triggs, 1996; Ozden et al., 2010; Resch et al., 2015).

The main idea of the factorization algorithm is to decompose the tracking matrix into the motion and structure components simultaneously by Singular Value Decomposition (SVD) with low-rank approximation. Most of the studies on the problem assume an affine camera model due to its linearity (Hartley and Vidal, 2008). Christy and Horaud (1996) extended the method to a perspective camera model by incrementally performing the affine factorization of a scaled tracking matrix. Triggs (1996) proposed a full projective factorization algorithm with projective depths recovered from epipolar geometry. The method was further studied, and different iterative schemes were proposed to recover the projective depths by minimizing image reprojection errors (Oliensis and Hartley, 2007; Wang and Wu, 2009). Oliensis and Hartley (2007) provided a complete theoretical convergence analysis for the iterative extensions.

The factorization algorithm was extended to non-rigid SfM by assuming that the 3D shape of a non-rigid object can be modeled as a weighted linear combination of a set of shape bases (Bregler et al., 2000). Thus, the shape bases and camera motions are factorized simultaneously for all time instants under a rank-3k constraint of the tracking matrix. The method has been extensively investigated and developed by Brand (2001) and Torresani et al. (2008). Recently, Rabaud and Belongie (2008) relaxed the Bregler’s assumption and proposed a manifold-learning framework to solve the problem. Yan and Pollefeys (2008) proposed a factorization approach to recover the structure of articulated objects. Akhter et al. (2011) proposed a dual approach to describe the non-rigid structure in trajectory space by a linear combination of basis trajectories. Gotardo and Martinez (2011) proposed to use kernels to model non-linear deformation. More recent study can be found in Agudo et al. (2014) and Newcombe et al. (2015).

Most factorization methods assume that all features are tracked across the sequence. In the presence of missing data, SVD factorization cannot be used directly, researches proposed to solve the motion and shape matrices alternatively, such as the alternative factorization (Ke and Kanade, 2005), power factorization (Hartley and Schaffalizky, 2003), and factor analysis (Gruber and Weiss, 2004). In practice, outlying data are inevitable during the process of feature tracking, as a consequence, performance of the algorithm will degrade. The most popular strategy to handle outliers in computer vision field is RANSAC, Least Median of Squares (Hartley and Zisserman, 2004), and other similar hypothesize-and-test frameworks (Scaramuzza, 2011). However, these methods are usually designed for two or three views, and they are computational expensive.

Aguiar and Moura (2003) proposed a scalar-weighted SVD algorithm that minimizes the weighted square errors. Gruber and Weiss (2004) formulated the problem as a factor analysis and derived an Expectation Maximization (EM) algorithm to enhance the robustness to missing data and uncertainties. Zelnik-Manor et al. (2006) defined a new type of motion consistency based on temporal consistency, and applied it to multi-body factorization with directional uncertainty. Zaharescu and Horaud (2009) introduced a Gaussian mixture model and incorporate it with the EM algorithm. Huynh et al. (2003) proposed an iterative approach to correct the outliers with “pseudo” observations. Ke and Kanade (2005) proposed a robust algorithm to handle outliers by minimizing a L1 norm of the reprojection errors. Eriksson and van den Hengel (2010) introduced the L1 norm to the Wiberg algorithm to handle missing data and outliers.

Okatani et al. (2011) proposed to incorporate a damping factor into the Wiberg method to solve the problem. Yu et al. (2011) presented a Quadratic Program formulation for robust multi-model fitting of geometric structures. Wang et al. (2012b) proposed an adaptive kernel-scale weighted hypotheses to segment multiple-structure data even in the presence of a large number of outliers. Paladini et al. (2012) proposed an alternating bilinear approach to SfM by introducing a globally optimal projection step of the motion matrices onto the manifold of metric constraints. Wang et al. (2012a) proposed a spatial-and-temporal-weighted factorization approach to handle significant noise in the measurement. The authors further proposed a rank-4 factorization algorithm to handle missing and outlying data (Wang et al., 2013b).

Most of the above robust algorithms are initially designed for SfM of rigid objects, and few studies have been carried out for non-rigid case. In our most recent study (Wang et al., 2013a), a robust non-rigid factorization approach is reported. The outlying data are detected from a new viewpoint via image reprojection residuals by exploring the fact that the reprojection residuals are largely proportional to the measurement errors. In this paper, the state-of-the-art techniques for structure from motion of non-rigid objects are reviewed, with some most recent development and results in this field.

The remaining part of this paper is organized as follows. Some background of structure and motion recovery of rigid objects is outlined in Section 2. Section 3 presents the formulation and development of non-rigid SfM. An augmented factorization framework for non-rigid SfM and a robust factorization strategy are introduced in Section 4, followed by some experimental results on both synthetic and real data in Section 5. Finally, the paper is concluded and discussed in Section 6.

2. Structure and Motion Factorization of Rigid Objects

In this section, a brief review to camera projection models and rigid structure and motion factorization are presented.

Under perspective projection, a 3D point X_j = [x_j, y_j, z_j]^T is projected onto an image point x_ij = [u_ij, v_ij]^T in frame i according to the imaging equation

${\mathrm{\lambda }}_{\mathit{ij}}{\tilde{\mathbf{x}}}_{\mathit{ij}}={\mathbf{P}}_i{\tilde{\mathbf{x}}}_j={\mathbf{K}}_i\left[{\mathbf{R}}_i|{\mathbf{t}}_i\right]{\tilde{\mathbf{x}}}_j$ (1)

where λ_ij is a non-zero scale factor; ${\tilde{\mathbf{x}}}_{\mathit{ij}}$ and ${\tilde{\mathbf{X}}}_j$ are the homogeneous form of x_ij and X_j, respectively; P_i is a 4 × 3 projection matrix of the i-th frame; R_i and t_i are the corresponding rotation matrix and translation vector of the camera with respect to the world system; K_i is the camera calibration matrix. When the object is far away from the camera with relatively small depth variation, one may safely assume a simplified affine camera model as below to approximate the perspective projection.

${\mathbf{x}}_{\mathit{ij}}={\mathbf{A}}_i{\mathbf{X}}_j+{\mathbf{c}}_i$ (2)

where the matrix A_i is a 2 × 3 affine projection matrix; c_i is a two-dimensional translation term of the frame. Under the affine projection, the mapping from space to the image becomes linear as the unknown depth scalar λ_ij in equation (1) is eliminated in equation (2). Consequently, the projection of all image points in the i-th frame can be denoted as

$\left[{\mathbf{x}}_{i1},{\mathbf{x}}_{i2},\cdots ,{\mathbf{x}}_{\mathit{in}}\right]={\mathbf{A}}_i\left[{\mathbf{X}}_1,{\mathbf{X}}_2,\cdots ,{\mathbf{X}}_n\right]+{\mathbf{C}}_i$ (3)

where C_i = [c_i, c_i, ⋅⋅⋅, c_i] is the translation matrix of the frame i. Therefore, the imaging process of an image sequence can be formulated by stacking equation (3) frame by frame.

$\underset{{\mathbf{W}}_{2m\times n}}{\underbrace{\left[\begin{array}{ccc}\hfill {\mathbf{x}}_{11}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{x}}_{1n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathbf{x}}_{m1}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{x}}_{\mathit{mn}}\hfill \end{array}\right]}}=\underset{{\mathbf{M}}_{2m\times 3}}{\underbrace{\left[\begin{array}{c}\hfill {\mathbf{A}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{A}}_m\hfill \end{array}\right]}}\underset{{\mathbf{S}}_{3\times n}}{\underbrace{\left[\begin{array}{ccc}\hfill {\mathbf{X}}_1,\hfill & \hfill \cdots ,\hfill & \hfill {\mathbf{X}}_n\hfill \end{array}\right]}}+\underset{{\mathbf{C}}_{2m\times n}}{\underbrace{\left[\begin{array}{c}\hfill {\mathbf{C}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{C}}_m\hfill \end{array}\right]}}$ (4)

where m is the frame number and n is the number of features. It is easy to verify that c_i in equation (2) is the image of the centroid of all space points. Thus, if all imaged points in each image are registered to the centroid and relative image coordinates with respect to the centroid are employed, the translation term vanishes, i.e., c_i = 0. Consequently, the imaging process [equation (4)] is written concisely as

${\mathbf{W}}_{2m\times n}={\mathbf{M}}_{2m\times 3}{\mathbf{S}}_{3\times n}$ (5)

where W is called the tracking matrix or measurement matrix, which is composed of all tracked features. Structure from motion is a reverse problem to the imaging process. Suppose the tracking matrix W is available, our purpose is to recover the motion matrix M and the shape matrix S.

It is obvious from equation (5) that the tracking matrix is highly rank deficient, and the rank of W is at most 3 if the translation term C is removed. In practice, the rank of a real tracking matrix is definitely >3 due to image noise and affine approximation error. Thus, one needs to find a rank-3 approximation of the tracking matrix. A common practice is to perform SVD decomposition on matrix W and truncate it to rank 3, then the motion matrix M and the shape matrix S can be easily decomposed from the tracking matrix. Nevertheless, this decomposition is not unique since it is only defined up to a non-singular linear transformation matrix $\mathrm{H}\in {\text{ℝ}}^{3\times 3}$ as

$\mathbf{W}=\left(\mathbf{MH}\right)\left({\mathbf{H}}^{-1}\mathbf{S}\right)$ (6)

In order to upgrade the solution from perspective space to the Euclidean space, the metric constraint on the motion matrix is usually adopted to recover the transformation matrix H (Quan, 1996; Wang and Wu, 2010). Then, the Euclidean structure is recovered from H^–1S and the camera motion parameters of each frame are decomposed from MH.

3. Structure and Motion Factorization of Non-Rigid Objects

We assumed rigid objects and static scenes in the last section. While in real world, many objects do not have fixed structure, such as human faces with different expressions, torsos, animals bodies, etc. In this section, the factorization algorithm is extended to handle non-rigid and deformable objects.

3.1. Bregler’s Deformation Model

For non-rigid objects, if their surfaces deform randomly at any time instance, there is currently no suitable method to recover its structure from images. A well-adopted assumption about the deformation is proposed by Bregler et al. (2000), where the 3D structure of non-rigid object is approximated by a weighted combination of a set of rigid shape bases. Figure 1 shows a very simple example of face models from neutral to smiling with only mouth movements. The deformation structure can be approximated by only two shape bases. If more face expressions, such as joy, sadness, surprise, and fear, are involved, then more shape bases are needed to model the structure.

FIGURE 1

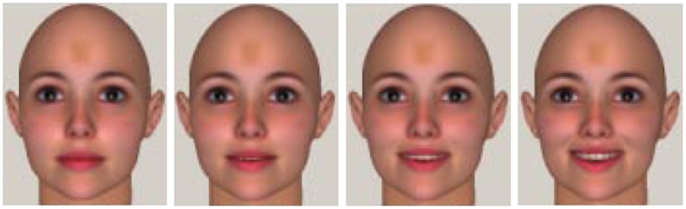
Figure 1. Four female face models carrying expressions from neutral to smiling. We may take any two models as shape bases, and then the other models can be derived as weighted linear combinations of the two bases. Courtesy of Jing Xiao.

Suppose the deformation structure ${\mathbf{S}}_i\in {\text{ℝ}}^{3\times \mathit{n}}$ is expressed as a weighted combination of k principal modes of deformation ${\mathbf{B}}_l\in {\text{ℝ}}^{3\times \mathit{n}}$, l = 1, ⋅⋅⋅, k. We formulate the model as

${\mathbf{S}}_i={\displaystyle \sum _{l=1}^k}{\mathrm{\hspace{0.17em}\omega }}_{\mathit{il}}{\mathbf{B}}_l$ (7)

where ${\omega }_{\mathit{il}}\in \text{ℝ}$ is the deformation weight for base l at frame i. A perfect rigid object corresponds to the situation of k = 1 and ω_il = 1.

3.2. Non-Rigid Factorization Under Affine Models

Under the assumption [equation (7)], the imaging process of one image can be modeled as

$\begin{array}{llll}\hfill {\mathbf{W}}_i& =\left[{\mathbf{x}}_{i1},\cdots ,{\mathbf{x}}_{\mathit{in}}\right]={\mathbf{A}}_i{\mathbf{S}}_i+\left[{\mathbf{c}}_i,\cdots ,{\mathbf{c}}_i\right]& \hfill & \\ \hfill & =\left[{\mathrm{\omega }}_{i1}{\mathbf{A}}_i,\cdots ,{\mathrm{\omega }}_{\mathit{ik}}{\mathbf{A}}_i\right]\left[\begin{array}{c}{\mathbf{B}}_1\\ ⋮\\ {\mathbf{B}}_k\end{array}\right]+\left[{\mathbf{c}}_i,\cdots ,{\mathbf{c}}_i\right]& \hfill & \end{array}$

It is easy to verify that if all image points in each frame are registered to the centroid and relative image coordinates are employed, the translation term vanishes, i.e., c_i = 0. Consequently, the non-rigid factorization under affine camera model is expressed as

$\underset{{\mathbf{W}}_{2m\times n}}{\underbrace{\left[\begin{array}{ccc}\hfill {\mathbf{x}}_{11}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{x}}_{1n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathbf{x}}_{m1}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{x}}_{\mathit{mn}}\hfill \end{array}\right]}}=\underset{{\mathbf{M}}_{2m\times 3k}}{\underbrace{\left[\begin{array}{ccc}\hfill {\mathrm{\omega }}_{11}{\mathbf{A}}_1\hfill & \hfill \cdots \hfill & \hfill {\mathrm{\omega }}_{1k}{\mathbf{A}}_1\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathrm{\omega }}_{m1}{\mathbf{A}}_m\hfill & \hfill \cdots \hfill & \hfill {\mathrm{\omega }}_{\mathit{mk}}{\mathbf{A}}_m\hfill \end{array}\right]}}\underset{{\mathbf{S}}_{3k\times n}}{\underbrace{\left[\begin{array}{c}\hfill {\mathbf{B}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{B}}_k\hfill \end{array}\right]}}$ (8)

Structure from motion is a reverse problem. Suppose the tracking matrix W is available, our purpose is to recover the camera motion parameters in M and the 3D structure from the shape matrix S_i. It is obvious from equation (8) that the rank of the tracking matrix W is at most 3k.

Following the idea of rigid factorization, we perform SVD decomposition on the non-rigid tracking matrix and impose the rank-3k constraint, W can be factorized into a 2m × 3k matrix $\widehat{\mathbf{M}}$ and a 3k × n matrix $\widehat{\mathbf{S}}$. However, the decomposition is not unique as any non-singular linear transformation matrix $\mathrm{H}\in {\text{ℝ}}^{\mathit{3k}\times \mathit{3k}}$ can be inserted into the factorization, which leads to an alternative factorization $\mathbf{W}=\left(\widehat{\mathbf{M}}\mathbf{H}\right)\left({\mathbf{H}}^{-1}\widehat{\mathbf{S}}\right)$. If we have a transformation matrix H that can resolve the affine ambiguity and upgrade the solution to Euclidean space, the shape bases are then easily recovered from $\mathbf{S}={\mathbf{H}}^{-1}\widehat{\mathbf{S}}$, while the rotation matrix and the weighting coefficient ω_ij can be decomposed from $\mathbf{M}=\widehat{\mathbf{M}}\mathbf{H}$ by Procrustes analysis (Bregler et al., 2000; Brand, 2001; Torresani et al., 2001).

Similar to the rigid situation, the upgrading matrix is usually recovered by application of metric constraint to the motion matrix (Wang and Wu, 2010). However, only the rotation constraints may be insufficient when the object deforms at varying speed, since most of the constraints are redundant. Xiao and Kanade (2005) proposed a basis constraint to solve this ambiguity. The main idea is based on the assumption that there exists k frames in the sequence, which include independent shapes that can be treated as a set of bases.

4. Materials and Methods

In non-rigid structure from motion, the input is an image sequence of a non-rigid object with the point features being tracked across the sequence. However, due to occlusion and lack of proper constraints, the tracking data are usually corrupted by outliers and missing points. This section will introduce a robust scheme to handle imperfect data (Wang et al., 2013a).

4.1. Augmented Affine Factorization Without Registration

One critical condition for the affine factorization equation (8) is that all image measurements are registered to the corresponding centroid of each frame. When the tracking matrix contains outliers and/or missing data, it is impossible to reliably retrieve the centroid. As will be shown in the experiments, the miscalculation of the centroid will cause a significant error to the final solution. Previous studies were either ignoring this problem or hallucinating the missing points with pseudo observations, which may lead to a biased estimation. In this section, a rank-(3k + 1) augmented factorization algorithm is proposed to solve this issue.

Let us formulate the affine imaging process [equation (2)] in the following form

${\mathbf{x}}_{\mathit{ij}}=\left[{\mathbf{A}}_i|{\mathbf{c}}_i\right]{\tilde{\mathbf{x}}}_j$ (9)

where ${\tilde{\mathbf{x}}}_j={\left[{\mathbf{X}}_j^T,t_j\right]}^T$ is a 4-dimensional homogeneous expression of X_j. Let ${\tilde{\mathbf{S}}}_i=\left[\begin{array}{c}\hfill {\mathbf{S}}_i\hfill \\ \hfill {\mathbf{t}}_i\hfill \end{array}\right]$ be the homogeneous form of the deformable structure, then the imaging process of frame i can be written as

$\begin{array}{llll}\hfill {\mathbf{W}}_i& =\left[{\mathbf{x}}_{i1},\cdots ,{\mathbf{x}}_{\mathit{in}}\right]=\left[{\mathbf{A}}_i|{\mathbf{c}}_i\right]\left[\begin{array}{c}{\sum }_{l=1}^k{\mathrm{\omega }}_{\mathit{il}}{\mathbf{B}}_l\\ {\mathbf{t}}_i\end{array}\right]& \hfill & \\ \hfill & =\left[{\mathrm{\omega }}_{i1}{\mathbf{A}}_i,\cdots ,{\mathrm{\omega }}_{\mathit{ik}}{\mathbf{A}}_i,{\mathbf{c}}_i\right]\left[\begin{array}{c}{\mathbf{B}}_1\\ ⋮\\ {\mathbf{B}}_k\\ {\mathbf{t}}_i\end{array}\right]& \hfill & \end{array}$

Thus, the structure and motion factorizations for the entire sequence are formulated as follows.

$\underset{{\mathbf{W}}_{2m\times n}}{\underbrace{\left[\begin{array}{ccc}\hfill {\mathbf{x}}_{11}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{x}}_{1n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathbf{x}}_{m1}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{x}}_{\mathit{mn}}\hfill \end{array}\right]}}=\underset{{\mathbf{M}}_{2m\times \left(3k+1\right)}}{\underbrace{\left[\begin{array}{cccc}\hfill {\mathrm{\omega }}_{11}{\mathbf{A}}_1\hfill & \hfill \cdots \hfill & \hfill {\mathrm{\omega }}_{1k}{\mathbf{A}}_1\hfill & \hfill {\mathbf{c}}_1\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\mathrm{\omega }}_{m1}{\mathbf{A}}_m\hfill & \hfill \cdots \hfill & \hfill {\mathrm{\omega }}_{\mathit{mk}}{\mathbf{A}}_m\hfill & \hfill {\mathbf{c}}_m\hfill \end{array}\right]}}\underset{{\mathbf{S}}_{\left(3k+1\right)\times n}}{\underbrace{\left[\begin{array}{c}\hfill {\mathbf{B}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{B}}_k\hfill \\ \hfill {\mathbf{t}}_i^T\hfill \end{array}\right]}}$ (10)

Obviously, the rank of the tracking matrix becomes 3k + 1 in this case. Given the tracking matrix, the factorization can be easily obtained via SVD decomposition and imposing rank-(3k + 1) constraint. The expression [equation (10)] does not require any image registration thus can directly work with outlying and missing data.

Both factorization algorithms [equations (8) and (10)] can be equivalently denoted as the following minimization scheme.

$f\left(\mathbf{M},\mathbf{S}\right)=\mathit{arg}\underset{\mathbf{M},\mathbf{S}}{\min }\parallel \mathbf{W}-\mathbf{MS}{\parallel }_F^2$ (11)

By enforcing different rank constraints, the Frobenius norm of equation (11) corresponding to the algorithms [equations (8) and (10)] would be

$E_{3k}={\displaystyle \sum _{i=3k+1}^N}{\mathrm{\hspace{0.17em}\sigma }}_i^2,E_{3k+1}={\displaystyle \sum _{i=3k+2}^N}{\mathrm{\hspace{0.17em}\sigma }}_i^2$ (12)

where σ_i, i = 1, ⋅⋅⋅, N are singular values of the tracking matrix in descending order, and N = min(2m, n). Clearly, the error difference by the two algorithm is ${\mathrm{\sigma }}_{3k+1}^2$. For noise free data, if all image points are registered to the centroid, then, σ_i = 0, ∀i > 3k, the equations (8) and (10) are actually equivalent. However, in the presence of outlying and missing data, the image centroid cannot be accurately recovered, the rank-3k algorithm [equation (8)] will yield a big error since σ_{3 k+1} does not approach zero in this situation.

4.2. Outlier Detection and Robust Factorization

Based on the foregoing proposed factorization algorithm, a fast and practical scheme for outlier detection is discussed in this section.

The best fit model of the factorization algorithm is obtained by minimizing the sum of squared residuals between the observed data and the fitted values provided by the model. Extensive empirical studies show that the algorithm usually yields reasonable solutions even in the presence of certain amount of outliers, and the reprojection residuals of the outlying data are usually significantly larger than those associated with inliers.

Suppose $\widehat{\mathbf{M}}$ and $\widehat{\mathbf{S}}$ are a set of initial solution of the motion and structure matrices, the reprojection residuals can be computed by reprojecting the solution back onto all images. Let us define a residual matrix as follows.

$\mathbf{E}=\mathbf{W}-\widehat{\mathbf{M}}\widehat{\mathbf{S}}={\left[\begin{array}{ccc}\hfill {\mathbf{e}}_{11}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{e}}_{1n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathbf{e}}_{m1}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{e}}_{\mathit{mn}}\hfill \end{array}\right]}_{2m\times n}$ (13)

where

${\mathbf{e}}_{\mathit{ij}}={\mathbf{x}}_{\mathit{ij}}-{\widehat{\mathbf{M}}}_i{\widehat{\mathbf{s}}}_j=\left[\begin{array}{c}\hfill \mathrm{\Delta }{u}_{\mathit{ij}}\hfill \\ \hfill \mathrm{\Delta }{v}_{\mathit{ij}}\hfill \end{array}\right]$ (14)

is the residual of point (i,j) in both image directions. The reprojection error of a point is defined by the Euclidean norm of the residual at that point as ||e_ij||.

Assuming Gaussian image noise, it is easy to prove that the reprojection residuals also follow Gaussian distribution (Wang et al., 2013a). Figure 2 shows an example from the synthetic data in Section 1. Three units Gaussian noise and 10% outliers were added to the synthetic images, and the residual matrix was calculated from equation (13). As shown in Figure 2, the residuals are obviously followed by Gaussian distribution. Thus, the points with large residuals will be classified as outliers.

FIGURE 2

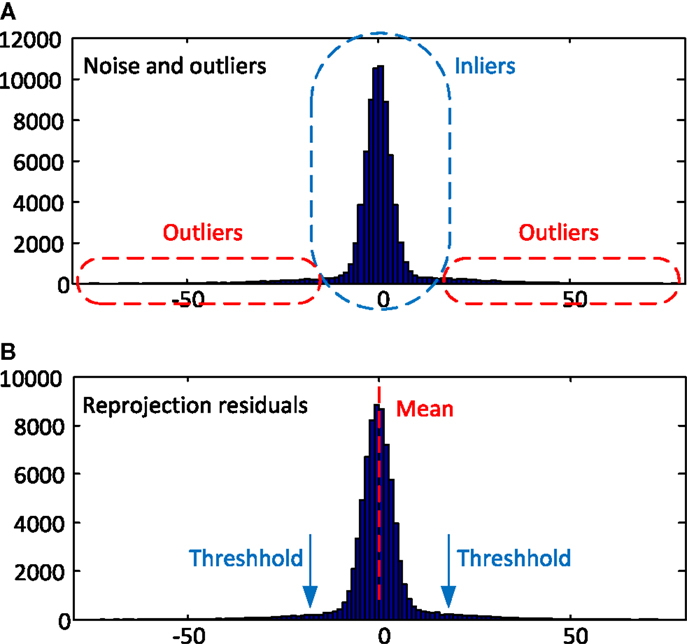
Figure 2. (A) Histogram distribution of the added noise and outliers; (B) histogram distribution of the reprojection residuals.

Inspired by this observation, a simple outlier detection and robust factorization scheme is proposed in Algorithm 1.

ALGORITHM 1

Algorithm 1. Robust non-rigid factorization algorithm.

Two important parameters are required in the robust algorithm: one is the outlier threshold, and the other is the weight matrix. A detailed discussion on how to recover these parameters can be found in Wang et al. (2013a).

5. Evaluations on Synthetic and Real Data

The section presents two examples of structure and motion recovery using the above robust factorization scheme.

5.1. Evaluations on Synthetic Data

The proposed technique was evaluated extensively on synthetic data and compared with previous algorithms. During the simulation, we generated a deformable space cube, which was composed of 21 evenly distributed rigid points on each side and three sets of dynamic points (33 × 3 points) on the adjacent surfaces of the cube that were moving outward. There are 252 space points in total as shown in Figure 3. Using the synthetic cube, 100 images were generated by affine projection with randomly selected camera parameter. Each image corresponds to a different 3D structure. The image resolution is 800 U × 800 U, and Gaussian white noise is added to the synthetic images.

FIGURE 3

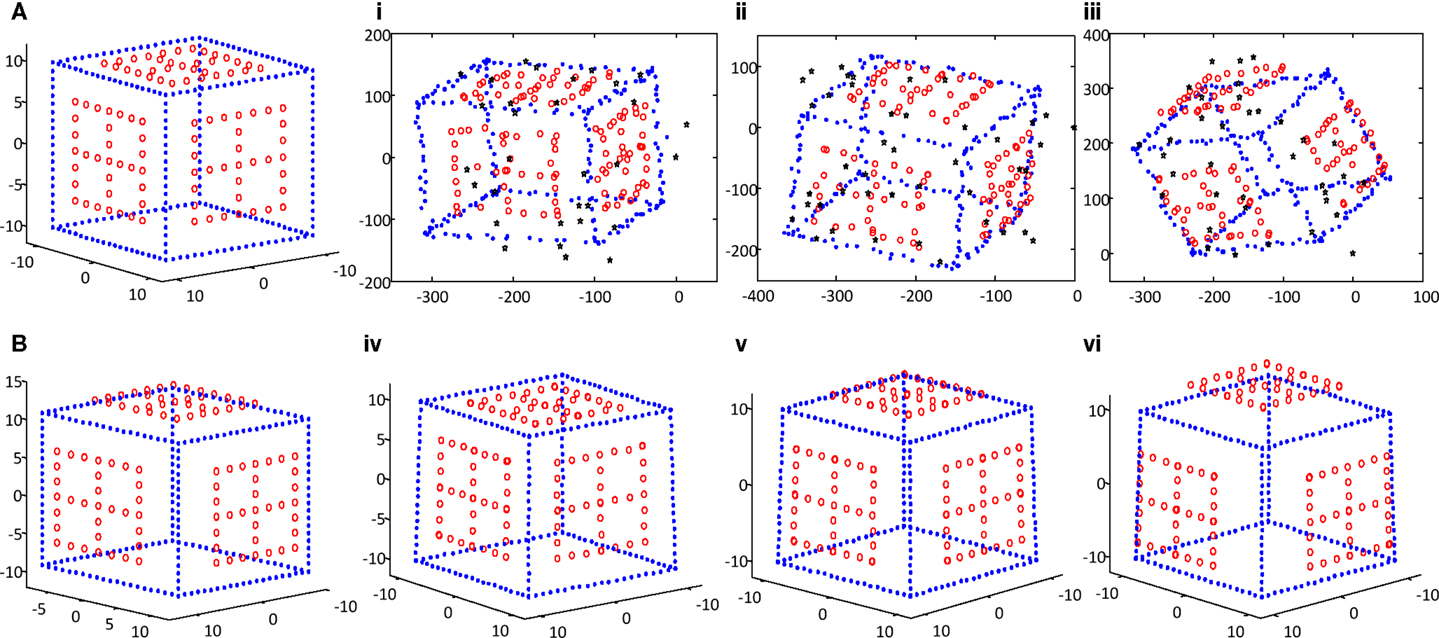
Figure 3. (A,B) Two simulated space cubes with three sets of moving points; (i–iii) three synthetic images with noise and outliers (black stars); (iv–vi) the reconstructed 3D structures corresponding to the three images.

For the above simulated image sequence, Gaussian noise was added to each image point, and the noise level was varied from 1 to 5 U in step 1. In the meantime, 10% outliers were added to the tracking matrix. Using the contaminated data, the foregoing proposed robust algorithm was employed to recover the motion and shape matrices. Figure 3 shows three noise and outlier-corrupted images and the corresponding 3D structures recovered by the proposed approach. It is evident that the deformable cube structures are correctly retrieved.

As a comparison, two popular algorithms in the literature were implemented as well, one is an outlier correction scheme proposed by Huynh et al. (2003), the other one is proposed by Ke and Kanade (2005) based on minimization of the L1 norm. The two algorithms were initially proposed for rigid SfM; here, they were extended to deal with non-rigid SfM. The mean reprojection variance at different noise levels and outliers ratios is shown in Figure 4.

FIGURE 4

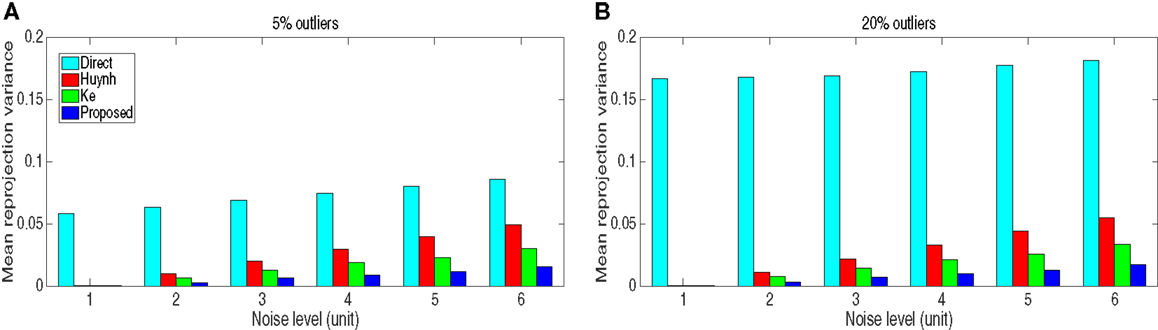
Figure 4. The mean reprojection variance of different algorithms with respect to different noise levels and outliers. (A) 5% outliers, (B) 20% outliers.

The results in Figure 4 were evaluated from 100 independent tests in order to yield a statistically meaningful result, where “Direct” stands for normal factorization algorithm without outlier rejection. In this test, the reprojection variance was estimated only using the original inlying data without outliers. Obviously, the proposed scheme outperforms other algorithms in terms of accuracy. The direct factorization algorithm yields significantly large errors due to the influence of outliers, and the error increases with the increase of the amount of outliers. The experiment also shows that all three robust algorithms are resilient to outliers, as can be seen in Figure 4, the ratio of outliers has little influence to the reprojection variance of the three robust algorithms.

5.2. Evaluations on Real Sequences

Two experimental results are reported in this section to test the robust scheme. The first one was on a dinosaur sequence (Akhter et al., 2011) is reported here. The sequence consists of 231 images with different movement and deformation of a dinosaur model. The image resolution is 570 × 338 pixel and 49 features were tracked across the sequence. In order to test the robustness of the algorithm, an additional 8% outliers were added to the tracking data as shown in Figure 5.

FIGURE 5

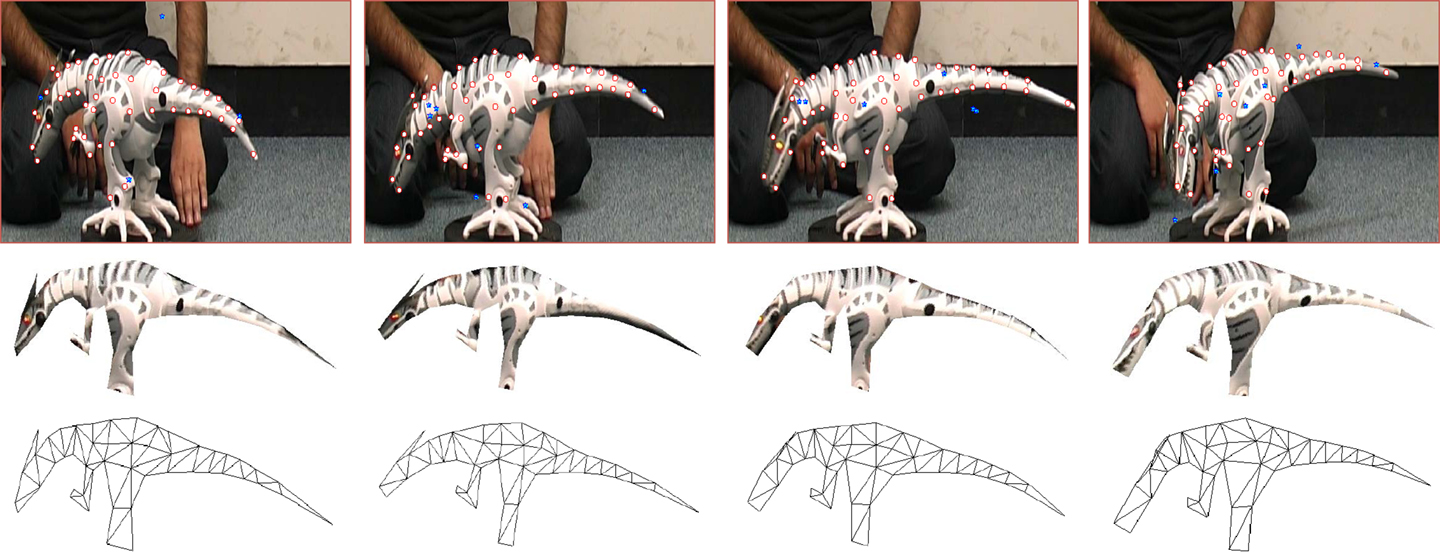
Figure 5. Four frames from the dinosaur sequence, the corresponding reconstructed VRML models, and triangulated wireframes. The tracked features (red circles) and added outliers (blue stars) are superimposed to the images.

Using the proposed approach, all outliers were successfully rejected; however, a few tracked features were also eliminated due to large tracking errors. The proposed approach was employed to recover the motion and structure matrices, and the solution was then upgraded to the Euclidean space. Figure 5 shows the reconstructed structure and wireframes. The VRML model is visually realistic, and the deformation at different instant is correctly recovered, although the initial tracking data are not very reliable.

The histogram distribution of the reprojection residual matrix [equation (13)] with outliers is shown in Figure 6. The residuals are largely conform to the assumption of normal distribution. As can be seen from the histogram, the outliers are obviously distinguished from inliers, and the computed threshold is shown in the figure. After rejecting outliers, the histogram distribution of the residuals produced by the final solution is also shown in Figure 6. Clearly, the residual error is reduced significantly. The final mean reprojection error given by the proposed approach is 0.597. In comparison, the reprojection errors by the algorithms of “Huynh” and “Ke” are 0.926 and 0.733, respectively. The proposed scheme outperforms other approaches.

FIGURE 6

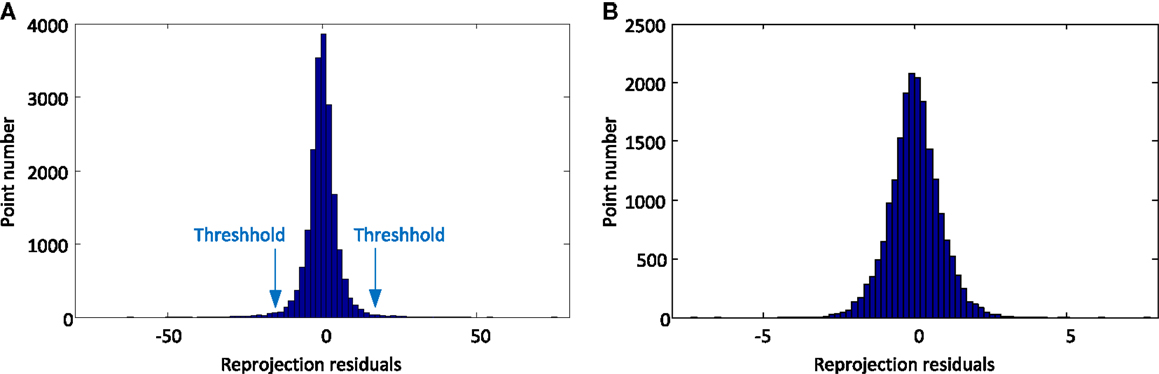
Figure 6. The histogram distribution of the residual matrix of the dinosaur sequence before (A) and after (B) outlier rejection.

The second test was on a non-rigid face sequence, as shown in Figure 7, with different facial expressions. This sequence was downloaded from FGnet (http://www-prima.inrialpes.fr/FGnet/html/home.html), and 200 consecutive images were used in the experiment. The resolution of each image is 720 × 576 and 68 feature points are automatically tracked across the sequence using the active appearance model (AAM). In order to test the robustness of the approach, 8% outliers were added randomly to the tracking data as shown in Figure 7.

FIGURE 7

Figure 7. Test results of the face sequence. (top) Four frames from the sequence overlaid with the tracked features (red circles) and added outliers (blue stars); (bottom) the corresponding 3D VRML models from two different viewpoints.

Figure 7 shows the reconstructed VRML models of four frames shown from front and right side. It is obvious that all outliers are removed successfully by the proposed algorithm, and different facial expressions have been correctly recovered. The reprojection errors obtained from “Huynh,” “Ke,” and the proposed algorithms are 0,697, 0.581, and 0.453, respectively. The proposed scheme again yields the lowest reprojection error in this test.

6. Conclusion and Discussion

The paper has presented an overview of the state-of-the-art techniques for non-rigid structure and motion factorization. A rank-(3k + 1) factorization algorithm, which is more accurate and more widely applicable than the classic rank-3k non-rigid factorization, has been presented, followed by a robust factorization scheme designed to deal with outlier-corrupted data. Comparative experiments demonstrated the effective and robustness of the proposed scheme. Although an outlier detection strategy and a robust factorization approach have been discussed in this paper, the problem remains far from being solved. Robustness is still a well-known bottleneck in practical applications of the algorithm. On the other hand, the non-rigid factorization approach discussed in this paper only works for a single simply non-rigid object, how to recover the 3D structure of general dynamic scenes, which may be coupled with rigid, non-rigid, articulated, and moving objects, is still an open problem in computer vision. New techniques have to be developed to handle the complex and challenging situations.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The work is partly supported by Kansas NASA EPSCoR Program and the National Natural Science Foundation of China (61273282, 61573351).

References

Agudo, A., Agapito, L., Calvo, B., and Montiel, J. (2014). “Good vibrations: a modal analysis approach for sequential non-rigid structure from motion,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Columbus, OH: IEEE), 1558–1565.

Google Scholar

Aguiar, P. M. Q., and Moura, J. M. F. (2003). Rank 1 weighted factorization for 3d structure recovery: algorithms and performance analysis. IEEE Trans. Pattern Anal. Mach. Intell. 25, 1134–1149. doi: 10.1109/TPAMI.2003.1227988

CrossRef Full Text | Google Scholar

Akhter, I., Sheikh, Y., Khan, S., and Kanade, T. (2011). Trajectory space: a dual representation for nonrigid structure from motion. IEEE Trans. Pattern Anal. Mach. Intell. 33, 1442–1456. doi:10.1109/TPAMI.2010.201

PubMed Abstract | CrossRef Full Text | Google Scholar

Brand, M. (2001). “Morphable 3d models from video,” in Proc. of IEEE Conference on Computer Vision and Pattern Recognition, Vol. 2 (Kauai, HI: IEEE), 456–463.

Google Scholar

Bregler, C., Hertzmann, A., and Biermann, H. (2000). “Recovering non-rigid 3d shape from image streams,” in Proc. of IEEE Conference on Computer Vision and Pattern Recognition, Vol. 2 (Hilton Head Island, SC: IEEE), 690–696.

Google Scholar

Christy, S., and Horaud, R. (1996). Euclidean shape and motion from multiple perspective views by affine iterations. IEEE Trans. Pattern Anal. Mach. Intell. 18, 1098–1104. doi:10.1109/34.544079

CrossRef Full Text | Google Scholar

Eriksson, A., and van den Hengel, A. (2010). “Efficient computation of robust low-rank matrix approximations in the presence of missing data using the L1 norm,” in CVPR (San Francisco, CA: IEEE), 771–778.

Google Scholar

Gotardo, P. F. U., and Martinez, A. M. (2011). “Kernel non-rigid structure from motion,” in IEEE International Conference on Computer Vision (ICCV), 2011 (Barcelona: IEEE), 802–809.

Google Scholar

Gruber, A., and Weiss, Y. (2004). “Multibody factorization with uncertainty and missing data using the EM algorithm,” in CVPR (1) (Washington, DC: IEEE), 707–714.

Google Scholar

Hartley, R., and Schaffalizky, F. (2003). “Powerfactorization: 3d reconstruction with missing or uncertain data,” in Proc. of Australia-Japan Advanced Workshop on Computer Vision. Adelaide.

Google Scholar

Hartley, R., and Vidal, R. (2008). “Perspective nonrigid shape and motion recovery,” in Proc. of European Conference on Computer Vision (ECCV) (1), Lecture Notes in Computer Science, Vol. 5302 (Marseille: Springer), 276–289.

Google Scholar

Hartley, R. I., and Zisserman, A. (2004). Multiple View Geometry in Computer Vision, Second Edn. Cambridge: Cambridge University Press. ISBN: 0521540518.

Google Scholar

Huynh, D. Q., Hartley, R., and Heyden, A. (2003). “Outlier correction in image sequences for the affine camera,” in ICCV (Nice: IEEE), 585–590.

Google Scholar

Ke, Q., and Kanade, T. (2005). “Robust L1 norm factorization in the presence of outliers and missing data by alternative convex programming,” in CVPR (1), 739–746.

Google Scholar

Newcombe, R. A., Fox, D., and Seitz, S. M. (2015). “Dynamicfusion: reconstruction and tracking of non-rigid scenes in real-time,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Boston, MA: IEEE), 343–352.

Google Scholar

Okatani, T., Yoshida, T., and Deguchi, K. (2011). “Efficient algorithm for low-rank matrix factorization with missing components and performance comparison of latest algorithms,” in ICCV (Barcelona: IEEE), 842–849.

Google Scholar

Oliensis, J., and Hartley, R. (2007). Iterative extensions of the sturm/triggs algorithm: convergence and nonconvergence. IEEE Trans. Pattern Anal. Mach. Intell. 29, 2217–2233. doi:10.1109/TPAMI.2007.1132

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozden, K. E., Schindler, K., and Van Gool, L. (2010). Multibody structure-from-motion in practice. IEEE Trans. Pattern Anal. Mach. Intell 32, 1134–1141. doi:10.1109/TPAMI.2010.23

PubMed Abstract | CrossRef Full Text | Google Scholar

Paladini, M., Bue, A. D., Xavier, J. M. F., de Agapito, L., Stosic, M., and Dodig, M. (2012). Optimal metric projections for deformable and articulated structure-from-motion. Int. J. Comput. Vis. 96, 252–276. doi:10.1007/s11263-011-0468-5

CrossRef Full Text | Google Scholar

Quan, L. (1996). Self-calibration of an affine camera from multiple views. Int. J. Comput. Vis. 19, 93–105. doi:10.1007/BF00131149

CrossRef Full Text | Google Scholar

Rabaud, V., and Belongie, S. (2008). “Re-thinking non-rigid structure from motion,” in IEEE Conference on Computer Vision and Pattern Recognition (Anchorage, AK: IEEE).

Google Scholar

Resch, B., Lensch, H., Wang, O., Pollefeys, M., and Sorkine-Hornung, A. (2015). “Scalable structure from motion for densely sampled videos,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Boston, MA: IEEE), 3936–3944.

Google Scholar

Scaramuzza, D. (2011). 1-Point-ransac structure from motion for vehicle-mounted cameras by exploiting non-holonomic constraints. Int. J. Comput. Vis. 95, 74–85. doi:10.1007/s11263-011-0441-3

CrossRef Full Text | Google Scholar

Tomasi, C., and Kanade, T. (1992). Shape and motion from image streams under orthography: a factorization method. Int. J. Comput. Vis. 9, 137–154. doi:10.1007/BF00129684

CrossRef Full Text | Google Scholar

Torresani, L., Hertzmann, A., and Bregler, C. (2008). Nonrigid structure-from-motion: estimating shape and motion with hierarchical priors. IEEE Trans. Pattern Anal. Mach. Intell. 30, 878–892. doi:10.1109/TPAMI.2007.70752

PubMed Abstract | CrossRef Full Text | Google Scholar

Torresani, L., Yang, D. B., Alexander, E. J., and Bregler, C. (2001). “Tracking and modeling non-rigid objects with rank constraints,” in Proc. of IEEE Conference on Computer Vision and Pattern Recognition, Vol. 1 (Kauai, HI: IEEE), 493–500.

Google Scholar

Triggs, B. (1996). “Factorization methods for projective structure and motion,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (San Francisco, CA: IEEE), 845–851.

Google Scholar

Wang, G., and Wu, Q. J. (2009). Perspective 3d Euclidean reconstruction with varying camera parameters. IEEE Trans. Circuits Syst. Video Technol. 19, 1793–1803. doi:10.1109/TCSVT.2009.2031380

CrossRef Full Text | Google Scholar

Wang, G., and Wu, Q. M. J. (2010). Quasi-perspective projection model: theory and application to structure and motion factorization from uncalibrated image sequences. Int. J. Comput. Vis. 87, 213–234. doi:10.1007/s11263-009-0267-4

CrossRef Full Text | Google Scholar

Wang, G., Zelek, J. S., and Wu, Q. M. J. (2012a). Structure and motion recovery based on spatial-and-temporal-weighted factorization. IEEE Trans. Circuits Syst. Video Technol. 22, 1590–1603. doi:10.1109/TCSVT.2012.2201795

CrossRef Full Text | Google Scholar

Wang, H., Chin, T.-J., and Suter, D. (2012b). Simultaneously fitting and segmenting multiple-structure data with outliers. IEEE Trans. Pattern Anal. Mach. Intell. 34, 1177–1192. doi:10.1109/TPAMI.2011.216

CrossRef Full Text | Google Scholar

Wang, G., Zelek, J. S., and Wu, Q. M. J. (2013a). “Robust structure from motion of nonrigid objects in the presence of outlying and missing data,” in CRV (Regina, SK: IEEE), 159–166.

Google Scholar

Wang, G., Zelek, J. S., Wu, Q. M. J., and Bajcsy, R. (2013b). “Robust rank-4 affine factorization for structure from motion,” in WACV (Tampa, FL: IEEE), 180–185.

Google Scholar

Xiao, J., and Kanade, T. (2005). “Uncalibrated perspective reconstruction of deformable structures,” in Proc. of the International Conference on Computer Vision, Vol. 2 (Beijing: IEEE), 1075–1082.

Google Scholar

Yan, J., and Pollefeys, M. (2008). A factorization-based approach for articulated nonrigid shape, motion and kinematic chain recovery from video. IEEE Trans. Pattern Anal. Mach. Intell. 30, 865–877. doi:10.1109/TPAMI.2007.70739

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, J., Chin, T.-J., and Suter, D. (2011). “A global optimization approach to robust multi-model fitting,” in CVPR (Colorado Springs: IEEE), 2041–2048.

Google Scholar

Zaharescu, A., and Horaud, R. (2009). Robust factorization methods using a Gaussian/uniform mixture model. Int. J. Comput. Vis. 81, 240–258. doi:10.1007/s11263-008-0169-x

CrossRef Full Text | Google Scholar

Zelnik-Manor, L., Machline, M., and Irani, M. (2006). Multi-body factorization with uncertainty: revisiting motion consistency. Int. J. Comput. Vis. 68, 27–41. doi:10.1007/s11263-005-4840-1

CrossRef Full Text | Google Scholar