Developing small satellite ground support software for orbit tracking and target acquisition of the HARP cubesat

Small satellites are efficient at performing Earth science from space due to their limited cost and size. Small satellites (cubesats) achieve much with limited power production/storage, heat dissipation, data storage, and ground contact points/bandwidth. As such it is beneficial to offload as much as possible to ground support systems. Consider the HyperAngular Rainbow Polarimeter (HARP) Cubesat. Its goals were to serve as a technical demonstration prior to the development of HARP2 aboard the NASA Plankton Aerosol Cloud and ocean Ecosystem (PACE) mission and to serve as an Earth viewing remote sensing platform which measured the characteristics of clouds and aerosols. HARP cubesat was limited to taking 5-minute capture sequences once every 24 h. It took approximately 10 such captures before it needed to perform data downlink and have its memory cleared for continued use. A ground station at NASA Wallops supported HARP with approximately three points of contact each day. To maximize the value of each capture, ground support software was developed leveraging public data to inform the schedule of each capture. In this paper, we review the algorithms and data sources that allowed us to: 1; predict the HARP orbital track a week in advance, 2; predict also the location of other remote sensing satellites and ground stations relative to HARP, 3; predict the ground view geometry of the instrument along its orbital track, 4; compare global climatological data products of clouds and aerosols along the predicted orbital tracks, and 5; identify and integrate important ground target locations based on remote sensing literature and ongoing natural phenomena. This HARP Orbital Prediction System (HOPS) made HARP into a successful technical demonstration which also offered significant science value. The HOPS system presents a valuable methodology for small satellites to operate efficiently despite their limited capabilities. HOPS is also a useful testbed for studying the sensitivity of scene geometry. Using HOPS, we show that for a wide field-of-view (FOV) instrument, like HARP, latitude/longitude geolocation varies by approximately ${0.1}^{\circ }$ at a height of 8–10 km. Scattering angles vary less than ${0.01}^{\circ }$ at similar heights, with the worst performance near direct backscatter $\left({180}^{\circ }\right)$.

1 Introduction

The HyperAngular Rainbow Polarimeter (HARP) Cubesat is an example of a science-quality payload designed to perform passive polarimetric measurements of Earth’s surface in a small, efficient 3U cubesat package (Martins et al., 2018). The payload was designed similarly to AirHARP, which was deployed and tested in two field campaigns, which proved the HARP concept for retrievals of cloud and aerosol microphysics (Puthukkudy et al., 2020; McBride et al., 2020).

HARP Cubesat was the first demonstration of the HARP concept in space and the first time HARP would fly autonomously without benefit from the careful daily flight planning of a field experiment. HARP Cubesat had no means of propulsion and was injected into orbit from the International Space Station (ISS) at around 400 km above the Earth’s surface, which subjected it to slow orbital decay and a 2-year limited lifespan. Further, HARP lacked a thermal control system and relied on its own small solar array for power and, as such, was much more operationally limited than payloads flown on larger platforms. For reference, the heritage polarimeter, Polarization and Directionality of the Earth’s Reflectances (POLDER; Deschamps et al., 1994) imaged the entire globe once every 48 h, whereas HARP could only acquire one 5-minute capture (With a swath-size on the order of 1,000 km²) once every 24 h at most. Capture frequency was further limited by the fact that HARP was limited to a single Ultra High Frequency (UHF) antenna station at NASA Wallops, VA, which underwent extended mechanical repairs between 2020 and 2022 when HARP was in orbit. Compared to a typical NASA mission such as Terra, Aqua or Aura that have several ground stations all around the world, HARP Cubesat data transmissions would be severely limited. HARP had data storage space for approximately 10 captures before it needed to have its memory read and cleared. Pass opportunities were limited to between 2 and 4 a day and were only minutes long which had to include downlink as well as uplink of future command actions.

Due to the limited capabilities of a small platform like HARP, a great deal of ground support was important for the success of the project. While HARP was budgeted as a technical demonstration, there was widespread scientific interest in the polarimetric data as the last NASA spaceborne polarimeter failed to reach orbit after a launch failure in 2011 (Dubovik et al., 2019), and no instrument with publicly available data took its place in the intervening period between the end of the 3rd POLDER mission in 2013 and 2020, when HARP Cubesat launched. Ground support for HARP consisted primarily of forward planning for the acquisitions done each day to maximize possible scientific or engineering data content of the precious few images we could acquire. While ground-station interrupts prevented HARP from working at its maximum rate of one capture every day, captures were still prepared with the assumption that once every 24 h a capture would be attempted and therefore software and field expertise had to be employed.

The primary science interests of HARP data were to image the Earth’s atmosphere and, through polarimetric retrieval techniques, provide information about the type, quantity, and size of aerosols as well as the size distribution and phase of cloud droplets. Aerosols, clouds, and the interaction between them remains the largest uncertainty in global climate models (National Academies of Sciences, Engineering, and Medicine, 2018). Polarization provides a large increase in the information content of passive remote sensing data (Remer et al., 2019; Li et al., 2022), as compared to the heritage passive radiometers like the Moderate Resolution Image Spectroradiometer (MODIS) aboard the Aqua satellite (Xiong and Butler, 2020). It is expected that MultiAngle Polarimeter (MAP) data can improve estimates of climate forcing by a factor of 2 (Chen et al., 2022). Additionally, as a technical precursor to HARP2, recently launched aboard the Plankton, Aerosol, Cloud, ocean Ecosystems (PACE) mission, we had interest in using HARP Cubesat to evaluate static surface targets for their candidacy as vicarious calibration targets for the much longer (3+ years) PACE mission. Both atmosphere and surface targets can be of increased interest in this regard if they exist close to a ground station of the Aerosol Robotic Network (AERONET; Holben et al., 1998; Giles et al., 2012) as these stations also perform aerosol retrievals and therefore can serve as atmospheric correction for viewing ground targets and/or validation data for aerosol retrievals. There also exist other ground-based remote sensing stations such as the European Aerosol Research Lidar Network (EARLIENT) (Pappalardo et al., 2014) and the NASA Micro-Pulse Lidar Network (MPLNET) (Lolli et al., 2019) which provide height-resolved lidar measurements of the atmosphere, unlike AERONET’s passive column-integrated measurements.

Further, there were several other active Earth remote sensing satellites in orbit at the same time as HARP Cubesat. It has been shown that bringing multiple instruments to bear on the same target can also improve retrieval information content (Dubovik et al., 2021); this concept informed the A-Train satellite constellation (Kelly and Macie, 2003) which has multiple instruments of differing design following one another in their orbit such that they can measure the same target with only a short time delay. Additionally, collocated captures such as these allow instruments to intercompare their raw measurements if they have design overlap in some regime (e.g., the same spectral band). This improves long term calibration monitoring and enables calibration transfer should one instrument drift. While no other public polarimeter data existed for HARP to readily compare to, radiometric measurements of intensity did overlap with the likes of MODIS and other heritage radiometers. Likewise, retrieval products can be intercompared regardless of instrument specific characteristics (Puthukkudy et al., 2020).

Finally, we note that retrievals from a passive imager such as HARP Cubesat, especially with polarization, depend heavily on scattering angle (Mishchenko, 2013; Li et al., 2022). Scattering angle is a function of the instrument’s viewing geometry as well as the solar illumination angle (dependent on time and location of the target). The polarimetric “cloudbow” is a good example of the importance of measuring a particular scattering angle range to be able to retrieve the mean size and size distribution range of liquid water droplets (Xu et al., 2018; McBride et al., 2020). Cloudbows are highly dependent on scattering angle and can only be seen in clouds with liquid water droplets in the upper layers. Not all of HARP Cubesat’s potential images supported cloudbow retrievals, and thus it became a serious effort on the ground to schedule HARP Cubesat captures when the geometry was favorable and liquid clouds likely to occur. Likeliness of liquid cloud droplets was a matter of climatology, as developed from long term level 3 cloud fraction and cloud thermodynamic phase measurements from MODIS (Pincus et al., 2023). Similar level 3 products exist for aerosol products (Gupta et al., 2020). These products were reviewed and provided overlays in HOPS and informed operator usage.

Therefore, the primary goals of the ground support designed for HARP involved: 1) the ability to predict when HARP would overfly ground targets of differing scientific potential, 2) the ability to predict events where HARP would be collocated in space and time with other remote sensing platforms in space or on the ground, and 3) the ability to assess the science validity of a target scene based on HARP’s measurement characteristics, viewing geometry and known, global climatological probabilities. The ground support system that performed these three needs for HARP, with the help of operator expertise, came to be known as the HARP Orbital Prediction System (HOPS). Broadly, it provides a framework that can support other small form-factor satellite imaging systems whose onboard capabilities are necessarily limited for the sake of efficiency. As cubesats carrying Earth-viewing sensors become more common place, the value of adapting HOPS to other nano satellites increases. The collection of algorithms within HOPS also provides the ability to assess the sensitivity of remote sensing measurements to orbital characteristics and instrument optical design.

For this article, Section 2 will review the theoretical basis for orbital prediction techniques, as well as the scattering angle and geolocation algorithms in common use and a summary of the external datasets used. In Section 3 results are shown, consisting primarily of selected collocation events for HARP Cubesat as well as a summary of the capture dataset for the entire HARP flight period. Section 3 will show the more generalized capabilities of HOPS by performing a sensitivity study of scattering angle with respect to ground projection height. In Section 4, there is a summary of the results of the overall HARP Cubesat technical demonstration and discussion of how HOPS may be improved and adapted for other uses. Section 5 contains conclusions derived from the construction of HOPS and the HARP Cubesat project overall.

2 Methodology

The HOPS system combines well established orbital prediction technologies with a geolocation algorithm developed for the aircraft instrument, AirHARP, and later used for HARP2 aboard PACE. It is based on simulations of the HARP optics and external data products of the Earth surface characteristics. Orbital prediction is handled by orbital propagators that take as input the state information of an orbiting body (e.g., position, speed, time of measurement) and applies basic Newtonian mechanics to predict its future state. Orbiting bodies are tracked by government entities, such as the North American Aerospace Defense Command (NORAD), and their state information is therefore publicly available. The data is posted online in a standardized Two-Line-Element (TLE) format which concisely provides everything a propagator needs to make its predictions. The Simplified General Perturbation (SGP4) propagator is a widely used open-source propagator which interfaces directly with TLE data and has been shown to propagate orbits accurately within 100 m for at least 10 days into the future (Vallado and Cefola, 2012), depending on the strength of atmospheric drag the object is experiencing and/or its own thrusters altering its state, both of which would diminish this accuracy window. Therefore, for HOPS we chose to limit predictions to be generated on weekly intervals from a given TLE of HARP Cubesat, whose orbit was constantly decaying due to atmospheric drag.

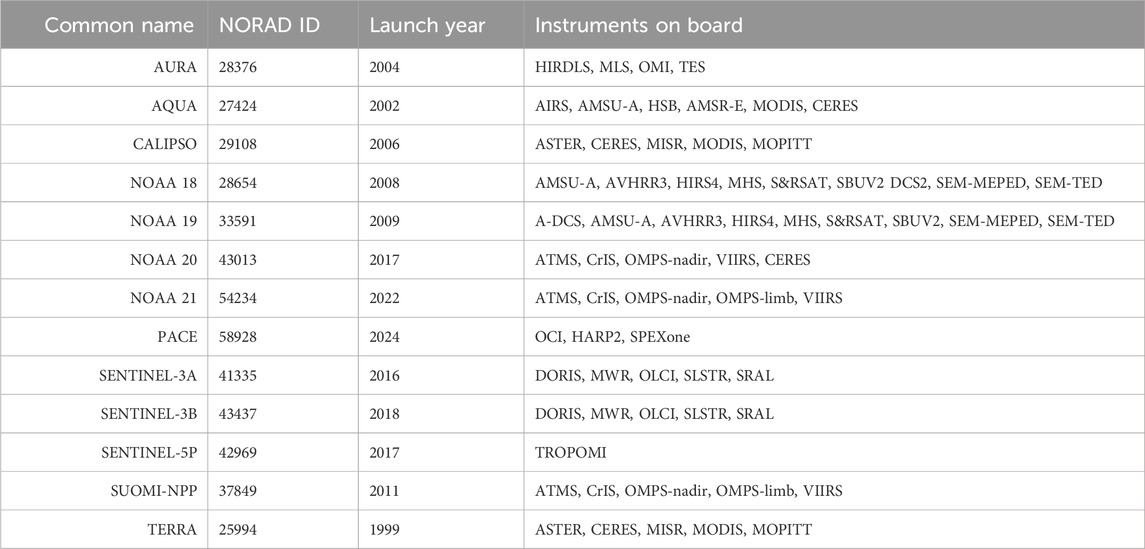
Table 1 provides a list of several major Earth remote sensing platforms, their associated TLE numerical identification codes, and a list of the instruments which they carry. These do not include the platforms which exist beyond Low-Earth Orbit (LEO), such as geostationary platforms like Himawari (Bessho et al., 2016), GOES-R (Castellanos et al., 2018), or the Deep Space Climate Observatory (DSCOVR) at the Lagrangian point between Earth and the Sun (Marshak et al., 2018), but by their very nature these platforms have static views of the Earth or are in orbit about the Sun and do not require orbital prediction to track the geographical extent of their Field of View (FOV).

Table 1

Table 1. Table of NORAD IDs for earth remote sensing satellites and their instrumentation.

There are also publicly available records of the locations of ground stations for AERONET, EARLINET, and MPLNET. Some stations are no-longer maintained, but public databases record a list of active and inactive sites to make sorting these out easy. What is not readily available are whether, at a particular time, these ground stations will have data as that depends on local conditions. Also of interest, Earth surface targets such as desert sites or solar reflection off of the ocean can be used for vicarious calibration of remote sensing platforms via stable natural phenomena (Dinguirard and Slater, 1999; Toubbé et al., 1999). Databases exist for remote sensing surface properties allowing seasonal variability of surface targets to be considered (Maignan et al., 2009). These well understood sites were used by operators to finalize targets fitting other criteria of interest via HOPS.

For further discussion on the nature of the SGP4 orbital propagator see (Vallado and Paul, 2008), and for a database of TLE records visit (Space-Track, 2024).

2.1 Geolocation and geometry

In general, geolocation of HARP image data occurs in a series of discrete, independent steps for each individual pixel in the image sensor. 1) identify the pointing vector in 3-D space with respect to the instrument optical axis using optical simulation and lab measurements, 2) rotate that pointing vector to the instrument body frame via the empirically derived “offset” angles, 3) rotate again using the instrument orbital attitude information to get the vector in an Earth-Centered reference frame, 4) extrapolate the pointing vector from the instrument to the Earth’s center and find the intercept point with the Earth’s surface, and 5) apply topography correction to the region around the intercept point to account for surface height variability of the planet intercepting the ray drawn from satellite to ground before it crosses the Earth ellipse. Additionally, once the intercept point is found we can use the pointing vector from the ground location back up to the instrument to calculate the viewing geometry angles and the time information to get the solar angles for the calculation of scattering angle.

The geolocation calculation is one of the most computationally expensive parts of the HARP Image Processing Pipeline (HIPP) that takes raw Level 0 data and produces calibrated and geolocated Level 1b data. HOPS avoids much of that computational expense by applying a simplified geolocation process that 1) reduces the resolution of the sensor because the scattering angle and its components are smoothly varying functions, so high resolution is not necessary for a summary view, and 2) ignores the instrument body offset rotation and topographic search algorithm; these are required for high accuracy in the satellite remote sensing data product but are not necessary for a summary view in the HOPS software. Topographic height can still be utilized in the base algorithm as a single valued height increase from the Earth ellipse for the entire image. This is done in Section 4 for sensitivity of scattering geometry to ground projection height. Here we are only ignoring the pixel-by-pixel topography changes for the sake of simplification.

The parts of the geolocation process that remain in HOPS will be described here. First off, the pointing vector of the instrument optics was determined via optical ray-tracing simulation. The HARP concept is based on wide field-of-view optics spanning ${114}^{\circ }\times {94}^{\circ }$ (along/cross-track) that uses a spherical front lens with a series of secondary lenses to create a telecentric beam. More on the HARP design is available in (McBride et al., 2024). The zenith angle from the optical center and the azimuth angle from the along-track direction can be calculated for each pixel by an empirically derived function determined from the ray-tracing.

${\theta }_{HARP}=a{r}^4+b{r}^3+c{r}^2+dr+e(1)$

${\theta }_{HARP}$ represents the instrument body-frame, pixel-resolved, zenith angle which is calculated as a polynomial of the pixel’s radial distance (in number of pixels), $r$, from the optical center. The polynomial coefficients as shown in Equation 1 come from the optical simulation of HARP. For an example, the order of magnitude of HARP’s coefficients are: $a\approx {10}^4,b\approx -{10}^3,c\approx {10}^2,d\approx {10}^1,e\approx {10}^{-3}$ where the exact coefficients depend not only on the optical system, but on the size of each pixel in the detector. By adjusting these parameters, different kinds of instruments can be easily implemented inside of HOPS. The pixel-azimuth $\left({\varphi }_{harp}\right)$ angle is even easier to calculate because of HARP’s spherical lens:

${\varphi }_{HARP}={\tan }^{-1}\left(\frac{y}{x}\right)(2)$

Where $y$ represents the along-track pixel coordinate, and $x$ the cross-track pixel coordinate, in number of pixels, with the origin at the instrument optical center. Assuming unit length, these two angles (Equations 1, 2) are sufficient to construct a cartesian vector of the view direction of each pixel in HARP using simple spherical coordinate transformations. The next step in the geolocation is to take this cartesian vector and rotate it to an intermediate local North-East-Down reference (NED) frame via Euler angle rotation. From that frame, we can rotate to the standard Earth-Centered-Earth-Fixed (ECEF) reference frame using an additional rotation matrix, both of which are described in Guowei et al. (2011). The ECEF frame is defined such that the x-axis extends out from the planet center through the geodetic latitude/longitude origin, and that the z-axis points along the rotational axis of the planet via the right-hand-rule, which also defines the y-axis.

The final step for geolocation is simply the intercept between the pixel pointing vector in the ECEF frame, and surface of the planet. This requires that we know the shape of the planet, for which standardized models exist such as the World Geodetic System 84 (WGS84). This provides radii measurements of the planetary ellipsoid, allowing us to construct a parameterized equation of the intercept.

$\mathit{P}=t\mathit{V}+{\mathit{P}}_0(3)$

Where $\mathit{P}$ represents the ECEF coordinate vector of the generalized Earth surface, $t$ is an unknown parameter which scales the ECEF pixel pointing vector found above, $\mathit{V}$, to the surface from the known coordinate of the spacecraft position vector in the ECEF frame, ${\mathit{P}}_0$. The vector components of $\mathit{P}$ can be found readily via the 3-D equation of an ellipse with the radii from the WGS84 representation of the planet. When solved for $t$, Equation 3 allows us to acquire our geolocation of a given pixel. Note that $\mathit{P}$ can be adjusted from the WGS84 Ellipse by an additive scalar to account for our ground projection height as mentioned previously.

Finally, we convert back from the ECEF coordinate to the geodetic coordinate system to obtain our latitude and longitude. Additionally, the ground view-zenith and view-azimuth angles can be found from the construction of the local North-East-Up (NEU) coordinate system at that geodetic position and the vector pointing to the satellite in that frame, which follow directly from spherical coordinate transform equations. The NEU frame transformation is again available from Guowei et al. (2011).

This methodology ignores inaccuracies due to the optical refraction of the light path from the instrument to the surface point as well as the previously mentioned instrument mounting offset parameters and the finely resolved ground topography, which are assumed to be negligible for general use. External information of local topography, such as from the Shuttle Radar Topography Mission (Farr et al., 2007), is needed alongside a search algorithm to see if a peak or valley near that expected point will be the actual endpoint of the projection ray. For the sake of simplicity HOPS does not account for these details as the search algorithm is very computationally expensive. Still, we retain the ability to raise the entire projection area by any amount we desire without implementation of a topographic search, such as to a cloud height of several kilometers (See Section 4). We could even prescribe a different height, without searching, to differing pixels if we knew the scene to have a significant FOV-dependent change in ground topography. Without an iterative search algorithm this addition would still not be fully accurate, nor does complex ground topography have much meaning at the resolution scale used for speedy HOPS evaluation (approximately 1/20 of the true HARP resolution in both along/cross-track dimensions).

To complete our full understanding of the geolocation point we must then also calculate the solar geometry at the given geolocation point, given the time of measurement. From there, we can define via spherical geometry the scattering angle of a HARP measurement at that location.

$\cos \left(\mathrm{\Theta }\right)=-\cos \left({\theta }_v\right)\cos \left({\theta }_s\right)+\sin \left({\theta }_v\right)\sin \left({\theta }_s\right)\cos \left({\varphi }_s-{\varphi }_v-\pi \right)(4)$

Where the scattering angle $\left(\mathrm{\Theta }\right)$ is defined as a function of the prior described viewing zenith and azimuth angles, ${\theta }_v$ and ${\varphi }_v$, as well as the solar zenith and azimuth angles, ${\theta }_s$ and ${\varphi }_s$, all in radians. Calculation of the solar angles as a function of time, latitude, and longitude is handled by a standard library (Reda and Afshin, 2004). The view angles follow from spherical geometry transformations of the vector pointing from the ground point to the satellite.

The “glint angle” differs from scattering angle only by the sign of the view-zenith cosine term, equivalent to taking $\pi -{\theta }_s$. Conceptually this corresponds to viewing the sunlight as “leaving” the water surface directly to the sensor (see Figure 1) and thereby provides a measurement of whether or not our satellite would be viewing the image of the sun on the ocean’s surface (the sunglint). It is widely used in satellite remote sensing when sunglint is of interest (Giglio et al., 2003).

$\cos \left({\mathrm{\Theta }}_{\mathrm{g}}\right)=\cos \left({\theta }_v\right)\cos \left({\theta }_s\right)+\sin \left({\theta }_v\right)\sin \left({\theta }_s\right)\cos \left({\varphi }_s-{\varphi }_v-\pi \right)(5)$

Figure 1

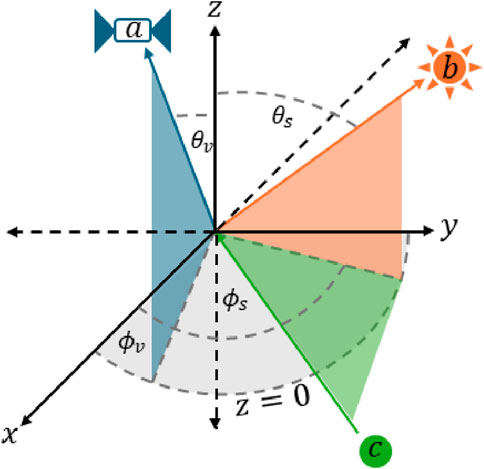
Figure 1. Scattering geometry visualization between satellite view $\left(a\right)$, solar $\left(b\right)$, and anti-solar $\left(c\right)$ rays. The satellite view zenith angle $a$ is defined as $\angle Za={\theta }_v$, the sun view zenith angle is defined as $\angle Zb={\theta }_s$, and the anti-sun vector is the supplementary angle to the solar zenith angle as $\cos \left(\theta \right)=-\cos \left(\pi -\theta \right)$. The view azimuth and zenith angles (${\varphi }_v$ and ${\varphi }_s$, respectively) are measured as the angle from the x-axis, but this selection is arbitrary as in both glint and scattering angle calculations only the difference between these angles matters, and the cosine function is an even function. Pictorially, the scattering angle is defined as $\mathrm{\Theta }=\angle ab$ and the glint angle is defined as ${\mathrm{\Theta }}_g=\angle ac$. The shaded color planes represent slices of the view meridional plane (blue), the solar meridional plane (orange), and the anti-solar meridional plane (green) between the principal ray of that plane and the $z=0$ plane shaded in grey.

Equation 5 shows the glint angle, ${\mathrm{\Theta }}_g$, as a function of the solar and viewing angles and it trends towards 0 with increasing sunglint signal, though the actual spread of relevant glint angles depends on the surface geometry, such as the sea surface perturbations from wind. A visualization of the scattering and glint geometry is provided in Figure 1.

3 Results

The primary result of the HOPS is an information-rich animation that simulates HARP Cubesat’s orbital track along with orbital tracks of other sensors with ground stations of interest marked. Figure 2 shows a single frame of one of the versions of the animation. HARP Cubesat is shown as a red marker with black lines indicating the along-track and cross-track extent of the FOV on the ground. The position of many remote sensing platforms is shown for the same timestamp, and ground stations are marked with different colored dots and/or numbers. The FOV of the Advanced Baseline Imager (ABI) instrument on GOES-R is also drawn. As the animation runs, the user can identify the times when HARP Cubesat is collocated with other sensors or when HARP Cubesat overflies an important ground target, often determined by operator expertise or Level 3 product overlays. Because daylight and night sections of the globe are indicated by shading, the user knows when HARP Cubesat is able to collect Earth view data. Solar and sensor viewing geometry are essential components of aerosol and cloud retrieval algorithms as noted in Section 2. A user planning when to schedule a capture for HARP Cubesat will want to know the scattering and glint geometry of the retrieval. This information is summarized by the scattering angle and the “glint angle” that are shown in the panels to the right in Figure 2, and these panels change with the timestamp. Scattering angle is given by Equation 4, and glint angle is given by Equation 5. Note that when glint angle is near 0 we expect HARP Cubesat to image the Sun’s reflection off water. The user would need this information when determining the value of a particular capture as glint can make aerosol retrieval difficult, or impossible, but it may otherwise provide a vicarious calibration target as the distribution of glint is well understood (Cox and Munk, 1954; Zhai et al., 2010).

Figure 2

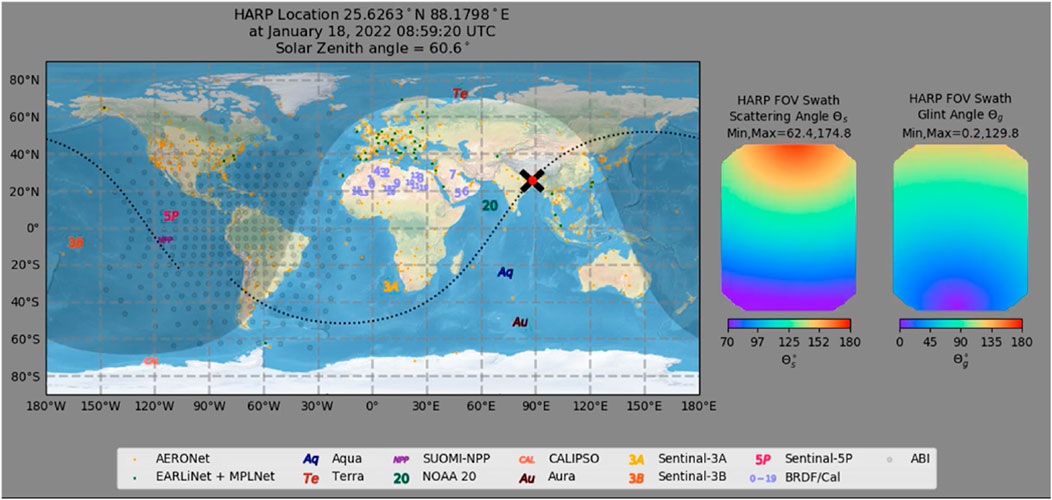
Figure 2. Screenshot of the original HARP Orbital Prediction System (HOPS) from January 2022 for a single time instance. HARP is shown as a red dot with black lines for the along/cross-track FOV extent. Other remote sensing satellites are marked by a common name, while active ground stations are marked by green and yellow markers. The geostationary Advanced Baseline Imager (ABI) aboard GOES-R has its FOV marked. Then, from the geolocation information, the scattering and glint angles are shown on the right, with the forward along-track view being depicted as the top of each image.

A newer, open-source form of HOPS will soon be made available (Fall 2024), which has an interactable GUI and improves this format. From the newer HOPS, Figure 3 was generated using a recent Aqua orbital TLE with the orbital height replaced with 300 km to make it more like HARP Cubesat. The scattering angle is calculated across the FOV for a given location in the central Atlantic Ocean. This particular time and location was selected to show the prediction of the range of scattering angles conducive to the measurement of the polarized cloudbow. The simulation runtime for this single frame is about 1 s and uses a ground projection height at sea level.

Figure 3

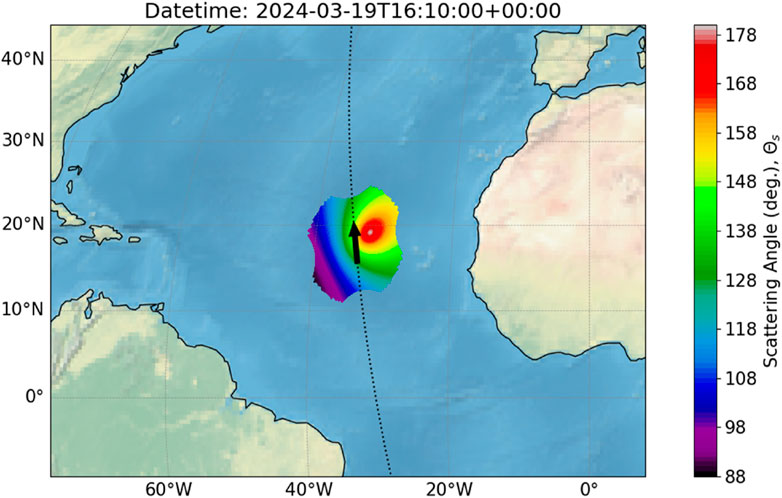
Figure 3. Footprint of HARP Cubesat using orbital track of AQUA satellite, but with orbital height replaced by a value of 300 km (similar to HARP Cubesat true orbit). The colors within the footprint indicate a calculation of scattering angle for this timestamp. The scattering angle range is indicative of a possible cloudbow measurement, pending cloud conditions. A black arrow indicates the direction of the orbit.

While HOPS was developed as an essential aide for determining HARP Cubesat captures, it has also proven to be a useful tool for understanding the assumptions needed to perform accurate geolocation for any HARP family sensor. For example, we can utilize the HOPS as a sandbox to evaluate the sensitivity of the calculated latitude/longitude and scattering angle as a function of ground projection height. Ground projection height may be different from expected due to clouds in a scene; similarly, aerosol plumes have a height about the surface and both may produce parallax in Level 1 data products if not accounted for, as we prove here using HOPS.

For the same scene as depicted in Figure 3, we changed the ground projection height across steps of 2 km, covering a range of typical cloud heights to evaluate how improper height projection of satellite geolocation data may influence cloudbow retrievals; results are shown in Figures 4, 5. In the former, two rows of images representing the HARP capture frame indicate the change of longitude and latitude with ground projection height. Significant fractions of a degree longitude and a degree latitude are indicated, which correspond to errors on the order tens of kilometers at the shown latitude in Figure 3. This would amount to several pixels of geolocation error for HARP2, with a pixel resolution of about 4 km. In Figure 5, the sensitivity of scattering angle under the same conditions is shown. Refer to Figure 3 to see the expected range of scattering angle in this case as Figure 5 shows only the difference at each height. Our result here, from HOPS, shows that that scattering angle is sensitive on the order ${0.1}^{\circ }$, or less, across typical water cloud heights, which is not significant for a measurement such as the polarimetric cloudbow which smoothly varies across a range of approximately ${40}^{\circ }$ (McBride et al., 2020). The most sensitivity to ground projection height exists for scattering angles around ${180}^{\circ }$, the direct backscatter position. This point is also of negligible importance to cloudbow measurements.

Figure 4

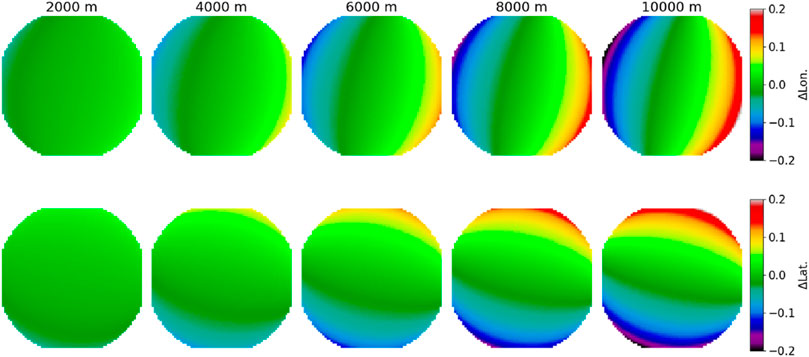
Figure 4. Difference map (in pixel coordinates) of the geodetic longitude (b) and latitude (a) for different ground projection heights. The HARP geolocation algorithm was run for differing topographic heights and the geolocation result for each was subtracted from the results with 0 m projection height (sea level). This demonstrates that projection height is a significant factor in accurate geolocation.

Figure 5

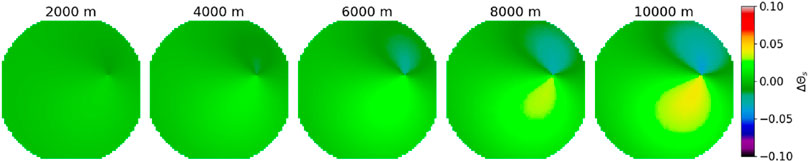
Figure 5. Difference map (in pixel coordinates) of the scattering angle for different ground projection heights. The HARP geolocation algorithm was run for differing heights, the scattering angle calculated from viewing/solar geometry angles, and the result was subtracted from the geolocation results with 0 m projection height. This demonstrates that projection height is a not a significant factor in accurate scattering angle, but that the greatest sensitivity is near direct backscatter.

4 Discussion

Small form-factor cubesats with limited capabilities can still carry science-relevant Earth-viewing sensors and fill an important niche in spaceborne observations. These instruments can be built for a fraction of the cost of larger space platforms, allowing for participation of nontraditional players in the space economy that include universities, countries with developing economies, Non-Governmental Organizations and the commercial sector (Cristóbal and Reza Emami, 2019). The inherent limited capabilities of cubesats require a strategy to maximize their usefulness. Of foremost concern are limitations in data volume downlinks. Earth-viewing sensors collect and transmit gigabytes of data that can challenge even the sophisticated downlinking capability of large observatories. Consider HARP Cubesat as our example, we note that after breaking up in the atmosphere in April 2022, HARP Cubesat had been in autonomous orbit for 777 days but had completed only 62 captures of some scientific merit, each less than 5 minutes in length. Expected capture frequency should have been close to the number of active days, but ground station down time limited this. Without a system such as HOPS enabling careful selection of captures, HARP Cubesat would have been much less successful.

Given the importance of each capture, having a tool that aides the quick evaluation of geometrical considerations, collocation potential and validation potential becomes fundamental to the overall goal of the mission like HARP. Using the HOPS system to predict capture times, we could choose wisely when/where science opportunities were present with a combination of external information and operator expertise. When such opportunities were unavailable, we could turn our attention to operational engineering captures important for the development of subsequent instruments without sacrificing science. Figure 6 shows a global map of HARP Cubesat captures in intensity using the red, green, and blue channels centered at 440, 550, and 665 nm respectively. These captures include water clouds with correct geometry for microphysical retrievals, dust plumes off the Sahara, pollution over Asia, smoke in North America, clear sky conditions over deserts and high-altitude lakes for calibration, and coccolithophore plumes in the northern Atlantic. These datasets are publicly available by request to the HARP team at the Earth and Space Institute housed on the University of Maryland Baltimore (UMBC) campus.

Figure 6

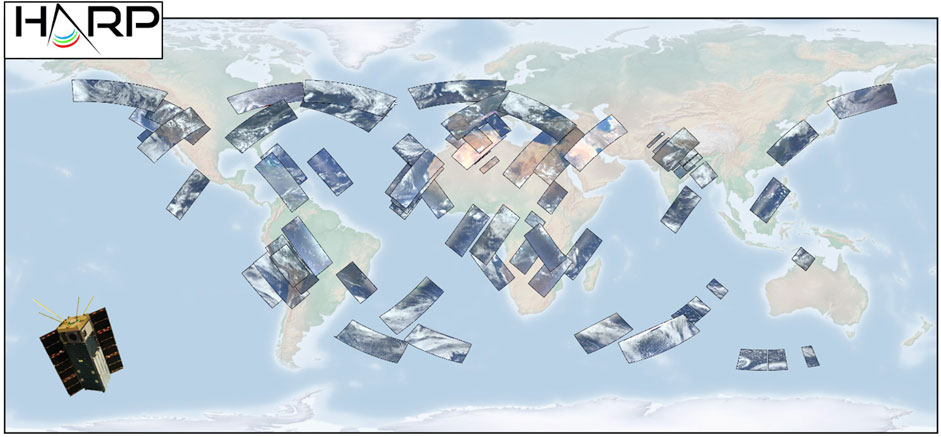
Figure 6. Global map of HARP Cubesat captures. Nadir pushrooms in intensity RGB format across the globe. Each pushroom spans an approximately 5-minute window spanning approximately 600 images per HARP detector.

Evaluations of the HARP Cubesat data informed the process of HARP2 aboard PACE, expanding the calibration pipeline to account for variations in wide-FOV polarization characteristics (Sienkiewicz et al., 2024). Construction of the HIPP system for construction of HARP Level 1 data products also directly contributed to the same process for PACE-HARP2. Much of the HARP Cubesat demonstration data remains to be fully evaluated with dedicated Level 2 retrieval products.

5 Conclusion

Since 1957 with the launch of the first Earth-orbiting satellites, space has been the sole domain of major national agencies who have developed an infrastructure for the building, launching and operations of their spacecraft. Only recently has the focused shifted from national agencies and major missions to a wide variety of space users and small affordable spacecraft. Now we see highly capable payloads fit for small spacecraft reaching orbit and producing science-quality data. This trend towards small spacecraft will continue (Baddock et al., 2021), but the infrastructure for operations of these spacecraft is lagging behind. HOPS is an important demonstration of the impact a smart tool can have in the operations and science productivity of a small satellite mission and the development of future missions.

While HOPS enabled, and doubtlessly enhanced, the HARP Cubesat mission, it also provides a framework for the evaluation of orbit sensitivities in Earth science. Measurement sensitivities and uncertainties remain a major effort in the production of Level 2 retrieval products (Gao et al., 2023). We determined that ground height projection was negligible $\left(<{0.1}^{\circ }\right)$ to the calculation of scattering angle in scenarios relevant to liquid water cloudbow droplet retrievals. For the same ground heigh projections (maximum of 10 km), determination of latitude and longitude with pixel-level accuracy in a HARP-like system was not possible as projection accuracy became approximately ${0.1}^{\circ }$ equivalent to several pixels of error. Final uncertainties for the PACE mission will depend on estimates such as these.

Here HOPS was used for a single satellite, but there is nothing preventing the use of HOPS for the evaluation of multiple cubesats in defining a constellation. Additional domain expertise in aerospace science to produce potential unique, simulated TLE information for such experiments is still a needed addition to HOPS. In addition to providing a service to the operation of small satellite platforms, HOPS can also help identify collocations of agency-led full-scale mission datasets as well to teams wishing to utilize colcated satellite data. HARP Cubesat stands as a successful technical demonstration of its own hardware as well as for ground support software such as HOPS. Going forward HOPS will continue to see development with an eventual open-source release to the community.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

NS: Conceptualization, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. JM: Conceptualization, Investigation, Project administration, Supervision, Writing–review and editing. XX: Conceptualization, Investigation, Project administration, Supervision, Writing–review and editing. BAM: Conceptualization, Supervision, Writing–review and editing. LAR: Methodology, Project administration, Resources, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors acknowledge the funding supports from the NASA FINESST (80NSSC21K1600) on behalf of NS NASA PACE mission, the NASA ESTO InVest project, and the UMBC START award. Additional funding support from NASA HARP/PACE (GSTR2178).

Acknowledgments

The authors acknowledge and thank the engineering and support staff at the Earth and Space Institute which have and continue to support all HARP iterations.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baddock, M. C., Bryant, R. G., Domínguez Acosta, M., and Gill, T. E. (2021). Understanding dust sources through remote sensing: making a case for CubeSats. J. Arid Environ. 184 (June 2020), 104335. doi:10.1016/j.jaridenv.2020.104335

CrossRef Full Text | Google Scholar

Bessho, K., Date, K., Hayashi, M., Ikeda, A., Imai, T., Inoue, H., et al. (2016). An introduction to himawari-8/9 — Japan’s new-generation geostationary meteorological satellites. J. Meteorological Soc. Jpn. 94 (2), 151–183. doi:10.2151/jmsj.2016-009

CrossRef Full Text | Google Scholar

Castellanos, P., da Silva, A. M., Darmenov, A. S., Buchard, V., Govindaraju, R. C., Ciren, P., et al. (2018). A geostationary instrument simulator for aerosol observing system simulation experiments. Atmosphere. 10 (1), 2. doi:10.3390/atmos10010002

CrossRef Full Text | Google Scholar

Chen, C., Dubovik, O., Schuster, G. L., Chin, M., Henze, D. K., Lapyonok, T., et al. (2022). Multi-angular polarimetric remote sensing to pinpoint global aerosol absorption and direct radiative forcing. Nat. Commun. 13 (1), 7459. doi:10.1038/s41467-022-35147-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Cox, C., and Munk, W. (1954). Measurement of the Roughness of the Sea Surface from Photographs of the Sun’s Glitter. J. Optical. Society. America. 44 (11), 838. doi:10.1364/josa.44.000838

CrossRef Full Text | Google Scholar

Cristóbal, N.-P., and Reza Emami, M. (2019). CubeSat mission: from design to operation. Appl. Sci. 9, 3110. doi:10.3390/app9153110

CrossRef Full Text | Google Scholar

Dinguirard, M., and Slater, P. N. (1999). Calibration of space-multispectral imaging sensors: a review. Remote Sens. Environ. 68 (3), 194–205. doi:10.1016/S0034-4257(98)00111-4

CrossRef Full Text | Google Scholar

Dubovik, O., Li, Z., Mishchenko, M. I., Tanré, D., Karol, Y., Bojkov, B., et al. (2019). Polarimetric remote sensing of atmospheric aerosols: instruments, methodologies, results, and perspectives. J. Quantitative Spectrosc. Radiat. Transf. 224, 474–511. doi:10.1016/j.jqsrt.2018.11.024

CrossRef Full Text | Google Scholar

Dubovik, O., Schuster, G. L., Xu, F., Hu, Y., Bösch, H., Landgraf, J., et al. (2021). Grand challenges in satellite remote sensing. Front. Remote Sens. 2 (February), 1–10. doi:10.3389/frsen.2021.619818

CrossRef Full Text | Google Scholar

Deschamps, P. Y., Breon, F. -M., Leroy, M., Podaire, A., Bricaud, A., and Buriez, J. -C. (1994). The POLDER mission: instrument characteristics and scientific objectives. IEEE Transactions on geoscience and remote sensing 32.3, 598–615.

CrossRef Full Text | Google Scholar

Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Riley, D., Scott, H., et al. (2007). The Shuttle radar topography mission. Rev. Geophys. 45 (2), 1–33. doi:10.1029/2005rg000183

CrossRef Full Text | Google Scholar

Gao, M., Knobelspiesse, K., Franz, B. A., Wang Zhai, P., Cairns, B., Xu, X., et al. (2023). The impact and estimation of uncertainty correlation for multi-angle polarimetric remote sensing of aerosols and ocean color. Atmos. Meas. Tech. 16 (8), 2067–2087. doi:10.5194/amt-16-2067-2023

CrossRef Full Text | Google Scholar

Giglio, L., Descloitres, J., Justice, C. O., and Kaufman, Y. J. (2003). An enhanced contextual fire detection algorithm for MODIS. Remote Sens. Environ. 87 (2–3), 273–282. doi:10.1016/S0034-4257(03)00184-6

CrossRef Full Text | Google Scholar

Giles, D. M., Holben, B. N., Eck, T. F., Sinyuk, A., Smirnov, A., Slutsker, I., et al. (2012). An analysis of AERONET aerosol absorption properties and classifications representative of aerosol source regions. J. Geophys. Res. Atmos. 117 (17), 1–16. doi:10.1029/2012JD018127

CrossRef Full Text | Google Scholar

Guowei, C., Lee, B. M., and Tong, H. (2011). Unmanned rotorcraft systems. London: Springer-Verlag. doi:10.1007/978-0-85729-635-1

CrossRef Full Text | Google Scholar

Gupta, P., Remer, L. A., Patadia, F., Levy, R. C., and Christopher, S. A. (2020). High-resolution gridded level 3 aerosol optical depth data from modis. Remote Sens. 12 (17), 2847–2922. doi:10.3390/rs12172847

CrossRef Full Text | Google Scholar

Holben, B. N., Eck, T. F., Slutsker, I., Tanré, D., Buis, J. P., Setzer, A., et al. (1998). AERONET - a federated instrument Network and data archive for aerosol characterization. Remote Sens. Environ. 66 (1), 1–16. doi:10.1016/S0034-4257(98)00031-5

CrossRef Full Text | Google Scholar

Kelly, A. C., and Macie, E. J. (2003). The A-train: NASA’s Earth observing system (eos) satellites and other Earth observation satellites. Berlin, Germany: Proceedings of the 4th IAA Symposium on Small Satellites for Earth Observation.

Google Scholar

Li, X., Han, Y., Wang, H., Liu, T., Chen, S. C., and Hu, H. (2022). Polarimetric imaging through scattering media: a review. Front. Phys. 10 (March), 1–24. doi:10.3389/fphy.2022.815296

CrossRef Full Text | Google Scholar

Lolli, S., Vivone, G., Lewis, J. R., Sicard, M., Welton, E. J., Campbell, J. R., et al. (2019). Overview of the new version 3 NASA micro-pulse lidar Network (MPLNET) automatic precipitation detection algorithm. Remote Sens. 12 (1), 71. doi:10.3390/rs12010071

CrossRef Full Text | Google Scholar

Maignan, F., Marie Bréon, F., Fédèle, E., and Bouvier, M. (2009). Polarized Reflectances of natural surfaces: spaceborne measurements and analytical modeling. Remote Sens. Environ. 113 (12), 2642–2650. doi:10.1016/j.rse.2009.07.022

CrossRef Full Text | Google Scholar

Marshak, A., Herman, J., Szabo, A., Blank, K., Carn, S., Alexander, C., et al. (2018). Earth observations from DSCOVR epic instrument. Bull. Am. Meteorological Soc. 99 (9), 1829–1850. doi:10.1175/BAMS-D-17-0223.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Martins, J. V., Fernandez-borda, R., Mcbride, B., Remer, L., and Barbosa, H. M. J. (2018). “The HARP hyperangular imaging polarimeter and the need for small satellite payloads with high science payoff for Earth science remote sensing,” in IGARSS 2018 - 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22-27 July 2018 (IEEE), 6304–6307. doi:10.1109/IGARSS.2018.8518823

CrossRef Full Text | Google Scholar

McBride, B., Barbosa, H. M., Birmingham, W., and Remer, L. (2020). Spatial distribution of cloud droplet size properties from airborne hyper-angular Rainbow polarimeter (AirHARP) measurements. Atmos. Meas. Tech. Discuss. 13, 1777–1796. doi:10.5194/amt-2019-380

CrossRef Full Text | Google Scholar

Mcbride, B. A., Vanderlei Martins, J., Dominik Cieslak, J., and Fernandez-borda, R. M. (2024). Pre-launch calibration and validation of the airborne hyper-angular Rainbow polarimeter (AirHARP) instrument. 2 (May 2023), 1–52.

CrossRef Full Text | Google Scholar

Mishchenko, M. I. (2013). “Electromagnetic scattering by particles and particle groups: an introduction,” in Electromagnetic scattering by particles and particle groups: an introduction (Cambridge: Cambridge University Press), 9780521519. doi:10.1017/CBO9781139019064

CrossRef Full Text | Google Scholar

National Academies of Sciences, Engineering, and Medicine (2018). Thriving on our changing planet: a decadal strategy for Earth observation from space. Washington, DC: The National Academic Press. doi:10.17226/24938

CrossRef Full Text | Google Scholar

Pappalardo, G., Amodeo, A., Apituley, A., Comeron, A., Freudenthaler, V., Linné, H., et al. (2014). EARLINET: towards an advanced sustainable European aerosol lidar Network. Atmos. Meas. Tech. 7 (8), 2389–2409. doi:10.5194/amt-7-2389-2014

CrossRef Full Text | Google Scholar

Pincus, R., Hubanks, P. A., Platnick, S., Meyer, K., Holz, R. E., Botambekov, D., et al. (2023). Updated observations of clouds by MODIS for global model assessment. Earth Syst. Sci. Data 15 (6), 2483–2497. doi:10.5194/essd-15-2483-2023

CrossRef Full Text | Google Scholar

Puthukkudy, A., Vanderlei Martins, J., Remer, L. A., Xu, X., Dubovik, O., Litvinov, P., et al. (2020). Retrieval of aerosol properties from airborne hyper angular Rainbow polarimeter (AirHARP) observations during ACEPOL 2017. Atmos. Meas. Tech. Discuss. 25. Available at: https://www.atmos-meas-tech-discuss.net/amt-2020-64/. doi:10.5194/amt-13-5207-2020

CrossRef Full Text | Google Scholar

Reda, I., and Afshin, A. (2004). Solar position algorithm for solar radiation applications. Sol. Energy 76 (5), 577–589. doi:10.1016/j.solener.2003.12.003

CrossRef Full Text | Google Scholar

Remer, L. A., Knobelspiesse, K., Zhai, P. W., Xu, F., Wu, L., Ahmad, Z., et al. (2019). Retrieving aerosol characteristics from the PACE mission, Part 2: multi-angle and polarimetry. Front. Environ. Sci. 7 (July), 1–21. doi:10.3389/fenvs.2019.00094

CrossRef Full Text | Google Scholar

Sienkiewicz, N., Martins, J. V., Fernandez-Borda, R., McBride, B. A., and Xu, X. (2024). “Exploring HARP’2 polarimetric precision for NASA PACE mission,” in Advances on the polarimetric remote sensing of aerosols and clouds (Baltimore: American Meteorological Society 104th Annual Meeting). Available at: https://ams.confex.com/ams/104ANNUAL/meetingapp.cgi/Paper/438277.

Google Scholar

Space-Track (2024). United States space command. Available at: https://www.space-track.org.

Google Scholar

Toubbé, B., Bailleul, T., Deuzé, J. L., Goloub, P., Hagolle, O., and Herman, M. (1999). In-flight calibration of the POLDER polarized channels using the Sun’s glitter. IEEE Trans. Geoscience Remote Sens. 37 (1), 513–524. doi:10.1109/36.739104

CrossRef Full Text | Google Scholar

Vallado, D. A., and Cefola, P. J. (2012). Two-lline element sets—practoce and use. Int. Astronaut. Congr. IAC7, 5812–5825.

Google Scholar

Vallado, D. A., and Paul, C. (2008). SGP4 orbit determination. AIAA/AAS Astrodyn. Specialist Conf. Exhib. doi:10.2514/6.2008-6770

CrossRef Full Text | Google Scholar

Xiong, X., and Butler, J. J. (2020). MODIS and VIIRS calibration history and future outlook. Remote Sens. 12 (16), 2523. doi:10.3390/RS12162523

CrossRef Full Text | Google Scholar

Xu, F., van Harten, G., Diner, D. J., Davis, A. B., Seidel, F. C., Rheingans, B., et al. (2018). Coupled retrieval of liquid water cloud and above-cloud aerosol properties using the airborne multiangle SpectroPolarimetric imager (AirMSPI). J. Geophys. Res. Atmos. 123 (6), 3175–3204. doi:10.1002/2017JD027926

CrossRef Full Text | Google Scholar

Zhai, P. W., Hu, Y., Chowdhary, J., Trepte, C. R., Lucker, P. L., and Josset, D. B. (2010). A vector radiative transfer model for coupled atmosphere and ocean systems with a rough interface. J. Quantitative Spectrosc. Radiat. Transf. 111 (7–8), 1025–1040. doi:10.1016/j.jqsrt.2009.12.005

CrossRef Full Text | Google Scholar