Corrigendum: Towards reliable retrievals of cloud droplet number for non-precipitating planetary boundary layer clouds and their susceptibility to aerosol

A Corrigendum on
Towards reliable retrievals of cloud droplet number for non-precipitating planetary boundary layer clouds and their susceptibility to aerosol

by Foskinis R, Nenes A, Papayannis A, Georgakaki P, Eleftheriadis K, Vratolis S, Gini MI, Komppula M, Vakkari V and Kokkalis P (2022). Front. Remote Sens. 3:958207. doi: 10.3389/frsen.2022.958207

A mistake was found in the Equation 1 of Zhu et al. (2018) which affects slightly the results in the original article, since this form was used to retrieve the satellite droplet number concentration using multiple beta-expressions (see Equation 4). Thus, in the published article, the error of Zhu et al. (2018) has been repeated, while the correct equation is found in Grosvenor's et al. (2018). Hence, the authors have made a series of changes based on the correct equation given by Grosvenor et al. (2018) which do not significantly affect their results. The changes, listed below, include updates to the text and to the figures.

1. Change in the abstract

A correction has been made to Abstract. This sentence previously stated:

“This methodology, used to study aerosol-cloud interactions for non-precipitating clouds formed over the Athens Metropolitan Area (AMA), Greece, during the springtime period from March to May 2020, shows that droplet closure can be achieved to within 30%, comparable to the level of closure obtained in many in situ studies.”

The corrected sentence appears below:

“This methodology, used to study aerosol-cloud interactions for non-precipitating clouds formed over the Athens Metropolitan Area (AMA), Greece, during the springtime period from March to May 2020, shows that droplet closure can be achieved to within ±33.4%, comparable to the level of closure obtained in many in situ studies.”2. Change in the Satellite relation from the one of Zhu et al. (2018) to Grosvenor et al. (2018).

A correction has been made to Modelling and data preprocessing, Satellite remote sensing—Optimal Cloud Analysis product and droplet number, 2.4.5. This sentence previously stated:

“According to Zhu et al. (2018), who further developed the Bennartz (2007) algorithm, N_d^sat, can be determined as:”

$N_d^{sat}=\sqrt{c\left(c_w\right)\tau }{\left(\frac{r_{eff}}{\beta }\right)}^{-\frac{5}{2}},(4)$

The corrected sentence appears below:

“According to Grosvenor et al. (2018) the, N_d^sat can be determined as:”

$N_d^{sat}=\sqrt{c\left(c_w\right)\tau }{\beta }^3{\left(r_{eff}\right)}^{-\frac{5}{2}},(4)$

3. Change in the numerical results.

A correction has been made to Modelling and data preprocessing, Satellite remote sensing—Optimal Cloud Analysis product and droplet number, 2.4.5. This sentence previously stated:

“We note here that $\frac{\partial N_d^{sat}}{\partial c_w}\delta c_w$ was on average relatively small (±5 cm⁻³), and contributes to ±1.7% on the total bias of $N_d^{sat}$. Therefore, we decided to omit it from Equation 5. $\frac{\partial {\mathrm{N}}_{\mathrm{d}}^{\text{sat}}}{\partial \mathrm{\tau }}\delta \tau$ and $\frac{\partial {\mathrm{N}}_{\mathrm{d}}^{\text{sat}}}{\partial r_{eff}}{\delta r}_{eff}$ were found on average equal to ±30 cm⁻³, ±76 cm⁻³, respectively, contributing ±12% and ±27%, respectively to the error. Furthermore, we estimated the $\frac{\partial {\mathrm{N}}_{\mathrm{d}}^{\text{sat}}}{\partial \beta }$ and found it equal to on average 593 cm⁻³ per unit of β. Since the uncertainty δβ is not available from published literature, we used $\delta \beta$ derived from the optimization process (see Section 3.1) and found it equals to 0.28. Thus, $\frac{\partial {\mathrm{N}}_{\mathrm{d}}^{\text{sat}}}{\partial \beta }\delta \beta$ is estimated equal to ±184 cm⁻³, which contributes ±57% to the droplet error.

The corrected sentence appears below:

“We note here that $\frac{\partial N_d^{sat}}{\partial c_w}\delta c_w$ was on average relatively small (±11 cm⁻³), and contributes ±3% on the total bias of $N_d^{sat}$. Therefore, we decided to omit it from Equation 5. $\frac{\partial {\mathrm{N}}_{\mathrm{d}}^{\text{sat}}}{\partial \mathrm{\tau }}\delta \tau$ and $\frac{\partial {\mathrm{N}}_{\mathrm{d}}^{\text{sat}}}{\partial r_{eff}}{\delta r}_{eff}$ were found on average equal to ±39 cm⁻³, ±84 cm⁻³, contributing ±13% and ±27% to the error, respectively. Furthermore, given that the uncertainty $\delta \beta$ is not available from published literature, we used the $\delta \beta$ which derived from the optimization process (see Section 3.1) and found it equals to 0.22, thus the $\frac{\partial {\mathrm{N}}_{\mathrm{d}}^{\text{sat}}}{\partial \beta }\delta \beta$ found to contribute ±52% to the droplet error which translates to ±165 cm⁻³. This implies that of all parameters considered in this study, optimally constraining β is of prime importance for the N_d^sat retrieval, compared to the other variables. The relevant results of the normalized bias of $N_d^{sat}$ from δc_w, δτ, δr_eff, and δβ can be found in the Supplement (c.f. Figure S 13).”

4. Change in the numerical results.

A correction has been made to Modelling and data preprocessing, Satellite remote sensing—Optimal Cloud Analysis product and droplet number, 2.4.5. This sentence previously stated:

“For expressions where β depends on N_d^sat, β(N_d^sat), the retrieval Equation 4 can be modified as follows:

$f{(N}_d^{sat})=N_d^{sat}-\sqrt{c\left(c_w\right)\tau }{\left(\frac{r_{eff}}{\beta \left(N_d^{sat}\right)}\right)}^{-\frac{5}{2}}=0(6)$

where N_d^sat is determined from the numerical solution of Equation 6 using the β(N_d^sat) expressions in Table 1. We discard the less reliable retrievals when the droplet uncertainty is significant, which correspond to the solutions of Equation 6 having δN_d^sat > 600 cm⁻³, δN_d^sat/ N_d^sat > 0.5, N_d^sat > 2000 cm⁻³, or N_d^sat<100 cm⁻³.

Finally, we performed closure studies between the accepted solutions of N_d^sat using each literature based β-expression, against to the estimations of in situ derived N_d from the parameterization (Section 2.4.3). By using the M94, RL03, PL03, Z06, GCMs, and F11 expressions, the corresponding averaged mean normalized bias (MNB) between N_d^sat and estimations of in situ N_d is equal to −17.37% ±32.66%, 51.34% ±69.25%, 23.51% ±56.09%, −21.25% ±24.91%, −28.80% ±22.52%, and −31.99% ±21.51%, respectively (c.f. Figure 4B; Table 3).

Table 3

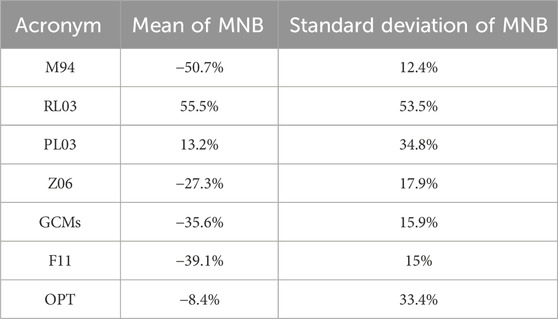
Table 3. Statistics of the performance of the closure study of N_d^sat − N_d for each β-expression used: OPT, RL03, M94, Z06, PL03, GCMs, and F12.

Therefore, in the case of using a constant value of β, such as Z06, GCMs, and F11, the N_d^sat values tend to be underestimated, since the estimated mean bias is of the order of 28%, while the standard deviation is reduced by 23% on average. On the other hand, by using the PL03 expression, the N_d^sat is overestimated, although comparable with those values derived when expressions of constant value of β are used (Z06, GCMs, and F11), with increased standard deviation values. In case of using the M94 explicit relation, N_d^sat is underestimated, but the mean bias is reduced by almost a factor of two, but with an increase in the standard deviation. Usage of the RL03 relation provides N_d^sat values that are considerable overestimated along with their standard deviation (c.f. Figure S12), while the MNBs presented in box plots can be found in Figure 4B.

Concluding, that the use of a constant value of β (or ε equivalently) or a linear relation between β and N_d^sat improves the closure error, we determined optimal parameters for a linear relationship between β and N_d^sat which minimizes the error with respect to the estimated in situ N_d (Section 3.1).”

The corrected sentence appears below:

“For expressions where β depends on N_d^sat, β(N_d^sat), the retrieval Equation 4 can be modified as follows:

$f{\left(N\right.}_d^{sat})=N_d^{sat}-\sqrt{c\left(c_w\right)\tau }{\beta }^3\left(N_d^{sat}\right){\left(r_{eff}\right)}^{-\frac{5}{2}}=0(6)$

where N_d^sat is determined from the numerical solution of Equation 6 using the β(N_d^sat) expressions in Table 1. We discard the less reliable retrievals when the droplet uncertainty is significant, which correspond to the solutions of Equation 6 having δN_d^sat > 600 cm⁻³, δN_d^sat/ N_d^sat > 0.5, N_d^sat > 2000 cm⁻³, or N_d^sat<100 cm⁻³.

Finally, we performed closure studies between the accepted solutions of N_d^sat using each literature based β-expression, against to the estimations of in situ derived N_d from the parameterization (Section 2.4.3). By using the M94, RL03, PL03, Z06, GCMs, and F11 expressions, the corresponding averaged mean normalized bias (MNB) between N_d^sat and estimations of in situ N_d is equal to −50.7 ± 12.4%, 55.5 ± 53.5%, 13.2 ± 34.8%, −27.3 ± 17.9%, −35.6 ± 15.9%, and −39.1 ± 15.0%, respectively (c.f. Figure 4B; Table 3).

Therefore, in the case of using a constant value of β, such as Z06, GCMs, and F11, the N_d^sat values tend to be underestimated, since the estimated mean bias is of the order of 34%, while the standard deviation is reduced by 16% on average. On the other hand, by using the RL03 expression, the N_d^sat is overestimated, although comparable compared to those values that were derived when expressions of constant value of β are used (Z06, GCMs, and F11), while in case of PL03 the average bias was found 13.2% ± 34.8%. In case of using the M94 explicit relation, N_d^sat is significantly underestimated, but the standard deviation is reduced by almost a factor of two compared to PL03. Usage of the RL03 relation provides N_d^sat values that are considerable overestimated along with their standard deviation (c.f. Figure S12, while the MNBs presented in box plots can be found in Figure 4B).

Concluding, that the use of a constant value of β (or ε equivalently) or a linear relation between β and N_d^sat improves the closure error, we determined optimal parameters for a linear relationship between β and N_d^sat which minimizes the error with respect to the estimated in situ N_d (Section 3.1).”

5. Change in the Equation.

A correction has been made to Results and Discussion, Optimization of β-expression, 3.1 This sentence previously stated:

“As a next step. we determined the β values from Equation 7, using each derived values of Ν_d and the corresponding values c(c_w), τ, r_eff as follows:

$\beta \left(N_d\right)={r_{eff}\left(\frac{\sqrt{c\left(c_w\right)\tau }}{N_d}\right)}^{\frac{5}{2}}(7)$

We then fit the β and N_d data to a linear relationship, β_opt = a + b N_d, to determine the “optimal β-expression” (OPT).”

The corrected sentence appears below:

$\beta \left(N_d\right)={\left(\frac{\sqrt{c\left(c_w\right)\tau }}{N_d}{r_{eff}}^{-\frac{5}{2}}\right)}^{-\frac{1}{3}}(7)$

“We then fit the β and N_d data to a relationship, β_opt = (1 + b N_d)^1/3, to determine the “optimal β- expression” (OPT).”

6. Change in the numerical results.

A correction has been made to Results and Discussion, Optimization of β-expression, 3.1 This sentence previously stated:

“The coefficients of OPT, a and b were estimated to be equal to 1.0421 ± 0.1979, and 4.8717 10^-4 ± 6.1084 10^-4, respectively (Figure 3), while the average δβ_opt was estimated to be equal to 0.28 for the whole dataset. Additionally, we calculated the P- value and R-value of the fit and found equal to 0.089 and 0.412, respectively, while the fitting confidence R² was found equal to ∼0.17. Then, we applied the OPT expression into Equation 6, to calculate the solutions of N_d^sat, while we disregarded the solutions where δβ_opt > 1, δβ_opt/ β_opt > 0.5, β_opt > 2, and β_opt < 1. Finally, we validated the accepted solutions in respect of the N_d. The results of this closure is presented in Figure 4A.”

Figure 3

Figure 3. The linear interpolations over the β-N_d data for the diabatic derived N_d; the labeling refers to the serial number of each cloud (c.f. Supplementary Figure S1).

Figure 4

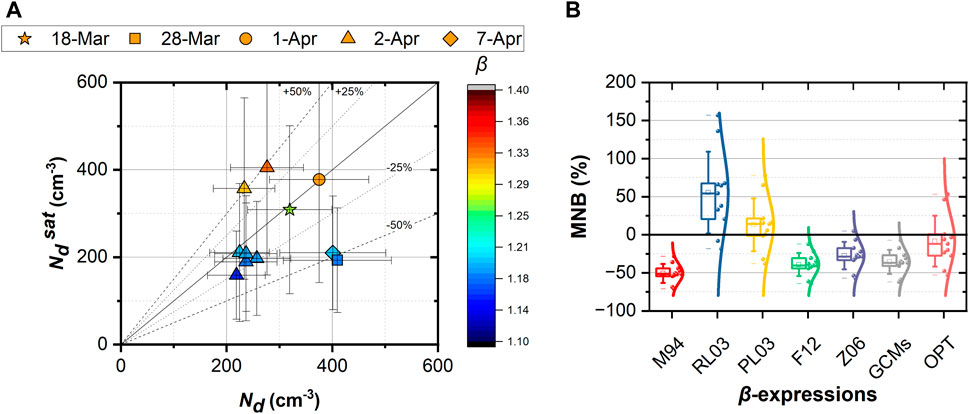
Figure 4. (A) Droplet number closure between Nd and N_d^sat using the OPT compared to N_d in respect of β_opt on the colorscale; (B) The MNB of the closure of N_d^sat − N_d by using each β-expression: (I) M94, ii) RL03, iii) PL03, iv) F12, v) Z06, vi) GCMs, and vii) OPT, respectively.

The corrected sentence appears below:

“The coefficient of OPT, b was estimated to be equal to 3.3541 10⁻³ ± 1.0623 10⁻³, respectively (Figure 3), while the average δβ_opt was estimated to be equal to 0.22 for the whole dataset. Additionally, we calculated the P- value of the fit and found equal to 0.05, respectively, while the fitting confidence R² was found equal to ∼0.57. Then, we applied the OPT expression into Equation 6, to calculate the solutions of N_d^sat, while we disregarded the solutions where δβ_opt > 1, δβ_opt/ β_opt > 0.5, β_opt > 2, and β_opt < 1. Finally, we validated the accepted solutions in respect of the N_d. The results of this closure are presented in Figure 4A.”

7. Change in the numerical results.

A correction has been made to Results and Discussion, Optimization of β-expression, 3.1 This sentence previously stated:

“Based on the results presented in Figure 4B and Table 3, we see that the proposed β-expression OPT exhibits the lowest mean MNB value (14.53%) with a standard deviation 36.33%. The performance of each β-expression can be ranked by their MNB values, as follows: OPT (−14.53%), M94 (−17.37%), Z06 (−21.25%), PL03 (23.51), GCMs (−28.80%), F11 (−31.99%), and RL03 (51.34%) (see also Table 3) along with the resulting standard deviation values (expressed as length of the box in the vertical axis) of MNB (c.f. Figure 4B).”

The corrected sentence appears below:

“Based on the results presented in Figure 4B and Table 3, we see that the OPT β-expression exhibits the lowest mean MNB value (−8.4%) with a standard deviation 33.4%, while the performance of the rest β-expression can be ranked by their MNB values, as follows: PL03 (13.2), Z06 (−27.3%), GCMs 35.6%), F11 (−39.1%), M94 (−50.7%), and RL03 (55.5%) (see also Table 3) along with the resulting standard deviation values (expressed as length of the box in the vertical axis) of MNB (c.f. Figure 4B).”

8. Change in the numerical results in Conclusions.

A correction has been made to Conclusions, 4.

This sentence previously stated:

“The study presented here expands an established droplet number retrieval algorithm for non-precipitating PBLCs (Bennartz et al., (2007) to explicitly account for the spectral dispersion of droplets and its dependence on droplet number in terms of β. The revised algorithm uses the cloud microphysical variables τ and r_eff, as derived from SEVIRI onboard the geostationary meteorological satellite (METEOSAT) with a temporal resolution of 15 min and with a spatial resolution 3.6 km × 4.6 km, along with an improved calculation of the total condensation rate (Zhu et al., 2018) with respect to cloud top height which can be obtained by using the ERA5 atmospheric pressure-temperature profiles (Hersbach et al., 2018). We found that the optimal retrieval of N_d^sat is most sensitive to biases of the β values, rather than biases in τ and r_eff, pointing to the need for a optimal β-expression for the most accurate N_d^sat retrievals.

We then calculated the retrieved N_d^sat values by using the literature-based β-expressions and we evaluated them against the in situ N_d estimations obtained by the droplet activation parameterization of the Nenes and Seinfeld (2003). We found that droplet number is captured to within ±29% and ±61%; based on these results we see that by using a constant value of β, or a linear relation between ε or β to N_d^sat, such as PL03, Z06, GCMs, and F11, the N_d^sat is captured to within ±35%. Additionally, we proposed a new β- N_d expression, based on the in situ N_d estimations, that optimizes the closure between N_d^sat and N_d within ±33% and underestimated by 14.53%. Furthermore, the new β-expression we obtained through the optimal fit between N_d^sat and N_d is remarkably similar to the PL03 relationship. Given that, the PL03 relationship derived from observation data suggests that our method to estimate N_d is realistic. The use of either RL03 or our optimized relationship, captures droplet number to within 30%, which is comparable to the closure levels obtained from in situ observations.

Although more work needs to be done to evaluate the extent to which our approach can be applied elsewhere in the globe, the results presented here are both encouraging and may suggest ways to develop high-value products for climate models that can take advantage of the rich ground-based aerosol datasets available to the community. ”

The corrected sentence appears below:

“The study presented here expands an established droplet number retrieval algorithm for non-precipitating PBLCs Grosvenor et al., (2018) to explicitly account for the spectral dispersion of droplets and its dependence on droplet number in terms of β. The revised algorithm uses the cloud microphysical variables $\tau$ and r_eff, as derived from SEVIRI onboard the geostationary meteorological satellite (METEOSAT) with a temporal resolution of 15 min and with a spatial resolution 3.6 km × 4.6 km, along with an improved calculation of the total condensation rate (Zhu et al., 2018) with respect to cloud top height which can be obtained by using the ERA5 atmospheric pressure-temperature profiles (Hersbach et al., 2018). The largest source of uncertainty in N_d^sat originates from β, rather than τ and r_eff. This points to the need for an optimal β-expression for more accurate N_d^sat retrievals.

We retrieved N_d^sat values by using the literature-based β-expressions and we evaluated them against the in situ N_d estimations obtained by a state-of-the-art droplet activation parameterization. We found that when using a constant value of β such as, Z06, GCMs, and F11, the droplet number is captured to on average ±16% and a bias of −34%. When using a linear relation between ε or β to N_d^sat, such as PL03, N_d^sat overestimates N_d by 13.2% ±34.8%. In the case of using more complex relation of β to N_d, such as of M94 or RL03, the bias of N_d^sat increases significantly. Additionally, we proposed a new β-N_d expression, based on the in situ N_d estimations, that minimize the bias of closure between $N_d^{sat}$ and N_d (8.4% ± 33.4%).

Although more work needs to be done to evaluate the extent to which our approach can be applied elsewhere in the globe, the results presented here are both encouraging and may suggest ways to develop high-value products for climate models that can take advantage of the rich ground-based aerosol datasets available to the community.”

The updated figures and tables based on the corrected results appear below:

The authors apologize for these errors and state that they do not change the scientific conclusions of the article in any way. The original article has been updated.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.