Summarizing multiple aspects of triple collocation analysis in a single diagram

With the ongoing expansion of global observation networks, it is expected that we shall routinely analyze records of geophysical variables such as temperature from multiple collocated instruments. Validating datasets in this situation is not a trivial task because every observing system has its own bias and noise. Triple collocation is a general statistical framework to estimate the error characteristics in three or more observational-based datasets. In a triple colocation analysis, several metrics are routinely reported but traditional multiple-panel plots are not the most effective way to display information. A new formula of error variance is derived for connecting the key terms in the triple collocation theory. A diagram based on this formula is devised to facilitate triple collocation analysis of any data from observations, as illustrated using three aerosol optical depth datasets from the recent Aerosol Cloud meTeorology Interactions oVer the western ATlantic Experiment (ACTIVATE). An observational-based skill score is also derived to evaluate the quality of three datasets by taking into account both error variance and correlation coefficient. Several applications are discussed and sample plotting routines are provided.

1 Introduction

The development of atmospheric sciences and other branches of Earth system science is inextricably linked to our capability of improving and expanding current atmospheric observing systems (Crutzen and Ramanathan, 2000; Stith et al., 2018; Bluestein et al., 2022). For instance, a dense weather station network provides us with synoptic weather conditions while sounding profiles from radiosondes and dropsondes give us a wealth of information for the vertical structure of the atmosphere over land and ocean (Stith et al., 2018). In addition to in situ observations, remotely sensed instruments such as weather radars are able to detect severe weather systems in a timely manner. The advent of satellite meteorology has reshaped our data inventory by making global observations possible (Atlas, 1997). Research aircraft in field campaigns provides a unique platform to collect measurements from both in situ and remotely sensed instruments for specific research problems with pressing societal needs (Bluestein et al., 2022).

With more and more new observing systems available, it has become commonplace for more than one instrument observing the same geophysical variable at the same location. Data validation and calibration then become necessary because no observing systems are perfectly built. Stoffelen (1998) recognized this issue and proposed a general statistical framework called triple collocation. For any geophysical variables, triple collocation estimates the error characteristics of three independent datasets without requiring any dataset being the ground truth. Since then, the method has been applied to a wide range of variables such as soil moisture (e.g., Dorigo et al., 2010), sea surface temperature (e.g., O’Carroll et al., 2008), and leaf area index (e.g., Fang et al., 2012), to name a few. The theory of triple collocation has also been clarified, tested, and extended over the years (e.g., Zwieback et al., 2012; Draper et al., 2013; McColl et al., 2014; Su et al., 2014; Yilmaz and Crow, 2014; Gruber et al., 2016; Tsamalis, 2022).

Several performance metrics such as standard error (Stoffelen, 1998) and correlation coefficient (McColl et al., 2014) have been developed for triple collocation analysis. These metrics are usually reported in the form of a map that shows one aspect such as a metric for one dataset (e.g., Dorigo et al., 2010) or a figure that shows another aspect for three datasets (e.g., Tsamalis, 2022). Multiple-panel plots are common in the literature (e.g., McColl et al., 2014; Deng et al., 2023) and some examples are given in Supplementary Material. But this kind of plot is not the most effective way to summarize results. A table that shows multiple aspects may help but different researchers have varying designs and notations (e.g., Su et al., 2014). The purpose of this study is to present a single diagram for the triple collocation analysis that can succinctly compare multiple aspects of multiple datasets. The diagram is facilitated by deriving a new formula of error variance. Some applications of the new triple collocation diagram are illustrated using datasets collected from a recent field campaign, i.e., the Aerosol Cloud meTeorology Interactions oVer the western ATlantic Experiment (ACTIVATE).

2 Methods

2.1 Classical and extended triple collocation

We first briefly review the derivation of classical and extended triple collocation. An error model is needed to specify each dataset as a function of the unknown ground truth (Zwieback et al., 2012). So far in the literature, linear error models are the most popular type with one example being the affine model,

$x_i=a_i+b_i\mathrm{\Theta }+{\epsilon }_i,(1)$

where $x_i$ $(i\in \{\mathrm{1,2,3}\})$ represents dataset $i$; $\mathrm{\Theta }$ is the unknown ground truth; $a_i$, $b_i$, and ${\epsilon }_i$ are the additive bias, multiplicative bias, and random error from dataset $i$, respectively.

Based on the affine error model, the variance/covariance equations for the collocated datasets are then given as.

$\mathrm{C}\mathrm{o}\mathrm{v}[x_i,x_j]=b_i{b}_j\mathrm{V}\mathrm{a}\mathrm{r}\left[\mathrm{\Theta }\right]+b_i\mathrm{C}\mathrm{o}\mathrm{v}[\mathrm{\Theta },{\epsilon }_j]+b_j\mathrm{C}\mathrm{o}\mathrm{v}\left[\mathrm{\Theta },{\epsilon }_i\right]+\mathrm{C}\mathrm{o}\mathrm{v}[{\epsilon }_i,{\epsilon }_j],\mathrm{i}\mathrm{f}i\ne j,(2)$

$\mathrm{V}\mathrm{a}\mathrm{r}\left[x_i\right]=b_i^2\mathrm{V}\mathrm{a}\mathrm{r}\left[\mathrm{\Theta }\right]+2b_i\mathrm{C}\mathrm{o}\mathrm{v}\left[\mathrm{\Theta },{\epsilon }_i\right]+\mathrm{V}\mathrm{a}\mathrm{r}\left[{\epsilon }_i\right],\mathrm{i}\mathrm{f}i=j,(3)$

where $\mathrm{V}\mathrm{a}\mathrm{r}[x_i]={\sigma }_i^2$ is the total variance, $\mathrm{V}\mathrm{a}\mathrm{r}[\mathrm{\Theta }]={\sigma }_{\mathrm{\Theta }}^2$ is the truth variance, and $\mathrm{V}\mathrm{a}\mathrm{r}[{\epsilon }_i]={\sigma }_{{\epsilon }_i}^2$ is the error variance. Note that $\mathrm{C}\mathrm{o}\mathrm{v}[x_i,x_j]=\mathrm{C}\mathrm{o}\mathrm{v}[x_j,x_i]$. Three datasets result in three equations for variance and three more for covariance, amounting to six equations in total.

Three further assumptions are usually made to simplify the equations (Gruber et al., 2020). First, the mean random error is zero $(E[{\epsilon }_i]=0)$. Second, the random error is uncorrelated with the ground truth $(\mathrm{C}\mathrm{o}\mathrm{v}[{\epsilon }_i,\mathrm{\Theta }]=0)$. Third, the random error of different datasets is uncorrelated with each other $(\mathrm{C}\mathrm{o}\mathrm{v}[{\epsilon }_i,{\epsilon }_j]=0,i\ne j)$. In virtue of these assumptions, Eqs 2, 3 become.

$\mathrm{C}\mathrm{o}\mathrm{v}[x_i,x_j]=b_i{b}_j{\sigma }_{\mathrm{\Theta }}^2,\mathrm{i}\mathrm{f}i\ne j,(4)$

$\mathrm{V}\mathrm{a}\mathrm{r}\left[x_i\right]=b_i^2{\sigma }_{\mathrm{\Theta }}^2+{\sigma }_{{\epsilon }_i}^2,\mathrm{i}\mathrm{f}i=j.(5)$

The six equations from Eqs. 4, 5 now have seven unknowns ($b_1,b_2,b_3,{\sigma }_{{\epsilon }_1},{\sigma }_{{\epsilon }_2},{\sigma }_{{\epsilon }_3}$, and ${\sigma }_{\mathrm{\Theta }}$) so the system has no unique solution. McColl et al. (2014) proposed that unknown variables can be combined to reduce the number of unknowns. Thus, in theory, the error variance can be solved using

${\sigma }_{{\epsilon }_i}^2={\sigma }_i^2-b_i^2{\sigma }_{\mathrm{\Theta }}^2.(6)$

In practice, the signal variance $b_i^2{\sigma }_{\mathrm{\Theta }}^2$ for different datasets (Eqs 7–9) can be computed from combining the covariance terms from Eq. 4.

${\sigma }_{{\epsilon }_1}^2=\mathrm{V}\mathrm{a}\mathrm{r}\left[x_1\right]-\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_2\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_3\right]}{\mathrm{C}\mathrm{o}\mathrm{v}\left[x_2,x_3\right]},(7)$

${\sigma }_{{\epsilon }_2}^2=\mathrm{V}\mathrm{a}\mathrm{r}\left[x_2\right]-\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_2\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_2,x_3\right]}{\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_3\right]},(8)$

${\sigma }_{{\epsilon }_3}^2=\mathrm{V}\mathrm{a}\mathrm{r}\left[x_3\right]-\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_3\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_2,x_3\right]}{\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_2\right]}.(9)$

To extend the classical triple collocation analysis, McColl et al. (2014) derived a new metric, the correlation coefficient, from the ordinary least squares framework.

$r_1=\pm \sqrt{\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_2\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_3\right]}{\mathrm{V}\mathrm{a}\mathrm{r}\left[x_1\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_2,x_3\right]}},(10)$

$r_2=\pm \mathrm{s}\mathrm{g}\mathrm{n}\left(\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_3\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_2,x_3\right]\right)\sqrt{\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_2\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_2,x_3\right]}{\mathrm{V}\mathrm{a}\mathrm{r}\left[x_2\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_3\right]}},(11)$

$r_3=\pm \mathrm{s}\mathrm{g}\mathrm{n}\left(\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_2\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_2,x_3\right]\right)\sqrt{\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_3\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_2,x_3\right]}{\mathrm{V}\mathrm{a}\mathrm{r}\left[x_3\right]\mathrm{C}\mathrm{o}\mathrm{v}\left[x_1,x_2\right]}},(12)$

where $r_i$ is correlation coefficient of the dataset $i$ with respect to an unknown ground truth, and sgn is signum function. Note that the sign of all correlation coefficients is ambiguous but practically all observing systems are positively correlated with the ground truth, i.e., taking the positive root.

2.2 Basis of the triple collocation diagram

To construct the triple collocation diagram, an alternative error variance equation is needed to connect all variance terms in Eq. 6 with the correlation coefficient (Eqs 10–12). To start with, we use the following basic statistical identities (Dekking et al., 2005; Thomson and Emery, 2014).

$\mathrm{V}\mathrm{a}\mathrm{r}\left[fD\pm h\right]=f^2\mathrm{V}\mathrm{a}\mathrm{r}\left[D\right],(13)$

$\mathrm{V}\mathrm{a}\mathrm{r}\left[D\pm E\right]=\mathrm{V}\mathrm{a}\mathrm{r}\left[D\right]+\mathrm{V}\mathrm{a}\mathrm{r}\left[E\right]\pm 2\mathrm{C}\mathrm{o}\mathrm{v}\left[D,E\right],(14)$

where $f$ and $h$ are constants; $D$ and $E$ are random variables.

Combining two identities (Eqs 13, 14) gives

$\mathrm{V}\mathrm{a}\mathrm{r}\left[fD\pm gE\right]=f^2\mathrm{V}\mathrm{a}\mathrm{r}\left[D\right]+g^2\mathrm{V}\mathrm{a}\mathrm{r}\left[E\right]\pm 2fg\mathrm{C}\mathrm{o}\mathrm{v}\left[D,E\right],(15)$

where $g$ is a constant.

Applying the above identity (Eq. 15) to the error model Eq. 1 gives Eq. 16, and subsequently Eqs 17, 18.

$\mathrm{V}\mathrm{a}\mathrm{r}\left[x_i-b_i\mathrm{\Theta }\right]=\mathrm{V}\mathrm{a}\mathrm{r}\left[x_i\right]+b_i^2\mathrm{V}\mathrm{a}\mathrm{r}\left[\mathrm{\Theta }\right]-2b_i\mathrm{C}\mathrm{o}\mathrm{v}\left[x_i,\mathrm{\Theta }\right],(16)$

$\mathrm{V}\mathrm{a}\mathrm{r}\left[a_i+{\epsilon }_i\right]={\sigma }_i^2+b_i^2{\sigma }_{\mathrm{\Theta }}^2-2b_i{\sigma }_{\mathrm{\Theta }}{\sigma }_i\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left[x_i,\mathrm{\Theta }\right]}{{\sigma }_{\mathrm{\Theta }}{\sigma }_i},(17)$

${\sigma }_{{\epsilon }_i}^2={\sigma }_i^2+b_i^2{\sigma }_{\mathrm{\Theta }}^2-2b_i{\sigma }_{\mathrm{\Theta }}{\sigma }_i{r}_i,(18)$

where the left hand side (lhs) of Eq. 17 uses Eq. 1, the lhs of Eq. 18 uses Eq. 13. On the right hand side (rhs) of Eq. 18, the correlation coefficient $r_i$ between each dataset $x_i$ and the ground truth $\mathrm{\Theta }$ follows the traditional definition, which is the ratio of the covariance of two datasets to the product of their corresponding standard deviations (Wilks, 2011). To our knowledge, Eq. 18 is derived here for the first time.

The alternative error variance Eq. 18 is inspired by the Taylor diagram (Taylor, 2001) which is based on the law of cosines. The alternative equation also resembles the law of cosines (Figure 1A): three sides for three standard deviation terms (error standard deviation ${\sigma }_{{\epsilon }_i}$, signal standard deviation $b_i{\sigma }_{\mathrm{\Theta }}$, and total standard deviation ${\sigma }_i$) and the angle $\varphi$ between ${\sigma }_i$ and $b_i{\sigma }_{\mathrm{\Theta }}$ for correlation coefficient. Triple collocation estimates error properties of observational-based datasets with respect to an unknown ground truth; on the contrary, the Taylor diagram aims to summarize model performance against an observational-based reference. Therefore, the three sides become model standard deviation, reference standard deviation, and the unbiased root-mean-square error between the model and reference fields, and the angle is the correlation coefficient between the two fields (Taylor, 2001).

Figure 1

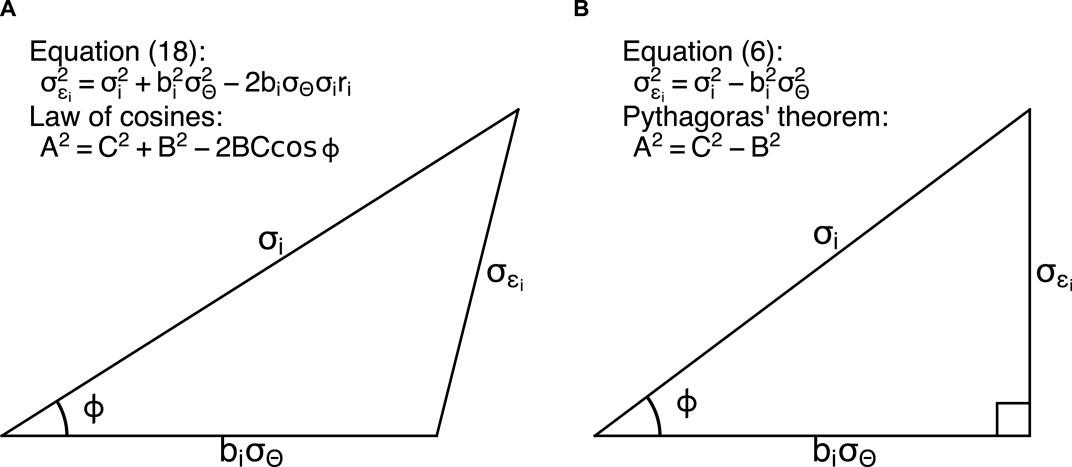
Figure 1. Geometrical meanings of (A) Eq. 18 and (B) Eq. 6. The error standard deviation ${\sigma }_{{\epsilon }_i}$, signal standard deviation $b_i{\sigma }_{\mathrm{\Theta }}$, and total standard deviation ${\sigma }_i$ form the three sides of a triangle, A, B, and C, respectively. The two sides $b_i{\sigma }_{\mathrm{\Theta }}$ and ${\sigma }_i$ form an angle $\varphi$. In both cases, $\varphi$ must be acute because in (A) the correlation coefficient must be positive and in (B) there is a right angle.

We emphasize that all datasets are assumed to be positively correlated with the ground truth in Eqs 10–12, i.e., taking the positive root. Therefore, $b_i$ is also positive using Eq. 8 in McColl et al. (2014). This assumption ensures that all standard deviation terms are positive and $\varphi$ is acute.

The original error variance Eq. 6 resembles the Pythagoras’ theorem (Figure 1B), a special case of the law of cosines. Therefore, the angle between $b_i{\sigma }_{\mathrm{\Theta }}$ and ${\sigma }_{{\epsilon }_i}$ has to be 90$°$. Note that there is nothing mysterious about the right angle as it is merely a consequence of the random error and ground truth being uncorrelated $(\mathrm{C}\mathrm{o}\mathrm{v}[{\epsilon }_i,\mathrm{\Theta }]=0)$ from one of our assumptions. It is clear that the alternative error variance equation is needed because the original equation does not provide information on the angle $\varphi$.

To summarize, the alternative error variance equation incorporates correlation coefficient, which is absent in the original equation. The new equation forms the basis of the proposed triple collocation diagram.

3 Data

To demonstrate applications of the new triple collocation diagram, we focus on a measurement related to the abundance of aerosol particles. Aerosols are highly variable in space and time leading to high uncertainty in estimating total anthropogenic radiative forcing (Forster et al., 2021). Three aerosol optical depth (AOD) retrieval datasets are used in this study. AOD quantifies the column-integrated aerosol loading, but more specifically the sum of light scattering and absorption by aerosols (Seinfeld and Pandis, 2006).

Two of the retrievals come from the Aerosol Cloud meTeorology Interactions oVer the western ATlantic Experiment (ACTIVATE) which is one of the National Aeronautics and Space Administration (NASA) Earth Venture Suborbital-3 (EVS-3) missions (Sorooshian et al., 2019; Sorooshian et al., 2023). During ACTIVATE, two NASA Langley Research Center aircraft, the low-flying HU-25 Falcon and high-flying King Air, were strategically deployed to collect in-situ and remotely-sensed measurements over the western North Atlantic Ocean. From February 2020 to June 2022, 174 and 168 flights were successfully completed by the King Air and Falcon, respectively. Among these, 162 were joint flights. AOD was retrieved by two remote sensing instruments onboard the King Air, the Research Scanning Polarimeter (RSP) (Cairns et al., 1999; Cairns et al., 2003) and Second Generation High Spectral Resolution Lidar (HSRL-2) (Hair et al., 2008). The third retrieval comes from the Moderate Resolution Imaging Spectroradiometer (MODIS). Two MODIS sensors have been onboard the Terra and Aqua satellites since 1999 and 2002, respectively. The two satellites observe the Earth along a sun-synchronous orbit at an altitude of around 700 km with a period of 99 min, providing MODIS data at three nadir spatial resolutions (Remer et al., 2005; Levy et al., 2013).

We compare AOD at 532 nm from the three retrievals. For RSP, the aerosol properties are retrieved using the Microphysical Aerosol Properties from Polarimetry (MAPP) algorithm (Stamnes et al., 2018), which then become part of the level 2 aerosol product. For HSRL-2, AOD is derived using extinction coefficients from the difference in molecular return signals (Hair et al., 2008). The original 1-km level 2 RSP and HSRL-2 AOD data are horizontally averaged to a spatial resolution of 3 km, which results in 6,988 pairs. For MODIS, we use the MODIS Collection 6.1 level 2 3-km aerosol product for both satellites: MOD04_3K from Terra and MYD04_3K from Aqua. This product is entirely retrieved using the Dark Target (DT) algorithm (Remer et al., 2013). The native MODIS AOD at 550 nm is converted to 532 nm using the Ångström exponent calculated from the MODIS AOD at 470 nm and 550 nm. For each pair of RSP and HSRL-2 data, we collocate the nearest MODIS data point within $\pm$ 60 min and 25 km, which results in 2,344 triplets for triple collocation analysis. All triplets are collocated over the ocean.

4 Applications

4.1 A bird’s-eye view of the triple collocation analysis

Based on the alternative error variance Eq. 18, a triple collocation diagram is designed to display multiple aspects of triple collocation analysis. A prototype is shown in Figure 2 with three AOD datasets: RSP, HSRL-2, and MODIS. For comparison, an additional figure (see Supplementary Figure S1) is prepared to display the same information using the traditional multi-panel method.

Figure 2

Figure 2. A sample diagram for displaying performance metrics of triple collocation analysis. Three colors represent three different 532-nm AOD datasets during ACTIVATE: RSP (blue), HSRL-2 (red), and MODIS (orange). Three open circles are drawn for each dataset. The radial distance between the origin and the circle on the polar grid is the total (system) standard deviation ${\sigma }_i$ of that dataset (e.g., 0.105 for RSP); the projection of the radial distance onto $x$-axis is the signal standard deviation $b_i{\sigma }_{\mathrm{\Theta }}$ (e.g., 0.084 for RSP); the project of the distance onto $y$-axis is the error standard deviation ${\sigma }_{{\epsilon }_i}$ (e.g., 0.064 for RSP). The polar angle between the total and signal standard deviations represents the correlation coefficient of a dataset with respect to the ground truth $r_i$ (e.g., 0.80 for RSP).

For those who are familiar with Taylor diagram, it is straightforward to use the schematic from Figure 1 to recognize the three standard deviation terms and correlation coefficient in Figure 2. The circles on the polar grid represents the total standard deviation. The projections of the total standard deviation on the $x$-axis and $y$-axis represent the signal standard deviation and error standard deviation, respectively. As a result, it is relatively easy to compare the magnitudes for either signal or error standard deviation.

During ACTIVATE, HSRL-2 has the smallest error standard deviation $({\sigma }_{{\epsilon }_{\text{HSRL}-2}}=0.027)$ and the highest correlation coefficient $(r_{\text{HSRL}-2}=0.93)$ while RSP has the largest error standard deviation $({\sigma }_{{\epsilon }_{\text{RSP}}}=0.064)$ and the lowest correlation coefficient $(r_{\text{RSP}}=0.80)$ among the three datasets. The different performance of RSP and HSRL-2 is justified from the perspectives of retrieval algorithm and instrument uncertainty. First, some assumptions in the RSP retrieval algorithm are not warranted during the field campaign. For example, the RSP algorithm assumes that all aerosols are spherical but the in-situ instruments and HSRL-2 show that non-spherical sea salt and dust are often detected in winter and summer, respectively. Second, past field campaigns showed that, compared to the Sun photometer measurements, the root-mean-squared difference for RSP and HSRL-2 are $\sim 0.04$ (Fu et al., 2020) and $\sim 0.01$ (Shinozuka et al., 2013), respectively.

Other metrics can also be easily estimated or computed from the diagram. The values of total standard deviation can be computed using ${\sigma }_i=\sqrt{{\sigma }_{{\epsilon }_i}^2/(1-r_i^2)}$. The values of signal standard deviation can then be computed using Eq. 6. Signal standard deviation is important for computing the unbiased signal-to-noise ratio $({\mathrm{S}\mathrm{N}\mathrm{R}}_{\text{ub}}=(b_i^2{\sigma }_{\mathrm{\Theta }}^2)/{\sigma }_{{\epsilon }_i}^2)$ or unbiased noise-to-signal ratio $({\mathrm{N}\mathrm{S}\mathrm{R}}_{\text{ub}}=1/{\mathrm{S}\mathrm{N}\mathrm{R}}_{\text{ub}})$, which indicates whether signal variations can be set apart from noise variations (Gruber et al., 2016). Total standard deviation is also important because fractional root mean square error (Draper et al., 2013) is defined as the ratio of error standard deviation to total standard deviation $(\mathrm{f}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}={\sigma }_{{\epsilon }_i}/{\sigma }_i)$. Total standard deviation also provides information on the measurement sensitivity $b_i$ through $b_i=(r_i{\sigma }_i)/{\sigma }_{\mathrm{\Theta }}$ (Rodgers and Nicewander, 1988).

4.2 Tracking performance metrics

The triple collocation diagram is not limited to handling three datasets only. For example, seeing that RSP exhibits the largest errors among three datasets (Figure 2), a simple data quality flag is devised to filter out data points with inferior retrievals based on a performance cost function in the RSP retrieval algorithm (Stamnes et al., 2018). Around 50% of triplets are filtered out, and the difference before and after applying the quality flag is shown in Figure 3. Filtered datasets are indicated by squares without changing the color theme. Colored arrows have also been added to follow the changes in performance metrics. Appreciable improvement is seen with RSP data after filtering as the correlation coefficient rises to 0.84 and error standard deviation falls to 0.044 (or a 31% decrease). Note also that if the correlation coefficient increases with the direction of the arrow, the signal-to-noise ratio also increases. An additional figure (see Supplementary Figure S2) is prepared to display the same information using the traditional multi-panel method.

Figure 3

Figure 3. Same as Figure 2 but adding the three datasets after applying an RSP data filter. The three original and filtered datasets are indicated by circles and squares, respectively. Colored arrows indicate the changes from original to filtered datasets.

4.3 Triple collocation skill score

While various performance metrics have been developed for the triple collocation analysis, it is beneficial to summarize the different aspects of the performance in a single measure. Similar problems have led to the development of skill scores such as Brier skill score and ranked probability skill score in weather and climate prediction (Wilks, 2011) and efficiencies such as Nash–Sutcliffe efficiency and Kling–Gupta efficiency in hydrology. For triple collocation, we propose a skill score,

$S=\left(1-{\alpha }_i\right)r_i=\left(1-\frac{{\sigma }_{{\epsilon }_i}^2}{{\sigma }_i^2+b_i^2{\sigma }_{\mathrm{\Theta }}^2}\right)r_i,(19)$

where $\alpha$ is the normalized error variance adopted from Koh et al. (2012). $S$ ranges between 0 and 1.

The same datasets in Figure 3 are shown in Figure 4, which is contoured with the proposed skill score (Eq. 19). Before filtering, HSRL-2 owns the highest skill score; after filtering, RSP gains $\sim 0.06$ in skill score. While $S$ is proportional to $r$ by definition, it varies in a more linear scale in the normal range between 0.1 and 0.9.

Figure 4

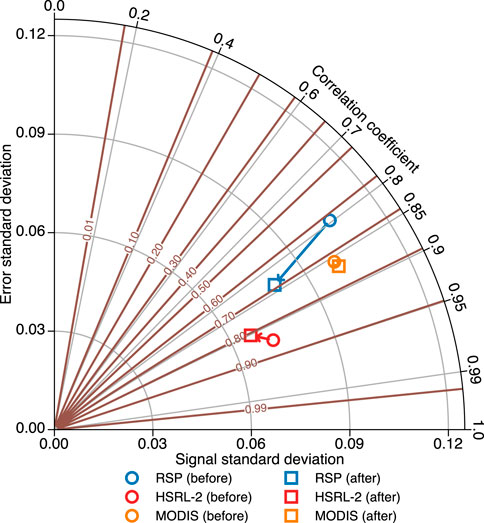
Figure 4. Same as Figure 3 but is contoured with a triple collocation skill score in brown.

5 Discussion

The utility of displaying multiple performance metrics in the triple collocation diagram deserves some discussion. The ACTIVATE field campaign provides a rare opportunity to validate the aerosol measurements from two airborne remote sensing instruments on the same platform. The common approach is to compare with Sun photometer measurements from the Aerosol Robotic Network (AERONET) but this is not feasible in our case because no AERONET site is available in the remote ocean over the study region. To get around this issue, we added one more independent satellite dataset and proceeded with the triple collocation analysis.

In the process, we got to be aware of the diverse applications in the literature and the development of various performance metrics. For example, $r$ was developed as an alternative of fRMSE (McColl et al., 2014). There are two reasons for showing multiple performance metrics in our current approach. First, it is impractical to predetermine a single performance metric for users as the choice is usually field or application dependent. For example, in aerosol studies, conventionally people are more concerned about the error standard deviation of an instrument compared to the Sun photometer because this quantity can be used to estimate the uncertainty of aerosol radiative forcing (Hansen et al., 1995; Chylek et al., 2003; Mishchenko et al., 2004), which remains the largest uncertainty of our future climate projection. There are usually no preference on the performance metrics for other variables, such as sea surface temperature and soil moisture. Second, it is in line with a current triple collocation community guideline (Gruber et al., 2020) to present a comprehensive picture of error characteristics. As such, our strategy is to display the various variance terms and correlation coefficient and provide guidance to compute other metrics (such as $\mathrm{S}\mathrm{N}{\mathrm{R}}_{\mathrm{u}\mathrm{b}}$ and $\mathrm{f}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}$) to suit the needs of individual practitioners. Note that the performance metrics including $\mathrm{S}\mathrm{N}{\mathrm{R}}_{\mathrm{u}\mathrm{b}}$, $\mathrm{N}\mathrm{S}{\mathrm{R}}_{\mathrm{u}\mathrm{b}}$, $\mathrm{f}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}$, and $\mathrm{S}$ are functions of $r$ under the triple collocation assumptions listed in Section 2.

6 Summary

Triple collocation is a statistical technique that considers three collocated datasets of any geophysical variable and estimates the error characteristics of each dataset without assuming any of the three datasets represent ground truth. Triple collocation analysis involves reporting several performance metrics which can at times become cumbersome using traditional ways of presentation such as multiple-panel plots and long tables.

An alternative equation is derived for the error variance which forms the basis of the proposed triple collocation diagram as a visual aid for condensing multiple aspects of the triple collocation analysis into a two-dimensional polar plot. An observational-based skill score is also obtained to compare performance of three datasets by considering both error variance and correlation coefficient. Three potential applications of the diagram, as illustrated in Figures 2–4, are showcased and discussed. The Taylor diagram has been used to compare the performance of multiple models with an observational-based reference dataset. The proposed diagram complements the Taylor diagram by comparing the performance of multiple observational-based datasets. For interested readers, a routine to draw the triple collocation diagram with several examples is available (see Data Availability Statement).

Data availability statement

All the data used in this work are publicly available. The ACTIVATE data can be downloaded from https://asdc.larc.nasa.gov/project/ACTIVATE (NASA/LARC/SD/ASDC, 2021). The MODIS Terra and Aqua data can be downloaded from https://doi.org/10.5067/MODIS/MOD04_3K.061 (MODIS Science Team, 2017b) and https://doi.org/10.5067/MODIS/MYD04_3K.061 (MODIS Science Team, 2017a). The code repository for this work is at https://github.com/leongwaisiu. Further inquiries can be directed to the corresponding author.

Author contributions

LWS: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. XZ: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing–review and editing, Data curation, Formal Analysis, Investigation, Software, Validation, Visualization. AS: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing–review and editing, Data curation, Formal Analysis, Investigation, Software, Validation, Visualization. BC: Data curation, Formal Analysis, Investigation, Software, Validation, Visualization, Writing–review and editing. CAH: Data curation, Formal Analysis, Investigation, Software, Validation, Visualization, Writing–review and editing. DP: Data curation, Formal Analysis, Investigation, Software, Validation, Visualization, Writing–review and editing. JSS: Data curation, Formal Analysis, Investigation, Software, Validation, Visualization, Writing–review and editing. RAF: Data curation, Formal Analysis, Funding acquisition, Investigation, Resources, Software, Validation, Visualization, Writing–review and editing. JWH: Data curation, Formal Analysis, Funding acquisition, Investigation, Resources, Software, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by NASA grant 80NSSC19K0442 for ACTIVATE, a NASA Earth Venture Suborbital-3 (EVS-3) investigation, which is funded by NASA’s Earth Science Division and managed through the Earth System Science Pathfinder Program Office.

Acknowledgments

We thank the pilots and aircraft maintenance personnel of NASA Langley Research Services Directorate for their work in conducting the ACTIVATE flights. Comments from two reviewers led to an improvement in presentation. We thank Karl Taylor for his comments on an earlier version of the manuscript.

Conflict of interest

Author DP was employed by Analytical Mechanics Associates Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Authors BC, RAF, and DP declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2024.1395442/full#supplementary-material

References

Atlas, R. (1997). Atmospheric observations and experiments to assess their usefulness in data assimilation (gtSpecial IssueltData assimilation in meteology and oceanography: theory and practice). J. Meteorological Soc. Jpn. Ser. II 75, 111–130. doi:10.2151/jmsj1965.75.1B_111

CrossRef Full Text | Google Scholar

Bluestein, H. B., Carr, F. H., and Goodman, S. J. (2022). Atmospheric observations of weather and climate. Atmosphere-Ocean 60, 149–187. doi:10.1080/07055900.2022.2082369

CrossRef Full Text | Google Scholar

Cairns, B., Russell, E. E., LaVeigne, J. D., and Tennant, P. M. W. (2003). “Research Scanning Polarimeter and airborne usage for remote sensing of aerosols,” in Proceedings of SPIE. Editors J. A. Shaw, and J. S. Tyo (Bellingham, WA: SPIE), 5158, 33–44. doi:10.1117/12.518320

CrossRef Full Text | Google Scholar

Cairns, B., Russell, E. E., and Travis, L. D. (1999). “Research Scanning Polarimeter: calibration and ground-based measurements,” in Proceedings of SPIE. Editors D. H. Goldstein, and D. B. Chenault (Denver, CO: SPIE), 3754, 186–196. doi:10.1117/12.366329

CrossRef Full Text | Google Scholar

Chylek, P., Henderson, B., and Mishchenko, M. (2003). Aerosol radiative forcing and the accuracy of satellite aerosol optical depth retrieval. J. Geophys. Res. Atmos. 108, 1–8. doi:10.1029/2003jd004044

CrossRef Full Text | Google Scholar

Crutzen, P. J., and Ramanathan, V. (2000). The ascent of atmospheric sciences. Science 290, 299–304. doi:10.1126/science.290.5490.299

PubMed Abstract | CrossRef Full Text | Google Scholar

Dekking, F. M., Kraaikamp, C., Lopuhaä, H. P., and Meester, L. E. (2005). A modern introduction to probability and statistics: understanding why and how. London, UK: Springer-Verlag.

Google Scholar

Deng, X., Zhu, L., Wang, H., Zhang, X., Tong, C., Li, S., et al. (2023). Triple collocation analysis and in situ validation of the CYGNSS soil moisture product. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 16, 1883–1899. doi:10.1109/JSTARS.2023.3235111

CrossRef Full Text | Google Scholar

Dorigo, W. A., Scipal, K., Parinussa, R. M., Liu, Y. Y., Wagner, W., de Jeu, R. A. M., et al. (2010). Error characterisation of global active and passive microwave soil moisture datasets. Hydrology Earth Syst. Sci. 14, 2605–2616. doi:10.5194/hess-14-2605-2010

CrossRef Full Text | Google Scholar

Draper, C., Reichle, R., de Jeu, R., Naeimi, V., Parinussa, R., and Wagner, W. (2013). Estimating root mean square errors in remotely sensed soil moisture over continental scale domains. Remote Sens. Environ. 137, 288–298. doi:10.1016/j.rse.2013.06.013

CrossRef Full Text | Google Scholar

Fang, H., Wei, S., Jiang, C., and Scipal, K. (2012). Theoretical uncertainty analysis of global MODIS, CYCLOPES, and GLOBCARBON LAI products using a triple collocation method. Remote Sens. Environ. 124, 610–621. doi:10.1016/j.rse.2012.06.013

CrossRef Full Text | Google Scholar

Forster, P., Storelvmo, T., Armour, K., Collins, W., Dufresne, J.-L., Frame, D., et al. (2021). “The earth’s energy budget, climate feedbacks, and climate sensitivity,” in Climate change 2021: the physical science basis. Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change. Editors V. Masson-Delmotte, P. Zhai, A. Pirani, S. Connors, C. Péan, S. Bergeret al. (Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press), 923–1054. doi:10.1017/9781009157896.009

CrossRef Full Text | Google Scholar

Fu, G., Hasekamp, O., Rietjens, J., Smit, M., Di Noia, A., Cairns, B., et al. (2020). Aerosol retrievals from different polarimeters during the acepol campaign using a common retrieval algorithm. Atmos. Meas. Tech. 13, 553–573. doi:10.5194/amt-13-553-2020

CrossRef Full Text | Google Scholar

Gruber, A., De Lannoy, G., Albergel, C., Al-Yaari, A., Brocca, L., Calvet, J.-C., et al. (2020). Validation practices for satellite soil moisture retrievals: what are (the) errors? Remote Sens. Environ. 244, 111806. doi:10.1016/j.rse.2020.111806

CrossRef Full Text | Google Scholar

Gruber, A., Su, C.-H., Zwieback, S., Crow, W., Dorigo, W., and Wagner, W. (2016). Recent advances in (soil moisture) triple collocation analysis. Int. J. Appl. Earth Observation Geoinformation 45, 200–211. doi:10.1016/j.jag.2015.09.002

CrossRef Full Text | Google Scholar

Hair, J. W., Hostetler, C. A., Cook, A. L., Harper, D. B., Ferrare, R. A., Mack, T. L., et al. (2008). Airborne high spectral resolution lidar for profiling aerosol optical properties. Appl. Opt. 47, 6734. doi:10.1364/ao.47.006734

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, J., Rossow, W., Carlson, B., Lacis, A., Travis, L., Del Genio, A., et al. (1995). Low-cost long-term monitoring of global climate forcings and feedbacks. Clim. Change 31, 247–271. doi:10.1007/BF01095149

CrossRef Full Text | Google Scholar

Koh, T., Wang, S., and Bhatt, B. C. (2012). A diagnostic suite to assess NWP performance. J. Geophys. Res. Atmos. 117, 1–20. doi:10.1029/2011jd017103

CrossRef Full Text | Google Scholar

Levy, R. C., Mattoo, S., Munchak, L. A., Remer, L. A., Sayer, A. M., Patadia, F., et al. (2013). The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 6, 2989–3034. doi:10.5194/amt-6-2989-2013

CrossRef Full Text | Google Scholar

McColl, K. A., Vogelzang, J., Konings, A. G., Entekhabi, D., Piles, M., and Stoffelen, A. (2014). Extended triple collocation: estimating errors and correlation coefficients with respect to an unknown target. Geophys. Res. Lett. 41, 6229–6236. doi:10.1002/2014gl061322

CrossRef Full Text | Google Scholar

Mishchenko, M. I., Cairns, B., Hansen, J. E., Travis, L. D., Burg, R., Kaufman, Y. J., et al. (2004). Monitoring of aerosol forcing of climate from space: analysis of measurement requirements. J. Quantitative Spectrosc. Radiat. Transf. 88, 149–161. doi:10.1016/j.jqsrt.2004.03.030

CrossRef Full Text | Google Scholar

MODIS Science Team (2017a). MODIS/Aqua aerosol 5-min L2 swath 3km. doi:10.5067/MODIS/MYD04_3K.061

CrossRef Full Text | Google Scholar

MODIS Science Team (2017b). MODIS/Terra Aerosol 5-Min L2 Swath 3km. doi:10.5067/MODIS/MOD04_3K.061

CrossRef Full Text | Google Scholar

NASA (2021). Aerosol Cloud meTeorology Interactions oVer the western ATlantic experiment (ACTIVATE). doi:10.5067/SUBORBITAL/ACTIVATE/DATA001

CrossRef Full Text | Google Scholar

O’Carroll, A. G., Eyre, J. R., and Saunders, R. W. (2008). Three-way error analysis between AATSR, AMSR-E, and in situ sea surface temperature observations. J. Atmos. Ocean. Technol. 25, 1197–1207. doi:10.1175/2007jtecho542.1

CrossRef Full Text | Google Scholar

Remer, L. A., Kaufman, Y. J., Tanré, D., Mattoo, S., Chu, D. A., Martins, J. V., et al. (2005). The MODIS aerosol algorithm, products, and validation. J. Atmos. Sci. 62, 947–973. doi:10.1175/jas3385.1

CrossRef Full Text | Google Scholar

Remer, L. A., Mattoo, S., Levy, R. C., and Munchak, L. A. (2013). MODIS 3 km aerosol product: algorithm and global perspective. Atmos. Meas. Tech. 6, 1829–1844. doi:10.5194/amt-6-1829-2013

CrossRef Full Text | Google Scholar

Rodgers, J. L., and Nicewander, W. A. (1988). Thirteen ways to look at the correlation coefficient. Am. Statistician 42, 59–66. doi:10.1080/00031305.1988.10475524

CrossRef Full Text | Google Scholar

Seinfeld, J. H., and Pandis, S. N. (2006). Atmospheric chemistry and physics: from Air pollution to climate change. 2nd edn. Hoboken, New Jersey: John Wiley & Sons, Inc.

Google Scholar

Shinozuka, Y., Johnson, R. R., Flynn, C. J., Russell, P. B., Schmid, B., Redemann, J., et al. (2013). Hyperspectral aerosol optical depths from TCAP flights. J. Geophys. Res. Atmos. 118 (12), 180–212. doi:10.1002/2013jd020596

CrossRef Full Text | Google Scholar

Sorooshian, A., Alexandrov, M. D., Bell, A. D., Bennett, R., Betito, G., Burton, S. P., et al. (2023). Spatially coordinated airborne data and complementary products for aerosol, gas, cloud, and meteorological studies: the NASA ACTIVATE dataset. Earth Syst. Sci. Data 15, 3419–3472. doi:10.5194/essd-15-3419-2023

CrossRef Full Text | Google Scholar

Sorooshian, A., Anderson, B., Bauer, S. E., Braun, R. A., Cairns, B., Crosbie, E., et al. (2019). Aerosol–cloud–meteorology interaction airborne field investigations: using lessons learned from the U.S. West Coast in the design of ACTIVATE off the U.S. East Coast. Bull. Am. Meteorological Soc. 100, 1511–1528. doi:10.1175/bams-d-18-0100.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Stamnes, S., Hostetler, C., Ferrare, R., Burton, S., Liu, X., Hair, J., et al. (2018). Simultaneous polarimeter retrievals of microphysical aerosol and ocean color parameters from the “MAPP” algorithm with comparison to high-spectral-resolution lidar aerosol and ocean products. Appl. Opt. 57, 2394. doi:10.1364/ao.57.002394

PubMed Abstract | CrossRef Full Text | Google Scholar

Stith, J. L., Baumgardner, D., Haggerty, J., Hardesty, R. M., Lee, W.-C., Lenschow, D., et al. (2018). 100 years of progress in atmospheric observing systems. Meteorol. Monogr. 59 (2), 2.1–2.55. doi:10.1175/amsmonographs-d-18-0006.1

CrossRef Full Text | Google Scholar

Stoffelen, A. (1998). Toward the true near-surface wind speed: error modeling and calibration using triple collocation. J. Geophys. Res. Oceans 103, 7755–7766. doi:10.1029/97jc03180

CrossRef Full Text | Google Scholar

Su, C.-H., Ryu, D., Crow, W. T., and Western, A. W. (2014). Beyond triple collocation: applications to soil moisture monitoring. J. Geophys. Res. Atmos. 119, 6419–6439. doi:10.1002/2013jd021043

CrossRef Full Text | Google Scholar

Taylor, K. E. (2001). Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 106, 7183–7192. doi:10.1029/2000jd900719

CrossRef Full Text | Google Scholar

Thomson, R. E., and Emery, W. J. (2014). Data analysis methods in physical oceanography. 3rd edn. Amsterdam, Netherlands: Elsevier.

Google Scholar

Tsamalis, C. (2022). Clarifications on the equations and the sample number in triple collocation analysis using SST observations. Remote Sens. Environ. 272, 112936. doi:10.1016/j.rse.2022.112936

CrossRef Full Text | Google Scholar

Wilks, D. S. (2011). Statistical methods in the atmospehric sciences. 3rd edn. San Diego, California: Academic Press.

Google Scholar

Yilmaz, M. T., and Crow, W. T. (2014). Evaluation of assumptions in soil moisture triple collocation analysis. J. Hydrometeorol. 15, 1293–1302. doi:10.1175/jhm-d-13-0158.1

CrossRef Full Text | Google Scholar

Zwieback, S., Scipal, K., Dorigo, W., and Wagner, W. (2012). Structural and statistical properties of the collocation technique for error characterization. Nonlinear Process. Geophys. 19, 69–80. doi:10.5194/npg-19-69-2012

CrossRef Full Text | Google Scholar