Land cover classification of the Alps from InSAR temporal coherence matrices

Land cover mapping is of great interest in the Alps region for monitoring the surface occupation changes (e.g. forestation, urbanization, etc). In this pilot study, we investigate how time series of radar satellite imaging (C-band single-polarized SENTINEL-1 Synthetic Aperture Radar, SAR), also acquired through clouds, could be an alternative to optical imaging for land cover segmentation. Concretely, we compute for every location (using SAR pixels over 45 × 45 m) the temporal coherence matrix of the Interferometric SAR (InSAR) phase over 1 year. This normalized matrix of size 60, ×, 60 (60 acquisition dates over 1 year) summarizes the reflectivity changes of the land. Two machine learning models, a Support Vector Machine (SVM) and a Convolutional Neural Network (CNN) have been developed to estimate land cover classification performances of 6 main land cover classes (such as forests, urban areas, water bodies, or pastures). The training database was created by projecting to the radar geometry the reference labeled CORINE Land Cover (CLC) map on the mountainous area of Grenoble, France. Upon evaluation, both models demonstrated good performances with an overall accuracy of 78% (SVM) and of 81% (CNN) over Chambéry area (France). We show how, even with a spatially coarse training database, our model is able to generalize well, as a large part of the misclassifications are due to a low precision of the ground truth map. Although some less computationally expensive approaches (using optical data) could be available, this land cover mapping based on very different information, i.e., patterns of land changes over a year, could be complementary and thus beneficial; especially in mountainous regions where optical imaging is not always available due to clouds. Moreover, we demonstrated that the InSAR temporal coherence matrix is very informative, which could lead in the future to other applications such as automatic detection of abrupt changes as snow fall or landslides.

1 Introduction

1.1 General context

C-band Synthetic Aperture Radar (SAR), onboard Sentinel-1A and 1B satellites launched between 2014 and 2016, offer new opportunities for monitoring France and its mountain ranges through remote sensing. On the French Alps, this active microwave radar acquisition is available every 6 days for both the ascending and the descending orbits, with a 15 × 4 m² resolution. A SAR signal contains both an amplitude and a phase information. The amplitude measures the strength of the radar response and the phase is the fraction of one complete sine wave cycle (a single SAR wavelength). The phase of the SAR image is determined by two components. One is deterministic and controlled by the propagation duration between the satellite antenna and the ground. The other is stochastic and results from the interaction of the wave with multiple targets present in a resolution cell. SAR has the advantage over optical imaging of being insensitive to cloud cover and meaningful information can be acquired regardless of solar illumination. SAR time-series monitoring has some drawbacks: the propagation phase delay is very sensitive to meteorologic perturbations, the phase of the signal can only be observed modulo 2π, and the signal is only relevant as a relative measure between two acquisition dates in order to cancel the stochastic phase contribution. Thus Interferometric SAR (InSAR) measure, calculating the complex (amplitude and phase) difference between dates, has been developed in order to assess precisely any changes of the ground. It has been in particular used for measurements of ground displacements due to earthquakes, volcanic activity, interseismic strain accumulation (Doin et al., 2011, 2015; Grandin et al., 2016). However, the InSAR technique requires that the stochastic phase component associated to the wave-ground interaction remains stable through time. The InSAR coherence, measured on the spatial neighborhood of a pixel, quantifies the ground changes due to vegetation evolution, snow, construction, landslides, etc. Relating the coherence properties to land cover is an important step to understand the sources of coherence loss and mitigate them as much as possible for accurate deformation measurement. It is, on the other hand, a new source of information on land cover with a classification based on the dynamics of land cover changes during the year. Here, we chose to focus on the coherence only and drop the information carried by radar backscatter amplitude and its evolution through time, despite the fact that it can be used for snow (Tsai et al., 2019a,b) and for avalanches (Eckerstorfer and Malnes, 2015; Karas et al., 2021) detection.

1.2 State-of-the-Art

1.2.1 Temporal SAR coherence matrix

1.2.1.1 Temporal and spatial coherence

The pixel stability through time, characterizing the land cover, could be in theory measured by the temporal coherence. If we denote by S₁ and S₂ the two complex values of SAR images at time 1 and 2 of the same pixel, the complex correlation coefficient can be written as (Touzi et al. (1999)):

$\mathbf{C}=e^{i\varphi }\cdot \rho =\frac{E\left({\mathbf{S}}_{\mathbf{1}}\cdot {\mathbf{S}}_{\mathbf{2}}^{*}\right)}{\sqrt{E\left({\left|{\mathbf{S}}_{\mathbf{1}}\right|}^2\right)E\left({\left|{\mathbf{S}}_{\mathbf{2}}\right|}^2\right)}}(1)$

where E() is the expectation, * is the complex conjugate, ϕ and ρ are respectively the interferometric phase and coherence. In this paper, we will focus on the coherence ρ. However, having such an estimation of the coherence ρ means that the expectation values should be obtained by using a suite of observations for every single pixel, i.e., a large number of interferograms acquired under almost exactly the same geometric conditions which is intractable. Yet, we can consider that the processes involved are spatially stationary at a local level, and we can thus consider spatial average instead of a temporal average from the ergodic assumption. Eq. 1 can be replaced for every pixel by the averaging of its neighborhood and the estimator $\widehat{C}$ is:

$\widehat{C}=\frac{\sum _{i=1}^L{\mathbf{S}}_{\mathbf{1}}\cdot {\mathbf{S}}_{\mathbf{2}}^{\ast }}{\sqrt{\sum _{i=1}^L{\left|{\mathbf{S}}_{\mathbf{1}}\right|}^2\sum _{i=1}^L{\left|{\mathbf{S}}_{\mathbf{2}}\right|}^2}}(2)$

where L is the set of pixels of the spatial neighborhood considered (typically 10 to 100 pixels). This neighborhood can be a squared box of fixed size, or a spatially homogeneous neighborhood selected as statistically similar pixels based on their amplitude distribution (Parizzi and Brcic, 2010). In the following, we will use the first option but our work could be extended to more complex neighborhoods.

1.2.1.2 Temporal coherence matrix representation

By estimating the coherence between all pairs of acquisitions of a period (for example 1 year), we can construct a 2D symmetric matrix representing the evolution of the temporal coherence of the signal:

$M=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill {\widehat{\rho }}_{\mathrm{1,2}}\hfill & \hfill \cdots \hfill & \hfill {\widehat{\rho }}_{1,T}\hfill \\ \hfill {\widehat{\rho }}_{\mathrm{2,1}}\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill {\widehat{\rho }}_{2,T}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\widehat{\rho }}_{T,1}\hfill & \hfill {\widehat{\rho }}_{T,2}\hfill & \hfill \cdots \hfill & \hfill 1\hfill \end{array}\right)(3)$

This visualization, also called sample correlation matrix, captures all pairing information: the short-term coherences, near the diagonal, as well as the long-term coherences, further off the diagonal. The drawback of the coherence matrix estimation is its high computational cost. Many studies using interferograms to estimate ground displacements calculate only a subset of the matrix (such as a few diagonals). Yet, recent studies point out the loss of information that such reductions can cause, coming back to the full matrix estimation (Ansari et al., 2020). The range of information contained in the coherence matrix has not yet been fully studied, while we believe that it could be beneficial in many applications (i.e., features related to the type, the cycles or the abrupt changes of the land cover, etc).

1.2.2 Land cover mapping

As a first proof-of-concept and investigation of the potentiality of SAR coherence information, estimating automatically the land cover mapping from SAR coherence matrices is particularly relevant. Land cover classification, consisting in segmenting the surface of the ground by type of coverage (forest, rock, building, etc.), has been one of the most important applications of remote sensing imaging. It has been fundamental, for example, for monitoring the evolution of anthropization and the evolution of forest regions for the last 30 years (Hansen et al., 2000).

1.2.2.1 Machine learning and deep learning for land cover mapping

Land cover mapping is a classification task at a pixel level, also called a segmentation task. From satellite imaging, this task has very early been tackled with supervised learning algorithms, requiring training regions where an external ground truth segmentation is available. First, the deployment of traditional machine learning methods, such as Random Forests (RF) or Support Vector Machine (SVM), has been very effective for pixel-based image analysis (Longépé et al., 2011; Balzter et al., 2015; Ullah et al., 2017; Fragoso-Campón et al., 2018). SVM is a classification method whose goal is to find a hyperplane, or class boundary, based on support vectors, i.e., data points that are closer to the hyperplane and influence the position and orientation of the hyperplane. SVM is capable to linearly separate classes of non-linear data by finding a hyperplane in a transformed feature space of higher dimensions than the original number of feature dimensions, without needing heavy calculations, based on what is called the kernel trick (Koutroumbas and Theodoridis, 2008). Although SVM is computationally efficient and accurate even with a small number of samples, it cannot take into account a particular feature organization, such as a grid-like pattern as in images.

More recently, the advent of deep neural networks, and particularly Convolutional Neural Network (CNN) specifically designed for gridded data, has proposed new opportunites for segmentation tasks and in particular for land cover mapping (Ndikumana et al., 2018; Gao et al., 2019; Liu et al., 2019). A CNN is a deep learning architecture widely adopted and a very effective model for analyzing images or image-like data for pattern recognition (Krizhevsky et al., 2012). A CNN is structured in layers: an input layer connected to the data, an output layer connected to the quantities to estimate, and multiple hidden layers in between. The hidden layers of a CNN typically consist of convolutional layers, pooling layers, fully connected layers and normalization layers. The convolutional operations are inspired by the cortex visual system, where each neuron only processes data for its receptive field. Fully connected (FC) layers, usually at the end of the CNN network, connect every neuron in one layer to every neuron in the following layer. The advantage of CNN is that it can learn to recognize spatial patterns by exploiting translation invariance (i.e., all parts of the image are processed in a similar way), and thus can extract features automatically and at different spatial scales while considerably reducing the number of parameters. While Ndikumana et al. (2018); Liu et al. (2019) performed the segmentation by sliding a classification encoder network over the region of interest, Gao et al. (2019) performed a direct pixel-based classification from a U-net (encoder followed by a decoder) architecture.

1.2.2.2 Optical land cover mapping

The majority of the land cover monitoring is done by optical imagery such as the Sentinel-2 data (Bruzzone et al., 2017; Phiri et al., 2020). It is also the case of the European Corine Land Cover (CLC), releasing new versions every 6 years: the 2018 CLC is based on Sentinel-2 and Landsat 8 data (Büttner et al., 2017). Mountainous areas, due to their difficulty of access on the ground, their rapid evolution and their importance in the sustainable management of natural resources, have been particularly monitored by remote sensing (Gao et al., 2019). Yet, the optical land cover products usually have a lower accuracy in mountainous areas, due to different issues: high relief and strong topographic variations, such as shadows, steep slopes and illumination variations (Tokola et al., 2001; Gao et al., 2019). Moreover, in many mountain ranges, the cloud cover is often particularly frequent leading to a smaller availability of optical imagery.

1.2.2.3 SAR land cover mapping

In contrast, SAR has also been employed for land cover mapping as it holds a very interesting characteristic: it is insensitive to cloud cover. Some land cover mapping studies rely only on SAR imagery (Longépé et al., 2011; Abdikan et al., 2014; Balzter et al., 2015; Hagensieker and Waske, 2018) while some other are combining optical and SAR acquisitions (Laurin et al., 2013; Liu et al., 2019).

SAR is affected by distortions in mountainous areas, but it is nearly independent of weather conditions and has a short revisit time. This provides the opportunity to monitor very efficiently the dynamic characteristics of land cover (from multiple acquisitions), which contain more information than a static representation (seasonal changes leading to a distinction between coniferous and broad-leaved forest for example). Moreover, SAR monitoring is particularly sensitive to changes (Rosen et al., 2000), which can be very useful for detecting either seasonal changes (such as snow, re-vegetation) or irremediable changes (such as constructions, landslides). Both are particularly relevant for mountainous and cold terrain. Yet, most of the current studies rely only on one acquisition time and do not benefit from this multitemporal information. This is why recently a few works have proposed to investigate the use of multitemporal InSAR data for land cover mapping (Waske and Braun, 2009; Ndikumana et al., 2018). The use of recurrent neural networks can be in particular interesting for this purpose (Ienco et al., 2017; Ndikumana et al., 2018), however this is at the cost of heavier computations or by using a pixel-based method (without spatial convolutions), and often only a few acquisitions are used in input.

1.2.2.4 InSAR coherence for land cover mapping

The computation of SAR coherence between different dates is very useful for temporal analysis as well as for unwrapping interferometric SAR phases (Abdelfattah et al., 2001; Zhang et al., 2019). It has been shown that land cover mapping results were improved when temporal coherence features were added to backscatter coefficients (Borlaf-Mena et al., 2021; Nikaein et al., 2021). Yet, the information captured in a coherence matrix is still poorly understood, and one can ask if land cover mapping classification can be solved only from temporal (normalized) coherence patterns. Sica et al. (2019) proposes a three-class land cover mapping based on short InSAR time-series (1 month), where temporal decorrelation is used as one of the input features of an RF classifier. Some recent studies seem to indicate that coherence could be even more efficient than image intensity for land cover mapping (Jacob et al., 2020; Mestre-Quereda et al., 2020). Jacob et al. (2020) compared different classification algorithms (RF, SVM, k-nearest neighbors, possibly coupled with a dimensionality reduction technique or a hand-crafted feature selection) based on the temporal coherence matrix or a subset of the matrix terms. The classification results are very promising, with accuracies ranging from 65 to 85% on up to 15 class evaluations. However, the 2D representation of the coherence matrix was not used to train a specific classifier such as CNN, that can take benefit of the multiscale patterns in the 2D matrix.

1.3 Contributions

In this work, we aim at studying the potential of the full temporal SAR coherence matrix representation on a mountainous area, summarizing the information of a pixel neighborhood by the normalized correlations between all acquisition dates. To do so, we will focus on a proof-of-concept case study: land cover mapping classification task, using the European CLC map as ground truth. Our goal is to assess the benefit of a 2D representation of the coherence matrix and treat it as an image-like input data in a CNN classifier. We will compare this approach to a more conventional method (SVM). Moreover, we will test the generalization of our method to a distinct area (Chambéry area, also in the French Alps). Finally, we will analyze in more details the obtained result mapping and discuss the benefits and limits of the proposed approach, in particular related to mountainous areas.The flowchart of the proposed land cover classification methods is represented in Figure 1.

2 Data processing

2.1 InSAR coherence pre-processing

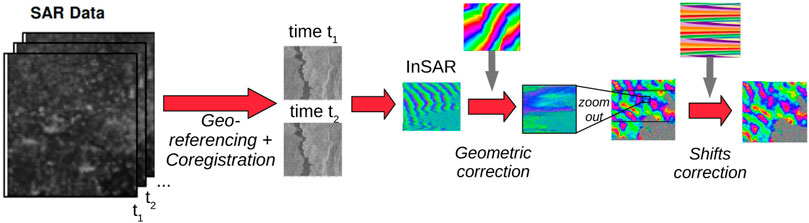
From the C-band Sentinel-1 satellite wide swath acquisitions, the complex SAR images are extracted on the region of interest during 1 year, from 09 to 03-2017 to 04-03-2018 (so 60 acquisitions, one acquisition every 6 days). We choose to process the descending track D139, subswath 2, and the VV polarization, that has a larger signal to noise ratio than the VH polarization. The processing is performed by the non-commercial NSBAS chain (Doin et al., 2011, 2015) in a few steps (see Figure 2):

1) Single Look Complex (SLC) burst images are first deramped using the burst phase function provided in the annotations and mosaicked into larger images.

2) Each image is then co-registered in a single radar geometry using a distortion field between secondary images and the reference image computed as follows: 1) subpixel offsets obtained by amplitude image correlation are computed for numerous points within the image, 2) an a priori range distortion field is computed using orbital information and the Digital Elevation Model (DEM), 3) the distortion field in azimuth is obtained by adjusting a bilinear model in range and azimuth on computed offsets, while iteratively removing outliers, 4) the distortion field in range corresponds to the modeled distortion field plus a constant, adjusted using computed offsets. Offsets in azimuth allow to refine the burst phase function, as described in Grandin et al. (2016).

3) We compute differential forward-backward interferograms, called Enhanced Spectral Diversity (ESD) phase (De Zan et al., 2014), on burst overlap regions, using a connected and redundant network of interferograms. ESD phase values are fitted by a polynomial, whose parameters are then inverted into time series (Thollard et al., 2021). The ESD polynomial function inverted for each time step is then used to correct the SLC images. This process avoids residual phase ramps within bursts and offsets across bursts due to slight azimuth misalignments.

4) Interferograms between all acquisition pairs are calculated by their Hadamard product and corrected from the geometrical phase modeled based on orbits and the DEM.

FIGURE 1

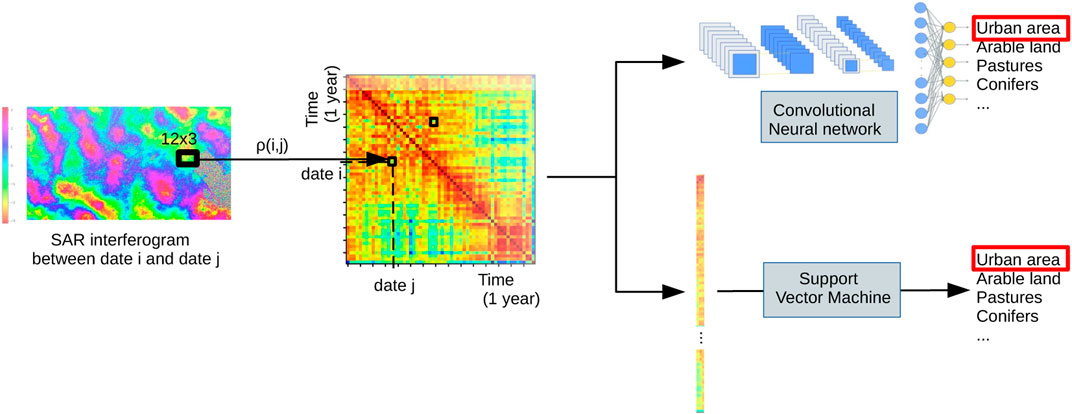
FIGURE 1. Flowchart of land cover classification from InSAR temporal coherence matrix, comparison of SVM and CNN methods.

FIGURE 2

FIGURE 2. Intererometric SAR processing pipeline.

For computing the coherence, we fix a patch size of 12 × 3 pixels, corresponding to a 45 × 45 m² land area (the radar geometry being anisotropic). For each patch of the studied area, we compute the full coherence symmetric matrix. By visualizing this matrix in a color-coded representation, we can already see how different types of land are expressing different patterns (Figure 3). Note that since the coherence is the normalized correlation, the diagonal is always filled with ones.

FIGURE 3

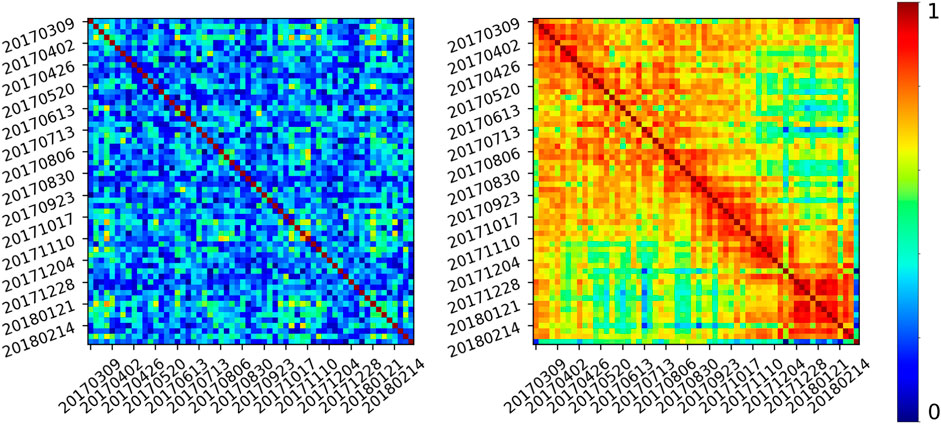
FIGURE 3. Examples of InSAR coherence matrices over 1 year. Left: broad-leaved forest. Right: urban area.

2.2 Ground truth land cover mapping

As with any supervised learning methods, the performance of the model and results are highly dependent on the training data inputs and their labels (associated ground truth classes). In our case, we used the open source labeled land cover map CORINE Land Cover (CLC). The CLC 2018 segments Europe in 44 types of terrain (many of which are different types of urban buildings), it has a resolution of 100m × 100m and is produced by a combined automated and manual interpretation of high-resolution optical satellite data (Büttner et al., 2017). We selected zones containing mountain areas, urban areas and cultivated areas, and we restricted our classification into 6 main categories that are the most present (Discontinuous Urban, Non-irrigated arable land, Pastures, Broad Leaved Forest, Coniferous Forest, Water Bodies).

As our coherence calculation is performed in the radar acquisition geometry, we projected the CLC segmentation product on the radar geometry using detailed lookup tables allowing the geometrical transformation. This operation is approximately equivalent to a rescaling, a range elongation (because the radar geometry is anisotropic), a flipping and a rotation of 9.7°. This allows us to directly define for every SAR pixel its CLC classification.

2.3 Data sets creation

We focused on Grenoble, France area for building the training and validation sets, and Chambéry, France for the test set (see Figure 4). The training set is used to train the machine learning model, the validation set to select the best hyperparameter setting, and the test set, kept unseen, is used to finally estimate the results. Both Grenoble and Chambéry regions contain urban areas, mountain areas, forests, cultivated areas and water areas, and they are completely disjoined.

FIGURE 4

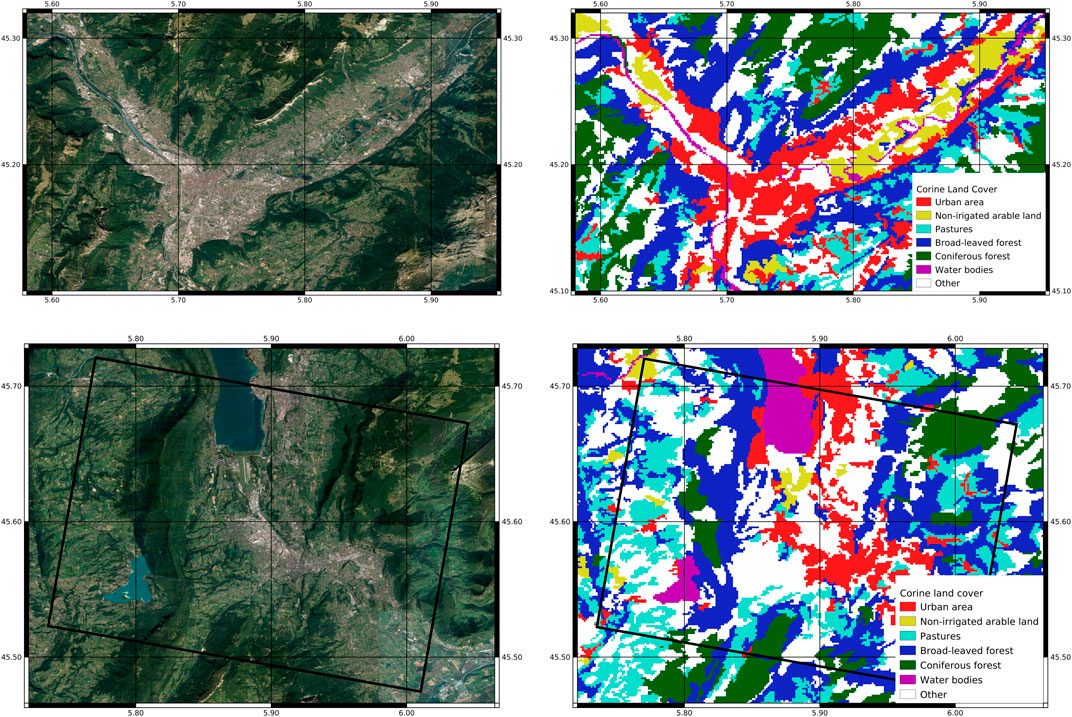
FIGURE 4. Top: Grenoble area, used for the training and validation phases. Bottom: Chambéry area, used for the testing phase. Left: Satellite view. Right: Corine land cover main classes.

For the training and validation sets, we extracted all the patches of size (range = 12, azimuth = 3) falling in the six classes defined above. Moreover, as the CLC resolution is larger than our patches, we decided to remove the samples located on the boundaries of the CLC segmented regions, i.e., between the classes regions, in order to have a cleaner dataset. Then, we selected the same number of samples (3,600) in every class so as to have a balanced dataset. Yet, since the arable land is too scarce in the region (944 samples), we decided to keep the 3,600 samples in the other classes and have a slightly less balanced dataset. Finally, 70% of each class was randomly assigned to the training set, and 30% to the validation set.

The test phase, performed on Chambéry area, will be used in two steps: firstly, a quantitative (balanced) evaluation with a similar selection of image patches for each of the six classes; secondly, an estimation of the full region in a sliding window process (for every 12 × 3 patch) in order to qualitatively assess the prediction.

3 Learning models

We compared different machine learning methods to classify the different coherence matrices in the six classes listed above. More formally, we want to learn a function f_θ such that f_θ(M) = y with M_T×T the coherence matrix of size T × T with T the number of acquisition times, y ∈ [1, 6] the class label. Concretely, we will optimize the function parameters θ during the training phase, and use the estimated f_θ to perform predictions on new samples. Here, M is the input of the model, and y the output.

3.1 Support Vector Machine Model

The first group of methods, from standard machine learning theory, is able to learn θ for problems in which the input is a vector of fixed size, i.e., a list of features. We will therefore linearize M. Since M is symmetric and its diagonal terms are always equal to one, we can restrict ourselves to the terms M_i,j, i + j > 0. We can then construct the input vector m of size [T × (T − 1)/2, 1] for every matrix M. From an evaluation of different state-of-the-art methods including RF, SVM and Multi-layer perceptron, we focused on SVM as it gave the best results for more details on SVM method). We used the Radial Basis Function (RBF) kernel with a regularization parameter C = 1. The RBF is a non-linear kernel, and thus can produce convoluted hyperplane separators in the high dimensional feature space able to make complex discrimination between sets that are not convex in the original space. The parameters of the model are optimized during the learning phase, by minimizing the hinge loss between the true class and the estimated class of every training sample.

3.2 Convolutional neural network model

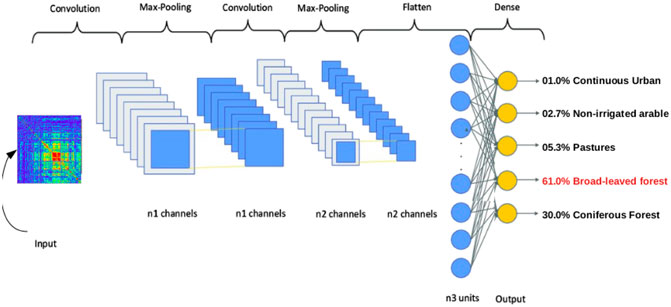
The second group of methods, based on CNN, is able to learn from spatially ordered data, in order to capture the information contained in the texture and the patterns rather than treating each pixel independently. A series of filtering operations at different scales (based on local convolutions) are performed in order to extract higher order features. While this family of methods was intended for natural images, in our case we can also view the coherence matrix as a 2D image, as nearby pixels can share common information. For example, by looking at Figure 3 (Right), the fact that the selected patch is coherent by pieces (visible by the red squares, meaning a coherence during a certain period of time) is important to capture, no matter the dates of coherency breaks. By linearizing the matrix, we loose the links between nearby pixels (i.e. dates). This is why we will compare the SVM approach with a CNN model for more details on CNN).

Figure 5 shows the structure of our CNN model with two pairs of convolution layers and pooling layers and one fully connected layer at the end. The convolution operations are performed by 3 × 3 filters: the values of these filters are optimized during the training in an iterative process. We used the Rectified Linear activation (ReLU) functions as activation functions after all the convolution and dense layers, and we perform a batch normalization after every convolution, as well as a 50% dropout, for regularizing the model (Srivastava et al., 2014; Ioffe and Szegedy, 2015). The max-pooling operations, performed after the convolutions, enables the model to extract highly abstract features in a multi-scale approach by downscaling the image by a factor of 2 with a max operator on every 2 × 2 window. The optimization is done by back-propagation and stochastic gradient descent, and the loss function is defined as the categorical crossentropy (used in multi-class classification tasks).

FIGURE 5

FIGURE 5. CNN architecture developed for land cover classification with InSAR coherence matrices.

4 Results

4.1 Quantitative results

We can evaluate the predictive power of our classification methods on the validation and test sets by first looking at the accuracy, i.e., the fraction of all predictions (classes) that are correct, in Table 1. We can confront the results to the theoretical power of a random guess predictor, which in case of a balanced dataset of 6 classes would give an accuracy of 17% (1/6 chances to randomly predict the correct class). With all accuracies larger than 77%, we can first conclude that the use of InSAR temporal coherence for classifying the land cover is indeed efficient, even when no amplitude information is used. For both methods, the accuracy on the test set (SVM: 77%, CNN: 81%) is smaller than on the validation set (SVM: 80%, CNN: 86%). This is due to the fact that the validation set is composed of samples coming from Grenoble area, i.e., the same area as the training set, while the test set is made of samples from a distinct region, Chambéry area. Even if the training and validation samples are different, they can be very similar and thus the prediction can be easier on the validation set than on the test set. Note that the accuracy on the test set are still very high, meaning that both methods are able to generalize well. Between the two models, the CNN has clearly a better predictive power.

TABLE 1

TABLE 1. Accuracy of the two tested methods on the balanced validation and test sets (both composed of equal number of samples from the 6 classes, validation: from Grenoble area, test: from Chambéry area).

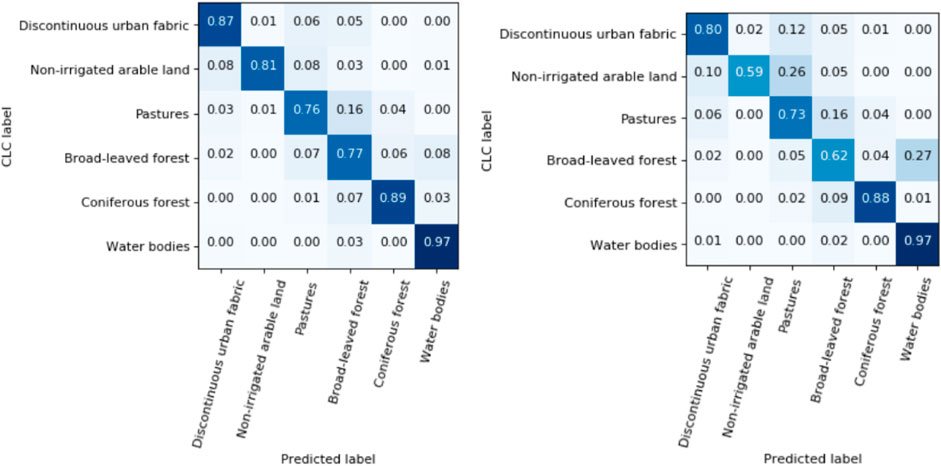
In Figures 6, 7 are represented the normalized confusion matrices of the two methods for both the validation and the test sets. A confusion matrix represents the proportion of class predictions for every ground truth class. Concretely, a perfect predictor would correspond to an identity matrix (ones on the main diagonal, and zero everywhere else). We can first notice that both models have high recall values (proportion of correctly classified, diagonal terms) for every of the 6 classes, in accordance with Table 1. Yet, we can see some differences in the predictive power between the classes. The water, urban and coniferous forest classes show high recalls (always $>0.8$, and even $>0.97$ for water bodies). On the other hand, we can see that pastures, arable lands and broad-leaved forest have higher errors. With a closer look, we notice that pastures are often misclassified as broad-leaved forest on both validation and test set (16% for CNN, 18–20% for SVM). This can be due to many reasons, the first one being that these land types might often overlap and the patches are then composed of a mix of both. The same phenomenon is also visible for arable land misclassified as urban areas (between 8% and 10% for CNN). By looking at the difference between validation and test results, we can notice some particular behaviors, such as the broad-leaved forest misclassified as water bodies (27% for CNN, 29% for SVM). This particular case, caused by SAR acquisition shadowing effect, will be investigated more in details in. Overall, both models show a similar behavior but CNN performs better in most of the cases.

FIGURE 6

FIGURE 6. SVM results, normalized confusion matrices. (left) validation set (right) test set.

FIGURE 7

FIGURE 7. CNN results, normalized confusion matrices. (left) validation set (right) test set.

4.2 Influence of the training set size

We represent in Figure 8 the influence of the training set size on the accuracy for both models. We performed multiple runs of every model, by randomly varying the weights initialization, in order to have a more robust comparison (represented by the box plots in both graphs). We can see that in both cases, a too small number of training samples causes a drop of performance (using 200 samples for every of the 6 classes, the accuracies are below 75%). For SVM, the performance improves quickly, then reaches a plateau at 1,200 samples and increasing further the number of samples does not change the result. On the other hand, the CNN model’s improvement is more gradual, and the performance keeps improving at least until 2,600 samples, surpassing then the SVM accuracy. Thus, it is interesting to point out that with a small database, the SVM is a satisfactory model. Yet, when having access to more data, the power of deep learning is revealed and it seems to be able to capture more complex features than the SVM model.

FIGURE 8

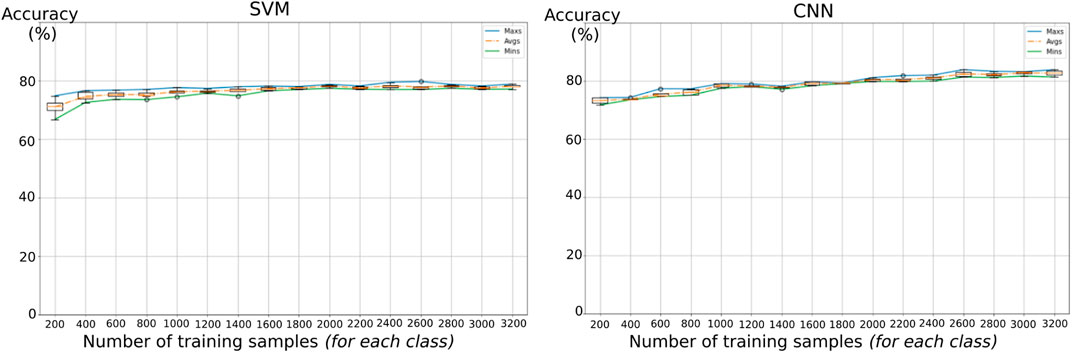
FIGURE 8. Influence of the training set size on the accuracy for (left) the SVM model (right) the CNN model on the test set.

4.3 Qualitative results and limits of the ground truth labelling

4.3.1 Segmentation of full testing area

We selected a region in the testing dataset (the Bourget du Lac area near Chambéry) and performed a complete segmentation by calculating the coherence matrix of every patch of the area and estimating its land cover class. The results of both SVM and CNN models are visible in Figure 9C,D, together with a satellite view (Figure 9A) and the Corine Land Cover of the same area (Figure 9B). We recall that the Corine Land Cover was used to create ground truth labels on Grenoble area for the training phase, using the 6 main types of lands. It is interesting to see that both models are performing well: the lake is clearly segmented, the zones of “Non-irrigated arable land” (zone D in the CLC map) is also well captured, as well as the forests.

FIGURE 9

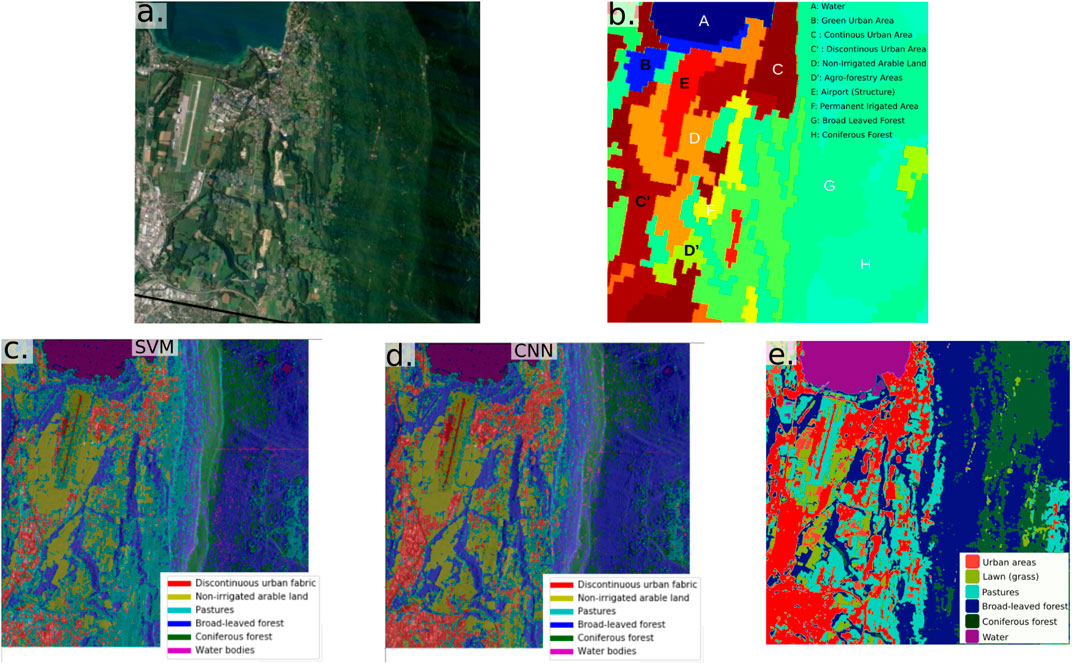
FIGURE 9. Results of automatic land cover classification by machine learning from InSAR temporal coherence matrices. (A) satellite view (Google Maps) of the Bourget du Lac study area. (B) extract from the Corine Land Cover land cover map of the same area (C) results of the classification by Support Vector Machine method (D) results of the classification by Convolutional Neural Network method (E) extract from the Theia land cover map (finer resolution than Corine Land Cover).

Moreover, we can also notice that the estimated segmentations are finer than the CLC map: we can see more details, such as the airport where the “urban” class is only restricted to the landing strip and the surroundings are identified as arable land or pastures. By looking at the satellite view, we can see that this segmentation is accurate. Moreover, by comparing with the Theia land cover¹ (Figure 9E), we can see how similar our segmentations perform with this finer scale map. We can draw three conclusions from these observations: firstly, in a future study, we might consider using a finer resolution for ground truth labelling (e.g., Theia land cover). Secondly, we can deduce that our models are robust as they were able to learn from a coarse labelling (i.e., with a consequent percentage of errors in the ground truth) and yet succeeded in correctly creating a more accurate model than the CLC map used as ground truth. Thirdly, our quantitative results should be reconsidered, as we can see that many misclassifications are clearly due to the too coarse ground truth labelling: a perfect accuracy score would be impossible and not desired.

Finally, we can see some small differences between SVM and CNN, as the contours of the urban areas: the CNN seems to better detect the urban areas and the segmentation is closer to the Theia land cover map.

4.3.2 Consequences of SAR acquisition artifacts in mountainous areas

An external bias that constitutes a source of classification errors is specific to the satellite data used and the terrain under study. Indeed, there are various phenomena that limit the quality of the original SAR data in steep terrain, particularly important in Grenoble and Chambéry areas, including foreshortening, layover and shadowing.

For example, we can see that for the class “Broad-leaved forest”, the prediction of the pixels in the middle area of the Figure 10 (Left) are mis-classified as “Water”. From Figure 10 (Right) we can see ,that is clearly not a water area. The background of Figure 10 (Left) represents the radar mean amplitude image, and we see that the central zone is completely dark: the original SAR data gets affected by the shadowing effect, as the area is behind a mountain and cannot be seen by the sensor. Geometrical artifacts, such as foreshortening and layover, could be corrected by mixing information from SAR data from Sentinel-1 on the descending orbit which complements the ascending data. However, shadows, also less frequent, may appear on slopes that are, for the other viewing angle, in layover or foreshortening areas. These areas cannot be mapped with radar data.

FIGURE 10

FIGURE 10. (Left) Prediction of the “Broad-Leaved Forest” class on a part of the test set. Background: radar amplitude mean image. The extent of the colored zone corresponds to the ground truth “Broad-leaved forest” CLC map zone. The colors are representing the prediction of the SVM model: in blue are the correct predictions (i.e., broad-leaved forest), while other colors represent mis-classifications. (Right) Optical image by Google Earth of the same area.

5 Conclusion and discussion

From this preliminary study, we can assess the potential of InSAR temporal coherence and in particular the temporal matrix representation for segmenting the land cover. The originality of this study resides on the fact that we consider the one-year coherence matrix as an image, while previous studies only considered 6, 12 or 18 days coherence time series (Sica et al., 2019; Mestre-Quereda et al., 2020). We have shown that it can distinguish between related classes such as coniferous and broad-leaved forests. Moreover, our model has the capacity to learn from a low-detailed ground truth, which is important for generalizing in different areas. Such an approach is particularly relevant for differentiating different crops having different dynamical seasonalities (as in Mestre-Quereda et al. (2020)), even if further studies would have to be made with more classes and more land diversity. Based on Sica et al. (2019); Mestre-Quereda et al. (2020), it would be interesting to assess the potential of using both polarizations (VV and VH) as well as adding the backscatter amplitude information. Moreover, one could perform a quantitative comparison with segmentation methods based on optical data in order to see if there would be a gain in combining both. In order to gain precision, the spatial neighboring could be adaptative by using the local spatial connectivity of the pixels (Parizzi and Brcic, 2010).

Lastly, we think that the potential of InSAR temporal coherence could be extended to other applications, such as abrupt soil change detection, as snow deposit, building constructions or landslides. The findings of this study also clearly show that such a change detection would have to be based on a prior land cover classification, as the temporal coherence patterns are very different between types of land cover.

Data availability statement

The raw data (C-band Synthetic Aperture Radar Sentinel-1) is freely available thought the Copernicus Open Access Hub. All data and codes supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SG-R wrote the paper and directed the study, SB developed the codes, computed the results and figures and helped in the writing; M-PD pre-processed the data, directed the study and proof-read the paper, AA and YY provided expertise and proofread the paper.

Funding

This work has been partially supported by the MIAI@Grenoble Alpes, (ANR-19-P3IA-0003) and by the APR CNES as part of the SHARE project. This work was also partly supported by the project “TRIPLETS” funded by the PNTS program of INSU-CNRS.

Acknowledgments

Thanks to GRICAD infrastructure (gricad.univ-grenoble-alpes.fr), which is supported by the Grenoble research communities, for the computations. ISTerre is part of Labex OSUG@2020 (ANR10 LABX56).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Value-added data processed by CNES for the Theia data cluster www.theia.land.fr from Copernicus data. The processing uses algorithms developed by Theia’s Scientific Expertise Centres.

References

Abdelfattah, R., Nicolas, J., Tupin, F., and Badredine, B. (2001). “Insar coherence estimation for temporal analysis and phase unwrapping applications,” in IGARSS 2001. Scanning the Present and Resolving the Future. Proceedings. IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No. 01CH37217) (IEEE), 2292–2294.5

Google Scholar

Abdikan, S., Sanli, F. B., Ustuner, M., and Calò, F. (2014). The international archives of the photogrammetry. Remote Sensing and Spatial Information Sciences, Volume XLI-B7, 2016 XXIII ISPRS Congress.Land cover mapping using sentinel-1 sar data

Google Scholar

Ansari, H., De Zan, F., and Parizzi, A. (2020). Study of systematic bias in measuring surface deformation with sar interferometry. IEEE Trans. Geosci. Remote Sens. 59, 1285–1301. doi:10.1109/tgrs.2020.3003421

CrossRef Full Text | Google Scholar

Balzter, H., Cole, B., Thiel, C., and Schmullius, C. (2015). Mapping corine land cover from sentinel-1a sar and srtm digital elevation model data using random forests. Remote Sens. 7, 14876–14898. doi:10.3390/rs71114876

CrossRef Full Text | Google Scholar

Borlaf-Mena, I., Badea, O., and Tanase, M. A. (2021). Assessing the utility of sentinel-1 coherence time series for temperate and tropical forest mapping. Remote Sens. 13, 4814. doi:10.3390/rs13234814

CrossRef Full Text | Google Scholar

Bruzzone, L., Bovolo, F., Paris, C., Solano-Correa, Y. T., Zanetti, M., and Fernández-Prieto, D. (2017). “Analysis of multitemporal sentinel-2 images in the framework of the esa scientific exploitation of operational missions,” in 2017 9th International Workshop on the Analysis of Multitemporal Remote Sensing Images (MultiTemp) (IEEE), 1–4.

CrossRef Full Text | Google Scholar

Büttner, G., Kosztra, B., Soukup, T., Sousa, A., and Langanke, T. (2017). Clc2018 technical guidelines. Copenhagen, Denmark 25: European Environment Agency.

Google Scholar

De Zan, F., Prats-Iraola, P., Scheiber, R., and Rucci, A. (2014). Interferometry with tops: Coregistration and azimuth shifts. In EUSAR 2014; 10th European Conference on Synthetic Aperture Radar (VDE), 1–4.

Google Scholar

Doin, M.-P., Guillaso, S., Jolivet, R., Lasserre, C., Lodge, F., Ducret, G., et al. (2011). “Presentation of the small baseline nsbas processing chain on a case example: The etna deformation monitoring from 2003 to 2010 using envisat data,” in Proceedings of the Fringe symposium (ESA SP-697, Frascati, Italy, 3434–3437.

Google Scholar

Doin, M.-P., Twardzik, C., Ducret, G., Lasserre, C., Guillaso, S., and Jianbao, S. (2015). Insar measurement of the deformation around siling co lake: Inferences on the lower crust viscosity in central tibet. J. Geophys. Res. Solid Earth 120, 5290–5310. doi:10.1002/2014jb011768

CrossRef Full Text | Google Scholar

Eckerstorfer, M., and Malnes, E. (2015). Manual detection of snow avalanche debris using high-resolution radarsat-2 sar images. Cold Regions Sci. Technol. 120, 205–218. doi:10.1016/j.coldregions.2015.08.016

CrossRef Full Text | Google Scholar

Fragoso-Campón, L., Quirós, E., Mora, J., Gutiérrez, J. A., and Durán-Barroso, P. (2018). Accuracy enhancement for land cover classification using lidar and multitemporal sentinel 2 images in a forested watershed. Multidiscip. Digit. Publ. Inst. Proc. 2, 1280. doi:10.3390/proceedings2201280

CrossRef Full Text | Google Scholar

Gao, L., Luo, J., Xia, L., Wu, T., Sun, Y., and Liu, H. (2019). Topographic constrained land cover classification in mountain areas using fully convolutional network. Int. J. Remote Sens. 40, 7127–7152. doi:10.1080/01431161.2019.1601281

CrossRef Full Text | Google Scholar

Grandin, R., Klein, E., Metois, M., and Vigny, C. (2016). Three‐dimensional displacement field of the 2015M_w8.3 Illapel earthquake (Chile) from across‐ and along‐track Sentinel‐1 TOPS interferometry. Geophys. Res. Lett. 43, 2552–2561. doi:10.1002/2016gl067954

CrossRef Full Text | Google Scholar

Hagensieker, R., and Waske, B. (2018). Evaluation of multi-frequency sar images for tropical land cover mapping. Remote Sens. 10, 257. doi:10.3390/rs10020257

CrossRef Full Text | Google Scholar

Hansen, M. C., DeFries, R. S., Townshend, J. R., and Sohlberg, R. (2000). Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. remote Sens. 21, 1331–1364. doi:10.1080/014311600210209

CrossRef Full Text | Google Scholar

Ienco, D., Gaetano, R., Dupaquier, C., and Maurel, P. (2017). Land cover classification via multitemporal spatial data by deep recurrent neural networks. IEEE Geosci. Remote Sens. Lett. 14, 1685–1689. doi:10.1109/lgrs.2017.2728698

CrossRef Full Text | Google Scholar

Ioffe, S., and Szegedy, C. (2015). “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in International conference on machine learning, Lille, France, July 6–11, 2015 (PMLR), 448–456.

Google Scholar

Jacob, A. W., Vicente-Guijalba, F., Lopez-Martinez, C., Lopez-Sanchez, J. M., Litzinger, M., Kristen, H., et al. (2020). Sentinel-1 insar coherence for land cover mapping: A comparison of multiple feature-based classifiers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 13, 535–552. doi:10.1109/jstars.2019.2958847

CrossRef Full Text | Google Scholar

Karas, A., Karbou, F., Giffard-Roisin, S., Durand, P., and Eckert, N. (2021). Automatic color detection-based method applied to sentinel-1 sar images for snow avalanche debris monitoring. IEEE Trans. Geosci. Remote Sens. 60, 1–17. doi:10.1109/tgrs.2021.3131853

CrossRef Full Text | Google Scholar

Koutroumbas, K., and Theodoridis, S. (2008). Pattern recognition. Elsevier Science.

Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. Adv. neural Inf. Process. Syst. 25, 1097–1105. doi:10.1145/3065386

CrossRef Full Text | Google Scholar

Laurin, G. V., Liesenberg, V., Chen, Q., Guerriero, L., Del Frate, F., Bartolini, A., et al. (2013). Optical and sar sensor synergies for forest and land cover mapping in a tropical site in west Africa. Int. J. Appl. Earth Observation Geoinformation 21, 7–16. doi:10.1016/j.jag.2012.08.002

CrossRef Full Text | Google Scholar

Liu, S., Qi, Z., Li, X., and Yeh, A. G.-O. (2019). Integration of convolutional neural networks and object-based post-classification refinement for land use and land cover mapping with optical and sar data. Remote Sens. 11, 690. doi:10.3390/rs11060690

CrossRef Full Text | Google Scholar

Longépé, N., Rakwatin, P., Isoguchi, O., Shimada, M., Uryu, Y., and Yulianto, K. (2011). Assessment of alos palsar 50 m orthorectified fbd data for regional land cover classification by support vector machines. IEEE Trans. Geosci. Remote Sens. 49, 2135–2150. doi:10.1109/tgrs.2010.2102041

CrossRef Full Text | Google Scholar

Mestre-Quereda, A., Lopez-Sanchez, J. M., Vicente-Guijalba, F., Jacob, A. W., and Engdahl, M. E. (2020). Time-series of sentinel-1 interferometric coherence and backscatter for crop-type mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 13, 4070–4084. doi:10.1109/jstars.2020.3008096

CrossRef Full Text | Google Scholar

Ndikumana, E., Ho Tong Minh, D., Baghdadi, N., Courault, D., and Hossard, L. (2018). Deep recurrent neural network for agricultural classification using multitemporal sar sentinel-1 for camargue, France. Remote Sens. 10, 1217. doi:10.3390/rs10081217

CrossRef Full Text | Google Scholar

Nikaein, T., Iannini, L., Molijn, R. A., and Lopez-Dekker, P. (2021). On the value of sentinel-1 insar coherence time-series for vegetation classification. Remote Sens. 13, 3300. doi:10.3390/rs13163300

CrossRef Full Text | Google Scholar

Parizzi, A., and Brcic, R. (2010). Adaptive insar stack multilooking exploiting amplitude statistics: A comparison between different techniques and practical results. IEEE Geosci. Remote Sens. Lett. 8, 441–445. doi:10.1109/lgrs.2010.2083631

CrossRef Full Text | Google Scholar

Phiri, D., Simwanda, M., Salekin, S., Nyirenda, V. R., Murayama, Y., and Ranagalage, M. (2020). Sentinel-2 data for land cover/use mapping: A review. Remote Sens. 12, 2291. doi:10.3390/rs12142291

CrossRef Full Text | Google Scholar

Rosen, P. A., Hensley, S., Joughin, I. R., Li, F. K., Madsen, S. N., Rodriguez, E., et al. (2000). Synthetic aperture radar interferometry. Proc. IEEE 88, 333–382. doi:10.1109/5.838084

CrossRef Full Text | Google Scholar

Sica, F., Pulella, A., Nannini, M., Pinheiro, M., and Rizzoli, P. (2019). Repeat-pass sar interferometry for land cover classification: A methodology using sentinel-1 short-time-series. Remote Sens. Environ. 232, 111277. doi:10.1016/j.rse.2019.111277

CrossRef Full Text | Google Scholar

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1929–1958.

Google Scholar

Thollard, F., Clesse, D., Doin, M.-P., Donadieu, J., Durand, P., Grandin, R., et al. (2021). Flatsim: The form@ ter large-scale multi-temporal sentinel-1 interferometry service. Remote Sens. 13, 3734. doi:10.3390/rs13183734

CrossRef Full Text | Google Scholar

Tokola, T., Sarkeala, J., and Van der Linden, M. (2001). Use of topographic correction in landsat tm-based forest interpretation in Nepal. Int. J. Remote Sens. 22, 551–563. doi:10.1080/01431160050505856

CrossRef Full Text | Google Scholar

Touzi, R., Lopes, A., Bruniquel, J., and Vachon, P. W. (1999). Coherence estimation for sar imagery. IEEE Trans. Geosci. Remote Sens. 37, 135–149. doi:10.1109/36.739146

CrossRef Full Text | Google Scholar

Tsai, Y.-L. S., Dietz, A., Oppelt, N., and Kuenzer, C. (2019a). Remote sensing of snow cover using spaceborne sar: A review. Remote Sens. 11, 1456. doi:10.3390/rs11121456

CrossRef Full Text | Google Scholar

Tsai, Y.-L. S., Dietz, A., Oppelt, N., and Kuenzer, C. (2019b). Wet and dry snow detection using sentinel-1 sar data for mountainous areas with a machine learning technique. Remote Sens. 11, 895. doi:10.3390/rs11080895

CrossRef Full Text | Google Scholar

Ullah, S., Shafique, M., Farooq, M., Zeeshan, M., and Dees, M. (2017). Evaluating the impact of classification algorithms and spatial resolution on the accuracy of land cover mapping in a mountain environment in Pakistan. Arab. J. Geosci. 10, 67. doi:10.1007/s12517-017-2859-6

CrossRef Full Text | Google Scholar

Waske, B., and Braun, M. (2009). Classifier ensembles for land cover mapping using multitemporal sar imagery. ISPRS J. photogrammetry remote Sens. 64, 450–457. doi:10.1016/j.isprsjprs.2009.01.003

CrossRef Full Text | Google Scholar

Zhang, Y., Fattahi, H., and Amelung, F. (2019). Small baseline insar time series analysis: Unwrapping error correction and noise reduction. Comput. Geosciences 133, 104331. doi:10.1016/j.cageo.2019.104331

CrossRef Full Text | Google Scholar